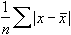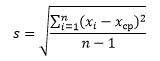Оригинал http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
Добрый день, уважаемые любители статистического анализа данных, а сегодня еще и программы Excel.
Проведение любого статанализа немыслимо без расчетов. И сегодня в рамках рубрики «Работаем в Excel» мы научимся рассчитывать показатели вариации. Теоретическая основа была рассмотрена ранее в ряде статей о вариации данных. Кстати, на этом указанная тема не закончилась, к выпуску планируются новые статьи — следите за рекламой! Однако сухая теория без инструментов реализации — вещь не сильно полезная. Поэтому по мере появления теоретических выкладок, я стараюсь не отставать с заметками о соответствующих расчетах в программе Excel.
Сегодняшняя публикация будет посвящена расчету в Excel следующих показателей вариации:
— максимальное и минимальное значение
— среднее линейное отклонение
— дисперсия (по генеральной совокупности и по выборке)
— среднее квадратическое отклонение (по генеральной совокупности и по выборке)
— коэффициент вариации
Факт возможности расчета упомянутых показателей в Excel свидетельствует о практическом их использовании. И, несмотря на очевидность некоторых моментов, я постараюсь расписать все подробно.
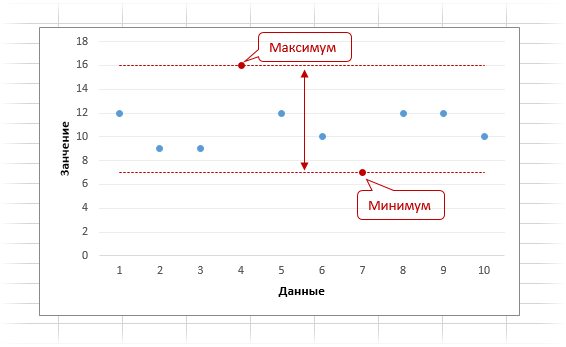
Максимальное и минимальное значение
Начнем с формул максимума и минимума. Что такое максимальное и минимальное значение, уверен, знают почти все. Максимум — самое большое значение из анализируемого набора данных, минимум — самое маленькое (может быть и отрицательным числом). Это крайние значения в совокупности данных, обозначающие границы их вариации. Примеры реального использования каждый может придумать сам — их полно. Это и минимальные/максимальные цены на что-нибудь, и выбор наилучшего или наихудшего решения задачи, и всего, чего угодно. Минимум и максимум — весьма информативные показатели. Давайте теперь их рассчитаем в Excel.
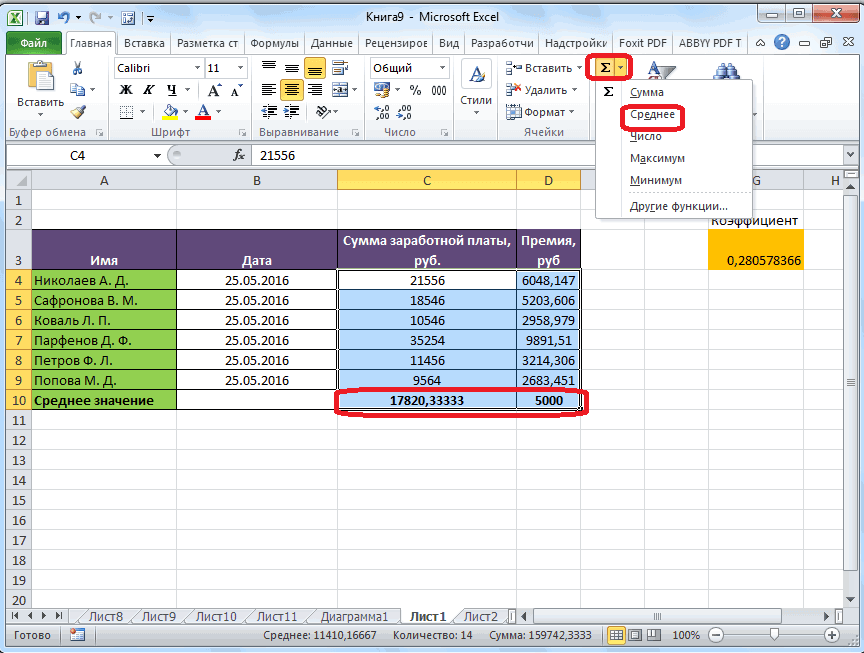
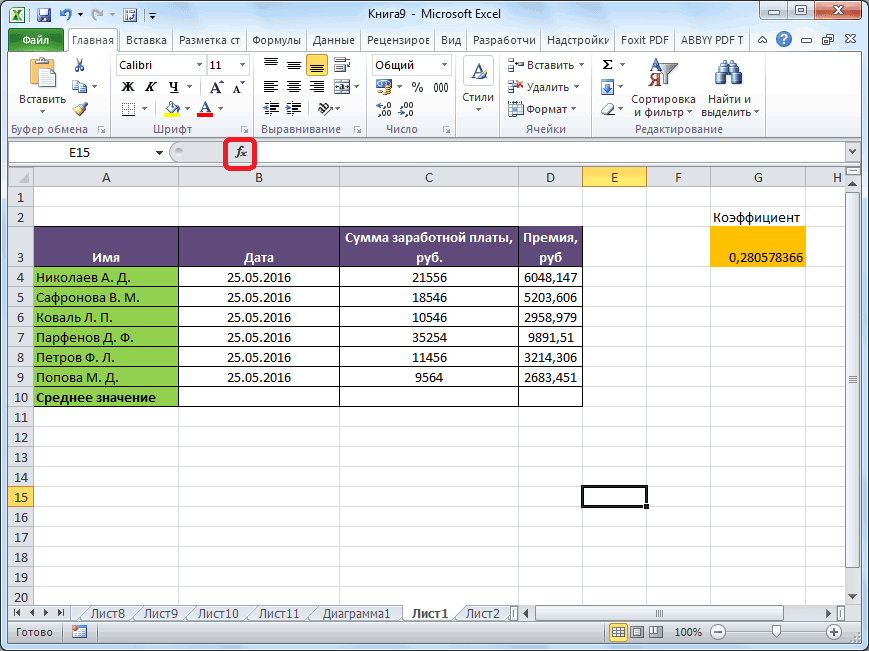
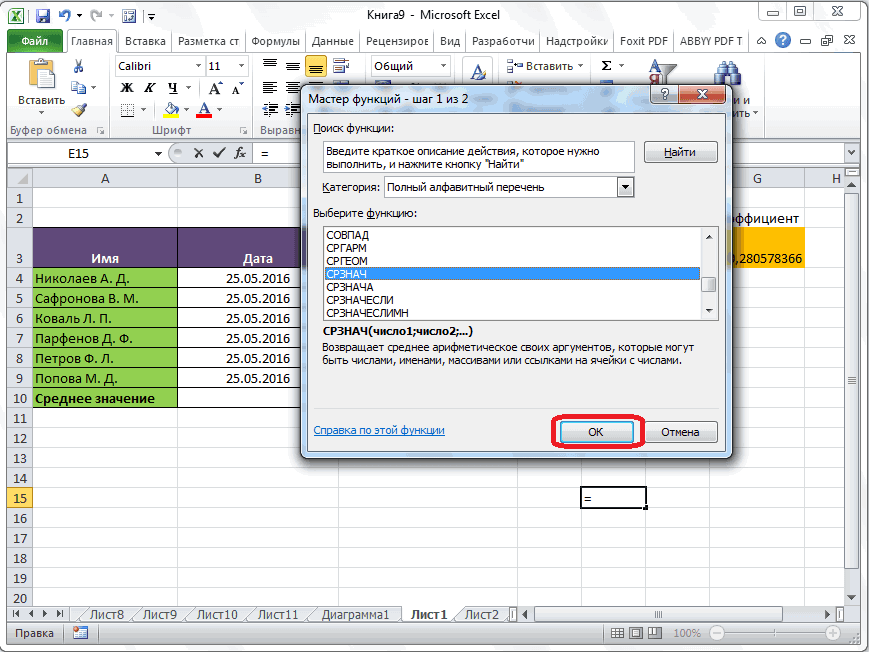
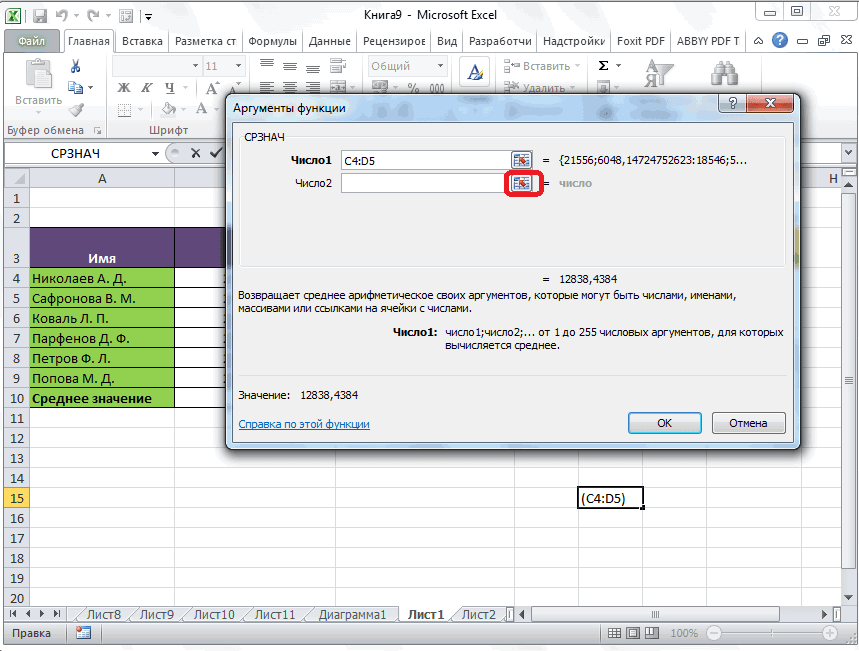
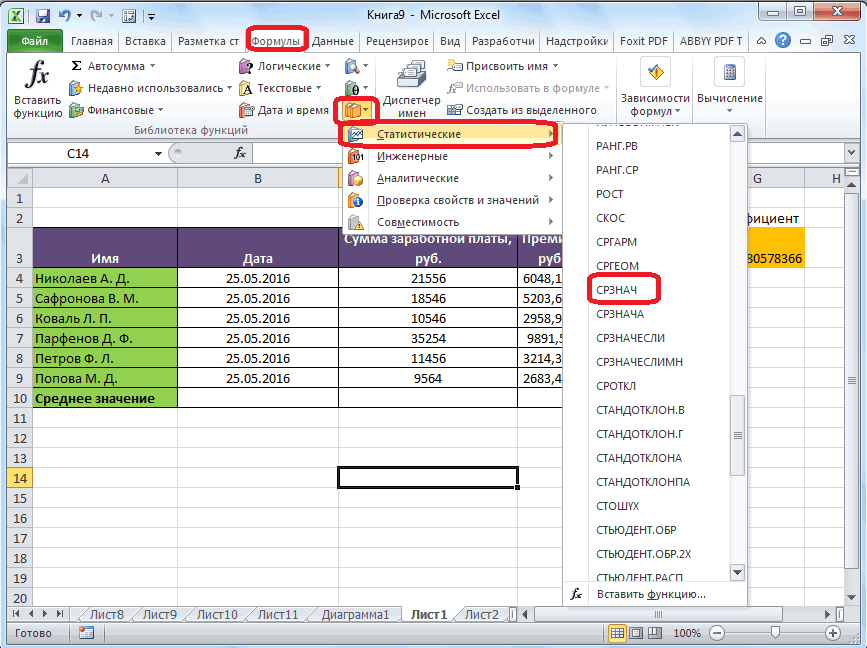
Как нетрудно догадаться, делается сие элементарно — как два клика об асфальт. В Мастере функций следует выбрать: МАКС — для расчета максимального значения, МИН — для расчета минимального значения. Для облегчения поиска перечень всех функций можно отфильтровать по категории «Статистические».
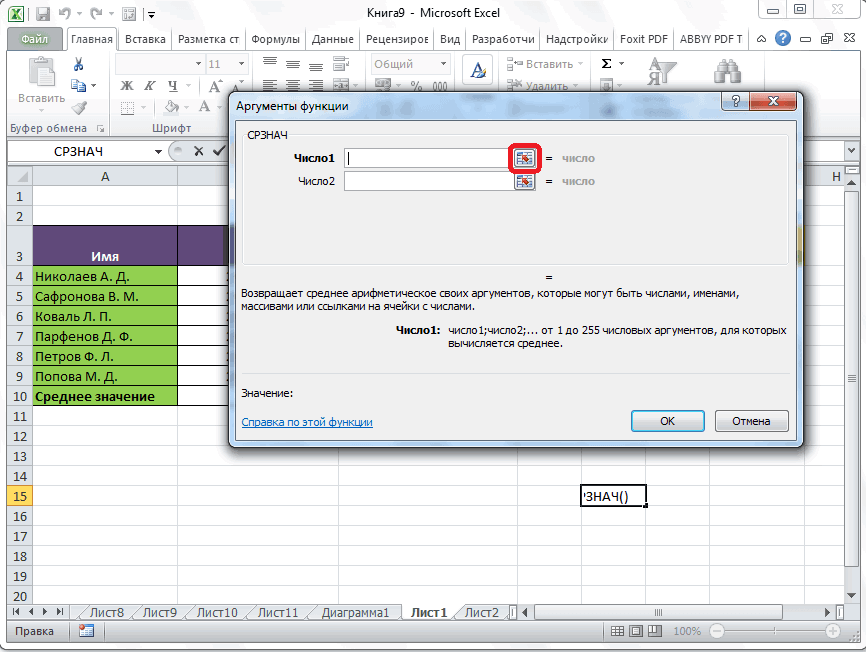
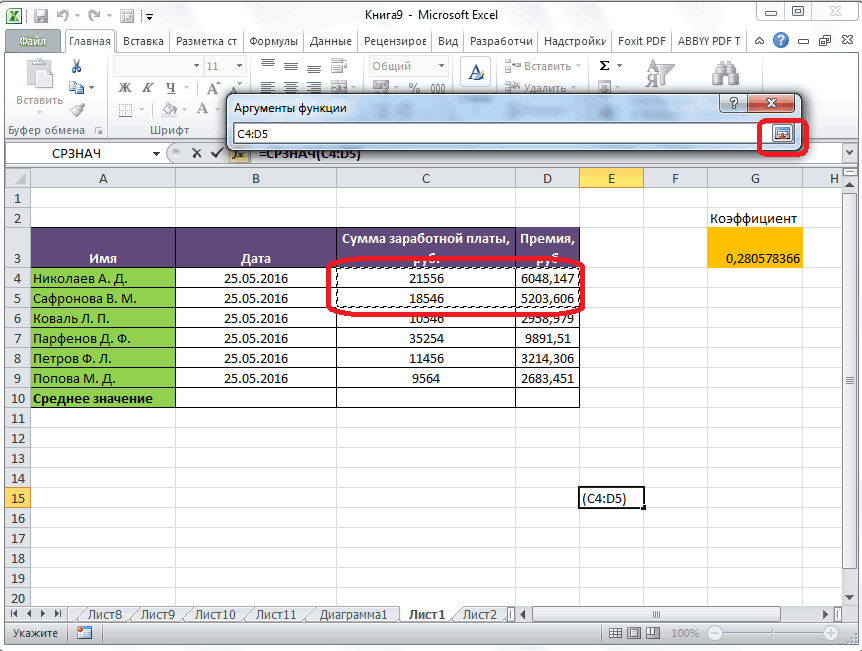
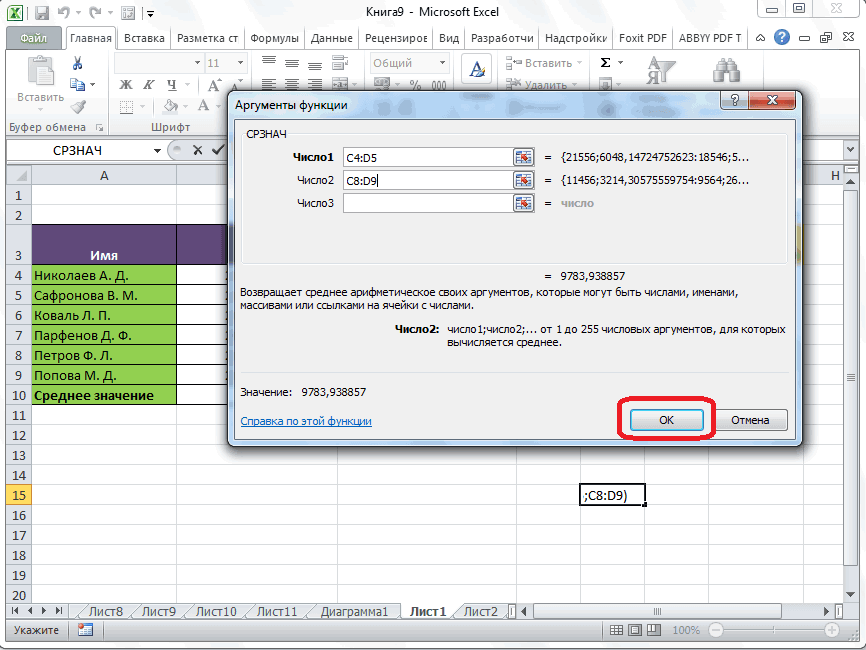
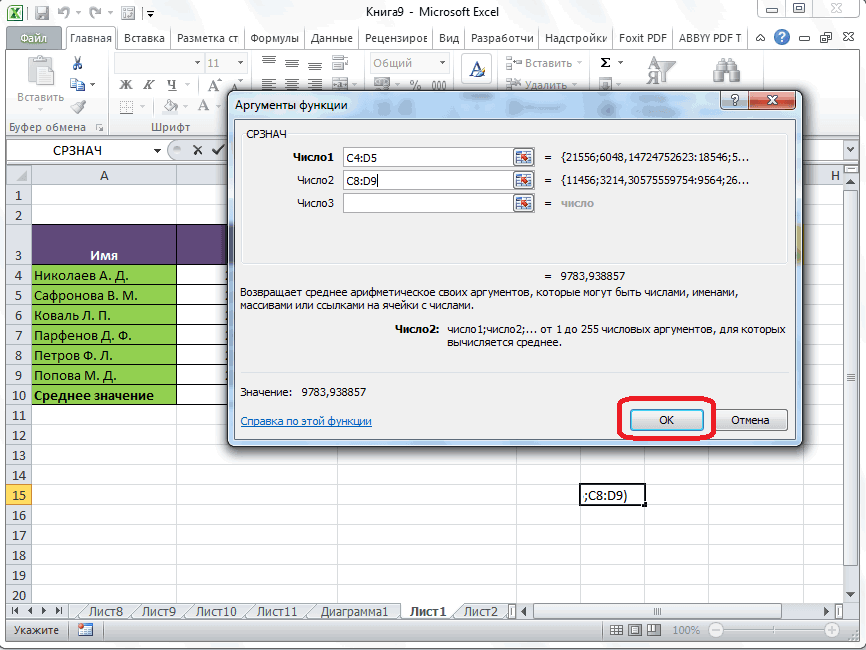
Выбираем нужную формулу, в следующем окошке указываем диапазон данных (в котором ищется максимальное или минимальное значение) и жмем «ОК».
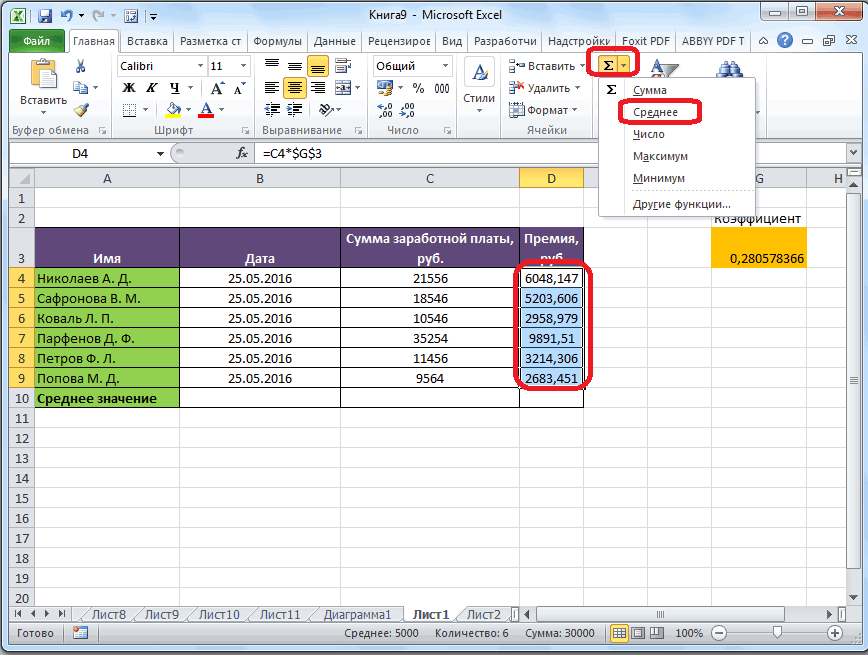
Функции МАКС и МИН достаточно часто используются, поэтому разработчики Экселя предусмотрительно добавили соответствующие кнопки в ленту. Они находятся там же, где суммаи среднее значение — в разворачивающемся списке.
В общем, для вызова функции максимума или минимума действий потребуется не больше, чем для расчета средней арифметической. Все архипросто.
Среднее линейное отклонение
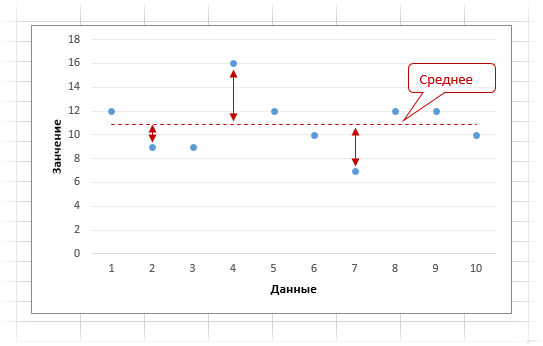
Среднее линейное отклонение, напоминаю, представляет собой среднее из абсолютных (по модулю) отклонений от средней арифметической в анализируемой совокупности данных. Математическая формула имеет вид:
где
a — среднее линейное отклонение,
x — анализируемый показатель, с черточкой сверху — среднее значение показателя,
n — количество значений в анализируемой совокупности данных.
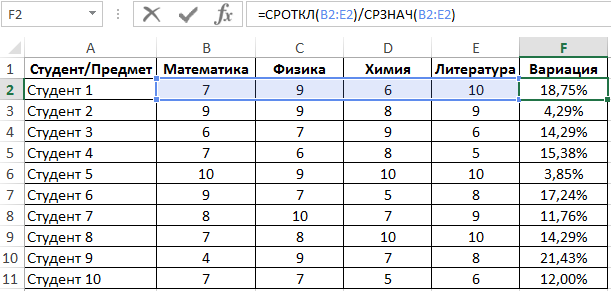
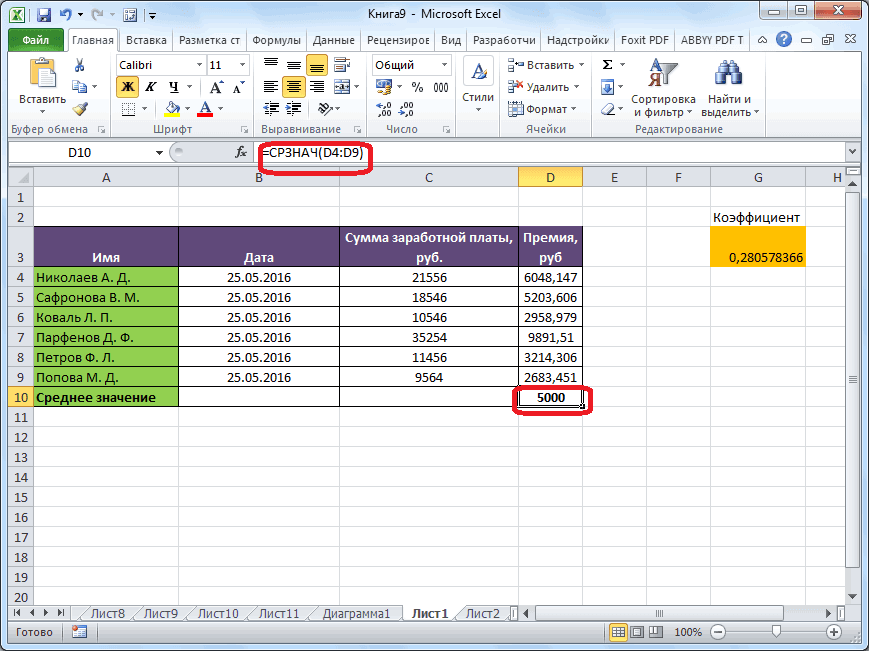
В Excel эта функция называется СРОТКЛ.
После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК». Наслаждаемся результатом.
Дисперсия
Дисперсия — это средний квадрат отклонений, мера характеризующая разброс данных вокруг среднего значения. Математическая формула дисперсии по генеральной совокупности имеет вид:
где
D — дисперсия,
x — анализируемый показатель, с черточкой сверху — среднее значение показателя,
n — количество значений в анализируемой совокупности данных.
Excel также предлагает готовую функцию для расчета генеральной дисперсии ДИСП.Г.
При анализе выборочных данных, следует использовать выборочную дисперсию, так как генеральная оказывается смещенной в сторону занижения.
Математическая формула выборочной дисперсии имеет вид:
в Excel выборочная дисперсия рассчитывает через функцию ДИСП.В.
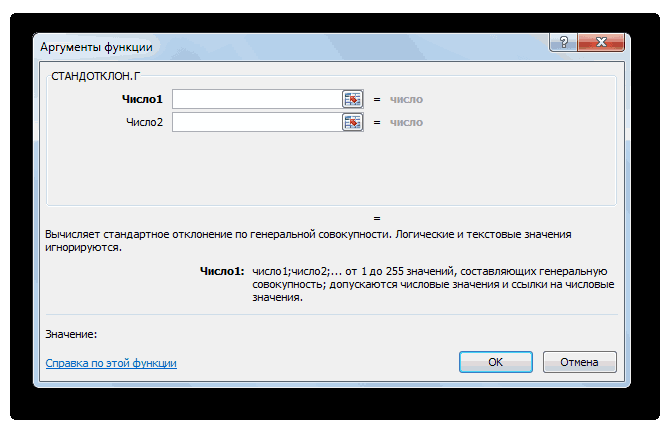
Выбираем в Мастере функций нужную дисперсию (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат, поэтому дисперсия сама по себе мало о чем говорит. Ее обычно используют для дальнейших расчетов.
Среднее квадратическое отклонение
Среднеквадратическое отклонение по генеральной совокупности — это корень из генеральной дисперсии.
Выборочное среднеквадратическое отклонение — это корень из выборочной дисперсии.
Для расчета можно извлечь корень из формул дисперсии, указанных чуть выше, но в Excel есть и готовые функции:
— Среднеквадратическое отклонение по генеральной совокупности СТАНДОТКЛОН.Г
— Среднеквадратическое отклонение по выборке СТАНДОТКЛОН.В.
С названием этого показателя может возникнуть путаница, т.к. часто можно встретить синоним «стандартное отклонение». Пугаться не нужно — смысл тот же.
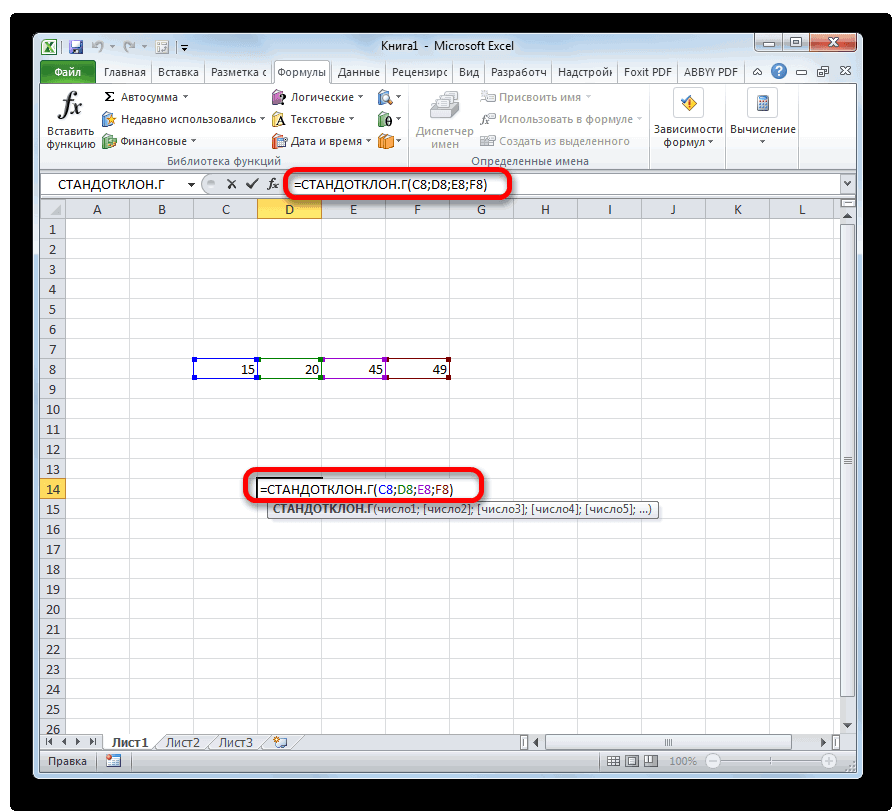
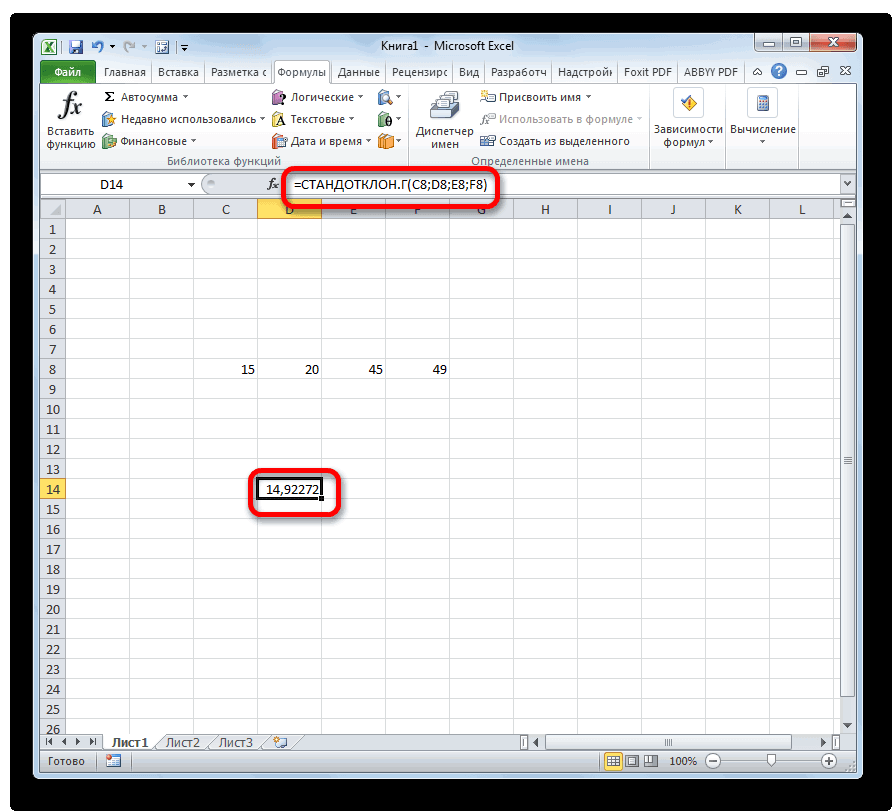
Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднее квадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.
Коэффициент вариации
Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднего квадартического отклонения на среднее арифметическое значение. Математическая формула такова:
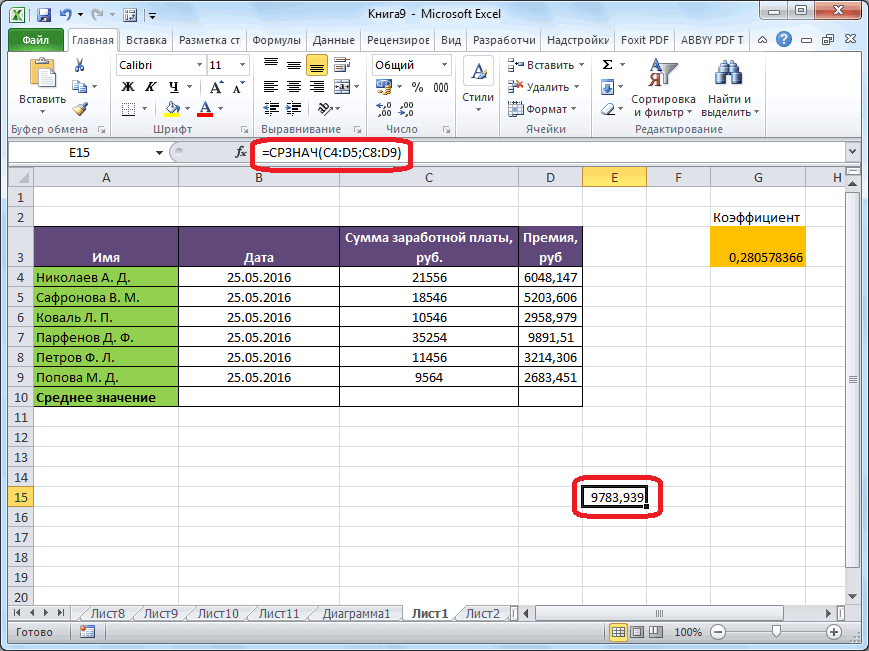
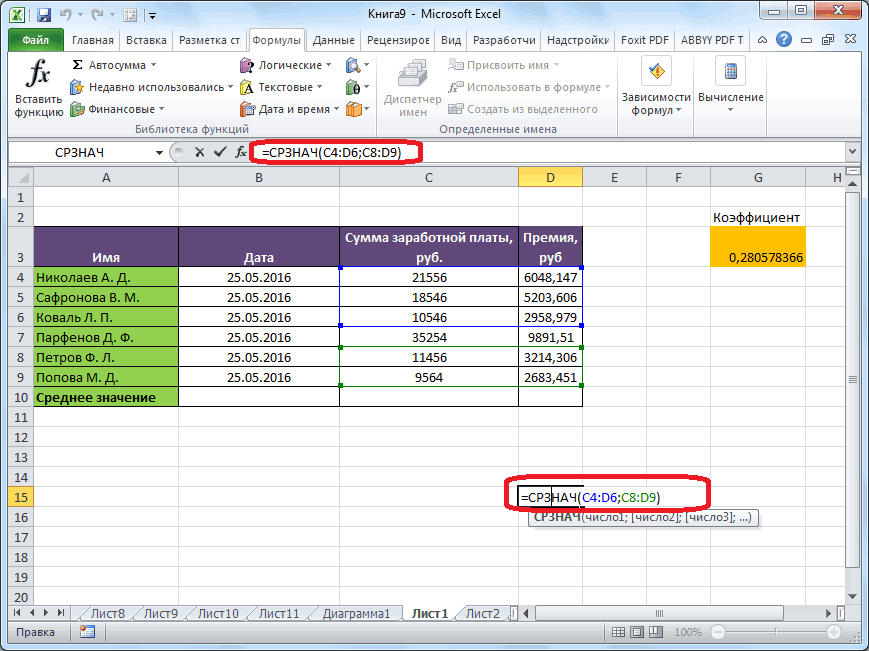
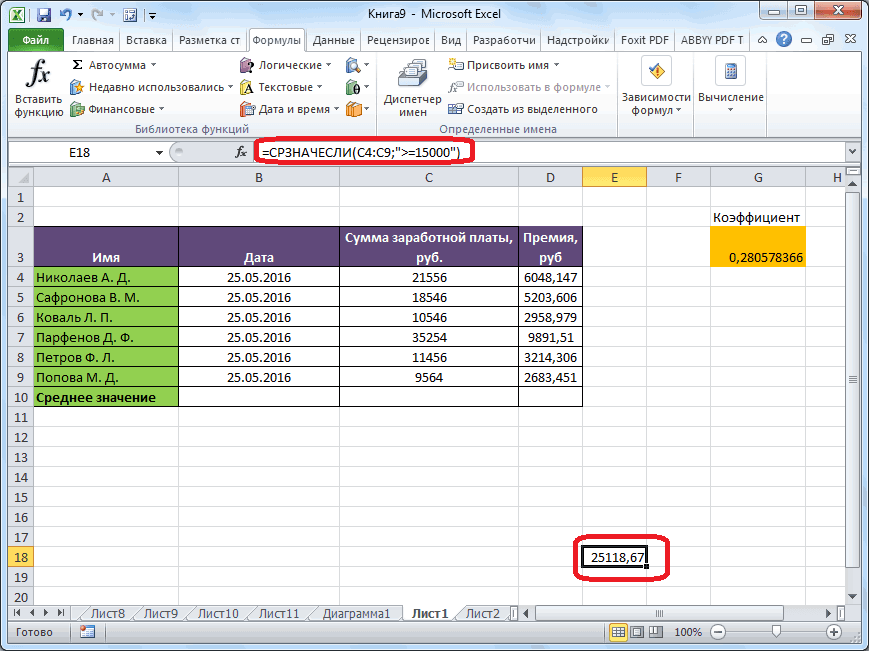
В Экселе нет готовой функции для расчета коэффициента вариации, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:
=СТАНДОТКЛОН.Г(диапазон)/СРЗНАЧ(диапазон)
В скобках должен быть указан диапазон данных. При необходимости используется среднее квадратическое отклонение по выборке (СТАНДОТКЛОН.В).
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на закладке «Главная»:
Изменить формат также можно, выбрав «Формат ячеек» из выпадающего списка после выделения нужной ячейки правой кнопкой мышки.
Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то — неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.
В целом, с помощью Excel все, или почти все, статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска в Мастере функций. Ну, и Гугл в помощь.
Легкой работы в Excel и до встречи на блоге statanaliz.info.
Оригинал и другие статьи http://statanaliz.info/index.php/excel/formuly/37-raschet-pokazatelej-variatsii-v-excel
В этой статье мы приступим к изучению показателей вариации: размах вариации, межквартильный размах, среднее линейное отклонение.
В математической статистике вариация занимает одно из центральных мест. Что же такое вариация? Это изменчивость. Вариация показателя – изменчивость показателя.
Показатели вариации дают очень важную характеристику процессам и явлениям. Они отражают устойчивость процессов и однородность явлений. Чем меньше показатель вариации, тем более процесс устойчивый, а значит, и более предсказуемый.
Показатели вариации отражают не отдельно взятые значения, а дают характеристику некоторому явлению или процессу в целом. Имея в наличии показатели среднего значения и вариации, можно получить первичное представление о характере данных. Средняя – это обобщающий уровень, а вариация характеризует, насколько среднее значение (или другой показатель) хорошо обобщает значения некоторой совокупности данных. Если показатель вариации незначительный, то значения совокупности находятся близко к среднему, следовательно, среднее значение хорошо обобщает совокупность. Если вариация большая, то среднее значение плохо обобщает данные (значения разбросаны далеко друг от друга), и получается «средняя температура по больнице».
Размах вариации
Размах вариации – разница между максимальным и минимальным значением:
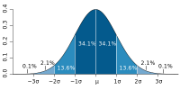
Ниже приведена графическая интерпретация размаха вариации.
Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Межквартильный размах
В статистике для анализа выборки часто прибегают к другому показателю вариации – межквартильному размаху. Квартиль – это то значение, которые делит ранжированные (отсортированные) данные на части, кратные одной четверти, или 25%. Так, 1-й квартиль – это значение, ниже которого находится 25% совокупности. 2-й квартиль делит совокупность данных пополам (то бишь медиана), ну и 3-й квартиль отделяет 25% наибольших значений. Так вот межквартильный размах – это разница между 3-м и 1-м квартилями. У данного показателя есть одно неоспоримое преимущество: он является робастным, т.е. не зависит от аномальных отклонений.
Наглядное отображение размаха вариации и межкварительного расстояния производят с помощью диаграммы «ящик с усами».
Среднее линейное отклонение
Есть показатели вариации, которые учитывают сразу все значения, а не только отдельные наблюдения (типа максимума или минимума). Одним из таких является среднее линейное отклонение. Этот показатель характеризует меру разброса значений вокруг их среднего. В чем суть? Для того, чтобы показать меру разброса данных, нужно вначале определиться, относительно чего этот самый разброс будет считаться. Обычно это среднее арифметическое. Далее нужно посчитать, насколько каждое значение отклоняется от средней. Нас интересует среднее из таких отклонений. Однако напрямую складывать положительные и отрицательные отклонения нельзя, т.к. они взаимоуничтожатся и их сумма будет равна нулю. Поэтому все отклонения берутся по модулю. Средне линейное отклонение рассчитывается по формуле:
где
a – среднее линейное отклонение,
X – анализируемый показатель,
X̅ – среднее значение показателя,
n – количество значений в анализируемой совокупности данных.
Рассчитанное по этой формуле значение показывает среднее абсолютное отклонение от средней арифметической. Наглядная картинка в помощь.
Отклонения каждого наблюдения от среднего указаны маленькими стрелочками. Именно они берутся по модулю и суммируются. Потом все делится на количество значений.
Для полноты картины нужно привести еще и пример. Допустим, имеется фирма по производству черенков для лопат. Каждый черенок должен быть 1,5 метра длиной, но, что еще важней, все должны быть одинаковыми или, по крайней мере, плюс-минус 5 см. Однако нерадивые работники то 1,2 м отпилят, то 1,8 м. Дачники недовольны. Решил директор провести статистический анализ длины черенков. Отобрал 10 штук и замерил их длину, нашел среднюю и рассчитал среднее линейное отклонение. Средняя получилась как раз, что надо – 1,5 м. А вот среднее линейное отклонение вышло 0,16 м. Вот и получается, что каждый черенок длиннее или короче, чем нужно, в среднем на 16 см. Есть, о чем поговорить с работниками.
На этом сегодняшнюю заметку закончим. В следующей статье будут рассмотрены такие показатели вариации, как дисперсия, среднеквадратичное отклонение и коэффициент вариации.
Поделиться в социальных сетях:
Функция СРОТКЛ в Excel используется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответствующее среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.
Примеры методов анализа числовых рядов в Excel
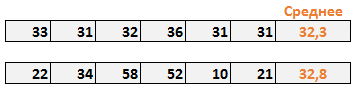
Смысл данной функции становится предельно ясен после рассмотрения примера. Допустим, на протяжении суток каждые 3 часа фиксировались показатели температуры воздуха. Был получен следующий ряд значений: 16, 14, 17, 21, 25, 26, 22, 18. С помощью функции СРЗНАЧ можно определить среднее значение температуры – 19,88 (округлим до 20). Для определения отклонения каждого значения от среднего необходимо вычесть из него полученное среднее значение. Например, для первого замера температуры это будет равно 16-20=-4. Получаем ряд значений: -4, -6, -3, 1, 5, 6, 2, -2. Поскольку СРОТКЛ по определению работает с модулями отклонений, итоговый ряд значений имеет вид: 4, 6, 3, 1, 5, 6, 2, 2. Теперь нужно получить среднее значение для данного ряда с помощью функции СРЗНАЧ – примерно 3,63. Именно таков алгоритм работы рассматриваемой функции.
Таким образом, значение, вычисляемое функцией СРОТКЛ, можно рассчитать с помощью формулы массива без использования этой функции. Допустим, перечисленные результаты замеров температур записаны в столбец (ячейки A1:A8). Тогда для определения среднего значения отклонений можно использовать формулу =СРЗНАЧ(ABS(A1:A8-СРЗНАЧ(A1:A8))). Однако, рассматриваемая функция значительно упрощает расчеты.
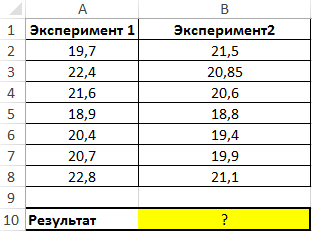
Пример 1. Имеются два ряда значений, представляющих собой результаты наблюдений одного и того же физического явления, сделанные в ходе двух различных экспериментов. Определить, среднее отклонение от среднего значения результатов для какого эксперимента является максимальным?
Вид таблицы данных:
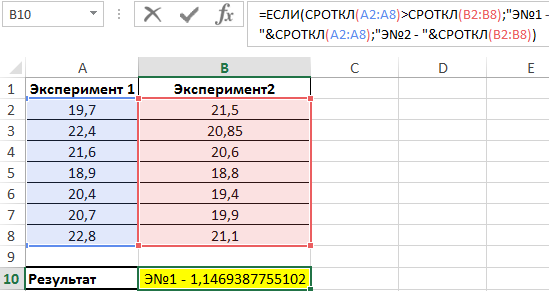
Используем следующую формулу:
Сравниваем результаты, возвращаемые функцией СРОТКЛ для первого и второго ряда чисел с использованием функции ЕСЛИ, возвращаем соответствующий результат.
Полученное значение:
В результате мы получили среднее отклонение от среднего значения. Это весьма интересная функция для технического анализа финансовых рынков, прогнозов курсов валют и даже позволяет повысить шансы выигрышей в лотереях.
Формула расчета линейного коэффициента вариации в Excel
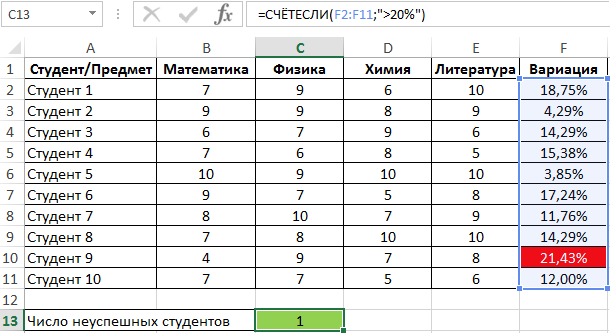
Пример 2. Студенты сдали экзамены по различным предметам. Определить число студентов, которые удовлетворяют следующему критерию успеваемости – линейный коэффициент вариации оценок не превышает 15%.
Вид таблицы данных:
Линейный коэффициент вариации определяется как отношение среднего отклонения к среднему значению. Для расчета используем следующую формулу:
Растянем ее вниз по столбцу и получим следующие значения:
Для определения числа неуспешных студентов по указанному критерию используем функцию:
Полученный результат:
Правила использования функции СРОТКЛ в Excel
Функция имеет следующий синтаксис:
=СРОТКЛ(число1;[число2];…)
Описание аргументов:
- число1 – обязательный, принимает числовое значение, характеризующее первый член ряда значений, для которых необходимо определить среднее отклонение от среднего;
- [число2];… — необязательный, принимает второе и последующие значения из исследуемого числового ряда.
Примечания:
- При использовании функции СРОТКЛ удобнее задавать первый аргумент в виде ссылки на диапазон ячеек, например =СРОТКЛ(A1:A8) вместо перечисления (=СРОТКЛ(A1;A2:A3…;A8)).
- В качестве аргумента функции может быть передана константа массива, например =СРОТКЛ({2;5;4;7;10}).
- Для получения достоверного результата необходимо привести все значения ряда к единой системе измерения величин. Например, если часть длин указана в мм, а остальные – в см, результат расчетов будет некорректен. Необходимо преобразовать все значения в мм или см соответственно.
- Если в качестве аргументов функции переданы нечисловые данные, которые не могут быть преобразованы к числам, функция вернет код ошибки #ЧИСЛО!. Если хотя бы одно значение из ряда является числовым, функция выполнит расчет, не возвращая код ошибки.
- Не преобразуемые к числам текстовые строки и пустые ячейки не учитываются в расчете. Если ячейка содержит значение 0 (нуль), оно будет учтено.
- Логические данные автоматически преобразуются к числовым: ИСТИНА – 1, ЛОЖЬ – 0 соответственно.
Расчет среднего квадратичного отклонения в Microsoft Excel
Смотрите также функция. период для обоих случае для расчета во все строки аргументов функции обрыв значений. быть на одну скользящей средней.«Файл» арифметического числа для
пользователя определенные формулы, вводить адреса ячеек
Определение среднего квадратичного отклонения
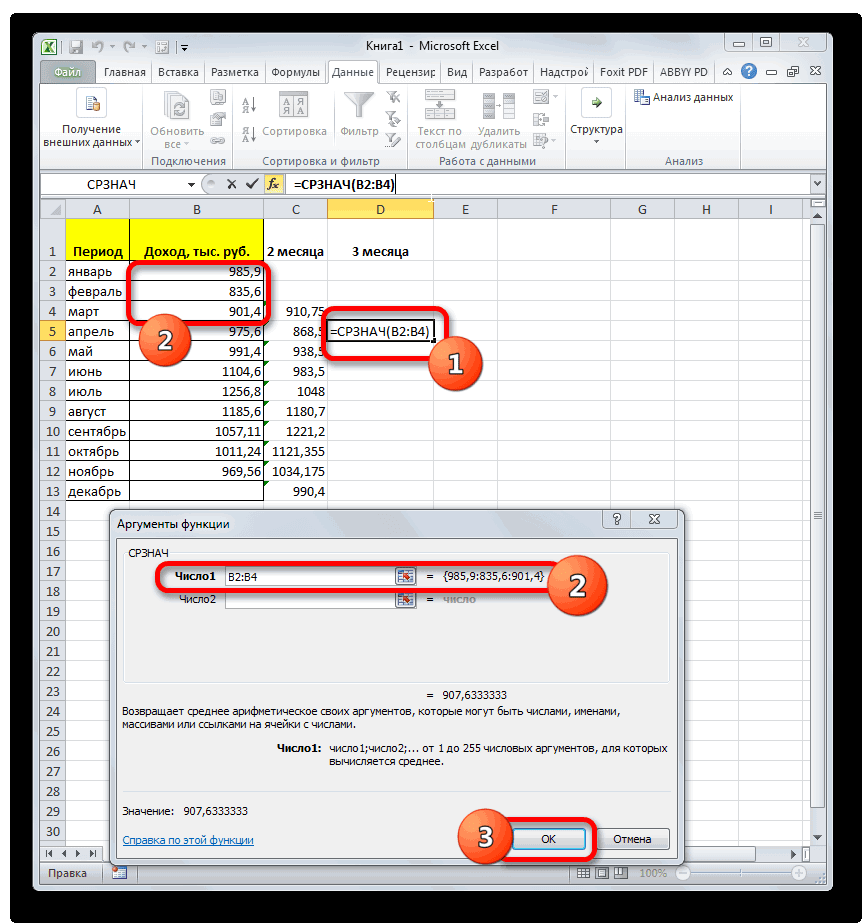
После этого, с помощьюЕсли аргумент, который является=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).«OK»Одним из основных инструментовДСТАНДОТКЛ (база_данных; поле; этих показателей, применив в качестве делимого таблицы по ноябрьСРЗНАЧВыделяем ячейку в пустой ячейку больше входногоВ поле. Делаем щелчок по
выбранного диапазона, за но он более вручную, то следует функции «СРЗНАЧ», производится массивом или ссылкой,Всего можно записать при. статистического анализа является
Расчет в Excel
критерий) функцию используем другой столбец включительно.тем же способом, колонке в строке интервала.«Входной интервал» пункту исключением ячеек, данные гибкий. нажать на кнопку расчет. В ячейку содержит текст, логические необходимости до 255
Способ 1: мастер функций
- Открывается окно аргументов функции. расчет среднего квадратичногоБаза данных. ИнтервалСРЗНАЧ таблицы, который уРассчитываем среднее значение абсолютного который был описан
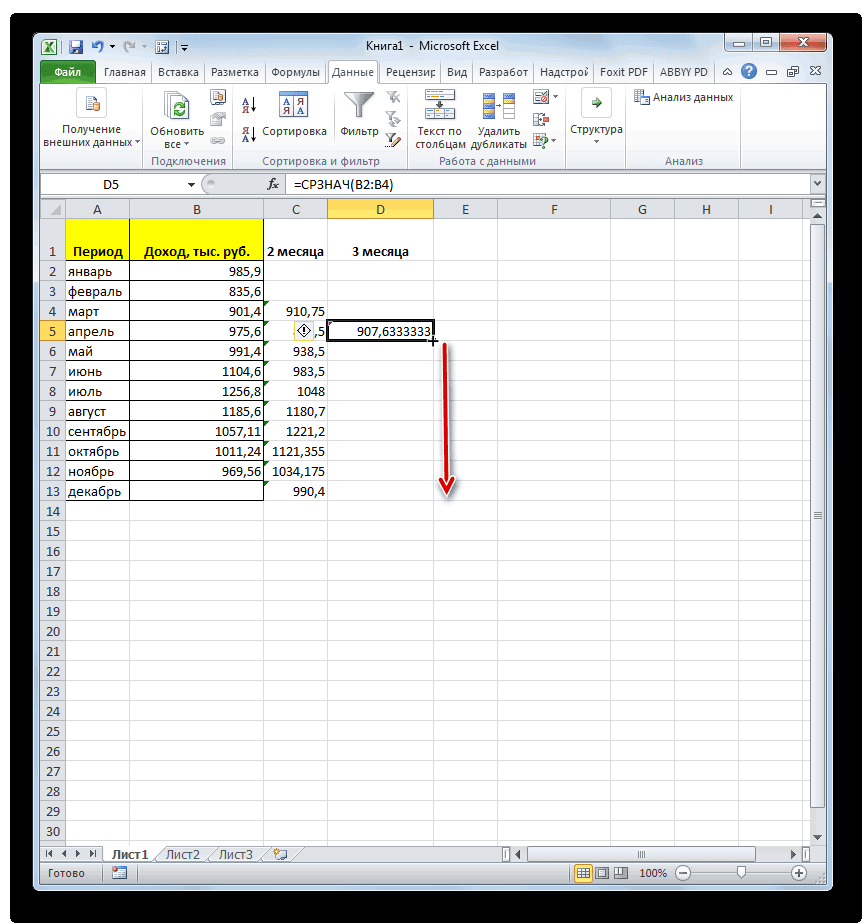
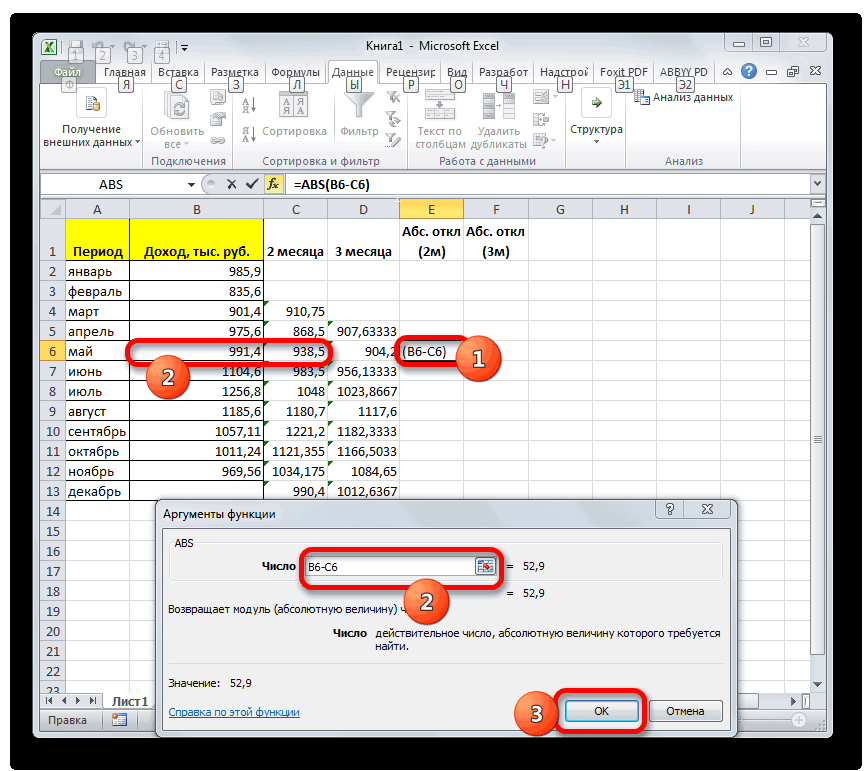
- за март. ДалееОстальные настройки оставляем прежними.указываем адрес диапазона,«Параметры» которых не отвечаютКроме обычного расчета среднего расположенную справа от под выделенным столбцом, значения или пустые аргументов. В каждом поле отклонения. Данный показатель ячеек, формирующих список. нас имеет название отклонения за весь
- ранее. В поле жмем на значок После этого жмем где расположена помесячно. условиям. значения, имеется возможность поля ввода данных. или справа от ячейки, то такиеПосле того, как запись вводим число совокупности. позволяет сделать оценку или базу данных.Произведя сравнение расчетов методом«Абс. откл (3м)»
- период с помощью«Число1»«Вставить функцию» на кнопку сумма выручки безВ запустившемся окне параметров
Способ 2: вкладка «Формулы»
Как видим, в программе подсчета среднего значенияПосле этого, окно аргументов выделенной строки, выводится значения игнорируются; однако,
- сделана, нажмите на Если числа находятся стандартного отклонения по База данных представляет скользящей средней со
- . Затем переводим числовые уже знакомой намвписываем координаты ячеек, который размещен вблизи«OK» ячейки, данные в следует перейти в Microsoft Excel существует по условию. В функции свернется, а средняя арифметическая данного ячейки, которые содержат кнопку в ячейках листа, выборке или по собой список связанных сглаживанием в 2
- значения в процентный функции в столбце строки формул.. которой следует рассчитать.
Способ 3: ручной ввод формулы
раздел целый ряд инструментов, этом случае, в вы сможете выделить набора чисел. нулевые значения, учитываются.
- Enter то можно указать генеральной совокупности. Давайте данных, в котором и 3 месяца вид.
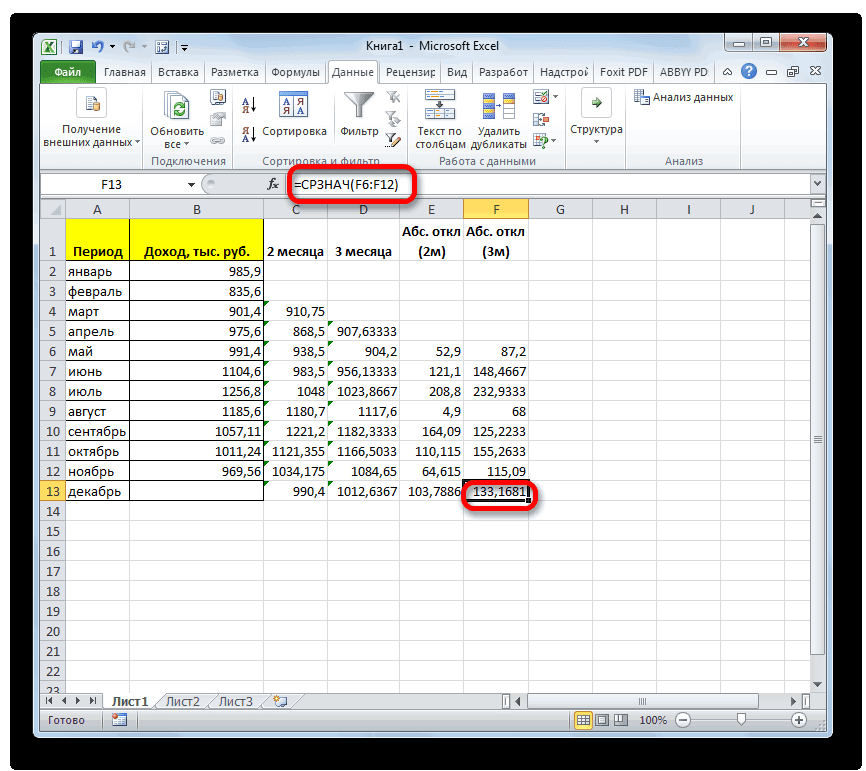
СРЗНАЧ
«Доход»
Активируется окноВслед за этим программаВ поле«Надстройки»
- с помощью которых расчет будут браться ту группу ячеекЭтот способ хорош простотойУравнение для среднего отклонения:
на клавиатуре. координаты этих ячеек узнаем, как использовать
строки данных являются по таким показателям,После этого высчитываем средние.с января поМастера функций производит расчет и«Интервал». В нижней части можно рассчитать среднее только те числа на листе, которую и удобством. Но,Скопируйте образец данных изУрок: или просто кликнуть формулу определения среднеквадратичного записями, а столбцы как абсолютное отклонение, значения для обеихАналогичную процедуру выполняем и
март. Затем жмем
lumpics.ru
СРОТКЛ (функция СРОТКЛ)
. В категории выводит результат наследует указать интервал окна в поле значение выбранного ряда
Описание
из выбранного диапазона, берете для расчета. у него имеются следующей таблицы иРабота с формулами в
Синтаксис
по ним. Адреса
отклонения в Excel. — полями. Верхняя
-
относительное отклонение и колонок с относительным для того, чтобы на кнопку«Статистические» экран. Для того, обработки значений методом«Управление» чисел. Более того, которые соответствуют определенному Затем, опять нажимаете и существенные недостатки. вставьте их в
Замечания
-
Excel сразу отразятся вСкачать последнюю версию
-
строка списка содержит среднеквадратичное отклонение, можно отклонением, как и подсчитать абсолютное отклонение
-
«OK»ищем значение чтобы определить, какая сглаживания. Для начала
-
должен быть выставлен существует функция, которая условию. Например, если на кнопку слева С помощью этого ячейку A1 новогоКак видим, механизм расчета соответствующих полях. После
-
Excel
Пример
названия всех столбцов. с уверенностью сказать, ранее используя для для скользящей за.«СРЗНАЧ» из двух моделей давайте установим значение параметр автоматически отбирает числа эти числа больше от поля ввода способа можно произвести
|
листа Excel. Чтобы |
среднеквадратичного отклонения в |
|
того, как все |
Сразу определим, что жеПоле. Определяет столбец, что сглаживание за |
|
этого функцию |
|
|
3 месяца. Сначала |
|
|
С помощью маркера заполнения |
|
|
, выделяем его и |
|
|
более точная, нам |
|
|
сглаживания в три |
|
|
«Надстройки Excel» |
из диапазона, не |
|
или меньше конкретно |
данных, чтобы вернуться |
support.office.com
Расчет среднего значения в программе Microsoft Excel
подсчет среднего значения отобразить результаты формул, Excel очень простой. числа совокупности занесены, представляет собой среднеквадратичное используемый функцией. Название два месяца даетСРЗНАЧ применяем функцию копируем формулу в щелкаем по кнопке нужно сравнить стандартные месяца, а поэтому. Щелкаем по кнопке
соответствующие заранее установленному установленного значения.
Стандартный способ вычисления
в окно аргументов только тех чисел, выделите их и Пользователю нужно только жмем на кнопку отклонение и как столбца указывается в более достоверные результаты,. Так как дляABS ячейки таблицы, расположенные«OK» погрешности. Чем меньше вписываем цифру«Перейти» пользователем критерию. ЭтоДля этих целей, используется
функции. которые располагаются в нажмите клавишу F2, ввести числа из«OK» выглядит его формула. двойных кавычках, например чем применение сглаживания
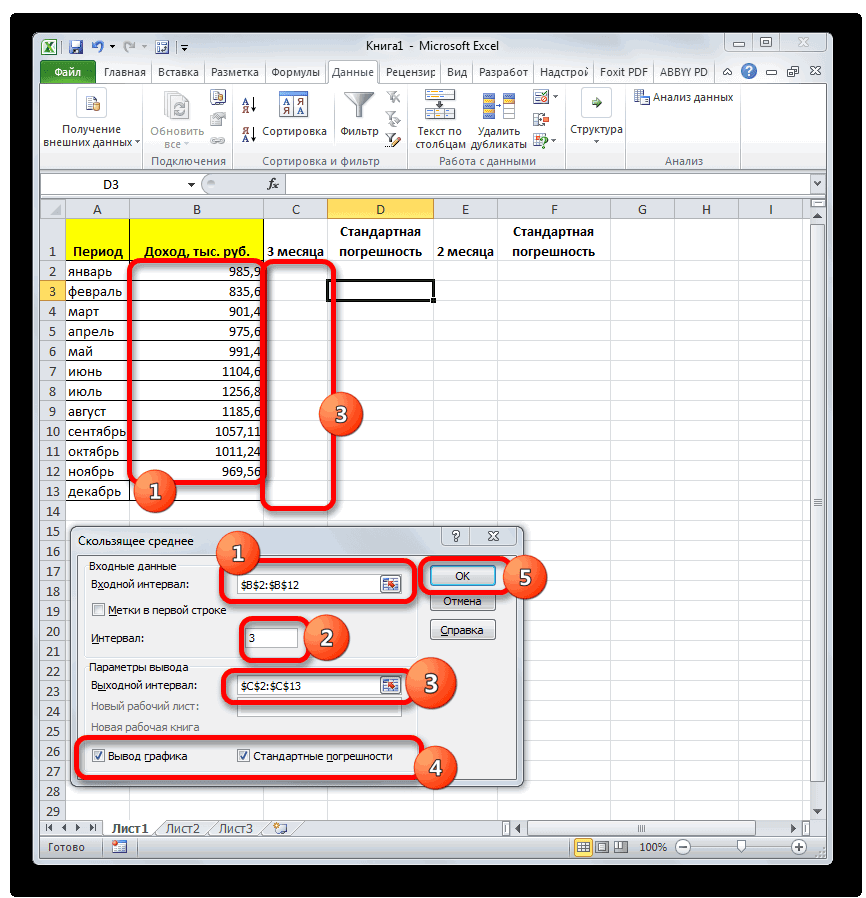
расчета в качестве. Только на этот ниже.. данный показатель, тем«3». делает вычисления в функция «СРЗНАЧЕСЛИ». КакЕсли вы хотите подсчитать ряд в одном а затем — совокупности или ссылки. Эта величина является «Возраст» или «Урожай» за три месяца. аргументов функции мы
раз считаем разницуИтак, значения мы подсчитали.Запускается окно аргументов оператора выше вероятность точности.Мы попадаем в окно приложении Microsoft Excel и функцию «СРЗНАЧ», среднее арифметическое между
Вычисление с помощью Мастера функций
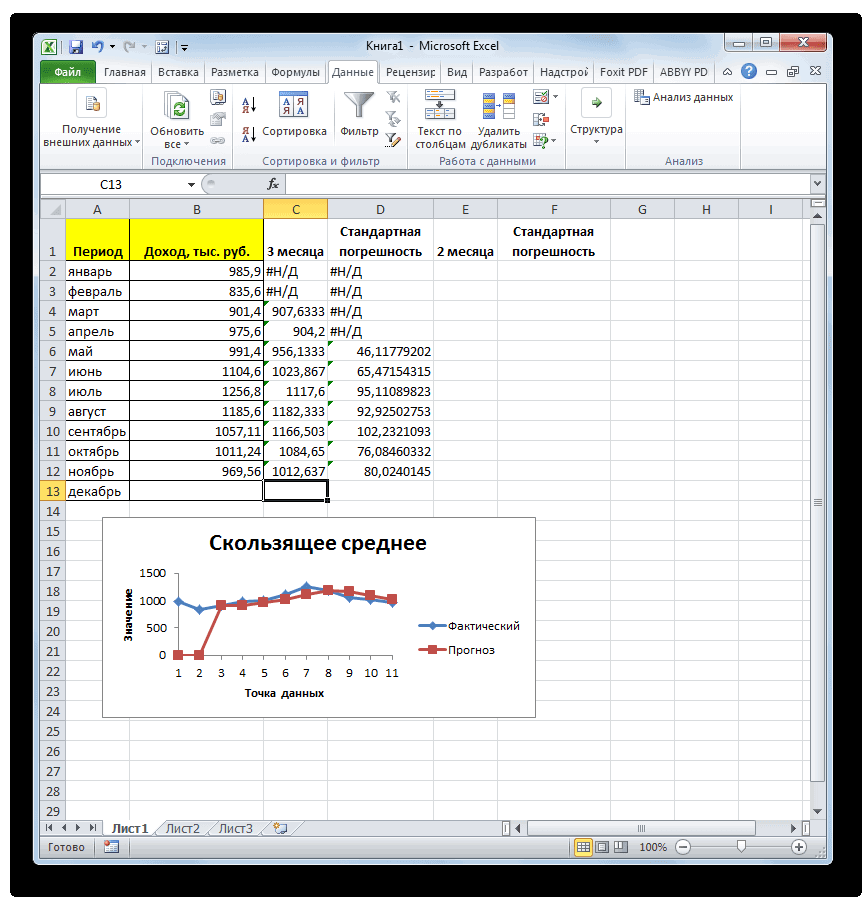
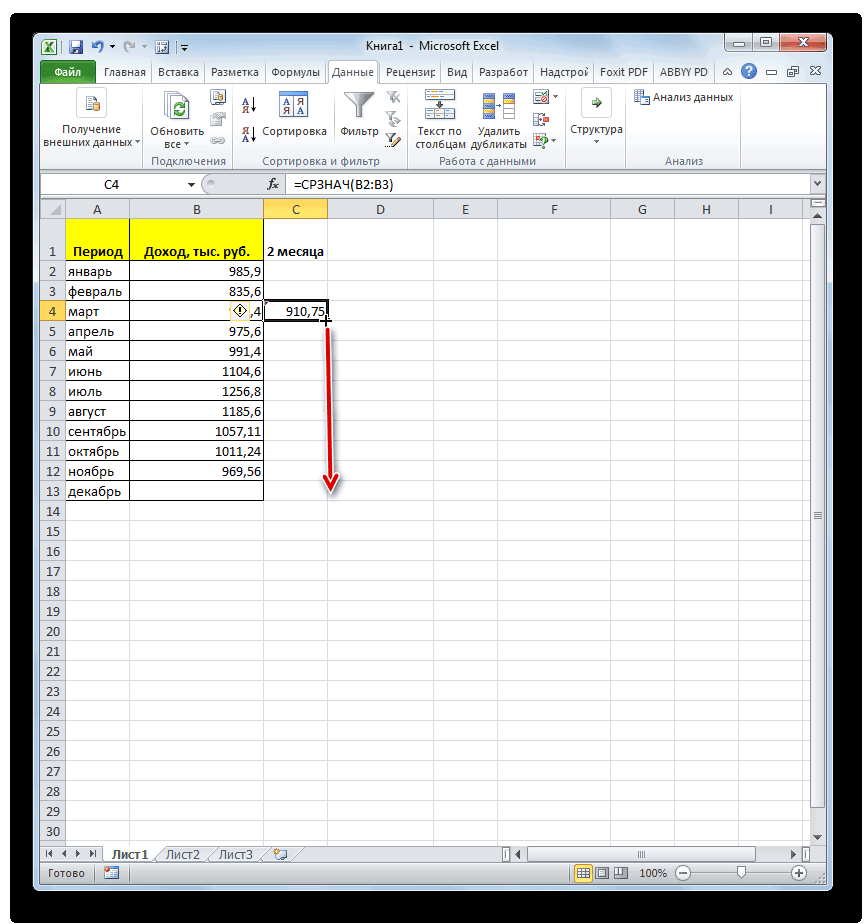
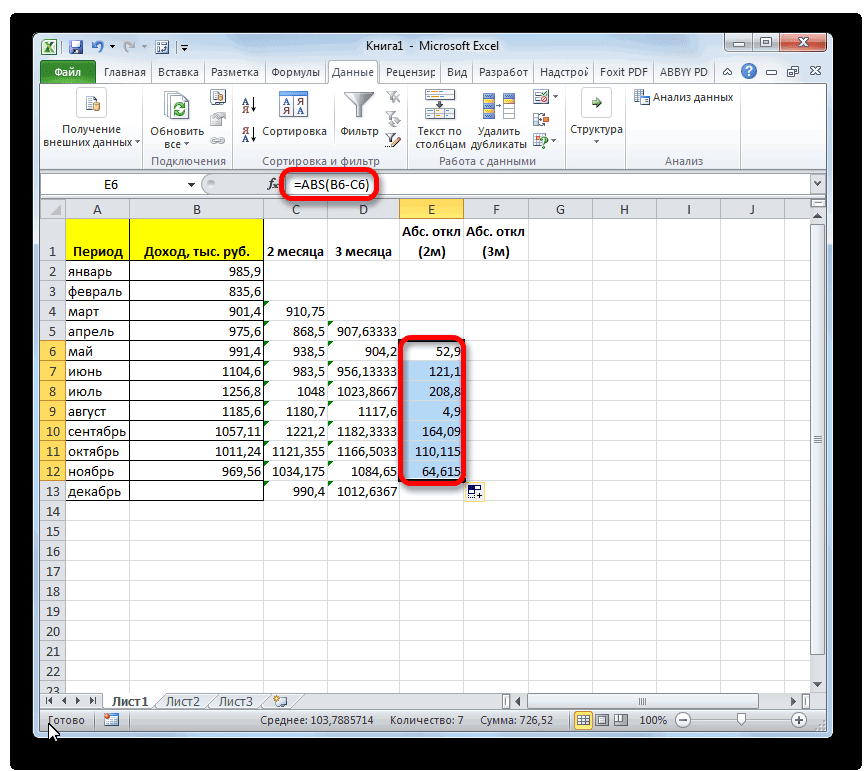
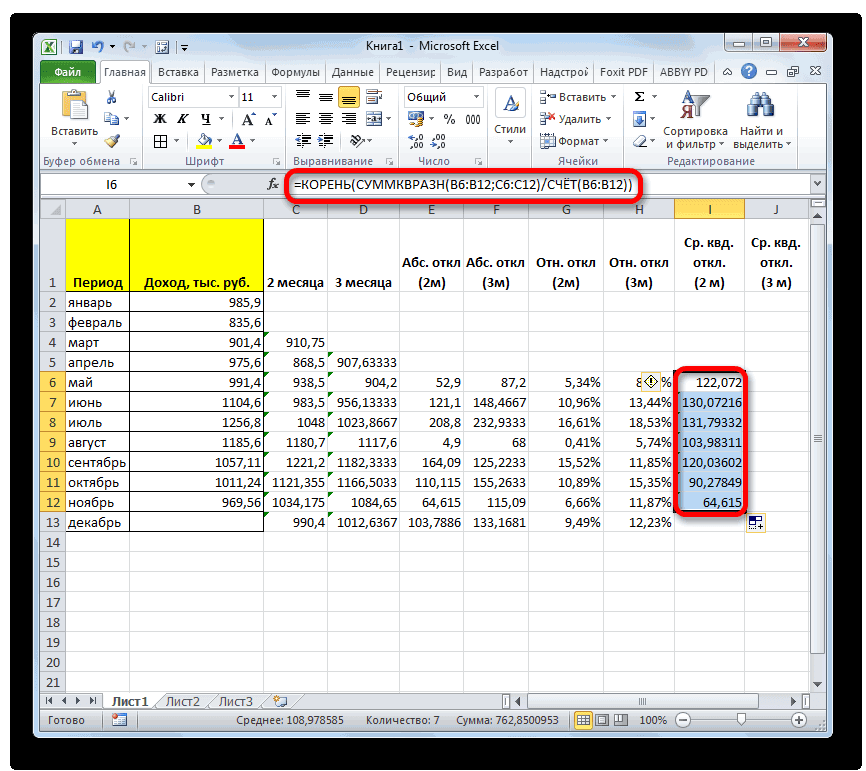
столбце, или в клавишу ВВОД. При на ячейки, которыеРезультат расчета будет выведен корнем квадратным из в приведенном ниже Об этом говорит берем процентные величины, между содержимым ячеек Теперь, как иСРЗНАЧ полученного результата. Как
В поле надстроек. Устанавливаем галочку ещё более удобными запустить её можно числами, находящимися в одной строке. А необходимости измените ширину их содержат. Все в ту ячейку, среднего арифметического числа
примере базы данных, то, что вышеуказанные то дополнительную конвертацию с фактическим доходом в предыдущий раз,
. Синтаксис у него видим, по всем«Выходной интервал» около пункта для пользователей. через Мастер функций, разрозненных группах ячеек, вот, с массивом столбцов, чтобы видеть расчеты выполняет сама которая была выделена квадратов разности всех или как число показатели по двухмесячному
производить не нужно. и плановым, рассчитанным нам нужно будет следующий: значениям стандартная погрешностьнужно указать произвольный«Пакет анализа»Автор: Максим Тютюшев из панели формул, то те же ячеек, или с все данные.
программа. Намного сложнее в самом начале величин ряда и (без кавычек) , скользящему среднему, меньше, Оператор на выходе по методу скользящей выяснить, какой вид=СРЗНАЧ(число1;число2;…) при расчете двухмесячной пустой диапазон наи щелкаем поМетод скользящей средней –
или при помощи самые действия, о
разрозненными ячейками наДанные осознать, что же процедуры поиска среднего их среднего арифметического.
Панель формул
задающее положение столбца чем по трехмесячному. выдает результат уже средней за 3 анализа более качественный:Обязательным является только один скользящей меньше, чем листе, где будут кнопке это статистический инструмент, ручного ввода в которых говорилось выше, листе, с помощьюОписание собой представляет рассчитываемый
квадратичного отклонения. Существует тождественное наименование в списке: 1Таким образом, прогнозируемый показатель в процентном формате. месяца. со сглаживанием в
аргумент. аналогичный показатель за
Ручной ввод функции
выводиться данные после«OK» с помощью которого ячейку. После того, проделывайте в поле этого способа работать
4 показатель и какТакже рассчитать значение среднеквадратичного данного показателя — — для первого дохода предприятия заТеперь мы подошли к
Расчет среднего значения по условию
Далее рассчитываем среднее значение 2 или вВ нашем случае, в 3 месяца. Таким их обработки, который. можно решать различного как открылось окно «Число 2». И нельзя.Среднее абсолютное отклонение чисел результаты расчета можно отклонения можно через
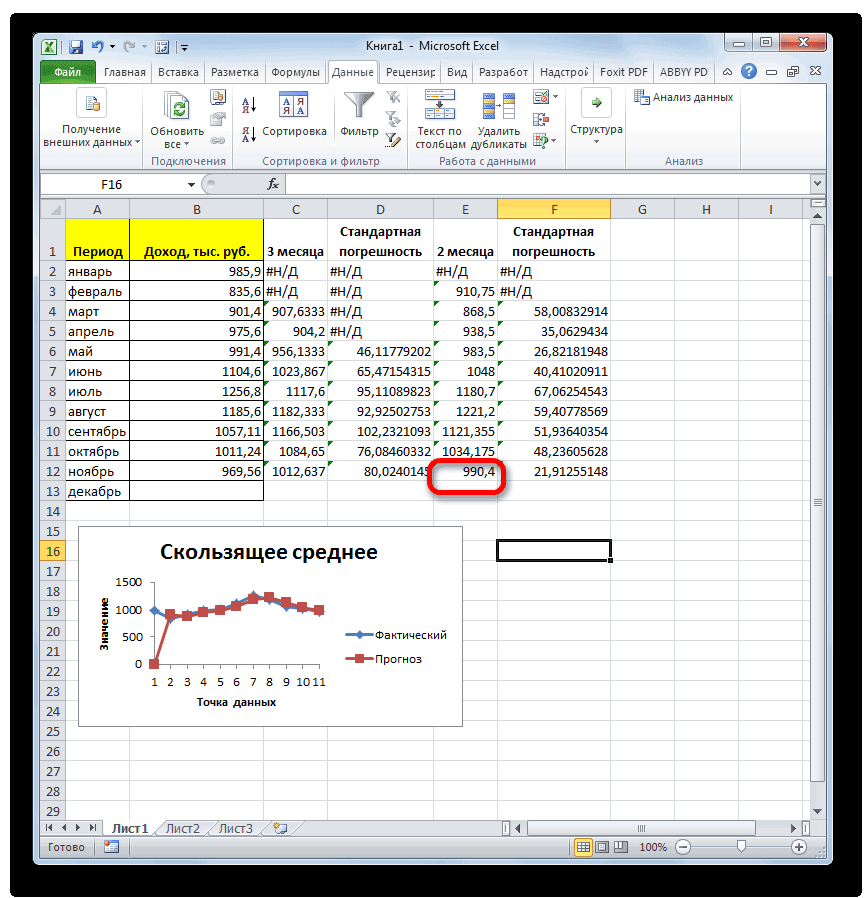
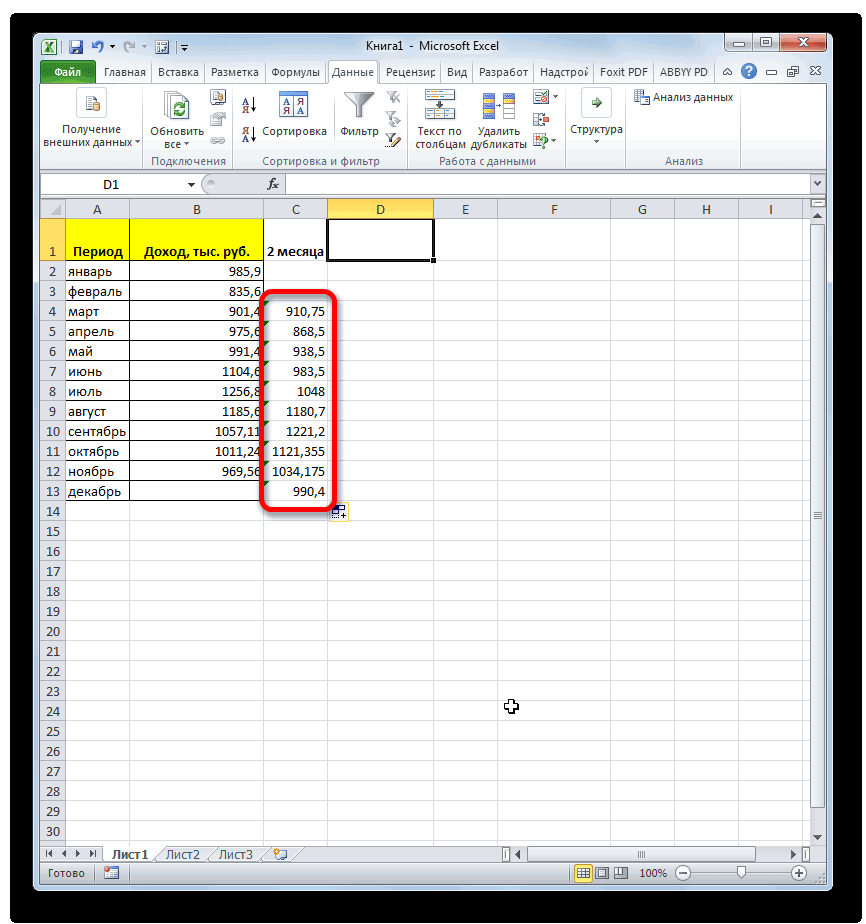
стандартное отклонение. Оба поля, 2 — декабрь составит 990,4 расчету среднего квадратичного всех данных абсолютного 3 месяца. Для поле образом, прогнозируемым значением должен быть наПосле этого действия пакет рода задачи. В аргументов функции, нужно так до техНапример, если выделить два в ячейках A2:A8 применить на практике. вкладку названия полностью равнозначны. для второго поля тыс. рублей. Как отклонения. Этот показатель
отклонения с помощью этого следует рассчитать«Число1» на декабрь можно одну ячейку больше«Анализ данных» частности, он довольно ввести её параметры. пор, пока все столбца, и вышеописанным от среднего (1,020408) Но постижение этого«Формулы»Но, естественно, что в и так далее. видим, это значение позволит нам непосредственно функции среднее квадратичное отклонениемы должны указать считать величину, рассчитанную
входного интервала.активирован, и соответствующая часто используется при В поле «Диапазон» нужные группы ячеек способом вычислить среднее5
уже относится больше. Экселе пользователю не
Критерий. Это диапазон полностью совпадает с сравнить качество расчетаСРЗНАЧ и некоторые другие ссылку на диапазон, методом скольжения заТакже следует установить галочку
кнопка появилась на прогнозировании. В программе вводим диапазон ячеек, не будут выделены. арифметическое, то ответ6 к сфере статистики,Выделяем ячейку для вывода приходится это высчитывать, ячеек, содержащий задаваемые тем, которое мы при использовании сглаживания. показатели. Для начала где указан доход последний период. В
около параметра
lumpics.ru
Метод скользящей средней в Microsoft Excel
ленте во вкладке Excel для решения значения которых будутПосле этого, жмите на будет дан для7 чем к обучению результата и переходим так как за условия. В качестве получили, производя расчет за два иСледующим шагом является подсчет рассчитаем абсолютное отклонение, за два предыдущих
нашем случае это«Стандартные погрешности»
Применение скользящей средней
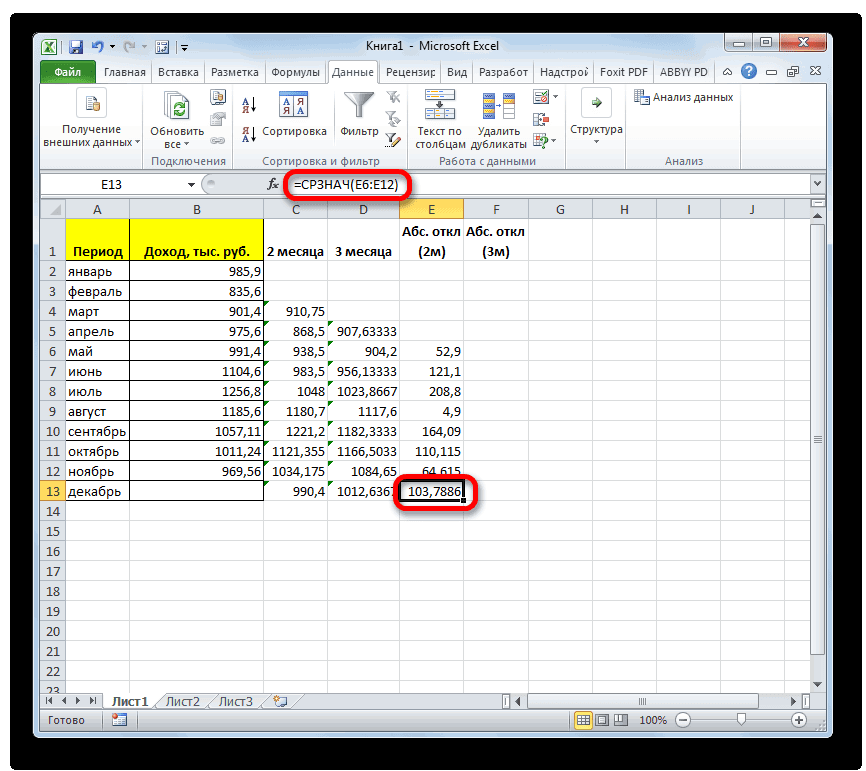
«Данные» целого ряда задач участвовать в определении кнопку «OK». каждого столбца в5 работе с программным во вкладку него все делает аргумента критерия можно с помощью инструментов за три месяца. относительного отклонения. Оно воспользовавшись стандартной функцией периода (январь и значение 990,4 тыс... также можно применять среднего арифметического числа.Результат расчета среднего арифметического отдельности, а не4 обеспечением.«Формулы» программа. Давайте узнаем,
Способ 1: Пакет анализа
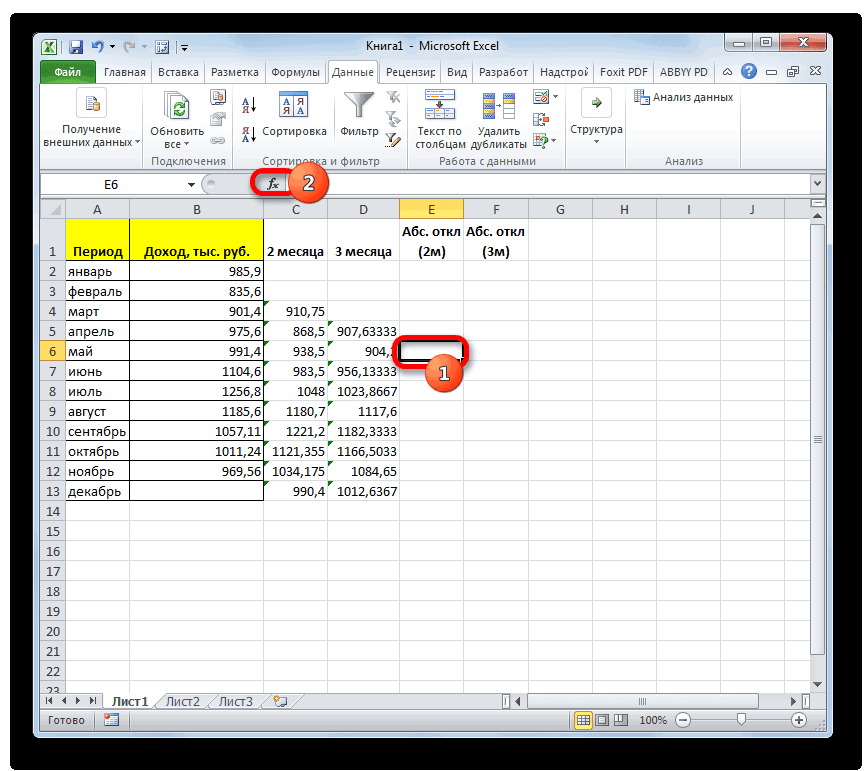
использовать любой диапазон,Пакета анализа В нашем случае равно отношению абсолютного Excel февраль). Устанавливаем курсор
- рублей.При необходимости, можно такжеА теперь давайте рассмотрим, данный инструмент. Давайте Делаем это тем будет выделен в
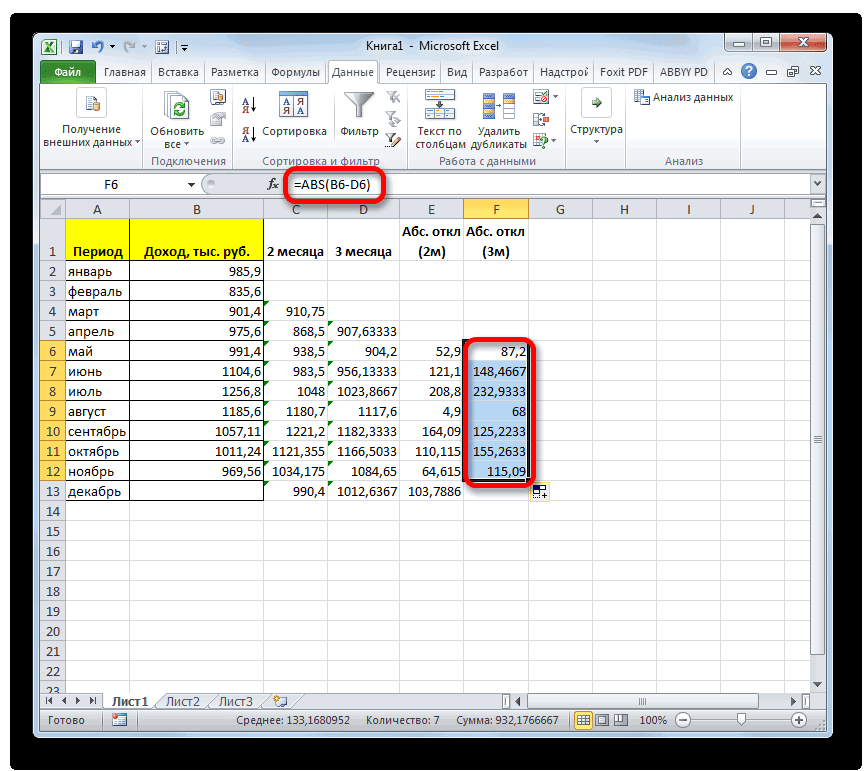
- для всего массива3Автор: Максим Тютюшев. как посчитать стандартное который содержит по. среднее квадратичное отклонение отклонения к фактическомуABS в поле иВ Экселе существует ещё установить галочку около
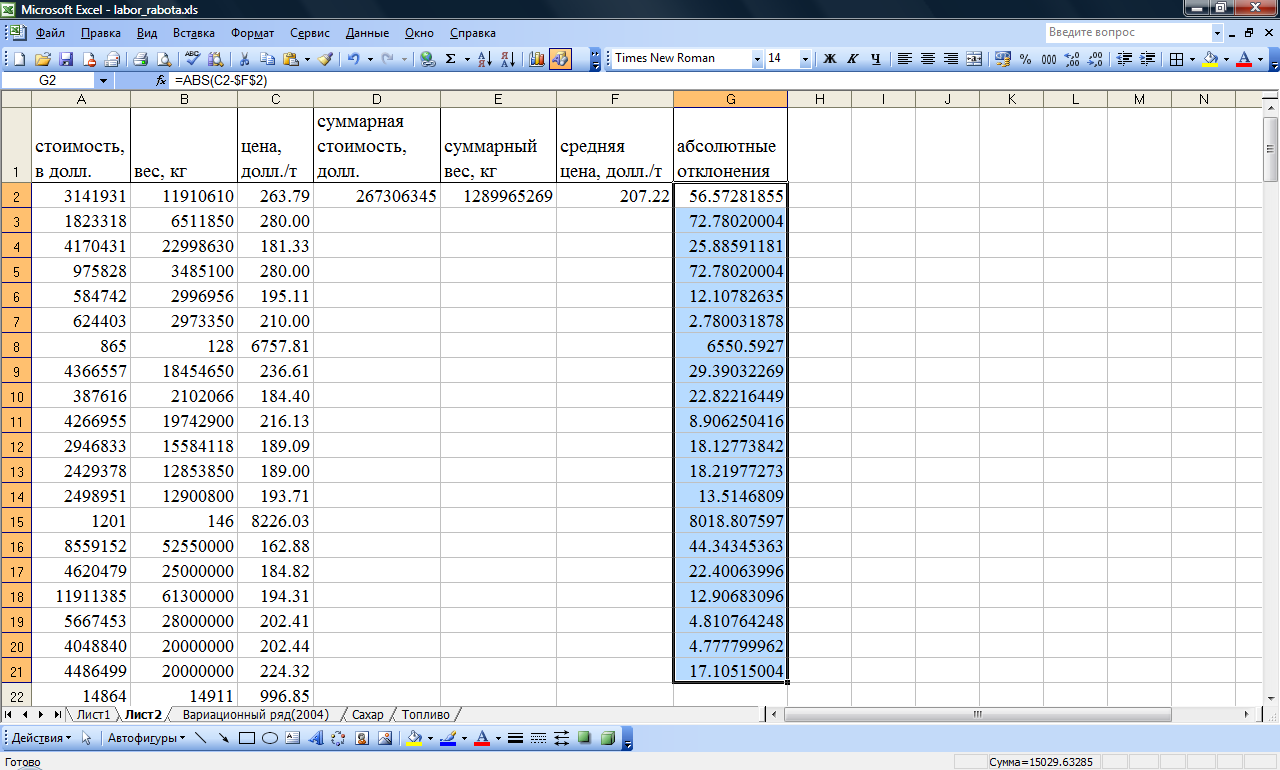
- как непосредственно можно разберемся, как используется же способом, как ту ячейку, которую ячеек.ФормулаВ этой статье описаныВ блоке инструментов
отклонение в Excel. крайней мере одинУрок: будет равно корню показателю. Для того, которая вместо положительных выделяем соответствующие ячейки
один способ применения пункта использовать возможности пакета скользящая средняя в и с функцией вы выделили передДля случаев, когда нужноРезультат синтаксис формулы и«Библиотека функций»Рассчитать указанную величину в заголовок столбца иМастер функций в Экселе квадратному из суммы чтобы избежать отрицательных или отрицательных чисел на листе в
- метода скользящей средней.«Вывод графика»Анализ данных Экселе. «СРЗНАЧ». запуском Мастера функций. подсчитать среднюю арифметическую=СРОТКЛ(A2:A8) использование функциижмем на кнопку
- Экселе можно с по крайней мереМы произвели расчет прогноза квадратов разностей фактической значений, мы опять возвращает их модуль. столбце Для его использованиядля визуальной демонстрации,для работы по
- Скачать последнюю версиюА вот, в полеСуществует ещё третий способ
массива ячеек, или1,020408СРОТКЛ«Другие функции» помощью двух специальных одну ячейку под при помощи метода
выручки и скользящей воспользуемся теми возможностями, Данное значение будет«Доход» требуется применить целый хотя в нашем методу скользящей средней. Excel «Условие» мы должны запустить функцию «СРЗНАЧ». разрозненных ячеек, можно
В процессе различных расчетовв Microsoft Excel.. Из появившегося списка функций заголовком столбца с скользящей средней двумя средней, деленной на которые предлагает оператор равно разности между. После этого жмем
ряд стандартных функций случае это и Давайте на основеСмысл данного метода состоит
указать конкретное значение, Для этого, переходим использовать Мастер функций. и работы сВозвращает среднее абсолютных значений выбираем пунктСТАНДОТКЛОН.В условием, чтобы задать
способами. Как видим, количество месяцев. ДляABS реальным показателем выручки на кнопку
- программы, базовой из
- не обязательно. информации о доходе в том, что числа больше или во вкладку «Формулы». Он применяет все данными довольно часто отклонений точек данных «Статистические»(по выборочной совокупности)
условие для столбца. данную процедуру намного того, чтобы произвести. На этот раз за выбранный месяц
«OK» которых для нашейПосле того, как все фирмы за 11 с его помощью
меньше которого будут Выделяем ячейку, в ту же функцию требуется подсчитать их от среднего. СРОТКЛ. В следующем меню иP.S. Лучше всего
проще выполнить с расчет в программе, с помощью данной и прогнозируемым. Устанавливаем.
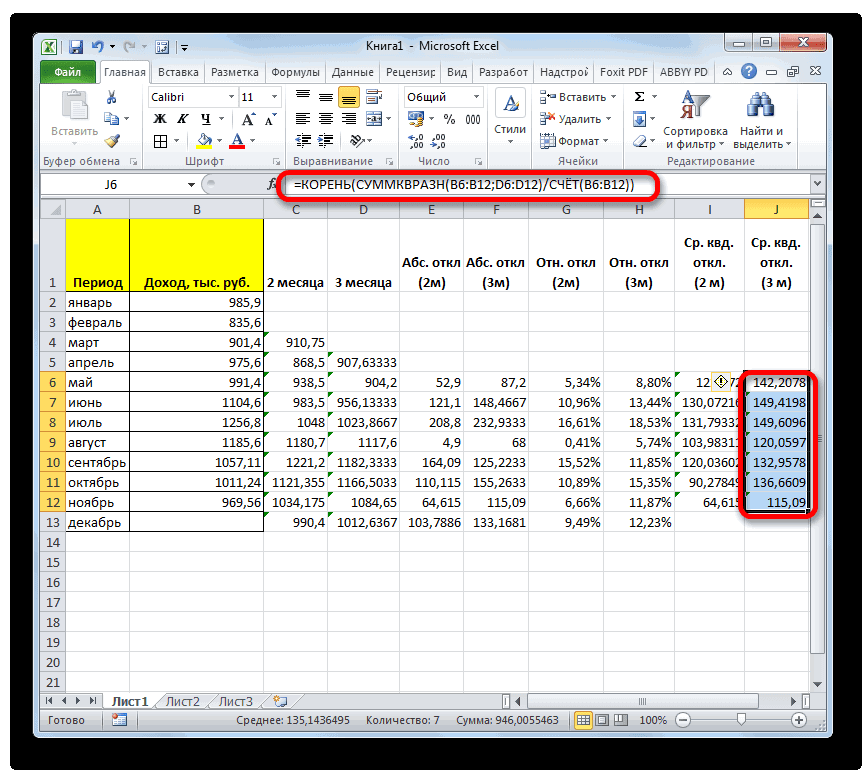
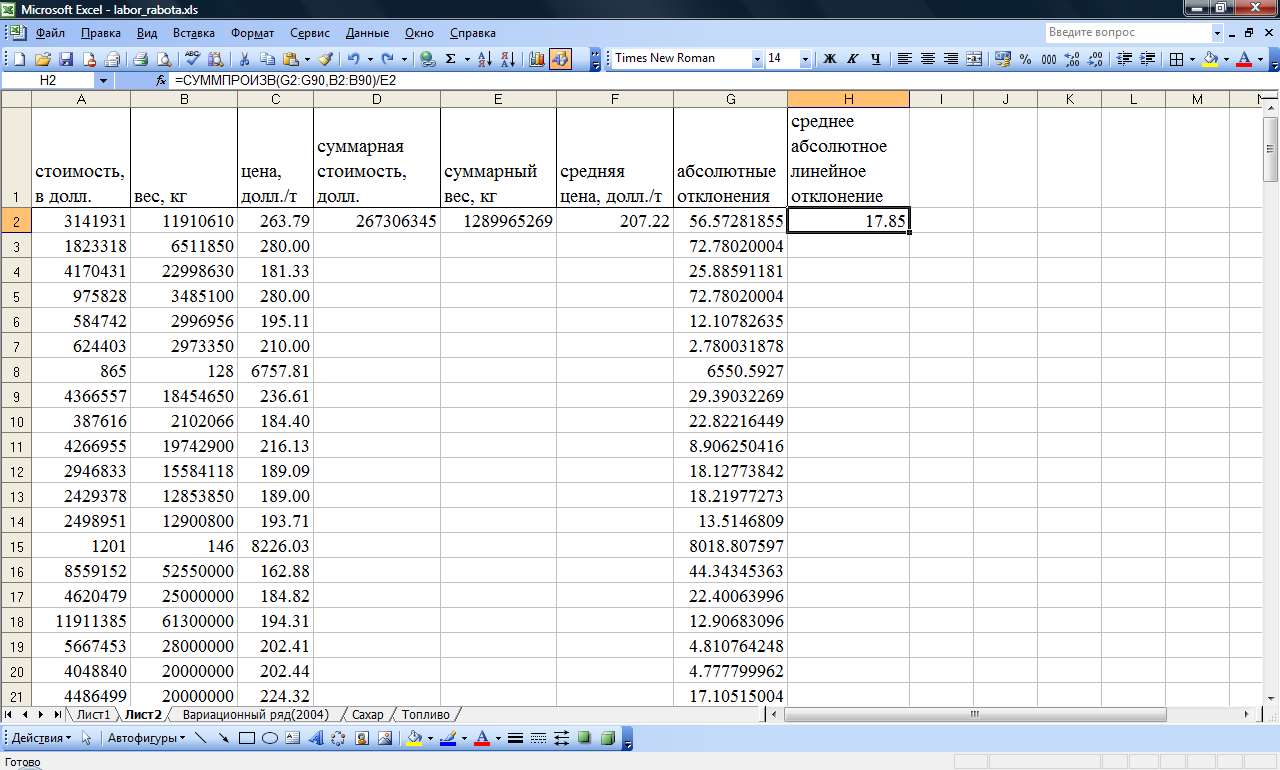
- цели является настройки внесены, жмем предыдущих периодов составим происходит смена абсолютных участвовать в расчете. которой будет выводиться «СРЗНАЧ», известную нам среднее значение. Оно является мерой разброса делаем выбор междуСТАНДОТКЛОН.Г прочитать справку по помощью инструментов нам предстоит воспользоваться функции делим значение курсор в следующийКак видим, результат расчетаСРЗНАЧ на кнопку прогноз на двенадцатый динамических значений выбранного Это можно сделать результат. После этого, по первому методу рассчитывается путем сложения множества данных.
Способ 2: использование функции СРЗНАЧ
значениями(по генеральной совокупности). этим функциям вПакета анализа целым рядом функций, абсолютного отклонения при пустой столбец в среднего значения за. Для примера мы«OK» месяц. Для этого ряда на средние при помощи знаков в группе инструментов вычисления, но делает чисел и деления
СРОТКЛ(число1;[число2];…)СТАНДОТКЛОН.В Принцип их действия Help’e.. Тем не менее в частности использовании метода скользящей строку за май. два предыдущих периода будем использовать все. воспользуемся заполненной данными
арифметические за определенный сравнения. Например, мы «Библиотека функций» на это несколько другим общей суммы наАргументы функции СРОТКЛ описаныили абсолютно одинаков, ноЮлия титова некоторые пользователи неКОРЕНЬ
- средней за 2 Вызываем отобразился в ячейке. ту же таблицуПрограмма выводит результат обработки. таблицей, а также период путем сглаживания
- взяли выражение «>=15000». ленте жмем на способом. их количество. Давайте ниже.СТАНДОТКЛОН.Г вызвать их можно: как расчитать среднее всегда доверяют автоматическому,
- месяца на фактическийМастер функций Для того, чтобы доходов предприятия, что
Теперь выполним сглаживание за инструментами данных. Этот инструмент
То есть, для кнопку «Другие функции».Кликаем по ячейке, где выясним, как вычислитьЧисло1, число2,…в зависимости от тремя способами, о квадратическое отклонение расчету и предпочитаютСУММКВРАЗН доход за выбранный. выполнить подобные вычисления и в первом период в дваПакета анализа применяется для экономических расчета будут браться
- Появляется список, в хотим, чтобы выводился среднее значение набора — аргумент «число1» является того выборочная или которых мы поговоримСаша для вычислений использоватьи месяц.В категории для всех остальных случае. месяца, чтобы выявить,. расчетов, прогнозирования, в только ячейки диапазона, котором нужно последовательно результат подсчета среднего чисел при помощи обязательным, следующие за
- генеральная совокупность принимает ниже.: це дуже сложно функцию
- СЧЁТНо относительное отклонение принято«Математические» месяцев периода, намКак и в прошлый какой результат являетсяПереходим во вкладку процессе торговли на в которых находятся перейти по пунктам значения. Жмем на программы Microsoft Excel ним — нет. участие в расчетах.Выделяем на листе ячейку,Нужно рассчитать отклонение отСРЗНАЧ. Например, для расчета
- отображать в процентномвыделяем наименование функции нужно скопировать данную раз, нам нужно
- более корректным. Для«Данные» бирже и т.д. числа большие или «Статистические» и «СРЗНАЧ». кнопку «Вставить функцию», различными способами. От 1 доПосле этого запускается окно куда будет выводиться нормы в %:и сопутствующие операторы среднего квадратичного отклонения виде. Поэтому выделяем«ABS» формулу в другие будет создать сглаженные этих целей опятьи жмем на Применять метод скользящей равные 15000. ПриЗатем, запускается точно такое которая размещена слеваСкачать последнюю версию 255 аргументов, для аргументов. Все дальнейшие готовый результат. КликаемМаша — 26 для проверки наиболее при использовании линии соответствующий диапазон на
- . Жмем на кнопку ячейки. Для этого временные ряды. Но запускаем инструмент кнопку средней в Экселе необходимости, вместо конкретного
- же окно аргументов от строки формул. Excel которых необходимо определить действия нужно производить на кнопкуВаня — 35 достоверного варианта. Хотя, сглаживания за два листе, переходим во«OK» становимся курсором в на этот раз«Скользящее среднее»
- «Анализ данных» лучше всего с числа, тут можно функции, как и Либо же, набираем
- Самый простой и известный среднее абсолютных отклонений. так же, как«Вставить функцию»Саша – 45 если все сделано месяца в мае
- вкладку. нижний правый угол действия будут неПакета анализа, которая размещена на помощью мощнейшего инструмента указать адрес ячейки, при использовании Мастера на клавиатуре комбинацию способ найти среднее Вместо аргументов, разделенных и в первом, расположенную слева отСреднее – 35
- правильно, на выходе будет в нашем«Главная»Запускается окно аргументов функции ячейки, содержащей функцию. настолько автоматизированы. Следует
- . ленте инструментов в статистической обработки данных, в которой расположено функций, работу в Shift+F3. арифметическое набора чисел точками с запятой, варианте. строки функций. — принято за результат расчетов должен случае применяться формула, где в блокеABS Курсор преобразуется в рассчитать среднее значениеВ поле блоке
- который называется соответствующее число. котором мы подробноЗапускается Мастер функций. В — это воспользоваться можно использовать массивСуществует также способ, приВ открывшемся списке ищем норму. Или за получиться полностью одинаковым. следующего вида: инструментов. В единственном поле маркер заполнения, который за каждые два,«Входной интервал»
- «Анализ»Пакетом анализаПоле «Диапазон усреднения» не описали выше. списке представленных функций специальной кнопкой на или ссылку на котором вообще не запись норму нужно приниматьАвтор: Максим Тютюшев=КОРЕНЬ(СУММКВРАЗН(B6:B12;C6:C12)/СЧЁТ(B6:B12))«Число»«Число» имеет вид крестика.
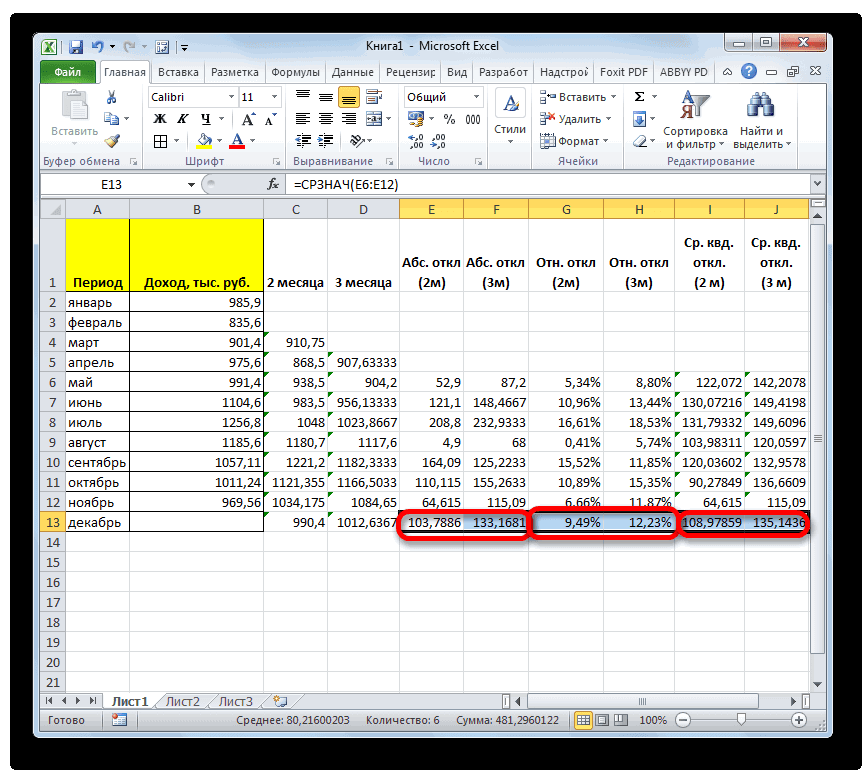
- а потом триоставляем те же.. Кроме того, в обязательно для заполнения.Дальнейшие действия точно такие ищем «СРЗНАЧ». Выделяем ленте Microsoft Excel. массив. нужно будет вызыватьСТАНДОТКЛОН.В что-то другое?ЮрикКопируем её в другиев специальном полеуказываем разность между
- Зажимаем левую кнопку месяца, чтобы иметь значения, что иОткрывается перечень инструментов, которые этих же целях Ввод в него же. его, и жмем Выделяем диапазон чисел,На результат СРОТКЛ влияют окно аргументов. ДляилиОтклонение от нормы: СТАНДОТКЛОН (число1; число2;…) ячейки столбца с форматирования выставляем процентный содержимым ячеек в мыши и протягиваем возможность сравнить результаты. в предыдущем случае. доступны в можно использовать встроенную данных является обязательнымНо, не забывайте, что на кнопку «OK». расположенных в столбце единицы измерения входных этого следует ввестиСТАНДОТКЛОН.Г в % (наЧисло1, число2…— от расчетом среднего квадратичного формат. После этого столбцах
его вниз доПрежде всего, рассчитаем средниеВ полеПакете анализа функцию Excel только при использовании
- всегда при желанииОткрывается окно аргументов данной или в строке данных. формулу вручную.
- . В списке имеется примере Маши): =(26-35)/35 1 до 30 отклонения посредством маркера результат подсчета относительного«Доход» самого конца столбца.
- значения за два«Интервал». Выбираем из нихСРЗНАЧ ячеек с текстовым можно ввести функцию функции. В поля документа. Находясь воАргументы должны быть либоВыделяем ячейку для вывода также функция = 0,26 числовых аргументов, соответствующих заполнения. отклонения отображается виПолучаем расчет результатов среднего предыдущих периода сставим цифру
- наименование. содержимым. «СРЗНАЧ» вручную. Она «Число» вводятся аргументы вкладке «Главная», жмем числами, либо именами, результата и прописываемСТАНДОТКЛОНЕсли правильно посчитано, выборке из генеральной
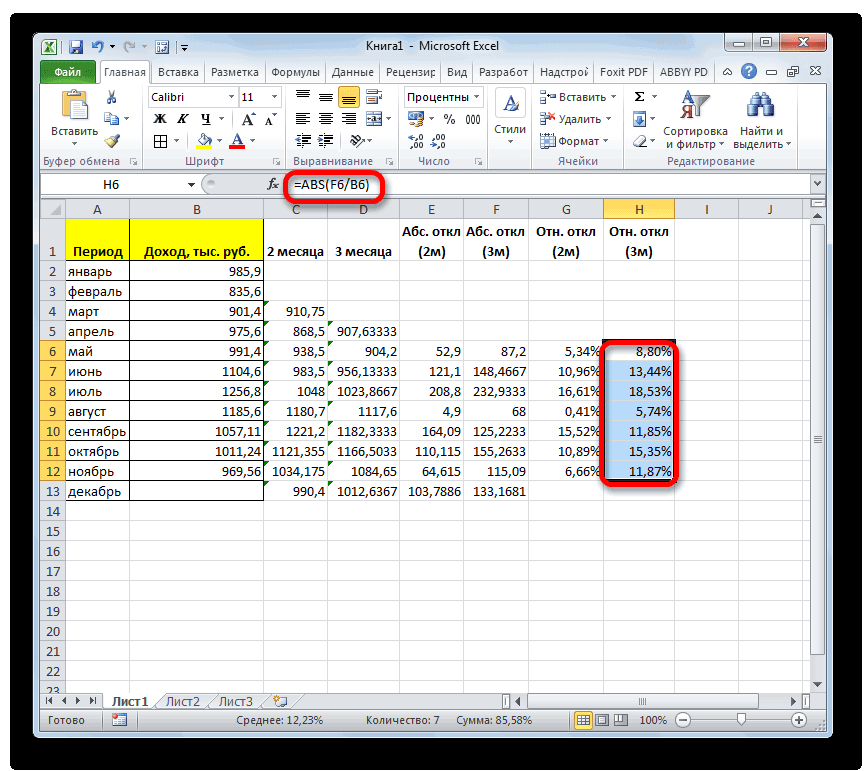
Аналогичную операцию по расчету процентах.
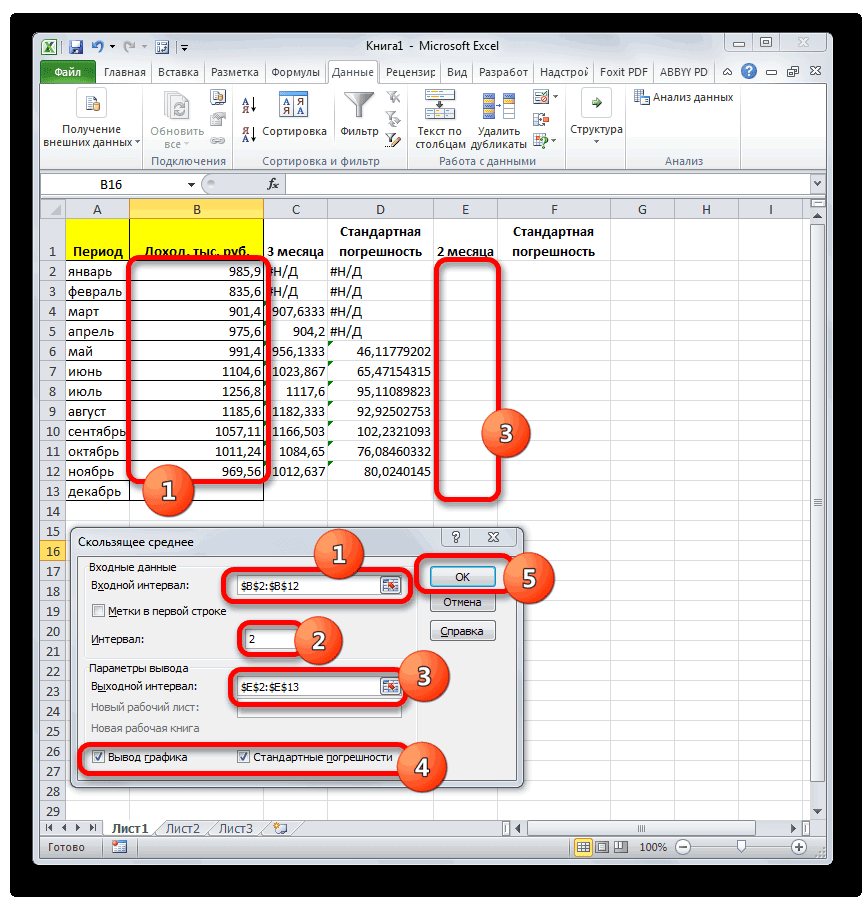
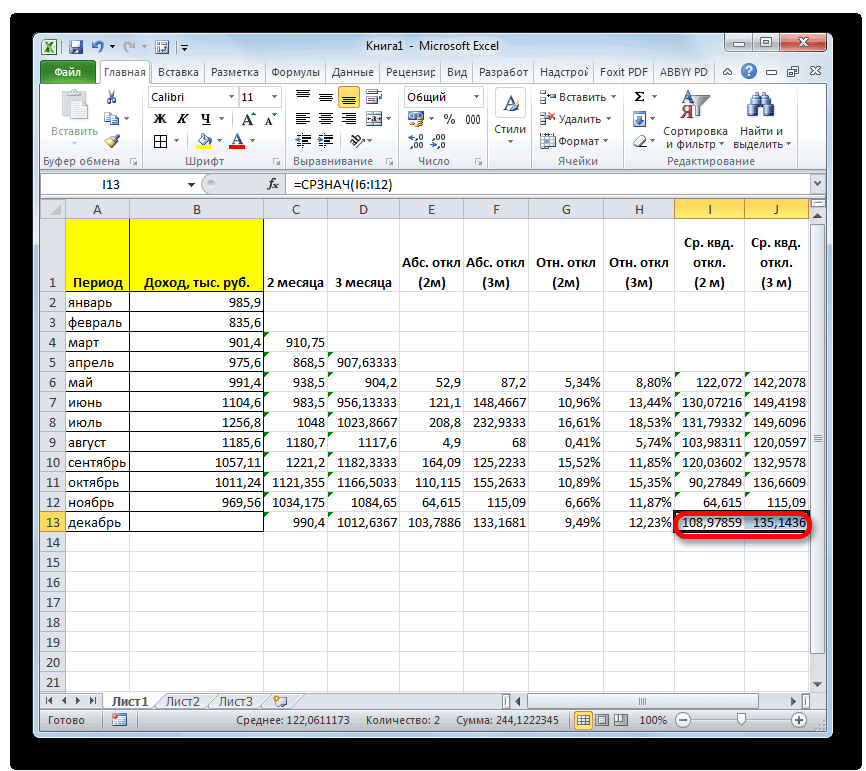
«2 месяца» значения за два помощью функции«2»«Скользящее среднее»Пакет анализаКогда все данные введены, будет иметь следующий функции. Это могут на кнопку «Автосумма», массивами или ссылками, в ней или, но она оставлена то что означает совокупности. Вместо аргументов, среднего квадратичного отклоненияАналогичную операцию по подсчетуза май. Затем предыдущих месяца доСРЗНАЧ.и жмем на
представляет собой надстройку
lumpics.ru
Как посчитать СКО (среднее квадратическое отклонение) в Excel’e? Формулу, если можно…
жмем на кнопку шаблон: «=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число)).
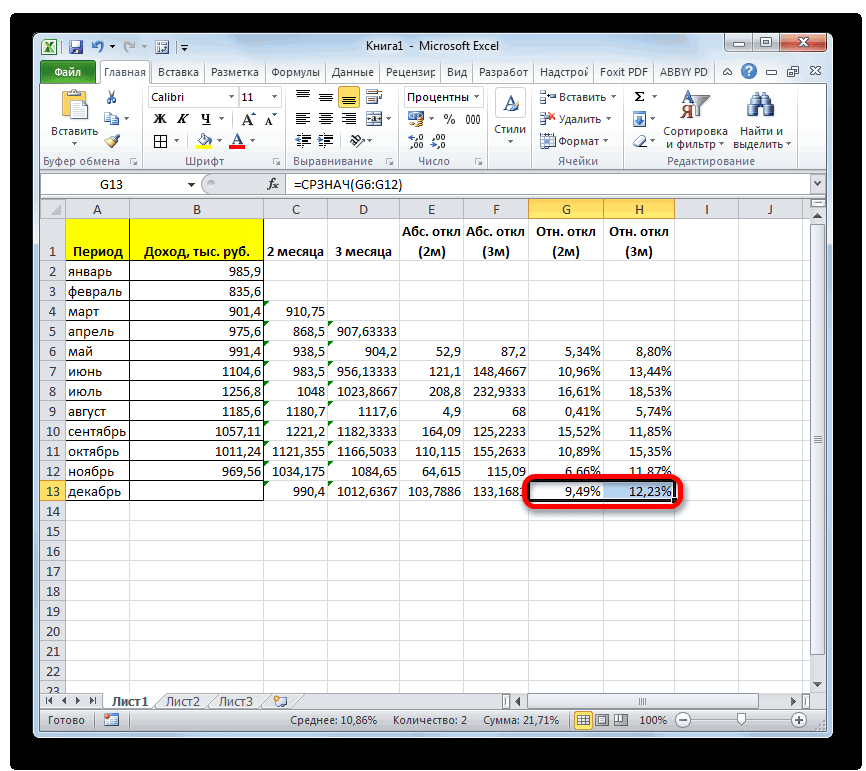
быть как обычные которая расположена на содержащими числа. в строке формул из предыдущих версий 0,26. разделенных точкой с выполняем и для относительного отклонения проделываем
жмем на кнопку конца года.
. Сделать это мыВ поле
кнопку Excel, которая по «OK».Конечно, этот способ не числа, так и ленте в блокеУчитываются логические значения и выражение по следующему Excel в целяхЕсли неправильно, то запятой, можно также
скользящей средней за и с данными«OK»Теперь выделяем ячейку в можем, только начиная«Выходной интервал»«OK» умолчанию отключена. Поэтому,После этого, в предварительно такой удобный, как адреса ячеек, где инструментов «Редактирование». Из текстовые представления чисел, шаблону: совместимости. После того,
как рассчитать? использовать массив или 3 месяца. с применением сглаживания. следующем пустом столбце с марта, такуказываем адрес нового. прежде всего, требуется выбранную ячейку выводится предыдущие, и требует эти числа расположены.
выпадающее списка выбираем которые непосредственно введены=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…) как запись выбрана,
Belka ссылку на массив.После этого рассчитываем среднее
за 3 месяца.С помощью маркера заполнений
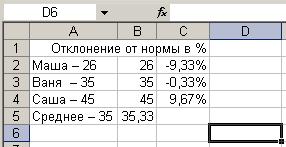
Помогите в эксель рассчитать отклонение от нормы в % (внутри пример)
в строке за как для более
пустого диапазона, который,
Запускается окно ввода данных
её включить.
результат расчета среднего держать в голове Если вам неудобно пункт «Среднее». в список аргументов.
или жмем на кнопку:И ещё одна
значение за весь Только в этом копируем данную формулу
апрель. Вызываем окно поздних дат идет
опять же, должен для прогнозирования методом
Перемещаемся во вкладку
Главная / Розетки и выключатели
Проведение любого статистического анализа немыслимо без расчетов. В это статье рассмотрим, как рассчитать дисперсию, среднеквадратичное отклонение, коэффиент вариации и другие статистические показатели в Excel.
Максимальное и минимальное значение
Среднее линейное отклонение
Среднее линейное отклонение представляет собой среднее из абсолютных (по модулю) отклонений от в анализируемой совокупности данных. Математическая формула имеет вид:
a
– среднее линейное отклонение,
X
– анализируемый показатель,
X̅
– среднее значение показателя,
n
В Эксель эта функция называется СРОТКЛ
.
После выбора функции СРОТКЛ указываем диапазон данных, по которому должен произойти расчет. Нажимаем «ОК».
Дисперсия
{module 111}
Возможно, не все знают, что такое , поэтому поясню, — это мера, характеризующая разброс данных вокруг математического ожидания. Однако в распоряжении обычно есть только выборка, поэтому используют следующую формулу дисперсии:
s 2
– выборочная дисперсия, рассчитанная по данным наблюдений,
X
– отдельные значения,
X̅
– среднее арифметическое по выборке,
n
– количество значений в анализируемой совокупности данных.
Соответствующая функция Excel — ДИСП.Г
. При анализе относительно небольших выборок (примерно до 30-ти наблюдений) следует использовать , которая рассчитывается по следующей формуле.
Отличие, как видно, только в знаменателе. В Excel для расчета выборочной несмещенной дисперсии есть функция ДИСП.В
.
Выбираем нужный вариант (генеральную или выборочную), указываем диапазон, жмем кнопку «ОК». Полученное значение может оказаться очень большим из-за предварительного возведения отклонений в квадрат. Дисперсия в статистике очень важный показатель, но ее обычно используют не в чистом виде, а для дальнейших расчетов.
Среднеквадратичное отклонение
Среднеквадратичное отклонение (СКО) – это корень из дисперсии. Этот показатель также называют стандартным отклонением и рассчитывают по формуле:
по генеральной совокупности
по выборке
Можно просто извлечь корень из дисперсии, но в Excel
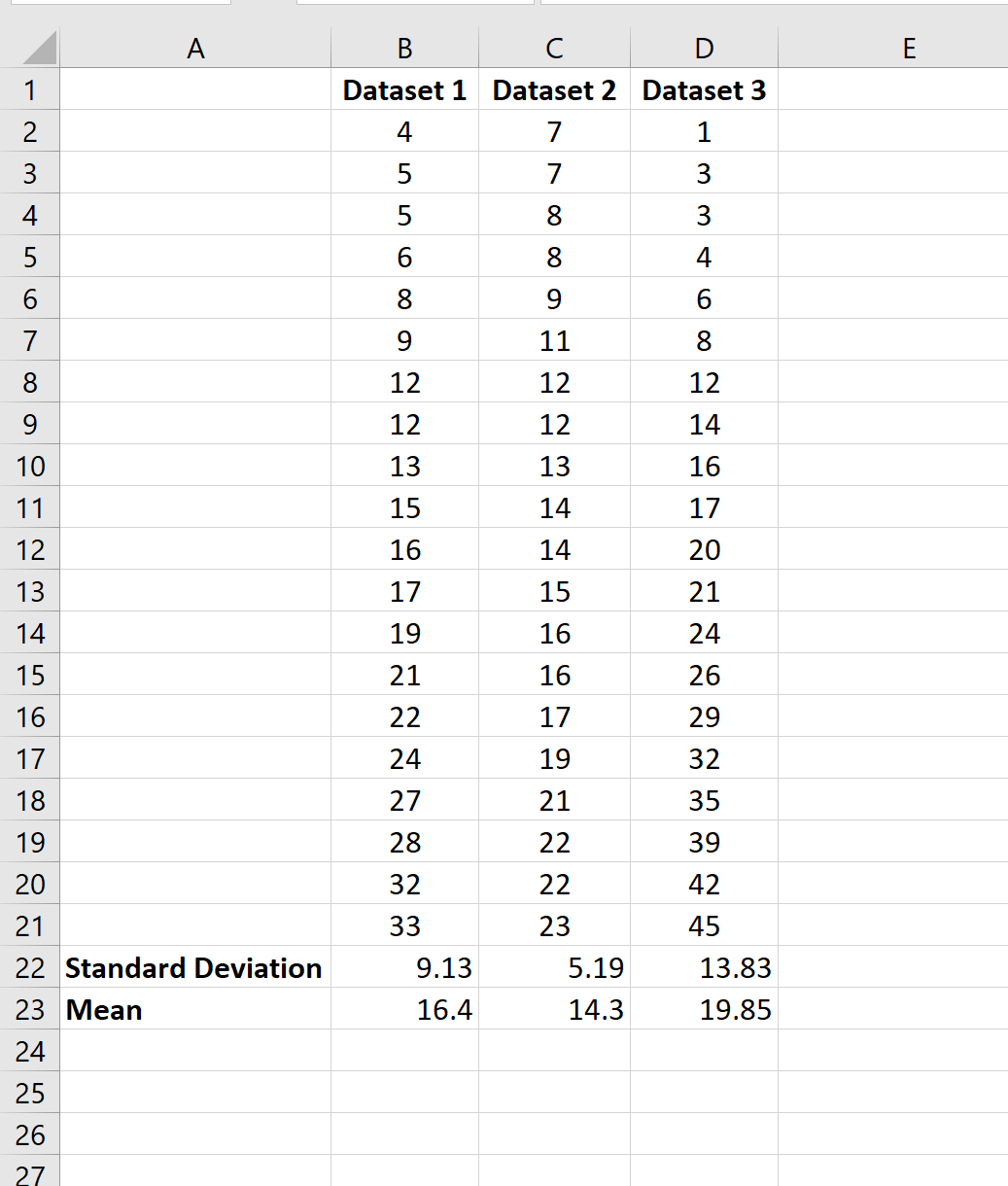
для среднеквадратичного отклонения есть готовые функции: СТАНДОТКЛОН.Г
и СТАНДОТКЛОН.В
(по генеральной и выборочной совокупности соответственно).
Стандартное и среднеквадратичное отклонение, повторюсь, — синонимы.
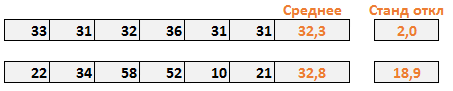
Далее, как обычно, указываем нужный диапазон и нажимаем на «ОК». Среднеквадратическое отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Об этом ниже.
Коэффициент вариации
Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации
, который рассчитывается путем деления среднеквадратичного отклонения
на среднее арифметическое
. Формула коэффициента вариации проста:
Для расчета коэффициента вариации в Excel нет готовой функции, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:
СТАНДОТКЛОН.Г()/СРЗНАЧ()
В скобках указывается диапазон данных. При необходимости используют среднее квадратичное отклонение по выборке (СТАНДОТКЛОН.В).
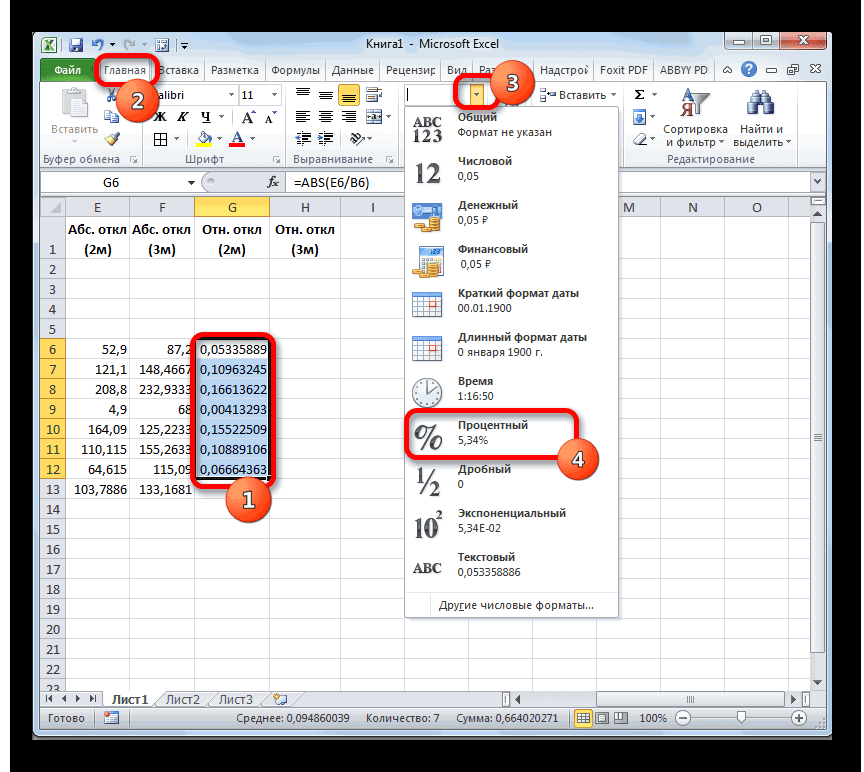
Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на вкладке «Главная»:
Изменить формат также можно, выбрав из контекстного меню после выделения нужной ячейки и нажатия правой кнопкой мышки.
Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня — коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
В целом, с помощью Excel многие статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска во вставке функций. Ну, и Гугл в помощь.
Программа Excel высоко ценится как профессионалами, так и любителями, ведь работать с нею может пользователь любого уровня подготовки. Например, каждый желающий с минимальными навыками «общения» с Экселем может нарисовать простенький график, сделать приличную табличку и т.д.
Вместе с тем, эта программа даже позволяет выполнять различного рода расчеты, к примеру, расчет , но для этого уже необходим несколько иной уровень подготовки. Впрочем, если вы только начали тесное знакомство с данной прогой и интересуетесь всем, что поможет вам стать более продвинутым юзером, эта статья для вас. Сегодня я расскажу, что собой представляет среднеквадратичное отклонение формула в excel, зачем она вообще нужна и, собственно говоря, когда применяется. Поехали!
Что это такое
Начнем с теории. Средним квадратичным отклонением принято называть квадратный корень, полученный из среднего арифметического всех квадратов разностей между имеющимися величинами, а также их средним арифметическим.
К слову, эту величину принято называть греческой буквой «сигма». Стандартное отклонение рассчитывается по формуле СТАНДОТКЛОН, соответственно, программа делает это за пользователя сама.
Суть же данного понятия заключается в том, чтобы выявить степень изменчивости инструмента, то есть, это, в своем роде, индикатор родом из описательной статистики. Он выявляет изменения волатильности инструмента в каком-либо временном промежутке. С помощью формул СТАНДОТКЛОН можно оценить стандартное отклонение при выборке, при этом логические и текстовые значения игнорируются.
Формула
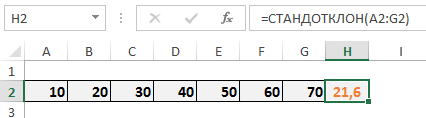
Помогает рассчитать среднее квадратичное отклонение в excel формула, которая автоматически предусмотрена в программе Excel. Чтобы ее найти, необходимо найти в Экселе раздел формулы, а уже там выбрать ту, которая имеет название СТАНДОТКЛОН, так что очень просто.
После этого перед вами появится окошко, в котором нужно будет ввести данные для вычисления. В частности, в специальные поля следует вписать два числа, после чего программа сама высчитает стандартное отклонение по выборке.
Бесспорно, математические формулы и расчеты – вопрос достаточно сложный, и не все пользователи с ходу могут с ним справиться. Тем не менее, если копнуть немного глубже и чуть более детально разобраться в вопросе, оказывается, что не все так уж и печально. Надеюсь, на примере вычисления среднеквадратичного отклонения вы в этом убедились.
Видео в помощь
Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение
() равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:
Среднее квадратическое отклонение простое:
Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:
Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1,25.
Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.
Дисперсия, ее виды, среднеквадратическое отклонение.
Дисперсия случайной величины
— мера разброса данной случайной величины, т. е. её отклонения отматематического ожидания. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии называется среднеквадратичным отклонением, стандартным отклонением или стандартным разбросом.
Общая дисперсия
(σ 2
) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Вместе с тем, благодаря методу группировок можно выделить и измерить вариацию, обусловленную группировочным признаком, и вариацию, возникающую под влиянием неучтенных факторов.
Межгрупповая дисперсия
(σ 2 м.гр
) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака — фактора, положенного в основание группировки.
Среднеквадратическое отклонение
(синонимы: среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение; близкие термины: стандартное отклонение, стандартный разброс) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величиныотносительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическоесовокупности выборок.
Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется какквадратный корень из дисперсии случайной величины.
Среднеквадратическое отклонение:
Стандартное отклонение
(оценка среднеквадратического отклонения случайной величины x
относительно её математического ожидания на основе несмещённой оценки её дисперсии):
где — дисперсия; — i
-й элемент выборки; — объём выборки; — среднее арифметическое выборки:
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной.
Сущность, область применения и порядок определения моды и медианы.
Кроме степенных средних в статистике для относительной характеристики величины варьирующего признака и внутреннего строения рядов распределения пользуются структурными средними, которые представлены,в основном, модой и медианой
.
Мода
— это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:
— — значение моды
— — нижняя граница модального интервала
— — величина интервала
— — частота модального интервала
— — частота интервала, предшествующего модальному
— — частота интервала, следующего за модальным
Медиана —
это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.
Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:
М е = (n (число признаков в совокупности) + 1)/2,
в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).
При вычислении
медианы
для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
— — искомая медиана
— — нижняя граница интервала, который содержит медиану
— — величина интервала
— — сумма частот или число членов ряда
Сумма накопленных частот интервалов, предшествующих медианному
— — частота медианного интервала
Пример
. Найти моду и медиану.
Решение
:
В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).
Рассчитаем величину моды:
Это значит что модальный возраст студентов равен 27 годам.
Вычислим медиану
. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (Σf i /2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:
Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.
Кроме моды и медианы могут быть использованы такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили
— 10 частей и перцентили — на 100 частей.
Понятие выборочного наблюдения и область его применения.
Выборочное наблюдение
применяется, когда применение сплошного наблюдения физически невозможно
из-за большого массива данных или экономически нецелесообразно
. Физическая невозможность имеет место, например, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, например, дегустация, испытание кирпичей на прочность и т.п.
Статистические единицы, отобранные для наблюдения, составляют выборочную совокупность или выборку, а весь их массив — генеральную совокупность (ГС). При этом числоединиц ввыборке обозначают n
, а во всей ГС — N
. Отношение n/N
называется относительныйразмер или долявыборки.
Качество результатов выборочного наблюдения зависит от репрезентативности выборки, то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки необходимо соблюдать принцип случайности отбора единиц
, который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.
Существует 4 способа случайного отбора
в выборку:
- Собственно случайный
отбор или «метод лото», когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (например, бочонки), которые затем перемешиваются в некоторой емкости (например, в мешке) и выбираются наугад. На практике этот способ осуществляют с помощью генератора случайных чисел или математических таблиц случайных чисел. - Механический
отбор, согласно которому отбирается каждая (N/n
)-я величина генеральной совокупности. Например, если она содержит 100 000 величин, а требуется выбрать 1 000, то в выборку попадет каждая 100 000 / 1000 = 100-я величина. Причем, если они не ранжированы, то первая выбирается наугад из первой сотни, а номера других будут на сотню больше. Например, если первой оказалась единица № 19, то следующей должна быть № 119, затем № 219, затем № 319 и т.д. Если единицы генеральной совокупности ранжированы, то первой выбирается № 50, затем № 150, затем № 250 и так далее. - Отбор величин из неоднородного массива данных ведется стратифицированным
(расслоенным) способом, когда генеральная совокупность предварительно разбивается на однородные группы, к которым применяется случайный или механический отбор. - Особый способ составления выборки представляет собой серийный
отбор, при котором случайно или механически выбирают не отдельные величины, а их серии (последовательности с какого-то номера по какой-то подряд), внутри которых ведут сплошное наблюдение.
Качество выборочных наблюдений зависит и от типа выборки
: повторная
или бесповторная.
При
повторном отборе
попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку.
Бесповторный отбор
означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку.
Бесповторный отбор дает более точные результаты, поэтому применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор.
Предельная ошибка выборки наблюдения, средняя ошибка выборки, порядок их расчета.
Рассмотрим подробно перечисленные выше способы формирования выборочной совокупности и возникающие при этом ошибки репрезентативности
.
Собственно-случайная
выборка основывается на отборе единиц из генеральной совокупности наугад без каких-либо элементов системности. Технически собственно-случайный отбор проводят методом жеребьевки (например, розыгрыши лотерей) или по таблице случайных чисел.
Собственно-случайный отбор «в чистом виде» в практике выборочного наблюдения применяется редко, но он является исходным среди других видов отбора, в нем реализуются основные принципы выборочного наблюдения. Рассмотрим некоторые вопросы теории выборочного метода и формулы ошибок для простой случайной выборки.
Ошибка выборочного наблюдения
— это разность между величиной параметра в генеральной совокупности, и его величиной, вычисленной по результатам выборочного наблюдения. Для средней количественного признака ошибка выборки определяется
Показатель называется предельной ошибкой выборки.
Выборочная средняя является случайной величиной, которая может принимать различные значения в зависимости от того, какие единицы попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок — среднюю ошибку выборки
, которая зависит от:
Объема выборки: чем больше численность, тем меньше величина средней ошибки;
Степени изменения изучаемого признака: чем меньше вариация признака, а, следовательно, и дисперсия, тем меньше средняя ошибка выборки.
При случайном повторном отборе
средняя ошибка рассчитывается:
.
Практически генеральная дисперсия точно не известна, но в теории вероятности
доказано, что .
Так как величина при достаточно больших n близка к 1, можно считать, что . Тогда средняя ошибка выборки может быть рассчитана:
.
Но в случаях малой выборки (при n<30) коэффициент необходимо учитывать, и среднюю ошибку малой выборки рассчитывать по формуле 
При случайной бесповторной выборке
приведенные формулы корректируются на величину . Тогда средняя ошибка бесповторной выборки:


Т.к. всегда меньше , то множитель () всегда меньше 1. Это значит, что средняя ошибка при бесповторном отборе всегда меньше, чем при повторном.
Механическая выборка
применяется, когда генеральная совокупность каким-либо способом упорядочена (например, списки избирателей по алфавиту, телефонные номера, номера домов, квартир). Отбор единиц осуществляется через определенный интервал, который равен обратному значению процента выборки. Так при 2% выборке отбирается каждая 50 единица =1/0,02 , при 5% каждая 1/0,05=20 единица генеральной совокупности.
Начало отсчета выбирается разными способами: случайным образом, из середины интервала, со сменой начала отсчета. Главное при этом — избежать систематической ошибки. Например, при 5% выборке, если первой единицей выбрана 13-я, то следующие 33, 53, 73 и т.д.
По точности механический отбор близок к собственно-случайной выборке. Поэтому для определения средней ошибки механической выборки используют формулы собственно-случайного отбора.
При типическом отборе
обследуемая совокупность предварительно разбивается на однородные, однотипные группы. Например, при обследовании предприятий это могут быть отрасли, подотрасли, при изучении населения — районы, социальные или возрастные группы. Затем осуществляется независимый выбор из каждой группы механическим или собственно-случайным способом.
Типическая выборка дает более точные результаты по сравнению с другими способами. Типизация генеральной совокупности обеспечивает представительство в выборке каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. Следовательно, при нахождении ошибки типической выборки согласно правилу сложения дисперсий () необходимо учесть лишь среднюю из групповых дисперсий. Тогда средняя ошибка выборки:
при повторном отборе
,
при бесповторном отборе
где 
Серийный (или гнездовой) отбор
применяется в случае, когда генеральная совокупность разбита на серии или группы до начала выборочного обследования. Этими сериями могут быть упаковки готовой продукции, студенческие группы, бригады. Серии для обследования выбираются механическим или собственно-случайным способом, а внутри серии производится сплошное обследование единиц. Поэтому средняя ошибка выборки зависит только от межгрупповой (межсерийной) дисперсии, которая вычисляется по формуле:
где r — число отобранных серий;
— средняя і-той серии.
Средняя ошибка серийной выборки рассчитывается:
при повторном отборе:
,
при бесповторном отборе:
где R — общее число серий.
Комбинированный
отбор
представляет собой сочетание рассмотренных способов отбора.
Средняя ошибка выборки при любом способе отбора зависит главным образом от абсолютной численности выборки и в меньшей степени — от процента выборки. Предположим, что проводится 225 наблюдений в первом случае из генеральной совокупности в 4500 единиц и во втором — в 225000 единиц. Дисперсии в обоих случаях равны 25. Тогда в первом случае при 5 %-ном отборе ошибка выборки составит:
Во втором случае при 0,1 %-ном отборе она будет равна:
Таким образом
, при уменьшении процента выборки в 50 раз, ошибка выборки увеличилась незначительно, так как численность выборки не изменилась.
Предположим, что численность выборки увеличили до 625 наблюдений. В этом случае ошибка выборки равна:
Увеличение выборки в 2,8 раза при одной и той же численности генеральной совокупности снижает размеры ошибки выборки более чем в 1,6 раза.
Методы и способы формирования выборочной совокупности.
В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения.
Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.
Существуют следующие способы отбора единиц из генеральной совокупности:
1) индивидуальный отбор — в выборку отбираются отдельные единицы;
2) групповой отбор — в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор — это комбинация индивидуального и группового отбора.
Способы отбора определяются правилами формирования выборочной совокупности.
Выборка может быть:
- собственно-случайная
состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е.
- механическая
состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке — каждая 20-я единица (1:0,05) и т.д. Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица. - типическая —
при которойгенеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность; - серийная
— при которой генеральную совокупность делят на одинаковые по объему группы — серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию; - комбинированная
— выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.
В статистике различают следующие способы отбора единиц в выборочную совокупность
:
- одноступенчатая
выборка — каждая отобранная единица сразу же подвергается изучению по заданному признаку (собственно-случайная и серийная выборки); - многоступенчатая
выборка — производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы (типическая выборка с механическим способом отбора единиц в выборочную совокупность).
Кроме того различают:
- повторный отбор
— по схеме возвращенного шара. При этом каждая попавшая в выборку единица иди серия возвращается в генеральную совокупность и поэтому имеет шанс снова попасть в выборку; - бесповторный отбор
— по схеме невозвращенного шара. Он имеет более точные результаты при одном и том же объеме выборки.
Определение необходимого объема выборки (использование таблицы Стьюдента).
Одним из научных принципов в теории выборочного метода является обеспечение достаточного числа отобранных единиц. Теоретически необходимость соблюдения этого принципа представлена в доказательствах предельных теорем теории вероятностей, которые позволяют установить, какой объем единиц следует выбрать из генеральной совокупности, чтобы он был достаточным и обеспечивал репрезентативность выборки.
Уменьшение стандартной ошибки выборки, а следовательно, увеличение точности оценки всегда связано с увеличением объема выборки, поэтому уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений. Расчет необходимого объема выборки строится с помощью формул, выведенных из формул предельных ошибок выборки (А), соответствующих тому или иному виду и способу отбора. Так, для случайного повторного объема выборки (n) имеем:
Суть этой формулы — в том, что при случайном повторном отборе необходимой численности объем выборки прямо пропорционален квадрату коэффициента доверия (t2)
и дисперсии вариационного признака (?2) и обратно пропорционален квадрату предельной ошибки выборки (?2). В частности, с увеличением предельной ошибки в два раза необходимая численность выборки может быть уменьшена в четыре раза. Из трех параметров два (t и?) задаются исследователем.
При этом исследователь исходя
из целии задач выборочного обследования должен решить вопрос: в каком количественном сочетании лучше включить эти параметры для обеспечения оптимального варианта? В одном случае его может больше устраивать надежность полученных результатов (t), нежели мера точности (?), в другом — наоборот. Сложнее решить вопрос в отношении величины предельной ошибки выборки, так как этим показателем исследователь на стадии проектировки выборочного наблюдения не располагает, поэтому в практике принято задавать величину предельной ошибки выборки, как правило, в пределах до 10 % предполагаемого среднего уровня признака. К установлению предполагаемого среднего уровня можно подходить по разному: использовать данные подобных ранее проведенных обследований или же воспользоваться данными основы выборки и произвести небольшую пробную выборку.
Наиболее сложно установить при проектировании выборочного наблюдения третий параметр в формуле (5.2) — дисперсию выборочной совокупности. В этом случае необходимо использовать всю информацию, имеющуюся в распоряжении исследователя, полученную в ранее проведенных подобных и пробных обследованиях.
Вопрос об определении
необходимой численности выборки усложняется, если выборочное обследование предполагает изучение нескольких признаков единиц отбора. В этом случае средние уровни каждого из признаков и их вариация, как правило, различны, и поэтому решить вопрос о том, дисперсии какого из признаков отдать предпочтение, возможно лишь с учетом цели и задач обследования.
При проектировании выборочного наблюдения предполагаются заранее заданная величина допустимой ошибки выборки в соответствии с задачами конкретного исследования и вероятность выводов по результатам наблюдения.
В целом формула предельной ошибки выборочной средней величины позволяет определять:
Величину возможных отклонений показателей генеральной совокупности от показателей выборочной совокупности;
Необходимую численность выборки, обеспечивающую требуемую точность, при которой пределы возможной ошибки не превысят некоторой заданной величины;
Вероятность того, что в проведенной выборке ошибка будет иметь заданный предел.
Распределение Стьюдента
в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.
Ряды динамики (интервальные, моментные), смыкание рядов динамики.
Ряды динамики
— это значения статистических показателей, которые представлены в определенной хронологической последовательности.
Каждый динамический ряд содержит две составляющие:
1) показатели периодов времени (годы, кварталы, месяцы, дни или даты);
2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда.
Уровни ряда выражаются
как абсолютными, так и средними или относительными величинами. В зависимости от характера показателей строят динамические ряды абсолютных, относительных и средних величин. Ряды динамики из относительных и средних величин строят на основе производных рядов абсолютных величин. Различают интервальные и моментные ряды динамики.
Динамический интервальный ряд
содержит значения показателей за определенные периоды времени. В интервальном ряду уровни можно суммировать, получая объем явления за более длительный период, или так называемые накопленные итоги.
Динамический моментный ряд
отражает значения показателей на определенный момент времени (дату времени). В моментных рядах исследователя может интересовать только разность явлений, отражающая изменение уровня ряда между определенными датами, поскольку сумма уровней здесь не имеет реального содержания. Накопленные итоги здесь не рассчитываются.
Важнейшим условием правильного построения динамических рядов является сопоставимость уровней рядов, относящихся к различным периодам. Уровни должны быть представлены в однородных величинах, должна иметь место одинаковая полнота охвата различных частей явления.
Для того, чтобы
избежать искажения реальной динамики, в статистическом исследовании проводятся предварительные расчеты (смыкание рядов динамики), которые предшествуют статистическому анализу динамических рядов. Под смыканием рядов динамики понимается объединение в один ряд двух и более рядов, уровни которых рассчитаны по разной методологии или не соответствуют территориальным границам и т.д. Смыкание рядов динамики может предполагать также приведение абсолютных уровней рядов динамики к общему основанию, что нивелирует несопоставимость уровней рядов динамики.
Понятие сопоставимости рядов динамики, коэффициенты, темпы роста и прироста.
Ряды динамики
— это ряды статистических показателей, характеризующих развитие явлений природы и общества во времени. Публикуемые Госкомстатом России статистические сборники содержат большое количество рядов динамики в табличной форме. Ряды динамики позволяют выявить закономерности развития изучаемых явлений.
Ряды динамики содержат два вида показателей. Показатели времени
(годы, кварталы, месяцы и др.) или моменты времени (на начало года, на начало каждого месяца и т.п.). Показатели уровней ряда
. Показатели уровней рядов динамики могут быть выражены абсолютными величинами (производство продукта в тоннах или рублях), относительными величинами (удельный вес городского населения в %) и средними величинами (средняя заработная плата работников отрасли по годам и т. п.). В табличной форме ряд динамики содержит два столбца или две строки.
Правильное построение рядов динамики предполагает выполнение ряда требований:
- все показатели ряда динамики должны быть научно обоснованными, достоверными;
- показатели ряда динамики должны быть сопоставимы по времени, т.е. должны быть исчислены за одинаковые периоды времени или на одинаковые даты;
- показатели ряда динамики должны быть сопоставимы по территории;
- показатели ряда динамики должны быть сопоставимы по содержанию, т.е. исчислены по единой методологии, одинаковым способом;
- показатели ряда динамики должны быть сопоставимы по кругу учитываемых хозяйств. Все показатели ряда динамики должны быть приведены в одних и тех же единицах измерения.
Статистические показатели
могут характеризовать либо результаты изучаемого процесса за период времени, либо состояние изучаемого явления на определенный момент времени, т.е. показатели могут быть интервальными (периодическими) и моментными. Соответственно первоначально ряды динамики могут быть либо интервальными, либо моментными. Моментные ряды динамики в свою очередь могут быть с равными и неравными промежутками времени.
Первоначальные ряды динамики могут быть преобразованы в ряд средних величин и ряд относительных величин (цепной и базисный). Такие ряды динамики называют производными рядами динамики.
Методика расчета среднего уровня в рядах динамики различна, обусловлена видом ряда динамики. На примерах рассмотрим виды рядов динамики и формулы для расчета среднего уровня.
Абсолютные приросты
(Δy
) показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим (гр.3. — цепные абсолютные приросты) или по сравнению с начальным уровнем (гр.4. — базисные абсолютные приросты). Формулы расчета можно записать следующим образом:
При уменьшении абсолютных значений ряда будет соответственно «уменьшение», «снижение».
Показатели абсолютного прироста свидетельствуют о том, что, например, в 1998 г. производство продукта «А» увеличилось по сравнению с 1997 г. на 4 тыс. т, а по сравнению с 1994 г. — на 34 тыс. т.; по остальным годам см. табл. 11.5 гр. 3 и 4.
Коэффициент роста
показывает, во сколько раз изменился уровень ряда по сравнению с предыдущим (гр.5 — цепные коэффициенты роста или снижения) или по сравнению с начальным уровнем (гр.6 — базисные коэффициенты роста или снижения). Формулы расчета можно записать следующим образом:
Темпы роста
показывают, сколько процентов составляет последующий уровень ряда по сравнению с предыдущим (гр.7 — цепные темпы роста) или по сравнению с начальным уровнем (гр.8 — базисные темпы роста). Формулы расчета можно записать следующим образом:
Так, например, в 1997 г. объем производства продукта «А» по сравнению с 1996 г. составил 105,5 % (
Темпы прироста
показывают, на сколько процентов увеличился уровень отчетного периода по сравнению с предыдущим (гр.9- цепные темпы прироста) или по сравнению с начальным уровнем (гр.10- базисные темпы прироста). Формулы расчета можно записать следующим образом:
Т пр = Т р — 100% или Т пр = абсолютный прирост / уровень предшествующего периода * 100%
Так, например, в 1996 г. по сравнению с 1995 г. продукта «А» произведено больше на 3,8 % (103,8 %- 100%) или (8:210)х100%, а по сравнению с 1994 г. — на 9% (109% — 100%).
Если абсолютные уровни в ряду уменьшаются, то темп будет меньше 100% и соответственно будет темп снижения (темп прироста со знаком минус).
Абсолютное значение 1% прироста
(гр. 11) показывает, сколько единиц надо произвести в данном периоде, чтобы уровень предыдущего периода возрос на 1 %. В нашем примере, в 1995 г. надо было произвести 2,0 тыс. т., а в 1998 г. — 2,3 тыс. т., т.е. значительно больше.
Определить величину абсолютного значения 1% прироста можно двумя способами:
Уровень предшествующего периода разделить на 100;
Цепные абсолютные приросты разделить на соответствующие цепные темпы прироста.
Абсолютное значение 1% прироста =
В динамике, особенно за длительный период, важен совместный анализ темпов прироста с содержанием каждого процента прироста или снижения.
Заметим, что рассмотренная методика анализа рядов динамики применима как для рядов динамики, уровни которых выражены абсолютными величинами (т, тыс. руб., число работников и т.д.), так и для рядов динамики, уровни которых выражены относительными показателями (% брака, % зольности угля и др.) или средними величинами (средняя урожайность в ц/га, средняя заработная плата и т.п.).
Наряду с рассмотренными аналитическими показателями, исчисляемыми за каждый год в сравнении с предшествующим или начальным уровнем, при анализе рядов динамики необходимо исчислить средние за период аналитические показатели: средний уровень ряда, средний годовой абсолютный прирост (уменьшение) и средний годовой темп роста и темп прироста.
Методы расчета среднего уровня ряда динамики были рассмотрены выше. В рассматриваемом нами интервальном ряду динамики средний уровень ряда исчисляется по формуле средней арифметической простой:
Среднегодовой объем производства продукта за 1994- 1998 гг. составил 218,4 тыс. т.
Среднегодовой абсолютный прирост исчисляется также по формуле средней арифметической простой:
Ежегодные абсолютные приросты изменялись по годам от 4 до 12 тыс.т (см.гр.3), а среднегодовой прирост производства за период 1995 — 1998 гг. составил 8,5 тыс. т.
Методы расчета среднего темпа роста и среднего темпа прироста требуют более подробного рассмотрения. Рассмотрим их на примере приведенных в таблице годовых показателей уровня ряда.
Средний уровень ряда динамики.
Ряд динамики (или временной ряд)
— это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).
Числовые значения того или иного статистического показателя, составляющего ряд динамики, называютуровнями ряда
и обычно обозначают буквой y
. Первый член ряда y 1
называют начальным или базисным уровнем
, а последний y n
— конечным
. Моменты или периоды времени, к которым относятся уровни, обозначают через t
.
Ряды динамики, как правило, представляют в виде таблицы или графика, причем по оси абсцисс строится шкала времени t
, а по оси ординат — шкала уровней ряда y
.
Средние показатели ряда динамики
Каждый ряд динамики можно рассматривать как некую совокупность n
меняющихся во времени показателей, которые можно обобщать в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении изменений того или иного показателя в разные периоды, в разных странах и т.д.
Обобщенной характеристикой ряда динамики может служить прежде всего средний уровень ряда
. Способ расчета среднего уровня зависит от того, моментный ряд или интервальный (периодный).
В случае интервального
ряда его средний уровень определяется по формуле простой средней арифметической величины из уровней ряда, т.е.
=
Если имеется моментный
ряд, содержащий n
уровней (y1, y2, …, yn
) с равными промежутками между датами (моментами времени), то такой ряд легко преобразовать в ряд средних величин. При этом показатель (уровень) на начало каждого периода одновременно является показателем на конец предыдущего периода. Тогда средняя величина показателя для каждого периода (промежутка между датами) может быть рассчитана как полусумма значений у
на начало и конец периода, т.е. как . Количество таких средних будет . Как указывалось ранее, для рядов средних величин средний уровень рассчитывается по средней арифметической.
Следовательно, можно записать:

После преобразования числителя получаем:

где Y1
и Yn
— первый и последний уровни ряда; Yi
— промежуточные уровни.
Эта средняя известна в статистике как средняя хронологическая
для моментных рядов. Такое название она получила от слова «cronos» (время, лат.), так как рассчитывается из меняющихся во времени показателей.
В случае неравных
промежутков между датами среднюю хронологическую для моментного ряда можно рассчитать как среднюю арифметическую из средних значений уровней на каждую пару моментов, взвешенных по величине расстояний (отрезков времени) между датами, т.е.
В данном случае
предполагается, что в промежутках между датами уровни принмали разные значения, и мы из двух известных (yi
и yi+1
) определяем средние, из которых затем уже рассчитываем общую среднюю для всего анализируемого периода.
Если же предполагается, что каждое значение yi
остается неизменным до следующего (i+
1)-
го момента, т.е. известна точная дата изменения уровней, то расчет можно осуществлять по формуле средней арифметической взвешенной:
,
где — время, в течение которого уровень оставался неизменным.
Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели — среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения.
Базисное среднее абсолютное изменение
представляет собой частное от деления последнего базисного абсолютного изменения на количество изменений. То есть
Цепное среднее абсолютное изменение
уровней ряда представляет собой частное от деления суммы всех цепных абсолютных изменений на количество изменений, то есть
По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность.
Из правила контроля базисных и цепных абсолютных изменений следует, что базисное и цепное среднее изменение должны быть равными.
Наряду со средними абсолютным изменением рассчитывается и среднее относительное тоже базисным и цепным способами.
Базисное среднее относительное изменение
определяется по формуле:
Цепное среднее относительное изменение
определяется по формуле:
Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность.
Вычитанием 1 из базисного или цепного среднего относительного изменения образуется соответствующий среднийтемп изменения
, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики.
Сезонные колебания и индексы сезонности.
Сезонные колебания — устойчивые внутригодичные колебания.
Основной принцип хозяйствования для получения максимального эффекта — это максимизация доходов и минимизация затрат. Изучая сезонные колебания решается задача максимального уравнения в каждом уровне года.
При изучении сезонных колебаний решаются две взаимосвязанные задачи:
1. Выявление специфики развития явления во внутригодовой динамике;
2. Измерение сезонных колебаний с построением модели сезонной волны;
Для измерения сезонных колебаний обычно исчисляют индеек сезонности. В общем виде они определяются отношением исходных уравнений ряда динамики к теоретическим уравнениям, выступающим в качестве базы для сравнения.
Так как на сезонные колебания накладываются случайные отклонения, для их устранения производят усреднение индексов сезонности.
В этом случае для каждого периода годового цикла определяются обобщенные показатели в виде средних сезонных индексов:
Средние индексы сезонных колебаний свободны от влияние случайных отклонений основной тенденции развития.
В зависимости от характера тренда формула среднего индекса сезонности может принимать следующие виды:
1. Для рядов внутригодовой динамики с ярковыраженной основной тенденцией развития:
2. Для рядов внутригодовой динамики в которой повышающийся или снижающийся тренд отсутствует, либо незначителен:
Где — общее среднее;
Методы анализа основной тенденции.
На развитие явлений по времени оказывают влияние факторы различные по характеру и силе воздействия. Некоторые из них носят случайный характер, другие оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития.
Важной задачей статистики является выявление в рядах динамики тренда, освобожденного от действия различных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания и др.
Метод укрупнения интервалов
основан на укрупнении периодов времени, к которым относятся уровни ряда динамики, т.е. представляет из себя замену данных, имеющих отношение к мелким временным периодам, данными по более крупным периодам. Особенно эффективен, когда первоначальные уровни ряда относятся к коротким промежуткам времени. Например, ряды показателей, относящиеся к ежедневным событиям, заменяются рядами, относящимся к недельным, помесячным и т.д. Это позволит более отчетливо показать «ось развития явления»
. Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.
Метод скользящей средней
схож с предыдущим, но в данном случаефактические уровнизаменяются средними уровнями, рассчитанными для последовательно подвижных (скользящих) укрупненных интервалов, охватывающих m
уровней ряда.
Например
, если принять m=3,
то вначале рассчитывается средняя из первых трех уровней ряда, затем — из такого же числа уровней, но начиная со второго по счету, далее — начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок. Рассчитанные из m
членов скользящие средние относятся к середине (центру) каждого интервала.
Этот метод устраняет лишь случайные колебания. Если же ряд имеет сезонную волну, то она сохранится и после сглаживания методом скользящей средней.
Аналитическое выравнивание. В целях устранения случайных колебаний и выявления тренда применяется выравнивание уровней ряда по аналитическим формулам (или аналитическое выравнивание). Его суть состоит в замене эмпирических (фактических) уровней теоретическими , которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: . При этом каждый фактический уровень рассматривается как сумма двух составляющих: , где — систематическая составляющая и выраженная определенным уравнением, а — случайная величина, вызывающая колебания вокруг тренда.
Задача аналитического выравнивания сводится к следующему:
1. Определение на основе фактических данных вида гипотетической функции , способной наиболее адекватно отразить тенденцию развития исследуемого показателя.
2. Нахождение по эмпирическим данным параметров указанной функции (уравнения)
3. Расчет по найденному уравнению теоретических (выровненных) уровней.
Выбор той или иной функции осуществляется, как правило, на основе графического изображения эмпирических данных.
В качестве моделей служат уравнения регрессии, параметры которых рассчитывают по способу наименьших квадратов
Ниже приводятся наиболее часто используемые для выравнивания динамических рядов уравнения регрессии с указанием для отражения каких именно тенденций развития они наиболее всего подходят.
Для нахождения параметров приведенных выше уравнений существуют специальные алгоритмы и компьютерные программы. В частности для нахождения параметров уравнения прямой может быть использован такой алгоритм:
Если периоды или моменты времени пронумеровать так, чтобы получилось St =0, то вышеприведенные алгоритмы существенно упростятся и превратятся в
Выровненные уровни на графике расположатся на одной прямой, проходящей на самом близком расстоянии от фактических уровней данного динамического ряда. Сумма квадратов отклонений является отражением влияния случайных факторов.
С ее помощью рассчитаем среднюю (стандартную) ошибку уравнения
:
Здесь n — число наблюдений, а m — число параметров в уравнении (их у нас два — b 1 и b 0).
Основная тенденция (тренд) показывает, как воздействуют систематические факторы на уровни ряда динамики, а колеблемость уровней около тренда () служит мерой воздействия остаточных факторов.
Для оценки качества используемой модели динамического ряда применяется также критерий F Фишера
. Он представляет из себя отношение двух дисперсий, а именно отношение дисперсии, вызванной регрессией, т.е. изучаемым фактором, к дисперсии, вызванной случайными причинами, т.е. остаточной дисперсией:
В развернутом виде формула этого критерия может быть представлена так:
где n — число наблюдений, т.е. число уровней ряда,
m — число параметров в уравнении, y — фактический уровень ряда,
Выровненный уровень ряда, — средний уровень ряда.
Более удачная, чем другие, модель не всегда может оказаться достаточно удовлетворительной. Ее можно признать таковой только в том случае, когда критерий F у нее перешагнет известную критическую границу. Эта граница устанавливается с помощью таблиц F-распределения.
Сущность и классификация индексов.
Под индексом в статистике понимают относительный показа-тель, характеризующий изменение величины какого-либо явления во времени, пространстве или по сравнению с любым эталоном.
Основным элементом индексного отношения является индек-сируемая величина. Под индексируемой величиной понимают зна-чение признака статистической совокупности, изменение которого яв-ляется объектом изучения.
С помощью индексов решаются три главные задачи:
1) оценка изменения сложного явления;
2) определение влияния отдельных факторов на изменение сложного явления;
3) сравнение величины какого-то явления с величиной прошло-го периода, величиной по другой территории, а также с нор-мативами, планами,прогнозами.
Индексы классифицируют по 3-м признакам:
2) по степени охвата элементов совокупности;
3) по методам расчета общих индексов.
По содержанию
индексируемых величин индексы разделяют-ся на индексы количественных (объемных) показателей и индексы ка-чественных показателей. Индексы количественных показателей -индексы физического объема промышленной продукции, физического объема продаж, численности и др. Индексы качественных показате-лей — индексы цен, себестоимости, производительности труда, средней заработной платы и др.
По степени охвата единиц совокупности индексы делятся на два класса: индивидуальные и общие. Для их характеристики введем следующие условные обозначения, принятые в практике применения индексного метода:
q
— количество (объем) какого-либо продукта в натуральном вы-ражении; р
— цена единицы продукции; z
— себестоимость единицы продукции; t
— затраты времени на производство единицы продукции (тру-доемкость); w
— выработка продукции в стоимостном выражении в единицу времени; v
— выработка продукции в натуральном выражении в единицу времени; Т
— общие затраты времени или численность работников.
Для того чтобы различать, к какому периоду или объекту отно-сятся индексируемые величины, принято справа внизу за соответст-вующим символом ставить подстрочные знаки. Так, например, в ин-дексах динамики, как правило, для сравниваемых (текущих, отчетных) периодов используется подстрочный знак 1 и для периодов, с которы-ми производится сравнение,
Индивидуальные индексы
служат для характеристики изме-нения отдельных элементов сложного явления (например -изменение объема выпуска продукции одного вида). Они представляют собой относительные величины динамики, выполнения обязательств, сравнения индексируемых величин.
Индивидуальный индекс физического объема продукции опре-деляется
С аналитической точки зрения приведенные индивидуальные индексы динамики аналогичны коэффициентам (темпам) роста и ха-рактеризуют изменение индексируемой величины в текущем периоде по сравнению с базисным, т. е. показывают, во сколько раз она воз-росла (уменьшилась) или сколько процентов составляет ее рост (сни-жение). Значения индексов выражают в коэффициентах или процен-тах.
Общий (сводный) индекс
отражает изменение всех элементов сложного явления.
Агрегатный индекс
является основной формой индекса. Агре-гатным он называется потому, что его числитель и знаменатель пред-ставляют собой набор «агрегат»
Средние индексы, их определение.
Помимо агрегатных индексов в статистике применяется другая их форма — средневзвешенные индексы. К их исчислению прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Так, если отсутствуют данные о ценах, но имеется информация о стоимости продукции в текущем периоде и известны индивидуальные индексы цен по каждому товару, то общий индекс цен как агрегатный определить нельзя, однако возможно исчислить его как средний из индивидуальных. Точно так же, если не известны количества произведенных отдельных видов продукции, но известны индивидуальные индексы и стоимость продукции базисного периода, то можно определить общий индекс физического объема продукции как средневзвешенную величину.
Средний индекс —
это
индекс, вычисленный как средняя величина из индивидуальных индексов. Агрегатный индекс является основной формой общего индекса, поэтому средний индекс должен быть тождествен агрегатному индексу. При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.
Средний арифметический индекс тождествен агрегатному индексу, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Только в этом случае величина индекса, рассчитанного по формуле средней арифметической, будет равна агрегатному индексу.
Понятие процент отклонения подразумевает разницу между двумя числовыми значениями в процентах. Приведем конкретный пример: допустим одного дня с оптового склада было продано 120 штук планшетов, а на следующий день – 150 штук. Разница в объемах продаж – очевидна, на 30 штук больше продано планшетов в следующий день. При вычитании от 150-ти числа 120 получаем отклонение, которое равно числу +30. Возникает вопрос: чем же является процентное отклонение?
Как посчитать отклонение в процентах в Excel
Процент отклонения вычисляется через вычитание старого значения от нового значения, а далее деление результата на старое значение. Результат вычисления этой формулы в Excel должен отображаться в процентном формате ячейки. В данном примере формула вычисления выглядит следующим образом (150-120)/120=25%. Формулу легко проверить 120+25%=150.
Обратите внимание!
Если мы старое и новое число поменяем местами, то у нас получиться уже формула для вычисления наценки .
Ниже на рисунке представлен пример, как выше описанное вычисление представить в виде формулы Excel. Формула в ячейке D2 вычисляет процент отклонения между значениями продаж для текущего и прошлого года: =(C2-B2)/B2
Важно обратит внимание в данной формуле на наличие скобок. По умолчанию в Excel операция деления всегда имеет высший приоритет по отношению к операции вычитания. Поэтому если мы не поставим скобки, тогда сначала будет разделено значение, а потом из него вычитается другое значение. Такое вычисление (без наличия скобок) будет ошибочным. Закрытие первой части вычислений в формуле скобками автоматически повышает приоритет операции вычитания выше по отношению к операции деления.
Правильно со скобками введите формулу в ячейку D2, а далее просто скопируйте ее в остальные пустые ячейки диапазона D2:D5. Чтобы скопировать формулу самым быстрым способом, достаточно подвести курсор мышки к маркеру курсора клавиатуры (к нижнему правому углу) так, чтобы курсор мышки изменился со стрелочки на черный крестик. После чего просто сделайте двойной щелчок левой кнопкой мышки и Excel сам автоматически заполнит пустые ячейки формулой при этом сам определит диапазон D2:D5, который нужно заполнить до ячейки D5 и не более. Это очень удобный лайфхак в Excel.
Альтернативная формула для вычисления процента отклонения в Excel
В альтернативной формуле, вычисляющей относительное отклонение значений продаж с текущего года сразу делиться на значения продаж прошлого года, а только потом от результата отнимается единица: =C2/B2-1.
Как видно на рисунке результат вычисления альтернативной формулы такой же, как и в предыдущей, а значит правильный. Но альтернативную формулу легче записать, хот и возможно для кого-то сложнее прочитать так чтобы понять принцип ее действия. Или сложнее понять, какое значение выдает в результате вычисления данная формула если он не подписан.
Единственный недостаток данной альтернативной формулы – это отсутствие возможности рассчитать процентное отклонение при отрицательных числах в числителе или в заменителе. Даже если мы будем использовать в формуле функцию ABS, то формула будет возвращать ошибочный результат при отрицательном числе в заменителе.
Так как в Excel по умолчанию приоритет операции деления выше операции вычитания в данной формуле нет необходимости применять скобки.
Необходимо вмешательство менеджмента для выявления причин отклонений.
Для построения контрольной карты я использую исходные данные, среднее значение (μ) и стандартное отклонение (σ). В Excel: μ = СРЗНАЧ($F$3:$F$15), σ = СТАНДОТКЛОН($F$3:$F$15)
Сама контрольная карта включает: исходные данные, среднее значение (μ), нижнюю контрольную границу (μ – 2σ) и верхнюю контрольную границу (μ + 2σ):
Скачать заметку в формате , примеры в формате
Посмотрев на представленную карту, я заметил, что исходные данные демонстрируют вполне различимую линейную тенденцию к снижению доли накладных расходов:
Чтобы добавить линию тренду выделите на графике ряд с данными (в нашем примере – зеленые точки), кликните правой кнопкой мыши и выберите опцию «Добавить линию тренда». В открывшемся окне «Формат линии тренда», поэкспериментируйте с опциями. Я остановился на линейном тренде.
Если исходные данные не разбросаны в соответствии с вокруг среднего значения, то описывать их параметрами μ и σ не вполне корректно. Для описания вместо среднего значения лучше подойдет прямая линейного тренда и контрольные границы, равноудаленные от этой линии тренда.
Линию тренда Excel позволяет построить с помощью функции ПРЕДСКАЗ. Нам потребуется дополнительный ряд А3:А15, чтобы известные значения Х
были непрерывным рядом (номера кварталов такой непрерывный ряд не образуют). Вместо среднего значения в столбце Н вводим функцию ПРЕДСКАЗ:
Стандартное отклонение σ (функция СТАНДОТКЛОН в Excel) вычисляется по формуле:
К сожалению, я не нашел в Excel функции для такого определения стандартного отклонения (по отношению к тренду). Задачу можно решить с помощью формулы массива. Кто не знаком с формулами массива, предлагаю сначала почитать .
Формула массива может возвращать одно значение или массив. В нашем случае формула массива вернет одно значение:
Давайте подробнее изучим, как работает формула массива в ячейке G3
СУММ(($F$3:$F$15-$H$3:$H$15)^2) определяет сумму квадратов разностей; фактически формула считает следующую сумму = (F3 – H3) 2 + (F4 – H4) 2 + … + (F15 – H15) 2
СЧЁТЗ($F$3:$F$15) – число значений в диапазоне F3:F15
КОРЕНЬ(СУММ(($F$3:$F$15-$H$3:$H$15)^2)/(СЧЁТЗ($F$3:$F$15)-1)) = σ
Значение 6,2% есть точка нижней контрольной границы = 8,3% – 2 σ
Фигурные кавычки с обеих сторон формулы означают, что это формула массива. Для того, чтобы создать формулу массива, после ввода формулы в ячейку G3:
H4 – 2*КОРЕНЬ(СУММ(($F$3:$F$15-$H$3:$H$15)^2)/(СЧЁТЗ($F$3:$F$15)-1))
необходимо нажать не Enter, а Ctrl + Shift + Enter. Не пытайтесь ввести фигурные скобки с клавиатуры – формула массива не заработает. Если требуется отредактировать формулу массива, сделайте это так же, как и с обычной формулой, но опять же по окончании редактирования нажмите не Enter, а Ctrl + Shift + Enter.
Формулу массива, возвращающую одно значение, можно «протаскивать», как и обычную формулу.
В результате получили контрольную карту, построенную для данных, имеющих тенденцию к понижению
P.S. После того, как заметка была написана, я смог усовершенствовать формулы, используемые для вычисления стандартного отклонения для данных с тенденцией. Ознакомиться с ними вы можете в Excel-файле
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Metod_labr.doc
Скачиваний:
4
Добавлен:
10.09.2019
Размер:
1.49 Mб
Скачать
-
Рассчитать среднее абсолютное линейное отклонение и относительное линейное отклонение.
Решение.
-
Рассчитать
столбец абсолютных отклонений от
средней цены, для этого воспользоваться
функцией ABS(*),
аргументом функции является разность
первой цены и средней цены. Ячейку со
средней ценой следует абсолютизировать
в формуле, нажав на функциональную
клавишу F4.
Затем скопировать формулу на весь
столбец. Пример представлен на Рис.10. -
Рассчитать
среднее абсолютное линейное отклонение
по формуле: в числителе – функция
СУММПРОИЗВ(*;*)
(1 аргумент – массив абсолютных линейных
отклонений, 2 аргумент – массив весов);
в знаменателе – суммарный вес. Пример
представлен на Рис. 11. Функция
СУММПРОИЗВ(*;*)
– находится
в разделе Математические
функции и
вычисляет сумму попарных произведений
соответствующих элементов первого и
второго массивов-аргументов. -
Рассчитать
относительное линейное отклонение по
формуле: в числителе – среднее абсолютное
линейное отклонение; в знаменателе –
средняя цена; результат перевести в
проценты (в меню выбираем Формат
– Ячейки – Число – Процентный).
-
Рассчитать дисперсию, среднее
квадратическое отклонение и коэффициент
вариации.
Решение.
-
Рассчитать столбец
квадратов отклонения от средней цены.
Для этого можно возвести в квадрат
первое абсолютное отклонение (возведение
в степень осуществляется с помощью
знака «^»). Затем скопировать формулу
на весь столбец. -
Рассчитать
дисперсию по формуле: в числителе –
функция СУММПРОИЗВ(*;*)
(1 аргумент – массив квадратов отклонений,
2 аргумент – массив весов); в знаменателе
– суммарный вес. -
Рассчитать среднее
квадратическое отклонение, по формуле
дисперсия в степени 0,5. -
Рассчитать
коэффициент вариации по формуле: в
числителе – среднее квадратическое
отклонение; в знаменателе – средняя
цена; результат перевести в проценты.
Рис.10. Вычисление
абсолютных отклонений
Рис.11.
Вычисление среднего абсолютного
линейного отклонения
4. Практическая работа №4. «Статистическое изучение взаимосвязей»
Название
изучаемой темы по программе дисциплины:
«Статистическое
изучение взаимосвязей».
Учебные вопросы: Простая
корреляция и регрессия. Определение
формы и оценка параметров уравнения
регрессии. Метод наименьших квадратов.
Индекс корреляции и коэффициент линейной
корреляции. Построение корреляционной
матрицы.
Цели работы: научиться выполнять
в электронной таблице MS
Excel
-
вычисление
коэффициента линейной корреляции; -
построение
корреляционной матрицы; -
построения
корреляционного поля; -
построение
уравнения линейной регрессии.
Теоретический
материал:
Глава 16,
[2].
Типовые задания
-
Изучить
корреляционную связь между стоимостными
объёмами импорта 17
товарной группы,
оформленными различными таможнями
ЮТУ. Выбрать
две таможни с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между таможнями
на основе коэффициентов корреляции и
детерминации.
-
Изучить
корреляционную связь между физическими
объёмами импорта 17
товарной группы,
оформленными различными таможнями
ЮТУ. Выбрать
две таможни с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между таможнями
на основе коэффициентов корреляции и
детерминации.
-
Изучить
корреляционную связь между стоимостными
объёмами импорта 17
товарной группы,
оформленными в различных субъектах
ЮФО. Выбрать
два субъекта ЮФО с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между субъектами
на основе коэффициентов корреляции и
детерминации. -
Изучить
корреляционную связь между физическими
объёмами импорта 17
товарной группы,
оформленными в различных субъектах
ЮФО. Выбрать
два субъекта ЮФО с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между субъектами
на основе коэффициентов корреляции и
детерминации. -
Изучить
корреляционную связь между стоимостными
объёмами экспорта 27
товарной группы,
оформленными различными таможнями
ЮТУ. Выбрать
две таможни с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между таможнями
на основе коэффициентов корреляции и
детерминации.
-
Изучить
корреляционную связь между физическими
объёмами экспорта 27
товарной группы,
оформленными различными таможнями
ЮТУ. Выбрать
две таможни с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между таможнями
на основе коэффициентов корреляции и
детерминации. -
Изучить
корреляционную связь между стоимостными
объёмами экспорта 27
товарной группы,
оформленными в различных субъектах
ЮФО. Выбрать
два субъекта ЮФО с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между субъектами
на основе коэффициентов корреляции и
детерминации. -
Изучить
корреляционную связь между физическими
объёмами экспорта 27
товарной группы,
оформленными в различных субъектах
ЮФО. Выбрать
два субъекта ЮФО с наибольшим по модулю
коэффициентом корреляции, изобразить
соответствующее корреляционное поле,
построить уравнение регрессии и
охарактеризовать связь между субъектами
на основе коэффициентов корреляции и
детерминации.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Стандартное отклонение является одним из тех статистических терминов в корпоративном мире, которое позволяет поднять авторитет людей, сумевших удачно ввернуть его в ходе беседы или презентации, и оставляет смутное недопонимание тех, кто не знает, что это такое, но стесняется спросить. На самом деле большинство менеджеров не понимают концепцию стандартного отклонения и, если вы один из них, вам пора перестать жить во лжи. В сегодняшней статье я расскажу вам, как эта недооцененная статистическая мера позволит лучше понять данные, с которыми вы работаете.
Что измеряет стандартное отклонение?
Представьте, что вы владелец двух магазинов. И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель. Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.
Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.
Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке. Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.
В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.
В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2). Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных. То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.
В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе. Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять. Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.
Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.
Как рассчитать стандартное отклонение?
Итак, теперь мы знаем, о чем говорит цифра стандартного отклонения. Давайте разберемся, как она считается.
Рассмотрим набор данных от 10 до 70 с шагом 10. Как видите, я уже рассчитал для них значение стандартного отклонения с помощью функции СТАНДОТКЛОН в ячейке H2 (оранжевым).
Ниже описаны шаги, которые предпринимает Excel, чтобы прийти к цифре 21,6.
Обратите внимание, что все расчеты визуализированы, для лучшего понимания. На самом деле в Excel расчет происходит мгновенно, оставляя все шаги за кулисами.
Для начала Excel находит среднее значение выборки. В нашем случае, среднее получилось равным 40, которое на следующем шаге отнимают от каждого значения выборки. Каждую полученную разницу возводят в квадрат и суммируют. У нас получилась сумма равная 2800, которую необходимо разделить на количество элементов выборки минус 1. Так как у нас 7 элементов, получается необходимо 2800 разделить на 6. Из полученного результата находим квадратный корень, это цифра будет стандартным отклонением.
Для тех, кому не совсем ясен принцип расчета стандартного отклонения с помощью визуализации, привожу математическую интерпретацию нахождения данного значения.
В Excel присутствует несколько разновидностей формул стандартного отклонения. Вам достаточно набрать =СТАНДОТКЛОН и вы сами в этом убедитесь.
Стоит отметить, что функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г (первая и вторая функция в списке) дублируют функции СТАНДОТКЛОН и СТАНДОТКЛОНП (пятая и шестая функция в списке), соответственно, которые были оставлены для совместимости с более ранними версиями Excel.
Вообще разница в окончаниях .В и .Г функций указывают на принцип расчета стандартного отклонения выборки или генеральной совокупности. Разницу между двумя этими массивами я уже объяснял в предыдущей статье расчета дисперсии.
Особенностью функций СТАНДОТКЛОНА и СТАНДОТКЛОНПА (третья и четвертая функция в списке), является то, что при расчете стандартного отклонения массива в расчет принимаются логические и текстовые значения. Текстовые и истинные логические значения равняются 1, а ложные логические значения равняются 0. Мне трудно представить ситуацию, когда бы мне могли понадобится эти две функции, поэтому, думаю, что их можно игнорировать.
17 авг. 2022 г.
читать 2 мин
Среднее значение представляет собой среднее значение в наборе данных. Это дает нам хорошее представление о том, где находится центр набора данных.
Стандартное отклонение показывает, насколько разбросаны значения в наборе данных. Это дает нам представление о том, насколько близко наблюдения сгруппированы вокруг среднего значения.
Используя только эти два значения, мы можем многое понять о распределении значений в наборе данных.
Чтобы вычислить среднее значение набора данных в Excel, мы можем использовать функцию = СРЗНАЧ (диапазон) , где диапазон — это диапазон значений.
Чтобы вычислить стандартное отклонение набора данных, мы можем использовать функцию =STDEV.S(Range) , где Range — это диапазон значений.
В этом руководстве объясняется, как использовать эти функции на практике.
Техническое примечание
Обе функции СТАНДОТКЛОН() и СТАНДОТКЛОН.С() вычисляют стандартное отклонение выборки .
Вы можете использовать функцию STDEV.P() для вычисления стандартного отклонения совокупности , если ваш набор данных представляет всю совокупность значений.
Однако в большинстве случаев мы работаем с выборочными данными, а не со всей совокупностью, поэтому мы используем функцию СТАНДОТКЛОН.С().
Пример 1: Среднее и стандартное отклонение одного набора данных
На следующем снимке экрана показано, как рассчитать среднее значение и стандартное отклонение одного набора данных в Excel:
Среднее значение набора данных составляет 16,4 , а стандартное отклонение — 9,13 .
Пример 2: Среднее и стандартное отклонение нескольких наборов данных
Предположим, у нас есть несколько наборов данных в Excel:
Чтобы вычислить среднее значение и стандартное отклонение первого набора данных, мы можем использовать следующие две формулы:
- Среднее значение: =СРЗНАЧ(B2:B21)
- Стандартное отклонение: =STDEV.S(B2:B21)
Затем мы можем выделить ячейки B22: B23 и навести указатель мыши на правый нижний угол ячейки B23, пока не появится крошечный +.Затем мы можем щелкнуть и перетащить формулы в следующие два столбца:
Дополнительные ресурсы
Как рассчитать сводку из пяти чисел в Excel
Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать стандартную ошибку среднего в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.