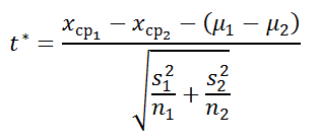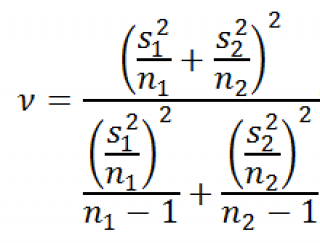17 авг. 2022 г.
читать 3 мин
Стьюдентный критерий для парных выборок используется для сравнения средних значений двух выборок, когда каждое наблюдение в одной выборке может быть сопоставлено с наблюдением в другой выборке.
В этом руководстве объясняется, как провести t-критерий парных выборок в Excel.
Как провести t-тест для парных выборок в Excel
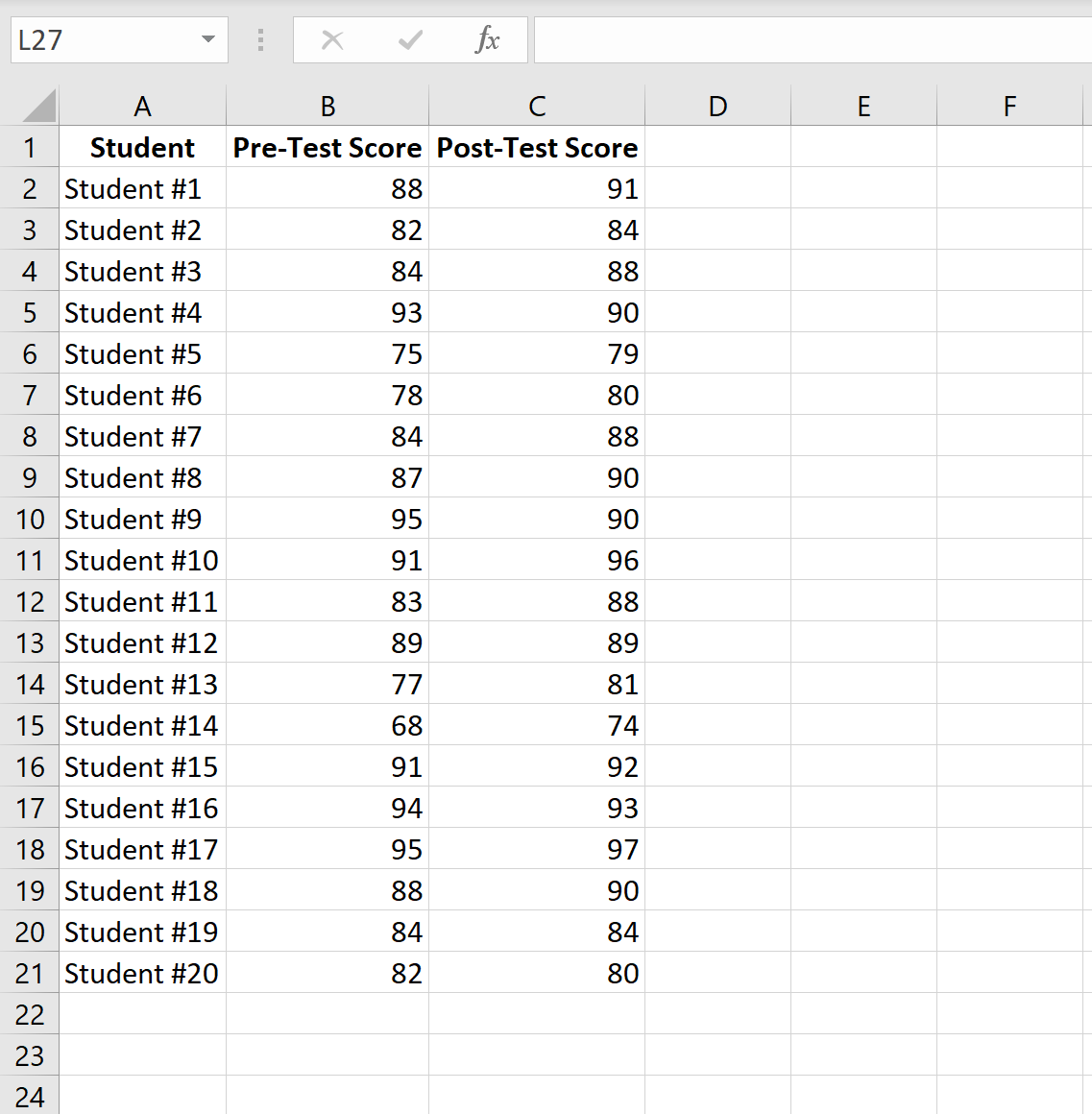
Предположим, мы хотим знать, значительно ли влияет определенная учебная программа на успеваемость студента на конкретном экзамене. Чтобы проверить это, у нас есть 20 учеников в классе, которые проходят предварительный тест. Затем каждый из студентов участвует в учебной программе в течение двух недель. Затем учащиеся пересдают тест аналогичной сложности.
Чтобы сравнить разницу между средними баллами по первому и второму тесту, мы используем t-критерий для парных выборок, потому что для каждого учащегося его балл за первый тест можно сопоставить с баллом за второй тест.
На следующем изображении показана оценка до теста и оценка после теста для каждого учащегося:
Выполните следующие шаги, чтобы провести t-критерий для парных выборок, чтобы определить, существует ли значительная разница в средних результатах теста между предварительным тестом и посттестом.
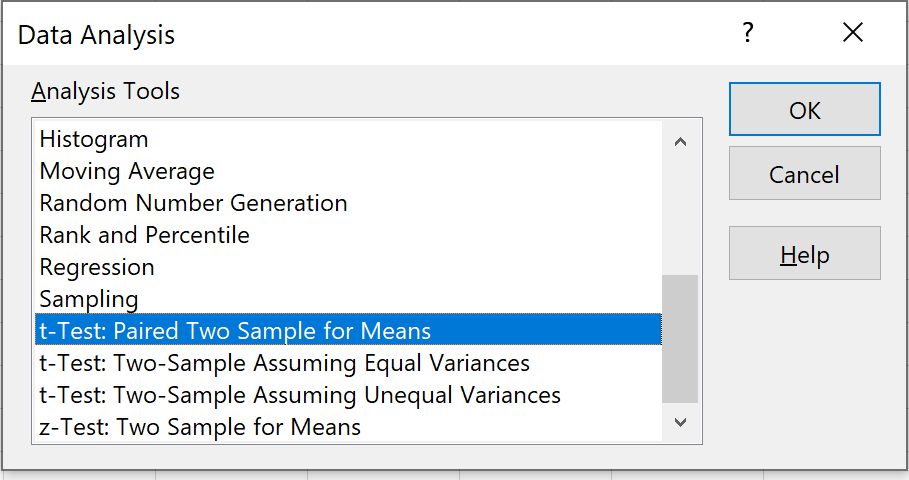
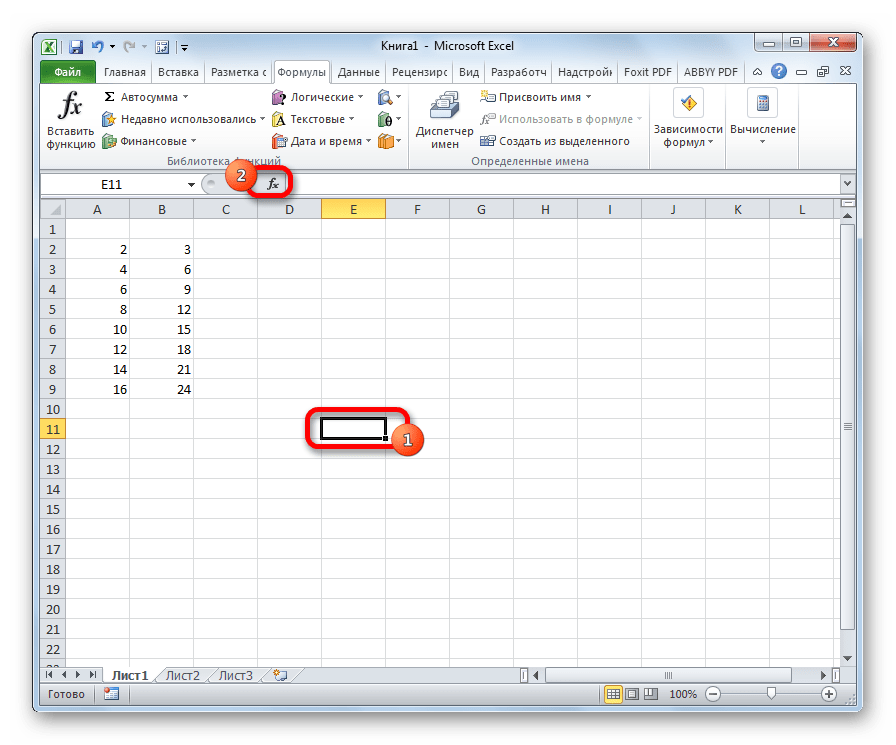
Шаг 1: Откройте пакет инструментов анализа данных.
На вкладке «Данные» на верхней ленте нажмите «Анализ данных».
Если вы не видите этот вариант для выбора, вам необходимо сначала загрузить пакет инструментов анализа , который является совершенно бесплатным.
Шаг 2: Выберите подходящий тест для использования.
Выберите вариант с надписью t-Test: Paired Two Sample for Means и нажмите OK.
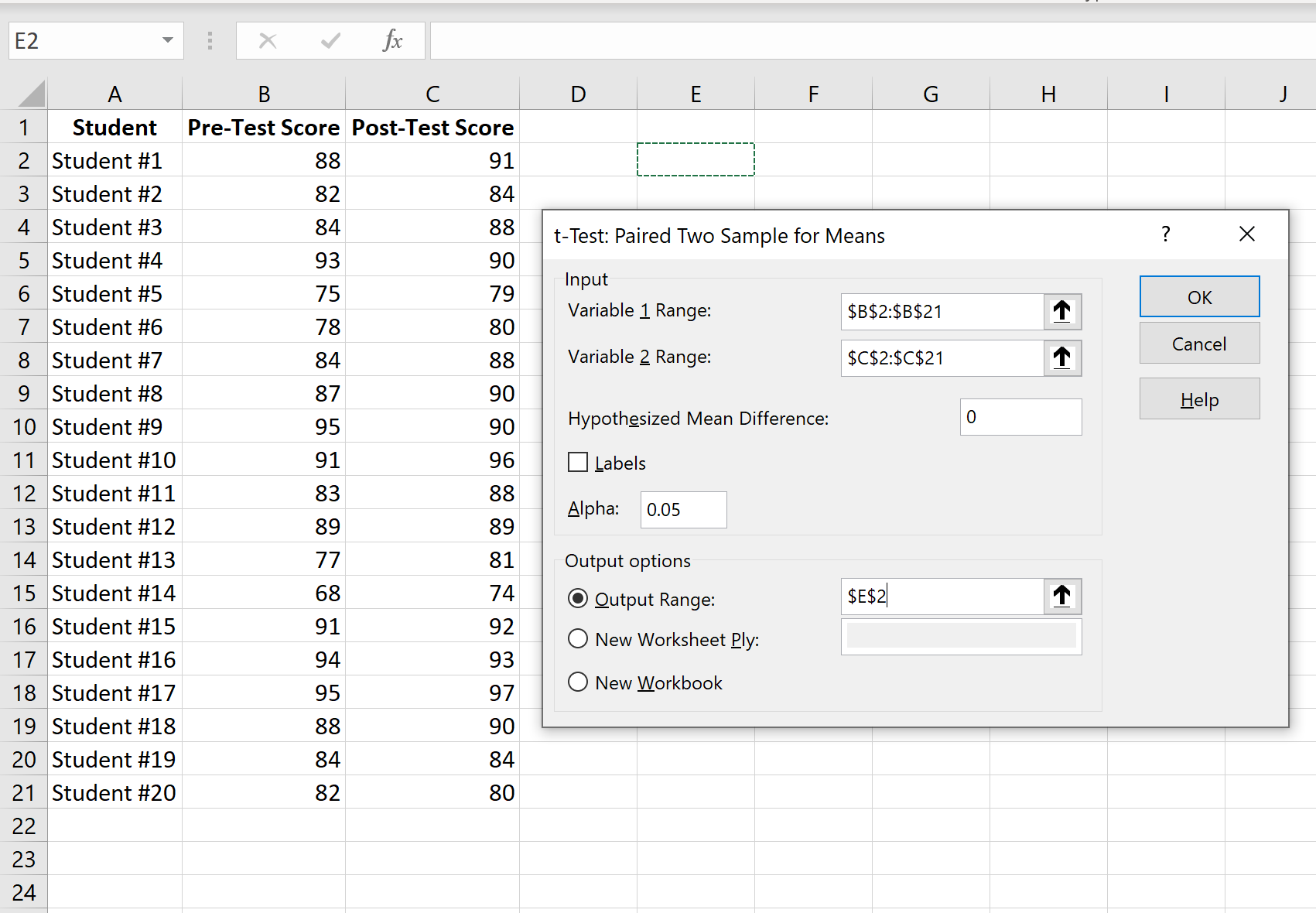
Шаг 3: Введите необходимую информацию.
Введите диапазон значений для Переменной 1 (оценки до теста), Переменной 2 (оценки после теста), гипотетической средней разницы (в этом случае мы поместили «0», потому что мы хотим знать, является ли истинная средняя разница между оценки до теста и оценки после теста равны 0), а выходной диапазон, в котором мы хотели бы видеть результаты теста, отображаются. Затем нажмите ОК.
Шаг 4: Интерпретируйте результаты.
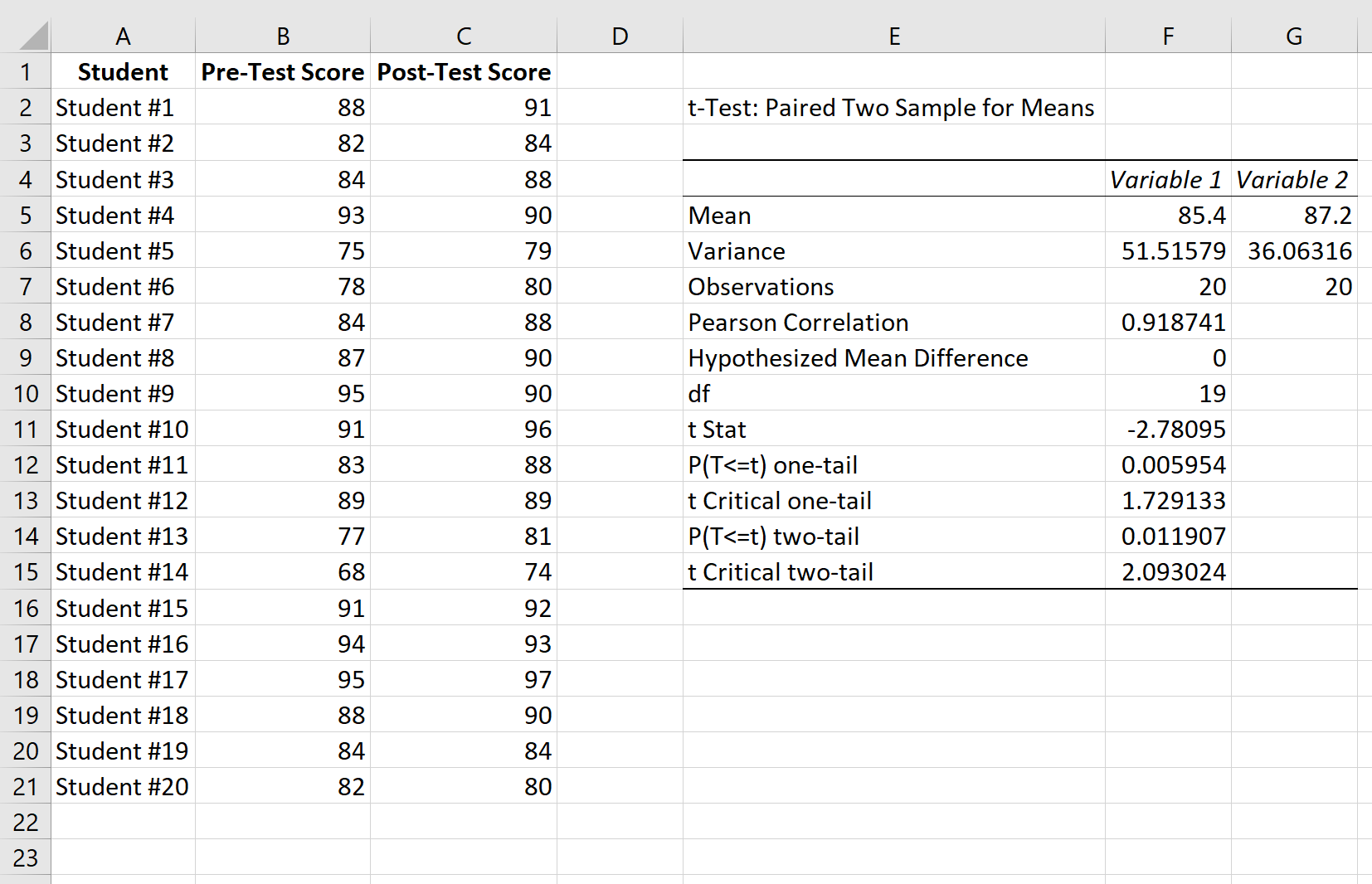
После того, как вы нажмете OK на предыдущем шаге, отобразятся результаты t-теста.
Вот как интерпретировать результаты:
Среднее значение: это среднее значение для каждого образца. Средний балл до теста — 85,4 , а средний балл после теста — 87,2 .
Дисперсия: это дисперсия для каждого образца. Дисперсия оценок до теста составляет 51,51 , а дисперсия оценок после теста — 36,06 .
Наблюдения: это количество наблюдений в каждой выборке. Обе выборки имеют по 20 наблюдений.
Корреляция Пирсона: корреляция между результатами до и после теста. Получается 0,918 .
Гипотетическая средняя разница: число, которое мы «предполагаем», представляет собой разницу между двумя средними значениями. В данном случае мы выбрали 0 , потому что хотим проверить, есть ли вообще какая-либо разница между результатами до и после теста.
df: Степени свободы для t-критерия. Это рассчитывается как n-1, где n — количество пар. В этом случае df = 20 – 1 = 19 .
t Stat: тестовая статистика t , которая оказывается равной -2,78 .
P(T<=t) двухсторонний: значение p для двустороннего t-критерия. В этом случае р = 0,011907.Это меньше, чем альфа = 0,05, поэтому мы отвергаем нулевую гипотезу. У нас есть достаточно доказательств, чтобы сказать, что существует статистически значимая разница между средним баллом до и после теста.
t Критический двухсторонний: это критическое значение теста, найденное путем определения значения в таблице распределения t , которое соответствует двустороннему тесту с альфа = 0,05 и df = 19. Получается 2,093024.Поскольку абсолютное значение нашей тестовой статистики t больше этого значения, мы отвергаем нулевую гипотезу. У нас есть достаточно доказательств, чтобы сказать, что существует статистически значимая разница между средним баллом до и после теста.
Обратите внимание, что подход с использованием p-значения и критического значения приведет к одному и тому же выводу.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие t-тесты в Excel:
Как провести одновыборочный t-тест в Excel
Как провести двухвыборочный t-тест в Excel
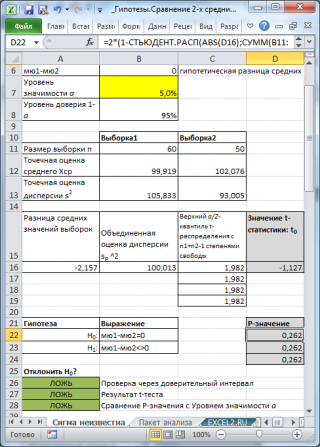
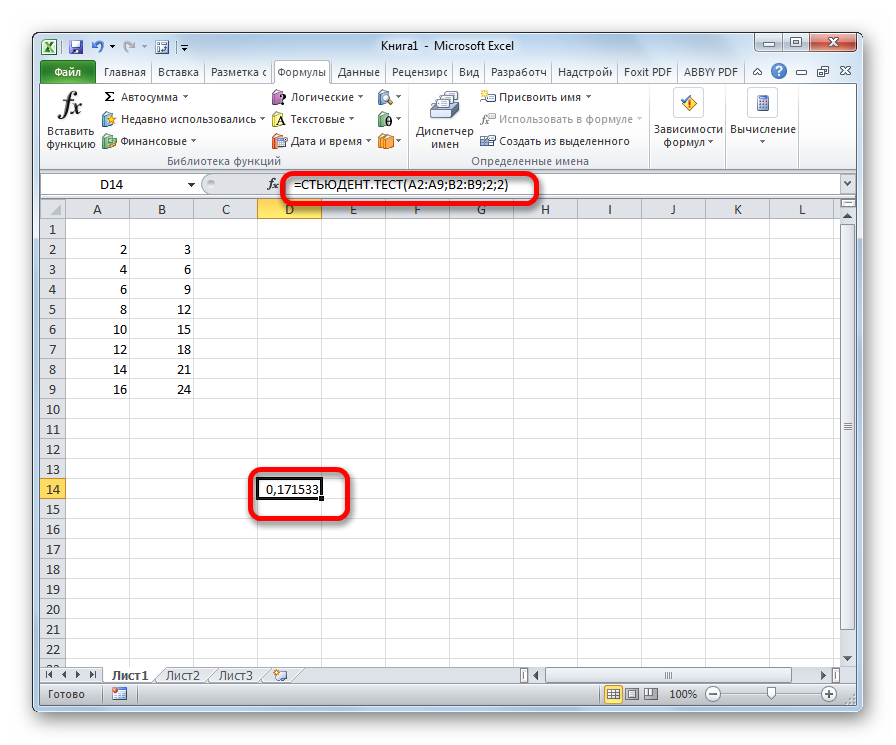
Рассмотрим использование MS EXCEL при проверке статистических гипотез о разнице средних значений 2-х распределений в случае неизвестных дисперсий (дисперсии этих 2-х распределений разные). Вычислим значение тестовой статистики t
0
*, рассмотрим соответствующую процедуру «двухвыборочный
t
-тест», вычислим Р-значение (Р-
value
). С помощью надстройки Пакет анализа сделаем «Двухвыборочный t-тест с различными дисперсиями».
Имеется две независимых случайных величины. Эти случайные величины имеют распределения с неизвестными
средними значениями
μ
1
и μ
2
.
Дисперсии
этих распределений неизвестны и не равны между собой (обозначим их σ
1
2
и σ
2
2
). Из этих распределений получены две
выборки
размером n
1
и n
2
.
Необходимо произвести
проверку гипотезы
о разнице
средних значений
этих распределений: μ
1
— μ
2
(англ. Hypothesis tests for a difference in means, populations with unknown and unequal variances).
Нулевая гипотеза
H
0
звучит так: разница
средних значений
равна Δ
0
, т.е. Δ
0
= (μ
1
— μ
2
). Часто предполагается, что Δ
0
=0, следовательно, μ
1
= μ
2
(значение Δ
0
задается исследователем исходя из условий решаемой задачи).
Альтернативная гипотеза H
1
: (μ
1
— μ
2
)<>Δ
0
. Т.е. нам требуется проверить
двухстороннюю гипотезу
.
СОВЕТ
: При первом знакомстве с процедурой
двухвыборочного
t
-теста
может быть полезным освежить в памяти
процедуру одновыброчного t-теста для среднего при неизвестной дисперсии
.
СОВЕТ
: Для
проверки гипотез
нам потребуется знание следующих понятий:
-
дисперсия и стандартное отклонение
,
-
выборочное распределение статистики
,
-
уровень доверия/ уровень значимости
,
-
нормальное распределение
,
-
t-распределение Стьюдента
и
его квантили
.
Примечание
: Вышеуказанные распределения не обязательно должны быть
нормальными
. Однако, требуется чтобы выполнялись условия применимости
Центральной предельной теоремы
. Если размеры
выборок
меньше 30, то для справедливости сделанных здесь выводов, необходимо, чтобы
выборки
были сделаны из
нормального распределения
.
Точечной оценкой
для Δ
0
или для μ
1
— μ
2
является разница между
средними значениями,
вычисленными на основании
выборок
из этих (независимых) распределений, т.е. Хср
1
— Хср
2
.
Когда
дисперсии
распределений, из которых сделаны
выборки,
не равны между собой, не существует точной
t
-статистики
для проверки
нулевой гипотезы
, как для случая с одинаковыми
дисперсиями
(см. статью
Двухвыборочный t-тест с одинаковыми дисперсиями
). Однако, при условии истинности
нулевой гипотезы
, статистика t*
:
приблизительно имеет
t
-распределение
с v (ню) степенями свободы:
Процедура
t
-теста в случае разных дисперсий
аналогична процедуре
t
-теста в случае одинаковых дисперсий
, за исключением того, что вместо
t
-статистики
используется вышеуказанная
статистики
t*. Значение, которое приняла
t
*-статистика
обозначим t
0
*.
Проверка
двухсторонней гипотезы
сводится к сравнению t
0
* с квантилями
эталонного распределения
, в данном случае распределения Стьюдента с v степенями свободы. Эта процедура носит название
двухвыборочный
t
-тест
в случае разных
дисперсий
(The two-sample t-Test with unequal variances).
Если вычисленное на основе
выборок
значение t
0
*, в случае
двухсторонней гипотезы
, не попадет в область значений ограниченной нижним и верхним
α
/2-квантилями
t
—
распределения
с v степенями свободы
,
то у нас будет основание отвергнуть
нулевую гипотезу.
Это утверждение эквивалентно случаю, когда Хср
1
— Хср
2
окажется вне пределов соответствующего
доверительного интервала
.
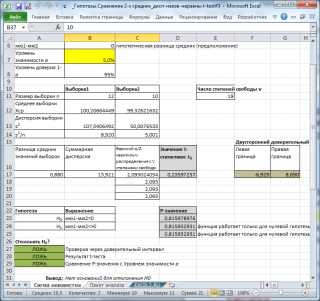
В
файле примера на листе Сигма неизвестн
а показана эквивалентность
доверительного интервала
и соответствующего
двухвыборочного
t
-теста.
Примечание
: Про построение соответствующего
двухстороннего доверительного интервала
можно прочитать в этой статье
Доверительный интервал для разницы средних значений 2-х распределений (дисперсии неизвестны и не равны) в MS EXCEL
.
Примечание
:
Верхний
α
/2-квантиль
— это такое значение случайной величины
t
v
,
что
P
(
t
v
>=
t
α
/2,
v
)=
α
/2.
Подробнее о
квантилях
распределений см. статью
Квантили распределений MS EXCEL
.
Чтобы в MS EXCEL вычислить значение
t
α
/2,
v
для различных
уровней значимости
(10%; 5%; 1%) и
степеней свобод
можно использовать несколько формул:
=СТЬЮДЕНТ.ОБР.2Х(
α
; v) =СТЬЮДЕНТ.ОБР(1-
α
/2; v) =-СТЬЮДЕНТ.ОБР(
α
/2; v) =СТЬЮДРАСПОБР(
α
; v)
Примечание
: Подробнее про функции MS EXCEL, связанные с
t
—
распределением
см.
статью t-распределение
.
Примечание
:
Число степеней свободы
v должно быть
округлено до ближайшего целого
.
Итак, если при проверке
двухсторонней гипотезы
формула
=ABS(t
0
*)
вернет значение больше, чем результат формулы
=СТЬЮДЕНТ.ОБР.2Х(
α
; v)
, то это означает, что необходимо отвергнуть
нулевую гипотезу
(вычисления приведены
файле примера на листе Сигма неизвестна
)
.
Для
односторонней
альтернативной гипотезы
(μ
1
— μ
2
)>Δ
0
,
нулевая гипотеза
будет отвергнута в случае t
0
*>
t
α
/2,
v
.
Для
односторонней
альтернативной гипотезы
(μ
1
— μ
2
)<Δ
0
,
нулевая гипотеза
будет отвергнута в случае t
0
*<-
t
α
/2,
v
.
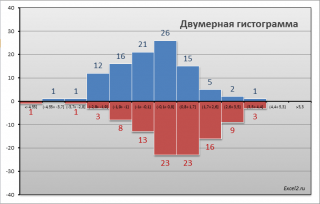
СОВЕТ
: Перед
проверкой гипотез
о равенстве средних значений
полезно построить
двумерную гистограмму
, чтобы визуально определить
центральную тенденцию
и
разброс данных
в обеих
выборок
.
Вычисление Р-значения
При
проверке гипотез,
помимо
t
-теста,
большое распространение получил еще один эквивалентный подход, основанный на вычислении
p
-значения
(p-value).
Если
p-значение
меньше чем заданный
уровень значимости α
, то
нулевая гипотеза
отвергается и принимается
альтернативная гипотеза
. И наоборот, если
p-значение
больше
α
, то
нулевая гипотеза
не отвергается.
В случае
двусторонней гипотезы
p-значение
равно суммарной вероятности, что
t
-статистика
примет значение больше |t
0
*| и меньше -|t
0
*|.
Подробнее про
p
-значение
см., например, статью про
двухвыборочный z-тест
.
В MS EXCEL
p
-значение
для
двухсторонней гипотезы
вычисляется по формуле:
=2*(1-СТЬЮДЕНТ.РАСП(ABS(t
0
*); v;ИСТИНА))
Примечание
: Вычисления приведены
файле примера на листе Сигма неизвестна
.
Для
односторонней гипотезы
μ
1
— μ
2
> Δ
0
p
-значение
вычисляется по формуле:
=1-СТЬЮДЕНТ.РАСП(t
0
*; v;ИСТИНА)
В этом случае
p-значение
равно вероятности, что
t
-статистика
примет значение больше t
0
*.
Для
односторонней гипотезы
μ
1
— μ
2
< Δ
0
p
-значение
вычисляется по формуле:
=СТЬЮДЕНТ.РАСП(t
0
*; v;ИСТИНА)
В этом случае
p-значение
равно вероятности, что
t
-статистика
примет значение меньше t
0
*.
В
файле примера на листе Сигма неизвестна
показана эквивалентность
проверки гипотезы
через
доверительный интервал
,
статистику
t
*
(
t
-тест)
и
p
-значение
.
В MS EXCEL есть функция
СТЬЮДЕНТ.TEСT()
, которая вычисляет
p-значение
для 3-х различных
двухвыборочных
t
-тестов
(см. следующий раздел статьи)
.
К сожалению, эта функция может быть использована только для
проверки гипотез
с Δ
0
=0, то есть для
проверки гипотез
о равенстве средних μ
1
= μ
2
. Об этом легко догадаться, т.к. среди ее параметров отсутствует параметр
Гипотетическая разность средних
, т.е. Δ
0
.
Функция
СТЬЮДЕНТ.ТЕСТ()
Функция
СТЬЮДЕНТ.ТЕСТ()
используется для оценки различия двух
выборочных средних
. До
MS EXCEL 2010
имелась аналогичная функция
ТТЕСТ()
.
Примечание
: В английской версии функция носит название T.TEST(), старая версия — TTEST().
Функция
СТЬЮДЕНТ.ТЕСТ()
имеет 4 параметра. Первые два – это ссылки на диапазоны ячеек, содержащие
выборки
из 2-х сравниваемых распределений.
Третий параметр имеет название «хвосты». Этот параметр задает тип проверяемой гипотезы: односторонняя (=1) или двухсторонняя (=2). Если мы проверяем
двухстороннюю гипотезу
, то смотрим, не попало ли значение
тестовой статистики
в один из 2-х хвостов соответствующего
t-распределения
. Если мы проверяем
одностороннюю гипотезу
(имеется ввиду гипотеза μ
1
< μ
2
), то «хвост» всего один.
Как было сказано выше, эта функция вычисляет
p
-значение
для 3-х различных
двухвыборочных
t
-тестов
. За это отвечает четвертый параметр функции, который принимает значения от 1 до 3:
-
Парный двухвыборочный t-тест для средних
;
-
Двухвыборочный t-тест с одинаковыми дисперсиями
;
Двухвыборочный t-тест с разными дисперсиями.
Таким образом,
p
-значение
для
двухсторонней гипотезы
(равные
дисперсии
) вычисляется по формуле (см.
файл примера
):
=СТЬЮДЕНТ.ТЕСТ(
выборка1
;
выборка2
; 2; 3)
или
=2*(1-СТЬЮДЕНТ.РАСП(ABS(t
0
*); v;ИСТИНА))
Для
односторонней гипотезы
μ
1
< μ
2
p
-значение
вычисляется по формуле:
=СТЬЮДЕНТ.ТЕСТ(
выборка1
;
выборка2
; 1; 3)
или
=СТЬЮДЕНТ.РАСП(t
0
*; v;ИСТИНА)
Для
односторонней гипотезы
μ
1
> μ
2
p
-значение
вычисляется по формуле:
=1-СТЬЮДЕНТ.ТЕСТ(
выборка1
;
выборка2
; 1; 3)
или
=1-СТЬЮДЕНТ.РАСП(t
0
*; v;ИСТИНА)
К сожалению, результаты, возвращаемые функцией
СТЬЮДЕНТ.ТЕСТ()
и формулой на основе функции
СТЬЮДЕНТ.РАСП()
незначительно отличаются (в 4-м знаке после запятой). Причем различие проявляется только для случая с неравными дисперсиями.
Какой результат правильный? В поддержку формулы на основе функции
СТЬЮДЕНТ.РАСП()
выступает надстройка
Пакет анализа
, которая возвращает аналогичный ей результат (см. ниже).
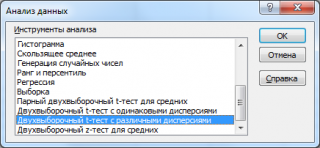
Пакет анализа
В
надстройке Пакет анализа
для проведения
двухвыборочного
t
-теста
с различными
дисперсиями
имеется специальный инструмент:
Двухвыборочный
t
-тест
с различными
дисперсиями
(t-Test: Two-Sample Assuming Unequal Variances).
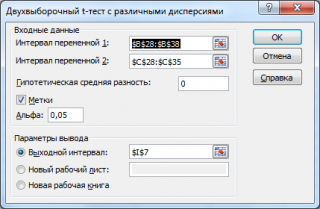
После выбора инструмента откроется окно, в котором требуется заполнить следующие поля (см.
файл примера лист Пакет анализа
):
интервал переменной 1
: ссылка на значения первой
выборки
. Ссылку указывать лучше с заголовком. В этом случае, при выводе результата надстройка выводит заголовки, которые делают результат нагляднее (в окне требуется установить галочку
Метки
);
интервал переменной 2
: ссылка на значения второй
выборки
;
гипотетическая средняя разность
: укажите значение Δ
0
, т.е. μ
1
— μ
2
. В нашем случае, введем 0;
Метки:
если в полях
интервал переменной 1
и
интервал переменной 2
указаны ссылки вместе с заголовками столбцов, то эту галочку нужно установить. В противном случае надстройка не позволит провести вычисления и пожалуется, что «
входной интервал содержит нечисловые данные
»;
Альфа:
уровень значимости;
Выходной интервал:
диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.
В результате вычислений будет заполнен указанный
Выходной интервал.
Тот же результат можно получить с помощью формул (см.
файл примера лист Пакет анализа
):
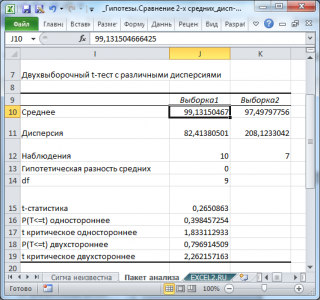
Разберем результаты вычислений, выполненных надстройкой:
Среднее
:
средние значения
обеих
выборок
Хср
1
— Хср
2
. Вычисления можно сделать с помощью функции
СРЗНАЧ()
;
Дисперсия
:
дисперсии
обеих
выборок.
Вычисления можно сделать с помощью функции
ДИСП.В()
Наблюдения
: размер
выборок.
Вычисления можно сделать с помощью функции
СЧЁТ()
Df
: число степеней свободы. Вычисление v приведено в ячейке
Е10
;
t
-статистика
: значение
тестовой статистики
t
(в наших обозначениях – это t
0
*). Вычисление t
0
* приведено в ячейке
Е16
;
P(T<=t) одностороннее
:
р-значение
в случае
односторонней альтернативной гипотезы
μ
1
— μ
2
>Δ
0
. Эквивалентная формула
=1-СТЬЮДЕНТ.РАСП(t
0
*;
v
; ИСТИНА)
;
t критическое одностороннее
: Верхний
α
-квантиль t-распределения. Эквивалентная формула
=СТЬЮДЕНТ.ОБР(1-
α
; v)
;
P(T<=t) двухстороннее: р-значение
в случае
двухсторонней альтернативной гипотезы
μ
1
— μ
2
<>Δ
0
. Эквивалентная формула
=2*(1-СТЬЮДЕНТ.РАСП(ABS(t
0
*); v; ИСТИНА))
;
t критическое двухстороннее: Верхний
α
/2-Квантиль t-распределения
. Эквивалентная формула
=СТЬЮДЕНТ.ОБР(1-
α
/2; v)
.
Отметим, что значения
P(T<=t) двухстороннее
и
P(T<=t) одностороннее
не совпадают в 4-м знаке после запятой с соответствующими результатами функции
СТЬЮДЕНТ.ТЕСТ()
. Например,
- 0,398457254347491 (результат, возвращаемый надстройкой)
- 0,398359475709341 (результат, возвращаемый функцией)
Это первый, замеченный мной случай в MS EXCEL, когда результат зависит от применяемого инструмента.
СОВЕТ
: О проверке других видов гипотез см. статью
Проверка статистических гипотез в MS EXCEL
.
Содержание
- Определение термина
- Расчет показателя в Excel
- Способ 1: Мастер функций
- Способ 2: работа со вкладкой «Формулы»
- Способ 3: ручной ввод
- Вопросы и ответы
Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.
Определение термина
Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
- Строим таблицу с двумя рядами переменных.
- Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.
- После того, как Мастер функций открылся. Ищем в списке значение ТТЕСТ или СТЬЮДЕНТ.ТЕСТ. Выделяем его и жмем на кнопку «OK».
- Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
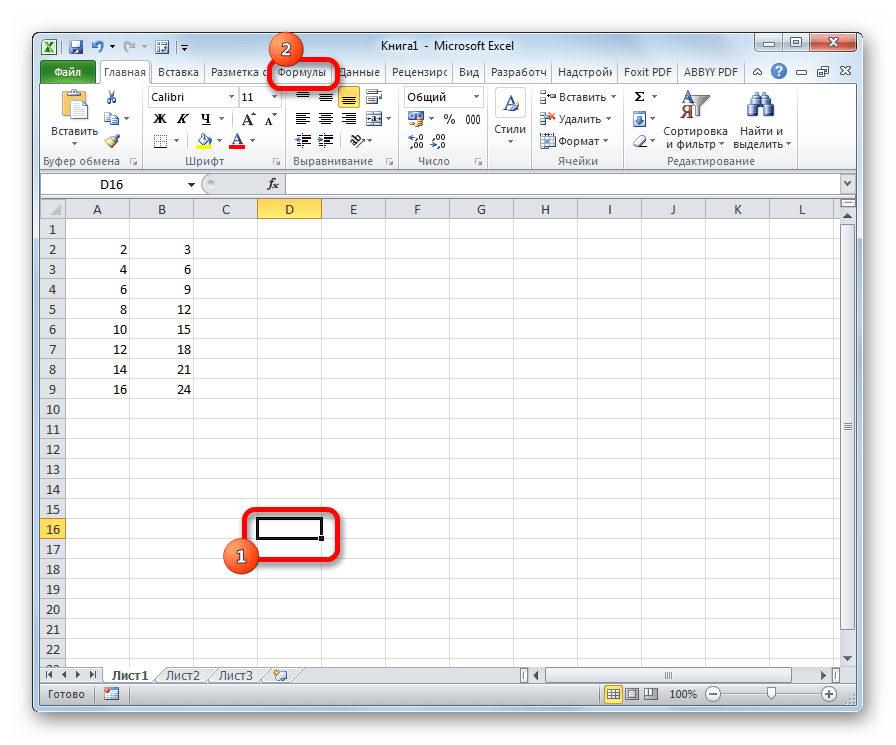
Способ 2: работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
- Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».
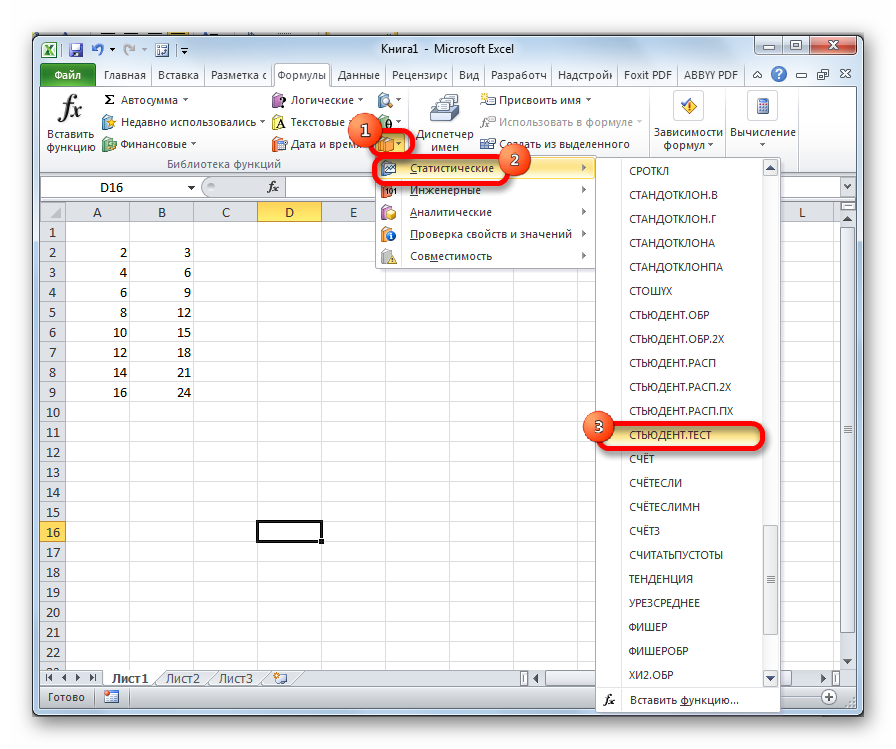
- Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».
- Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.
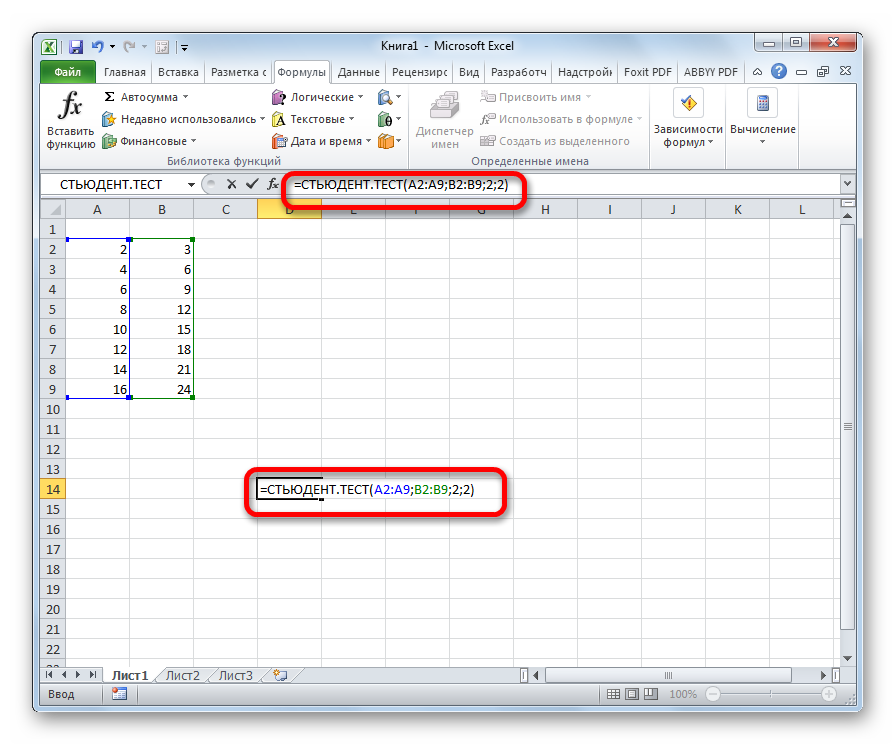
Способ 3: ручной ввод
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.
После того, как данные введены, жмем кнопку Enter для вывода результата на экран.
Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
Еще статьи по данной теме:
Помогла ли Вам статья?
A T-test is a way of deciding if there are statistically significant differences between datasets, using a Student’s t-distribution. The T-Test in Excel is a two-sample T-test comparing the means of two samples. This article explains what statistical significance means and shows how to do a T-Test in Excel.
Instructions in this article apply to Excel 2019, 2016, 2013, 2010, 2007; Excel for Microsoft 365 and Excel Online.
What is Statistical Significance?
Imagine you want to know which of two dice will give a better score. You roll the first die and get a 2; you roll the second die and get a 6. Does this tell you the second die usually gives higher scores? If you answered, “Of course not,” then you already have some understanding of statistical significance. You understand the difference was due to the random change in the score, each time a die is rolled. Because the sample was very small (only one roll) it didn’t show anything significant.
Now imagine you roll each die 6 times:
- The first die rolls 3, 6, 6, 4, 3, 3; Mean = 4.17
- The second die rolls 5, 6, 2, 5, 2, 4; Mean = 4.00
Does this now prove the first die gives higher scores than the second? Probably not. A small sample with a relatively small difference between the means makes it likely the difference is still due to random variations. As we increase the number of dice rolls it becomes difficult to give a common sense answer to the question — is the difference between the scores the result of random variation or is one actually more likely to give higher scores than the other?
Significance is the probability that an observed difference between samples is due to random variations. Significance is often called the alpha level or simply ‘α.’ The confidence level, or simply ‘c,’ is the probability that the difference between the samples is not due to random variation; in other words, that there’s a difference between the underlying populations. Therefore: c = 1 – α
We can set ‘α’ at whatever level we want, to feel confident we’ve proven significance. Very often α=5% is used (95% confidence), but if we want to be really sure that any differences are not caused by random variation, we might apply a higher confidence level, using α=1% or even α=0.1%.
Various statistical tests are used to calculate significance in different situations. T-tests are used to determine whether the means of two populations are different and F-tests are used to determine whether the variances are different.
Why Test for Statistical Significance?
When comparing different things, we need to use significance testing to determine if one is better than the other. This applies to many fields, for example:
- In business, people need to compare different products and marketing methods.
- In sports, people need to compare different equipment, techniques, and competitors.
- In engineering, people need to compare different designs and parameter settings.
If you want to test whether something performs better than something else, in any field, you need to test for statistical significance.
What is a Student’s T-Distribution?
A Student’s t-distribution is similar to a normal (or Gaussian) distribution. These are both bell-shaped distributions with most results close to the mean, but some rare events are quite far from the mean in both directions, referred to as the tails of the distribution.
The exact shape of the Student’s t-distribution depends on the sample size. For samples of more than 30 it’s very similar to the normal distribution. As the sample size is reduced, the tails get larger, representing the increased uncertainty that comes from making inferences based on a small sample.
How to Do a T-Test in Excel
Before you can apply a T-Test to determine whether there’s a statistically significant difference between the means of two samples, you must first perform an F-Test. This is because different calculations are performed for the T-Test depending on whether there’s a significant difference between the variances.
You will need the Analysis Toolpak add-in enabled to perform this analysis.
Checking and Loading the Analysis Toolpak Add-In
To check and activate the Analysis Toolpak follow these steps:
-
Select the FILE tab >select Options.
-
In the Options dialogue box, select Add-Ins from the tabs on the left-hand side.
-
At the bottom of the window, select the Manage drop-down menu, then select Excel Add-ins. Select Go.
-
Ensure the check-box next to Analysis Toolpak is checked, then select OK.
-
The Analysis Toolpak is now active and you are ready to apply F-Tests and T-Tests.
Performing an F-Test and a T-Test in Excel
-
Enter two datasets into a spreadsheet. In this case, we’re considering the sales of two products during a week. The mean daily sales value for each product is also calculated, together with its standard deviation.
-
Select the Data tab > Data Analysis
-
Select F-Test Two-Sample for Variances from the list, then select OK.
The F-Test is highly sensitive to non-normality. It may therefore be safer to use a Welch test, but this is more difficult in Excel.
-
Select the Variable 1 Range and Variable 2 Range; set the Alpha (0.05 gives 95% confidence); select a cell for the top left corner of the output, considering that this will fill 3 columns and 10 rows. Select OK.
For the for Variable 1 Range, the sample with the largest standard deviation (or variance) must be selected.
-
View the F-Test results to determine whether there is a significant difference between the variances. The results give three important values:
- F: The ratio between the variances.
- P(F<=f) one-tail: The probability that variable 1 doesn’t actually have a larger variance than variable 2. If this is larger than alpha, which is generally 0.05, then there’s no significant difference between the variances.
- F Critical one-tail: The value of F that would be required to give P(F<=f)=α. If this value is greater than F, this also indicates there’s no significant difference between the variances.
P(F<=f) can also be calculated using the FDIST function with F and the degrees of freedom for each sample as its inputs. Degrees of freedom is simply the number of observations in a sample minus one.
-
Now that you know whether there is a difference between the variances you can select the appropriate T-Test. Select the Data tab > Data Analysis, then select either t-Test: Two-Sample Assuming Equal Variances or t-Test: Two-Sample Assuming Unequal Variances.
-
Regardless of which option you chose in the previous step, you will be presented with the same dialogue box to enter the details of the analysis. To start, select the ranges containing the samples for Variable 1 Range and Variable 2 Range.
-
Assuming you want to test for no difference between the means, set the Hypothesized Mean Difference to zero.
-
Set the significance level Alpha (0.05 gives 95% confidence), and select a cell for the top left corner of the output, considering that this will fill 3 columns and 14 rows. Select OK.
-
Review the results to decide if there’s a significant difference between the means.
Just as with the F-Test, if the p-value, in this case P(T<=t), is greater than alpha, then there’s no significant difference. However, in this case there are two p-values given, one for a one-tail test and the other for a two-tail test. In this case, use the two-tail value since either variable having a greater mean would be a significant difference.
Thanks for letting us know!
Get the Latest Tech News Delivered Every Day
Subscribe
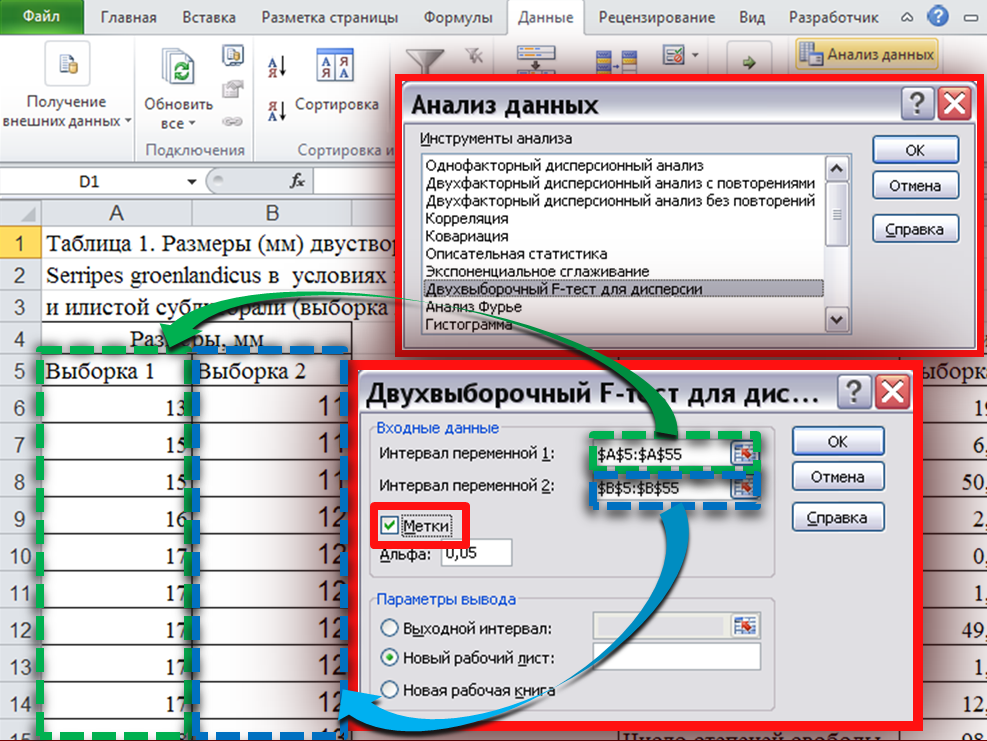
А. Сравнение
выборочных дисперсий.
Выбираем
раздел меню Данные
— «Анализ
данных»-«Двухвыборочный тест для
дисперсии» (Рис. 
Рис. 8
В появившимся окне
указываем
диапазоны ячеек с вариантами обеих
выборок («Интервал
переменной 1»
и «Интервал
переменной 2),
если диапазон ячеек выделяем вместе с
названием столбцов ставим отметку в
окошке «Метки»,
нажимаем «ОК»
(как показано на Рисунке
8)
и получаем таблицу с результатами.
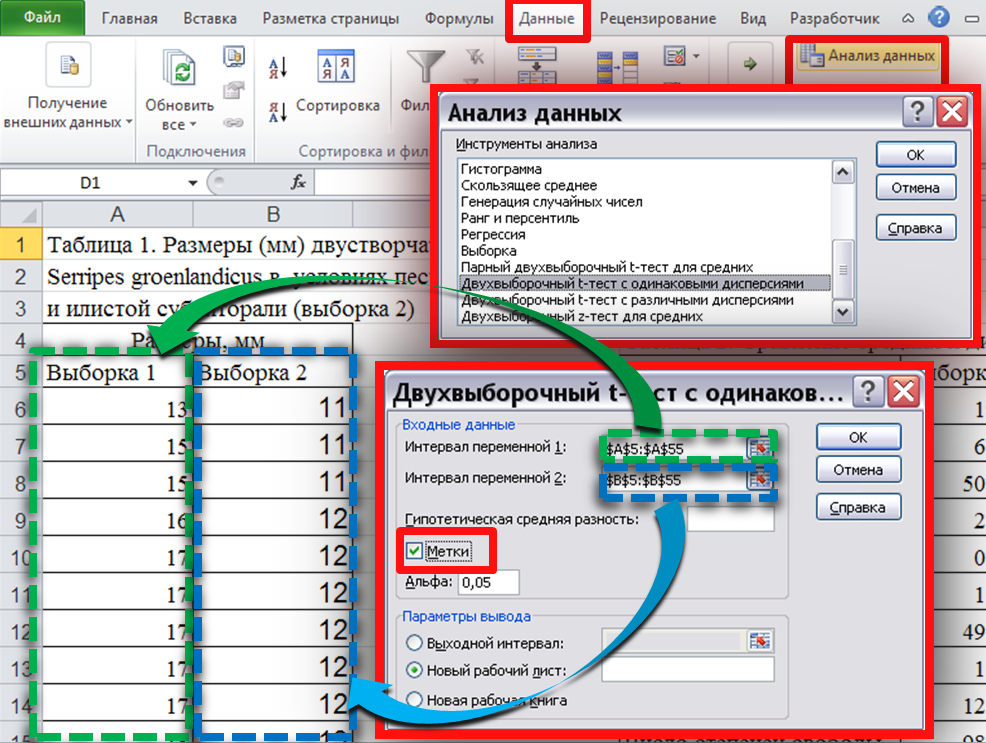
Б. Сравнение
средних.
Выбираем
раздел меню «Данные»-«Анализ
данных»-«Двухвыборочный t-тест
с одинаковыми дисперсиями» (Рис. 9).
В
Рис. 9.
появившимся окнеуказываем
диапазоны ячеек с вариантами обеих
выборок («Интервал
переменной
1
»
и «Интервал
переменной
2
).
Если диапазон ячеек выделяем вместе с
названием столбцов, ставим отметку в
окошке «Метки»,
нажимаем «ОК»
(как показано на Рисунке
9) и получаем
таблицу с результатами.
3. Сравнение двух выборок с помощью приложения «Статистика».
Для начала подготовим
наши данные: сгруппируем данные обеих
выборок в единый ряд и введем еще одну
переменную — код выборки: значениям
признака из выборки 1 соответствует 1,
значениям признака из выборки 2 –
соответствует цифра 2 (Таблица
3).
Таблица 3. Исходные
данные
|
Варианты |
Код |
Вставляем данные
(оба столбца) в специальную таблицу
Spreadsheet.
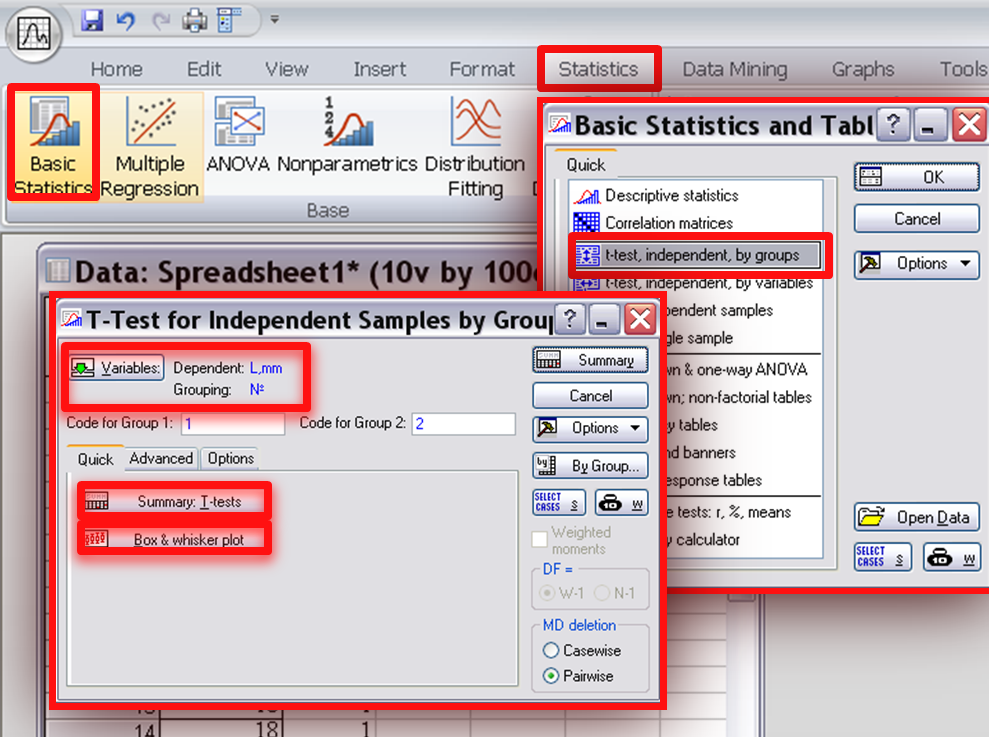
Выбираем последовательно разделы
Statistics-Basic
Statistics/Tables-t—test,
idependent
by
groups
(как показано на Рисунке
10).
Рис. 10-11
В открывшейся
вкладке (Рис.
11) нажимаем
кнопку Variables,
чтобы указать,
в каком столбце находятся значения
изучаемого признака (Dependent
variables),
в каком — значения группирующей переменной
(Grouping
variables), в
данном случае это коды выборки.
Нажимая кнопки
Summary:
T—tests
и Box&whisker
plot
соответственно получим таблицу с
итогами сравнения выборок и графическое
изображение средних значений в выборках
с различными видами интервалов.
Для более точного
графического изображения доверительного
интервала для средних обеих выборок
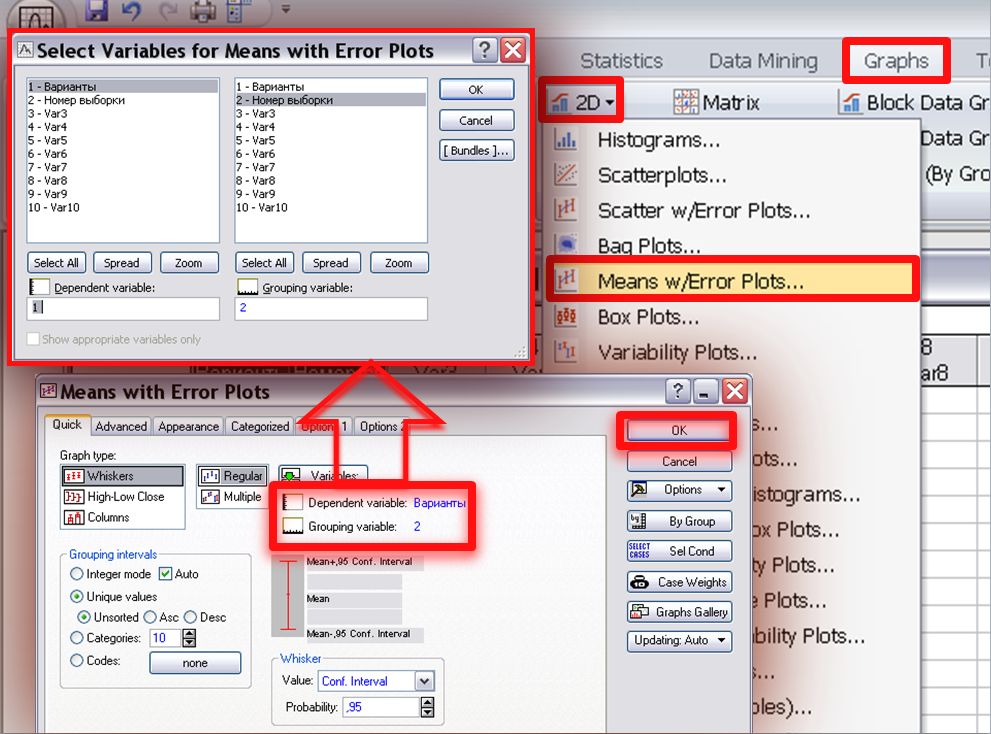
следует воспользоваться разделом меню
Graphs-Means
w/Error
Plots….(Рис.
12). В появившемся
окне нажимаем кнопку Variables
и указываем,
в каком столбце находятся данные:
Dependent
variable
(значения
признака) и Grouping
variable
(коды выборки).
Все остальные отметки оставляем
неизменными (тип графика
Graph
type–
Whiskers;
группировка данных в б/интервальный
вариационный ряд – Grouping
intervals
— Unique
value,
тип интервала – 95% доверительный интервал
— Whiskers
— Conf. Interval)
и нажимаем ОК.
Рис. 12
4. Непараметрическое
сравнение выборочных статистик.
U-критерий Манна-Уитни Ограничения применимости критерия
-
В каждой из выборок
должно быть не менее 3 значений признака.
Допускается, чтобы в одной выборке было
два значения, но во второй тогда не
менее пяти. -
В каждой выборке
должно быть не более 60 значений параметра,
но уже при выборках в 20 и более единиц
ранжирование становится довольно
трудоемким.
Для применения
U-критерия Манна-Уитни нужно произвести
следующие операции.
-
Составить единый
ранжированный (в порядке возрастания)
ряд из обоих сопоставляемых выборок,
каждому значению признака присвоить
ранг (ранги –числа натурального ранга;
меньшему значению присваивается меньший
ранг; одинаковым значениям признака
присваивается одинаковый средний
ранг). -
Разделить единый
ранжированный ряд на два, состоящие
соответственно из единиц первой и
второй выборок. Подсчитать отдельно
сумму рангов, пришедшихся на долю
элементов первой выборки, и отдельно
— на долю элементов второй выборки.
Определить большую из двух ранговых
сумм (Tx),
соответствующую выборке с nx
единиц. -
Определить значение
U-критерия Манна-Уитни по формуле:
.
-
По таблице
определить критические значения
критерия для данных n1
и n2.
Если полученное значение U меньше
табличного или равно ему для избранного
уровня статистической значимости, то
признается наличие существенного
различия между уровнем признака в
рассматриваемых выборках (принимается
альтернативная гипотеза). Если же
полученное значение U больше табличного,
принимается нулевая гипотеза.
Достоверность различий тем выше, чем
меньше значение U.
Задача.
Но: Наблюдаемые
различия между значениями признака в
рассматриваемых выборках случайны.
На: Наблюдаемые
различия между значениями признака в
рассматриваемых выборках не случайны.
А. Ранжируем
варианты обеих выборок в один общий
ряд. Для этого:
-
Создадим еще одну
таблицу (Табл.
4): 1 столбец
– значения признака (в обеих выборках),
2 столбец – номер выборки. -
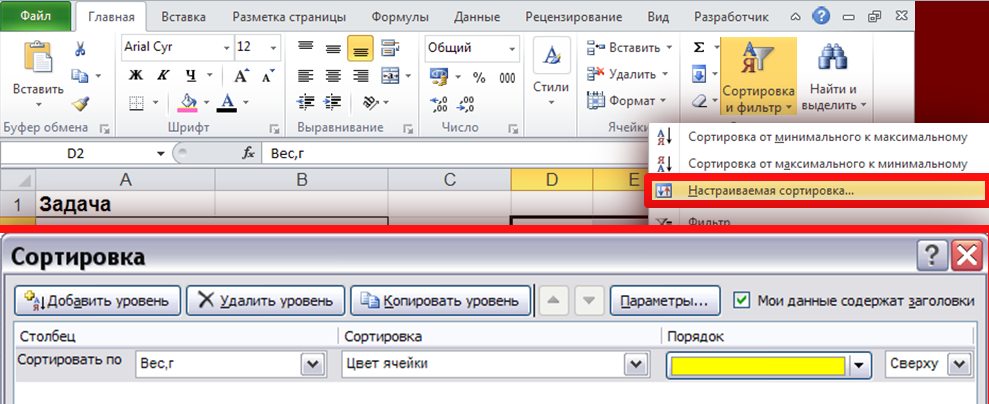
В
Рис. 13
ыделяем оба столбца (без названий)
и сортируем (Данные-Сортировка)
данные по столбцу со значениями признака
(Рис. 13).
-
Вводим еще два
столбца: 1- с порядковыми значениями
вариант и 2 – где вычисляем для каждой
варианты ранг (одинаковым значениям
признака присваивается одинаковый
ранг) (Табл.
4).
Табл. 4.
Ранжирование данных обеих выборок в
единый ряд и присвоение рангов отдельным
значениям признака.
|
Варианты |
Номер |
Порядковый |
Ранги |
Находим сумму
рангов отдельно для каждой выборки
(можно опять воспользоваться сортировкой
данных – выделить всю таблицу и
отсортировать по столбцу Номер
выборки),
результаты оформляем в виде таблицы —
Табл. 5.
Таблица 5.
Сравнение выборок с помощью критерия
Манна-Уитни
|
Показатели |
Выборка |
Выборка |
|
Сумма |
||
|
Объем |
||
|
Критерий |
||
|
Ust |
Примечание: N1
и N2
– ранги вариант первой и второй выборки
Но принимается
если U>Ust.
Ust
берем из таблицы (файл табл.кр.
знач.Манна_Уитни.pdf).
Соседние файлы в папке Задание 6
- #
- #
16.04.201552.74 Кб68Схема_отчета_6.xls