Задание
Для
случайной выборки объемом n=50
с несовпадающими числами выполнить
следующую последовательность действий:
1.Вывести
на лист Excel
исходные статистические данные.
2. Построить
вариационный ряд.
3. Вычислить
статистические характеристики.
4. Построить
интервальный статистический ряд.
5.Построить
гистограмму частот.
6. Составить
статистическую функцию распределения
статистического ряда.
7.
Составить и постоить статистическую
функцию распределения группированного
статистического ряда.
В качестве примера
рассмотрим следующую выборку
Порядок выполнения работы
1.Ввод исходных статистических данных.
Вводим данные в
первый столбец таблицы (рис.1).
рис.1
2. Построение вариационного ряда.
Производим
сортировку данных в порядке возрастания.
Для этого:
а) выделяем первый
столбец;
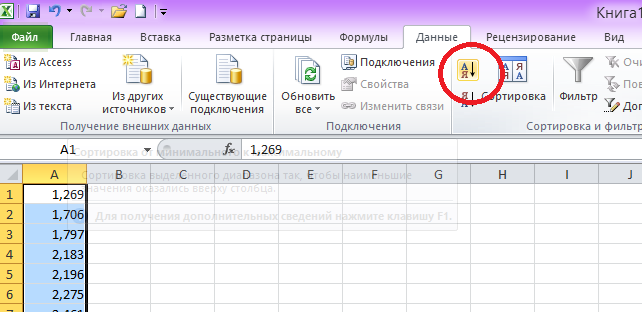
б)
на ленте
во вкладке «Данные» выбираем «Сортировка
и фильтр» (рис.2)
рис. 2
3. Вычисление статистических характеристик.
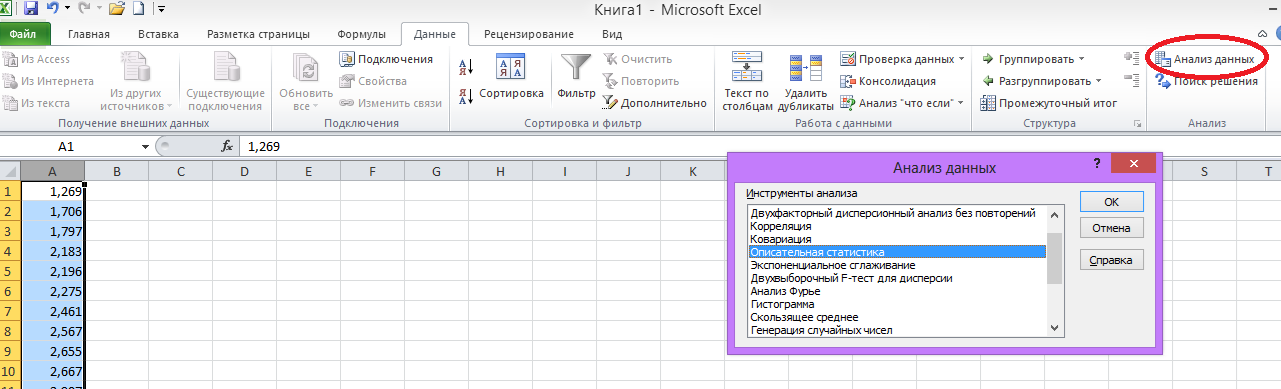
На ленте
во вкладке «Данные» выбираем «Анализ
данных» меню «Описательная статистика»
нажимаем ОК.
рис. 3
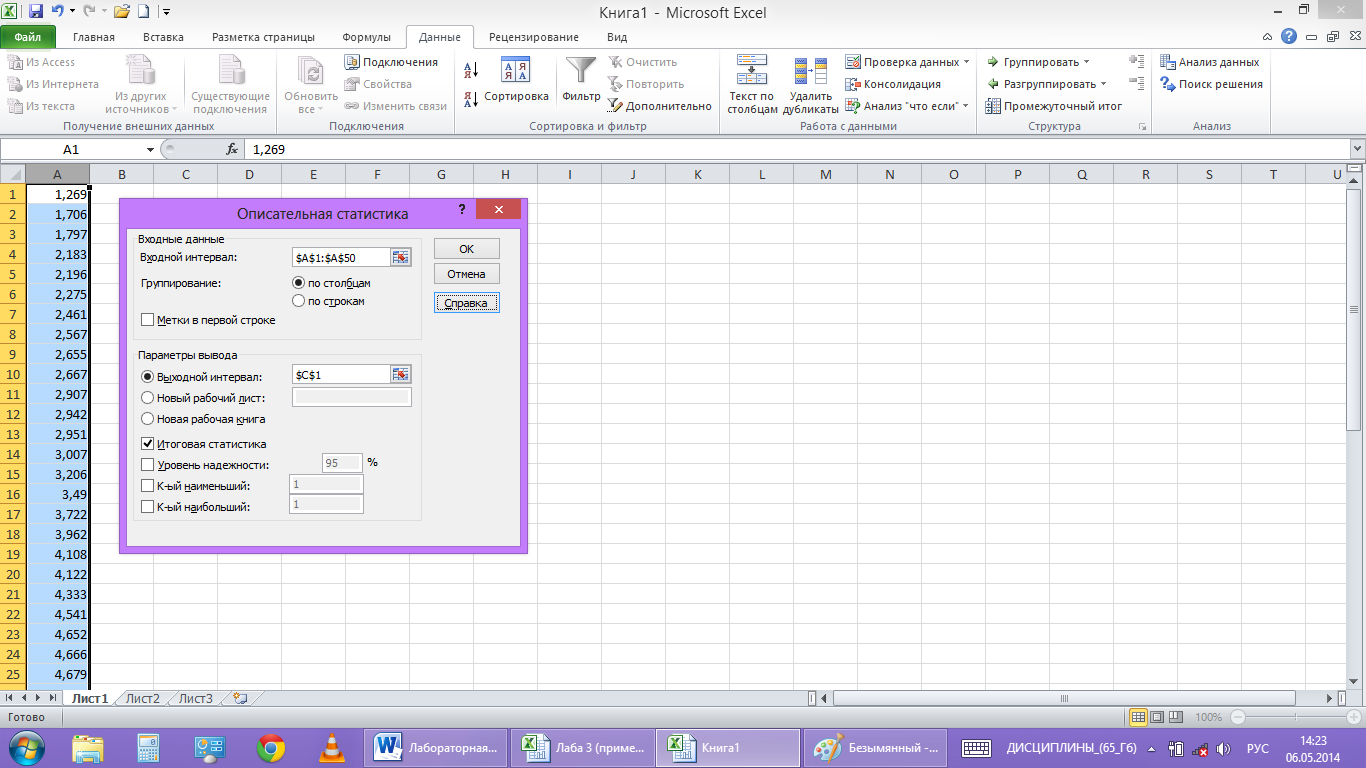
В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
а в пункте «Выходной интервал» обозначим
первую ячейку для записи результаов
$C$1.
Ставим флажок напротив пункта «Итоговая
статистика» и нажимаем ОК.(рис.4)
рис. 4
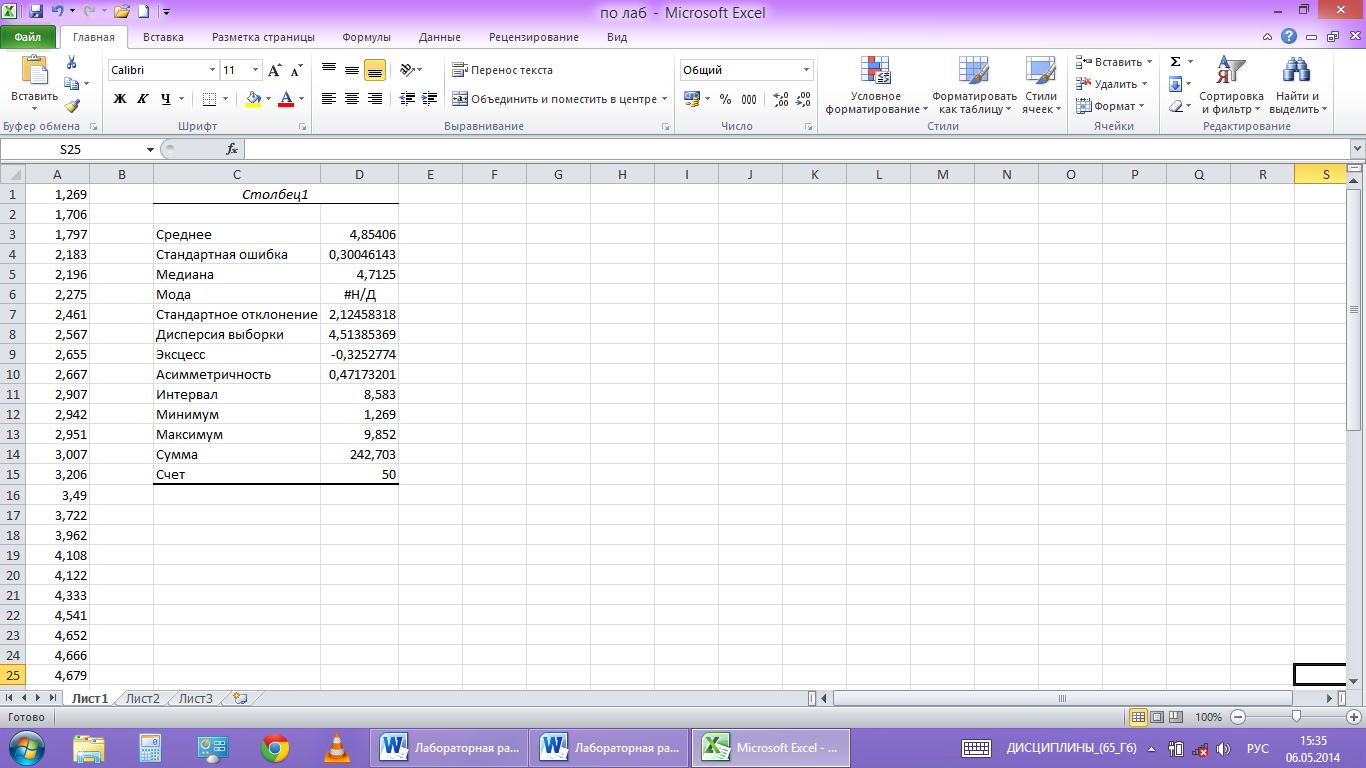
На
рабочем листе появляется таблица с
вычисленными значениями числовых
характеристик выборки (рис.5)
рис. 5
Здесь
«Среднее»означает математическое
ожидание выборки, а «Стандартная ошибка»
— погрешность ее значения. «Дисперсия
выборки» означает исправленную выборочную
дисперсию, а «Стандартное отклонение»
— исправленное среднее квадратичное
отклонение. Положительное значение
«Асимметричности» означает, что «длинная
часть» кривой лежит правее моды.
Отрицательное значение «Эксцесса»
означает, что кривая имеет более низкую
и «плоскую» вершину, чем нормальная
кривая. «Интервал» равен разности
Xmax−Xmin.
«Сумма»
дает результат суммирования всех
элементов выборки. «Счет» задает общее
число элементов выборки.
4. Построение интервального статистического ряда.
Длину интервала
группировки определяем по формуле
Необходимые данные
имеем в таблице: Xmax
– в ячейке D13,
Xmin–
в ячейке D12,
число элементов выборки n
— в ячейке D15.
В ячейку С16 вводим
слово «Интервал», в ячейку D16
вводим формулу
в ячейке D16
появится значение числа h.
В ячейку C17
вводим букву h.
В ячейку D17
вводим формулу
В ячейке
D17
получаем округленное до одного знака
после запятой значение интерала h.
Проведем формирование
интервалов. Для этого от Xmin
отступим влево примерно на h/2
и получим начальную точку отсчета.
Последовательно прибавляя к ней целое
число отрезков h,
получим все граничные точки интервалов.
В ячейку
F1
вводим формулу
В этой
ячейке появляется значение начальной
точки отсчета. В ячейку F2
вводим формулу
В этой
ячейке появляется значение второй
граничной точки первого интервала.
Возвращаемся в ячейку F2,
ставим курсор в правый нижний угол рамки
и двигаем его вниз, не отпуская левую
кнопку мыши. В результате такой процедуры
(протяжка) столбец F
заполнят граничные точки интервалов.
Самый нижний интервал должен включать
Xmax
(рис.6).
Проведем подсчет
числа вариант, попавших в каждый интервал,
определим относительные частоты и
серединные точки этих интервалов.
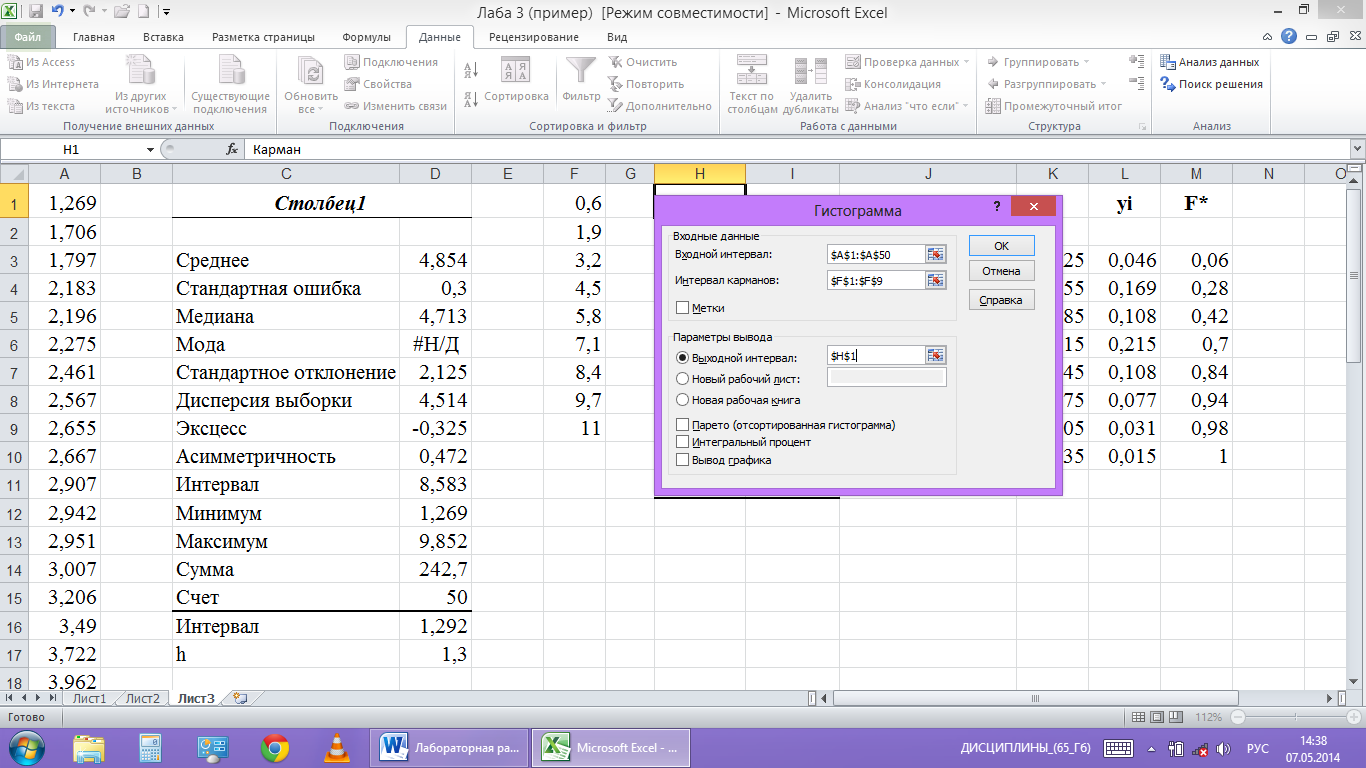
Для
этого на ленте во вкладке «Данные»
выбираем «Анализ данных» меню
«Гистограмма». (рис.
7)
|
|
|
|
рис. 6 |
рис. 7 |
В пункт
«Входной интервал» вводим диапазон
ячеек с исходными данными $A$1:$A$50,
в пункт «Интервал карманов» — диапазон
ячеек с границами интервалов $F$1:$F$9.
Отметим точкой пункт «Выходной интервал»
и введем в него адрес первой ячейки для
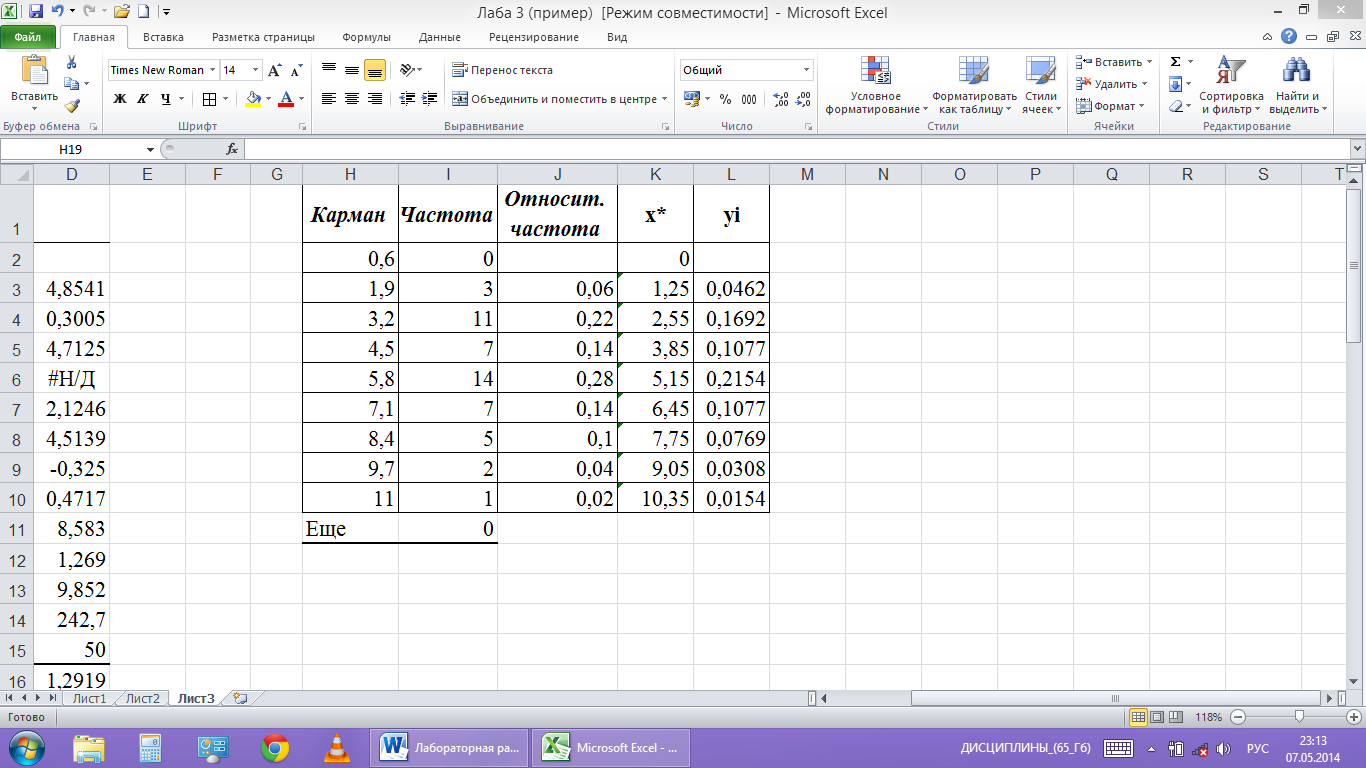
записи результатов $Н$1. Появится таблица
из двух столбцов с обозначениями «Карман»
и «Частота» (рис.8).
Определим
относительные частоты рi*,
значения серединных точек интервалов
и высоты
прямоугольников
Для этого
-
в ячейку
J1
введем заголовок «Относительная
частота»; -
В ячейку
J3
введем формулу
и
протягиваем её вниз до ячейки J10.
В результате к таблице из двух столбцов
добавится третий столбец (рис.8). В этой
таблице частота появления случайной
величины в каждом интервале записана
в одной строке с концом интервала;
-
в ячейку
K1
введем заголовок столбца Х*; -
в ячейку
К3 введем формулу
Протягиваем
эту формулу до ячейки К10. В результате
в четвертом столбце таблицы (рис.8)
появятся значения серединных точек
интервалов;
-
в ячейку
L1
введем заголовок столбца Уi; -
в ячейку
L3
введем формулу
Протягиваем
её вниз до ячейки L10.
В
результате в пятом столбце таблицы
(рис.8) появятся значения Уi.
рис.8
Соседние файлы в папке Лаб.работы
- #
- #
- #
- #
- #
- #
- #
Как построить вариационный ряд в Excel
Вариационный ряд может быть:
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Решение.
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда
7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
Примечание: можно скачать готовый шаблон построение дискретного вариационного ряда в Excel
Следующая тема: Построение интервального вариационного ряда в Excel.
Построение вариационных рядов, графическое изображение вариационного ряда с помощью MS Office Excel
При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение — это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.
Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, — генеральной совокупностью.
Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Элементами выборки (x1 х2, . хп) являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (а, b).
Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если вариационный ряд содержит значения признака и соответствующие ему частоты,то такой ряд носит название дискретный вариационный ряд. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала, то строим интервальный вариационный.
Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Пример 2.1.
Известны следующие данные о результатах сдачи студентами экзамена (в баллах):
| 18 | 16 | 20 | 17 | 19 | 20 | 17 |
| 17 | 12 | 15 | 20 | 18 | 19 | 18 |
| 18 | 16 | 18 | 14 | 14 | 17 | 19 |
| 16 | 14 | 19 | 12 | 15 | 16 | 20 |
Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.
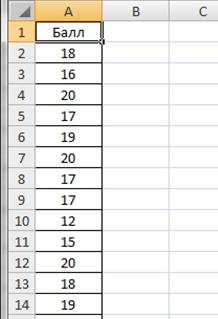
Введем данные в диапазоне A1: A29, в ячейку A1 введем текст «Балл» (рис.2.6).
Рисунок 2.6. Баллы успеваемости студентов
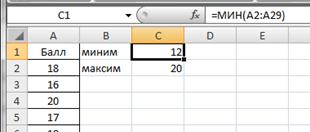
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).
Рисунок 2.7. Минимальный и максимальный балл
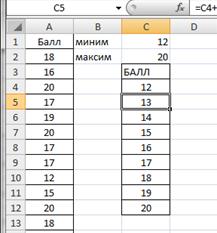
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.
Рисунок 2.8. Значения признака
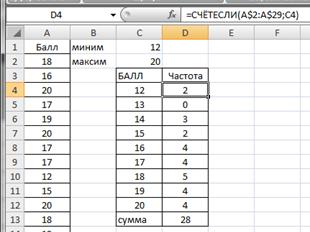
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).
Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.
Рис.2.9. Частоты вариационного ряда
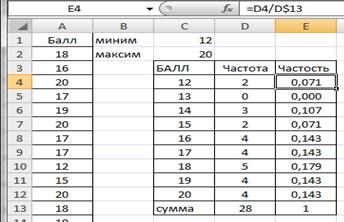
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).
Рисунок 2.10. Частости ряда распределения
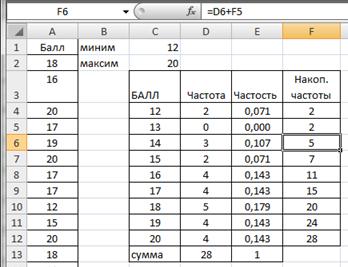
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).
Рисунок 2.11. Накопленные частоты ряда
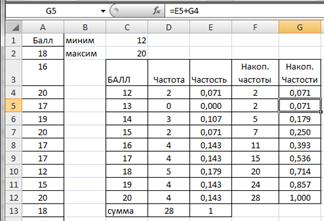
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.
Рисунок 2.12. Накопленные частости ряда
Построим полигон распределения частот и частостей. Выделим диапазон ячеек С4:D12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частот представлен на рисунке 2.13.
Рисунок 2.13. Полигон распределения частот
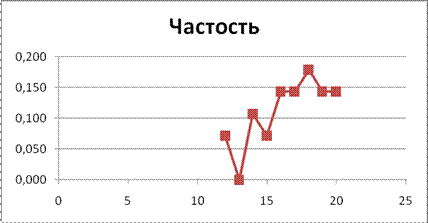
Выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон Е4:Е12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.
Рисунок 2.14. Полигон распределения частостей
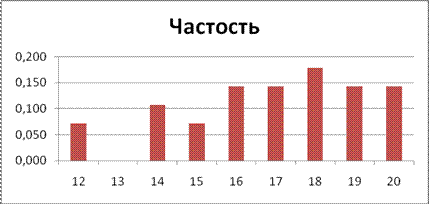
Построим гистограмму распределения частостей, для чего выделим диапазон Е4:Е12, выберем тип диаграммы «Гистограмма». Щелкнем правой кнопкой в области диаграммы, выберем «Выбрать данные», выберете «Ряд» — «Изменить», левой кнопкой щелкнем в строке «Подписи оси Х» и выделим диапазон С4:С12 (рис.2.15).
Рисунок 2.15. Гистограмма распределения частостей
Построим кумуляту частостей, для чего выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон G4:G12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками». Кумулята представлена на рис.2.16.
Рисунок 2.16. Кумулята
Пример 2.2.
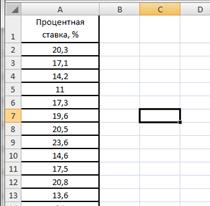
В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.
Банковские процентные ставки
| № Банка | Процентная ставка, % |
| 1 | 20,3 |
| 2 | 17,1 |
| 3 | 14,2 |
| 4 | 11,0 |
| 5 | 17,3 |
| 6 | 19,6 |
| 7 | 20,5 |
| 8 | 23,6 |
| 9 | 14,6 |
| 10 | 17,5 |
| 11 | 20,8 |
| 12 | 13,6 |
| 13 | 24,0 |
| 14 | 17,5 |
| 15 | 15,0 |
| 16 | 21,1 |
| 17 | 17,6 |
| 18 | 15,8 |
| 19 | 18,8 |
| 20 | 22,4 |
| 21 | 16,1 |
| 22 | 17,9 |
| 23 | 21,7 |
| 24 | 18,0 |
| 25 | 16,4 |
| 26 | 26,0 |
| 27 | 18,4 |
| 28 | 16,7 |
| 29 | 12,2 |
| 30 | 13,9 |
Построим интервальный вариационный ряд. Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.
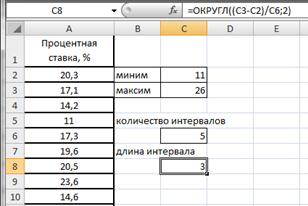
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).
Рисунок 2.17. Процентные ставки банков
Рисунок 2.18. Число интервалов
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).
Рисунок 2.19. Длина интервала
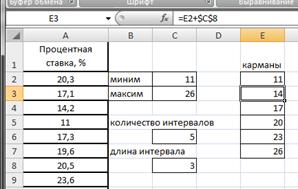
Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).
Рисунок 2.20. Границы интервалов
Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.
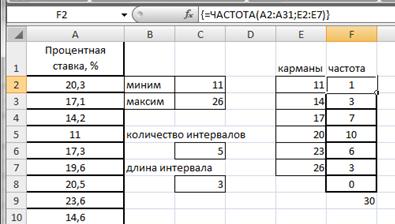
Воспользуемся функцией ЧАСТОТА. Для этого в ячейке F2 введем формулу =ЧАСТОТА(A2:A31;E2:E7). Протянем F2 маркером заполнения вниз до F8.
Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).
Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.
Рисунок 2.21. Частоты значений признака
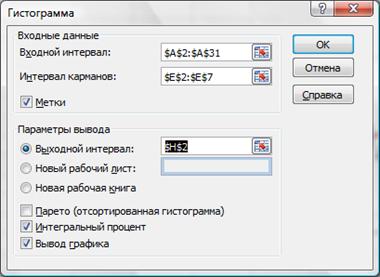
Также можно воспользоваться средством Пакета анализа (Анализ данных в Office 2007) ГИСТОГРАММА (рис.2.22). Выберем входной интервал, интервал карманов, метки, интегральный процент, поместим результаты на этом же листе (укажем ячейку $H$2).
Рисунок 2.22. Построение гистограммы
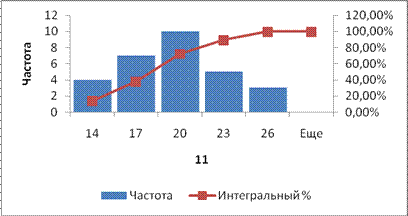
Полученная гистограмма представлена на рис.2.23.
Рис.2.23. Гистограмма частот
Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
Источник
2.2. Методика построения вариационных рядов и их графиков с помощью электронных таблиц Excel
Построим дискретный вариационный ряд по затратам труда на 1 ц зерна.
Открываем лист Excel, в ячейку А1 записываем условное обозначение результативного признака – у, а в ячейки А2:А31 значения затрат труда на 1 ц зерна. В ячейки В2:В3 введём наименьшее и следующее за ним значения признака 0,7 и 0,8; выделим обе ячейки (В2 и В3). Щёлкнем мышью правый нижний угол выделительной рамки и потянем вниз до значения 1,5 (наибольшее значение признака). В ячейках В2:В10 получим варианты признака в ранжированном порядке. Для определения частот проделаем следующие шаги:
1.Поставим курсор в ячейку С2.
2.Выберем Вставка, Функция.
Выберем в категории Статистические функции функцию Частота и нажмём ОК.
3.В поле данных укажем ячейки А2:А31, а в поле интервалов В2:В10.
4.Нажмём кнопку ОК.
5.Выделим ячейки С2:С10.
6.Нажмём F2, а затем комбинацию клавиш Shift+Ctrl+Enter.
В ячейках С2:С10 появятся частоты.
Вычислим накопленные частоты, которые потребуются для дальнейших расчётов, путём последовательного суммирования локальных частот (нарастающим итогом). Так, первая плюс вторая частоты дают накопленную частоту второго варианта (1+2=3); прибавляя к ней третью частоту, получим накопленную частоту третьего варианта (3+4=7) и т.д.
Скопируем полученный в Excel вариационный ряд и построим таблицу.
Дискретный вариационный ряд распределения затрат труда на 1 ц зерна
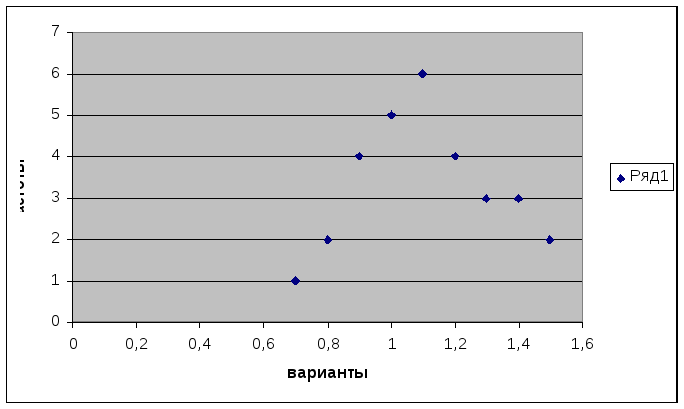
Построим полигон распределения частот с помощью Мастера диаграмм. Выберем точечную диаграмму, соединим полученные точки отрезками, а крайние точки с осью абсцисс в точках, отстоящих от крайних на расстоянии шага.
Р
Рассмотрим построение интервального вариационного ряда.
Рис. 2. Построение интервального вариационного ряда
На листе Excel в ячейку А1 записываем условное обозначение факторного признака – х, в ячейки А2:А31 – значения факторного признака – урожайности озимой пшеницы. Произведём сортировку данных, для чего выделяем диапазон данных, выбираем Данные – Сортировка и в появившемся окне «Сортировка диапазона» указываем «по возрастанию», нажимаем ОК. Данные в ячейках А2:А31 расположатся в ранжированном порядке по возрастанию признака. По формуле Стерджесса определяем количество групп (интервалов). Для вычисления десятичного логарифма lg30 выбираем Мастер функций – Математические – LOG10. В появившемся окне в поле Число записываем число 30, десятичный логарифм которого необходимо найти. Нажатием ОК получаем этот логарифм 1,477121. . Подставляя числовые данные в формулу (1), получим число групп (интервалов) 5,9, округляем до 6. По формуле (2) определяем величину интервалов – шаг с такой же точностью, с которой даны исходные данные (в данном случае с точностью до десятых: (30-20)/6≈1,7. Следовательно, совокупность надо разбить на 6 интервалов. Получаем шаг 1,7. Озаглавим следующие столбцы в Excel словами «Интервалы», «Частоты», «Накопленные частоты», «Середины интервалов». В ячейку В2 вписываем минимальное значение признака Хmin=20, в ячейку В3 формулу =В2+1,7, т.е. минимальное значение плюс шаг. Копируем эту формулу на 5 строк вниз. В результате в этих шести строках (В3:В8) получим верхние границы всех интервалов. Нижними границами интервалов будут данные в соседних верхних ячейках, т.е. для первого интервала нижней границей будет содержание ячейки В2, для второго В3 и для шестого В7.
Для расчёта частот выберем Сервис — Анализ данных – Гистограмма и нажмём ОК. В появившемся окне «Гистограмма» в поле «Входной интервал» копируем исходные данные (ячейки А2:А31), в поле «Интервал карманов» — верхние границы интервалов (ячейки В3:В8), в поле «Выходной интервал» ячейки частот (С3:С8), нажимаем ОК. В ячейки D3:D8 будут записаны частоты для всех шести интервалов. Накопленные частоты подсчитываем нарастающим итогом.
Для построения диаграммы необходимо найти середины интервалов. Для этого вводим формулу расчёта середины интервала: 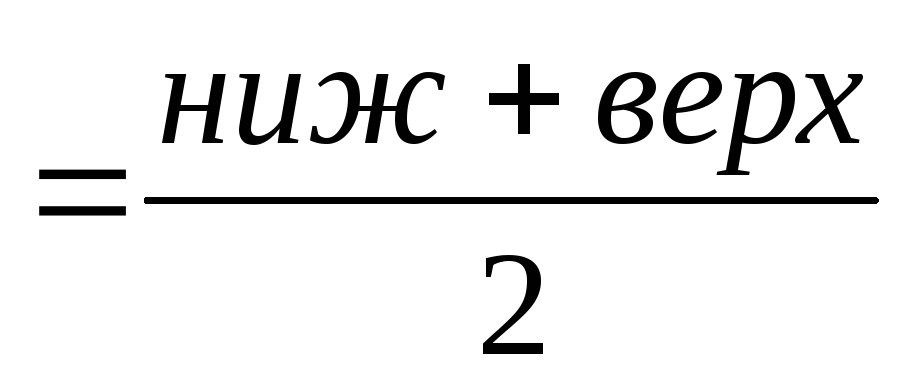
Для построения диаграммы выделяем массив частот и середин интервалов. Далее в Мастере диаграмм выбираем вид диаграммы — гистограмму определённого вида. Нажимаем кнопку Далее. В появившемся окне выбираем вкладку Ряд, удаляем ряд 1, а в поле «Подписи оси х» копируем середины интервалов. Нажимаем далее, в появившемся окне выбираем вкладку Заголовки. В поле «ось х (категорий)» вписываем название факторного признака (в данном случае урожайность, ц/га), в поле «Ось у (значений)» вписываем частоты. Нажимаем Далее, Готово. Появится диаграмма, состоящая из столбиков, отделённых друг от друга некоторым зазором. Щёлкаем правой кнопкой мыши на одном из столбиков диаграммы. В раскрывающемся списке элементов щёлкаем по кнопке Формат рядов данных. В появившемся диалоговом окне активизируем вкладку Параметры и в поле Ширина зазора устанавливаем значение 0. Нажимаем ОК, в результате чего гистограмма принимает стандартный вид.
Источник
Интервальные графики (статистические диаграммы) представляют собой полезный инструмент для анализа частотных данных, предлагая пользователям возможность сортировать данные в группы (называемые рядами) на визуальном графике, аналогичном гистограмме. В этой статье пошагово описано как создать статистическую диаграмму и выполнить её настройку в Microsoft Excel.
Если вы хотите создавать статистические диаграммы в Excel, вам нужно будет использовать Excel 2016 или более позднюю версию. В более ранних версиях Office (Excel 2013 и до неё) эта функция отсутствует.
Говоря простым языком, частотный анализ данных состоит в том, что берутся собранные результаты и определяется, как часто встретились те или иные значения. В качестве примера можно взять результаты тестов учащихся и посчитать, в каких диапазонах чаще всего встречаются полученные студентами результаты.
Статистические диаграммы позволяют легко получать данные такого рода и визуализировать их в диаграмме Excel.
Начните с того, что введите данные в Microsoft Excel и выделите данные, на основе которых будет строится интервальный график. Вы можете выбрать данные вручную или кликните на любую ячейку в нужном диапазоне и нажмите Ctrl+A на клавиатуре.

Выбрав данные, перейдите во вкладку «Вставить» на панели ленты. Различные доступные вам варианты графиков будут перечислены в разделе «Диаграммы» в середине. Нажмите кнопку «Вставить статистическую диаграмму», чтобы просмотреть список доступных диаграмм. В разделе «Гистограмма» раскрывающегося меню выберите первый верхний график слева.

В результате в вашу таблицу Excel будет вставлена гистограмма. Excel попытается параметры для данных, например, ширину интервалов, но вам может потребоваться внести изменения вручную после вставки диаграммы.
Форматирование гистограммы
Excel попытается определить интервалы и тип представления данных, но возможно вам придётся самостоятельно это настроить под ваши нужды. К примеру, в моём случае данные разбиты на 3 интервала, но я могу выбрать разбивку на интервалы с шагом в 10, либо отобразить данные по категориям. Рассмотрим это на конкретных примерах.
Кликните правой кнопкой мыши по надписям осей и выберите «Формат оси…»:
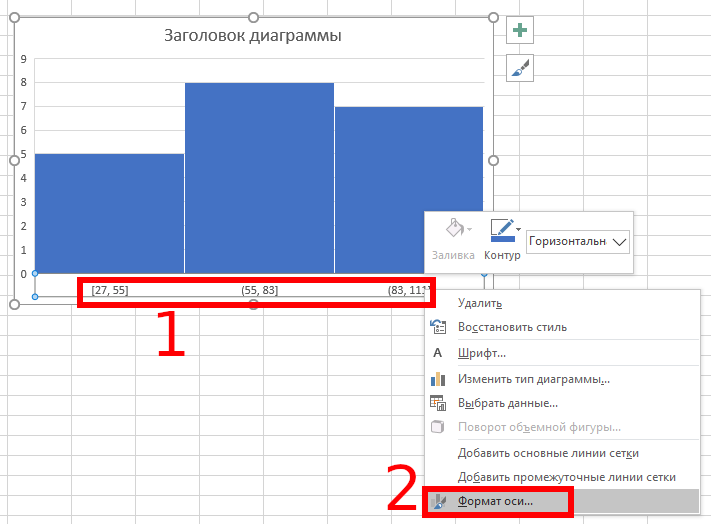
В открывшемся окне справа «Формат оси» выберите интервалы «По категориям»:

Теперь вы можете видеть каждое значение — в нашем случае это результаты тестов каждого из учеников.
Если нужен интервальный график, но с настраиваемой длиной интервала, то выберите вариант «Длина интервала» и установите нужную длину, например, 10:
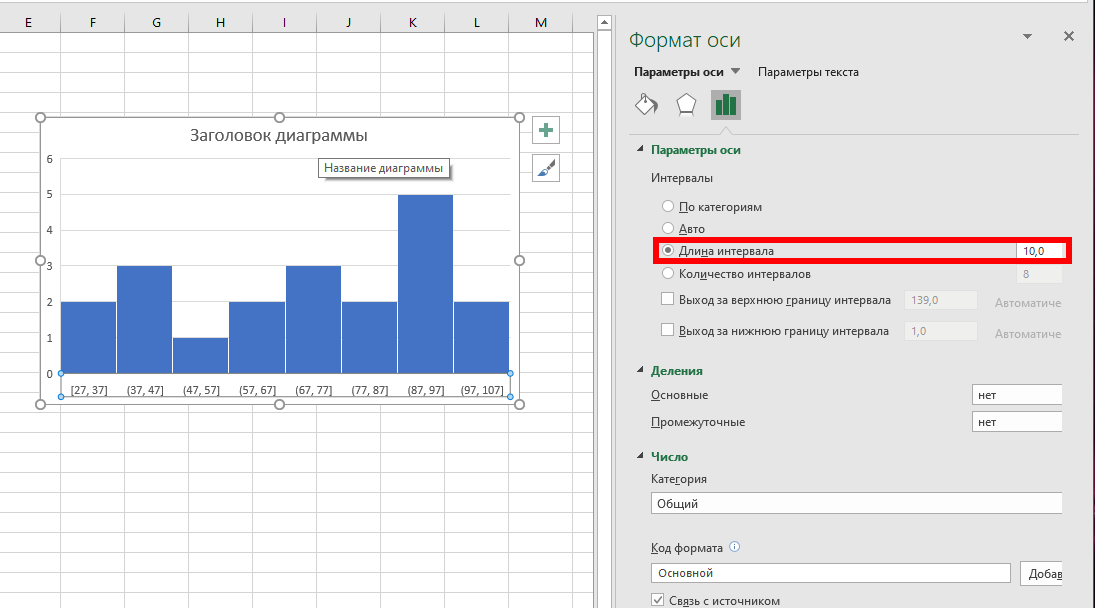
Диапазоны нижней оси начинаются с наименьшего числа. Например, первая группа ячеек отображается как «[27, 37]», а самый большой диапазон заканчивается «[97, 107]», несмотря на то, что максимальный результат теста равен 100.
Вы можете выбрать определённое количество интервалов, в этом случае из максимального значения будет вычтено минимальное и полученный результат поделён на указанное количество интервалов — в результате интервалы могут заканчиваться на дробные числа:
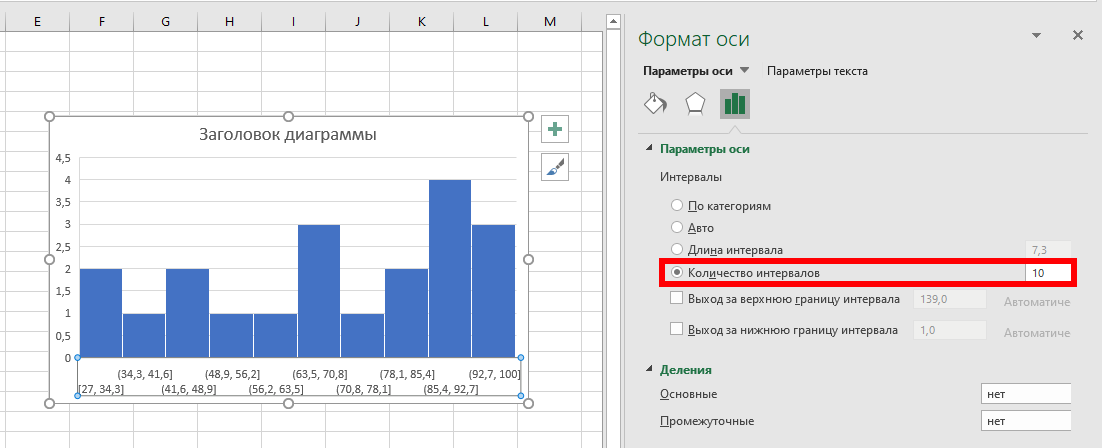
Вы можете собрать все данные, которые больше определённого значения, в одном интервале, независимо от его длины. Для этого поставьте флажок «Выход за верхнюю границу интервала» и укажите значение, выше которого все результаты будут помещены в один интервал:
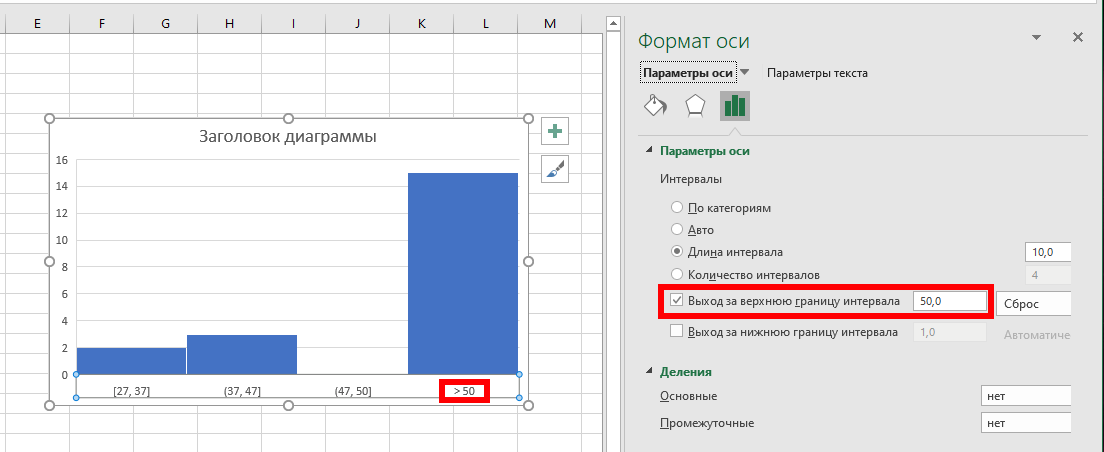
Аналогично в один интервал можно собрать все значения, ниже определённой величины, для этого поставьте флажок «Выход за нижнюю границу интервала» и укажите значение, ниже которого все результаты будут помещены в один интервал:
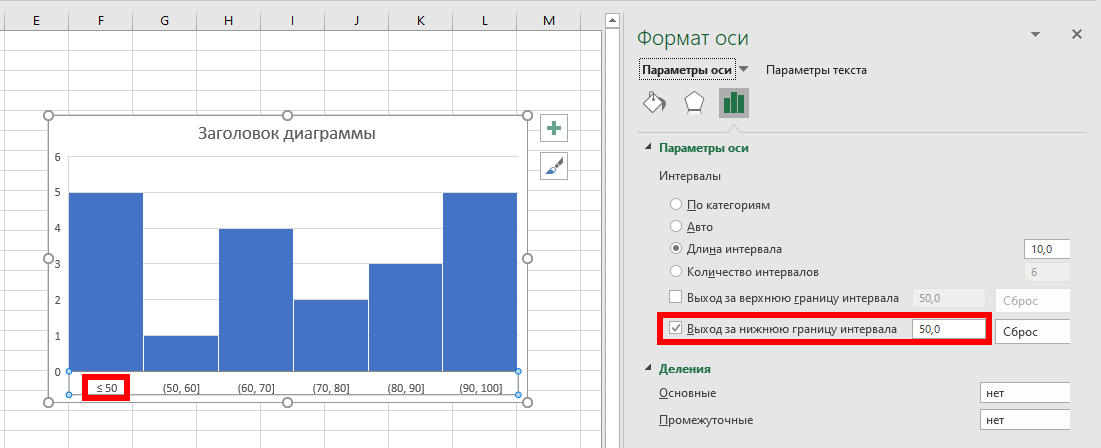
Эти опции работают в сочетании с другими форматами группировки интервалов, такими как ширина или количество интервалов.
Вы также можете вносить косметические изменения в вид интервального графика, включая замену заголовков и меток осей — для этого дважды кликните по области, которую вы хотите отредактировать. Дальнейшие изменения в тексте и цветах и параметрах панели можно выполнить, щёлкнув правой кнопкой мыши саму диаграмму и выбрав опцию «Форматировать область диаграммы».
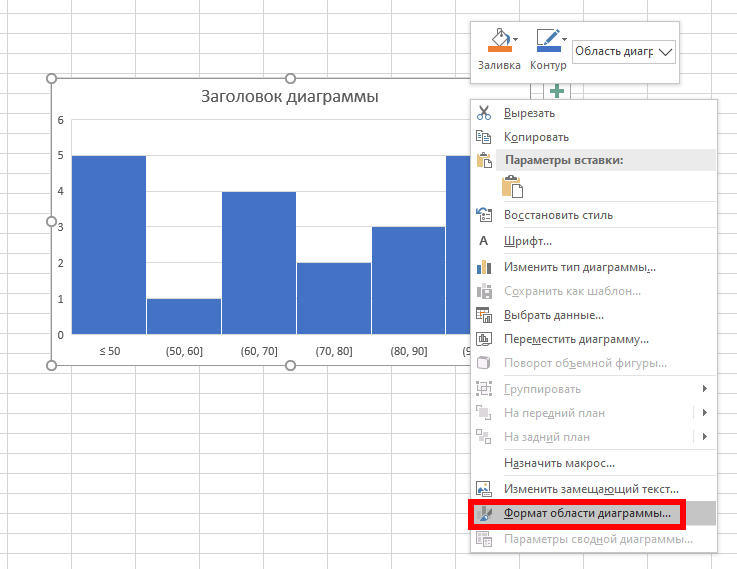
Стандартные параметры форматирования диаграммы, в том числе изменение границ и параметров столбцов, появятся в меню «Формат области диаграммы» справа.
Если вас интересуют вопросы редактирования внешнего вида, то они более подробно рассмотрены в статье «Как сделать гистограмму в Microsoft Excel», где показано, как применять готовые стили или вручную настроить любые параметры графиков, в том числе формат текста.
Связанные статьи:
- Как сделать палочковый график в Microsoft Excel (82.5%)
- Как сделать изогнутый график в Excel (69.3%)
- Как добавить подписи в графики Microsoft Excel (69.3%)
- Как сделать гистограмму в Microsoft Excel (69.3%)
- Функции Excel на русском (63.2%)
- Как в Word узнать количество символов во фрагменте текста и во всём тексте (RANDOM — 17.6%)
Построение рядов распределения
Любой ряд распределения характеризуется двумя элементами:
— варианта(хi) – это отдельные значения признака единиц выборочной совокупности. Для вариационного ряда варианта принимает числовые значения, для атрибутивного – качественные (например, х=«государственный служащий»);
— частота (ni) – число, показывающее, сколько раз встречается то или иное значение признака. Если частота выражена относительным числом (т.е. долей элементов совокупности, соответствующих данному значению варианты, в общем объеме совокупности), то она называется относительной частотойили частостью.
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Интервальный ряд может строиться как с интервалами равной длины (равноинтервальный ряд) так и с неодинаковыми интервалами, если это диктуется условиями статистического исследования. Например, может рассматриваться ряд распределения доходов населения со следующими интервалами:
где k – число интервалов, n – объем выборки. (Конечно, формула обычно дает число дробное, а в качестве числа интервалов выбирается ближайшее целое к полученному число.) Длина интервала в таком случае определяется по формуле
При работе в Excel для построения вариационных рядов могут быть использованы следующие функции:
— СЧЁТ(массив данных) – для определения объема выборки. Аргументом является диапазон ячеек, в котором находятся выборочные данные.
— СЧЁТЕСЛИ(диапазон; критерий) – может быть использована для построения атрибутивного или вариационного ряда. Аргументами являются диапазон массива выборочных значений признака и критерий – числовое или текстовое значение признака или номер ячейки, в которой оно находится. Результатом является частота появления этого значения в выборке.
Проиллюстрируем процесс первичной обработки данных на следующих примерах.
Пример 1.1. имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17. Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Теперь построим полигон: выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Пример 1.2. Имеются данные о выбросах загрязняющих веществ из 50 источников:
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Составить равноинтервальный ряд, построить гистограмму
Внесем массив данных в лист Excel, он займет диапазон А1:J5 Как и в предыдущей задаче, определим объем выборки n, минимальное и максимальное значения в выборке. Поскольку теперь требуется не дискретный, а интервальный ряд, и число интервалов в задаче не задано, вычислим число интервалов k по формуле Стерджесса. Для этого в ячейку В10 введем формулу =1+3,322*LOG10(B7).
Рис.1.4. Пример 2. Построение равноинтервального ряда
Полученное значение не является целым, оно равно примерно 6,64. Поскольку при k=7 длина интервалов будет выражаться целым числом (в отличие от случая k=6) выберем k=7, введя это значение в ячейку С10. Длину интервала d вычислим в ячейке В11, введя формулу =(В9-В8)/С10.
Рис.1.5. Пример 2. Построение равноинтервального ряда
Теперь заполним массив «карманов» при помощи функции ЧАСТОТА, как это было сделано в примере 1.
Рис.1.6. Пример 2. Построение равноинтервального ряда
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Если выбор количества интервалов или их диапазонов не устраивает, то можно в диалоговом окне указать нужный массив интервалов если интервал карманов включает текстовый заголовок, то нужно установить галочку напротив поля Метка. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Расчет ширины интервала и таблица интервалов приведены в файле примера на листе Гистограмма . Для вычисления количества значений, попадающих в каждый интервал, использована формула массива на основе функции ЧАСТОТА() . О вводе этой функции см. статью Функция ЧАСТОТА() – Подсчет ЧИСЛОвых значений в MS EXCEL .
Для построений необходимо выделить всю таблицу вместе с заголовком и выполнить команду вкладка Вставка — инструмент Точечная. Выбираем вариант Точечная с гладкими кривыми и маркерами как более показательный.
| 10,4 | 18,6 | 10,3 | 26,0 | 45,0 | 18,2 | 17,3 | 19,2 | 25,8 | 18,7 |
| 28,2 | 25,2 | 18,4 | 17,5 | 41,8 | 14,6 | 10,0 | 37,8 | 10,5 | 16,0 |
| 18,1 | 16,8 | 38,5 | 37,7 | 17,9 | 29,0 | 10,1 | 28,0 | 12,0 | 14,0 |
| 14,2 | 20,8 | 13,5 | 42,4 | 15,5 | 17,9 | 19, | 10,8 | 12,1 | 12,4 |
| 12,9 | 12,6 | 16,8 | 19,7 | 18,3 | 36,8 | 15,0 | 37,0 | 13,0 | 19,5 |
Стиль и внешний вид гистограммы
После того, как вы создали гистограмму, вам может потребоваться внести корректировки в то, как выглядит ваш график. Для изменения дизайна и стиля используйте вкладку “Конструктор”. Эта вкладка отображается на Панели инструментов, когда вы выделяете левой клавишей мыши гистограмму. С помощью дополнительных настроек в разделе “Конструктор” вы сможете:
- добавить заголовок и другие дополнительные данные для отображения. Для того, чтобы добавить данные на график, кликните на пункт “Добавить элемент диаграммы”, затем, выберите нужный пункт из выпадающего списка:
Вы также можете использовать кнопки быстрого доступа к редактированию элементов гистограммы, стиля и фильтров:
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Получили следующий набор данных 18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29 Постройте интервальный ряд и исследуйте его. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Например:
Для распределения учеников по росту получаем: begin S^2=fraccdot 104,1approx 105,1\ sapprox 10,3 end Коэффициент вариации: $ V=fraccdot 100textapprox 6,0textlt 33text $ Выборка однородна. Найденное значение среднего роста (X_)=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
Интервальный вариационный ряд и его характеристики: построение, гистограмма, выборочная дисперсия и СКО
- автоматически рассчитаны интервалы значений (карманы);
- подсчитано количество значений из указанного массива данных, попадающих в каждый интервал (построена таблица частот);
- если поставлена галочка напротив пункта Вывод графика , то вместе с таблицей частот будет выведена гистограмма.
Ряды распределения одна из разновидностей статистических рядов (кроме них в статистике используются ряды динамики), используются для анализа данных о явлениях общественной жизни. Построение вариационных рядов вполне посильная задача для каждого. Однако есть правила, которые необходимо помнить.