Как построить вариационный ряд в Excel
Вариационный ряд может быть:
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Решение.
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда
7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
Примечание: можно скачать готовый шаблон построение дискретного вариационного ряда в Excel
Следующая тема: Построение интервального вариационного ряда в Excel.
Создание вариационного
ряда, вариационной кривой, определение среднего значения и среднеквадратичного
отклонения.
Для селекционера,
например, важно знать, сколько зерен содержит колос выведенного (выводимого) им
нового сорта пшеницы. В этой ситуации совершенно ясно, что подсчетом количества
зерен только в одном колосе не обойтись. Для определения числа зерен надо
воспользоваться достаточно большим количеством колосьев, скажем не менее сотни.
Приведем пример математической обработки результатов селекции.
Все поле
пшеницы, которое вырастил селекционер можно на математическом языке назвать
генеральной совокупностью. Подсчитать количество зерен в колосьях всей
генеральной совокупности, очевидно, не представляется возможным, но из всей
генеральной совокупности можно выбрать, скажем, сто колосьев и подсчитать
количество зерен в них. Эти сто колосьев будут называться выборкой из генеральной
совокупности, и они с определенной точностью будут отражать число зерен во всем
поле (генеральной совокупности). Чтобы по данным выборки иметь возможность
судить обо всей генеральной совокупности, она должна быть отобрана случайно.
Так в нашем случае селекционер ни в коем случае не должен отдавать предпочтение
тем или иным колосьям (по размерам, внешнему виду, месту произрастания на поле
и т.п.) в процессе их выборки. Наиболее целесообразно в данной ситуации
совершать выбор колосьев из непрозрачного мешка наугад. У всех выбранных
колосьев производится подсчет числа зерен, и результаты фиксируются в виде ряда
чисел, с которыми в дальнейшем и предстоит совершать математические действия. В
данном примере можно предложить следующую их последовательность.
2.1 Создание вариационного ряда.
Вариационным
рядом называется ранжированный в порядке возрастания или убывания ряд вариантов
с соответствующими им весами (частотами или частностями). Вариационный ряд
будет дискретным, если любые его варианты отличаются на постоянную величину, и
непрерывным, если варианты могут отличатся один от другого на сколь угодно
малую величину.
Иными словами в вариационном ряду
полученные значения располагаются в порядке их увеличения и, если значение
повторяется, то рядом записывается число его повторений. Т.е. в данном примере
по числу зерен в колосьях ряд может выглядеть так (таб. 2):
Таблица 2
|
Число зерен в колосе |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
Число колосьев |
1 |
2 |
2 |
4 |
6 |
8 |
8 |
9 |
10 |
|
Число зерен в колосе |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
|
Число колосьев |
9 |
9 |
9 |
8 |
6 |
4 |
3 |
1 |
1 |
Полученный вариационный ряд
позволяет выявить закономерности распределения колосьев по числу зерен в них.
2.2 Создание вариационной
кривой.
Закономерности распределения
можно представить более наглядно, создав вариационную кривую, называемую
полигоном (рис 3), или представить в виде столбчатой диаграммы, которая здесь
будет называться гистограммой (рис 4).
Из полученных схем уже можно наглядно судить о закономерностях
распределения.
Диаграммы
строятся при помощи «Excel»
так:
Ø Ввести в окно программы данные вариационного
ряда.
Ø Запустить «Мастер диаграмм», нажатием
кнопки 
Ø В графе «тип» выбирать или «гистограмма», или
«график».
Ø Нажать кнопку «Далее».
Ø В «шаге 2 из 4» найти строку с названием
«Диапазон» и щелкнуть по кнопке, расположенной справа от надписи и пустого
поля, при этом «Мастер диаграмм» несколько свернется.
Ø Выделить данные в окне программы (в примере это
значения в ячейках В1 – В18).
Ø Снова щелкнуть по кнопке в «Мастере диаграмм».
«Мастер» развернется. В окне «Мастера» появится эскиз гистограммы или полигона.
Ø В этом же шаге (2 из 4) щелкнуть по закладке с
надписью «Ряд».
Ø В открывшейся страничке найти строчку с надписью
«Подписи оси Х».
Ø Щелкнуть по кнопке справа от надписи и пустого
поля.
Ø Выделить значения в окне программы, которые
будут на диаграмме представляться в качестве данных оси Х. (в примере значения
в ячейках А1 – А18).
Ø Щелкнуть по кнопке в свернутом «Мастере».
Ø Щелкнуть по кнопке «Далее» (шаг 3 из 4).
Ø При необходимости, в графе «Заголовки» выполнить
подписи осей Х и Y, а
так же дать диаграмме название.
Ø Щелкнуть по кнопке далее, затем готово и в
результате получится готовая гистограмма или полигон (рис 3).
2.3 Определение среднего значения признака.
Среднее
значение ряда данных находится обычным образом. Суммируются все значения
признака и делятся на количество этих значений. Т.е. здесь общее число зерен в
100 колосках равно 2551, то среднее значение будет равно 2551/100 = 25.51.
Для определения
среднего значения признака с использованием «Excel» надо выполнить следующие шаги:
Ø Ввести в столбец А окна программы все значения
признака, в том числе и повторяющиеся. Т.е. здесь все 100 значений зерен в
колосках. Ввод можно осуществлять в любой последовательности – по возрастанию,
по убыванию или в разнобой. Введенный массив чисел лучше сохранить, так как он
пригодится для расчета отклонения.
Ø Щелкнуть в окне программы по любой пустой
ячейке. По окончании расчетов в ней появится соответствующее среднее значение.
Ø В меню «Вставка» выбрать «Функция».
Ø В появившемся списке функций выбрать функцию
«СРЗНАЧ».
Ø Щелкнуть по кнопке «ОК». Появится окно
«Аргументы функции».
Ø Щелкнуть по кнопке правее надписи «Число 1» и
поля (окно свернется).
Ø Выделить в окне программы весь числовой массив,
среднее значение которого необходимо определить.
Ø Щелчком по кнопке справа от поля с надписями
развернуть окно «Аргументы функции».
Ø Щелкнуть по кнопке «ОК». В выбранной
предварительно ячейке появится среднее значение массива чисел.
2.4 Определение среднего квадратического
отклонения.
Вариационная кривая имеет
определенную ширину. Нетрудно догадаться, что чем больше ширина вариационной
кривой, тем сильнее разброс значений относительно средней величины.
Как показано на рисунках 5 и 6 при
одном и том же среднем значении, равном 25.51, полигон первого рисунка шире
полигона второго.
Оценить
степень разброса данных относительно среднего значения можно рассчитав значение
дисперсии S2,
или среднее квадратическое отклонение S, равное корню квадратному из дисперсии. Дисперсией вариационного ряда называется
средняя арифметическая квадратов отклонений вариантов от их средней
арифметической. Значением среднего квадратического отклонения пользоваться
удобнее, так как оно выражается в тех же единицах, что и значение признака. Так
среднее квадратическое отклонение данных, представленных графически на первом
полигоне равно 3.70, а на втором полигоне 2.65. Видим, что отклонение первое
больше второго и это как раз и отражается на ширине полигона.
Алгоритм
расчета среднего квадратического отклонения
и дисперсии такой же, как и для расчета среднего арифметического
значения, только в списке функций надо выбрать «СТАНДОТКЛОН» для вычисления отклонения, или «ДИСП» для расчета дисперсии.
Построим дискретный вариационный ряд
по затратам труда на 1 ц зерна.
Открываем лист Excel,
в ячейку А1 записываем условное обозначение
результативного признака – у, а в ячейки
А2:А31 значения затрат труда на 1 ц зерна.
В ячейки В2:В3 введём наименьшее и
следующее за ним значения признака 0,7
и 0,8; выделим обе ячейки (В2 и В3). Щёлкнем
мышью правый нижний угол выделительной
рамки и потянем вниз до значения 1,5
(наибольшее значение признака). В ячейках
В2:В10 получим варианты признака в
ранжированном порядке. Для определения
частот проделаем следующие шаги:
1.Поставим курсор в ячейку С2.
2.Выберем Вставка,
Функция.
Выберем в категории
Статистические функции
функцию Частота и
нажмём ОК.
3.В поле данных
укажем ячейки А2:А31, а в поле интервалов
В2:В10.
4.Нажмём кнопку ОК.
5.Выделим ячейки
С2:С10.
6.Нажмём F2,
а затем комбинацию клавиш Shift+Ctrl+Enter.
В ячейках С2:С10 появятся
частоты.
Вычислим накопленные
частоты, которые потребуются для
дальнейших расчётов, путём последовательного
суммирования локальных частот (нарастающим
итогом). Так, первая плюс вторая частоты
дают накопленную частоту второго
варианта (1+2=3); прибавляя к ней третью
частоту, получим накопленную частоту
третьего варианта (3+4=7) и т.д.
Скопируем полученный
в Excel
вариационный ряд и построим таблицу.
Таблица 2
Дискретный вариационный ряд распределения
затрат труда на 1 ц зерна
|
Варианты |
Частоты |
Накопленные |
|
0,7 |
1 |
1 |
|
0,8 |
2 |
3 |
|
0,9 |
4 |
7 |
|
1,0 |
5 |
12 |
|
1,1 |
6 |
18 |
|
1,2 |
4 |
22 |
|
1,3 |
3 |
25 |
|
1,4 |
3 |
28 |
|
1,5 |
2 |
30 |
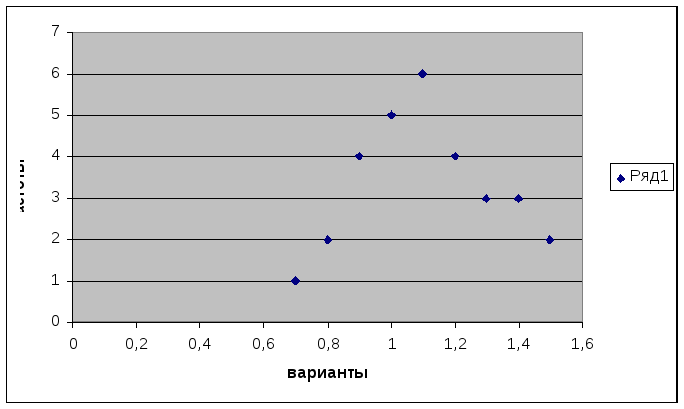
Построим
полигон распределения частот с помощью
Мастера
диаграмм.
Выберем точечную диаграмму, соединим
полученные точки отрезками, а крайние
точки с осью абсцисс в точках, отстоящих
от крайних на расстоянии шага.
Р
1. Полигон распределения сельскохозяйственных
предприятий по затратам труда на 1 ц
зерна
Рассмотрим
построение интервального вариационного
ряда.
Рис. 2. Построение интервального
вариационного ряда
На
листе Excel в ячейку А1 записываем условное
обозначение факторного признака – х,
в ячейки А2:А31 – значения факторного
признака – урожайности озимой пшеницы.
Произведём сортировку данных, для чего
выделяем диапазон данных, выбираем
Данные – Сортировка и в появившемся
окне «Сортировка диапазона» указываем
«по возрастанию», нажимаем ОК. Данные
в ячейках А2:А31 расположатся в ранжированном
порядке по возрастанию признака. По
формуле Стерджесса определяем количество
групп (интервалов). Для вычисления
десятичного логарифма lg30 выбираем
Мастер функций – Математические –
LOG10. В появившемся окне в поле Число
записываем число 30, десятичный логарифм
которого необходимо найти. Нажатием ОК
получаем этот логарифм 1,477121. . Подставляя
числовые данные в формулу (1), получим
число групп (интервалов) 5,9, округляем
до 6. По формуле (2) определяем величину
интервалов – шаг с такой же точностью,
с которой даны исходные данные (в данном
случае с точностью до десятых:
(30-20)/6≈1,7. Следовательно, совокупность
надо разбить на 6 интервалов. Получаем
шаг 1,7. Озаглавим следующие столбцы в
Excel словами «Интервалы», «Частоты»,
«Накопленные частоты», «Середины
интервалов». В ячейку В2 вписываем
минимальное значение признака Хmin=20,
в ячейку В3 формулу =В2+1,7, т.е. минимальное
значение плюс шаг. Копируем эту формулу
на 5 строк вниз. В результате в этих шести
строках (В3:В8) получим верхние границы
всех интервалов. Нижними границами
интервалов будут данные в соседних
верхних ячейках, т.е. для первого интервала
нижней границей будет содержание ячейки
В2, для второго В3 и для шестого В7.
Для
расчёта частот выберем Сервис — Анализ
данных – Гистограмма и нажмём ОК. В
появившемся окне «Гистограмма» в поле
«Входной интервал» копируем исходные
данные (ячейки А2:А31), в поле «Интервал
карманов» — верхние границы интервалов
(ячейки В3:В8), в поле «Выходной интервал»
ячейки частот (С3:С8), нажимаем ОК. В ячейки
D3:D8 будут записаны частоты для всех
шести интервалов. Накопленные частоты
подсчитываем нарастающим итогом.
Для
построения диаграммы необходимо найти
середины интервалов. Для этого вводим
формулу расчёта середины интервала:
,
рассчитаем середину первого интервала.
Копируем формулу для остальных пяти
групп.
Для
построения диаграммы выделяем массив
частот и середин интервалов.
Далее в
Мастере диаграмм выбираем вид диаграммы
— гистограмму определённого вида.
Нажимаем кнопку Далее. В появившемся
окне выбираем вкладку Ряд, удаляем ряд
1, а в поле «Подписи оси х» копируем
середины интервалов. Нажимаем далее, в
появившемся окне выбираем вкладку
Заголовки. В поле «ось х (категорий)»
вписываем название факторного признака
(в данном случае урожайность, ц/га), в
поле «Ось у (значений)» вписываем частоты.
Нажимаем Далее, Готово. Появится
диаграмма, состоящая из столбиков,
отделённых друг от друга некоторым
зазором. Щёлкаем правой кнопкой мыши
на одном из столбиков диаграммы. В
раскрывающемся списке элементов щёлкаем
по кнопке Формат рядов данных. В
появившемся диалоговом окне активизируем
вкладку Параметры и в поле Ширина зазора
устанавливаем значение 0. Нажимаем ОК,
в результате чего гистограмма принимает
стандартный вид.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1. Построение вариационного ряда
Нужно выделить ячейки содержащие результаты эксперимента, и воспользоваться операцией сортировка по возрастанию (либо с панели инструментов, либо через главное меню Данные>Сортировка), и в появившемся окне сообщения – «обнаружены данные выходящие за пределы выделенного диапазона» выбрать действие – «сортировать в пределах указанного выделения»
2. Построение группировочного статистического ряда
Для вычисления абсолютной частоты нужна статистическая функция ЧАСТОТА. При её использовании нужно выполнить следующие действия:
а) выделить весь диапазон ячеек, в которых будет располагаться результат подсчёта частот (т.е. это ячейки под заголовком Абсолютная частота в количестве равном числу промежутков)
b) не снимая выделения, поставить курсор в строку формул и нажать на кнопку вставка функции (чуть левее курсора) или Главное меню – вставка – формула.
с) выбрать функцию ЧАСТОТА
d) ввести Массив_данных – диапазон, содержащий элементы выборки (в файле 2.xls это ячейки) B2:B101
e) ввести Массив_интервалов – диапазон ячеек под заголовком Начало промежутка начиная со строчки, соответствующей промежутку под номером 2 до строчки, соответствующей последнему промежутку.
f) нажмите на кнопку ОК и после закрытия окна для ввода аргументов функции ЧАСТОТА поставьте курсор обратно в строку формул.
g) Нажмите на три кнопки Ctrl+Shift+Enter (сначала на первые две, а потом, не отпуская их, нажмите на Enter).
Примечание. Формулу вычисления абсолютной частоты необходимо ввести как формулу массива. Нажатие комбинации клавиш CTRL+SHIFT+ENTER позволяет определить формулу как формулу массива. Если формула не будет введена как формула массива, единственное значение будет равно 1.
В результате изначально выделенный диапазон будет содержать абсолютные частоты попадания во все промежутка. Проверьте, что сумма всех абсолютных частот равна общему числу элементов выборки (100).
3. Построение гистограммы группировочного статистического ряда
ВАРИАЦИОННЫЕ РЯДЫ.
ВЫБОРОЧНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
- Авторы
- Файлы работы
- Сертификаты
Растеряев Н.В. 1, Елисеев С.А. 1
1Филиал Федерального государственного автономного образовательного учреждения высшего образования «Южный федеральный университет» в г. Новошахтинске Ростовской области (филиал ЮФУ в г. Новошахтинске)
Комментарии
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
овладеть навыками составления дискретных и интервальных вариационных рядов выборки, построения выборочной (эмпирической) функции распределения в среде ЭТ MS.
Краткая теория
Для решения задач, связанных с анализом данных при наличии случайных непредсказуемых воздействий, разработан математический аппарат ‒ математическая статистика, что позволяет выявлять закономерности на основе случайностей, делать на их основе обоснованные выводы и прогнозы.
Важнейшими понятиями математической статистики являются понятия генеральной совокупности и выборки.
Генеральной совокупностью наблюдаемого признака (случайной величины) Х называют множество всевозможных значений, принимаемых наблюдаемым признаком Х.
Часть отобранных объектов из генеральной совокупности называется выборочной совокупностью, или выборкой. Результаты измерений изучаемого признака nобъектов выборочной совокупности порождают nзначений х1, х2, … , хn случайной величины X . Число nназывается объемом выборки.
Выборку можно рассматривать двояко:
а) как случайный вектор длины n, каждая компонента которого имеет такое же распределение, как и наблюдаемый признак;
б) как на результаты измерений, т.е. набор n чисел.
Случайная величина Х называется дискретной случайной величиной, если она принимает свое значение из некоторого конечного фиксированного набора, например, случайная величина Х ‒ число появления шестерки при двух бросках игрального кубика
Х: 0,1,2 .
Случайная величина Х называется непрерывной случайной величиной, если она принимает любое значение из некоторого интервала (в том числе ‒ ∞ и +∞), например, рост человека.
После получения выборки имеем данные, которые представляют собой множество чисел, расположенных в беспорядке. Анализ таких данных весьма затруднителен, и для изучения скрытых закономерностей их подвергают определенной обработке.
Простейшая операция – ранжирование опытных данных, результатом которого являются значения, расположенные в порядке неубывания. Если среди элементов встречаются одинаковые, то они объединяются в одну группу. Значение случайной величины, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называется вариантом, а изменение этого значения – варьированием. Варианты будем обозначать строчными буквами с соответствующими порядковому номеру группы индексами x(1) , x(2) , …, x(N) , где N – число групп. При этом x(1)< x(2)< … < x(N).
Численность отдельной группы сгруппированного ряда данных называется частотой ni , где i – индекс варианта, а отношение частоты данного варианта к общей сумме частот называется частностью (или относительной частотой) и обозначается ωi , i = 1, …,N , т.е.
ωi=nij=1Nnj ,
при этом j=1Nnj=n ‒ объему выборки.
Дискретным вариационным рядомназывается ранжированная совокупность вариантов x(i) с соответствующими им частотами niили частностями ωi .
Если число возможных значений дискретной случайной величины достаточно велико или наблюдаемая случайная величина является непрерывной, то строят интервальный вариационный ряд, под которым понимают упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частностями попаданий в каждый из них значений случайной величины.
Как правило, частичные интервалы, на которые разбивается весь интервал варьирования, имеют одинаковую длину Δ, которая может быть вычислена по следующей формуле
∆=RN=xmax-xminN .
где R – размах варьирования (изменения) случайной величины;
xmax , xmin – наибольшее и наименьшее значения исследуемой случайной величины;
N – число частичных интервалов группировки.
Некоторые авторы рекомендуют пользоваться следующими эмпирическими формулами для определения числа интервалов:
, N = 5.lg(n) ,
N = 1 + 3,322.lg(n) ‒ формула Стерджеса.
В рекомендациях по стандартизации Р 50.1.033-2001 «Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат» рекомендует следующие значения N в зависимости от объема выборки n:
|
Объем выборки n |
Число интервалов группировки N |
|
40 ‒ 100 |
7 ‒ 9 |
|
100 ‒ 500 |
8 ‒ 12 |
|
500 ‒ 1000 |
10 ‒ 16 |
|
1000 ‒ 10000 |
12 ‒ 22 |
В теории вероятностей для характеристики распределения случайной величины служит функция распределения
,
определяющую для каждого значения х вероятность того, что случайная величина Х примет значение, меньшее х, т.е. равная вероятности события , где – любое действительное число.
Одной из основных характеристик выборки является выборочная (эмпирическая) функция распределения
,
где – количество элементов выборки, меньших чем . Другими словами, есть относительная частота появления события в n независимых испытаниях. Главное различие между и состоит в том, что определяет вероятность события A, а выборочная функция распределения – относительную частоту этого события.
Свойства функции :
1. .
2. – неубывающая функция.
3.
Функция является «ступенчатой», имеются разрывы в точках, которым соответствуют наблюдаемые значения вариантов. Величина скачка равна относительной частоте варианта.
Аналитически задается следующим соотношением:
Fn*x= 0 при x≤x1 ;j=1i-1ωj при x(i-1)x(N) ,
где – соответствующие относительные частоты;
– элементы вариационного ряда (варианты).
Замечание. В случае интервального вариационного ряда под понимается середина i-го частичного интервала. Эмпирическую функцию распределения непрерывной случайной величины так же называют «накопленная частота».
Перед вычислением полезно построить дискретный или интервальный вариационный ряд.
Пример выполнения
Постановка задачи 1. На телефонной станции проводились наблюдения над числом неправильных соединений в минуту. Наблюдения в течение 30 минут дали следующие результаты (табл. 1).
Таблица 1.
|
3 |
0 |
1 |
5 |
1 |
2 |
4 |
5 |
3 |
4 |
|
2 |
4 |
2 |
0 |
2 |
3 |
1 |
3 |
2 |
1 |
|
4 |
3 |
0 |
2 |
1 |
0 |
4 |
2 |
3 |
2 |
Требуется найти дискретный вариационный ряд, выборочную (эмпирическую) функцию распределения данной выборки и построить ее график в среде ЭТ MS Excel.
Решение.
Очевидно, что число X является дискретной случайной величиной, а полученные данные есть значения этой случайной величины.
В результате выполнения операций ранжирования и группировки были получены шесть значений случайной величины (варианты): 0; 1; 2; 3; 4; 5. При этом значение 0 в этой группе встречается 4 раза, значение 1 – 5 раз, значение 2 – 8 раз, значение 3 – 6 раз, значение 4 – 5 раз, значение 5 – 2 раза. Вычисленные значения частот и частностей приведены в табл. 2.
Таблица 2.
|
Индекс |
1, 2, 3, 4, 5, 6 |
|
|
Вариант |
0, 1, 2, 3, 4, 5 |
|
|
Частота |
4, 5, 8, 6, 5, 2 |
|
|
Частность |
Используя данный дискретный вариационный ряд (см. табл. 2), вычислим значения по формуле, приведенной выше, и занесем их в табл. 3.
Таблица 3.
|
x |
|
|
x 0 |
0 |
|
0 < x 1 |
|
|
1 < x 2 |
|
|
2 < x 3 |
|
|
3 < x 4 |
|
|
4 < x 5 |
|
|
x > 5 |
По данным таблицы 3 построим график эмпирической функции распределения.
Решение задачи в среде ЭТ MSExcel. Для решения задачи в среде ЭТ MS Excel необходимо выполнить следующие действия:
1. Идентифицируйте свою работу, переименовав Лист1 в Титульный лист и записав номер лабораторной работы, ее название, кто выполнил и проверил.
2. Переименуйте Лист 2 в Дискретный. Наберите массив 30 значений исходных данных выборки.
3. Найдите величины хmax, хmin, n, используя встроенные функции Excel МАКС, МИН и СЧЕТ.
4. Сформируйте столбец вариант x(i)от 0 до 5 и с помощью функции ЧАСТОТА найдите частоту появления значений случайной величины Х в данном интервале.
Синтаксис функции:
ЧАСТОТА(массив данных;массив интервалов).
Массив данных ‒ массив или ссылка на множество данных, для которых вычисляются частоты. В нашем случае это диапазон B2:K2. Если массив данных не содержит значений, то функция ЧАСТОТА возвращает массив нулей.
Массив интервалов ‒ массив или ссылка на множество интервалов, в которые группируются значения аргумента массив данных. В нашем случае это диапазон F7:F12. Если массив интервалов не содержит значений, то функция ЧАСТОТА возвращает количество элементов в аргументе Массив данных.
Функция ЧАСТОТА вводится как формула массива после выделения интервала смежных ячеек, в которые нужно вернуть полученный массив частот.
Количество элементов в возвращаемом массиве на единицу больше числа элементов в массиве интервалов. Дополнительный элемент в возвращаемом массиве содержит количество значений, больших, чем максимальное значение в интервалах, т.е. больше 5 в нашем случае.
Поскольку данная функция возвращает массив, она должна задаваться в качестве формулы массива и работа с ней завершается трехклавишной комбинацией CTRL+SHIFT+ENTER.
Функция ЧАСТОТА игнорирует пустые ячейки и тексты.
5. Сформируйте столбец частностей, вычислив значения ωi , i = 1, …,6 по формуле
ωi=nin .
6. Сформируйте столбец значений выборочной функции распределения . При этом первое значение в ячейке I7 просто копируется из ячейки Н7.
Следующее значение вычисляется как накопленная сумма предыдущего значения ω1 из ячейки I7 и текущего значения ω2 из ячейки Н8:
=I7+H8 .
Затем данная формула копируется автозаполнением в остальные ячейки диапазона, с выходом на значение, равное 1.
7. Построим график эмпирической функции распределения. С использованием штатных средств Мастера диаграмм ЭТ MS Excel построить ступенчатый график функции распределения дискретной случайной величины нельзя.
Покажем, как в MS Excel все-таки можно построить такой график.
7.1. Расположим данные полученного дискретного вариационного ряда так, как показано на рисунке ниже.
При этом данные копируются из предыдущей таблицы. Используют контекстное меню команды Вставка: Параметры вставки → Значения
7.2. В разреженную таким образом таблицу введем ряд дополнений. В ячейку К7 введем значение -2, а в ячейку К20 значение 7, это границы интервала [-2 ;7] на котором будет построен наш график. В оставшиеся пустые ячейки введем значения, чуть меньшие значений полученных вариант (см. случай а) ниже).
Два первых значения функции F(x) в ячейках L7 и L8 примем равным нулю, т.к. при x ≤ x(1) . В оставшиеся пустые ячейки скопируем значения функции, расположенные выше (см. случай б) выше).
7.3. По данным, находящимся в диапазоне ячеек K7:L20, с помощью Мастера диаграмм, построим диаграмму типа Точечная без маркеров. Отформатируем диаграмму, убрав маркеры и задав линию, соединяющую табличные значения.
Т.к. функция ‒ непрерывна слева в любой точке x, т. е. , то устраним неоднозначность в точках разрыва, “вырезав” соответствующие значения. Для этого построим точечный график по данным первого и последнего столбца полученного дискретного вариационного ряда.
8. Постройте пунктирные линии в вырезанных точках графика. Для этого выделим точки графика и на вкладке Макет в группе Анализ нажмём кнопку Планки погрешностей, а затем выберем строку Дополнительные параметры планок погрешностей … .
В диалоговом окне Формат планок погрешностей выполните установки, представленные ниже. Установите радиокнопку – пользовательская и в появившемся окне, в поле ввода Отрицательное значение ошибки введите значения столбца F(x).
Получили график функции распределения с пунктирными линиями.
9. Сделайте выводы и сохраните работу в вашем каталоге.
Постановка задачи 2. Исследуется рост учащихся (в сантиметрах) в студенческой группе из 25 человек. Получена выборка (см. табл. 4) из следующих 25 значений.
Таблица 4.
|
184 |
182 |
182 |
180 |
177 |
|
179 |
173 |
179 |
192 |
173 |
|
190 |
163 |
177 |
186 |
170 |
|
178 |
185 |
173 |
179 |
165 |
|
179 |
173 |
179 |
166 |
170 |
Требуется: найти интервальныйвариационный ряд, выборочную (эмпирическую) функцию распределения данной выборки и построить ее график в среде ЭТ MS Excel.
Решение.
Найдем максимальное и минимальное значения в исследуемой выборке
xmax=192 , xmin=163 см.
Вычислим размах варьирования R исследуемого признака по формуле
R=xmax-xmin=29.
Для нахождения числа интервалов группировки N воспользуемся формулой
N≈n=25=5.
Далее следует группировка выборки. При этом интервал варьирования признака [xmin, xmax] разбивается на N интервалов группировки одинаковой длины ∆, а затем подсчитывается число попаданий признака в j-й интервал группировки – ni,i=.
∆=RN=xmax-xminN =5,8≈6.
При этом каждый интервал группировки Δi= (ai;bi) характеризуется своим правым и левым концом, числом ni – попаданием признака в этот интервал. Иногда интервал характеризуют не границами, а его средним значением.
Дальнейшие вычисления удобно представить в табл. 5.
Таблица 5.
|
i |
Интервал группировки Δi |
Кол-во попаданий в интервал |
Частоты ni |
Относительные частоты ωi=nin |
Накопленные частоты |
|
1 |
162,5-168,5 |
│││ |
3 |
3/25 |
3/25 |
|
2 |
168,5-174,5 |
│││││ │ |
6 |
6/25 |
9/25 |
|
3 |
174,5-180,5 |
│││││ ││││ |
9 |
9/25 |
18/25 |
|
4 |
180,5-186,5 |
│││││ |
5 |
5/25 |
23/25 |
|
5 |
186,5-192,5 |
││ |
2 |
2/25 |
252/25 = 1 |
|
∑ |
25 |
1 |
Чтобы значение исследуемого признака не попадало на границы интервала группировки, примем минимальное значение признака не 163, а 162,5 и от этого значения начнем строить интервалы длиной Δ = 6 (см. второй столбец табл. 5).
Откладывая по оси абсцисс средние значения интервалов группировки, а по оси ординат – значения накопленных частот, строим график эмпирической функции растределения.
Решение задачи в среде ЭТ MSExcel. Для решения задачи в среде ЭТ MS Excel необходимо выполнить следующие действия:
1. Переименуйте Лист 3 в Непрерывный. Наберите массив 25 значений исходных данных выборки.
2. Найдите величины хmax, хmin, n, N, Δокругл используя встроенные функции Excel МАКС, МИН, СЧЕТ, КОРЕНЬ и ОКРУГЛ.
3. Сформируйте столбец интервалов варьирования от значения 162,5 с шагом Δ = 6. Первое значение набираем с клавиатуры, а второе вычисляем с помощью формулы
=E9+$C$13 .
Остальные значения получим копированием с помощью Автозаполнения.
4. Сформируйте столбец Частота и с помощью функции ЧАСТОТА найдите частоту появления значений исследуемой случайной величины Х в каждом из интервалов.
5. Заполните столбец относительных частот, рассчитав значение в ячейке G9 по формуле
=F9/$C$10 .
Остальные значения получим копированием формулы с помощью Автозаполнения.
6. Вычислите середины интервалов группировки, рассчитав значение в ячейке Н9 по формуле
=(E9+E10)/2 .
Остальные значения в диапазоне Н10:Н13 получим копированием формулы с помощью Автозаполнения.
7. Заполните столбец накопленных частот. При этом, значение в ячейке I9 получим, копируя значение ячейки G10 по формуле
=G10 .
Значение в ячейке I10 получим по формуле
=I9+G11 .
Остальные значения в диапазоне I11:I13 получим, копируя формулу с помощью Автозаполнения.
8. По данным двух последних столбцов построим график эмпирической функции распределения.
9. Сделайте выводы и сохраните работу в вашем каталоге.
Лист Excel лабораторной работы имеет вид, представленный на рисунке.
Исходные данные для самостоятельного решения
Задание 1. Имеется выборка непрерывной случайной величины объема n = 26 (табл. 6).
Задание 2. Имеется выборка дискретной случайной величины объема n = 30 (табл. 7).
Требуется: найти дискретный и интервальныйвариационные ряды, выборочную (эмпирическую) функцию распределения данных выборок и построить их графики в среде ЭТ MS Excel.
Таблица 6.
|
№ варианта |
Выборка |
||||||||||||
|
1 |
11,7 |
9,83 |
5,49 |
7,43 |
9,92 |
3,41 |
6,83 |
8,22 |
8,30 |
8,14 |
9,29 |
9,27 |
7,43 |
|
7,41 |
3,56 |
7,72 |
12,1 |
6,06 |
10,6 |
6,76 |
8,21 |
9,86 |
8,13 |
9,04 |
4,75 |
9,33 |
|
|
2 |
4,49 |
9,25 |
7,94 |
9,10 |
6,27 |
6,77 |
3,47 |
8,84 |
6,48 |
4,92 |
6,98 |
10,1 |
6,32 |
|
6,36 |
5,16 |
7,92 |
12,0 |
7,46 |
7,01 |
13,0 |
7,34 |
6,71 |
5,48 |
9,95 |
11,9 |
8,89 |
|
|
3 |
6,13 |
8,56 |
9,77 |
9,17 |
8,89 |
6,19 |
7,70 |
6,96 |
6,72 |
6,08 |
4,41 |
5,52 |
9,59 |
|
9,02 |
6,22 |
4,86 |
6,33 |
6,28 |
8,60 |
7,38 |
7,84 |
7,24 |
6,85 |
6,50 |
8,28 |
4,98 |
|
|
4 |
6,52 |
9,27 |
7,91 |
5,77 |
8,02 |
3,07 |
2,22 |
5,76 |
11,6 |
6,62 |
7,07 |
12,5 |
1,65 |
|
10,5 |
3,67 |
7,62 |
4,94 |
5,39 |
3,64 |
4,62 |
8,88 |
6,75 |
5,77 |
6,38 |
10,3 |
5,74 |
|
|
5 |
8,18 |
9,56 |
6,06 |
5,85 |
6,78 |
5,60 |
10,8 |
7,70 |
6,44 |
8,64 |
6,95 |
5,66 |
4,84 |
|
4,96 |
4,62 |
5,57 |
6,47 |
5,97 |
8,02 |
3,66 |
9,24 |
4,13 |
6,58 |
7,51 |
5,67 |
7,89 |
|
|
6 |
10,2 |
9,23 |
8,77 |
10,4 |
9,44 |
9,09 |
6,30 |
9,42 |
6,12 |
9,69 |
8,59 |
8,68 |
7,97 |
|
8,64 |
6,45 |
5,29 |
5,00 |
8,42 |
8,84 |
8,26 |
6,66 |
6,96 |
6,51 |
6,72 |
6,00 |
5,36 |
|
|
7 |
7,13 |
9,12 |
9,77 |
9,17 |
8,89 |
6,19 |
7,71 |
6,96 |
6,72 |
6,08 |
4,41 |
5,52 |
9,59 |
|
8,06 |
6,26 |
4,86 |
6,33 |
6,28 |
8,60 |
7,38 |
7,84 |
7,24 |
6,85 |
6,50 |
8,28 |
4,98 |
|
|
8 |
3,53 |
9,56 |
7,03 |
9,18 |
7,45 |
5,59 |
6,85 |
11,3 |
7,90 |
6,00 |
6,68 |
5,66 |
8,64 |
|
8,87 |
4,58 |
11,3 |
5,02 |
4,33 |
9,31 |
10,3 |
5,99 |
6,98 |
5,23 |
8,75 |
7,73 |
9,16 |
|
|
9 |
3,38 |
7,87 |
4,04 |
8,21 |
4,08 |
3,46 |
4,37 |
6,66 |
1,46 |
5,59 |
3,78 |
8,73 |
5,57 |
|
8,22 |
3,25 |
3,38 |
4,20 |
2,49 |
6,11 |
4,54 |
6,53 |
5,20 |
3,84 |
5,35 |
9,72 |
4,63 |
|
|
10 |
4,21 |
5,68 |
3,45 |
6,79 |
3,39 |
2,99 |
3,88 |
3,77 |
1,43 |
5,96 |
4,94 |
6,55 |
5,92 |
|
4,20 |
4,25 |
5,64 |
5,58 |
5,87 |
5,05 |
3,55 |
7,95 |
4,45 |
5,85 |
6,68 |
1,24 |
7,09 |
Таблица 7.
|
№ варианта |
Выборка |
||||||||||||||
|
1 |
4 |
0 |
2 |
5 |
1 |
2 |
4 |
5 |
3 |
4 |
4 |
0 |
1 |
5 |
1 |
|
2 |
3 |
2 |
0 |
2 |
3 |
1 |
3 |
2 |
1 |
2 |
4 |
2 |
0 |
2 |
|
|
2 |
2 |
0 |
3 |
5 |
1 |
2 |
4 |
5 |
3 |
4 |
4 |
0 |
1 |
5 |
1 |
|
1 |
3 |
4 |
0 |
2 |
3 |
1 |
3 |
2 |
1 |
2 |
4 |
2 |
0 |
2 |
|
|
3 |
2 |
3 |
2 |
0 |
2 |
3 |
1 |
1 |
2 |
3 |
2 |
4 |
2 |
0 |
2 |
|
2 |
0 |
3 |
5 |
1 |
2 |
4 |
5 |
3 |
4 |
4 |
0 |
1 |
5 |
1 |
|
|
4 |
4 |
2 |
1 |
5 |
1 |
2 |
4 |
5 |
3 |
4 |
4 |
0 |
1 |
5 |
1 |
|
3 |
3 |
4 |
0 |
2 |
3 |
1 |
3 |
2 |
1 |
2 |
4 |
2 |
0 |
2 |
|
|
5 |
2 |
3 |
4 |
0 |
2 |
1 |
2 |
3 |
2 |
1 |
2 |
2 |
4 |
0 |
2 |
|
4 |
3 |
2 |
2 |
1 |
3 |
1 |
3 |
2 |
2 |
1 |
4 |
2 |
2 |
0 |
|
|
6 |
2 |
3 |
2 |
1 |
2 |
2 |
4 |
0 |
2 |
4 |
4 |
0 |
1 |
5 |
1 |
|
1 |
3 |
2 |
2 |
1 |
4 |
2 |
2 |
0 |
1 |
2 |
4 |
2 |
0 |
2 |
|
|
7 |
4 |
3 |
2 |
2 |
5 |
3 |
1 |
3 |
2 |
2 |
1 |
4 |
2 |
2 |
0 |
|
2 |
3 |
2 |
1 |
2 |
2 |
4 |
0 |
2 |
4 |
4 |
0 |
1 |
5 |
1 |
|
|
8 |
5 |
3 |
4 |
4 |
0 |
1 |
5 |
1 |
2 |
2 |
1 |
4 |
2 |
2 |
0 |
|
3 |
2 |
1 |
2 |
4 |
2 |
0 |
2 |
2 |
0 |
4 |
0 |
1 |
5 |
1 |
|
|
9 |
2 |
3 |
2 |
1 |
2 |
2 |
4 |
0 |
2 |
4 |
4 |
0 |
1 |
5 |
1 |
|
5 |
3 |
4 |
4 |
0 |
1 |
5 |
1 |
2 |
2 |
1 |
4 |
2 |
2 |
0 |
|
|
10 |
0 |
2 |
3 |
5 |
1 |
2 |
4 |
5 |
3 |
4 |
4 |
0 |
1 |
5 |
1 |
|
4 |
2 |
1 |
5 |
1 |
2 |
4 |
5 |
3 |
4 |
4 |
0 |
1 |
5 |
1 |
Просмотров работы: 10657
Код для цитирования: