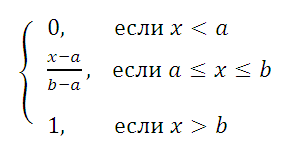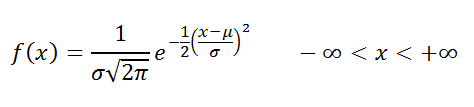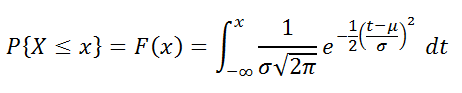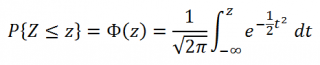Рассмотрим равномерное непрерывное распределение. Вычислим математическое ожидание и дисперсию. Сгенерируем случайные значения с помощью функции MS EXCEL
СЛЧИС()
и надстройки Пакет Анализа, произведем оценку среднего значения и стандартного отклонения.
Равномерно распределенная
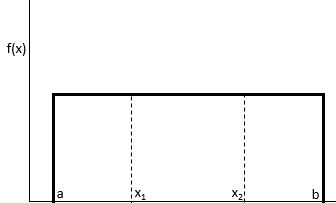
на отрезке [a; b] случайная величина имеет
плотность распределения (вероятности)
:
Функция распределения
определяется следующим образом:
Равномерное непрерывное распределение
(англ.
Continuous
uniform d
istribution
или
Rectangular
distribution
) часто встречается на практике.
Пример1.
Например, известно, что гейзер извергается каждые 50 минут. Найти вероятность, того что турист увидит извержение, если будет ждать у гейзера 20 минут. В соответствии с вышеуказанными формулами вероятность увидеть извержение в течение времени наблюдения равна 20/50=0,4, т.е. 40%.
Пример2.
Симметричный волчок после раскручивания падает набок. Вертикальная ось волчка после падения указывает на определенный угол от 0 до 360 градусов. Найти вероятность, того что ось волчка укажет на сектор от 90 до 180 градусов. Вероятность равна (180-90)/(360-0)=0,25.
В
файле примера
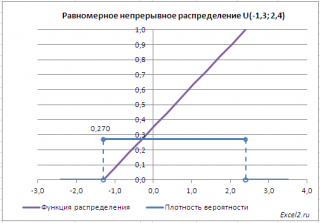
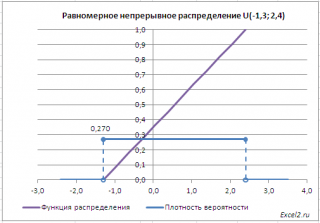
приведены графики
плотности распределения вероятности
и
интегральной функции распределения
.
Математическое ожидание и дисперсия
Математическое ожидание
для
равномерного непрерывного распределения
вычисляется по формуле =(a+b)/2.
Дисперсия (квадрат стандартного отклонения)
вычисляется по формуле =((b-a)^2)/12.
Генерация случайных чисел
Случайные числа, имеющие
равномерное непрерывное распределение
на отрезке [0; 1), можно сгенерировать с помощью функции MS EXCEL
СЛЧИС()
. В функции нельзя задать нижнюю и верхнюю границу интервала, но записав формулу
=СЛЧИС()*(b-a)+a
можно сгенерировать равномерно распределенные числа на любом интервале [a; b).
Примечание
: Чтобы сгенерировать случайные числа, имеющие
равномерное дискретное распределение
, воспользуйтесь функцией
СЛУЧМЕЖДУ()
.
Сгенерировать случайные числа, извлеченные из
непрерывного равномерного
распределения,
можно также с помощью надстройки
Пакет анализа
.
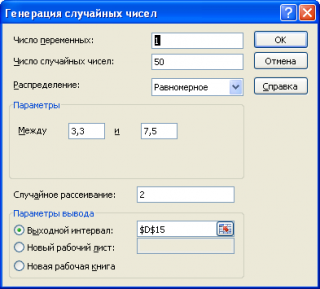
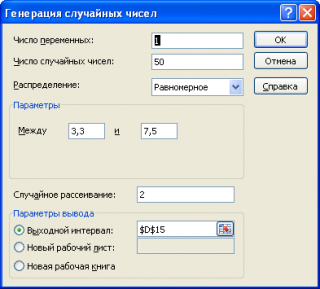
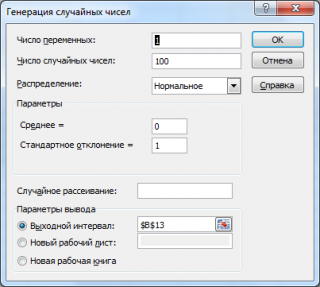
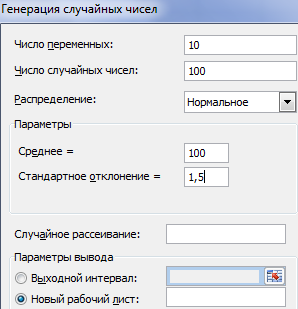
Сгенерируем массив из 50 чисел из диапазона [3,3; 7,5). Для этого в окне
Генерация случайных чисел
установим следующие параметры (см.
файл примера лист Генерация
):
Как видно из рисунка выше, в поле
Случайное рассеивание
установлен необязательный параметр равный 2. Параметр
Случайное рассеивание
может принимать значение от 1 до 32767. Если установить этот параметр, то MS EXCEL будет каждый раз генерировать один и тот же массив чисел, соответствующий этот значению. Этот подход удобен для генерации одинаковых массивов, например, на различных компьютерах.
Оценка среднего и стандартного отклонения
Нижнюю и верхнюю границу интервала возьмем [3,3; 7,5) и разместим их в ячейках
B4:B5
. Сгенерируем 50 чисел (
выборку
) и поместим их в диапазоне
С14:С63
.
Математическое ожидание
этого распределения
=(B4+B5)/2
и равно 5,4.
Стандартное отклонение
распределения равно
=КОРЕНЬ(((B5-B4)^2)/12)=1,21
Чтобы оценить
математическое ожидание
воспользуемся значениями
выборки
=СУММ(C14:C63)/СЧЁТ(C14:C63)
.
Оценить
стандартное отклонение
можно с помощью формулы
=СТАНДОТКЛОН.В(C14:C63)
в MS EXCEL 2010 или
=СТАНДОТКЛОН(C14:C63)
для более ранних версий.
Чтобы оценить
дисперсию
используйте формулу
=ДИСП.В(C14:C63)
в MS EXCEL 2010 или
=ДИСП(C14:C63)
для более ранних версий. Также можно использовать формулу
=СТАНДОТКЛОН.В(C14:C63)^2
.
СОВЕТ
: О других распределениях MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Распределение вероятностей – одно из центральных понятий теории
вероятности и математической статистики. Определение распределения вероятности
равносильно заданию вероятностей всех СВ, описывающих некоторое случайное
событие. Распределение вероятностей некоторой СВ, возможные значения которой x1, x2, … xn образуют
выборку, задается указанием этих значений и соответствующих им вероятностей p1, p2,… pn. (pn должны быть
положительны и в сумме давать единицу).
В данной лабораторной работе будут рассмотрены и построены с помощью MS Excel наиболее
распространенные распределения вероятности: биномиальное и нормальное.
1 Биномиальное распределение
Представляет собой распределение вероятностей числа наступлений
некоторого события («удачи») в n повторных
независимых испытаниях, если при каждом испытании вероятность наступления этого
события равна p. При этом
распределении разброс вариант (есть или нет события) является следствием
влияния ряда независимых и случайных факторов.
Примером практического использования биномиального распределения
может являться контроль качества партии фармакологического препарата. Здесь
требуется подсчитать число изделий (упаковок), не соответствующих требованиям.
Все причины, влияющие на качество препарата, принимаются одинаково вероятными и
не зависящими друг от друга. Сплошная проверка качества в этой ситуации не
возможна, поскольку изделие, прошедшее испытание, не подлежит дальнейшему
использованию. Поэтому для контроля из партии наудачу выбирают определенное
количество образцов изделий (n). Эти образцы всестороннее
проверяют и регистрируют число бракованных изделий (k). Теоретически число
бракованных изделий может быть любым, от 0 до n.
В Excel функция БИНОМРАСП
применяется для вычисления вероятности в задачах с фиксированным числом тестов
или испытаний, когда результатом любого испытания может быть только успех или
неудача.
Функция использует следующие
параметры:
БИНОМРАСП (число_успехов;
число_испытаний; вероятностъ_успеха; интегральная), где
число_успехов — это количество успешных
испытаний;
число_испытаний — это число независимых
испытаний (число успехов и число испытаний должны быть целыми числами);
вероятность_ успеха — это вероятность успеха
каждого испытания;
интегральный — это логическое значение,
определяющее форму функции.
Если данный параметр имеет
значение ИСТИНА (=1), то считается интегральная функция распределения
(вероятность того, что число успешных испытаний не менее значения число_
успехов);
если этот параметр имеет
значение ЛОЖЬ (=0), то вычисляется значение функции плотности
распределения (вероятность того, что число успешных испытаний в точности равно
значению аргумента число_ успехов).
Пример 1. Какова вероятность того,
что трое из четырех новорожденных будут мальчиками?
Решение:
1. Устанавливаем табличный курсор в свободную
ячейку, например в А1. Здесь должно оказаться значение искомой
вероятности.
2. Для получения значения вероятности
воспользуемся специальной функцией: нажимаем на панели инструментов кнопку Вставка
функции (fx).
3. В появившемся диалоговом окне Мастер
функций — шаг 1 из 2 слева в поле Категория указаны виды функций.
Выбираем Статистическая. Справа в поле Функция выбираем функцию БИНОМРАСП
и нажимаем на кнопку ОК.
Появляется диалоговое окно
функции. В поле Число_s вводим с клавиатуры
количество успешных испытаний (3). В поле Испытания вводим с клавиатуры
общее количество испытаний (4). В рабочее поле Вероятность_s
вводим с клавиатуры вероятность успеха в отдельном испытании (0,5). В поле Интегральный
вводим с клавиатуры вид функции распределения — интегральная или весовая (0).
Нажимаем на кнопку ОК.
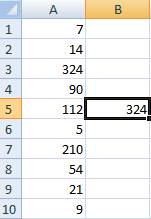
В ячейке А1 появляется
искомое значение вероятности р = 0,25. Ровно 3 мальчика из 4
новорожденных могут появиться с вероятностью 0,25.
Если изменить формулировку
условия задачи и выяснить вероятность того, что появится не более трех
мальчиков, то в этом случае в рабочее поле Интегральный вводим 1 (вид
функции распределения интегральный). Вероятность этого события будет равна
0,9375.
Задания для самостоятельной работы
1. Какова вероятность того, что восемь из десяти студентов,
сдающих зачет, получат «незачет». (0,04)
2.
Нормальное распределение
Нормальное распределение — это совокупность объектов, в которой крайние значения
некоторого признака — наименьшее и наибольшее — появляются редко; чем ближе значение признака к математическому ожиданию,
тем чаще оно встречается. Например, распределение студентов по их весу приближается
к нормальному распределению. Это распределение имеет очень широкий круг приложений в
статистике, включая проверку гипотез.
Диаграмма нормального
распределения симметрична относительно точки а (математического
ожидания). Медиана нормального распределения равна тоже а. При этом в
точке а функция f(x) достигает своего максимума, который равен
.
В Excel для вычисления значений
нормального распределения используются функция НОРМРАСП, которая
вычисляет значения вероятности нормальной функции распределения для указанного
среднего и стандартного отклонения.
Функция имеет параметры:
НОРМРАСП (х; среднее;
стандартное_откл; интегральная), где:
х — значения выборки, для
которых строится распределение;
среднее — среднее арифметическое
выборки;
стандартное_откл — стандартное отклонение
распределения;
интегральный — логическое значение,
определяющее форму функции. Если интегральная имеет значение ИСТИНА(1), то
функция НОРМРАСП возвращает интегральную функцию распределения; если это
аргумент имеет значение ЛОЖЬ (0), то вычисляет значение функция плотности
распределения.
Если среднее = 0 и
стандартное_откл = 1, то функция НОРМРАСП возвращает стандартное
нормальное распределение.
Пример 2. Построить график
нормальной функции распределения f(x) при x, меняющемся от 19,8 до 28,8
с шагом 0,5, a=24,3 и
=1,5.
Решение
1. В ячейку А1 вводим символ
случайной величины х, а в ячейку B1 — символ функции
плотности вероятности — f(x).
2. Вводим в диапазон А2:А21
значения х от 19,8 до 28,8 с шагом 0,5. Для этого воспользуемся
маркером автозаполнения: в ячейку А2 вводим левую границу диапазона (19,8), в
ячейку A3 левую границу плюс шаг (20,3). Выделяем блок А2:А3. Затем за правый
нижний угол протягиваем мышью до ячейки А21 (при нажатой левой кнопке мыши).
3. Устанавливаем табличный курсор в ячейку В2 и
для получения значения вероятности воспользуемся специальной функцией —
нажимаем на панели инструментов кнопку Вставка функции (fx). В появившемся диалоговом
окне Мастер функций — шаг 1 из 2 слева в поле Категория указаны виды
функций. Выбираем Статистическая. Справа в поле Функция выбираем
функцию НОРМРАСП. Нажимаем на кнопку ОК.
4. Появляется диалоговое
окно НОРМРАСП. В рабочее поле X вводим адрес ячейки А2
щелчком мыши на этой ячейке. В рабочее поле Среднее вводим с клавиатуры
значение математического ожидания (24,3). В рабочее поле Стандартное_откл
вводим с клавиатуры значение среднеквадратического отклонения (1,5). В рабочее
поле Интегральная вводим с клавиатуры вид функции распределения (0).
Нажимаем на кнопку ОК.
5. В ячейке В2 появляется
вероятность р = 0,002955. Указателем мыши за правый нижний угол табличного
курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В21
копируем функцию НОРМРАСП в диапазон В3:В21.
6. По полученным данным строим искомую диаграмму
нормальной функции распределения. Щелчком указателя мыши на кнопке на панели
инструментов вызываем Мастер диаграмм. В появившемся диалоговом окне
выбираем тип диаграммы График, вид — левый верхний. После нажатия кнопки
Далее указываем диапазон данных — В1:В21 (с помощью мыши). Проверяем,
положение переключателя Ряды в: столбцах. Выбираем закладку Ряд и с
помощью мыши вводим диапазон подписей оси X: А2:А21. Нажав на кнопку Далее,
вводим названия осей Х и У и нажимаем на кнопку Готово.
Рис. 1 График нормальной функции распределения
Получен приближенный график
нормальной функции плотности распределения (см. рис.1).
Задания для самостоятельной работы
1. Построить график нормальной
функции плотности распределения f(x) при x, меняющемся от 20 до 40 с
шагом 1 при
= 3.
3. Генерация случайных величин
Еще одним аспектом
использования законов распределения вероятностей является генерация случайных величин. Бывают ситуации, когда необходимо
получить последовательность случайных чисел. Это, в частности, требуется для
моделирования объектов, имеющих случайную природу, по известному распределению
вероятностей.
Процедура генерации
случайных величин используется для заполнения диапазона ячеек случайными числами, извлеченными из
одного или нескольких распределений.
В MS Excel для генерации СВ используются функции из категории Математические:
СЛЧИС () – выводит на экран равномерно
распределенные случайные числа больше или равные 0 и меньшие 1;
СЛУЧМЕЖДУ (ниж_граница; верх_граница) – выводит на экран
случайное число, лежащее между произвольными заданными
значениями.
В случае использования
процедуры Генерация случайных чисел из пакета Анализа необходимо
заполнить следующие поля:
— число переменных
вводится число столбцов значений, которые необходимо разместить в выходном диапазоне. Если это число не введено, то все
столбцы в выходном диапазоне будут заполнены;
— число случайных чисел
вводится число случайных значений, которое необходимо вывести для
каждой переменной, если число случайных чисел не будет введено, то все строки выходного диапазона будут заполнены;
— в поле распределение необходимо выбрать тип распределения,
которое следует использовать для генерации случайных переменных:
1. равномерное — характеризуется
верxней и нижней границами. Переменные извлекаются с одной и
той же вероятностью для всех значений интервала.
2. нормальное
— характеризуется средним значением и стандартным отклонением. Обычно для
этого распределения используют среднее значение
0 и стандартное отклонение 1.
3. биномиальное
— характеризуется вероятностью успеха (величина р) для некоторого числа попыток. Например, можно сгенерировать случайные двухальтернативные переменные по числу попыток, сумма которых будет биномиальной случайной
переменной;
4. дискретное
— характеризуется значением СВ и соответствующим ему интервалом вероятности, диапазон должен состоять из двух столбцов: левого,
содержащего значения, и правого, содержащего
вероятности, связанные со значением в данной строке. Сумма вероятностей должна быть
равна 1;
5. распределения Бернулли, Пуассона
и Модельное.
— в поле случайное рассеивание
вводится произвольное значение, для которого необходимо
генерировать случайные числа. Впоследствии можно снова использовать это
значение для получения тех же самых случайных чисел.
— выходной диапазон
вводится ссылка на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и
на экран будет выведено сообщение в случае
возможного наложения выходного диапазона на исходные
данные.
Рассмотрим пример.
Пример 3. Повар столовой может готовить 4 различных первых блюда (уха, щи, борщ, грибной суп). Необходимо составить меню на месяц, так чтобы
первые блюда чередовались в случайном порядке.
Решение
1.
Пронумеруем первые
блюда по порядку: 1 — уха, 2 — щи, 3 — борщ, 4 — грибной суп. Введем числа 1-4 в диапазон А2:А5 рабочей таблицы.
2.
Укажем желаемую вероятность появления
каждого первого блюда. Пусть все блюда будут
равновероятны (р=1/4). Вводим число 0,25 в диапазон В2:В5.
3.
В меню Сервис
выбираем пункт Анализ данных и далее указываем строку Генерация
случайных чисел. В появившемся диалоговом окне указываем Число
переменных — 1, Число случайных чисел — 30 (количество
дней в месяце). В поле Распределение указываем Дискретное (только натуральные числа). В поле Входной
интервал значений и вероятностей
вводим (мышью) диапазон, содержащий номера супов и их
вероятности. – А2:В5.
4.
Указываем выходной
диапазон и нажимаем ОК. В столбце С появляются случайные числа: 1, 2, 3,
4.
Задание для
самостоятельной работы
1. Сформировать
выборку из 10 случайных чисел, лежащих в диапазоне от 0 до 1.
2. Сформировать
выборку из 20 случайных чисел, лежащих в диапазоне от 5 до 20.
3. Пусть
спортсмену необходимо составить график тренировок на 10 дней, так чтобы
дистанция, пробегаемая каждый день, случайным образом менялась от 5 до 10 км.
4. Составить
расписание внеклассных мероприятий на неделю для случайного проведения:
семинаров, интеллектуальных игр, КВН и спец. курса.
5. Составить
расписание на месяц для случайной демонстрации на телевидении одного из четырех
рекламных роликов турфирмы. Причем вероятность появления рекламного ролика №1
должна быть в два раза выше, чем остальных рекламных роликов.
Содержание
- Как использовать равномерное распределение в Excel
- Примеры: Равномерное распределение в Excel
- Равномерное непрерывное распределение в EXCEL
- Математическое ожидание и дисперсия
- Генерация случайных чисел
- Оценка среднего и стандартного отклонения
- Функция СЛЧИС
- Описание
- Синтаксис
- Замечания
- Пример
- Дополнительные сведения
- Как сгенерировать случайное число в Excel
- Создаём генератор случайных чисел с помощью функции СЛЧИС
- Генерация случайной величины, распределенной по равномерному закону
- Способ применения функции «СЛУЧМЕЖДУ( ; )»:
- Способ применения функции «СЛЧИС()»:
- Функция случайного числа в Excel
- Выборка случайных чисел с помощью СЛЧИС
- Функция СЛУЧМЕЖДУ
- Выбор рандом чисел в заданном диапазоне
- Дробные числа больше единицы
- Как сделать генератор чисел в экселе. Генератор случайных чисел в Excel
- Случайное число в определенном диапазоне. Функция
- Случайное число с определенным шагом
- Как применять рандом для проверки модели?
- Использование надстройки Analysis ToolPack
- Произвольное дискретное распределение
- Генератор случайных чисел нормального распределения
- Как предотвратить повторное вычисление СЛЧИС и СЛУЧМЕЖДУ
Как использовать равномерное распределение в Excel
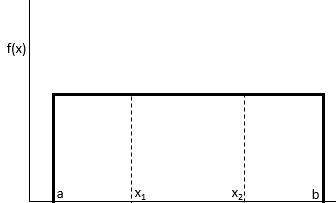
Равномерное распределение — это такое распределение вероятностей, при котором каждое значение в интервале от a до b будет выбрано с равной вероятностью.
Вероятность того, что мы получим значение между x 1 и x 2 на интервале от a до b , можно найти по формуле:
P(получить значение между x 1 и x 2 ) = (x 2 – x 1 ) / (b – a)
Равномерное распределение обладает следующими свойствами:
- Среднее значение распределения равно μ = (a + b)/2.
- Дисперсия распределения σ 2 = (b – a) 2 / 12
- Стандартное отклонение распределения равно σ = √σ 2
В следующих примерах показано, как рассчитать вероятности для равномерного распределения в Excel.
Примечание. Вы можете перепроверить решение каждого приведенного ниже примера с помощьюКалькулятора равномерного распределения .
Примеры: Равномерное распределение в Excel
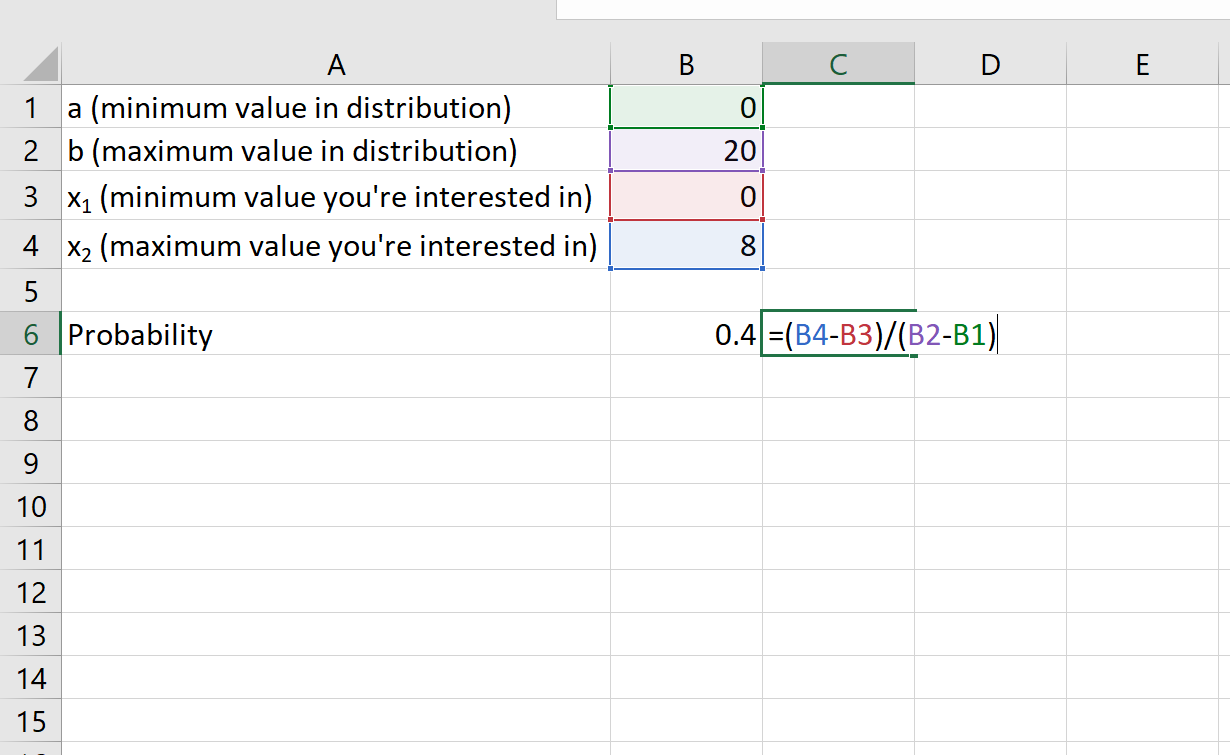
Пример 1: Автобус появляется на автобусной остановке каждые 20 минут. Если вы прибываете на автобусную остановку, какова вероятность того, что автобус приедет через 8 минут или меньше?
Решение:
- а: 0 минут
- б: 20 минут
- х 1 : 0 минут
- х 2 : 8 минут
Вероятность того, что автобус приедет через 8 минут или меньше, равна 0,4 .
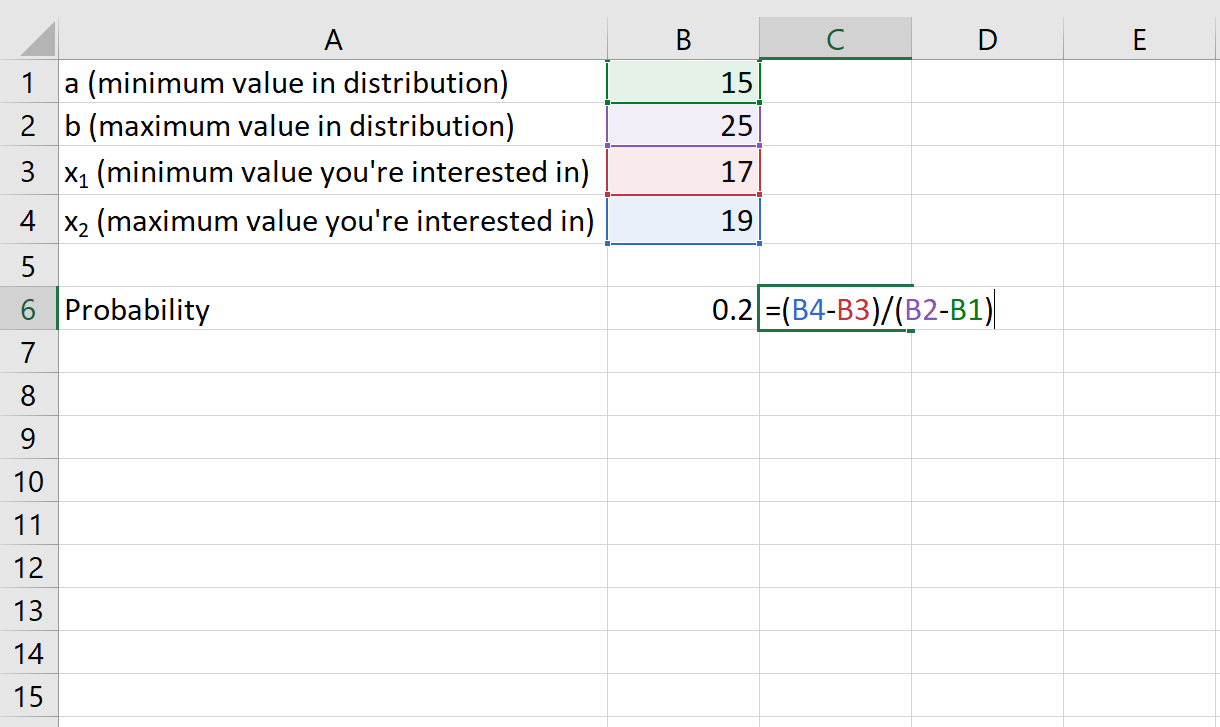
Пример 2: Вес определенного вида лягушек равномерно распределен между 15 и 25 граммами. Если вы случайно выберете лягушку, какова вероятность того, что она весит от 17 до 19 граммов?
Решение:
- а: 15 грамм
- б: 25 грамм
- х 1 : 17 грамм
- х 2 : 19 грамм
Вероятность того, что лягушка весит от 17 до 19 граммов, равна 0,2 .
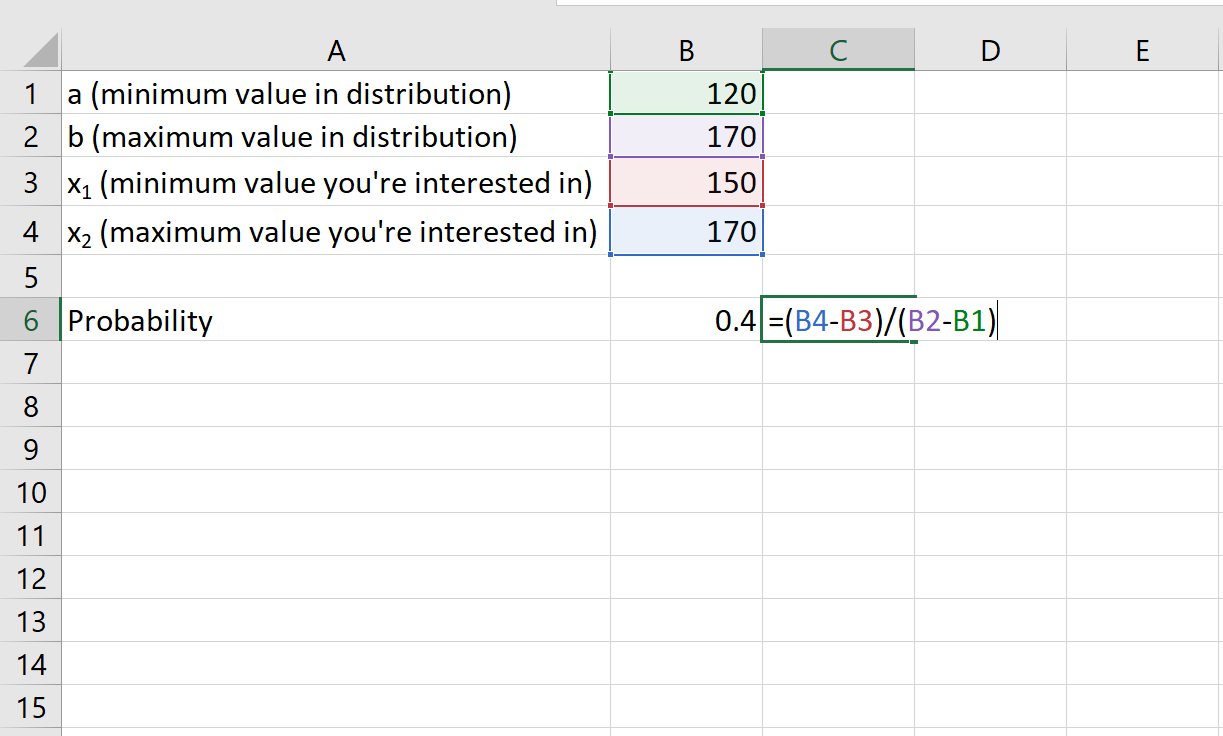
Пример 3. Продолжительность игры НБА равномерно распределена между 120 и 170 минутами. Какова вероятность того, что случайно выбранная игра НБА продлится более 150 минут?
Решение:
- а: 120 минут
- б: 170 минут
- х 1 : 150 минут
- х 2 : 170 минут
Вероятность того, что случайно выбранная игра НБА продлится более 150 минут, равна 0,4 .
Найдите больше руководств по Excel на этой странице .
Источник
Равномерное непрерывное распределение в EXCEL
history 8 ноября 2016 г.
Рассмотрим равномерное непрерывное распределение. Вычислим математическое ожидание и дисперсию. Сгенерируем случайные значения с помощью функции MS EXCEL СЛЧИС() и надстройки Пакет Анализа, произведем оценку среднего значения и стандартного отклонения.
Равномерно распределенная на отрезке [a; b] случайная величина имеет плотность распределения (вероятности) :
Функция распределения определяется следующим образом:
Равномерное непрерывное распределение (англ. Continuous uniform d istribution или Rectangular distribution ) часто встречается на практике.
Пример1. Например, известно, что гейзер извергается каждые 50 минут. Найти вероятность, того что турист увидит извержение, если будет ждать у гейзера 20 минут. В соответствии с вышеуказанными формулами вероятность увидеть извержение в течение времени наблюдения равна 20/50=0,4, т.е. 40%.
Пример2. Симметричный волчок после раскручивания падает набок. Вертикальная ось волчка после падения указывает на определенный угол от 0 до 360 градусов. Найти вероятность, того что ось волчка укажет на сектор от 90 до 180 градусов. Вероятность равна (180-90)/(360-0)=0,25.
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Математическое ожидание и дисперсия
Математическое ожидание для равномерного непрерывного распределения вычисляется по формуле =(a+b)/2.
Генерация случайных чисел
Случайные числа, имеющие равномерное непрерывное распределение на отрезке [0; 1), можно сгенерировать с помощью функции MS EXCEL СЛЧИС() . В функции нельзя задать нижнюю и верхнюю границу интервала, но записав формулу =СЛЧИС()*(b-a)+a можно сгенерировать равномерно распределенные числа на любом интервале [a; b).
Примечание : Чтобы сгенерировать случайные числа, имеющие равномерное дискретное распределение , воспользуйтесь функцией СЛУЧМЕЖДУ() .
Сгенерировать случайные числа, извлеченные из непрерывного равномерного распределения, можно также с помощью надстройки Пакет анализа .
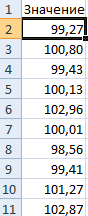
Сгенерируем массив из 50 чисел из диапазона [3,3; 7,5). Для этого в окне Генерация случайных чисел установим следующие параметры (см. файл примера лист Генерация ):
Как видно из рисунка выше, в поле Случайное рассеивание установлен необязательный параметр равный 2. Параметр Случайное рассеивание может принимать значение от 1 до 32767. Если установить этот параметр, то MS EXCEL будет каждый раз генерировать один и тот же массив чисел, соответствующий этот значению. Этот подход удобен для генерации одинаковых массивов, например, на различных компьютерах.
Оценка среднего и стандартного отклонения
Нижнюю и верхнюю границу интервала возьмем [3,3; 7,5) и разместим их в ячейках B4:B5 . Сгенерируем 50 чисел ( выборку ) и поместим их в диапазоне С14:С63 .
Математическое ожидание этого распределения =(B4+B5)/2 и равно 5,4. Стандартное отклонение распределения равно =КОРЕНЬ(((B5-B4)^2)/12)=1,21
Чтобы оценить математическое ожидание воспользуемся значениями выборки =СУММ(C14:C63)/СЧЁТ(C14:C63) .
Оценить стандартное отклонение можно с помощью формулы =СТАНДОТКЛОН.В(C14:C63) в MS EXCEL 2010 или =СТАНДОТКЛОН(C14:C63) для более ранних версий.
Чтобы оценить дисперсию используйте формулу =ДИСП.В(C14:C63) в MS EXCEL 2010 или =ДИСП(C14:C63) для более ранних версий. Также можно использовать формулу =СТАНДОТКЛОН.В(C14:C63)^2 .
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Источник
Функция СЛЧИС
В этой статье описаны синтаксис формулы и использование функции СЛЧИС в Microsoft Excel.
Описание
Функция СЛЧИС возвращает равномерно распределенное случайное вещественное число, большее или равное 0, но меньшее 1. При каждом пересчете листа возвращается новое случайное вещественное число.
Примечание: начиная с версии Excel 2010, в Excel для генерации случайных чисел используется алгоритм «вихрь Мерсенна» (MT19937).
Синтаксис
У функции СЛЧИС нет аргументов.
Замечания
Чтобы получить случайное вещественное число в диапазоне между a и b, можно использовать следующую формулу:
Если требуется применить функцию СЛЧИС для генерации случайного числа, но изменение этого числа при каждом вычислении значения ячейки нежелательно, вы можете ввести в строке формулы =СЛЧИС(), а затем нажать клавишу F9, чтобы заменить формулу случайным числом. Формула вычисляется и оставляет только значение.
Пример
Скопируйте образец данных из приведенной ниже таблицы и вставьте их в ячейку A1 на новом листе Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.
Случайное число, большее или равное 0, но меньшее 1
Случайное число, большее или равное 0 и меньшее 100
Случайное целое число, большее или равное 0 и меньшее 100
Примечание. При пересчете листа после ввода формулы или данных в другую ячейку или при выполнении пересчета вручную (по нажатию клавиши F9) каждая формула, в которой используется функция СЛЧИС, создает новое случайное число.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Источник
Как сгенерировать случайное число в Excel
Создаём генератор случайных чисел с помощью функции СЛЧИС
С помощью функции СЛЧИС, мы имеем возможность генерировать любое случайное число в диапазоне от 0 до 1 и эта функция будет выглядеть так:

=СЛЧИС()*100; 
=ОТБР((СЛЧИС()*100);0) 
- a – представляет нижнюю границу,
- b – верхний предел
и полная формула будет выглядеть: =СЛЧИС()*(6-1)+1, а без дробных частей вам нужно написать: =ОТБР(СЛЧИС()*(6-1)+1;0)
Генерация случайной величины, распределенной по равномерному закону
Дискретное равномерное распределение – это такое распределение, для которого вероятность каждого из значений случайной величины одна и та же, то есть
где N – количество возможных значений случайной величины
Для получения случайной величины, распределенной по равномерному закону, в библиотеке Мастера функций табличного процессора в категории Математические есть специальная функция СЛЧИС() , которая генерирует случайные вещественные числа в диапазоне 0 -1. Функция не имеет параметров
Если необходимо сгенерировать случайные числа в другом диапазоне, то для этого нужно использовать формулу:
= СЛЧИС() * (b – a) +a , где
a – число, устанавливающее нижнюю границу диапазона;
b – число, устанавливающее верхнюю границу диапазона.
Например, для генерации чисел распределенных по равномерному закону в диапазоне 10 – 20, нужно в ячейку рабочего листа ввести формулу:
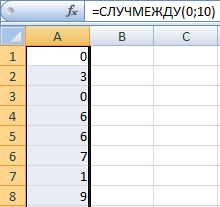
Для генерации целых случайных чисел, равномерно распределенных в диапазоне между двумя заданными числами в библиотеке табличного процессора есть специальная функция СЛУЧМЕЖДУ. Функция имеет параметры:
СЛУЧМЕЖДУ(Нижн_гран; Верхн_гран) , где
Нижн_гран – число, устанавливающее нижнюю границу диапазона;
Верхн_гран – число, устанавливающее верхнюю границу диапазона. Применение функций СЛЧИС и СЛУЧМЕЖДУ рассмотрим на примере.
Пример 1 . Требуется создать массив из 10 чисел, распределенных равномерно в диапазоне 50 – 100.
Решение
1. Выделим диапазон, включающий десять ячеек рабочего листа, например B2:B11 (рис. 1).
2. На ленте Формулы в группе Библиотека функций кликнем на пиктограмме Вставить функцию .
3. В открывшемся окне диалога Мастер функций выберем категорию Математические , в списке функций – СЛЧИС , кликнем на ОК – появится окно диалога Аргументы функции .
4. Нажмем комбинацию клавиш + + – в выделенном диапазоне будут помещены числа, распределенные по равномерному закону в диапазоне 0 – 1 (рис. 1).
5. Щелкнем указателем мыши в строке формул и изменим имеющуюся там формулу, приведя ее к виду: =СЛЧИС()*(100-50)+50.
6. Нажмем комбинацию клавиш + + – в выделенном диапазоне будут размещены числа, распределенные по равномерному закону в диапазоне 50 – 100 (рис. 2).
Способ применения функции «СЛУЧМЕЖДУ( ; )»:
- Установить курсор в ячейку, которой присваиваете значение;
- Выбрать функцию «СЛУЧМЕЖДУ( ; )»;
- В меню указать начальное и конечное число диапазона или ячейки, содержащие эти числа;
- Нажать «ОК»
Наряду с функцией «СЛУЧМЕЖДУ» существует «СЛЧИС()», эта функция в отличие от «СЛУЧМЕЖДУ» выбирает случайное число из диапазона от 0 до 1. То есть присваивает ячейке случайное дробное число до единицы.
Способ применения функции «СЛЧИС()»:
- Установить курсор в ячейку, которой присваиваете значение;
- Выбрать функцию «СЛЧИС()»;
- Нажать «ОК»
У нас есть последовательность чисел, состоящая из практически независимых элементов, которые подчиняются заданному распределению. Как правило, равномерному распределению.
Сгенерировать случайные числа в Excel можно разными путями и способами.
Функция случайного числа в Excel
- Функция СЛЧИС возвращает случайное равномерно распределенное вещественное число. Оно будет меньше 1, больше или равно 0.
- Функция СЛУЧМЕЖДУ возвращает случайное целое число.
Выборка случайных чисел с помощью СЛЧИС
Данная функция аргументов не требует (СЛЧИС()).
Чтобы сгенерировать случайное вещественное число в диапазоне от 1 до 5, например, применяем следующую формулу: =СЛЧИС()*(5-1)+1.
Возвращаемое случайное число распределено равномерно на интервале .
При каждом вычислении листа или при изменении значения в любой ячейке листа возвращается новое случайное число. Если нужно сохранить сгенерированную совокупность, можно заменить формулу на ее значение.
- Щелкаем по ячейке со случайным числом.
- В строке формул выделяем формулу.
- Нажимаем F9. И ВВОД.
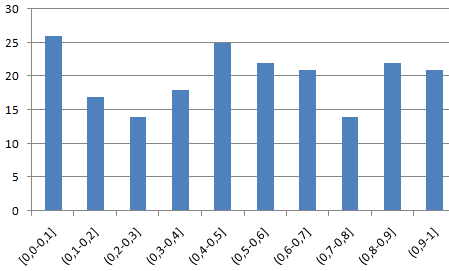
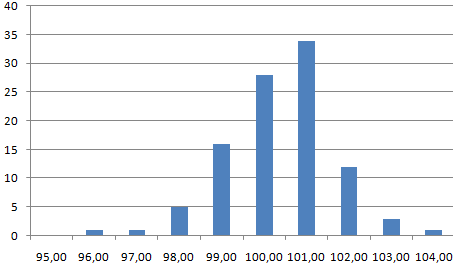
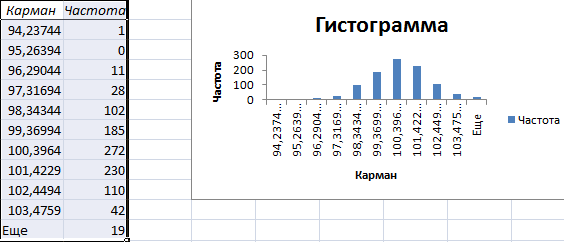
Проверим равномерность распределения случайных чисел из первой выборки с помощью гистограммы распределения.
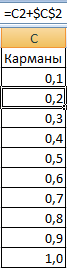
- Сформируем «карманы». Диапазоны, в пределах которых будут находиться значения. Первый такой диапазон – 0-0,1. Для следующих – формула =C2+$C$2.
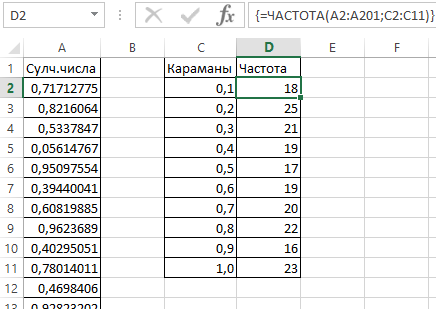
- Определим частоту для случайных чисел в каждом диапазоне. Используем формулу массива <=ЧАСТОТА(A2:A201;C2:C11)>.
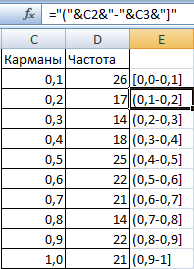
- Сформируем диапазоны с помощью знака «сцепления» (=»»).
- Строим гистограмму распределения 200 значений, полученных с помощью функции СЛЧИС ().
Диапазон вертикальных значений – частота. Горизонтальных – «карманы».
Функция СЛУЧМЕЖДУ
Синтаксис функции СЛУЧМЕЖДУ – (нижняя граница; верхняя граница). Первый аргумент должен быть меньше второго. В противном случае функция выдаст ошибку. Предполагается, что границы – целые числа. Дробную часть формула отбрасывает.
Пример использования функции:
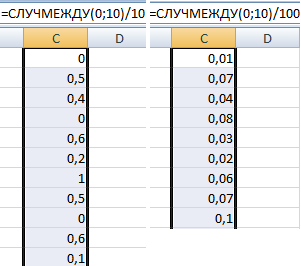
Случайные числа с точностью 0,1 и 0,01:
Выбор рандом чисел в заданном диапазоне
Вы можете получить случайное целое число в нужном диапазоне. Для этого используем функцию =СЛУЧМЕЖДУ(мин ;>макс) . Первым аргументом функции будет минимальное допустимое число, вторым – максимальное.
Например, так можно получить число в промежутке от -100 до 100:
Функции СЛЧИС и СЛУЧМЕЖДУ изменяют свой результат при каждом пересчёте листа. Если Вам нужно этого избежать – замените формулы на значения с помощью специальной вставки .
А теперь немного примеров использования приведенных функций.
Дробные числа больше единицы
Как вы уже поняли, функция СЛЧИС всегда возвращает дробное число от 0 до 1, а СЛУЧМЕЖДУ – целое в указанном диапазоне. А как выбрать число рандомно, дробное и больше единицы? К примеру, нам нужно случайное дробное число в пределах от 10 до 90. Поможет такая формула:
Как сделать генератор чисел в экселе. Генератор случайных чисел в Excel
В Excel есть функция нахождения случайных чисел =СЛЧИС(). Возможность же найти случайное число в Excel, важная составляющая планирования или анализа, т.к. вы можете спрогнозировать результаты вашей модели на большом количестве данных или просто найти одно рандомное число для проверки своей формулы или опыта.
Чаще всего эта функция применяется для получения большого количества случайных чисел. Т.е. 2-3 числа всегда можно придумать самому, для большого количества проще всего применить функцию.
В большинстве языков программирования подобная функция известная как Random (от англ. случайный), поэтому часто можно встретить обрусевшее выражение «в рандомном порядке» и т.п.
В английском Excel функция СЛЧИС числится как RAND
Начнем с описания функции =СЛЧИС(). Для этой функции не нужны аргументы.
А работает она следующим образом — выводит случайное число от 0 до 1. Число будет вещественное, т.е. по большому счету любое, как правило это десятичные дроби, например 0,0006.
При каждом сохранении число будет меняться, чтобы обновить число без обновления нажмите F9.
Случайное число в определенном диапазоне. Функция
Что делать если вам не подходит имеющийся диапазон случайных чисел, и нужно набор случайных чисел от 20 до 135. Как это можно сделать?
Нужно записать следующую формулу.
Т.е. к 20 будет случайным образом прибавляться число от 0 до 115, что позволит получать каждый раз число в нужном диапазоне (см. первую картинку).
- Кстати, если вам необходимо найти целое число в таком же диапазоне, для этого существует специальная функция, где мы указываем верхнюю и нижнюю границу значений
- СЛУЧМЕЖДУ(20;135)
- Просто, но очень удобно!
- Если нужно множество ячеек случайных чисел просто протяните ячейку ниже.
Случайное число с определенным шагом
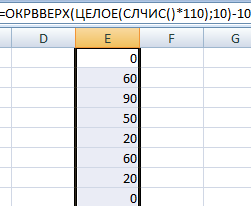
Если нам нужно получить рандомное число с шагом, к примеру пять, то мы воспользуемся одной из . Это будет ОКРВВЕРХ()
Где мы находим случайное число от 0 до 50, а затем округляем его до ближайшего сверху значения кратного 5. Удобно, когда вы делаете расчет для комплектов по 5 штук.
Как применять рандом для проверки модели?
Проверить придуманную модель можно при помощи большого количества случайных чисел. Например проверить будет ли прибыльным бизнес-план
Использование надстройки Analysis ToolPack
Другой способ получения случайных чисел в листе состоит в использовании надстройки Analysis ToolPack (которая поставлялась вместе с Excel). Этот инструмент может генерировать неравномерные случайные числа. Они генерируются не формулами, поэтому, если вам нужен новый набор случайных чисел, необходимо перезапустить процедуру.
Получите доступ к пакету Analysis ToolPack, выбрав Данные Анализ Анализ данных.
Если эта команда отсутствует, установите пакет Analysis ToolPack с помощью диалогового окна Надстройки . Самый простой способ вызвать его — нажать Atl+TI.
В диалоговом окне Анализ данныхвыберите Генерация случайных чисели нажмите ОК. Появится окно, показанное на рис. 130.1.
Выберите тип распределения в раскрывающемся списке Распределение, а затем задайте дополнительные параметры (они изменяются в зависимости от распределения). Не забудьте указать параметр Выходной интервал, в котором хранятся случайные числа.
Чтобы выбрать из таблицы случайные данные, нужно воспользоваться функцией в Excel «Случайные числа». Это готовый генератор случайных чисел в Excel.
Эта функция пригодится при проведении выборочной проверки или при проведении лотереи, т.д. Итак, нам нужно провести розыгрыш призов для покупателей.
В столбце А стоит любая информация о покупателях – имя, или фамилия, или номер, т.д. В столбце в устанавливаем функцию случайных чисел. Выделяем ячейку В1. На закладке «Формулы» в разделе «Библиотека функций» нажимаем на кнопку «Математические» и выбираем из списка функцию «СЛЧИС». Заполнять в появившемся окне ничего не нужно. Просто нажимаем на кнопку «ОК».
Случайное число из диапазона Excel.
Чтобы получить случайные числа в определенном диапазоне, установим функцию «СЛУЧМЕЖДУ» в математических формулах. Установим формулы в столбце С. Диалоговое окно заполнили так. 

Внимание!
В таблице случайные числа располагаем в первом столбце. У нас такая таблица. 
=НАИМЕНЬШИЙ($A$1:$A$6;E1)
Копируем формулу на ячейки F2 и F3 – мы выбираем трех призеров.
В ячейке G1 пишем такую формулу. Она выберет имена призеров по случайным числам из столбца F. =ВПР(F1;$A$1:$B$6;2;0)
Получилась такая таблица победителей.

=НАИМЕНЬШИЙ($A$1:$A$6;E1)
Копируем формулу на ячейки F2 и F3 – мы выбираем трех призеров.
В ячейке G1 пишем такую формулу. Она выберет имена призеров по случайным числам из столбца F. =ВПР(F1;$A$1:$B$6;2;0)
Получилась такая таблица победителей.
Если нужно выбрать призеров по нескольким номинациям, то нажимаем на клавишу F9 и произойдет не только замена случайных чисел, но и связанных с ними имен победителей.
Как отключить обновление случайных чисел в Excel.
Чтобы случайное число не менялось в ячейке, нужно написать формулу вручную и нажать клавишу F9 вместо клавиши «Enter», чтобы формула заменилась на значение.
В Excel есть несколько способов, как копировать формулы, чтобы ссылки в них не менялись. Смотрите описание простых способов такого копирования в статье »
Доброго времени суток, уважаемый, читатель!
Недавно, возникла необходимость создать своеобразный генератор случайных чисел в Excel в границах нужной задачи, а она была простая, с учётом количества человек выбрать случайного пользователя, всё очень просто и даже банально. Но меня заинтересовало, а что же ещё можно делать с помощью такого генератора, какие они бывают, каковые их функции для этого используются и в каком виде. Вопросом много, так что постепенно буду и отвечать на них.
Итак, для чего же собственно мы можем использовать этом механизм:
- во-первых: мы можем для тестировки формул, заполнить нужный нам диапазон случайными числами;
- во-вторых: для формирования вопросов различных тестов;
- в-третьих: для любого случайно распределения заранее задач между вашими сотрудниками;
- в-четвёртых: для симуляции разнообразнейших процессов.
Произвольное дискретное распределение
С помощью надстройки Пакет Анализа можно сгенерировать числа, имеющие произвольное дискретное распределение , т.е. распределение, где пользователь сам задает значения случайной величины и соответствующие вероятности.
В поле Входной интервал значений и вероятностей необходимо ввести ссылку на двухстолбцовый диапазон (см. файл примера ).
Необходимо следить, чтобы сумма вероятностей модельного распределения была равна 1. Для этого в MS EXCEL имеется специальная функция ВЕРОЯТНОСТЬ() .
СОВЕТ : О генерации чисел, имеющих произвольное дискретное распределение , см. статью Генерация дискретного случайного числа с произвольной функцией распределения в MS EXCEL . В этой статье также рассмотрена функция ВЕРОЯТНОСТЬ() .
Генератор случайных чисел нормального распределения
Функции СЛЧИС и СЛУЧМЕЖДУ выдают случайные числа с единым распределением. Любое значение с одинаковой долей вероятности может попасть в нижнюю границу запрашиваемого диапазона и в верхнюю. Получается огромный разброс от целевого значения.
Нормальное распределение подразумевает близкое положение большей части сгенерированных чисел к целевому. Подкорректируем формулу СЛУЧМЕЖДУ и создадим массив данных с нормальным распределением.
Себестоимость товара Х – 100 рублей. Вся произведенная партия подчиняется нормальному распределению. Случайная переменная тоже подчиняется нормальному распределению вероятностей.
При таких условиях среднее значение диапазона – 100 рублей. Сгенерируем массив и построим график с нормальным распределением при стандартном отклонении 1,5 рубля.
Используем функцию: =НОРМОБР(СЛЧИС();100;1,5).
Программа Excel посчитала, какие значения находятся в диапазоне вероятностей. Так как вероятность производства товара с себестоимостью 100 рублей максимальная, формула показывает значения близкие к 100 чаще, чем остальные.
Перейдем к построению графика. Сначала нужно составить таблицу с категориями. Для этого разобьем массив на периоды:
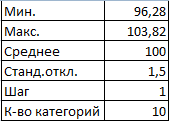
- Определим минимальное и максимальное значение в диапазоне с помощью функций МИН и МАКС.
- Укажем величину каждого периода либо шаг. В нашем примере – 1.
- Количество категорий – 10.
На основе полученных данных сможем сформировать диаграмму с нормальным распределением. Ось значений – число переменных в промежутке, ось категорий – периоды.
График с нормальным распределением готов. Как и должно быть, по форме он напоминает колокол.
Сделать то же самое можно гораздо проще. С помощью пакета «Анализ данных». Выбираем «Генерацию случайных чисел».
О том как подключить стандартную настройку «Анализ данных» читайте здесь .
Заполняем параметры для генерации. Распределение – «нормальное».
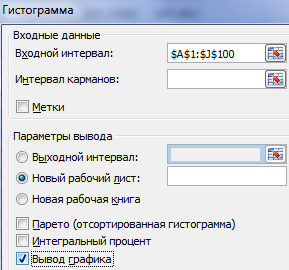
Жмем ОК. Получаем набор случайных чисел. Снова вызываем инструмент «Анализ данных». Выбираем «Гистограмма». Настраиваем параметры. Обязательно ставим галочку «Вывод графика».
График с нормальным распределением в Excel построен.
Как предотвратить повторное вычисление СЛЧИС и СЛУЧМЕЖДУ
Если вы хотите получить постоянный набор случайных чисел, дат или текстовых строк, которые не будут меняться каждый раз, то есть зафиксировать случайные числа, когда лист пересчитывается, используйте один из следующих способов:
- Чтобы остановить функции СЛЧИС или СЛУЧМЕЖДУ от пересчета в одной ячейке , выберите эту ячейку, переключитесь на панель формул и нажмите F9 , чтобы заменить формулу на ее значение.
- Чтобы предотвратить функцию случайных чисел в Excel от автоматического обновления значений в нескольких ячейках , используйте функцию Вставить. Выберите все ячейки с формулой генерации случайных значений, нажмите Ctrl+C, чтобы скопировать их, затем щелкните правой кнопкой мыши выбранный диапазон и нажмите « Вставить специальные »–> « Значения ».
Источник
При решении задач в Microsoft Office Excel с помощью макросов иногда необходимо сгенерировать произвольные числа для проверки правильности работы программы. Или нужно создать большой массив различных цифр без повторений. Для подобных заданий в редакторе заложены специализированные функции, и сегодня разберемся, как задать случайное число в excel.
Функции
Excel содержит две функции, которые позволяют генерировать произвольные цифры –СЛЧИС и СЛУЧМЕЖДУ. Рассмотрим каждую из них более подробно.
Функция СЛЧИС не имеет аргументов, поэтому просто вписываете ее в строку формул и нажимаете Enter.
При помощи маркера автозаполнения можно применить формулу к нужному количеству ячеек.
Важно! При любом действии с ячейкой число автоматически изменяется. Чтобы его зафиксировать, необходимо поставить курсор в нужную ячейку, выделить выражение в строке формул и нажать клавишу F9.
Особенностью этой функции является то, что она работает в пределах от нуля включительно до единицы с нормальным распределением.
Чтобы сгенерировать цифры в заданном диапазоне, например от 3 до 8, необходимо дополнять формулу.
Чтобы сгенерировать случайное целое число, отлично подойдет функция СЛУЧМЕЖДУ. Где в качестве аргументов выступают два числа – верхняя и нижняя границы. При этом существует несколько особенностей:
- Первая часть формулы должна быть меньше второй.
- Границы должны быть целыми числами.
- Цифры после запятой отбрасываются.
Если умножить формулу на определенный коэффициент, то можно создать случайное дробное число с десятыми, сотыми, тысячными и так далее.
В качестве бонуса рассмотрим, как использовать excel для лотереи. Для начала нужно выгрузить базу данных участников в программу любым известным способом, а затем провести розыгрыш. Формула будет выглядеть следующим образом:
Где СЧЕТЗ возвращает количество непустых ячеек, а ИНДЕКС позволяет вывести значение ячейки, которая находится на пересечении конкретной строки и столбца.
Специальный инструмент
Генератор случайных чисел можно найти в пакете анализа данных, который активируется через надстройки Excel. Чтобы воспользоваться этой функцией, необходимо нажать отдельную кнопку во вкладке Данные на Панели инструментов и из списка выбрать нужную строку.
Откроется окно настроек, в котором задаете число переменных и количество случайных чисел, затем указываете дополнительные параметры и место вывода полученных данных. Для примера используем нормальное распределение, которое можно выбрать из отдельного списка.
В результате получилось следующее:
Этот метод намного проще, чем описанные выше способы. Однако он не позволяет накладывать дополнительные условия, поэтому генерация не всегда может удовлетворять требованиям пользователя.
Как видите, в редакторе существует несколько способов задания произвольного числа. Если нужны какие-то ограничения, то используйте встроенные функции, а если важно наличие случайного значения, то генератор из анализа данных подойдет лучше.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Рассмотрим Нормальное распределение. С помощью функции MS EXCEL НОРМ.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по нормальному закону, произведем оценку параметров распределения, среднего значения и стандартного отклонения.
Нормальное распределение (также называется распределением Гаусса) является самым важным как в теории, так в приложениях системы контроля качества. Важность значения Нормального распределения (англ. Normal distribution) во многих областях науки вытекает из Центральной предельной теоремы теории вероятностей.
Определение: Случайная величина x распределена по нормальному закону, если она имеет плотность распределения:
Нормальное распределение зависит от двух параметров: μ (мю) — является математическим ожиданием (средним значением случайной величины), и σ (сигма) — является стандартным отклонением (среднеквадратичным отклонением). Параметр μ определяет положение центра плотности вероятности нормального распределения, а σ — разброс относительно центра (среднего).
Примечание: О влиянии параметров μ и σ на форму распределения изложено в статье про Гауссову кривую, а в файле примера на листе Влияние параметров можно с помощью элементов управления Счетчик понаблюдать за изменением формы кривой.
Нормальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Нормального распределения имеется функция НОРМ.РАСП() , английское название — NORM.DIST(), которая позволяет вычислить плотность вероятности (см. формулу выше) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по нормальному закону, примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Вышеуказанное распределение имеет обозначение N(μ; σ). Так же часто используют обозначение через дисперсию N(μ; σ 2 ).
Примечание: До MS EXCEL 2010 в EXCEL была только функция НОРМРАСП() , которая также позволяет вычислить функцию распределения и плотность вероятности. НОРМРАСП() оставлена в MS EXCEL 2010 для совместимости.
Стандартное нормальное распределение
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ=0 и дисперсией σ=1. Вышеуказанное распределение имеет обозначение N(0;1).
Примечание: В литературе для случайной величины, распределенной по стандартному нормальному закону, закреплено специальное обозначение z.
Любое нормальное распределение можно преобразовать в стандартное через замену переменной z=(x-μ)/σ. Этот процесс преобразования называется стандартизацией.
Примечание: В MS EXCEL имеется функция НОРМАЛИЗАЦИЯ() , которая выполняет вышеуказанное преобразование. Хотя в MS EXCEL это преобразование называется почему-то нормализацией. Формулы =(x-μ)/σ и =НОРМАЛИЗАЦИЯ(х;μ;σ) вернут одинаковый результат.
В MS EXCEL 2010 для стандартного нормального распределения имеется специальная функция НОРМ.СТ.РАСП() и ее устаревший вариант НОРМСТРАСП() , выполняющий аналогичные вычисления.
Продемонстрируем, как в MS EXCEL осуществляется процесс стандартизации нормального распределения N(1,5; 2).
Для этого вычислим вероятность, что случайная величина, распределенная по нормальному закону N(1,5; 2), меньше или равна 2,5. Формула выглядит так: =НОРМ.РАСП(2,5; 1,5; 2; ИСТИНА) =0,691462. Сделав замену переменной z=(2,5-1,5)/2=0,5, запишем формулу для вычисления Стандартного нормального распределения: =НОРМ.СТ.РАСП(0,5; ИСТИНА) =0,691462.
Естественно, обе формулы дают одинаковые результаты (см. файл примера лист Пример ).
Обратите внимание, что стандартизация относится только к интегральной функции распределения (аргумент интегральная равен ИСТИНА), а не к плотности вероятности.
Примечание: В литературе для функции, вычисляющей вероятности случайной величины, распределенной по стандартному нормальному закону, закреплено специальное обозначение Ф(z). В MS EXCEL эта функция вычисляется по формуле
=НОРМ.СТ.РАСП(z;ИСТИНА) . Вычисления производятся по формуле
В силу четности функции плотности стандартного нормального распределения f(x), а именно f(x)=f(-х), функция стандартного нормального распределения обладает свойством Ф(-x)=1-Ф(x).
Обратные функции
Функция НОРМ.СТ.РАСП(x;ИСТИНА) вычисляет вероятность P, что случайная величина Х примет значение меньше или равное х. Но часто требуется провести обратное вычисление: зная вероятность P, требуется вычислить значение х. Вычисленное значение х называется квантилем стандартного нормального распределения.
В MS EXCEL для вычисления квантилей используют функцию НОРМ.СТ.ОБР() и НОРМ.ОБР() .
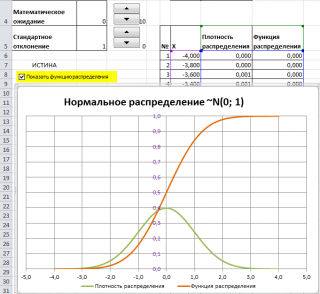
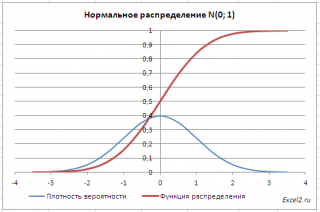
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения.
Как известно, около 68% значений, выбранных из совокупности, имеющей нормальное распределение, находятся в пределах 1 стандартного отклонения (σ) от μ(среднего или математического ожидания); около 95% — в пределах 2-х σ, а в пределах 3-х σ находятся уже 99% значений. Убедиться в этом для стандартного нормального распределения можно записав формулу:
которая вернет значение 68,2689% — именно такой процент значений находятся в пределах +/-1 стандартного отклонения от среднего (см. лист График в файле примера ).
В силу четности функции плотности стандартного нормального распределения: f(x)=f(-х), функция стандартного нормального распределения обладает свойством F(-x)=1-F(x). Поэтому, вышеуказанную формулу можно упростить:
Для произвольной функции нормального распределения N(μ; σ) аналогичные вычисления нужно производить по формуле:
Вышеуказанные расчеты вероятности требуются для построения доверительных интервалов.
Примечание: Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм.
Примечание: Для удобства написания формул в файле примера созданы Имена для параметров распределения: μ и σ.
Генерация случайных чисел
С помощью надстройки Пакет анализа можно сгенерировать случайные числа, распределенные по нормальному закону.
СОВЕТ: О надстройке Пакет анализа можно прочитать в статье Надстройка Пакет анализа MS EXCEL.
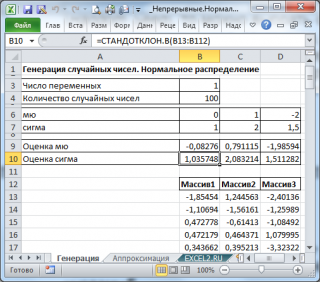
Сгенерируем 3 массива по 100 чисел с различными μ и σ. Для этого в окне Генерация случайных чисел установим следующие значения для каждой пары параметров:
Примечание: Если установить опцию Случайное рассеивание (Random Seed), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию равной 25, можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции Случайное рассеивание может запутать. Лучше было бы ее перевести как Номер набора со случайными числами.
В итоге будем иметь 3 столбца чисел, на основании которых можно, оценить параметры распределения, из которого была произведена выборка: μ и σ. Оценку для μ можно сделать с использованием функции СРЗНАЧ() , а для σ – с использованием функции СТАНДОТКЛОН.В() , см. файл примера лист Генерация .
Примечание: Для генерирования массива чисел, распределенных по нормальному закону, можно использовать формулу =НОРМ.ОБР(СЛЧИС();μ;σ) . Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Задачи
Задача1. Компания изготавливает нейлоновые нити со средней прочностью 41 МПа и стандартным отклонением 2 МПа. Потребитель хочет приобрести нити с прочностью не менее 36 МПа. Рассчитайте вероятность, что партии нити, изготовленные компанией для потребителя, будут соответствовать требованиям или превышать их.
Решение1: = 1-НОРМ.РАСП(36;41;2;ИСТИНА)
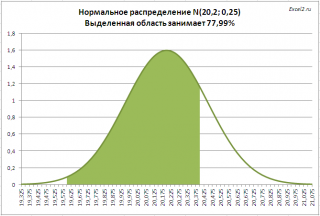
Задача2. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Согласно техническим условиям, трубы признаются годными, если диаметр находится в пределах 20,00+/- 0,40 мм. Какая доля изготовленных труб соответствует ТУ?
Решение2: = НОРМ.РАСП(20,00+0,40;20,20;0,25;ИСТИНА)- НОРМ.РАСП(20,00-0,40;20,20;0,25)
На рисунке ниже, выделена область значений диаметров, которая удовлетворяет требованиям спецификации.
Решение приведено в файле примера лист Задачи .
Задача3. Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Внешний диаметр не должен превышать определенное значение (предполагается, что нижняя граница не важна). Какую верхнюю границу в технических условиях необходимо установить, чтобы ей соответствовало 97,5% всех изготавливаемых изделий?
Решение3: = НОРМ.ОБР(0,975; 20,20; 0,25) =20,6899 или
= НОРМ.СТ.ОБР(0,975)*0,25+20,2 (произведена «дестандартизация», см. выше)
Задача 4. Нахождение параметров нормального распределения по значениям 2-х квантилей (или процентилей).
Предположим, известно, что случайная величина имеет нормальное распределение, но не известны его параметры, а только 2-я процентиля (например, 0,5-процентиль, т.е. медиана и 0,95-я процентиль). Т.к. известна медиана, то мы знаем среднее, т.е. μ. Чтобы найти стандартное отклонение нужно использовать Поиск решения.
Решение приведено в файле примера лист Задачи .
Примечание: До MS EXCEL 2010 в EXCEL были функции НОРМОБР() и НОРМСТОБР() , которые эквивалентны НОРМ.ОБР() и НОРМ.СТ.ОБР() . НОРМОБР() и НОРМСТОБР() оставлены в MS EXCEL 2010 и выше только для совместимости.
Линейные комбинации нормально распределенных случайных величин
Известно, что линейная комбинация нормально распределённых случайных величин x(i) с параметрами μ(i) и σ(i) также распределена нормально. Например, если случайная величина Y=x(1)+x(2), то Y будет иметь распределение с параметрами μ(1)+ μ(2) и КОРЕНЬ(σ(1)^2+ σ(2)^2). Убедимся в этом с помощью MS EXCEL.
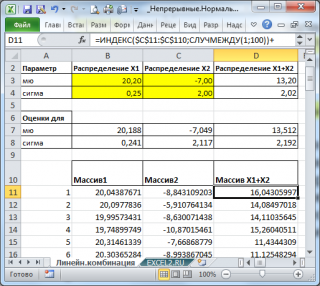
С помощью надстройки Пакет анализа сгенерируем 2 массива по 100 чисел с различными μ и σ.
Теперь сформируем массив, каждый элемент которого является суммой 2-х значений, взятых из каждого массива.
С помощью функций СРЗНАЧ() и СТАНДОТКЛОН.В() вычислим среднее и дисперсию получившейся выборки и сравним их с расчетными.
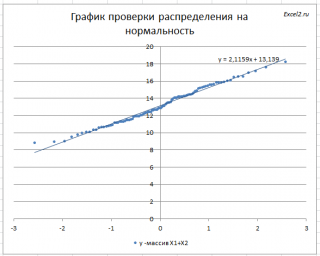
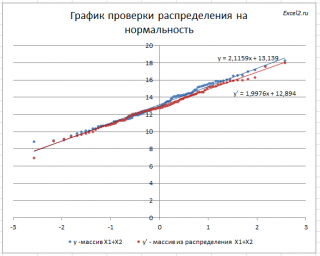
Кроме того, построим График проверки распределения на нормальность (Normal Probability Plot), чтобы убедиться, что наш массив соответствует выборке из нормального распределения.
Прямая линия, аппроксимирующая полученный график, имеет уравнение y=ax+b. Наклон кривой (параметр а) может служить оценкой стандартного отклонения, а пересечение с осью y (параметр b) – среднего значения.
Для сравнения сгенерируем массив напрямую из распределения N(μ(1)+ μ(2); КОРЕНЬ(σ(1)^2+ σ(2)^2)).
Как видно на рисунке ниже, обе аппроксимирующие кривые достаточно близки.
В качестве примера можно провести следующую задачу.
Задача. Завод изготавливает болты и гайки, которые упаковываются в ящики парами. Пусть известно, что вес каждого из изделий является нормальной случайной величиной. Для болтов средний вес составляет 50г, стандартное отклонение 1,5г, а для гаек 20г и 1,2г. В ящик фасуется 100 пар болтов и гаек. Вычислить какой процент ящиков будет тяжелее 7,2 кг.
Решение. Сначала переформулируем вопрос задачи: Вычислить какой процент пар болт-гайка будет тяжелее 7,2кг/100=72г. Учитывая, что вес пары представляет собой случайную величину = Вес(болта) + Вес(гайки) со средним весом (50+20)г, и стандартным отклонением =КОРЕНЬ(СУММКВ(1,5;1,2)) , запишем решение
= 1-НОРМ.РАСП(72; 50+20; КОРЕНЬ(СУММКВ(1,5;1,2));ИСТИНА)
Ответ: 15% (см. файл примера лист Линейн.комбинация )
Аппроксимация Биномиального распределения Нормальным распределением
Если параметры Биномиального распределения B(n;p) находятся в пределах 0,1 10, то Биномиальное распределение можно аппроксимировать Нормальным распределением.
При значениях λ>15, Распределение Пуассона хорошо аппроксимируется Нормальным распределением с параметрами: μ=λ, σ 2 =λ.
Подробнее о связи этих распределений, можно прочитать в статье Взаимосвязь некоторых распределений друг с другом в MS EXCEL. Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL.
У нас есть последовательность чисел, состоящая из практически независимых элементов, которые подчиняются заданному распределению. Как правило, равномерному распределению.
Сгенерировать случайные числа в Excel можно разными путями и способами. Рассмотрим только лучше из них.
Функция случайного числа в Excel
- Функция СЛЧИС возвращает случайное равномерно распределенное вещественное число. Оно будет меньше 1, больше или равно 0.
- Функция СЛУЧМЕЖДУ возвращает случайное целое число.
Рассмотрим их использование на примерах.
Выборка случайных чисел с помощью СЛЧИС
Данная функция аргументов не требует (СЛЧИС()).
Чтобы сгенерировать случайное вещественное число в диапазоне от 1 до 5, например, применяем следующую формулу: =СЛЧИС()*(5-1)+1.
Возвращаемое случайное число распределено равномерно на интервале [1,10].
При каждом вычислении листа или при изменении значения в любой ячейке листа возвращается новое случайное число. Если нужно сохранить сгенерированную совокупность, можно заменить формулу на ее значение.
- Щелкаем по ячейке со случайным числом.
- В строке формул выделяем формулу.
- Нажимаем F9. И ВВОД.
Проверим равномерность распределения случайных чисел из первой выборки с помощью гистограммы распределения.
- Сформируем «карманы». Диапазоны, в пределах которых будут находиться значения. Первый такой диапазон – 0-0,1. Для следующих – формула =C2+$C$2.
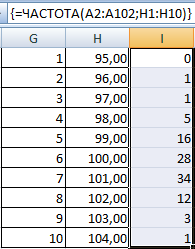
- Определим частоту для случайных чисел в каждом диапазоне. Используем формулу массива <=ЧАСТОТА(A2:A201;C2:C11)>.
- Сформируем диапазоны с помощью знака «сцепления» (=»[0,0-«&C2&»]»).
- Строим гистограмму распределения 200 значений, полученных с помощью функции СЛЧИС ().
Диапазон вертикальных значений – частота. Горизонтальных – «карманы».
Функция СЛУЧМЕЖДУ
Синтаксис функции СЛУЧМЕЖДУ – (нижняя граница; верхняя граница). Первый аргумент должен быть меньше второго. В противном случае функция выдаст ошибку. Предполагается, что границы – целые числа. Дробную часть формула отбрасывает.
Пример использования функции:
Случайные числа с точностью 0,1 и 0,01:
Как сделать генератор случайных чисел в Excel
Сделаем генератор случайных чисел с генерацией значения из определенного диапазона. Используем формулу вида: =ИНДЕКС(A1:A10;ЦЕЛОЕ(СЛЧИС()*10)+1).
Сделаем генератор случайных чисел в диапазоне от 0 до 100 с шагом 10.
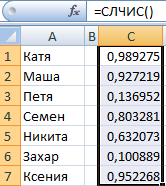
Из списка текстовых значений нужно выбрать 2 случайных. С помощью функции СЛЧИС сопоставим текстовые значения в диапазоне А1:А7 со случайными числами.
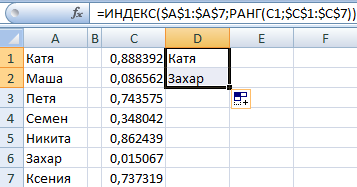
Воспользуемся функцией ИНДЕКС для выбора двух случайных текстовых значений из исходного списка.
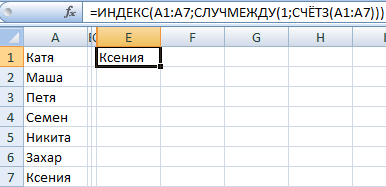
Чтобы выбрать одно случайное значение из списка, применим такую формулу: =ИНДЕКС(A1:A7;СЛУЧМЕЖДУ(1;СЧЁТЗ(A1:A7))).
Генератор случайных чисел нормального распределения
Функции СЛЧИС и СЛУЧМЕЖДУ выдают случайные числа с единым распределением. Любое значение с одинаковой долей вероятности может попасть в нижнюю границу запрашиваемого диапазона и в верхнюю. Получается огромный разброс от целевого значения.
Нормальное распределение подразумевает близкое положение большей части сгенерированных чисел к целевому. Подкорректируем формулу СЛУЧМЕЖДУ и создадим массив данных с нормальным распределением.
Себестоимость товара Х – 100 рублей. Вся произведенная партия подчиняется нормальному распределению. Случайная переменная тоже подчиняется нормальному распределению вероятностей.
При таких условиях среднее значение диапазона – 100 рублей. Сгенерируем массив и построим график с нормальным распределением при стандартном отклонении 1,5 рубля.
Используем функцию: =НОРМОБР(СЛЧИС();100;1,5).
Программа Excel посчитала, какие значения находятся в диапазоне вероятностей. Так как вероятность производства товара с себестоимостью 100 рублей максимальная, формула показывает значения близкие к 100 чаще, чем остальные.
Перейдем к построению графика. Сначала нужно составить таблицу с категориями. Для этого разобьем массив на периоды:
- Определим минимальное и максимальное значение в диапазоне с помощью функций МИН и МАКС.
- Укажем величину каждого периода либо шаг. В нашем примере – 1.
- Количество категорий – 10.
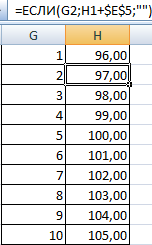
- Нижняя граница таблицы с категориями – округленное вниз ближайшее кратное число. В ячейку Н1 вводим формулу =ОКРВНИЗ(E1;E5).
- В ячейке Н2 и последующих формула будет выглядеть следующим образом: =ЕСЛИ(G2;H1+$E$5;»»). То есть каждое последующее значение будет увеличено на величину шага.
- Посчитаем количество переменных в заданном промежутке. Используем функцию ЧАСТОТА. Формула будет выглядеть так:
На основе полученных данных сможем сформировать диаграмму с нормальным распределением. Ось значений – число переменных в промежутке, ось категорий – периоды.
График с нормальным распределением готов. Как и должно быть, по форме он напоминает колокол.
Сделать то же самое можно гораздо проще. С помощью пакета «Анализ данных». Выбираем «Генерацию случайных чисел».
О том как подключить стандартную настройку «Анализ данных» читайте здесь.
Заполняем параметры для генерации. Распределение – «нормальное».
Жмем ОК. Получаем набор случайных чисел. Снова вызываем инструмент «Анализ данных». Выбираем «Гистограмма». Настраиваем параметры. Обязательно ставим галочку «Вывод графика».
График с нормальным распределением в Excel построен.
Перейти к содержанию
На чтение 3 мин Просмотров 52 Опубликовано 01.01.1970
Обновлено 09.03.2023
Для исследования экономической информации задач бизнес – анализа широко используются статистические методы обработки. Электронная таблица Excel содержит набор встроенных функций категории Статистические, а также предоставляет специальные информационные технологии, выполняемые в среде Пакета анализа.
Для загрузки пакета анализа выполните следующие действия:
- Выполните команду Сервис Надстройки. На экране появится окно диалога “ Надстройки ”.
- Выберите Пакет анализа, а затем нажмите кнопку ОК.
После окончания загрузки в списке опций пункта Сервис основного меню появится строка Анализ данных. При выборе этой строки появляется окно диалога “ Анализ данных ”.
В окне диалога “ Анализ данных ” отображается список инструментов.
При статистическом моделировании и первичной обработке данных используются следующие инструменты: Генерация случайных чисел, Гистограмма.
Инструмент Генерация случайных чисел заполняет интервал независимыми случайными числами.
При помощи параметра Число переменных вы можете получить многомерную выборку. Для этого введите число столбцов в выходной таблице.
Параметром Число случайных чисел определяется число точек данных, которое вы хотите генерировать для каждой переменной.
Выбор закона распределения случайных чисел задаётся параметром Распределение.
- Равномерное распределение характеризуется верхней и нижней границами. Вероятность попадания переменной в отрезок фиксированной длины зависит только от длины отрезка и не зависит от его расположения на интервале. Как правило, в приложениях используют равномерное распределение в интервале [0,1].
- Нормальное распределение характеризуется средним значением и стандартным отклонением. Обычно приложения для этого распределения используют среднее значение 0 и стандартное отклонение 1.
- Распределение Бернулли характеризуется вероятностью успеха в данном испытании. Случайная величина принимает значение 0 или 1. Например, при бросании игральной кости или выпадет 6 очков с вероятностью 1/6 или выпадет не 6 очков с вероятностью 5/6, то есть случайная величина принимает значение 1 с вероятностью 1/6 или 0 с вероятностью 5/6.
- Биноминальное распределение характеризуется вероятностью успеха для некоторого числа испытаний. Например, вы можете генерировать случайные числа, моделирующие процесс бросания монеты с вероятностью успеха ровно в “k” случаях из “n” испытаний.
- Распределение Пуассона характеризуется значением Лямбда, равным 1/среднее. Распределение Пуассона часто используется для характеристики числа событий, случающихся в единицу времени, например, число телефонных соединений в минуту.
- Модельное распределение характеризуется нижней и верхней границей, шагом, числом повторений значений и числом повторений последовательности.
- Дискретное распределение характеризуется значением и связанным с ним интервалом вероятности. Интервал должен содержать два столбца: левый содержит значения, правый – вероятности, связанные со значением в данной строке. Сумма вероятностей должна быть равна 1.
При помощи параметра Случайное рассеивание вы фиксируйте последовательность выводимых случайных чисел. При повторных запусках генератора можно использовать это значение для получения тех же самых случайных чисел.