Сложные математические статистические функции в excel - Word и Excel

Содержание

Статистические функции
- МАКС
- МИН
- СРЗНАЧ
- СРЗНАЧЕСЛИ
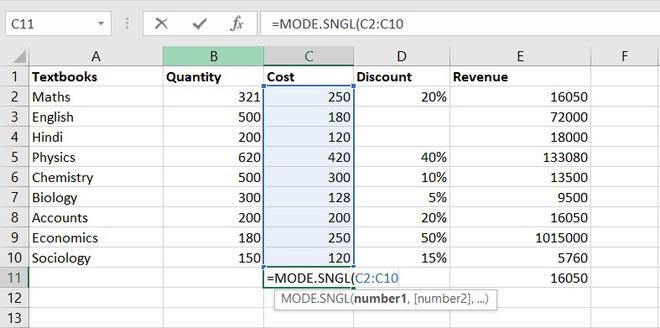
- МОДА.ОДН
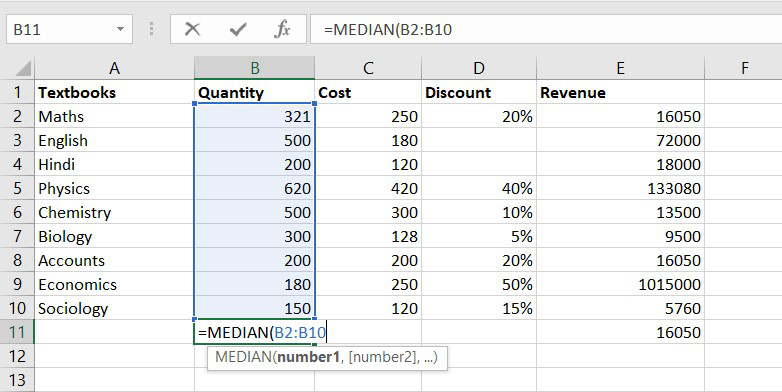
- МЕДИАНА
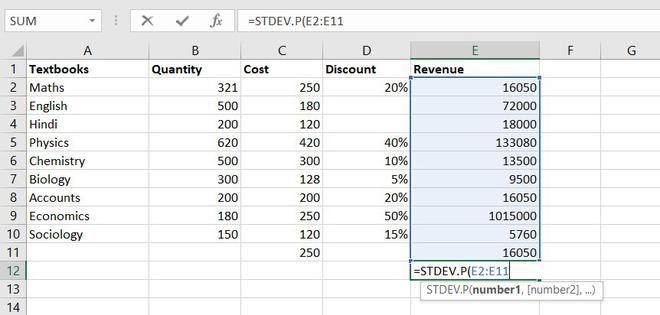
- СТАНДОТКЛОН
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- РАНГ.СР
Вопросы и ответы

Статистическая обработка данных – это сбор, упорядочивание, обобщение и анализ информации с возможностью определения тенденции и прогноза по изучаемому явлению. В Excel есть огромное количество инструментов, которые помогают проводить исследования в данной области. Последние версии этой программы в плане возможностей практически ничем не уступают специализированным приложениям в области статистики. Главными инструментами для выполнения расчетов и анализа являются функции. Давайте изучим общие особенности работы с ними, а также подробнее остановимся на отдельных наиболее полезных инструментах.

Статистические функции

Как и любые другие функции в Экселе, статистические функции оперируют аргументами, которые могут иметь вид постоянных чисел, ссылок на ячейки или массивы.

Выражения можно вводить вручную в определенную ячейку или в строку формул, если хорошо знать синтаксис конкретного из них. Но намного удобнее воспользоваться специальным окном аргументов, которое содержит подсказки и уже готовые поля для ввода данных. Перейти в окно аргумента статистических выражений можно через «Мастер функций» или с помощью кнопок «Библиотеки функций» на ленте.

Запустить Мастер функций можно тремя способами:

Кликнуть по пиктограмме «Вставить функцию» слева от строки формул.

Находясь во вкладке «Формулы», кликнуть на ленте по кнопке «Вставить функцию» в блоке инструментов «Библиотека функций».

Набрать на клавиатуре сочетание клавиш Shift+F3.

При выполнении любого из вышеперечисленных вариантов откроется окно «Мастера функций».

Затем нужно кликнуть по полю «Категория» и выбрать значение «Статистические».

После этого откроется список статистических выражений. Всего их насчитывается более сотни. Чтобы перейти в окно аргументов любого из них, нужно просто выделить его и нажать на кнопку «OK».

Для того, чтобы перейти к нужным нам элементам через ленту, перемещаемся во вкладку «Формулы». В группе инструментов на ленте «Библиотека функций» кликаем по кнопке «Другие функции». В открывшемся списке выбираем категорию «Статистические». Откроется перечень доступных элементов нужной нам направленности. Для перехода в окно аргументов достаточно кликнуть по одному из них.

Урок: Мастер функций в Excel

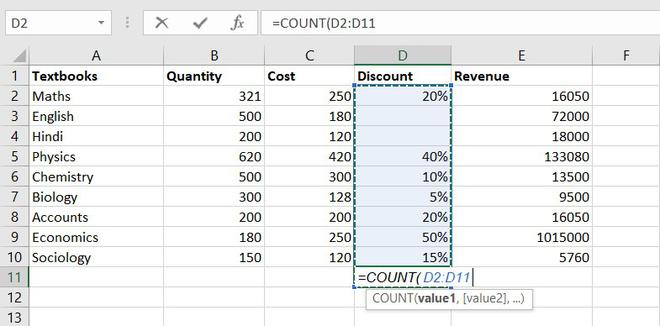
МАКС

Оператор МАКС предназначен для определения максимального числа из выборки. Он имеет следующий синтаксис:

=МАКС(число1;число2;…)

В поля аргументов нужно ввести диапазоны ячеек, в которых находится числовой ряд. Наибольшее число из него эта формула выводит в ту ячейку, в которой находится сама.

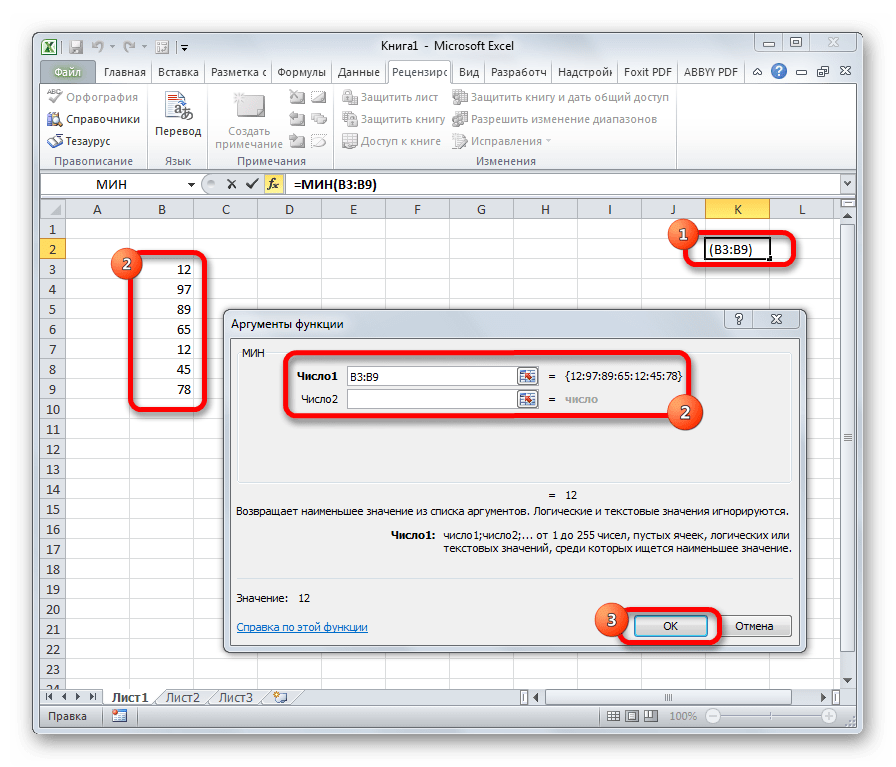
МИН

По названию функции МИН понятно, что её задачи прямо противоположны предыдущей формуле – она ищет из множества чисел наименьшее и выводит его в заданную ячейку. Имеет такой синтаксис:

=МИН(число1;число2;…)

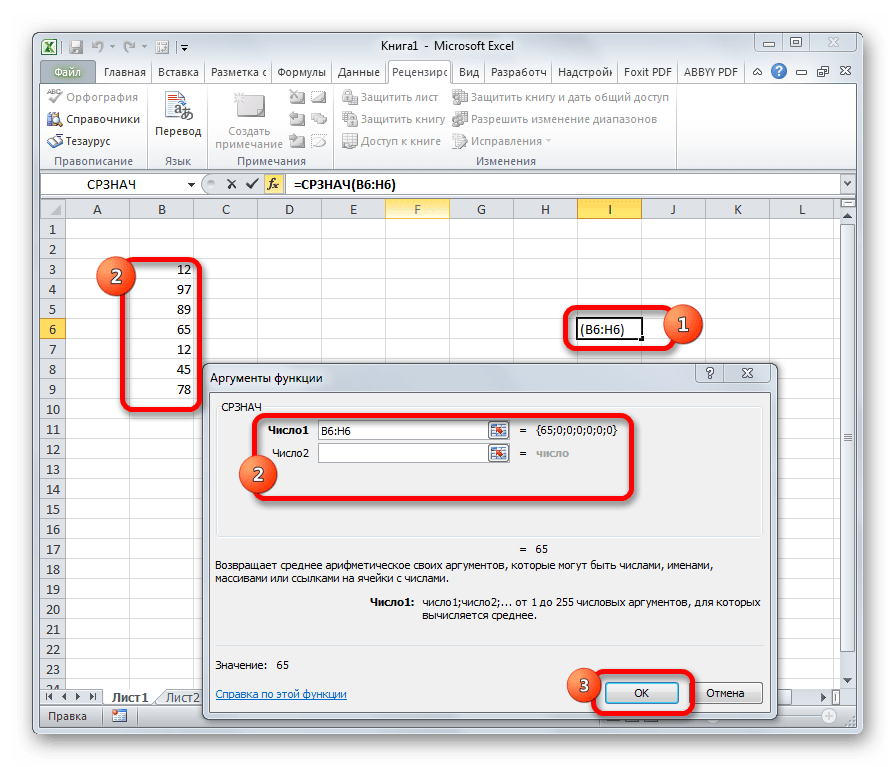
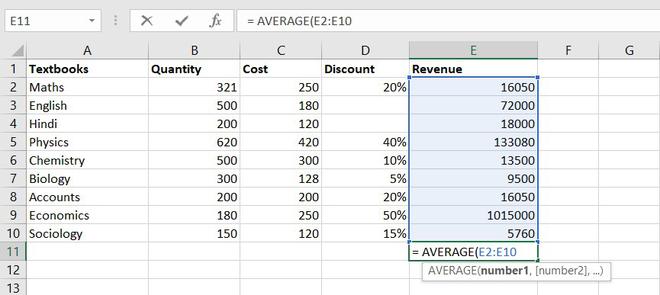
СРЗНАЧ

Функция СРЗНАЧ ищет число в указанном диапазоне, которое ближе всего находится к среднему арифметическому значению. Результат этого расчета выводится в отдельную ячейку, в которой и содержится формула. Шаблон у неё следующий:

=СРЗНАЧ(число1;число2;…)

СРЗНАЧЕСЛИ

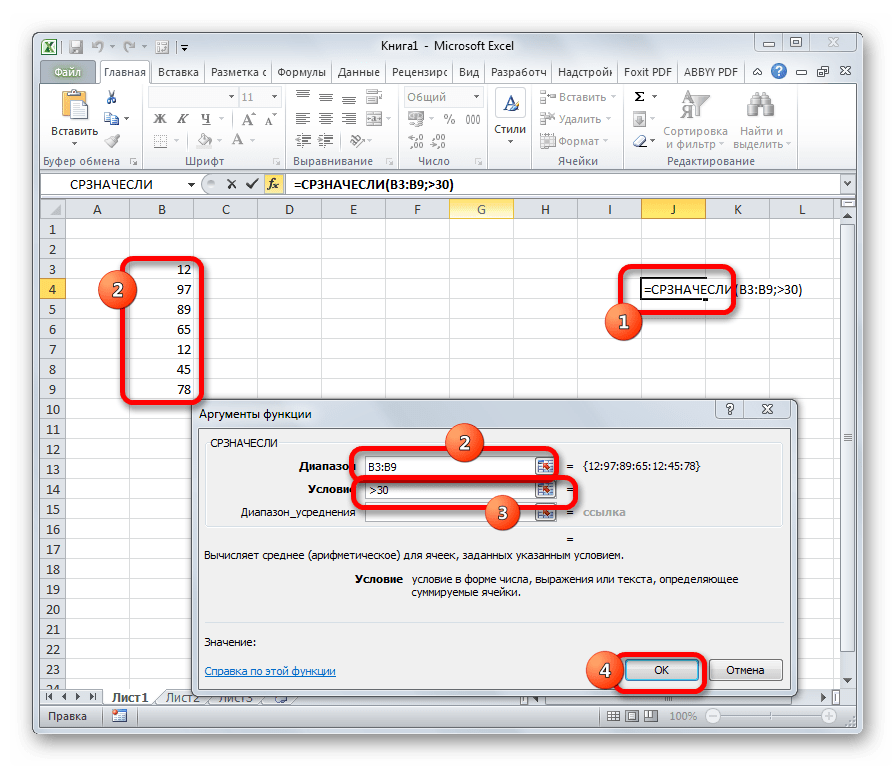
Функция СРЗНАЧЕСЛИ имеет те же задачи, что и предыдущая, но в ней существует возможность задать дополнительное условие. Например, больше, меньше, не равно определенному числу. Оно задается в отдельном поле для аргумента. Кроме того, в качестве необязательного аргумента может быть добавлен диапазон усреднения. Синтаксис следующий:

=СРЗНАЧЕСЛИ(число1;число2;…;условие;[диапазон_усреднения])

МОДА.ОДН

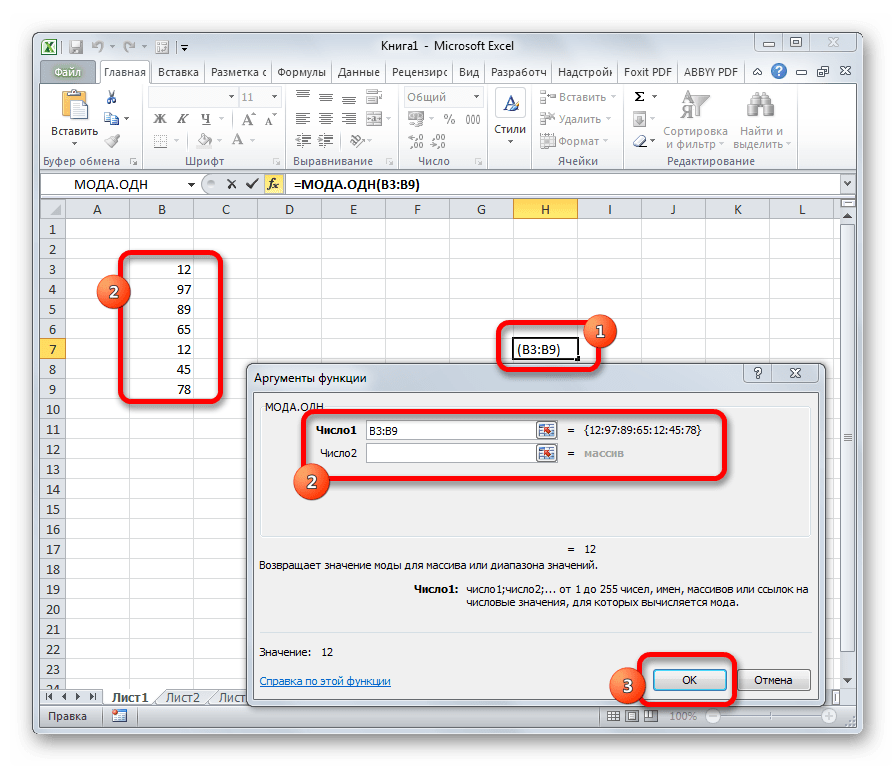
Формула МОДА.ОДН выводит в ячейку то число из набора, которое встречается чаще всего. В старых версиях Эксель существовала функция МОДА, но в более поздних она была разбита на две: МОДА.ОДН (для отдельных чисел) и МОДА.НСК(для массивов). Впрочем, старый вариант тоже остался в отдельной группе, в которой собраны элементы из прошлых версий программы для обеспечения совместимости документов.

=МОДА.ОДН(число1;число2;…)

=МОДА.НСК(число1;число2;…)

МЕДИАНА

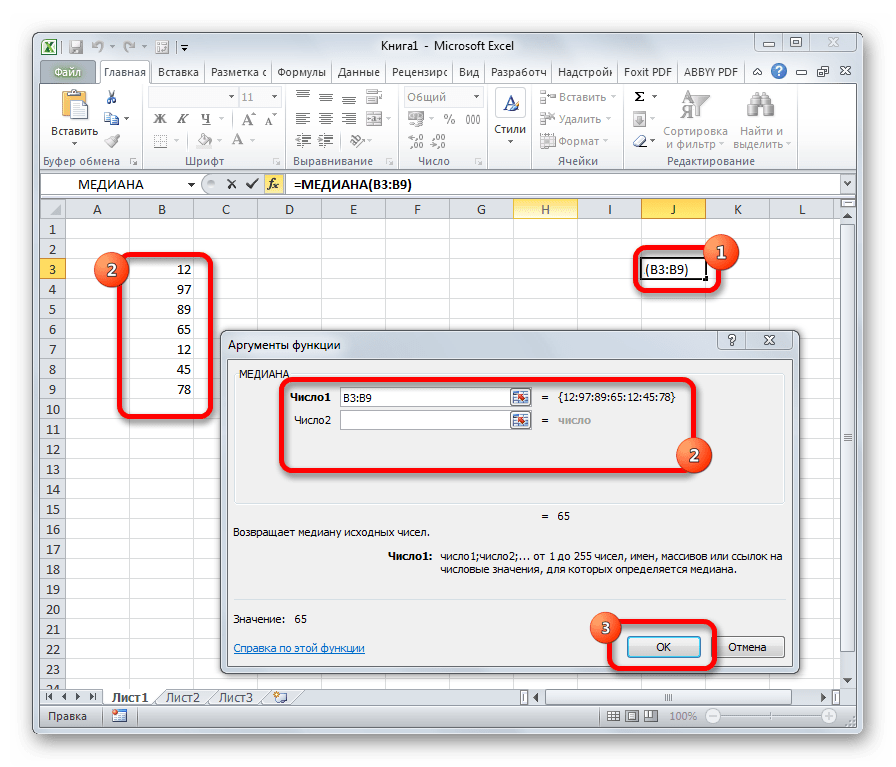
Оператор МЕДИАНА определяет среднее значение в диапазоне чисел. То есть, устанавливает не среднее арифметическое, а просто среднюю величину между наибольшим и наименьшим числом области значений. Синтаксис выглядит так:

=МЕДИАНА(число1;число2;…)

СТАНДОТКЛОН

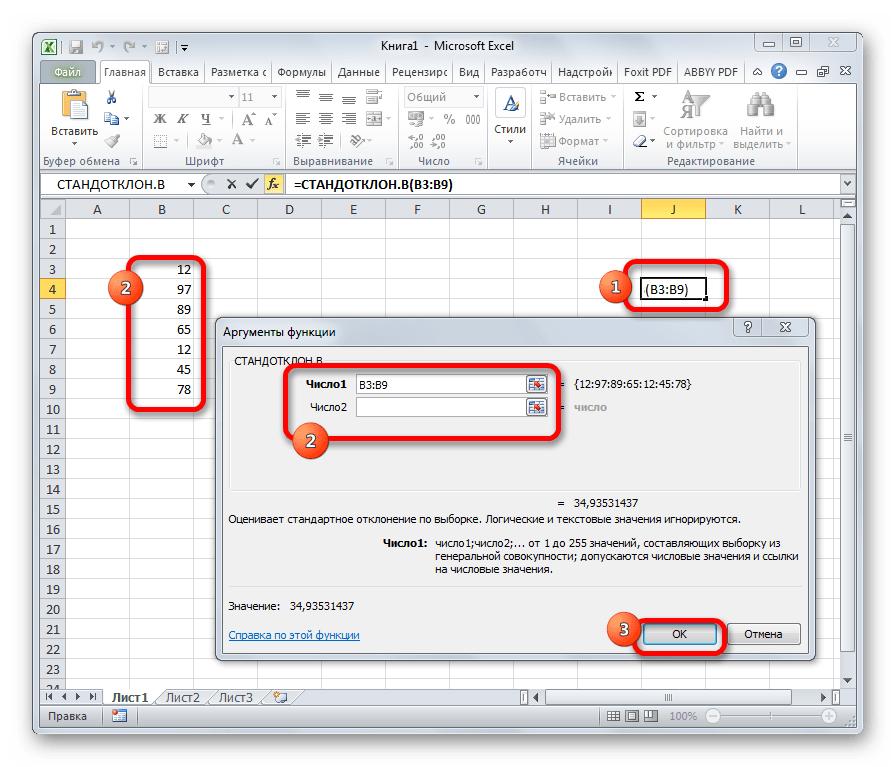
Формула СТАНДОТКЛОН так же, как и МОДА является пережитком старых версий программы. Сейчас используются современные её подвиды – СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г. Первая из них предназначена для вычисления стандартного отклонения выборки, а вторая – генеральной совокупности. Данные функции используются также для расчета среднего квадратичного отклонения. Синтаксис их следующий:

=СТАНДОТКЛОН.В(число1;число2;…)

=СТАНДОТКЛОН.Г(число1;число2;…)

Урок: Формула среднего квадратичного отклонения в Excel

НАИБОЛЬШИЙ

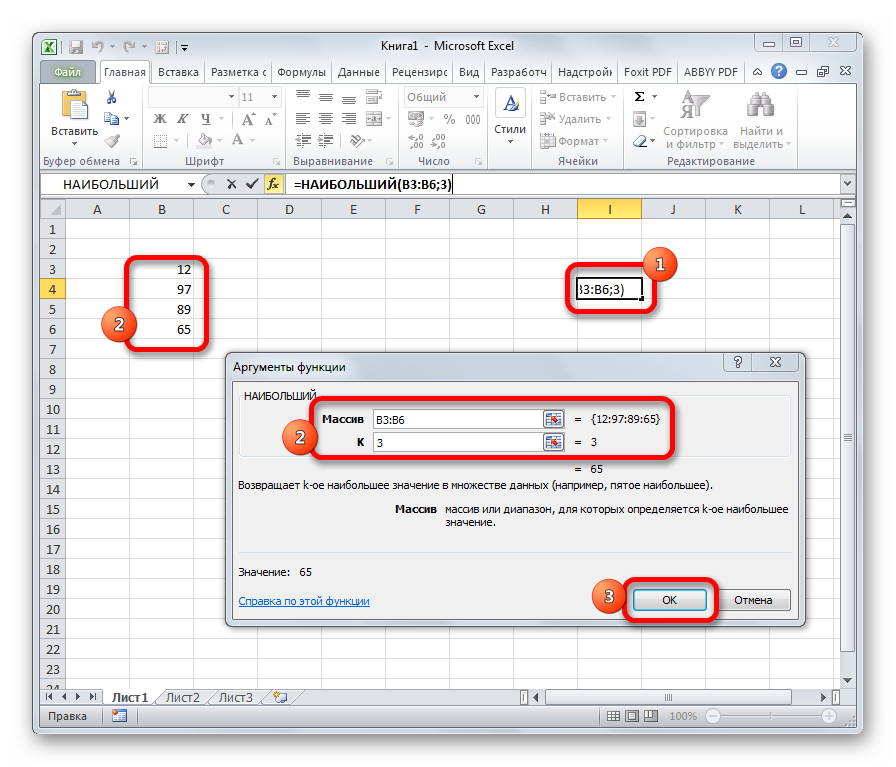
Данный оператор показывает в выбранной ячейке указанное в порядке убывания число из совокупности. То есть, если мы имеем совокупность 12,97,89,65, а аргументом позиции укажем 3, то функция в ячейку вернет третье по величине число. В данном случае, это 65. Синтаксис оператора такой:

=НАИБОЛЬШИЙ(массив;k)

В данном случае, k — это порядковый номер величины.

НАИМЕНЬШИЙ

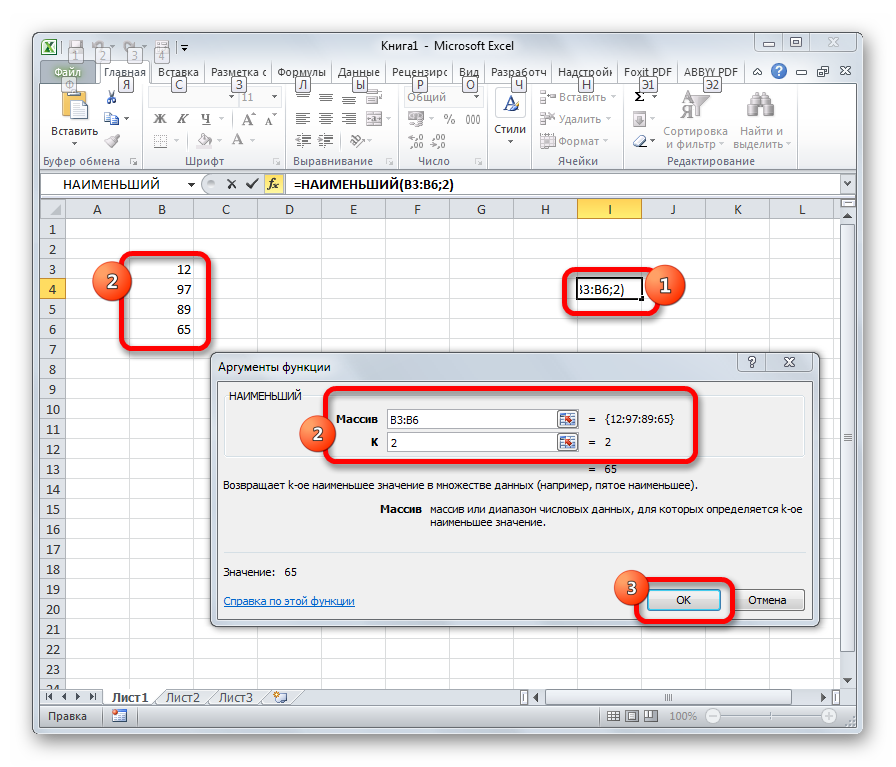
Данная функция является зеркальным отражением предыдущего оператора. В ней также вторым аргументом является порядковый номер числа. Вот только в данном случае порядок считается от меньшего. Синтаксис такой:

=НАИМЕНЬШИЙ(массив;k)

РАНГ.СР

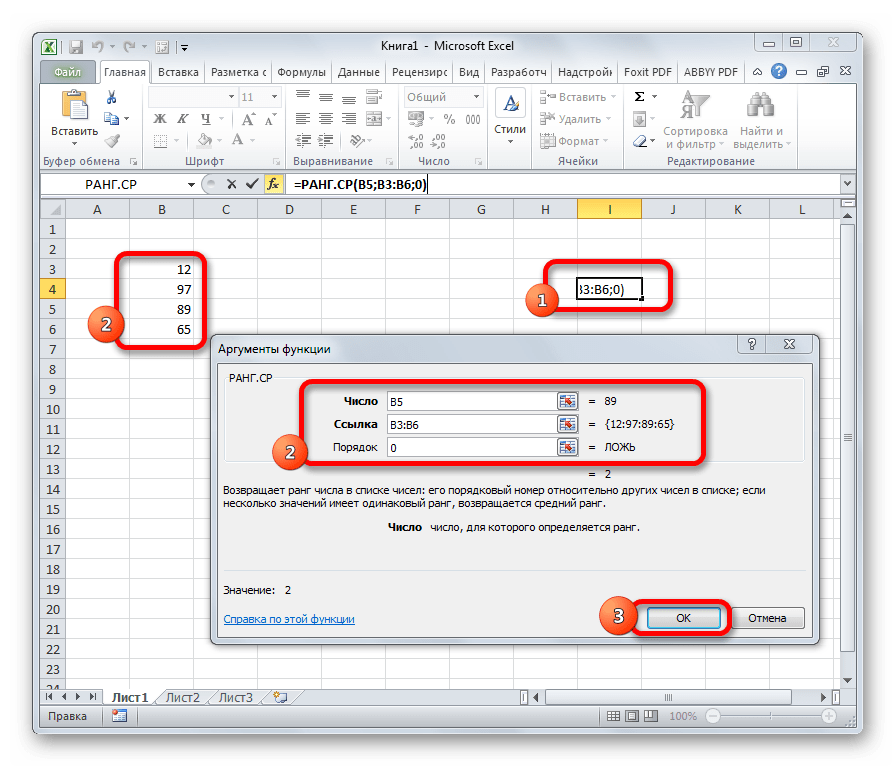
Эта функция имеет действие, обратное предыдущим. В указанную ячейку она выдает порядковый номер конкретного числа в выборке по условию, которое указано в отдельном аргументе. Это может быть порядок по возрастанию или по убыванию. Последний установлен по умолчанию, если поле «Порядок» оставить пустым или поставить туда цифру 0. Синтаксис этого выражения выглядит следующим образом:

=РАНГ.СР(число;массив;порядок)

Выше были описаны только самые популярные и востребованные статистические функции в Экселе. На самом деле их в разы больше. Тем не менее, основной принцип действий у них похожий: обработка массива данных и возврат в указанную ячейку результата вычислительных действий.

Источник

Зная статистические формулы и приемы можно обработать, проанализировать и упорядочить большое количество информации. В Эксель инструменты статистики выведены в отдельную категорию функций. Давайте посмотрим, как их найти, а также, какие из них являются наиболее популярными среди пользователей.

Использование статистических функций
- СРЗНАЧ
- МАКС
- МИН
- СРЗНАЧЕСЛИ
- МЕДИАНА
- НАИБОЛЬШИЙ
- НАИМЕНЬШИЙ
- МОДА.ОДН
- СТАНДОТКЛОН
- СРГЕОМ
Заключение

Использование статистических функций

Формулы функций в Excel можно вводить вручную непосредственно в той ячейке, где планируется выполнить соответствующие расчеты. Это легко применимо к таким простым действиям, как сложение, вычитание, умножение и деление. Но запомнить формулы сложных функций уже непросто, поэтому проще воспользоваться специальным помощником, который встроен в программу.

Итак, чтобы вставить функцию в ячейку, выполняем одно из следующих действий:

Находясь в любой вкладке программы щелкаем по значку “Вставить функцию” (fx), которая находится с левой стороны от строки формул.
Переходим во вкладку “Формулы”, где видим в левом углу ленты инструментов кнопку “Вставить функцию”.
Используем сочетание клавиш Shift+F3.

Независимо от выбранного способа выше перед нами появится окно вставки функций. Щелкаем по текущей категории и из раскрывшегося списка выбираем пункт “Статистические”.

Далее будет предложен на выбор один из статистических операторов. Отмечаем нужный и жмем OK.

На экране отобразится окно с аргументами выбранной функции, которые нужно заполнить.

Примечание: существует еще один способ выбора требуемой функции. Находясь во вкладке “Формулы” в блоке инструментов “Библиотека функций” щелкаем по значку “Другие функции”, затем выбираем пункт “Статистические” и, наконец, в открывшемся перечне (который можно листать вниз) – нужный оператор.

Давайте теперь рассмотрим наиболее популярные функции.

СРЗНАЧ

Оператор вычисляет среднее арифметическое значение из указанных значений (диапазона). Формула функции выглядит таким образом:

=СРЗНАЧ(число1;число2;…)

В качестве аргументов функции можно указать:

конкретные числа;
ссылки на ячейки, которые можно указать как вручную (напечатать с помощью клавиатуры), так и находясь в соответствующем поле щелкнуть по нужному элементу в самой таблице;
диапазон ячеек – указывается вручную или путем выделения в таблице.
переход к следующему аргументу происходит путем щелчка по соответствующему полю напротив него или просто нажатием клавиши Tab.

МАКС

Функция помогает определить максимальное значение из заданных чисел (диапазона). Формула оператора следующая:

=МАКС(число1;число2;…)

В аргументах функции, также, как и в случае с оператором СРЗНАЧ можно указать конкретные числа, ссылки на ячейки или диапазоны ячеек.

МИН

Функция находит минимальное число из указанных значений (диапазона ячеек). В общем виде синтаксис выглядит так:

=МИН(число1;число2;…)

Аргументы функции заполняются так же, как и для оператора МАКС.

СРЗНАЧЕСЛИ

Функция позволяет найти среднее арифметическое значение, но при выполнении заданного условия. Формула оператора:

=СРЗНАЧЕСЛИ(диапазон;условие;диапазон_усреднения)

В аргументах указываются:

Диапазон ячеек – вручную или с помощью выделения в таблице;
Условие отбора значений из заданного диапазона (больше, меньше, не равно) – в кавычках;
Диапазон_усреднения – не является обязательным аргументом для заполнения.

МЕДИАНА

Оператор находит медиану заданного диапазона значений. Синтаксис функции:

=МЕДИАНА(число1;число2;…)

В аргументах указываются: конкретные числа, ссылки на ячейки или диапазоны элементов.

НАИБОЛЬШИЙ

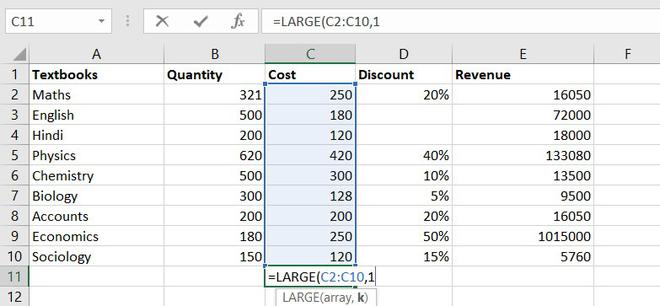
Функция позволяет найти из указанного диапазона значений с заданной позицией (по убыванию). Формула оператора:

=НАИБОЛЬШИЙ(массив;k)

Аргумента функции два: массив и номер позиции – K.

Допустим, имеется ряд чисел 4, 6, 12, 24, 15, 9. Если мы укажем в качестве аргумента “K” число 2, результатом будет значение, равное 15, т.к. оно второе по величине в выбранном диапазоне.

НАИМЕНЬШИЙ

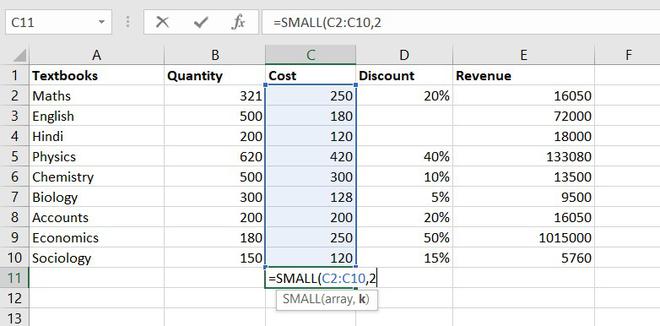
Функция также, как и оператор НАИБОЛЬШИЙ, выполняет поиск из указанного диапазона значений. Правда, в данном случае счет идет по возрастанию. Синтаксис оператора следующий:

=НАИМЕНЬШИЙ(массив;k)

МОДА.ОДН

Функция пришла на замену более старому оператору “МОДА” (теперь находится в категории “Полный алфавитный перечень”). Позволяет определять число, которое повторяется чаще остальных в выбранном диапазоне. Работает функция по формуле:

=МОДА.ОДН(число1;число2;…)

В значениях аргументов указываются конкретные числовые значения, отдельные ячейки или их диапазоны.

Для вертикальных массивов, также, используется функция МОДА.НСК.

СТАНДОТКЛОН

Функция СТАНДОТКЛОН также устарела (но ее все еще можно найти, выбрав алфавитный перечень) и теперь представлена двумя новыми:

СТАДНОТКЛОН.В – находит стандартное отклонение выборки
СТАДНОТКЛОН.Г – определяет стандартное отклонение по генеральной совопкупности

Формулы функций выглядят следующим образом:

=СТАДНОТКЛОН.В(число1;число2;…)
=СТАДНОТКЛОН.Г(число1;число2;…)

СРГЕОМ

Оператор находит среднее геометрическое значение для заданного массива или диапазона. Формула функции:

=СРГЕОМ(число1;число2;…)

Заключение

В программе Excel более 100 статистических функций. Мы лишь рассмотрели те, которые используются пользователями чаще других, а также, где их можно найти и как заполнить аргументы для получения корректного результата.

Источник

Создание сложных формул с помощью встроенных логических функций Excel

Логические выражения в Excel используются для записи условий, в которых сравниваются числа, функции, формулы, текстовые или логические значения. Любое логическое выражение должно содержать, по крайней мере, один оператор сравнения, который определяет отношение между элементами логического выражения.

Ниже представлен список операторов сравнения Excel:

Больше или равно

Результатом логического выражения является логическое значение ИСТИНА (1) или логическое значение ЛОЖЬ (0).

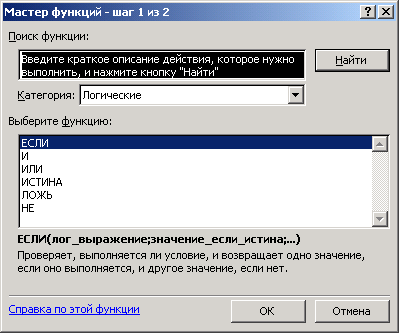
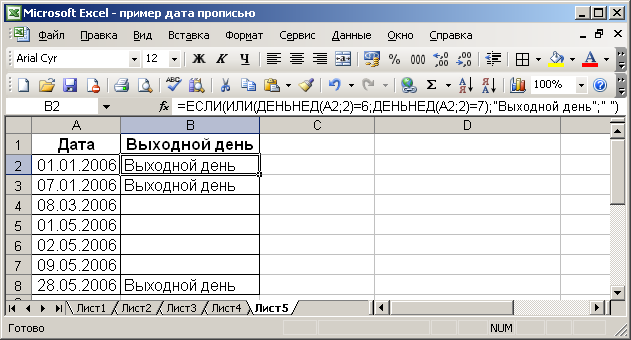
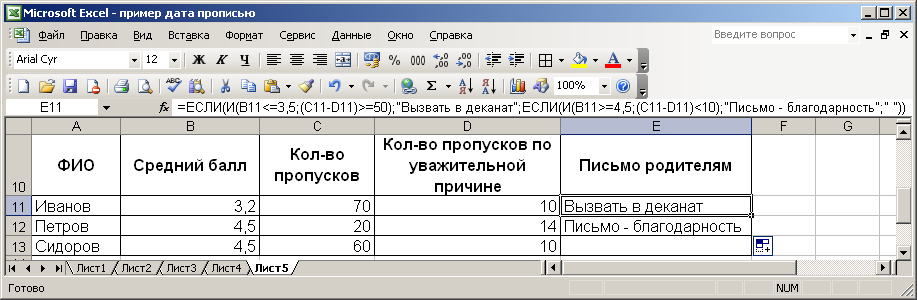
Функция ЕСЛИ – это функция, которая позволяет вывести в ячейку одно значение, если заданное пользователем условие выполняется и другое – если условие не выполняется.

ЕСЛИ(лог_выраж.; знач._если_истина; знач._если_ложь)

Рассчитать стоимость товара с учетом того, что если количество превысило 5 шт., то магазин дает скидку 10%. Исходные данные приведены на рис. 26.

Для того чтобы рассчитать стоимость товара с учетом скидки необходимо:

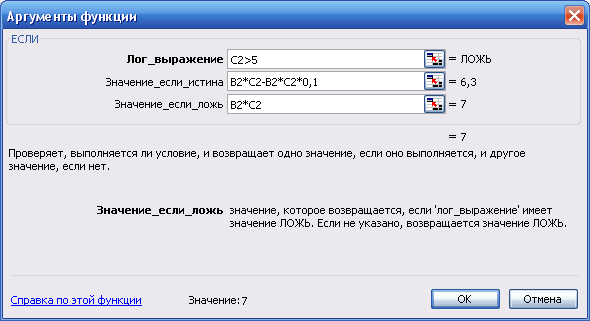
Переместить курсор в ячейку D2. С помощью мастера функций выбрать из категории Логические функцию ЕСЛИ (рис. 27), а затем щелкнуть на кнопке ОК.

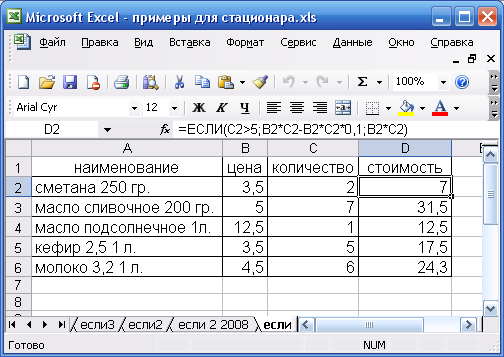
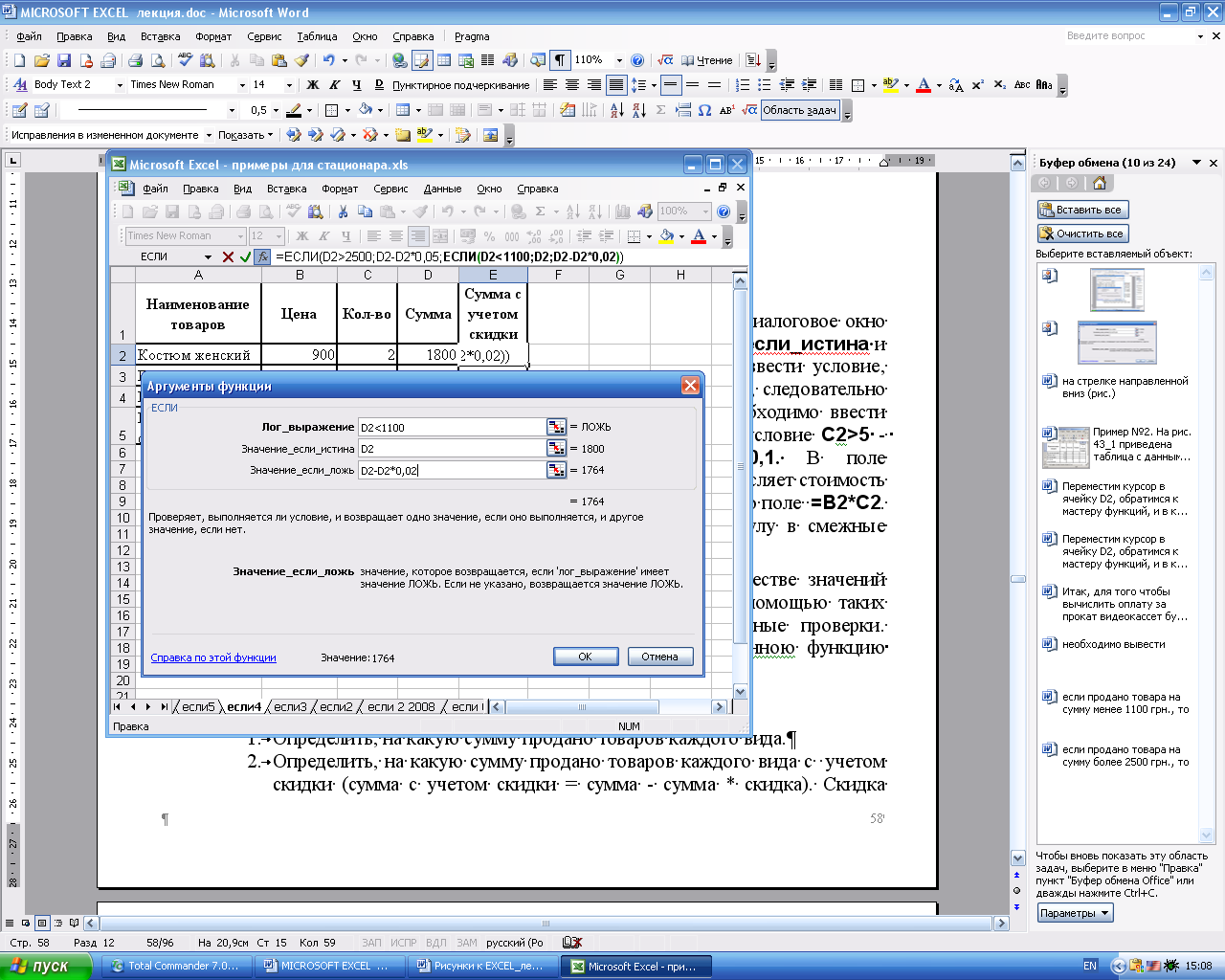
Диалоговое окно Аргументы функции (рис. 28) содержит три поля ввода. В поле Лог_выражение необходимо ввести условие, которое определяет, превышает ли проданное кол-во товара 5 шт., следовательно введем в это поле С2>5. В поле Значение_если_истина необходимо ввести формулу, которая вычисляет стоимость товара с учетом скидки, тогда введем в это поле B2*C2-B2*C2*0,1. В поле Значение_если_ложь необходимо ввести формулу, которая вычисляет стоимость товара без учета скидки (условие С2>5 — Ложь), в тогда введем в это поле B2*C2 (см. рис. 29). Теперь щелкнем на кнопке OK.

Скопировать полученную формулу в смежные ячейки. Результаты вычислений формул приведены на рис. 30.

Функции ЕСЛИ могут быть вложены друг в друга в качестве значений аргументов значение_если_истина и значение_если_ложь. С помощью таких вложенных функций Если можно конструировать более сложные проверки. Рассмотрим на примерах, как необходимо использовать вложенной функцией ЕСЛИ.

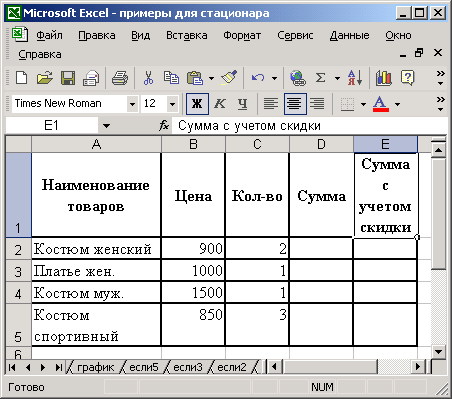
На рис. 31 приведена таблица с данными. Необходимо:

Определить, на какую сумму продано товаров каждого вида.

Определить, на какую сумму продано товаров каждого вида с учетом скидки (сумма с учетом скидки = сумма — сумма * скидка). Скидка начисляется по следующему принципу: если продано товара на сумму более 2500 грн., то скидка составит 5%, если продано товара на сумму менее 1100 грн., то скидка составит 0%, в остальных случаях скидка составит 2%.

Для того чтобы выполнить первый пункт задания необходимо в ячейку D2 ввести формулу =C2*B2.

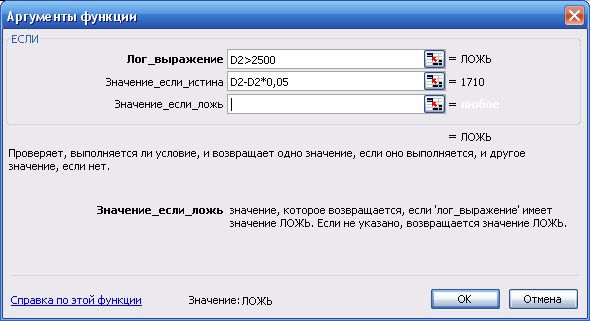
Для того чтобы вычислить сумму со скидкой будем использовать вложенную функцию ЕСЛИ, так как существует три варианта начисления скидки.

Переместим курсор в ячейку E2 и с помощью мастера функций введем следующую формулу (рис. 33 – 34). Результаты решения приведены на рис. 35.

Рис. 35

Функции ИЛИ, И

Функции И и функция ИЛИ из категории Логические способны заметно улучшить наглядность и понятность сложных логических проверок. Функция ИЛИ и функция И позволяют задавать в формуле одновременно несколько условий, т.е. дают возможность создавать сложные логические выражения. Эти функции работают в сочетании с простыми операторами сравнения. Функции И и ИЛИ могут иметь до 30 логических аргументов и имеют синтаксис:

Аргументы функций И, ИЛИ могут быть логическими выражениями, массивами или ссылками на ячейки, содержащие логические значения.

Функция ИЛИ возвращает логическое значение ИСТИНА, если хотя бы одно из логических выражений истинно, а функция И возвращает логическое значение ИСТИНА, только если все логические выражения истинны.

Предположим, что нужно вывести сообщение «Светофор», если содержимое ячейки B4 или «красный», или «зеленый», или «желтый». Если же она содержит любую другую информацию, то необходимо вывести сообщение «Это не светофор. ».

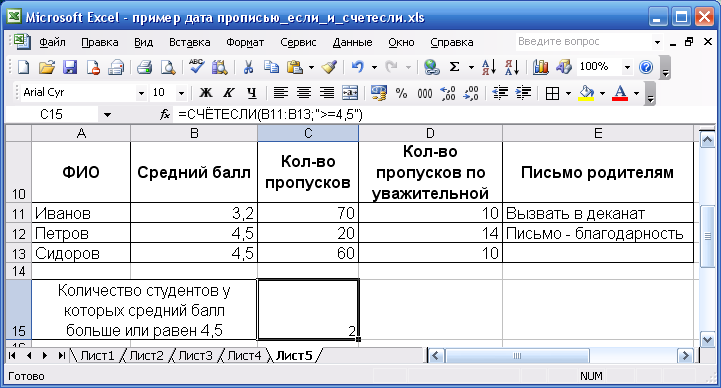
Предположим, что нужно вывести на экран содержимое ячейки B4, если она содержит число строго между 1 и 100 (1 =1; B4 =4.5.

Тогда в ячейку С15 необходимо ввести формулу: =СЧЁТЕСЛИ(B11:B13;»>=4,5″). Результат приведен на рис. 40

СУММЕСЛИ (диапазон; критерий; диапазон_суммирования)

диапазон — диапазон ячеек проверяемых на критерий (условие).

критерий — критерий (условие) в форме числа, выражения или текста, определяющего суммируемые ячейки.

диапазон_суммирования — фактические ячейки для суммирования.

Функция СУММЕСЛИ работает следующим образом: ячейки из «диапазон_суммирования» суммируются, только если соответствующие им ячейки в аргументе «диапазон» удовлетворяют условию (критерию). В тех случаях, когда диапазон вычисляемых ячеек (где проверяется условие) и диапазон фактических ячеек для суммирования совпадают, аргумент «диапазон_суммирования» можно не указывать.

В таблице на рис. 41 приведены объемы партий товара, полученные магазином. Необходимо просуммировать только объемы тех партий, значения которых превышают 20. Решение на рис. 42

Логические функции в excel с примерами их использования

Логические функции в Excel проверяют данные и возвращают результат «ИСТИНА», если условие выполняется, и «ЛОЖЬ», если нет.

Рассмотрим синтаксис логических функций и примеры применения их в процессе работы с программой Excel.

Использование логических функций в Excel

Логические функции в Excel и примеры решения задач

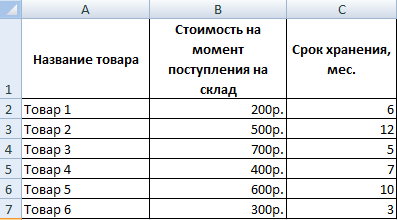
Задача 1. Необходимо переоценить товарные остатки. Если продукт хранится на складе дольше 8 месяцев, уменьшить его цену в 2 раза.

Сформируем таблицу с исходными параметрами:

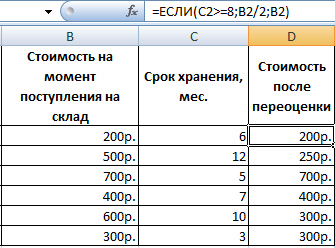
Чтобы решить поставленную задачу, воспользуемся логической функцией ЕСЛИ. Формула будет выглядеть так: =ЕСЛИ(C2>=8;B2/2;B2).

Логическое выражение «С2>=8» построено с помощью операторов отношения «>» и «=». Результат его вычисления – логическая величина «ИСТИНА» или «ЛОЖЬ». В первом случае функция возвращает значение «В2/2». Во втором – «В2».

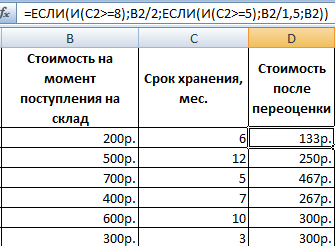
Усложним задачу – задействуем логическую функцию И. Теперь условие такое: если товар хранится дольше 8 месяцев, то его стоимость уменьшается в 2 раза. Если дольше 5 месяцев, но меньше 8 – в 1,5 раза.

Формула приобретает следующий вид: =8);B2/2;ЕСЛИ(И(C2>=5);B2/1,5;B2))’ class=’formula’>.

В функции ЕСЛИ можно использовать в качестве аргументов текстовые значения.

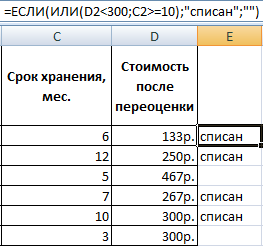
Задача 2. Если стоимость товара на складе после уценки стала меньше 300 р. или продукт хранится дольше 10 месяцев, его списывают.

Для решения используем логические функции ЕСЛИ и ИЛИ: =10);»списан»;»»)’ class=’formula’>. Условие, записанное с помощью логической операции ИЛИ, расшифровывается так: товар списывается, если число в ячейке D2 = 10.

При невыполнении условия функция ЕСЛИ возвращает пустую ячейку.

В качестве аргументов можно использовать другие функции. К примеру, математические.

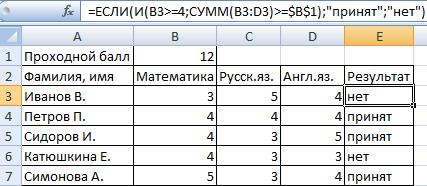
Задача 3. Ученики перед поступлением в гимназию сдают математику, русский и английский языки. Проходной балл – 12. По математике для поступления нужно получить не менее 4 баллов. Составить отчет о поступлении.

Составим таблицу с исходными данными:

Нужно общее количество баллов сравнить с проходным баллом. И проверить, чтобы по математике оценка была не ниже «4». В графе «Результат» поставить «принят» или «нет».

Введем формулу вида: =4;СУММ(B3:D3)>=$B$1);»принят»;»нет»)’ class=’formula’>. Логический оператор «И» заставляет функцию проверять истинность двух условий. Математическая функция «СУММ» используется для подсчета итогового балла.

Функция ЕСЛИ позволяет решать многочисленные задачи, поэтому используется чаще всего.

Статистические и логические функции в Excel

Задача 1. Проанализировать стоимость товарных остатков после уценки. Если цена продукта после переоценки ниже средних значений, то списать со склада этот продукт.

Работаем с таблицей из предыдущего раздела:

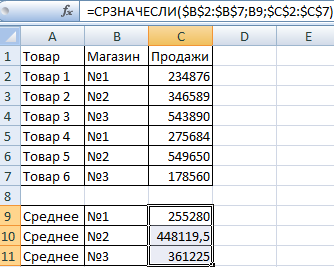
Для решения задачи используем формулу вида: . В логическом выражении «D2 . Первый аргумент – $B$2:$B$7 – диапазон ячеек для проверки. Второй аргумент – В9 – условие. Третий аргумент – $C$2:$C$7 – диапазон усреднения; числовые значения, которые берутся для расчета среднего арифметического.

Функция СРЗНАЧЕСЛИ сопоставляет значение ячейки В9 (№1) со значениями в диапазоне В2:В7 (номера магазинов в таблице продаж). Для совпадающих данных считает среднее арифметическое, используя числа из диапазона С2:С7.

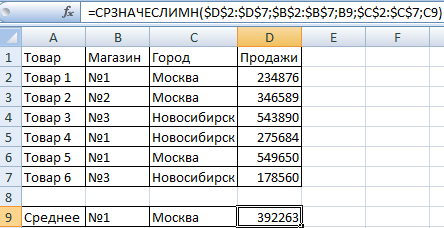
Задача 3. Найти средние продажи в магазине №1 г. Москва.

Видоизменим таблицу из предыдущего примера:

Нужно выполнить два условия – воспользуемся функцией вида: .

Функция СРЗНАЧЕСЛИМН позволяет применять более одного условия. Первый аргумент – $D$2:$D$7 – диапазон усреднения (откуда берутся цифры для нахождения среднего арифметического). Второй аргумент – $B$2:$B$7 – диапазон для проверки первого условия.

Третий аргумент – В9 – первое условие. Четвертый и пятый аргумент – диапазон для проверки и второе условие, соответственно.

Функция учитывает только те значения, которые соответствуют всем заданным условиям.

БЛОГ

Только качественные посты

Практический справочник функций Microsoft Excel с примерами их использования

На сегодняшний день программа Microsoft Excel является самой популярной программой в бизнесе, которая позволяет решать различные задачи — от анализа до учета данных. Самым популярным инструментом в Excel являются встроенные функции, количество которых приближается к 1000 штук.

Отсюда вытекает вопрос: Сколько нужно знать функций Excel, чтобы решать практически любую задачу в Excel?

Могу с уверенностью, опираясь на свой 17 летний профессиональный опыт работы в Excel, сказать, что достаточно освоить всего около 100 функций…

Представляю Вам ТОП-50 самых главных функций в Microsoft Excel с примерами их использования

– изучив данные Excel функции, у Вас будет достаточно теоретических знаний, чтобы решать практически любую задачу в Excel

( Для перехода к примерам нажмите на название функции. Все примеры — это ссылки на лучшие статьи уважаемых специалистов по Excel и наших партнеров)

1. СУММ / СРЗНАЧ / СЧЁТ / МАКС / МИН (SUM / AVERAGE / COUNT / MAX / MIN) — [Базовые формулы Excel]
2. ВПР (VLOOKUP) — [Ищет значение в первом столбце массива и выдает значение из ячейки в найденной строке и указанном столбце]
3. ИНДЕКС (INDEX) — [По индексу получает значение из ссылки или массива]
4. ПОИСКПОЗ (MATCH) — [Ищет значения в ссылке или массиве]
5. СУММПРОИЗВ (SUMPRODUCT) — [Вычисляет сумму произведений соответствующих элементов массивов (позволяет работать с массивами без формул массива)]
6. АГРЕГАТ / ПРОМЕЖУТОЧНЫЕ.ИТОГИ (AGGREGATE / SUBTOTALS) — [Возвращает общий итог или промежуточный итог в списке или базе данных с учетом фильтров или без учета фильтров]
7. ЕСЛИ (IF) — [Выполняет проверку условия]
8. И / ИЛИ / НЕ (AND / OR / NOT) — [Логические условия, как правило для функции ЕСЛИ]
9. ЕСЛИОШИБКА (IFERROR) — [Если формула возвращает ошибку то что]
10. СУММЕСЛИМН (SUMIFS) — [Суммирует ячейки, удовлетворяющие заданным критериям. Допускается указывать более одного условия]
11. СРЗНАЧЕСЛИМН (AVERAGEIFS) — [Возвращает среднее арифметическое значение всех ячеек, которые соответствуют нескольким условиям]
12. СЧЁТЕСЛИМН (COUNTIFS) — [Подсчитывает количество ячеек, которые соответствуют нескольким условиям]
13. МИНЕСЛИ / МАКСЕСЛИ (MINIFS / MAXIFS) — [Возвращает минимальное/максимальное значение всех ячеек, которые соответствуют нескольким условиям]
14. НАИБОЛЬШИЙ / НАИМЕНЬШИЙ (LARGE / SMALL) — [Возвращает k-ое наибольшее/наименьшее значение в множестве данных]
15. ДВССЫЛ (INDIRECT) — [Определяет ссылку, заданную текстовым значением]
16. ВЫБОР (CHOOSE) — [Выбирает значение из списка значений по индексу]
17. ПРОСМОТР (LOOKUP) — [Ищет значения в массиве]
18. СМЕЩ (OFFSET) — [Определяет смещение ссылки относительно заданной ссылки]
19. СТРОКА / СТОЛБЕЦ (ROW / COLUMN) — [Возвращает номер строки/столбца, на который указывает ссылка]
20. ЧИСЛСТОЛБ / ЧСТРОК (COLUMNS / ROWS) — [Возвращает количество столбцов/строк в ссылке]
21. ОКРУГЛ / ОКРУГЛТ / ОКРУГЛВНИЗ / ОКРУГЛВВЕРХ (ROUND / MROUND / ROUNDDOWN / ROUNDUP) — [Округляет число до указанного количества десятичных разрядов]
22. СЛЧИС / СЛУЧМЕЖДУ / РАНГ (RAND / RANDBETWEEN / RANK) — [Возвращает случайное число]
23. Ч (N) — [Возвращает значение, преобразованное в число]
24. ЧАСТОТА (FREQUENCY) — [Находит распределение частот в виде вертикального массива]
25. СЦЕПИТЬ / СЦЕП / ОБЪЕДИНИТЬ / & (CONCATENATE / CONCAT / TEXTJOIN / &) — [Объединения двух или нескольких текстовых строк в одну]
26. ПСТР (MID) — [Выдает определенное число знаков из строки текста, начиная с указанной позиции]
27. ЛЕВСИМВ / ПРАВСИМВ (LEFT / RIGHT) — [Возвращает заданное количество символов текстовой строки слева / права]
28. ДЛСТР (LEN) — [Определяет количество знаков в текстовой строке]
29. НАЙТИ / ПОИСК (FIND / SEARCH) — [Поиск текста в ячейке с учетом / без учета регистр]
30. ПОДСТАВИТЬ / ЗАМЕНИТЬ (SUBSTITUTE / REPLACE) — [Заменяет в текстовой строке старый текст новым]
31. СТРОЧН / ПРОПИСН / ПРОПНАЧ (LOWER / UPPER) — [Преобразует все буквы текста в строчные/прописные/ или первую букву в каждом слове текста в прописную]
32. ГИПЕРССЫЛКА (HYPERLINK) — [Создает ссылку, открывающую документ, находящийся на жестком диске, сервере сети или в Интернете]
33. СЖПРОБЕЛЫ (TRIM) — [Удаляет из текста все пробелы, за исключением одиночных пробелов между словами]
34. ПЕЧСИМВ (CLEAN) — [Удаляет все непечатаемые знаки из текста]
35. СОВПАД (EXACT) — [Проверяет идентичность двух текстов]
36. СИМВОЛ / ПОВТОР (CHAR / REPT) — [Возвращает знак с заданным кодом/Повторяет текст заданное число раз]
37. СЕГОДНЯ / ТДАТА (TODAY / NOW) — [Возвращает текущую дату в числовом формате / Возвращает текущую дату и время в числовом формате]
38. МЕСЯЦ / ГОД (MONTH / YEAR) — [Вычисляет год / месяц от заданной даты]
39. НОМНЕДЕЛИ (WEEKNUM) — [Преобразует дату в числовом формате в число, которое указывает, на какую неделю года приходится дата]
40. ДАТАЗНАЧ (DATEVALUE) — [Преобразует дату из текстового формата в числовой]
41. РАЗНДАТ (DATEDIF) — [Вычисляет количество дней, месяцев или лет между двумя датами]
42. РАБДЕНЬ (WORKDAY) — [Возвращает дату в числовом формате, отстоящую вперед или назад на заданное количество рабочих дней]
43. ЯЧЕЙКА (CELL) — [Возвращает сведения о формате, расположении или содержимом ячейки]
44. ТРАНСП (TRANSPOSE) — [Выдает транспонированный массив]
45. ПРЕОБР (CONVERT) — [Преобразует число из одной системы мер в другую]
46. ПРЕДСКАЗ (FORECAST) — [Вычисляет или предсказывает будущее значение по существующим значениям линейным трендом]
47. ТИП.ОШИБКИ (ERROR.TYPE) — [Возвращает числовой код, соответствующий типу ошибки]
48. ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ (GETPIVOTDATA) — [Возвращает данные, хранящиеся в сводной таблице]
49. БДСУММ (DSUM) — [Суммирует числа в поле (столбце) записей списка или базы данных, которые удовлетворяют заданным условиям]
50. В качестве бонуса рекомендую изучить Пользовательские форматы в Excel.

После освоения данных функций, следующим этапом рекомендую осваивать инструменты Бизнес- аналитики Business Intelligence (BI)

В Excel к инструментам бизнес-аналитики уровня Self-Service BI относятся бесплатные надстройки «Power»:

Power Query — это технология подключения к данным, с помощью которой можно обнаруживать, подключать, объединять и уточнять данные из различных источников для последующего анализа.
Power Pivot — это технология моделирования данных, которая позволяет создавать аналитические модели данных, устанавливать отношения и добавлять аналитические вычисления.
Power View — это технология визуализации данных, с помощью которой можно создавать интерактивные диаграммы, графики, карты и другие наглядные элементы, позволяющие визуализировать различную информацию.

Ну и если Вы со временем поймете, что возможностей Excel для решения ваших аналитических задач недостаточно, то вам пора переходить к изучению промышленных решений уровня Business Intelligence (BI)

6 малоизвестных, но очень полезных функций Excel

Microsoft Excel на сегодняшний день просто незаменим, особенно когда дело касается обработки больших объемов данных. Однако у этой программы столько функций, что непросто разобраться, какие их них действительно нужные и полезные.

И поэтому сегодня AdMe.ru расскажет, какими способами можно эффективно систематизировать информацию и разложить все по полочкам.

Сводные таблицы

С помощью сводных таблиц очень удобно сортировать, рассчитывать сумму или получать среднее значение из данных электронной таблицы, при этом никакие формулы выводить не нужно.

Как применять:

Выберите Вставка > Рекомендуемые сводные таблицы.
В диалоговом окне Рекомендуемые сводные таблицы щелкните любой макет сводной таблицы, чтобы увидеть его в режиме предварительного просмотра, а затем выберите тот из них, в котором данные отображаются нужным вам образом. Нажмите кнопку ОК.
Excel добавит сводную таблицу на новый лист и отобразит список полей, с помощью которого можно упорядочить данные в таблице.

Подбор параметра

Если вы знаете, какой результат вычисления формулы вам нужен, но не можете определить входные значения, позволяющие его получить, используйте средство подбора параметров.

Как применять:

Выберите Данные > Работа с данными > Анализ «что если» > Подбор параметра.
В поле Установить в ячейке введите ссылку на ячейку, в которой находится нужная формула.
В поле Значение введите нужный результат формулы.
В поле Изменяя значениеячейки введите ссылку на ячейку, в которой находится корректируемое значение, и нажмите кнопку ОК.

Условное форматирование

Условное форматирование позволяет быстро выделить на листе важные сведения.

Как применять:

На вкладке Главная в группе Стили щелкните стрелку рядом с кнопкой Условное форматирование и выберите формулу, которая вам понадобится.

Например, если вам нужно выделить все значения меньше 100, выберите Правила выделения ячеек > Меньше, а затем наберите 100. Перед тем как нажать ОК, можно выбрать формат, который будет применяться для подходящих значений.

ИНДЕКС и ПОИСКПОЗ

Если ВПР помогает находить нужные данные только в первом столбце, то, благодаря функциям ИНДЕКС и ПОИСКПОЗ, можно искать информацию внутри таблицы.

Как применять:

Убедитесь, что ячейки с данными образуют сетку, где есть заголовки и названия строк.
Используйте функцию ПОИСКПОЗ: сначала, чтобы найти столбец, в котором расположен искомый элемент, и затем еще раз, чтобы перейти к строке с ответом.
Вставьте ответы в ИНДЕКС, и Excel сможет указать на ячейку, где эти значения пересекаются.

Например: ИНДЕКС (array, ПОИСКПОЗ (lookup_value, lookup_array, 0), ПОИСКПОЗ (lookup_value, lookup_array, 0)).

Диаграмма «водопад»

Это одна из форм визуализации данных, которая позволяет увидеть, в какую сторону менялись показатели в течение определенного периода. Очень полезная штука для тех, чья работа связана с финансами или статистикой.

Как применять:

В версии Excel 2016 необходимо выделить нужные данные и выбрать Вставка > Водопад или Диаграмма > Водопад.

Данная функция позволяет вычислять и предсказывать будущие значения на основе уже имеющихся данных.

Использование логических функций в Excel

Табличный редактор Эксель – очень гибкий и мощный инструмент для структурированной работы с данными. Среди большого количества его эффективных инструментов стоит отдельно выделить логические операторы, в основе использования которых лежит признание выражения истинным или ложным. Эти функции эффективно встроены в инструментарий формул и позволяют создавать гибкие условия для различных вычислений или заполнения ячеек на основе логических выражений. В данной статье будут описаны основные используемые функции, а также приведен практический пример использования логических операторов в Excel.

Основные логические функции, используемые в Эксель

Перечень наиболее часто используемых логических операторов можно ограничить следующим набором:

В большинстве случаев их достаточно для построения сложных логических конструкций и задания условий.

Для каждого из указанных выше операторов существуют аргументы (за исключением функций ИСТИНА и ЛОЖЬ) – это могут быть как цифровые или текстовые значения, так и ссылки на данные, содержащиеся в других ячейках.

Операторы ИСТИНА и ЛОЖЬ

Функция ИСТИНА не имеет собственных аргументов и практически всегда используется, как структурный компонент для других логических выражений, так как принимает одно конкретно заданное значение.

Функция ЛОЖЬ, напротив, может принимать любые значения, не являющиеся истинными. Как и ИСТИНА, практически всегда используется, как структурный компонент для других сложных выражений.

Операторы И и ИЛИ

Синтаксис оператора И выглядит следующим образом:

=И(лог_значение1; лог_значение2; …), возможное количество используемых аргументов – от 1 до 255.

Оператор И используется в качестве элемента-связки для нескольких условий логического выражения. Важно, чтобы все аргументы оператора имели значение ИСТИНА (если в выражении их несколько), в противном случае вся логическая цепочка будет возвращать значение ЛОЖЬ.

Синтаксис оператора ИЛИ:

=ИЛИ(лог_значение1; лог_значение2; …), возможное количество используемых аргументов – от 1 до 255.

В отличие от И, функция ИЛИ будет возвращать значение ИСТИНА даже в случае, когда хотя бы один из используемых аргументов ему соответствует, а все остальные – ложные.

Оператор НЕ

Синтаксис функции НЕ: =НЕ(лог_значение).

Количество аргументов оператора НЕ – всегда один. Соответственно, результат функции (ИСТИНА/ЛОЖЬ) полностью зависит только от значения аргумента.

Операторы ЕСЛИ и ЕСЛИОШИБКА

Общий синтаксис функции ЕСЛИ представляет собой конструкцию:

=ЕСЛИ(логическое_выражение;значение_если_истина;значение_если-ложь).

Оператор ЕСЛИ используется для построения сложных развернутых логических цепочек. Суть функции – в проверке внесенного в качестве логического выражения условия. Если условие выполняется, и оно истинно, то в качестве результата функции возвращается одно выражение, если же логическое выражение ложно, то в качестве результата функции возвращается другое условие.

Синтаксис оператора ЕСЛИОШИБКА имеет вид:

=ЕСЛИОШИБКА(значение;значение_если_ошибка).

Функция проверяет истинность логического выражения для первого аргумента, и если он соблюдается, то возвращает в качестве результата его значение. Если же выражение ложно, то в качестве результата выдается значение второго аргумента, указанное в функции.

Операторы ЕОШИБКА и ЕПУСТО

Оператор ЕОШИБКА имеет следующую структуру:

=ЕОШИБКА(значение)

Он позволяет осуществить проверку корректности уже заполненных ячеек (одной или диапазона), и, если ячейка некорректно заполнена, возвращает результат ИСТИНА, в противном случае – ЛОЖЬ.

Примеры значений в некорректно заполненных ячейках:

Аргумент функции – адрес конкретной ячейки или ссылка на диапазон ячеек.

Формула функции ЕПУСТО выглядит следующим образом:

=ЕПУСТО(значение)

Функционал оператора проверяет ячейку или диапазон ячеек и возвращает ИСТИНА, если в ячейке/диапазоне ячеек нет данных, и ЛОЖЬ, если в ячейке/диапазоне ячеек присутствуют данные. Аргумент функции – адрес конкретной ячейки или ссылка на диапазон ячеек.

Практический пример использования логических функций

В примере ниже попробуем частично использовать описанные выше функции для решения задачи, приближенной к реальной ситуации с расчетом премии, зависящей от определенных условий.

В качестве исходных данных – таблица со сведениями о работниках, в которой указан их пол и возраст.

Нам необходимо произвести расчет премии. Ключевые условия, от которых зависит размер премии:

величина обычной премии, которую получат все сотрудники без исключения – 3 000 руб.;
сотрудницам женского пола положена повышенная премия – 7 000 руб.;
молодым сотрудникам (младше 1984 г. рождения) положена повышенная премия – 7 000 руб.;

Выполним необходимые расчеты, используя логические функции.

Встаем в первую ячейку столбца, в которой хотим посчитать размеры премий и щелкаем кнопку “Вставить функцию” (слева от сроки формул).
В открывшемся Мастере функций выбираем категорию “Логические”, затем в предложенном перечне операторов кликаем по строке “ЕСЛИ” и жмем OK.
Теперь нам нужно задать аргументы функции. Так как у нас не одно, а два условия получения повышенной премии, причем нужно, чтобы выполнялось хотя бы одно из них, чтобы задать логическое выражение, воспользуемся функцией ИЛИ. Находясь в поле для ввода значения аргумента “Лог_выражение” кликаем в основной рабочей области книги на небольшую стрелку вниз, расположенную в левой верхней части окна программы, где обычно отображается адрес ячейки. В открывшемся списке функций выбираем оператор ИЛИ, если он представлен в перечне (или можно кликнуть на пункт “Другие функции” и выбрать его в новом окне Мастера функций, как мы изначально сделали для выбора оператора ЕСЛИ).
Мы переключимся в окно аргументов функци ИЛИ. Здесь задаем наши условия получения премии в 7000 руб.:
- год рождения позже 1984 года;
- пол – женский;
Теперь обращаем внимание на строку формул. Кликаем в ней на название первоначального оператора ЕСЛИ, чтобы переключиться в аргументы этой функции.
Заполняем аргументы функции и щелкаем OK:
- в значении “Истина” пишем цифру 7000;
- в значении “Ложь” указываем цифру 3000;
Результат работы логических операторов отобразится в первой ячейке столбца, которую мы выбрали. Как мы можем видеть, окончательный вид формулы выглядит следующим образом:
=ЕСЛИ(ИЛИ(C2>1984;D2=»жен.»);7000;3000) .
Кстати, вместо использования Мастера функций можно было вручную составить и прописать данную формулу в требуемой ячейке.
Чтобы рассчитать премию для всех сотрудников, воспользуемся Маркером заполнения. Наведем курсор на правый нижний угол ячейки с формулой. После того, как курсор примет форму черного крестика (это и есть Маркер заполнения), зажимаем левую кнопку мыши и протягиваем выделение вниз, до последней ячейки столбца.
Все готово. Благодаря логическим операторам мы получили заполненные данные для столбца с премиями.

Заключение

Логические операторы используются практически во всех сложных формулах, в которых значение в ячейке зависит от соблюдения одного или нескольких условий и позволяют строить гибкие конструкции, объединяя простые функции и расчеты в одной ячейке. Это дает возможность значительно сократить время на обработку данных и повысить эффективность работы, так как снимает большое количество промежуточных шагов в расчетах и вычислениях.

Источник

Содержание

Использование описательной статистики
Подключение «Пакета анализа»
Размах вариации
Вычисление коэффициента вариации
Шаг 1: расчет стандартного отклонения
Шаг 2: расчет среднего арифметического
Шаг 3: нахождение коэффициента вариации
Простая формула для расчета объема выборки
Пример расчета объема выборки
Задачи о генеральной доле
По части судить о целом
Как рассчитать объем выборки
Как определить статистические выбросы и сделать выборку для их удаления в Excel
Способ 1: применение расширенного автофильтра
Способ 2: применение формулы массива
СРЗНАЧ()
СРЗНАЧЕСЛИ()
МАКС()
МИН()

Использование описательной статистики

Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.

В Экселе существует отдельный инструмент, входящий в «Пакет анализа», с помощью которого можно провести данный вид обработки данных. Он так и называется «Описательная статистика». Среди критериев, которые высчитывает данный инструмент следующие показатели:

Медиана;
Мода;
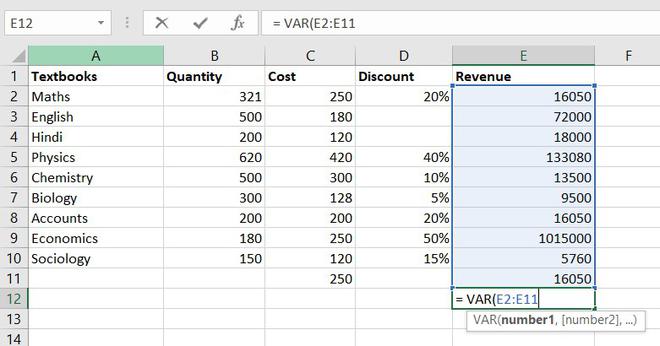
Дисперсия;
Среднее;
Стандартное отклонение;
Стандартная ошибка;
Асимметричность и др.

Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.

Подключение «Пакета анализа»

Как уже было сказано выше, инструмент «Описательная статистика» входит в более широкий набор функций, который принято называть Пакет анализа. Но дело в том, что по умолчанию данная надстройка в Экселе отключена. Поэтому, если вы до сих пор её не включили, то для использования возможностей описательной статистики, придется это сделать.

Переходим во вкладку «Файл». Далее производим перемещение в пункт «Параметры».

В активировавшемся окне параметров перемещаемся в подраздел «Надстройки». В самой нижней части окна находится поле «Управление». Нужно в нем переставить переключатель в позицию «Надстройки Excel», если он находится в другом положении. Вслед за этим жмем на кнопку «Перейти…».

Запускается окно стандартных надстроек Excel. Около наименования «Пакет анализа» ставим флажок. Затем жмем на кнопку «OK».

После вышеуказанных действий надстройка Пакет анализа будет активирована и станет доступной во вкладке «Данные» Эксель. Теперь мы сможем использовать на практике инструменты описательной статистики.

Размах вариации

Размах вариации – разница между максимальным и минимальным значением:

Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.

С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.

Вычисление коэффициента вариации

Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.

В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.

Шаг 1: расчет стандартного отклонения

Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.

Синтаксис данных функций выглядит соответствующим образом:

= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)

Для того, чтобы рассчитать стандартное отклонение, выделяем любую свободную ячейку на листе, которая удобна вам для того, чтобы выводить в неё результаты расчетов. Щелкаем по кнопке «Вставить функцию». Она имеет внешний вид пиктограммы и расположена слева от строки формул.

Выполняется активация Мастера функций, который запускается в виде отдельного окна с перечнем аргументов. Переходим в категорию «Статистические» или «Полный алфавитный перечень». Выбираем наименование «СТАНДОТКЛОН.Г» или «СТАНДОТКЛОН.В», в зависимости от того, по генеральной совокупности или по выборке следует произвести расчет. Жмем на кнопку «OK».

Открывается окно аргументов данной функции. Оно может иметь от 1 до 255 полей, в которых могут содержаться, как конкретные числа, так и ссылки на ячейки или диапазоны. Ставим курсор в поле «Число1». Мышью выделяем на листе тот диапазон значений, который нужно обработать. Если таких областей несколько и они не смежные между собой, то координаты следующей указываем в поле «Число2» и т.д. Когда все нужные данные введены, жмем на кнопку «OK»

В предварительно выделенной ячейке отображается итог расчета выбранного вида стандартного отклонения.

Шаг 2: расчет среднего арифметического

Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.

«Вставить функцию»

В статистической категории Мастера функций ищем наименование «СРЗНАЧ». После его выделения жмем на кнопку «OK».

Запускается окно аргументов СРЗНАЧ. Аргументы полностью идентичны тем, что и у операторов группы СТАНДОТКЛОН. То есть, в их качестве могут выступать как отдельные числовые величины, так и ссылки. Устанавливаем курсор в поле «Число1». Так же, как и в предыдущем случае, выделяем на листе нужную нам совокупность ячеек. После того, как их координаты были занесены в поле окна аргументов, жмем на кнопку «OK».

Результат вычисления среднего арифметического выводится в ту ячейку, которая была выделена перед открытием Мастера функций.

Шаг 3: нахождение коэффициента вариации

Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.

«Главная»

«Число»

«Процентный»

Снова возвращаемся к ячейке для вывода результата. Активируем её двойным щелчком левой кнопки мыши. Ставим в ней знак «=». Выделяем элемент, в котором расположен итог вычисления стандартного отклонения. Кликаем по кнопке «разделить» (/) на клавиатуре. Далее выделяем ячейку, в которой располагается среднее арифметическое заданного числового ряда. Для того, чтобы произвести расчет и вывести значение, щёлкаем по кнопке Enter на клавиатуре.

Как видим, результат расчета выведен на экран.

Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.

Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:

Вместо наименования «Диапазон значений» вставляем реальные координаты области, в которой размещен исследуемый числовой ряд. Это можно сделать простым выделением данного диапазона. Вместо оператора СТАНДОТКЛОН.В, если пользователь считает нужным, можно применять функцию СТАНДОТКЛОН.Г.

После этого, чтобы рассчитать значение и показать результат на экране монитора, щелкаем по кнопке Enter.

Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.

Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.

Разделы: Математика

Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.

Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).

Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.

Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):

23 25 24 25 30 24 30 26 28 26
32 33 31 31 25 33 25 29 30 28
23 30 29 24 33 30 30 28 26 25
26 29 27 29 26 28 27 26 29 28
29 30 27 30 28 32 28 26 30 26
31 27 30 27 33 28 26 30 31 29
27 30 30 29 27 26 28 31 29 28
33 27 30 33 26 31 34 28 32 22
29 30 27 29 34 29 32 29 29 30
29 29 36 29 29 34 23 28 24 28

рассчитать числовые характеристики:

моду
медиану
размах ряда
построить полигон частот
построить столбчатую и круговую диаграммы
раскрыть смысловую сторону каждой характеристики

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наибольшее значение = 36.

Вставка – Функция – Статистические – МИН.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_i случайной величины меняются от 22 до 36 включительно шагом 1.

x_i	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
n_i

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

x_i	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
n_i	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).

Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)

Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.

Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

Диаграмма – Стандартные – Гистограмма.

4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.

Простая формула для расчета объема выборки

где: n – объем выборки;

z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности. Этот показатель характеризует возможность, вероятность попадания ответов в специальный – доверительный интервал. На практике уровень доверительности часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58;

p – вариация для выборки, в долях. По сути, p – это вероятность того, что респонденты выберут той или иной вариант ответа. Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;

q = (1 – p);

e – допустимая ошибка, в долях.

Пример расчета объема выборки

Компания планирует провести социологическое исследование с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».

Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95%, тогда нормированное отклонение z = 1,96. Вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они – «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. Допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.

Подставляем эти данные в формулу и считаем:

Получаем объем выборки n = 96 человек.

Задачи о генеральной доле

На вопрос «Накрывает ли доверительный интервал заданное значение p₀?» — можно ответить, проверив статистическую гипотезу H₀:p=p₀. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p^* появления события A: где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H₀ используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 – Гипотезы о генеральной доле

Гипотеза	H₀:p=p₀	H₀:p₁=p₂
Предположения	Схема испытаний Бернулли	Схема испытаний Бернулли
Оценки по выборке
Статистика K
Распределение статистики K	Стандартное нормальное N(0,1)	Стандартное нормальное N(0,1)

Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле

Значение u_кр находим по таблице функции Лапласа из соотношения 2Ф(u_кр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при u_кр=1.96. Следовательно, предельная ошибка Функция Лапласа (приложение 1) принимает значение 0.475 при u_кр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.

Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет
По таблице функции Лапласа найдем значение u_кр при заданной
доверительной вероятности
По таблице функции Лапласа найдем значение u_кр при заданной
доверительной вероятности
Ф(2.23) = 0.49, u_кр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку:
где n=40, N = 365 (дней). Отсюда
где n=40, N = 365 (дней). Отсюда
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.

Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.

Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01

Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H₀:p=p₀=0,97 — неизвестная генеральная доля p равна заданному значению p₀=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H₁:p<0,97 – вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p₀=0,97, n=200, m=193

Критическое значение находим по таблице функции Лапласа из равенства

По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-K_kp)= (-∞;-2,05). Наблюдаемое значение К_набл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.

Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H₀:p₁=p₂ — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H₀:p₁≠p₂ — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.

Наблюдаемое значение равно

Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение K_набл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.

По части судить о целом

О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при

достаточном числе наблюдений

. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.
А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.
Строгие формулировки:

С увеличением числа случайных величин их среднее арифметическое стремится к среднему арифметическому математических ожиданий и перестает быть случайным. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.
Таким образом з.б.ч. гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.

Распределение случайной величины, которая получена в результате сложения большого числа независимых случайных величин (ни одно из которых не доминирует, не вносит в сумму определяющего вклада и имеет дисперсию значительно меньшею по сравнению с дисперсией суммы) имеет распределение, близкое к нормальному.
Из ц.п.т. следует, что ошибки выборки также подчиняется нормальному распределению.

Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.

Как рассчитать объем выборки

Достаточный размер выборки зависит от следующих составляющих:

изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)

ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента

Формулы для расчета объема выборки:

Формулы расчета объема выборки

Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.

График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.

Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.

Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.

Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.

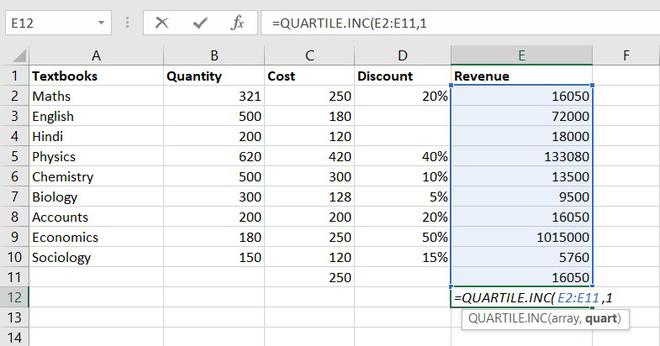
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.

В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:

Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.

В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:

Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.

Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.

Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.

Способ 1: применение расширенного автофильтра

Наиболее простым способом произвести отбор является применение расширенного автофильтра. Рассмотрим, как это сделать на конкретном примере.

Выделяем область на листе, среди данных которой нужно произвести выборку. Во вкладке «Главная» щелкаем по кнопке «Сортировка и фильтр». Она размещается в блоке настроек «Редактирование». В открывшемся после этого списка выполняем щелчок по кнопке «Фильтр».

Есть возможность поступить и по-другому. Для этого после выделения области на листе перемещаемся во вкладку «Данные». Щелкаем по кнопке «Фильтр», которая размещена на ленте в группе «Сортировка и фильтр».

После этого действия в шапке таблицы появляются пиктограммы для запуска фильтрования в виде перевернутых острием вниз небольших треугольников на правом краю ячеек. Кликаем по данному значку в заглавии того столбца, по которому желаем произвести выборку. В запустившемся меню переходим по пункту «Текстовые фильтры». Далее выбираем позицию «Настраиваемый фильтр…».

Активируется окно пользовательской фильтрации. В нем можно задать ограничение, по которому будет производиться отбор. В выпадающем списке для столбца содержащего ячейки числового формата, который мы используем для примера, можно выбрать одно из пяти видов условий:
- равно;
- не равно;
- больше;
- больше или равно;
- меньше.
Давайте в качестве примера зададим условие так, чтобы отобрать только значения, по которым сумма выручки превышает 10000 рублей. Устанавливаем переключатель в позицию «Больше». В правое поле вписываем значение «10000». Чтобы произвести выполнение действия, щелкаем по кнопке «OK».

Как видим, после фильтрации остались только строчки, в которых сумма выручки превышает 10000 рублей.

Но в этом же столбце мы можем добавить и второе условие. Для этого опять возвращаемся в окно пользовательской фильтрации. Как видим, в его нижней части есть ещё один переключатель условия и соответствующее ему поле для ввода. Давайте установим теперь верхнюю границу отбора в 15000 рублей. Для этого выставляем переключатель в позицию «Меньше», а в поле справа вписываем значение «15000».
Кроме того, существует ещё переключатель условий. У него два положения «И» и «ИЛИ». По умолчанию он установлен в первом положении. Это означает, что в выборке останутся только строчки, которые удовлетворяют обоим ограничениям. Если он будет выставлен в положение «ИЛИ», то тогда останутся значения, которые подходят под любое из двух условий. В нашем случае нужно выставить переключатель в положение «И», то есть, оставить данную настройку по умолчанию. После того, как все значения введены, щелкаем по кнопке «OK».

Теперь в таблице остались только строчки, в которых сумма выручки не меньше 10000 рублей, но не превышает 15000 рублей.

Аналогично можно настраивать фильтры и в других столбцах. При этом имеется возможность сохранять также фильтрацию и по предыдущим условиям, которые были заданы в колонках. Итак, посмотрим, как производится отбор с помощью фильтра для ячеек в формате даты. Кликаем по значку фильтрации в соответствующем столбце. Последовательно кликаем по пунктам списка «Фильтр по дате» и «Настраиваемый фильтр».

Снова запускается окно пользовательского автофильтра. Выполним отбор результатов в таблице с 4 по 6 мая 2016 года включительно. В переключателе выбора условий, как видим, ещё больше вариантов, чем для числового формата. Выбираем позицию «После или равно». В поле справа устанавливаем значение «04.05.2016». В нижнем блоке устанавливаем переключатель в позицию «До или равно». В правом поле вписываем значение «06.05.2016». Переключатель совместимости условий оставляем в положении по умолчанию – «И». Для того, чтобы применить фильтрацию в действии, жмем на кнопку «OK».

Как видим, наш список ещё больше сократился. Теперь в нем оставлены только строчки, в которых сумма выручки варьируется от 10000 до 15000 рублей за период с 04.05 по 06.05.2016 включительно.

Мы можем сбросить фильтрацию в одном из столбцов. Сделаем это для значений выручки. Кликаем по значку автофильтра в соответствующем столбце. В выпадающем списке щелкаем по пункту «Удалить фильтр».

Как видим, после этих действий, выборка по сумме выручки будет отключена, а останется только отбор по датам (с 04.05.2016 по 06.05.2016).

В данной таблице имеется ещё одна колонка – «Наименование». В ней содержатся данные в текстовом формате. Посмотрим, как сформировать выборку с помощью фильтрации по этим значениям.
Кликаем по значку фильтра в наименовании столбца. Последовательно переходим по наименованиям списка «Текстовые фильтры» и «Настраиваемый фильтр…».

Опять открывается окно пользовательского автофильтра. Давайте сделаем выборку по наименованиям «Картофель» и «Мясо». В первом блоке переключатель условий устанавливаем в позицию «Равно». В поле справа от него вписываем слово «Картофель». Переключатель нижнего блока так же ставим в позицию «Равно». В поле напротив него делаем запись – «Мясо». И вот далее мы выполняем то, чего ранее не делали: устанавливаем переключатель совместимости условий в позицию «ИЛИ». Теперь строчка, содержащая любое из указанных условий, будет выводиться на экран. Щелкаем по кнопке «OK».

Как видим, в новой выборке существуют ограничения по дате (с 04.05.2016 по 06.05.2016) и по наименованию (картофель и мясо). По сумме выручки ограничений нет.

Полностью удалить фильтр можно теми же способами, которые использовались для его установки. Причем неважно, какой именно способ применялся. Для сброса фильтрации, находясь во вкладке «Данные» щелкаем по кнопке «Фильтр», которая размещена в группе «Сортировка и фильтр».

Второй вариант предполагает переход во вкладку «Главная». Там выполняем щелчок на ленте по кнопке «Сортировка и фильтр» в блоке «Редактирование». В активировавшемся списке нажимаем на кнопку «Фильтр».

При использовании любого из двух вышеуказанных методов фильтрация будет удалена, а результаты выборки – очищены. То есть, в таблице будет показан весь массив данных, которыми она располагает.

Способ 2: применение формулы массива

Сделать отбор можно также применив сложную формулу массива. В отличие от предыдущего варианта, данный метод предусматривает вывод результата в отдельную таблицу.

На том же листе создаем пустую таблицу с такими же наименованиями столбцов в шапке, что и у исходника.

Выделяем все пустые ячейки первой колонки новой таблицы. Устанавливаем курсор в строку формул. Как раз сюда будет заноситься формула, производящая выборку по указанным критериям. Отберем строчки, сумма выручки в которых превышает 15000 рублей. В нашем конкретном примере, вводимая формула будет выглядеть следующим образом:
=ИНДЕКС(A2:A29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Естественно, в каждом конкретном случае адрес ячеек и диапазонов будет свой. На данном примере можно сопоставить формулу с координатами на иллюстрации и приспособить её для своих нужд.

Так как это формула массива, то для того, чтобы применить её в действии, нужно нажимать не кнопку Enter, а сочетание клавиш Ctrl+Shift+Enter. Делаем это.

Выделив второй столбец с датами и установив курсор в строку формул, вводим следующее выражение:
=ИНДЕКС(B2:B29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Жмем сочетание клавиш Ctrl+Shift+Enter.

Аналогичным образом в столбец с выручкой вписываем формулу следующего содержания:
=ИНДЕКС(C2:C29;НАИМЕНЬШИЙ(ЕСЛИ(15000<=C2:C29;СТРОКА(C2:C29);"");СТРОКА()-СТРОКА($C$1))-СТРОКА($C$1))

Опять набираем сочетание клавиш Ctrl+Shift+Enter.

Во всех трех случаях меняется только первое значение координат, а в остальном формулы полностью идентичны.

Как видим, таблица заполнена данными, но внешний вид её не совсем привлекателен, к тому же, значения даты заполнены в ней некорректно. Нужно исправить эти недостатки. Некорректность даты связана с тем, что формат ячеек соответствующего столбца общий, а нам нужно установить формат даты. Выделяем весь столбец, включая ячейки с ошибками, и кликаем по выделению правой кнопкой мыши. В появившемся списке переходим по пункту «Формат ячейки…».

В открывшемся окне форматирования открываем вкладку «Число». В блоке «Числовые форматы» выделяем значение «Дата». В правой части окна можно выбрать желаемый тип отображения даты. После того, как настройки выставлены, жмем на кнопку «OK».

Теперь дата отображается корректно. Но, как видим, вся нижняя часть таблицы заполнена ячейками, которые содержат ошибочное значение «#ЧИСЛО!». По сути, это те ячейки, данных из выборки для которых не хватило. Более привлекательно было бы, если бы они отображались вообще пустыми. Для этих целей воспользуемся условным форматированием. Выделяем все ячейки таблицы, кроме шапки. Находясь во вкладке «Главная» кликаем по кнопке «Условное форматирование», которая находится в блоке инструментов «Стили». В появившемся списке выбираем пункт «Создать правило…».

В открывшемся окне выбираем тип правила «Форматировать только ячейки, которые содержат». В первом поле под надписью «Форматировать только ячейки, для которых выполняется следующее условие» выбираем позицию «Ошибки». Далее жмем по кнопке «Формат…».

В запустившемся окне форматирования переходим во вкладку «Шрифт» и в соответствующем поле выбираем белый цвет. После этих действий щелкаем по кнопке «OK».

На кнопку с точно таким же названием жмем после возвращения в окно создания условий.

Теперь у нас имеется готовая выборка по указанному ограничению в отдельной надлежащим образом оформленной таблице.

СРЗНАЧ()

Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.

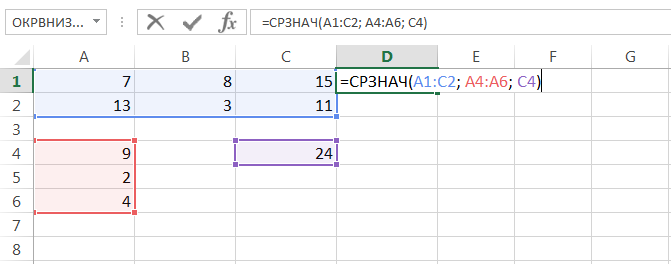
Данная функция может принимать до 255 аргументов и находить среднее сразу в нескольких несмежных диапазонах и ячейках:

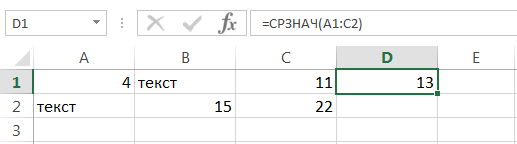
Если в рассчитываемом диапазоне встречаются пустые или содержащие текст ячейки, то они игнорируются. В примере ниже среднее ищется по четырем ячейкам, т.е. (4+15+11+22)/4 = 13

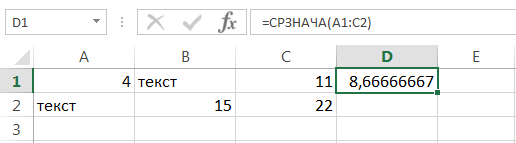
Если необходимо вычислить среднее, учитывая все ячейки диапазона, то можно воспользоваться статистической функцией СРЗНАЧА. В следующем примере среднее ищется уже по 6 ячейкам, т.е. (4+15+11+22)/6 = 8,6(6).

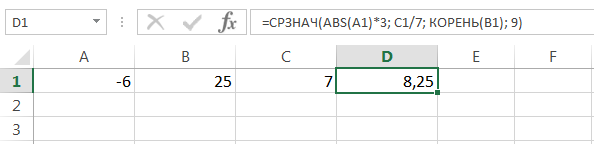
Статистическая функция СРЗНАЧ может использовать в качестве своих аргументов математические операторы и различные функции Excel:

СРЗНАЧЕСЛИ()

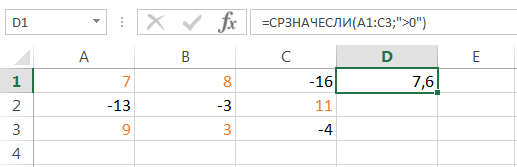
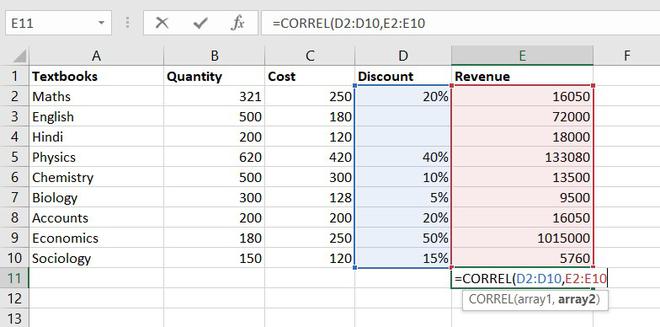
Если необходимо вернуть среднее арифметическое значений, которые удовлетворяют определенному условию, то можно воспользоваться статистической функцией СРЗНАЧЕСЛИ. Следующая формула вычисляет среднее чисел, которые больше нуля:

В данном примере для подсчета среднего и проверки условия используется один и тот же диапазон, что не всегда удобно. На этот случай у функции СРЗНАЧЕСЛИ существует третий необязательный аргумент, по которому можно вычислять среднее. Т.е. по первому аргументу проверяем условие, по третьему – находим среднее.

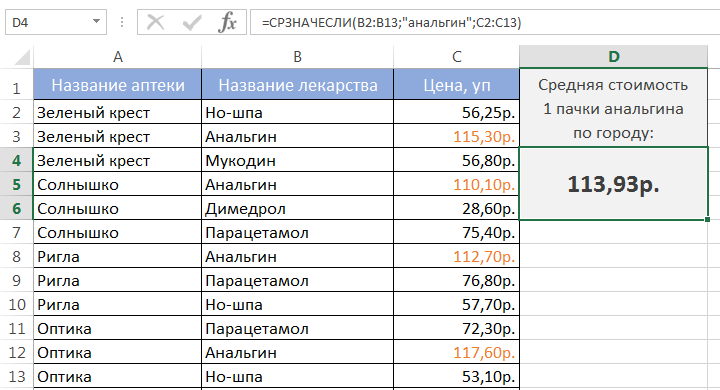
Допустим, в таблице ниже собрана статистика по стоимости лекарств в городе. В одной аптеке лекарство стоит дороже, в другой дешевле. Чтобы посчитать стоимость анальгина в среднем по городу, воспользуемся следующей формулой:

Если требуется соблюсти несколько условий, то всегда можно применить статистическую функцию СРЗНАЧЕСЛИМН, которая позволяет считать среднее арифметическое ячеек, удовлетворяющих двум и более критериям.

МАКС()

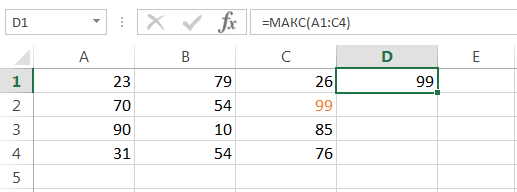
Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:

МИН()

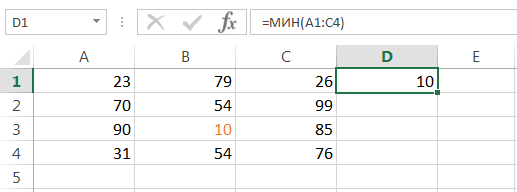
Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:

Источники

https://lumpics.ru/descriptive-statistics-in-excel/
https://statanaliz.info/statistica/opisanie-dannyx/variatsiya-razmakh-srednee-linejnoe-otklonenie/
https://www.hd01.ru/info/kak-poschitat-razmah-v-excel/
http://galyautdinov.ru/post/formula-vyborki-prostaya
https://math.semestr.ru/group/interval-estimation-share.php
https://tidydata.ru/sample-size
https://exceltable.com/formuly/raschet-statisticheskih-vybrosov
https://lumpics.ru/how-to-make-a-sample-in-excel/
https://office-guru.ru/excel/statisticheskie-funkcii-excel-kotorye-neobhodimo-znat-96.html

Источник

Функции категории Статистические предназначены в первую очередь для анализа диапазонов ячеек в Excel. С помощью данных функций Вы можете вычислить наибольшее, наименьшее или среднее значение, подсчитать количество ячеек, содержащих заданную информацию, и т.д.

Данная категория содержит более 100 самых различных функций Excel, большая часть из которых предназначена исключительно для статистических расчетов и обычному рядовому пользователю покажется темным лесом. Мы же в рамках этого урока рассмотрим самые полезные и распространенные функции данной категории.

В рамках данной статьи мы не будем затрагивать такие популярные статистические функции Excel, как СЧЕТ и СЧЕТЕСЛИ, для них подготовлен отдельный урок.

Содержание

СРЗНАЧ()
СРЗНАЧЕСЛИ()
МАКС()
МИН()
НАИБОЛЬШИЙ()
НАИМЕНЬШИЙ()
МЕДИАНА()
МОДА()

СРЗНАЧ()

Статистическая функция СРЗНАЧ возвращает среднее арифметическое своих аргументов.

СРЗНАЧЕСЛИ()

МАКС()

Статистическая функция МАКС возвращает наибольшее значение в диапазоне ячеек:

МИН()

Статистическая функция МИН возвращает наименьшее значение в диапазоне ячеек:

НАИБОЛЬШИЙ()

Возвращает n-ое по величине значение из массива числовых данных. Например, на рисунке ниже мы нашли пятое по величине значение из списка.

Чтобы убедиться в этом, можно отсортировать числа в порядке возрастания:

НАИМЕНЬШИЙ()

Возвращает n-ое наименьшее значение из массива числовых данных. Например, на рисунке ниже мы нашли четвертое наименьшее значение из списка.

Если отсортировать числа в порядке возрастания, то все станет гораздо очевидней:

Статистическая функция МЕДИАНА возвращает медиану из заданного массива числовых данных. Медианой называют число, которое является серединой числового множества. Если в списке нечетное количество значений, то функция возвращает то, что находится ровно по середине. Если же количество значений четное, то функция возвращает среднее для двух чисел.

Например, на рисунке ниже формула возвращает медиану для списка, состоящего из 14 чисел.

Если отсортировать значения в порядке возрастания, то все становится на много понятней:

МОДА()

Возвращает наиболее часто встречающееся значение в массиве числовых данных.

Если отсортировать числа в порядке возрастания, то все становится гораздо понятней:

Статистическая функция МОДА на данный момент устарела, точнее, устарела ее форма записи. Вместо нее теперь используется функция МОДА.ОДН. Форма записи МОДА также поддерживается в Excel для совместимости.

Как известно, категория Статистические в Excel содержит более 100 самых разноплановых функций. Но, как показывает практика, львиная доля этих функций практически не применяется, а особенно начинающими пользователями. В этом уроке мы постарались познакомить Вас только с самыми популярными статистическими функциями Excel, которые Вы рано или поздно сможете применить на практике. Надеюсь, что данный урок был для Вас полезен. Удачи Вам и успехов в изучении Excel.

Оцените качество статьи. Нам важно ваше мнение:

Источник

Обновлено: 16.04.2023

Аннотация: Цель работы: научиться работать с Мастером функций, проводить анализ данных. Содержание работы: Использование Мастера функций. Анализ статистических данных. Инструменты пакета анализа. Порядок выполнения работы: Изучить методические указания. Выполнить задания. Оформить отчет и ответить на контрольные вопросы.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Математические функции

MS EXCEL обеспечивает 10 разных категорий функций: математические/тригонометрические, инженерные, логические, текстовые, статистические, функции категории дата/время, функции для работы с базами данных/списками, финансовые, информационные и функции категории ссылки/массивы.

Программа EXCEL содержит более 400 встроенных функций, которые можно выбрать с помощью Мастера функций.

После её нажатия появится окно Мастера функций (рис. 3.1 рис. 3.1).

В открывшемся диалоговом окне выберите категорию и имя функции, а затем в полях с соответствующими подсказками введите аргументы (рис. 3.2 рис. 3.2). После нажатия кнопки ОК, готовая функция появится в строке формул

Вызов функции состоит в указании в формуле имени функции, после которого в скобках указывается список параметров (аргументов). Отдельные параметры (аргументы) разделяются в списке точкой с запятой.

В качестве аргумента может использоваться число, адрес ячейки или произвольное выражение, для вычисления которого также могут использоваться функции.

числовые константы, например, функция ПРОИЗВЕД(2;3) вычисляет произведение чисел 2 и 3, т.е. 2•3.
ссылки на ячейки и блоки ячеек (функция ПРОИЗВЕД (А1;С1:СЗ) вычисляет произведение содержимого ячеек А1,С1,С2 и С3, т.е. А1•С1•С2•СЗ.
текстовые константы (заключенные в кавычки).
логические значения.
массивы.
имена ссылок, например, если ячейке А10 присвоить имя СУММА –последовательность команд Формулы Присвоить имя. – рис. 3.3 рис. 3.3), а блоку ячеек В10:Е10 – имя ИТОГИ, то допустима следующая запись: =СУММ(СУММА;ИТОГИ).
смешанные аргументы, например, =СРЗНАЧ (Группа;АЗ;5*3)

Пример 1. Вычислить значения функции

Y=e x *sin(x) для

Заполним столбец А значениями аргумента функции. Чтобы не вводить их вручную, применим следующий прием. Введите в ячейку А1 начальное значения аргумента (-1). Во вкладке Главная> Редактирование выберите кнопку Заполнить, затем Прогрессия и в открывшемся диалоговом окне укажите предельное значение (1), шаг(0,2) и направление По столбцам (рис. 3.4 рис. 3.4). После нажатия кнопки ОК в столбце А будут введены все значения аргумента

В ячейку В1 введите формулу =exp(А1)*sin(A1). Размножьте эту формулу на остальные ячейки столбца B , ухватив левой мышью маркер заполнения (черный квадратик в правом нижнем углу рамки выделенной ячейки B1 ) и протащив маркер до конца изменения аргумента. В итоге будут вычислены соответствующие значения функции.

Логические функции

Принцип действия большинства логических функций EXCEL заключается в проверке некоторого условия и выполнения в зависимости от него тех или иных действий.

Так, функция ЕСЛИ выполняет проверку условия, задаваемого первым аргументом логич_выр:

=ЕСЛИ(логич_выр; знач_да; знач_нет) и возвращает знач_да, если условие выполнено (ИСТИНА), и знач_нет, в противном случае (ЛОЖЬ).

Если значение в ячейке А6 80, то в ячейке с приведенной формулой будет записано «Сданы», иначе – «Не сданы».

Если сумма значений в столбце А1:А10 больше 0, то вычислится сумма значений в столбце В1:В10, в противном случае результат – 0.

Дополнительные логические функции

позволяют создавать сложные условия, например:

Если суммы и в столбце А1:А10 и в столбце В1:В10 положительны, то вычислить суму значений в ячейках А1:В10, иначе – 0.

Статистические функции

MS EXCEL предоставляет широкие возможности для анализа статистических данных. Для решения простых задач можно использовать встроенные функции. Рассмотрим некоторые из них.

Вычисление среднего арифметического последовательности чисел:

=СРЗНАЧ (числа).

Нахождение максимального (минимального) значения:

Вычисление медианы (числа, являющегося серединой множества):

=МЕДИАНА(числа).

Вычисление моды (наиболее часто встречающегося значения в множестве):

Следующие функции предназначены для анализа выборок генеральной совокупности данных.

=СТАНДОТКЛОН( числа).

Статистический анализ с помощью Пакета анализа

Для решения сложных задач применяется Пакет анализа. Пакет анализа – это дополнение EXCEL , расширяющее его аналитические возможности и позволяющие строить гистограммы, составлять таблицы рангперсентиль, делать случайные или периодические выборки данных и находить их статистические характеристики, генерировать неравномерно распределенные случайные числа, проводить регрессивный анализ и многое другое.

Чтобы воспользоваться инструментами анализа, выполните следующие действия.

В меню Данные > Анализ выберите команду Анализ данных.

Выберите из списка название нужного инструмента анализа и нажмите кнопку ОК.

В большинстве случаев в открывшемся диалоговом окне нужно просто указать интервал исходных данных интервал для вывода результатов и задать некоторые параметры.

Инструмент Описательная статистика формирует таблицу статистических данных, ускоряя и упрощая этот процесс по сравнению с использованием формул 1- 6 (рис. 3.6 рис. 3.6).

Инструмент Генерация случайных чисел дает возможность получать равномерное и неравномерное распределение.

Инструмент Гистограмма позволяет создавать гистограммы распределения данных. Область значений измеряемой величины разбивается на несколько интервалов, называемых карманами, в которых в виде столбцов откладывается количество попавших в этот интервал измерений, называемое частотой.

Пример 2. Пусть дана таблица с данными о температуре воздуха в Краснодаре летом 2014г. Интервал изменения температуры от 18 до 38 градуса по Цельсию (его можно определить с помощью функций МАКС() и МИН()).

Разобьем этот интервал на подинтервалы – карманы шириной, например, 2 градуса по Цельсию (ширина карманов не обязательно должна быть равной).
Воспользуемся командой Заполнить из меню Главная в группе Редактирование для быстрого заполнения столбца карманов (значения в столбце будут изменятся от 18 до 38 градусов по Цельсию с шагом 2 градуса).
Выполним команду Анализ данных из меню Данные. В открывшемся диалоговом окне зададим входной интервал (это ячейки с данными о температуре), интервал карманов, выходной интервал (надо указать только верхнюю, левую ячейку для вывода результатов) и установим флажок Вывод графика.
После нажатия кнопки ОК на экран будет выведена гистограмма, а рядом со столбцом карманов появится столбец частот, показывающий, сколько дней летом в Краснодаре имели температуру, попадающую в каждый интервал.

ЗАДАНИЕ

Каждый вариант состоит из двух заданий. Для выполнения первого задания необходимо:

На рабочем листе № 4 построить таблицу значений функции согласно варианта задания и ее график.
Определите среднее, минимальное и максимальное значение функции и вывести эти данные на графике.
Используя логическую формулу, вычислить сумму значений функций, если среднее, минимальное и максимальное значения имеют одинаковые знаки и произведение в противном случае.
Произвольной ячейке присвоить имя и сгенерировать в ней случайное число. В таблице значений функции добавить еще один столбец, полученный умножением у на случайное число. Добавить на графике функции второй график, соответствующий полученному столбцу данных.

Исходными данными для второго задания являются варианты заданий к лабораторной работе № 1. Необходимо:

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Выберите документ из архива для просмотра:

приложения для студентов.xlsx

Выбранный для просмотра документ pril5.docx

К какой категории относятся функции МИН, МАКС, СРЗНАЧ, СЧЁТЕСЛИ?

В ячейку В15 ввели формулу =(С6+В$6)*$Е$6 . Затем эту формулу заполнили вниз. Какая формула содержится в ячейки В18?

В ячейку А3 ввели формулу =$ C $8+ C 9*25% . Затем формулу заполни вниз. Какая формула содержится в ячейки А7?

К какой категории относятся функции СУММ, КОРЕНЬ, СУММЕСЛИ, ПРОИЗВЕД?

Как называется документ Excel ?

Какие из функций написаны неверно?

= РАНГ(В1: $B$1 ; $B$7 ;1)

= РАНГ(В1; $B$1 : $B$7 ;2)

В первую ячейку ряда ввели некоторую формулу, которую затем заполнили вправо. В одной из ячеек оказалась следующая формула.

Что получиться в ячейках, если известно, что маркер заполнения протянули вниз на четыре ячейки?

Отдел 1, Отдел 2, Отдел 3, Отдел 4;

Ничего, пустые ячейки.

В электронных таблицах выделена группа ячеек В1: D 2. Сколько ячеек входит в этот диапазон.

Результатом вычислений в ячейке С1 будет:

ФИО ____________________________________________________

Дополнения __________________________________________________________________

Замечания ____________________________________________________________________

Оценка _________________________

Выбранный для просмотра документ Конспект урока.docx

Microsoft Excel 2007. Статистические функции

Закрепить на практике работу с мастером функций;

Научиться использовать статистические функции Excel.

Программное обеспечение:

Ms Office: Ms Excel 2007.

1. Организационная часть

1.1. Проверить присутствующих на уроке.
1.2. Проверить готовность учащихся к уроку.

2. Вводный инструктаж

2.1. Проверка техники безопасности и охраны труда;
2.2. Проверка знаний пройденного материала (фронтальный опрос)

Вопросы:

Что такое функция?

Сколько функций входит в Excel, и на какие категории распределяются?

Какие существуют способы вызова окна “Мастера функций”?

Математические функции и их синтаксис ?

В процессе повторения, на экране отображается презентация по прошлому уроку при изучении темы “Математические функции”.

2.3. Сообщить тему и цели нового урока;
2.4. Объяснение нового материала;
2.4.1. Объяснить и показать при помощи проектора синтаксис статистических функций в Excel (МАКС, МИН, СРЗНАЧ, РАНГ, СЧЁТЕСЛИ ).

3. Текущий инструктаж.

3.1. Выдать раздаточный материал;
3.2. Целевой обход;
3.3. Проверка правильной организации рабочих мест;
3.4. Проверка правильности выполнения приемов;
3.5. Работа с отстающими;
3.6. Контроль знаний.

4. Заключительный инструктаж.

4.1. Провести анализ выполненного задания;
4.2. Разобрать ошибки;
4.3. Дать краткую характеристику работы каждого учащегося и сообщить оценки;
4.4. Сообщить тему следующего урока и выдать домашние задание.

Конспект вводного инструктажа

Создание формул с использованием мастера функций

Функция – стандартная формула, которая обеспечивает выполнение определенных действий над значениями, выступающими в качестве аргументов. Функции позволяют упростить формулы, особенно если они длинные или сложные. Функции используют не только для непосредственных вычислений, но также и для преобразования чисел, например для округления, для поиска значений, сравнения и т. д.

Для создания формул с функциями обычно используют группу Библиотека функций вкладки Формулы (рис.1).

Рис. 1. Вкладка Формулы

Выделите ячейку, в которую требуется ввести формулу;

Щелкните по кнопке нужной категории функций в группе Библиотека функций и выберите нужную функцию;

В окне Аргументы функции в соответствующем поле (полях) введите аргументы функции. Ссылки на ячейки можно вводить с клавиатуры, но удобнее пользоваться выделением ячеек мышью. Для этого поставьте курсор в соответствующее поле и на листе выделите необходимую ячейку или диапазон ячеек. Для удобства выделения ячеек окно Аргументы функции можно сдвинуть или свернуть. Текст, числа и логические выражения в качестве аргументов обычно вводят с клавиатуры. В качестве подсказки в окне отображается назначение функции, а в нижней части окна отображается описание аргумента, в поле которого в данный момент находится курсор. Следует иметь в виду, что некоторые функции не имеют аргументов;

В окне Аргументы функции нажмите кнопку ОК .

Например , в таблице на рис.1 в ячейке Е14 необходимо создать формулу для подсчета минимальной стоимости заказа на мягкую мебель:

Выделите ячейку Е14;

Щелкните по кнопке категории Другие функции в группе Библиотека функций и выберите категорию Статистические функцию МИН (рис.2);

Рис. 2. Выбор функции

В окне Аргументы функции (рис.3) установите курсор в поле Число1 и на листе выделите ячейку Е14, затем введите диапазон аргументов для расчета минимальной стоимости заказа;

Рис. 3. Ввод аргументов функции

Для вставки функции не обязательно использовать кнопки категорий функций в группе Библиотека функций . Для выбора нужной функции можно использовать мастер функций. Причем, это можно сделать при работе в любой вкладке.

В окне Мастер функций: шаг 1 из 2 (рис.4) в раскрывающемся списке Категория выберите категорию функции, затем в списке Выберите функцию выберите функцию;

Рис. 4. Выбор функции в Мастере функций

Имена функций при создании формул можно вводить с клавиатуры. Для упрощения процесса создания и снижения количества опечаток используйте автозавершение формул.

Рис. 5. Ввод формулы с использованием автозавершения

Выберите нужную функцию, для чего дважды щелкните по ней мышью;

С использованием клавиатуры и мыши введите аргументы функции. Подтвердите ввод формулы.

Статистические функции используются для автоматизации статистической обработки данных.

Изучаем синтаксис функций МИН, МАКС, СРЗНАЧ, РАНГ, СЧЕТЕСЛИ.

=МИН (число1; число2;…; число _n )

Функция возвращает наименьшее значение из списка аргументов. Логические и текстовые значение игнорируются;

Ячейки А1:А5 содержать значения 10,7,9,27 и 2

Чему будет равно значение функции?

=МИН(А1:А5) 2

=МИН(А1:А5;0) 0

=МАКС(число1; число2;…; число _n )

Функция возвращает наибольшие значение из списка аргументов. Логические и текстовые значение игнорируются;

Ячейки А1:А5 содержать значения 10,7,9,27 и 2

Чему будет равно значение функции?

=МАКС(А1:А5) 27

=МАКС(А1:А5;30) 30

=СРЗНАЧ (число1; число2;…; число _n )

Функция возвращает среднее арифметическое своих аргументов, которые могут быть числами, именами, массивами или ссылками на ячейки с числами. Если аргумент текстовый, логический или пустая ячейка, то значения игнорируются.

Ячейки А1:А5 содержат значения 10,7,9,27 и 2

Чему будет равно значение функции?

=СРЗНАЧ(А1:А5) 11

Мы могли бы этот пример решить по иному, не используя функцию СРЗНАЧ:

=(А1+А2+А3+А4+А5)/5 или =СУММ(А1:А5)/5

А если написать такую функцию =СРЗНАЧ(А1:А5;5), то чему будет равно значение этой функции? 10

Функция возвращает ранг числа в списке чисел относительно других чисел в списке.

Если требуется не только вычислить наибольшее или наименьшее число из списка значений, но и расположить числа в порядке возрастания или убывания применяется функция ранжирования, которая записывается следующим образом:

=РАНГ (число; ссылка на список; порядок)

Число – это число, для которого определяется ранг (порядок);

Ссылка на список – которому принадлежит число, нечисловые значения в ссылке игнорируются (ссылка на список должна быть абсолютной);

Порядок – способ упорядочения значений списка:

0 или ничего – определяет ранг числа, так как если бы список сортировался в порядке убывания (т.е. максимальному значению присваивается ранг равный 1, чуть меньшему числу ранг 2 и т.д.);

Число не равное 0 – определяет ранг числа, так как если бы список сортировался в порядке возрастания (т.е. минимальному числу присваивается ранг равный 1, чуть большему числу ранг 2 и т.д.).

Разберем примеры:

Ячейки А1:А5 содержат числа 7 3,5 4 1 2

Чему будет равно значение функции для ячейки А2:
=РАНГ(А1;$А$1:$А$5;1)
Обратите внимание, что порядок (последняя цифра) в этой функции равен 1, число не равное 0.
Значит, иными словами я хочу узнать, какой порядок занимает число А2 равное 3,5 в списке чисел, отсортированном в порядке возрастания.
Согласно определения, функция присвоит наименьшему числу ранг 1.

Ответ нашего примера 3

Ячейки А1:А5 содержат числа 7 3,5 4 1 2

Чему будет равно значение функции для ячейки А1:

Обратите внимание, что порядок в этой функции отсутствует. Значит, иными словами я хочу узнать какой порядок занимает число А1, равное 7 в списке чисел, отсортированному в порядке убывания.

Ответ нашего примера 1

ПРИМЕЧАНИЕ : Функция РАНГ присваивает повторяющимся числам одинаковый ранг. Однако, наличие повторяющихся чисел влияет на ранг последующих чисел.

Например, ячейки А1:А7 содержат числа 1 2 3 4 5 5 6. Нужно узнать чему будет равен ранг для ячеек А5 и А6.

Согласно определению и примечанию, функция присвоит наибольшему числу ранг 1

Как мы видим, число 5 повторяется дважды и имеет ранг 2

Число 4 имеет ранг 4 и нет чисел, имеющего ранг 3

=СЧЕТЕСЛИ (диапазон; критерий)

Функция подсчитывает количество непустых ячеек в диапазоне, удовлетворяющих заданному условию.

В диапазоне А1:А6, нужно подсчитать количество ячеек со значением 35

Ответ примера 1

В диапазоне А1:А6, нужно подсчитать количество ячеек со значением книга

Ответ примера 2

Для закрепления нового материала, учащимся предлагается выполнить практические задания на компьютере.

Практическая работа 1

В ячейках выделенных зелёным цветом произведите соответствующие вычисления, используя математические функции;

В ячейках выделенных желтым цветом произведите соответствующие вычисления, используя статистические функции.

Практическая работа 2

В выделенных ячейках произведите соответствующие вычисления:

в столбце D рассчитайте налог 13% от начисленной заработной платы;

в столбце Е рассчитайте заработную плату к выдаче без учета НДФЛ;

в столбце F рассчитайте РАНГ числа ЗП по возрастанию;

в ячейках С12, С13, С14 воспользуйтесь статистическими функциями.

Практическая работа 3

Продажи в день найдите с помощью умножения объёма продаж на цену;

В выделенных ячейках произведите соответствующие вычисления с помощью функции СЧЕТЕСЛИ.

В программе Excel разработчиками заложено огромное количество различных функций, но, пользователи чаще всего пользуются математическими. Давайте рассмотрим их и подробнее остановимся на самых популярных.

Использование математических функций в программе

В категорию математических функций входит более 60 различных операторов, которые позволяют выполнять различные вычисления.

Вставить функцию в свободную ячейку таблицы можно по-разному:

Результатом любого из вышеописанных способов будет открытие окна вставки функции. Здесь мы выбираем категорию “Математические”.

Теперь, когда категория выбрана, в поле ниже отмечаем требуемую функцию и щелкаем OK.

После этого откроется окно с аргументами для заполнения.

Примечание: Если мы, находясь во вкладке “Формулы”, в группе инструментов “Библиотека функций” нажмем по значку математических функций, сразу откроется список операторов, которые мы можем выбрать, минуя окно вставки функции.

Стоит учитывать, что в предлагаемом перечне присутствуют не все операторы, но самые необходимые здесь все же есть, и в большинстве случаев их достаточно.

Теперь перейдем к детальному рассмотрению самых популярных функций.

Пожалуй, это самая популярная функция, которая используется в Эксель. С помощью нее выполняется суммирование числовых данных. Формула функции:

В аргументах можно указать как конкретные числа, так и ссылки на ячейки, содержащие числовые значения. Причем указать координаты можно вручную (с помощью клавиш клавиатуры) или методом клика/выделения непосредственно в самой таблице.

Для перехода к заполнению следующего аргумента достаточно кликнуть по полю напротив него или нажать клавишу Tab.

СУММЕСЛИ

Данная функция позволяет считать сумму чисел с заданным условиями, с помощью которых будет выполняться отбор значений, учитывающихся в суммировании. Формула выглядит следующим образом:

В аргументах функции указывается диапазон ячеек (вручную или путем выделения в таблице), значения которых нужно просуммировать. В качестве критерия можно задать следующие условия (в кавычках):

Аргумент “Диапазон_сумирования” заполнять не обязательно.

ПРОИЗВЕД

С помощью данного оператора выполняется умножение чисел. Синтаксис выглядит следующим образом:

В аргументах функции, как и в СУММ, можно указывать как конкретные числа, так и адреса ячеек (диапазоны ячеек), которые содержат числовые значения.

ЧАСТНОЕ

Чаще всего для деления используется формула со знаком “/” между делимым и делителем: =Число1/Число2 .

Однако в программе также есть отдельная функция для выполнения деления, синтаксис которой представлен ниже:

Заполнить нужно два аргумента: Числитель (Делимое) и Знаменатель (Делитель).

СТЕПЕНЬ

Оператор позволяет возвести число в указанную степень. Формула выглядит так:

В аргументах функции указывается само число, а также, степень, в которую нужно его возвести.

КОРЕНЬ

С помощью данного оператора можно извлечь квадратный корень из числа. Синтаксис выглядит следующим образом:

Заполнить требуется только один аргумент – “Число”.

ОКРУГЛ

Функция применяется для выполнения еще одного распространенного математического действия – округления чисел (по общематематическим правилам, т.е., к ближайшему по модулю значению). Синтаксис функции представлен ниже:

В аргументе “Число” указывается значение, которое требуется округлить. В числе разрядов, соответственно, пишем количество цифр, которые хотим оставить после запятой.

Также, в Excel доступны операторы ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые, как следует из их названий, используются для округления до ближайшего верхнего и нижнего числа, соответственно (по модулю).

Позволяет получить модуль числа. Формула функции представлена ниже:

Заполнить нужно всего один аргумент – “Число”, модуль которого требуется найти.

С помощью этого оператора определяется логарифм числа по заданному основанию. Синтаксис функции представлен в виде:

Необходимо заполнить два аргумента: Число и Основание логарифма (если его не указать, программа примет значение по умолчанию, равное 10).

Также для десятичного логарифма предусмотрена отдельная функция – LOG10.

ОСТАТОК

Применяется для получения остатка от деления чисел. Формула оператора выглядит следующим образом:

Для того, чтобы получить результат, требуется заполнить значения двух аргументов: Число и Делитель.

Заключение

Таким образом, мы разобрали самые популярные математические функции, которые используются в Excel. Однако возможности программы гораздо шире, и в ее инструментарии можно найти функцию для успешного выполнения практически любой задачи.

Учебное занятие по данной теме поможет обучающимся изучить функцию ЕСЛИ из категории Логические, изучить функции СРЗНАЧ и СЧЁТЕСЛИ из категории Статистические, изучить функцию ЦЕЛОЕ из категории Математические и научиться использовать их при решении задач.

ПЛАН-КОНСПЕКТ

Цели учебного занятия: научиться решать задачи в Microsoft Excel 2010 с помощью логических, статистических и математических функций.

Задачи учебного занятия:

Образовательная:

изучить функцию ЕСЛИ из категории Логические;

изучить функции СРЗНАЧ и СЧЁТЕСЛИ из категории Статистические;

изучить функцию ЦЕЛОЕ из категории Математические;

научиться использовать их при решении задач.

Развивающая:

способствовать формированию у обучающихся логического и алгоритмического мышления;

развивать познавательный интерес к учебной дисциплине и навыки ИКТ;

развивать умения оперировать ранее полученными знаниями;

выполнять в процессе учебной деятельности все требуемые этапы решения задач с помощью компьютера.

Воспитательная:

формировать информационную культуру, умения и навыки самостоятельного овладения знаниями;

воспитывать информационную культуру обучающихся, внимательность, аккуратность, дисциплинированность, усидчивость.

Тип учебного занятия: комбинированный.

Метод обучения: объяснительно-иллюстративный.

Методические приемы обучения: словесный, наглядный.

Формы работы: индивидуальная.

Оборудование: персональные компьютеры, доска, мел.

Программное обеспечение: операционная система Windows 7, пакет прикладных программ Microsoft Office 2010.

План занятия:

Организационный момент (3 минуты).

Актуализация базовых знаний (12 минут).

Изложение нового материала (25 минут).

Практическая работа (1 час 30 минут).

Подведение итогов учебного занятия. Рефлексия (5 минут).

Ход учебного занятия:

Организационный момент.

Учебное занятие начинается с приветствия обучающихся. Затем педагог дополнительного образования отмечает присутствующих в группе.

Актуализация базовых знаний.

Педагог дополнительного образования старается подвести обучающихся к новой теме, задает несложные вопросы:

1. Установите соответствие между Функцией и Назначением.

2. Впишите категорию функции (Математические или Статистические) (на листках распечатать или на доске).

Вычисление суммы значений в заданном диапазоне

Вычисление корня квадратного

Округляет вещественное число до ближайшего меньшего целого

Вычисление тригонометрической функции

Позволяет найти число ячеек по определенному критерию. Работает с числовыми и текстовыми значениями, датами.

Вычисление минимального значения в заданном диапазоне

Вычисляет среднее арифметическое значение диапазона аргументов

СУММ, КОРЕНЬ, ЦЕЛОЕ, SIN — Математические

МИН, СРЗНЧ, СЧЁТЕСЛИ — Статистические

После выполнения задания оцените себя, пожалуйста, в листе самооценки!

Изложение нового материала.

Педагог дополнительного образования поясняет тему нового учебного занятия, цель работы. Затем педагог дополнительного образования приступает к объяснению новой темы.

Для решения задач в Microsoft Excel часто используется логическая функция ЕСЛИ:

Функция ЕСЛИ проверяет, выполняется ли условие, и возвращает одно значение, если оно выполняется, и другое значение, если нет.

Синтаксис функции ЕСЛИ очень простой:

ЕСЛИ(лог_выражение; [значение_если_истина]; [значение_если_ложь])

лог_выражение – это любое значение или выражение, которое при вычислении дает значение ИСТИНА или ЛОЖЬ.

Что это значит? Выражение при вычислении дает значение ИСТИНА если это выражение верно.

В этой части необходимо проверить на соответствие выражения.

=ЕСЛИ(А1=10; [значение_если_истина]; [значение_если_ложь]) — если А1 равно 10, то выражение А1=10 даст значение ИСТИНА, а если не равно 10, то ЛОЖЬ

=ЕСЛИ(С1=”Да”; [значение_если_истина]; [значение_если_ложь]) — если в ячейки C1 содержится слово “Да” то выражение вернет значение ИСТИНА, а если нет, то С1=”Да” вернет ЛОЖЬ

Надеюсь с этим понятно. Рассмотрим следующие компоненты функции ЕСЛИ

=ЕСЛИ(лог_выражение; [значение_если_истина]; [значение_если_ложь])

значение_если_истина, значение_если_ложь – как видно из их названия, это то что необходимо сделать в зависимости от того, что вернул лог выражения: ИСТИНА и ЛОЖЬ.

3. А теперь посмотрите, пожалуйста, на доску. Перед Вами представлена задача (Приложение 1).

2. А давайте подумаем, какую формулу можно задать, если необходимо вычислить среднюю оценку за каждую четверть для каждого обучающегося? Ответ необходимо записать в ячейку таблицы.

=ЕСЛИ(СРЗНАЧ(C3:E3)-ЦЕЛОЕ(СРЗНАЧ(C3:E3))C3:E3)); ЦЕЛОЕ(СРЗНАЧ(C3:E3))+1)

3. А теперь подумаем какую формулу можно задать, если необходимо вычислить итоги года для каждого обучающегося?

= ЕСЛИ(СРЗНАЧ(G3;L3;Q3;V3)-ЦЕЛОЕ(СРЗНАЧ(G3;L3;Q3;V3))G3;L3;Q3;V3)); ЦЕЛОЕ(СРЗНАЧ(G3;L3;Q3;V3))+1)

Молодцы! Справились!

Подведение итогов учебного занятия. Рефлексия.

Педагог дополнительного образования демонстрирует работы, выполненные обучающимися и предлагает обучающимся оценить себя самостоятельно.

Читайте также:

Конспект как правильно мыть руки

Конспект наука о русском языке

Расселение древнейшего человека человек разумный конспект

Конспект урока отражение света 11 класс

Сергий радонежский конспект урока

Источник

Создание
сложных формул с помощью встроенных
логических функций Excel

Логические
выражения

Логические выражения
в Excel
используются для записи условий, в
которых сравниваются числа, функции,
формулы, текстовые или логические
значения. Любое логическое выражение
должно содержать, по крайней мере, один
оператор сравнения, который определяет
отношение между элементами логического
выражения.

Ниже
представлен список операторов сравнения
Excel:

=	Равно
>	Больше
<	Меньше
>=	Больше или равно
<=	Меньше или равно
<>	Не равно

Результатом
логического выражения является логическое
значение ИСТИНА (1) или логическое
значение ЛОЖЬ (0).

Функция ЕСЛИ

Функция ЕСЛИ
– это функция, которая позволяет вывести
в ячейку одно значение, если заданное
пользователем условие выполняется и
другое – если условие не выполняется.

Синтаксис:

ЕСЛИ(лог_выраж.;
знач._если_истина; знач._если_ложь)

Пример:

Рассчитать стоимость
товара с учетом того, что если количество
превысило 5 шт., то магазин дает скидку
10%. Исходные данные приведены на рис.
26.

Рис. 26

Для того чтобы
рассчитать стоимость товара с учетом
скидки необходимо:

Переместить курсор
в ячейку D2.
С помощью мастера функций выбрать из
категории Логические функцию ЕСЛИ
(рис. 27), а затем щелкнуть на кнопке
ОК.
Диалоговое окно
Аргументы функции (рис. 28) содержит
три поля ввода. В поле Лог_выражение
необходимо ввести условие, которое
определяет, превышает ли проданное
кол-во товара 5 шт., следовательно введем
в это поле С2>5.
В поле Значение_если_истина
необходимо ввести формулу, которая
вычисляет стоимость товара с учетом
скидки, тогда введем в это поле
B2*C2-B2*C2*0,1. В
поле Значение_если_ложь
необходимо ввести формулу, которая
вычисляет стоимость товара без учета
скидки (условие С2>5 —
Ложь),
в тогда введем в это поле B2*C2
(см. рис. 29). Теперь щелкнем на
кнопке OK.
Скопировать
полученную формулу в смежные ячейки.
Результаты вычислений формул приведены
на рис. 30.

Рис. 27

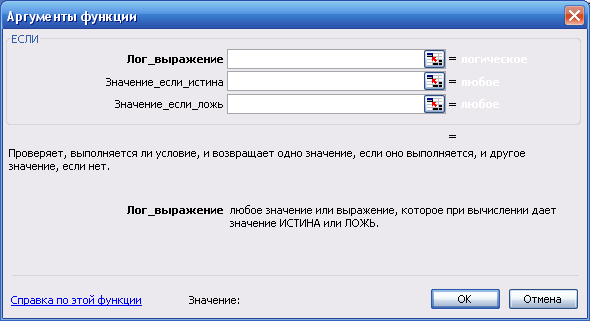
Рис. 28

Рис. 29

Рис. 30

Функции ЕСЛИ
могут быть вложены друг в друга в качестве
значений аргументов значение_если_истина
и значение_если_ложь.
С помощью таких вложенных функций Если
можно
конструировать более сложные проверки.
Рассмотрим на примерах, как необходимо
использовать вложенной функцией
ЕСЛИ.

Пример.

На рис. 31 приведена
таблица с данными. Необходимо:

Определить, на
какую сумму продано товаров каждого
вида.
Определить, на
какую сумму продано товаров каждого
вида с учетом скидки (сумма с учетом
скидки = сумма — сумма * скидка). Скидка
начисляется по следующему принципу:
если продано товара на сумму более 2500
грн., то скидка составит 5%, если продано
товара на сумму менее 1100 грн., то скидка
составит 0%, в остальных случаях скидка
составит 2%.

Рис. 31

Для того чтобы
выполнить первый пункт задания необходимо
в ячейку D2 ввести
формулу =C2*B2.

Для того чтобы
вычислить сумму со скидкой
будем использовать вложенную
функцию ЕСЛИ, так как существует
три варианта начисления скидки.

Рис. 32

Переместим курсор
в ячейку E2 и с
помощью мастера функций введем следующую
формулу (рис. 33 – 34). Результаты решения
приведены на рис. 35.

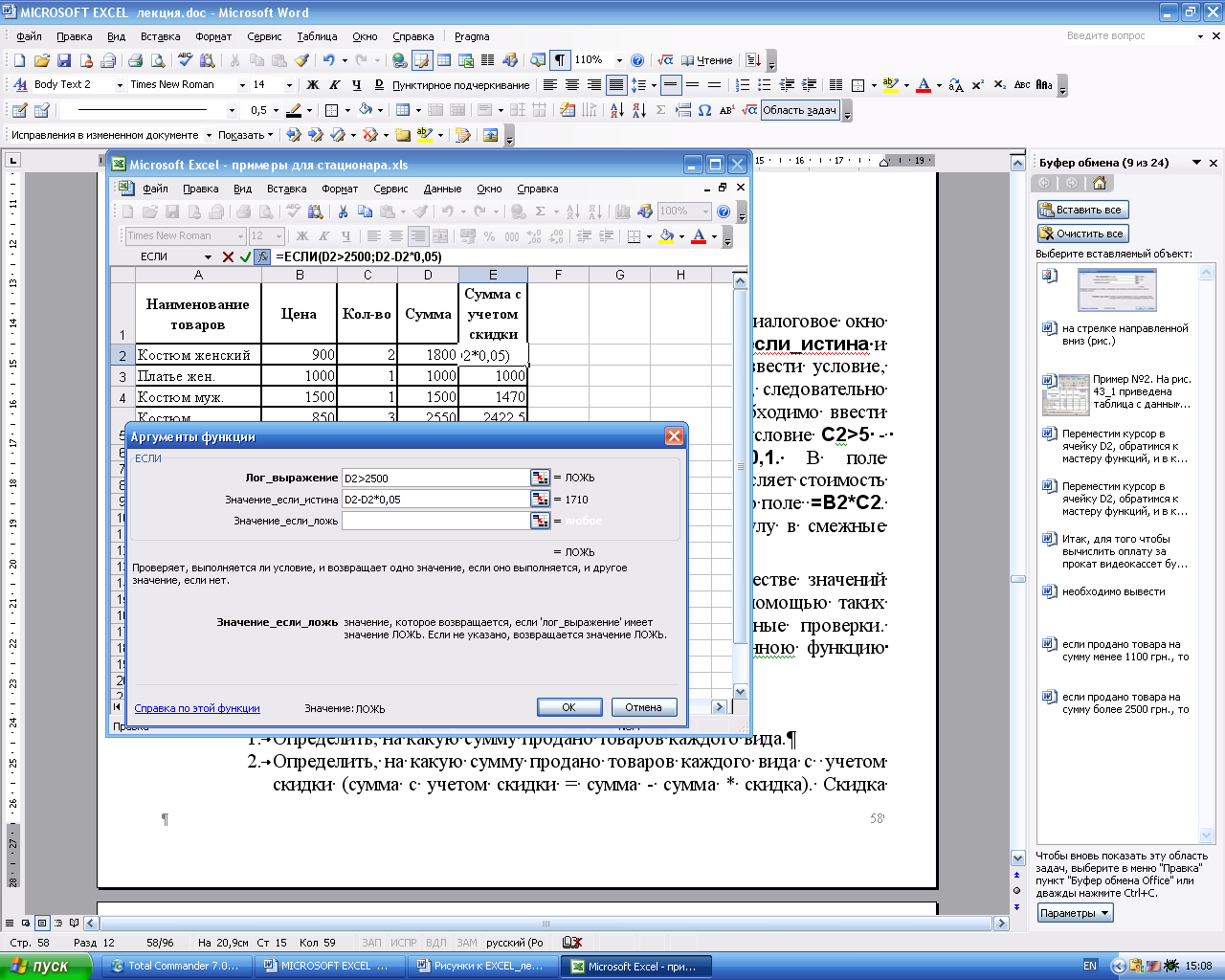
Щелкнуть
тут

Рис. 33

Рис. 34

Рис.
35

Функции
ИЛИ, И

Функции И
и функция ИЛИ
из категории Логические
способны заметно улучшить наглядность
и понятность сложных логических проверок.
Функция ИЛИ
и функция И
позволяют задавать в формуле одновременно
несколько условий, т.е. дают возможность
создавать сложные логические выражения.
Эти функции работают в сочетании с
простыми операторами сравнения. Функции
И
и ИЛИ
могут иметь до 30 логических аргументов
и имеют синтаксис:

ИЛИ(логическое_значение1;логическое_значение2;
…)

И(логическое_значение1;
логическое_значение2; …)

Аргументы функций
И, ИЛИ
могут быть логическими выражениями,
массивами или ссылками на ячейки,
содержащие логические значения.

Функция ИЛИ
возвращает логическое значение ИСТИНА,
если хотя бы одно из логических выражений
истинно, а функция И
возвращает логическое значение ИСТИНА,
только если все логические выражения
истинны.

Пример

Предположим, что
нужно вывести сообщение «Светофор»,
если содержимое ячейки B4
или
«красный», или «зеленый», или «желтый».
Если же она содержит любую другую
информацию, то необходимо вывести
сообщение «Это не светофор!!!».

ЕСЛИ(ИЛИ(B4=«зеленый»;B4=«красный»;B4=«желтый»);»Светофор»;
«Это не светофор!!!» )

Пример

Предположим, что
нужно вывести на экран содержимое ячейки
B4,
если она содержит число строго между 1
и 100 (1<=B4<=100),
и сообщение «Значение вне интервала»
в противном случае.

ЕСЛИ(И(B4>=1;
B4<=100); B4; «Значение вне интервала»)

Пример

Есть список дат,
необходимо определить, является ли
выходным днем введенная дата. Решения
задачи на рис. 36

Рис. 36

Формулу в ячейке
В2
можно вводить с клавиатуры (необходимо
помнить синтаксис используемых вложенных
функций) или с помощью мастера функции.
Рассмотрим, как вводить формулу с
помощью мастера функций:

Переместим курсор
в ячейку В2,
щелкнем
на кнопке вставка функции и в категории
логические выберем функцию Если.
Щелкнем в поле
Лог_выражение
функции
Если,
а затем
щелкнем на стрелке вниз в строке формул
и выберем Другие
функции (см.
рис. 37). Теперь в категории Логические
можно выбрать функцию ИЛИ.
Щелкнем в поле
Логическое_выражение_1
функции ИЛИ,
а затем щелкнем на стрелке вниз в строке
формул и выберем Другие
функции. В
категории Дата
и время
выберем функцию ДЕНЬНЕД
и в поле Дата_в_числом_формате
введем А2,
а в поле Тип
введем 2.
В строке формул
щелкнем мышкой внутри слова ИЛИ
и таким образом, сможем вернуться в
диалоговое окно функции ИЛИ,
для того чтобы закончить ввод условия
в первое поле этой функции (набираем =
6).
Щелкнем в поле
Логическое_выражение_2
функции ИЛИ
и повторим
действия пункта 3 и 4, чтобы ввести второе
условие ДЕНЬНЕД(А2;2)=7.
В строке формул
щелкнем мышкой внутри слова ЕСЛИ
и таким образом, сможем вернуться в
диалоговое окно функции ЕСЛИ,
для того чтобы закончить ввод формулы
(в поле Значение_если_истина
вводим
Выходной
день, в поле
Значение_если_ложь
вводим
пробел).

Рис. 37

Пример

Информация о
результатах первого модульного контроля
и посещаемости студентами занятий
выведена в таблице см. рис. 38. Необходимо
вывести следующую информацию: Если
средний бал студента меньше или равен
3,5 и он пропустил более 49 часов занятий
по неуважительной причине, то необходимо
вызвать родителей в деканат; если средний
бал студента больше или 4,5 и он пропустил
не более 10 часов занятий по неуважительной
причине, то необходимо отправить
родителям письмо благодарность. Решение
задачи представлено на рис. 39.

Рис. 38

Рис. 39

Функции
СЧЁТЕСЛИ и СУММЕСЛИ

Эти функции надо
искать не в категории Логические,
а в категориях Статистические
и Математические,
соответственно (или в полном алфавитном
перечне).

СЧЁТЕСЛИ
— подсчитывает количество ячеек в
диапазоне, удовлетворяющих заданному
условию, а СУММЕСЛИ
— суммирует значения ячеек, удовлетворяющих
заданному условию. Функция СУММЕСЛИ
используется в тех случаях, когда
необходимо суммировать не весь диапазон,
а только ячейки, отвечающие некоторым
условиям (критериям).

Синтаксис:

СЧЁТЕСЛИ
(диапазон; критерий)

где,

диапазон
—
диапазон, в котором нужно подсчитать
ячейки.

критерий
— критерий
(условие) в форме числа, выражения или
текста, который определяет, какие ячейки
надо подсчитывать.

Функция СЧЁТЕСЛИ
работает следующим образом: вычисляется
количество ячеек диапазона, значение
которых удовлетворяют условию
(критерию).

Пример

В задаче, рассмотренной
в примере 10 необходимо определить
количество студентов, у которых средний
балл >=4.5.

Тогда в ячейку С15
необходимо ввести формулу:
=СЧЁТЕСЛИ(B11:B13;»>=4,5″).
Результат
приведен на рис. 40

Рис. 40

Синтаксис:

СУММЕСЛИ
(диапазон; критерий; диапазон_суммирования)

где,

диапазон
— диапазон ячеек проверяемых на критерий
(условие).

критерий
— критерий (условие) в форме числа,
выражения или текста, определяющего
суммируемые ячейки.

диапазон_суммирования
— фактические
ячейки для суммирования.

Функция СУММЕСЛИ
работает следующим образом: ячейки из
«диапазон_суммирования»
суммируются, только если соответствующие
им ячейки в аргументе «диапазон»
удовлетворяют условию
(критерию).
В тех случаях, когда диапазон вычисляемых
ячеек (где проверяется условие) и диапазон
фактических ячеек для суммирования
совпадают, аргумент «диапазон_суммирования»
можно не указывать.

Пример

В таблице на рис.
41 приведены объемы партий товара,
полученные магазином. Необходимо
просуммировать только объемы тех партий,
значения которых превышают 20. Решение
на рис. 42

Рис. 41

Рис.42

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

To begin with, statistical function in Excel let’s first understand what is statistics and why we need it? So, statistics is a branch of sciences that can give a property to a sample. It deals with collecting, organizing, analyzing, and presenting the data. One of the great mathematicians Karl Pearson, also the father of modern statistics quoted that, “statistics is the grammar of science”.

We used statistics in every industry, including business, marketing, governance, engineering, health, etc. So in short statistics a quantitative tool to understand the world in a better way. For example, the government studies the demography of his/her country before making any policy and the demography can only study with the help of statistics. We can take another example for making a movie or any campaign it is very important to understand your audience and there too we used statistics as our tool.

Ways to approach statistical function in Excel:

In Excel, we have a range of statical functions, we can perform basic mead, median mode to more complex statistical distribution, and probability test. In order to understand statistical Functions we will divide them into two sets:

Basic statistical Function
Intermediate Statistical Function.

Statistical Function in Excel

Excel is the best tool to apply statistical functions. As discussed above we first discuss the basic statistical function, and then we will study intermediate statistical function. Throughout the article, we will take data and by using it we will understand the statistical function.

So, let’s take random data of a book store that sells textbooks for classes 11th and 12th.

Example of statistical function.

Basic statistical Function

These are some most common and useful functions. These include the COUNT function, COUNTA function, COUNTBLANK function, COUNTIFS function. Let’s discuss one by one:

1. COUNT function

The COUNT function is used to count the number of cells containing a number. Always remember one thing that it will only count the number.

Formula for COUNT function = COUNT(value1, [value2], …)

Example of statistical function.

Thus, there are 7 textbooks that have a discount out of 9 books.

2. COUNTA function

This function will count everything, it will count the number of the cell containing any kind of information, including numbers, error values, empty text.

Formula for COUNTA function = COUNTA(value1, [value2], …)

Example of statistical function.

So, there are a total of 9 subjects that being sold in the store

3. COUNTBLANK function

COUNTBLANK function, as the term, suggest it will only count blank or empty cells.

Formula for COUNTBlANK function = COUNTBLANK(range)

Example of statistical function.

There are 2 subjects that don’t have any discount.

4. COUNTIFS function

COUNTIFS function is the most used function in Excel. The function will work on one or more than one condition in a given range and counts the cell that meets the condition.

Formula for COUNTIFS function = COUNTIFS (range1, criteria1, [range2], [criteria2], ...)

Intermediate Statistical Function

Let’s discuss some intermediate statistical functions in Excel. These functions used more often by the analyst. It includes functions like AVERAGE function, MEDIAN function, MODE function, STANDARD DEVIATION function, VARIANCE function, QUARTILES function, CORRELATION function.

1. AVERAGE value1, [value2], …)

The AVERAGE function is one of the most used intermediate functions. The function will return the arithmetic mean or an average of the cell in a given range.

Formula for AVERAGE function = AVERAGE(number1, [number2], …)

Example of statistical function.

So the average total revenue is Rs.144326.6667

2. AVERAGEIF function

The function will return the arithmetic mean or an average of the cell in a given range that meets the given criteria.

Formula for AVERAGEIF function = AVERAGEIF(range, criteria, [average_range])

3. MEDIAN function

The MEDIAN function will return the central value of the data. Its syntax is similar to the AVERAGE function.

Formula for MEDIAN function = MEDIAN(number1, [number2], …)

Example of statistical function.

Thus, the median quantity sold is 300.

4. MODE function

The MODE function will return the most frequent value of the cell in a given range.

 Formula for MODE function = MODE.SNGL(number1,[number2],…)

Example of statistical function.

Thus, the most frequent or repetitive cost is Rs. 250.

5. STANDARD DEVIATION

This function helps us to determine how much observed value deviated or varied from the average. This function is one of the useful functions in Excel.

Formula for STANDARD DEVIATION function = STDEV.P(number1,[number2],…)

Example of statistical function.

Thus, Standard Deviation of total revenue =296917.8172

6. VARIANCE function

To understand the VARIANCE function, we first need to know what is variance? Basically, Variance will determine the degree of variation in your data set. The more data is spread it means the more is variance.

Formula for VARIANCE function = VAR(number1, [number2], …)

Example of statistical function.

So, the variance of Revenue= 97955766832

7. QUARTILES function

Quartile divides the data into 4 parts just like the median which divides the data into two equal parts. So, the Excel QUARTILES function returns the quartiles of the dataset. It can return the minimum value, first quartile, second quartile, third quartile, and max value. Let’s see the syntax :

Formula for QUARTILES function = QUARTILE (array, quart)

Example of statistical function.

So, the first quartile = 14137.5

8. CORRELATION function

CORRELATION function, help to find the relationship between the two variables, this function mostly used by the analyst to study the data. The range of the CORRELATION coefficient lies between -1 to +1.

Formula for  CORRELATION function = CORREL(array1, array2)

Example of statistical function.

So, the correlation coefficient between discount and revenue of store = 0.802428894. Since it is a positive number, thus we can conclude discount is positively related to revenue.

9. MAX function

The MAX function will return the largest numeric value within a given set of data or an array.

Formula for  MAX function = MAX (number1, [number2], ...)

The maximum quantity of textbooks is Physics,620 in numbers.

10. MIN function

The MIN function will return the smallest numeric value within a given set of data or an array.

Formula for MIN function = MIN (number1, [number2], ...)

The minimum number of the book available in the store =150(Sociology)

11. LARGE function

The LARGE function is similar to the MAX function but the only difference is it returns the nth largest value within a given set of data or an array.

Formula for  LARGE function = LARGE (array, k)

Let’s find the most expensive textbook using a large function, where k = 1

Example of statistical function.

The most expensive textbook is Rs. 420.

12. SMALL function

The SMALL function is similar to the MIN function, but the only difference is it return nth smallest value within a given set of data or an array.

Formula for  SMALL function = SMALL (array, k)

Similarly, using the SMALL function we can find the second least expensive book.

Example of statistical function.

Thus, Rs. 120 is the least cost price.

Conclusion

So these are some statistical functions of Excel. We have learned some of the most simple functions like COUNT functions to complex ones like the CORRELATION function. So far we learn, we understand how much these functions are useful for analyzing any data. You can explore more functions and learn more things of your own.

Источник

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28