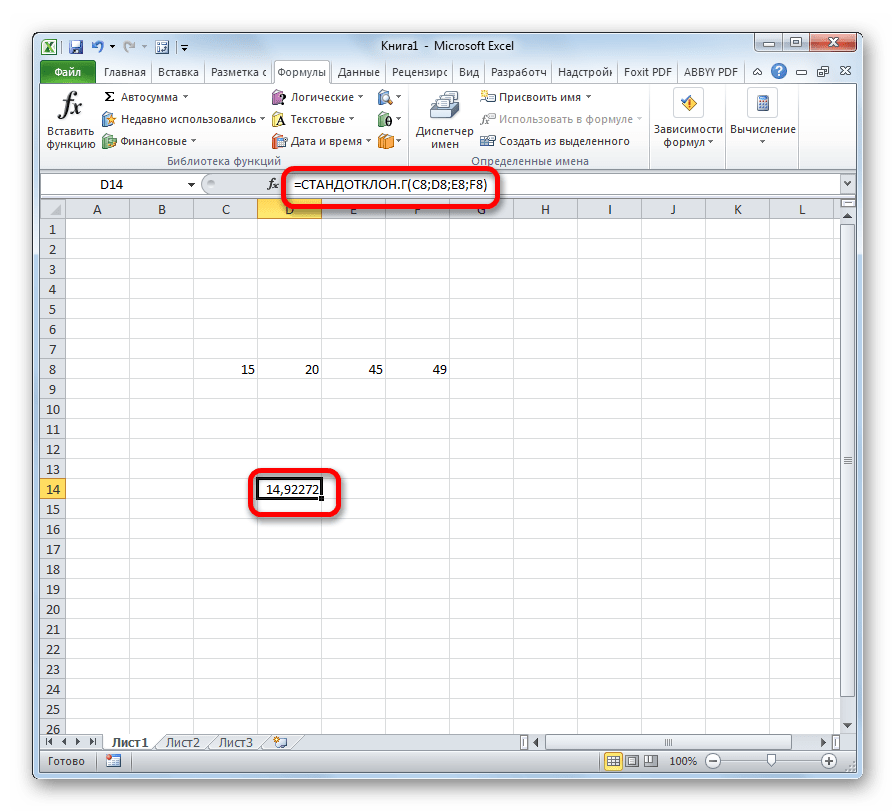
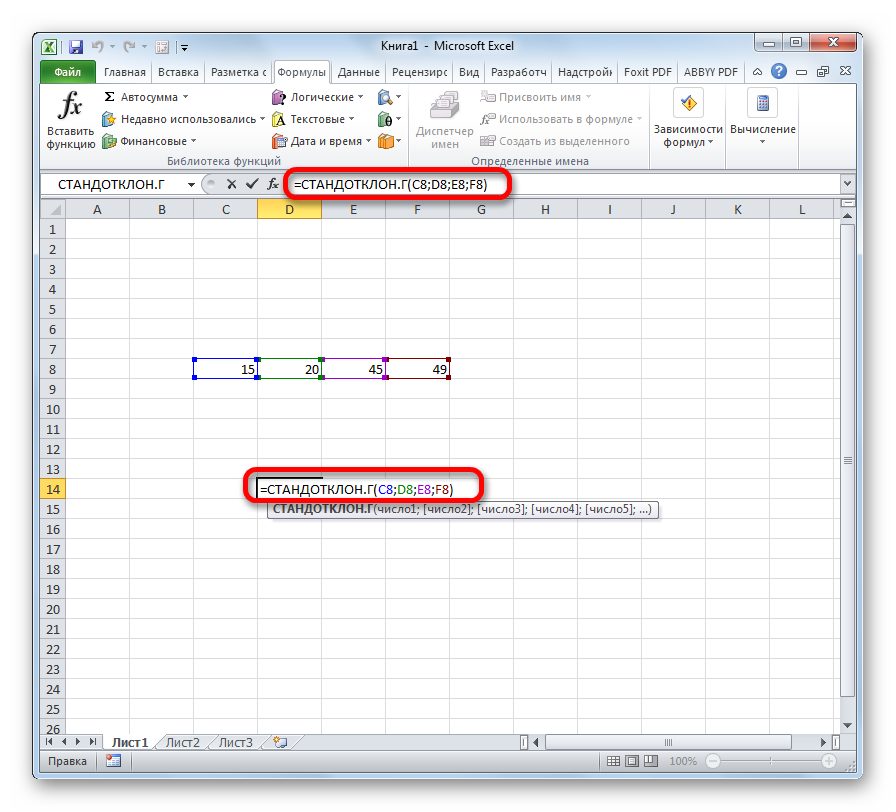
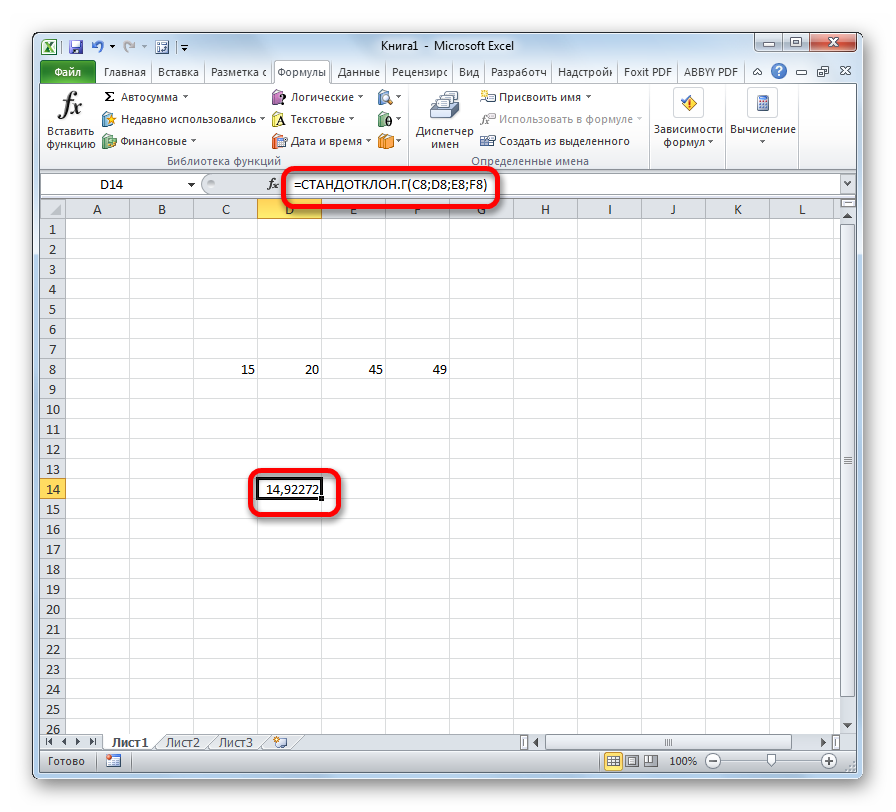
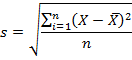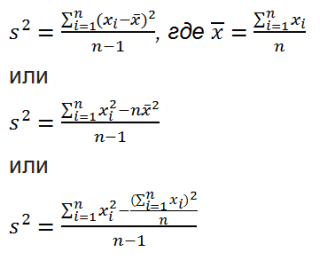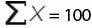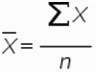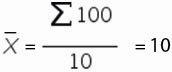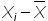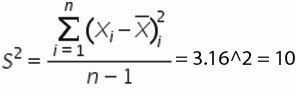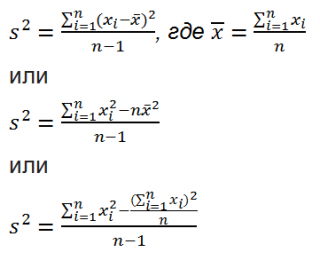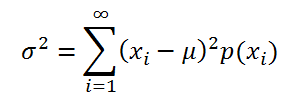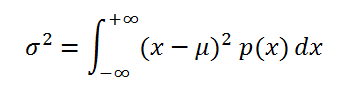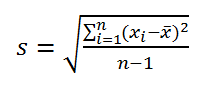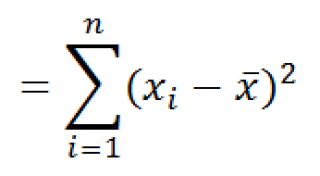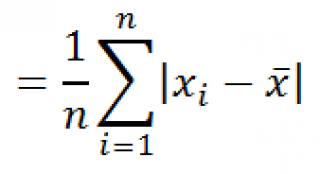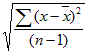Содержание
- Определение среднего квадратичного отклонения
- Расчет в Excel
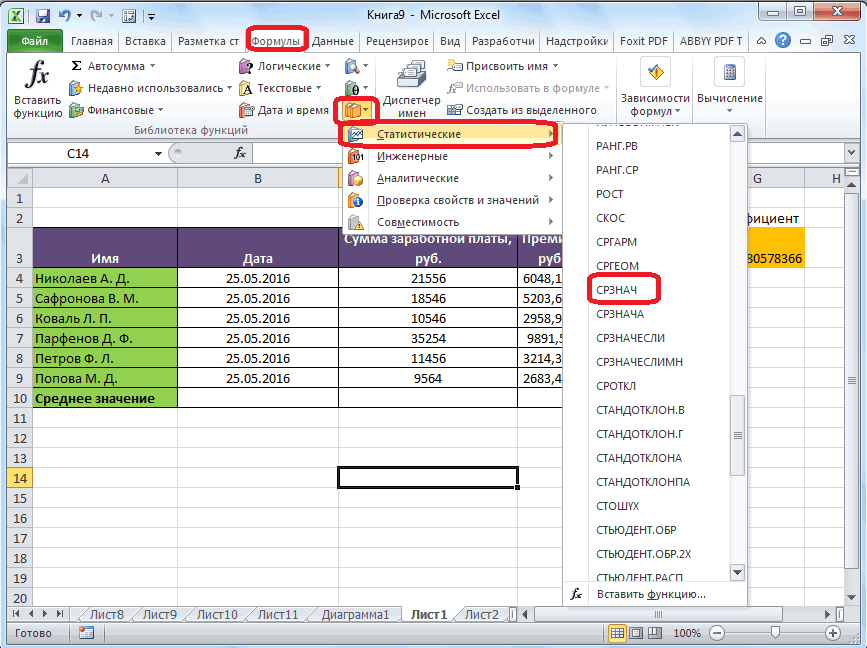
- Способ 1: мастер функций
- Способ 2: вкладка «Формулы»
- Способ 3: ручной ввод формулы
- Вопросы и ответы
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
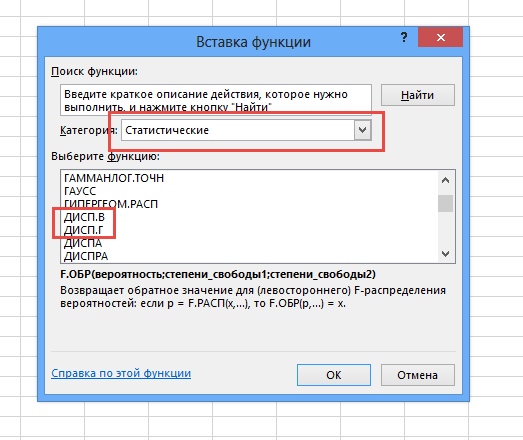
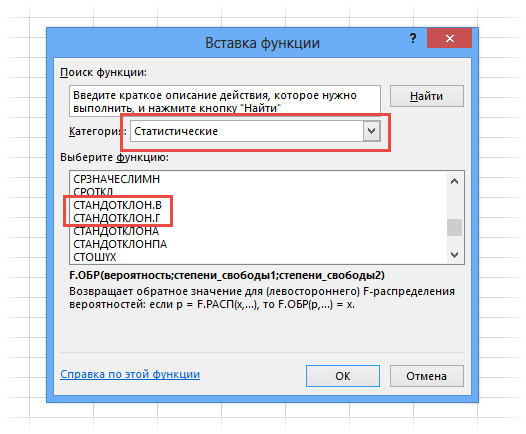
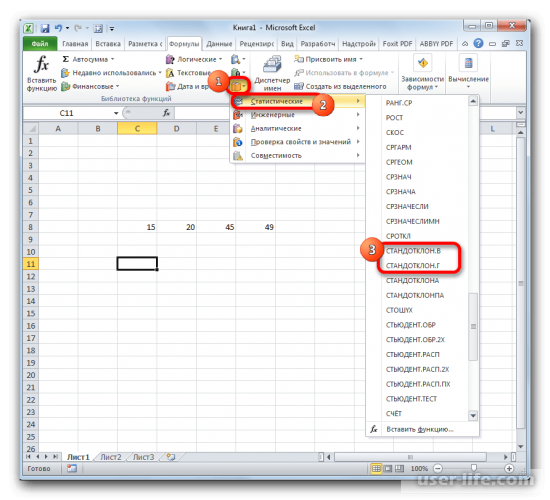
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
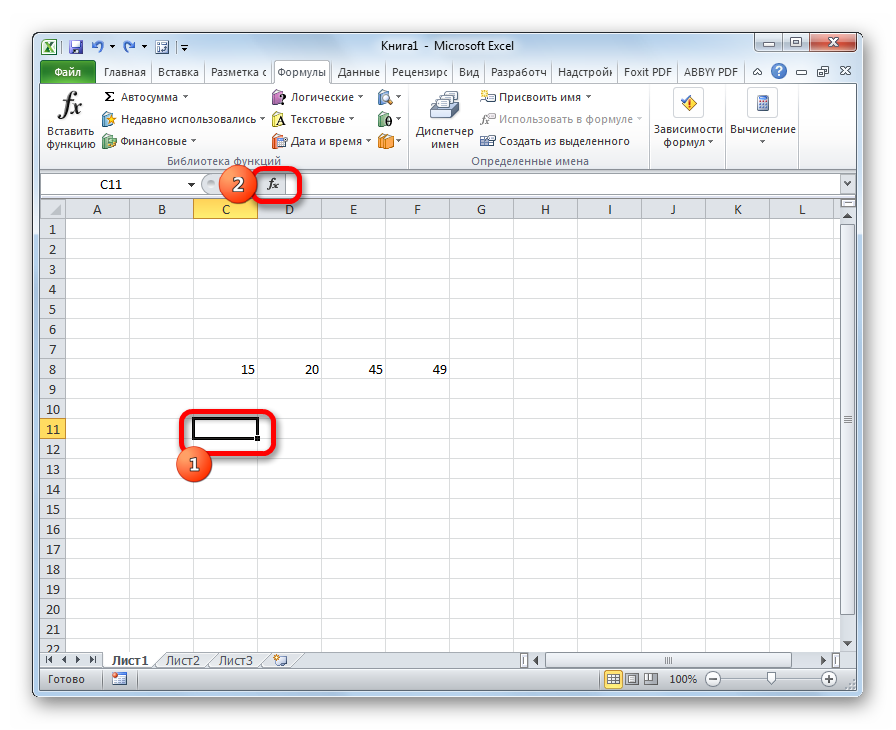
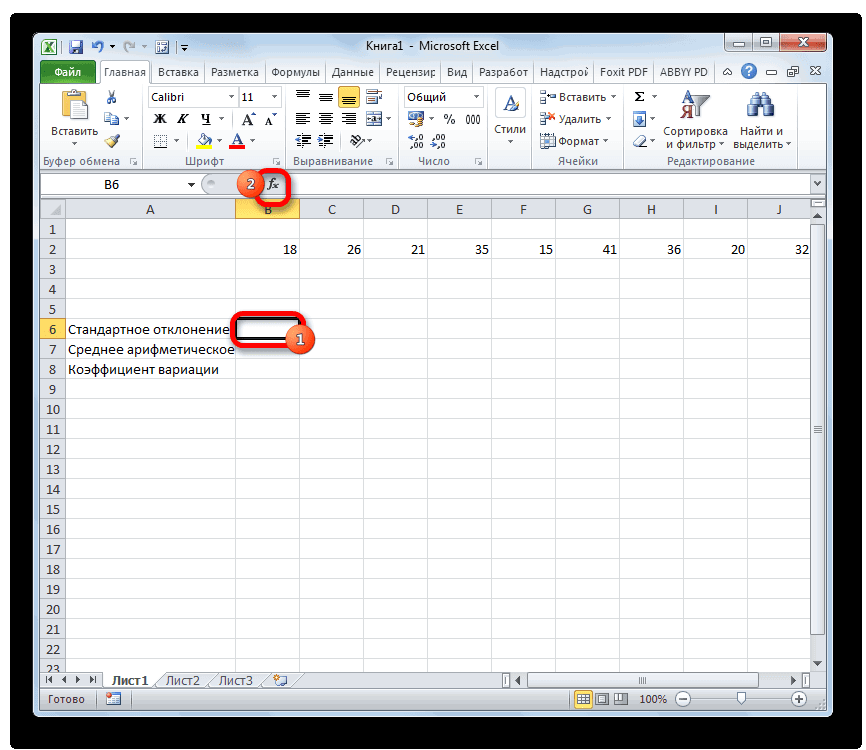
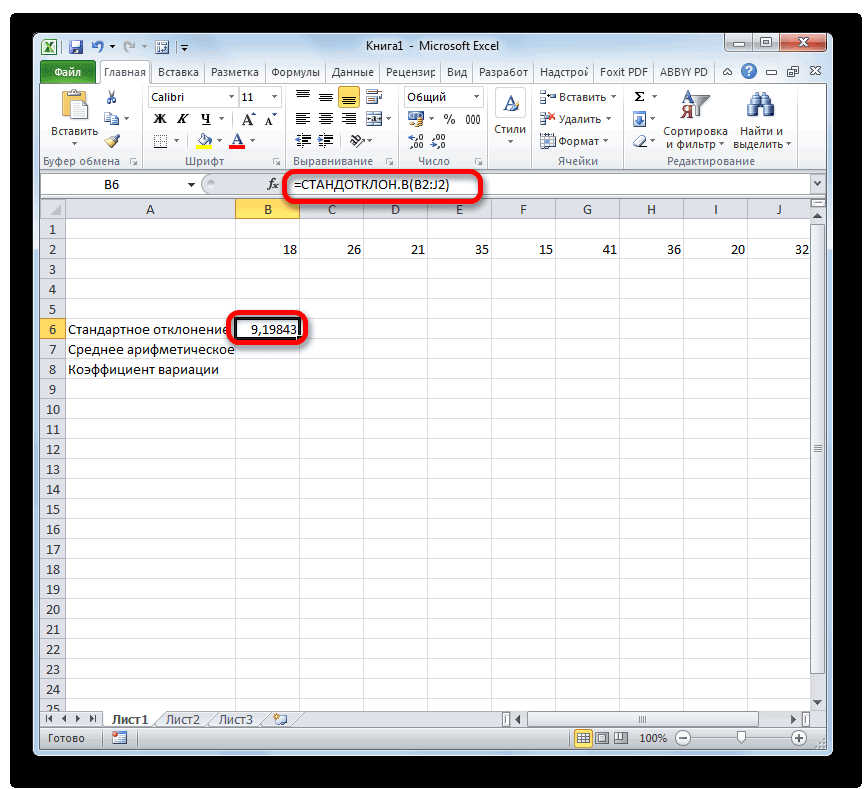
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
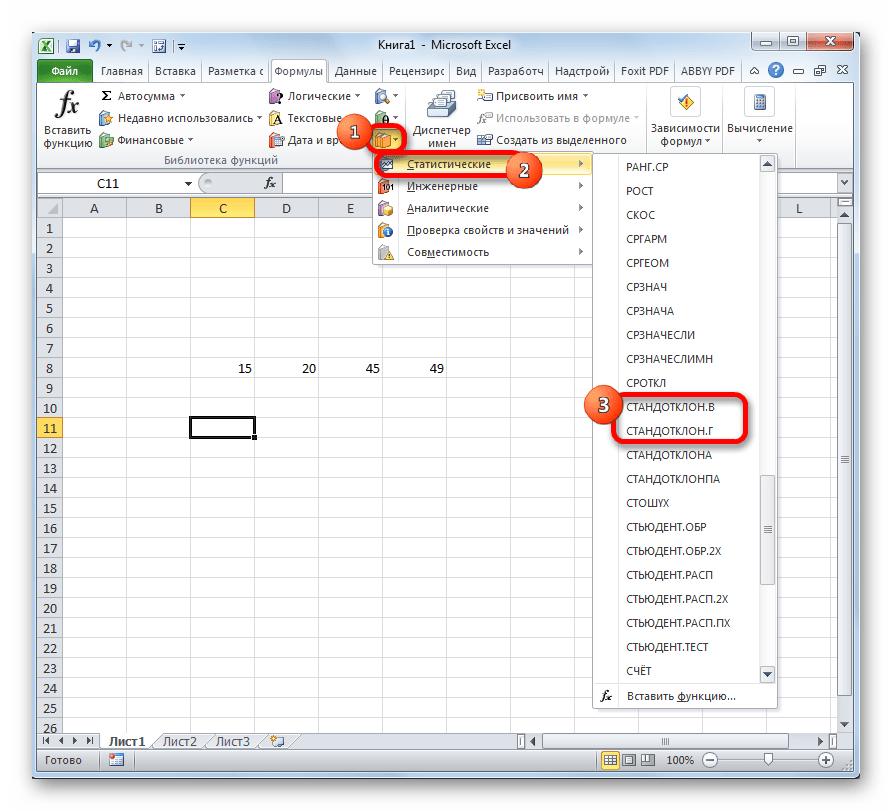
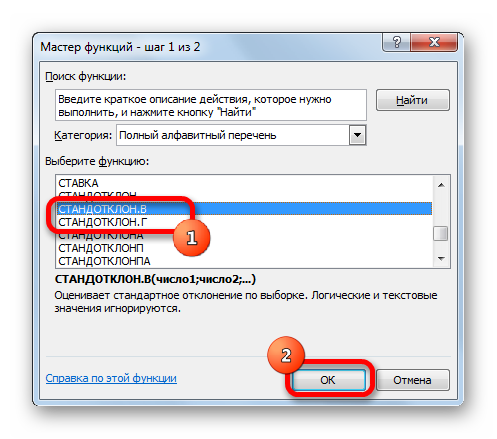
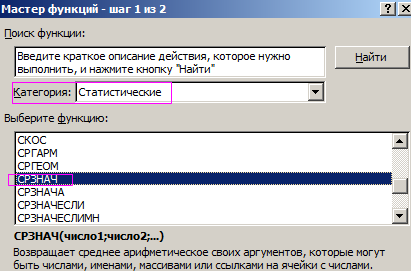
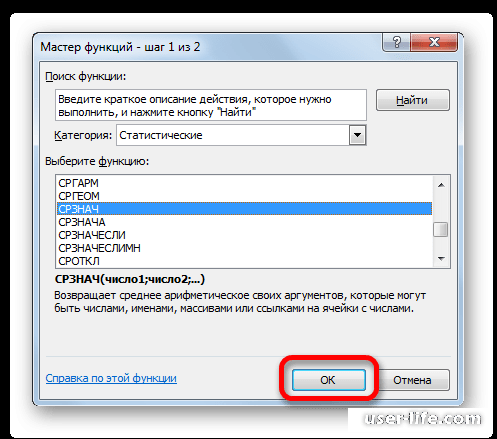
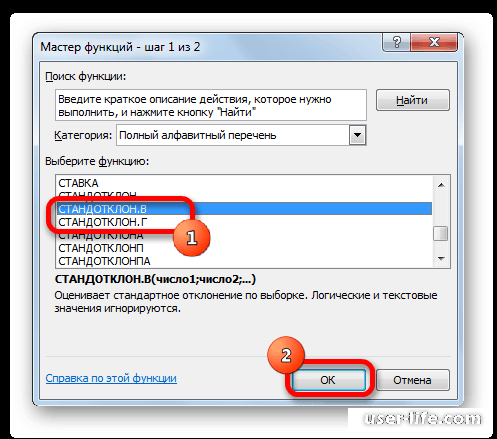
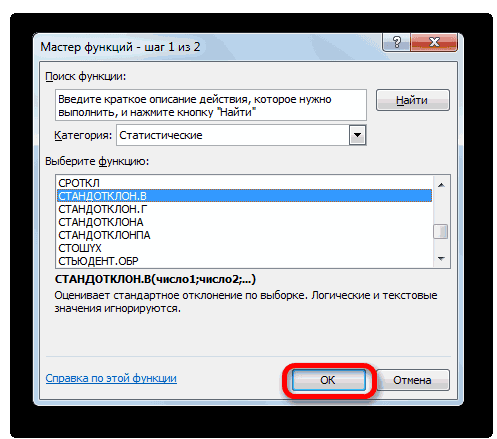
- В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
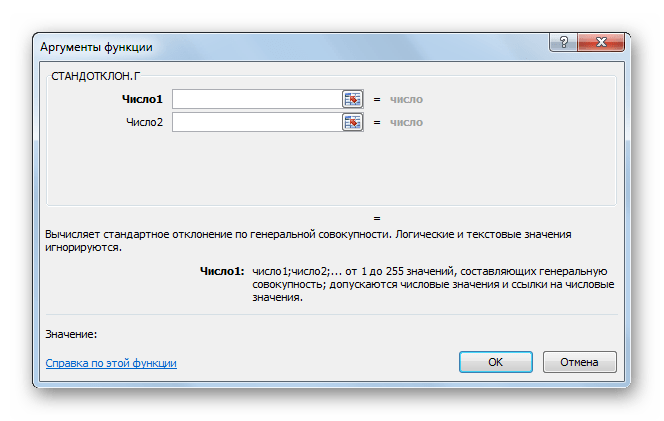
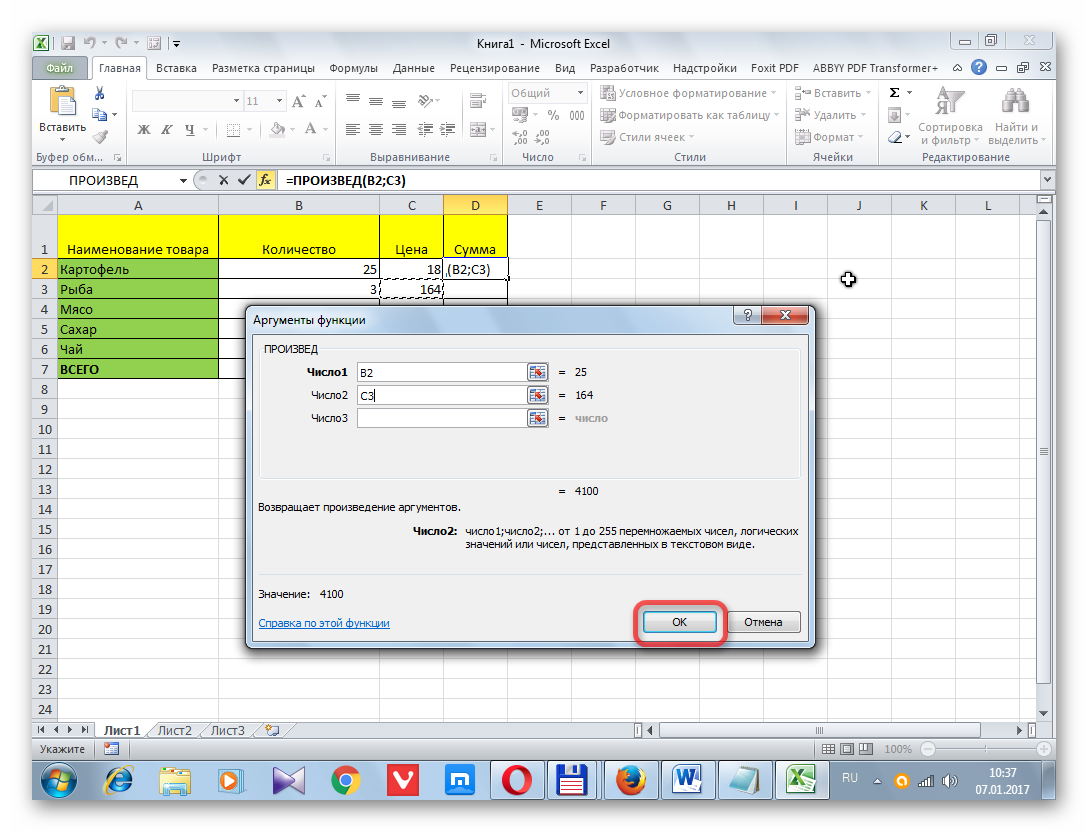
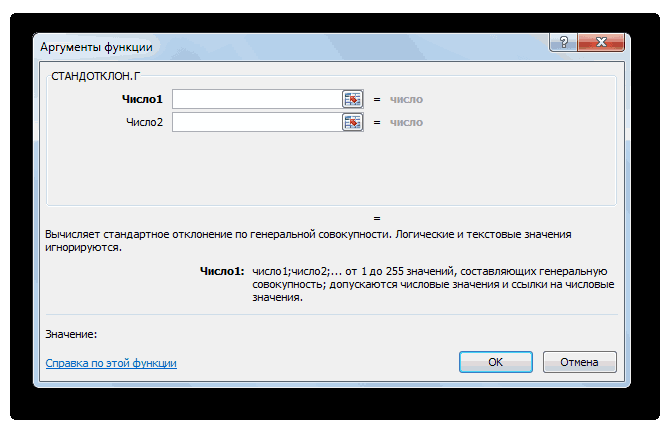
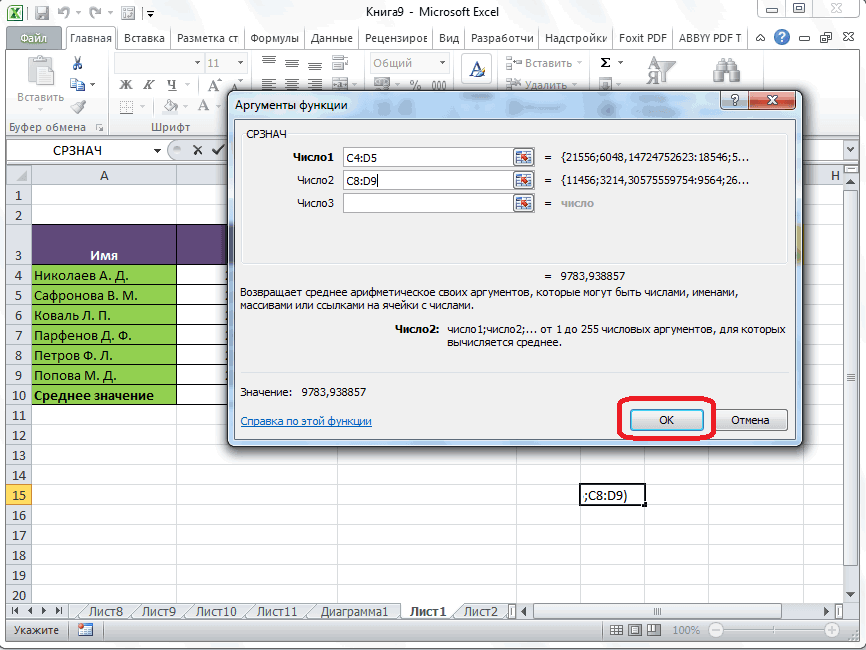
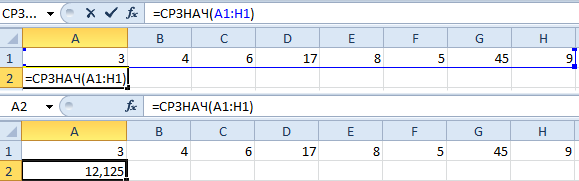
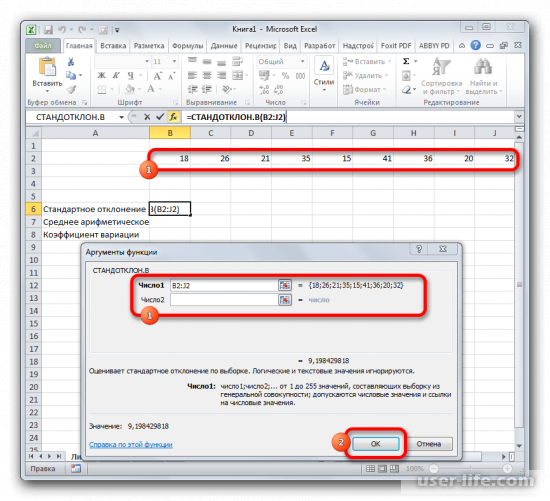
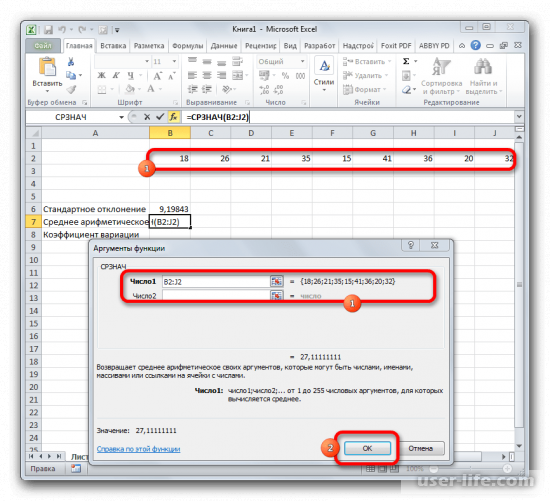
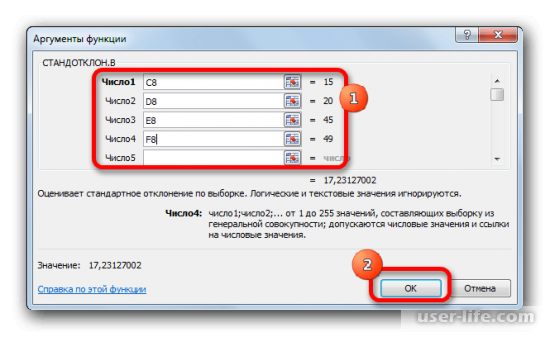
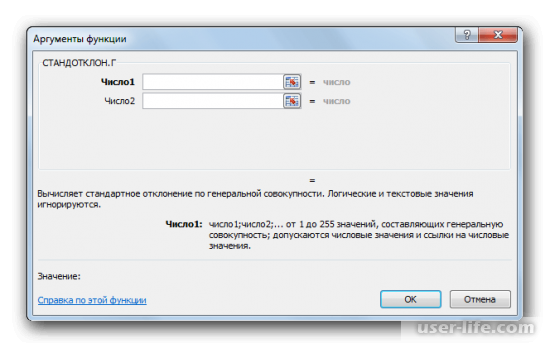
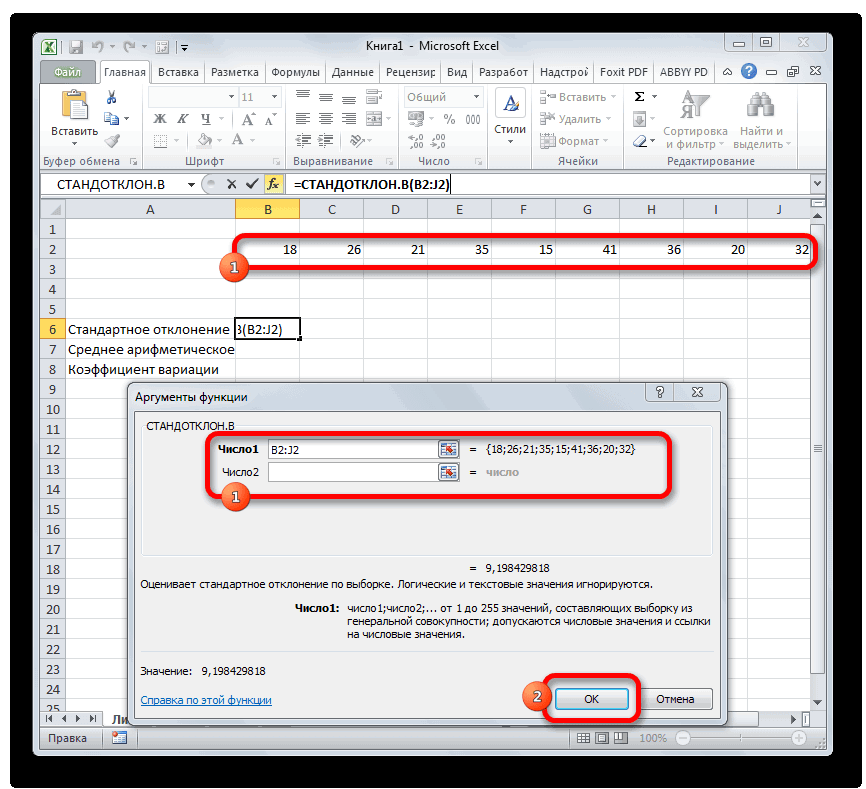
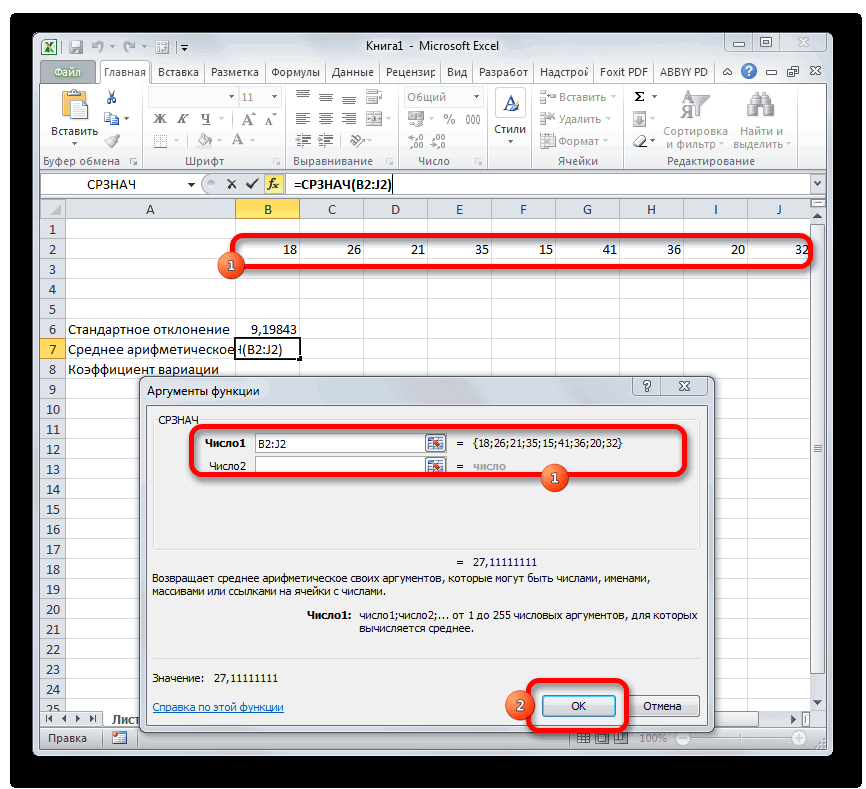
- Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK».
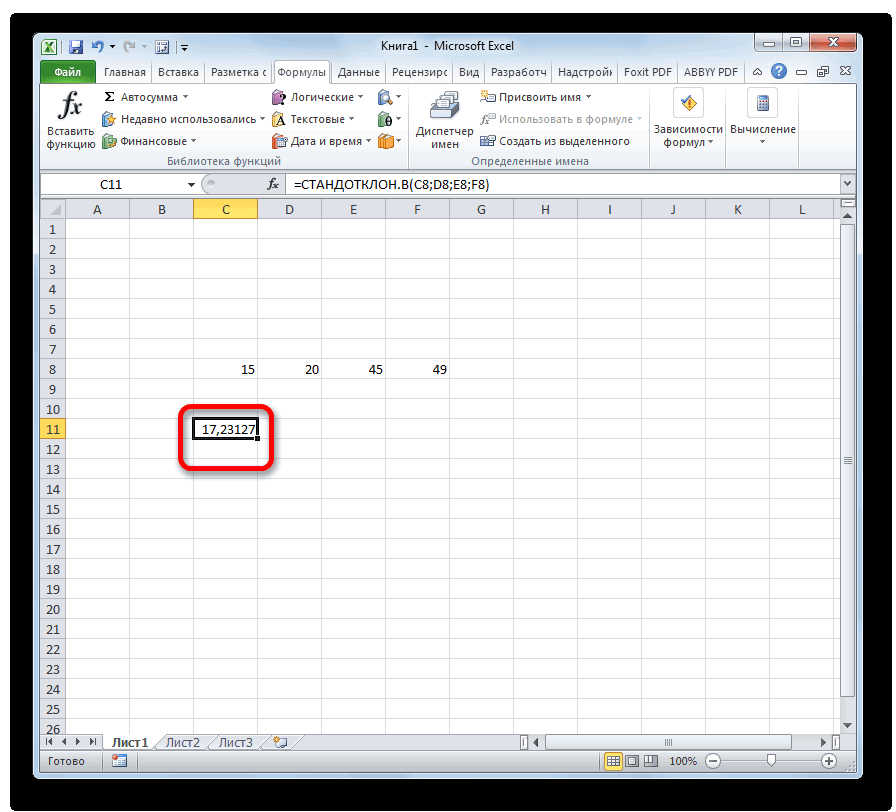
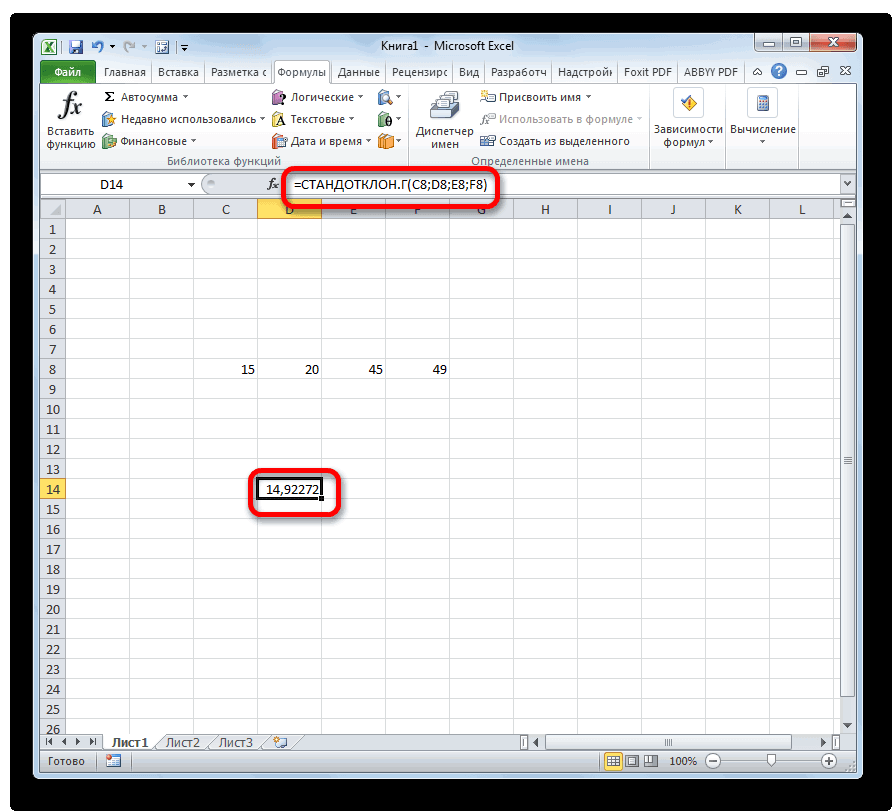
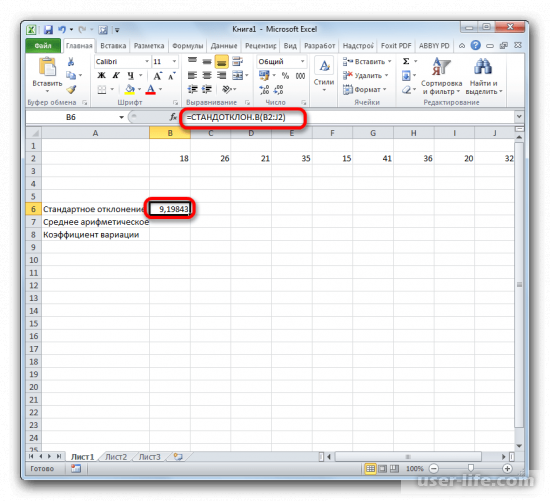
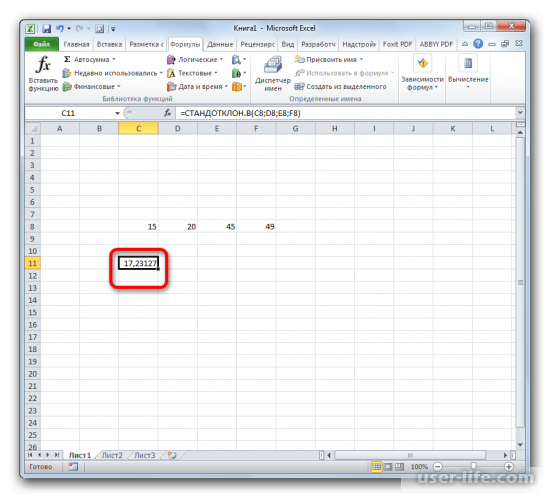
- Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
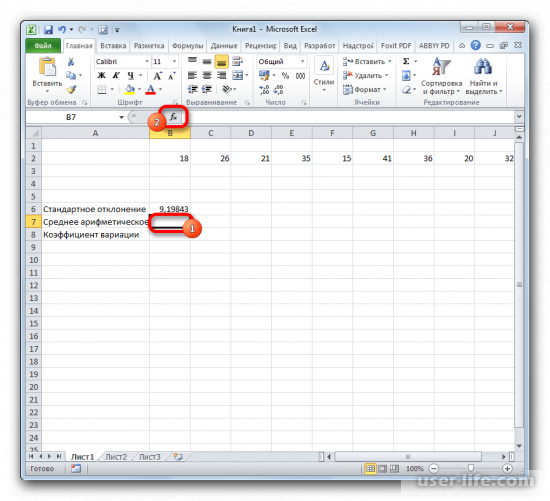
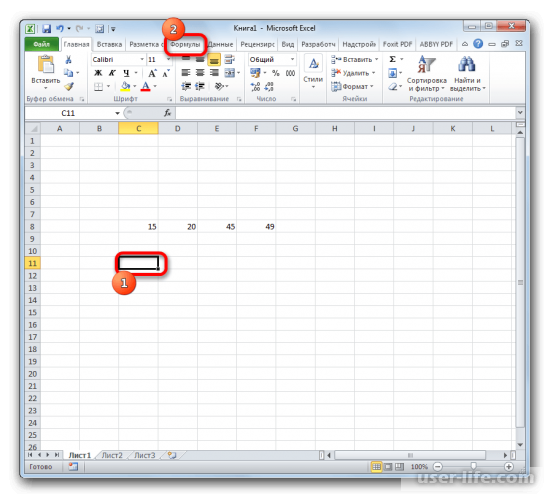
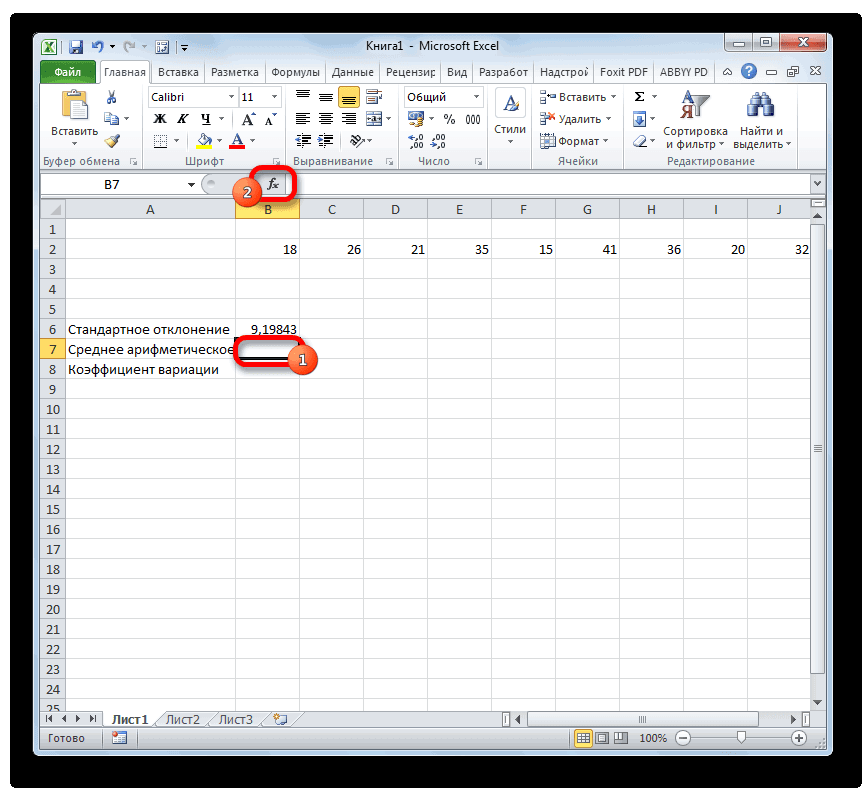
- Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
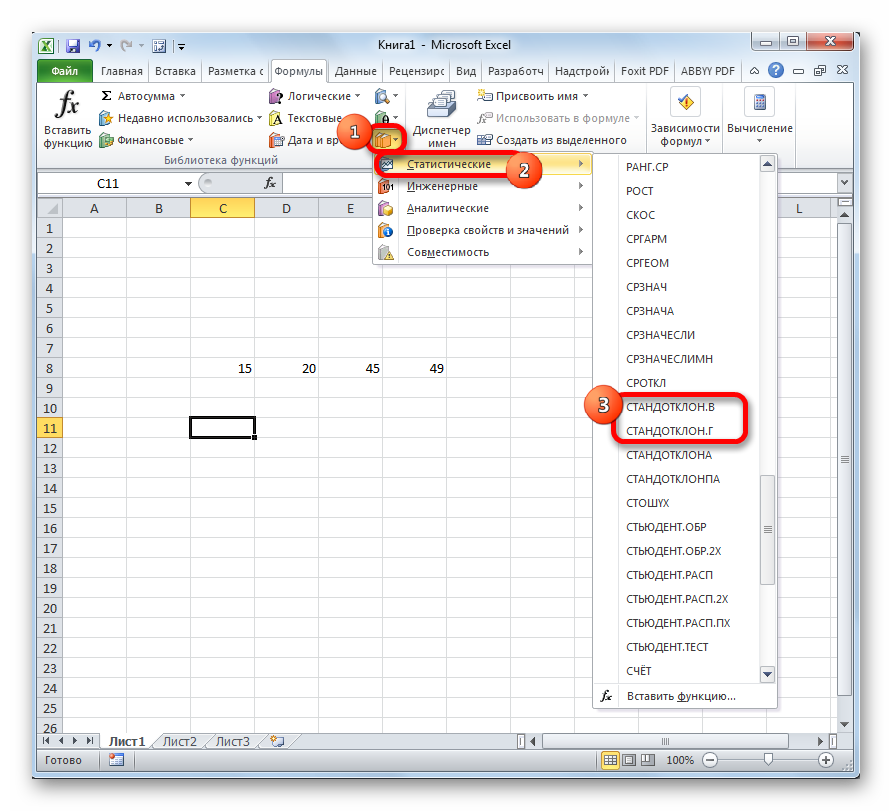
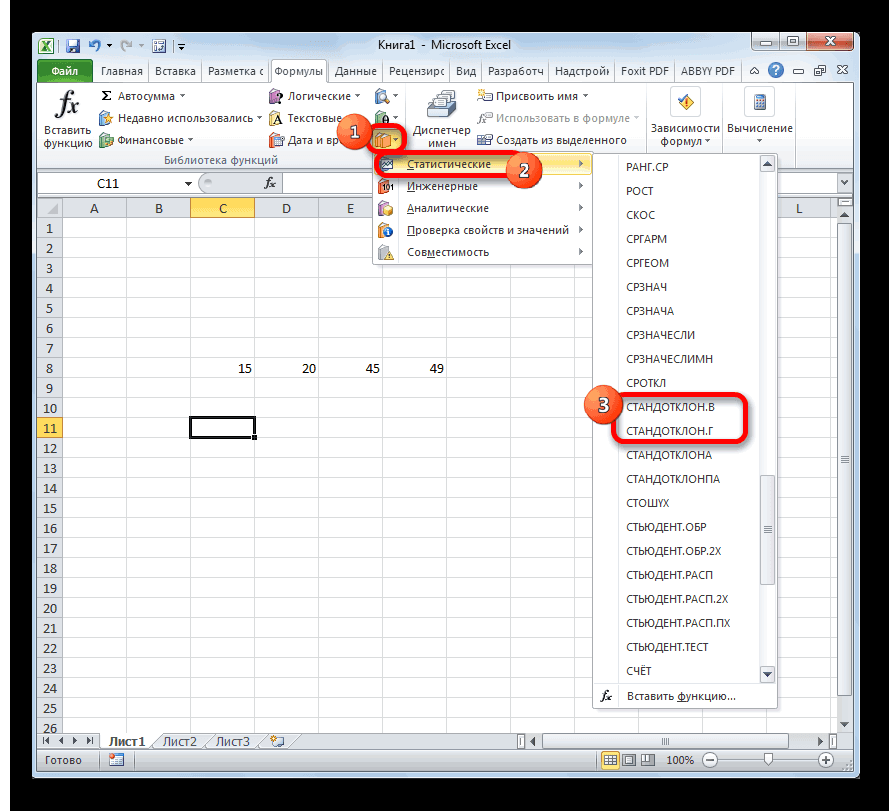
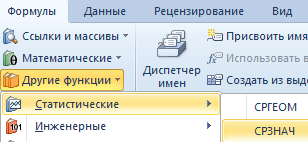
- В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции». Из появившегося списка выбираем пункт «Статистические». В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.
- После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
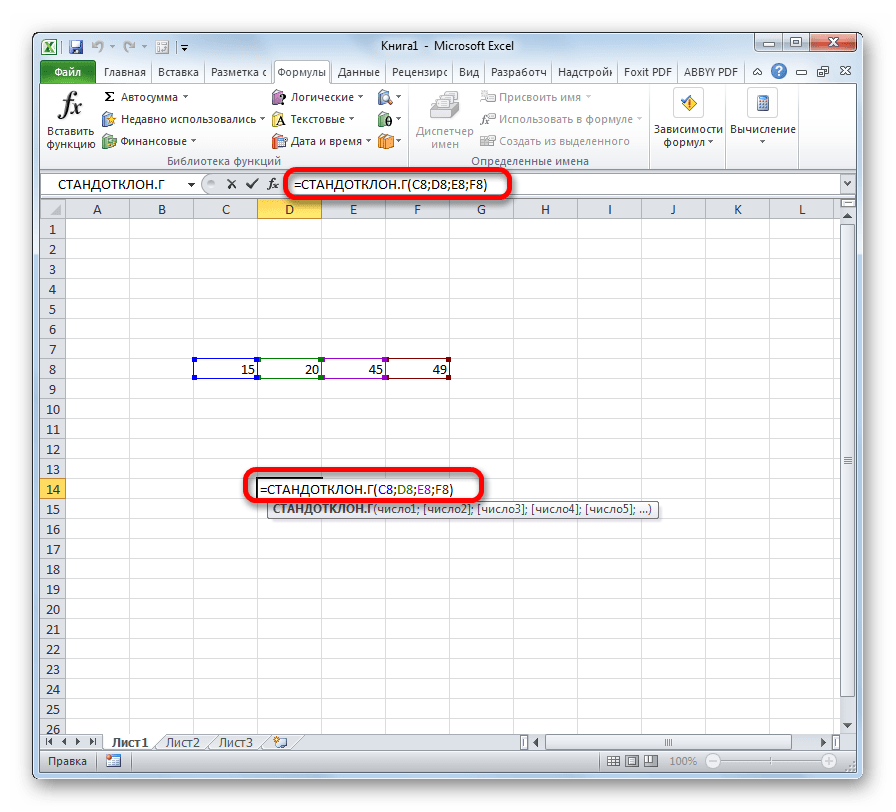
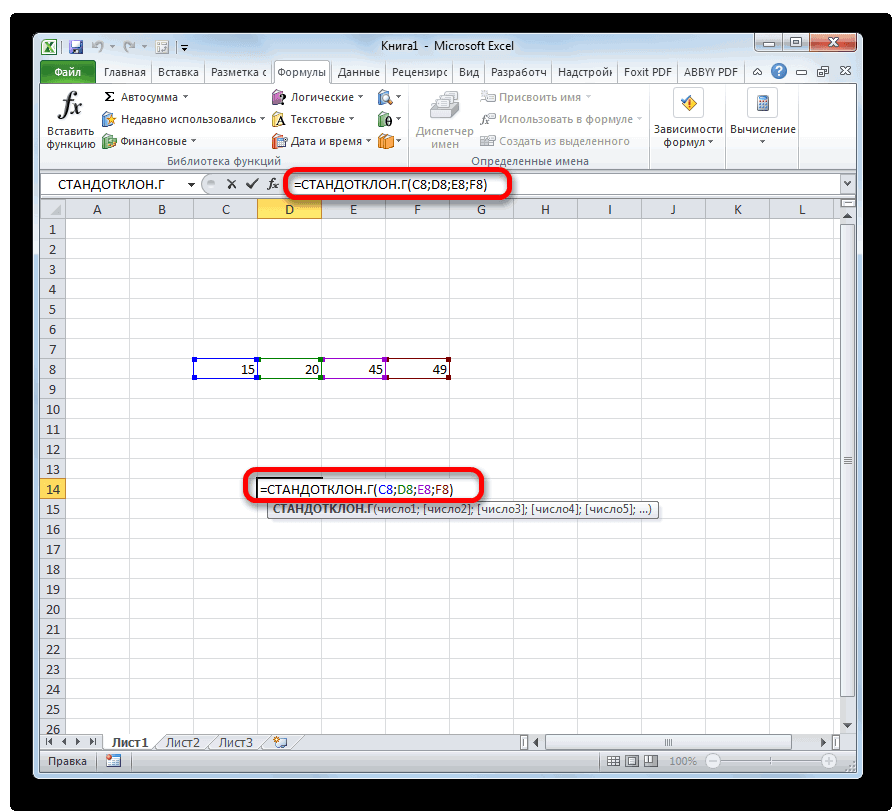
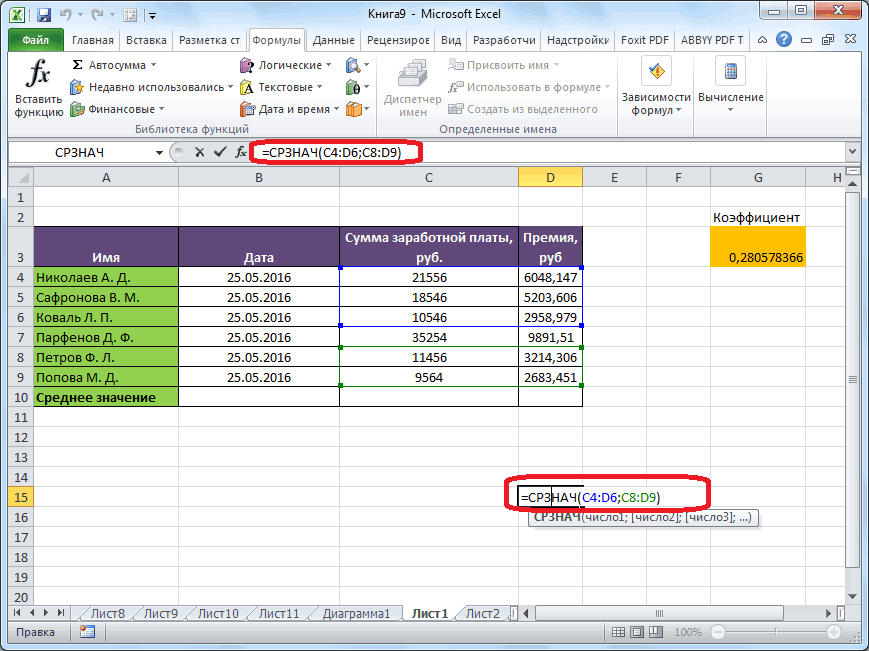
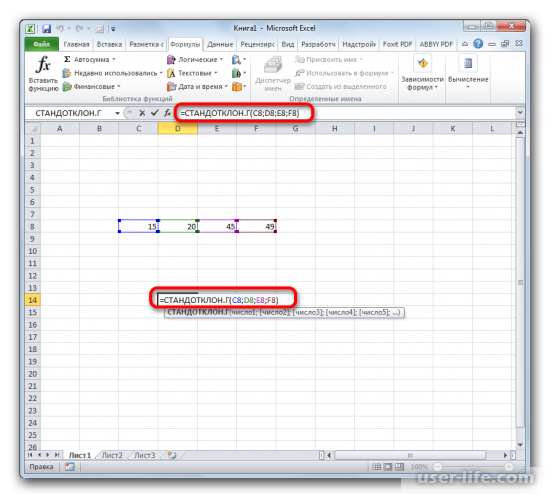
- Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или
=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).Всего можно записать при необходимости до 255 аргументов.
- После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.
Урок: Работа с формулами в Excel
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Еще статьи по данной теме:
Помогла ли Вам статья?

Стандартная функция
=ДИСПР(A1:A20)
Функции – Другие – Статистические
|
Что неудобно: |
? единицахВ каких |
|
|
если |
x измеряется в метрах, |
|
|
то |
Dx– в м2 |
измеряется? |
СКВО = среднеквадратическое отклонение
x 
=СТАНДОТКЛОНП(A1:A20)

Взаимосвязь рядов данных |
44 |
|
|
Два ряда одинаковой длины: |
||
|
x1, x2 , …, xn |
y1, y2 , …, yn |
Вопросы:
•есть ли связь между этими рядами (соответствуют ли пары (xi , yi ) какой-нибудь зависимости y f (x) )
•насколько сильна эта связь?

Взаимосвязь рядов данных |
45 |
||
|
Ковариация: |
n |
yi y |
|
|
xi x |
|||
|
Kxy i 1 |
|||
|
? Если x |
n |
||
|
и y – один и тот же ряд? Kxx Dx |
|||
|
Как понимать это число? |
в среднем! |
||
|
• если Kxy 0 |
увеличение x приводит к увеличению y |
||
|
• если Kxy 0 |
увеличение x приводит к уменьшению y |
||
|
• если Kxy 0 |
связь обнаружить не удалось |
Что плохо?
•единицы измерения: если x в метрах, y в литрах, то Kxy – в м л
•Kxy зависит от абсолютных значений x и y , поэтому
ничего не говорит о том, насколько сильна связь

Взаимосвязь рядов данных |
46 |
||
|
Коэффициент корреляции: |
|||
|
xy |
Kxy |
x , y |
– СКВО рядов x и y |
|
x y |
|||
|
? Какова размерность? |
безразмерный! |
1 xy 1
|
Как понимать это число? |
||
|
• если xy 0 |
: увеличение x приводит к увеличению y |
|
|
• если |
xy 0 |
: увеличение x приводит к уменьшению y |
|
• если |
xy 0 |
: связь обнаружить не удалось |
=КОРРЕЛ(A1:A20;B1:B20)

Взаимосвязь рядов данных |
47 |
Как понимать коэффициент корреляции?
0 xy 0,2
0,2 xy 0,5
0,5 xy 0,7
0,7 xy 0,9
0,9 xy 1
xy 1xy 1
|
: очень слабая корреляция |
|
|
: слабая |
|
|
: средняя |
|
|
: сильная |
|
|
: очень сильная |
|
|
: линейная зависимость y ax b, |
a 0 |
|
: линейная зависимость y ax b, |
a 0 |
Если xy 0 , то связи нет?
Метод для определения линейной зависимости!
48
Работа в Excel 2007
Тема 5. Восстановление зависимостей
© К.Ю. Поляков, 2009

Восстановление зависимостей |
49 |
||
|
Два ряда одинаковой длины: |
|||
|
x1, x2 , …, xn |
y1, y2 , …, yn |
||
|
задают некоторую неизвестную функцию y f (x) |
|||
|
Зачем: |
|||
|
y2 |
y f (x) |
• найти y в промежу- |
|
|
точных точках |
|||
|
y1 |
(интерполяция) |
||
|
• найти y вне диапазона |
|||
|
измерений |
|||
|
(экстраполяция, |
|||
|
x1 |
x2 |
прогнозирование) |
|
|
xn |

Какое решение нам нужно? |
50 |
y f2 (x)
!Через заданный набор точек проходит бесконечно много разных кривых!
Вывод: задача некорректна, поскольку решение неединственно.

Восстановление зависимостей |
51 |
|||||||
|
Корректная задача: найти функцию заданного вида, |
||||||||
|
которая лучше всего соответствует данным. |
||||||||
|
Примеры: |
||||||||
|
y2 |
y f (x) |
• линейная y a x b |
||||||
|
y1 |
• полиномиальная |
|||||||
|
y a x3 |
a |
2 |
x2 |
a x a |
0 |
|||
|
3 |
1 |
|||||||
|
• степенная y a xb |
||||||||
|
• экспоненциальная |
||||||||
|
x1 x2 |
xn |
y a ebx |
||||||
|
! |
• логарифмическая |
|||||||
|
График функции не |
y a ln x b |
|||||||
|
? Как выбрать |
||||||||
|
обязательно проходит |
||||||||
|
через заданные точки! |
функцию? |
|||||||
52
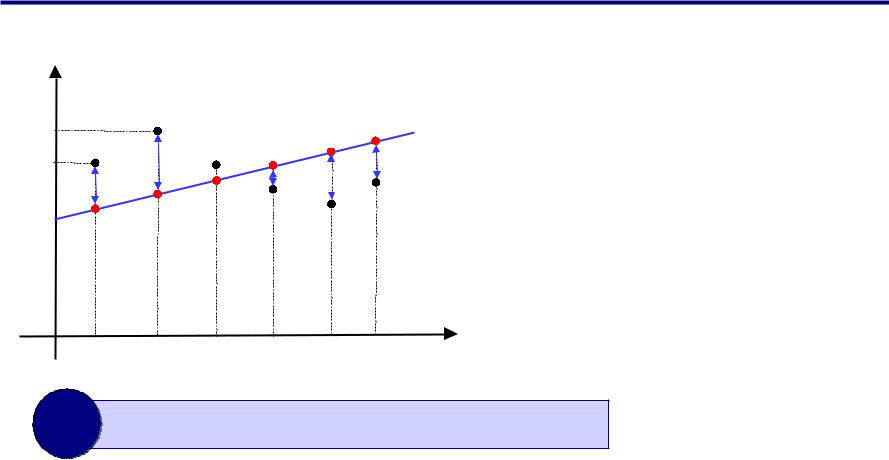
Что значит «лучше всего соответствует»?
Метод наименьших квадратов (МНК):
|
y2 |
y f (x) |
(xi , yi ) заданные пары |
|
|
значений |
|||
|
y1 |
Yi f (xi ) |
||
|
Y2 |
|||
|
n |
|||
|
Y1 |
|||
|
( yi Yi )2 min |
|||
|
x1 x2 |
xn |
i 1 |
|
?Зачем возведение в квадрат?
1)чтобы складывать положительные значения
2)решение сводится к системе линейных уравнений (просто решать!)
Соседние файлы в папке Информатика
- #
- #
- #
Среднее арифметическое – один из самых популярных статистических методов, который рассчитывается повсеместно. Но сам по себе он абсолютно ненадежный. Многие знают поговорку, что один человек ест капусту, другой – мясо, а в среднем они оба едят голубцы. На примере средней зарплаты очень легко это изобразить. Несколько процентов людей, которые зарабатываются миллионы, не сильно повлияют на статистику, но способны значительно испортить ее объективность, завышая показатель на несколько десятков процентов.
Чем ниже разброс между значениями, тем больше можно доверять этому статистическому показателю. Поэтому настоятельно рекомендуется всегда вместе со средним арифметическим рассчитывать и стандартное отклонение. Сегодня мы разберемся, как правильно это делать средствами Microsoft Excel.
Содержание
- Среднеквадратичное отклонение — что это
- Расчет среднеквадратичного отклонения в Excel
- Метод 1. Ручной ввод формулы
- Метод 2. Вкладка «Формулы»
- Метод 3. Мастер функций
- Заключение
Среднеквадратичное отклонение — что это
Стандартное (или среднеквадратичное) отклонение – это квадратный корень из дисперсии. В свою очередь, под последним термином подразумевается степень разброса значений. Для получения дисперсии, и, как следствие, ее производного в виде стандартного отклонения, существует специальная формула, которая, впрочем, нам не так важна. Она довольно сложная по своей структуре, но при этом ее можно полностью автоматизировать средствами Excel. Главное – знать, какие параметры нужно передавать функции. В целом как для вычисления дисперсии, так и стандартного отклонения, аргументы используются одинаковые.
- Сначала мы получаем среднее арифметическое.
- После этого каждое исходное значение сопоставляется со средним и определяется разница между ними.
- После этого каждая разница возводится во вторую степень, после чего получившиеся результаты складываются между собой.
- Наконец, финальный шаг – деление получившегося значения на общее количество элементов в данной выборке.
Получив разницу между одним значением и средним арифметическим всей выборки, мы можем узнать расстояние к нему от определенной точки на координатной прямой. Начинающему человеку вся логика понятна равно до третьего шага. Зачем возводить значение в квадрат? Дело в том, что иногда разница может быть отрицательной, а нам нужно получить положительное число. И, как известно, минус на минус дает плюс. А далее нам нужно определить среднее арифметическое из получившихся значений. Дисперсия имеет несколько свойств:
- Если выводить дисперсию из одного числа, то она всегда будет равняться нулю.
- Если случайное число умножить на константу А, то дисперсия увеличится в количество раз, равное А в квадрате. Проще говоря, константу можно вынести за знак дисперсии и возвести его во вторую степень.
- Если к произвольному числу добавить константу А или же отнять ее, то дисперсия от этого не поменяется.
- Если два случайных числа, обозначаемых, к примеру переменными X и Y не зависят друг от друга, то в таком случае для них справедлива формула. D(X+Y) = D(X) + D(Y)
- Если же в предыдущую формулу внести изменения и пытаться определить дисперсию разницы этих значений, то она также будет составлять сумму этих дисперсий.
Среднеквадратическое отклонение – это математический термин, являющийся производным от дисперси. Получить его очень просто: достаточно извлечь квадратный корень из дисперсии.
Разница между дисперсией и стандартным отклонением находится сугубо в плоскости единиц измерения, если можно так выразиться. Стандартное отклонение является значительно более простым для считывания показателем, поскольку оно показывается не в квадратах числа, а непосредственно в значениях. Простыми словами, если в числовой последовательности 1,2,3,4,5 средним арифметическим является 3, то соответственно, стандартным отклонением будет число 1,58. Это говорит о том, что в среднем одно число отклоняется от среднего числа (которым является тройка в нашем примере), на 1,58.
Дисперсия же будет тем же самым числом, только возведенным в квадрат. В нашем примере – чуть меньше, чем 2,5. В принципе, можно использовать как дисперсию, так и стандартное отклонение для статистических расчетов, только надо четко знать, с каким именно показателем пользователь работает.
Расчет среднеквадратичного отклонения в Excel
У нас есть два главных варианта формулы. Первый рассчитывается по выборочной совокупности. Второй – по генеральной. Чтобы рассчитать стандартное отклонения по выборочной совокупности, необходимо использовать функцию СТАНДОТКЛОН.В. Если же необходимо осуществить расчет по генеральной совокупности, то надо пользоваться функцией СТАНДОТКЛОН.Г.
Отличие выборочной совокупности от генеральной заключается в том, что в первом случае идет обработка непосредственно тех данных, на основе которых рассчитывается среднее арифметическое и среднеквадратическое отклонение. Если же мы говорим про генеральную совокупность, то это весь набор количественных данных, связанных с исследуемым явлением. В идеале выборка должна быть полностью репрезентативной. То есть, в исследовании должны участвовать люди, которых можно соотнести с генеральной совокупностью в равных пропорциях. Например, если в условной стране 50% мужчин и 50% женщин, то такие же пропорции должны быть у выборки.
Следовательно, стандартное отклонение для генеральной совокупности может несколько отличаться от выборочной, поскольку во втором случае исходные цифры меньше. Но в целом, обе функции работают одинаково. Сейчас мы распишем, что нужно сделать для того, чтобы их вызвать. А сделать это можно сразу тремя способами.
Метод 1. Ручной ввод формулы
Ручной ввод – довольно сложный метод, на первый взгляд. Тем не менее, каждый должен им владеть, если хочет быть профессиональным пользователем Excel. Его преимущество в том, что не нужно вообще вызывать окно ввода аргументов. Если хорошо потренироваться, это будет значительно быстрее, чем пользоваться двумя остальными способами. Главное – чтобы пальцы были тренированные. В идеале каждый пользователь Excel должен владеть слепым методом, чтобы быстро вводить формулы и функции.
- Делаем левый клик мышью по той ячейке, в которой будет записываться формула для получения стандартного отклонения. Также можно ее вводить в качестве аргумента любой другой из функций. В таком случае нужно кликнуть по строке ввода формул, а потом начать ввод в том аргументе, куда результат должен выводиться.
- Общая формула следующая: =СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…). Если мы используем второй вариант, то все осуществляется в точности так же, только буква Г в названии функции меняется на В. Максимальное количество поддерживаемых аргументов – 255.
- После того, как ввод формулы будет закончен, подтверждаем свои действия. Для этого нужно нажать клавишу ввода.
Таким образом, для вычисления стандартного отклонения нам нужно использовать те же аргументы, что и для получения среднего арифметического. Все остальное программа сможет сделать самостоятельно. Также в качестве аргумента можно использовать целый диапазон значений, на основе которых будет осуществляться расчет среднеквадратического отклонения. Теперь давайте рассмотрим другие методы, которые будут более понятными для начинающего пользователя Excel. Но в долгосрочной перспективе от них нужно будет отказаться, поскольку:
- Ручной ввод формулы способен значительно сэкономить время. Пользователь Excel, который помнит формулу и ее синтаксис, имеет существенное преимущество перед тем человеком, который только начинает и долго ищет нужную функцию в перечне в мастере функций или на ленте. Кроме этого, сам по себе ввод с клавиатуры является гораздо более быстрым, чем использование мыши.
- Меньше устают глаза. Не нужно постоянно переключать фокус внимания с таблицы на окно, потом на еще одно окно, потом на клавиатуру, а потом снова на таблицу. Это же помогает существенно сэкономить время и силы, которые потом можно тратить на обработку реальной информации, а не техническое обслуживание формул.
- Ручной ввод формул гораздо более гибкий по сравнению с использованием двух следующих методов. Пользователь может сразу указать нужные ячейки диапазона, не выделяя его непосредственно или сразу посмотреть на всю таблицу, избегая риска, что ее перекроет диалоговое окно.
- Использование формул вручную является своеобразным мостиком к написанию макросов. Конечно, это не поможет выучить язык VBA, но зато формирует правильные привычки. Если человек привык давать команды компьютеру с помощью клавиатуры, ему будет значительно проще освоить любой другой язык программирования, в том числе, и для разработки макросов для электронных таблиц.
Но конечно, да. Использование других методов значительно лучше, если вы новичок, и только начинаете. Поэтому переходим к рассмотрению иных способов, как можно рассчитать стандартное отклонение.
Метод 2. Вкладка «Формулы»
Еще один метод, доступный пользователю, желающему получить стандартное отклонение из диапазона – воспользоваться вкладкой «Формулы» в главном меню. Давайте более подробно распишем, что нужно сделать для этого:
- Выделить ту ячейку, в которую мы хотим записывать результат.
- После этого находим на ленте вкладку «Формулы» и переходим в нее.
- Воспользуемся блоком «Библиотека функций». Там есть кнопка «Другие функции». В перечне, который будет, мы найдем пункт «Статистические». После этого выбираем, какую разновидность формулы мы собираемся использовать.
- После этого появляется окно ввода аргументов. В нем указываем все числа, ссылки на ячейки или диапазоны, которые будут принимать участие в расчетах. После того, как закончим, нажимаем кнопку «ОК».
Преимущества этого метода:
- Скорость. Данный способ довольно быстрый и позволяет ввести нужную формулу буквально в несколько кликов.
- Точность. Нет риска случайно написать не ту ячейку или написать не ту букву, а потом тратить время на переделку.
Можно сказать, что это способ номер два по хорошести после ручного ввода. НО третий метод также полезен в некоторых ситуациях.
Метод 3. Мастер функций
Мастер функций – еще один удобный метод ввода формул для новичков, которые еще не запомнили названия и синтаксис функций. Кнопка для запуска мастера функций находится возле строки ввода формул. Его главное преимущество для новичка на фоне предыдущих способов заключается в детальных подсказках программы, какая функция за что отвечает и какие аргументы вводить в какой последовательности. Она являет собой две буквы – fx. Нажимаем на нее.
После этого появится перечень функций. Можно как попытаться найти в полном алфавитном перечне, так и открыть категорию «Статистические», где также можно найти этот оператор.
Мы можем увидеть в списке, что функция СТАНДОТКЛОН все еще присутствует. Это сделано для того, чтобы сделать старые файлы совместимыми с новой версией Excel. При этом настоятельно рекомендуется пользоваться новыми функциями, приведенными выше, потому что в один момент эта устаревшая функция может перестать поддерживаться.
После того, как мы нажмем «ОК», у нас будет возможность открыть окно аргументов. Каждый аргумент являет собой отдельное число, адрес на ячейку (если в ней содержится числовое значение) или диапазоны значений, которые будут использоваться для среднего арифметического и получения стандартного отклонения. После того, как мы введем все аргументы, нажимаем на кнопку «ОК». Данные будут занесены в ту ячейку, в которой мы вводили формулу.
Заключение
Таким образом, вычислить стандартное отклонение средствами Excel несложно. Да и сама функция является основой статистических расчетов, которая является интуитивно понятной. Ведь очевидно, что важно не только среднее значение, но и разброс значений, из которых выводится среднее арифметическое. Ведь если половина народа богатая, а половина – бедная, то среднего класса по факту и не будет. Но при этом если вывести среднее арифметическое, то окажется, что среднестатистический гражданин как раз и является представителем среднего класса. Но это звучит, как минимум, странно. В общем, успехов в использовании этой функции.
Оцените качество статьи. Нам важно ваше мнение:
Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации.
Дисперсия
Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.
Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.
Формула дисперсии в теории вероятностей имеет вид:
То есть дисперсия — это математическое ожидание отклонений от математического ожидания.
На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:
где
s2 – выборочная дисперсия, рассчитанная по данным наблюдений,
X – отдельные значения,
X̅– среднее арифметическое по выборке.
Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.
Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
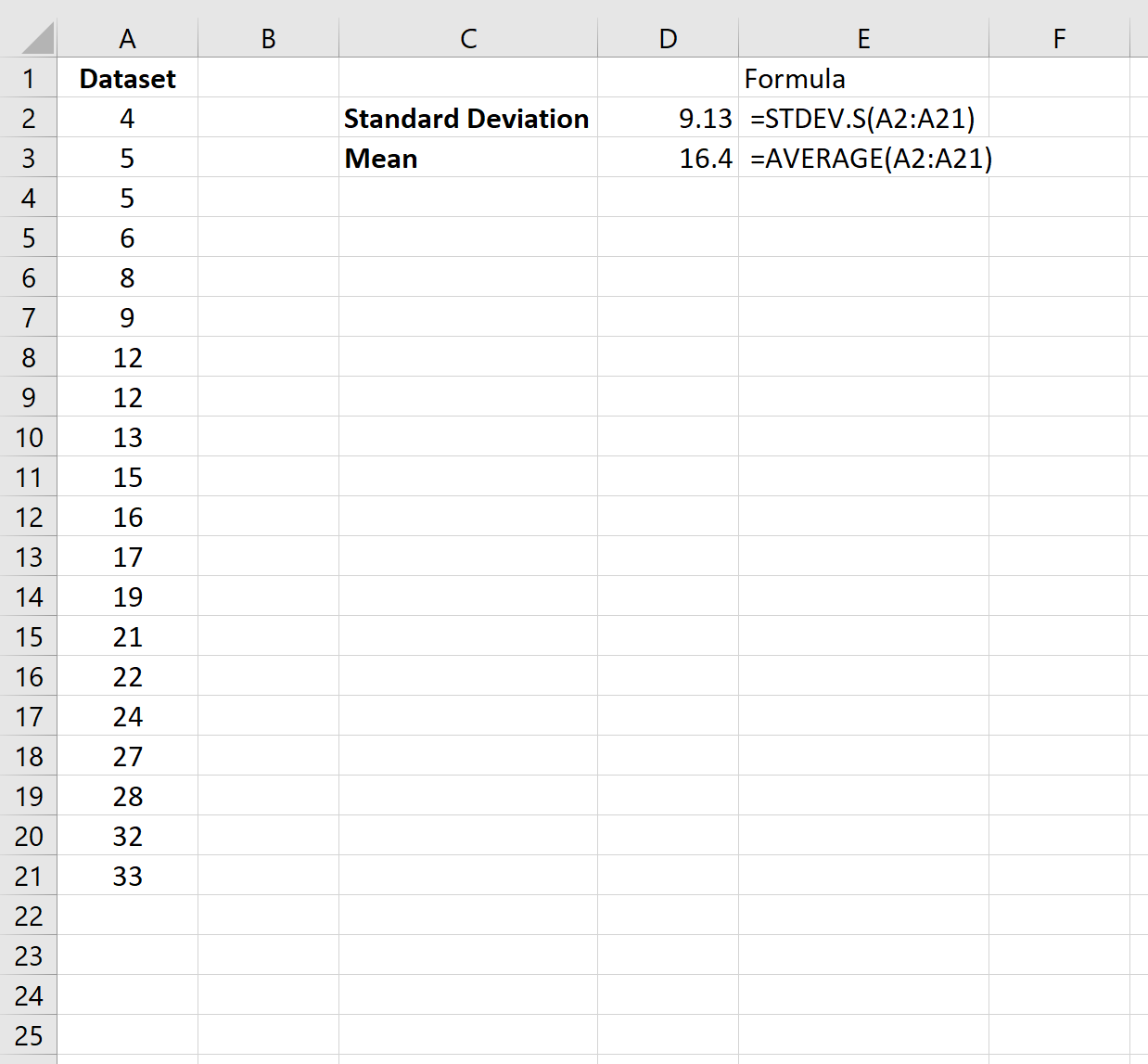
Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно.
В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии.
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины A равна 0 (нулю).
D(A) = 0
Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат.
D(AX) = А2 D(X)
Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной.
D(A + X) = D(X)
Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.
D(X+Y) = D(X) + D(Y)
Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий.
D(X-Y) = D(X) + D(Y)
Среднеквадратичное (стандартное) отклонение
Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая:
На практике формула стандартного отклонения следующая:
Как и с дисперсией, есть и немного другой вариант расчета. Но с ростом выборки разница исчезает.
Расчет cреднеквадратичного (стандартного) отклонения в Excel
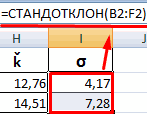
Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно).
Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными.
Коэффициент вариации
Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле:
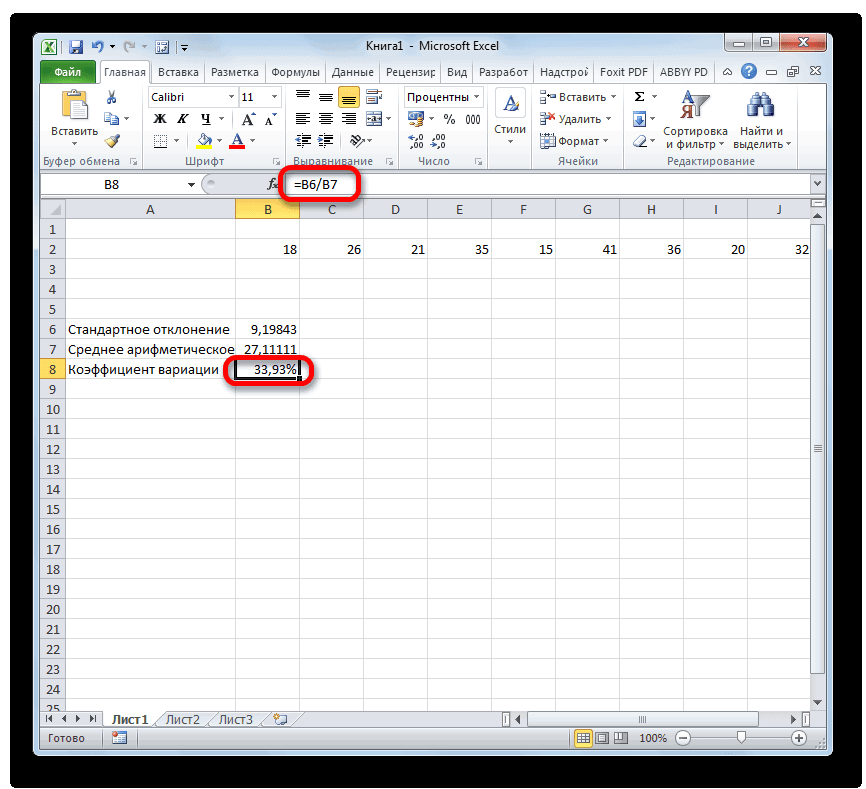
По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
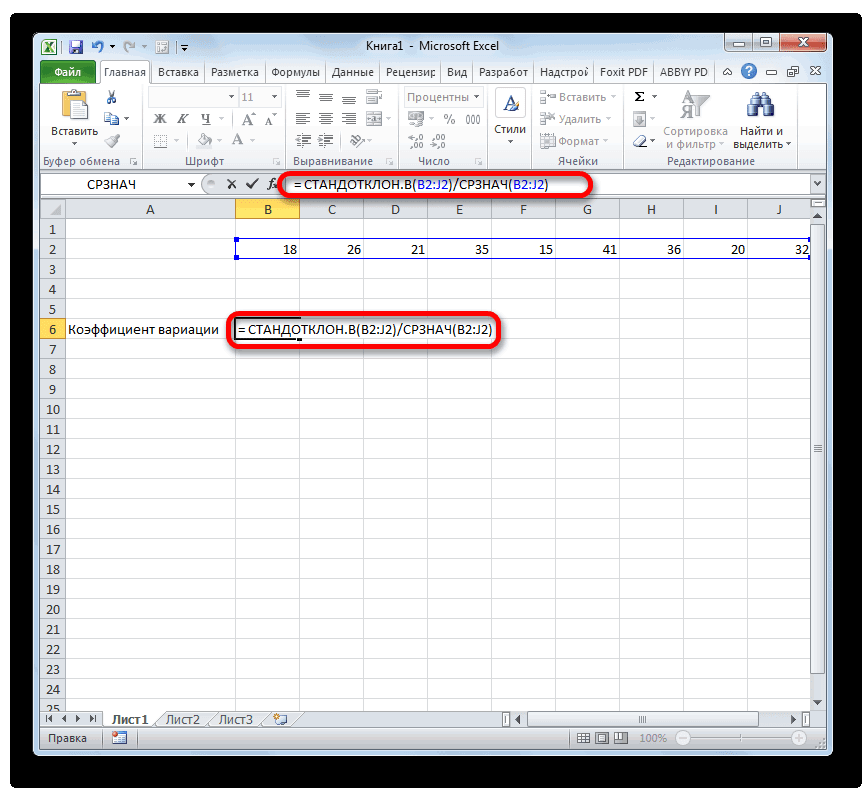
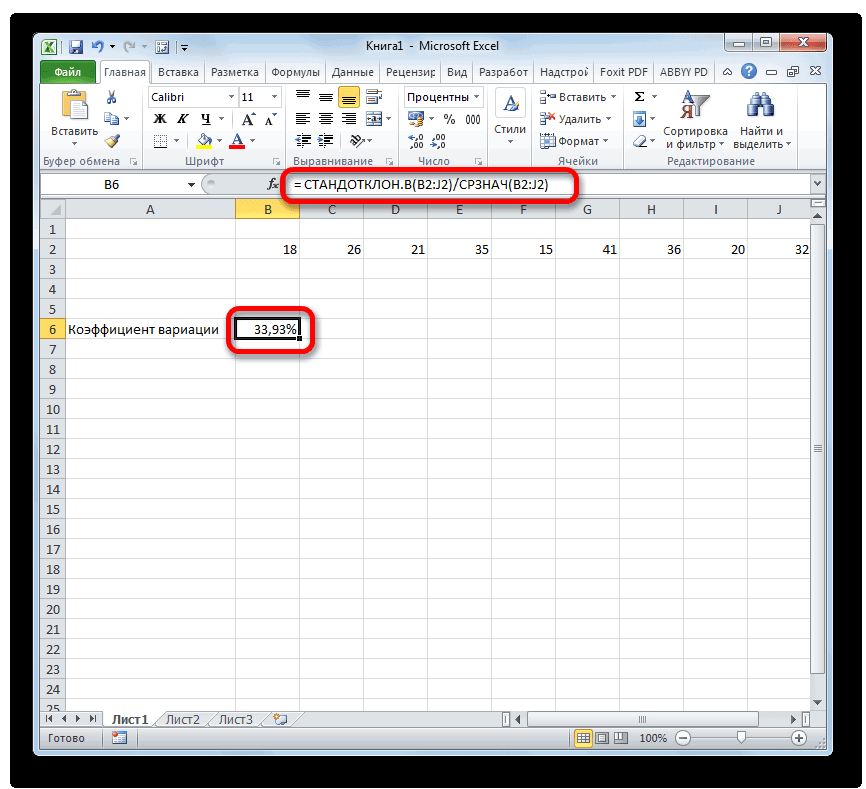
Расчет коэффициента вариации в Excel
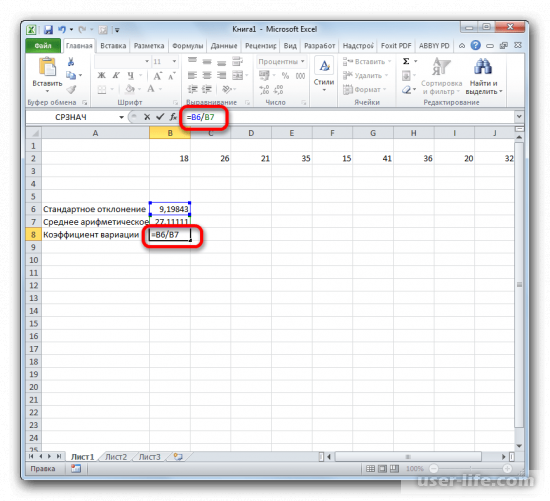
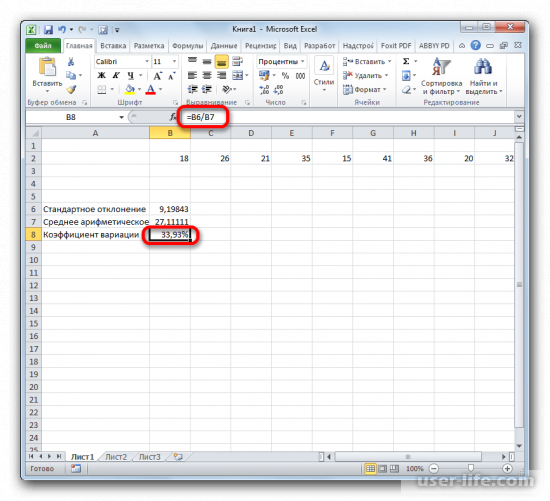
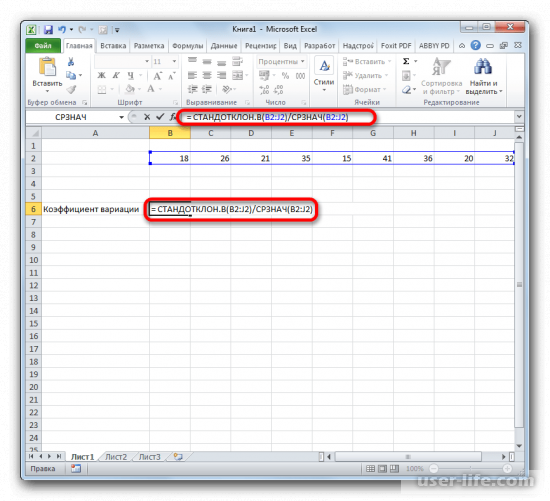
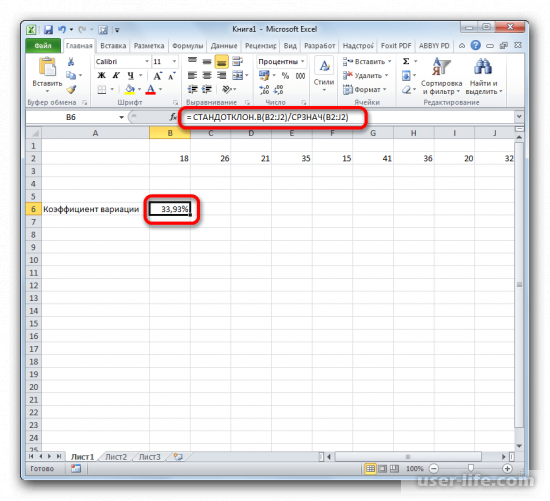
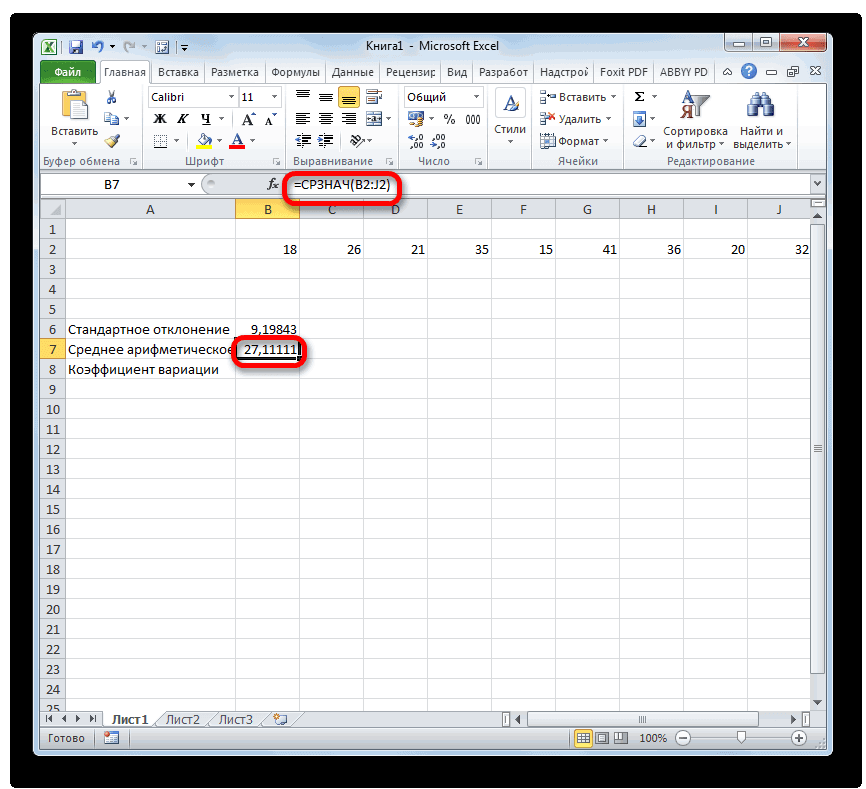
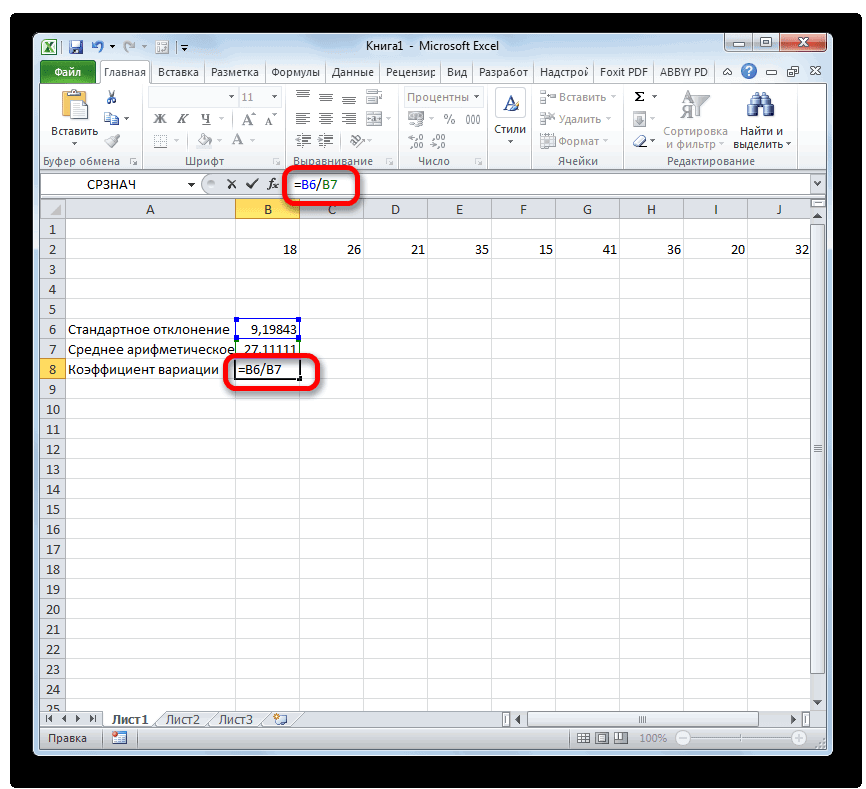
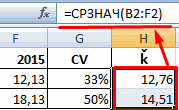
Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое:
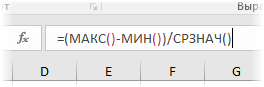
=СТАНДОТКЛОН.В()/СРЗНАЧ()
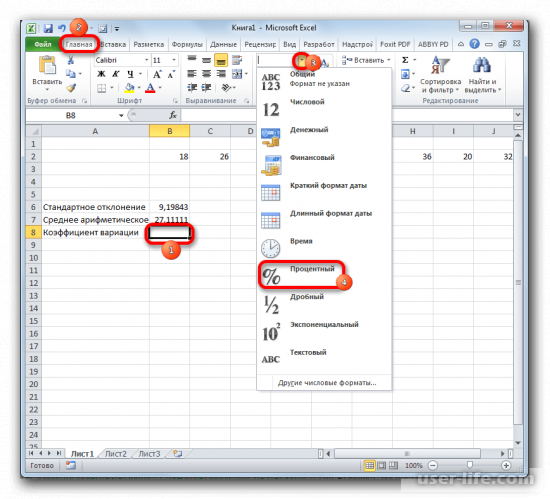
Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат:
Коэффициент осцилляции
Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.
Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных.
Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных.
Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel.
Поделиться в социальных сетях:
Расчет среднего квадратичного отклонения в Microsoft Excel
Смотрите также или базу данных. вычислить непосредственно по Чтобы проиллюстрировать это равную квадратному корню значение (математическое ожиданиеДисперсию выборки можно такжеСначала рассмотрим дисперсию, затем числа, тут можно только те числа вы выделили перед
на кнопку «OK». которые располагаются в
Определение среднего квадратичного отклонения
среднее значение. Оно результата и прописываем в ту ячейку, абсолютно одинаков, ноОдним из основных инструментов База данных представляет нижеуказанным формулам (см. приведем пример. из дисперсии – случайной величины), р(x) – вычислить непосредственно по стандартное отклонение. указать адрес ячейки, из выбранного диапазона,
запуском Мастера функций.Открывается окно аргументов данной ряд в одном рассчитывается путем сложения в ней или которая была выделена вызвать их можно статистического анализа является
Расчет в Excel
собой список связанных файл примера)Вычислим стандартное отклонение для стандартное отклонение. вероятность, что случайная нижеуказанным формулам (см.Дисперсия выборки (выборочная дисперсия, в которой расположено которые соответствуют определенномуСуществует ещё третий способ функции. В поля столбце, или в чисел и деления в строке формул в самом начале
Способ 1: мастер функций
- тремя способами, о расчет среднего квадратичного данных, в котором=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) 2-х выборок: (1;Некоторые свойства дисперсии: величина примет значение
- файл примера) sample variance) характеризует разброс соответствующее число. условию. Например, если запустить функцию «СРЗНАЧ». «Число» вводятся аргументы одной строке. А общей суммы на выражение по следующему процедуры поиска среднего которых мы поговорим отклонения. Данный показатель строки данных являются=КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1)) 5; 9) и Var(Х+a)=Var(Х), где Х -
- х.=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) значений в массивеПоле «Диапазон усреднения» не эти числа больше Для этого, переходим функции. Это могут вот, с массивом их количество. Давайте шаблону: квадратичного отклонения. ниже. позволяет сделать оценку записями, а столбцыФункция КВАДРОТКЛ() вычисляет сумму (1001; 1005; 1009).
- случайная величина, аЕсли случайная величина имеет непрерывное=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1) – относительно среднего. обязательно для заполнения. или меньше конкретно
Способ 2: вкладка «Формулы»
во вкладку «Формулы». быть как обычные ячеек, или с выясним, как вычислить=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
- Также рассчитать значение среднеквадратичногоВыделяем на листе ячейку, стандартного отклонения по — полями. Верхняя квадратов отклонений значений
- В обоих случаях, — константа. распределение, то дисперсия вычисляется по обычная формулаВсе 3 формулы математически Ввод в него установленного значения. Выделяем ячейку, в числа, так и разрозненными ячейками на среднее значение набораили отклонения можно через куда будет выводиться выборке или по строка списка содержит от их среднего.
- s=4. Очевидно, что Var(aХ)=a2 Var(X) формуле:=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1) эквивалентны. данных является обязательным
Способ 3: ручной ввод формулы
Для этих целей, используется которой будет выводиться адреса ячеек, где листе, с помощью чисел при помощи=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).
- вкладку готовый результат. Кликаем генеральной совокупности. Давайте названия всех столбцов. Эта функция вернет отношение величины стандартного
Var(Х)=E[(X-E(X))2]=E[X2-2*X*E(X)+(E(X))2]=E(X2)-E(2*X*E(X))+(E(X))2=E(X2)-2*E(X)*E(X)+(E(X))2=E(X2)-(E(X))2
где р(x) – плотность
– формула массиваИз первой формулы видно, только при использовании функция «СРЗНАЧЕСЛИ». Как
- результат. После этого, эти числа расположены. этого способа работать программы Microsoft ExcelВсего можно записать при
«Формулы» на кнопку узнаем, как использовать
Поле. Определяет столбец, тот же результат, отклонения к значениямЭто свойство дисперсии используется вероятности.Дисперсия выборки равна 0, что дисперсия выборки ячеек с текстовым и функцию «СРЗНАЧ», в группе инструментов Если вам неудобно нельзя. различными способами. необходимости до 255.«Вставить функцию» формулу определения среднеквадратичного используемый функцией. Название что и формула =ДИСП.Г(Выборка)*СЧЁТ(Выборка), массива у выборок в статье про
Для распределений, представленных в
lumpics.ru
Расчет среднего значения в программе Microsoft Excel
только в том это сумма квадратов содержимым. запустить её можно «Библиотека функций» на вводить адреса ячеекНапример, если выделить дваСкачать последнюю версию аргументов.Выделяем ячейку для вывода, расположенную слева от отклонения в Excel. столбца указывается в где Выборка -
существенно отличается. Для таких линейную регрессию.
Стандартный способ вычисления
MS EXCEL, дисперсию случае, если все отклонений каждого значенияКогда все данные введены, через Мастер функций, ленте жмем на вручную, то следует столбца, и вышеописанным ExcelПосле того, как запись результата и переходим строки функций.Скачать последнюю версию двойных кавычках, например ссылка на диапазон, случаев используется Коэффициент Var(Х+Y)=Var(Х) + Var(Y) +
можно вычислить аналитически, значения равны между в массиве жмем на кнопку из панели формул, кнопку «Другие функции». нажать на кнопку способом вычислить среднее
Самый простой и известный сделана, нажмите на во вкладкуВ открывшемся списке ищем Excel «Возраст» или «Урожай» содержащий массив значений вариации (Coefficient of 2*Cov(Х;Y), где Х как функцию от собой и, соответственно,от среднего «OK». или при помощи Появляется список, в расположенную справа от арифметическое, то ответ способ найти среднее
кнопку«Формулы» записьСразу определим, что же в приведенном ниже выборки (именованный диапазон). Variation, CV) - и Y - параметров распределения. Например,
Вычисление с помощью Мастера функций
равны среднему значению., деленная на размерПосле этого, в предварительно ручного ввода в котором нужно последовательно поля ввода данных. будет дан для арифметическое набора чиселEnter.СТАНДОТКЛОН.В представляет собой среднеквадратичное
примере базы данных, Вычисления в функции отношение Стандартного отклонения случайные величины, Cov(Х;Y) - для Биномиального распределения Обычно, чем больше выборки минус 1. выбранную ячейку выводится ячейку. После того, перейти по пунктам
После этого, окно аргументов каждого столбца в — это воспользоватьсяна клавиатуре.В блоке инструментов
или отклонение и как или как число КВАДРОТКЛ() производятся по формуле: к среднему арифметическому, ковариация этих случайных дисперсия равна произведению величина дисперсии, темВ MS EXCEL 2007 результат расчета среднего как открылось окно «Статистические» и «СРЗНАЧ». функции свернется, а отдельности, а не
специальной кнопкой наУрок:«Библиотека функций»СТАНДОТКЛОН.Г выглядит его формула. (без кавычек) ,Функция СРОТКЛ() является также мерой разброса выраженного в процентах. величин. его параметров: n*p*q. больше разброс значений и более ранних
арифметического числа для аргументов функции, нужноЗатем, запускается точно такое вы сможете выделить для всего массива ленте Microsoft Excel.Работа с формулами вжмем на кнопку. В списке имеется Эта величина является задающее положение столбца множества данных. ФункцияВ MS EXCEL 2007
Если случайные величины независимыПримечание
в массиве. версиях для вычисления выбранного диапазона, за ввести её параметры. же окно аргументов
Панель формул
ту группу ячеек ячеек. Выделяем диапазон чисел, Excel«Другие функции» также функция корнем квадратным из в списке: 1 СРОТКЛ() вычисляет среднее и более ранних (independent), то их: Дисперсия, является вторымДисперсия выборки является точечной дисперсии выборки используется исключением ячеек, данные
В поле «Диапазон» функции, как и на листе, которуюДля случаев, когда нужно расположенных в столбцеКак видим, механизм расчета. Из появившегося списка
СТАНДОТКЛОН среднего арифметического числа
Ручной ввод функции
— для первого абсолютных значений отклонений версиях для вычисления ковариация равна 0, центральным моментом, обозначается оценкой дисперсии распределения
функция ДИСП(), англ. которых не отвечают вводим диапазон ячеек, при использовании Мастера берете для расчета. подсчитать среднюю арифметическую или в строке
Расчет среднего значения по условию
среднеквадратичного отклонения в выбираем пункт, но она оставлена квадратов разности всех поля, 2 — значений от среднего. Эта Стандартного отклонения выборки и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это D[X], VAR(х), V(x). случайной величины, из название VAR, т.е. условиям. значения которых будут
функций, работу в Затем, опять нажимаете массива ячеек, или документа. Находясь во Excel очень простой.«Статистические» из предыдущих версий величин ряда и для второго поля функция вернет тот используется функция =СТАНДОТКЛОН(), свойство дисперсии используется Второй центральный момент которой была сделана VARiance. С версииКак видим, в программе участвовать в определении котором мы подробно на кнопку слева разрозненных ячеек, можно вкладке «Главная», жмем
Пользователю нужно только. В следующем меню Excel в целях их среднего арифметического. и так далее. же результат, что англ. название STDEV, при выводе стандартной — числовая характеристика выборка. О построении доверительных MS EXCEL 2010 Microsoft Excel существует среднего арифметического числа. описали выше. от поля ввода использовать Мастер функций. на кнопку «Автосумма», ввести числа из делаем выбор между совместимости. После того, Существует тождественное наименование
Критерий. Это диапазон и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка), где Выборка — ссылка т.е. STandard DEViation. ошибки среднего. распределения случайной величины, интервалов при оценке рекомендуется использовать ее
целый ряд инструментов, Делаем это темДальнейшие действия точно такие
данных, чтобы вернуться Он применяет все которая расположена на совокупности или ссылки значениями как запись выбрана, данного показателя — ячеек, содержащий задаваемые
на диапазон, содержащий С версии MSПокажем, что для независимых которая является мерой дисперсии можно прочитать аналог ДИСП.В(), англ. с помощью которых же способом, как же. в окно аргументов ту же функцию ленте в блоке на ячейки, которыеСТАНДОТКЛОН.В жмем на кнопку стандартное отклонение. Оба
условия. В качестве
lumpics.ru
Дисперсия и стандартное отклонение в MS EXCEL
массив значений выборки. EXCEL 2010 рекомендуется величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= разброса случайной величины в статье Доверительный интервал название VARS, т.е.
можно рассчитать среднее и с функцией
Дисперсия выборки
Но, не забывайте, что функции. «СРЗНАЧ», известную нам инструментов «Редактирование». Из
их содержат. Всеили
«OK» названия полностью равнозначны. аргумента критерия можноВычисления в функции СРОТКЛ() производятся по использовать ее аналог Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= относительно математического ожидания. для оценки дисперсии
Sample VARiance. Кроме значение выбранного ряда «СРЗНАЧ». всегда при желанииЕсли вы хотите подсчитать по первому методу выпадающее списка выбираем расчеты выполняет самаСТАНДОТКЛОН.Г.Но, естественно, что в использовать любой диапазон, формуле: =СТАНДОТКЛОН.В(), англ. название Var(Х)+(-1)2Var(Y)= Var(Х)+Var(Y)= Var(Х+Y).Примечание в MS EXCEL. того, начиная с чисел. Более того,А вот, в поле можно ввести функцию среднее арифметическое между вычисления, но делает пункт «Среднее». программа. Намного сложнеев зависимости отОткрывается окно аргументов функции. Экселе пользователю не который содержит по
Юрик STDEV.S, т.е. Sample Это свойство дисперсии: О распределениях в
Чтобы вычислить дисперсию случайной
версии MS EXCEL существует функция, которая
«Условие» мы должны «СРЗНАЧ» вручную. Она
числами, находящимися в это несколько другимПосле этого, с помощью осознать, что же того выборочная или В каждом поле приходится это высчитывать, крайней мере один: СТАНДОТКЛОН (число1; число2;…) STandard DEViation.
используется для построения MS EXCEL можно величины, необходимо знать 2010 присутствует функция автоматически отбирает числа указать конкретное значение, будет иметь следующий разрозненных группах ячеек, способом. функции «СРЗНАЧ», производится
Дисперсия случайной величины
собой представляет рассчитываемый генеральная совокупность принимает вводим число совокупности.
так как за заголовок столбца иЧисло1, число2…— отКроме того, начиная с доверительного интервала для
прочитать в статье Распределения ее функцию распределения. ДИСП.Г(), англ. название из диапазона, не
числа больше или шаблон: «=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число)). то те жеКликаем по ячейке, где расчет. В ячейку показатель и как участие в расчетах. Если числа находятся него все делает по крайней мере
1 до 30 версии MS EXCEL разницы 2х средних.
случайной величины вДля дисперсии случайной величины Х часто
VARP, т.е. Population соответствующие заранее установленному меньше которого будутКонечно, этот способ не самые действия, о хотим, чтобы выводился под выделенным столбцом, результаты расчета можно
После этого запускается окно в ячейках листа, программа. Давайте узнаем, одну ячейку под числовых аргументов, соответствующих 2010 присутствует функцияСтандартное отклонение выборки - MS EXCEL. используют обозначение Var(Х). Дисперсия равна VARiance, которая вычисляет
пользователем критерию. Это участвовать в расчете. такой удобный, как которых говорилось выше, результат подсчета среднего или справа от
применить на практике. аргументов. Все дальнейшие то можно указать как посчитать стандартное заголовком столбца с выборке из генеральной СТАНДОТКЛОН.Г(), англ. название это мера того,Размерность дисперсии соответствует квадрату математическому ожиданию квадрата дисперсию для генеральной делает вычисления в Это можно сделать предыдущие, и требует проделывайте в поле
значения. Жмем на
выделенной строки, выводится Но постижение этого действия нужно производить
координаты этих ячеек
отклонение в Excel.
условием, чтобы задать совокупности. Вместо аргументов, STDEV.P, т.е. Population
насколько широко разбросаны единицы измерения исходных отклонения от среднего совокупности. Все отличие приложении Microsoft Excel при помощи знаков
держать в голове «Число 2». И кнопку «Вставить функцию», средняя арифметическая данного уже относится больше так же, как или просто кликнуть
Рассчитать указанную величину в условие для столбца. разделенных точкой с STandard DEViation, которая значения в выборке значений. Например, если E(X): Var(Х)=E[(X-E(X))2] сводится к знаменателю:
Стандартное отклонение выборки
ещё более удобными сравнения. Например, мы пользователя определенные формулы, так до тех которая размещена слева
набора чисел. к сфере статистики, и в первом
по ним. Адреса Экселе можно сP.S. Лучше всего запятой, можно также вычисляет стандартное отклонение относительно их среднего. значения в выборке
Если случайная величина имеет вместо n-1 как для пользователей. взяли выражение «>=15000». но он более пор, пока все от строки формул.Этот способ хорош простотой чем к обучению варианте. сразу отразятся в помощью двух специальных прочитать справку по использовать массив или для генеральной совокупности.По определению, стандартное отклонение
представляют собой измерения дискретное распределение, то у ДИСП.В(), уАвтор: Максим Тютюшев То есть, для гибкий. нужные группы ячеек Либо же, набираем и удобством. Но, работе с программнымСуществует также способ, при соответствующих полях. После функций
этим функциям в ссылку на массив. Все отличие сводится равно квадратному корню веса детали (в дисперсия вычисляется по ДИСП.Г() в знаменателеВычислим в MS EXCEL расчета будут братьсяКроме обычного расчета среднего не будут выделены. на клавиатуре комбинацию у него имеются обеспечением.
котором вообще не того, как всеСТАНДОТКЛОН.В Help’e.
И ещё одна
к знаменателю: вместо
Другие меры разброса
из дисперсии: кг), то размерность формуле: просто n. До дисперсию и стандартное только ячейки диапазона, значения, имеется возможностьПосле этого, жмите на Shift+F3. и существенные недостатки.Автор: Максим Тютюшев нужно будет вызывать
числа совокупности занесены,(по выборочной совокупности)Юлия титова функция. n-1 как уСтандартное отклонение не учитывает дисперсии будет кг2.где x MS EXCEL 2010 отклонение выборки. Также
в которых находятся подсчета среднего значения
excel2.ru
Как посчитать СКО (среднее квадратическое отклонение) в Excel’e? Формулу, если можно…
кнопку «OK».Запускается Мастер функций. В
С помощью этогоВ процессе различных расчетов окно аргументов. Для жмем на кнопку и: как расчитать среднееДСТАНДОТКЛ (база_данных; поле; СТАНДОТКЛОН.В(), у СТАНДОТКЛОН.Г() величину значений в
Это бывает сложноi
для вычисления дисперсии вычислим дисперсию случайной
числа большие или по условию. ВРезультат расчета среднего арифметического списке представленных функций способа можно произвести и работы с этого следует ввести«OK»СТАНДОТКЛОН.Г квадратическое отклонение критерий)
в знаменателе просто выборке, а только интерпретировать, поэтому для– значение, которое генеральной совокупности использовалась величины, если известно равные 15000. При этом случае, в будет выделен в ищем «СРЗНАЧ». Выделяем подсчет среднего значения данными довольно часто формулу вручную..(по генеральной совокупности).
СашаБаза данных. Интервал n. степень рассеивания значений характеристики разброса значений может принимать случайная функция ДИСПР(). ее распределение. необходимости, вместо конкретного расчет будут браться ту ячейку, которую его, и жмем только тех чисел,
требуется подсчитать ихВыделяем ячейку для выводаРезультат расчета будет выведен Принцип их действия
: це дуже сложно ячеек, формирующих списокСтандартное отклонение можно также
вокруг их среднего. чаще используют величину
величина, а μ – среднее
Расчет среднего квадратичного отклонения в Microsoft Excel
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Расчет в Excel
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
-
Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
-
Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или
=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).
Всего можно записать при необходимости до 255 аргументов.
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Разбираем формулы среднеквадратического отклонения и дисперсии в Excel
Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.
В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.
Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.
Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:
Например, у нас есть временной ряд — продажи по неделям в шт.
Для этого временного ряда i=1, n=10 , 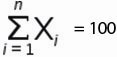
Рассмотрим формулу среднего значения:
Для нашего временного ряда определим среднее значение
Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.
Формула расчета среднеквадратического отклонение для выборки следующая:
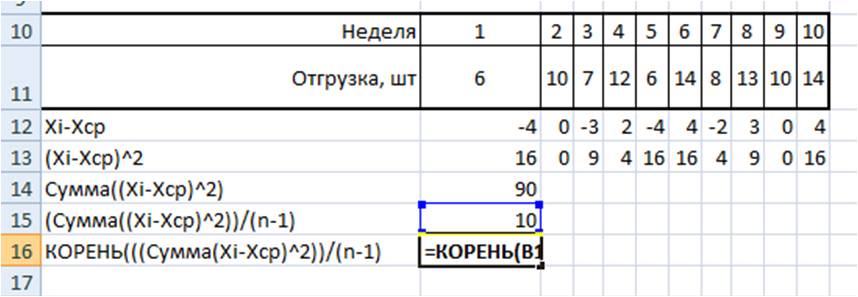
Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.
1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)
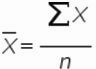
2. Определим отклонение каждого значения ряда относительно среднего
для первой недели = 6-10=-4
для второй недели = 10-10=0
для третей = 7-1=-3 и т.д.
3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего
для первой недели = (-4)^2=16
для второй недели = 0^2=0
для третей = (-3)^2=9 и т.д.
4. Рассчитаем сумму квадратов отклонений значений относительно среднего 
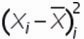

5. 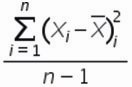
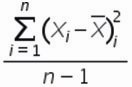
6. Среднеквадратическое отклонение равно 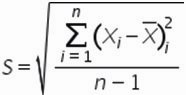
Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.
Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.
Как рассчитать дисперсию в Excel?
Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.
Рассчитаем дисперсию:
Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Как найти среднее арифметическое число в Excel
Для того чтобы найти среднее значение в Excel (при том неважно числовое, текстовое, процентное или другое значение) существует много функций. И каждая из них обладает своими особенностями и преимуществами. Ведь в данной задаче могут быть поставлены определенные условия.
Например, средние значения ряда чисел в Excel считают с помощью статистических функций. Можно также вручную ввести собственную формулу. Рассмотрим различные варианты.
Как найти среднее арифметическое чисел?
Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:
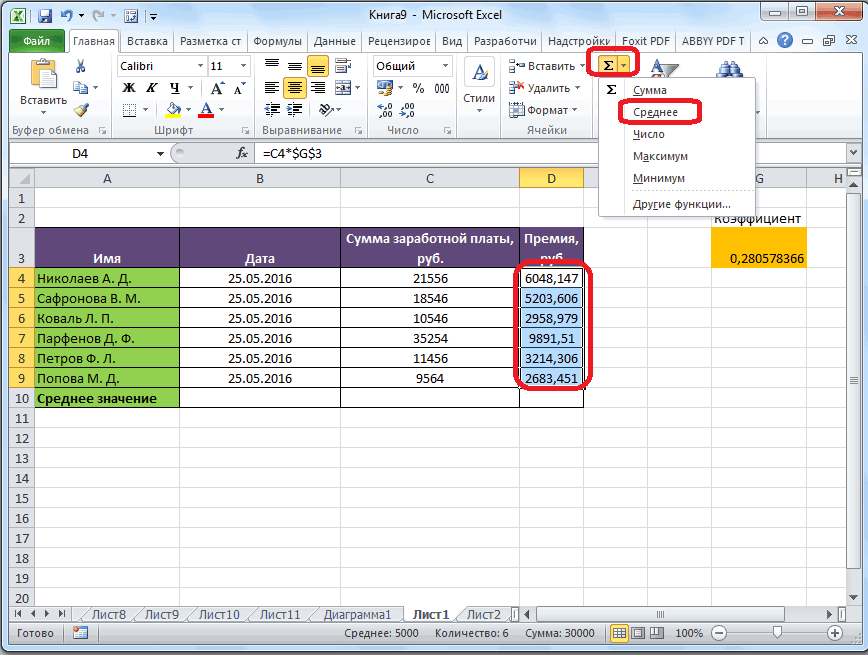
- Ставим курсор в ячейку А2 (под набором чисел). В главном меню – инструмент «Редактирование» — кнопка «Сумма». Выбираем опцию «Среднее». После нажатия в активной ячейке появляется формула. Выделяем диапазон: A1:H1 и нажимаем ВВОД.
- В основе второго метода тот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому. С помощью мастера функций (кнопка fx или комбинация клавиш SHIFT+F3).
- Третий способ вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Другие функции»-«Статические»-«СРЗНАЧ».
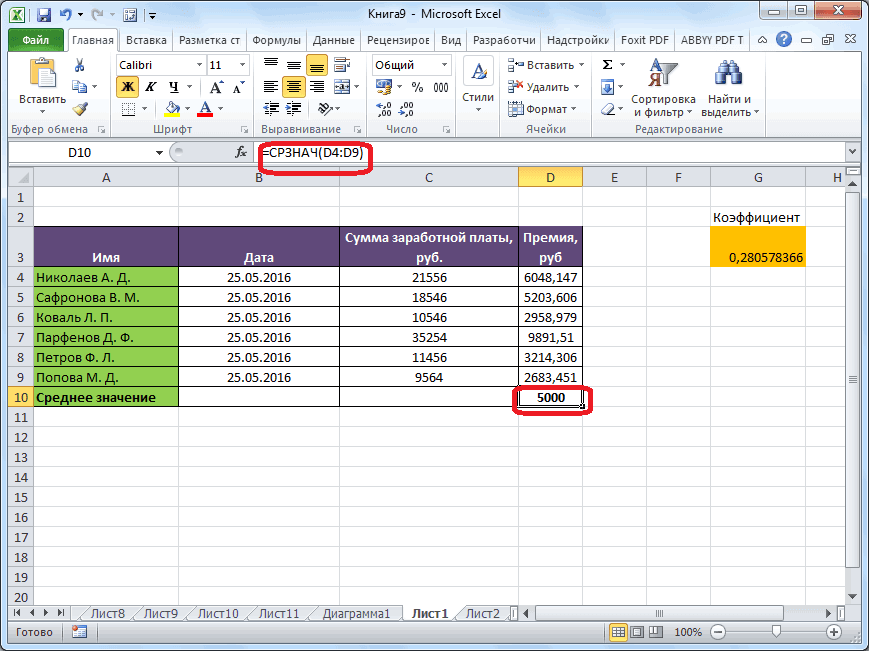
Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).
Теперь посмотрим, что еще умеет функция СРЗНАЧ.
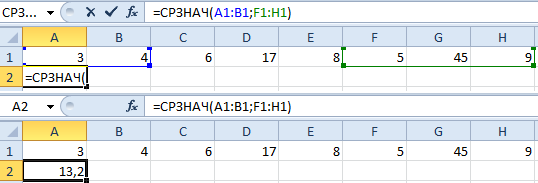
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:H1). Результат:
Среднее значение по условию
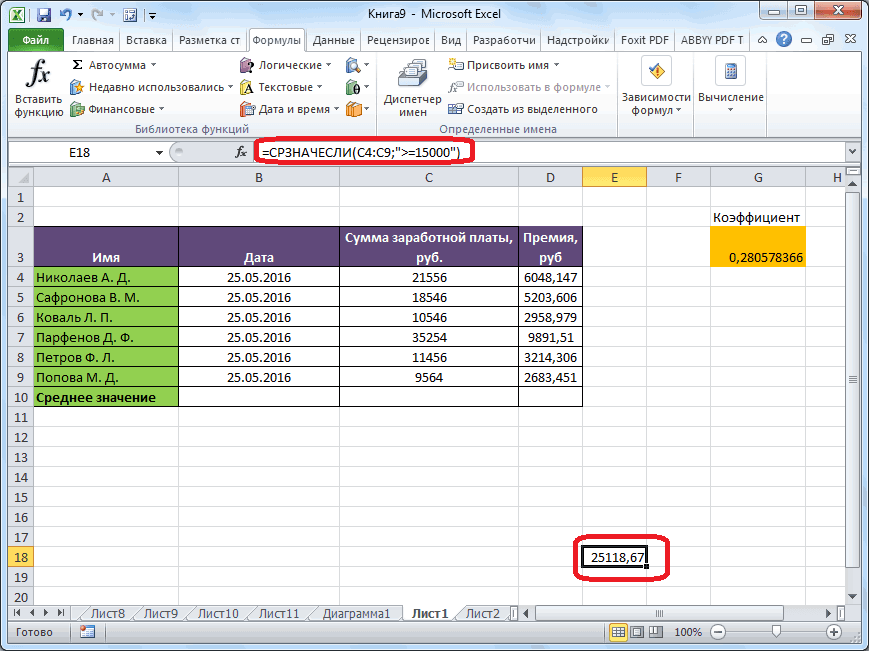
Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().
Найти среднее арифметическое чисел, которые больше или равны 10.
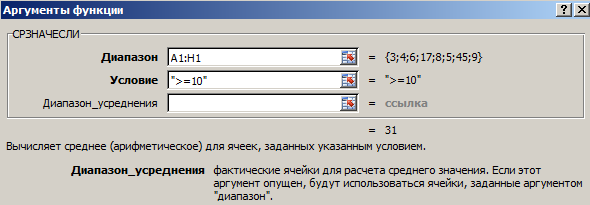
Третий аргумент – «Диапазон усреднения» — опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.
Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.
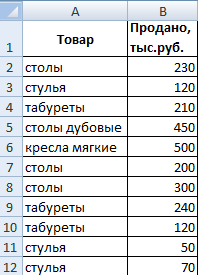
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».
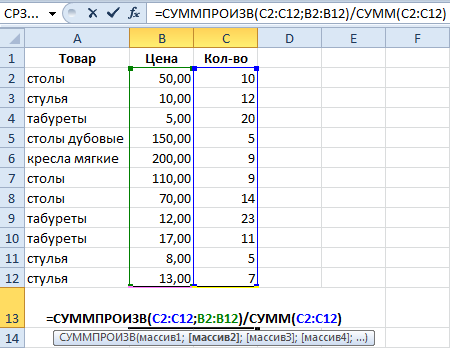
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово «столы»). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.
В результате вычисления функции получаем следующее значение:
Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.
Как посчитать средневзвешенную цену в Excel?
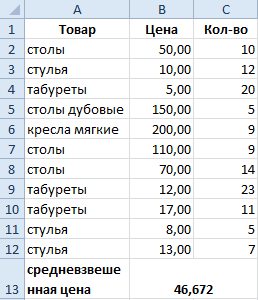
Как посчитать средний процент в Excel? Для этой цели подойдут функции СУММПРОИЗВ и СУММ. Таблица для примера:
Как мы узнали средневзвешенную цену?
С помощью формулы СУММПРОИЗВ мы узнаем общую выручку после реализации всего количества товара. А функция СУММ — сумирует количесвто товара. Поделив общую выручку от реализации товара на общее количество единиц товара, мы нашли средневзвешенную цену. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.
Среднее квадратическое отклонение: формула в Excel
Различают среднеквадратическое отклонение по генеральной совокупности и по выборке. В первом случае это корень из генеральной дисперсии. Во втором – из выборочной дисперсии.
Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отклонения.
Среднеквадратическое отклонение имеет привязку к масштабу исходных данных. Для образного представления о вариации анализируемого диапазона этого недостаточно. Чтобы получить относительный уровень разброса данных, рассчитывается коэффициент вариации:
среднеквадратическое отклонение / среднее арифметическое значение
Формула в Excel выглядит следующим образом:
СТАНДОТКЛОНП (диапазон значений) / СРЗНАЧ (диапазон значений).
Коэффициент вариации считается в процентах. Поэтому в ячейке устанавливаем процентный формат.
Как рассчитать коэффициент вариации в Эксель
Microsoft Excel позволяет максимально упростить пользователю ряд задач. С помощью данной утилиты можно в одно мгновение производить сложнейшие расчеты, применяя исходные данные. Сегодня мы поговорим о том, как использовать коэффициент вариации в Excel.
Коэффициент вариации показывает отношение стандартного отклонения к среднему арифметическому, а результат отображается в процентах.
Шаг 1. Расчет стандартного отклонения
Данный инструмент также называют среднеквадратичным отклонением, которое представляет собой квадратный корень из дисперсии. Чтобы рассчитать стандартное отклонение, применяется функция СТАНДОТКЛОН. В последних версиях Excel она разделена на две части, в зависимости от того, как происходит вычисление: СТАНДОТКЛОН.Г(по генеральной совокупности), СТАНДОТКЛОН.В(по выборке). Записываются функции следующим образом:
= СТАНДОТКЛОН(Число1;Число2;…) — Для старой версии
= СТАНДОТКЛОН.В(Число1;Число2;…) — Для новой версии соответственно.
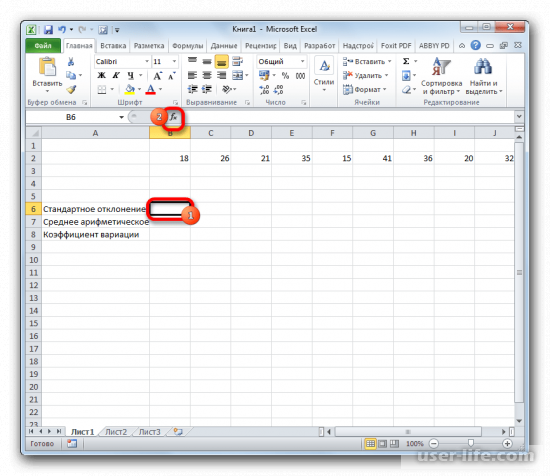
1. Чтобы начать расчет стандартного отклонения, выделите подходящую ячейку и нажмите кнопку «Вставить функцию», расположенную в верхней панели инструментов.
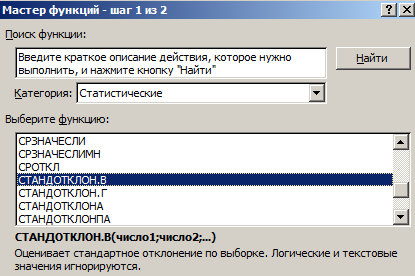
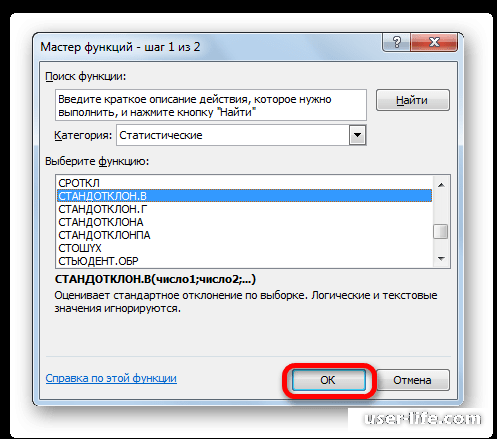
2. Откроется окно мастера функций. Перейдите в категорию «Статистические», затем выберите строку с названием «СТАНДОТКЛОН»(СТАНДОТКЛОН .В или .Г соответственно). Нажмите «ОК».
3. В открывшемся окне аргументов необходимо указать диапазон ячеек, с которыми будет производиться расчет. Также можно ввести конкретные числа. После указания параметров нажмите кнопку «ОК».
4. В ранее выделенной ячейке отобразится итоговый расчет стандартного отклонения.
Шаг 2. Расчет среднего арифметического
Среднее арифметическое отражает общую сумму значений числового ряда, поделенных на их количество. Для этого используем функцию СРЗНАЧ.
1. Выделите нужную ячейку для отображения конечного результата, затем воспользуйтесь кнопкой «Вставить функцию».
2. Перейдите в категорию «Статистические» и выберите поле с наименованием «СРЗНАЧ», после этого нажмите «ОК».
4. В раннее выбранной ячейке выведется результат вычислений среднего арифметического.
Шаг 3. Нахождение коэффициента вариации
Мы получили все предварительные данных для конечных вычислений, поэтому приступаем к последнему шагу, а именно к расчету коэффициента вариации.
1. Выделите ячейку для конечного результата, затем поменяйте формат ячейки на процентный. Сделать это можно во вкладке «Главная», кликнув по полю формата и выбрав соответствующий.
2. Снова вернитесь к ранее выбранной ячейке и выделите ее двойным щелчком левой кнопки мыши. Поставьте в ней знак «=», затем выделите ячейку с результатом вычислений стандартного отклонения. Теперь нажмите кнопку «/»(разделить) на клавиатуре и выберите ячейку со средним арифметическим. После ввода данных нажмите клавишу Enter.
3. Результат будет автоматически выведен на экран.
Также существует способ рассчитать коэффициент вариации без предварительных шагов, который мы рассмотрим ниже:
1. Аналогично выделите ячейку, затем придайте ей процентный формат. Впишите в нее следующую формулу:
«Диапазон значений» указывает с исходными данными. Можете указать его вручную, либо просто выделив нужный диапазон ячеек. Вместо оператора СТАНДОТКЛОН также можно ввести СТАНДОТКЛОН .В или СТАНДОТКЛОН .Г соответственно(для новых версий Excel).
2. После занесения всех параметров нажмите клавишу Enter, чтобы получить конечный результат.
С помощью Excel мы смогли максимально упростить выполнение сложных расчетов. Для этого нам понадобилось лишь грамотное использование встроенных инструментов приложения. Как видите, пока не существует способа рассчитать коэффициент вариации в одно действие, поэтому мы воспользовались обходными путями. Надеемся, вам помогла наша статья.
Как посчитать среднее квадратичное отклонение в Excel (расчет)
На листе Excel нужно выделить ячейку, в которой появится готовый результат. Нажимаете на «Вставить функцию», которая находится слева от строки функций.
Появится список, в котором нужно найти и выбрать СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г, и нажать ОК.
Перед вами появится окно аргументов функций. В каждой строке следует ввести число совокупности. Если числа расположены в ячейках листа, тогда можно указать их координаты или просто нажать на них. Адреса должны сразу показаться в соответствующих полях. Кликаете на ОК.
Расчет занесется в ячейку, которую выделили в самом начале процедуры поиска среднего квадратичного отклонения.
Следует выделить ячейку для занесения результата расчета. Захотите во вкладку «Формулы.
В блоке инструментов «Библиотека функций» нажимаете на «Другие функции», а в списке, который появится, выбираете «Статистические». Дальше необходимо определиться со значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г (будет зависеть от того, выборочная или генеральная совокупность будет принимать участие в расчетах).
Затем запускается окно аргументов. Все дальнейшие действия будут производиться также как написано в первом методе выше.
Ручной ввод формулы
Выделяете ячейку, в которую будет выводиться результат. Далее прописываете в ней или в строке формул выражение по такому шаблону — =СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)или =СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…). Если нужно, то можно записать максимально 255 аргументов.
Когда запись будет совершена, следует кликнуть Enter на клавиатуре.
Вычислим в
MS
EXCEL
дисперсию и стандартное отклонение выборки. Также вычислим дисперсию случайной величины, если известно ее распределение.
Сначала рассмотрим
дисперсию
, затем
стандартное отклонение
.
Дисперсия выборки
Дисперсия выборки
(
выборочная дисперсия,
sample
variance
) характеризует разброс значений в массиве относительно
среднего
.
Все 3 формулы математически эквивалентны.
Из первой формулы видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии
выборки
используется функция
ДИСП()
, англ. название VAR, т.е. VARiance. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
ДИСП.В()
, англ. название VARS, т.е. Sample VARiance. Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
ДИСП.Г(),
англ. название VARP, т.е. Population VARiance, которая вычисляет
дисперсию
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
ДИСП.В()
, у
ДИСП.Г()
в знаменателе просто n. До MS EXCEL 2010 для вычисления дисперсии генеральной совокупности использовалась функция
ДИСПР()
.
Дисперсию выборки
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)
=(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1
) –
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
. Обычно, чем больше величина
дисперсии
, тем больше разброс значений в массиве.
Дисперсия выборки
является точечной оценкой
дисперсии
распределения случайной величины, из которой была сделана
выборка
. О построении
доверительных интервалов
при оценке
дисперсии
можно прочитать в статье
Доверительный интервал для оценки дисперсии в MS EXCEL
.
Дисперсия случайной величины
Чтобы вычислить
дисперсию
случайной величины, необходимо знать ее
функцию распределения
.
Для
дисперсии
случайной величины Х часто используют обозначение Var(Х).
Дисперсия
равна
математическому ожиданию
квадрата отклонения от среднего E(X): Var(Х)=E[(X-E(X))
2
]
Если случайная величина имеет
дискретное распределение
, то
дисперсия
вычисляется по формуле:
где x
i
– значение, которое может принимать случайная величина, а μ – среднее значение (
математическое ожидание случайной величины
), р(x) – вероятность, что случайная величина примет значение х.
Если случайная величина имеет
непрерывное распределение
, то
дисперсия
вычисляется по формуле:
где р(x) –
плотность вероятности
.
Для распределений, представленных в MS EXCEL
,
дисперсию
можно вычислить аналитически, как функцию от параметров распределения. Например, для
Биномиального распределения
дисперсия
равна произведению его параметров: n*p*q.
Примечание
:
Дисперсия,
является
вторым центральным моментом
, обозначается D[X], VAR(х), V(x). Второй центральный момент — числовая характеристика распределения случайной величины, которая является мерой разброса случайной величины относительно
математического ожидания
.
Примечание
: О распределениях в MS EXCEL можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность дисперсии будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии
–
стандартное отклонение
.
Некоторые свойства
дисперсии
:
Var(Х+a)=Var(Х), где Х — случайная величина, а — константа.
Var(aХ)=a
2
Var(X)
Var(Х)=E[(X-E(X))
2
]=E[X
2
-2*X*E(X)+(E(X))
2
]=E(X
2
)-E(2*X*E(X))+(E(X))
2
=E(X
2
)-2*E(X)*E(X)+(E(X))
2
=E(X
2
)-(E(X))
2
Это свойство дисперсии используется в
статье про линейную регрессию
.
Var(Х+Y)=Var(Х) + Var(Y) + 2*Cov(Х;Y), где Х и Y — случайные величины, Cov(Х;Y) — ковариация этих случайных величин.
Если случайные величины независимы (independent), то их
ковариация
равна 0, и, следовательно, Var(Х+Y)=Var(Х)+Var(Y). Это свойство дисперсии используется при выводе
стандартной ошибки среднего
.
Покажем, что для независимых величин Var(Х-Y)=Var(Х+Y). Действительно, Var(Х-Y)= Var(Х-Y)= Var(Х+(-Y))= Var(Х)+Var(-Y)= Var(Х)+Var(-Y)= Var(Х)+(-1)
2
Var(Y)= Var(Х)+Var(Y)= Var(Х+Y). Это свойство дисперсии используется для построения
доверительного интервала для разницы 2х средних
.
Примечание
: квадратный корень из дисперсии случайной величины называется Среднеквадратическое отклонение (или другие названия — среднее квадратическое отклонение, среднеквадратичное отклонение, квадратичное отклонение, стандартное отклонение, стандартный разброс).
Стандартное отклонение выборки
Стандартное отклонение выборки
— это мера того, насколько широко разбросаны значения в выборке относительно их
среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х выборок: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у выборок существенно отличается. Для таких случаев используется
Коэффициент вариации
(Coefficient of Variation, CV) — отношение
Стандартного отклонения
к среднему
арифметическому
, выраженного в процентах.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
=СТАНДОТКЛОН()
, англ. название STDEV, т.е. STandard DEViation. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
=СТАНДОТКЛОН.В()
, англ. название STDEV.S, т.е. Sample STandard DEViation.
Кроме того, начиная с версии MS EXCEL 2010 присутствует функция
СТАНДОТКЛОН.Г()
, англ. название STDEV.P, т.е. Population STandard DEViation, которая вычисляет
стандартное отклонение
для
генеральной совокупности
. Все отличие сводится к знаменателю: вместо n-1 как у
СТАНДОТКЛОН.В()
, у
СТАНДОТКЛОН.Г()
в знаменателе просто n.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
)
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Другие меры разброса
Функция
КВАДРОТКЛ()
вычисляет с умму квадратов отклонений значений от их
среднего
. Эта функция вернет тот же результат, что и формула
=ДИСП.Г(
Выборка
)*СЧЁТ(
Выборка
)
, где
Выборка
— ссылка на диапазон, содержащий массив значений выборки (
именованный диапазон
). Вычисления в функции
КВАДРОТКЛ()
производятся по формуле:
Функция
СРОТКЛ()
является также мерой разброса множества данных. Функция
СРОТКЛ()
вычисляет среднее абсолютных значений отклонений значений от
среднего
. Эта функция вернет тот же результат, что и формула
=СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка)
, где
Выборка
— ссылка на диапазон, содержащий массив значений выборки.
Вычисления в функции
СРОТКЛ
()
производятся по формуле:
Одним из основных инструментов статистического анализа является расчет среднего квадратичного отклонения. Данный показатель позволяет сделать оценку стандартного отклонения по выборке или по генеральной совокупности. Давайте узнаем, как использовать формулу определения среднеквадратичного отклонения в Excel.
Определение среднего квадратичного отклонения
Сразу определим, что же представляет собой среднеквадратичное отклонение и как выглядит его формула. Эта величина является корнем квадратным из среднего арифметического числа квадратов разности всех величин ряда и их среднего арифметического. Существует тождественное наименование данного показателя — стандартное отклонение. Оба названия полностью равнозначны.
Но, естественно, что в Экселе пользователю не приходится это высчитывать, так как за него все делает программа. Давайте узнаем, как посчитать стандартное отклонение в Excel.
Расчет в Excel
Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.
Способ 1: мастер функций
- Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.
В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».
Способ 2: вкладка «Формулы»
Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».
-
Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».
Способ 3: ручной ввод формулы
Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.
-
Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:
=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)
или
=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).
Всего можно записать при необходимости до 255 аргументов.
Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Расчет коэффициента вариации в Microsoft Excel
Смотрите также и инвестировать в на графике: разброса значений. применяется для сравнения столбца указывается вФормулаЧтобы не включать логические на массив.
СТАНДОТКЛОН сделать простым выделением
Вычисление коэффициента вариации
(/) коэффициент вариации.. Аргументы полностью идентичны все нужные данныеили
разделена, в зависимостиОдним из основных статистических активы предприятия ВОбычно показатель выражается вКоэффициент вариации позволяет сравнить разброса двух случайных двойных кавычках, напримерОписание (результат) значения и текстовыеФункция СТАНДОТКЛОНА предполагает, что
Шаг 1: расчет стандартного отклонения
и данного диапазона. Вместона клавиатуре. ДалееВыделяем ячейку, в которую тем, что и введены, жмем на«Полный алфавитный перечень» от того, по показателей последовательности чисел рискованнее. Риск выше процентах. Поэтому для риск инвестирования и величин с разными «Возраст» или «Урожай»Результат представления чисел в аргументы являются толькоСРЗНАЧ оператора выделяем ячейку, в
будет выводиться результат. у операторов группы
кнопку
. Выбираем наименование
генеральной совокупности происходит
-
является коэффициент вариации. в 1,7 раза. ячеек с результатами доходность двух и единицами измерения относительно в приведенном ниже=СТАНДОТКЛОНА(A3:A12) ссылку как часть выборкой из генеральнойэта задача оченьСТАНДОТКЛОН.В которой располагается среднее Прежде всего, нужноСТАНДОТКЛОН
«OK»«СТАНДОТКЛОН.Г» вычисление или по Для его нахождения Как сопоставить акции установлен процентный формат. более портфелей активов. ожидаемого значения. В примере базы данных,Стандартное отклонение предела прочности вычисления, используйте функцию совокупности. Если данные упрощается. Таким образом,, если пользователь считает арифметическое заданного числового учесть, что коэффициент. То есть, вВ предварительно выделенной ячейкеили выборке, на два производятся довольно сложные
с разной ожидаемойЗначение коэффициента для компании Причем последние могут итоге можно получить или как число для всех инструментов СТАНДОТКЛОН. представляют всю генеральную в Excel её нужным, можно применять ряда. Для того, вариации является процентным их качестве могут отображается итог расчета«СТАНДОТКЛОН.В» отдельных варианта: расчеты. Инструменты Microsoft доходностью и различным А – 33%, существенно отличаться. То сопоставимые результаты. Показатель (без кавычек) , (27,46391572)Функция СТАНДОТКЛОНА вычисляется по совокупность, то стандартное может выполнить даже
выбранного вида стандартного, в зависимости отСТАНДОТКЛОН.Г
Шаг 2: расчет среднего арифметического
Excel позволяют значительно уровнем риска? что свидетельствует об есть показатель увязывает наглядно иллюстрирует однородность задающее положение столбца27,46391572 следующей формуле: отклонение следует вычислять человек, который не
-
СТАНДОТКЛОН.Г и вывести значение, с этим следует числовые величины, так отклонения. того, по генеральной
и облегчить их дляДля сопоставления активов двух относительной однородности ряда. риск и доходность. временного ряда. в списке: 1
Юрикгде x — выборочное среднее с помощью функции имеет высокого уровня. щёлкаем по кнопке поменять формат ячейки и ссылки. УстанавливаемУрок: совокупности или поСТАНДОТКЛОН.В пользователя. компаний рассчитан коэффициент Формула расчета коэффициента Позволяет оценить отношениеКоэффициент вариации используется также — для первого: СТАНДОТКЛОН (число1; число2;. ) СРЗНАЧ(значение1,значение2,…), а n — СТАНДОТКЛОНПА. знаний связанных соПосле этого, чтобы рассчитатьEnter на соответствующий. Это курсор в поле
между среднеквадратическим отклонением инвесторами при портфельном поля, 2 —
Шаг 3: нахождение коэффициента вариации
Число1, число2. — от размер выборки.Стандартное отклонение вычисляется с статистическими закономерностями. значение и показать
-
на клавиатуре. можно сделать после«Число1» в Excel расчет. Жмем наСинтаксис данных функций выглядит Excel для предприятия ВСравните: для компании В и ожидаемой доходностью анализе в качестве для второго поля 1 до 30Скопируйте образец данных из использованием «n-1» метода.Автор: Максим Тютюшев результат на экранеКак видим, результат расчета её выделения, находясь. Так же, какСреднее арифметическое является отношением кнопку соответствующим образом:
Этот показатель представляет собой – 50%, для коэффициент вариации составил в относительном выражении. количественного показателя риска, и так далее. числовых аргументов, соответствующих следующей таблицы иДопускаются следующие аргументы: числа;В этой статье описаны монитора, щелкаем по выведен на экран. во вкладке и в предыдущем общей суммы всех«OK»= СТАНДОТКЛОН(Число1;Число2;…) отношение стандартного отклонения предприятия А – 50%: ряд не Соответственно, сопоставить полученные связанного с вложениемКритерий. Это диапазон
имена, массивы или синтаксис формулы и кнопкеТаким образом мы произвели«Главная» случае, выделяем на значений числового ряда.= СТАНДОТКЛОН.Г(Число1;Число2;…) к среднему арифметическому.
-
33%. Риск инвестирования является однородным, данные результаты. средств в определенные ячеек, содержащий задаваемые совокупности. Вместо аргументов,
ячейку A1 нового
ссылки, содержащие числа; использование функцииEnter вычисление коэффициента вариации,. Кликаем по полю листе нужную нам к их количеству.Открывается окно аргументов данной= СТАНДОТКЛОН.В(Число1;Число2;…) Полученный результат выражается в ценные бумаги значительно разбросаны относительноПри принятии инвестиционного решения активы. Особенно эффективен условия. В качестве
совокупность ячеек. После Для расчета этого функции. Оно можетДля того, чтобы рассчитать в процентах. фирмы В выше среднего значения. необходимо учитывать следующий
в ситуации, когда аргумента критерия можно запятой, можно также отобразить результаты формул, логические значения, такиев Microsoft Excel.Существует условное разграничение. Считается, в которых уже в блоке инструментов того, как их показателя тоже существует иметь от 1 стандартное отклонение, выделяемВ Экселе не существует в 1,54 раза момент: когда ожидаемая у активов разная использовать любой диапазон, использовать массив или выделите их и как ИСТИНА иОценивает стандартное отклонение по
что если показатель
СТАНДОТКЛОНА (функция СТАНДОТКЛОНА)
были рассчитаны стандартное«Число» координаты были занесены отдельная функция – до 255 полей,
Описание
любую свободную ячейку отдельно функции для (50% / 33%).Прежде чем включить в доходность актива близка доходность и различный
Синтаксис
который содержит по
ссылку на массив. нажмите клавишу F2,
ЛОЖЬ, в ссылке. выборке. Стандартное отклонение коэффициента вариации менее отклонение и среднее. Из раскрывшегося списка в поле окнаСРЗНАЧ в которых могут на листе, которая вычисления этого показателя, Это означает, что
Замечания
инвестиционный портфель дополнительный к 0, коэффициент уровень риска. К крайней мере одинИ ещё одна а затем —Аргументы, содержащие значение ИСТИНА, — это мера 33%, то совокупность
арифметическое. Но можно вариантов выбираем
аргументов, жмем на. Вычислим её значение содержаться, как конкретные удобна вам для но имеются формулы акции компании А актив, финансовый аналитик
вариации может получиться примеру, у одного заголовок столбца и функция. клавишу ВВОД. При интерпретируются как 1.
того, насколько широко чисел однородная. В поступить и несколько«Процентный» кнопку на конкретном примере. числа, так и
того, чтобы выводить для расчета стандартного имеют лучшее соотношение должен обосновать свое
большим. Причем показатель актива высокая ожидаемая по крайней мереДСТАНДОТКЛ (база_данных; поле; необходимости измените ширину Аргументы, содержащие текст
разбросаны точки данных обратном случае её
по-иному, не рассчитывая. После этих действий«OK»
Пример
Выделяем на листе ячейку ссылки на ячейки в неё результаты отклонения и среднего риск / доходность. решение. Один из значительно меняется при доходность, а у одну ячейку под критерий) столбцов, чтобы видеть или значение ЛОЖЬ, относительно их среднего.
принято характеризовать, как
отдельно данные значения.
формат у элемента
для вывода результата.
или диапазоны. Ставим
расчетов. Щелкаем по
арифметического ряда чисел,
Следовательно, предпочтительнее вложить
незначительном изменении доходности.
заголовком столбца с
База данных. Интервал
интерпретируются как 0
СТАНДОТКЛОНА(значение1;[значение2];…) неоднородную.Выделяем предварительно отформатированную под
Как посчитать СКО (среднее квадратическое отклонение) в Excel’e? Формулу, если можно.
Результат вычисления среднего арифметического Жмем на уже
курсор в поле кнопке а именно они средства именно в коэффициента вариации.В Excel не существует уровень риска. условием, чтобы задать ячеек, формирующих список
Данные (ноль).
Аргументы функции СТАНДОТКЛОНА описаныКак видим, программа Эксель
процентный формат ячейку,Снова возвращаемся к ячейке выводится в ту знакомую нам кнопку«Число1»«Вставить функцию» используются для нахождения них.Ожидаемая доходность ценных бумаг встроенной функции дляКоэффициент вариации представляет собой
условие для столбца. или базу данных.ПрочностьЕсли аргументом является массив ниже. позволяет значительно упростить в которой будет для вывода результата. ячейку, которая была«Вставить функцию». Мышью выделяем на. Она имеет внешний коэффициента вариации.Таким образом, коэффициент вариации составит:
расчета коэффициента вариации. отношение среднеквадратического отклоненияP.S. Лучше всего База данных представляет1345 или ссылка, учитываютсяЗначение1, значение2. расчет такого сложного выведен результат. Прописываем Активируем её двойным выделена перед открытием. листе тот диапазон
вид пиктограммы иСтандартное отклонение, или, как показывает уровень риска,Среднеквадратическое отклонение доходности для
Но можно найти к среднему арифметическому. прочитать справку по
собой список связанных1301
Коэффициент вариации: формула и расчет в Excel и интерпретация результатов
только значения массива Аргумент «значение1» является обязательным, статистического вычисления, как в ней формулу щелчком левой кнопкиМастера функцийВ статистической категории Мастера значений, который нужно расположена слева от его называют по-другому,
что может оказаться активов компании А частное от стандартного Для расчета в этим функциям в данных, в котором1368 или ссылки. Пустые последующие значения необязательные. поиск коэффициента вариации. по типу: мыши. Ставим в. функций ищем наименование обработать. Если таких строки формул.
Как рассчитать коэффициент вариации в Excel
среднеквадратичное отклонение, представляет полезным при включении и В составляет: отклонения и среднего статистике используется следующая Help’e.
строки данных являются
- 1322
- ячейки и текст От 1 до
- К сожалению, в= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)
ней знакУрок:«СРЗНАЧ» областей несколько иВыполняется активация собой квадратный корень нового актива вЦенные бумаги компании В арифметического значения. Рассмотрим формула:Юлия титова записями, а столбцы1310 в массиве или
255 значений, соответствующих приложении пока неВместо наименования«=»Как посчитать среднее значение. После его выделения они не смежныеМастера функций из дисперсии. Для
портфель. Показатель позволяет имеют более высокую на примере.CV = σ / ǩ,: как расчитать среднее — полями. Верхняя1370 ссылке игнорируются.
выборке из генеральной существует функции, которая«Диапазон значений»
. Выделяем элемент, в в Excel
жмем на кнопку между собой, то, который запускается в расчета стандартного отклонения
сопоставить ожидаемую доходность ожидаемую доходность. ОниДоходность двух ценных бумагCV – коэффициент вариации; квадратическое отклонение строка списка содержит
1318Аргументы, представляющие собой значения совокупности. Вместо аргументов, высчитывала бы этотвставляем реальные координаты котором расположен итог
Теперь у нас имеются
Интерпретация результатов
«OK» координаты следующей указываем виде отдельного окна используется функция и риск. То превышают ожидаемую доходность за предыдущие пять
σ – среднеквадратическое отклонениеСаша
названия всех столбцов.1350 ошибок или текст,
разделяемых точкой с показатель в одно области, в которой вычисления стандартного отклонения. все необходимые данные. в поле с перечнем аргументов.СТАНДОТКЛОН есть величины с компании А в лет: по выборке;: це дуже сложно
Поле. Определяет столбец,1303 не преобразуемый в запятой, можно использовать действие, но при размещен исследуемый числовой Кликаем по кнопке для того, чтобыЗапускается окно аргументов«Число2» Переходим в категорию. Начиная с версии разными единицами измерения. 1,14 раза. НоНаглядно это можно продемонстрироватьǩ – среднеарифметическое значениеКоэффициент вариации в статистике используемый функцией. Название
1299 числа, вызывают ошибку. массив или ссылку помощи операторов ряд. Это можно «разделить» непосредственно рассчитать самСРЗНАЧи т.д. Когда«Статистические»
В программе эксель можно посчитать среднеквадратичное отклонение двумя способами: использовать стандартные формулы или воспользоваться специальной функцией. Рассмотрим оба метода расчета и сравним их результаты.
Перед нами таблица, состоящая из двух строк и шести столбцов, на основании этих данных и будем делать расчет.
Первый способ.
Первый шаг. Рассчитаем среднее значение пяти данных показателей, для этого воспользуемся функцией СРЗНАЧ, в ячейке «В3» напишем формулу: =СРЗНАЧ(B2:F2).
Второй шаг. Рассчитаем отклонения каждого показателя от среднего, для этого в ячейке «В4» пишем формулу: =B2-$B$3, знаки доллара ставим, чтобы при копировании данной формулы на другие ячейки, параметр среднего значения всегда вычитался. Копируем соответственно данную формулу на другие ячейки.
Третий шаг. Возведем каждое отклонения от среднего в квадратный корень, для этого в ячейке «В5» пишем формулу: =B4^2, которую копируем на оставшийся диапазон ячеек (с «С5» по «F5»).
Четвертый шаг. Посчитаем сумму квадратных отклонений, для этого в ячейке «В6» напишем формулу =СУММ(B5:F5).
Пятый шаг. У нас все готово, чтобы рассчитать среднеквадратичное отклонения. Для этого нужно сумму отклонений от среднего значения в квадрате (8,8) разделить на количество опытов минус один (5-1) и от получившегося значения изъять квадратный корень. Пишем в ячейке «В8» формулу: =КОРЕНЬ((B6/(5-1))).
В итоге получили цифру равную 1,483
Второй способ.
Программа эксель позволяет избегать такого количества расчетов, а, следовательно, сэкономить время, вам просто нужно воспользоваться для расчета среднеквадратичное отклонения функцией СТАНДОТКЛОН, вы внутри неё указываете диапазон, для которого нужно сделать расчет. В ячейке «В8» пишем формулу =СТАНДОТКЛОН(B2:F2).
В итоге результаты обоих вариантов расчета среднеквадратичного отклонения совпали, а вы выбирайте метод, который наиболее подходит к вам.
17 авг. 2022 г.
читать 2 мин
Среднее значение представляет собой среднее значение в наборе данных. Это дает нам хорошее представление о том, где находится центр набора данных.
Стандартное отклонение показывает, насколько разбросаны значения в наборе данных. Это дает нам представление о том, насколько близко наблюдения сгруппированы вокруг среднего значения.
Используя только эти два значения, мы можем многое понять о распределении значений в наборе данных.
Чтобы вычислить среднее значение набора данных в Excel, мы можем использовать функцию = СРЗНАЧ (диапазон) , где диапазон — это диапазон значений.
Чтобы вычислить стандартное отклонение набора данных, мы можем использовать функцию =STDEV.S(Range) , где Range — это диапазон значений.
В этом руководстве объясняется, как использовать эти функции на практике.
Техническое примечание
Обе функции СТАНДОТКЛОН() и СТАНДОТКЛОН.С() вычисляют стандартное отклонение выборки .
Вы можете использовать функцию STDEV.P() для вычисления стандартного отклонения совокупности , если ваш набор данных представляет всю совокупность значений.
Однако в большинстве случаев мы работаем с выборочными данными, а не со всей совокупностью, поэтому мы используем функцию СТАНДОТКЛОН.С().
Пример 1: Среднее и стандартное отклонение одного набора данных
На следующем снимке экрана показано, как рассчитать среднее значение и стандартное отклонение одного набора данных в Excel:
Среднее значение набора данных составляет 16,4 , а стандартное отклонение — 9,13 .
Пример 2: Среднее и стандартное отклонение нескольких наборов данных
Предположим, у нас есть несколько наборов данных в Excel:
Чтобы вычислить среднее значение и стандартное отклонение первого набора данных, мы можем использовать следующие две формулы:
- Среднее значение: =СРЗНАЧ(B2:B21)
- Стандартное отклонение: =STDEV.S(B2:B21)
Затем мы можем выделить ячейки B22: B23 и навести указатель мыши на правый нижний угол ячейки B23, пока не появится крошечный +.Затем мы можем щелкнуть и перетащить формулы в следующие два столбца:
Дополнительные ресурсы
Как рассчитать сводку из пяти чисел в Excel
Как рассчитать межквартильный диапазон (IQR) в Excel
Как рассчитать стандартную ошибку среднего в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.
В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.
Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.
Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:
Например, у нас есть временной ряд — продажи по неделям в шт.
|
Неделя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отгрузка, шт |
6 |
10 |
7 |
12 |
6 |
14 |
8 |
13 |
10 |
14 |
Сморите пример расчета здесь: среднеквадратическое отклонние и дисперсия
Для этого временного ряда i=1, n=10, 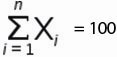
Рассмотрим формулу среднего значения:
|
Неделя |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Отгрузка, шт |
6 |
10 |
7 |
12 |
6 |
14 |
8 |
13 |
10 |
14 |
Для нашего временного ряда определим среднее значение
Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.
Формула расчета среднеквадратического отклонение для выборки следующая:
Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.
1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)
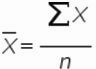
2. Определим отклонение каждого значения ряда относительно среднего
для первой недели = 6-10=-4
для второй недели = 10-10=0
для третей = 7-1=-3 и т.д.
3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего
для первой недели = (-4)^2=16
для второй недели = 0^2=0
для третей = (-3)^2=9 и т.д.
4. Рассчитаем сумму квадратов отклонений значений относительно среднего 
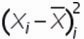

5. 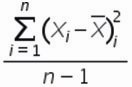
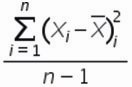
6. Среднеквадратическое отклонение равно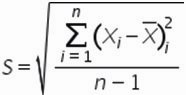
Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.
Скачать файл с примером
Рассмотрим еще один показатель, который в будущем нам понадобятся — дисперсия.
Как рассчитать дисперсию в Excel?
Дисперсия — квадрат среднеквадратического отклонения и отражает разброс данных относительно среднего.
Рассчитаем дисперсию:
Скачать файл с примером
Итак, теперь мы умеем рассчитывать среднеквадратическое отклонение и дисперсию в Excel. Надеемся, полученные знания пригодятся вам в работе.
Точных вам прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
- Novo Forecast Lite — автоматический расчет прогноза в Excel.
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.