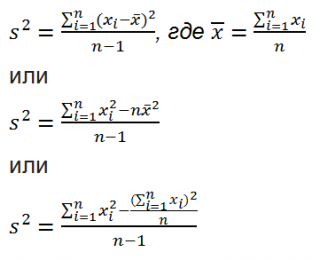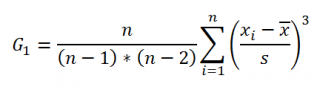Рассмотрим инструмент Описательная статистика, входящий в надстройку Пакет Анализа. Рассчитаем показатели выборки: среднее, медиана, мода, дисперсия, стандартное отклонение и др.
Задача
описательной статистики
(descriptive statistics) заключается в том, чтобы с использованием математических инструментов свести сотни значений
выборки
к нескольким итоговым показателям, которые дают представление о
выборке
.В качестве таких статистических показателей используются:
среднее
,
медиана
,
мода
,
дисперсия, стандартное отклонение
и др.
Опишем набор числовых данных с помощью определенных показателей. Для чего нужны эти показатели? Эти показатели позволят сделать определенные
статистические выводы о распределении
, из которого была взята
выборка
. Например, если у нас есть
выборка
значений толщины трубы, которая изготавливается на определенном оборудовании, то на основании анализа этой
выборки
мы сможем сделать, с некой определенной вероятностью, заключение о состоянии процесса изготовления.
Содержание статьи:
- Надстройка Пакет анализа;
-
Среднее выборки
;
-
Медиана выборки
;
-
Мода выборки
;
-
Мода и среднее значение
;
-
Дисперсия выборки
;
-
Стандартное отклонение выборки
;
-
Стандартная ошибка
;
-
Ассиметричность
;
-
Эксцесс выборки
;
-
Уровень надежности
.
Надстройка Пакет анализа
Для вычисления статистических показателей одномерных
выборок
, используем
надстройку Пакет анализа
. Затем, все показатели рассчитанные надстройкой, вычислим с помощью встроенных функций MS EXCEL.
СОВЕТ
: Подробнее о других инструментах надстройки
Пакет анализа
и ее подключении – читайте в статье
Надстройка Пакет анализа MS EXCEL
.
Выборку
разместим на
листе
Пример
в файле примера
в диапазоне
А6:А55
(50 значений).
Примечание
: Для удобства написания формул для диапазона
А6:А55
создан
Именованный диапазон
Выборка.
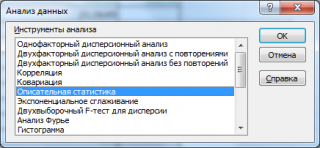
В диалоговом окне
Анализ данных
выберите инструмент
Описательная статистика
.
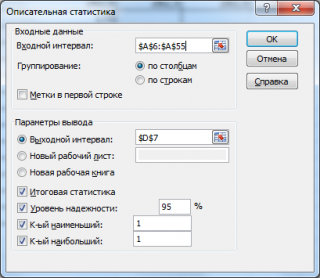
После нажатия кнопки
ОК
будет выведено другое диалоговое окно,
в котором нужно указать:
входной интервал
(Input Range) – это диапазон ячеек, в котором содержится массив данных. Если в указанный диапазон входит текстовый заголовок набора данных, то нужно поставить галочку в поле
Метки в первой строке (
Labels
in
first
row
).
В этом случае заголовок будет выведен в
Выходном интервале.
Пустые ячейки будут проигнорированы, поэтому нулевые значения необходимо обязательно указывать в ячейках, а не оставлять их пустыми;
выходной интервал
(Output Range). Здесь укажите адрес верхней левой ячейки диапазона, в который будут выведены статистические показатели;
Итоговая статистика (
Summary
Statistics
)
. Поставьте галочку напротив этого поля – будут выведены основные показатели выборки:
среднее, медиана, мода, стандартное отклонение
и др.;-
Также можно поставить галочки напротив полей
Уровень надежности (
Confidence
Level
for
Mean
)
,
К-й наименьший
(Kth Largest) и
К-й наибольший
(Kth Smallest).
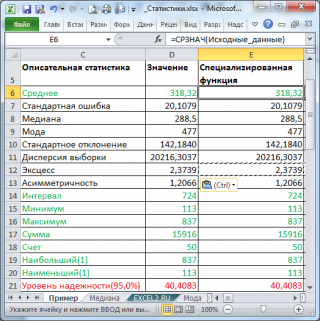
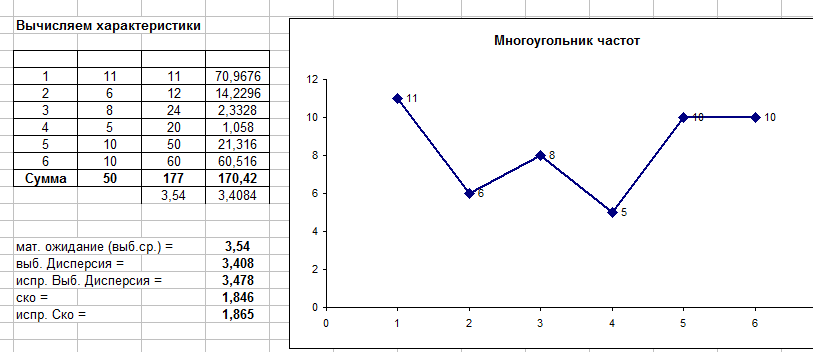
В результате будут выведены следующие статистические показатели:
Все показатели выведены в виде значений, а не формул. Если массив данных изменился, то необходимо перезапустить расчет.
Если во
входном интервале
указать ссылку на несколько столбцов данных, то будет рассчитано соответствующее количество наборов показателей. Такой подход позволяет сравнить несколько наборов данных. При сравнении нескольких наборов данных используйте заголовки (включите их во
Входной интервал
и установите галочку в поле
Метки в первой строке
). Если наборы данных разной длины, то это не проблема — пустые ячейки будут проигнорированы.
Зеленым цветом на картинке выше и в
файле примера
выделены показатели, которые не требуют особого пояснения. Для большинства из них имеется специализированная функция:
Интервал
(Range) — разница между максимальным и минимальным значениями;
Минимум
(Minimum) – минимальное значение в диапазоне ячеек, указанном во
Входном интервале
(см.статью про функцию
МИН()
);
Максимум
(Maximum)– максимальное значение (см.статью про функцию
МАКС()
);
Сумма
(Sum) – сумма всех значений (см.статью про функцию
СУММ()
);
Счет
(Count) – количество значений во
Входном интервале
(пустые ячейки игнорируются, см.статью про функцию
СЧЁТ()
);
Наибольший
(Kth Largest) – выводится К-й наибольший. Например, 1-й наибольший – это максимальное значение (см.статью про функцию
НАИБОЛЬШИЙ()
);
Наименьший
(Kth Smallest) – выводится К-й наименьший. Например, 1-й наименьший – это минимальное значение (см.статью про функцию
НАИМЕНЬШИЙ()
).
Ниже даны подробные описания остальных показателей.
Среднее выборки
Среднее
(mean, average) или
выборочное среднее
или
среднее выборки
(sample average) представляет собой
арифметическое среднее
всех значений массива. В MS EXCEL для вычисления среднего выборки используется функция
СРЗНАЧ()
.
Выборочное среднее
является «хорошей» (несмещенной и эффективной) оценкой
математического ожидания
случайной величины (подробнее см. статью
Среднее и Математическое ожидание в MS EXCEL
).
Медиана выборки
Медиана
(Median) – это число, которое является серединой множества чисел (в данном случае выборки): половина чисел множества больше, чем
медиана
, а половина чисел меньше, чем
медиана
. Для определения
медианы
необходимо сначала
отсортировать множество чисел
. Например,
медианой
для чисел 2, 3, 3,
4
, 5, 7, 10 будет 4.
Если множество содержит четное количество чисел, то вычисляется
среднее
для двух чисел, находящихся в середине множества. Например,
медианой
для чисел 2, 3,
3
,
5
, 7, 10 будет 4, т.к. (3+5)/2.
Если имеется длинный хвост распределения, то
Медиана
лучше, чем
среднее значение
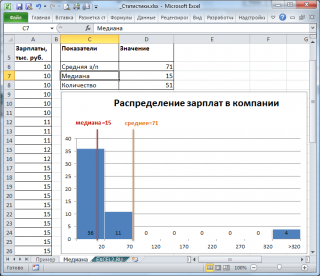
, отражает «типичное» или «центральное» значение. Например, рассмотрим несправедливое распределение зарплат в компании, в которой руководство получает существенно больше, чем основная масса сотрудников.
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что
как минимум
у 50% сотрудников зарплата меньше или равна 15 тыс. руб.
Для определения
медианы
в MS EXCEL существует одноименная функция
МЕДИАНА()
, английский вариант — MEDIAN().
Медиану
также можно вычислить с помощью формул
=КВАРТИЛЬ.ВКЛ(Выборка;2) =ПРОЦЕНТИЛЬ.ВКЛ(Выборка;0,5).
Подробнее о
медиане
см. специальную статью
Медиана в MS EXCEL
.
СОВЕТ
: Подробнее про
квартили
см. статью, про
перцентили (процентили)
см. статью.
Мода выборки
Мода
(Mode) – это наиболее часто встречающееся (повторяющееся) значение в
выборке
. Например, в массиве (1; 1;
2
;
2
;
2
; 3; 4; 5) число 2 встречается чаще всего – 3 раза. Значит, число 2 – это
мода
. Для вычисления
моды
используется функция
МОДА()
, английский вариант MODE().
Примечание
: Если в массиве нет повторяющихся значений, то функция вернет значение ошибки #Н/Д. Это свойство использовано в статье
Есть ли повторы в списке?
Начиная с
MS EXCEL 2010
вместо функции
МОДА()
рекомендуется использовать функцию
МОДА.ОДН()
, которая является ее полным аналогом. Кроме того, в MS EXCEL 2010 появилась новая функция
МОДА.НСК()
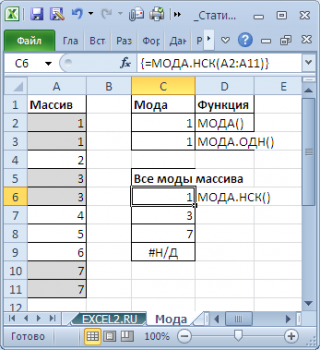
, которая возвращает несколько наиболее часто повторяющихся значений (если количество их повторов совпадает). НСК – это сокращение от слова НеСКолько.
Например, в массиве (1; 1;
2
;
2
;
2
; 3;
4
;
4
;
4
; 5) числа 2 и 4 встречаются наиболее часто – по 3 раза. Значит, оба числа являются
модами
. Функции
МОДА.ОДН()
и
МОДА()
вернут значение 2, т.к. 2 встречается первым, среди наиболее повторяющихся значений (см.
файл примера
, лист
Мода
).
Чтобы исправить эту несправедливость и была введена функция
МОДА.НСК()
, которая выводит все
моды
. Для этого ее нужно ввести как
формулу массива
.
Как видно из картинки выше, функция
МОДА.НСК()
вернула все три
моды
из массива чисел в диапазоне
A2:A11
: 1; 3 и 7. Для этого, выделите диапазон
C6:C9
, в
Строку формул
введите формулу
=МОДА.НСК(A2:A11)
и нажмите
CTRL+SHIFT+ENTER
. Диапазон
C
6:
C
9
охватывает 4 ячейки, т.е. количество выделяемых ячеек должно быть больше или равно количеству
мод
. Если ячеек больше чем м
о
д, то избыточные ячейки будут заполнены значениями ошибки #Н/Д. Если
мода
только одна, то все выделенные ячейки будут заполнены значением этой
моды
.
Теперь вспомним, что мы определили
моду
для выборки, т.е. для конечного множества значений, взятых из
генеральной совокупности
. Для
непрерывных случайных величин
вполне может оказаться, что выборка состоит из массива на подобие этого (0,935; 1,211; 2,430; 3,668; 3,874; …), в котором может не оказаться повторов и функция
МОДА()
вернет ошибку.
Даже в нашем массиве с
модой
, которая была определена с помощью
надстройки Пакет анализа
, творится, что-то не то. Действительно,
модой
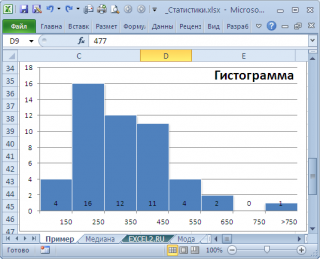
нашего массива значений является число 477, т.к. оно встречается 2 раза, остальные значения не повторяются. Но, если мы посмотрим на
гистограмму распределения
, построенную для нашего массива, то увидим, что 477 не принадлежит интервалу наиболее часто встречающихся значений (от 150 до 250).
Проблема в том, что мы определили
моду
как наиболее часто встречающееся значение, а не как наиболее вероятное. Поэтому,
моду
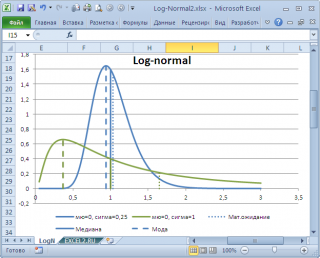
в учебниках статистики часто определяют не для выборки (массива), а для функции распределения. Например, для
логнормального распределения
мода
(наиболее вероятное значение непрерывной случайной величины х), вычисляется как
exp
(
m
—
s
2
)
, где m и s параметры этого распределения.
Понятно, что для нашего массива число 477, хотя и является наиболее часто повторяющимся значением, но все же является плохой оценкой для
моды
распределения, из которого взята
выборка
(наиболее вероятного значения или для которого плотность вероятности распределения максимальна).
Для того, чтобы получить оценку
моды
распределения, из
генеральной совокупности
которого взята
выборка
, можно, например, построить
гистограмму
. Оценкой для
моды
может служить интервал наиболее часто встречающихся значений (самого высокого столбца). Как было сказано выше, в нашем случае это интервал от 150 до 250.
Вывод
: Значение
моды
для
выборки
, рассчитанное с помощью функции
МОДА()
, может ввести в заблуждение, особенно для небольших выборок. Эта функция эффективна, когда случайная величина может принимать лишь несколько дискретных значений, а размер
выборки
существенно превышает количество этих значений.
Например, в рассмотренном примере о распределении заработных плат (см. раздел статьи выше, о Медиане),
модой
является число 15 (17 значений из 51, т.е. 33%). В этом случае функция
МОДА()
дает хорошую оценку «наиболее вероятного» значения зарплаты.
Примечание
: Строго говоря, в примере с зарплатой мы имеем дело скорее с
генеральной совокупностью
, чем с
выборкой
. Т.к. других зарплат в компании просто нет.
О вычислении
моды
для распределения
непрерывной случайной величины
читайте статью
Мода в MS EXCEL
.
Мода и среднее значение
Не смотря на то, что
мода
– это наиболее вероятное значение случайной величины (вероятность выбрать это значение из
Генеральной совокупности
максимальна), не следует ожидать, что
среднее значение
обязательно будет близко к
моде
.
Примечание
:
Мода
и
среднее
симметричных распределений совпадает (имеется ввиду симметричность
плотности распределения
).
Представим, что мы бросаем некий «неправильный» кубик, у которого на гранях имеются значения (1; 2; 3; 4; 6; 6), т.е. значения 5 нет, а есть вторая 6.
Модой
является 6, а среднее значение – 3,6666.
Другой пример. Для
Логнормального распределения
LnN(0;1)
мода
равна =EXP(m-s2)= EXP(0-1*1)=0,368, а
среднее значение
1,649.
Дисперсия выборки
Дисперсия выборки
или
выборочная дисперсия (
sample
variance
) характеризует разброс значений в массиве, отклонение от
среднего
.
Из формулы №1 видно, что
дисперсия выборки
это сумма квадратов отклонений каждого значения в массиве
от среднего
, деленная на размер выборки минус 1.
В MS EXCEL 2007 и более ранних версиях для вычисления
дисперсии выборки
используется функция
ДИСП()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог — функцию
ДИСП.В()
.
Дисперсию
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1) =(СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/ (СЧЁТ(Выборка)-1)
– обычная формула
=СУММ((Выборка -СРЗНАЧ(Выборка))^2)/ (СЧЁТ(Выборка)-1)
–
формула массива
Дисперсия выборки
равна 0, только в том случае, если все значения равны между собой и, соответственно, равны
среднему значению
.
Чем больше величина
дисперсии
, тем больше разброс значений в массиве относительно
среднего
.
Размерность
дисперсии
соответствует квадрату единицы измерения исходных значений. Например, если значения в выборке представляют собой измерения веса детали (в кг), то размерность
дисперсии
будет кг
2
. Это бывает сложно интерпретировать, поэтому для характеристики разброса значений чаще используют величину равную квадратному корню из
дисперсии – стандартное отклонение
.
Подробнее о
дисперсии
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартное отклонение выборки
Стандартное отклонение выборки
(Standard Deviation), как и
дисперсия
, — это мера того, насколько широко разбросаны значения в выборке
относительно их среднего
.
По определению,
стандартное отклонение
равно квадратному корню из
дисперсии
:
Стандартное отклонение
не учитывает величину значений в
выборке
, а только степень рассеивания значений вокруг их
среднего
. Чтобы проиллюстрировать это приведем пример.
Вычислим стандартное отклонение для 2-х
выборок
: (1; 5; 9) и (1001; 1005; 1009). В обоих случаях, s=4. Очевидно, что отношение величины стандартного отклонения к значениям массива у
выборок
существенно отличается.
В MS EXCEL 2007 и более ранних версиях для вычисления
Стандартного отклонения выборки
используется функция
СТАНДОТКЛОН()
. С версии MS EXCEL 2010 рекомендуется использовать ее аналог
СТАНДОТКЛОН.В()
.
Стандартное отклонение
можно также вычислить непосредственно по нижеуказанным формулам (см.
файл примера
):
=КОРЕНЬ(КВАДРОТКЛ(Выборка)/(СЧЁТ(Выборка)-1)) =КОРЕНЬ((СУММКВ(Выборка)-СЧЁТ(Выборка)*СРЗНАЧ(Выборка)^2)/(СЧЁТ(Выборка)-1))
Подробнее о
стандартном отклонении
см. статью
Дисперсия и стандартное отклонение в MS EXCEL
.
Стандартная ошибка
В
Пакете анализа
под термином
стандартная ошибка
имеется ввиду
Стандартная ошибка среднего
(Standard Error of the Mean, SEM).
Стандартная ошибка среднего
— это оценка
стандартного отклонения
распределения
выборочного среднего
.
Примечание
: Чтобы разобраться с понятием
Стандартная ошибка среднего
необходимо прочитать о
выборочном распределении
(см. статью
Статистики, их выборочные распределения и точечные оценки параметров распределений в MS EXCEL
) и статью про
Центральную предельную теорему
.
Стандартное отклонение распределения выборочного среднего
вычисляется по формуле σ/√n, где n — объём
выборки, σ — стандартное отклонение исходного
распределения, из которого взята
выборка
. Т.к. обычно
стандартное отклонение
исходного распределения неизвестно, то в расчетах вместо
σ
используют ее оценку
s
—
стандартное отклонение выборки
. А соответствующая величина s/√n имеет специальное название —
Стандартная ошибка среднего.
Именно эта величина вычисляется в
Пакете анализа.
В MS EXCEL
стандартную ошибку среднего
можно также вычислить по формуле
=СТАНДОТКЛОН.В(Выборка)/ КОРЕНЬ(СЧЁТ(Выборка))
Асимметричность
Асимметричность
или
коэффициент асимметрии
(skewness) характеризует степень несимметричности распределения (
плотности распределения
) относительно его
среднего
.
Положительное значение
коэффициента асимметрии
указывает, что размер правого «хвоста» распределения больше, чем левого (относительно среднего). Отрицательная асимметрия, наоборот, указывает на то, что левый хвост распределения больше правого.
Коэффициент асимметрии
идеально симметричного распределения или выборки равно 0.
Примечание
:
Асимметрия выборки
может отличаться расчетного значения асимметрии теоретического распределения. Например,
Нормальное распределение
является симметричным распределением (
плотность его распределения
симметрична относительно
среднего
) и, поэтому имеет асимметрию равную 0. Понятно, что при этом значения в
выборке
из соответствующей
генеральной совокупности
не обязательно должны располагаться совершенно симметрично относительно
среднего
. Поэтому,
асимметрия выборки
, являющейся оценкой
асимметрии распределения
, может отличаться от 0.
Функция
СКОС()
, английский вариант SKEW(), возвращает коэффициент
асимметрии выборки
, являющейся оценкой
асимметрии
соответствующего распределения, и определяется следующим образом:
где n – размер
выборки
, s –
стандартное отклонение выборки
.
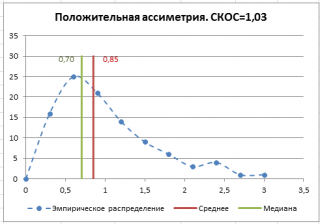
В
файле примера на листе СКОС
приведен расчет коэффициента
асимметрии
на примере случайной выборки из
распределения Вейбулла
, которое имеет значительную положительную
асимметрию
при параметрах распределения W(1,5; 1).
Эксцесс выборки
Эксцесс
показывает относительный вес «хвостов» распределения относительно его центральной части.
Для того чтобы определить, что относится к хвостам распределения, а что к его центральной части, можно использовать границы μ +/-
σ
.
Примечание
: Не смотря на старания профессиональных статистиков, в литературе еще попадается определение
Эксцесса
как меры «остроконечности» (peakedness) или сглаженности распределения. Но, на самом деле, значение
Эксцесса
ничего не говорит о форме пика распределения.
Согласно определения,
Эксцесс
равен четвертому
стандартизированному моменту:
Для
нормального распределения
четвертый момент равен 3*σ
4
, следовательно,
Эксцесс
равен 3. Многие компьютерные программы используют для расчетов не сам
Эксцесс
, а так называемый Kurtosis excess, который меньше на 3. Т.е. для
нормального распределения
Kurtosis excess равен 0. Необходимо быть внимательным, т.к. часто не очевидно, какая формула лежит в основе расчетов.
Примечание
: Еще большую путаницу вносит перевод этих терминов на русский язык. Термин Kurtosis происходит от греческого слова «изогнутый», «имеющий арку». Так сложилось, что на русский язык оба термина Kurtosis и Kurtosis excess переводятся как
Эксцесс
(от англ. excess — «излишек»). Например, функция MS EXCEL
ЭКСЦЕСС()
на самом деле вычисляет Kurtosis excess.
Функция
ЭКСЦЕСС()
, английский вариант KURT(), вычисляет на основе значений выборки несмещенную оценку
эксцесса распределения
случайной величины и определяется следующим образом:
Как видно из формулы MS EXCEL использует именно Kurtosis excess, т.е. для выборки из
нормального распределения
формула вернет близкое к 0 значение.
Если задано менее четырех точек данных, то функция
ЭКСЦЕСС()
возвращает значение ошибки #ДЕЛ/0!
Вернемся к
распределениям случайной величины
.
Эксцесс
(Kurtosis excess) для
нормального распределения
всегда равен 0, т.е. не зависит от параметров распределения μ и σ. Для большинства других распределений
Эксцесс
зависит от параметров распределения: см., например,
распределение Вейбулла
или
распределение Пуассона
, для котрого
Эксцесс
= 1/λ.
Уровень надежности
Уровень
надежности
— означает вероятность того, что
доверительный интервал
содержит истинное значение оцениваемого параметра распределения.
Вместо термина
Уровень
надежности
часто используется термин
Уровень доверия
. Про
Уровень надежности
(Confidence Level for Mean) читайте статью
Уровень значимости и уровень надежности в MS EXCEL
.
Задав значение
Уровня
надежности
в окне
надстройки Пакет анализа
, MS EXCEL вычислит половину ширины
доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Тот же результат можно получить по формуле (см.
файл примера
):
=ДОВЕРИТ.СТЬЮДЕНТ(1-0,95;s;n)
s —
стандартное отклонение выборки
, n – объем
выборки
.
Подробнее см. статью про
построение доверительного интервала для оценки среднего (дисперсия неизвестна)
.
Добавил:
Вуз:
Предмет:
Файл:
Скачиваний:
0
Добавлен:
15.11.2022
Размер:
1.67 Mб
Скачать
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования «Оренбургский государственный университет»
Кафедра математических методов и моделей в экономике
Н.П. ФОТ, А.Г. ГАНСКАЯ, О.Н. ЯРКОВА
МЕТОДЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ С ПРИМЕНЕНИЕМ ЭЛЕКТРОННОЙ ТАБЛИЦЫ EXCEL
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОМУ ПРАКТИКУМУ И САМОСТОТЕЛЬНОЙ РАБОТЕ СТУДЕНТОВ
Рекомендовано к изданию Редакционно-издательским советом государственного образовательного учреждения
высшего профессионального образования «Оренбургский государственный университет»
Оренбург 2006
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
УДК 519.23 (076.5) ББК 22.172 я 73
Ф 81
Рецензент кандидат экономических наук, доцент С.В. Дьяконова
Фот Н.П.
Ф81 Методы математической статистики с применением электронной таблицы Excel [Текст]: методические указания к лабораторному практикуму и самостоятельной работе студентов/ Н.П.Фот, А.Г.- Ганская, О.Н. Яркова– Оренбург: ГОУ ОГУ, 2006. – 29 с.
Методические указания предназначены для выполнения лабораторного практикума и самостоятельной работы по дисциплине «Теория вероятностей и математическая статистика» для студентов экономических специальностей.
ББК 22.172 я 73
© Фот Н.П., 2006 Ганская А.Г. Яркова О.Н.
© ГОУ ОГУ, 2006
2
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
Содержание |
||
|
Введение………………………………………………………………………………………………………………………………………………………… |
5 |
|
|
1 |
Постановка задачи……………………………………………………………………………………………………………………………………….. |
6 |
|
2 |
Построение гистограммы и статистической функции распределения в среде пакета Excel…………………………….. |
6 |
|
3 |
Оценка основных выборочных характеристик: среднего значения, дисперсии, среднеквадратического откло- |
|
|
нения. Нахождение их посредством электронной таблицы Excel……………………………………………………………………. |
12 |
|
|
4Проверка гипотезы о законе распределения генеральной совокупности с помощью критерия согласия ……….. |
14 |
|
|
5 |
Построение доверительных интервалов для основных характеристик генеральной совокупности………………… |
17 |
|
6 |
Оценка парного коэффициента корреляции (нахождение его в таблице Excel). Проверка его значимости и по- |
|
|
строение доверительного интервала………………………………………………………………………………………………………………. |
19 |
|
|
7 |
Оценка уравнения регрессии. Проверка значимости и построение доверительных интервалов для значимых |
|
|
параметров регрессии……………………………………………………………………………………………………………………………………. |
22 |
|
|
8Вопросы к защите……………………………………………………………………………………………………………………………………….. |
25 |
|
|
Список использованных источников……………………………………………………………………………………………………………… |
26 |
|
|
Приложение А………………………………………………………………………………………………………………………………………………. |
28 |
3
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Введение
Математическая статистка изучает различные методы обработки и осмысления результатов многократно повторяемых случайных событий. Обработка данных и получения на ее основе каких-либо рекомендаций относительно принятия того или иного управленческого решения – процесс многоэтапный.
Для выявления закономерностей, присущих экономическим и социальноэкономическим показателями, выборочные данные подвергают первичной обработке (построение гистограммы и функции распределения), производят оценку числовых характеристик показателей (математического ожидания и дисперсии) и выявляют степень тесноты линейной статистической связи (расчет коэффициента корреляции).
Целью данных методических указаний является:
1)наработка навыков получения точечных и интервальных оценок с помощью электронной таблицы Excel;
2)проверка статистических гипотез по выборочным данным;
3)выявление взаимосвязей между признаками посредством корреляционнорегрессионного анализа.
4
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
1 Постановка задачи
Предприятия машиностроительной отрасли характеризуются двумя основными показателями производственно – хозяйственной деятельности.
На основании выборочных данных из генеральной совокупности по двум, указанным в варианте (приложение А), признакам:
1)по выборочным данным построить гистограмму и график эмпирической функции распределения;
2)определить основные числовые характеристики: среднее значение, дисперсию, среднеквадратическое отклонение;
3)на основании выборочных данных X и Y с помощью критерия согласия при уровне значимости α=0,05, проверить гипотезу о законе распределения генеральной совокупности;
4)построить 95%-ые доверительные интервалы для основных числовых характеристик генеральной совокупности;
5)найти коэффициент корреляции между признаками X и Y, проверить его значимость, для значимого параметра связи с α=0,05 построить доверительный интервал, сделать выводы;
6)оценить уравнение регрессии, проверить значимость коэффициентов регрессии, для значимых параметров построить доверительные интервалы, сделать выводы (α=0,05).
2 Построение гистограммы и статистической функции распределения в среде пакета Excel
Пример приведен с использованием электронной таблицы Excel и рассмотрен для 0 варианта приложения А.
Данные вводятся в среду электронного пакета Excel, где переменной А – соответствуют значения Х1, переменной В– значения X4 (фрагмент таблицы представлен на рисунке 1).
5
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Рисунок 1 – Ввод исходных данных Для построения гистограммы на панели инструментов, в меню «Сервис»
выбирают функцию «Анализ данных», окно которого представлено на рисунке 2 (при отсутствии данной категории — в меню «Сервис»: в модуле «Настройка» активизируйте пункт «Пакет анализа», после чего появляется запрашиваемая функция).
Рисунок 2 – Выбор меню «Анализ данных»
На следующем этапе производится выбор категории «Гистограмма» — в диалоговом окне указывают основные параметры для построения гистограммы по исходным данным (рисунок 3).
Рисунок 3 – Окна ввода данных
Квводимым параметрам относятся:
i.входной диапазон — ссылка на диапазон, содержащий анализируемые данные;
ii.интервал карманов (необязательный) — вводится диапазон ячеек, определяющих отрезки (карманы). Эти значения должны быть введены в возрастающем порядке. В Microsoft Excel вычисляется число попаданий данных между текущим началом отрезка и соседним большим по порядку, если такой есть. При этом включаются значения на нижней границе отрезка и не включаются значения на верхней границе. Если диапазон карманов не введен, то набор отрезков, равномерно распреде-
6
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
ленных между минимальным и максимальным значениями данных, будет создан автоматически;
iii.выходной диапазон — вводят ссылку на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные;
iv.новый лист — устанавливают переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1. Если в этом есть необходимость, вводят имя нового листа в поле, расположенном напротив соответствующего положения переключателя;
v.новая книга — устанавливают переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге;
vi.Парето (отсортированная диаграмма) — устанавливают флажок, чтобы представить данные в порядке убывания частоты. Если флажок снят, то данные в выходном диапазоне будут представлены в порядке возрастания отрезков, а трех самых правых столбцов с отсортированными данными не будет;
vii.интегральный процент — устанавливают флажок для генерации интегральных процентных отношений включения в гистограмму графика интегральных процентов. Чтобы не вычислять интегральные процентные соотношения флажок снимают;
viii.вывод графика — устанавливают флажок для автоматического создания встроенной диаграммы на листе, содержащем выходной диапазон.
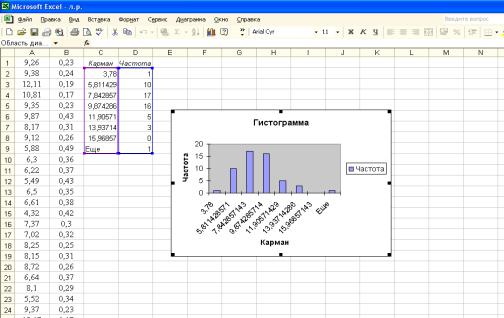
Для построения гистограммы переменной Х1 в окне ввода данных указываем входной интервал — «А1:А53», выходной интервал – ячейку «С1» и ставим флажок для вывода графика. Далее нажимаем на кнопку «ОК». Вывод результатов представлен на рисунке 4.
7
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Рисунок 4 – Вывод результатов
Вследствие того, что не был указан параметр – «Интервал карманов», все исходные значения автоматически разделены на равные промежутки (в выводе результатов – столбец «Карманы»), и для каждого из них посчитано количество заданных значений, попавших в соответствующий интервал (столбец – «Частота»). Графическим представлением полученных выводов является график «Гистограмма».
Построение графика эмпирической функции распределения не предусмотрено статистическим модулем «Анализ данных» и поэтому на первом этапе построения проделывают несколько дополнительных вычислений.
Геометрическим представлением эмпирической функции распределения называют кумулятой или кумулятивной прямой, где по оси х – расположены границы интервалов (карманов), а по оси y – накопленная частота ν Нk, равная сумме частот всех предшествующих интервалов.
Найдем накопленные частоты для рассматриваемого примера, путем последовательного сложения ячеек столбца «Частоты» (рисунок 5). Таким образом, получаем столбец, состоящий из найденных накопленных частот. Отметим, что для ввода формулы используем в меню «Вставка» категорию «Функция», в которой выбираем операцию сложения. Все формулы в среде электронной таблицы Excel вводятся в свободную ячейку и начинаются со знака «=».
8

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Рисунок 5 – Вычисление накопленных частот
На следующем этапе для каждого интервала вычисляем эмпирическую функцию распределения по формуле:
принимающую значение равное нулю при ν kH =0 и значение единицы при ν kH =53 (n – объем выборки, равен 53 для каждого интервала).
Для этого в свободную ячейку вводим формулу (1) и составляем столбец значений функции распределения, последнее значение должно быть =1 (рисунок 6).
Рисунок 6 — Вычисление значений функции распределения
9

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Для построения графика на панели инструментов щелкаем на значке
и в меню «Мастер диаграмм» последовательно указываем необходимые параметры, после каждого шага нажимая кнопку «Далее».
На первом шаге предлагается выбор типа и вида диаграммы (рисунок 7а). На втором шаге указываем диапазон данных для построения путем выделения их левой кнопкой мыши (рисунок 7б). Для указания дополнительных параметров: подписей по оси Х и имени построенного ряда переходят в окно «Ряд» (рисунок 7в). На третьем шаге предлагается указать следующие параметры диаграммы: заголовки, оси, линии сетки, легенды, подписи данных и таблицы данных (рисунок 7г).
Рисунок 7 – Построение графика функции распределения
10
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
О книге «Практикум по математической статистике с примерами в Excel»
Рассмотрены задачи оценки законов распределения, точечного и интервального оценивания числовых характеристик и параметров распределения, проверки статистических гипотез, а также элементы корреляционного, регрессионного и дисперсионного анализа. Материал изложен таким образом, что сначала вводятся основные понятия, перечисляются основные формулы и алгоритмы с указанием условий их применения и получения, затем рассматривается решение типовых задач, многие из которых прикладного характера. После этого приводятся задания и методики выполнения лабораторных работ в среде MS Excel. В конце каждой главы приведены задания для самостоятельного решения. Предназначено для укрупненных групп специальностей среднего профессионального образования «Экономика и управление», «Сельское, лесное и рыбное хозяйство» и специальности «Прикладная информатика».
На нашем сайте можно скачать книгу «Практикум по математической статистике с примерами в Excel» в формате fb2, rtf, epub, pdf, txt или читать онлайн. Здесь так же можно перед прочтением обратиться к отзывам читателей, уже знакомых с книгой, и узнать их мнение. В интернет-магазине нашего партнера вы можете купить и прочитать книгу в бумажном варианте.
В книгу включены все разделы, входящие в программы стандартных учебных дисциплин «Математическая статистика», «Теория статистики», «Статистика» для широкого спектра экономических и технических направлений подготовки специалистов высших учебных заведений.
Каждая глава (соответствующий раздел курса) содержит справочный материал, а также минимальные теоретические сведения, достаточные для обоснования применяемых алгоритмов и объяснения полученных результатов. Алгоритмы решения задач в программе Excel описаны достаточно подробно, и с их применением пользователь может справиться самостоятельно. Большое количество разобранных примеров позволяет использовать данное пособие не только для аудиторной, но и для самостоятельной работы студентов. Задания для самостоятельной работы содержат задачи, встречающиеся в технике, экономике и маркетинговых исследованиях, и способствуют закреплению отработанных навыков.
Полнота изложения материала и относительная компактность данного издания позволяют рекомендовать его преподавателям и студентам, а также всем пользователям, включая экономистов, менеджеров, инженеров, маркетологов, которым приходится сталкиваться с необходимостью обрабатывать статистические данные и готовить отчеты, содержащие статистические графики и диаграммы.
Рассмотрены основные вопросы теории вероятностей и математической статистики с соответствующими примерами, контрольными и индивидуальными заданиями. Описывается методика статистического анализа данных с использованием табличного процессора Excel. Электронная версия примеров, контрольных и индивидуальных заданий, а так же исходные данные для их выполнения размещены на WEB-сайте КГАУ
Пособие в известной мере отражает практику преподавания авторами предмета в Кубанском государственном аграрном университете, Таганрогском государственном радиотехническом университете и Таганрогском институте управления и экономики. Многие примеры и задания сформулированы по результатам научных исследований авторов.
Предназначается для студентов вузов, обучающихся по экономическим специальностям, преподавателей, аспирантов и слушателей курсов повышения квалификации, применяющих в своей практике вероятностные и статистические методы.
Названия программных продуктов являются товарными знаками соответствующих компаний.
Представленные в книге примеры, упражнения и задачи предназначены для углубленного изучения возможностей процессора электронных таблиц Excel (в основном версии Excel 97, Excel 2000, но большинство примеров могут выполняться в среде Excel 5.0/7.0). Задачи разнообразны по тематике и уровню трудности. Особое внимание уделено методам адресации, построению табличных формул (формул массива), работе с электронными таблицами как с базами данных.
Для широкого круга читателей: от начинающих до опытных пользователей. Большая часть материала доступна учащимся старших классов и студентам младших курсов экономических и технических вузов. Книгу можно использовать для самообразования и для проведения занятий с преподавателем.
В учебном пособии изложены основные методы статистического анализа (средние величины, выборочный метод, проверка статистических гипотез, корреляционный и дисперсионный анализ, индексы, ряды динамики), приведены соответствующие расчетные формулы, раскрыт содержательный смысл статистических показателей. Подробно, вплоть до пошаговых инструкций, описаны способы решения статистических задач на персональном компьютере с помощью Microsoft Excel — самой известной и наиболее часто используемой программы для осуществления подобных расчетов.
Для студентов вузов по специальности 060800 «Экономика и управление на предприятии АПК», а также специалистов любого профиля, интересующихся методами статистической обработки данных на ПК.
Рассматриваются функциональные возможности табличного процессора Excel для проведения статистического анализа данных на персональном компьютере. Описывается технология работы с программной надстройкой «Пакет анализа» и встроенными статистическими функциями. Приводится большое количество примеров по обработке экономической информации. Содержатся краткие сведения из теории статистики, помогающие читателю быстрее разобраться с существом реализованных в Excel статистических методов.
Для студентов, аспирантов, преподавателей, экономистов, инженерно-технических работников, занимающихся статистической обработкой данных.
Рассматриваются функциональные возможности табличного процессора Excel для проведения статистического анализа данных на персональном компьютере. Описывается технология работы с программной надстройкой «Пакет анализа» и встроенными статистическими функциями. Приводится большое количество примеров по обработке экономической информации. Содержатся краткие сведения из теории статистики, помогающие читателю быстрее разобраться с существом реализованных в Excel статистических методов.
Для студентов, аспирантов, преподавателей, экономистов, инженерно-технических работников, занимающихся статистической обработкой данных.
СКАЧАТЬ КНИГУ
Книга представляет собой вводный курс бизнес-статистики. В ней рассмотрены практически все традиционные темы, касающиеся анализа данных — от описательных статистик до регрессионного анализа и карт контроля. Особенную ценность книге придает огромное количество примеров, почерпнутых из практики, а также компакт-диск c большим количеством приложений, иллюстрирующих методы статистического анализа данных с помощью программы Microsoft Excel.
Книга предназначена для студентов, изучающих основы менеджмента, преподавателей бизнес-школ, а также менеджеров, желающих повысить качество своей работы.
Рассмотрены вопросы обшей теории статистики и практики современных статистических исследований в соответствии с требованиями государственного образовательного стандарта высшего профессионального образования. Приведены основные концепции, понятия и показатели теоретической статистики. Описана на конкретных примерах методика использования табличного процессора Excel для статистической обработки информации.
Для студентов, аспирантов, преподавателей и практических работников, заинтересованных в изучении и использовании современных методов анализа статистических данных. Может быть использовано как справочное издание для анализа исходного статистического массива в Excel.
СКАЧАТЬ КНИГУ
Описываются способы, приемы и рекомендации построения средствами Excel диаграмм различного типа, широко используемых в экономических исследованиях. Большинство этих способов и приемов разработаны автором и ранее не публиковались. Рассматриваются способы решения средствами Excel типовых вычислительных задач. Большое внимание уделяется способам рациональной организации таблиц. Материал излагается в доступной форме и сопровождается примерами и упражнениями.
Для преподавателей, студентов, магистрантов и аспирантов экономических специальностей, а также для пользователей Excel.
В книгу вошли основные сведения по MS Excel и классическим методам непараметрической статистики, применяемым к независимым выборкам, парным наблюдениям и таблицам сопряженности, реализующие эти методы программы VBA и технологии решения типовых задач в MS Excel. Данные технологии представлены, как пошаговыми решениями (без применения макросов), так и автоматическими, когда задача решается одним макросом, возвращающим значение статистики, критерий принятия основной гипотезы и вывод о том, какую гипотезу следует принять.
Книга ориентирована на студентов вузов, изучающих статистические методы, но будет полезна и более широкому кругу пользователей MS Excel.
В этом разделе вы найдете полезные статьи, формулы и шаблоны, которые помогут решать задачи по ТВиМС (или проверять решение) с помощью Excel.
Если говорить о теории вероятностей или комбинаторике, эксель — не панацея. Все равно вам нужно самим научиться вычленять данные задачи, определять ее тип, подходящую формулу и порядок решения для нахождения вероятности. А вот сделать вычисления, проверить ответ, быстро и точно подсчитать — с этим справится пакет электронных таблиц.
В математической статистике Excel более полезен. Безн него не обойтись в объемных расчетных задачах: обработка выборки, построении линий регрессии, дисперсионный анализ и т.п., так как ручные расчеты утомительны и нерациональны. Удобно использовать специальные шаблоны для решения типовых задач (некоторые вы найдете у нас) или модифицировать их под свои задачи.
Ну и конечно, эксель пригодится для построения графиков и диаграмм: многоугольник закона распределения дискретной случайной величины, плотность нормального распределения, гистограмма выборочных наблюдений, линии регрессии и т.п.
Примеры решений задач в Excel
Путеводитель по Excel
- Таблица формул ТВиМС в Excel
- Комбинаторика в Excel
- Факториал в Excel
- Решение задач по формуле Бернулли в Excel
Все обучающие статьи о теории вероятностей
Проконсультируем по теории вероятностей
Если решения нужны срочно
Более 11000 задач с полными и подробными решениями по теории вероятностей и математической статистике в онлайн-решебнике.
А еще!
|
|