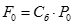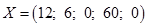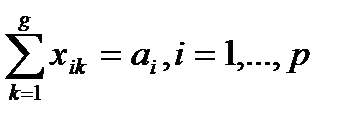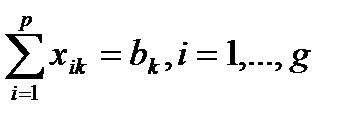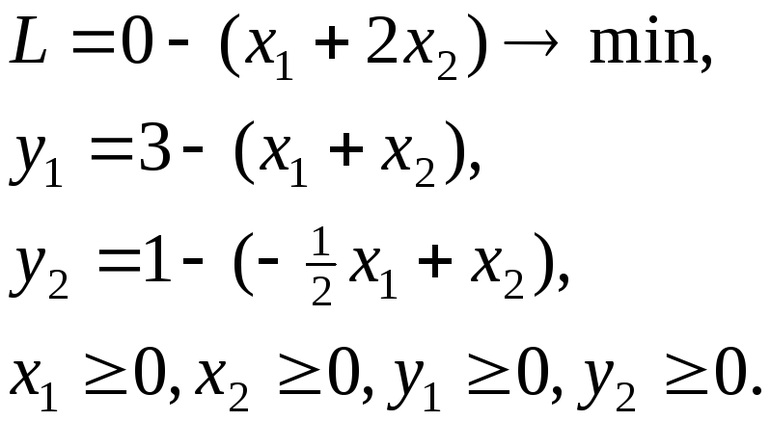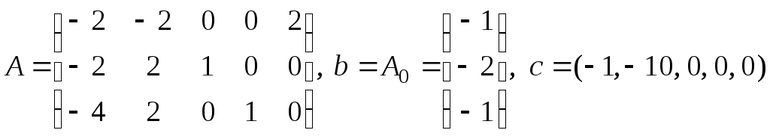Skip to content
Рассмотрим решение задачи линейного программирования с помощью симплекс-метода в Excel на примере
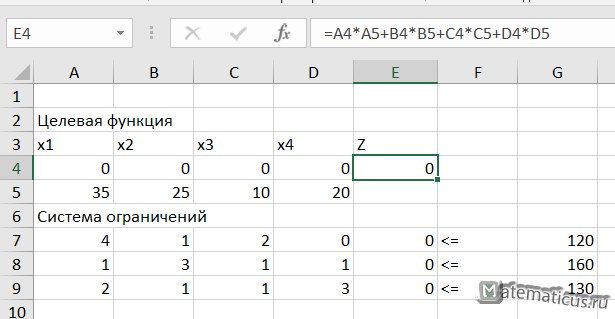
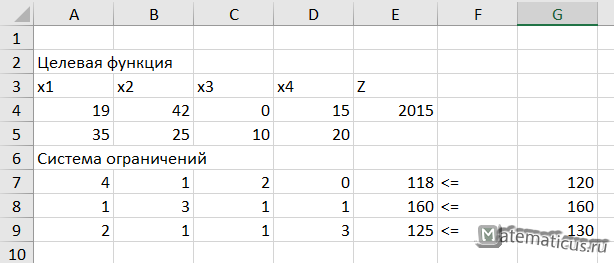
Целевая функция имеет вид
Z = 35∙x1+25∙x2+10∙x3+20∙x4→ max
Ограничения, записанные в виде системы линейных уравнений
4∙x1+1∙x2+2∙x3+0∙x4 ≤ 120
1∙x1+3∙x2+1∙x3+1∙x4 ≤ 160∙
2∙x1+1∙x2+1∙x3+3∙x4 ≤ 130
x1, x2, x3, x4 ≥ 0 – целые
Теперь данную задачу для решения запишем в Excel
В ячейке E4 вставим формулу
=A4*A5+B4*B5+C4*C5+D4*D5
Для ячейки E7, E8 и E9 формула будет иметь вид
=$A$4*A7+$B$4*B7+$C$4*C7+$D$4*D7
=$A$4*A8+$B$4*B8+$C$4*C8+$D$4*D8
=$A$4*A9+$B$4*B9+$C$4*C9+$D$4*D9
Также можно воспользоваться формулой:
=СУММПРОИЗВ(A4:D4;A7:D7)
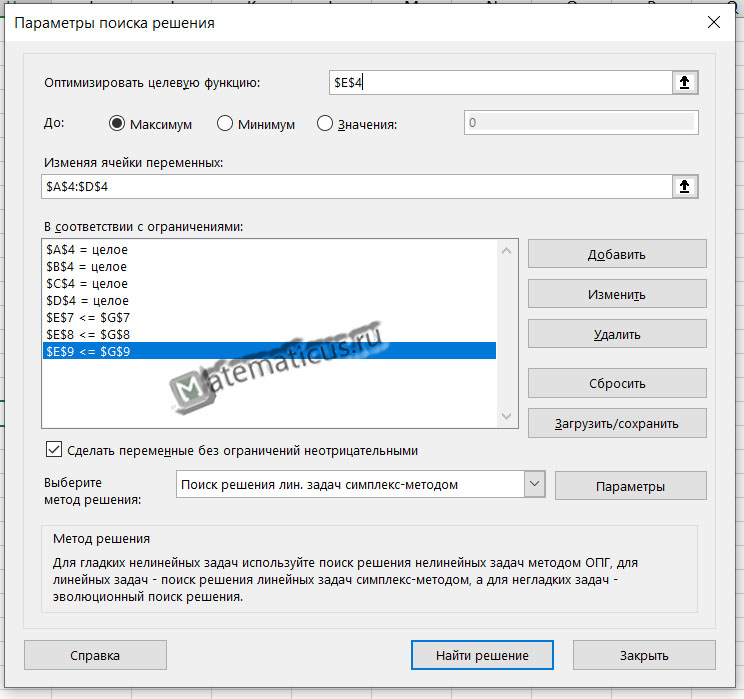
На вкладке данные переходим в Поиск решения
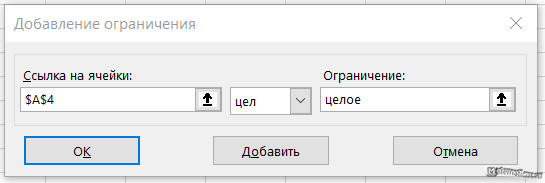
Выбираем ячейку с целевой функцией, ставим галочку максимум, далее выбираем ячейки изменяемых переменных ($A$4:$D$4) и добавляем ограничения при помощи кнопки Добавить. Также ставим галочку переменные без ограничений неотрицательные, выбираем, выбираем метод решения – симплекс-метод решения линейных задач.
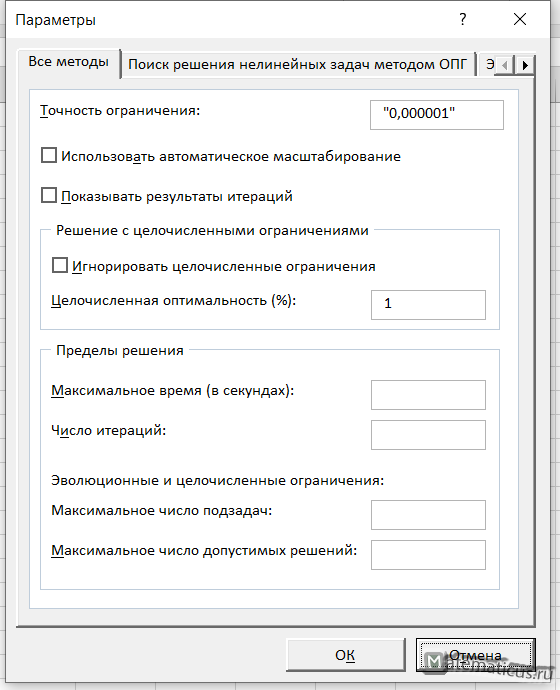
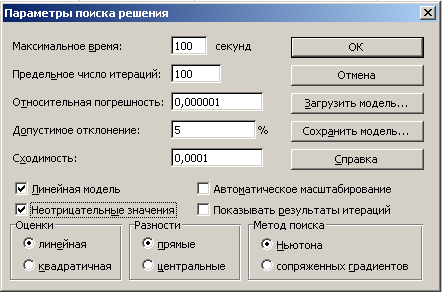
Можно также перейти в параметры и настроить точность.
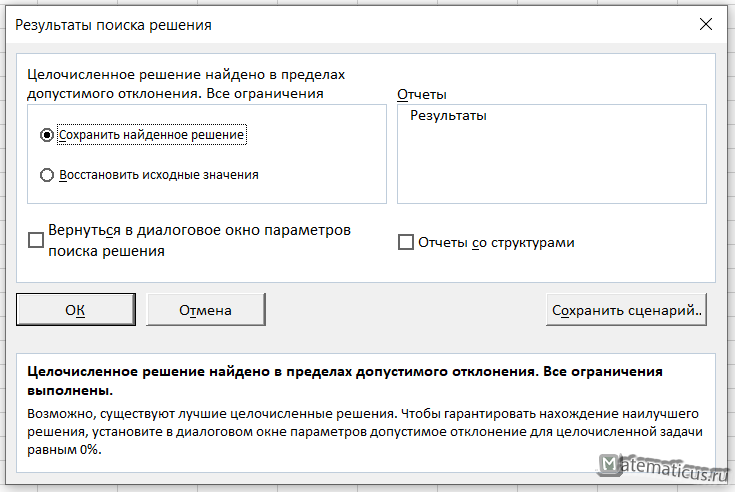
Итак, нажимаем Найти решение, появляется окно результаты поиска решений, выбираем сохранить найденное решение.
В итоги получили решения задачи
Z=2015
x1=19; x2=42; x3=0; x4=15
21609
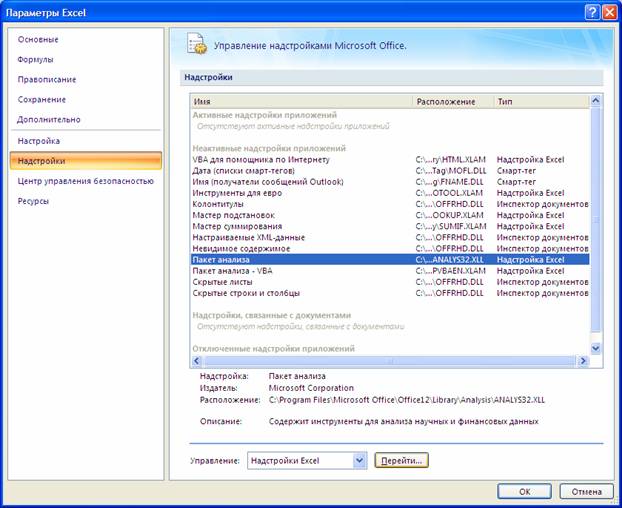
В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel, нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel» внизу окна:
Если данная команда отсутствует в списке, необходимо выполнить команду Сервис / Надстройки
вид поиска (максимальное значение)
в поле изменяя ячейки : $B$2:$D$2
в поле Ограничения добавьте заданные ограничения
Поле должно иметь следующее содержание:
$B$2:$D$2>=0
$G$6 Выполнить
Иногда задание звучит следующим образом: расчеты осуществить на ЭВМ, привести распечатку полученных результатов.
MS Excel позволяет представить результаты поиска решения в форме отчета. Существует три типа таких отчетов:
- Результаты (Answer). В отчет включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях.
- Устойчивость (Sensitivity). Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.
- Пределы (Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.
Пример. В библиотеке работают 6 пожилых уборщиц. Каждая из них по своим физическим возможностям и состоянию здоровья может выполнять только определенные виды работ, причем с определенной производительностью. Площадь каждой из работ известна. Нужно добиться минимума времени на уборку помещений.
| ПРОИЗВОДИТЕЛЬНОСТЬ БАБУШЕК м 2 . /мин | |||||||
| Баба Аня | Белла Петровна | Баба Варя | Баба Галя | Домна Ивановна | Евгения Карловна | Площадь работ | |
| Мытье окон | 2 | 1 | 46 | ||||
| Мытье полов | 1 | 300 | |||||
| Протирка столов | 2 | 0.2 | 1 | 50 | |||
| Чистка дорожек | 2 | 4 | 100 |
Пример.На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество корма каждого вида, которое должны ежедневно получать лисицы и песцы, приведено в таблице. В ней же указаны общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца.
Найти оптимальное соотношение количества кормов и численности поголовья лис и песцов.
Для упрощения процесса вычислений при решении ЗЛП симплекс-методом можно использовать Microsoft Excel.
Найдем решение нашей задачи симплекс-методом с помощью Microsoft Excel.
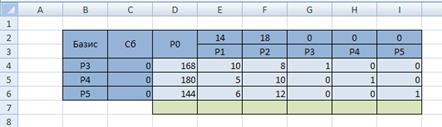
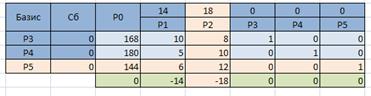
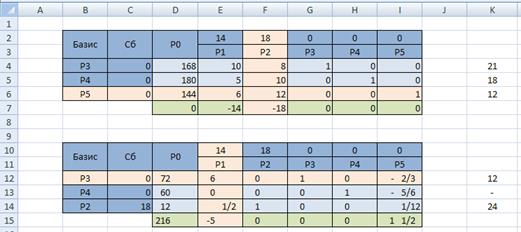
Запустите Excel и подготовьте начальную симплекс таблицу по образцу:
Вычислим значение 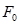
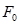
Для вычисления скалярного произведения двух векторов используется функция
СУММПРОИЗВ(массив1, [массив2], [массив3]. ),
В ячейку D7 вводится формула, вычисляющая значение 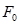
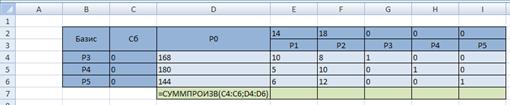
Для вычисления оценок 
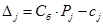
Выделите ячейку D7 и введите формулу:
Аналогично вычислите значения других оценок.
Определим разрешающий столбец – столбец с наибольшей по модулю отрицательной оценкой и найдем отношение элементов столбца 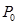
Скопируйте формулу на диапазон K4 : K6
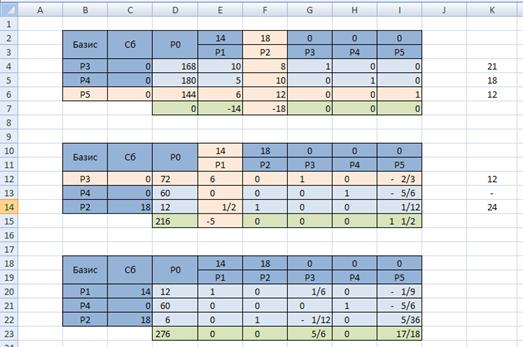
Таким образом, разрешающий столбец – столбец 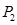
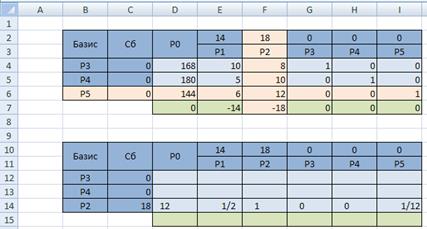
Создайте вторую симплекс-таблицу (скопируйте предыдущую и удалите все ненужно). Произведите замену в базисе вектора 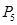
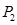
Выделите диапазон D12:I15 и укажите смените формат числовых данных на дробный
Вычислите новые элементы разрешающей строки: разделить элементы разрешающей строки на разрешающий элемент.
В ячейку D14 введите формулу
Скопируйте формулу на диапазон E14 : I14:
| В ячейку D12 введите формулу: =D14*(-$F$4)+D4 Скопируйте формулу на диапазон E12:I12. В ячейку D13 введите формулу: =D14*(-$F$5)+D5 Скопируйте формулу на диапазон E13:I13. В ячейку D15 введите формулу: =D14*(-$F$5)+D5 Скопируйте формулу на диапазон E15:I15. |  |
Так как строка оценок содержит отрицательное число, и соответствующий столбец содержит положительные числа, то план можно улучшить.
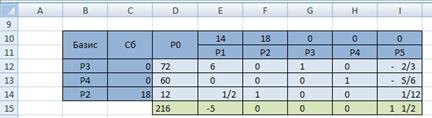
Выбираем разрешающую строку и разрешающий столбец:
Строим новую симплекс-таблицу и заменяем вектор 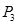
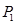
Так как строка оценок не содержит отрицательных значений, то полученный план оптимален и имеет вид:
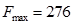
Ответ: 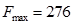
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9622 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Для решения задач линейного программирования симплекс-методом в среде MS Excel заполняются ячейки исходными данными в режиме чисел и формулами математической модели.
MS Excel позволяет получить оптимальное решение без ограничения размерности системы неравенств целевой функции.
Решим задачу о выпускаемых изделиях симплекс-методом применяя надстройку «Поиск решения» в MS Excel.
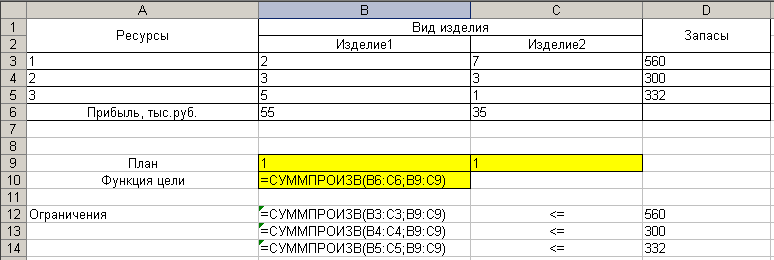
1. Заполните таблицу Excel в режиме чисел (рис.1)
2. Заполните таблицу Excel в режиме формул (рис.2)
Рис.1 Таблица в режиме чисел
Рис.1 Таблица в режиме формул
Здесь: В9:С9 – результат (оптимальное количество изделий каждого вида);
В6:С6 – коэффициенты целевой функции;
В10 – значение целевой функции;
В3:С5 – коэффициенты ограничений;
D12:D14 – правая часть ограничений;
B12:B14 – вычисляемые (фактические) значения левой части ограничений.
Решим задачу с помощью команды Данные/Поиск решения. На экране появляется диалоговое окно Поиск решения.
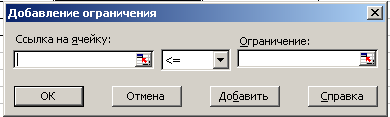
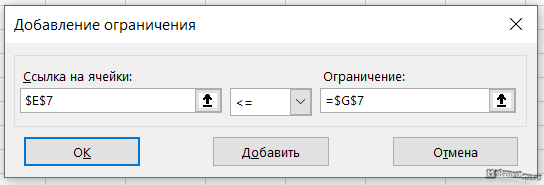
В поле Установить целевую функция будет показана ссылка на активную ячейку, т.е. на В10. Причем эта ссылка абсолютная. В секции Равной устанавливаем переключатель Максимальному (минимальному) значению в зависимости от целевой функции. Ограничения устанавливаются с помощью кнопки Добавить, которая вызывает диалоговое окно их ввода Добавление ограничения.
В поле ввода Ссылка на ячейку: указывается адрес ячейки, содержащей формулу левой части ограничения. Затем выбирается из списка знак соотношения. В поле Ограничение указывается адрес ячейки, содержащей правую часть ограничения. Щёлкаем на кнопку Добавить и повторяем до следующего ограничения. После ввода всех ограничений нажимаем ОК.
Так как все переменные несут условия неотрицательности, то их положительность задается через кнопку Параметры в окне диалога Поиск решения. После щелчка по ней, на экране окно Параметры поиска решения.
Устанавливаем флажок Сделать переменные без ограничений неотрицательными и выбрать Метод решения Поиск решения линеных задач симплекс-методом. Щёлкаем на кнопке Найти решение.
Excel предъявит окно Результаты поиска решения с сообщением о том, что решение найдено, или о том, что не может найти подходящего решения.
Если вычисления оказались успешными, Excel предъявит следующее окно итогов. Их можно сохранить или отказаться. Кроме того, можно получить один из трёх видов отчётов (Результаты,Устойчивость,Пределы), позволяющие лучше осознать полученные результаты, в том числе, оценить их достоверность.
После найденного решения, в ячейках В9:С9 появится оптимальное количество изделий каждого вида.
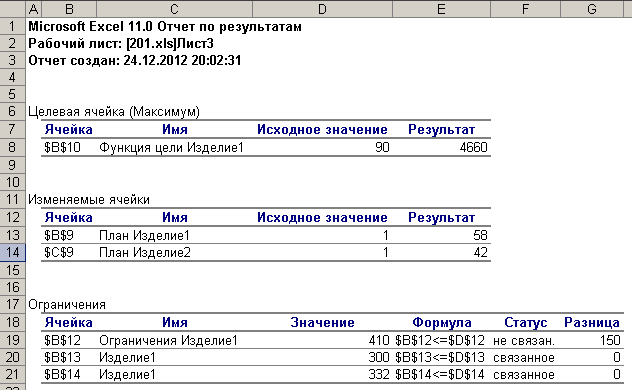
При сохранении отчета выберите – Отчет по результатам (рис.3).
Из отчета видно, что ресурс 1 не используется полностью на 150 кг, а ресурс 2 и 3 используется полностью.
В результате получен оптимальный план, при котором изделий 1 вида необходимо выпустить в количестве 58 шт., а изделий 2 вида в количестве 42 шт. При этом прибыль от их реализации максимальная и составляет 4660 тыс.руб.
Рис.3 Отчет по результатам
1. Со станции формирования ежедневно отправляются пассажирские и скорые поезда, составленные из плацкартных, купейных и мягких вагонов. Число мест в плацкартном вагоне – 54, в купейном – 36, в мягком – 18. В таблице указаны состав поезда каждого типа и количество имеющихся в парке вагонов различного типа. Определить число скорых и пассажирских поездов, которые необходимо формировать ежедневно, чтобы число перевозимых пассажиров было максимальным.
| 1 | плац | куп | мягк |
| скор | 2 | 6 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 50 | 60 | 26 |
| 2 | плац | куп | мягк |
| скор | 2 | 6 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 50 | 66 | 26 |
| 3 | плац | куп | мягк |
| скор | 2 | 6 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 55 | 60 | 26 |
| 4 | плац | куп | мягк |
| скор | 2 | 6 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 55 | 66 | 26 |
| 5 | плац | куп | мягк |
| скор | 2 | 7 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 55 | 77 | 28 |
| 6 | плац | куп | мягк |
| скор | 2 | 7 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 55 | 84 | 28 |
| 7 | плац | куп | мягк |
| скор | 4 | 6 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 60 | 60 | 26 |
| 8 | плац | куп | мягк |
| скор | 4 | 6 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 60 | 66 | 26 |
| 9 | плац | куп | мягк |
| скор | 4 | 6 | 2 |
| пасс | 5 | 2 | 2 |
| парк | 60 | 72 | 26 |
| 10 | плац | куп | мягк |
| скор | 2 | 7 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 55 | 91 | 28 |
| 11 | плац | куп | мягк |
| скор | 3 | 7 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 60 | 70 | 28 |
| 12 | плац | куп | мягк |
| скор | 2 | 6 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 50 | 72 | 26 |
| 13 | плац | куп | мягк |
| скор | 3 | 7 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 60 | 70 | 28 |
| 14 | плац | куп | мягк |
| скор | 3 | 7 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 60 | 84 | 28 |
| 15 | плац | куп | мягк |
| скор | 3 | 6 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 55 | 72 | 26 |
| 16 | плац | куп | мягк |
| скор | 3 | 7 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 60 | 91 | 28 |
| 17 | плац | куп | мягк |
| скор | 2 | 8 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 60 | 96 | 30 |
| 18 | плац | куп | мягк |
| скор | 2 | 8 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 60 | 96 | 30 |
| 19 | плац | куп | мягк |
| скор | 2 | 8 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 60 | 104 | 30 |
| 20 | плац | куп | мягк |
| скор | 2 | 8 | 2 |
| пасс | 5 | 7 | 2 |
| парк | 60 | 112 | 30 |
| 21 | плац | куп | мягк |
| скор | 1 | 8 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 55 | 96 | 30 |
| 22 | плац | куп | мягк |
| скор | 1 | 8 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 55 | 104 | 30 |
| 23 | плац | куп | мягк |
| скор | 4 | 7 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 65 | 91 | 28 |
| 24 | плац | куп | мягк |
| скор | 4 | 7 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 65 | 84 | 28 |
| 25 | плац | куп | мягк |
| скор | 4 | 7 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 65 | 70 | 28 |
| 26 | плац | куп | мягк |
| скор | 4 | 7 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 65 | 77 | 28 |
| 27 | плац | куп | мягк |
| скор | 1 | 7 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 50 | 70 | 28 |
| 28 | плац | куп | мягк |
| скор | 1 | 7 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 50 | 77 | 28 |
| 30 | плац | куп | мягк |
| скор | 1 | 7 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 50 | 91 | 28 |
| 29 | плац | куп | мягк |
| скор | 1 | 7 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 50 | 84 | 28 |
Решение транспортных задач
Транспортными задачами называются задачи определения оптимального плана перевозок груза из данных пунктов отправления в заданные пункты потребления.
| b1 | b2 | … | bk | … | bg | |
| a1 | [c11 x11 | [c12 x12 | … | [c1k x1k | … | [c1g x1g |
| a2 | [c21 x21 | [c22 X22 | … | [c2k x2k | … | [c2g x2g |
| … | … | … | … | … | … | … |
| ai | [ci2 xi2 | [ci2 xi2 | … | [cik xik | … | [cig xig |
| … | … | … | … | … | … | … |
| ap | [cp2 xp2 | [cp2 xp2 | … | [cpk xpk | … | [cpg xpg |
Если 
Переменные должны удовлетворять условиям
Суммарные затраты на перевозки
Решение такой задачи разбивается на два этапа:
1. Определение опорного (базисного) решения;
2. Построение последовательных итераций, т.е. приближение к оптимальному решению.
Для каждого из этих этапов существует несколько методов.
Для построения опорного решения чаще всего используют метод «северо-западного угла» и метод минимальных тарифов.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Понятие и алгоритм
Под симплексным методом понимается последовательный переход от одного базисного нахождения системы решений к другому. Эта перестановка повторяется до тех пор, пока переменная величина цели не достигнет своего наибольшего или наименьшего значения. Такой подход является универсальным, его можно использовать для решения любой задачи последовательного программирования.
Метод был разработан в 1947 году математиком из США Бернардом Данцигом. Предложенный способ оказался весьма эффективным для решения задач, связанных с оптимизацией использования ограниченных ресурсов. То есть он позволяет оценить и откорректировать параметры системы, а также получить качественные аналитические результаты.
Существует два подхода решения задачи:
- графический;
- симплексный.
Первый можно использовать для оптимизационного решения двухмерных задач. Например, существует два производственных цикла по сборке ящиков. Выпуск товара характеризуется ограничением в поставках древесины и временем формовки изделия. Для одного необходимо 30 досок, а для другого — 40. Поставщики доставляют в неделю 2 тыс. единиц материала. Первый ящик собирается за 15 минут, а второй — за 30. Нужно определить, какое количество ящиков необходимо производить за неделю на первом конвейере и на втором. При этом первое изделие приносит 10 рублей прибыли, а второе — пять. Время изготовление ограничено 160 часами.
Решение заключается в принятии за Х1 и Х2 количество выпущенных ящиков. Затем — в нахождении максимальной еженедельной прибыли и описании процесса ограничения в виде уравнения.
Это типовая двухмерная задача, условия неотрицательности которой определяются границами прямых: 30*Х1 + 4 0*Х 2 ≤ 2000 (для досок) и 20*Х 1 ≤ 50*Х 2 = 1600 (для сборки). Отложив по оси ординат Х1, а Х2 по абсцисс, и указав на них точки соответствующие уравнениям, можно будет подобрать оптимальное решение для использования сырья и времени.
Графический метод удобно применять для двухмерных задач, но его невозможно использовать при решениях, связанных с размерностью, превышающей три. При этом во всех алгоритмах оптимальный результат принимается допустимым базисному. Симплекс-метод же является вычислительной процедурой, использующей принятое положение, описываемое в алгебраической форме.
Симплекс-метод при базисном решении
Впервые способ был изложен Данцигом в книге «Линейное программирование, его обобщения и применения», изданной на русском языке в 1966 году. Эта теория основывалась на вычислительной процедуре и представлялась в виде стандартных алгебраических форм. Основное направление метода заключается в указании способа нахождения опорного решения, переходе к другому, более оптимальному расчёту и определении критериев, позволяющих остановить перебор опорных вариантов.
Алгоритм решения задачи линейного программирования симплекс методом следующий:
- Свести поставленную задачу к канонической форме путём переноса свободных членов в правую часть и ввода дополнительных переменных. В случае отрицательных переменных неравенство умножается на -1. Если в записи используется знак «меньше или равно», переменная используется положительная, в противном случае — отрицательная.
- В зависимости от количества вводимых значений все переменные принимаются за основные. Их необходимо выразить через неосновные и перейти к базовому решению.
- Через неосновные переменные выражается функция цели.
- Если при решении отыскивается ответ с максимумом или минимумом линейной формы и все неосновные переменные получаются только положительными, то задача считается выполненной.
- Если найденный максимум (минимум) линейной формы в функции имеет одну или несколько неосновных переменных с отрицательными коэффициентами, необходимо перейти к новому базисному решению.
- Из переменных, входящих в форму с отрицательными или положительными коэффициентами, выбирается наибольшая (по модулю) и переводится в основные.
Другими словами, указывается оптимальное опорное решение, способ перехода от одного нахождения ответа к другому, варианты улучшения расчётов. После нахождения первоначального решения с «единичным базисом» вычисляется оценка разложения векторов по базису и заполняется симплексная таблица.
В тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи, используют метод с искусственным базисом. Это симплекс-метод с так называемой М-задачей (ММЭ), решаемый способом добавления к левой части системы уравнений искусственных единичных векторов. При этом новая матрица должна содержать группу единичных линейно-независимых векторов.
Двухфазный способ
Двойственный метод используется при анализе задач линейного программирования, записанного в форме основной задачи. При этом среди векторов, m уравнений, составленных из коэффициентов, должны быть единичные. Такой метод можно использовать, когда свободные члены уравнений являются любыми числами.
Например, существует ограниченность, описываемая функцией:
F = C 1 X 1+ C 2 X 2+…+ CnXn. Используется условие, что Х1Р1+Х2Р2+…+Х(m +1) P (m +1)+ +… XnPn = Р0, где Х j больше либо равно 0 (j =1, n). Принимается, что среди чисел bi (i =1, m) имеются отрицательные.
Решением будет выражение: х= (b1; b2;…; bm ;0;…;0), однако этот ответ не будет разрешать задание, так как к нему могут относиться и отрицательные числа. Так как векторы Р1, Р2… Рм единичные, то каждый из них можно описать линейной областью, состоящей из них же. При этом коэффициентами разложения векторов Рj по области будут числа: Xij = aij (i =1, m; j =1, n) по модулю.
Выражение х= ( b1; b2;…; bm ;0;…;0) определяется базисом. Называют его псевдоплан. Считается, что если дельта j больше либо равна нулю, то для любого: j ( j =1, n ) по модулю. В то же время если в псевдоплане с находимым базисом существует хотя бы одно отрицательное число, то тогда задача вообще не будет иметь планов. Но когда для этих отрицательных чисел верно, что аij меньше нуля, то можно будет перейти к новому псевдоплану.
Объяснение псевдоплана помогает построить алгоритм двойственного метода. Если взять за основу х = (b1; b2;…; bm ;0;…;0) и представить это выражение псевдопланом, то, учитывая исходные данные, можно составить симплекс-таблицу. В ней часть элементов будет отрицательная. Так как дельта j должна быть больше либо равна нулю, то при отсутствии таких чисел в таблице уже будет записан оптимальный план. В обратном случае выбирается по модулю наибольшее из чисел с минусом.
Принцип решения задачи включает следующее:
- нахождение псевдоплана;
- проверка его на оптимальность;
- выбор разрешающей строки путём нахождения абсолютной величины отрицательного числа, отношения элементов (m+1) и соответствующей им строке;
- нахождение нового псевдоплана.
Если анализ оптимален, считается, что найдено верное решение. В другом случае устанавливается неразрешимость задачи либо составляется новый псевдоплан. Делается это в результате пересчёта табличных данных, например, методом Жордана-Гаусса.
Пример задачи
Использование метода линейного программирования распространено в решениях транспортных задач. Он помогает в целевых расчётах и нужен для минимизации затрат в условиях ограниченной грузоподъёмности и времени обслуживания заказчиков.
Задачи линейного программирования (ЗЛП) позволяют выбрать оптимальную загрузку при перемещении какого-либо товара из одних мест в другие. Во вводных данных указывается число пунктов отправления (м) и количество мест назначения (n). Первые обозначаются как А1, А2…Ам, а вторые – В1, В2…Вn. За аi принимается объём продукции на складе, а bi – потребность. Затраты на перевозку с i пункта в j обозначаются Сij.
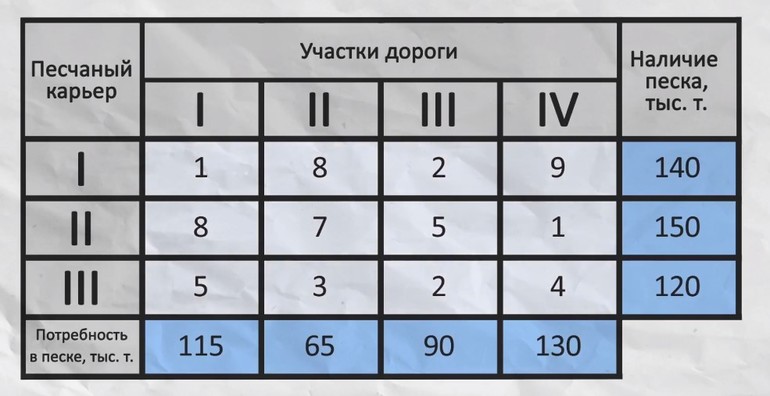
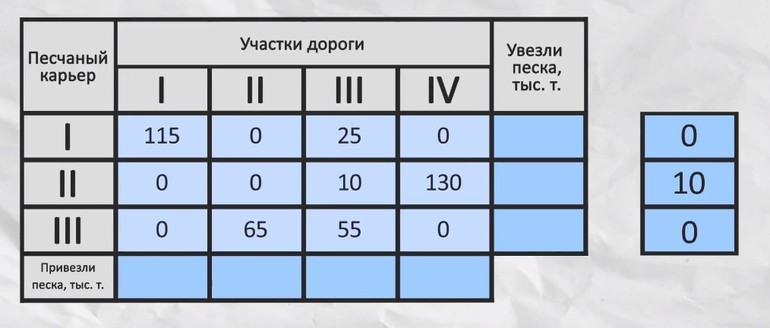
Главная задача — составить план таким образом, чтобы общая стоимость была минимальна. Пусть дано четыре песчаных карьера, с которых необходимо поставить песок на четыре склада. При этом осуществляться перевозки должны за определённую стоимость. Составляем таблицу.
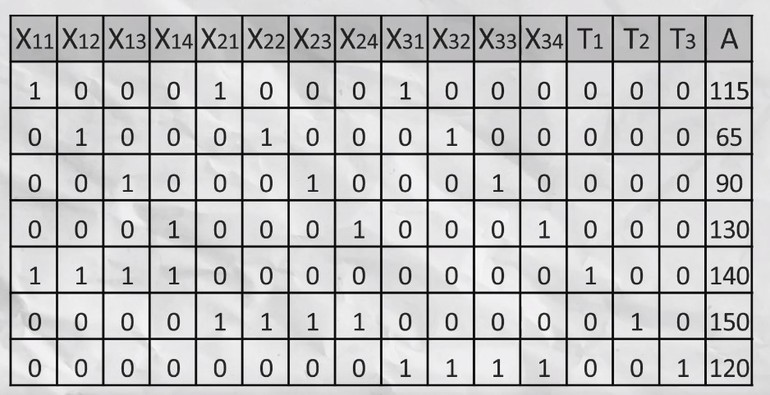
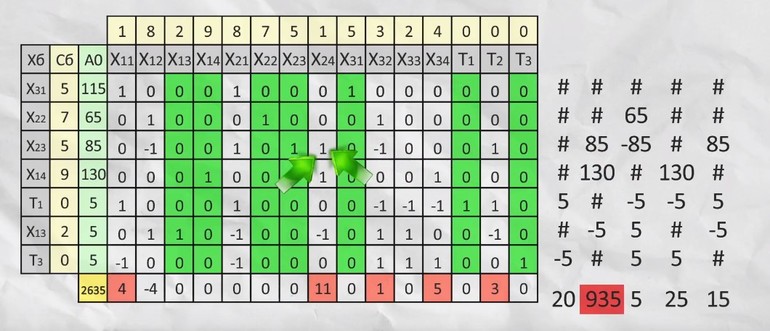
Записываем уравнение ограничения. Сумма всего перевезённого песка с первого карьера должна быть меньше или равна 140. Поэтому можно записать: x11+x12+x12+x14+T1 = 140, где Т1 переменная для хранения остатка. Сумма ограничений будет записана как х11+х21+х31 =115. Аналогичные уравнения составляют и для оставшихся карьеров.
Теперь формируют матрицу, на основании которой с помощью свойства матриц ищется единичный базис. Например, вычесть из одной строки другую. Все отрицательные значения последнего столбца убирают. Для этого из каждой строки вычитают наименьшее значение, а последнее отрицательное число умножают на -1. Теперь составляют подробную симплекс-таблицу, где:
- A0 – последний столбец из матрицы;
- Сб – стоимость перевозок;
- Х11, Т3 – данные из полученной матрица.
В последней строчке прямоугольника проставляют сумму произведений Сб на этот столбец и вычитают значение суммы перемножения Сб с А0. Делают дополнительное вычисление. Для каждой строки А0 делят на выделенное число, ищут наименьший результат и умножают его на положительные числа из последней строки.
Наибольшее число определяется пересечением ранее выбранных значений, на базе которых создают новый базис. После в соответствии с единичными базисами меняют Сб и Хб. Операцию повторяют до тех пор, пока не исчезнут все положительные числа из последней строки. Заполняют новую таблицу.
Расчёт в Excel
Для включения пакета анализа в программе необходимо перейти в раздел «Параметры» и выбрать строчку «Перейти». В новом окне найти строчку «Пакет анализа», кликнуть по ней и нажать кнопку ОК.
Затем понадобится загрузить и открыть шаблон для проверки в Excel. Используя манипулятор типа «мышь» или клавиатуру, выбрать ячейку G4 и выполнить команду «Сервис/Поиск решения». Далее указать исходные данные, а после нажать кнопку «Выполнить».
Полученное решение можно представить в форме отчёта, содержащего:
- Результаты – содержит информацию об исходных и конечных значениях целевой и влияющих ячеек, дополнительные сведения об ограничениях.
- Устойчивость — отчёт, включающий данные о чувствительности решения к малым изменениям.
- Пределы – включают исходные и конечные значения, а также верхние и нижние границы значений, которые принимают влияющие ячейки при введённых ограничениях.
Онлайн-сервис для чайников
Метод решения относится к высшей математике, поэтому в нём довольно трудно разобраться даже подготовленному человеку, не говоря уже о чайнике. Существует некоторое количество сайтов с подробным онлайн-решением методом симплекса. На таких сервисах предлагается ввести количество переменных и строк (ограничений). А далее просто заполнить симплекс-таблицу и нажать расчёт. Причём при необходимости вводимые данные можно править, тем самым видеть, как изменяется результат от изменения исходной информации.
Удобным является ещё и то, что обычно на сайтах предлагается создать шаблон решения в Excel или Maple. Решаться любая задача будет почти мгновенно. Подробно можно выполнить расчёт онлайн-калькулятор по методу симплекса на следующих сайтах:
- «Семестр» (semestr.ru).
- «Мир математики» (matworld.ru).
- «Высшая математика» (math-pr.com).
- «Матзона» (mathzone.ru).
- «Контрольная работа» (kontrolnaya-rabota.ru).
Выполнить расчёт с помощью онлайн-сервисов сможет любой. При этом вероятность ошибки в ответе стремится к нулю. Тем более что для решения задачи даже необязательно знать принцип симплекс-метода.
Цель
работы.
Освоение
технологии решения задач линейного
программирования симплекс-методом в
табличном процессоре Excel.
Содержание
лабораторной работы.
Дана
задача линейного программирования.
Требуется найти решение ЗЛП в табличном
процессоре EXCEL
симплекс – методом.
Задание
на лабораторную работу.
Вариант
6.
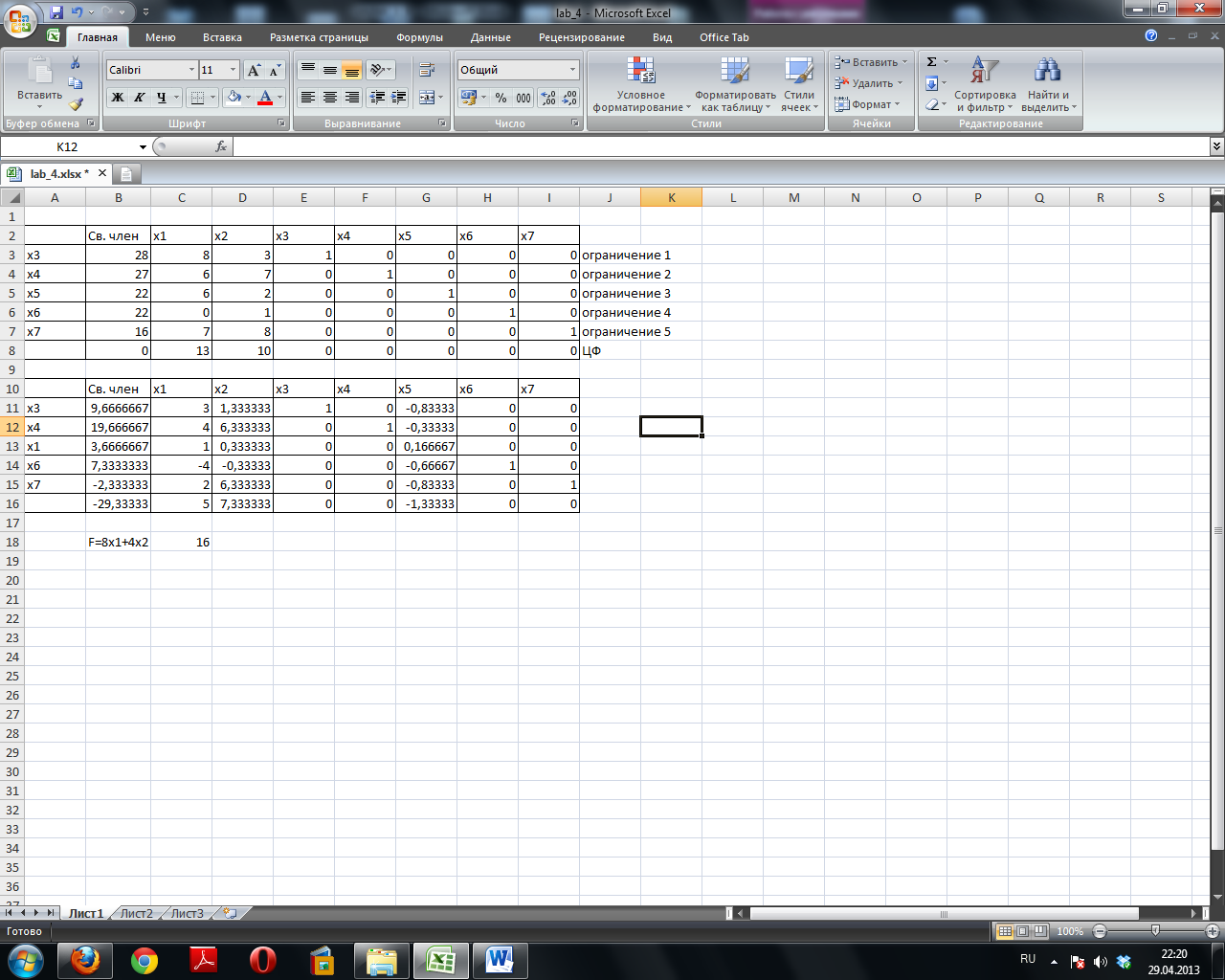
Задача:
На
арендном предприятии для изготовления
двух типов кабеля Аи В выполняется пять
технологических операций. Нормы затрат
времени на изготовление1000 м кабеля
каждого вида по каждой операции, доход
от реализации 1000 м кабеля, а также общий
фонд рабочего времени по каждой операции
приведены в табл. 4.5. Определить оптимальный
выпуск продукции, при котором будет
получен наибольший доход.
Таблица
1.
|
Вид технологической операции |
Нормы |
Общий |
|
|
Типа |
Типа |
||
|
Получение |
8 |
3 |
28 |
|
Изоляция |
6 |
7 |
27 |
|
Скручивание |
6 |
2 |
22 |
|
Освинцовывание |
0 |
1 |
22 |
|
Испытание |
7 |
8 |
16 |
|
Доход |
13 |
10 |
Построим
модель:

Избавимся
от неравенств в ограничениях, введя в
ограничения неотрицательные балансовые
переменные, и перейдём к каноническому
виду:


Составим
опорный план
Рис.
1
Теперь
выберем разрешающий столбец. В нашем
случае это столбец С, поскольку в нём
находится наибольшее положительное
значение целевой функции. После этого
выбираем разрешающий элемент( min
{bi/aij}),
в нашем случае это элемент С7.
Рис.
2
Далее
составляем новую симплекс – таблицу,
в которой элементы разрешающей строки
делятся на разрешающий элемент. Элементы
разрешающей строки и столбца становятся
равны 0, кроме разрешающего элемента.
Остальные элементы определяются по
правилу прямоугольника (сумма произведений
главной и побочной диагонали делить на
разрешающий элемент).
Рис.
3
В
новой симплекс – таблице значения
целевой функции равны нулю или меньше
нуля, а это значит, что найдено оптимальное
решение:
х1
= 2,3; х2
= 0; х3
= 9,71; х4
= 13,29; х5
= 8,29; х6
= 22; x7
= 0; Fmax
= 29,71
Ответ:
для достижения максимального дохода,
который составит 26 ед. необходимо
выпустить 2 единицы изделий типа А и
отказаться от выпуска изделий типа В.
Ответы
на контрольные вопросы.
1.
Как построить первоначальный опорный
план задачи линейного программирования?
Для
построения опорного плана необходимо
построить модель ЗЛП в каноническом
виде и преобразовать её в симплекс –
таблицу для дальнейших преобразований.
2.
Перечислите условия оптимальности
опорного плана.
План
считается оптимальным, если в строке
целевой функции симплекс – таблицы все
элементы равны нулю или меньше него.
Если есть положительные числа, то
необходимо перейти к новому опорному
плану, который даст более оптимальное
значение.
3.
Как определяется вектор для включения
в базис, если первоначальный план
неоптимальный?
Для
определения разрешающего столбца нужно,
для задачи на максимум, в целевой строке
выбрать из отрицательных элементов
наибольший по модулю, а в задаче на
минимум выбрать наибольший положительный
элемент. Столбец, в котором расположен
выбранный элемент и будет являться
разрешающим.
4.
Когда линейная функция не ограничена
на многограннике решений?
Если
существует такая угловая точка
многогранника решений, в которой линейная
функция задачи линейного программирования
достигает своего оптимума, то эта точка
называется оптимальным решением, если
такой точки нет, значит функция не
ограничена на многограннике решений.
5.
Как определить вектор, подлежащий
исключению из базиса?
Чтобы
определить вектор подлежащий исключению
из базиса, необходимо найти отношение
свободных членов к элементам разрешающего
столбца. Строку с наименьшим отношением
исключают.
Элемент,
расположенный на пересечении разрешающей
строки и разрешающего столбца называется
разрешающим.
6.
Какой метод решения систем линейных
уравнений лежит в основе симплексного
метода?
В
основе решения задач линейного
программирования лежит метод замещения
одного опорного плана другим, в котором
целевая функция достигает своего
оптимального значения. Указанное
замещение возможно, если известен
некоторый исходный опорный план.
7.
Какую простейшую геометрическую
интерпретацию можно дать симплексному
методу?
Геометрической
интерпретацией симплексного метода
является выпуклый многогранник.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #