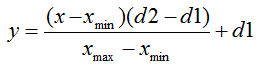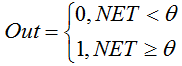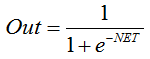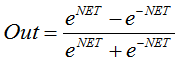A sigmoid function is a mathematical function that has an “S” shaped curve when plotted.
The most common example of a sigmoid function is the logistic sigmoid function, which is calculated as:
F(x) = 1 / (1 + e-x)
To calculate the value of a sigmoid function for a given x value in Excel, we can use the following formula:
=1/(1+EXP(-A1))
This formula assumes the x value is located in cell A1.
The following example shows how to use this formula in practice.
Example: Calculate Sigmoid Function in Excel
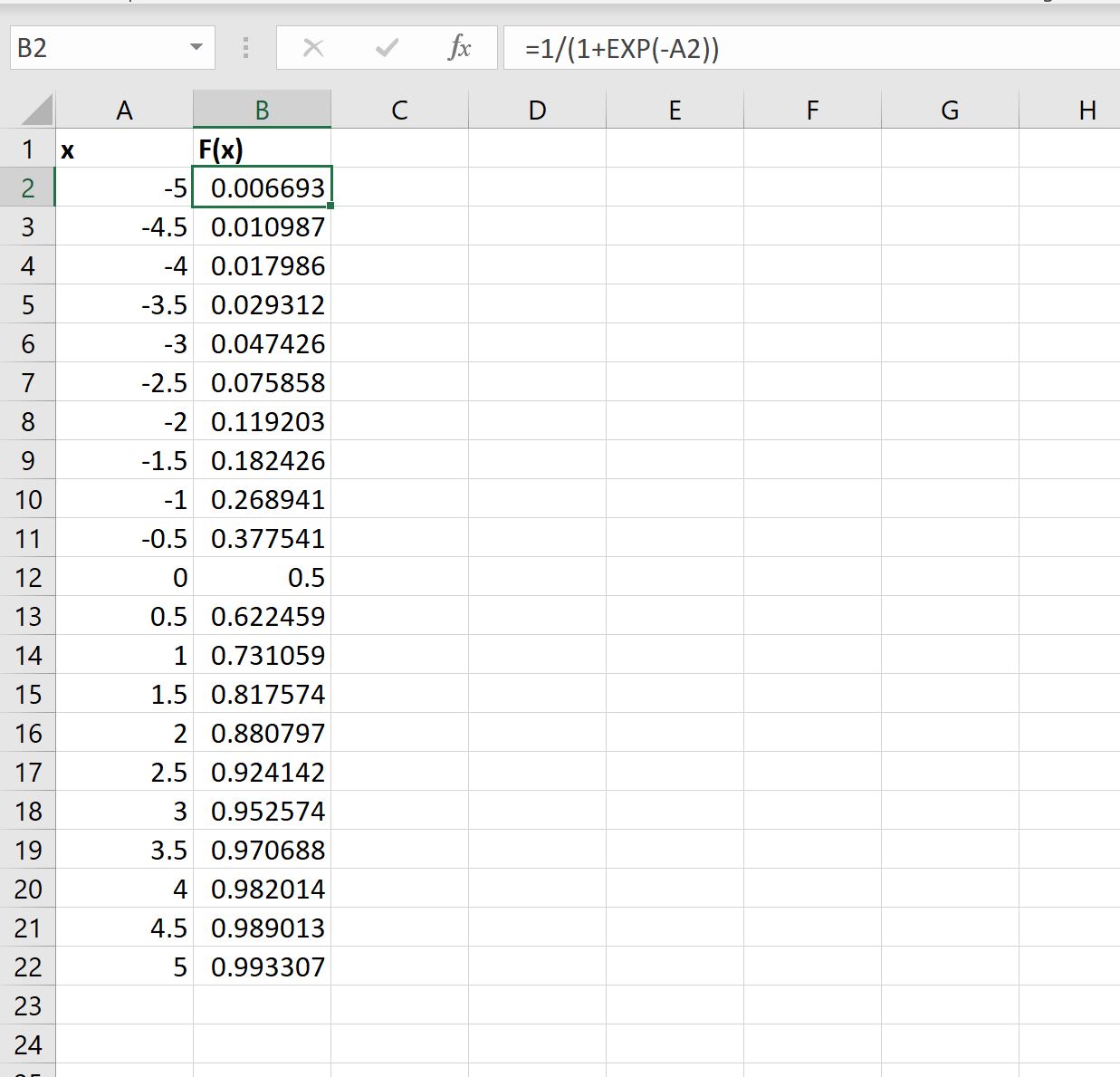
Suppose we have the following list of x values in a column in Excel:
To calculate the value of the sigmoid function for each x value, I can type the following formula into cell B2:
=1/(1+EXP(-A2))
I can then drag this formula down to every remaining cell in column B to calculate the value of the sigmoid function for each x value:
We can then create a line plot to visualize the values of the sigmoid function.
First, highlight every value in column A and B:
Then click the Insert tab along the top ribbon. Then click the Charts group and click the chart titled Scatter with Smooth Lines and Markers:
Once you click this, the following line chart will appear:
The x-axis displays the x values and the y-axis displays the value of the sigmoid function for each x value.
Notice that the plot exhibits the “S” shaped curve that is characteristic of a sigmoid function.
Additional Resources
The following tutorials explain how to perform other common operations in Excel:
How to Perform Curve Fitting in Excel
How to Fit a Polynomial Curve in Excel
How to Create a Bell Curve in Excel
17 авг. 2022 г.
читать 2 мин
Сигмовидная функция — это математическая функция, которая при построении имеет S-образную кривую.
Наиболее распространенным примером сигмовидной функции является логистическая сигмоидальная функция, которая рассчитывается как:
F(x) = 1/(1 + e- x )
Чтобы вычислить значение сигмовидной функции для заданного значения x в Excel, мы можем использовать следующую формулу:
=1/(1+EXP(- A1 ))
Эта формула предполагает, что значение x находится в ячейке A1 .
В следующем примере показано, как использовать эту формулу на практике.
Пример: расчет сигмовидной функции в Excel
Предположим, у нас есть следующий список значений x в столбце Excel:
Чтобы вычислить значение сигмовидной функции для каждого значения x, я могу ввести следующую формулу в ячейку B2 :
=1/(1+EXP(- A2 ))
Затем я могу перетащить эту формулу в каждую оставшуюся ячейку в столбце B, чтобы вычислить значение сигмовидной функции для каждого значения x:
Затем мы можем создать линейный график для визуализации значений сигмовидной функции.
Сначала выделите каждое значение в столбцах A и B:
Затем щелкните вкладку « Вставка » на верхней ленте. Затем щелкните группу « Диаграммы » и щелкните диаграмму « Разброс с плавными линиями и маркерами» :
После того, как вы нажмете на нее, появится следующая линейная диаграмма:
По оси x отображаются значения x, а по оси y — значение сигмовидной функции для каждого значения x.
Обратите внимание, что на графике изображена S-образная кривая, характерная для сигмовидной функции.
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные операции в Excel:
Как выполнить подбор кривой в Excel
Как подогнать полиномиальную кривую в Excel
Как создать кривую нормального распределения в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
DColin
asked on 1/15/2012
Hi Experts,
Please look at the attached Excel worksheet. I would like to know how to change the formula in column B so that the Y axis goes from 0 to +1 instead of -1 to +1.
sigmoid-01.xls
Math / ScienceMicrosoft Excel
Last Comment
TommySzalapski
8/22/2022 — Mon
Try Formula in A1:
=1/(1+EXP(-A1))
THIS SOLUTION ONLY AVAILABLE TO MEMBERS.
View this solution by signing up for a free trial.
Members can start a
7-Day free trial
and enjoy unlimited access to the platform.
THIS SOLUTION ONLY AVAILABLE TO MEMBERS.
View this solution by signing up for a free trial.
Members can start a
7-Day free trial
and enjoy unlimited access to the platform.
@Ankit27
Ok, it seems you want econometric models, for which you will probably need to use maximum likelihood to calculate the parameters of the distributions. Not that it can’t be done in Excel, but I don’t remember how to go about fitting the logistic function to the data (and the logistic IS sigmoidal, so I don’t understand part of your question). But this isn’t an Excel issue, but one of econometrics (or biostatistics, …). You’ll have better luck getting a book on the subject and finding a user group on, say, usenet, replete with statisticians.
I asked for your objective in order to get an idea of the intended use for your curve-fits. There are so many criteria that determine what you even mean by a fit. Some objectives — say Monte Carlo simulation — even obviate the need for a fit.
When posting, explain the axes; are you looking for, say,how the probability of the cream being useful varies with time of application? That points towards the logistic (aka logit) model; I don’t see how the Weibul comes into the picture, which isn’t to say it doesn’t.
Excel’s trendline/regression routines are using ordinary least squares for the fits. You cannot adapt them to what you stated you wanted: again, someone who knows statistics well will almost certainly recommend maximizing the likelihood (in this case the log-likelihood) of your data, which by the way seem overly aggregated for the task.
There are other ways to «fit a curve» that are nonparametric and might be more useful. Posting your intended use of the curve will make answering your question easier.
Groups dealing with R (the language) might be the first place to look. Given the breadth of topics on Usenet, there are probably groups just devoted to statistics. Worth a look. You could also try a local university: a lot of marketing professors and economists are well-versed in the use of the logit model, among others. And perhaps try Redit?
Hope this helped.
Введение
В наше время, наверное, каждый трейдер слышал о нейронных сетях и знает, как это круто. В представлении большинства те, которые в них разбираются, это какие-то чуть ли не сверхчеловеки. В этой статье я постараюсь рассказать, как устроена нейросеть, что с ней можно делать и покажу практические примеры её использования.
Понятие о нейронных сетях
Нейронные сети – это одно из направлений исследований в области искусственного интеллекта, основанное на попытках воспроизвести нервную систему человека, а именно: способность нервной системы обучаться и исправлять ошибки, что должно позволить смоделировать, хотя и достаточно грубо, работу человеческого мозга.
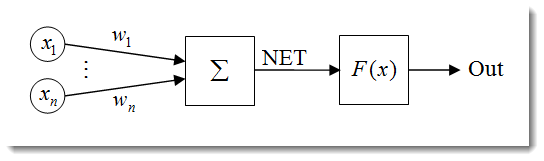
Нейронная сеть состоит, как это ни странно, из нейронов.
Рис. 1. Структурная схема нейрона
Структуру нейрона можно представить из следующих блоков:
- Входные сигналы
;
- Весовые коэффициенты
;
- Сумматор
и его выход
;
- Функция активации нейрона
;
- Выходной сигнал
.
У нейронной сети много свойств, но самым главным является ее способность к обучению. Процесс обучения сети сводится к изменению весовых коэффициентов .
в данном случае и есть результат вычислений нейрона.
Результаты вычислений предаются на выход не напрямую, а через функцию активации, о которой мы поговорим позже. Одним словом, нейронную сеть можно представить в виде «черного ящика», на вход которого мы подаем сигналы, а на выходе получаем результат.
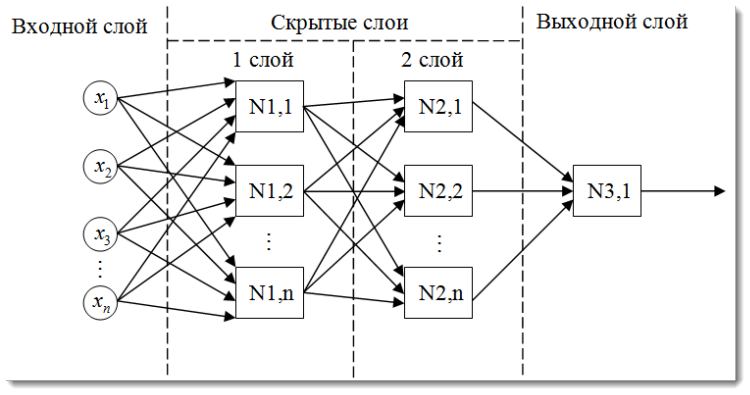
Рис. 2. Структурная схема многослойной нейронной сети
А так будет выглядеть многослойная нейронная сеть. Она включает в себя:
- Входной слой — служит для распределения данных по сети и не производит никаких вычислений. Выходы этого слоя передают сигналы на входы следующего слоя (скрытого или выходного);
- Выходной слой — обычно содержит один нейрон (может и больше), который выдает результат расчетов всей нейронной сети. На основании это сигнала строится дальнейшая логика управления советника;
- Скрытые слои — слои обычных нейронов, которые передают сигналы от входа к выходу. Их входом служит выход предыдущего слоя, а выход — входом следующего слоя.
В данном примере была рассмотрена нейронная сеть с двумя скрытыми слоями, хотя возможны варианты и с большим количеством слоев.
Нормализация входных данных
Нормализация входных данных — это процесс, при котором все входные данные проходят процесс «выравнивания», т.е. приведения к интервалу [0,1] или [-1,1]. Если не провести нормализацию, то входные данные будут оказывать дополнительное влияние на нейрон, что приведет к неверным решениям. Другими словами, как можно сравнивать величины разных порядков?
В общем виде формула нормализации выглядит так:
где:
Поясню сказанное на примере:
Пусть есть n входных данных из интервала [0,10], тогда = 0, а
= 10. Данные будем приводить к интервалу [0,1], тогда
= 0, а
= 1. Теперь, подставив все значения в формулу, можно вычислить нормализованные значения для любого x из n входных данных.
На языке MQL5 это выглядит следующим образом:
double d1=0.0; double d2=1.0; double x_min=iMA_buf[ArrayMinimum(iMA_buf)]; double x_max=iMA_buf[ArrayMaximum(iMA_buf)]; for(int i=0;i<ArraySize(iMA_buf);i++) { inputs[i]=(((iMA_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; }
Сначала мы указываем крайние значения для выходного значения, после получаем минимальное и максимальное значения индикатора (копирование данных с индикатора пропущено, но к примеру там может быть 10 последних значений). Последним шагом произведем в цикле нормализацию каждого входного элемента (значения индикатора на различных барах) и сохраним в массив для дальнейшей работы с ним.
Функции активации нейронов
Функция активации нейрона — это функция, которая вычисляет выходной сигнал нейрона. На вход этой функции подается сумма всех произведений сигналов и весов этих сигналов (далее, средневзвешенная сумма):
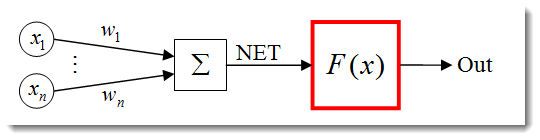
Рис. 3. Структурная схема нейрона с выделенной функцией активации
Функция активации в общем виде будет выглядеть так:
где:
Основные виды функций активации:
-
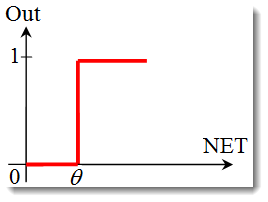
Единичный скачок или жесткая пороговая функция.
Функция описывается следующей формулой:
Пока средневзвешенная сумма меньше определенного значения, функция активации возвращает ноль, а когда становится больше — единицу. -
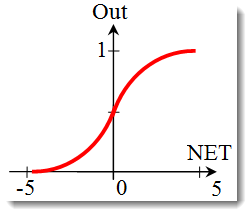
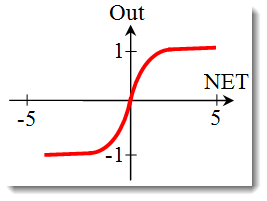
Сигмоидальная функция или сигмоид.
Формула, описывающая сигмоид:
Часто применяется в многослойных нейронных и других сетях с непрерывными сигналами. Гладкость и непрерывность функции — важные положительные качества. -
Гиперболический тангенс.
Формула:
или
Также часто применяется в сетях с непрерывными сигналами. Ее особенность в том, что она может возвращать отрицательные значения результата.
Изменение формы функции активации нейрона
В предыдущем разделе мы рассмотрели функции активации. Но есть еще очень важный момент — крутизна функции (кроме жесткой пороговой функции). Рассмотрим более подробно сигмоидальную функцию.
Если обратиться к графику функции, легко заметить, что функция имеет гладкую форму на отрезке [-5,5]. Допустим, у нас есть сеть, состоящая из одного нейрона с 10 входами и одним выходом. Теперь попробуем рассчитать «крайние» значения переменной . На каждый вход будет подаваться нормализованное значение (как я уже говорил в разделе Нормализация входных данных), допустим из интервала [-1,1].
Возьмем отрицательные входные значения, так как функция дифференцируема и при отрицательном аргументе. Весовые коэффициенты будем выбирать тоже из этого интервала. При всех возможных вариантах сочетаний входных данных и весовых коэффициентов получим крайние значения в интервале [-10,10], так как:
На языке MQL5 эта формула будет выглядеть следующим образом:
for(int n=0; n<10; n++) { NET+=Xn*Wn; }
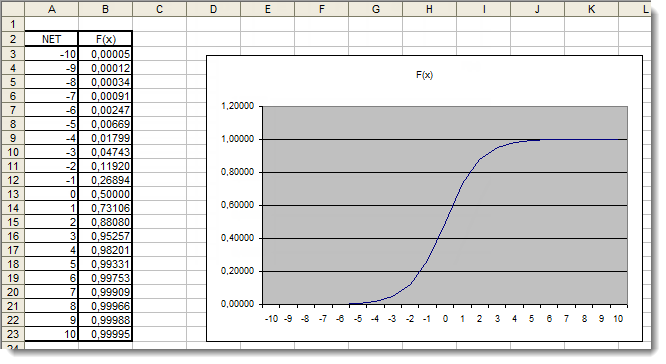
Теперь нужно построить график функции активации в найденном интервале. Для примера возьмем сигмоидальную функцию. Проще всего это сделать в Excel.
Рис. 4. График сигмоидальной функции в Excel
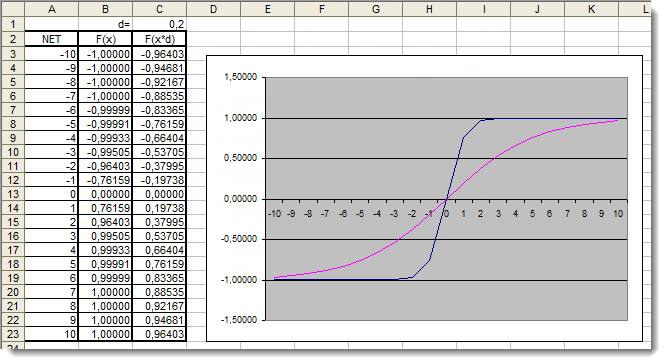
Тут мы видим наглядно, что значения аргумента за пределами интервала [-5,5] никак не влияют на результат. Значит, область значений неполная. Попробуем это исправить. Добавим к аргументу некий добавочный коэффициент d, который расширит область значений.
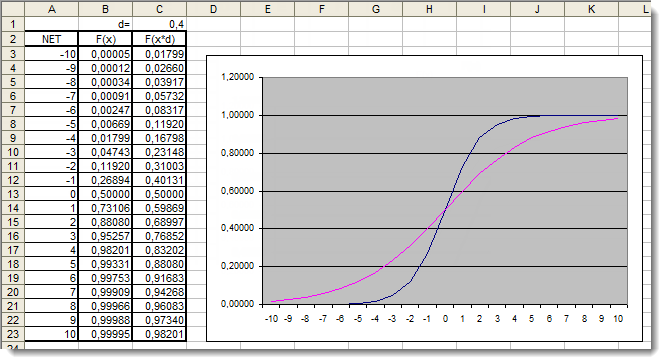
Рис. 5. График сигмоидальной функции в Excel с добавочным коэффициентом
Теперь снова посмотрим графики. Мы добавили добавочный коэффициент d=0.4, который исправил форму функции. Сравнив значения в таблице мы видим, что распределение стало более равномерным. Значит, результат запишем следующим образом:
for(int n=0; n<10; n++) { NET+=Xn*Wn; } NET*=0.4;
Теперь рассмотрим функцию активации гиперболический тангенс. Опуская всю теорию, рассмотренную в предыдущей функции, перейдем сразу к практике. Единственное, что в ней по другому — выход может принадлежать интервалу [-1,1]. Средневзвешенная сумма может принимать значения также из интервала [-10,10].
Рис. 6. График функции гиперболического тангенса в Excel с добавочным коэффициентом
Из рисунка видно, что добавочный коэффициент d=0.2 исправил форму этой функции. Значит, результат запишем следующим образом:
for(int n=0;n<10;n++) { NET+=Xn*Wn; } NET*=0.2;
Таким образом можно править форму любой функции активации.
Практическое занятие
Теперь перейдем к практике. Для начала попробуем описать программно вычисление нейрона, а затем подключим к нему функцию активации. Вспомним, как вычисляется значение нейрона:
double NET; double x[3]; double w[3]; int OnInit() { x[0]=0.1; x[1]=0.8; x[2]=0.5; w[0]=0.5; w[1]=0.6; w[2]=0.3; for(int n=0;n<3;n++) { NET+=x[n]*w[n]; } }
Разберемся:
- Для начала мы объявили переменную для хранения решения нейрона
и два массива: входные данные
и весовые коэффициенты
;
- Расположили мы эти переменные в самом начале, ни в одном из тел функций, для того чтобы сделать глобальными (доступными из любого места программы);
- В функции инициализации OnInit() (вообще можно в любой) мы заполняем массивы входных данных и весовых коэффициентов;
- Далее следует цикл суммирования, n<3 так как у нас всего три входа и соответственно три весовых коэффициента к ним;
- Суммируем средневзвешенные значения входов и записываем все это в переменную
.
С первой задачей разобрались — сумму получили. Теперь очередь функции активации. Приведу код расчета функций активации, описанных в разделе Функции активации нейронов.
Единичный скачок или жесткая пороговая функция
double Out; if(NET>=x) Out=1; else Out=0;
Сигмоидальная функция или сигмоид
double Out = 1/(1+exp(-NET));
Гиперболический тангенс
double Out = (exp(NET)-exp(-NET))/(exp(NET)+exp(-NET));
Соберем все вместе
Для простоты реализации возьмем сеть, состоящую из одного нейрона. Конечно, сетью назвать это тяжело, но главное — понять принцип. Ведь многослойная нейронная сеть состоит из таких же нейронов, где выход предыдущего слоя нейронов является входом для следующего.
Мы воспользуемся уже готовым советником, собранным в статье Быстрый старт или краткий курс для начинающих, но немного его изменив. К примеру, заменим трендовый индикатор Moving Average на осциллятор Relative Strength Index. Параметры индикатора и порядок их следования можно посмотреть во встроенной справке.
#property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "http://www.mql5.com" #property version "1.00" #include <TradeTrade.mqh> #include <TradePositionInfo.mqh> input double w0=0.5; input double w1=0.5; input double w2=0.5; input double w3=0.5; input double w4=0.5; input double w5=0.5; input double w6=0.5; input double w7=0.5; input double w8=0.5; input double w9=0.5; int iRSI_handle; double iRSI_buf[]; double inputs[10]; double weight[10]; double out; string my_symbol; ENUM_TIMEFRAMES my_timeframe; double lot_size; CTrade m_Trade; CPositionInfo m_Position; int OnInit() { my_symbol=Symbol(); my_timeframe=PERIOD_CURRENT; lot_size=SymbolInfoDouble(my_symbol,SYMBOL_VOLUME_MIN); iRSI_handle=iRSI(my_symbol,my_timeframe,14,PRICE_CLOSE); if(iRSI_handle==INVALID_HANDLE) { Print("Не удалось получить хендл индикатора"); return(-1); } ChartIndicatorAdd(ChartID(),0,iRSI_handle); ArraySetAsSeries(iRSI_buf,true); weight[0]=w0; weight[1]=w1; weight[2]=w2; weight[3]=w3; weight[4]=w4; weight[5]=w5; weight[6]=w6; weight[7]=w7; weight[8]=w8; weight[9]=w9; return(0); } void OnDeinit(const int reason) { IndicatorRelease(iRSI_handle); ArrayFree(iRSI_buf); } void OnTick() { int err1=0; err1=CopyBuffer(iRSI_handle,0,1,10,iRSI_buf); if(err1<0) { Print("Не удалось скопировать данные из индикаторного буфера"); return; } double d1=0.0; double d2=1.0; double x_min=iRSI_buf[ArrayMinimum(iRSI_buf)]; double x_max=iRSI_buf[ArrayMaximum(iRSI_buf)]; for(int i=0;i<ArraySize(inputs);i++) { inputs[i]=(((iRSI_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; } out=CalculateNeuron(inputs,weight); if(out<0.5) { if(m_Position.Select(my_symbol)) { if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol); if(m_Position.PositionType()==POSITION_TYPE_BUY) return; } m_Trade.Buy(lot_size,my_symbol); } if(out>=0.5) { if(m_Position.Select(my_symbol)) { if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol); if(m_Position.PositionType()==POSITION_TYPE_SELL) return; } m_Trade.Sell(lot_size,my_symbol); } } double CalculateNeuron(double &x[],double &w[]) { double NET=0.0; for(int n=0;n<ArraySize(x);n++) { NET+=x[n]*w[n]; } NET*=0.4; return(ActivateNeuron(NET)); } double ActivateNeuron(double x) { double Out; Out=1/(1+exp(-x)); return(Out); }
Первое, что нам понадобится, так это обучить нашу сеть. Проведем оптимизация весовых коэффициентов
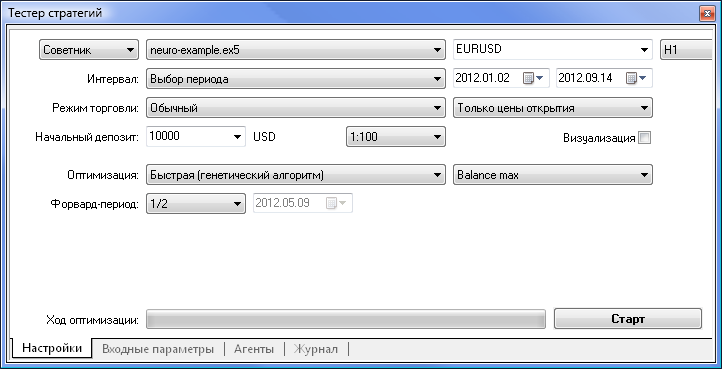
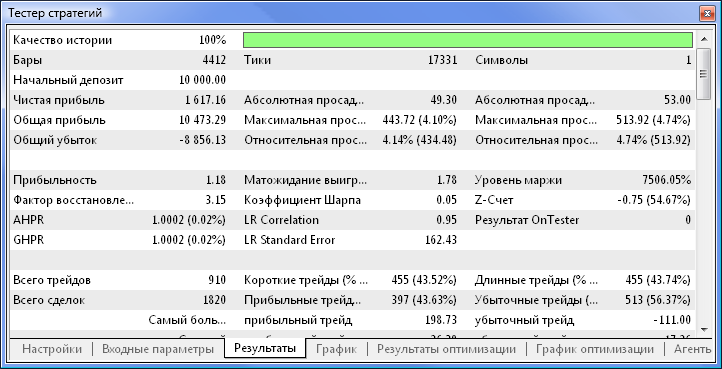
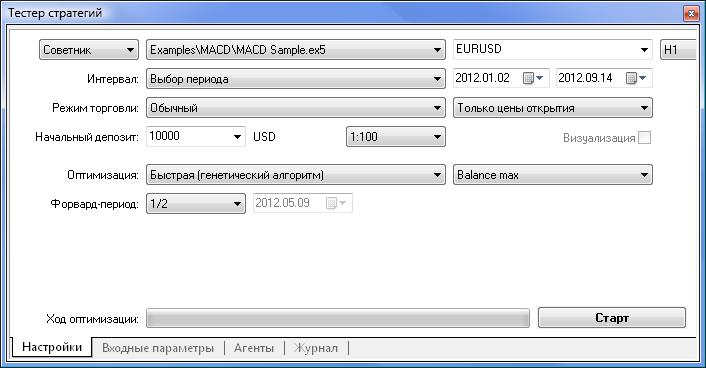
Рис. 7. Тестер стратегий с установленными параметрами
Оптимизацию будем проводить со следующими параметрами:
- Интервал — ну, к примеру, с начала года. Чем больше период, тем меньше будет подгонки под историю и тем качественнее будет результат.
- Режим торговли — обычный, только цены открытия. Нет смысла тестировать на всех тиках, так как наш советник берет 10 последних значений с индикатора, кроме текущего.
- Оптимизация — можно поставить полный перебор, хотя я для быстрого результата воспользовался генетическим алгоритмом. Удобно для оценки алгоритма. Если результат удовлетворяет, можно протестировать полным перебором для более точного результата.
- Форвард-период — 1/2 и больше, позволит оценить, как долго советник сможет работать с полученными результатами до следующей переоптимизации.
- Таймфрейм и Валютная пара — по желанию.
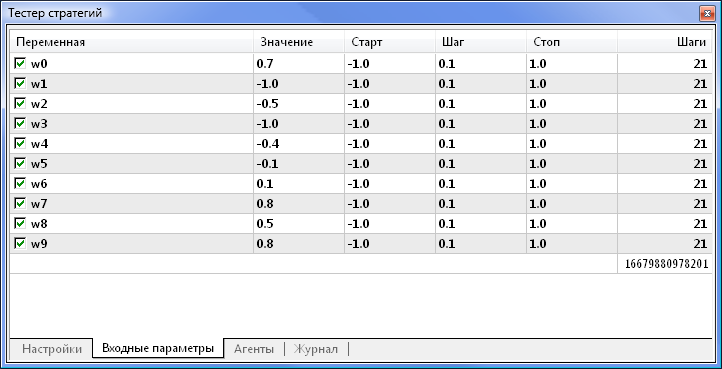
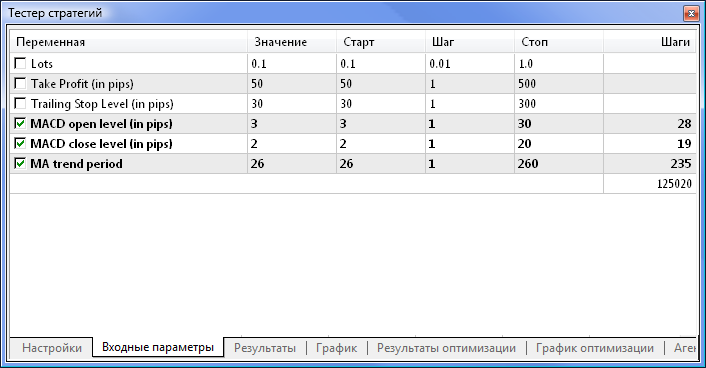
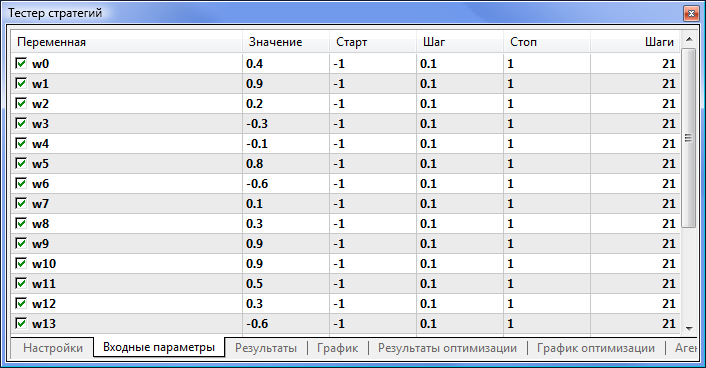
Рис. 8. Указываем параметры для оптимизации и их пределы
Укажем, что будут оптимизироваться все весовые коэффициенты и интервалы для них. Запустим оптимизацию, вернувшись на вкладку «Настройки» и нажав кнопку «Старт».
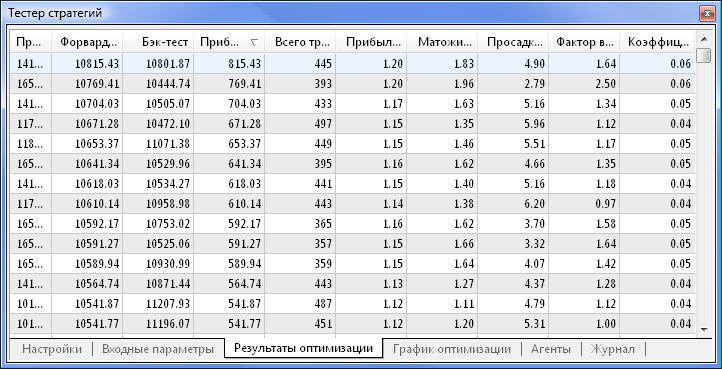
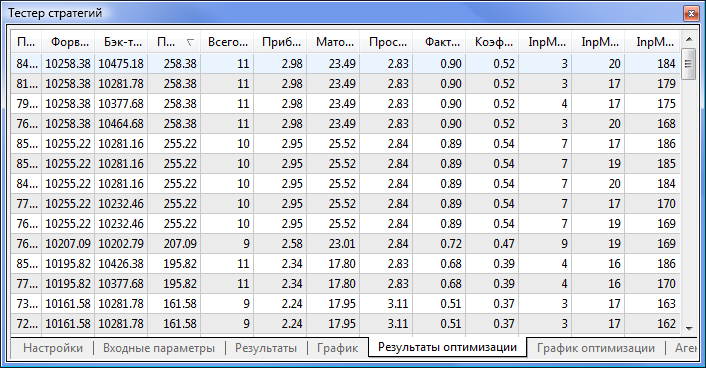
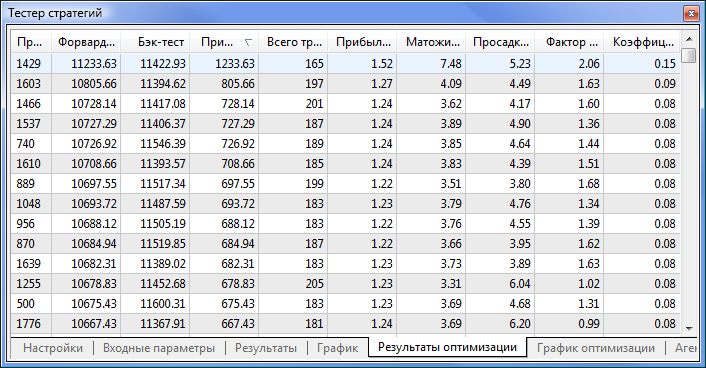
Рис. 9. Полученные данные после оптимизации
После оптимизации на вкладке «Результаты оптимизации» выбираем тот проход, у которого максимальная прибыль (для сортировки по одному из параметров необходимо кликнуть на названию колонки). После можно оценить остальные параметры и при необходимости выбрать желаемый проход.
После делаем двойной клик на нужном проходе — проходит тестирование, с результатами которого можно ознакомиться на вкладках «Результаты» и «График».
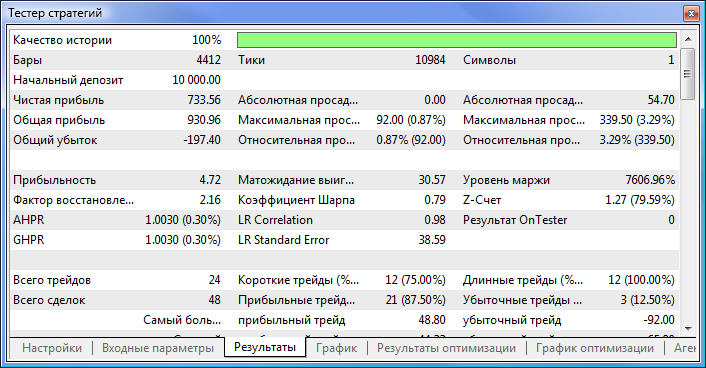
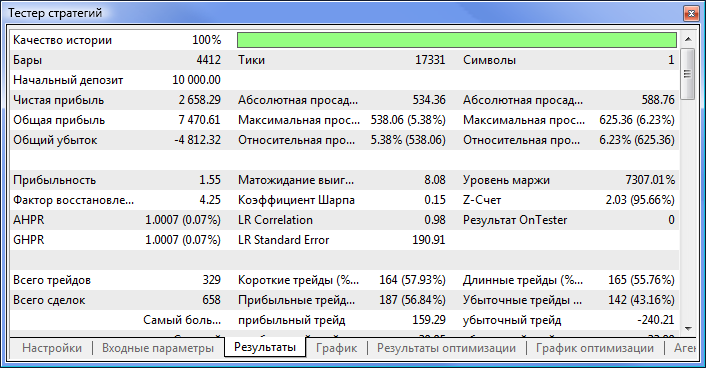
Рис. 10. Отчет тестирования
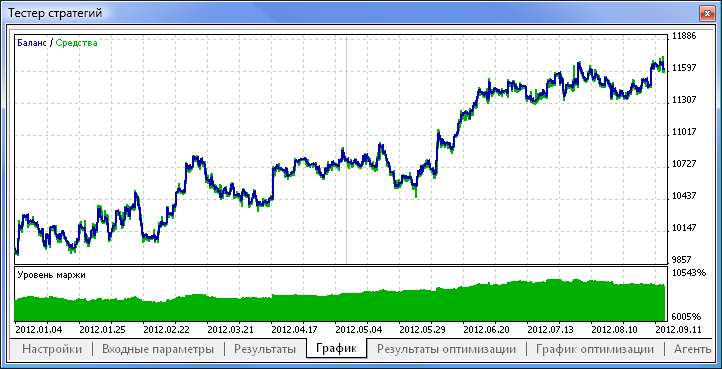
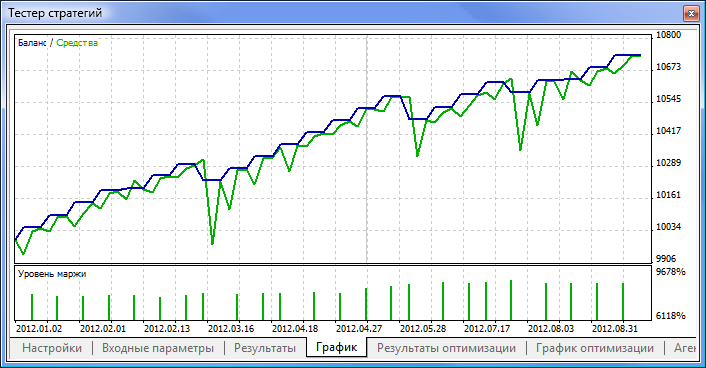
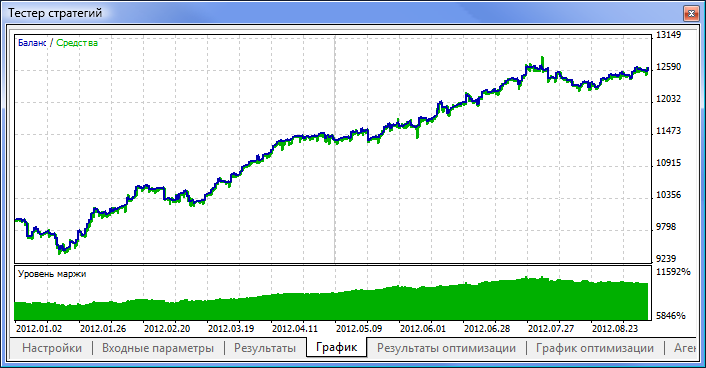
Рис. 11. График баланса
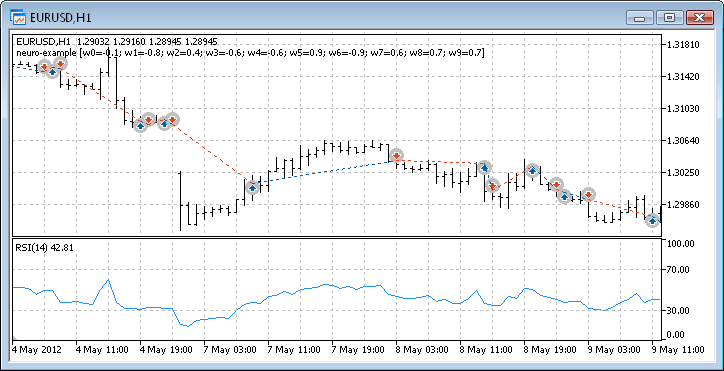
Рис. 12. Пример торговли советника
Вот мы и получили результат. Скажем так, для начала очень даже неплохо. Нужно учесть, что это работа только одного нейрона. Да, пример примитивен, но согласись, что даже он может приносить прибыль.
Преимущества нейронных сетей
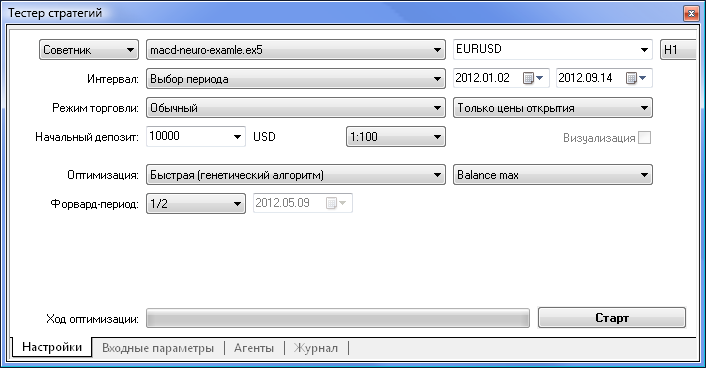
Теперь попробуем сравнить советник на обычной логике с советником на основе нейронной сети. Для примера сравним результаты оптимизации и тестирования советника MACD Sample, идущего в стандартной поставке терминала, с нейронным советником на основе MACD.
Параметры тейк-профита и трейлинг-стопа оптимизировать не будем, так как в нейросетевом советнике они отсутствуют. Попытаемся протестировать советники с одинаковыми показателями: в обоих советниках используется MACD со следующими параметрами:
- Период быстрой средней: 12;
- Период медленной средней: 26;
- Период усреднения разности: 9;
- Тип цены: цена закрытия.
Валютную пару и тайм-фрейм можно задать при тестировании, оставим без изменения EURUSD, H1. Период тестирования одинаковый: по ценам открытия, с начала года.
| MACD Sample | macd-neuro-examle |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Теперь сравним основные параметры протестированных советников:
| Параметр | MACD Sample | macd-neuro-examle |
|---|---|---|
| Чистая прибыль | 733,56 | 2 658,29 |
| Абсолютная просадка по балансу | 0,00 | 534,36 |
| Максимальная просадка по средствам | 339,50 (3,29%) | 625,36 (6,23%) |
| Прибыльность | 4,72 | 1,55 |
| Фактор восстановления | 2,16 | 4,25 |
| Матожидание выигрыша | 30,57 | 8,08 |
| Коэффициент Шарпа | 0,79 | 0,15 |
| Всего трейдов | 24 | 329 |
| Всего сделок | 48 | 658 |
| Прибыльные трейды (% от всех) | 21 (87,50%) | 187 (56,84%) |
| Средний прибыльный трейд | 44,33 | 39,95 |
| Средний непрерывный выигрыш | 5 | 2 |
Рис. 13. Сравнение основных параметров
Заключение
В данной статье мы рассмотрели основные моменты, которые необходимо знать при проектировании советников с использование нейронных сетей. Узнали о структуре нейрона и нейронной сети, видах функций активации и процессе оптимизации, методах исправления формы функции активации и процессе нормализации входных данных. Провели сравнение советников на стандартной логике и на основе нейронных сетей.