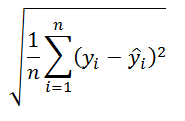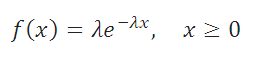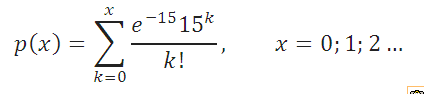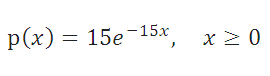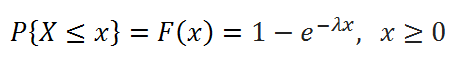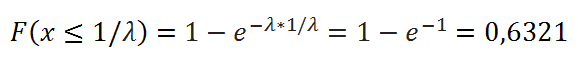17 авг. 2022 г.
читать 3 мин
Экспоненциальное сглаживание — это метод «сглаживания» данных временных рядов, который часто используется для краткосрочного прогнозирования.
Основная идея заключается в том, что данные временных рядов часто имеют связанный с ними «случайный шум», который приводит к пикам и впадинам в данных, но, применяя экспоненциальное сглаживание, мы можем сгладить эти пики и впадины, чтобы увидеть истинную основную тенденцию данных. .
Основная формула для применения экспоненциального сглаживания выглядит следующим образом:
F t = αy t-1 + (1 – α) F t-1
куда:
F t = прогнозируемое значение для текущего периода времени t
α = значение константы сглаживания в диапазоне от 0 до 1.
y t-1 = Фактическое значение данных за предыдущий период времени
F t-1 = Прогнозируемое значение для предыдущего периода времени t-1
Чем меньше значение альфа, тем больше сглаживаются данные временного ряда.
В этом руководстве мы покажем, как выполнить экспоненциальное сглаживание данных временных рядов с помощью встроенной функции в Excel.
Пример: экспоненциальное сглаживание в Excel
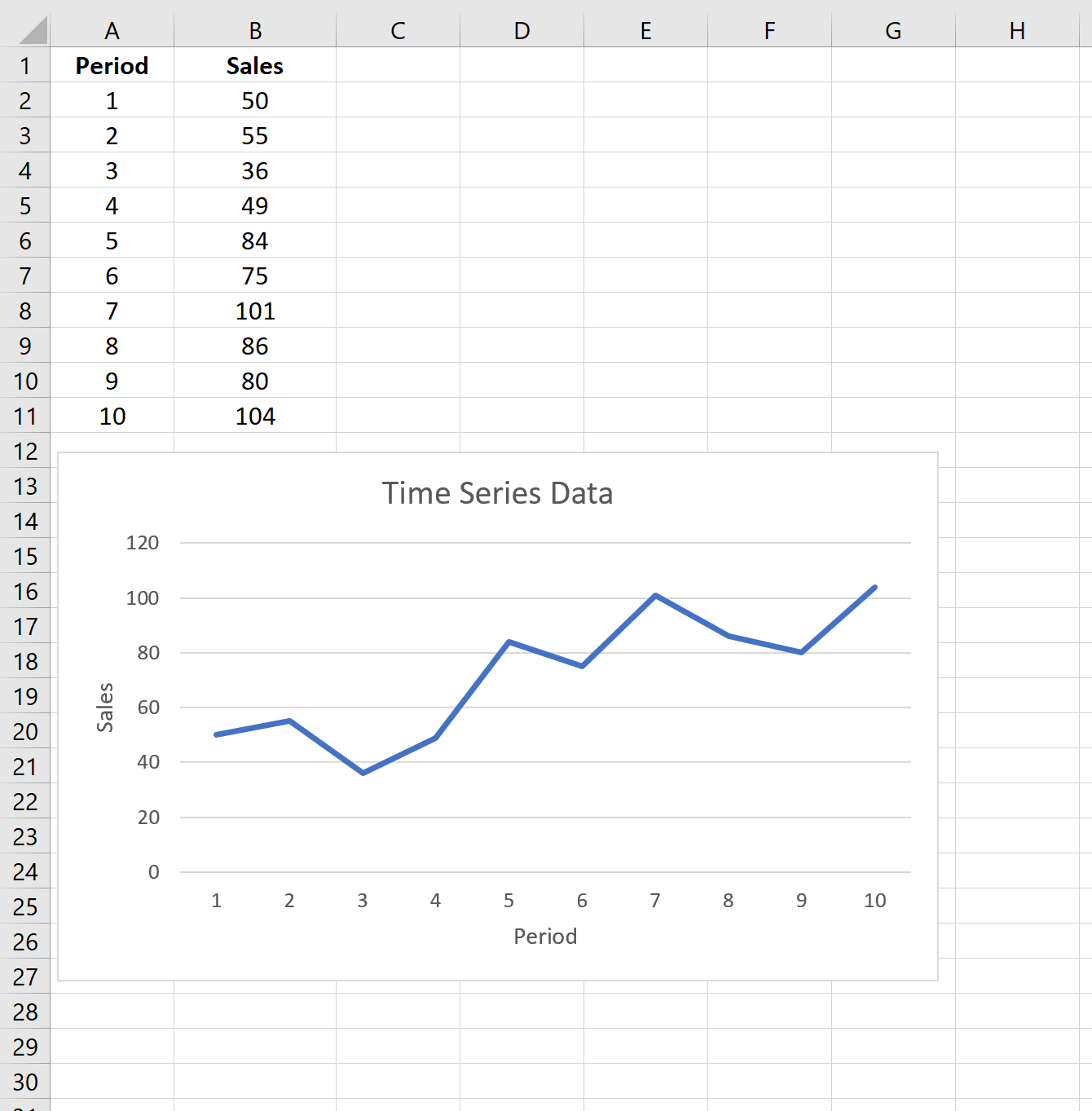
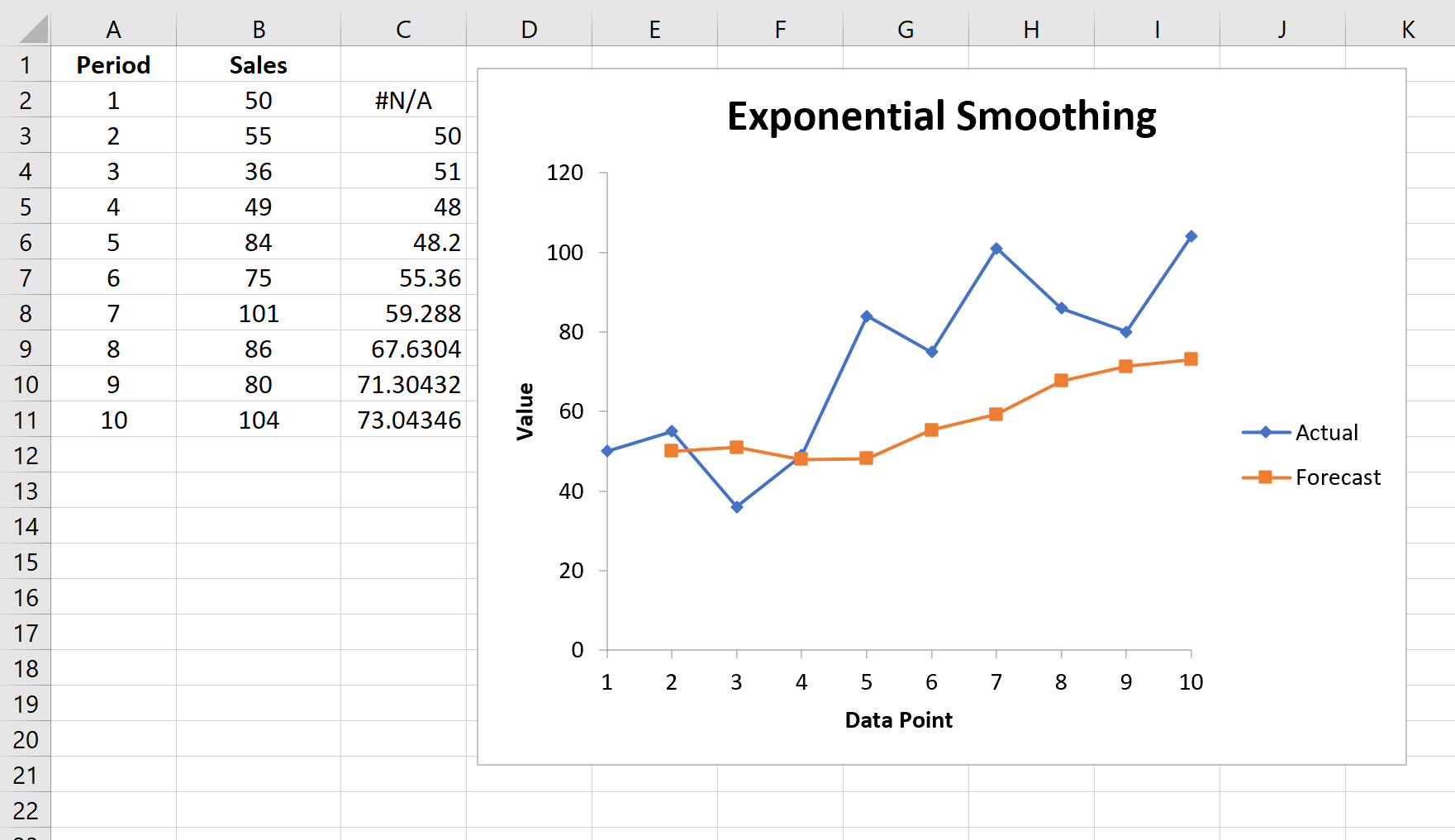
Предположим, у нас есть следующий набор данных, который показывает продажи конкретной компании за 10 периодов продаж:
Выполните следующие шаги, чтобы применить экспоненциальное сглаживание к этим данным временного ряда.
Шаг 1: Нажмите кнопку «Анализ данных».
Перейдите на вкладку «Данные» на верхней ленте и нажмите кнопку «Анализ данных». Если вы не видите эту кнопку, вам нужно сначала загрузить Excel Analysis ToolPak , который можно использовать совершенно бесплатно.
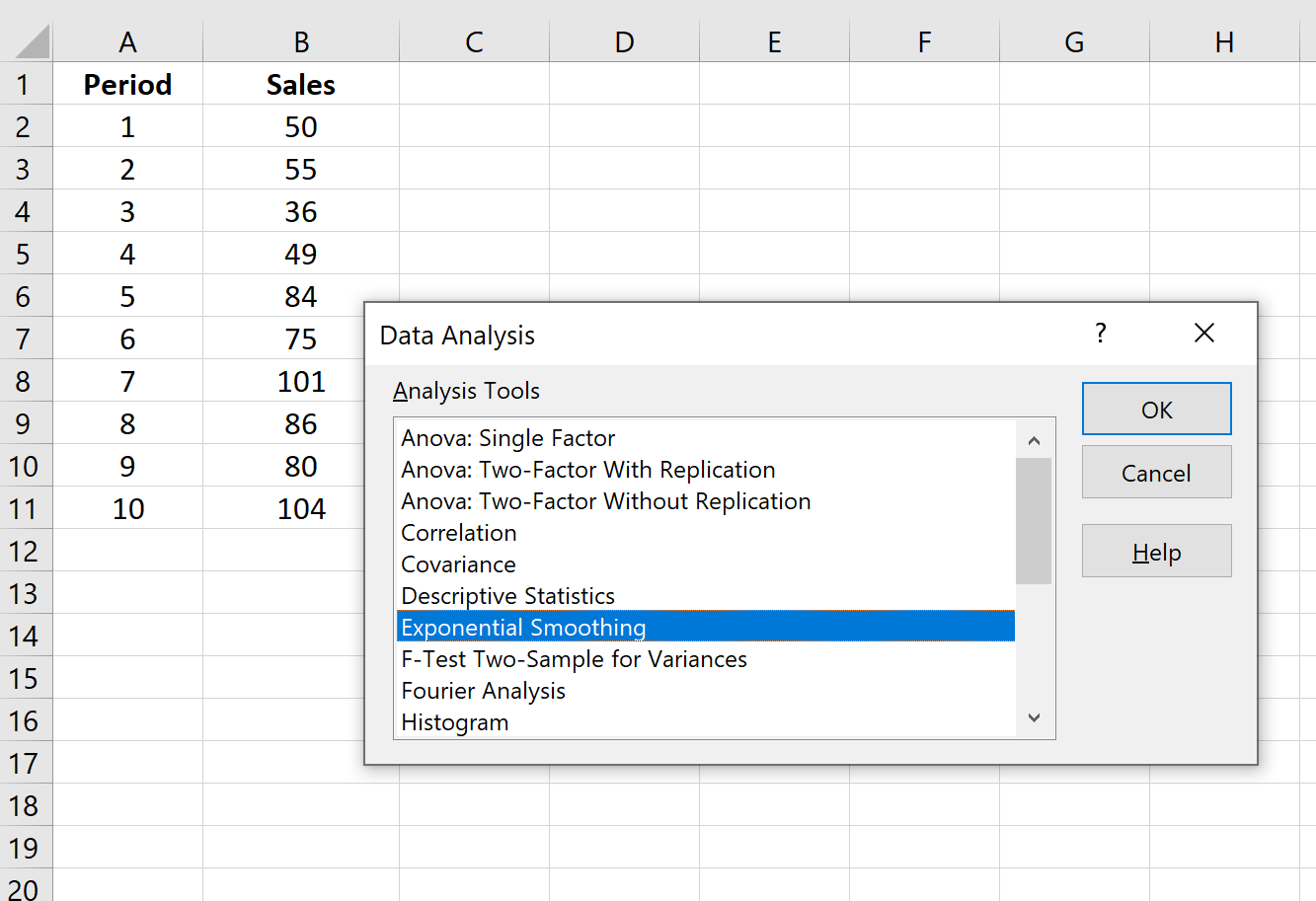
Шаг 2: Выберите параметр «Экспоненциальное сглаживание» и нажмите «ОК».
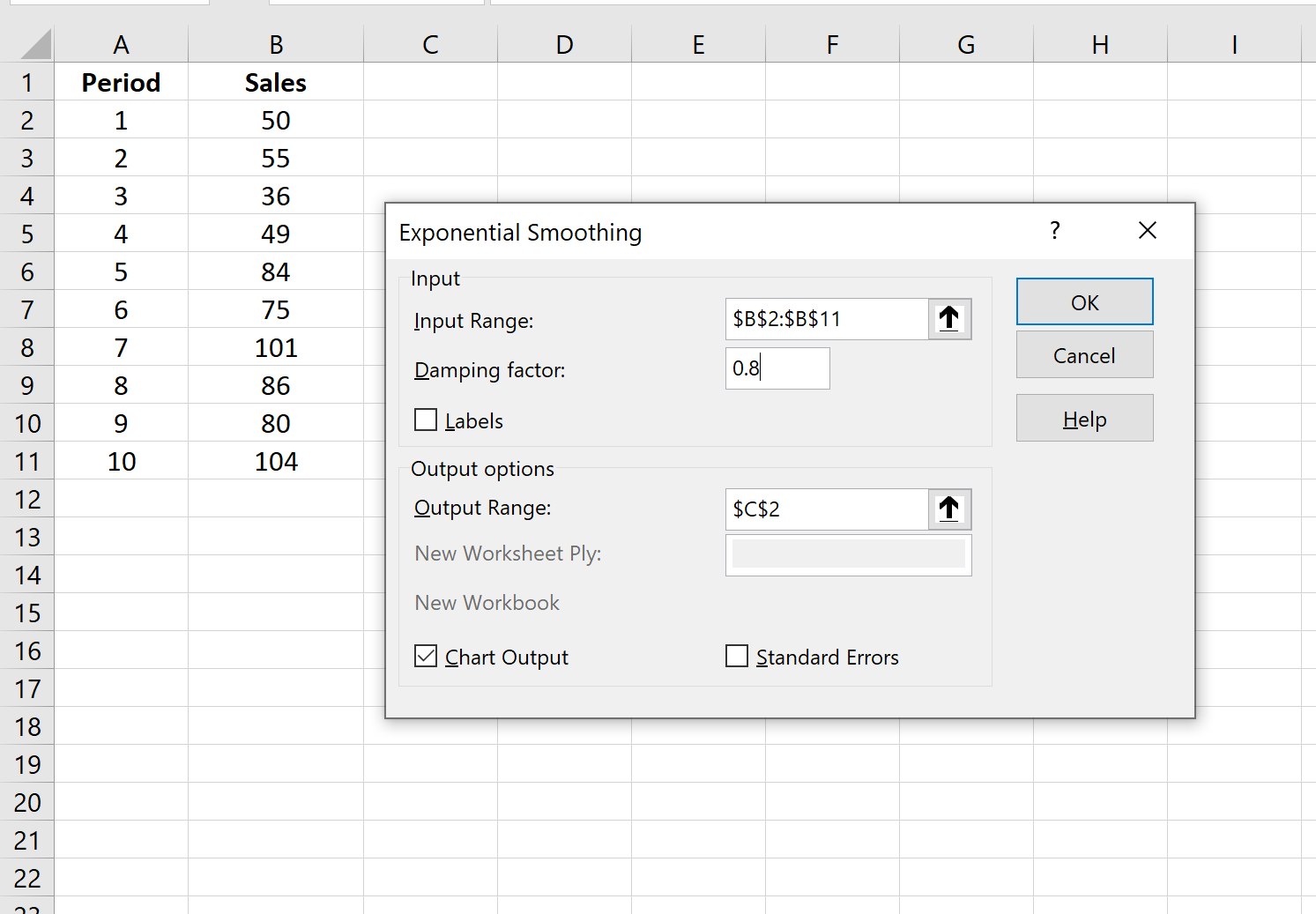
Шаг 3: Заполните необходимые значения.
- Заполните значения данных для Input Range .
- Выберите значение, которое вы хотели бы использовать для коэффициента затухания , которое равно 1-α. Если вы хотите использовать α = 0,2, то ваш коэффициент демпфирования будет 1-0,2 = 0,8.
- Выберите выходной диапазон , в котором должны отображаться прогнозируемые значения. Рекомендуется выбрать этот выходной диапазон рядом с вашими фактическими значениями данных, чтобы вы могли легко сравнивать фактические значения и прогнозируемые значения рядом друг с другом.
- Если вы хотите увидеть диаграмму с фактическими и прогнозируемыми значениями, установите флажок « Вывод диаграммы ».
Затем нажмите ОК.
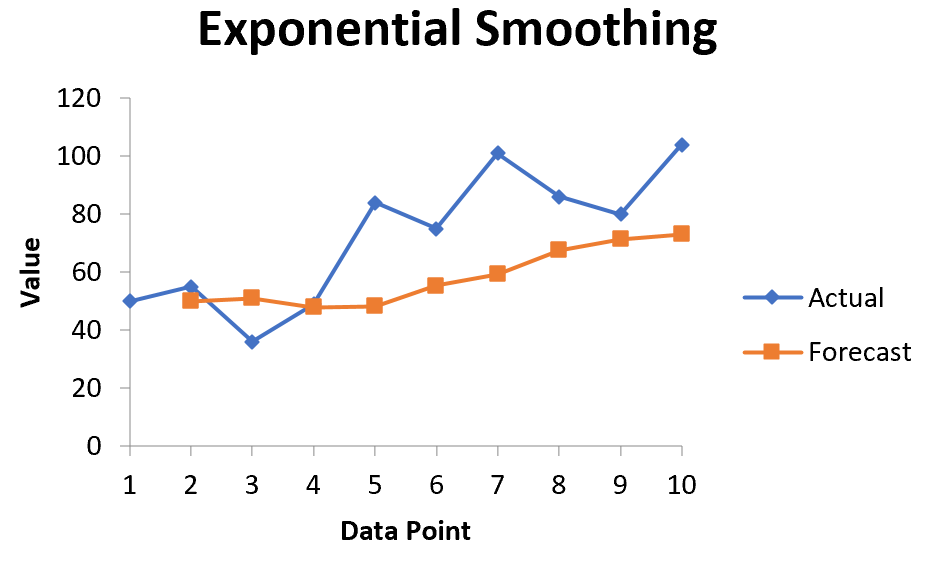
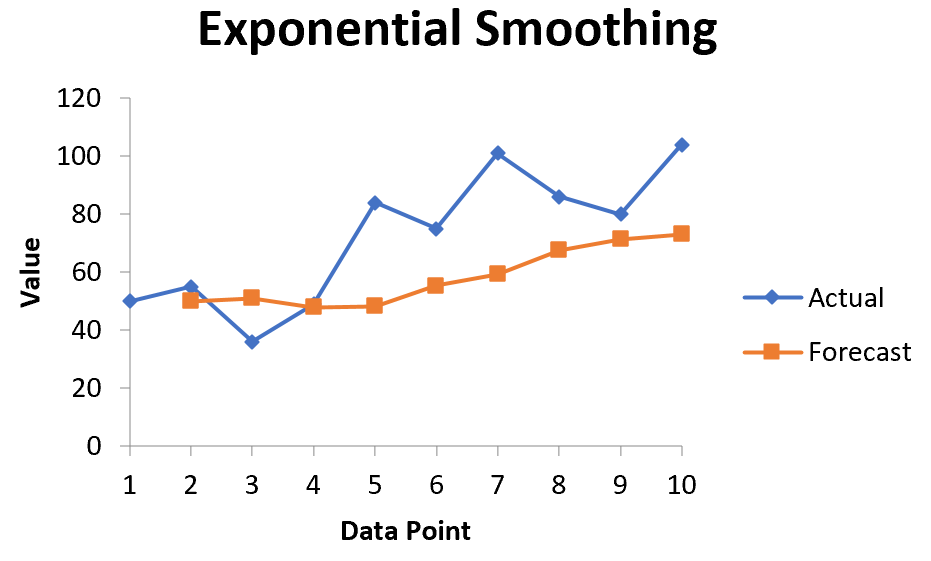
Автоматически появится список прогнозируемых значений и диаграмма:
Обратите внимание, что первый период времени имеет значение #N/A, поскольку нет предыдущего периода времени, который можно было бы использовать для расчета прогнозируемого значения.
Эксперименты с коэффициентами сглаживания
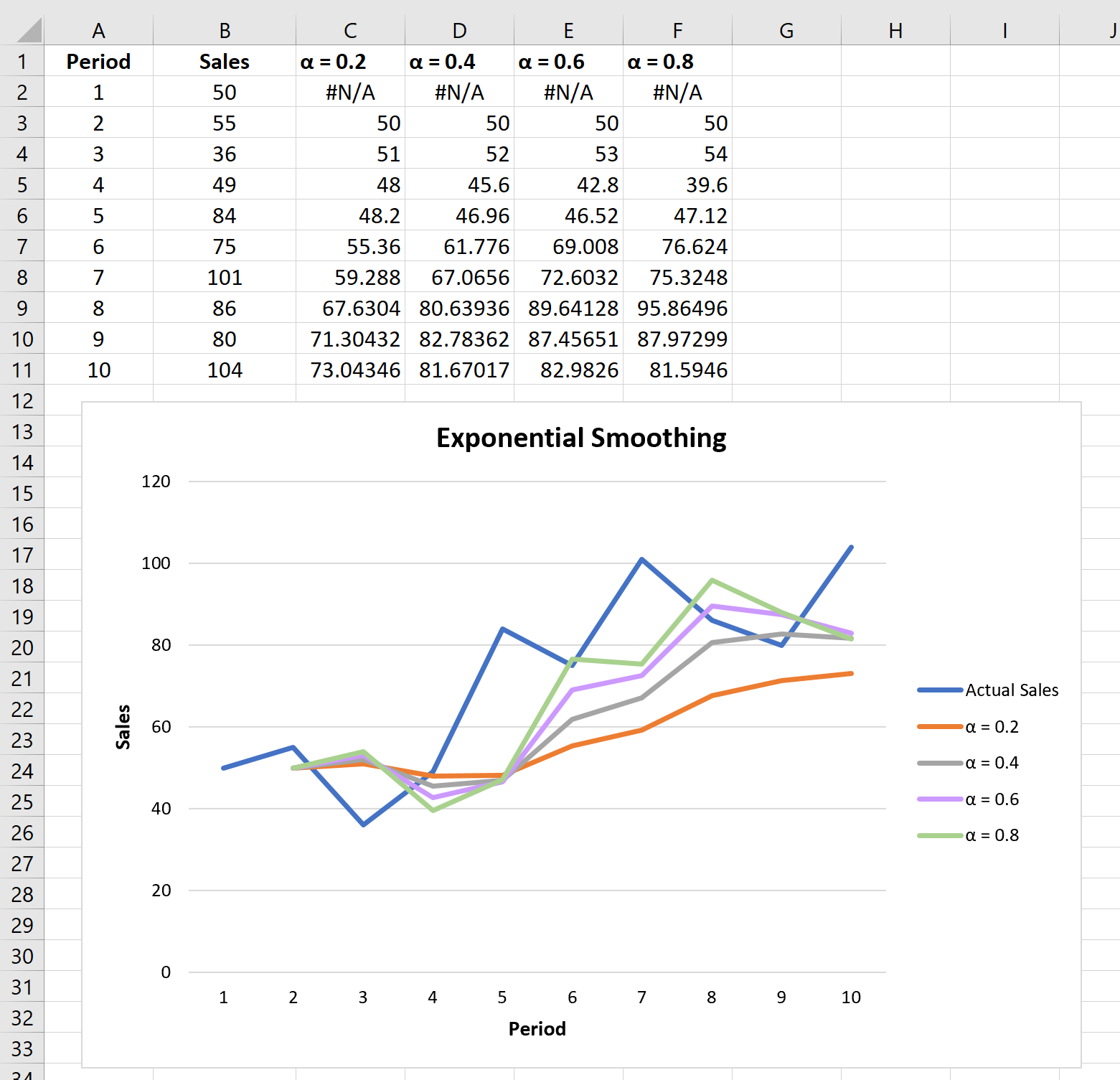
Вы можете поэкспериментировать с различными значениями коэффициента сглаживания α и посмотреть, как он повлияет на прогнозируемые значения. Вы заметите, что чем меньше значение α (больше значение коэффициента затухания), тем более сглаженными будут прогнозируемые значения:
Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашим полным списком руководств по Excel .
history 10 января 2021 г.
- Группы статей
Экспоненциальное сглаживание используется для сглаживания краткосрочных колебаний во временных рядах, чтобы облегчить определение долгосрочного тренда, а также для прогнозирования. Произведем экспоненциальное сглаживание с помощью надстройки MS EXCEL Пакет анализа и формулами. Рассмотрим двойное и тройное экспоненциальное сглаживание для прогнозирования рядов с трендом и сезонностью.
Экспоненциальное сглаживание один из наиболее распространённых методов для сглаживания временных рядов. В отличие от метода Скользящего среднего, где прошлые наблюдения имеют одинаковый вес, Экспоненциальное сглаживание присваивает им экспоненциально убывающие веса, по мере того как наблюдения становятся старше. Другими словами, последние наблюдения дают относительно больший вес при прогнозировании, чем старые наблюдения.
Примечание: Перед прочтением этой статьи рекомендуется прочитать про Скользящее среднее.
Примечание: В англоязычной литературе для экспоненциального сглаживания используется термин Single Exponential Smoothing или Simple Exponential Smoothing (SES).
Напомним, что при усреднении методом Скользящего среднего веса, присвоенные наблюдениям, одинаковы и равны 1/n, где n – количество периодов усреднения. Например, в случае усреднения за 3 периода скользящее среднее равно:
Yскол.i=(Yi+ Yi-1+ Yi-2)/3 = Yi/3+ Yi-1/3+ Yi-2/3
В случае Экспоненциального сглаживания формула выглядит следующим образом:
Yэксп.i=альфа*Yi-1+ (1-альфа)*Yэксп.i-1
или
Yэксп.i= Yэксп.i-1 + альфа*(Yi-1 — Yэксп.i-1)
где 0<альфа<1, i>2
Параметр альфа определяет степень сглаживания. При малых значениях альфа (0,1 – 0,2) имеет место сильное сглаживание. При значениях близких к 1, сглаженный ряд практически повторяет исходный ряд с задержкой (лагом) на один период. Для медленно меняющегося ряда часто берут небольшие значения альфа=0,1; а для быстро меняющегося 0,3-0,5.
Примечание: Формулы представляют собой рекуррентное соотношение – это когда последующий член ряда вычисляется на основе предыдущего.
Примечание: Существует альтернативный подход к Экспоненциальному сглаживанию: в нем в формуле вместо Yi-1 заменяют на Yi. Этот подход используется в контрольных картах экспоненциально взвешенного скользящего среднего (EWMA).
Надстройка Пакет анализа
Получить Экспоненциально сглаженный ряд можно с помощью надстройки Пакет анализа (Analysis ToolPak). Надстройка доступна из вкладки Данные, группа Анализ.
СОВЕТ: Подробнее о других инструментах надстройки Пакет анализа и ее подключении – читайте в статье.
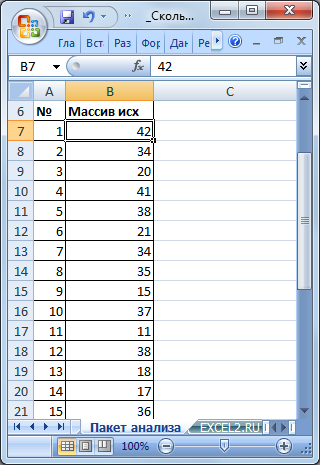
Разместим исходный числовой ряд в диапазоне B7:B32.
Для наглядности пронумеруем каждое значение ряда (столбец А).
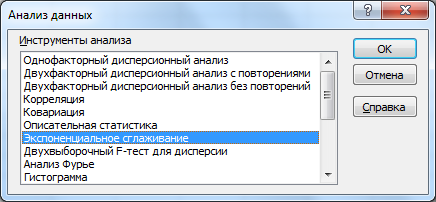
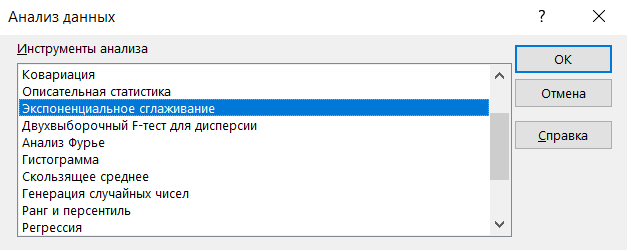
Вызовем надстройку Пакет анализа, выберем инструмент Экспоненциальное сглаживание.
и нажмем ОК.
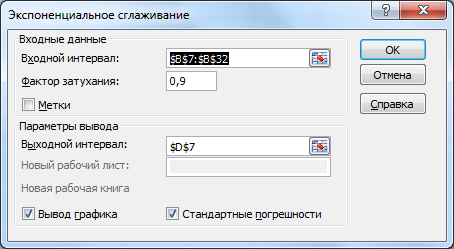
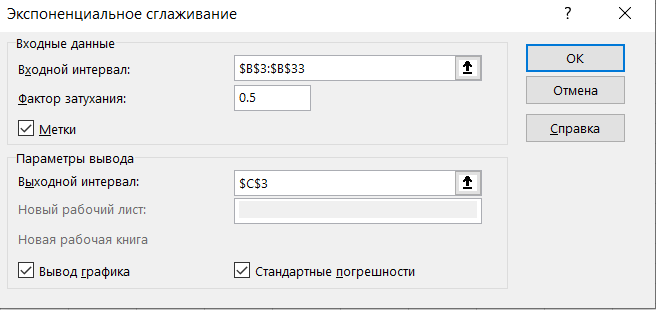
В появившемся диалоговом окне в поле Входной интервал введите ссылку на диапазон с данными ряда, т.е. на B7:B32.
Если диапазон включает и заголовок, то нужно установить галочку в поле Метки. В нашем случае устанавливать галочку не требуется, т.к. заголовок столбца не входит в диапазон B7:B32.
Поле Фактор затухания, как и параметр альфа в вышеуказанной формуле, определяет степень сглаживания ряда. Фактор затухания равен (1- альфа). Чем больше Фактор затухания тем глаже получается ряд. Установим значение 0,8.
В поле Выходной интервал достаточно ввести ссылку на левую верхнюю ячейку диапазона с результатами (укажем ячейку D7).
Также поставим галочки в поле Вывод графика и Стандартные погрешности (будет выведен столбец с расчетами погрешностей, англ. Standard Errors).
Нажмем ОК.
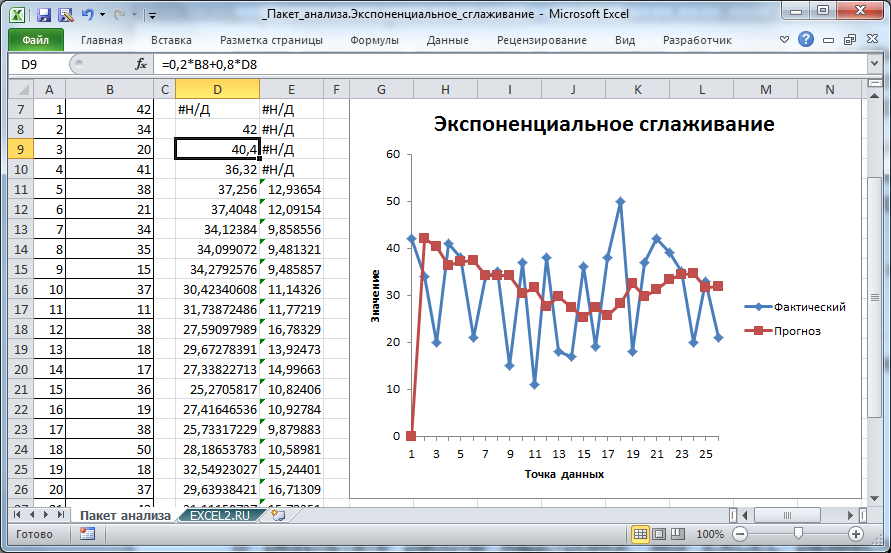
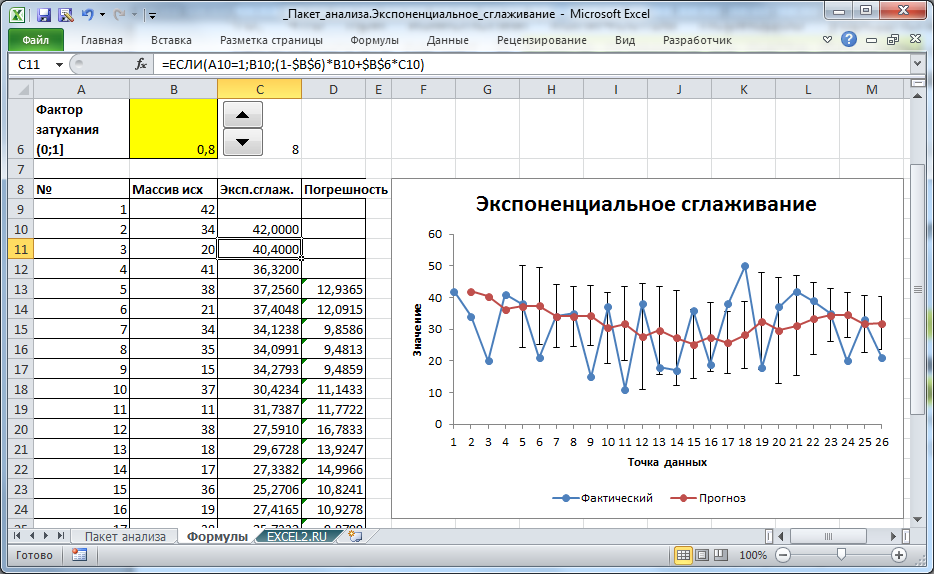
В результате работы надстройки, MS EXCEL разместил значения ряда, полученного методом Экспоненциального сглаживания, в столбце D (см. файл примера лист Пакет анализа).
В ячейке D7 содержится текстовое значение ошибки #Н/Д, т.к. для получения первого значения Экспоненциального сглаживания требуется значение исходного ряда за предыдущий период.
Первое значение сглаженного ряда, точнее формула =B7, содержится в ячейке D8. Второе значение вычисляется с помощью формулы =0,2*B8+0,8*D8.
Таким образом, Фактор затухания (0,8) определяет вес (вклад) предыдущего значения сглаженного ряда. Соответственно, (1-Фактор затухания)=альфа определяет вес предыдущего значения исходного ряда.
Диаграмма
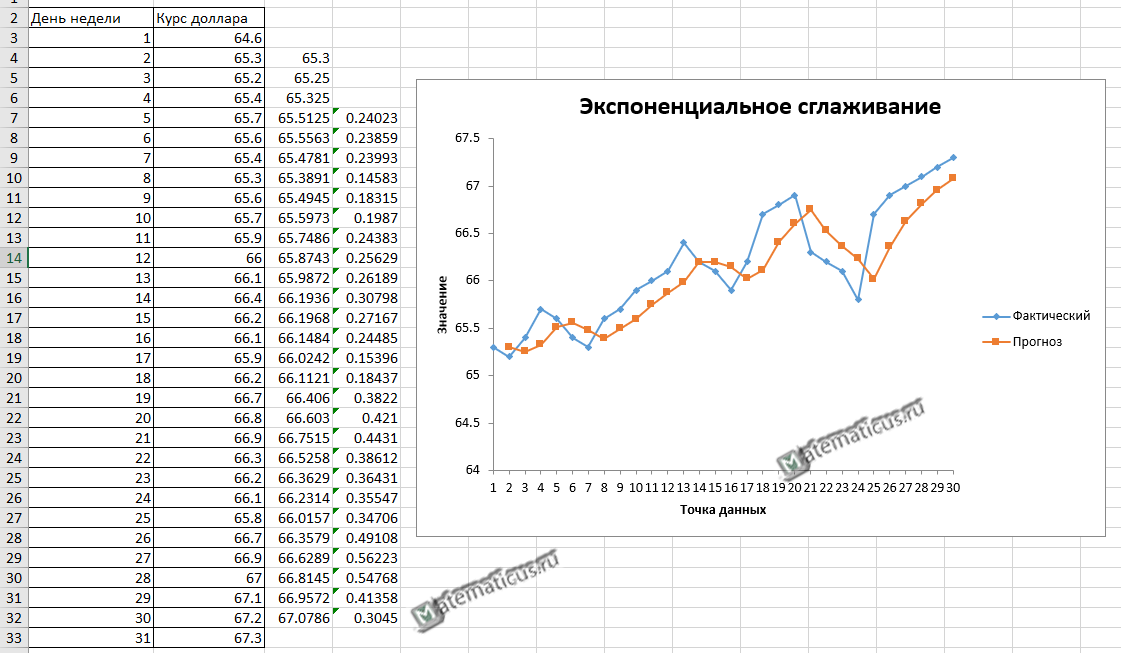
Для отображения рядов MS EXCEL создал диаграмму типа график. Сглаженный ряд на диаграмме называется «Прогноз» (ряд красного цвета).
Первое значение сглаженного ряда, которое равно ошибке #Н/Д, отражаются как 0, и может ввести в заблуждение (особенно, если последующие значения ряда близки к 0). Поэтому его лучше удалить из ячейки D7.
Примечание: Значение #Н/Д в ячейке D7 является просто текстовым значением, что принципиально отличается от результата возвращаемого формулами, например, функцией НД(), хотя визуально они неразличимы. При построении диаграммы текстовые значения всегда отображаются как 0. Но, если ошибка #Н/Д является результатом формулы, то воспринимается диаграммой как пустая ячейка и на ней не отображается.
Диаграмма позволяет визуально определить «выбросы», т.е. значения исходного ряда, которые существенно отличаются от средних значений. Такие «выбросы» могут быть следствием ошибки, но они оказывают существенное влияние на вид сглаженного ряда.
Вычисление погрешности
В столбце E, начиная с ячейки Е11, MS EXCEL разместил формулы для вычисления погрешностей (англ. Standard Errors):
=КОРЕНЬ(СУММКВРАЗН(B8:B10;D8:D10)/3)
Т.е. данная погрешность вычисляется по формуле:
Значения y – это значения исходного ряда в период i. Значения «y с крышечкой» — значения ряда, полученного методом Экспоненциального сглаживания, в тот же в период i. Значение n для экспоненциального сглаживания всегда равно 3, т.е. ошибка вычисляется за 3 последних периода (последние 3 значения учитываются с макимальным весом при расчете текущего значения сглаженного ряда и, соответственно, вносят более 50% вклада в его значение. Величина вклада сильно зависит от альфа).
Подробнее об этой погрешности см. соответствующий раздел в статье про Скользящее среднее.
Почему сглаживание называется экспоненциальным?
Как было показано в статье про Взвешенное скользящее среднее веса значений исходного ряда берутся в зависимости от их удаленности от текущего периода. Например, для 3-х периодов усреднения для Взвешенного скользящего среднего можно использовать формулу:
Yскол.i=0,5*Yi+ 0,4*Yi-1+ 0,1*Yi-2
Экспоненциальное сглаживание по сути является модификацией Взвешенного скользящего среднего – при расчете значения сглаженного ряда используются ВСЕ предыдущие значения исходного ряда с весами уменьшающимися в геометрической прогрессии по мере удаления от текущего периода.
Чтобы это показать воспользуемся формулой
Yэксп.i=альфа*Yi-1+ (1-альфа)*Yэксп.i-1
и вычислим Yэксп.5, т.е. значения сглаженного ряда для 5-го периода. После очевидных преобразований получим:
Yэксп.5=альфа*[(1-альфа)0* Yэксп.4+ (1-альфа)1* Yэксп.3+(1-альфа)2* Yэксп.2] +(1-альфа)3* Y1
Таким образом, вес 4-го (предыдущего) члена ряда =(1-альфа)0, а вес 3-го =(1-альфа)1 и т.д. Пусть t – текущий период (в нашем случае =5). Вес (t-i)-го члена ряда =(1-альфа)t-1-i. Т.к. (1-альфа)<1, то с ростом i растет и вес, и для члена t-1 достигает максимума =1.
Как известно, экспоненциальный рост y=a*EXP(b*x) в случае дискретной области определения с равными интервалами x называют геометрическим ростом (значения экспоненциальной функции y=a*EXP(b*x) являются в этом случае членами геометрической прогрессии m^x).
В нашем случае, приравняв i-й вес (1-альфа)t-1-i соответствующему значению экспоненциальной функции a*EXP(b*i) получим уравнение, которое позволит вычислить коэффициенты a и b (понадобится еще одно уравнение, например, для i-1 веса).
Решив систему из 2-х уравнений получим, a= EXP((t-1)*LN(1-альфа)) и b= LN(1-альфа).
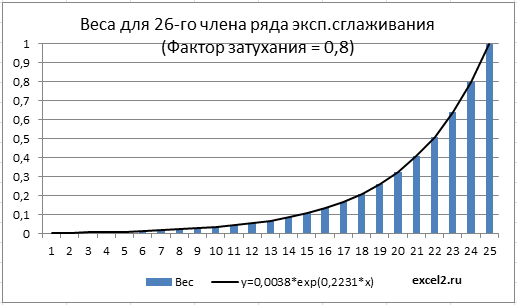
В файле примера для 26-го члена сглаженного ряда (t=26) вычислены веса всех предыдущих членов. На диаграмме ниже показано, что веса уменьшаются с ростом i в геометрической прогрессии, что соответствует экспоненциальной функции y=0,0038*exp(0,2231*x), где x=i. Вычисления параметров экспоненциальной кривой сделаны с помощью надстройки Поиск решения.
Экспоненциальное сглаживание с настраиваемым Фактором затухания
Недостатком формул, получаемых с помощью Пакета анализа, является то, что при изменении Фактора затухания (1-альфа) приходится перезапускать расчет. В файле примера на листе Формулы создана форма для быстрого пересчета Экспоненциального сглаживания в зависимости от значения Фактора затухания (полученный результат, естественно, полностью совпадает с расчетами надстройки Пакет анализа).
Значения ряда вычисляются с помощью формулы:
=ЕСЛИ(A10=1;B10;(1-$B$6)*B10+$B$6*C10)
в ячейке В6 содержится значение Фактора затухания.
Выбор значения Фактора затухания для удобства осуществляется с помощью элемента управления Счетчик с шагом 0,1.
Exponential smoothing is a technique for “smoothing” out time series data and is often used for short-term forecasting.
The basic idea is that time series data often has “random noise” associated with it, which leads to peaks and valleys in the data, but by applying exponential smoothing we can smooth out these peaks and valleys to see the true underlying trend of the data.
The basic formula for applying exponential smoothing is as follows:
Ft = αyt-1 + (1 – α) Ft-1
where:
Ft = Forecasted value for current time period t
α = The value for the smoothing constant, between 0 and 1
yt-1 = The actual data value for the previous time period
Ft-1 = Forecasted value for previous time period t-1
The smaller the alpha value, the more the time series data is smoothed out.
In this tutorial, we show how to perform exponential smoothing for time series data using a built-in function in Excel.
Suppose we have the following dataset that shows the sales for a particular company for 10 sales periods:
Perform the following steps to apply exponential smoothing to this time series data.
Step 1: Click on the “Data Analysis” button.
Go to the “Data” tab along the top ribbon and click the “Data Analysis” button. If you don’t see this button, you need to first load the Excel Analysis ToolPak, which is completely free to use.
Step 2: Choose the “Exponential Smoothing” option and click OK.
Step 3: Fill in the necessary values.
- Fill in the data values for Input Range.
- Select the value you’d like to use for Damping Factor, which is 1-α. If you’d like to use α = 0.2, then your damping factor will be 1-0.2 = 0.8.
- Select the Output Range where you’d like the forecasted values to appear. It’s a good idea to choose this output range right next to your actual data values so you can easily compare the actual values and the forecasted values side by side.
- If you would like to see a chart displayed with the actual and the forecasted values, select the box that says Chart Output.
Then, click OK.
A list of forecasted values and a chart will automatically appear:
Note that the first time period has a value of #N/A because there is no previous time period to use to calculate the forecasted value.
Experimenting with Smoothing Factors
You can experiment with different values for the smoothing factor α and see how it impacts the forecasted values. You’ll notice that the smaller the value for α (larger value for Damping Factor), the more smoothed out the forecasted values will be:
For more tutorials in Excel, be sure to check out our complete list of Excel Guides.
Содержание
- Экспоненциальное сглаживание в Excel
- Экспоненциальное распределение. Непрерывные распределения в EXCEL
- Экспоненциальное распределение в MS EXCEL
- Графики функций
- Генерация случайных чисел
- Задачи
- Как использовать экспоненциальное распределение в Excel
- Пример 1: время до прихода следующего клиента
- Пример 2: Время до следующего землетрясения
- Пример 3: время до следующего телефонного звонка
- Как выполнить экспоненциальное сглаживание в Excel
- Пример: экспоненциальное сглаживание в Excel
- Эксперименты с коэффициентами сглаживания
Экспоненциальное сглаживание в Excel
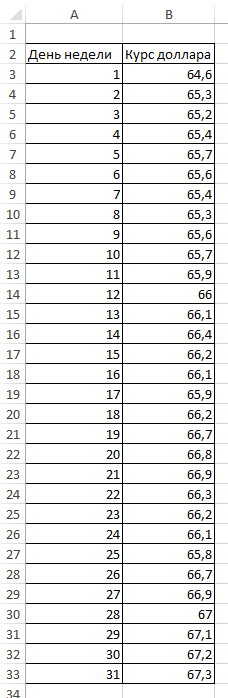
Дана таблица курса доллара за месяц.
Для того чтобы применить экспоненциальное сглаживание в Excel переходим на Анализ данных.
Переходим на вкладку Данные -> Анализ данных -> Экспоненциальное сглаживание
Если у вас в Excel не отображается на вкладке расширение Анализ данных, как его настроить см. здесь.
В окне экспоненциальное сглаживание указываем входной и выходной интервал, фактор затухания укажем 0.5. Ставим галочки метки, вывод графика и стандартные погрешности и нажимаем Ок.
Получаем график прогноза при применение экспоненциального сглаживания и фактический график в Excel
Экспоненциальное сглаживание часто применяется для прогнозирования.
Источник
Экспоненциальное распределение. Непрерывные распределения в EXCEL
history 8 ноября 2016 г.
Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ЭКСП.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.
Экспоненциальное распределение (англ. Exponential distribution ) часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение Экспоненциального распределения :
- Промежутки времени между появлением посетителей в кафе;
- Промежутки времени нормальной работы оборудования между появлением неисправностей (неисправности возникают из-за случайных внешних влияний, а не по причине износа, см. Распределение Вейбулла );
- Затраты времени на обслуживание одного покупателя.
Плотность вероятности Экспоненциального распределения задается следующей формулой:
График плотности распределения вероятности и интегральной функции Экспоненциального распределения выглядит следующим образом (см. ниже).
Экспоненциальное распределение тесно связано с дискретным распределением Пуассона . Если Распределение Пуассона описывает число случайных событий, произошедших за определенный интервал времени, то Экспоненциальное распределение должноописывать длину интервала времени между двумя последовательными событиями.
Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается распределением Пуассона со средним значением равным 15 машин в час (параметр распределения λ =15). Вероятность того, что на стоянку в течение часа приедет k машин равно:
Т.к. в среднем в час на стоянку приезжает 15 машин, то среднее время между 2-мя приезжающими машинами равно 1час/15машин=0,067. Т.к. среднее время между 2-мя событиями равно обратному значению параметра экспоненциального распределения , то параметр λ =15 , а плотность соответствующего экспоненциального распределения равна:
Экспоненциальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Экспоненциального распределения имеется функция ЭКСП.РАСП() , английское название — EXPON.DIST(), которая позволяет вычислить плотность вероятности (см. формулу в начале статьи) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по экспоненциальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Экспоненциальное распределение имеет обозначение Exp ( λ ).
Примечание : До MS EXCEL 2010 в EXCEL была функция ЭКСПРАСП() , которая позволяет вычислить кумулятивную (интегральную) функцию распределения и плотность вероятности . ЭКСПРАСП() оставлена в MS EXCEL 2010 для совместимости.
В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции экспоненциального распределения :
- =1-EXP(- λ *x) ;
- =ГАММА.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем Гамма распределения ;
- =ВЕЙБУЛЛ.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем распределения Вейбулла ;
Примечание : Для удобства написания формул в файле примера создано Имя для параметра распределения — λ .
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Генерация случайных чисел
Для генерирования массива чисел, распределенных по экспоненциальному закону , можно использовать формулу =-LN(СЛЧИС())/ λ
Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Если случайные числа содержатся в диапазоне B14:B213 , то оценку параметра экспоненциального распределения λ можно сделать с использованием формулы =1/СРЗНАЧ(B14:B213) .
Задачи
Экспоненциальное распределение широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр λ называется интенсивность отказов , а 1/ λ – среднее время до отказа .
Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый Экспоненциальным распределением с интенсивностью отказа равной 10^(-3) в час, таким образом, λ = 10^(-3). Среднее время до отказа равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за Среднее время до отказа, то нужно записать формулу:
Т.е. результат не зависит от параметра λ .
В MS EXCEL решение выглядит так: =ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)
Задача . Среднее время до отказа некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы. =ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Источник
Как использовать экспоненциальное распределение в Excel
Экспоненциальное распределение — это распределение вероятностей, которое используется для моделирования времени, в течение которого мы должны ждать, пока не произойдет определенное событие.
Это распределение может быть использовано для ответа на такие вопросы, как:
- Как долго владельцу магазина нужно ждать, пока покупатель войдет в его магазин?
- Как долго батарея будет продолжать работать, прежде чем она умрет?
- Как долго компьютер будет продолжать работать, прежде чем он сломается?
В каждом сценарии нас интересует вычисление того, как долго нам придется ждать, пока не произойдет определенное событие. Таким образом, каждый сценарий может быть смоделирован с использованием экспоненциального распределения.
Если случайная величина X следует экспоненциальному распределению, то кумулятивная функция плотности X может быть записана как:
F (х; λ) = 1 – e -λx
- λ: параметр скорости (рассчитывается как λ = 1/μ)
- e: константа, примерно равная 2,718.
Чтобы рассчитать вероятности, связанные с кумулятивной функцией плотности экспоненциального распределения в Excel, мы можем использовать следующую формулу:
- x : значение экспоненциально распределенной случайной величины
- lambda : параметр скорости
- cumulative : использовать функцию кумулятивной плотности или нет (ИСТИНА или ЛОЖЬ)
Следующие примеры показывают, как использовать эту формулу на практике.
Пример 1: время до прихода следующего клиента
В среднем новый покупатель заходит в магазин каждые две минуты. После прихода клиента найти вероятность того, что новый клиент прибудет менее чем за одну минуту.
Решение: Среднее время между клиентами составляет две минуты. Таким образом, ставка может быть рассчитана как:
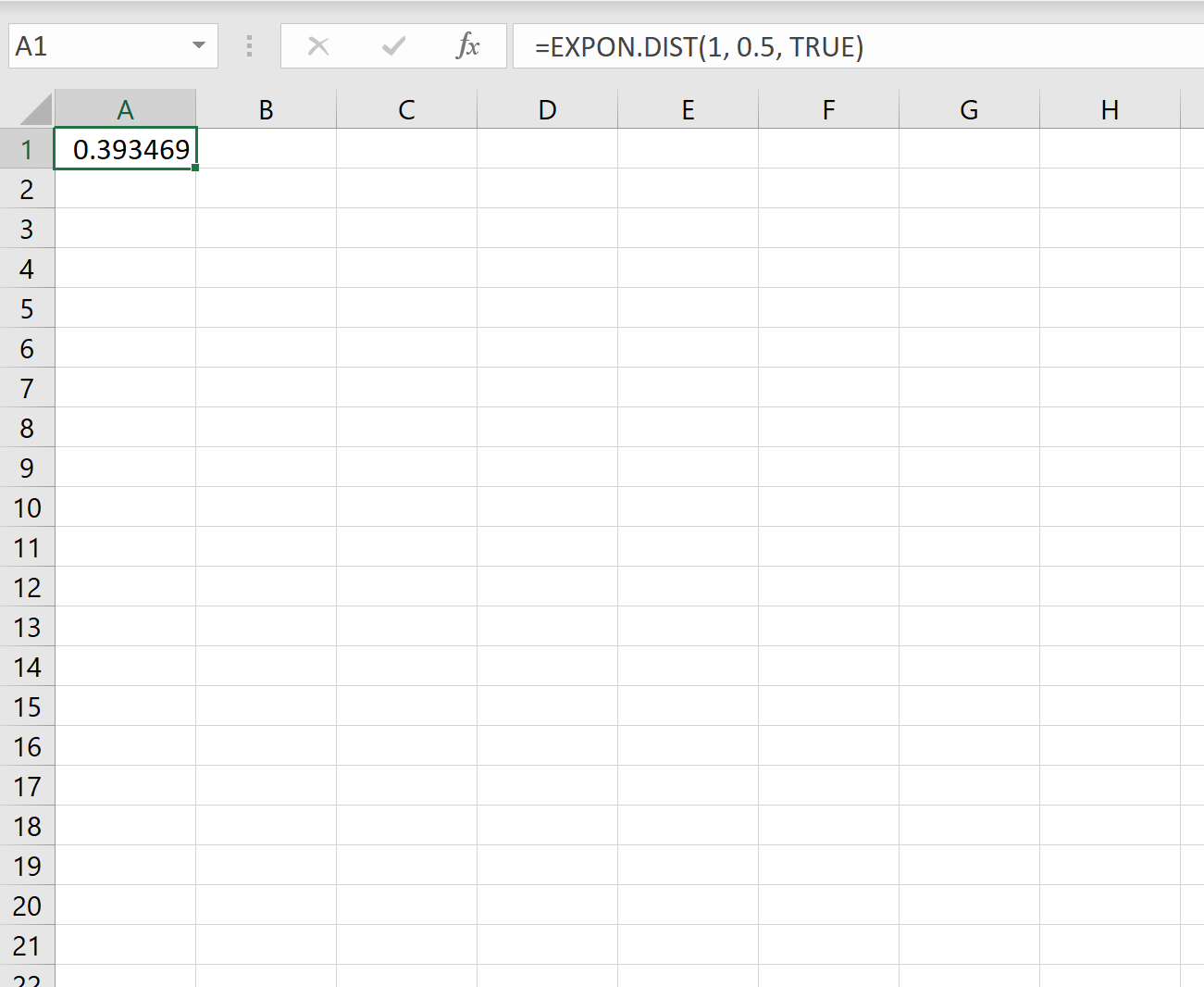
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что новый клиент прибудет менее чем за одну минуту:
Вероятность того, что следующего клиента придется ждать менее одной минуты, равна 0,393469 .
Пример 2: Время до следующего землетрясения
Предположим, землетрясение происходит в среднем каждые 400 дней в определенном регионе. После землетрясения найти вероятность того, что следующее землетрясение произойдет не ранее, чем через 500 дней.
Решение: Среднее время между землетрясениями составляет 400 дней. Таким образом, ставка может быть рассчитана как:
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что следующее землетрясение произойдет менее чем через 500 дней:
Вероятность того, что следующее землетрясение произойдет менее чем через 500 дней, равна 0,7135.
Таким образом, вероятность того, что следующего землетрясения придется ждать более 500 дней, равна 1 – 0,7135 = 0,2865 .
Пример 3: время до следующего телефонного звонка
Предположим, колл-центр получает новый звонок в среднем каждые 10 минут. После звонка клиента найти вероятность того, что новый клиент позвонит в течение 10–15 минут.
Решение: Среднее время между вызовами составляет 10 минут. Таким образом, ставка может быть рассчитана как:
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что следующий клиент позвонит в течение 10-15 минут:
Вероятность того, что новый клиент позвонит в течение 10-15 минут. составляет 0,1447 .
Источник
Как выполнить экспоненциальное сглаживание в Excel
Экспоненциальное сглаживание — это метод «сглаживания» данных временных рядов, который часто используется для краткосрочного прогнозирования.
Основная идея заключается в том, что данные временных рядов часто имеют связанный с ними «случайный шум», который приводит к пикам и впадинам в данных, но, применяя экспоненциальное сглаживание, мы можем сгладить эти пики и впадины, чтобы увидеть истинную основную тенденцию данных. .
Основная формула для применения экспоненциального сглаживания выглядит следующим образом:
F t = αy t-1 + (1 – α) F t-1
F t = прогнозируемое значение для текущего периода времени t
α = значение константы сглаживания в диапазоне от 0 до 1.
y t-1 = Фактическое значение данных за предыдущий период времени
F t-1 = Прогнозируемое значение для предыдущего периода времени t-1
Чем меньше значение альфа, тем больше сглаживаются данные временного ряда.
В этом руководстве мы покажем, как выполнить экспоненциальное сглаживание данных временных рядов с помощью встроенной функции в Excel.
Пример: экспоненциальное сглаживание в Excel
Предположим, у нас есть следующий набор данных, который показывает продажи конкретной компании за 10 периодов продаж:
Выполните следующие шаги, чтобы применить экспоненциальное сглаживание к этим данным временного ряда.
Шаг 1: Нажмите кнопку «Анализ данных».
Перейдите на вкладку «Данные» на верхней ленте и нажмите кнопку «Анализ данных». Если вы не видите эту кнопку, вам нужно сначала загрузить Excel Analysis ToolPak , который можно использовать совершенно бесплатно.
Шаг 2: Выберите параметр «Экспоненциальное сглаживание» и нажмите «ОК».
Шаг 3: Заполните необходимые значения.
- Заполните значения данных для Input Range .
- Выберите значение, которое вы хотели бы использовать для коэффициента затухания , которое равно 1-α. Если вы хотите использовать α = 0,2, то ваш коэффициент демпфирования будет 1-0,2 = 0,8.
- Выберите выходной диапазон , в котором должны отображаться прогнозируемые значения. Рекомендуется выбрать этот выходной диапазон рядом с вашими фактическими значениями данных, чтобы вы могли легко сравнивать фактические значения и прогнозируемые значения рядом друг с другом.
- Если вы хотите увидеть диаграмму с фактическими и прогнозируемыми значениями, установите флажок « Вывод диаграммы ».
Затем нажмите ОК.
Автоматически появится список прогнозируемых значений и диаграмма:
Обратите внимание, что первый период времени имеет значение #N/A, поскольку нет предыдущего периода времени, который можно было бы использовать для расчета прогнозируемого значения.
Эксперименты с коэффициентами сглаживания
Вы можете поэкспериментировать с различными значениями коэффициента сглаживания α и посмотреть, как он повлияет на прогнозируемые значения. Вы заметите, что чем меньше значение α (больше значение коэффициента затухания), тем более сглаженными будут прогнозируемые значения:
Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашим полным списком руководств по Excel .
Источник
Содержание
- Формула расчета метода экспоненциального сглаживания в Excel
- Инструменты сглаживания программы MS EXCEL
- Сглаживание графика в excel. Сглаживание линий в графиках и точечных диаграммах
- Экспоненциальное сглаживание в Excel
- Метод средней взвешенной
- Метод скользящей средней
- Метод экспертных оценок
- Как рассчитать прогноз по методу экспоненциального сглаживания в Excel?
- Возможно, у вас есть тренд
- Выявление закономерностей в данных
- Мультипликативное экспоненциальное сглаживание Холта-Винтерса
Ниже на рисунке изображен отчет спроса на определенный продукт за 26 недель. Столбец «Спрос» содержит информацию о количестве проданного товара. В столбце «Прогноз» – формула:

В столбце «Скользящая средняя» определяется прогнозируемый спрос, рассчитанный с помощью обычного вычисления скользящей средней с периодом 6 недель:

В последнем столбце «Прогноз», с описанной выше формулой применяется метод экспоненциального сглаживания данных в которых значения последних недель имеет больший вес чем предыдущих.
Коэффициент «Альфа:» вводится в ячейке G1, он значит вес присвоения наиболее актуальным данным. В данном примере он имеет значение 30%. Остальные 70% веса распределяется на остальные данные. То есть второе значение с точки зрения актуальности (с право на лево) имеет вес равный 30% от оставшихся 70% веса – это 21%, третье значение имеет вес равен 30% от остальной части 70% веса – 14,7% и так далее.
Инструменты сглаживания программы MS EXCEL
В программе EXCEL имеется всего два инструмента анализа, используемые для сглаживания временного ряда. Элементы диалогового окна «Скользящее среднее» представлены на рис. 3.1.
Рис. 3.1. Инструмент анализа «Скользящее среднее»
Необходимо ввести следующие аргументы:
- «Входной интервал» — анализируемый ряд (должен состоять из одного столбца или одной строки).
- «Интервал» — «размер окна» (по умолчанию используется 3).
- «Метки в первой строке» — необходимо установить флажок, если первая строка (или столбец) входного интервала содержит заголовок.
- «Выходной диапазон» — должен находиться на одном листе с исходными данными. По этой причине параметры «Новый лист» и «Новая книга» недоступны. Необходимо ввести ссылку на левую верхнюю ячейку выходного диапазона.
- «Стандартные погрешности» — если установлен флажок, то выходной диапазон состоит из двух столбцов, и значения стандартных погрешностей содержатся в правом столбце.
- «Вывод графика» — если установлен флажок, то создаётся встроенная диаграмма на листе, содержащем выходной диапазон.
Элементы диалогового окна «Экспоненциальное сглаживание» представлены на рис. 3.2.
Читайте также: Как сделать схему для вязания в excel?
Здесь имеется ранее не представленный аргумент «Фактор затухания», представляющий собой константу экспоненциального сглаживания — корректировочный фактор, минимизирующий нестабильность данных генеральной совокупности. По умолчанию значение аргумента «Фактор затухания» равно 0,3. Наиболее подходящим интервалом значений этого параметра сглаживания считается промежуток от 0,2 до 0,3.
Обнаружение и анализ тренда
Обычно анализ временного ряда начинается с выявления тренда.Выделение тренда очень важно, т.к. его исключение позволяет перейти к дальнейшей идентификации других компонент ряда.
Окончательная проверка реализаций на наличие трендов может быть выполнена различными способами.
При этом желательно знание закона распределения, например, нормального, или применение непараметрических критериев, при использовании которых не требуется знание выборочных распределений оценок.
Показатели динамики
Наличие или отсутствие тренда обычно хорошо видно по графику временного ряда (см., например, рис. 8.1) или по специальным аналитическим «показателям динамики ВР».
Показатели динамики разделяются на следующие важнейшие виды:
«абсолютный прирост» равен разности Δ двух сравниваемых уровней и характеризует изменение показателя за определенный промежуток текущей переменной.
- «темп роста» Т (всегда положителен) характеризует отношение двух сравниваемых уровней ряда, как правило, выраженное в процентах.
- «темп прироста» K.
- Причем каждый из указанных видов показателей может быть трех типов:
- «цепной» — если сравнение осуществляется при переменной базе, и каждый последующий уровень сравнивается с предыдущим
- «базисный» — если сравнение осуществляется с одним и тем же уровнем, принятым за базу сравнения;
- «средний».
Например, «средний абсолютный прирост» — это обобщающая характеристика скорости изменения исследуемого показателя во времени (скоростью будем называть прирост в единицу времени). Для его определения за весь период наблюдения используется формула простой средней арифметической «цепного абсолютного прироста».
«Средний темп роста» — обобщающая характеристика, отражающая интенсивность изменения уровней ряда. Он показывает, сколько в среднем процентов последующий уровень составляет от предыдущего на всем периоде наблюдения. Этот показатель рассчитывается по формуле средней геометрической n последовательных цепных темпов роста.
Формулы расчёта всех видов и типов показателей динамики представлены в табл. 8.1.
Таблица 8.1. Основные показатели динамики ВР
| Вид показателя | Абсолютный прирост | Темп роста % | Темп прироста % |
| Цепной |  |
||
| Базисный |  |
||
| Средний |  |
 |
Сглаживание графика в excel. Сглаживание линий в графиках и точечных диаграммах
Данные, получаемые в процессе экспериментов, как правило, содержат случайные отклонения (погрешности), поэтому построенные по ним графики не являются плавными линиями, они чаще всего имеют вид зубчатых линий, т.е. линий, отличающихся от плавных наличием “выбросов” и “впадин”.
Наличие таких выбросов и впадин иногда затрудняет не только визуальное восприятие закономерности изменения данной величины и, соответственно, анализ полученных графиков, но и выбор гипотезы возможного математического описания графика.
Поэтому экспериментальные данные в большинстве случаев необходимо сглаживать, используя методы усреднения ординат на основе интерполяционных формул.
Идея, положенная в основу всех методик математического сглаживания графиков, аналогична идее выравнивания пересеченной местности с помощью бульдозера – срезание выступов почвы и перемещение полученного материала в ближайшие ямы.
Все методики сглаживания графиков
основаны на использовании нечетного количества ординат (3, 5, 7, …) и работоспособны только в том случае, когда шаг точек по оси абсцисс одинаков.
Самым простым методом сглаживания является метод сглаживания по трем ординатам.
Сглаживание по методу трех ординат выполняется следующим образом. Пусть в результате экспериментов получена зависимость у = f(x),
данные сведены в соответствующую таблицу и по ним построен график. В таблице выбираются первые три соседние ординаты, начиная с крайней левой, и они условно
обозначаются:
Левая в рассматриваемой тройке ординат (т.е. в данном случае самая первая ордината);
- Средняя из выделенных ординат;
- Правая в данной тройке ординат.
Сглаженное значение крайней левой ординаты определяется по следующей формуле:
Сглаженное значение второй (средней) ординаты определяется по формуле:
Далее сдвигаются вправо на одну точку и выделяют вторую тройку соседних ординат, в которой та ордината, которая была средней в первой тройке, станет крайней левой в новой тройке ординат. В этой новой тройке ординат определяют сглаженное значение только средней ординаты
по формуле (2).
Затем сдвигаются на один шаг вправо и получают следующую тройку соседних ординат, в которой средняя ордината предыдущей тройки станет крайней левой, определяют сглаженное значение средней ординаты в полученной новой тройке ординат
и так поступают до тех пор, пока в последней тройке соседних ординат в качестве третьей ординаты не окажется крайняя правая ордината.
В последней тройке ординат определяют сглаженное значение средней ординаты
по формуле (2), а затем сглаженное значение крайней правой ординаты по формуле:
Если в исходных экспериментальных данных имеются точки с половинным шагом по оси абсцисс по сравнению с шагом остальных точек, то усредненное (сглаженное) значение ординаты каждой такой точки определяется точно так же, как и описано выше, т.е.
выделяется тройка соседних ординат, в которой условной средней ординатой является ордината точки с половинным шагом по оси абсцисс, а условной левой ординатой и условной правой ординатами считаются ординаты, находящиеся непосредственно слева и справа от нее.
В случае, если исходная зависимость имеет большой разброс точек (большие “выбросы” и “впадины“), то однократного сглаживания может быть недостаточно, и будет необходимо провести еще одно или несколько повторных сглаживаний. В качестве исходных значений ординат при каждом повторном сглаживании следует использовать результаты предыдущего сглаживания.
Методы сглаживания по пяти, семи и большему количеству ординат позволяют получить сглаженный график более быстро, но при этом более сильно искажают вид исходного графика. Из всех известных методов сглаживания метод сглаживания по трем ординатам является самым «нежным» и щадящим.
Следует иметь ввиду, что при многократном повторении сглаживания исходного графика по любому количеству ординат любой исходный график превратится в конечном итоге в прямую линию
, поэтому ко многократному повторению сглаживания следует относиться осторожно.
Если исходный график похож на некую пилообразную или кусочно-линейную фигуру, состоящую из более или менее прямолинейных отрезков, то представляется целесообразным сглаживать по отдельности эти отрезки. При этом крайние сглаженные ординаты соседних отрезков, как правило, совпадать не будут. За сглаженное значение таких ординат следует принять их среднее арифметическое.
Рисунок 20. — Чтобы изменить форму конкретного маркера данных или всех маркеров выделенного ряда, выберите один из вариантов на вкладке Фигура.
Excel не допускает изменения формы маркеров данных в объемных диаграммах, содержащих ось рядов.
Варианты 2 и 3, а также 5 и 6 почти аналогичны друг другу. Отличие заключается в том, что при выборе вариантов 3 и 6 маркеры, представляющие меньшие значения в ряду данных, отображаются в виде усеченной фигуры. Например, при выборе варианта 3 короткие маркеры ряда данных появятся в виде усеченных пирамид.
Сглаживание линий в графиках и точечных диаграммах
Excel может применять сглаживание к рядам данных на графиках и точечных диаграммах. Чтобы воспользоваться этой возможностью, выделите ряд данных, который хотите сгладить, и выберите первую команду в меню Формат. Затем на вкладке Вид (Patterns) открывшегося окна диалога Формат ряда данных установите флажок Сглаженная линия (Smoothed Line).
Изменение линий и маркеров в графиках, точечных и лепестковых диаграммах
Чтобы изменить тип, толщину и цвет линии на графике, лепестковой или точечной диаграмме, выделите ряд данных и затем выберите первую команду в меню Формат. После открытия окна диалога Формат ряда данных перейдите на вкладку Вид (Patterns), представленную на рисунке 21. На этой же вкладке можно изменить вид, цвет и размер маркеров или вовсе удалить их из ряда данных.
Для форматирования линий и маркеров установите нужные значения параметров на вкладке Вид.
Отображение в графиках коридоров колебания и полос повышения и понижения
Коридор колебания — это линия, соединяющая минимальное и максимальное значения и наглядно показывающая диапазон, в пределах которого изменяются значения в данной категории. На рисунке 8 показана диаграмма, иллюстрирующая применение коридора колебания. Коридор колебания может быть показан только на плоских графиках.
Полоса повышения и понижения — это прямоугольник, нарисованный между точками данных первого и последнего ряда.
Excel заполняет прямоугольник одним цветом или узором, если первый ряд расположен выше последнего, и контрастным цветом или узором в противном случае.
Полосы повышения и понижения обычно используются в биржевых диаграммах для отслеживания изменения цен открытия и закрытия, но вы можете отобразить их и на плоских графиках, содержащих, по крайней мере, два ряда данных.
Чтобы отобразить в диаграмме коридоры колебания или полосы повышения и понижения, выделите любой ряд данных и выберите первую команду в меню Формат. Затем на вкладке Параметры (Options) открывшегося окна диалога Формат ряда данных (Format Data Series) установите флажок Минимум-максимум (High-Low Lines) или Открытие-закрытие (Up-Down Bars).
При использовании в диаграмме полос повышения и понижения Excel позволяет изменять ширину зазора. Этот параметр обычно доступен только для гистограмм и линейчатых диаграмм, но Excel рассматривает график с полосами повышения и понижения как вид гистограммы. При увеличении ширины зазора полосы повышения и понижения становятся уже, а при уменьшении — шире.
Вы можете изменить внешний вид коридоров колебания или полос повышения и понижения. Для этого выделите один (одну) из них и затем выберите первую команду в меню Формат.
Excel откроет окно диалога, позволяющее изменять цвет, толщину и тип линии коридоров колебания или цвет, узор и рамку полос повышения и понижения.
Для заливки полос повышения и понижения можно даже использовать текстуру или рисунок.
Отображение линий проекций в графиках и диаграммах с областями
Линия проекции — это прямая, которая проходит от точки данных до оси категорий.
Линии проекций особенно полезны в диаграммах с областями, содержащих несколько рядов данных, но их можно добавить в любую диаграмму с областями, в плоский или объемный график.
Для этого выделите ряд данных и выберите первую команду в меню Формат. Затем на вкладке Параметры открывшегося окна диалога Формат ряда данных установите флажок Линии проекции (Drop Lines).
Чтобы отформатировать линии проекции для ряда данных, выделите одну из них и затем выберите первую команду в меню Формат.
Отделение секторов круга и кольца
Ваша мышь может разорвать круг или кольцо на отдельные секторы. Просто перетащите любой сектор по направлению от центра диаграммы. (Но учтите, что в кольцевой диаграмме можно отделять секторы только внешнего кольца.) Чтобы вернуть кругу или кольцу первоначальный вид, просто перетащите сектор назад в центр диаграммы.
Чтобы отделить только конкретный сектор круга или кольца в плоской или объемной диаграмме, щелкните на этом секторе два раза. Первый щелчок выделит ряд данных, а второй — конкретный сектор. После выделения сектора перетащите его в сторону от центра.
Форматирование вторичной круговой диаграммы и вторичной гистограммы
Вторичная круговая диаграмма и вторичная гистограмма — это круговая диаграмма, в которой несколько точек данных отображаются на вспомогательной круговой диаграмме или гистограмме. Вспомогательная диаграмма предоставляет более подробную информацию о некоторой части основной диаграммы.
Чтобы преобразовать обычную круговую диаграмму во вторичную круговую диаграмму или гистограмму, выделите любую ее часть и затем в меню Диаграмма выберите команду Тип диаграммы. В правой части галереи видов круговой диаграммы вы найдете вторичную круговую диаграмму и вторичную гистограмму.
По умолчанию при построении вспомогательной диаграммы Excel использует два последних значения ряда данных, но допустимы и другие способы разделения значений между основной и вспомогательной диаграммами.
Для этого выделите ряд данных во вторичной круговой диаграмме или гистограмме и выберите первую команду в меню Формат.
После открытия окна диалога Формат ряда данных перейдите на вкладку Параметры, представленную на рисунке 22.
Ряд данных можно разделить по положению (последние n точек данных отойдут к вспомогательной диаграмме), по значению (к вспомогательной диаграмме отойдут все точки данных, значение которых меньше n), по доле (к вспомогательной диаграмме отойдут все секторы, значение которых составляет меньше n процентов от общей суммы). Кроме того, вы можете выбрать пункт Дополнительно (Custom) в списке Разделение рядов (Split Series By) и затем просто перетащить часть секторов из основной диаграммы во вспомогательную.
Изменение параметров вторичной круговой диаграммы и вторичной гистограммы.
Параметры настройки для вторичной круговой диаграммы и вторичной гистограммы одинаковы, и единственным их отличием является форма вспомогательной диаграммы.
После изменения параметров разделения Excel перерисует основную диаграмму и покажет на ней единый сектор, представляющий все точки данных, отображаемые на вспомогательной диаграмме.
По умолчанию Excel рисует линии от этого общего сектора ко всей вспомогательной диаграмме. Вы можете удалить эти линии, сняв флажок Соединить значения ряда (Series Lines).
У меня есть некоторые зазубренные контурные сюжеты, которые мне нужно сгладить. Мне нужно сгладить их, не теряя ни одной из линий контура. Я упомянул эти , но они не совсем предлагают решение моей проблемы. Без какого-либо фильтра мои сюжеты выглядят так:
Вы можете видеть, что внешние контуры очень неровные, и поэтому качество презентации не является. Если я запустил данные через гауссовский фильтр порядка 0 и сигма 2 (т.е. scipy.ndimage.gaussian_filter(z, 2)), он сглаживает графики, но я потеряет внутренние контуры:
Каков наилучший способ сглаживания графика без потери внутренних контуров? Характер данных, с которыми я работаю, заключается в том, что он всегда имеет самые высокие значения вблизи центра. Фильтрация расширяет информацию и устраняет внутренние контуры. Это наиболее важные контуры: контуры представляют собой риск гибели людей, поэтому, как правило, чем выше значение, тем важнее оно.
Я рассмотрел два метода сглаживания контурных линий.
- Получите каждую координату контурной линии через contour_object.collections.get_paths().vertices и сгладьте/перерисуйте каждый. Это кажется возможным, но неэлегантным, и я не уверен, с чего начать.
- Примените гауссовский фильтр только к данным, превышающим определенное значение: например, 5 * 10 -6 . Это легко сделать (процитировать массив данных и взять из исходного набора, если значение больше, чем обрезание, и отфильтрованный набор, если это не так), но кажется довольно произвольным и трудно оправдавшимся.
Я хотел бы сделать что-то вроде первого варианта, но это похоже на хак. Каков наилучший способ сгладить эти контурные графики?
Сглаживание данных → потеря данных.
Моя первая реакция: почему вы хотите отображать сглаженные данные? Я редко когда-либо видел презентации данных, в которых сглаживание данных было действительно полезно для понимания последствий данных. Фактически, это то, что Туфте часто критиковали (это не повод, чтобы избежать этого, конечно, но, возможно, для того, чтобы попросить себя придумать больше оправдания, чем обычно).
- Если сюжет должен выглядеть красиво для некоторых причин, не связанных с данными, это полностью нормально, но если вы пытаетесь сделать его более приятным для глаз, когда задача состоит в том, чтобы понять что-то о природе контуров, вам гораздо лучше просто представить исходные данные, как есть.
- Если у вас есть разные контуры, хранящиеся в виде отдельных наборов данных (например, если вы просто украли разные наборы данных сюжетной линии, которые использует контурный плоттер), вы можете применить сглаживание только к тем контурам, где потеря данных от сглаживания и оставлять меньшие внутренние контуры несжимаемыми и зубчатыми.
- Или вы можете возиться с параметрами сглаживания, чтобы ваше сглаживающее ядро было достаточно узким, чтобы не полностью убить крошечные внутренние кольца из вашего набора данных.
- В принципе, нет никакого способа «сгладить» данные без «потери» данных в некотором смысле, и любой способ сделать это, который не применяется равномерно ко всему набору данных, будет подозрительным.
Экспоненциальное сглаживание в Excel
- В Excel можно подключить пакет анализа для сглаживания самих данных.
- Такое сглаживание это метод применяемый для сглаживания временных рядом — статья википедии
- Зайдите в меню — Параметры Excel — Надстройки — Пакет анализа (в правом окне) и в самом низу нажимайте Перейти
В открывшемся окне находим Экспоненциальное сглаживание.
Метод средней взвешенной
Метод средней взвешенной основан на использовании среднего арифметического, взвешенного по временным периодам, с наибольшим весом у самых близких к прогнозируемому и с учетом сезонности. После этого находится сумма всех значений прогнозируемого показателя за периоды и делится на сумму весов. Преимуществом данного метода является его простота и скорость расчетов, поэтому он прекрасно подходит для ситуаций, где необходимо составить прогноз движения денежных средств в очень сжатые сроки. Однако для принятия долгосрочных стратегических решений этот метод не является наиболее оптимальным, поскольку процент отклонения его прогнозного значения от фактического наибольший, кроме того он не позволяет оценить и другие факторы, помимо временного и фактора сезонности.
Метод скользящей средней
Это еще один метод прогнозирования денежных потоков «на скорую руку». Скользящая средняя — это средняя стоимость какого-нибудь показателя за определенный период (например, последние 3 месяца), которые с течением времени сдвигаются вперед (таким образом, происходит сглаживание сезонности).
Метод экспертных оценок
Экспертный метод позволяет получить самую субъективную оценку будущего денежного потока компании, поскольку основан на субъективных оценках экспертов (в роли которых выступают обычно сотрудники соответствующих подразделений компании). Преимуществом данного метода является то, что он может быть применен в условиях, когда исторических данных или технических средств для построения объективного прогноза не хватает, или в условиях полной неопределенности. В таком случае, например, сотрудники, отвечающие за собираемость дебиторской задолженности, составляют прогноз поступлений денежных средств от операционной деятельности с учетом качества дебиторской задолженности, сроков ее погашения и классифицируют ожидаемые поступления по курируемым клиентам и степени вероятности (базовый прогноз, оптимистичный и пессимистичный).
Как рассчитать прогноз по методу экспоненциального сглаживания в Excel?
Формула расчета прогноза проста:
Ŷt+1=k*Yt +(1-k)* Ŷt
Где:
- Ŷt+1 – прогноз на следующий период t+1;
- Yt – данные для прогноза за текущий период t (например, продажи по месяцам);
- k – коэффициент сглаживания ряда , k задается вами вручную и находится в диапазоне от 0 до 1, 0 < k < 1
- Ŷt – значение прогноза на текущий период t. Причем в первый период (месяц, день…) Ŷ1=Y1, т.е. Ŷt в первый период равны продажам в этот период.
Прогноз по методу экспоненциального сглаживания = коэффициент сглаживания * последнее фактическое значение продаж + (1- коэффициент сглаживания)*предыдущий прогноз по методу экспоненциального сглаживания.
Важно отметить, что данная модель предполагает регулярный пересчет прогноза по окончании последнего периода и появлении новых данных для прогноза за последний период.
Возможно, у вас есть тренд
Чтобы проверить это предположение достаточно подогнать линейную регрессию под данные спроса и выполнить тест на соответствие критерию Стьюдента на подъеме этой линии тренда (как в главе 6). Если уклон линии ненулевой и статистически значимый (в проверке по критерию Стьюдента величина р менее 0,05), у данных есть тренд (рис. 6).
Рис. 6. Тест Стьюдента показывает наличие тренда
Мы воспользовались функцией ЛИНЕЙН, которая возвращает 10 описательных статистик (если вы ранее не пользовались этой функцией, рекомендую Функция массива ЛИНЕЙН) и функцией ИНДЕКС, которая позволяет «вытащить» только три требуемые статистики, а не весь набор. Получилось, что наклон равен 2,54, и он значим, так как тест Стьюдента показал, 0,000000012 существенно меньше 0,05. Итак, тренд есть, и осталось включить его в прогноз.
Выявление закономерностей в данных
Есть способ испытать прогностическую модель на прочность — сравнить погрешности сами с собой, сдвинутыми на шаг (или несколько шагов). Если отклонения случайны, то улучшить модель нельзя. Однако, возможно, в данных о спросе есть сезонный фактор. Концепция погрешности, коррелирующей с собственной версией за другой период, называется автокорреляцией (подробнее об автокорреляции см. Простая линейная регрессия). Чтобы рассчитать автокорреляцию, начните с данных об ошибке прогноза за каждый период (столбец F на рис. 7 переносим в столбец В на рис. 10). Далее определите среднюю ошибку прогноза (рис. 10, ячейка В39; формула в ячейке: =СРЗНАЧ(B3:B38)). В столбце С рассчитайте отклонение ошибки прогноза от среднего; формула в ячейке С3: =B3-B$39. Далее последовательно сдвигайте столбец С на столбец вправо и строку вниз. Формулы в ячейках D39: =СУММПРОИЗВ($C3:$C38;D3:D38), D41: =D39/$C39, D42: =2/КОРЕНЬ(36), D43: =-2/КОРЕНЬ(36).
Рис. 10. Расчет автокорреляции
Что может значить для одного из столбцов D:O «синхронное движение» со столбцом С. Например, если столбцы С и D синхронны, то число, отрицательное в одном из них, должно быть отрицательным и в другом, положительное в одном, положительное – в другом. Это означает, что сумма произведений двух столбцов будет значительной (отличия накапливаются). Или, что тоже самое, чем ближе значение в диапазоне D41:О41 к нулю, тем ниже корреляция столбца (соответственно от D до О) со столбцом С (рис. 11).
Рис. 11. Диаграмма автокорреляции
Одна автокорреляция выше критического значения. Погрешность, сдвинутая на год, коррелирует сама с собой. Это означает 12-месячный сезонный цикл. И это неудивительно. Если вы посмотрите на график спроса (рис. 2), то окажется, что есть пики спроса на каждое Рождество и провалы в апреле-мае. Рассмотрим технику прогнозирования, учитывающую сезонность.
Мультипликативное экспоненциальное сглаживание Холта-Винтерса
Метод называется мультипликативным (от multiplicate — умножать), поскольку использует умножение для учета сезонности:
Спрос в момент t = (уровень + t × тренд) × сезонная поправка для момента t × все оставшиеся нерегулярные поправки, которые мы не можем учесть
Сглаживание Холта-Винтерса также называют тройным экспоненциальным сглаживанием, потому что у него три сглаживающих параметра (альфа, гамма и сезонный фактор – дельта). Например, если имеется 12-месячный сезонный цикл:
Прогноз на месяц 39 = (уровень36 + 3 × тренд36) х сезонность27
Анализируя данные, необходимо выяснить, что в серии данных является трендом, а что — сезонностью. Чтобы выполнить вычисления по методу Холта-Винтерса, необходимо:
- Сгладить исторические данные методом скользящего среднего.
- Сравнить сглаженную версию временного ряда данных с оригиналом, чтобы получить приблизительную оценку сезонности.
- Получить новые данные без сезонного компонента.
- Найти приближения уровня и тренда на основе этих новых данных.
Начните с исходных данных (столбцы А и В на рис. 12) и добавьте столбец С со сглаженными значениями на основе скользящего среднего. Так как сезонность имеет 12-месячные циклы, имеет смысл использовать среднее за 12 месяцев. С этим средним есть небольшая проблема. 12 – четное число. Если вы сглаживаете спрос за месяц 7, стоит ли считать его средним спросом с 1-го по 12-й месяц или со 2-го по 13-й? Чтобы справиться с этим затруднением, нужно сгладить спрос с помощью «скользящего среднего 2×12». Т.е., взять половину от двух средних с 1 по 12-й месяц и со 2 по 13. Формула в ячейке С8: =(СРЗНАЧ(B3:B14)+СРЗНАЧ(B2:B13))/2.
Рис. 12. Данные, очищенные от сезонного фактора
Сглаженные данных для месяцев 1–6 и 31–36 получить нельзя, так как не хватает предыдущих и последующих периодов. Для наглядности исходные и сглаженные данные можно отразить на диаграмме (рис. 13).
Рис. 13. Сглаженные данные спроса
Теперь в столбце D разделите оригинальную величину на сглаженную и получите приблизительное значение сезонной поправки (столбец D на рис. 12). Формула в ячейке D8: =B8/C8. Обратите внимание на всплески в 20% выше нормального спроса в месяцах 12 и 24 (декабрь), в то время как весной наблюдаются провалы. Эта техника сглаживания дала вам две точечные оценки для каждого месяца (всего 24 месяца). В столбце Е найдено среднее значение этих двух факторов. Формула в ячейке Е1: =СРЗНАЧ(D14;D26). Для наглядности уровень сезонных колебаний можно представить графически (рис. 14).
Рис. 14. Сезонные колебания
Теперь можно получить данные, скорректированные на сезонные колебания. Формула в ячейке G1: =B2/E2. Постройте график на основе данных столбца G, дополните его линией тренда, выведите уравнение тренда на диаграмму (рис. 15), и используйте коэффициенты в последующих расчетах.
Рис. 15. Данные, скорректированные на сезонные колебания
Сформируйте новый лист, как показано на рис. 16. Значения в диапазон Е5:Е16 подставьте с рис. 12 области Е2:Е13. Значения С16 и D16 возьмите из уравнения линии тренда на рис. 15. Значения констант сглаживания установите для начала на отметке 0,5. Растяните значения в строке 17 на диапазон месяцев с 1 по 36. Запустите Поиск решения для оптимизации коэффициентов сглаживания (рис. 18). Формула в ячейке В53: =(C$52+(A53-A$52)*D$52)*E41.
Рис. 16. Данные для прогноза Холта-Винтера
Рис. 17. График прогноза Холта-Винтерса
Теперь в сделанном прогнозе нужно проверить автокорреляции (рис. 18). Так как все значения расположились между верхней и нижней границами, вы понимаете, что модель неплохо поработала над пониманием структуры значений спроса.
Рис. 18. Коррелограмма модели Холта-Винтерса
Источники
- https://exceltable.com/formuly/metod-eksponencialnogo-sglazhivaniya
- https://iiorao.ru/excel/kak-sdelat-sglazhivanie-grafika-v-excel.html
- https://zen.yandex.ru/media/id/5ad880039e29a252e4838439/5b04959c1aa80cf17bff526c
- https://4analytics.ru/prognozirovanie/malo-dannix-dlya-prognoza-model-eksponencialnogo-sglajivaniya.html
- https://baguzin.ru/wp/prognozirovanie-na-osnove-eksponents/