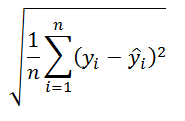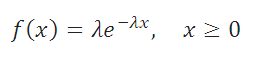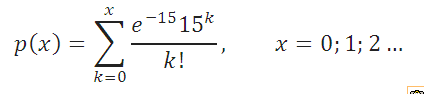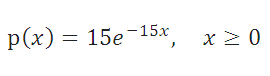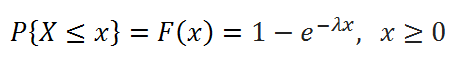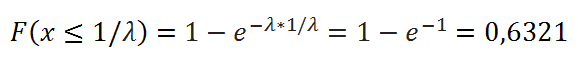history 10 января 2021 г.
- Группы статей
Экспоненциальное сглаживание используется для сглаживания краткосрочных колебаний во временных рядах, чтобы облегчить определение долгосрочного тренда, а также для прогнозирования. Произведем экспоненциальное сглаживание с помощью надстройки MS EXCEL Пакет анализа и формулами. Рассмотрим двойное и тройное экспоненциальное сглаживание для прогнозирования рядов с трендом и сезонностью.
Экспоненциальное сглаживание один из наиболее распространённых методов для сглаживания временных рядов. В отличие от метода Скользящего среднего, где прошлые наблюдения имеют одинаковый вес, Экспоненциальное сглаживание присваивает им экспоненциально убывающие веса, по мере того как наблюдения становятся старше. Другими словами, последние наблюдения дают относительно больший вес при прогнозировании, чем старые наблюдения.
Примечание: Перед прочтением этой статьи рекомендуется прочитать про Скользящее среднее.
Примечание: В англоязычной литературе для экспоненциального сглаживания используется термин Single Exponential Smoothing или Simple Exponential Smoothing (SES).
Напомним, что при усреднении методом Скользящего среднего веса, присвоенные наблюдениям, одинаковы и равны 1/n, где n – количество периодов усреднения. Например, в случае усреднения за 3 периода скользящее среднее равно:
Yскол.i=(Yi+ Yi-1+ Yi-2)/3 = Yi/3+ Yi-1/3+ Yi-2/3
В случае Экспоненциального сглаживания формула выглядит следующим образом:
Yэксп.i=альфа*Yi-1+ (1-альфа)*Yэксп.i-1
или
Yэксп.i= Yэксп.i-1 + альфа*(Yi-1 — Yэксп.i-1)
где 0<альфа<1, i>2
Параметр альфа определяет степень сглаживания. При малых значениях альфа (0,1 – 0,2) имеет место сильное сглаживание. При значениях близких к 1, сглаженный ряд практически повторяет исходный ряд с задержкой (лагом) на один период. Для медленно меняющегося ряда часто берут небольшие значения альфа=0,1; а для быстро меняющегося 0,3-0,5.
Примечание: Формулы представляют собой рекуррентное соотношение – это когда последующий член ряда вычисляется на основе предыдущего.
Примечание: Существует альтернативный подход к Экспоненциальному сглаживанию: в нем в формуле вместо Yi-1 заменяют на Yi. Этот подход используется в контрольных картах экспоненциально взвешенного скользящего среднего (EWMA).
Надстройка Пакет анализа
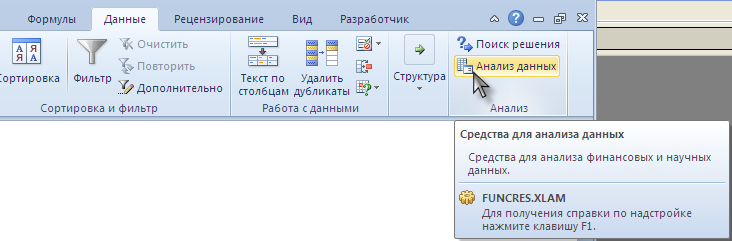
Получить Экспоненциально сглаженный ряд можно с помощью надстройки Пакет анализа (Analysis ToolPak). Надстройка доступна из вкладки Данные, группа Анализ.
СОВЕТ: Подробнее о других инструментах надстройки Пакет анализа и ее подключении – читайте в статье.
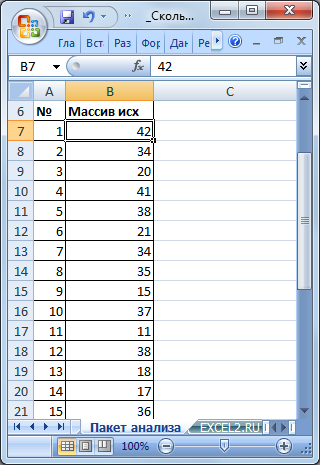
Разместим исходный числовой ряд в диапазоне B7:B32.
Для наглядности пронумеруем каждое значение ряда (столбец А).
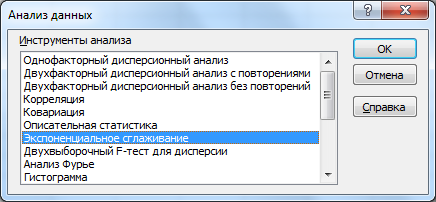
Вызовем надстройку Пакет анализа, выберем инструмент Экспоненциальное сглаживание.
и нажмем ОК.
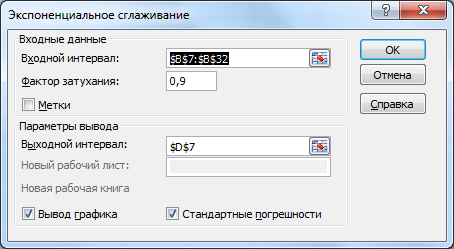
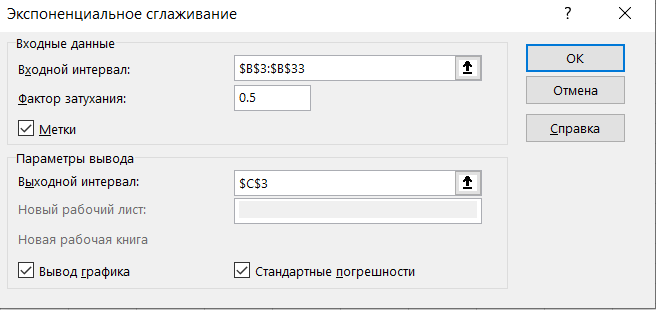
В появившемся диалоговом окне в поле Входной интервал введите ссылку на диапазон с данными ряда, т.е. на B7:B32.
Если диапазон включает и заголовок, то нужно установить галочку в поле Метки. В нашем случае устанавливать галочку не требуется, т.к. заголовок столбца не входит в диапазон B7:B32.
Поле Фактор затухания, как и параметр альфа в вышеуказанной формуле, определяет степень сглаживания ряда. Фактор затухания равен (1- альфа). Чем больше Фактор затухания тем глаже получается ряд. Установим значение 0,8.
В поле Выходной интервал достаточно ввести ссылку на левую верхнюю ячейку диапазона с результатами (укажем ячейку D7).
Также поставим галочки в поле Вывод графика и Стандартные погрешности (будет выведен столбец с расчетами погрешностей, англ. Standard Errors).
Нажмем ОК.
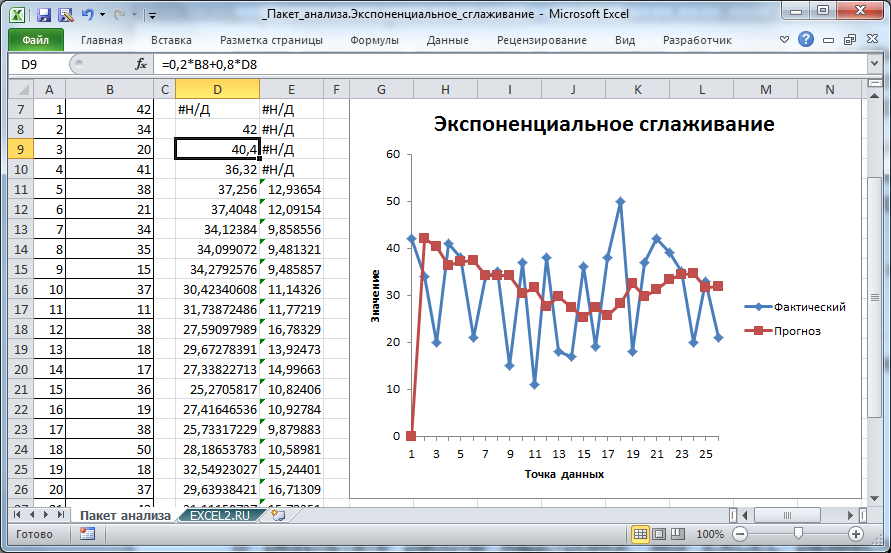
В результате работы надстройки, MS EXCEL разместил значения ряда, полученного методом Экспоненциального сглаживания, в столбце D (см. файл примера лист Пакет анализа).
В ячейке D7 содержится текстовое значение ошибки #Н/Д, т.к. для получения первого значения Экспоненциального сглаживания требуется значение исходного ряда за предыдущий период.
Первое значение сглаженного ряда, точнее формула =B7, содержится в ячейке D8. Второе значение вычисляется с помощью формулы =0,2*B8+0,8*D8.
Таким образом, Фактор затухания (0,8) определяет вес (вклад) предыдущего значения сглаженного ряда. Соответственно, (1-Фактор затухания)=альфа определяет вес предыдущего значения исходного ряда.
Диаграмма
Для отображения рядов MS EXCEL создал диаграмму типа график. Сглаженный ряд на диаграмме называется «Прогноз» (ряд красного цвета).
Первое значение сглаженного ряда, которое равно ошибке #Н/Д, отражаются как 0, и может ввести в заблуждение (особенно, если последующие значения ряда близки к 0). Поэтому его лучше удалить из ячейки D7.
Примечание: Значение #Н/Д в ячейке D7 является просто текстовым значением, что принципиально отличается от результата возвращаемого формулами, например, функцией НД(), хотя визуально они неразличимы. При построении диаграммы текстовые значения всегда отображаются как 0. Но, если ошибка #Н/Д является результатом формулы, то воспринимается диаграммой как пустая ячейка и на ней не отображается.
Диаграмма позволяет визуально определить «выбросы», т.е. значения исходного ряда, которые существенно отличаются от средних значений. Такие «выбросы» могут быть следствием ошибки, но они оказывают существенное влияние на вид сглаженного ряда.
Вычисление погрешности
В столбце E, начиная с ячейки Е11, MS EXCEL разместил формулы для вычисления погрешностей (англ. Standard Errors):
=КОРЕНЬ(СУММКВРАЗН(B8:B10;D8:D10)/3)
Т.е. данная погрешность вычисляется по формуле:
Значения y – это значения исходного ряда в период i. Значения «y с крышечкой» — значения ряда, полученного методом Экспоненциального сглаживания, в тот же в период i. Значение n для экспоненциального сглаживания всегда равно 3, т.е. ошибка вычисляется за 3 последних периода (последние 3 значения учитываются с макимальным весом при расчете текущего значения сглаженного ряда и, соответственно, вносят более 50% вклада в его значение. Величина вклада сильно зависит от альфа).
Подробнее об этой погрешности см. соответствующий раздел в статье про Скользящее среднее.
Почему сглаживание называется экспоненциальным?
Как было показано в статье про Взвешенное скользящее среднее веса значений исходного ряда берутся в зависимости от их удаленности от текущего периода. Например, для 3-х периодов усреднения для Взвешенного скользящего среднего можно использовать формулу:
Yскол.i=0,5*Yi+ 0,4*Yi-1+ 0,1*Yi-2
Экспоненциальное сглаживание по сути является модификацией Взвешенного скользящего среднего – при расчете значения сглаженного ряда используются ВСЕ предыдущие значения исходного ряда с весами уменьшающимися в геометрической прогрессии по мере удаления от текущего периода.
Чтобы это показать воспользуемся формулой
Yэксп.i=альфа*Yi-1+ (1-альфа)*Yэксп.i-1
и вычислим Yэксп.5, т.е. значения сглаженного ряда для 5-го периода. После очевидных преобразований получим:
Yэксп.5=альфа*[(1-альфа)0* Yэксп.4+ (1-альфа)1* Yэксп.3+(1-альфа)2* Yэксп.2] +(1-альфа)3* Y1
Таким образом, вес 4-го (предыдущего) члена ряда =(1-альфа)0, а вес 3-го =(1-альфа)1 и т.д. Пусть t – текущий период (в нашем случае =5). Вес (t-i)-го члена ряда =(1-альфа)t-1-i. Т.к. (1-альфа)<1, то с ростом i растет и вес, и для члена t-1 достигает максимума =1.
Как известно, экспоненциальный рост y=a*EXP(b*x) в случае дискретной области определения с равными интервалами x называют геометрическим ростом (значения экспоненциальной функции y=a*EXP(b*x) являются в этом случае членами геометрической прогрессии m^x).
В нашем случае, приравняв i-й вес (1-альфа)t-1-i соответствующему значению экспоненциальной функции a*EXP(b*i) получим уравнение, которое позволит вычислить коэффициенты a и b (понадобится еще одно уравнение, например, для i-1 веса).
Решив систему из 2-х уравнений получим, a= EXP((t-1)*LN(1-альфа)) и b= LN(1-альфа).
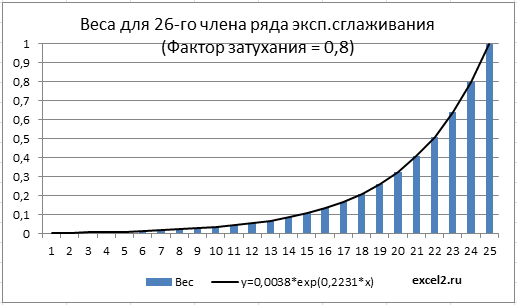
В файле примера для 26-го члена сглаженного ряда (t=26) вычислены веса всех предыдущих членов. На диаграмме ниже показано, что веса уменьшаются с ростом i в геометрической прогрессии, что соответствует экспоненциальной функции y=0,0038*exp(0,2231*x), где x=i. Вычисления параметров экспоненциальной кривой сделаны с помощью надстройки Поиск решения.
Экспоненциальное сглаживание с настраиваемым Фактором затухания
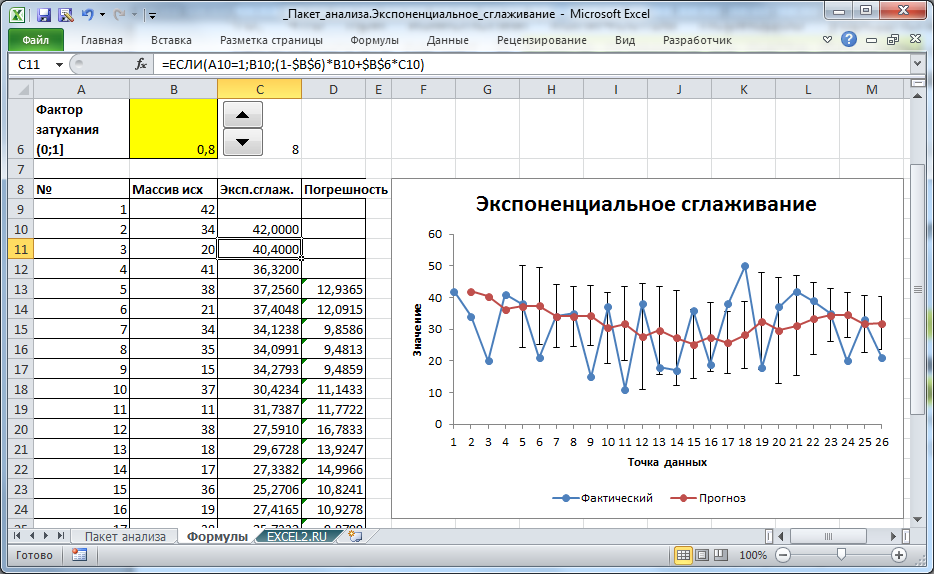
Недостатком формул, получаемых с помощью Пакета анализа, является то, что при изменении Фактора затухания (1-альфа) приходится перезапускать расчет. В файле примера на листе Формулы создана форма для быстрого пересчета Экспоненциального сглаживания в зависимости от значения Фактора затухания (полученный результат, естественно, полностью совпадает с расчетами надстройки Пакет анализа).
Значения ряда вычисляются с помощью формулы:
=ЕСЛИ(A10=1;B10;(1-$B$6)*B10+$B$6*C10)
в ячейке В6 содержится значение Фактора затухания.
Выбор значения Фактора затухания для удобства осуществляется с помощью элемента управления Счетчик с шагом 0,1.
17 авг. 2022 г.
читать 3 мин
Экспоненциальное сглаживание — это метод «сглаживания» данных временных рядов, который часто используется для краткосрочного прогнозирования.
Основная идея заключается в том, что данные временных рядов часто имеют связанный с ними «случайный шум», который приводит к пикам и впадинам в данных, но, применяя экспоненциальное сглаживание, мы можем сгладить эти пики и впадины, чтобы увидеть истинную основную тенденцию данных. .
Основная формула для применения экспоненциального сглаживания выглядит следующим образом:
F t = αy t-1 + (1 – α) F t-1
куда:
F t = прогнозируемое значение для текущего периода времени t
α = значение константы сглаживания в диапазоне от 0 до 1.
y t-1 = Фактическое значение данных за предыдущий период времени
F t-1 = Прогнозируемое значение для предыдущего периода времени t-1
Чем меньше значение альфа, тем больше сглаживаются данные временного ряда.
В этом руководстве мы покажем, как выполнить экспоненциальное сглаживание данных временных рядов с помощью встроенной функции в Excel.
Пример: экспоненциальное сглаживание в Excel
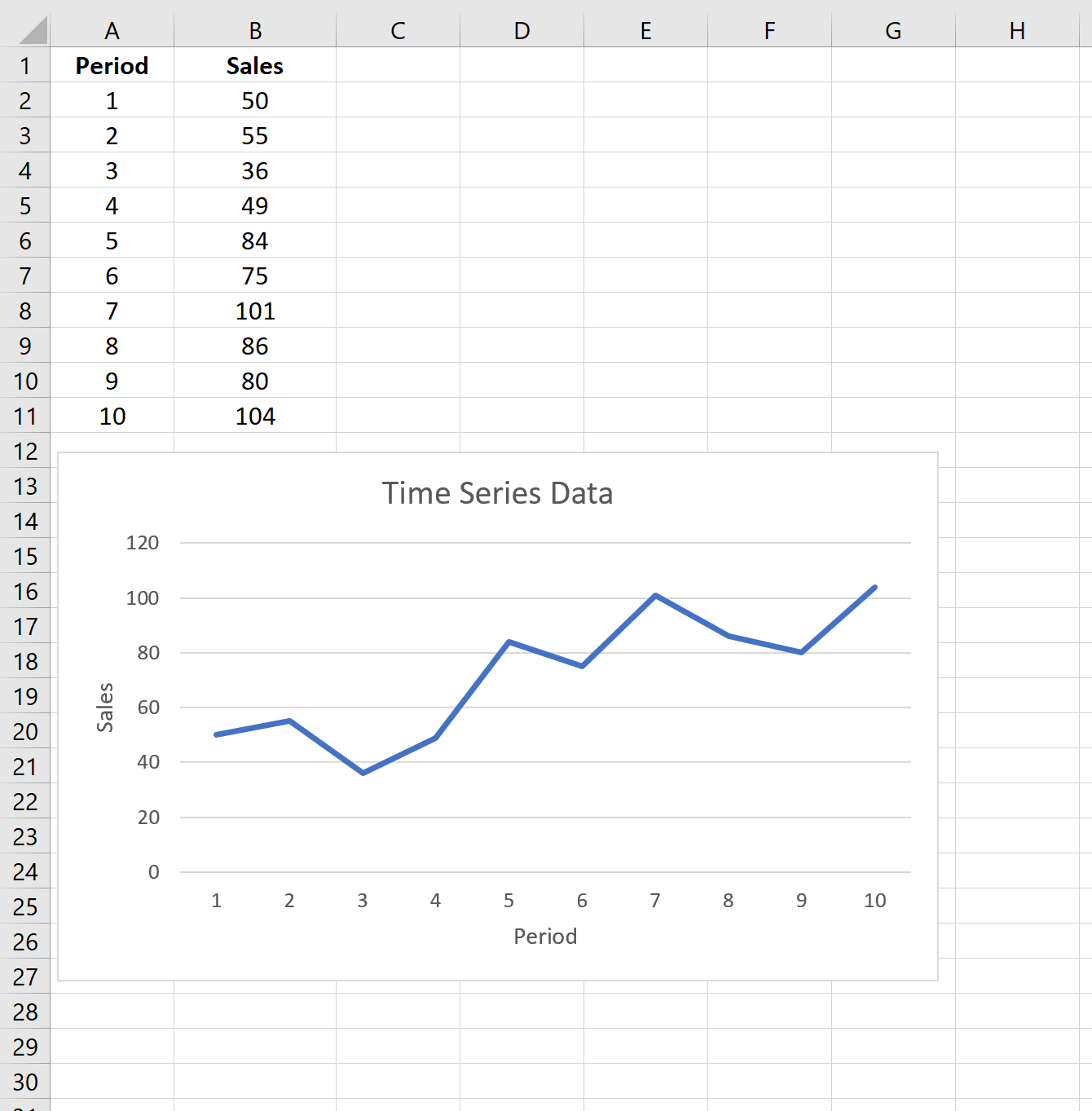
Предположим, у нас есть следующий набор данных, который показывает продажи конкретной компании за 10 периодов продаж:
Выполните следующие шаги, чтобы применить экспоненциальное сглаживание к этим данным временного ряда.
Шаг 1: Нажмите кнопку «Анализ данных».
Перейдите на вкладку «Данные» на верхней ленте и нажмите кнопку «Анализ данных». Если вы не видите эту кнопку, вам нужно сначала загрузить Excel Analysis ToolPak , который можно использовать совершенно бесплатно.
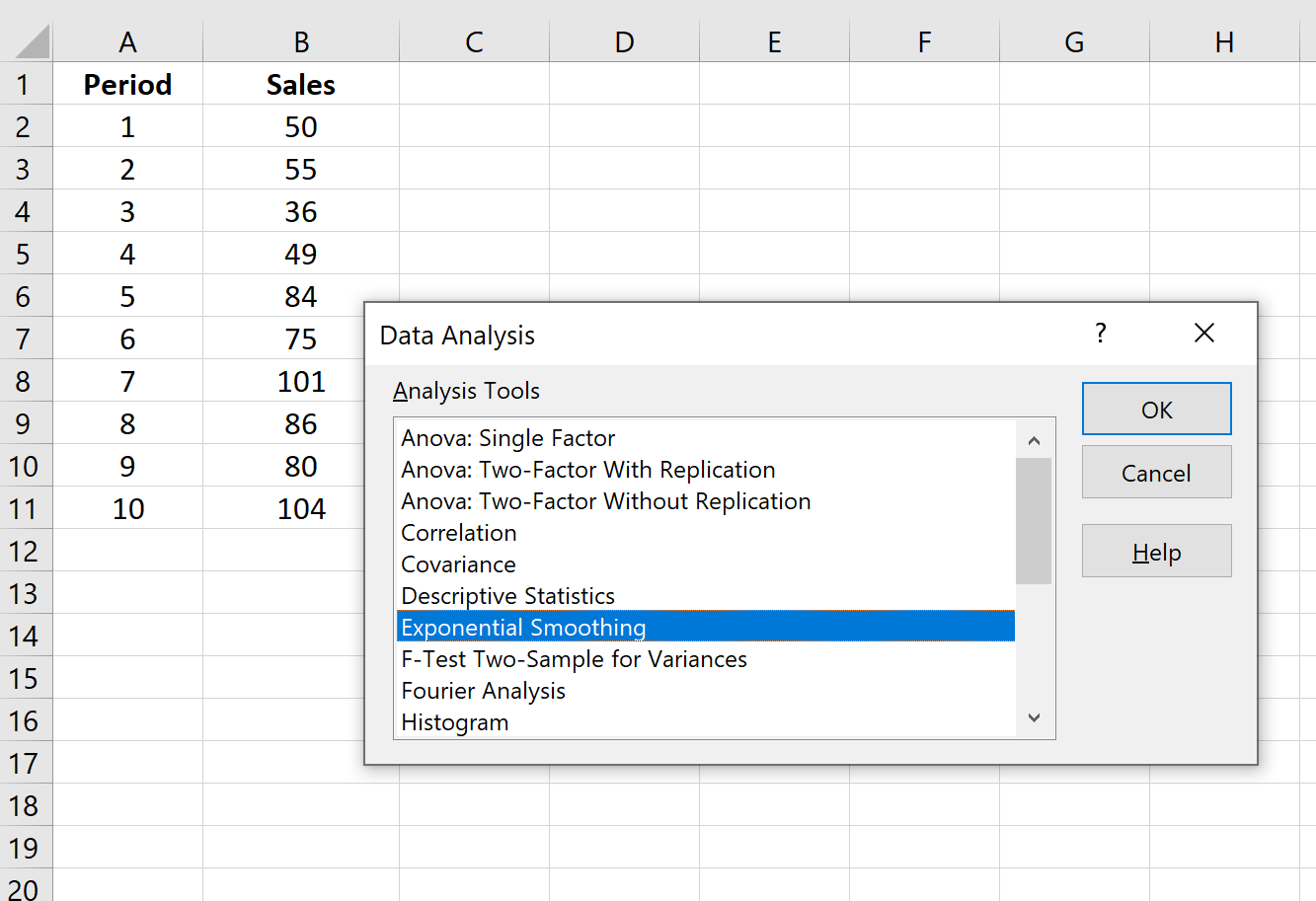
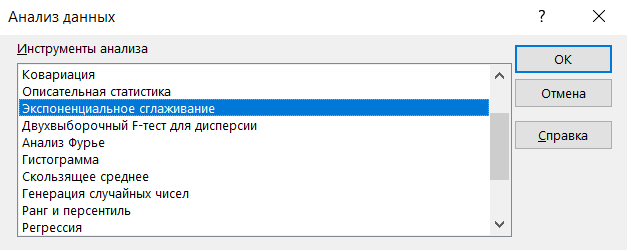
Шаг 2: Выберите параметр «Экспоненциальное сглаживание» и нажмите «ОК».
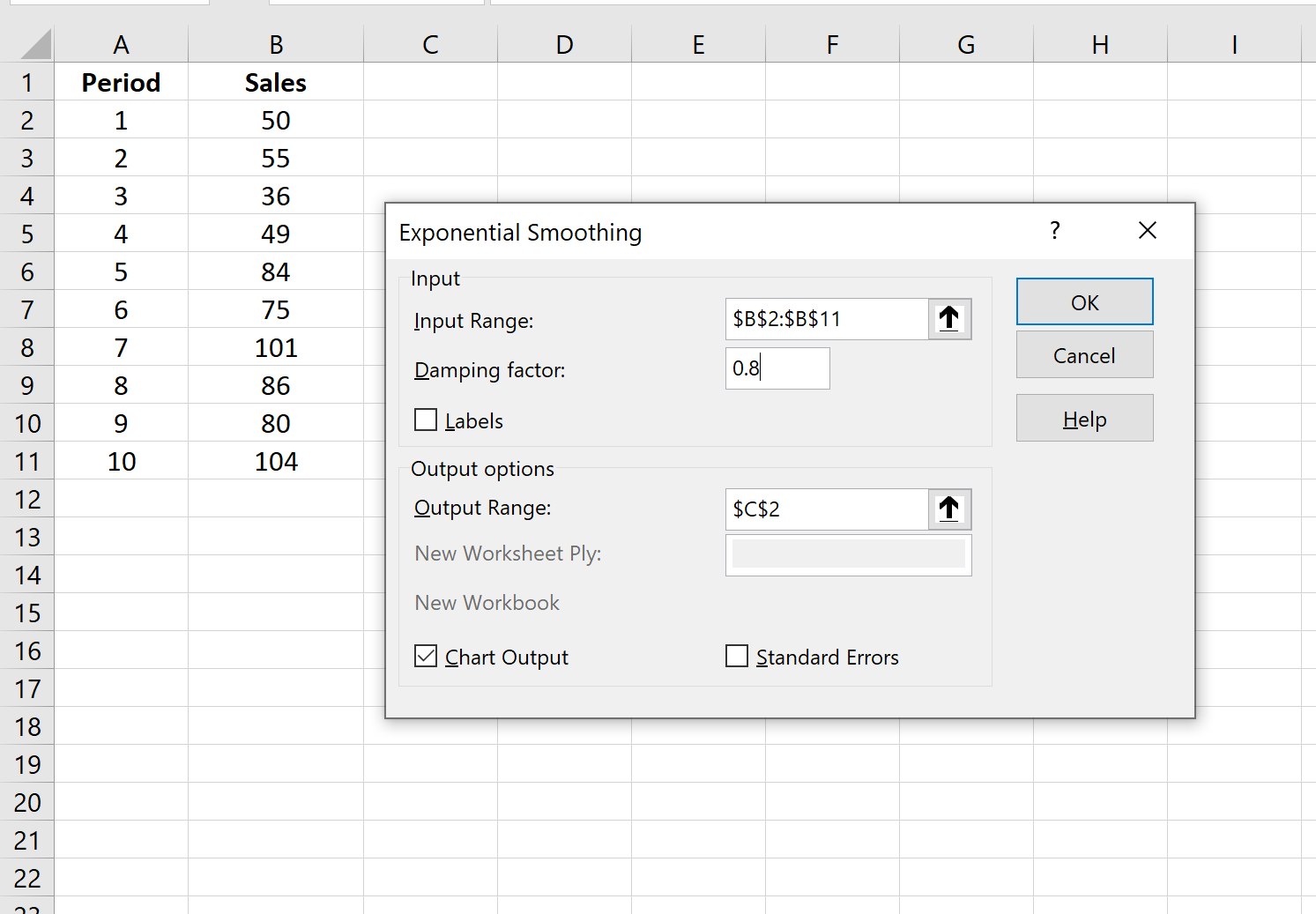
Шаг 3: Заполните необходимые значения.
- Заполните значения данных для Input Range .
- Выберите значение, которое вы хотели бы использовать для коэффициента затухания , которое равно 1-α. Если вы хотите использовать α = 0,2, то ваш коэффициент демпфирования будет 1-0,2 = 0,8.
- Выберите выходной диапазон , в котором должны отображаться прогнозируемые значения. Рекомендуется выбрать этот выходной диапазон рядом с вашими фактическими значениями данных, чтобы вы могли легко сравнивать фактические значения и прогнозируемые значения рядом друг с другом.
- Если вы хотите увидеть диаграмму с фактическими и прогнозируемыми значениями, установите флажок « Вывод диаграммы ».
Затем нажмите ОК.
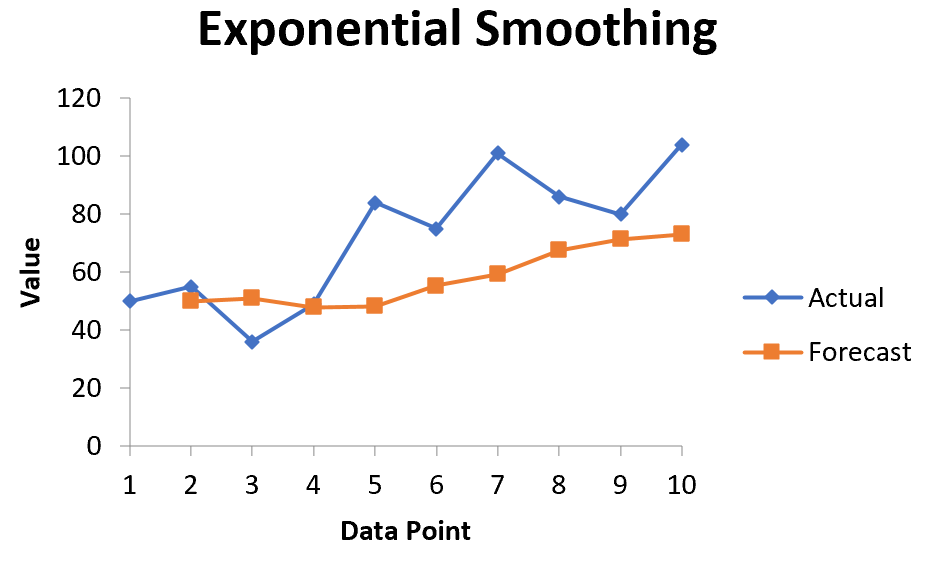
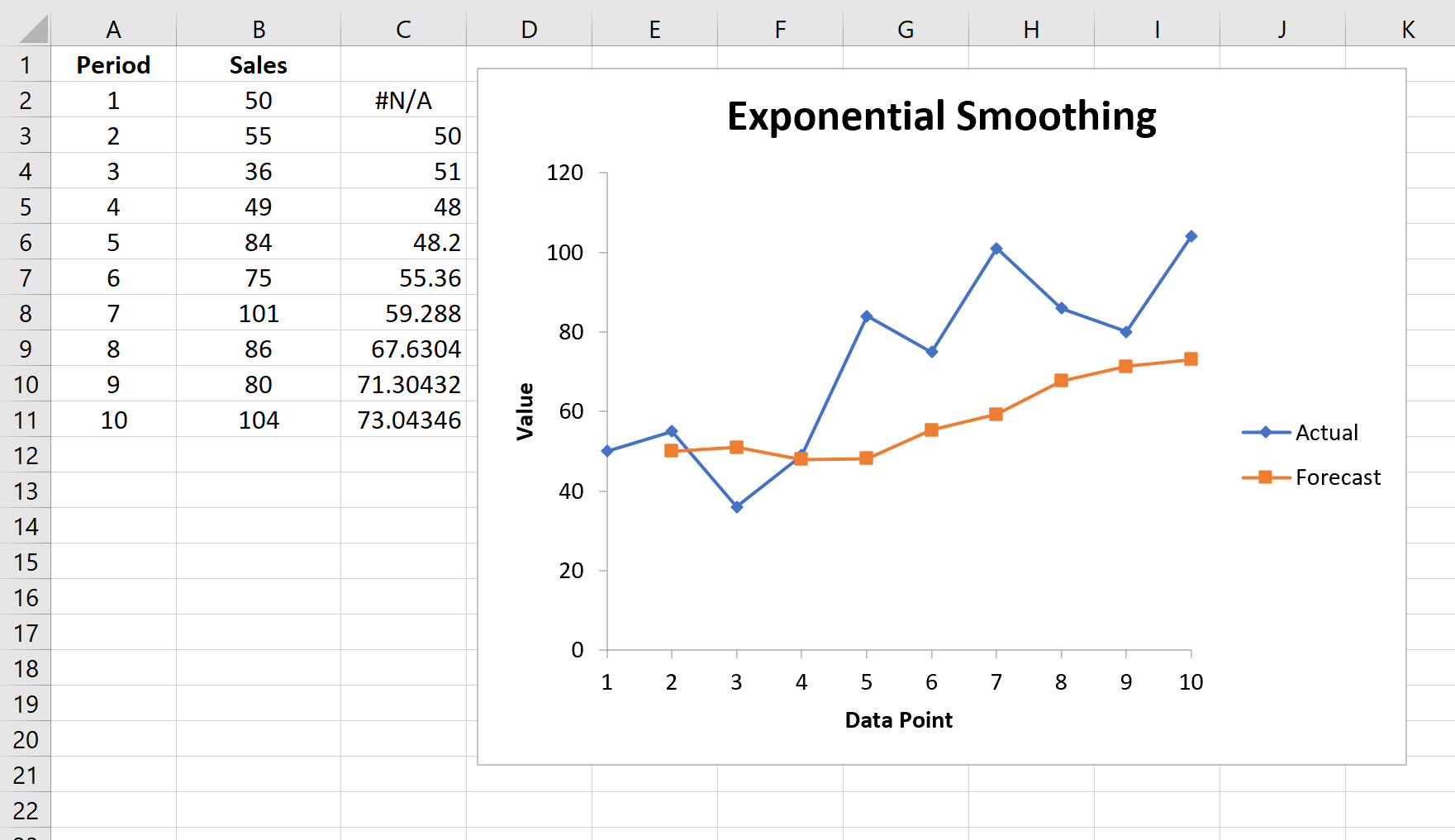
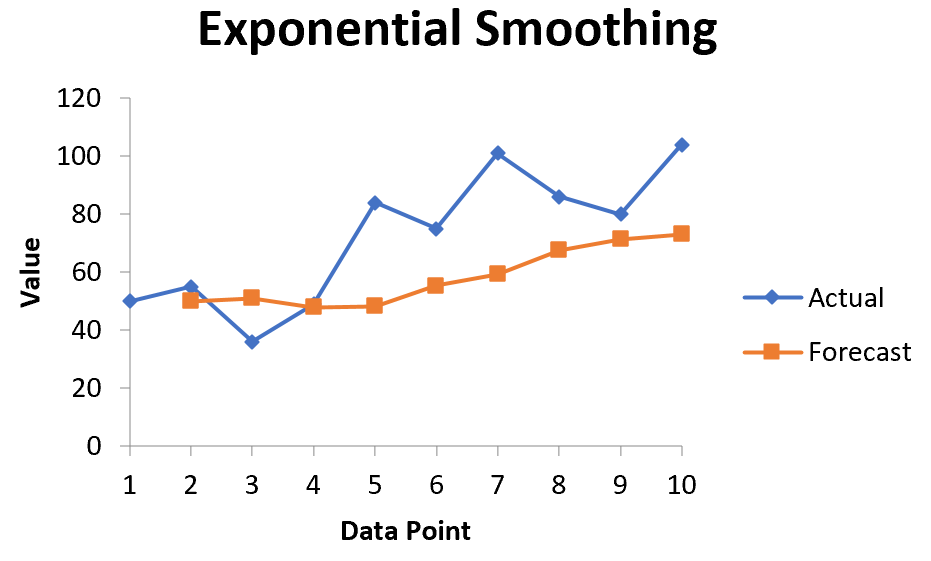
Автоматически появится список прогнозируемых значений и диаграмма:
Обратите внимание, что первый период времени имеет значение #N/A, поскольку нет предыдущего периода времени, который можно было бы использовать для расчета прогнозируемого значения.
Эксперименты с коэффициентами сглаживания
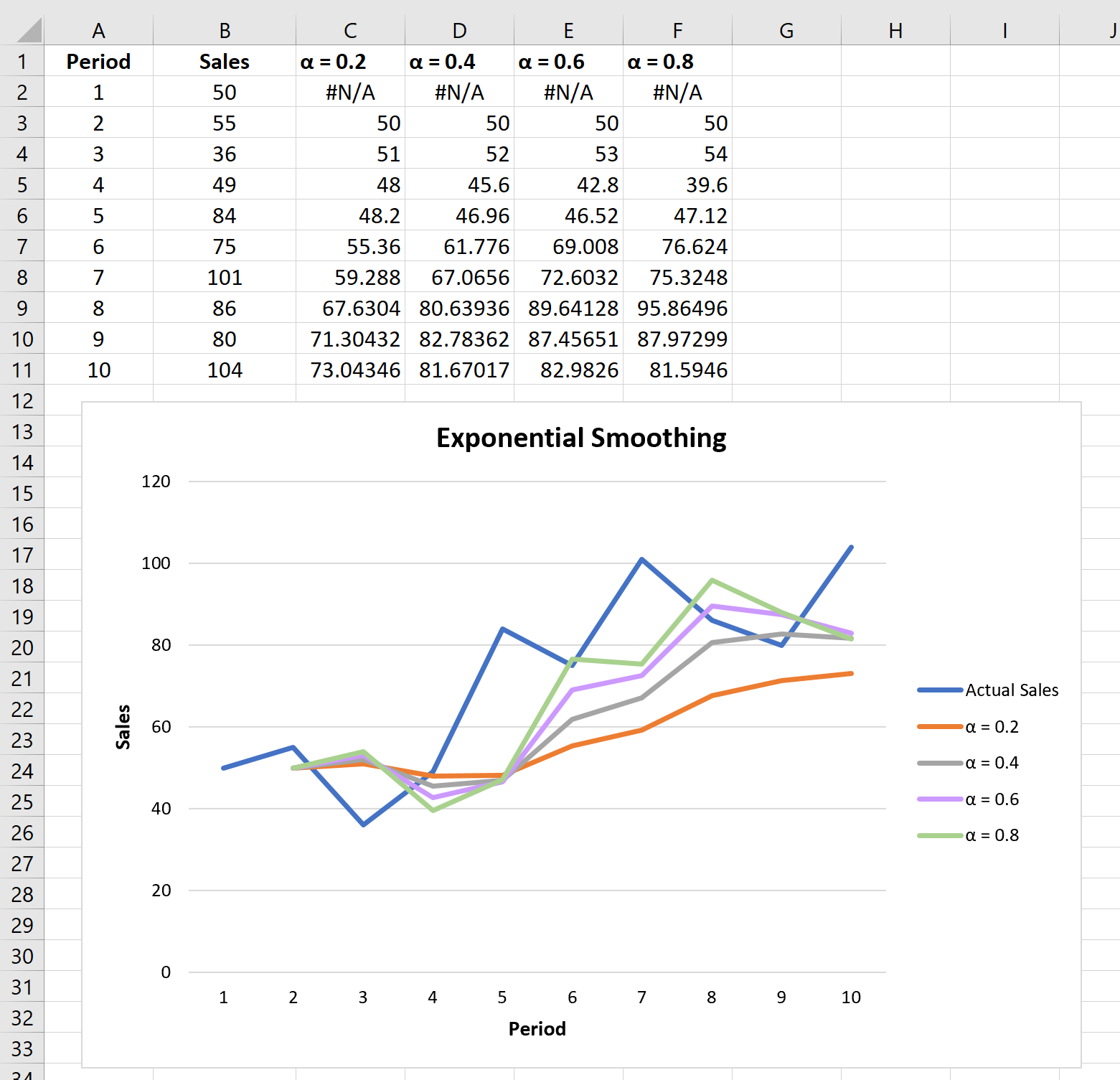
Вы можете поэкспериментировать с различными значениями коэффициента сглаживания α и посмотреть, как он повлияет на прогнозируемые значения. Вы заметите, что чем меньше значение α (больше значение коэффициента затухания), тем более сглаженными будут прогнозируемые значения:
Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашим полным списком руководств по Excel .
Содержание
- Экспоненциальное сглаживание в Excel
- Экспоненциальное распределение. Непрерывные распределения в EXCEL
- Экспоненциальное распределение в MS EXCEL
- Графики функций
- Генерация случайных чисел
- Задачи
- Как использовать экспоненциальное распределение в Excel
- Пример 1: время до прихода следующего клиента
- Пример 2: Время до следующего землетрясения
- Пример 3: время до следующего телефонного звонка
- Как выполнить экспоненциальное сглаживание в Excel
- Пример: экспоненциальное сглаживание в Excel
- Эксперименты с коэффициентами сглаживания
Экспоненциальное сглаживание в Excel
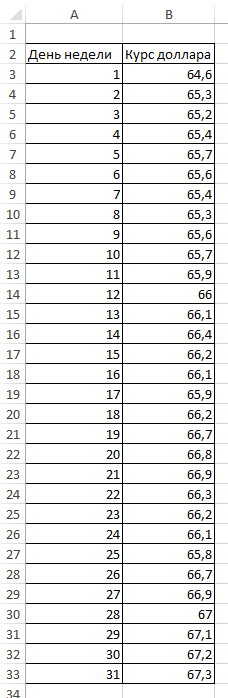
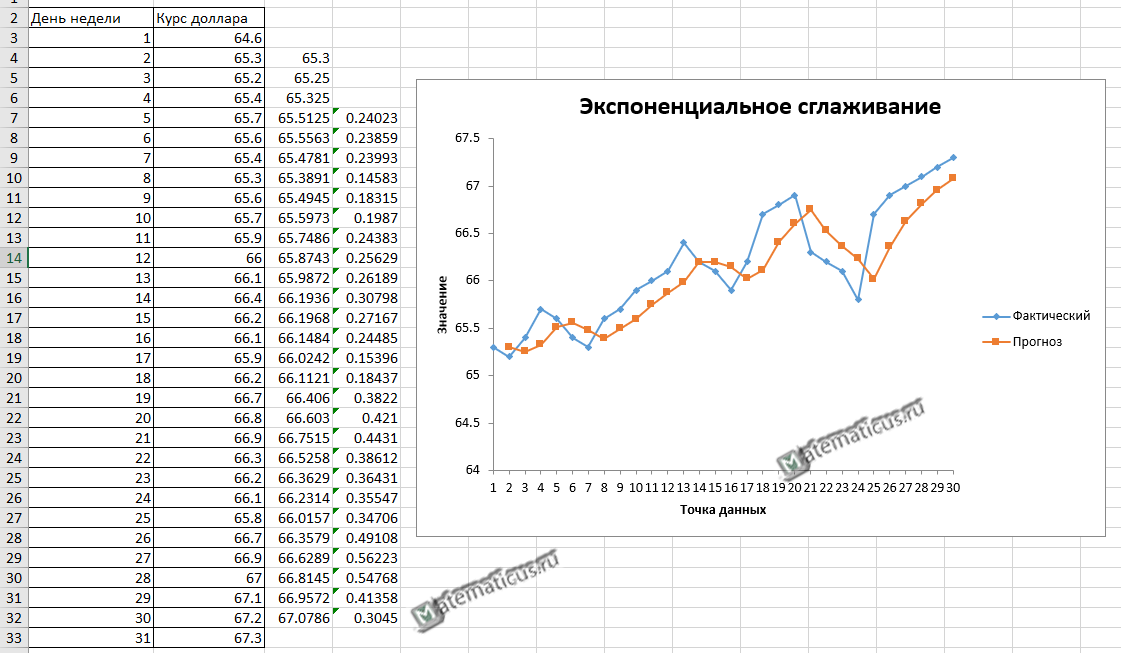
Дана таблица курса доллара за месяц.
Для того чтобы применить экспоненциальное сглаживание в Excel переходим на Анализ данных.
Переходим на вкладку Данные -> Анализ данных -> Экспоненциальное сглаживание
Если у вас в Excel не отображается на вкладке расширение Анализ данных, как его настроить см. здесь.
В окне экспоненциальное сглаживание указываем входной и выходной интервал, фактор затухания укажем 0.5. Ставим галочки метки, вывод графика и стандартные погрешности и нажимаем Ок.
Получаем график прогноза при применение экспоненциального сглаживания и фактический график в Excel
Экспоненциальное сглаживание часто применяется для прогнозирования.
Источник
Экспоненциальное распределение. Непрерывные распределения в EXCEL
history 8 ноября 2016 г.
Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ЭКСП.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.
Экспоненциальное распределение (англ. Exponential distribution ) часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение Экспоненциального распределения :
- Промежутки времени между появлением посетителей в кафе;
- Промежутки времени нормальной работы оборудования между появлением неисправностей (неисправности возникают из-за случайных внешних влияний, а не по причине износа, см. Распределение Вейбулла );
- Затраты времени на обслуживание одного покупателя.
Плотность вероятности Экспоненциального распределения задается следующей формулой:
График плотности распределения вероятности и интегральной функции Экспоненциального распределения выглядит следующим образом (см. ниже).
Экспоненциальное распределение тесно связано с дискретным распределением Пуассона . Если Распределение Пуассона описывает число случайных событий, произошедших за определенный интервал времени, то Экспоненциальное распределение должноописывать длину интервала времени между двумя последовательными событиями.
Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается распределением Пуассона со средним значением равным 15 машин в час (параметр распределения λ =15). Вероятность того, что на стоянку в течение часа приедет k машин равно:
Т.к. в среднем в час на стоянку приезжает 15 машин, то среднее время между 2-мя приезжающими машинами равно 1час/15машин=0,067. Т.к. среднее время между 2-мя событиями равно обратному значению параметра экспоненциального распределения , то параметр λ =15 , а плотность соответствующего экспоненциального распределения равна:
Экспоненциальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Экспоненциального распределения имеется функция ЭКСП.РАСП() , английское название — EXPON.DIST(), которая позволяет вычислить плотность вероятности (см. формулу в начале статьи) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по экспоненциальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:
Экспоненциальное распределение имеет обозначение Exp ( λ ).
Примечание : До MS EXCEL 2010 в EXCEL была функция ЭКСПРАСП() , которая позволяет вычислить кумулятивную (интегральную) функцию распределения и плотность вероятности . ЭКСПРАСП() оставлена в MS EXCEL 2010 для совместимости.
В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции экспоненциального распределения :
- =1-EXP(- λ *x) ;
- =ГАММА.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем Гамма распределения ;
- =ВЕЙБУЛЛ.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем распределения Вейбулла ;
Примечание : Для удобства написания формул в файле примера создано Имя для параметра распределения — λ .
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Генерация случайных чисел
Для генерирования массива чисел, распределенных по экспоненциальному закону , можно использовать формулу =-LN(СЛЧИС())/ λ
Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Если случайные числа содержатся в диапазоне B14:B213 , то оценку параметра экспоненциального распределения λ можно сделать с использованием формулы =1/СРЗНАЧ(B14:B213) .
Задачи
Экспоненциальное распределение широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр λ называется интенсивность отказов , а 1/ λ – среднее время до отказа .
Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый Экспоненциальным распределением с интенсивностью отказа равной 10^(-3) в час, таким образом, λ = 10^(-3). Среднее время до отказа равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за Среднее время до отказа, то нужно записать формулу:
Т.е. результат не зависит от параметра λ .
В MS EXCEL решение выглядит так: =ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)
Задача . Среднее время до отказа некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы. =ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Источник
Как использовать экспоненциальное распределение в Excel
Экспоненциальное распределение — это распределение вероятностей, которое используется для моделирования времени, в течение которого мы должны ждать, пока не произойдет определенное событие.
Это распределение может быть использовано для ответа на такие вопросы, как:
- Как долго владельцу магазина нужно ждать, пока покупатель войдет в его магазин?
- Как долго батарея будет продолжать работать, прежде чем она умрет?
- Как долго компьютер будет продолжать работать, прежде чем он сломается?
В каждом сценарии нас интересует вычисление того, как долго нам придется ждать, пока не произойдет определенное событие. Таким образом, каждый сценарий может быть смоделирован с использованием экспоненциального распределения.
Если случайная величина X следует экспоненциальному распределению, то кумулятивная функция плотности X может быть записана как:
F (х; λ) = 1 – e -λx
- λ: параметр скорости (рассчитывается как λ = 1/μ)
- e: константа, примерно равная 2,718.
Чтобы рассчитать вероятности, связанные с кумулятивной функцией плотности экспоненциального распределения в Excel, мы можем использовать следующую формулу:
- x : значение экспоненциально распределенной случайной величины
- lambda : параметр скорости
- cumulative : использовать функцию кумулятивной плотности или нет (ИСТИНА или ЛОЖЬ)
Следующие примеры показывают, как использовать эту формулу на практике.
Пример 1: время до прихода следующего клиента
В среднем новый покупатель заходит в магазин каждые две минуты. После прихода клиента найти вероятность того, что новый клиент прибудет менее чем за одну минуту.
Решение: Среднее время между клиентами составляет две минуты. Таким образом, ставка может быть рассчитана как:
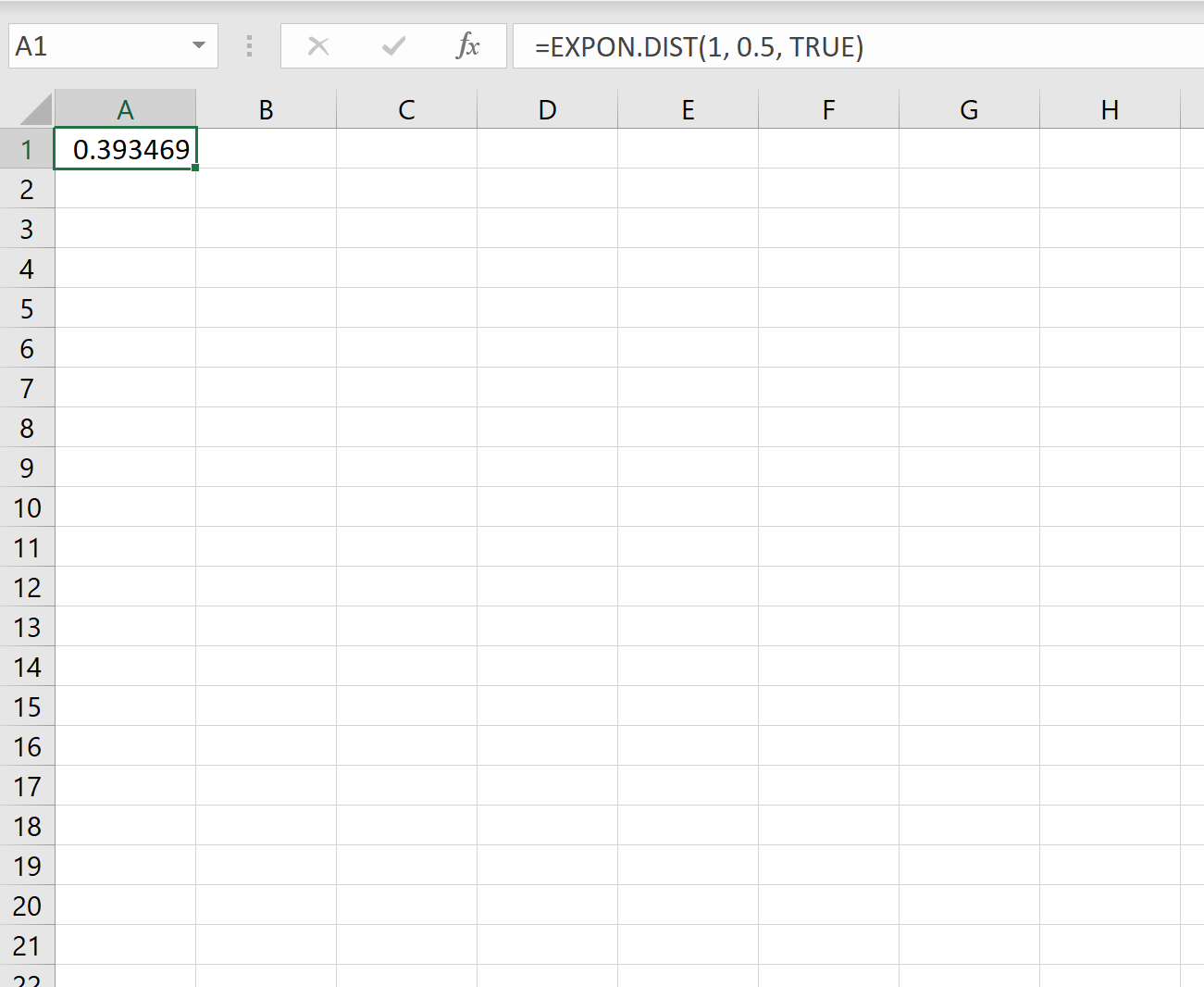
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что новый клиент прибудет менее чем за одну минуту:
Вероятность того, что следующего клиента придется ждать менее одной минуты, равна 0,393469 .
Пример 2: Время до следующего землетрясения
Предположим, землетрясение происходит в среднем каждые 400 дней в определенном регионе. После землетрясения найти вероятность того, что следующее землетрясение произойдет не ранее, чем через 500 дней.
Решение: Среднее время между землетрясениями составляет 400 дней. Таким образом, ставка может быть рассчитана как:
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что следующее землетрясение произойдет менее чем через 500 дней:
Вероятность того, что следующее землетрясение произойдет менее чем через 500 дней, равна 0,7135.
Таким образом, вероятность того, что следующего землетрясения придется ждать более 500 дней, равна 1 – 0,7135 = 0,2865 .
Пример 3: время до следующего телефонного звонка
Предположим, колл-центр получает новый звонок в среднем каждые 10 минут. После звонка клиента найти вероятность того, что новый клиент позвонит в течение 10–15 минут.
Решение: Среднее время между вызовами составляет 10 минут. Таким образом, ставка может быть рассчитана как:
Таким образом, мы можем использовать следующую формулу в Excel для расчета вероятности того, что следующий клиент позвонит в течение 10-15 минут:
Вероятность того, что новый клиент позвонит в течение 10-15 минут. составляет 0,1447 .
Источник
Как выполнить экспоненциальное сглаживание в Excel
Экспоненциальное сглаживание — это метод «сглаживания» данных временных рядов, который часто используется для краткосрочного прогнозирования.
Основная идея заключается в том, что данные временных рядов часто имеют связанный с ними «случайный шум», который приводит к пикам и впадинам в данных, но, применяя экспоненциальное сглаживание, мы можем сгладить эти пики и впадины, чтобы увидеть истинную основную тенденцию данных. .
Основная формула для применения экспоненциального сглаживания выглядит следующим образом:
F t = αy t-1 + (1 – α) F t-1
F t = прогнозируемое значение для текущего периода времени t
α = значение константы сглаживания в диапазоне от 0 до 1.
y t-1 = Фактическое значение данных за предыдущий период времени
F t-1 = Прогнозируемое значение для предыдущего периода времени t-1
Чем меньше значение альфа, тем больше сглаживаются данные временного ряда.
В этом руководстве мы покажем, как выполнить экспоненциальное сглаживание данных временных рядов с помощью встроенной функции в Excel.
Пример: экспоненциальное сглаживание в Excel
Предположим, у нас есть следующий набор данных, который показывает продажи конкретной компании за 10 периодов продаж:
Выполните следующие шаги, чтобы применить экспоненциальное сглаживание к этим данным временного ряда.
Шаг 1: Нажмите кнопку «Анализ данных».
Перейдите на вкладку «Данные» на верхней ленте и нажмите кнопку «Анализ данных». Если вы не видите эту кнопку, вам нужно сначала загрузить Excel Analysis ToolPak , который можно использовать совершенно бесплатно.
Шаг 2: Выберите параметр «Экспоненциальное сглаживание» и нажмите «ОК».
Шаг 3: Заполните необходимые значения.
- Заполните значения данных для Input Range .
- Выберите значение, которое вы хотели бы использовать для коэффициента затухания , которое равно 1-α. Если вы хотите использовать α = 0,2, то ваш коэффициент демпфирования будет 1-0,2 = 0,8.
- Выберите выходной диапазон , в котором должны отображаться прогнозируемые значения. Рекомендуется выбрать этот выходной диапазон рядом с вашими фактическими значениями данных, чтобы вы могли легко сравнивать фактические значения и прогнозируемые значения рядом друг с другом.
- Если вы хотите увидеть диаграмму с фактическими и прогнозируемыми значениями, установите флажок « Вывод диаграммы ».
Затем нажмите ОК.
Автоматически появится список прогнозируемых значений и диаграмма:
Обратите внимание, что первый период времени имеет значение #N/A, поскольку нет предыдущего периода времени, который можно было бы использовать для расчета прогнозируемого значения.
Эксперименты с коэффициентами сглаживания
Вы можете поэкспериментировать с различными значениями коэффициента сглаживания α и посмотреть, как он повлияет на прогнозируемые значения. Вы заметите, что чем меньше значение α (больше значение коэффициента затухания), тем более сглаженными будут прогнозируемые значения:
Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашим полным списком руководств по Excel .
Источник
Exponential smoothing is a technique for “smoothing” out time series data and is often used for short-term forecasting.
The basic idea is that time series data often has “random noise” associated with it, which leads to peaks and valleys in the data, but by applying exponential smoothing we can smooth out these peaks and valleys to see the true underlying trend of the data.
The basic formula for applying exponential smoothing is as follows:
Ft = αyt-1 + (1 – α) Ft-1
where:
Ft = Forecasted value for current time period t
α = The value for the smoothing constant, between 0 and 1
yt-1 = The actual data value for the previous time period
Ft-1 = Forecasted value for previous time period t-1
The smaller the alpha value, the more the time series data is smoothed out.
In this tutorial, we show how to perform exponential smoothing for time series data using a built-in function in Excel.
Suppose we have the following dataset that shows the sales for a particular company for 10 sales periods:
Perform the following steps to apply exponential smoothing to this time series data.
Step 1: Click on the “Data Analysis” button.
Go to the “Data” tab along the top ribbon and click the “Data Analysis” button. If you don’t see this button, you need to first load the Excel Analysis ToolPak, which is completely free to use.
Step 2: Choose the “Exponential Smoothing” option and click OK.
Step 3: Fill in the necessary values.
- Fill in the data values for Input Range.
- Select the value you’d like to use for Damping Factor, which is 1-α. If you’d like to use α = 0.2, then your damping factor will be 1-0.2 = 0.8.
- Select the Output Range where you’d like the forecasted values to appear. It’s a good idea to choose this output range right next to your actual data values so you can easily compare the actual values and the forecasted values side by side.
- If you would like to see a chart displayed with the actual and the forecasted values, select the box that says Chart Output.
Then, click OK.
A list of forecasted values and a chart will automatically appear:
Note that the first time period has a value of #N/A because there is no previous time period to use to calculate the forecasted value.
Experimenting with Smoothing Factors
You can experiment with different values for the smoothing factor α and see how it impacts the forecasted values. You’ll notice that the smaller the value for α (larger value for Damping Factor), the more smoothed out the forecasted values will be:
For more tutorials in Excel, be sure to check out our complete list of Excel Guides.
Анализ временных рядов позволяет изучить показатели во времени. Временной ряд – это числовые значения статистического показателя, расположенные в хронологическом порядке.
Подобные данные распространены в самых разных сферах человеческой деятельности: ежедневные цены акций, курсов валют, ежеквартальные, годовые объемы продаж, производства и т.д. Типичный временной ряд в метеорологии, например, ежемесячный объем осадков.
Временные ряды в Excel
Если фиксировать значения какого-то процесса через определенные промежутки времени, то получатся элементы временного ряда. Их изменчивость пытаются разделить на закономерную и случайную составляющие. Закономерные изменения членов ряда, как правило, предсказуемы.
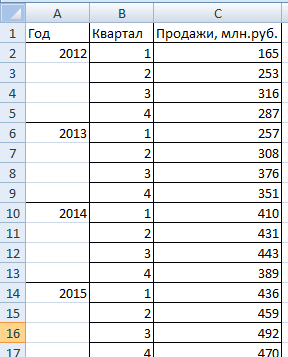
Сделаем анализ временных рядов в Excel. Пример: торговая сеть анализирует данные о продажах товаров магазинами, находящимися в городах с населением менее 50 000 человек. Период – 2012-2015 гг. Задача – выявить основную тенденцию развития.
Внесем данные о реализации в таблицу Excel:
На вкладке «Данные» нажимаем кнопку «Анализ данных». Если она не видна, заходим в меню. «Параметры Excel» — «Надстройки». Внизу нажимаем «Перейти» к «Надстройкам Excel» и выбираем «Пакет анализа».
Подключение настройки «Анализ данных» детально описано здесь.
Нужная кнопка появится на ленте.
Из предлагаемого списка инструментов для статистического анализа выбираем «Экспоненциальное сглаживание». Этот метод выравнивания подходит для нашего динамического ряда, значения которого сильно колеблются.
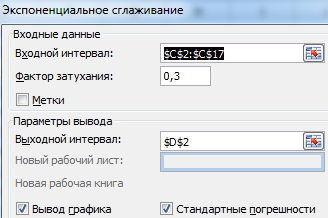
Заполняем диалоговое окно. Входной интервал – диапазон со значениями продаж. Фактор затухания – коэффициент экспоненциального сглаживания (по умолчанию – 0,3). Выходной интервал – ссылка на верхнюю левую ячейку выходного диапазона. Сюда программа поместит сглаженные уровни и размер определит самостоятельно. Ставим галочки «Вывод графика», «Стандартные погрешности».
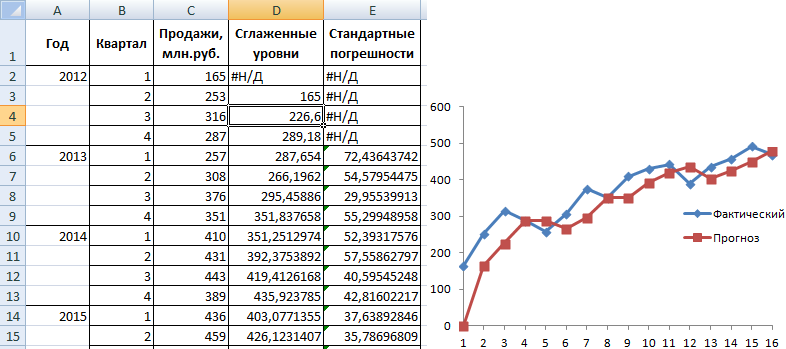
Закрываем диалоговое окно нажатием ОК. Результаты анализа:
Для расчета стандартных погрешностей Excel использует формулу: =КОРЕНЬ(СУММКВРАЗН(‘диапазон фактических значений’; ‘диапазон прогнозных значений’)/ ‘размер окна сглаживания’). Например, =КОРЕНЬ(СУММКВРАЗН(C3:C5;D3:D5)/3).
Прогнозирование временного ряда в Excel
Составим прогноз продаж, используя данные из предыдущего примера.
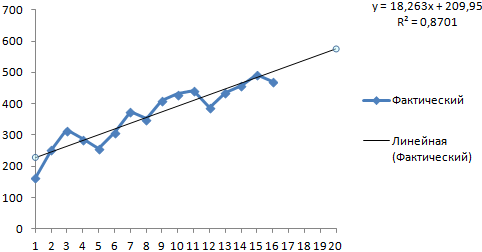
На график, отображающий фактические объемы реализации продукции, добавим линию тренда (правая кнопка по графику – «Добавить линию тренда»).
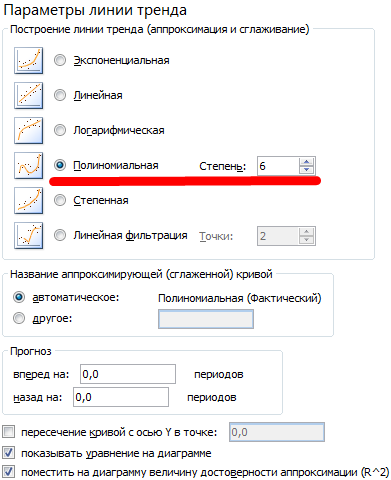
Настраиваем параметры линии тренда:
Выбираем полиномиальный тренд, что максимально сократить ошибку прогнозной модели.
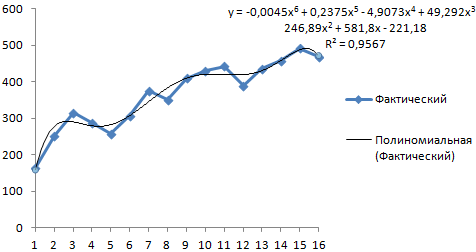
R2 = 0,9567, что означает: данное отношение объясняет 95,67% изменений объемов продаж с течением времени.
Уравнение тренда – это модель формулы для расчета прогнозных значений.
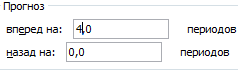
Большинство авторов для прогнозирования продаж советуют использовать линейную линию тренда. Чтобы на графике увидеть прогноз, в параметрах необходимо установить количество периодов.
Получаем достаточно оптимистичный результат:
В нашем примере все-таки экспоненциальная зависимость. Поэтому при построении линейного тренда больше ошибок и неточностей.
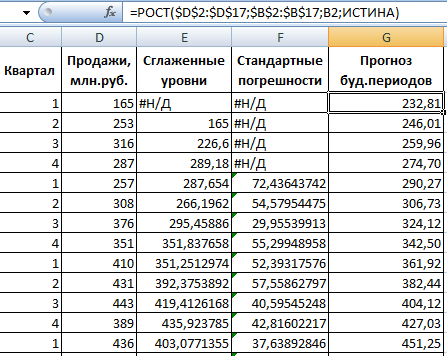
Для прогнозирования экспоненциальной зависимости в Excel можно использовать также функцию РОСТ.
Для линейной зависимости – ТЕНДЕНЦИЯ.
При составлении прогнозов нельзя использовать какой-то один метод: велика вероятность больших отклонений и неточностей.