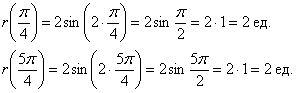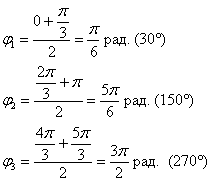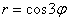Муниципальное
общеобразовательное учреждение «Лицей №1» г. Новотроицка
Исследовательская
работа
Построение
кривых в программе Microsoft Excel
Выполнила:
ученица
9 «В» класса
МОАУ
«Лицей №1»
Фролова
Ксения
Руководитель:
Хоменко Н. В.
Новотроицк
2020
ОГЛАВЛЕНИЕ
Введение..……………………………………………………………………….…………..3
1.1.
Полярная система координат…………………………………………………………………….5
1.2.
Инструкция по построению кривых с помощью программы Microsoft Excel……7
1.3.
Спирали ………………………………………………………………………………………..10
1.4.
Розы ……………….…………..……………………………………………………….13
Заключение…………….…………………………………………….…………………….17
Список
литературы………………………………………………………………………18
Приложение
1………………………………………………..…………………………………..20
Приложение
2………………………………………………………..……….……….…..26
ВВЕДЕНИЕ
Кроме привычной для нас прямоугольной
декартовой системы координат, в математике используются и другие способы
задания положения точки в пространстве или на плоскости. Чаще всего применяются
полярные координаты. Положение точки определяется при помощи луча,
выходящего из полюса и пересекающего в заданном месте соответствующую
окружность. В такие координаты очень естественно укладываются многие природные
формы и биологические объекты. Их формы порой самым удивительным образом
напоминают фигуры, образуемые в криволинейных координатах достаточно простыми и
лаконичными математическими выражениями. Это сходство указывает на то, что тела
живых организмов, биологические структуры, образуются по принципам, сходным с
принципами построения «полярных» объектов. Живой организм
«начинается» из одной исходной точки, и затем развивается и растет во
все стороны по определенному математическому закону. По крайней мере, такое
предположение совсем не противоречит наблюдаемому в природе обилию
«математических», «полярных» форм. Природа как бы сама
использует полярные координаты, что особенно бросается в глаза на примере
растений, многоклеточных животных и насекомых. Вероятно поэтому фигуры,
построенные в полярных координатах, обладают неповторимой эстетической
привлекательностью. Они плотно ассоциируются с формами цветов, бабочек, словом,
всем тем, что так много удовольствия доставляет нашему взору в живой природе.
Использование
компьютерных программ для построения графиков функций, изучение их свойств и
закономерностей, дает возможность рассмотреть большое количество примеров с
минимальными усилиями. Данная работа предназначена в помощь учителям при
изучении функции, а также ученикам с целью заинтересовать их математикой,
информатикой, показав возможности использования информационных технологий на
уроках математики.
Актуальность
работы. При изучении программы Microsoft Excel на уроках информатики построение
подобных графиков не оговаривалось. Также не оговаривался переход от декартовой
системы к полярной, поэтому выполняя данную работу я получаю возможность узнать
что-то новое для себя в обоих направлениях.
Вопрос (мотивация): Как построить графический образ уравнения
третьей (и выше) Microsoft Excel?
Проблема:
необходимо научиться переходить к полярной системе координат и строить различные
кривые этих уравнений в программе Microsoft Excel.
Гипотеза:
в ходе изучения построения графиков кривых в полярной системе координат я узнаю
некоторые особые возможности программы Microsoft Excel.
Поэтому,
объектом моего исследования стала полярная система координат.
Исходя
из этого, предметом моего исследования стала программа Microsoft Excel.
Цель
моей работы – показать принцип построения линий в
полярной системе координат с помощью программы Microsoft Excel, так как она должна значительно
облегчить построение кривых.
Результаты
исследования.
В
процессе работы я:
Ø изучила
переход от декартовой системы координат к полярной и обратно;
Ø исследовала
изменения вида кривой, в зависимости от параметров входящих в её уравнение;
Ø лучше
поняла принципы работы в программе Microsoft
Excel и оценила преимущества построения графиков именно в
ней.
Планы
и перспективы: продолжить изучение плоских кривых.
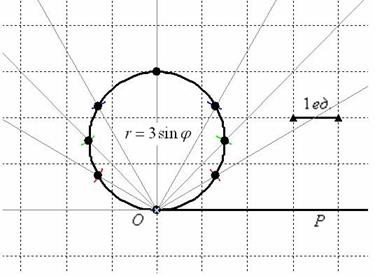
1.1. Полярная
система координат.
В полярной системе
координат положение точки определяется полярным радиусом R и углом , образуемым полярным радиусом с полярной
осью. Следовательно, полярная система координат — система координат, ставящая в
соответствие каждой точке на плоскости пару чисел .
Основными понятиями этой системы являются точка отсчёта (полюс) и луч,
начинающийся в этой точке (полярная ось).
Если в декартовой
системе координат предельно простое выражение определяет
прямую линию, то это же выражение, переписанное в форме ,
уже превращается в спираль. Фигуры в полярных координатах образуются как след
конца бегающего по кругу полярного радиуса переменной длины. Длина полярного
радиуса определяется величиной угла, который в данный момент времени он
образует с полярной осью. Координата берётся со знаком «+»,
если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «-»
в противоположном случае. Любая точка в этой системе имеет бесконечное число
координат вида, которым соответствует одна и
та же точка при любых натуральных . Для полюса
, угол
произвольный.
 Связь
Связь
между полярной и декартовой системами координат.
Точка О
— полярный полюс, луч ОЕ будем называть полярной осью,
отрезок ОМ — называют длиной полярного
радиуса R, положительный
угол от луча ОЕ до луча F — полярный угол.
Если известны полярные координаты R
и , точки М, то можно уставить связь
с её декартовыми координатами.
Построим прямоугольный ОМЕ. В этом треугольнике гипотенуза
ОМ=R, ЕОМ =
, катет ЕМ = у, катет ОЕ =
х координаты точки М.
Для того, чтобы перейти от полярных
координат к декартовой системе, используют формулы: ,
,
.
Обратно, чтобы, имея прямоугольные координаты, получить расстояние нужное для
задания полярных координат, надо воспользоваться теоремой Пифагора: , затем
,
.
Некоторые замечательные
кривые. На протяжении многих лет ученые собирали
информацию о формулах, рисующих разные фигуры. Многие фигуры получили свои
названия. Список таких названий внушителен: спираль Архимеда, Ферма, Галлилея,
Фибоначчи, кардиоида, овалы Кассини, лемниската Бернулли, фигуры Лиссажу,
розы Гвидо Гранди, кривые Маклорена, верзьера (локон Марии Аньези) и т.д.
1.2.
Инструкция по построению кривых с помощью
программы Microsoft Excel.
Если уравнение
задано в декартовых координатах, то следует перевести его в полярные, используя
формулы: X=R*COS(F),
Y=R*SIN(F).
Следовательно, математическая модель у нас уже есть. Рассмотрим пример
построения кривой.
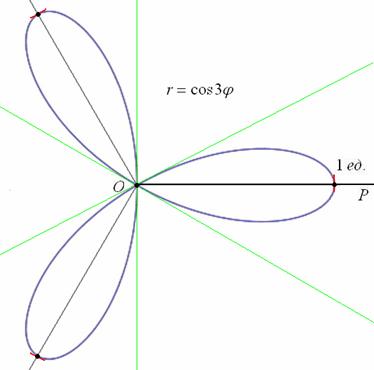
Задача.
Построить кривую, заданную уравнением .
Решение.
Найдем уравнение данной линии в полярных координатах.
Для программы
Microsoft Excel: R=4*COS(3*F)
Предположим, что угол F изменяется в
интервалах от 0 до 2. Для того, чтобы построить эту
кривую наиболее точно, с малым шагом изменения угла F, как мы это делали при
построении тригонометрических функций, мы выберем шаг изменения 0,1.
Построим
компьютерную модель исследования.
Формулы будут
записаны в терминах электронных таблиц следующим образом:
А2
0,1
А3 =А2+0,1
B2 =4*COS(3*F)
C2 =SIN(А2)
D2 =COS(А2)
E2 =B2*D2
F2 =В2*C2
Тогда получаем следующее распределение по
столбцам электронной таблицы:
|
1 |
F |
R |
SIN(F) |
COS(F) |
X |
Y |
|
2 |
0,1 |
3,821346 |
0,099833 |
0,995004 |
3,802255 |
0,381498 |
|
3 |
0,2 |
3,301342 |
0,198669 |
0,980067 |
3,235535 |
0,655875 |
|
4 |
0,3 |
2,48644 |
0,29552 |
0,955336 |
2,375387 |
0,734793 |
|
5 |
0,4 |
1,449431 |
0,389418 |
0,921061 |
1,335014 |
0,564435 |
|
6 |
0,5 |
0,282949 |
0,479426 |
0,877583 |
0,248311 |
0,135653 |
Для построения графика выделим
информационный блок E2..F63, так как аргумент F, будем изменять от 0,1 до 6,3
радиана. Возможно изменение и до 9,42, 12,56, и т. д.
Получим
следующий график.
Исследование
формы кривой, в зависимости от изменения значений входящих
в её уравнение. Внося изменения в ячейку В2 , не меняя более ничего, мы можем
получать различные виды уравнения .
1.3. 
В
математике спираль — это кривая, которая огибает некоторую центральную точку
или ось, постепенно приближаясь или удаляясь от неё, в зависимости от
направления обхода кривой.
Спираль Архимеда может
быть определена как траектория точки, участвующей одновременно в двух
равномерных движениях, одно из которых совершается вдоль прямой, а другое – по
окружности. Изобретение этой спирали приписывается, по некоторым источникам,
Кокону Самосскому, однако свойства ее были изучены Архимедом.
Уравнение кривой в декартовом
представлении: , в полярных координатах:
, где а — коэффициент
пропорциональности (получили прямо-пропорциональную зависимость). Расстояния
между соседними витками спирали есть величина постоянная и равна — а.
Различают правую и левую спираль, закрученную по- или против- часовой стрелки.
Применение.
По спирали Архимеда идет звуковая дорожка на грампластинке. Туго свернутый
рулон бумаги в профиль также представляет собой спираль Архимеда. Одна из
деталей швейной машины – механизм для равномерного наматывания ниток на шпульку
– имеет форму спирали Архимеда.

В истории математики логарифмическая спираль упоминается впервые в письме
Декарта к Мерсену в 1638 г., в котором Декарт определяет новую спираль как
линию, отношение длины дуги которой к радиус-вектору является постоянным.
Независимо от Декарта логарифмическая спираль была открыта Торичелли. Особенно
много внимания логарифмической спирали уделил Я. Бернулли, назвавший ее —
дивная спираль. Само же название логарифмической спирали было предложено
Вариньоном. Уравнение кривой в полярных координатах: .
Логарифмическая спираль имеет
многочисленные применения в технике, основанные на свойстве этой кривой
пересекать все свои радиус-векторы под одним и тем же углом. Это свойство
применяют в режущих машинах. Вращающиеся ножи в режущих машинах имеют профиль,
очерченный по дуге спирали, благодаря чему угол резания остается постоянным.

(частный случай логарифмической спирали).
Эту кривую можно заметить в созданиях природы. Например, раковины многих
моллюсков, улиток, рога архаров закручиваются по золотой спирали. Один из
наиболее распространенных пауков, эпейра, сплетает свою паутину по золотой
спирали. Cемечки в подсолнухе
располагаются по золотой спирали, точно так же, как и многие галактики, в том
числе и галактика Солнечной системы. В гидротехнике по золотой спирали изгибают
трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды
используется с наибольшей производительностью.

сказать, что золотая спираль является математическим символом идеального
соотношения формы и роста. Великий немецкий поэт Гёте считал ее даже
математическим символом жизни и духовного развития.
Спираль Ферма: . Любопытное отличие спирали Ферма от
других спиралей заключается в том, что расстояние между ее витками
неограниченно убывает по мере удаления от полюса.

. По мере роста
спираль устремляется к полюсу, делая
вокруг него бесконечное множество витков, расстояние между которыми убывает.

,
. Спираль
Галилея вошла в историю математики в 17 столетии в связи с постановкой проблемы
определения формы линии, по которой должна двигаться свободно падающая в
области экватора точка, если бы она не обладала начальной скоростью, сообщаемой
ей вращением земного шара.
Спираль «жезл»: .
Еще
одна спираль. По форме напоминает жезл египетских фараонов.
1.4. 
Впервые исследованием роз занимался
итальянский геометр Гвидо Гранди. Полная теория этих кривых была изложена им в
сочинении «Flores geometrici ex rhodanearum et claelarum deskriptione
resultants», изданном в 1728 году.
Задача.
Отрезок длины 2а движется так, что его концы все время находятся на
координатных осях. Составить уравнение траектории основания М перпендикуляра,
опущенного из начала координат на отрезок.
Решением данной задачи будет уравнение так
называемой четырехлепестковой розы или
.
В полярных координатах общее уравнение для
роз записывается в виде: или в виде
, где a и k – положительные
числа.
Обратимся к исследованию формы роз.
Поскольку правая часть уравнения не может превышать величины a, то и вся
роза, очевидно, уменьшается внутри круга радиусом a. Количество же
лепестков розы зависит от величины модуля k:
1. Если модуль k
– целое число, то роза состоит из k лепестков, при нечетном k,
и из 2k лепестков при k четном.
 |
|||
 |
2.Если модуль k – рациональное
число, равное то
роза состоит из m лепестков в случае, когда оба числа m
и n
нечетные, и из 2m
лепестков, если одно из этих чисел является четным.
При этом, в отличие от первого случая
каждый следующий лепесток будет частично перекрывать предыдущий.
3.Если модуль k – иррациональное
число, то роза состоит из бесчисленного множества лепестков, частично
накладывающихся друг на друга.
1.5.
Математическим исследованием формы цветов и листьев занимался также Хабеннихт
– геометр 19 столетия. Им был получен целый ряд уравнений, которые с весьма
хорошим приближением выражали аналитически формы листьев клена, щавеля, ивы и
т. д. Вот некоторые из этих кривых:
В полярных координатах можно описать при
помощи косинусов кратных дуг линии, которые обрисовывают контуры листьев
некоторых растений:
• кувшинки: ;
• кислицы: ;
• настурции: ;
• стрелолиста: .
Интересные «цветы» получаются при
построении кривых заданных уравнением: ,
которое задает на плоскости две линии: окружность и розу
.
Исследование формы кривой при постоянном
значении радиуса , и изменяющемся значения
коэффициента при угле .







«Цветочная
фантазия» на основе кривых Хабенихта,
(получены
с помощью графопостроителя Advanced Grapher).
ЗАКЛЮЧЕНИЕ.
Еще во время изучения графического
решения уравнений и неравенств на уроках алгебры меня заинтересовали графики,
имеющие необычную форму. Поэтому я была рада возможности изучить построение
графиков в полярной системе координат. Выполняя эту работу, я узнала много
нового для себя, а также овладела дополнительными навыками использования
программы Microsoft Excel. Перед началом изучения темы, я поставила перед
собой следующую цель: выявить преимущества построения графиков в полярной
системе координат с помощью программы Microsoft Excel. Выполняя
исследовательскую, я поняла, что это действительно так, ведь строить различные
спирали, точки которых имеют дробные, а иногда и иррациональные, координаты,
было бы весьма проблематично, а программа Microsoft Excel дает возможность без
особых усилий «рисовать» различные фигуры на экране компьютера.
Я надеюсь, что изученный мною материал
пригодится мне в будущем и проделанная работа окажется ненапрасной. Однако для
меня много большое значение имеет уже то, что изучение этой темы вызвало у меня
искренний интерес, а значит я не потратила время даром.
Список используемой литературы
1.
Д.В. Беклемишев. Курс аналитической
геометрии и линейной алгебры. Москва, Наука, 1980
г.
2.
И.М. Гельфанд и др. Метод координат.
Москва, Наука, 1973 г.
3.
В.С. Шипачёв. Основы высшей математики.
Москва, Высшая школа, 1989 г.
4.
И.А. Каплан. Практические занятия по
высшей математике, Харьков, Харьковский университет, 1970
г.
5.
И.И. Привалов. Аналитическая геометрия,
Москва, Высшая школа, 1966 г.
6.
Н.В. Ефимов. Краткий курс аналитической
геометрии. Москва, Высшая школа, 1972
7.
Г.И. Запорожец. Руководство к решению
задач по математическому анализу. Москва, Высшая школа, 1974
г.
8.
Б.П. Демидович. Сборник задач и упражнений
по математическому анализу, Москва, Наука, 1969
г.
9.
Егерев В.К. Радунский Б.А., Тальский Д.А.
Методика построения графиков функций. Москва, 1970
г.
10.
Дороднов А.М. Краткие сведения о
построении графиков в полярной системе координат. Москва, 1972
г.
11.
Линии: определение, исследование и
построение: Метод. рекомендации / Краснояр. гос. ун-т; Сост. А.П. Ляпин.
Красноярск, 2001
12.
М.Я. Выгодский. Справочник по высшей математике.
Москва, 1977 г.
Сайты
и ссылки
1.
http://www.ipfw.edu/math/Coffman/pov/spiric.html
— рассказано о сечениях тора с картинками на английском языке. Там же ссылки на
биографии математиков и на замечательные кривые.
2.
http://www.didaktik.mathematik.uni-wuerzburg.de/mathei/cinderella/cassoval.html
— ссылка на апплет, рисующий овалы Кассини, на немецком языке.
3.
http://164.8.13.169/Enciklopedija/math/math/c/c084.htm
страничка овалов Кассини сайта, посвященному замечательным кривым.
4. http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Cassini.html
подробная биография Кассини
5. http://rusgraf.ru/graf4
6.
http://www.2dcurves.com/higher/highercc.html
прекрасная страничка для любителей красивых кривых, из нее мы узнали об овалах
с тремя и более фокусами.
7. http://center.fio.ru/som/Resources/Karpuhina/2003/10/pedsovet
8. http://arbuz.uz/x_stati.html
ПРИЛОЖЕНИЕ 1.
Изменение
вида кривой в зависимости от параметров,
входящих в её уравнение.
ПРИЛОЖЕНИЕ 2.
Изменение вида кривой в
зависимости от параметров, входящих в её уравнение.
Работа, представленная на фестиваль
Разделы:
Математика, Информатика
Учебный год: 2008 / 2009
Автор:
Тимофеев Максим Валерьевич
Руководитель:
Чудаева Елена Владимировна
Материалы работы:
570275.zip
* (2 МБ)
Описание работы:
Использование компьютерных программ для построения графиков функций и уравнений, изучение их свойств и закономерностей, дает возможность рассмотреть большое количество примеров с минимальными затратами времени. Данная работа предназначена в помощь учителям при изучении построения графиков функций, заданных уравнениями выше второй степени, а также ученикам с целью заинтересовать их математикой и информатикой, показав возможности использования информационных технологий на уроках математики. В работе рассматривается построение различных спиралей, роз Гвидо Гранди и кривых Хабенихта.
Контактная информация:
- Эл. почта: echudaeva@yandex.ru
* Для распаковки архива вы можете воспользоваться бесплатной программой 7-Zip или любой другой программой, поддерживающей архивы 7z и Zip.
1
Полярные координаты. Построение графиков кривых в программе Microsoft Office Еxcel
2
В полярной системе координат основными постоянными элементами, по отношению к которым определяется положение точки на плоскости, является точка O — полюс и ось OP, которая называется полярной осью. В полярной системе координат основными постоянными элементами, по отношению к которым определяется положение точки на плоскости, является точка O — полюс и ось OP, которая называется полярной осью. Если M — произвольная точка плоскости, не совпадающая с полюсом O, то ее положение на плоскости вполне определено заданием двух чисел: r — ее расстояния от полюса, выраженного в единицах масштаба, и — угла φ, на который следует повернуть полярную ось против часовой стрелки, чтобы она совпала с лучом OM. Числа r и φ называются полярными координатами точки M. Если M — произвольная точка плоскости, не совпадающая с полюсом O, то ее положение на плоскости вполне определено заданием двух чисел: r — ее расстояния от полюса, выраженного в единицах масштаба, и — угла φ, на который следует повернуть полярную ось против часовой стрелки, чтобы она совпала с лучом OM. Числа r и φ называются полярными координатами точки M. Полярные координаты M O P φ r
3
Переход из полярной системы координат в декартовую систему координат. Если полюс полярной системы координат находится в начале прямоугольной системы координат, а положительная полуось Ox совпадает с полярной осью, ось же Oy перпендикулярна оси Ox и направлена так, что ей соответствует полярный угол φ, то по известным полярным координатам точки ее прямоугольные координаты вычисляются из формул Если полюс полярной системы координат находится в начале прямоугольной системы координат, а положительная полуось Ox совпадает с полярной осью, ось же Oy перпендикулярна оси Ox и направлена так, что ей соответствует полярный угол φ, то по известным полярным координатам точки ее прямоугольные координаты вычисляются из формул
4
Пример 1 Построить кривую, заданную уравнением r=4cos3 φ Внесем данные и получим следующее распределение по столбцам электронной таблицы: где аргумент F (угол в радианах) будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 12,6; 18,9; 25,2 и т.д.
5
Далее выделим те данные, которые получились в столбцах «Х» и «У», нажмём кнопку «Мастер диаграмм» на панели инструментов и выберем тип диаграммы «Точечная диаграмма со значениями, соединёнными сглаживающими линиями без маркеров» Получим кривую: r = a cos k φ r = a sin kφ Данная кривая является частным случаем семейства кривых, имеющих общее уравнение r = a cos k φ или r = a sin kφ и называемых «Розами Гранди»
6
РОЗЫ ГРАНДИ РОЗЫ ГРАНДИ Гвидо Гранди ( ) – итальянский математик, историк и священник В уравнении «роз» параметр а отвечает за радиус лепестков, а параметр k – за их количество k=2 k=7 k=7 k=3 k=4 k=2 k=10 k=5
7
Вариации роз
8
k=59 k=15 k=13,97 k=9,5 k=9,5 k=74 k=10,4
9
Пример 2 Спираль Архимеда r = a φ
10
Пример 3 Гиперболическая спираль R=a/ φ
11
Пример 4 Кривые Хабеннихта Математическим исследованием формулы цветов и листьев занимался также немецкий геометр Л. Хабеннихт Лист кислицы Лист плюща
12
Лист стрелолиста Лист кувшинкиЛист клёна r = a (1 + cosφ)
13
r = 1 + 7cos(k φ ) + 4sin 2 (k φ ) + 3sin 4 (k φ ) Цветы
14
Цветы При к=5При к=6 При к=6,3При к=7,5
15
Цветы
16
Над презентацией работали учащиеся 11Б класса МОУ «Ломоносовская СОШ 3» Наталья Ващенко Самсон Приёмышев Учитель – Торопова Елена Владимировна
Обновлено: 16.04.2023
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №4 г.Ессентуки Исследовательская работа на тему: „Замечательные математические кривые — розы и спирали ” Автор: Ненашева Елизавета, ученица 10А класса Руководитель: Казанова А.В., учитель математики г.Ессентуки 2019
Введение: Актуальность темы исследования: в школьном курсе не достаточно рассматриваются свойства и применение таких замечательных кривых, как розы и спирали. Объект и предмет исследования: Роза Гранди и спирали Цель исследовательской работы: Исследовать зависимость внешнего вида кривой от параметров входящих в её уравнение. Изучить применение роз Гранди и спирали Архимеда в нашей жизни.
Задачи: — Выяснить, что такое роза Гранди и спирали; — Установить какие виды роз и спиралей существуют; — Выяснить их применение; — Построить свои розы Гранди; — Опытным путем показать, как изменяются кривые Гранди и спирали в зависимости от различных значений параметров; — Сделать выводы и дать общее заключение; Гипотеза: при изучении замечательных кривых и их свойств можно объяснить различные явления окружающего мира.
Понятие кривой Кривая линия – это множество точек пространства, координаты которых являются функциями одной переменной. Плоские кривые — это кривые линии, все точки которых принадлежат одной плоскости. Парабола Гипербола Эллипс
Розы Гвидо Гранди Гвидо Луиджи Гранди Роза в природе Роза Гвидо Гранди — плоская кривая, заданная в полярной системе координат, напоминающее символическое изображение цветка.
Полярная система координат Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости однозначно определяется двумя величинами — полярным углом и полярным радиусом.
Уравнение розы Гранди R=ASINK K – количество лепестков А – размер кривой
Графики роз Гранди K=2 K=3
Анализирование K — четное число, то K – нечетное число, то лепестков в 2 раза больше лепестков столько же K=2 K=3 K – число в виде отношения чисел, то лепестки перекрывают друг друга K=5/2
Применение роз Гранди Розы Гранди используются в архитектуре, ландшафтном дизайне, в дизайнерских решениях при создании интерьеров.
Спирали Спираль — это траектория равномерного движения точки по равномерно вращающемуся вокруг своего начала лучу.
Спираль Архимеда Спираль Архимеда — плоская кривая, которую описывает точка, движущаяся равномерно и поступательно от центра по равномерно-вращающемуся радиусу.
Уравнение спирали Архимеда R=Kф K — смещение точки M по лучу r, при повороте на угол равный одному радиану.
Свойства Архимедовой спирали Шаг спирали – постоянное расстояние между витками, равное 2πk. Правая спираль — положительные значения (+) Левая спираль — отрицательные значения (-)
Применение Архимедовой спирали
Спираль Ферма Спираль Ферма — плоская кривая, которая задается на плоскости в полярной системе координат при помощи уравнения: R*2=A*2ф Спираль Ферма Подсолнечник
Логарифмическая спираль Логарифмическая спираль — кривая, которая задается в полярной системе координат с помощью уравнения R=Ae*Bф. Свойства логарифмической спирали: 1.Размер витков увеличивается, но форма неизменна. 2.Прирост радиуса на единицу длины окружности постоянен
Спираль Фибоначчи или Золотая спираль Золотая спираль — это частный случай логарифмической спирали, коэффициент роста которой равен ф*4 , где — ф золотое сечение. Золотая спираль
Вывод Личностные навыки Знакомство с красотой роз Гранди и спиралей Получение различных видов роз Гранди
Спасибо за внимание!
Выбранный для просмотра документ Проект по математике(текст).docx
Муниципальное бюджетное общеобразовательное учреждени е средняя общеобразовательная школа № 4 г.Ессентуки
на тему: „Замечательные математические кривые — розы и спирали ”
Автор : Ненашева Елизавета, ученица 10А класса
Руководитель: Казанова А.В., учитель математики
Актуальность темы исследования : я считаю, что тема моей исследовательской работы достаточно актуальна, так как в школьном курсе не достаточно рассматриваются свойства и применение таких замечательных кривых, как розы и спирали.
Объект и предмет исследования : Роза Гранди и спирали
Цель исследовательской работы : Целями моей исследовательской работы является исследование зависимости внешнего вида кривой от параметров входящих в её уравнение и изучение применения роз Гранди и спирали Архимеда в нашей жизни.
— Выяснить, что такое роза и спираль, как замечательные кривые;
— Установить какие виды роз и спиралей существуют;
— Выяснить их применение;
— Построить свои розы Гранди;
— Показать, как изменяются кривые в зависимости от различных значений параметров;
— Сделать выводы и дать общее заключение;
Гипотеза : при изучении замечательных кривых и их свойств можно объяснить различные явления окружающего мира.
Понятие кривой
Для начала вспомним понятие кривой.
Кривая линия – это множество точек пространства, координаты которых являются функциями одной переменной. Каждая кривая включает в себя геометрические элементы, которые составляют её определитель, т.е. совокупность независимых условий, однозначно определяющих эту кривую. Мы знакомы с некоторыми алгебраическими плоскими кривыми, с такими как парабола, гипербола, эллипс и т.д. Плоские кривые — это кривые линии, все точки которых принадлежат одной плоскости. Плоская кривая линия называется алгебраической, если её уравнение f (xy) = 0.
Парабола Гипербола Эллипс
Розы Гвидо Гранди
Полярная ночь холодна и морозна,
Укутавшись в плед изо льда и ветров,
Розы вычерчивает осторожно,
Чтобы шипы не острить мягкотой.
Жёлтый свет лампы, термометра след,
Холода не было, трещины нет.
Роза прекрасна, синяя тень,
Циркуля холод, угла единица,
Что ж это мне по ночам-то не спится?
В этом стихотворении красной нитью проходит тема о розах Гвидо Гранди.
Гвидо Луиджи Гранди (1671 — 1742) был итальянским монахом, священником,
философом, математиком и инженером.
Он родился 1 октября 1671 в Кремоне, Италия и окрещен Луиджи. В 18 веке Гранди создал кривые линии похожие на цветки роз. Он собрал все свои восхитительные розы в одну книгу и назвал ее «Цветник роз».
Гвидо Гранди, работая с полярной системой координат, решил воссоздать с помощью линий такие прекрасные растения, как розы. Розы Гвидо Гранди радуют глаз правильными и плавными линиями, но их очертания не каприз природы — они предопределены специально подобранными математическими зависимостями.
Роза Гвидо Гранди — плоская кривая, заданная в полярной системе координат, напоминающее символическое изображение цветка.
Так как мы затронули понятие полярной системы координат, разберемся что это значит.
Полярная система координат
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости однозначно определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат задаётся лучом, который называют полярной осью(обозначается . Точка, из которой выходит этот луч, называется полюсом(обычно обозначается r ).
Координатные линии в полярной системе координат.
Уравнение Розы Гранди
Розы Гранди задаются уравнением в полярной системе координат, и это уравнение выглядит таким образом: r= a sin k , где k– положительное число, которое
определят кол-во лепестков, a – положительное число, которое определяет размер. Также k можно представить в виде рационального числа ( k = )
Графики Роз Гранди
На основе полученных знаний, я провела свои исследования и выяснила, как же меняется замечательная кривая роза Гранди при изменении параметров в её уравнении.
Я выполняла свои построения в программе Microsoft Excel . Для более удобного построения необходимо перевести значения кривой из полярной системы координат в привычную нам декартовую систему (грубо говоря с x и y ). Затем я составила таблицу с величинами и в итоге получила график кривой.
5-ти лепестковая роза
На первом графике представлена роза с параметрами K =2 и A =4. Во всех дальнейших построениях я использовала один и тот же параметр A =4 и это означает, что все розы имели один и тот размер. Но что касается параметра K , то на всех графиках он был разным.
Также я попробовала взять в качестве параметра K рациональное число, представленное в виде дроби и вот, что у меня получилось.
Проанализировав полученные результаты, я сделала некоторые выводы.
1) Если k является четным числом, то количество лепестков увеличивается в два раза
(например, k =2, но лепестков в розе ровно 4)
Если k является нечетным число, то количество лепестков соответствует модулю k .
2) Если k — рациональное число, равное отношению , то каждый лепесток будет частично перекрывать предыдущий.
Применение роз Гранди
Розы Гранди радуют своими плавными и красивыми формами глаза человека. Поэтому данные кривые широко используются в архитектуре, ландшафтном дизайне, в дизайнерских решениях при создании интерьеров.
Розы Гранди были особенно красивы и популярны на окнах зданий во времена готики.

С такими замечательными кривыми, как розы, мы закончили и теперь перейдем к изучению спиралей.
Многие имеют представление, что такое спираль и как она выглядит. Сегодня мы познакомимся с этим понятием более подробно.
По определению Архимеда: Спираль — это траектория равномерного движения точки по равномерно вращающемуся вокруг своего начала лучу.
Так же есть еще одно определение спирали — плоская кривая линия, многократно обходящую одну из точек на плоскости.
Зачастую, мы сталкиваемся с данной кривой, изучая различные явления природы: смерчи, водовороты, циклоны и антициклоны, спиральные галактики, раковины брюхоногих, молекула ДНК, рога у животных и даже семена в подсолнечнике распределяются согласно законам построения спирали.
В этом есть своя красота, которую задает природа. Спираль как будто воплощает саму жизнь, ее бесконечность, ее развитие, непрерывность жизни.
Существует большое количество видов спиралей, которые отличаются друг от друга формой и уравнением, которое задает спираль.
Первой из спиралей, с которой мы познакомимся, будет спираль Архимеда
Спираль Архимеда
Спираль Архимеда — плоская кривая, которую описывает точка, движущаяся равномерно и поступательно от центра по равномерно-вращающемуся радиусу.
Архимедова спираль была открыта, не трудно догадаться кем, самим Архимедом. Это произошло в III веке до н.э., когда он экспериментировал с компасом. Он тянул стрелку компаса с постоянной скоростью, вращая сам компас по часовой стрелке. Получившаяся кривая была спиралью, которая сдвигались на ту же величину, на которую поворачивался компас, и между витками спирали сохранялось одно и то же расстояние.
Архимедова спираль задается уравнением в полярной системе координат таким образом: r = k , где k — смещение точки M по лучу r , при повороте на угол равный одному радиану.
Свойства Архимедовой спирали
Геометрическим свойством, характеризующим спираль Архимеда, является постоянство расстояний между витками; каждое из них равно 2 π k , и равно шагу спирали . На картинке шаг спирали показан в виде расстояния между точками B , M и A .
Также интересным свойством спирали Архимеда является и то, что если вращать луч, который образует спираль против часовой стрелки, то получается правая спираль ( на картинке она показана синим цветом ) и этой правой спирали будут соответствовать положительные значения угла , а левая спираль (показана зеленым цветом ), которая образуется путем вращения луча по часовой стрелке , будет соответствовать отрицательным значениям угла .
Применение спирали Архимеда
В III веке до нашей эры Архимед на основе своей спирали изобрёл винт , который успешно применяли для передачи воды. Позже на основе винта Архимеда создали шнек . Его очень известная разновидность – винтовой ротор в мясорубке . Шнек используют в механизмах для перемешивания материалов различной консистенции. Также на основе спирали Архимеда работает часовой механизм в механических часах. Звуковые дорожки на CD и DVD дисках также имеют форму спирали Архимеда.
И это лишь только малая часть всевозможных способов применений данной спирали. Спираль Архимеда нашла огромное практическое применение в математике, технике, архитектуре и машиностроении.
Теперь мы познакомимся с остальными видами спиралей, но не на столько подробно, как со спиралью Архимеда, а более кратко.
Спираль Ферма
Спираль Ферма — один из видов спирали Архимеда. Данная спираль задается на плоскости в полярных координатах при помощи уравнения = . По траектории спирали Ферма растут семечки в подсолнечнике.
Гиперболическая спираль — плоская кривая , уравнение которой в полярной системе координат является обратным для уравнения Архимедовой спирали и записывается так: r = a
Логарифмическая спираль
Логарифмическая спираль — кривая, которая задается в полярной системе координат с помощью уравнения r = a .
Некоторые интересные свойства логарифмической спирали:
1. Размер витков логарифмической спирали постепенно увеличивается, но их форма остаётся неизменной.
2. Прирост радиуса на единицу длины окружности постоянен. Возможно, в результате этого свойства логарифмическая спираль появляется в определённых растущих формах, подобных раковинам моллюсков , спиралям циклонов и галактик .
Спираль Фибоначчи или Золотая спираль
Золотая спираль — это частный случай логарифмической спирали, коэффициент роста которой равен , где — золотое сечение. Данная спираль расположена в квадратах, размеры которых соответствуют последовательности Фибоначчи.
На данном рисунке изображены квадраты с размерами 1, 1, 2,3, 5,8, 13 и 21. Спираль изображенная синим цветом и является золотой спиралью.
Подводя итоги моей презентации, я хотела бы сказать, что я получила огромный опыт нахождения, обработки, анализирования и использования информации из сети Интернет.
Также данная исследовательская работа позволила нам взглянуть, на казавшиеся скучные и неинтересные замечательные кривые, совершенно иначе. Мы увидели, что Розы Гранди и спирали имеют красивые и интересные графики и самое главное то, что данная красота окружает нас повсюду.
В ходе исследования мы получили огромное разнообразие видов и форм роз Гранди и увидели, как один параметр уравнения может коренным образом изменить всю кривую.
Содержание Аннотация проекта Основные понятия геометрии, необходимые для построения кривых Виды уравнений в плоскости Основные системы координат Переход от ДСК в ПСК Инструкция по построению кривых с помощью программы Microsoft Excel Исследование форм роз от изменений коэффициентов
Аннотация проекта Я увлекаюсь математикой очень давно и мне постоянно хочется узнавать что-то новое по этому предмету. Так, расширяя границы знаний в области математики, я узнал о цветах Гвидо Гранди. Эта тема показалась мне необычной и интересной, и я захотел показать, насколько красивой может быть эта наука.
Цели и задачи Цели проекта: Вывести закономерности построения цветов Гвидо Гранди. Показать ученикам всю красоту и простоту «графической» математики. Применение систем координат в жизни. Задачи проекта : Повторить основные понятия геометрии И зучить различные виды систем координат Научиться переходить из одной системы координат в другую Научиться строить графики с помощью программы Microsoft Excel .
Основные понятия геометрии Точка — абстрактный объект в пространстве, не имеющий никаких измеримых характеристик Плоскость — это поверхность, образованная кинематическим движением образующей по направляющей, представляющей из себя прямую Прямая – линия, путь вдоль которой равен расстоянию между двумя точками. Вектор – математический объект, характеризующийся величиной и направлением.
Основные системы координат Декартова система координат — прямолинейная система координат взаимно перпендикулярными осями на плоскости или в пространстве. Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Сферическая система координат — система координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат.
Применение полярных систем координат В медицине: Компьютерная томография сердца в системе полярных координат.
Применение полярных систем координат В геодезии: получение координат точек объекта основано на измерении полярных углов и расстояний до объекта.
Чтобы правильно занять свое место в кинотеатре, нужно знать две координаты — ряд и место. Применение декартовой системы координат
Система географических координат широта – параллели, долгота -меридианы Применение декартовой системы координат
Переход от ДСК к ПСК Пусть (x; y) – координаты точки в декартовой системе координат, – в полярной. Тогда очевидно, что: Формулы обратного перехода: Замечание: число в полярной системе определено не однозначно: парам чисел соответствует одна и та же точка при любых натуральных n.
Инструкция по построению кривых с помощью программы Microsoft Excel Переведем уравнение из декартовых координат в полярные, используя формулы: X = R * COS ( F ), Y = R * SIN ( F ). Задача. Построить кривую, заданную уравнением Решение. Найдем уравнение линии в полярных координатах Для программы Microsoft Excel : R= 4*COS(3*F) Пусть угол Выберем шаг изменения 0,1 Построим компьютерную модель исследования
Инструкция по построению кривых с помощью программы Microsoft Excel А2 0,1 А3 =А2+0,1 B2 =4*COS(3*F) C2 =SIN(А2) D2 =COS(А2) E2 =С2* D 2 F2 =С2* E 2 Внесем данные и получим следующее распре- деление по столбцам электронной таблицы: 1 F R SIN(F) COS(F) X Y 2 0,1 3,821346 0,099833 0,995004 3,802255 0,381498 3 0,2 3,301342 0,198669 0,980067 3,235535 0,655875 4 0,3 2,48644 0,29552 0,955336 2,375387 0,734793 5 0,4 1,449431 0,389418 0,921061 1,335014 0,564435 6 0,5 0,282949 0,479426 0,877583 0,248311 0,135653 Для построения графика выделим информационный блок E2..F63, так как аргумент F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д.
Инструкция по построению кривых с помощью программы Microsoft Excel Получим следующую кривую
Инструкция по построению кривых с помощью программы Microsoft Excel Исследование формы кривой. Внося изменения в ячейку В2 , не меняя более ничего, мы можем получать различные кривые заданные уравнением
В математике спираль — это кривая, которая огибает некоторую центральную точку или ось, постепенно приближаясь или удаляясь от неё, в зависимости от направления обхода кривой. Спирали Спираль Архимеда может быть определена как траектория точки, участвующей одновременно в двух равномерных движениях, одно из которых совершается вдоль прямой, а другое – по окружности. прямо-пропорциональная зависимость
Спираль Архимеда. Спираль Архимеда — плоская кривая, которую описывает точка, движущаяся равномерно-поступательно от центра 0 по равномерно-вращающемуся радиусу. Изобретение этой кривой приписывается Конону Самосскому, хотя ее основные свойства описал именно Архимед. Ему (Архимеду), в частности, было известно, что расстояние между двумя последовательными витками спирали является постоянной величиной и равно 2р. Число a — называется шагом спирали . Положительным значениям соответствует правая спираль, отрицательным — левая спираль.
Спираль Ферма Любопытное отличие спирали Ферма от других спиралей заключается в том, что расстояние между ее витками убывает по мере удаления от полюса. Гиперболическая спираль По мере роста спираль устремляется к полюсу, делая вокруг него бесконечное множество витков, расстояние между которыми убывает.
Логарифмическая спираль В истории математики логарифмическая спираль упоминается впервые в письме Декарта к Мерсену в 1638 г., в котором Декарт определяет новую спираль как линию, отношение длины дуги которой к радиус-вектору является постоянным. Уравнение кривой в полярных координатах:
Семейство роз Гранди . Полярная роза — известная математическая кривая, похожая на цветок с лепестками . В силу периодичности тригонометрических функций роза состоит из одинаковых лепестков, симметричных относительно наибольших радиусов, каждый из которых равен 1.
Четырехлепестковая Роза Гранди Ч етырехлепестковая роза Гвидо Гранди в декартовых координатах задаётся уравнением: В полярных координатах общее уравнение для роз записывается в виде: или
Исследование формы роз «Роза» — располагается внутри круга радиусом a. Количество же лепестков розы зависит от величины модуля k: Если модуль k – целое число, то роза состоит: из k лепестков, при нечетном k, из 2k лепестков при k четном
2. Если I k I – рациональное число, равное то роза состоит из m лепестков в случае, когда оба числа m и n нечетные, и из 2 m лепестков, если одно из этих чисел является четным. 3.Если модуль k – иррациональное число, то роза состоит из бесчисленного множества лепестков, частично накладывающихся друг на друга. Исследование формы роз
«Пируэты роз » ( получены с помощью графопостроителя для Word версия 1.50 и компьютерной программы «Розы», язык Visual Basic ).
Лист кувшинки Лист конопли Лист клевера Кривые Хабеннихта
Интересные «цветы» получаются при построении кривых заданных уравнением которое задает на плоскости две линии: окружность и розу Форма кривой при постоянном значении радиуса r = 2 , и изменяющемся значения коэффициента k
Читайте также:
- R studio формат даты
- Программа для восстановления лицензии windows 7
- Как сделать зин в фотошопе
- Как прошить psp ютуб
- Как поменять местоположение ос в 1с
«Районная научно-практическая конференция
«От исследования — к научному поиску»
Учреждение: МБОУ «Многопрофильная гимназия г. Лагани»
Секция: Естественно-научная
Тема работы:
«Построение и исследование графиков
функций при помощи электронных
Таблиц Excel.»
Автор работы: Белкин Алексей Васильевич,
ученик 10 класса МБОУ «Многопрофильная гимназия г. Лагани»
Научный руководитель: Никифоров Евгений Алексеевич,
учитель математики МБОУ «Многопрофильная гимназия г. Лагани»
г. Лагань — 2013
ОГЛАВЛЕНИЕ
|
Введение |
2 |
Microsoft Excel. |
3-5 |
|
1.2. Полярная система координат |
5-6 |
|
1.3. Инструкция по построению кривых в полярных координатах с помощью программы Microsoft Excel |
6-10 |
|
1.4. Построение кусочно-заданной функции на примере построения эскиза национального орнамента |
11-12 |
|
Заключение |
13 — 14 |
|
Список литературы |
15 |
ВВЕДЕНИЕ
Актуальность работы. При изучении, темы преобразования графиков функций возникла необходимость построения графиков элементарных функций и уравнений выше второй степени. Для изучения свойств этих функций Microsoft Excel предлагает широкие возможности, которые в школьных учебниках по информатике не оговариваются.
Вопрос (мотивация): Как построить график с изменяющимся параметром, для дальнейшего его изучения?
Проблема: необходимо найти удобный (сравнительно простой, наглядный, доступный) способ построения графиков элементарных функций и уравнений степеней выше второй с двумя переменными.
Гипотеза: для решения поставленной проблемы, возможно использовать инструменты прикладной программы Microsoft Excel, а для построения графиков уравнений высших порядков ввести новые переменные, или новую систему координат, или и то и другое одновременно.
Поэтому, объект нашего исследования — прикладная программа Microsoft Excel, ее возможности для построений графиков функций и исследования их.
Исходя из этого, предметом нашего исследования стали уравнения элементарных функций и кривых высших порядков.
Цель работы – показать алгоритм построение графиков функций в Excel, принцип построения линий высших порядков в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам. Результаты исследования: в процессе работы я:
- Научился строить графики функций, с дальнейшей возможностью изучения их свойств
- изучил переход от декартовой системы координат к полярной и обратно;
- исследовал изменения вида графиков функций и кривых, в зависимости от параметров входящих в её уравнение;
- познакомились с некоторыми замечательными кривыми известных математиков.
Планы и перспективы: продолжить изучение плоских кривых.
- Инструкция по построению кривых с помощью программы
Microsoft Excel.
Пусть задана функция y= f(x), где х – независимая переменная , а y – переменная зависящая от х.
Для начала нам необходимо задать значения независимой переменной с заданным шагом (шаг лучше выбрать дробным значением). Чем меньше шаг вычисления независимой переменной тем точнее построенный график.
Задаем формулу по которой определяется зависимая переменная. Вычисляем для каждого значения независимой переменной ее соответствующее значение функции.
По построенным данным строим график функции.
Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения уравнения графика и ее исследования
. Рассмотрим в качестве примера тригонометрическую функцию
Построим компьютерную модель исследования.
Для дальнейших исследований будем одновременно строить график исходной элементарной функции y= sinx и преобразованной функции и сравнивать полученные результаты.
Формулы будут записаны в терминах электронных таблиц следующим образом:
|
А3= -7 |
d3= -7 d4 =d3+0,1 E3 =sin($f$1*d3) В ячейке F1 будем задавать значение параметра k, и рассматривать полученные изменения графика функции |
Фрагмент произведенных расчетов из электронной таблицы приведен ниже
В приложенном к работе файле Microsoft Excel работа графики можно увидеть полные вычисления и полученные результаты
Для детального изучения преобразований графики построил в одной системе координат, что дает возможность сравнить полученные результаты.
Для дальнейших исследований достаточно теперь изменить значение в ячейке f1, и получим иную картину. Например f1=-4
Как видно значения функции автоматически пересчитаны, и построен уже другой график. Данные возможности мною были продемонстрированы одноклассникам на уроке математики. В дальнейшем мои товарищи на уроки изучили свойства полученных графиков функций и наглядно изучили преобразования графиков следующих функций
( и др.)
1.2. Полярная система координат.
Мои исследования, на этом не закончились, возник вопрос в построении более сложных графиков. В качестве примера мною рассмотрено уравнение
В полярной системе координат положение точки определяется полярным радиусом R и углом , образуемым полярным радиусом с полярной осью. Следовательно, полярная система координат — система координат, ставящая в соответствие каждой точке на плоскости пару чисел
. Основными понятиями этой системы являются точка отсчёта (полюс) и луч, начинающийся в этой точке (полярная ось).
Если в декартовой системе координат предельно простое выражение определяет прямую линию, то это же выражение, переписанное в форме
, уже превращается в спираль. Фигуры в полярных координатах образуются как след конца бегающего по кругу полярного радиуса переменной длины. Длина полярного радиуса определяется величиной угла, который в данный момент времени он образует с полярной осью. Координата
берётся со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «-» в противоположном случае. Любая точка в этой системе имеет бесконечное число координат вида
, которым соответствует одна и та же точка при любых натуральных
. Для полюса
, угол
произвольный.
Связь между полярной и декартовой системами координат.
Точка О — полярный полюс, луч ОЕ будем называть полярной осью, отрезок ОМ — называют длиной полярного радиуса R, положительный угол от луча ОЕ до луча F — полярный угол.
Если известны полярные координаты R и , точки М, то можно уставить связь с её декартовыми координатами.
Построим прямоугольный ОМЕ. В этом треугольнике гипотенуза ОМ=R,
ЕОМ =
, катет ЕМ = у, катет ОЕ = х координаты точки М.
Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы: ,
,
. Обратно, чтобы, имея прямоугольные координаты, получить расстояние нужное для задания полярных координат, надо воспользоваться теоремой Пифагора:
, затем
,
.
Некоторые замечательные кривые. На протяжении многих лет ученые собирали информацию о формулах, рисующих разные фигуры. Многие фигуры получили свои названия. Список таких названий внушителен: спираль Архимеда, Ферма, Галлилея, Фибоначчи, кардиоида, овалы Кассини, лемниската Бернулли, фигуры Лиссажу, розы Гвидо Гранди, кривые Маклорена, верзьера (локон Марии Аньези) и т.д.
1.3. Инструкция по построению кривых
в полярных координатахс помощью программы Microsoft Excel.
Если уравнение задано в декартовых координатах, то следует перевести его в полярные, используя формулы: X=R*COS(F), Y=R*SIN(F). Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения кривой.
Задача. Построить кривую, заданную уравнением .
Решение. Найдем уравнение данной линии в полярных координатах.
Для программы Microsoft Excel: R=4*COS(3*F)
Предположим, что угол F изменяется в интервалах от 0 до 2. Для того, чтобы построить эту кривую наиболее точно, с малым шагом изменения угла F, как мы это делали при построении тригонометрических функций, мы выберем шаг изменения 0,1.
Построим компьютерную модель исследования.
Формулы будут записаны в терминах электронных таблиц следующим образом:
А2 0,1 А3 =А2+0,1 B2 =4*COS(3*F)
C2 =SIN(А2) D2 =COS(А2) E2 =B2*D2 F2 =В2*C2
Тогда получаем следующее распределение по столбцам электронной таблицы:
|
f |
r |
sin(f) |
cos(f) |
x |
y |
|
0,1 |
3,821346 |
0,099833 |
0,995004 |
3,802255 |
0,381498 |
|
0,2 |
3,301342 |
0,198669 |
0,980067 |
3,235535 |
0,655875 |
|
0,3 |
2,48644 |
0,29552 |
0,955336 |
2,375387 |
0,734793 |
|
0,4 |
1,449431 |
0,389418 |
0,921061 |
1,335014 |
0,564435 |
|
0,5 |
0,282949 |
0,479426 |
0,877583 |
0,248311 |
0,135653 |
|
0,6 |
-0,90881 |
0,564642 |
0,825336 |
-0,75007 |
-0,51315 |
|
0,7 |
-2,01938 |
0,644218 |
0,764842 |
-1,54451 |
-1,30092 |
|
0,8 |
-2,94957 |
0,717356 |
0,696707 |
-2,05499 |
-2,1159 |
|
0,9 |
-3,61629 |
0,783327 |
0,62161 |
-2,24792 |
-2,83274 |
|
1 |
-3,95997 |
0,841471 |
0,540302 |
-2,13958 |
-3,3322 |
|
1,1 |
-3,94992 |
0,891207 |
0,453596 |
-1,79167 |
-3,5202 |
и т. д.
Для построения графика выделим информационный блок E2..F64, так как аргумент F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д. Получим следующий график.
Исследование формы кривой, в зависимости от изменения значений входящих в её уравнение. Внося изменения в ячейку H27 , не меняя более ничего, мы можем получать различные виды уравнения
Еще примеры …
Обратимся к исследованию формы роз. Поскольку правая часть уравнения не может превышать величины a, то и вся роза, очевидно, уменьшается внутри круга радиусом a. Количество же лепестков розы зависит от величины модуля k:
1. Если модуль k – целое число, то роза состоит из k лепестков, при нечетном k, и из 2k лепестков при k четном.
2.Если модуль k – рациональное число, равное то роза состоит из m лепестков в случае, когда оба числа m и n нечетные, и из 2m лепестков, если одно из этих чисел является четным.
При этом, в отличие от первого случая каждый следующий лепесток будет частично перекрывать предыдущий.
3.Если модуль k – иррациональное число, то роза состоит из бесчисленного множества лепестков, частично накладывающихся друг на друга.
Математическим исследованием формы цветов и листьев занимался также Хабеннихт – геометр 19 столетия. Им был получен целый ряд уравнений, которые с весьма хорошим приближением выражали аналитически формы листьев клена, щавеля, ивы и т. д. Вот некоторые из этих кривых:
В полярных координатах можно описать при помощи косинусов кратных дуг линии, которые обрисовывают контуры листьев некоторых растений:
• кувшинки: (рис. а);
• кислицы: (рис. б);
• настурции: (рис. в);
• стрелолиста: (рис. г).
Рис. А Рис. Б Рис. В Рис. Г
1.4. Построение кусочно-заданной функции на примере построения эскиза национального орнамента
Свои исследования я продолжил, возник вопрос в построении графиков функций состоящих из нескольких кривых на заданном интервале. В качестве примера мною рассмотрено построение эскиза калмыцкого орнамента (геометрического) в Excel.
Если рассмотреть любой геометрический орнамент, то с математической точки он представляет собой набор прямых или кривых на заданном интервале, иногда на одном интервале может быть задано несколько различных линий. Совокупность этих линий и кривых образует рисунок который и будем считать орнаментом.
Также можно заметить, что орнамент представляет собой периодическую функцию (рисунок повторяется, через заданный интервал). Для того, чтобы построить заданный орнамент мы его построим на определенном интервале, а затем перенесем все вычисления на заданный шаг и т. д.
Приведенный ниже орнамент представляет собой семейство прямых заданных на отрезках, причем прямые параллельны одной из осей координат т.е. их уравнения принимают вид у =a или х =а.
Построим эти прямые.
Примеры таблиц вычислений:
|
|
|
(Полные вычисления можно увидеть в файле приложении1)
График функции приведен ниже:
Заключение
Проделав данную исследовательскую работу я пришел к следующим выводам: Microsoft Excel предоставляет большие возможности для построения и исследования графиков функций.
Использование компьютерных программ для построения графиков функций, изучение их свойств и закономерностей, дает возможность рассмотреть большое количество примеров с минимальными усилиями. Данная работа предназначена в помощь учителям при изучении функции, а также ученикам с целью заинтересовать их математикой, информатикой, показав возможности использования информационных технологий на уроках математики.
В классе котором я обучаюсь, мною была дана обзорная лекция с практическим ознакомлением, на которой одноклассников я ознакомил учащихся с принципами построения графиков функций на примере тригонометрических функций, был предложен вариант построения графика функции с параметром. Построение графиков с параметром позволяет рассмотреть особенности графика в зависимости от параметра, изучить свойства функции, научиться строить графики функций путем преобразований исходной. В какой то мере благодаря этой работе мои одноклассники разобрались на отлично с темой построение графиков тригонометрических функций и их преобразований.
Мне удалось добиться поставленных целей работы. Был проработан алгоритм построения графиков элементарных функций, для построения кривых высших порядков мною был изучен дополнительный материал: построение кривых высших порядков в полярных координатах, где основополагающим является угол преобразования и радиус вектор. Был проработан алгоритм решения данной задачи: при помощи формул перехода от полярных координат к декартовым и обратно.
Изучая кривые линии высших порядков, ведь используя Microsoft excel, это не составляет труда, мне представился удивительный мир графиков различных функций. Оказывается таким образом можно построить, меняя параметры в данных уравнениях графики, которые напоминают листья растений и деревьев (например: кувшинки или лотоса). Оказывается математика — живая наука.
Опыт, приобретенный мною в процессе выполнения работы, несомненно, пригодится мне в дальнейшей жизни. Так, например, умея строить графики уравнений с параметрами можно найти корни уравнений и их зависимость от введенного параметра, что даст наглядную картину решения данного уравнения. Это позволяет решать задания ЕГЭ по математике части С5.
Также данные навыки будут необходимы при построении графиков и диаграмм в дальнейшей профессиональной деятельности, так excel прикладная программа применимая во многих сферах деятельности человека, например бухгалтерии, дизайн, аналитика, инженерия и другие.
Строя график функции на примере орнамента у меня возник вопрос, который остался не разрешенным. Как вы видели, я строил график по интервалам, что конечно занимает некоторое время. Возникает вопрос, как упростить данные построения. У меня есть три способа решения данной проблемы: 1) попытаться найти оптимальное уравнение функции, которое позволить заменить одновременно несколько этапов построения. Для решения этого вопроса нужно провести поиск в математических источниках.
2) найти возможности программы Excel для решения этой задачи. Как я говорил, в данной программе, много возможностей, многие из них, я еще не изучил.
3) найти другие программы построения графиков, которые позволят построить график данных функций. Такие программы существуют, например Adgrapher или DPlot и др. Данные программы, я планирую изучить в дальнейшем. Оптимальным решением, конечно же, будет создание своей программы, используя языки программирования.
Список используемой литературы
- Б.П. Демидович. Сборник задач и упражнений по математическому анализу, Москва, Наука, 1969 г.
- Дороднов А.М. Краткие сведения о построении графиков в полярной системе координат. Москва, 1972 г.
- И.М. Гельфанд и др. Метод координат. Москва, Наука, 1973 г.
- И.И. Привалов. Аналитическая геометрия, Москва, Высшая школа, 1966 г.
- Н.В. Ефимов. Краткий курс аналитической геометрии. Москва, Высшая школа, 1972
- Г.И. Запорожец. Руководство к решению задач по математическому анализу. Москва, Высшая школа, 1974 г.
- Егерев В.К. Радунский Б.А., Тальский Д.А. Методика построения графиков функций. Москва, 1970 г.
- Линии: определение, исследование и построение: Метод. рекомендации / Краснояр. гос. ун-т; Сост. А.П. Ляпин. Красноярск, 2001
Сайты и ссылки
- http://ru.wikipedia.org
2. http://www-gap.dcs.st-and.ac.uk/~history/Mathematicians/Cassini.html
подробная биография Кассини
3. http://www.2dcurves.com/higher/highercc.html прекрасная страничка для любителей красивых кривых, из нее мы узнали об овалах с тремя и более фокусами.
4. http://arbuz.uz/x_stati.html
5. http://otherreferats.allbest.ru/mathematics/00125991_0.html — Построение кривых высшего порядка
Существует два подхода к построению полярной розы. Сначала пойдём по накатанной колее, считая, что полярный радиус не может быть отрицательным:
Такое тригонометрическое неравенство тоже нетрудно решить графически: из материалов статьи Геометрические преобразования графиков известно, что если аргумент функции удвоить, то её график сожмётся к оси ординат в 2 раза. Пожалуйста, найдите график функции 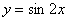
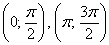
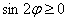
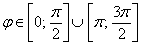
Вообще говоря, решение рассматриваемых неравенств представляет собой бесконечное множество отрезков, но, повторюсь, нас интересует только один период.
Возможно, некоторым читателям более лёгким покажется аналитический способ нахождения области определения, условно назову его «нарезка круглого пирога». Резать будем на равные части и, прежде всего, найдём границы первого куска. Рассуждаем следующим образом: синус неотрицателен, когда его аргумент находится в пределах от 0 до 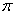
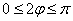
Теперь начинаем последовательно «нарезать равные куски по 90 градусов» против часовой стрелки:
– и, наконец, интервал 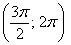
Прямо, как по ромашке – «любит, не любит, любит, не любит» =) С тем отличием, что тут не гадание. Да, прямо какая-то любовь по-китайски получается….
Итак, 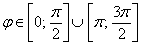
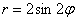
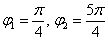
Вот закономерный результат заботливого садовника:
Следует отметить, что длину лепестка легко сразу усмотреть из уравнения 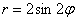
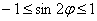
б) Построим линию, заданную уравнением 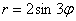
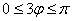
Далее начинаем «нарезку пирога кускам» по 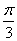
– отрезок 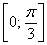
– интервал 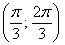
– отрезок 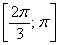
– интервал 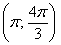
– отрезок 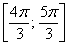
– интервал 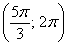
Процесс успешно завершён на отметке 360 градусов.
Таким образом, область определения: 
Проводимые действия полностью либо частично несложно осуществлять и мысленно.
Построение. Если в предыдущем пункте всё благополучно обошлось прямыми углами и углами в 45 градусов, то здесь придётся немного повозиться. Найдём вершины лепестков. Их длина 
Обратите внимание, что между вершинами лепестков должны обязательно получиться равные промежутки, в данном случае 120 градусов.
Чертёж желательно разметить на 60-градусные секторы (отграничены зелёными линиями) и провести направления вершин лепестков (серые линии). Сами вершины удобно наметить с помощью циркуля – единожды отмерять расстояние в 2 единицы и нанести три засечки на прочерченных направлениях в 30, 150 и 270 градусов:
Готово. Понимаю, что занятие хлопотное, но если хотите всё оформить по уму, то придётся потратить время.
Сформулируем общую формулу: уравнение вида 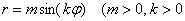


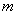
Например, уравнение 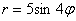
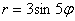
О втором подходе я хотел вообще умолчать, однако не могу пройти мимо – уж слишком он распространён. Суть состоит в том, что полярная роза часто рассматривается в обобщённых полярных координатах, где полярный радиус может быть отрицательным. Вопрос области определения отпадает, но появляются другие приколы.
Во-первых, разберёмся, как строить точки с отрицательным значением «эр». Если 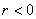
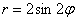
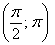
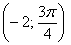
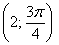
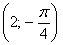
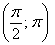
И, соответственно, когда угол проходит значения 
Интересно отметить, что при таком подходе вторая полярная роза 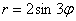
Сформулируем правило розы для обобщенной системы координат: уравнение вида 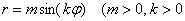

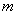
1) если 
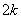
2) если 

Например, роза 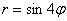
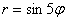
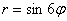
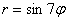
А почему закономерность столь необычна, я только что проиллюстрировал геометрически.
Какой способ выбрать, решать вам, …но я бы не особо рекомендовал использовать обобщенные полярные координаты – у преподавателя могут появиться дополнительные вопросы на счет отрицательных значений полярного радиуса (а то и вообще всё будет забраковано по этой причине)
Короткая задача для самостоятельного решения:
Построить линии, заданные уравнением в полярных координатах
а) 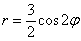
б)
Сформулировать общее правило о количестве и длине лепестков полярной розы вида 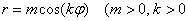

В моём образце решение проведено 1-ым способом. Повторим порядок действий:
– Сначала находим область определения. При этом для лучшего понимания своих действий рекомендую соотносить аналитический способ «нарезки» с графической интерпретацией. По материалам урока Геометрические преобразования графиков выясните, как выглядят, и при необходимости начертите графики функций 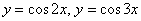
– Находим угловые координаты вершин лепестков – они расположены ровно посередине промежутков области определения.
– Выполняем чертёж. Пойдёт схематическая версия, однако желательно разметить найдённые секторы и угловые направления вершин лепестков (в случае необходимости – с помощью транспортира). Вершины удобно засекать циркулем, предварительно установив раствор, равный длине лепестка.
Существуют более солидные и общие формулы окружности, полярной розы и желающие могут с ними ознакомиться в других источниках информации. Я лишь ограничился практически значимыми (с моей точки зрения) примерами.
Предлагаю перейти ко 2-ой части занятия под названием Как построить линию в полярной системе координат?, где мы продолжим рассматривать типовые задачи, и усовершенствуем свои навыки.
Решения и ответы:
Пример 3: Решение: найдём область определения:
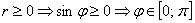
Вычислим полярные координаты точек, принадлежащих данной линии:
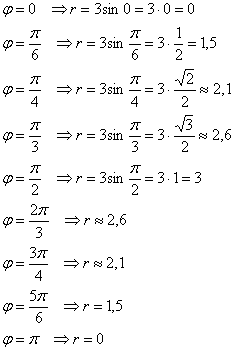
Выполним чертёж:
Найдём уравнение линии в декартовой системе координат:
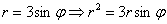
Проведём замены 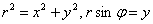
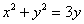
Выделим полный квадрат:
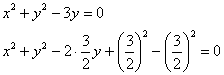
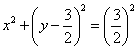
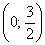
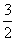
Дополнительная информация: уравнение вида 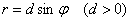
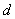
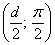
Пример 5: Решение:
а) Найдём область определения: косинус неотрицателен, когда его аргументнаходится в пределах от 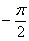
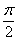
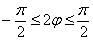
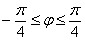
Таким образом:
– отрезок 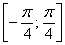
– интервал 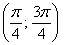
– отрезок 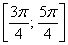
– интервал 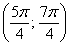
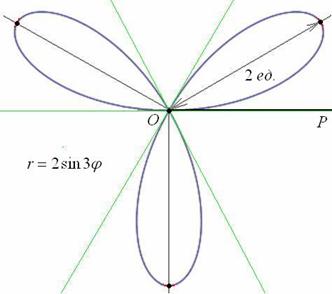
Область определения: 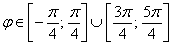
Роза имеет два лепестка, вершины которых находятся на полярной оси и её продолжении, длина лепестка равна 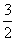
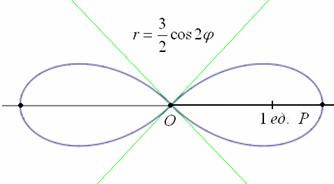
б) область определения: 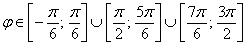
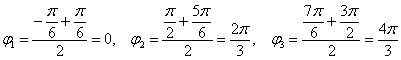
Выполним чертёж:
Уравнение вида 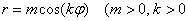


Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Уравнения кривых. Роза.
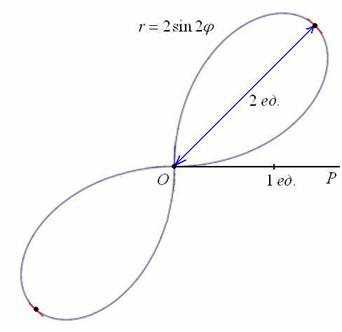
Роза — плоская кривая, ее чертеж схож с рисунком цветка. Эта кривая в полярной системе координат характеризуется выражением:
где a и k — константы, обуславливающие размер (a) и численность лепестков (k) выбранной розы.
Вся линия размещена внутри окружности с радиусом а и при k > 1состоит из идентичных по форме и размеру лепестков. Численность лепестков характеризуется величиной k.
При целом k численность лепестков будет k, когда k нечётное и 2 k,- когда чётное.
При дробном k вида k = m /n, где m и n взаимно простые, количество лепестков розы будет m, когда оба числа нечётные и 2m, если хотя бы одно — чётно.
При k иррациональном лепестков бесчисленное множество.
Трехлепестковая роза.
Уравнение имеет вид:
Данное уравнение сходно с линией, образованной вращением против часовой стрелки по кривой 30 o либо π/6 радиан.
В общем, r = acosnθ или r = asinnθ формирует k лепестков когда k — нечетное.
Четырехлепестковая роза.
Данное уравнение сходной с линией, образованной вращением против часовой стрелки по кривой 45 o или π/4 радиан.
В общем r = acosnθ или r = asinnθ формирует 2k лепестков если k — четное.
Исследовательская работа «Розы Гвидо Гранди»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
САМАРСКИЙ КОЛЛЕДЖ СТРОИТЕЛЬСТВА И ПРЕДПРИНИМАТЕЛЬСТВА (ФИЛИАЛ) ФГБОУ ВО «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
РОЗЫ ГВИДО ГРАНДИ
Окунев Игорь, студент Самарского колледжа строительства и предпринимательства ФГБОУ ВО «Национальный исследовательский Московский государственный строительный университет». Научный руководитель – Егорова Н. С., преподаватель естественно-научных дисциплин.
1. Введение. Цель и задачи работы
2. Основная часть
2.1 Историческая справка
2.2 Разнообразие роз Гвидо Гранди
2.3 Полярная система координат
2.4 Общие свойства роз Гвидо Гранди
2.5 Связь с другими замечательными кривыми
«Узоры математики, как и узоры художника или узоры поэта, должны быть красивы, идеи, как и краски или слова, должны сочетаться гармонически. Красота является первым критерием: в мире нет места для безобразной математики» (Дж.Х. Харди).
Математика-это наука, которая изучает величины, количественные отношения и пространственные формы, описывает процессы, происходящие в окружающем нас мире. Законы математики и решения математических задач приложены ко всем областям человеческой деятельности. Линии занимают особое положение в математике. Используя линии, можно создать наглядные модели многих процессов и проследить их течение во времени. Линии позволяют установить и исследовать функциональную зависимость между различными величинами. С помощью линий удается решать многие научные, инженерные задачи в различных отраслях жизни. Меня заинтересовали кривые, заданные в полярных координатах. Среди них можно назвать спираль Архимеда, логарифмическую спираль, кардиоиду, лемнискату, астроиду, розы Гвидо Гранди. Больше других мое внимание привлекла математическая кривая, похожая на цветок — полярная роза или роза Гвидо Гранди, и я в своей работе хочу исследовать многообразие форм «роз» Гвидо Гранди.
Исследовать, как изменяются кривые Гвидо Гранди, заданные в полярной системе координат в зависимости от различных значений параметров
1. Установить связь между количеством лепестков, их формул и симметричности получившегося рисунка.
2. Получить большое разнообразие форм «роз» Гвидо Гранди.
3. Изучить использование полярных координат в жизни, искусстве, науке, технике и применить на практике.
2.1 Историческая справка
В 18 веке итальянский геометр Гвидо Гранди (1671-1742) создал кривые линии с точными плавными очертаниями. Они были похожи на цветок. Семейство этих кривых было названо семейством роз Гвидо Гранди. Их точные черты не причуды природы, они предопределены особо подобранными математическими зависимостями. Эти зависимости были подсказаны самой природой, ведь в большинстве случаев абрис листа или цветка представляет собой кривую, симметричную относительно оси. Свои очаровательные цветы Гвидо Гранди собрал в одну книгу и назвал ее «Цветник роз» . Гранди извест ен своей работ ой «Flores geometrici» (1728). Данная работа позволяет изучать крив ые , котор ые име ю т форму лепестков цветка. Он назвал розы кривой rhodonea и назвал крив ую Clelia в честь графин и Клели и Борромео .
Уравнение розы Гвидо Гранди в полярных координатах имеет вид
Задавая параметр 
2.2. Разнообразие роз Гвидо Гранди
Рассмотрим уравнение кривой
Возьмём для начала любое a и k -чётное число, тогда получим «розу» с количеством лепестков 2 k , и длина от начала координат до вершины лепестков будет равна радиусу описанной окружности a . Кривые симметричны относительно оси ординат, оси абсцисс и начала координат.
Если мы возьмём любое a и k -нечётное число, то получим цветок из k лепестков. Мы замечаем, что в одном случаи есть лепесток, направленный по оси ординат вверх, а в другом вниз. Это зависит от значения k . Вниз лепесток будет направлен при k =3 и при всех последующих нечётных через одно число, вверх – при k =5 и при всех следующих нечетных числах через одно. Кривые симметричны относительно оси ординат.
Рассмотрим уравнение кривой 
Мы замечаем, что количество лепестков стало зависеть от c и b .Если c=1, а b =2 получаем кривую, напоминающую 2 кардиоиды, «наползшие» друг на друга. Если b=3, то мы получим кардиоиду с петлей «внутри себя». Если b>3 мы получим закольцованную спираль, в центре которой будет кардиоида (1 или 2). Если c > b , c -любое нечётное число, b -любое нечётное число и получившаяся дробь не сокращается до целого числа, тогда мы получаем «розу» из c -лепестков, у которого они находят друг на друга. При c =5 и всех последующих нечётных чисел через одни, один лепесток «розы» будет направлении вниз по оси ординат. По аналогии при c =7 и при всех последующих нечётных числах один лепесток направлен вверх по оси ординат. Кривая симметрична относительно оси ординат.
Если c > b , c -любое чётное число, b -любое нёчетное и получившаяся дробь не сокращается до целого числа, то мы имеем «розу» из лепестков количеством 2 c . Они ложатся друг на друга. Кривые симметричны относительно начала координат, оси ординат и абсцисс.
Если мы зададим значения c > b , c -любое нечётное число, b -любое чётное и получившаяся дробь не сокращается до целого числа, тогда увидим цветы с количеством лепестков 2 c . Они будут накладываться друг на друга. Кривые симметричны относительно начала координат, оси ординат и абсцисс.
Рассмотрим уравнение кривой 
Если k -чётное число, и мы будем прибавлять | m |>5 , то наша «роза» из 2k лепестков будет переходить в кривую, стремящуюся к форме окружности. Чем больше m и чем меньше a , тем более округленный цветок мы получим
Если k -нечётное число, и если будем прибавлять числа | m |>5 , то наша кривая в форме цветка будет переходить в окружность. Чем больше m и чем меньше a , тем более округленный цветок мы получим.
2.3. Полярная система координат.
Положение любой точки P в пространстве (в частности, на плоскости) может быть определено при помощи той или иной системы координат. Числа (или другие символы), определяющие положение точки, называются координатами этой точки. В зависимости от целей и характера исследований выбирают различные системы координат. Рассмотрим полярную систему координат.
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Итак: положительным направлением отсчета углов считается направление «против часовой стрелки»
Основными понятиями этой системы являются точка отсчёта – полюс, и луч, начинающийся в этой точке – полярная ось.
Полярный радиус ρ – длина отрезка О P
Полярный угол φ – величина угла между полярной осью и отрезком О P .
Переход от полярной системы координат к декартовой
Если полюс полярной системы координат совместить с началом прямоугольной системы координат, а полярную ось с положительной полуосью Ox, то по известным полярным координатам точки А (ρ;φ) её прямоугольные координаты вычисляются по формулам:
2.5 Общие свойства роз Гвидо Гранди
Семейство роз Гранди имеет свойство, которое в природе не сразу и заметишь: так как

то вся кривая расположена внутри круга единичного радиуса. В силу периодичности тригонометрических функций роза состоит из одинаковых лепестков, симметричных относительно наибольших радиусов, каждый из которых равен 1.
Наиболее красивые «цветы» получаются при k = 2 (четырехлепестковая роза) и при k = 3 (трехлепестковая роза).
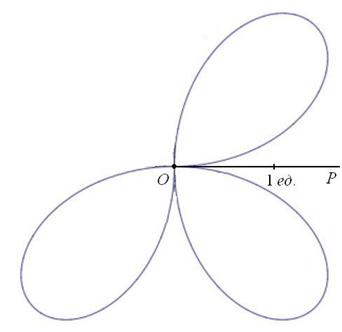
Покажем, как построить трёхлепестковую розу. Для построения этой кривой сначала заметим, что поскольку полярный радиус неотрицателен, то должно выполняться неравенство 

В силу периодичности функции 














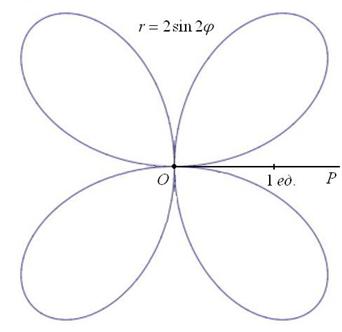
Рассмотрим теперь, как построить кривую, заданную в полярной системе координат уравнением ρ= sin(2 ∗ 𝜑) .
Функция 

поэтому достаточно построить кривую в первой четверти, потом зеркально отразить ее относительно оси Оу и использовать периодичность для построения кривой в третьей и четвертой четвертях.
Функция 


Отметим следующие интересные свойства четырехлепестковой розы:
• четырехлепестковая роза есть геометрическое место оснований перпендикуляров, опущенных из начала координат на отрезок длиной 1, концы которого скользят по координатным осям;
• площадь, ограничиваемая четырехлепестковой розой, равна 
Вообще, если k — натуральное число, то роза состоит из 2k лепестков при четном k и из k лепестков при k нечетном.
2.6.Связь с другими кривыми
Замечательные кривые
Кардиоида (от греческих слов сердце и вид) – получила свое название из-за схожести своих очертаний со стилизованным изображением сердца.
Определяется уравнением в полярных координатах

(a — радиус окружности)
В Древней Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя в спортивных играх. Эту лемнискату называют в честь швейцарского математика Якоба Бернулли, положившего начало ее изучению.
Определяется уравнением в полярных координатах:
(с – половина расстояния между фокусами лемнискаты)
Полярная роза – известная математическая кривая, похожая на цветок. Определяется уравнением в полярных координатах
Спираль Архимеда – названа в честь ее изобретателя, древнегреческого математика Архимеда. Определяется уравнением в полярных координатах
Применение полярных координат
В фотографии
Вертикальные линии после того, как к ним применен фильтр (переводящий координаты точек из прямоугольной системы в полярную), стали расходиться из центральной точки.
В экономике
Необычный формат биржевых графиков предложил в 1990-е годы российский математик Владимир Иванович Елисеев
Ф – время её совершения
Используя такую систему координат, относительно просто связать градусы и время (в году 365 дней, в окружности – 360 градусов)
В военном деле
Координаты цели могут выдаваться в полярной системе координат (азимут, дальность), прямоугольной (X, Y), геодезической (широта, долгота).
В медицине
Компьютерная томография сердца в системе полярных координат .
В системах идентификации человека
Результат преобразования кольца радужной оболочки из декартовой системы координат в полярную.
В различных областях науки и техники
Измерительный проектор предназначен для измерения различных параметров в прямоугольной и полярной системах координат
Применяется в измерительных лабораториях и цехах предприятий точного приборостроения, машиностроения, микроэлектроники, в инструментальном производстве, а также в лабораториях НИИ.
В математическом дизайне и архитектуре малых форм
С помощью выращенных цветов, различных кривых в полярных координатах и графических редакторов можно сделать, например различные рисунки, рамки-орнаменты, или украсить ими различные предметы. Орнамент — украшение, узор, состоящий из ритмически организованных повторяющихся элементов, которые композиционно могут образовывать орнаментальный ряд.
В ландшафтном дизайне

2.7 Практическая часть
Так как я обучаюсь в Самарском колледже строительства и предпринимательства, то данная тема мне близка и актуальна. На отделении садово-парковое и ландшафтное строительство студенты создают эскизы и макеты цветников, клумб и альпийских горок. 
На отделении строительство зданий и сооружений, на уроках архитектуры изучают и создают современные орнаменты.
Мной созданы несколько эскизов орнамента. Изучение линий Гвидо Гранди натолкнуло меня выполнить эскизы орнамента в виде кардиоид и роз. Несколько моих разработок я здесь представлю.
источники:
http://www.calc.ru/Uravneniya-Krivykh-Roza.html
http://infourok.ru/issledovatelskaya-rabota-rozy-gvido-grandi-5489747.html