Решения задач в excel менеджмент - Word и Excel - помощь в работе с программами

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

Делаем таблицу со значениями матрицы А.
Выделяем на этом же листе область для обратной матрицы.
Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
В поле аргумента «Массив» вписываем диапазон матрицы А.
Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Источник

Время на прочтение
5 мин

Количество просмотров 172K

Я работаю обычным аналитиком и, так получилось, что летом 2014 года, участвуя в одном e-commerce проекте, на коленке за 3 недели сделал управленческий учет в MS Excel. Давно планировал и наконец-то решил выложить на Хабр. Думаю, будет полезно малым предпринимателям, понимающим важность управления финансовыми потоками, но не желающим тратить значительное количество времени и средств на ведение управленческого учета. Не претендую на истину в последней инстанции и буду рад иным решениям, предложенным участниками сообщества.

Бизнес, к которому я летом имел отношение, был обычным интернет-магазином одежды премиум и выше сегмента с оборотом около 1 млн рублей в месяц. Бизнес работал, не сказать, чтобы очень успешно, но работал и продолжает работать. Собственник понимал необходимость ведения управленческого учета и, с этим пониманием, взял меня в качестве финансового директора (аналитика/менеджера …), так как предыдущий ушел из бизнеса за 3 месяца до моего прихода. Собственно, дыра такой же продолжительности была и в ведении управленческого учета. Забегая вперед скажу, что дыру не устранил (решили не ворошить прошлое), но создал систему, которая успешно работает при минимальных трудозатратах и по сей день.

Мой предшественник вёл управленку в Финграде, который оказался весьма мощным инструментом. Например, он позволял автоматически грузить информацию из 1С и выписок разных банк-клиентов, создавая проводки по заранее сформулированным правилам. Вещь, безусловно полезная, однако, при соблюдении системы двойной записи увеличивала время работы в разы. Чтобы избежать увеличения работы этот инструмент позволял генерировать «зависимые проводки». В создании этих дополнительных проводок и была зарыта собака. И тут выяснилось, что за всей мощью Финграда крылась уникальность, обусловившая полное отсутствие экспертизы в свободном доступе. Обычным пользователям (платившим, кстати, 3000 рублей в месяц за доступ к системе) были доступны лишь «Руководство пользователя» на официальном сайте, да 6 видео-уроков там же. Youtube, дававший доступ к ещё паре десятков видеоуроков, также не сильно помогал. Форумов с информацией «how to…» не было в принципе. Поддержка, на конкретные вопросы о правилах создания «зависимых проводок» и просьбах помочь именно в моем случае — морозилась фразами «у нас с вами не заключен договор на поддержку, поэтому на такие специфические вопросы мы не готовы отвечать». Хотя казалось бы — чего специфического в таких просьбах, да ещё и со скриншотами с моей стороны? Понятно, что все можно бить руками, но спрашивается, а зачем тогда вообще платить за инструмент, который сильно увеличивает время, необходимое на ведение управленки и не дает никаких преимуществ для малого бизнеса?

Убедив собственника в нецелесообразности использования «Финграда» при таких объемах бизнеса и выгрузив всю информацию из системы, я поставил на нем БОЛЬШОЙ и жирный крест. При этом решение уйти именно в MS Excel было не спонтанным. Хорошенько загуглив на тему ведения управленческого учета находил монстров, похожих на «Финград», либо ссылки на веб-приложения для ведения личных финансов, в то время как основными требованиями к системе были:

— возможность ведения БДДС и БДР на основе изменяемого плана счетов;
— простота в дальнейшем ведении управленческого учета (в том числе силами «финансово-неграмотных» пользователей);
— гибкость (возможность на ходу расширять/убирать функционал);
— отсутствие перегруженности инструмента/интерфейса.

Для начала проясним термины: будучи не финансистом, под БДДС понимаю «Баланс Движения Денежных Средств», БДР — «Бюджет Доходов и Расходов». БДДС считаем кассовым методом (днем совершения операции — колонка «Дата операции») и используем для операционного day-to-day планирования, а БДР методом начисления (колонка «Период начисления») для стратегического, в рамках года и более.

Итак, как все устроено и как оно работает (в идеале):

1. Управленческий учет собирается на основе информации вводимой конечными пользователями при помощи формы в Google Docs. Красным помечены названия полей и кодировки вариантов в конечном файле управленческого учета — своего рода мапинг полей.

2. В итоге выглядит оно так (зеленым залито то, что перенесено в итоговый файл управленки).

3. Управленческий учет построен на базе .xls выгрузки из Финграда (отсюда странные для сторонних пользователей названия и, в целом избыточное количество колонок). Убедительная просьба не воспринимать всерьез значения колонок «Приход», «Расход» — многое рандомно изменено.

Механизм заполнения прост: аккуратно переносим во вкладку «Общая книга» из формы Google Docs и банковских выписок. Красным выделены строки, используемые для формирования БДР, зеленым — БДДС., которые представляют собой сводные таблицы и строятся на основе промежуточных вкладок с говорящими названиями. Единственные колонки, информация в которых не связана с иными источниками: «Исходный ID» (уникальные значения строк) и «Дата создания» (=ТДАТА(), а затем копируем и вставляем как значение)

4. Статьи ДДС (движения денежных средств) располагаются на отдельной вкладке «ПС_служебный» и вполне могут регулярно пересматриваться в зависимости от конкретных потребностей (не забываем обновлять формулы на листах «Данные_БДДС», «Данные_БДР»).

5. На картинке образец БДДС, в формате по умолчанию, свернутый до понедельной «актуальности».

6. Образец БДС (помесячный). Обратите внимание на уже упоминавшийся выше тезис об использовании строк из «Общей книги»: Бюджет и Факт для БДР, План и Факт — для БДДС.

7. Работа с БДДС подразумевает поддержание строк «План» в максимально актуальном состоянии. Я достаточно педантичен в работе с первичной информацией и комментарии сделанные мной сохраняли всю историю изменений. Как будет у Вас — вопрос к Вам. Мой подход позволил мне отлавливать примерно 1 существенную ошибку в неделю, грозившую расхождениями на десятки-сотни тысяч рублей. Время, кстати, съедалось немного.

8. Собственно сам файл управленческого учета.

PS: Долго думал над тем, как автоматизировать процесс «перелива» информации из формы Google Docs, пока не пришел к мысли о необходимом ручном контроле вводимой разнородной информации (много людей заполняет формы + наличие минимум одного банк-клиента + 1С). Тем более не знаю VBA… Отдаю на суд хабрасообщества как есть, надеюсь, кому-нибудь поможет или просто будет интересно.

UPD от 30.04.2020: ввиду текущей экономической ситуации решил вспомнить Excel и бесплатно помочь малому бизнесу созданием подобных инструментов. Все интеллектуальные права останутся за мной и будут опубликованы в виде статей (без данных, содержащих коммерческую тайну).

Критерии попадания в выборку кому хочу помочь:

Обязательный:
Вы не МММ, продавцы алкоголя возле школ, микрофинансовые организации

~~и прочие лохотронщики~~

Опциональные(достаточно соответствовать одному из):
Ваше дело имеет очевидную ценность для общества (благотворительные фонды, волонтерские движения и т.д.)
или
Вы платите белые зарплаты и приемлемый для оборота объем налогов (придется доказать выписками перечислений в фонды и на счета ФНС)

Источник

1
Построение моделей задач линейного
программирования 2

2
Решение задачи ЛП при помощи надстройки
«Поиск решения» в MS Excel 3

3
Анализ оптимального решения задач ЛП 8

4
Двойственная задача. Теневые цены 11

5
Транспортная задача 26

6
Задача коммивояжера 35

Контрольные
вопросы 45

Линейное программирование

1 Построение моделей задач линейного программирования

Математическое
программирование («планирование») —
это раздел математики, занимающийся
разработкой методов отыскания
экстремальных значений функции, на
аргументы которой наложены ограничения.
Методы математического программирования
используются в экономических,
организационных, военных и др. системах
для решения так называемых распределительных
задач. Распределительные
задачи (РЗ) возникают в случае, когда
имеющихся в наличии ресурсов не хватает
для выполнения каждой из намеченных
работ эффективным образом и необходимо
наилучшим образом распределить ресурсы
по работам в соответствии с выбранным
критерием оптимальности.

Линейное программирование (ЛП)
является наиболее простым и лучше всего
изученным разделом математического
программирования. Характерные черты
задач ЛП следующие:

1) показатель оптимальности
(целевая функция) L(X)
представляет собой линейную
функцию от элементов решения
;

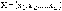
2) ограничительные условия,
налагаемые на возможные решения, имеют
вид линейных
равенств или неравенств.

Общая форма записи модели
задачи ЛП

Целевая функция (ЦФ)

при ограничениях

((1.1)

Допустимое решение —
это совокупность чисел (план) ,
удовлетворяющих ограничениям задачи
(1.1).

Оптимальное решение —
это план, при котором
ЦФ принимает свое максимальное
(минимальное) значение.

2 Решение задачи лп при помощи надстройки «Поиск решения» в ms Excel

Пример:
Оптимальный план выпуска продукции
мебельного цеха

Цех может
выпускать два вида продукции: шкафы и
тумбы для телевизора. На каждый шкаф
расходуется 3,5 м стандартных ДСП, 1 м
лицевого стекла и 1 человеко-день
трудозатрат. На тумбу -1м ДСП, 2 м стекла
и 1 человеко-день трудозатрат. Прибыль
от продажи 1 шкафа составляет 200 у. е., а
1 тумбы -100 у е. Материальные и трудовые
ресурсы ограниченны: в цехе работают
150 рабочих, в день нельзя израсходовать
больше 350 м ДСП и более 240 м стекла. Какое
количество шкафов и тумб должен выпускать
цех, чтобы сделать прибыль максимальной?

2.1 Формализация примера и основные соотношения (математическая модель)

Сведем все данные в
следующую таблицу

Таблица 1 –
Параметры задачи

Ресурсы	Запасы	Продукты
Шкаф	Тумба
ДСП	350	3,5	1
Стекло	240	1	2
Труд	150	1	1
Прибыль, у.е.	200	100

В колонке «Ресурсы»запишем предельный расход ресурсов
(ДСП, стекла и труда). В колонках«Шкаф»и«Тумба»(продукция, выпускаемая цехом) запишем
расход сырья на единицу продукции.
Наконец, на пересечении колонок«Шкаф»и«Тумба»
и строки«Прибыль»запишем величины
прибыли от продаж 1 шкафа и 1 тумбы.

Определим теперь все элементы
математической модели данной ситуации
(таблица 2):

— переменные решения;

— целевую функцию;

— ограничения.

В данном случае
очевидно, что переменные решения (иначе —
неизвестные), от которых зависит целевая
функция (прибыль) цеха, —
это количество шкафов и тумб, выпускаемых
цехом. Обозначим эти переменные
соответственноx₁их₂.

Таблица
2 – Элементы модели

Переменные решения	Целевая функция
x₁— количество шкафов х₂— количество тумб, производимых цехом	прибыль цеха
Ограничения

Нетрудно
также понять, как в данном случае
записывается выражение для целевой
функции.

Прибыль
от продажи одного шкафа равна 200 у. е.,
значит, прибыль от продажи x₁шкафов будет 6∙x₁. Аналогично
прибыль от продажиx₂тумб
равна 5∙x₂, что и отражено в
соответствующей графе таблицы. Глядя
на выражение для целевой функции
(типичное для моделей линейного
программирования), можно легко увидеть,
что, чем больше будут значения переменныхx₁иx₂, тем больше
будет и прибыльР. Если бы было
возможно беспредельно увеличивать
ежедневный выпуск шкафов и тумб, прибыль
росла бы беспредельно. Ясно, однако, что
это невозможно, поскольку доступные
запасы ресурсов ограничены. Это приводит
к ограничениям на значения переменныхx₁иx₂.

Займемся
теперь этими ограничениями. Запишем
неравенство, отражающее ограниченность
запасов шкафов. Поскольку на 1 шкаф
расходуется 3,5 м ДСП, а на 1 тумбу — 1 м,
то суммарный расход ДСП на x₁шкафов иx₂тумб будет, очевидно,,
что не должно превышать запаса ДСП в
цехе, т.е. 350 м ДСП. Это отражено первым
неравенством, записанным в таблице 2.
Точно так же получаются второе и третье
неравенства, отражающие ограниченность
запасов стекла ичеловеко-день
трудозатрат. Естественно, переменные
решения не могут быть отрицательными
числами, что отражено в последнем
ограничении в таблице 2.

Определение
переменных решения, целевой функции и
ограничений — это почти все, что должен
сделать менеджер, чтобы воспользоваться
результатами оптимизации и анализа
линейной модели. Далее необходимо только
правильно организовать данные для
компьютера, а все остальное сделает
компьютерный алгоритм оптимизации.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Применение команды «Поиск решений»

в работе с профессионально-ориентированными задачами

Постановка задачи

В ресторане установлены 7 графиков работы официантов:

График	Выходные
1	Суббота. Воскресение
2	Воскресение, Понедельник
3	Понедельник, Вторник
4	Вторник, Среда
5	Среда, Четверг
6	Четверг, Пятница
7	Пятница, Суббота

Количество работающих по ним соответственно – №1, №2, №3, №4, №5, №6, №7. Опытным путём было определено требуемое количество официантов на каждый день недели:

День недели	Пн	Вт	Ср	ЧТ	Пт	Сб	Вс
Требуется, чел.	11	10	9	10	12	12	13

Необходимо распределить работающих официантов по каждому графику таким образом, чтобы затраты на еженедельную зарплату всем официантам были минимальными (найти N1, N2, N3, N4, N5, N6, N7). При этом нужно учитывать следующие факторы:

Ежедневно фактическое количество работающих официантов должно быть не менее ежедневной потребности.
Число работников, работающих по каждому графику, не может быть отрицательным.
Число работников, работающих по каждому графику, должно быть целочисленным.

Рассмотреть ситуацию, когда по графику 1 обязательно должно работать 3 человека.

Создание таблицы для анализа данных

Исходя из условий постановки задачи, создадим в табличном процессоре Excel таблицу, где будем потом рассматривать и анализировать ситуации.

Открываем программу Excel, например, щёлкнув два раза её ярлык на рабочем столе или через Пуск – Программы – Microsoft Excel.
Устанавливаем поля документа через Файл — Параметры страницы:
Сохраняем книгу (файл в Excel) через Файл – Сохранить как под именем Анализ графиков работы.xls.
Начиная с ячейки A1, оформляем таблицу (см. следующий лист). В те дни недели, где предусмотрен по графику рабочий день, ставим 1, а где выходной – 0. при этом формат данных в этих ячейках оставляем по умолчанию – Общий.
После заполнения таблицы данными, отформатируем ячейки так, чтобы текст и числа в них располагались по горизонтали и вертикали По центру. Для этого выделим мышкой всю таблицу и используем меню Формат – Ячейки – вкладка Выравнивание (или по правой клавише мыши).
Оформим внешние и внутренние границы ячеек.
Получим таблицу следующего вида:

Здесь A2…G2 – количество официантов, работающих в соответствующий день недели, A1..G1 – требуемое (определённое опытным путём, меньше нельзя).

Всего работников – N.

K – дневная заработная плата одного официанта, она составляет, к примеру, 200 рублей.

Поскольку файл в программе Excel называется книга, а каждая книга состоит из листов, переименуем ярлычок первого листа книги, где создана таблица, и назовём его Заготовка. Переименовать можно щелчком правой клавишей по ярлычку листа, выбрать пункт Переименовать или просто два раза щёлкнуть по ярлычку листа, название Лист1 выделиться, можно вводить новое название.
Мышкой выделим всю таблицу и скопируем её в Буфер обмена.
Перейдём на Лист2 книги, щёлкнув ярлычок этого листа.
Вставим из буфера скопированную таблицу: щёлкнем значок на панели Стандартная.
В ячейках C2:C8 удалим набранный текст. В этих ячейках будут вычисляться значения при применении команды Поиск решения.
В ячейки D10:J10 введём определённое опытном путём минимальное количество официантов по дням недели.

Требуется (определено опыт. путём)

Цвет шрифта этих ячеек для лучшей наглядности сделаем синим.

В ячейках D9:J9 также удалим текст. Сюда необходимо вписать формулы.
В ячейку C12 запишем 200, изменим формат данных в ячейке на Денежный в рублях, получим 200р.
Переименуем Лист2 в Ситуация 1.

Таблица для проведения анализа готова.

Ввод формул для получения решения

Чтобы в дальнейшем проанализировать ситуации, необходимо в ячейки D9:J9 ввести формулы. рассчитывающие фактическое количество официантов по дням недели и по графикам работы.

Формулы для вычислений могут быть простыми, такими как сложение содержимого двух ячеек, а могут быть сложными, такими как определение отклонения какой-либо величины от других значений последовательности.

Ввод формулы в Excel начинается со знака =. За ним записывается функция, потом в скобках () аргументы. Некоторые функции, например, многие статистические, финансовые используют несколько аргументов. Тогда аргументы отделяются друг от друга запятыми.

Простейшие формулы, такие как сложение, вычитание, умножение, деление состоят из двух частей: арифметического оператора и хотя бы одного адреса ячейки.

При составлении формул для вычислений или преобразований данных необходимо указать содержимое каких именно ячеек используется в формулах.

Введём в ячейку D9 формулу =D2*C2+D5*C5+D6*C6+D7*C7+C8.

Она рассчитывает сколько официантов должно работать в понедельник с учётом графиков их работы. Там, где в таблице 0, т.е. выходной, ячейки не обсчитываем.

Для подсчёта работников во вторник в ячейку E9 запишем формулу

=C2*E2+E3*C3+E6*C6+E7*C7+E8*C8.

Для ячейки F9 – =F2*C2+F3*C3+F4*C4+F7*C7+F8*C8. Среда.

Для ячейки G9 – =G2*C2+G3*C3+G4*C4+G5*C5+G8*C8. Четверг.

Для ячейки H9 – =H2*C2+H3*C3+H4*C4+H5*C5+H6*C6. Пятница.

Для ячейки I9 – =I3*C3+I4*C4+I5*C5+I6*C6+I7*C7. Суббота.

Для ячейки J9 – =J4*C4+J5*C5+J6*C6+J7*C7+J8*C8. Воскресенье.

В ячейку C11 нужно записать формулу подсчёта общего количества официантов с учётом всех семи графиков работы: =СУММ(C2:C8), т.е. просуммировать всех официантов, работающих по графикам 1…7.

В ячейку C13 введём формулу подсчёта недельной зарплаты всех официантов:

=(C11*C12).

Все необходимые формулы и данные введены в таблицу. Теперь можно приступать к поиску решения поставленной задачи.

Поиск решения

Команда Поиск решения из меню Сервис анализирует ситуацию с учётом ограничений, накладываемых на отдельные ячейки, рассчитывает значение целевой ячейки, изменяя значения указанных нами ячеек.

При поиски решения целевая ячейка должна содержать формулу, но ячейки, которые будут изменяться, должны содержать значения, а не формулу.

Для решения нашей задачи выполним следующие действия:

Выделим ячейку C13. (Еженедельная зарплата, она должна быть минимальной.)
Сервис — Поиск решения.
Установим целевую ячейку $C$13 равной минимальному значению.

Укажем, что будут меняться значения ячеек $C$2:$C$8. Это можно сделать, щёлкнув по красной стрелке в правом углу окошечка, перейдя в таблицу и выделив нужные ячейки.
Введём ограничения на значения отдельных ячеек: в ячейках C2…C8 должно быть целое число; ячейка D9>=11, E9>=10, F9>=9, G9>=10, H9>=12, I9>=12, J9>=13. Ввод ограничений проводим через кнопку.
Через кнопку Параметры установим, что значения в изменяемых ячейках должны быть неотрицательными. Другие параметры в открывшемся окне Параметры поиска решения оставляем внесёнными по умолчанию.

Нажимаем кнопку Выполнить. Получаем решение задачи для первой ситуации, когда определяем минимальное количество официантов с учётом всех графиков их работы при условии, что ежедневно фактическое количество работающих официантов должно быть не менее ежедневной потребности. Решение представлено в Приложении.
В ситуации 2 официантов, работающих по графику №1, должно быть обязательно 3. Для учёта этого обстоятельства при новом поиске решения введём ещё одно ограничение: $C$2 =3. Тогда после нажатия кнопки Выполнить получим решение для этой ситуации. Это решение представлено также в Приложении.
Проанализировав обе ситуации видим, что общее количество официантов одинаково (16). Это минимальное количество при заданных условиях. Соответственно подсчитана и еженедельная зарплата всех официантов. Но в ситуации 2 распределение официантов по графикам работы другое. Фактическое количество работающих по дням недели также изменилось.

Заключение

Табличный процессор Excel обладает удобными возможностями для анализа и обработки данных. Такие команды или средства программы как Подбор параметров и Поиск решения можно использовать для решения задач прогнозирования различных ситуаций в работе менеджера, финансиста и других специалистов, гибкого подбора новых параметров при изменении ситуации, поиска более гибкого и многовариантного решения задачи с учётом различных обстоятельств и ограничений.

Приложение

Решение задачи, найденное с помощью программы MS Excel

Ситуация 1

Ситуация 2

Источник

На этой странице вы найдете примеры решений различных оптимизационных задач с использованием пакета электронных таблиц MS Excel (используется как надстройка Поиск решения, так и ручные вычисления).

Задачи оптимизации и Excel

Задачи оптимизации имеют огромное прикладное значение и возникают в самых разных разделах экономики, техники, военного дела и т.п. В таких задачах нас интересуют поиск некоторого оптимального решения (минимизующего или максимизирующего целевую функцию: прибыль, затраты, калорийность и т.п.) в условиях ограничений (наличия ресурсов, дорог, времени, продуктов и т.п.).

Вот некоторые примеры экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация калорийности и стоимости рациона (как для людей, так и для животных), минимизация расходов на перевозку грузов по маршрутам, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.

Часто эти задачи (даже учебные, даже в случае линейности) содержат более десяти переменных(а в случае, например, транспортных задач, и вовсе десятки), что делает ручные расчеты нерациональными. В то же время привычная для всех программа Excel прекрасно подходит для поиска решения.

Алгоритм решения с помощью надстройки «Поиск решения» следующий:

составить математическую модель задачи: выделить и обозначить переменные, ограничения на них в виде равенств и неравенств (естественные, например, неотрицательность количества, и дополнительные, например, «запасов железной руды не более 10 т»), целевую функцию (то, что нужно оптимизировать) выразить через переменные.
выделить место под переменные задачи; внести ограничения (левые части — в виде формул от переменных, правые — в виде констант) в файл электронной таблицы Excel,
внести в ячейку формулу для целевой функции,
запустить надстройку Поиск решения,
установить нужные параметры решения (ограничения в листе, ограничения неотрицательности, условие линейности при необходимости и т.п.) и запустить выполнение.

Excel вычислит оптимальные значения переменных и покажет их в ячейках, а также значение целевой функции. Дополнительно можно построить отчеты для анализа решения задачи.

Некоторые задачи оптимизации решаются не с помощью надстройки Поиск решения, а путем подбора параметра или ручных расчетов. Ниже вы найдете примеры разных задач, а также ссылки на другие разделы со сходными заданиями.

Понравилось? Добавьте в закладки

Задачи оптимизации: примеры в Excel

Задача 1. Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля $R_j$. Определена экономическая эффективность $К$ — каждого проекта в зависимости от рентабельности производства. По истечении трех сроков $S_i$ рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д. е.):

Выберите оптимальное решение в соответствии с критериями Лапласа, Вальда, Сэвиджа и Гурвица (при $а = 0,5$).

Задача 2. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода каждого вида сырья на изготовление единицы продукции данного вида в таблице 6. В ней же указаны прибыль от реализации единицы изделия каждого вида и общее количество сырья данного, которое может быть использовано предприятием.
Требуется такой составить такой план производства изделий А и В, при котором прибыль от реализации будет максимальной?

Задача 3. Фирма N, имеющая филиалы (k), производит продукцию. Каждый филиал фирмы выпускает четыре вида продукции из пяти (i=1-5). Данные, характеризующие производство филиалов $b_{ki}$, приведены в табл.1.
Филиалы фирмы закупают сырье, из которого производят продукцию, у семи АО (j =1-7). Выход готового продукта из 1 тонны сырья $a_{ij}$ показан в табл.2.
Прибыль филиалов фирмы при закупке 1тн сырья у разных АО, $С_{kj}$ , показана в табл.3.
В разделе 1 работы требуется:
1.1.Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, ($x_j$), максимизируя прибыль филиала. Далее, студент формулирует экономико-математическую модель общей задачи линейного программирования (ОЗЛП).
1.2.С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции.

Задача 4. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки?
Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5.
Для решения задачи используется ППП Excel.

Задача 5. Менеджер проекта по строительству нового торгового гипермаркета компании Наше дело надеется завершить проект за пару недель до Рождества.
После обзора оценок времени выполнения отдельных стадий выяснилось, что потребуются дополнительные инвестиции, чтобы сократить длительность проекта так, чтобы он действительно завершился вовремя. В таблице приведены оценки длительностей стадий и стоимость их сокращения на 1 и на 2 недели.
a. Нарисуйте сетевую диаграмму проекта и найдите критический путь.
b. Определите минимальную стоимость сокращения проекта на 5 недель.

Решаем задачи вручную и в Excel с отчетом

Полезные ссылки

Решение транспортной задачи в Excel
Решение ЗЛП в Excel

Другие виды задач, решаемые в Эксель
Готовые контрольные по ЛП

Методички

Решение оптимизационных задач в среде MS Excel 2013 Методические указания небольшого объема. Разобраны стандартные задачи: ЛП, транспортная, нелинейная, приведены скриншоты решения и пояснения.
Решение задач оптимизации в Microsoft Excel 2010 Учебное пособие ТОГУ, 101 страница, более увесистый и подробный документ. Разбирается надстройка Поиск решения, решение задач линейного и нелинейного программирования и СЛАУ.

Источник