|
В общем виде задача о рюкзаке формулируется следующим способом: имеется рюкзак определенного объема и неограниченное количество предметов. Для каждого предмета известен его объем (вес) и ценность (стоимость, эффективность). В рюкзак можно положить целое число предметов различного типа. Цель состоит в том, чтобы суммарная ценность всех находящихся в рюкзаке предметов была максимальна, а их объем (вес) не превышал заданной величины. К подобной формулировке может быть сведена задача максимального использования грузоподъемности подвижного состава, грузовместимости судна, автомобиля и т.п. Такая задача часто возникает при выборе оптимального управления в экономико-финансовых областях (например распределение бюджета отдела по проектам). Решение задачи в классической постановке Подобные задачи легко решаются с помощью надстройки «Поиск решения». Подготовлены исходные данные (рисунок ниже). Задача состоит в том, чтобы за счет подбора значений ячеек B16:B19 добиться максимального значения целевой функции (значение ячейки D20).
На первом рисунке ниже показаны ограничения на значения изменяемых ячеек. На втором рисунке ниже приводится результат расчета. Во многих практических случаях данная постановка задачи является слишком упрощенной. Далее будут рассмотрены варианты усложнения постановки задачи.
Модифицированная задача Одним из дополнительных ограничений, возникающих при практическом использовании данной задачи, могут быть ограничения на необходимое количество предметов определенных видов, которые можно положить в рюкзак. При этом могут возникать варианты задачи, когда требуется строго определенное количество предметов или требуется не менее (не более) заданного количества предметов. На рисунке ниже показаны исходные данные модифицированного варианта задачи. В этом случае предполагается, что в рюкзак может быть положено не менее некоторого количества предметов.
На следующем рисунке показаны ограничения на значения изменяемых ячеек B16:B19. В данном случае к ограничениям добавлено условие 16:19>=8:11, то есть задано минимальное необходимое количество предметов различных видов.
Решение задачи представлено последнем рисунке.
При необходимости дополнительное условие 16:19>=8:11 может быть изменено. Например, можно установить отдельные ограничения для всех предметов, назначив для некоторых из них точное количество предметов, в то время как для других — условие «не менее» или «не более»
|
|
Создадим модель для одной из модификаций классической задачи о рюкзаке: укладка как можно большего числа вещей в рюкзак при условии, что общий объём (или вес) всех предметов, способных поместиться в рюкзак, ограничен. Расчет будем проводить с помощью надстройки Поиск решения.
Существует множество разновидностей задачи о рюкзаке, отличия заключаются в условиях, наложенных на рюкзак, на предметы или их выбор. Рассмотрим Рюкзак 0-1 (англ. 0-1 Knapsack Problem): не более одного экземпляра каждого предмета (пример с сайта
www.solver.com
).
Задача
Бензовоз с 4-мя цистернами разного объема должен выполнить заказ: перевезти определенное количество топлива трех разных типов. К сожалению, суммарный объем цистерн меньше, чем объем заказа. За невыполненный заказ взимается штраф, размер которого пропорционален объему невыполненного заказа. Необходимо минимизировать размер штрафа, заполнив цистерны топливом оптимальным образом.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см.
файл примера
).
Переменные (выделено зеленым)
. В качестве переменных модели следует взять загрузку цистерн разными видами топлива.
Поиск решения
подбирает как сам вид топлива, который нужно перевозить, так и его объем.
Ограничения (выделено синим)
. Объем перевозимого топлива не должен превышать объем цистерн, а также как можно ближе к требованиям заказа.
Целевая функция (выделено красным)
.
Сумма штрафа должна быть минимальна.
Примечание
: для удобства настройки
Поиска решения
используются
именованные диапазоны
.
Вводная статья про
Поиск решения
в MS EXCEL 2010
находится здесь
.
|
Задача о рюкзаке |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
Программа-калькулятор для решения задачи о рюкзаке 0-1 или 0-1 knapsack problem (достаточно большого размера) LargeKnapsack здесь
- Динамическое программирование. Что меня поразило в этом алгоритме
- Пример решений задачи на VBA Excel
- Пример решений задачи на C# Visual Studio 2012
- Пример решений задачи на C++ Visual Studio 2012
- Пример решений задачи на Delphi 7, XE
Условие 0-1 knapsack problem:
Из множества предметов со свойствами «стоимость» и «вес», отобрать некоторое их число таким образом,
чтобы получить максимальную суммарную стоимость при одновременном соблюдении ограничения на суммарный вес.
Динамическое программирование. Что меня поразило в этом алгоритме
Ведь задан вес — Р.
Кажется, кратчайшее решение — это рассматривать наборы только этого веса.
Число сочетаний С из n по m возрастает с увеличением m [от 1 до n/2], а затем будет убывать.
Так зачем рассматривать промежуточные наборы и тратить время.
Отсортировать предметы по убыванию «стоимости» и перебирать в цикле, проверяя условие: вес <=P.
Машина посчитает
Можно, даже, отсортировать по параметру удельной стоимости каждого предмета (стоимость/вес предмета),
тогда каждый выше расположенный в ряду предмет будет предпочтительней, чем нижние.
А оказывается, нет.
Рассматривая варианты для весов от 1 до Р (внутренний цикл > ячейки одной строки) и увеличивая
количество предметов от 1 до n (внешний цикл > увеличение номера строки) становится возможной
автоматическая оптимизация.
Делая выбор для очередной ячейки, выбирается максимум из двух вариантов:
Первый вариант: ячейка в этой же колонке, но на строку выше (т.е. просто, не брать этот предмет в ранец,
т.к. предыдущий набор предметов для данного веса «ценнее»).
Второй вариант: стоимость предмета + ячейка, которая на строку выше и левее на величину веса предмета
(т.е. берем предмет, но выбрасываем из ранца другие предметы на величину его веса).
Гениально…
А как красиво заполняется таблица Иногда, оказывается, следует выбрасывать предметы с большей удельной
стоимостью, чтобы достичь максимальной загрузки ранца и от этого получить максимум стоимости в результат.
И даже сортировка излишня. Без нее результат абсолютно тот же. Предмет с большим удельным весом всегда
будет размещаться алгоритмом (в строке таблицы) левее, чем остальные.
Экспериментируйте. Все наглядно.
В желтых ячейках можно задать параметры.
Кнопки Random, Sort, Massiv запускают определенные макросы.
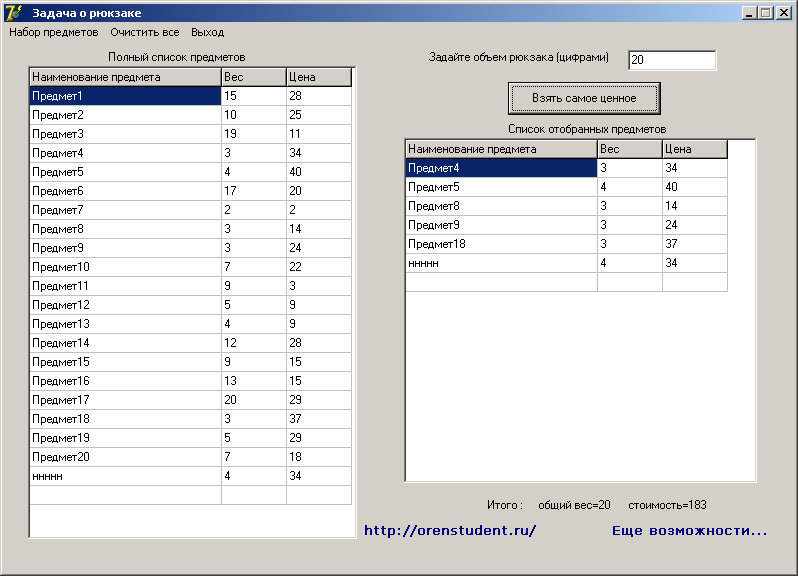
Пример решений задачи на VBA Excel 2007 и выше
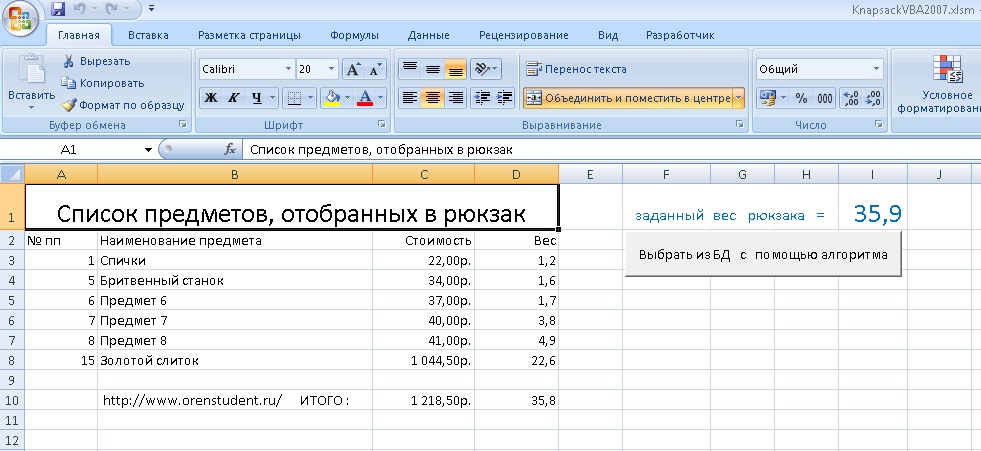
А это Задача о ранце (рюкзаке) на VBA Excel 2010…
Рис.1 Пример решений задачи на VBA Excel
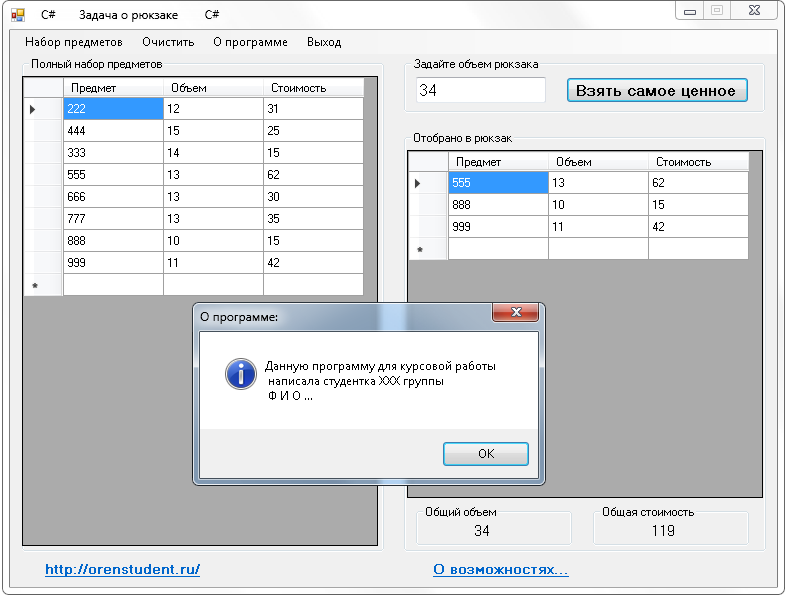
Пример решений задачи на C# Visual Studio 2012
Так может выглядеть главная форма…
Рис.2 Пример решений задачи на C# Visual Studio 2012
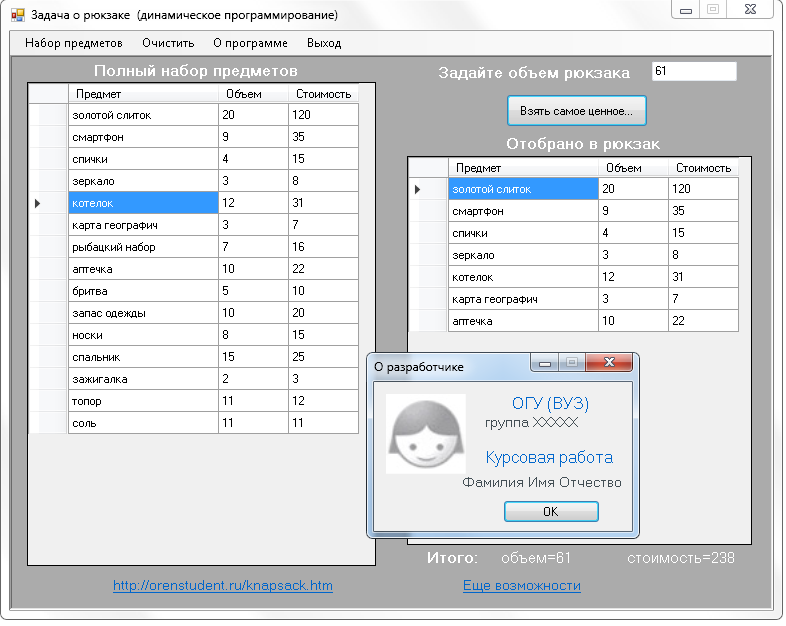
Пример решений задачи на C++ Visual Studio 2012
Так может выглядеть главная форма…
Рис.3 Пример решений задачи на C++ Visual Studio 2012
Замена фото (файл the_foto.jpg) на форме AboutForm — вопрос на любителя… Можно форму «О разработчике» удалить, если не требуется.
Пример решений задачи на Delphi 7, XE
Главная форма…
Рис.5 Пример решений задачи на Delphi 7, XE
Если у Вас остались вопросы, то задать их Вы можете, нажав на эту кнопочку …
Если на этой странице не нашлось того, что Вы так искали…
Не расстраивайтесь, не все потеряно… Смело щелкайте…
телефон:
+7(919) 572-59-92
+7(987) 848-79-61
1)
6x1+
2x2+
3x3+
7x4
→
max
5x1+
2x2+
4x3+
5x4
≤
14
xi
≥
0, xi
є
Z,
i
=
1,..,4.
2)
2x1+
4x2+
4x3+
3x4
→
max
2x1+5x2+
3x3+4x4
≤ 12
xi
≥
0, xi
є
Z,
i =
1,..,4.
3)
3x1+
6x2+
5x3+
x4
→
max
2x1+
5x2+4x3+
x4
≤
15
xi
≥
0, xi
є
Z,
i =
1,..,4.
4)
2x1+
2x2+
x3+3x4
→
max
2x1+
3x2+
2x3+
3x4
≤
13
xi
≥
0, xi
є
Z,
i =
1,..,4.
5)
5x1+
x2+
x3+
3x4
→
max
4x1+
3x2+
x3
+
3x4
≤
13
xi
≥
0, xi
є
Z,
i =
1,..,4.
6)
x1+
5x2+
2x3+
3x4
→
max
2x1+
4x2+
5x3+
3x4
≤
14
xi
≥
0, xi
є
Z,
i =
1,..,4.
7)
5x1+
7x2+
6x3+
3x4
→
max
4x1+
5x2+
8x3+
3x4
≤
14
xi
≥
0, xi
є
Z,
i =
1,..,4.
x1+
7x2+
3x3+
4x4
→
max
x1+
5x2+
2x3+
3x4
≤
13
xi
≥
0, xi
є
Z,
i =
1,..,4.
9)
x1+
7x2+
7x3+
4x4
→
max
2x1+
6x2+
4x3+
3x4
≤
15
xi
≥
0, xi
є
Z,
i =
1,..,4.
10)
3x1+
5x2+
2x3+
8x4
→
max
2x1+
4x2+
x3+
6x4
≤
15
xi
≥
0, xi
є
Z,
i =
1,..,4.
11)
x1+
5x2+
6x3+
3x4
→
max
2x1+
4x2+
5x3
+ 3x4
≤
15
xi
≥
0, xi
є
Z,
i =
1,..,4.
12)
4x1+
5x2+
2x3+4x4
→
max
2x1+2x2+
x3+
3x4
≤
13
xi
≥
0, xi
є
Z,
i =
1,..,4.
13)
3x1+
7x2+
7x3+
5x4
→
max
4x1+
7x2+
5x3+
6x4
≤
13
xi
≥
0, xi
є
Z,
i =
1,..,4.
14)
2x1+
4x2+
5x3+
6x4
→
max
2x1+
3x2+
4x3+
5x4
≤
14
xi
≥
0, xi
є
Z,
i =
1,..,4.
15)
5x1+
6x2+
3x3+
4x4
→
max
4x1+
7x2+
3x3+
5x4
≤
18
xi
≥
0, xi
є
Z,
i =
1,..,4.
16)
5x1+
6x2+
9x3+
4x4
→
max
4x1+
5x2+
8x3+
3x4
≤
14
xi
≥
0, xi
є
Z,
i =
1,..,4.
17)
x1+
7x2+
3x3+
8x4
→
max
x1+
4x2+
2x3+
5x4
≤
14
xi
≥
0, xi
є
Z,
i =
1,..,4.
18)
9x1+
x2+
2x3+5x4
→
max
8x1+
x2+3x3+4x4
≤
15
xi
≥
0, xi
є
Z,
i =
1,..,4.
19)
2x1+
3x2+
6
x3+9x4
→
max
4x1+
7x2+
8x3+10x4
≤
20
xi
≥
0, xi
є
Z,
i =
1,..,4.
20)
x1+
8x2+
9x3+7x4
→
max
x1+
5x2+
8x3+
6x4
≤
14
xi
≥
0, xi
є
Z,
i =
1,..,4.
21)
2x1+
3x2+
3x3+
4x4
→
max
4x1+
4x2+
5x3+
5x4
≤
19
xi
≥
0, xi
є
Z,
i =
1,..,4.
22)
4x1+
3x2+
7x3+
x4
→
max
4x1+
5x2+
8x3+
2x4
≤
14
xi
≥
0, xi
є
Z,
i =
1,..,4.
23)
x1+
4x2+
3x3+
9x4
→
max
x1+
3x2+
2x3+
5x4
≤
17
xi
≥
0, xi
є
Z,
i =
1,..,4.
24)
7x1+
x2+
3x3+2x4
→
max
6x1+
x2+2x3+3x4
≤
20
xi
≥
0, xi
є
Z,
i =
1,..,4.
25)
2x1+
3x2+
6
x3+9x4
→
max
4x1+
7x2+
8x3+10x4
≤
20
xi
≥
0, xi
є
Z,
i =
1,..,4.
26)
x1+
6x2+
7x3+4x4
→
max
x1+
5x2+
4x3+
3x4
≤
19
xi
≥
0, xi
є
Z,
i =
1,..,4.
27)
2x1+
5x2+
3x3+
7x4
→
max
x1+
3x2+
2x3+
5x4
≤
27
xi
≥
0, xi
є
Z,
i =
1,..,4.
28)
5x1+
x2+
3x3+7x4
→
max
4x1+
x2+2x3+3x4
≤
26
xi
≥
0, xi
є
Z,
i =
1,..,4.
29)
2x1+
3x2+
6
x3+7x4
→
max
3x1+
7x2+
8x3+
9x4
≤
25
xi
≥
0, xi
є
Z,
i =
1,..,4.
30)
x1+
6x2+
4x3+4x4
→
max
x1+
5x2+
4x3+
3x4
≤
29
xi
≥
0, xi
є
Z,
i =
1,..,4.
Содержание
- Задача о ранце (рюкзаке) на VBA (EXCEL), C++, C# (Visual Studio 2012) и DELPHI
- Динамическое программирование. Что меня поразило в этом алгоритме
- Пример решений задачи на VBA Excel 2007 и выше
- Поиск решения EXCEL (3.2). Минимизация потерь (задача о рюкзаке)
- Задача
- Создание модели
- Задача о рюкзаке в Excel
- Задача рюкзака решение excel
- Лабораторная работа 3. Решение задачи о рюкзаке приближенными и точными алгоритмами.
- «Жадный» алгоритм.
Задача о ранце (рюкзаке) на VBA (EXCEL), C++, C# (Visual Studio 2012) и DELPHI
Программа-калькулятор для решения задачи о рюкзаке 0-1 или 0-1 knapsack problem (достаточно большого размера) LargeKnapsack здесь
Калькулятор-Упаковщик «Packer1» тоже использует алгоритм «задачи рюкзака» Программа-калькулятор расчета укладки продукции в упаковки
Условие 0-1 knapsack problem:
Из множества предметов со свойствами «стоимость» и «вес», отобрать некоторое их число таким образом, чтобы получить максимальную суммарную стоимость при одновременном соблюдении ограничения на суммарный вес.
Динамическое программирование. Что меня поразило в этом алгоритме
Ведь задан вес — Р.
Кажется, кратчайшее решение — это рассматривать наборы только этого веса.
Число сочетаний С из n по m возрастает с увеличением m [от 1 до n/2], а затем будет убывать.
Так зачем рассматривать промежуточные наборы и тратить время.
Отсортировать предметы по убыванию «стоимости» и перебирать в цикле, проверяя условие: вес ячейки одной строки) и увеличивая количество предметов от 1 до n (внешний цикл > увеличение номера строки) становится возможной автоматическая оптимизация.
Делая выбор для очередной ячейки, выбирается максимум из двух вариантов:
Первый вариант: ячейка в этой же колонке, но на строку выше (т.е. просто, не брать этот предмет в ранец, т.к. предыдущий набор предметов для данного веса «ценнее»).
Второй вариант: стоимость предмета + ячейка, которая на строку выше и левее на величину веса предмета (т.е. берем предмет, но выбрасываем из ранца другие предметы на величину его веса).
А как красиво заполняется таблица Иногда, оказывается, следует выбрасывать предметы с большей удельной стоимостью, чтобы достичь максимальной загрузки ранца и от этого получить максимум стоимости в результат.
И даже сортировка излишня. Без нее результат абсолютно тот же. Предмет с большим удельным весом всегда будет размещаться алгоритмом (в строке таблицы) левее, чем остальные.
Экспериментируйте. Все наглядно.
В желтых ячейках можно задать параметры.
Кнопки Random, Sort, Massiv запускают определенные макросы.
Пример решений задачи на VBA Excel 2007 и выше
А это Задача о ранце (рюкзаке) на VBA Excel 2010.
Источник
Поиск решения EXCEL (3.2). Минимизация потерь (задача о рюкзаке)
history 27 марта 2015 г.
Создадим модель для одной из модификаций классической задачи о рюкзаке: укладка как можно большего числа вещей в рюкзак при условии, что общий объём (или вес) всех предметов, способных поместиться в рюкзак, ограничен. Расчет будем проводить с помощью надстройки Поиск решения.
Существует множество разновидностей задачи о рюкзаке, отличия заключаются в условиях, наложенных на рюкзак, на предметы или их выбор. Рассмотрим Рюкзак 0-1 (англ. 0-1 Knapsack Problem): не более одного экземпляра каждого предмета (пример с сайта ]]> www.solver.com ]]> ).
Задача
Бензовоз с 4-мя цистернами разного объема должен выполнить заказ: перевезти определенное количество топлива трех разных типов. К сожалению, суммарный объем цистерн меньше, чем объем заказа. За невыполненный заказ взимается штраф, размер которого пропорционален объему невыполненного заказа. Необходимо минимизировать размер штрафа, заполнив цистерны топливом оптимальным образом.
Создание модели
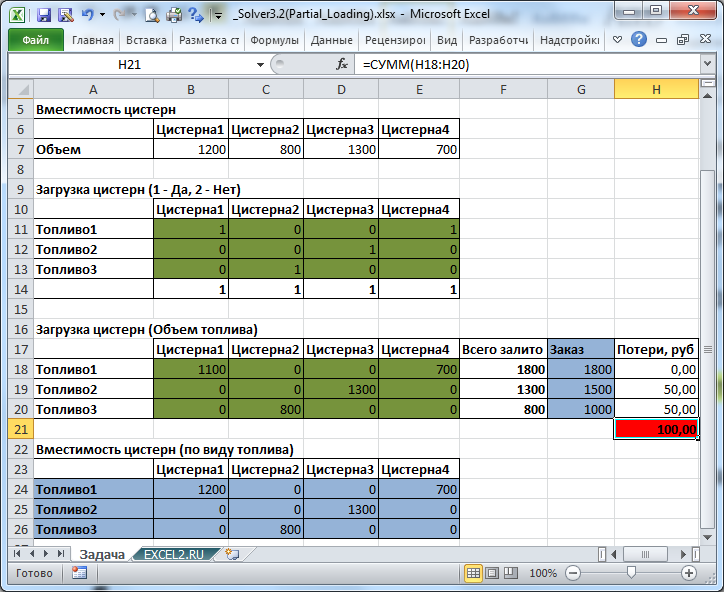
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера ).
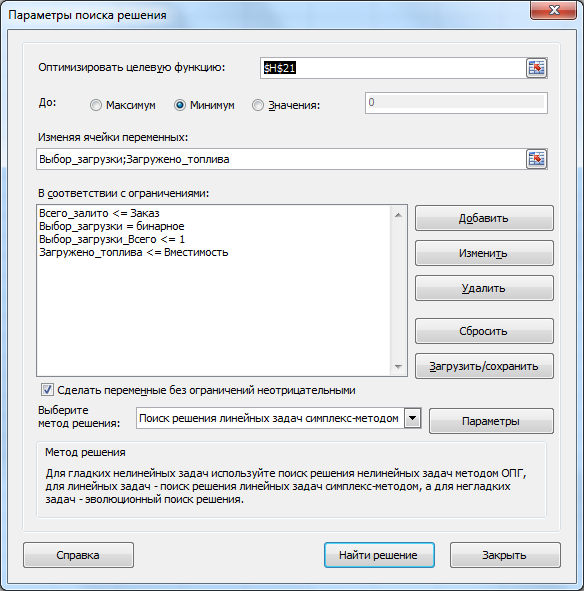
Переменные (выделено зеленым) . В качестве переменных модели следует взять загрузку цистерн разными видами топлива. Поиск решения подбирает как сам вид топлива, который нужно перевозить, так и его объем. Ограничения (выделено синим) . Объем перевозимого топлива не должен превышать объем цистерн, а также как можно ближе к требованиям заказа. Целевая функция (выделено красным) . Сумма штрафа должна быть минимальна.
Примечание : для удобства настройки Поиска решения используются именованные диапазоны .
Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь .
Источник
Задача о рюкзаке в Excel
В общем виде задача о рюкзаке формулируется следующим способом: имеется рюкзак определенного объема и неограниченное количество предметов. Для каждого предмета известен его объем (вес) и ценность (стоимость, эффективность). В рюкзак можно положить целое число предметов различного типа. Цель состоит в том, чтобы суммарная ценность всех находящихся в рюкзаке предметов была максимальна, а их объем (вес) не превышал заданной величины. К подобной формулировке может быть сведена задача максимального использования грузоподъемности подвижного состава, грузовместимости судна, автомобиля и т.п. Такая задача часто возникает при выборе оптимального управления в экономико-финансовых областях (например распределение бюджета отдела по проектам).
Решение задачи в классической постановке
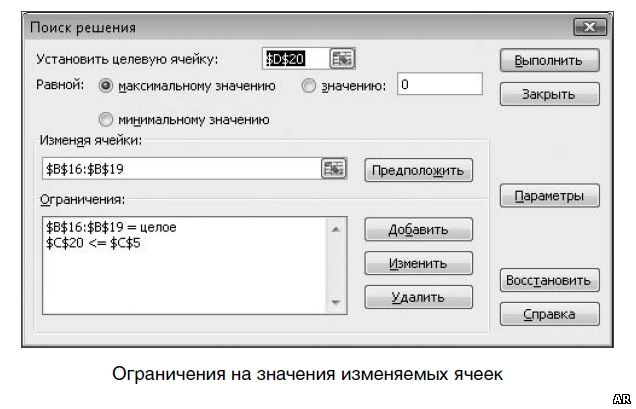
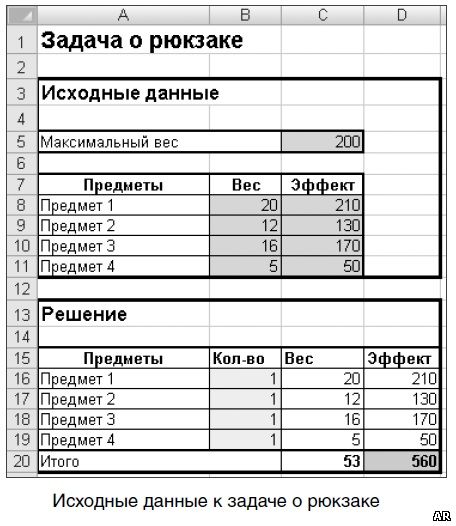
Подобные задачи легко решаются с помощью надстройки «Поиск решения». Подготовлены исходные данные (рисунок ниже). Задача состоит в том, чтобы за счет подбора значений ячеек B16:B19 добиться максимального значения целевой функции (значение ячейки D20).
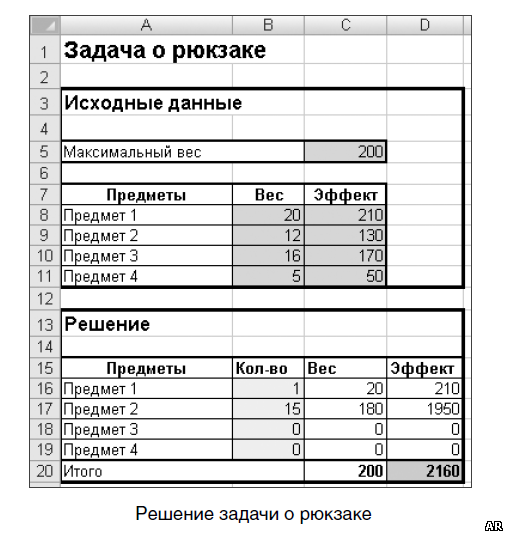
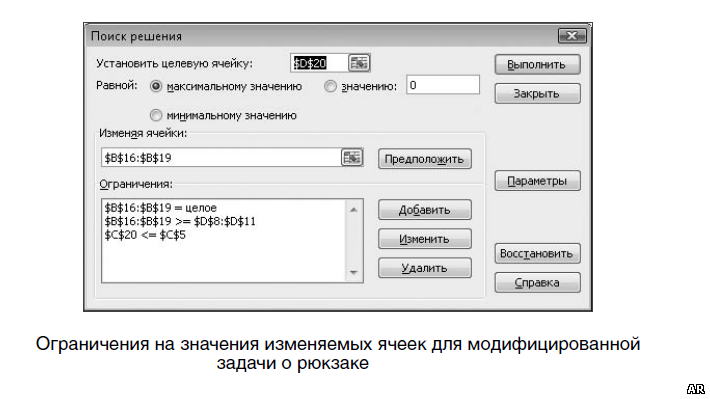
На первом рисунке ниже показаны ограничения на значения изменяемых ячеек. На втором рисунке ниже приводится результат расчета. Во многих практических случаях данная постановка задачи является слишком упрощенной. Далее будут рассмотрены варианты усложнения постановки задачи.
Модифицированная задача
Одним из дополнительных ограничений, возникающих при практическом использовании данной задачи, могут быть ограничения на необходимое количество предметов определенных видов, которые можно положить в рюкзак. При этом могут возникать варианты задачи, когда требуется строго определенное количество предметов или требуется не менее (не более) заданного количества предметов.
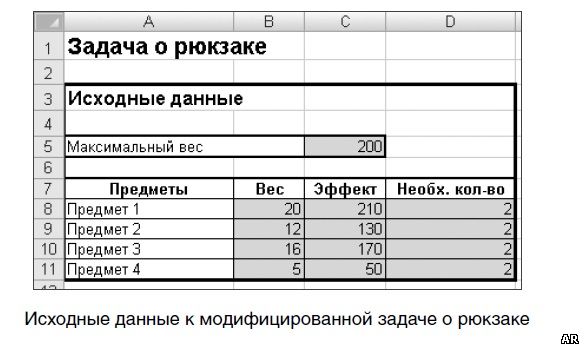
На рисунке ниже показаны исходные данные модифицированного варианта задачи. В этом случае предполагается, что в рюкзак может быть положено не менее некоторого количества предметов.
На следующем рисунке показаны ограничения на значения изменяемых ячеек B16:B19. В данном случае к ограничениям добавлено условие 16:19>=8:11, то есть задано минимальное необходимое количество предметов различных видов.
Решение задачи представлено последнем рисунке.
При необходимости дополнительное условие 16:19>=8:11 может быть изменено. Например, можно установить отдельные ограничения для всех предметов, назначив для некоторых из них точное количество предметов, в то время как для других — условие «не менее» или «не более»
Источник
Задача рюкзака решение excel
= Мир MS Excel/Задача о рюкзаке — Мир MS Excel
Войти через uID
Войти через uID
Модератор форума: _Boroda_, китин
Мир MS Excel » Вопросы и решения » Готовые решения » Задача о рюкзаке (Excel)
Задача о рюкзаке
| MCH | Дата: Среда, 12.08.2015, 20:40 | Сообщение № 1 |
|
В продолжении темы «Подбор слагаемых под нужную сумму» (сумма подмножеств) Во вложении два алгоритма: В основе решения динамическое программирование, отсюда ограничения — работа с целыми числами, и существенное увеличение времени решения и количество выделяемой памяти от размеров рюкзака. UPD 13/08/2015 В продолжении темы «Подбор слагаемых под нужную сумму» (сумма подмножеств) Во вложении два алгоритма: В основе решения динамическое программирование, отсюда ограничения — работа с целыми числами, и существенное увеличение времени решения и количество выделяемой памяти от размеров рюкзака. UPD 13/08/2015 Сообщение В продолжении темы «Подбор слагаемых под нужную сумму» (сумма подмножеств) Во вложении два алгоритма: В основе решения динамическое программирование, отсюда ограничения — работа с целыми числами, и существенное увеличение времени решения и количество выделяемой памяти от размеров рюкзака. UPD 13/08/2015 Источник Лабораторная работа 3. Решение задачи о рюкзаке приближенными и точными алгоритмами.Задача о рюкзаке и ее варианты широко используются для моделирования большого числа практических задач управления, таких как выбор проектов, распределение капитала, комбинаторные аукционы, расположение предметов в системах сборки по заказу и др. [3, 6, 7]. Одним из частных случаев задачи о рюкзаке является одномерная булева задача о рюкзаке, которая может быть сформулирована следующим образом. Рассмотрим рюкзак с объемом равным b. Пусть существует n различных предметов. Предмет j занимает объем aj, при этом его ценность равна cj. Цель задачи состоит в максимизации выгоды от помещенных в рюкзак предметов. Таким образом, задача может быть сформулирована как задача булева линейного программирования в следующем виде:
Если условие Для решения задачи о рюкзаке разработан целый ряд алгоритмов и методов: динамическое программирование [6], метод ветвей и границ [3], метод перебора L-классов [2] и другие. В случае небольших n одномерная задача о рюкзаке может быть также решена в табличном процессоре MS Excel. При этом исходные данные задачи записываются также, как и для задачи ЛП, но в окне Поиск решения, Ограничения необходимо указать, что переменные являются целыми, либо булевыми (рис. 10).
Рис. 10. Диалоговое окно Поиск решения для задачи о рюкзаке. При больших n точное решение задачи может потребовать значительных затрат машинного времени. Поэтому актуальной является разработка приближенных алгоритмов. Самый известный приближенный алгоритм – это так называемый “жадный” алгоритм. Опишем этот алгоритм по шагам для булевого случая. «Жадный» алгоритм.т.е. так, чтобы выполнялось соотношение
положить k:=1 и перейти на шаг 2. Увеличить k на единицу и перейти на шаг 3. Шаг 3. Если k > n, то алгоритм завершает работу, иначе перейти на шаг 2. Варианты заданий. Решить задачу о рюкзаке в пакете MS Excel. Разработать алгоритм полного перебора и «жадный» алгоритм для задачи о рюкзаке [8]. Найти точное и приближенное решение задачи о рюкзаке, используя реализованные алгоритмы. Источник Adblock |
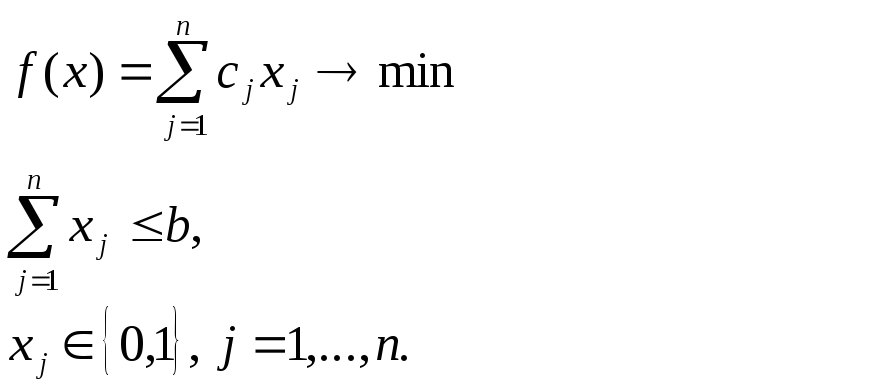
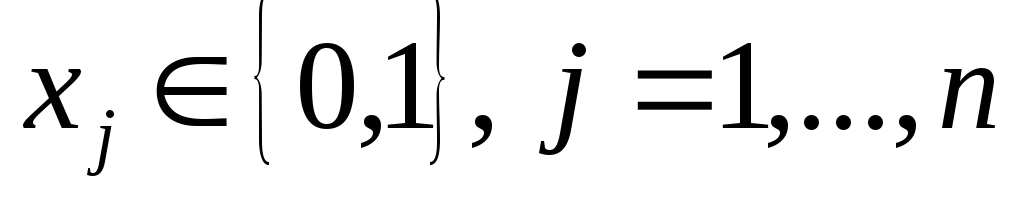заменить условием
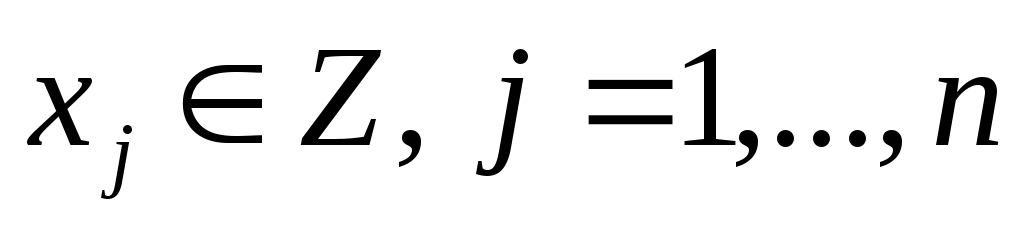, то получим задачу об одномерном целочисленном рюкзаке. В этом случае имеетсяn типов предметов и требуется определить, сколько предметов каждого типа нужно поместить в рюкзак, чтобы они имели максимальную суммарную ценность.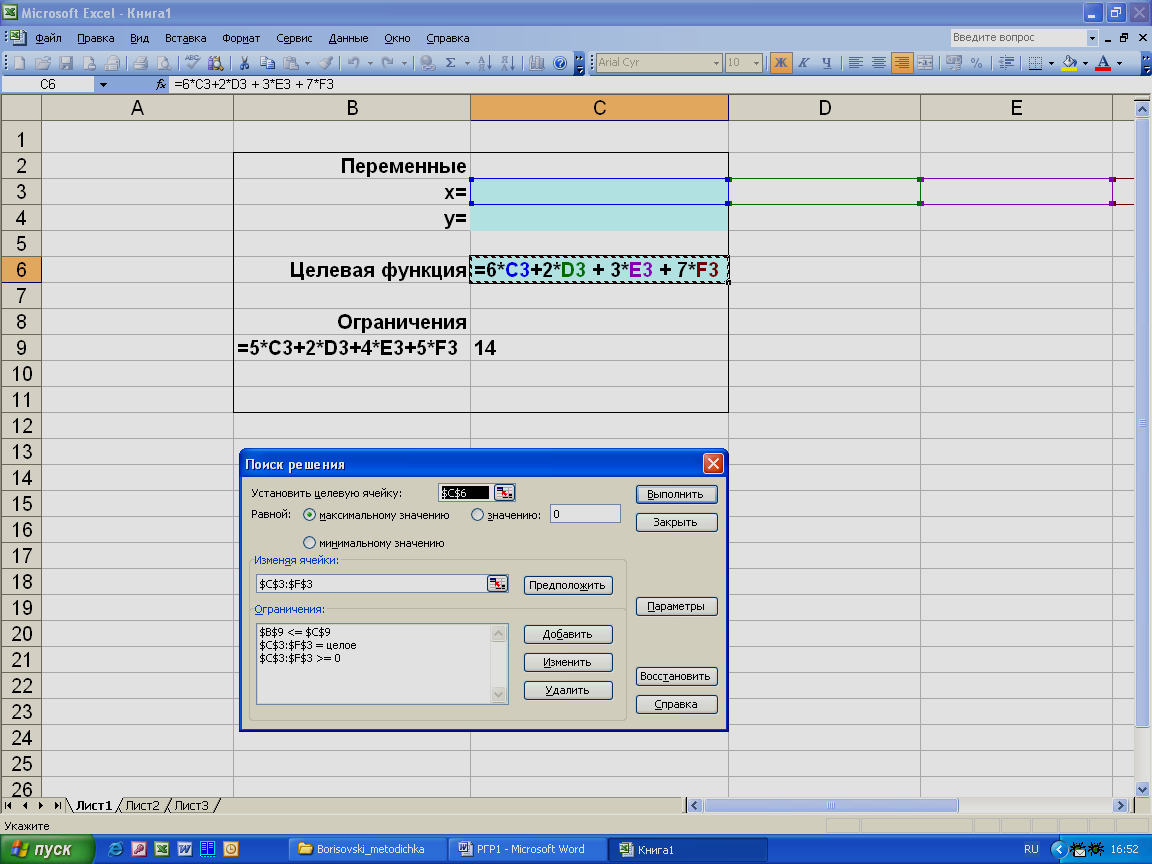
,
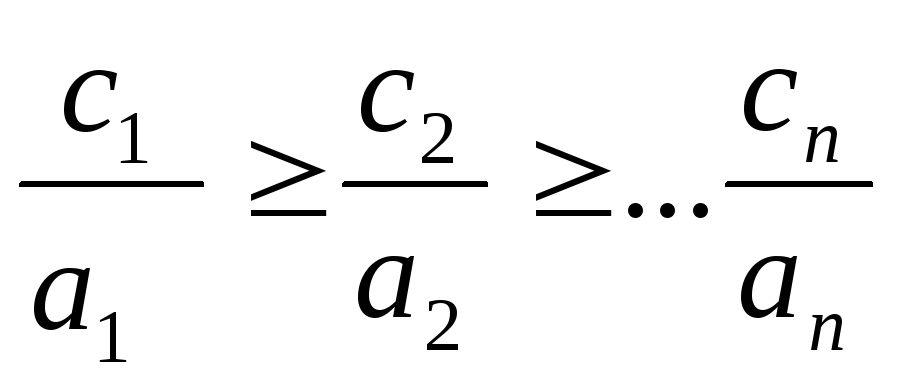