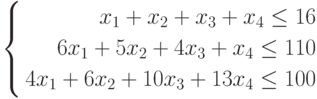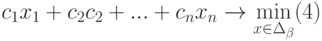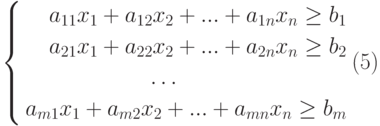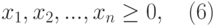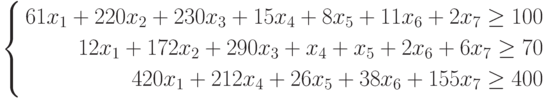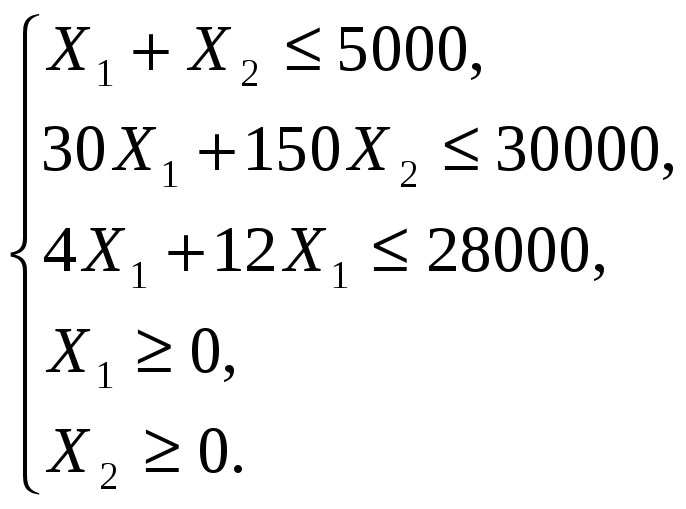Решение задачи об оптимальном плане в excel

во втором поле выбрать оператор ограничения (>, Поиск решения).

Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:

1. В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
2. В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.

С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.

Каждый отчет создается на отдельном листе текущей рабочей книги.

Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша ).

• Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
• Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
• Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.

Рассмотрим применение процессора Excel для решения ЗЛП на примерах.

Задача 1. Планирование производства

Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.

МП выпускает товары х₁,х₂,х₃,х₄, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.

Затраты	х1	х2	x3	х4	Всего
Трудовые	1	1	1	1	16
Сырьевые	6	5	4	1	110
Финансы	4	6	10	13	100

1. Максимум прибыли в зависимости от оптимального распределения затрат.
2. Минимум ресурсов, необходимых для получения максимальной прибыли.

Решение задачи средствами Excel состоит из 4 этапов:

1. Создание математической модели задачи ЛП.
2. Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
3. Ввод данных из формы в окно Excel Поиск решения из меню Данные.
4. Задание параметров поиска и решение задачи.

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

— целевая функция прибыли.

— граничные условия модели, так как количество производимых товаров не может быть отрицательной величиной.

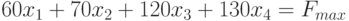
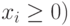
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.

Создание формы

• Составление формы в виде:

A	B	C	D	E	F	G	H
1	Переменная	х7	х2	x3	х4	Формула	Знак	Св.член
2	Значение
3	Коэф. ЦФ	60	70	120	130	=СУММПРОИЗВ(В$2:Е$2;В3:Е3)	Max
4	Трудовые	1	1	1	1	=СУММПРОИЗВ(В$2:Е$2;В4:Е4)		16
5	Сырьевые	6	5	4	1	=СУММПРОИЗВ(В$2:Е$2;В5:Е5)		110
6	Финансы	4	6	10	13	=СУММПРОИЗВ(В$2:Е$2;В6:Е6)		100

• Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
• Ввод формул с помощью f_x – Мастера функций.

Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3 , затем по значку Мастера функций f_x на панели инструментов, в появившемся окне «Мастер функций, Шаг 1» выбрать категорию «Математические», далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне «Мастер функций Шаг 2» в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х₁..х₄), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).

Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.

Нажать клавишу ОК, в ячейку F3 запишется формула 60х₁+70х₂+120х₃+ 130х₄ в виде СУММПРОИЗВ(В2:Е2;В3:Е3).

Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2 , установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4 , затем повторить эти действия для адреса E2 . Формула примет следующий вид:

После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3 , содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.

В результате копирования мы увидим следующие формулы:

• в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
• в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
• в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).

Заполнение окна Поиск решения

Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение «Максимальному значению» (см. рис. 12.1 рис. 12.1). В поле «Изменяя ячейки» ввести $В$2:$Е$2(с клавиатуры или протащив мышью).

Нажать клавишу «Добавить», в окне «Добавление ограничения» в поле «Ссылка на ячейку» ввести F4 , выбрать через «стрелка вниз» знак ««, в поле справа ввести Н4 (рис. 12. рис. 12.2).

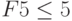
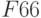
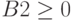
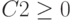
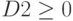
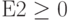
Аналогично через «Добавить» ввести , для системы ограничений (2), а также , , и .

Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.

После ввода последнего граничного условия вместо «Добавить» нажать клавишу ОК, появится окно «Поиск решения».

Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.

Параметры поиска

В окне «Поиск решения» нажать клавишу «Параметры», выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке «Линейная модель», нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).

Результаты поиска решения с таблицей результатов:

A	B	C	D	E	F	G	H
1	Переменная	X1	X2	X3	X4	Формула	Знак	Св.член
2	Значение	10	0	6	0
3	Коэф. ЦФ	60	70	120	130	1320	Max
4	Трудовые	1	1	1	1	16		16
5	Сырьевые	6	5	4	1	84		110
6	Финансы	4	6	10	13	100		100

Таким образом оптимальный план Х(Х₁,Х₂,Х₃,Х₄)=(10,0,6,0) при минимальном использовании ресурсов

• Трудовые – 16 (У₁)
• Сырьевые – 84 (У₂)
• Финансы – 100 (У₃)

даёт максимум прибыли F в 1320 руб.

_Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х₁ и Х₃ в количестве 10 и 6 штук соответственно, товары Х₃ и Х₄ выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У₁) и финансовые (У₃) ресурсы используются полностью, по сырьевым ресурсам (У₂) есть запас в 110-84=26 ед.

Кроме того, это означает, что изменение трудовых ( y₁ ) и финансовых ( y₃ ) ресурсов приведёт к изменению прибыли F , а изменение сырьевых ресурсов ( y₂ ) – нет.

Разности между плановыми ресурсами и использованными являются двойственными переменными y₁, y₂ и y₃ сопряжённой задачи линейного программирования. В данном случае y₁=y₃=0 , а y₂=26 ед. Таким образом, ресурс y₂ можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.

Задача 2. Задача об оптимальной диете

Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа содержится а_i единиц питательного вещества j-го вида . Известна минимальная суточная потребность b _j (j in <1,2. т>) человека в каждом из видов питательных веществ. Задана калорийность с_i одной весовой единицы i-го продукта ( i принадлежит <1, 2, . n>).

Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.

Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:

где множество допустимых альтернатив 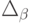формируется следующей системой ограничений типа неравенств:

Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.

Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3).

Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂= 70, в углеводах b3 = 400.

Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	61	220	230	15	8	11	6
Жиры	12	172	290	1	1	2	2
Углеводы	420	0	0	212	26	38	155

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

– целевая функция (суммарная калорийность продуктов).

– граничные условия

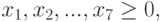
Создание формы

Для решения поставленной задачи выполним следующие подготовительные действия:

1. Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4 .
2. В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с₁ = 2060, с₂ = 2430, с₃ = 3600, с₄ = 890, с₅ = 140, с₆ = 230, с₇ = 650.
3. В ячейку I2 введем формулу: =СУММПРОИЗВ( b ₂:Н2;B3:H3), которая представляет целевую функцию (4).
4. В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.

1. В ячейки J5 :J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b ₁=100 , жирах b ₂= 70 и углеводах b3 = 400.
2. В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
3. Скопируем формулу, введенную в ячейку I5 , в ячейки I6 и I7 .
4. Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).

Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.

Заполнение окна Поиск решения

Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения.

После появления диалогового окна Поиск решения следует выполнить следующие действия:

1. В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2 .
2. Для группы Равной: выбрать вариант поиска решения – минимальному значению.
3. В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2 .
4. Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
   • для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
   • в появившемся дополнительном окне выбрать ячейку $I$5 , которая должна отобразиться в поле с именем Ссылка на ячейку;
   • в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство » «;
   • в качестве значения правой части ограничения выбрать ячейку $J$5 ;
   • для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
   • аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).

Параметры

В окне «Поиск решения» нажать клавишу «Параметры», выбрать «Поиск решения Линейных задач симплекс-методом», нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).

После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.

Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х₁ = 0, х₂ = 0,211, 3 = 0,109, х₄= 1,887, х₅ = 0, х₆ = 0, х₇ = 0, которым соответствует значение целевой функции: f_опт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.

Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.

ЗАДАНИЕ

1. Составить математическую модель задачи линейного программирования.
2. Решить задачу линейного программирования в Excel с помощью Поиска решения.
3. Сохранить в виде модели установочные параметры.

Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Фирма производит два вида продукции – А и B . Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.

Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.

Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:

• не менее 0.8%, но не более 1.2% кальция;
• не менее 22% белка;
• не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.

Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа содержится а_i единиц питательного вещества j-го вида . Известна минимальная суточная потребность b _j человека в каждом из видов питательных веществ. Задана калорийность сi одной весовой единицы i-го продукта ( i принадлежит <1, 2, . n >). Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

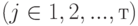
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	66	225	235	20	13	16	11
Жиры	17	177	295	1	1	7	7
Углеводы	425	0	0	217	31	43	200

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 105, в жирах b ₂ = 75, в углеводах b ₃ = 405.

Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.

Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Фирма производит два вида продукции – A и B . Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.

Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.

Таблица 1. Расход химических веществ на изготовления клея, их запас на складе

Вид клея /Химические вещества	Клей № 1	Клей № 2	Клей № 3	Запас на складе
Крахмал	0,4	0,3	0,2	20
Желатин	0,2	0,3	0,4	35
Квасцы	0,05	0,07	0,1	7
Мел	0,01	0,05	0,15	10

Стоимость каждого вида клея для оптовых покупателей следующая:с₁ = 380 руб/кг,с₂ =430 руб/кг,с₃ = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.

Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:

• не менее 0.8%, но не более 1.2% кальция;
• не менее 22% белка;
• не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.

Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб «Бородинский», картофель ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность 1 кг каждого из продуктов следующая:с₁ = 470,с₂= 380,с₃ = 350,с₄ = 1460,с₅ = 2150,с₆ = 2070, с₇ = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂ = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).

Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Поиск решения задач в Excel с примерами

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

1.
Организуйте данные на листе MS Excel так,
как это показано на рисунке 1.

a) В ячейку G9 введена
целевая функция,
представляющая собой прибыль от продажиx₁десятков свитеров иx₂десятков кофточек.

b) В ячейки G6,G7,G8 — формулы, отражающие
расход сырья при изготовленииx₁десятков свитеров иx₂десятков
кофточек.

Рисунок 1 –
Организация данных на листе MS Excel для
примера «Оптимальный план производства
трикотажной фабрики»

2.
Выберите вкладку «Данные» 
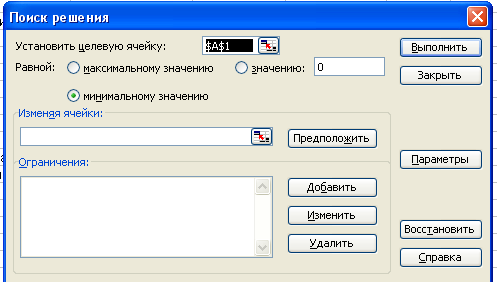
«Поиск решения». Появится окно,
озаглавленное«Поиск решения» (рисунок
2).

а) В поле окна «Установить целевую
ячейку»отметьте ячейкуG9
(щелкните сначала по полю окна, а затем
по ячейкеG9);

b) Установите переключатель на отметке
«Равной максимальному значению»;

c) В поле окна «Изменяя ячейки»отметьте ячейки В12:С12.

Рисунок 2 –
Общий вид и работа с окном «Поиск решения»

Добавьте
ограничения, щелкая по кнопке «Добавить».
В появившемся окне, озаглавленном«Добавление ограничения»(рисунок
3), щелкните по полю «Ссылка на ячейку»,
а затем отметьте ячейки В12:С12, выберите
знак ограничения, щелкните по правому
полю «Ограничение» и введите в него
значение 0. Таким образом, вы ввели
ограничение.
Вновь щелкните по кнопке«Добавить».

.

Рисунок 3 –
Общий вид и работа с окном «Добавление
ограничения»

e) В появившемся окне «Добавление
ограничения»щелкните в поле«Ссылка
на ячейку», а затем отметьте ячейкуG6, выберите знак ограничения
(≤), щелкните по правому полю«Ограничение»и отметьте в нем ячейкуD6,
содержащую ограничение на ресурс«ДСП».
Таким образом, вы ввели ограничение;

f) Продолжайте процесс, пока не введете
остальные два ограничения.

3.
Щелкните по кнопке «Параметры».
Появится окно«Параметры поиска
решения»(рисунок 4), в котором можно
(но не нужно) менять многочисленные
параметры оптимизации. Вас интересует
только, установлен ли флажок«Линейная
модель». Если нет, установите его,
щелкните по кнопкеOkи вернитесь к
окну«Поиск решения».

Рисунок 4 –
«Параметры поиска решения» в MSExcel

Установка
параметров оптимизации в окне «Поиск
решения» должна выглядеть так, как
показано на рисунке 5.

Рисунок 5 – Ввод
данных для примера «Оптимальный план
выпуска продукции мебельного цеха» в
окно «Поиск решения»

Замечание

а) Первое ограничение ()
можно не добавлять в список ограничений
в окне«Поиск решения», вместо этого
можно поставить флажок«Неотрицательные
значения»в окне«Параметры поиска
решения»;

b) Если ограничения имеют
один и тот же знак и расположены на листеMSExcelв
смежных ячейках (и если запасы ресурсов
также расположены в смежных ячейках),
то в окне«Добавление ограничения»в полях«Ссылка на ячейку» и«Ограничение» можно указывать не
отдельные ячейки, а диапазоны ячеек
(рисунок 6).

Рисунок 6 –
Пример ввода ограничений в окно
«Добавление ограничения»

4. Щелкните по
кнопке «Выполнить». Оптимизационная
программа MS Excel выполнит поиск решения,
после чего появится окно«Результаты
поиска решения»(рисунок 7). Прочтите
сообщение программы в этом окне. Если
вы все сделали правильно, программа
сообщит:«Решение найдено. Все
ограничения и условия оптимальности
выполнены».

Рисунок 7 – Вид
окна «Результаты поиска решения»

Вид
листа MS Excel, соответствующий оптимальному
решению, показан на рисунке 8.

Рисунок 8 – Вид
листа MS Excel, соответствующий оптимальному
решению

В этом случае
убедитесь, что переключатель в окне
«Результаты поиска решения»находится
в положении«Сохранить найденное
решение», щелкните по кнопкеOkи
прочтите ответ в ячейках В12:С12. В ячейкахG6:G8 содержатся
значения ресурсов, которые необходимы
для полученного оптимального плана. В
случае, если вы неверно задали знак
ограничений, ввели неверные формулы
для целевой функции или для ограничений
и оптимизационная программа не может
найти решения, в окне появятся сообщения«Значения целевой ячейки не сходятся»
или«Поиск не может найти решения»,
или«Условия линейной модели не
выполняются». В этом случае следует
переставить переключатель в окне«Результаты поиска решения» в
положение«Восстановить исходные
данные», щелкнуть по кнопкеOkи
проверить организацию данных на листе
Excel и в установках окна«Поиск решения».

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Урок
№___

Тема: Практическая
работа №18

«Решение задач оптимального
планирования в Microsoft Excel»

Тип урока: практическая работа

Цели:

·       
Получение представления о построении оптимального плана методом
линейного программирования;

·       
Практическое освоение раздела Microsoft
Excel «Поиск
решения» для построения оптимального плана;

·       
Формирование навыка по работе в MS Excel;

·       
Развитие системного мышления, позволяющего выделять
в окружающей действительности системы, элементы систем, адекватные поставленной
задаче;

·       
Формирование профессиональных навыков работы.

Оборудование:

·       
ПК;

·       
Интерактивная доска;

·       
MS Excel

Ход
урока:

I. Организационный момент (5 мин.)

Приветствие.
Сообщение темы.

II. Актуализация
знаний (5 мин.)

Проверка
домашнего задания.

III. Практическая
работа (30 мин.)

Практическая работа

Справочная информация

Средство,
которое используется в данной работе, называется Поиск решения.
Соответствующая команда находится в меню Сервис. Поиск решения —
одно из самых мощных средств табличного процессора Excel.
Покажем на простейшем примере («пирожки и пирожные», см. учебник, § 39), как
воспользоваться указанным средством.

Задание 1

Реализовать
поиск оптимального решения для задачи планирования работы школьного
кондитерского цеха, описанной в § 39 учебника.

1. Подготовить таблицу к решению задачи
оптимального планирования.

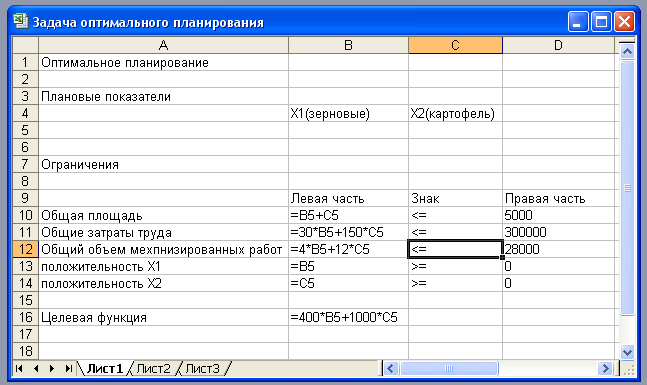
В
режиме отображения формул таблица показана на рисунке. Ячейки В5 и С5
зарезервированы соответственно для значений х (план по
изготовлению пирожков) и у (план по изготовлению
пирожных). Ниже представлена система неравенств, определяющая ограничения на
искомые решения. Неравенства разделены на левую часть (столбец В) и правую
часть (столбец D).
Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая
функция занесена в ячейку В15.

	А	В	С	D
1	Оптимальное планирование
2
3	Плановые показатели
4		X (пирожки)	У (пирожные)
5
6
7	Ограничения
8
9		Левая часть	Знак	Правая часть
10	Время производства:	1000	<=	1000
11	Общее количество:	700	<=	700
12	Положительность X:	600	>=	0
13	Положительность Y:	100	>=	0
14
15	Целевая функция	=B5+2*C5

2.
Вызвать программу оптимизации и сообщить ей, где расположены данные. Для этого
выполнить следующие действия:

1.    
Перейти на вкладку Данные

2.    
В группе Анализ щелкнуть на
кнопку Поиск решений

На
экране откроется соответствующая форма:

3.
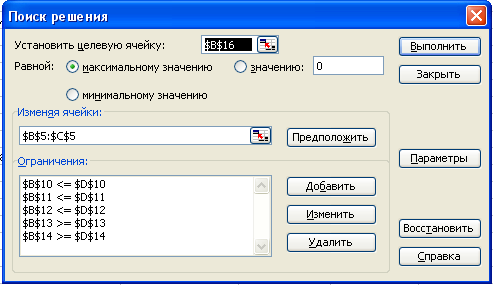
Выполнить следующий алгоритм:

1.     ввести
адрес ячейки с целевой функцией. В нашем случае это $В$15 (заметим, что если
перед этим установить указатель мыши на ячейку В15, то ввод произойдет
автоматически);

2.     поставить
отметку максимальному значению, т. е. сообщить программе, что нас
интересует нахождение максимума целевой функции;

3.     в
поле Изменяя ячейки ввести $В$5:$С$5, т. е. сообщить, какое место
отведено под значения переменных — плановых показателей;

4.     в
поле Ограничения ввести неравенства-ограничения, которые имеют вид: B10<=D10;
B11<=D11;
B12>=D12;
B13>=D13.
Огра­ничения вводятся следующим образом:

a.      щелкнуть
на кнопке Добавить;

b.     в
появившемся диалоговом окне Добавление ограничения ввести ссылку на
ячейку В10, выбрать из меню знак неравенства <= и ввести ссылку на ячейку D10;

c.      снова
щелкнуть на кнопке Добавить и аналогично ввести второе ограничение B11<=D11
и т. д.

d.     в
конце щелкнуть на кнопке ОК.

5.     закрыть
диалоговое окно Добавление ограничения. Перед нами снова форма Поиск
решения:

6.     указать,
что задача является линейной (это многократно облегчит программе ее решение).
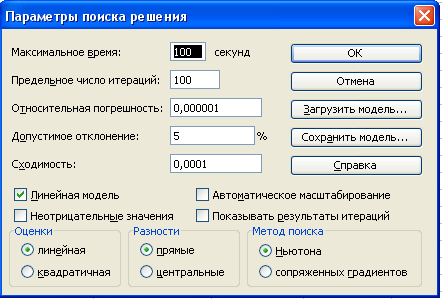
Для этого щелкнуть на кнопке Параметры, после чего открывается форма Параметры
поиска решения:

7.    
установить флажок линейная
модель. Остальная информация на форме Параметры поиска решения чисто
служебная, автоматически устанавливаемые значения нас устраивают, и вникать в
их смысл не будем. Щелкнуть на кнопке ОК. Снова откроется форма Поиск
решения.

8.     щелкнуть
на кнопке Выполнить — в ячейках В5 и С5 появляется оптимальное решение:

Справочная
информация

В
результате применения инструмента Поиск решения, получен следующий
оптимальный план дневного производства кондитерского цеха: нужно выпускать 600
пирожков и 100 пирожных. Эти плановые показатели соответствуют положению точки В на рис.
6.9 в учебнике. В этой точке значение целевой функции f(600,
100) = 800. Если один пирожок стоит 5 руб., то полученная выручка составит 4000
руб.

Задание
2

Требуется
решить задачу поиска оптимального плана производства школьного кондитерского
цеха с измененными условиями.

Представьте
себе, что в школе учатся неисправимые сладкоежки. И, кроме всех прочих
ограничений, перед кондитерским цехом ставится обязательное условие: число
пирожных должны быть не меньше числа пирожков. При такой постановке задачи
система неравенств (см. § 39) примет вид:

1.        
Внести соответствующие изменения в
электронную таблицу, построенную при выполнении предыдущего задания.

2.        
Получить оптимальный план с помощью
средства Поиск решения.

Проанализировать
полученные результаты. Сопоставить их с результатами задания 1.

Задание для самостоятельного выполнения по теме

«Оптимальное
планирование»

Задание

Составить
оптимальный план проведения экскурсионных поездок школьников во время каникул в
следующей ситуации. Областной департамент образования может профинансировать
поездки школьников из пяти районов области (районы будем обозначать номерами) в
три города (назовем эти города X, У и Z).

Количество
учащихся, которых следует отправить в поездки, таково:

Экскурсионное
бюро может в данные каникулы обеспечить поездку следующего количества учащихся
в каждый из трех городов:

Стоимость
поездки (в рублях) приведена в следующей таблице.

Город	Номер района
1	2	3	4	5
X	500	700	750	1000	1100
Y	700	600	400	500	800
Z	1200	1000	800	600	500

Смысл
чисел в таблице таков: если в ячейке Y2
стоит 600, то это значит, что поездка одного учащегося из района 2 в город У
обходится в 600 рублей.

Необходимо составить такой план экскурсий,
который бы:

·       
позволил каждому из намеченных к
поездке учащихся побывать на экскурсии;

·       
удовлетворил условию об общем числе
экскурсантов в каждый из городов;

·       
обеспечил максимально низкие
суммарные расходы финансирующей стороны.

Поскольку
эта задача непроста, поможем вам с ее математической фор­мулировкой.

План
перевозок, который нам надлежит составить, будет отражен в следующей таблице:

Величины,
стоящие в этой таблице, и являются объектами поиска. Так, X₃
есть число учащихся из района № 3, которые
по разрабатываемому плану поедут в город X.

Первое
условие (ограничение задачи) состоит в том, что все учащиеся из каждого района
поедут на экскурсию. Математически оно выражается следующими уравнениями:

                     (1)

Второе
условие — в каждый город поедут столько учащихся, сколько этот город в
состоянии принять:

                          (2)

Кроме
того, искомые величины, разумеется, неотрицательны:

 
           (3)

Теперь
запишем общую стоимость расходов на экскурсии. Поскольку привести, например, на
экскурсию X₁
учащихся в целом стоит X₁*500
рублей (см. таблицу стоимости поездки), то общие
расходы составят:

(4)

Теперь
имеется все для полной математической формулировки задачи: требуется найти
наименьшее значение функции (4) при
условии, что входящие в нее переменные удовлетворяют системам уравнений (1) и
(2)
и неравенств (3).

Это
весьма непростая задача. Однако ее решение (как и задач, существенно более
сложных) вполне «по плечу» программе Excel
с помощью средства Поиск решений, которым вам и надлежит воспользоваться.

Приведем результат решения задачи:

X1	X2	X3	X4	X5	Y1	Y2	Y3	Y4	Y5	Z1	Z2	Z3	Z4	Z5
300	100	0	0	0	0	100	400	0	0	0	50	0	350	200

Итог:
в город X поедут
на экскурсию 300 учащихся из района №1 и 100 учащихся из района № 2, в город У —
100 учащихся из района № 2 и 400 из района № 3, в город Z
— 50 учащихся из района № 2, 350 — из
района № 4 и 200 — из района № 5.

Полученный
результат можно сформулировать следующим образом: все учащиеся из района №1
уедут в город X, учащиеся из района № 2 поделятся между городами X, У и
Z
(соответственно 100, 100 и 5), все
учащиеся из района № 3 уедут в город У, а все учащиеся из районов № 4 и № 5
поедут в город Z.
Такое неочевидное, на первый взгляд,
разделение обеспечивает в данном случае наибольшую экономию средств.

IV. Итог урока (2 мин.) Объявляются оценки.

V.
Домашнее задание (3 мин.) Подготовка к к/р. Подготовка
докладов по § 40-43

Урок № Класс 11 предмет информатика дата 29.04.2021

Тема: Практическая работа     «Решение задачи оптимального планирования».

Цели урока: научить учащихся решать задачи оптимального планирования средствами MS Excel.

1. Образовательная- познакомить учащихся с особым видом экономических задач – задач оптимального планирования, способом их решения в среде MS Excel

2. Развивающая- закрепить навыки работы с формулами в среде электронных таблиц;

3. Воспитательная- воспитывать самостоятельность и ответственность в принятии решения.

Тип урока:

1. Компьютер преподавателя

2. Компьютеры учащихся – 10 шт.

3. Локальная сеть

4. Программное обеспечение: MS PowerPoint, MS Excel

Ход урока

1. Организующее начало урока.

2. Выявление имеющихся знаний и умений.

1.        а)  Что такое корреляционная зависимость?

б)         Что такое корреляционный анализ?

в)         Какие типы задач можно решать с помощью корреляционного анализа?

г)         Какая величина является количественной мерой корреляции? Какие значения она может принимать?

1. С помощью какого средства табличного процессора можно вычислить коэффициент корреляции?

2. а) Для данных из таблицы, представленной на рис. 2.18, постройте две линейные регрессионные модели.

б) Для этих же данных вычислите коэффициент корреляции. Сравните с приведенными на рис. 2.18 результатами.

4. Практическая работа  3.6 «Решение задачи оптимального планированияl»

Цели работы:

•        получение   представления   о   построении   оптимального плана методом линейного программирования;

•        практическое освоение раздела MS Excel «Поиск решения» для построения оптимального плана.

Используемое программное обеспечение: табличный процессор Microsofxt Excel.

Задание1.

Средство, о котором идет речь, называется «Поиск решения». Соответствующая команда находится в меню Сервис. «Поиск решения» — одно из самых мощных средств ТП Excel, и мы не будем даже пытаться освоить все его возможности. Покажем на рассмотренном нами простейшем примере («зерно и картофель»), как воспользоваться указанным средством.

Вначале надо подготовить электронную таблицу к решению задачи оптимального планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки В5 и С5 зарезервированы соответственно для значений х₁ га  (площадь отведенная для посевов зерна ) и х₂ га (площадь отведенная под картофель). Ниже этих ячеек представлена система неравенств (а), определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция (Р) занесена в ячейку В15.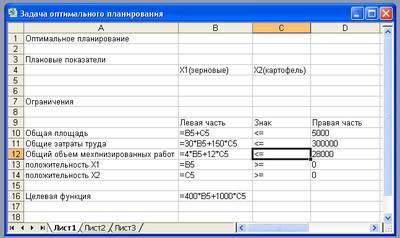

Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей, где расположены данные. Для этого надо выполнить команду = Сервис = Поиск решения. На экране откроется соответствующая форма (рис. 2)

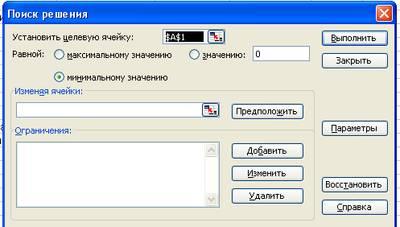
Далее надо выполнить следующий алгоритм:

1. Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически).

2. Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.

3. В поле «Изменяя ячейки» ввести В5:С5, то есть сообщить, какое место отведено под значения переменных -плановых показателей.

4. В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10=D12; B13=D13. Ограничения вводятся следующим образом:

= щелкнуть по кнопке «Добавить»;

в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку В10, выбрать из меню знак неравенства

5.        Закрыть диалоговое окно «Добавление ограничения».
Снова появится форма «Поиск решения» (рис. 3).

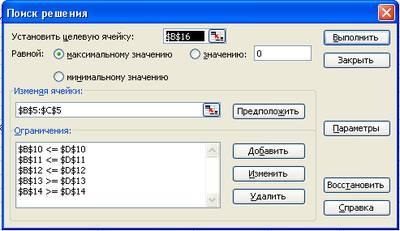
6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры» — появится форма «Параметры поиска решения» (рис. 4).

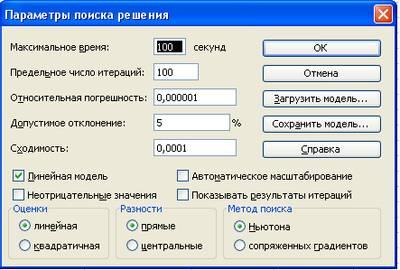
1. Надо выставить флажок на переключателе «Линейная модель» Остальная информация в форме «Параметры поиска решения» служебная, автоматически устанавливаемые значения нас устраивают и вникать в их смысл мы не будем. Следует щелкнуть по кнопке ОК, что возвратит нас в форму «Поиск решения».

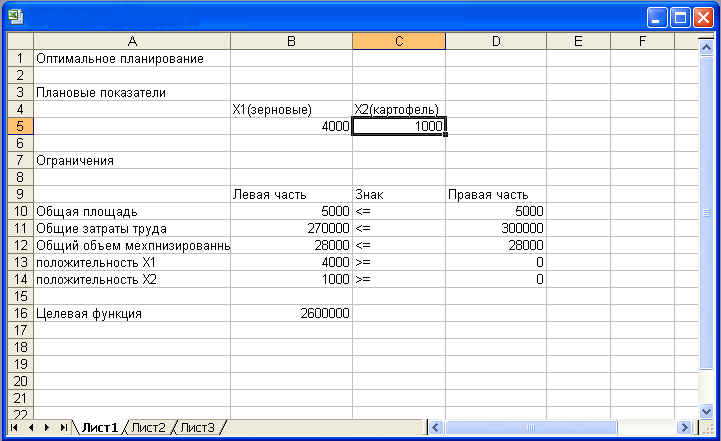
Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение (числа 4000 и 1000), а также число 2600000 в ячейке В16 — максимальное значение целевой функции (рис. 5).

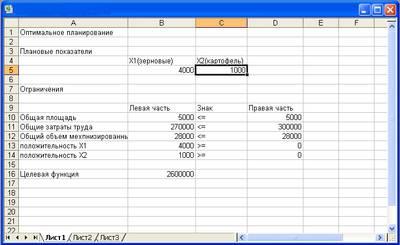
Этап III. Оптимальное сочетание посевных площадей культур: зерновые — 4000 га, картофель—1000 га. Существенно провести экономический анализ оптимального решения задачи.

При х₁=4000 и х₂=1000 х₁ +  х₂=5000, а это значит, что пашня используется полностью.

4 х₁ + 12 х₂≤ 300 000= 4·4000+ 12·1000 = 28 000. Это означает, что ресурсы тракторного парка используются полностью.

30 х₁ + 150 х₂= 30·4000+150·1000 = 270 000. Мы выяснили, что трудовые ресурсы недоиспользованы на 30 000 чел.·ч. Полное использование трудовых ресурсов сдерживается ограниченностью пашни и мощностью тракторного парка. Как видим, для рассмотренного в задаче совхоза ресурсы имеют разную ценность: человеческих рук в избытке, а механизированный труд дефицитен.

5. Закрепление новой темы по вопросам:

1. В чем состоит задача оптимального планирования?

2. Что такое плановые показатели, ресурсы, стратегическая цель? Приведите примеры.

3. Попробуйте сформулировать содержание оптимального планирования своей учебной деятельности.

4. Что такое математическое программирование, линейное программирование?

6.       Д/З   § 20, читать конспект, составить математическую модель для решения 1 задачи

Список используемой литературы:

1. Семакин И.Г  Учебник  Информатика и ИКТ. Базовый уровень 11 класс..  М. Бином 2019г.

2. И.М. Шапиро.  Использование задач с практическим содержанием в преподавании математики. М. Просвещение 1990 г.

«Решение задачи оптимального планирования в MS Excel»

Цели работы:

• получение представления о построении оптимального плана методом

линейного программирования;

• практическое освоение раздела MS Excel «Поиск решения» для построения

оптимального плана.

Средство, о котором идет речь, называется «Поиск решения». Соответствующая

команда находится в меню Сервис. «Поиск решения» — одно из самых мощных

средств ТП Excel, и мы не будем даже пытаться освоить все его возможности.

Покажем на рассмотренном нами простейшем примере («зерно и картофель»), как

воспользоваться указанным средством.

Вначале надо подготовить электронную таблицу к решению задачи оптимального

планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки

В5 и С5 зарезервированы соответственно для значений х

1

га (площадь отведенная для

посевов зерна ) и х

2

га (площадь отведенная под картофель). Ниже этих ячеек

представлена система неравенств (а), определяющая ограничения на искомые

решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец

D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая

функция (Р) занесена в ячейку В15.

Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей,

где расположены данные. Для этого надо выполнить команду => Сервис => Поиск

решения. На экране откроется соответствующая форма (рис. 2)

На этой странице вы найдете примеры решений различных оптимизационных задач с использованием пакета электронных таблиц MS Excel (используется как надстройка Поиск решения, так и ручные вычисления).

Задачи оптимизации и Excel

Задачи оптимизации имеют огромное прикладное значение и возникают в самых разных разделах экономики, техники, военного дела и т.п. В таких задачах нас интересуют поиск некоторого оптимального решения (минимизующего или максимизирующего целевую функцию: прибыль, затраты, калорийность и т.п.) в условиях ограничений (наличия ресурсов, дорог, времени, продуктов и т.п.).

Вот некоторые примеры экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация калорийности и стоимости рациона (как для людей, так и для животных), минимизация расходов на перевозку грузов по маршрутам, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.

Часто эти задачи (даже учебные, даже в случае линейности) содержат более десяти переменных(а в случае, например, транспортных задач, и вовсе десятки), что делает ручные расчеты нерациональными. В то же время привычная для всех программа Excel прекрасно подходит для поиска решения.

Алгоритм решения с помощью надстройки «Поиск решения» следующий:

• составить математическую модель задачи: выделить и обозначить переменные, ограничения на них в виде равенств и неравенств (естественные, например, неотрицательность количества, и дополнительные, например, «запасов железной руды не более 10 т»), целевую функцию (то, что нужно оптимизировать) выразить через переменные.
• выделить место под переменные задачи; внести ограничения (левые части — в виде формул от переменных, правые — в виде констант) в файл электронной таблицы Excel,
• внести в ячейку формулу для целевой функции,
• запустить надстройку Поиск решения,
• установить нужные параметры решения (ограничения в листе, ограничения неотрицательности, условие линейности при необходимости и т.п.) и запустить выполнение.

Excel вычислит оптимальные значения переменных и покажет их в ячейках, а также значение целевой функции. Дополнительно можно построить отчеты для анализа решения задачи.

Некоторые задачи оптимизации решаются не с помощью надстройки Поиск решения, а путем подбора параметра или ручных расчетов. Ниже вы найдете примеры разных задач, а также ссылки на другие разделы со сходными заданиями.

Задачи оптимизации: примеры в Excel

Задача 1. Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля $R_j$. Определена экономическая эффективность $К$ — каждого проекта в зависимости от рентабельности производства. По истечении трех сроков $S_i$ рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д. е.):


Выберите оптимальное решение в соответствии с критериями Лапласа, Вальда, Сэвиджа и Гурвица (при $а = 0,5$).

Задача 2. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода каждого вида сырья на изготовление единицы продукции данного вида в таблице 6. В ней же указаны прибыль от реализации единицы изделия каждого вида и общее количество сырья данного, которое может быть использовано предприятием.
Требуется такой составить такой план производства изделий А и В, при котором прибыль от реализации будет максимальной?

Задача 3. Фирма N, имеющая филиалы (k), производит продукцию. Каждый филиал фирмы выпускает четыре вида продукции из пяти (i=1-5). Данные, характеризующие производство филиалов $b_{ki}$, приведены в табл.1.
Филиалы фирмы закупают сырье, из которого производят продукцию, у семи АО (j =1-7). Выход готового продукта из 1 тонны сырья $a_{ij}$ показан в табл.2.
Прибыль филиалов фирмы при закупке 1тн сырья у разных АО, $С_{kj}$ , показана в табл.3.
В разделе 1 работы требуется:
1.1.Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, ($x_j$), максимизируя прибыль филиала. Далее, студент формулирует экономико-математическую модель общей задачи линейного программирования (ОЗЛП).
1.2.С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции.

Задача 4. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки?
Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5.
Для решения задачи используется ППП Excel.

Задача 5. Менеджер проекта по строительству нового торгового гипермаркета компании Наше дело надеется завершить проект за пару недель до Рождества.
После обзора оценок времени выполнения отдельных стадий выяснилось, что потребуются дополнительные инвестиции, чтобы сократить длительность проекта так, чтобы он действительно завершился вовремя. В таблице приведены оценки длительностей стадий и стоимость их сокращения на 1 и на 2 недели.
a. Нарисуйте сетевую диаграмму проекта и найдите критический путь.
b. Определите минимальную стоимость сокращения проекта на 5 недель.

Полезные ссылки

Методички

• Решение оптимизационных задач в среде MS Excel 2013 Методические указания небольшого объема. Разобраны стандартные задачи: ЛП, транспортная, нелинейная, приведены скриншоты решения и пояснения.
• Решение задач оптимизации в Microsoft Excel 2010 Учебное пособие ТОГУ, 101 страница, более увесистый и подробный документ. Разбирается надстройка Поиск решения, решение задач линейного и нелинейного программирования и СЛАУ.

МБОУ «Учхозская средняя общеобразовательная школа» Краснослободского муниципального района Республики Мордовия

Конспект урока по информатике в 11 классе

«Решение задачи оптимального планирования в MS Excel»

Урок подготовил и провел: учитель информатики и ИКТ Бахарев Юрий Владимирович

п. Преображенский -2013

Цель урока: научить учащихся решать задачи оптимального планирования средствами MS Excel.

Задачи:

1. познакомить учащихся с особым видом экономических задач – задач оптимального планирования, способом их решения в среде MS Excel;

2. закрепить навыки работы с формулами в среде электронных таблиц;

3. развивать умение анализировать и обобщать материал, строить математическую модель задачи;

4. воспитывать самостоятельность и ответственность в принятии решения.

Оборудование:

1. Компьютер преподавателя

2. Компьютеры учащихся – 10 шт.

3. Локальная сеть

4. Программное обеспечение: MS PowerPoint, MS Excel

Продолжительность урока: 40 мин.

Ход урока

1. Организующее начало урока.

2. Выявление имеющихся знаний и умений.

1. а) Что такое корреляционная зависимость?

б) Что такое корреляционный анализ?

в) Какие типы задач можно решать с помощью корреляционного анализа?

г) Какая величина является количественной мерой корреляции? Какие значения она может принимать?

1. С помощью какого средства табличного процессора можно вычислить коэффициент корреляции?

2. а) Для данных из таблицы, представленной на рис. 2.18, постройте две линейные регрессионные модели.

б) Для этих же данных вычислите коэффициент корреляции. Сравните с приведенными на рис. 2.18 результатами.

3. Изучение нового материала.

Решение задачи оптимального планирования в MS Excel.

Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец, государства.

Постановка задачи планирования выглядит следующим образом:

• имеются некоторые плановые показатели: х, у и другие;

имеются некоторые ресурсы: R1, R2 и другие, за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены; имеется определенная стратегическая цель, зависящая от значений х, у и других плановых показателей, на которую следует ориентировать планирование.

Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.

Рассмотрим пример, из которого вы получите представление об одном из подходов к решению задачи оптимального планирования.

Пусть совхоз занимается возделыванием только двух культур — зерновых и картофеля — и располагает следующими ресурсами: пашня — 5000 га, труд — 300 тыс. чел.-ч, возможный объем тракторных работ — 28 000 условных га.

Цель производства—получение максимального объема валовой продукции (в стоимостном выражении).

Найдите оптимальное сочетание посевных площадей культур.

Решение.

Этап I. Для составления математической модели воспользуемся нормативами затрат и выхода продукции для данного совхоза.

Таблица 10

Культуры	Затраты на 1 га посева	Стоимость валовой продукции с 1 га, р.
труда, чел.-ч	тракторных работ, усл. га
Зерновые Картофель	30 150	4 12	400 1000

Критерием оптимальности является максимум стоимости валовой продукции. Этот максимум должен достигаться в условиях использования ограниченных ресурсов пашни, труда и механизированных работ.

Задача является многовариантной, так как имеется множество допустимых вариантов сочетания посевных площадей двух культур, но не все они равнозначны с точки зрения требования оптимальности.

Допустим, что примем решение всю площадь засеять картофелем, который обеспечивает наибольший выход валовой продукции с 1 га. Но для возделывания картофеля на площади 5000 та потребуется 150·5000 = 750 000 Чел.-ч., а мы такими ресурсами не располагаем. Ясно, что такое решение не является приемлемым. Если же засеем всю площадь зерновыми, объем валовой продукции не окажется наибольшим, да и значительная часть трудовых ресурсов не будет использована.

Для поиска оптимального решения задачи обозначим через х₁ -га площадь, отводимую под зерновые, а через х₂ га — площадь, отводимую под картофель. Тогда стоимость зерновых составит 400 х₁ р., а стоимость картофеля — 1000 х₂ р. Отсюда стоимость всей валовой продукции составит ( 400 х₁ + 1000 х₂) р. Обозначим это выражение через у и назовем его целевой функцией:

у = 400 х₁ + 1000 х₂

Нам надо найти максимум этой целевой функции при соблюдении следующих условий:

а) общая площадь зерновых и картофеля не должна превышать 5000 га, т. е. х₁ + х₂≤5000;

б) общие затраты труда не должны превосходить 300 тыс. человеко-часов, т. е. 30 х₁ + 150 х₂≤ 300 000;

в) общий объем механизированных работ не должен превосходить 28 000 усл. га, т. е. 4 х₁ + 12 х₂≤28 000;

г) площади, отводимые под зерновые и картофель, могут принимать только неотрицательные значения: х₁≥0 и х₂ ≥0.

Таким образом, условия задачи выражаются следующей системой неравенств

Требуется найти такие значения х₁ и х₂, при которых целевая функция у = 400 х₁ + 1000 х₂ принимает наибольшее значение.

х₁≥0 и х₂ ≥0xi^O и х2^0.

Этап II. Решим задачу графически.

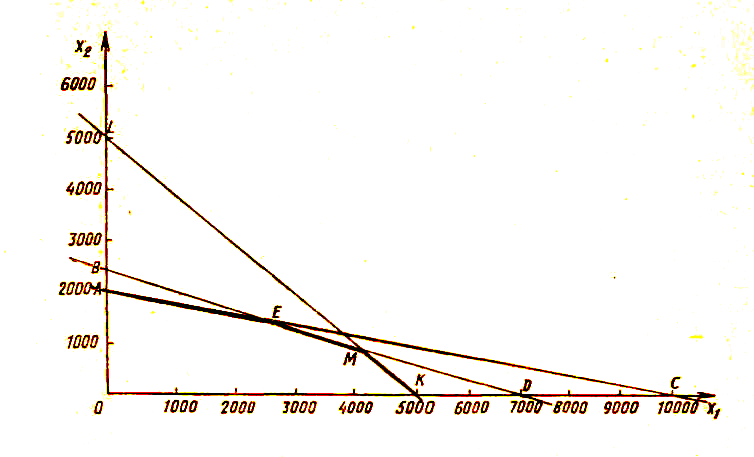
Построим прямую х₁ + х₂=5000. Координаты всех точек треугольника LOK удовлетворяют неравенству х₁ + х₂≤5000.

Построим прямую 30 х₁ + 150 х₂=300 000. Координаты всех точек треугольника АОС удовлетворяют неравенству 30 х₁ + 150 х₂≤ 300 000.

Построим прямую 4 х₁ + 12 х₂=28 000. Координаты всех точек треугольника BOD удовлетворяют неравенству 4 х₁ + 12 х₂≤28 000.

Неравенствам х₁≥0 и х₂ ≥0 удовлетворяют все точки I четверти координатной плоскости х₁0х₂ .

Любая точка многоугольник» АЕМКО удовлетворяет системе неравенств. Для нахождения наибольшего значения целевой функции найдем ее значения в вершинах многоугольника АЕМКО.

Таким образом, наибольшее значение целевой функции достигается в вершине М, что соответствует варианту плана, по которому под зерновые отводится 4000 га, а под картофель — 1000 га.

В связи с тем что введение понятия о линейном программировании в массовой школе не предусмотрено, такая задачу мы можем выполнить используя средство «Поиск решения» которая реализована в MS Ехsel.

1. Практическая работа 19.

«Решение задачи оптимального планирования в MS Excel»

Цели работы:

• получение представления о построении оптимального плана методом линейного программирования;

• практическое освоение раздела MS Excel «Поиск решения» для построения оптимального плана.

Средство, о котором идет речь, называется «Поиск решения». Соответствующая команда находится в меню Сервис. «Поиск решения» — одно из самых мощных средств ТП Excel, и мы не будем даже пытаться освоить все его возможности. Покажем на рассмотренном нами простейшем примере («зерно и картофель»), как воспользоваться указанным средством.

Вначале надо подготовить электронную таблицу к решению задачи оптимального планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки В5 и С5 зарезервированы соответственно для значений х₁ га (площадь отведенная для посевов зерна ) и х₂ га (площадь отведенная под картофель). Ниже этих ячеек представлена система неравенств (а), определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция (Р) занесена в ячейку В15.

Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей, где расположены данные. Для этого надо выполнить команду = Сервис = Поиск решения. На экране откроется соответствующая форма (рис. 2)

Далее надо выполнить следующий алгоритм:

1. Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически).

2. Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.

3. В поле «Изменяя ячейки» ввести В5:С5, то есть сообщить, какое место отведено под значения переменных -плановых показателей.

4. В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10D10; B1K=D11; B12=D12; B13=D13. Ограничения вводятся следующим образом:

= щелкнуть по кнопке «Добавить»;

в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку В10, выбрать из меню знак неравенства D10; снова щелкнуть по кнопке «добавить» и аналогично ввести второе ограничение B11D11 и так далее. В конце надо щелкнуть на кнопке ОК.

5. Закрыть диалоговое окно «Добавление ограничения».
Снова появится форма «Поиск решения» (рис. 3).

6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры» — появится форма «Параметры поиска решения» (рис. 4).

1. Надо выставить флажок на переключателе «Линейная модель» Остальная информация в форме «Параметры поиска решения» служебная, автоматически устанавливаемые значения нас устраивают и вникать в их смысл мы не будем. Следует щелкнуть по кнопке ОК, что возвратит нас в форму «Поиск решения».

Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение (числа 4000 и 1000), а также число 2600000 в ячейке В16 — максимальное значение целевой функции (рис. 5).

Этап III. Оптимальное сочетание посевных площадей культур: зерновые — 4000 га, картофель—1000 га. Существенно провести экономический анализ оптимального решения задачи.

При х₁=4000 и х₂=1000 х₁ + х₂=5000, а это значит, что пашня используется полностью.

4 х₁ + 12 х₂≤ 300 000= 4·4000+ 12·1000 = 28 000. Это означает, что ресурсы тракторного парка используются полностью.

30 х₁ + 150 х₂= 30·4000+150·1000 = 270 000. Мы выяснили, что трудовые ресурсы недоиспользованы на 30 000 чел.·ч. Полное использование трудовых ресурсов сдерживается ограниченностью пашни и мощностью тракторного парка. Как видим, для рассмотренного в задаче совхоза ресурсы имеют разную ценность: человеческих рук в избытке, а механизированный труд дефицитен.

5. Закрепление новой темы по вопросам:

1. В чем состоит задача оптимального планирования?

2. Что такое плановые показатели, ресурсы, стратегическая цель? Приведите примеры.

3. Попробуйте сформулировать содержание оптимального планирования своей учебной деятельности.

4. Что такое математическое программирование, линейное программирование?

6. Д/З § 38, читать конспект, составить математическую модель для решения 1 задачи

Список используемой литературы:

1. Семакин И.Г Учебник Информатика и ИКТ. Базовый уровень 10-11 класс.. М. Бином.

2. И.М. Шапиро. Использование задач с практическим содержанием в преподавании математики. М. Просвещение 1990 г.