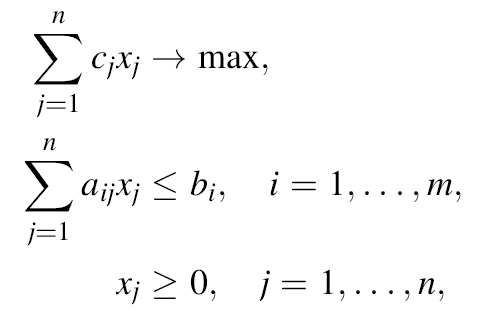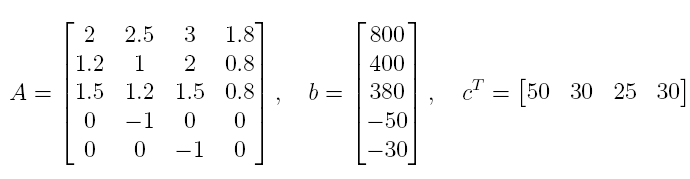Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.
Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.
При решении данной задачи должны быть учтены следующие ограничения:
- общий объем производства – всего 300 изделий;
- должно быть произведено не менее 50 изделий А;
- должно быть произведено не менее 40 изделий В;
- должно быть произведено не более 40 изделий С.
Технология:
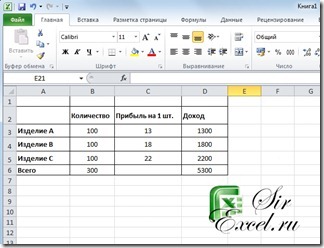
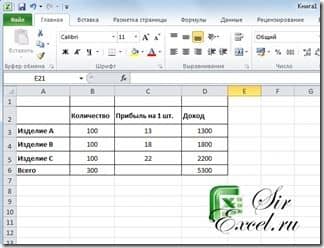
1. Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.
2. Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения)
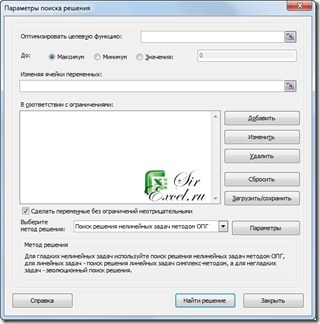
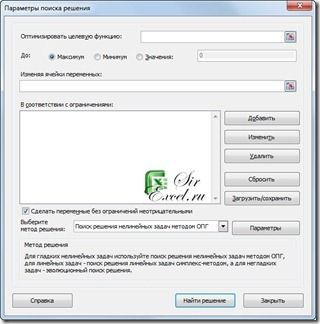
и в окне “Поиск решений” ввести данные:
- в поле «Установить целевую ячейку» указать адрес D6;
- установить флажок «Равной максимальному значению»;
- в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
- в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300; B3>=50; B4>=40; B5<=40). Для этого щелкнуть по кнопке «Добавить» и в появившемся окне «Добавление ограничения» ввести ссылку на ячейку (B6), оператор ограничения (=) и значение (300), для добавления следующего ограничения щелкнуть кнопку «Добавить» и повторить процедуру добавления ограничения; после ввода последнего ограничения щелкнуть кнопку «ОК».
- в диалоговом окне «Поиск решения» щелкнуть кнопку “Выполнить”;
- в диалоге “Результаты поиска решения” установить переключатель «Сохранить найденное решение», в окне «Тип отчета» выбрать «Результаты» и нажать кнопку “Ok”;
В результате с помощью средства Поиск решения будут найдены оптимальные объемы выпуска продукции для максимизации прибыли.
Скачать пример
Очень надеемся, что наша статья помогла Вам. Будем благодарны, если Вы нажмете +1 и/или Мне нравится внизу данной статьи или поделитесь с друзьями с помощью кнопок расположенных ниже.
Спасибо
-
Решение задачи максимизации прибыли
Программа
Excel
имеет достаточный набор инструментальных
средств, для решения задач такого
класса. Рассмотрим задачу линейной
оптимизации на следующем примере.
Пример_1:
Предприятие
выпускает 4 вида продукции: П1, П2, П3, П4.
Для изготовления используется 3 вида
ресурсов: р1, р2, р3, объем которых ограничен.
Известны потребности в ресурсах для
каждого вида продукции, а также прибыль,
получаемая от ее реализации.
Требуется
определить оптимальное количество
выпуска каждого вида продукции, при
котором будет получена максимальная
прибыль для предприятия. Исходные данные
приведены в таблице 1.
Таблица
1
|
Исходные |
Тип |
Значение |
||||
|
Показатель |
Вид |
|||||
|
П1 |
П2 |
П3 |
П4 |
|||
|
Прибыль |
60 |
70 |
120 |
130 |
||
|
Ресурс |
1 |
1 |
1 |
1 |
<= |
16 |
|
Ресурс |
4 |
6 |
10 |
13 |
<= |
100 |
|
Ресурс |
6 |
5 |
4 |
3 |
<= |
110 |
|
Нижняя |
1 |
2 |
2 |
1 |
||
|
Верхняя |
4 |
— |
— |
1 |
Постановка
задачи.
Целью решения данной оптимизационной
задачи является нахождение максимальной
прибыли при оптимальном количестве
выпуска каждого вида продукции (n1,
n2, n3, n4) с учетом существующих ограничений.
Целевая
функция (прибыль):
60*n1+70*n2+120*n3+130*n4max.
-
Подготовка исходных данных
Создайте
на рабочем столе папку под своим именем
и скопируйте в нее файлы Максимизация
прибыли и Транспортная
задача с
жесткого диска, например с диска Е:
из папки
1550ПТ_1550_09.
-
Запустите
программу Microsoft
Excel.
Откройте файл
Максимизация прибыли. -
В
соответствии с данными таблицы 1,
заполните ячейки таблицы:
-
начальные
значения объема производства изделий
вида П1,
П2,
П3,
П4,
равные нулю, введите в
C6:F6,
-
значения
единичной прибыли в ячейки C7:F7. -
нормы
расходов ресурсов (р1 – р3) на каждый
вид продукции в ячейки: C10:С12
для П1, D10:D12
для П2, E10:E12
для П3, F10:F12
для П4.
тип
ограничения в G10:G12,
значения ограничения на ресурсы – в
Н10:Н12.
-
граничные
условия в ячейки C14:F15.
-
В
ячейку Н5
введите целевую функцию:
=C7*C6+D7*D6+E7*E6+F7*F6. -
В
ячейки I10:I12
введите формулы
для подсчета объема потребления каждого
ресурса: р1 — C10*$C$6+D10*$D$6+E10*$E$6+F10*$F$6,
Р2
— C11*$C$6+D11*$D$6+E11*$E$6+F11*$F$6,
Р3
— C12*$C$6+D12*$D$6+E12*$E$6+F12*$F$6.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Видео: Поиск решения. Задача о выборе инвестиций
Чтобы познакомиться с мощным инструментом Excel Поиск решения, рассмотрим и решим с вами задачу.
Необходимо найти оптимальные объемы выпуска трех видов продукции для получения максимальной прибыли от их продажи.
При решении данной задачи должны быть учтены следующие ограничения:
- общий объем производства – всего 300 изделий;
- должно быть произведено не менее 50 изделий А;
- должно быть произведено не менее 40 изделий В;
- должно быть произведено не более 40 изделий С.
- Внести в новый рабочий лист данные для вычисления прибыли от продажи трех видов продукции, причем в ячейки столбца D, и в ячейку B6 должны быть введены формулы.
- Запустить задачу поиска решений. Для этого: выполнить команду в Excel 2003 Сервис | Поиск решений … (В Excel 2007 и 2010 необходимо зайти в раздел Данные | Поиск решения)
и в окне “Поиск решений” ввести данные:
Видео: Урок 1.Поиск решения, оптимизация, оптимальный план производства
- в поле «Установить целевую ячейку» указать адрес D6;
- установить флажок «Равной максимальному значению»;
- в поле «Изменяя ячейки» определить изменяемые ячейки (B3:B5);
- в поле «Ограничения» по одному добавить каждое из следующих четырех ограничений задачи (B6=300- B3>=50- B4>=40- B5<=40). Для этого щелкнуть по кнопке «Добавить» и в появившемся окне «Добавление ограничения» ввести ссылку на ячейку (B6), оператор ограничения (=) и значение (300), для добавления следующего ограничения щелкнуть кнопку «Добавить» и повторить процедуру добавления ограничения- после ввода последнего ограничения щелкнуть кнопку «ОК».
- в диалоговом окне «Поиск решения» щелкнуть кнопку “Выполнить”;
- в диалоге “Результаты поиска решения” установить переключатель «Сохранить найденное решение», в окне «Тип отчета» выбрать «Результаты» и нажать кнопку “Ok”;
В результате с помощью средства Поиск решения будут найдены оптимальные объемы выпуска продукции для максимизации прибыли.
Видео: Поиск решения. Задача о выпуске продукции
Очень надеемся, что наша статья помогла Вам. Будем благодарны, если Вы нажмете +1 и/или Мне нравится внизу данной статьи или поделитесь с друзьями с помощью кнопок расположенных ниже.
Видео: Решение транспортной задачи закрытого типа с помощью Поиска решений
Ранее я писал, что для принятия решений с учетом ограничивающих факторов может использоваться линейное программирование. Напомню, что этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы.
При решении задач линейного программирования, во-первых, необходимо составить модель, то есть сформулировать условия на математическом языке. После этого решение может быть найдено графически (см., например, здесь), с использованием надстройки Excel «Поиск решения» (рассмотрено в настоящей заметке) или с помощью специализированных компьютерных программ (см., например, здесь).
Рассмотрим линейное программирование в Excel на примере задачи, ранее решенной графическим методом.
Задача. Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно. Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд. На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц. Необходимо определить количество единиц продуктов А и В, которые Николай доложен производить в следующем месяце для максимизации маржинальной прибыли.
Скачать заметку в формате Word, пример в формате Excel
1. Воспользуемся математической моделью построенной в упомянутой заметке. Вот эта модель:
Максимизировать: Z = 2500 * х1 + 3500 *х2
При условии, что: 3 * х1 + 10 * х2 ≤ 330
16 * х1 + 4 * х2 ≤ 400
6 * х1 + 6 * х2 ≤ 240
х2 ≥ 12
х1 ≥ 0
2. Создадим экранную форму и введем в нее исходные данные (рис. 1).
Рис. 1. Экранная форма для ввода данных задачи линейного программирования
Обратите внимание на формулу в ячейке С7. Это формула целевой функции. Аналогично, в ячейки С16:С18 введены формулы для расчета левой части ограничений.
3. Проверьте, если у вас установлена надстройка «Поиск решения» (рис. 2), пропустите этот пункт.
Рис. 2. Надстройка Поиск решения установлена; вкладка «Данные», группа «Анализ»
Если надстройки «Поиск решения» вы на ленте Excel не обнаружили, щелкните на кнопку Microsoft Office, а затем Параметры Excel (рис. 3).
Рис. 3. Параметры Excel
Выберите строку Надстройки, а затем в самом низу окна «Управление надстройками Microsoft Excel» выберите «Перейти» (рис. 4).
Рис. 4. Надстройки Excel
В окне «Надстройки» установите флажок «Поиск решения» и нажмите Ok (рис. 5). (Если «Поиск решения» отсутствует в списке поля «Надстройки», чтобы найти надстройку, нажмите кнопку Обзор. В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.)
Рис. 5. Активация надстройки «Поиск решения»
После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения (рис. 2).
4. Следующим этапом заполняем окно Excel «Поиск решения» (рис. 6)
Рис. 6. Заполнение окна «Поиск решения»
В поле «Установить целевую ячейку» выбираем ячейку со значением целевой функции – $C$7. Выбираем, максимизировать или минимизировать целевую функцию. В поле «Изменяя ячейки» выбираем ячейки со значениями искомых переменных $C$4:$D$4 (пока в них нули или пусто). В области «Ограничения» с помощью кнопки «Добавить» размещаем все ограничения нашей модели. Жмем «Выполнить». В появившемся окне «Результат поиска решения» выбираем все три типа отчета (рис. 7) и жмем Ok. Эти отчеты нужны для анализа полученного решения. Подробнее о данных, представленных в отчетах, можно почитать здесь.
Рис. 7. Выбор типов отчета
На основном листе появились значения максимизированной целевой функции – 130 000 руб. и изменяемых параметров х1 = 10 и х2 = 30. Таким образом, для максимизации маржинального дохода Николаю в следующем месяце следует произвести 10 единиц продукта А и 30 единиц продукта В.
Если вместо окна «Результат поиска решения» появилось что-то иное, Excel`ю найти решение не удалось. Проверьте правильность заполнения окна «Поиск решения». И еще одна маленькая хитрость. Попробуйте уменьшить точность поиска решения. Для этого в окне «Поиск решения» щелкните на Параметры (рис. 8.) и увеличьте погрешность вычисления, например, до 0,001. Иногда из-за высокой точности Excel не успевает за 100 итераций найти решение. Подробнее о параметрах поиска решения можно почитать здесь.
Рис. 8. Увеличение погрешности вычислений

Твой путь к знаниям!
- Учеба
- Академии
- Учителя
- Рейтинг
- Вопросы
- Магазин
- Новости
- Помощь
- О проекте
- Курсы
- Школа
- Мини-МБА
- Профессиональная переподготовка
- Повышение квалификации
- Сертификации
-
О курсе- Информация
- Глоссарий
- Дипломы
- Вопросы и ответы
- Студенты
- Рейтинг выпускников
- Мнения
- Курс на youtube
- Учебные программы
-
План занятий- Экзамен экстерном
- Тест 1
- Тест 2
- Тест 3
- Тест 4
- Тест 5
- Тест 6
- Тест 7
- Тест 8
- Контрольная работа 1
- Тест 9
- Тест 10
- Тест 11
- Тест 12
- Тест 13
- Тест 14
- Тест 15
- Тест 16
- Контрольная работа 2
- Экзамен
Курский институт менеджмента, экономики и бизнеса
Опубликован: 05.02.2014 | Доступ: свободный | Студентов: 2660 / 26 | Длительность: 07:51:00
Смотреть на youtube || на ИНТУИТ в качестве: низком | среднем | высоком
© НОУ «ИНТУИТ»,
2003 – 2023
Телефон: +7 (499) 253-9312, WhatsApp, Telegram, Viber: +7 (977) 954-84-50, факс: +7 (499) 253-9310, e-mail: info@intuit.ru, Skype: Intuit.ru
Решим задачу линейного программирования с помощью надстройки Поиск решения.
В этой статье мы отойдем от формулировки практических задач и решим задачу линейного программирования в абстрактных терминах: вектор переменных х, матрица ограничений
A
х
, вектор
b
, целевая функция
cTx
(вместо более привычных: объем производства, количество комплектующих разного вида, максимальный доход). Задача линейного программирования (ЛП) есть задача максимизации линейной функции при линейных ограничениях. Задачу ЛП можно записать несколькими стандартными способами. Мы сформулируем ее в форме
max
{
cTx
:
Ax
<
b
,
x
>0}
Задача
Необходимо максимизировать целевую функцию cTx: max 50*
x1
+ 30*
x2
+ 25*
x3
+ 30*
x4
при условии, что: 2*
x1
+ 2,5*
x2
+ 3*
x3
+ 1,8*
x4
<= 800 1,2*
x1
+
x2
+ 2*
x3
+ 0,8*
x4
<= 400 1,5*
x1
+ 1,2*
x2
+ 1,5*
x3
+ 0,8*
x4
<=380
x2
>= 50
x3
>= 30
x1; x2; x3; x4
>= 0
cTx — это векторное произведение векторов cT (транспонированный вектор с) и х.
Примечание
: эта задача эквивалентна задаче определения оптимальной структуры производства с целью максимизации дохода (см. статью
Поиск решения MS EXCEL (1.1). Оптимальная структура выпускаемой продукции
). Сформулируем эту задачу в общем виде:
Предприятие планирует производить n видов продукции, используя m видов ресурсов. Для производства единицы j-го продукта требуется aij единиц i-го ресурса. Стоимость единицы j-го продукта равна cj. В наличии имеется bi единиц i-го ресурса. Нужно определить план производства с целью максимизировать прибыль.
Обозначив хj — объем выпуска продукции j-го вида (j =1;…;n), мы можем записать задачу поиска оптимального производственного плана следующим образом:
Или в матричной форме:
Получается, что в исходной задаче:
-
вектор
с
(стоимость продукции) равен (50; 30; 25; 30) -
вектор
x
(количество продукции) необходимо найти для заданных условий - n=4 (4 вида продукции)
- m=3 (3 вида ресурсов)
-
вектор
b
(количество ресурсов) равен (800; 400; 380) -
матрица
A
(количество единиц ресурсов для изготовления продукта) равна (2; 2,5; 3; 1,8
:
1,2; 1; 2; 0,8
:
1,5; 1,2; 1,5; 0,8)
Теперь создадим модель.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см.
файл примера
).
Для решения задачи на листе MS EXCEL необходимо записать матрицу
А
, вектора
b
и
cT
(предварительно все неравенства переведены в форму меньше или равно путем умножения соответствующих уравнений на -1):
Примечание
: для удобства настройки
Поиска решения
используются
именованные диапазоны
.
Совет
: Вводная статья про
Поиск решения
в MS EXCEL 2010
находится здесь
.
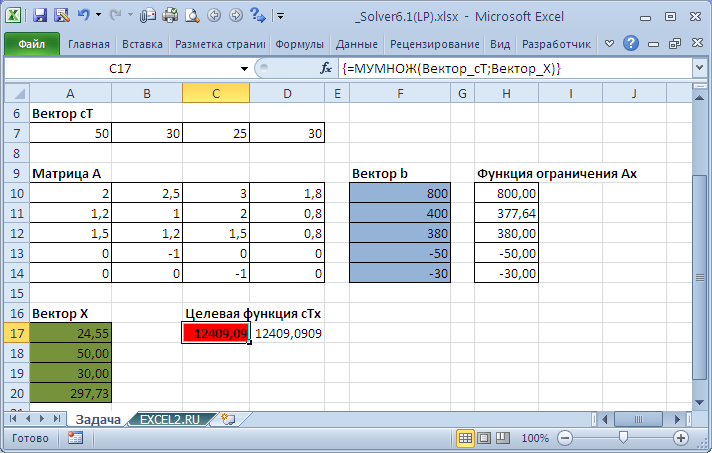
Значение целевой функции
cTx
получено путем матричного умножения векторов
cT
и
x
(используйте функцию
МУМНОЖ()
, которая вводится как
формула массива
). Аналогично получена функция ограничений
Ах
, путем умножения матрицы
А
на
х
. Так как матрица
Ах
имеет размерность 5х1, то перед вводом формулы =
МУМНОЖ(Матрица_А;Вектор_Х)
необходимо выделить столбец из 5 ячеек, затем после записи формулы в
Строке формул
, нажмите
CTRL
+
SHIFT
+
ENTER
для ее ввода.
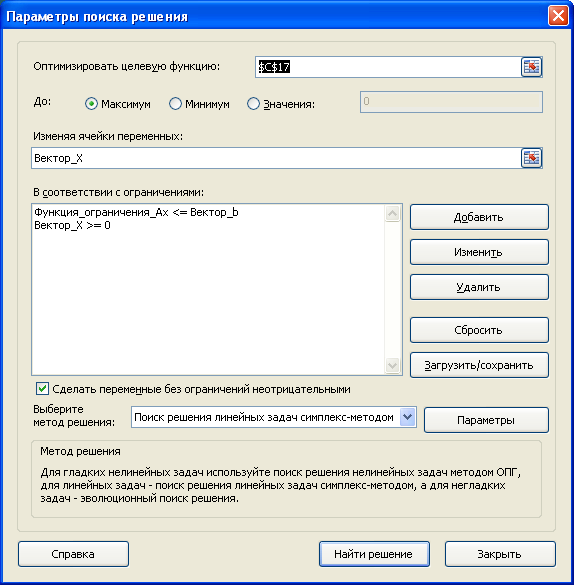
Настроить
Поиск решения
нужно следующим образом: