Решение задач в табличном процессоре ms excel

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

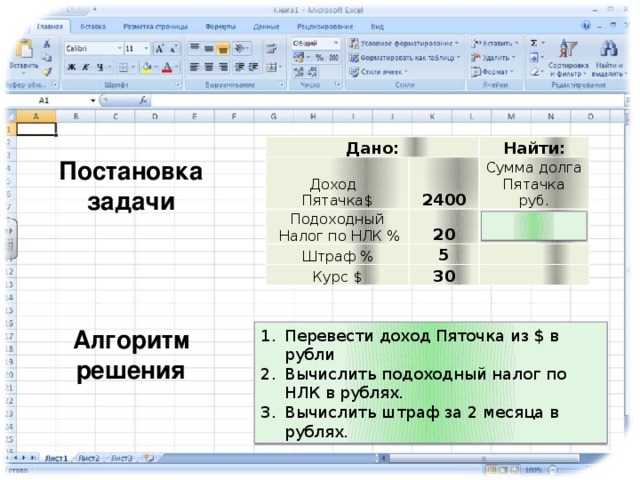
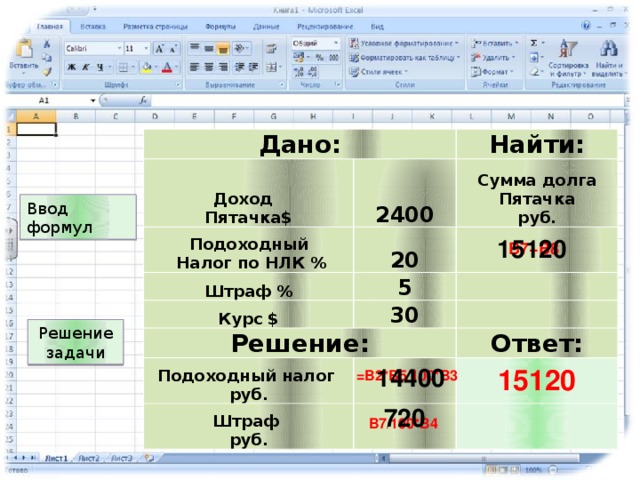
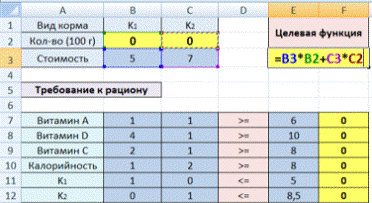
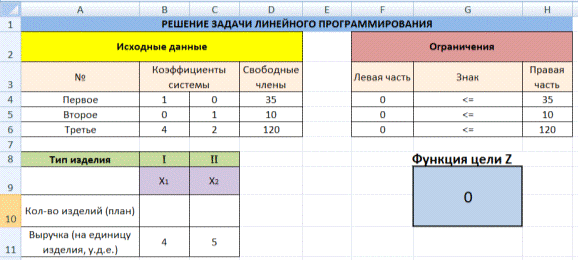
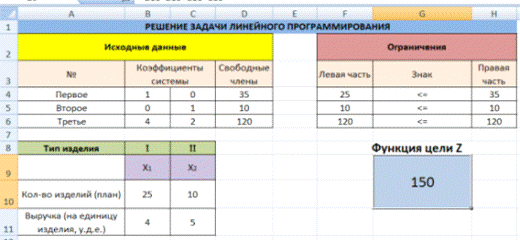
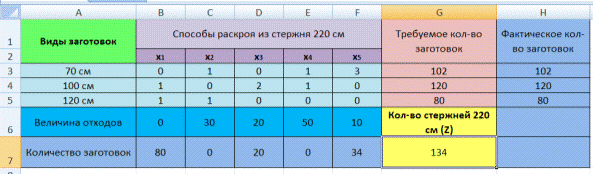
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

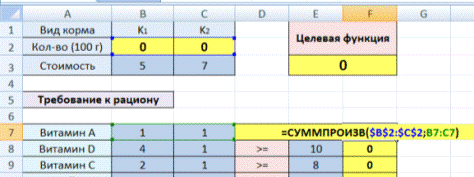
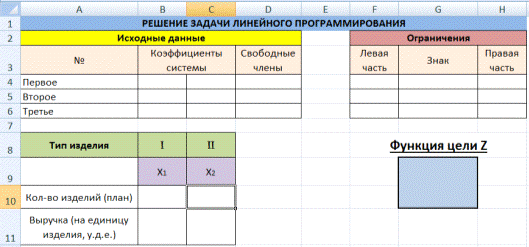
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

Известные данные.

На основании этих данных составим рабочую таблицу:

Рабочая таблица.

  1. Количество изделий нам пока неизвестно. Это переменные.
  2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
  3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
  4. Цель – найти максимально возможную прибыль. Это ячейка С14.

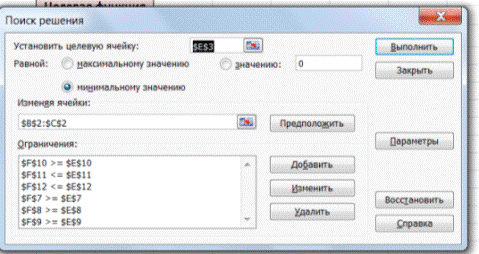
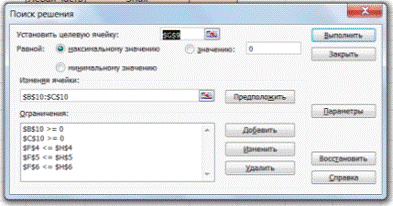
Активизируем команду «Поиск решения» и вносим параметры.

Параметры настройки.

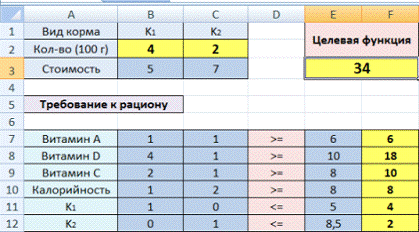
После нажатия кнопки «Выполнить» программа выдает свое решение.

Результат решения.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.



Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Исходные данные.

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

  1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
  2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
  3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
  4. Тип – 0.
  5. БС – сумма, которую мы хотим получить в конце срока вклада.

Параметры функции БС.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Результат функции БС.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Диапазон значений.

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Функция КОРРЕЛ.

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Пример задачи.

  1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
  2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
  3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение задачи.

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

  1. Делаем таблицу со значениями матрицы А.
  2. Выделяем на этом же листе область для обратной матрицы.
  3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
  4. В поле аргумента «Массив» вписываем диапазон матрицы А.
  5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Результат выполнения массива.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Источник

Для
решения задач линейного программирования
в MS
Excel
имеется
надстройка Поиск
решения. По
умолчанию в Excel надстройка Поиск решения
отключена. Чтобы активизировать ее в
MS
Excel
2007,
щелкните значок Кнопка
Microsoft Office
, щелкните Параметры
MS
Excel,
а затем выберите категорию Надстройки.
В поле Управление
выберите значение Надстройки
MS
Excel
и нажмите кнопку Перейти
(см. рис. 5.1).

В поле Доступные
надстройки
установите флажок рядом с пунктом Поиск
решения
и нажмите кнопку ОК
(см. рис. 5.2).

В Excel
2003 и
ниже выберите команду Сервис→Надстройки,
в появившемся диалоговом окне Надстройки
установите флажок Поиск
решения
и щелкните на кнопке ОК. Если вслед за
этим на экране появится диалоговое окно
с предложением подтвердить ваши
намерения, щелкните на кнопке Да.
(Возможно, вам понадобится установочный
компакт-диск MS
 Office).

рис.
рис 5.1


рис.
5.2

Рассмотрим
использование данной надстройки для
решения задачи
линейного программирования из примера
6.

1. Для решения
задачи с помощью функции Поиск
решения
необходимо внести исходные данные –
это диапазон ячеек (A5:F10)
на рис. 5.3.

2

рис. 5.3

. Затем определить ячейки для
результата решения задачи-неизвестные
величиныxj,
отражающие план
производства изделий A,
B,
С и D.
 Ячейки для неизвестных
величин заполнить нулями – это диапазон
ячеек (B15:E15)
на рис. 5.3.


рис.
5.3

3. В
ячейке F15
для вычисления значения общей стоимости
всей произведенной предприятием
продукции — ввести формулу
=СУММПРОИЗВ(В10:E10;В15:E15),
которая находит
сумму попарных произведений ячеек с
ценами (В10:E10)
на ячейки со значениями неизвестных
величин (В15:E15).

4. Для
задания ограничений по видам сырья
в
ячейку G7
скопировать
формулу из ячейки F15.
Она скопируется в виде СУММПРОИЗВ(C2:F2;C7:F7).
Необходимо
заменить диапазон (C2:F2)
на
диапазон параметров расхода сырья
(В7:E7),
а диапазон (C7:F7)
на диапазон (В15:E15)-
значения неизвестных величин .

Диапазон
(В15:E15)
преобразуется
к абсолютному виду для удобства
дальнейшего копирования формулы в
ячейки с ограничениями. Для
такого преобразования необходимо при
наборе формулы после
выделения нужного диапазона ячеек в
таблице (В15:E15)
нажать
клавишу F4,
чтобы получилась формула
=СУММПРОИЗВ(B7:E7;$B$15:$E$15).

Для
задания остальных ограничений скопировать
вновь введенную
формулу в ячейки G8
и G9.
На рис. 5.3 ячейки содержащие формулы
закрашены серым цветом.

5. После
создания таблицы с исходными данными
установить курсор
в ячейку с формулой целевой функции
(F15)
и выбрав в
меню Сервис
функцию
Поиск
решения в
Excel
2003 или

Данные→Анализ→Поиск
решения в
Excel
2007.
Затем
заполнить поля в
появившемся окне

в

рис.
5.3

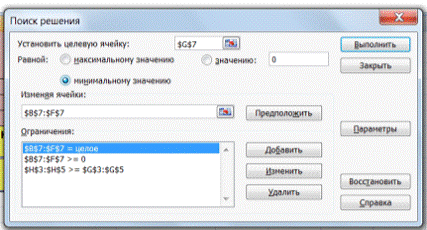
полеУстановить
целевую ячейку должен
появиться адрес ячейки
с формулой целевой функции (в данном
случае $F$15);

•
установить
переключатель вида оптимизации в поле
Равной:
в
положение максимальное
(минимальное) значение, при
необ­ходимости
найти максимум или минимум целевой
функции;

• в
поле Изменяя
ячейки указать
диапазон ячеек со значениями неизвестных
задачи, выделив его в таблице. В данном
примере это
ячейки $B$15:$E$15;

• в
поле Ограничения
задать
вид и значения ограничений. Для этого
установить курсор в поле ввода ограничений
и нажать кнопку
Добавить. После
чего в появившемся окне Добавление
ограничения
ввести в поле Ссылка
на ячейку адрес
ячейки с формулой соответствующего
ограничения (например,
$G$7 для ресурса I
–го вида). Затем
ввести в поле Огра­ничение
предельное
значение соответствующего ресурса (оно
находится в ячейке $F$7)
и выбрать вид от­ношения
(<, >, = и т.п.). (см. рис. 5.4).


рис.
5.4

После
нажатия кнопки
Добавить (или
OK
для ввода послед­него
ограничения) данное ограничение попадает
в список огра­ничений
задачи.

С
помощью кнопок Удалить
и
Изменить
можно
удалять вы­деленные в списке ограничения
или вносить в них исправления.

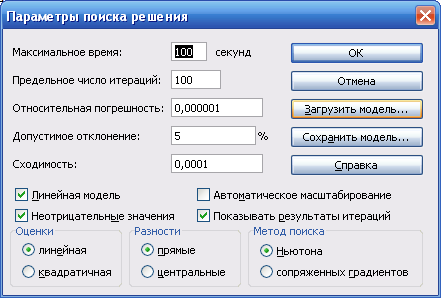
После заполнения
всех полей окна нажать кнопку Параметры
 в открывшемся
окне Параметры
поиска решения (рис
5.5)
установить
флажки Линейная
модель для
решения задачи линей­ного
программирования и Неотрицательные
значения, если
такие ограничения
накладываются на все переменные задачи.

В
этом окне можно так же определить
параметры процесса решения:
предельное время поиска решения,
максимальное ко­личество
итераций, точность и т.п.

Флажок
Показывать
результа­ты
итераций
позволяет по шагам следить за поиском
решения.

Флажок
Автоматическое
масштабирование включается
в том случае,
когда разброс значений параметров очень
велик.


рис.
5.5

Параметры
средства Поиск решения.

Таблица 5.1

Максимальное
время

-служит для
ограничения времени, отпущенного на
поиск решения задачи. В этом поле можно
ввести время в секундах, не превышающее
32 767 (примерно девять часов); значение
100, используемое по умолчанию, вполне
приемлемо для решения большинства
простых задач.

Предельное
число итераций

-управляет
временем решения задачи путем
ограничения числа вычислительных
циклов (итераций).

Относительная
погрешность

— определяет
точность вычислений. Чем меньше
значение этого параметра, тем выше
точность вычислений.

Допустимое
отклонение

— предназначен
для задания допуска на отклонение от
оптимального решения, если множество
значений влияющей ячейки ограничено
множеством целых чисел. Чем больше
значение допуска, тем меньше времени
требуется на поиск решения.

Сходимость

— применяется
только к нелинейным задачам. Когда
относительное изменение значения в
целевой ячейке за последние пять
итераций становится меньше числа,
указанного в поле Сходимость, поиск
прекращается.

Линейная
модель

— служит для
ускорения поиска решения путем
применения к задаче оптимизации
линейной модели. Нелинейные модели
предполагают использование нелинейных
функций, фактора роста и экспоненциального
сглаживания, что замедляет вычисления.

Неотрицательные
значения

— позволяет
установить нулевую нижнюю границу
для тех влияющих ячеек, для которых
не было задано соответствующее
ограничение в диалоговом окне Добавить
ограничение.

Автоматическое
масштабирование

— используется,
когда числа в изменяемых ячейках и в
целевой ячейке существенно различаются.

Показывать
результаты итераций

— приостанавливает
поиск решения для просмотра результатов
отдельных итераций.

Загрузить
модель

— после
щелчка на этой кнопке отрывается
одноименное диалоговое окно, в котором
можно ввести ссылку на диапазон ячеек,
содержащих модель оптимизации.

Сохранить
модель

— служит для
отображения на экране одноименного
диалогового окна, в
котором можно
ввести ссылку на диапазон ячеек,
предназначенный для хранения модели
оптимизации.

Оценка
линейная

— выберите
этот переключатель для работы с
линейной моделью.

Оценка
квадратичная

— выберите
этот переключатель для работы с
нелинейной моделью.

Разности
прямые

— используется
в большинстве задач, где скорость
изменения ограничений относительно
невысока. Увеличивает скорость работы
средства Поиск решения.

Разности
центральные

— используется
для функций, имеющих разрывную
производную. Данный способ требует
больше вычислений, однако его применение
может быть оправданным, если выдано
сообщение о том, что получить более
точное решение не удается.

Метод
поиска Ньютона

— требует
больше памяти, но выполняет меньше
итераций, чем в методе сопряженных
градиентов.

Метод
поиска сопряженных градиентов

— реализует
метод сопряженных градиентов, для
которого требуется меньше памяти, но
выполняется больше итераций, чем в
методе Ньютона. Данный метод следует
использовать, если задача достаточно
большая и необходимо экономить память
или если итерации дают слишком малое
отличие в последовательных приближениях.

Задав все параметры,
нажать кнопку Выполнить
для поиска
решения задачи. Если решение найдено,
то появляется окно, с
соответствующим сообщением (рис. 5.6).

рис.
5.6

Результаты
решения
могут быть сохранены в файле задачи в
виде сценарии или
добавлены в виде отдельных листов Отчет
по результатам, Отчет
по устойчивости, Отчет по пределам. Для
сохранения результатов
в виде листов необходимо предварительно
в поле Тип
отчета выделить
требуемые типы отчетов. В этом же окне
можно
отказаться от полученных решений и
восстановить ис­ходные
значения переменных.

Отчет
по результатам приведен
ниже на рис. 5.7. В данном отче­те
в графах Результат
выводятся
значения целевой функции и оптимального
плана, а также значения исходного
опорного пла­на
(графа Исходное
значение). Кроме
того, указывается, какие ограничения
являются связанными, т.е. ограничения
с дефи­цитным
ресурсом (т.е его количество ограничивает
план производства), а какие — нет (графа
Статус),
и
приведены значения
соответствующих дефицитов по всем
ограничениям (графа
Разница).

Отчеты
по устойчивости и по пределам позволяют
проанализировать модель на устойчивость.
Устойчивость модели имеет важную роль
на практике. Если значение оптимального
решения резко изменяется при небольших
отклонениях переменных, то такой моделью
сложно пользоваться на практике, где
изменения цен и запасов – явление
обыденное. Возможности
MS Excel анализировать модель на устойчивость
в данном пособии не рассматриваются.


рис.
5.7

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ, НАУКИ И МОЛОДЕЖНОЙ ПОЛИТИКИ               ВОРОНЕЖСКОЙ ОБЛАСТИ

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВОРОНЕЖСКОЙ ОБЛАСТИ

“ВОРОНЕЖСКИЙ ТЕХНИКУМ СТРОИТЕЛЬНЫХ ТЕХНОЛОГИЙ”

(ГБПОУ ВО “ВТСТ”)

Методические указания

для выполнения Практических работ

в табличном процессоре Microsoft Excel

по предмету    “Информатика и ИКТ ”

ВОРОНЕЖ

2019

ОДОБРЕНО

Предметной (цикловой)

Комиссией естественнонаучных дисциплин

Протокол заседания №7

от “____” _____________ 2019 года.

Председатель П(Ц)К

________________________/ Болычева А. В./

Настоящее пособие разработано на основе Федерального государственного образовательного стандарта среднего профессионального образования для всех специальностей 1 курса и полностью соответствует программе информатике и ИКТ для СПО.

Данное пособие содержит методические рекомендации  для выполнения  практических работ в Microsoft  Excel  по теме  “Методы вычисления в Excel ”.

      Цель данных рекомендаций – оказать помощь студентам при выполнении практических работ, закрепления и применения на практике теоретических знаний, полученных студентами по предметам  «Информатика» и «Информационные технологии».

Автор-составитель: Радычева Екатерина Александровна,

преподаватель информатики и ИКТ.

СОДЕРЖАНИЕ

Практическая работа 1 Тема: ОРГАНИЗАЦИЯ РАСЧЕТОВ В ТАБЛИЧНОМ ПРОЦЕССОРЕ MS EXCEL        4

Практическая работа 2  Тема: СОЗДАНИЕ ЭЛЕКТРОННОЙ КНИГИ. ОТНОСИТЕЛЬНАЯ И АБСОЛЮТНАЯ АДРЕСАЦИИ В MS Excel.        8

Практическая работа 3 Тема: СВЯЗАННЫЕ ТАБЛИЦЫ. РАСЧЕТ ПРОМЕЖУТОЧНЫХ ИТОГОВ В ТАБЛИЦАХ MS Excel        11

Практическая работа 4 Тема: ПОДБОР ПАРАМЕТРА. ОРГАНИЗАЦИЯ ОБРАТНОГО РАСЧЕТА        14

Практическая работа 5. Тема: ЗАДАЧИ ОПТИМИЗАЦИИ (ПОИСК РЕШЕНИЯ)        18

Практическая работа 6 Тема: СВЯЗИ МЕЖДУ ФАЙЛАМИ И КОНСОЛИДАЦИЯ ДАННЫХ В MS EXCEL.        22

Практическая работа 7. Тема: ЭКОНОМИЧЕСКИЕ РАСЧЕТЫ В MS EXCEL        26

Практическая работа 8. Тема: КОМПЛЕКСНОЕ ИСПОЛЬЗОВАНИЕ ПРИЛОЖЕНИЙ MICROSOFT OFFICE ДЛЯ СОЗДАНИЯ ДОКУМЕНТОВ        31

Практическая работа 1 Тема: ОРГАНИЗАЦИЯ РАСЧЕТОВ В ТАБЛИЧНОМ ПРОЦЕССОРЕ MS EXCEL

Цель занятия. Изучение информационной технологии использования встроенных вычислительных функций Excel для финансового анализа.

Задание 1. Создать таблицу финансовой сводки за неделю, произвести расчеты, построить диаграмму изменения финансового результата, произвести фильтрацию данных.

Исходные данные представлены в табл. 1.

Порядок работы

  1. Запустите редактор электронных таблиц Microsoft Excel и создайте новую электронную книгу (при стандартной установке MS office выполните Пуск/Программы/Microsoft Excel).

Таблица 1

Финансовая сводка за неделю

Дни недели

Доход

Расход

Финансовый результат

Понедельник

3245,20

3628,50

?

Вторник

4572,50

5320,50

?

Среда

6251,66

5292,10

?

Четверг

2125,20

3824,30

?

Пятница

3896,60

3020,10

?

Суббота

5420,30

4262,10

?

Воскресенье

6050,60

4369,50

?

Ср. значение

?

?

Общий финансовый результат за неделю:

?

2. Введите заголовок таблицы «Финансовая сводка за неделю (тыс. р.)», начиная с ячейки А1.

3. Для оформления шапки таблицы выделите ячейки на третьей строке АЗ:DЗ и создайте стиль для оформления. Для этого выполните команду Формат/Стиль и в открывшемся окне Стиль наберите имя стиля «Шапка таблиц» и нажмите кнопку Изменить. В открывшемся окне на вкладке Выравнивание задайте Переносить по словам и выберите горизонтальное и вертикальное выравнивание — по центру), на вкладке Число укажите формат — Текстовый. После этого нажмите кнопку Добавить.

4. На третьей строке введите названия колонок таблицы — «Дни недели», «Доход», «Расход», «Финансовый результат», далее заполните таблицу исходными данными согласно Заданию 1.

Краткая справка. Для ввода дней недели наберите «Понедельник» и произведите автокопирование до «Воскресенья» (левой кнопкой мыши за маркер автозаполнения в правом нижнем углу ячейки).

5. Произведите расчеты в графе «Финансовый результат» по следующей формуле:        

Финансовый результат = Доход — Расход,

для этого в ячейке D4 наберите формулу = В4-С4.

Краткая справка. Введите расчетную формулу только для расчета по строке «Понедельник», далее произведите автокопирование формулы (так как в графе «Расход» нет незаполненных данными ячеек, можно производить автокопирование двойным щелчком мыши по маркеру автозаполнения в правом нижнем углу ячейки).

6. Для ячеек с результатом расчетов задайте формат — «Денежный» с выделением отрицательных чисел красным цветом  (Формат/‘Ячейки/вкладка Число/формат — Денежный/ отрицательные числа — красные. Число десятичных знаков задайте равное 2).

Обратите внимание, как изменился цвет отрицательных значений финансового результата на красный.

7. Рассчитайте средние значения Дохода и Расхода, пользуясь мастером функций. Функция «Среднее значение» (СРЗНАЧ) находится в разделе «Статистические». Для расчета функции СРЗНАЧ дохода установите курсор в соответствующей ячейке для расчета среднего значения (В 11), запустите мастер функций (Вставка/Функция/категория — Статистические/СРЗНАЧ). В качестве первого числа выделите группу ячеек с данными для расчета среднего значения — В4:В10.

Аналогично рассчитайте «Среднее значение» расхода.

8. В ячейке D13 выполните расчет общего финансового результата (сумма по столбцу «Финансовый результат»). Для выполнения автосуммы удобно пользоваться кнопкой Автосуммирования (∑) на панели инструментов или функцией СУММ . В качестве первого числа выделите группу ячеек с данными для расчета суммы – D4:D10.

9. Проведите форматирование заголовка таблицы. Для этого выделите интервал ячеек от А1 до D1, объедините их кнопкой панели инструментов Объединить и поместить в центре или командой меню Формат/Ячейки/вкладка Внимание/отображение — Объединение ячеек). Задайте начертание шрифта — полужирное; цвет — по вашему усмотрению.

10. Постройте диаграмму (линейчатого типа) изменения финансовых результатов по дням недели с использованием мастера диаграмм.

Для этого выделите интервал ячеек с данными финансового результата и выберите команду Вставка/Диаграмма. На первом шаге работы с мастером диаграмм выберите тип диаграммы — линейчатая; на втором шаге на вкладке Ряд в окошке Подписи оси X  укажите интервал ячеек с днями недели — А4:А10.

Далее введите название диаграммы и подписи осей; дальнейшие шаги построения диаграммы осуществляются автоматически по подсказкам мастера.

11. Произведите фильтрацию значений дохода, превышающих 4000 р.

Краткая справка. В режиме фильтра в таблице видны только те данные, которые удовлетворяют некоторому критерию, при этом остальные строки скрыты. В этом режиме все операции форматирования, копирования, автозаполнения, автосуммирования и т.д. применяются только к видимым ячейкам листа.

Для установления режима фильтра установите курсор внутри таблицы и воспользуйтесь командой Данные/ Фильтр/Автофильтр. В заголовках полей появятся стрелки выпадающих списков. Щелкните по стрелке в заголовке поля, на которое будет  наложено условие (в столбце «Доход»), и вы увидите список всех неповторяющихся значений этого поля. Выберите команду для фильтрации — Условие.

В открывшемся окне Пользовательский автофильтр задайте условие «Больше 4000».

Произойдет отбор данных по заданному условию.

Проследите, как изменились вид таблицы и построенная диаграмма.

12. Сохраните созданную электронную книгу в своей

      папке.

Дополнительные задания

Задание 2. Заполнить таблицу, произвести расчеты, выделить минимальную и максимальную суммы покупки (табл.2); по ре-расчета построить круговую диаграмму суммы продаж.

Таблица 2

Анализ продаж

№

Наименование

Цена, руб.

Кол-во

Сумма , руб.

1

Туфли

820,00

150

?

2

Сапоги

1530,00

60

?

3

Куртки

1500,00

25

?

4

Юбки

250,00

40

?

5

Шарфы  

125,00

80

?

6

Зонты

80,00

50

?

7

Перчатки

120,00

120

?

8

Варежки

50,00

40

?

Всего:

?

Минимальная сумма покупки

?

Максимальная сумма покупки

?

Используйте созданный стиль (Формат/Стиль/Шапка таблиц).

Формулы для расчета:

Сумма = Цена * Количество;

Всего = сумма значений колонки «Сумма».

Краткая справка. Для выделения максимального/минимального значений установите курсор в ячейке расчета, выберите встроенную функцию Excel МАКС (МИН) из категории «Статистические», в качестве первого числа выделите диапазон ячеек значений столбца «Сумма» (ячейки ЕЗ:Е10).

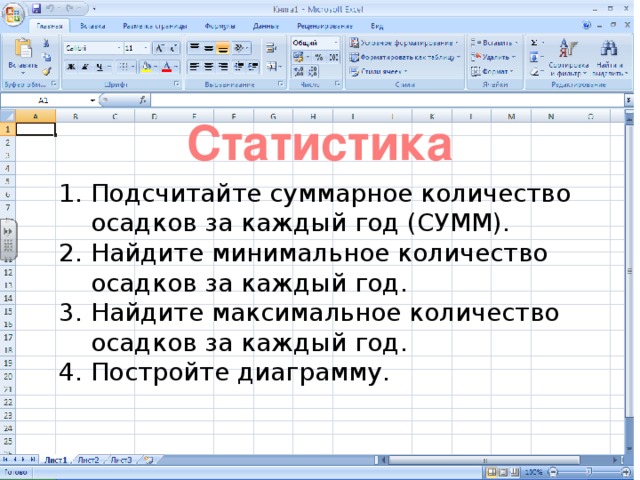
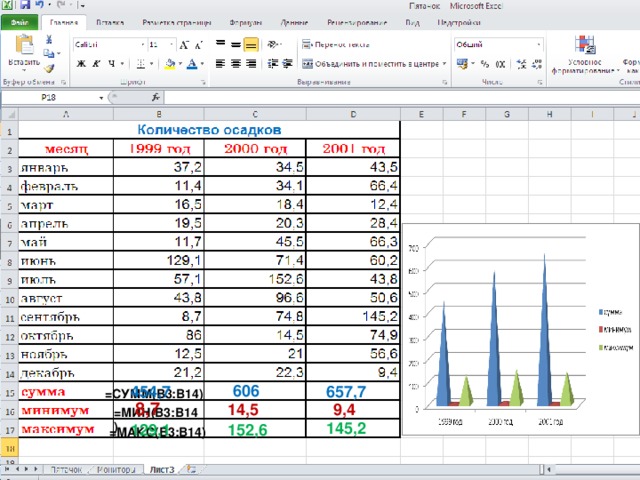
Задание 3. Заполнить ведомость учета брака, произвести расчеты, выделить минимальную, максимальную и среднюю суммы брака, а также средний процент брака; произвести фильтрацию данных по условию процента брака < 8 %, построить график отфильтрованных значений изменения суммы брака по месяцам .

Формула для расчета:

Сумма брака = Процент брака * Сумма зарплаты.

Краткая справка. В колонке «Процент брака» установите процентный формат чисел (Формат/Ячейки/вкладка Число/формат — Процентный).

Таблица 3

Ведомость учета брака

месяц

ФИО

Табельный номер

Процент брака

Сумма зарплаты

Сумма брака

Январь

Иванов

245

10%

3265

?

Февраль

Петров

289

8%

4568

?

Март

Сидоров

356

5%

4500

?

Апрель

Панчук

657

11%

6804

?

Май

Васин

568

9%

6759

?

Июнь

Борисова

849

12%

4673

?

Июль

Сорокина

409

21%

5677

?

Август

Федорова

386

46%

6836

?

Сентябрь

Титова

598

6%

3534

?

Октябрь

Пирогов

4569

3%

5789

?

Ноябрь

Светов

239

2%

4673

?

Декабрь

Козлов

590

1%

6785

?

        Максимальная  сумма брака

?

Минимальная сумма брака

?

Средняя сумма брака

?

Средний процент брака

?

Задание 4. Заполнить таблицу анализа продаж, произвести расчеты, выделить минимальную и максимальную продажи (количество и сумму); произвести фильтрацию по цене, превышающей 9000 р., построить гистограмму отфильтрованных значений изменения выручки по видам продукции.

Формулы для расчета:

Всего = Безналичные платежи + Наличные платежи;

Выручка от продажи = Цена * Всего.

Практическая работа 2  Тема: СОЗДАНИЕ ЭЛЕКТРОННОЙ КНИГИ. ОТНОСИТЕЛЬНАЯ И АБСОЛЮТНАЯ АДРЕСАЦИИ В MS Excel.

Цель занятия. Применение относительной и абсолютной адресаций для финансовых расчетов. Сортировка, условное форматирование и копирование созданных таблиц. Работа с листами электронной книги.

Задание 1. Создать таблицы ведомости начисления заработной платы за два месяца на разных листах электронной книги, произвести расчеты, форматирование, сортировку и защиту данных.

Исходные данные представлены в табл. 1.

Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel и создайте новую электронную книгу.

2. Создайте таблицу расчета заработной платы по образцу (см. табл.1). Введите исходные данные — Табельный номер, ФИО и Оклад, % Премии = 27%,% Удержания = 13 %.

Примечание. Выделите отдельные ячейки для значений % Премии (D4) и % Удержания (F4).

Таблица 1

Ведомость начисления заработной платы

за октябрь 2003 года

табельный номер

Фамилия И.О.

оклад

(руб.)

премия

(руб.)

всего начислено

(руб.)

удержания

(руб.)

к выдаче

(руб.)

27%

13%

200

Петров И.Л.

4500,00

?

?

?

?

201

Иванов И.Г.

4850,00

?

?

?

?

202

Степанов А.Ш.

5200,00

?

?

?

?

203

Шорохова С.М.

5550,00

?

?

?

?

204

Галкин В.Ж.

5900,00

?

?

?

?

205

Портнов М.Т.

6250,00

?

?

?

?

206

Орлова Н.Н

6600,00

?

?

?

?

207

Степкина А.В.

6950,00

?

?

?

?

208

Жарова Г.А.

7300,00

?

?

?

?

209

Стольникова О.Д.

7650,00

?

?

?

?

210

Дрынкина С.С.

8000,00

?

?

?

?

211

Шпаро Н.Г.

8350,00

?

?

?

?

212

Шашкин Р.Н.

8700,00

?

?

?

?

213

Стелков Р.Х.

9050,00

?

?

?

?

Всего:

?

?

?

?

?

Максимальный доход        ?

Минимальный доход         ?

Средний доход        ?

Произведите расчеты во всех столбцах таблицы.

При расчете Премии используется формула Премия = Оклад * % Премии, в ячейке D5 наберите формулу = $D$ * С5 (ячейка D4 используется в виде абсолютной адресации) и скопируйте автозаполнением.

Рекомендации. Для удобства работы и формирования навыков работы с абсолютным видом адресации рекомендуется при оформлении констант окрашивать ячейку цветом, отличным от цвета расчетной таблицы. Тогда при вводе формул в расчетную окрашенная ячейка (т. е. ячейка с константой) будет вам напоминанием, что следует установить абсолютную адресацию (набором символов $ с клавиатуры или нажатием клавиши [F4]).

Формула для расчета «Всего начислено»:

Всего начислено = Оклад + Премия.

При расчете Удержания используется формула

Удержание = Всего начислено * % Удержания,

для этого в ячейке  F5 наберите формулу = $$4 * Е5.

 Формула для расчета столбца «К выдаче»:

К выдаче = Всего начислено — Удержания.

3. Рассчитайте итоги по столбцам, а также максимальный, минимальный и средний доходы по данным колонки «К выдаче» (Вставка/Функция/категория — Статистические функции).

4. Переименуйте ярлычок Листа 1, присвоив ему имя «Зарплата октябрь». Для этого дважды щелкните мышью по ярлычку и наберите новое имя. Можно воспользоваться командой Переименовать контекстного меню ярлычка, вызываемого правой кнопкой мыши.

Краткая справка. Каждая рабочая книга Excel может содержать до 255 рабочих листов. Это позволяет, используя несколько листов, создавать понятные и четко структурированные документы, вместо того, чтобы хранить большие последовательные наборы данных на одном листе.

5. Скопируйте содержимое листа «Зарплата октябрь» на новый лист (Правка/Переместить/Скопировать лист). Можно воспользоваться командой Переместить/Скопировать контекстного меню ярлычка. Не забудьте для копирования поставить галочку в окошке Создавать копию .

Краткая справка. Перемещать и копировать листы можно, перетаскивая их корешки (для копирования удерживайте нажатой клавишу [Ctrl]).

6. Присвойте скопированному листу название «Зарплата ноябрь». Исправьте название месяца в названии таблицы. Измените значение Премии на 32 %. Убедитесь, что программа произвела пересчет формул.

7. Между колонками «Премия» и «Всего начислено» вставьте новую колонку «Доплата» (Вставка/ Столбец) и рассчитайте значение доплаты по формуле Доплата = Оклад * % Доплаты. Значение доплаты примите равным 5 %.

8. Измените формулу для расчета значений колонки «Всего начислено»:

Всего начислено = Оклад + Премия + Доплата.

9. Проведите условное форматирование значений колонки «К выдаче». Установите формат вывода значений между 7000 и 10000 — зеленым цветом шрифта; меньше 7000 — красным; больше или равно 10 000 — синим цветом шрифта (Формат/Условное форматирование) .

10. Проведите сортировку по фамилиям в алфавитном порядке по возрастанию (выделите фрагмент с 5 по 18 строки таблицы — без итогов, выберите меню Данные/Сортировка, сортировать по — Столбец В) .

И. Поставьте к ячейке D3 комментарии «Премия пропорциональна окладу» (Вставка/Примечание), при этом в правом верхнем углу ячейки появится красная точка, которая свидетельствует о наличии примечания.

12. Защитите лист «Зарплата ноябрь» от изменений (Сервис/Защита/Защитить лист). Задайте пароль на лист , сделайте подтверждение пароля .

Убедитесь, что лист защищен и невозможно удаление данных. Снимите защиту листа (Сервис/Защита/Снять защиту листа).

13. Сохраните созданную электронную книгу под именем «Зарплата» в своей папке.

Дополнительные задания

Задание 2. Сделать примечания к двум-трем ячейкам.

Задание 3. Выполнить условное форматирование оклада и премии за ноябрь месяц:

до 2000 р. — желтым цветом заливки;

от 2000 до 10 000 р. — зеленым цветом шрифта;

свыше 10000 р. — малиновым цветом заливки, белым цветом шрифта.

Задание 4. Защитить лист зарплаты за октябрь от изменений.

Проверьте защиту. Убедитесь в неизменяемости данных. Снимите защиту со всех листов электронной книги «Зарплата».

Задание 5. Построить круговую диаграмму начисленной суммы к выдаче всех сотрудников за ноябрь месяц.

Практическая работа 3 Тема: СВЯЗАННЫЕ ТАБЛИЦЫ. РАСЧЕТ ПРОМЕЖУТОЧНЫХ ИТОГОВ В ТАБЛИЦАХ MS Excel

Цель занятия. Связывание листов электронной книги. Расчет промежуточных итогов. Структурирование таблицы.

Задание 1. Рассчитать зарплату за декабрь и построить диаграмму. Создать итоговую таблицу ведомости квартального начисления заработной платы, провести расчет промежуточных итогов по подразделениям.

Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel и откройте созданный в Практической работе 9 файл «Зарплата».

2. Скопируйте содержимое листа «Зарплата ноябрь» на новый лист электронной книги (Правка/Переместить/Скопировать лист). Не забудьте для копирования поставить галочку в окошке Создавать копию.

3. Присвойте скопированному листу название «Зарплата декабрь». Исправьте название месяца в ведомости на декабрь.

4. Измените значение Премии на 46 %, Доплаты — на 8 %. Убедитесь, что программа произвела пересчет формул .

5. По данным таблицы «Зарплата декабрь» постройте гистограмму доходов сотрудников. В качестве подписей оси X выберите фамилии сотрудников. Проведите форматирование диаграммы. Конечный вид гистограммы приведен на рис. 10.2.

6. Перед расчетом итоговых данных за квартал проведите сортировку по фамилиям в алфавитном порядке (по возрастанию) в ведомостях начисления зарплаты за октябрь—декабрь.

7. Скопируйте содержимое листа «Зарплата октябрь» на новый лист (Правка/Переместить/Скопировать лист). Не забудьте для копирования поставить галочку в окошке Создавать копию.

8. Присвойте скопированному листу название «Итоги за квартал». Измените название таблицы на «Ведомость начисления заработной платы за 4 квартал».

9. Отредактируйте лист «Итоги за квартал» согласно образцу на рис. 10.3. Для этого удалите в основной таблице колонки Оклада и Премии, а также строку 4 с численными значениями % Премии и % Удержания и строку 19 «Всего». Удалите также строки с расчетом максимального, минимального и среднего доходов под основной таблицей. Вставьте пустую третью строку.

10. Вставьте новый столбец «Подразделение» (Вставка/Столбец) между столбцами «Фамилия» и «Всего начислено». Заполните столбец «Подразделение» данными по образцу (см. табл. 1).

11. Произведите расчет квартальных начислений, удержаний и суммы к выдаче как сумму начислений за каждый месяц (данные по месяцам располагаются на разных листах электронной книги, поэтому к адресу ячейки добавится адрес листа).

Краткая справка. Чтобы вставить в формулу адрес или диапазон ячеек с другого листа, следует во время ввода формулы щелкнуть по закладке этого листа и выделить на нем нужные ячейки. Вставляемый адрес будет содержать название этого листа.

В ячейке В5 для расчета квартальных начислений «Всего начислено» формула имеет вид

= ‘Зарплата декабрь’!F5 + ‘Зарплата ноябрь’!F5 +

+ ‘Зарплата октябрь’!Е5.

Таблица 1

Ведомость начисления заработной платы

за 4 квартал  2003 года

табельный номер

Фамилия И.О.

Подразделение

всего начислено

(руб.)

удержания

(руб.)

к выдаче

(руб.)

204

Галкин В.Ж.

Отдел менеджмента

?

?

?

210

Дрынкина С.С.

Отдел менеджмента

?

?

?

208

Жарова Г.А.

Отдел реализации

?

?

?

201

Иванова И.Г

Бухгалтерия

?

?

?

206

Петров И.Л.

Отдел реализации

?

?

?

205

Портнов М.Т.

Отдел реализации

?

?

?

213

Стелков Р.Х.

Отдел менеджмента

?

?

?

202

Степанов А.Ш.

Отдел менеджмента

?

?

?

207

Степкина А.В.

Бухгалтерия

?

?

?

209

Стольникова О.Д.

Отдел реализации

?

?

?

212

Шашкин Р.Н.

Бухгалтерия

?

?

?

203

Шорохов С.М.

Отдел реализации

?

?

?

211

Шпаро Н.Г.

Отдел реализации

?

?

?

Аналогично произведите квартальный расчет «Удержания» и «К выдаче».

Примечание. При выборе начислений за каждый месяц делайте ссылку на соответствующую ячейку из таблицы соответствующего листа электронной книги «Зарплата». При этом произойдет связывание информации соответствующих ячеек листов электронной книги.

12. В силу однородности расчетных таблиц зарплаты по месяцам для расчета квартальных значений столбцов «Удержание» и «К выдаче» достаточно скопировать формулу из ячейки D5 в ячейки Е5 и F5 (рис. 10.4).

Для расчета квартального начисления заработной платы для всех сотрудников скопируйте формулы в столбцах D, Е и F.

13. Для расчета промежуточных итогов проведите сортировку по подразделениям, а внутри подразделений — по фамилиям.

14. Подведите промежуточные итоги по подразделениям, используя формулу суммирования. Для этого выделите всю таблицу и выполните команду Данные/Итоги .Задайте параметры подсчета промежуточных итогов:

при каждом изменении в — Подразделение;

операция — Сумма;

добавить итоги по: Всего начислено, Удержания, К выдаче.

Отметьте галочкой операции «Заменить текущие итоги» и «Итоги под данными».

15. Изучите полученную структуру и формулы подведения промежуточных итогов, устанавливая курсор на разные ячейки таблицы. Научитесь сворачивать и разворачивать структуру до разных уровней (кнопками «+» и «-»).

Краткая справка. Под структурированием понимается многоуровневая группировка строк и столбцов таблицы и создание элементов управления, с помощью которых легко можно скрывать и раскрывать эти группы.

16. Сохраните файл «Зарплата» с произведенными изменениями (Файл/ Сохранит ь).

Дополнительные задания

Задание  2. Исследовать графическое отображение зависимостей ячеек друг от друга.

Порядок работы

Скопируйте содержимое листа «Зарплата октябрь» на новый лист. Копии присвойте имя «Зависимости». Откройте панель «Зависимости» (Сервис/Зависимости/Панель зависимостей). Изучите назначение инструментов панели, задерживая на них указатель мыши.

Устанавливайте курсор на ячейку в каждом столбце и вызывайте зависимости кнопками Влияющие ячейки и Зависимые ячейки панели «Зависимости». Появятся стрелки, указывающие на зависимость ячейки от других ячеек и ее влияние на другие ячейки. Сохраните файл «Зарплата» с произведенными изменениями.

Практическая работа 4 Тема: ПОДБОР ПАРАМЕТРА. ОРГАНИЗАЦИЯ ОБРАТНОГО РАСЧЕТА

Цель занятия. Изучение технологии подбора параметра при обратных расчетах.

Задание 1. Используя режим подбора параметра, определить, при каком значении % Премии общая сумма заработной платы за октябрь будет равна 250000 р. (на основании файла «Зарплата», созданного в Практических работах 2… 3).

Краткая справка. К исходным данным этой таблицы относятся значения Оклада и % Премии, одинакового для всех сотрудников. Результатом вычислений являются ячейки, содержащие формулы, при этом изменение исходных данных приводит к изменению результатов расчетов. Использование операции «Подбор параметра» в MS Excel позволяет производить обратный расчет, когда задается конкретное значение рассчитанного параметра, и по этому значению подбирается некоторое удовлетворяющее заданным условиям, значение исходного параметра расчета.

Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel и откройте созданный в Практических работ 2… 3 файл «Зарплата».

2. Скопируйте содержимое листа «Зарплата октябрь» на новый лист электронной книги (Правка/Переместить/ Скопировать лист). Не забудьте для копирования поставить галочку в окошке Создавать копию. Присвойте скопированному листу имя «Подбор параметра».

3. Осуществите подбор параметра командой Сервис/Подбор параметра.

В диалоговом окне Подбор параметра на первой строке в качестве подбираемого параметра укажите адрес общей итоговой суммы зарплаты (ячейка 019), на второй строке наберите заданное значение 250000, на третьей строке укажите адрес подбираемого значения % Премии (ячейка В4), затем нажмите кнопку ОК. В окне Результат подбора параметра дайте подтверждение подобранному параметру нажатием кнопки ОK.

Произойдет обратный пересчет % Премии. Результаты подбора :

если сумма к выдаче равна 250000 р., то % Премии должен быть 203 %.

Задание 2. Используя режим подбора параметра, определить штатное расписания фирмы. Исходные данные приведены в табл. 1.

Краткая справка. Известно, что в штате фирмы состоит:

• 6 курьеров;

• 8 младших менеджеров;

• 10 менеджеров;

• 3 заведующих отделами;

• 1 главный бухгалтер;

• 1 программист;

• 1 системный аналитик;

• 1 генеральный директор фирмы.

Общий месячный фонд зарплаты составляет 100000 р. Необходимо определить, какими должны быть оклады сотрудников фирмы.

Каждый оклад является линейной функцией от оклада курьера, а именно: зарплата =Аi*х+Bi,  где х — оклад курьера; Аi и Вi, — коэффициенты, показывающие:

Аi — во сколько раз превышается значение х;

Bi— на сколько превышается значение х.

Таблица 1

Штатное расписание фирмы

Зарплата курьера  

?

Должность

Коэф. А

Коэф. В

Зарплата

сотрудника

Кол-во

сотрудников

Суммарная зарплата

Курьер

1

0

?

6

?

Младший менеджер

1,5

0

?

8

?

Менеджер

3

0

?

10

?

Зав. Отделением

5

1000

?

3

?

Главный бухгалтер

1,5

0

?

1

?

Программист

4

1500

?

1

?

Системный аналитик

5

0

?

1

?

Ген. директор

2000

?

1

?

Фонд заработной платы:

?

Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel.

2. Создайте таблицу штатного расписания фирмы по приведенному образцу (см. табл. 1). Введите исходные данные в рабочий лист электронной книги.

3. Выделите отдельную ячейку DЗ для зарплаты курьера (переменная «х») и все расчеты задайте с учетом этого. В ячейку DЗ временно введите произвольное число.

4. В столбце D введите формулу для расчета заработной платы по каждой должности. Например, для ячейки D6 формула расчета имеет следующий вид: = В6 * $D$3 + С6 (ячейка DЗ задана в виде абсолютной адресации). Далее скопируйте формулу из ячейки D6 вниз по столбцу автокопированием.

В столбце F задайте формулу расчета заработной платы всех работающих в данной должности. Например, для ячейки F6 формула расчета имеет вид = D6 * Е6. Далее скопируйте формулу из ячейки F6 вниз по столбцу автокопированием.

В ячейке F14 автосуммированием вычислите суммарный фонд заработной платы фирмы.

5. Произведите подбор зарплат сотрудников фирмы для суммарной заработной платы, равной 100000 р. Для этого в меню Сервис активизируйте команду Подбор параметра.

В поле Установить в ячейке появившегося окна введите ссылку на ячейку F14, содержащую формулу расчета фонда заработной платы;

в поле Значение наберите искомый результат 100 000;

в поле Изменяя значение ячейки введите ссылку на изменяемую ячейку DЗ, в которой находится значение зарплаты курьера, и щелкните по кнопке ОК. Произойдет обратный расчет зарплаты сотрудников по заданному условию при фонде зарплаты, равном 100 000 р.

6. Присвойте рабочему листу имя «Штатное расписание 1». Сохраните созданную электронную книгу под именем «Штатное расписание» в своей папке.

Анализ задач показывает, что с помощью MS Excel можно решать линейные уравнения. Задания 1 и 2 показывают, что поиск значения параметра формулы — это не что иное, как численное решение уравнений. Другими словами, используя возможности программы MS Excel, можно решать любые уравнения с одной переменной.

Задание  3. Используя режим подбора параметра и таблицу расчета штатного расписания (см. задание 2), определить заработные платы сотрудников фирмы для ряда заданных значений фонда заработной платы.

Порядок работы

1. Скопируйте содержимое листа «Штатное расписание 1» на новый лист и присвойте копии листа имя «Штатное расписание 2». Выберите коэффициенты уравнений для расчета согласно табл. 2 (один из пяти вариантов расчетов).

2. Методом подбора параметра последовательно определите зарплаты сотрудников фирмы для различных значений фонда заработной платы: 100000, 150000, 200000, 250000, 300000, 350000, 400000 р. Результаты подбора значений зарплат скопируйте в табл. 3. в виде специальной вставки.

Таблица 2.

Должность

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Коэффициент А

Коэффициент В

Коэффициент А

Коэффициент В

Коэффициент А

Коэффициент В

Коэффициент А

Коэффициент В

Коэффициент А

Коэффициент В

Курьер

1

0

1

0

1

0

1

0

1

0

Младший менеджер

1,2

500

1,3

0

1,3

700

1,4

0

1,45

500

Менеджер

2,5

800

2,6

500

2,7

700

2,6

300

2,5

1000

Зав.отделением

3

1500

3,1

1200

3,2

800

3,3

700

3,1

1000

Главный бухгалтер

4

1000

4,1

1200

4,2

500

4,3

0

4,2

1200

Программист

1,5

1200

1,6

800

1,7

500

1,6

1000

1,5

1300

Системный аналитик

3,5

0

3,6

500

3,7

800

3,6

1000

3,5

1500

Ген. директор

5

2500

5,2

2000

5,3

1500

5,5

1000

5,4

3000

Таблица 3

Фонд заработной платы

100000

150000

200000

250000

300000

350000

400000

Должность

Зарплата

сотрудни

ка

Зарплата

сотрудни

ка

Зарплата

сотрудни

ка

Зарплата

сотрудни

ка

Зарплата

сотрудни

ка

Зарплата

сотрудни

ка

Зарплата

сотрудни

Ка

Курьер

?

?

?

?

?

?

?

Младший инженер

?

?

?

?

?

?

?

Менеджер

?

?

?

?

?

?

?

Зав.

Отделением

?

?

?

?

?

?

?

Главный бухгалтер

?

?

?

?

?

?

?

Программист

?

?

?

?

?

?

?

Системный

Аналитик

?

?

?

?

?

?

?

Ген. директор

?

?

?

?

?

?

?

Краткая справка. Для копирования результатов расчетов в виде значений необходимо выделить копируемые данные, произвести запись в буфер памяти (Правка/Копировать), установить курсор в соответствующую ячейку таблицы ответов, задать режим специальной вставки (Правка/Специальная вставка), отметив в качестве объекта вставки — значения (Правка/Специальная вставка/ вставить — значения) .

Специальная вставка информации в виде значений позволяет копировать значения, полученные в результате расчетов, без дальнейшей их зависимости от пересчета формул.

Практическая работа 5. Тема: ЗАДАЧИ ОПТИМИЗАЦИИ (ПОИСК РЕШЕНИЯ)

Цель занятия. Изучение технологии поиска решения для задач оптимизации (минимизации, максимизации).

Задание 1. Минимизация фонда заработной платы фирмы.

Пусть известно, что для нормальной работы фирмы требуется 5… 7 курьеров, 8. ..10 младших менеджеров, 10 менеджеров, 3 заведующих отделами, главный бухгалтер, программист, системный аналитик, генеральный директор фирмы.

Общий месячный фонд зарплаты должен быть минимален. Необходимо определить, какими должны быть оклады сотрудников фирмы, при условии, что оклад курьера не должен быть меньше 1400 р.

В качестве модели решения этой задачи возьмем линейную модель. Тогда условие задачи имеет вид

N1 * A1  * x + (A2 * x + B2)+ . . . + N8 * (A8 * x + B8)  = Минимум,

где N — количество работников данной специальности; x: — зарплата курьера; АI и ВI — коэффициенты заработной платы сотрудников фирмы.

Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel и откройте созданный в Практической работе 4 файл «Штатное расписание».

Скопируйте содержимое листа «Штатное расписание 1» на новый лист и присвойте копии листа имя «Штатное расписание 2».

2. В меню Сервис активизируйте команду Поиск решения .

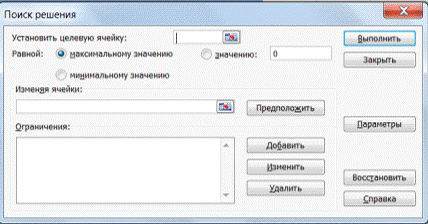
3. В окне Установить целевую ячейку укажите ячейку Р14, содержащую модель — суммарный фонд заработной платы.

Поскольку необходимо минимизировать общий месячный фонд зарплаты, активизируйте кнопку равный — Минимальному значению.

В окне Изменяя ячейки укажите адреса ячеек, в которых будет отражено количество курьеров и младших менеджеров, а также зарплата курьера — $Е$6:$Е$7:$D$3 (при задании ячеек Е6, Е7 и DЗ держите нажатой клавишу [Ctrl]).

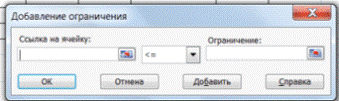
Используя кнопку Добавить в окнах Поиск решения и Добавление ограничений, опишите все ограничения задачи: количество курьеров изменяется от 5 до 7, младших менеджеров от 8 до 10, а зарплата курьера > 1400 (рис. 12.2). Ограничения наберите в виде

$В$3 > = 1400 $Е$6 > = 5 $Е$6 < = 7 $Е$7 > = 8 $Е$7 < = 10.

Активизировав кнопку Параметры, введите параметры поиска.

Запустите процесс поиска решения нажатием кнопки Выполнить. В открывшемся диалоговом окне Результаты поиска решения задайте опцию Сохранить найденное решение.

Решение задачи тривиально: чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд заработной платы

Таблица 1.

Сырье

Нормы расхода сырья

Запас сырья

А

В

С

Сырье 1

18

15

12

350

Сырье 2

6

4

8

200

Сырье 3

5

3

3

100

Прибыль

10

15

20

Задание 2.  Составление плана выгодного производства.

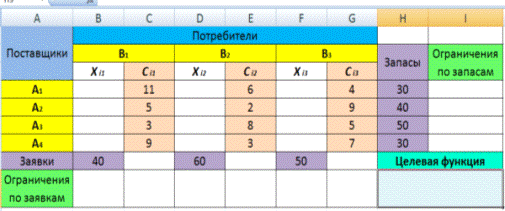
Фирма производит несколько видов продукции из одного и того же сырья — А, В и С. Реализация продукции А дает прибыль 10 р., В — 15 р. и С — 20 р. на единицу изделия.

Продукцию можно производить в любых количествах, поскольку известно, что сбыт обеспечен, но ограничены запасы сырья. Необходимо определить, какой продукции и сколько надо произвести, чтобы общая прибыль от реализации была максимальной.

Нормы расхода сырья на производство продукции каждого вида приведены в табл. 1.

Порядок работы

1. Запустите редактор электронных таблиц Microsoft  Excel и создайте новую электронную книгу.

2. Создайте расчетную таблицу как в табл. 2.. Введите исходные данные и формулы в электронную таблицу. Расчетные формулы имеют такой вид:

Таблица 2

Сырье

Нормы расхода сырья

Запас сырья

Расход сырья

А

В

С

Сырье 1

18

15

12

350

?

Сырье 2

6

4

8

200

?

Сырье 3

5

3

3

100

?

Прибыль  на ед. изд.

10

15

20

Количество

?

?

?

Общая прибыль

?

?

?

?

Расход сырья 1 = (количество сырья 1) * (норма расхода сырья А) + (количество сырья 1) * (норма расхода сырья В) + (количество сырья 1) * (норма расхода сырья С).

Значит, в ячейку F5 нужно ввести формулу = В5 * $В$9 + С5 * * $С$9 + D5 * $D$9.

Обратите внимание, что значения количества сырья каждого вида пока не известны и будут подобраны в процессе решения задания (ячейки В9:D9 пока пустые).

(Общая прибыль по А) = (прибыль на ед. изделий А) * (количество А), следовательно в ячейку В10 следует ввести формулу = В 8 * В9.

Итоговая общая прибыль = (Общая прибыль по А) + (Общая прибыль по В) + (Общая прибыль по С), значит в ячейку Е10 следует ввести формулу = СУММ(В10:D10).

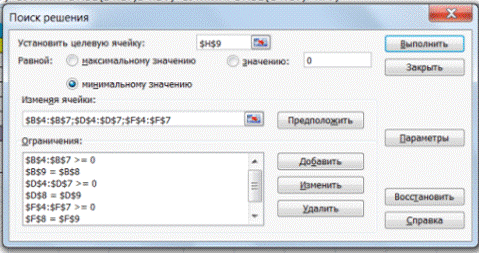
3. В меню Сервис активизируйте команду Поиск решения и введите параметры поиска.

В качестве целевой ячейки укажите ячейку «Итоговая общая прибыль» (Е10), в качестве изменяемых ячеек — ячейки количества сырья — (В9:D9).

Не забудьте задать максимальное значение суммарной прибыли и указать ограничения на запас сырья:

расход сырья 1 < = 350; расход сырья 2 < = 200; расход сырья 3 < = 100, а также положительные значения количества сырья А, В, C = 0.

Установите параметры поиска решения. Для этого кнопкой Параметры откройте диалоговое окно Параметры поиска решения, установите параметры по образцу, задайте линейную модель расчета (Линейность модели).

4. Кнопкой Выполнить запустите Поиск решения.

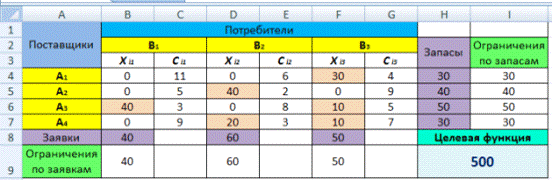
5. Сохраните созданный документ под именем «План производства».

Выводы. Из решения видно, что оптимальный план выпуска предусматривает изготовление 5,56 кг продукции В и 22,22 кг продукции С. Продукцию А производить не стоит. Полученная прибыль при этом составит 527,78 р.

Дополнительные задания

Используя файл «План производства» (см. задание 2), определить план выгодного производства, т.е. какой продукции и сколько необходимо произвести, чтобы общая прибыль от реализации была максимальной.

Выберите нормы расхода сырья на производство продукции каждого вида и ограничения по запасам сырья из таблицы соответствующего варианта (5 вариантов):

Вариант 1

Сырье

Нормы расхода сырья

Запас сырья

А

В

С

Сырье 1

25

17

11

500

Сырье 2

9

7

10

400

Сырье 3

15

8

5

300

Прибыль на ед. изделия

5

10

12

Количество продукции

?

?

?

Общая прибыль

?

?

?

?

Вариант 2

Сырье

Нормы расхода сырья

Запас сырья

А

В

С

Сырье 1

12

11

8

3500

Сырье 2

14

15

2

280

Сырье 3

8

9

10

711

Прибыль на ед. изделия

10

9

8

Количество продукции

?

?

?

Общая прибыль

?

?

?

?

Вариант 3

Сырье

Нормы расхода сырья

Запас сырья

А

В

С

Сырье 1

25

17

11

500

Сырье 2

9

7

10

400

Сырье 3

15

8

5

300

Прибыль на ед. изделия

5

10

12

Количество продукции

?

?

?

Общая прибыль

?

?

?

?

Вариант 4

Сырье

Нормы расхода сырья

Запас сырья

А

В

С

Сырье 1

14

15

19

460

Сырье 2

7

8

12

820

Сырье 3

17

24

6

214

Прибыль на ед. изделия

15

10

25

Количество продукции

?

?

?

Общая прибыль

?

?

?

?

Вариант 5

Сырье

Нормы расхода сырья

Запас сырья

А

В

С

Сырье 1

12

18

3

625

Сырье 2

16

25

13

227

Сырье 3

8

9

10

176

Прибыль на ед. изделия

18

15

9

Количество продукции

?

?

?

Общая прибыль

?

?

?

?

Практическая работа 6 Тема: СВЯЗИ МЕЖДУ ФАЙЛАМИ И КОНСОЛИДАЦИЯ ДАННЫХ В MS EXCEL.

Цель занятия. Изучение технологии связей между файлами и консолидации данных в MS Excel.

Задание 1. Задать связи между файлами.

Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel и создайте новую электронную книгу.

2. Создайте таблицу «Отчет о продажах 1 квартал». Введите исходные данные (Доходы и Расходы):

Доходы = 234,58 р.;

Расходы = 75,33 р.

и проведите расчет Прибыли: Прибыль = Доходы — Расходы. Сохраните файл под именем «1 квартал».

3. Создайте таблицу «Отчет о продажах 2 квартал»  в виде нового файла. Для этого создайте новый документ (Файл/Создать) и скопируйте таблицу отчета о продаже за первый квартал, после чего исправьте заголовок таблицы и измените исходные данные:

Доходы = 452,6 р.;

Расходы = 185,8 р.

Обратите внимание, как изменился расчет Прибыли. Сохраните файл под именем «2 квартал».

4. Создайте таблицу «Отчет о продажах за полугодие» в виде нового файла. Для этого создайте новый документ (Файл/Создать) и скопируйте таблицу отчета о продаже за первый квартал, после чего подправьте заголовок таблицы и в колонке В удалите все значения исходных данных и результаты расчетов. Сохраните файл под именем «Полугодие».

5. Для расчета полугодовых итогов свяжите формулами файлы «1 квартал» и «2 квартал».

Краткая справка. Для связи формулами файлов Excel выполните действия:

• откройте эти файлы (все три файла);

• начните ввод формулы в файле-клиенте (в файле «Полугодие» введите формулу для расчета «Доход за полугодие»).

Формула для расчета:

Доход за полугодие = Доход за 1 квартал + Доход за 2 квартал.

Чтобы вставить в формулу адрес ячейки или диапазона ячеек из другого файла (файла-источника), щелкните мышью по этим ячейкам, при этом расположите окна файлов на экране так, чтобы они не перекрывали друг друга.

Полный адрес ячейки состоит из названия рабочей книги в квадратных скобках, имени листа, восклицательного знака и адреса ячейки на листе.

В ячейке ВЗ файла «Полугодие» формула для расчета полугодового дохода имеет следующий вид:

= ‘[1 квартал.xls] Лист1’!$В$3 + ‘[2 квартал.xls]Лист1’!$В$3.

Аналогично рассчитайте полугодовые значения Расходов и Прибыли, используя данные файлов «1 квартал» и «2 квартал». Сохраните текущие результаты расчетов.

Примечание. Если файл-источник данных закрыт, в формуле, которая на него ссылается, будет указан весь путь для этого файла.

Задание 2. Обновить связи между файлами.

Порядок работы

1. Закройте файл «Полугодие» предыдущего задания.

2. Измените значения «Доходы» в файлах» первого и второго кварталов, увеличив их на 100 р.:                                              Доходы 1 квартала = 334,58 р.;

Доходы 2 квартала = 552,6 р.

Сохраните изменения и закройте файлы.

3. Откройте файл «Полугодие». Одновременно с открытием файла появится окно с предложением обновить связи. Для обновления связей нажмите кнопку Да. Проследите, как изменились данные файла «Полугодие» (величина «Доходы» должна увеличиться на 200 р. и принять значение 887,18 р.).

В случае, когда вы отказываетесь от автоматического обновления связи, вам приходится выполнить это действие вручную.

4. Изучим процесс ручного обновления связи. Сохраните файл «Полугодие» и закройте его.

5. Вновь откройте файлы первого и второго кварталов и измените исходные данные Доходов, увеличив значения на 100 р.:

Доходы 1 квартала = 434,58 р.;

Доходы 2 квартала = 652,6 р.

Сохраните изменения и закройте файлы.

6. Откройте файл «Полугодие». Одновременно с открытием файла появится окно с предложением обновить связи, нажмите кнопку Нет. Для ручного обновления связи в меню Правка выберите команду Связи, появится окно. В окне перечислены все файлы, данные из которых используются в активном файле «Полугодие»

Расположите его так, чтобы были видны данные файла «Полугодие», выберите файл «1 квартал» и нажмите кнопку Обновить и проследите, как изменились данные файла «Полугодие». Аналогично выберите файл «2 квартал» и нажмите кнопку Обновить. Проследите, как вновь изменились данные файла «Полугодие».

Примечание. При изменении данных в нескольких исходных файлах обновление связи производится для каждого файла.

Задание 3. Консолидация данных для подведения итогов по таблицам данных сходной структуры.

Краткая справка. В Excel существует удобный инструмент для подведения итогов по таблицам данных сходной структуры, расположенных на разных листах или разных рабочих книгах, — Консолидация данных. При этом одна и та же операция (суммирование, вычисление среднего и др.) выполняется по всем ячейкам нескольких прямоугольных таблиц, и все формулы Excel строит автоматически.

Порядок работы

1. Откройте все три файла задания 2 и в файле «Полугодие» в колонке В удалите все численные значения данных. Установите курсор в ячейку ВЗ.

2. Выполните команду Данные/Консолидация. В появившемся окне Консолидация выберите функцию — «Сумма».

В строке «Ссылка» сначала выделите в файле «1 квартал» диапазон ячеек ВЗ:В5 и нажмите кнопку Добавить, затем выделите в файле «2 квартал» диапазон ячеек ВЗ:В5 и опять нажмите кнопку Добавить. В списке диапазонов будут находиться две области данных за первый и второй кварталы для консолидации. Далее нажмите кнопку ОК, произойдет консолидированное суммирование данных за первый и второй кварталы.

Дополнительные задания

Задание 4. Консолидация данных для подведения итогов по таблицам неоднородной структуры.

Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel и создайте новую электронную книгу. Наберите отчет по отделам за третий квартал по образцу (табл. 1). Произведите расчеты и сохраните файл с именем «3 квартал».

Таблица 1

 Отчет о продажах по отделам 3 квартал

Отдел 1ё

Отдел 3

Отдел 4

Всего:

Доходы

124,52  р.

248,56 р.

741,55 р.

?

Расходы  

125,30 р.

198,36 р.

625,80 р.

?

Прибыль

?

?

?

?

2. Создайте новую электронную книгу. Наберите отчет по отделам за четвертый квартал по образцу (табл. 2). Произведите расчеты и сохраните файл с именем «4 квартал».

Таблица 2

Отчет о продажах по отделам 4 квартал

Отдел 1

Отдел 2

Всего:

Доходы

128,66 р.

279,60 р.

?

Расходы  

117,50 р.

255,40 р.

?

Прибыль

?

?

?

3. Создайте новую электронную книгу. Наберите название таблицы «Полугодовой отчет о продажах по отделам». Установите курсор на ячейку АЗ и проведите консолидацию за третий и четвертый кварталы по заголовкам таблиц. Для этого выполните команду Данные/Консолидация. В появившемся окне консолидации данных сделайте ссылки на диапазон ячеек АЗ:Е6 файла «3 квартал» и АЗ:D6 файла «4 квартал». Обратите внимание, что интервал ячеек включает имена столбцов и строк таблицы.

В окне Консолидация активизируйте опции (поставьте галочку):

• подписи верхней строки;

• значения левого столбца;

• создавать связи с исходными данными (результаты будут не константами, а формулами).

После нажатия кнопки ОК произойдет консолидация. Сохраните все файлы в папке вашей группы.

Обратите внимание, что все данные корректно сгруппированы по их заголовкам (по отделам). В левой части экрана появятся так называемые кнопки управления контуром (иерархической структурой). С их помощью можно скрывать или показывать исходные данные.

Практическая работа 7. Тема: ЭКОНОМИЧЕСКИЕ РАСЧЕТЫ В MS EXCEL

Цель занятия. Изучение технологии экономических расчетов в табличном процессоре.

Задание 1. Оценка рентабельности рекламной кампании фирмы.

Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel и создайте новую электронную книгу.

2. Создайте таблицу оценки рекламной кампании по образцу табл. 1. Введите исходные данные: Месяц, Расходы на рекламу А(0) (р.), Сумма покрытия В(0) (р.), Рыночная процентная ставка (i) = 13,7%.

Выделите для рыночной процентной ставки, являющейся константой, отдельную ячейку — СЗ, и дайте этой ячейке имя «Ставка».

Таблица 1

Оценка рекламной кампании

Рыночная процент-ная ставка

13,7 %

Месяц (n)

Расходы на рекламу А(0) (руб.)

Текущая стоимость расходов на рекламу А (n) (руб.)

Расходы на рекламу нараста-ющим итогом (руб.)

Сумма покрытия В(0) (руб.)

Текущая стоимость  суммы покрытия В(n) (поступаю-щих доходов) (руб.)

Сумма покрытия нарастающим итогом (руб.)

Сальдо дисконтиро-ванных денежных потоков нарастающим итогом (руб.)

1

75250,00

?

?

?

?

?

2

125700,00

?

?

25250,00

?

?

?

3

136940,00

?

?

75950,00

?

?

?

4

175020,00

?

?

105700,00

?

?

?

5

170600,00

?

?

1683000,00

?

?

?

6

?

?

145500,00

?

?

?

7

?

?

137450,00

?

?

?

8

?

?

127420,00

?

?

?

9

?

?

43100,00

?

?

?

10

?

?

?

?

?

11

?

?

?

?

?

12

?

?

?

?

?

Краткая справка. Присваивание имени ячейке или группе ячеек.

• Выделите ячейку (группу ячеек или несмежный диапазон), которой необходимо присвоить имя.

• Щелкните на поле Имя, которое расположено слева в строке формул.

• Введите имя ячеек.

• Нажмите клавишу [Enter].

Помните, что по умолчанию имена являются абсолютными ссылками.

3. Произведите расчеты во всех столбцах таблицы.

Краткая справка. Расходы на рекламу осуществлялись в течение нескольких месяцев, поэтому выбираем динамический инвестиционный учет. Это предполагает сведение всех будущих платежей и поступлений путем дисконтирования на сумму рыночной процентной ставки к текущему значению.

Формулы для расчета:

А(n) = А(0) * (1 + i/12)(1-n), в ячейке С6 наберите формулу

= В6 * (1 + ставка/12)^(1 — $А6).

Примечание. Ячейка А6 в формуле имеет комбинированную адресацию: абсолютную адресацию по столбцу и относительную по строке, и записывается в виде $А6.

При расчете расходов на рекламу нарастающим итогом надо учесть, что первый платеж равен значению текущей стоимости расходов на рекламу, значит в ячейку D6 введем значение = С6, но в ячейке D7 формула примет вид = D6 + С7. Далее формулу ячейки D7 скопируйте в ячейки D8:D17.

Обратите внимание, что в ячейках нарастающего итога с мая по декабрь будет находиться одно и то же значение, поскольку после мая месяца расходов на рекламу не было.

Выберем сумму покрытия в качестве ключевого показателя целесообразности инвестиций в рекламу. Она определяет, сколько приносит продажа единицы товара в копилку возврата инвестиций.

Для расчета текущей стоимости покрытия скопируйте формулу из ячейки С6 в ячейку F6. В ячейке F6 должна быть формула

= Е6 * (1 + ставка/12)^(1 — $А6).

Далее с помощью маркера автозаполнения скопируйте формулу в ячейки F7:F17.

Сумма покрытия нарастающим итогом рассчитывается аналогично расходам на рекламу нарастающим итогом, поэтому в ячейку G6 поместим содержимое ячейки F6 (= F6), а в G7 введем формулу

=G6 + F7.

Далее формулу из ячейки G7 скопируем в ячейки G8:G17. В последних трех ячейках столбца будет представлено одно и то же значение, ведь результаты рекламной кампании за последние три месяца на сбыте продукции уже не сказывались.

Сравнив значения в столбцах D и G, уже можно сделать вывод о рентабельности рекламной кампании, однако расчет денежных потоков в течение года (колонка Н), вычисляемый как разница колонок G и D, показывает, в каком месяце была пройдена точка окупаемости инвестиций. В ячейке Н6 введите формулу = Gб – D6, и скопируйте ее на всю колонку.

Проведите условное форматирование результатов расчета колонки Н: отрицательных чисел — синим курсивом, положительных чисел — красным цветом шрифта. По результатам условного форматирования видно, что точка окупаемости приходится на июль месяц.

4. В ячейке Е19 произведите расчет количества месяцев, в которых сумма покрытия имеется (используйте функцию «Счет» (Вставка/ Функция/ Статистические), указав в качестве диапазона «Значение 1» интервал ячеек Е7:Е14). После расчета формула в ячейке Е19 будет иметь вид = СЧЕТ(Е7:Е14).

5. В ячейке Е20 произведите расчет количества месяцев, в которых сумма покрытия больше 100000 р. (используйте функцию СЧЕТЕСЛИ, указав в качестве диапазона «Значение» интервал ячеек Е7:Е14, а в качестве условия >100 000). После расчета формула в ячейке Е20 будет иметь вид = СЧЕТЕСЛИ(Е7:Е14) .

6. Постройте графики по результатам расчетов : «Сальдо дисконтированных денежных потоков нарастающим итогом» по результатам расчетов колонки Н;

«Реклама: расходы и доходы» по данным колонок D и G (диапазоны D5:D17 и G5:G17 выделяйте, удерживая нажатой клавишу

Графики дают наглядное представление об эффективности расходов на рекламу и графически показывают, что точка окупаемости инвестиций приходится на июль месяц.

7. Сохраните файл в папке вашей группы.

Задание 2. Фирма поместила в коммерческий банк 45 000 р. на 6 лет под 10,5 % годовых. Какая сумма окажется на счете, если проценты начисляются ежегодно? Рассчитать, какую сумму надо поместить в банк на тех же условиях, чтобы через 6 лет накопить 250 000 р.?

Порядок работы

1. Запустите редактор электронных таблиц Microsoft Excel и создайте новую электронную книгу или перейдите на новый лист книги, созданной в Задании 1.

2. Создайте таблицу констант и таблицу для расчета наращенной суммы вклада по образцу (табл.2).

3. Произведите расчеты А(n) двумя способами:

с помощью формулы А(n) = А(0) * (1 +i)n (в ячейку D10 ввести формулу = $В$3 * (1 + $В$4)^А10 или использовать функцию СТЕПЕНЬ);

с помощью функции БЗ (см. табл. 2).

Таблица 2

Накопление финансовых средств фирмы

А(0)

45000

Процентная ставка (i)

10,50%

Расчет наращенной суммы

Период n

А(n) расчет по формуле

А(n) расчет по функции БЗ

1

?

?

2

?

?

3

?

?

4

?

?

5

?

?

6

?

?

Краткая справка. Функция БЗ возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки.

Синтаксис функции БЗ: БЗ (ставка; кпер; плата; нз; тип), где ставка — это процентная ставка за период; кпер — это общее число периодов выплат годовой ренты; плата — это выплата, производимая в каждый период, вводится со знаком «-», это значение не может меняться в течение всего периода выплат. Обычно плата состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов; нз — это текущая стоимость, или общая сумма всех будущих платежей с настоящего момента. Если аргумент нз опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента плата; тип — это число 0 или 1, обозначающее, когда должна производиться выплата. Если аргумент тип опущен, то он полагается равным 0 (0 — платеж в конце периода; 1 — платеж в начале периода).

Все аргументы, обозначающие деньги, которые платятся (например, депозитные вклады), представляются отрицательными числами. Деньги, которые получены (например, дивиденды), представляются положительными числами.

Для ячейки С10 задание параметров расчета функции БЗ имеет вид.

4. Используя режим Подбор параметра (Сервис/Подбор параметра) рассчитайте, какую сумму надо поместить в банк на тех же условиях, чтобы через 6 лет накопить 250 000 р. Задание параметров подбора значения суммы вклада для накопления 250 000 р.  В результате подбора выясняется, что первоначальная сумма для накопления в 137330,29 р. позволит накопить заданную сумму в 250 000 р.

Дополнительное задание

Задание 3. Сравнить доходность размещения средств организации, положенных в банк на один год, если проценты начисляются т раз в год, исходя из процентной ставки) = 9,5 % годовых (табл. 3); по результатам расчета построить график изменения доходности инвестиционной операции от количества раз начисления процентов в году (капитализации).

Таблица 3

Зависимость доходности от условий капитализации

Таблица констант

i

9,50%

число начислений процентов в год (m)

доходность

1

?

2

?

3

?

4

?

5

?

6

?

7

?

8

?

9

?

10

?

11

?

12

?

Выясните, при каком значении  i доходность (при капитализации т = 12) составит 15 %.

Краткая справка. Формула для расчета доходности

Доходность = (1 + i/m)m— 1.

Примечание. Установите формат значений доходности — «Процентный».

Для проверки правильности ваших расчетов сравните полученный результат с правильным ответом:

для m = 12 доходность = 9,92 %.

Произведите обратный расчет (используйте режим Подбор параметра) для выяснения, при каком значении i доходность (при капитализации m = 12) составит 15 % .

Практическая работа 8. Тема: КОМПЛЕКСНОЕ ИСПОЛЬЗОВАНИЕ ПРИЛОЖЕНИЙ MICROSOFT OFFICE ДЛЯ СОЗДАНИЯ ДОКУМЕНТОВ

Цель занятия. Закрепление и проверка навыков создания комплексных текстовых документов с встроенными расчетными таблицами и графиками.

Порядок работы

Применяя все известные вам приемы создания и форматирования текстовых и табличных документов, выполните задания по образцу, стараясь создать по внешнему виду документ как можно ближе к оригиналу задания.

Задание 1. Создать таблицу расчета прибыли фирмы, произвести расчеты суммарных доходов, расходов (прямых и прочих) и прибыли; произвести пересчет прибыли в условные единицы по курсу (рис. 15.1).

Таблица 1

Расчет прибыли фирмы

Доходы всего

?

Расходы всего

?

в т.ч.

в т.ч.

собственное производство

1725245,90

прямые

прочие

субподрядные организации

2974965,30

зарплата

320352,38

обслуж. Банков

3363,66

ЕСН

131948,98

налоги

21338,00

амортизация ОС

25861,03

налоги на дороги

13478,00

амортизация НА

2423,16

налог на имущество

7860,00

материалы

695882,84

всего:

услуги связ. с производством

78952,86

субпдряд

2974965,30

всего:

?

прибыль

?

прибыль (у.е.)

?

курс  1 у.е.

32,45 р.

Выясните, при каком значении зарплаты прибыль будет равна 500000 р. (используйте режим Подбор параметра).

Краткая справка. Формулы для расчета:

Расходы: всего = Прямые расходы + Прочие расходы;

Прибыль = Доходы: всего — Расходы: всего;

Прибыль (у. е.) = Прибыль х Курс 1 у.е.

Задание 2. Создать «Ведомость учета остатков продуктов и товаров на складе».

Текстовую часть документа создайте в текстовом редакторе MS Excel, таблицу учета продуктов и товаров создайте в MS Ехсе1, проведите расчеты и скопируйте в текстовый документ.

Задание 3. Фирма хочет накопить деньги для реализации нового проекта. С этой целью в течение пяти лет она кладет на счет ежегодно по 1250 $ в конце каждого года под 8 % годовых (табл. 2). Определить сколько будет на счете фирмы к концу пятого года (в MS Ехсе1). Построить диаграмму по результатам расчетов. Выясните, какую сумму надо ежегодно класть на счет, чтобы к концу пятого года накопить 10 000 $.

Таблица 2

Процентная ставка (годовая)

Внесенные раз в год платежи

i

D

8%

$ 1250,00

 число лет действия ренты (n)

Величина суммы на счете, рассчитанная по формуле

Величина суммы на счете, рассчитанная по функции БЗ

1

?

?

2

?

?

3

?

?

4

?

?

5

?

?

Краткая справка. Формула для расчета

Сумма на счете = D * ((1 + i)^n — 1)/i.

Сравните полученный результат с правильным ответом:

для n = 5 сумма на счете = 7333,25 $.

Для расчета суммы ежегодного вклада для накопления к концу пятого года 10 000 $ используйте режим Подбор параметра.

Наименование организации

ВЕДОМОСТЬ №

УЧЕТА ОСТАТКОВ ПРОДУКТОВ И ТОВАРОВ НА СКЛАДЕ
      от «      »        200     г.

№

п/п

Продукты и товары

Единицы

измерения

Учетная цена

р. к.

Остаток на

«01» июля 2004 г.

Наименование

Код

Наимено-вание

Код по

ОКЕИ

Коли-чество

Сумма

 р. к.

1

2

3

4

5

6

7

8

1

Бульон из кубика

шт.

5,00

2

Ветчина

кг.

118,89

3

Говядина вырезка

кг.

85,00

4

Говядина зад

кг.

60,00

5

Колбаса с/к.

кг.

165,00

6

Купаты

кг.

31,39

7

Куры

кг.

65,20

8

Крылья куриные

кг.

49,44

9

Легкие

кг.

45,00

10

Окорочка куриные

кг.

33,06

11

Пельмени

кг.

49,17

12

Печень говяжья

кг.

40,83

13

Сардельки (сосиски)

кг.

50,56

14

Свинина корейка

кг.

90,00

15

Свинина зад.

кг.

65,00

16

Сердце

кг.

40,00

Итого по странице:

количество порядковых номеров ___

общее количество единиц фактически

на сумму фактически _________

Материально ответственное лицо:

Задание 4. Создать «Акт о порче товарно-материальных ценностей».

Текстовую часть документа создайте в текстовом редакторе MS Word, таблицу расчета стоимости товарно-материальных ценностей (ТМЦ) для списания создайте в MS Ехсе1, проведите расчеты и скопируйте в текстовый документ.

Наименование организации ___                                   «Утверждаю»
Отдел ________________                                      Руководитель организации

                                                                                              200    г.

АКТ

О ПОРЧЕ ТОВАРНО-МАТЕРИАЛЬНЫХ ЦЕННОСТЕЙ

ОТ «__»___________ 200_ г.

Комиссия в составе: председатель __________________, члены комиссии _________________________ на основании приказа от _________ № _______ составила настоящий акт в том, что указанные ниже ценности пришли в негодность и подлежат списанию.

Итого по акту _____ наименование на сумму ___ р. __ к.

(прописью по розничным ценам или по ценам приобретения)

Председатель комиссии ________________________

Задание 5. Фирма собирается инвестировать проект в течение трех лет.

Имеется два варианта инвестирования:

1-й вариант: под 12 % годовых в начале каждого года;

2-й вариант. под 14 % годовых в конце каждого года.

Предполагается ежегодно вносить по 500 000 р.

Определить, в какую сумму обойдется проект (табл. 4).

Таблица 4

i

Вариант 1

12%

Вариант 2

14%

D

500000,00 р.

Период (n)

Вариант 1

Вариант 2

Сумма проекта (расчет по формуле)

Сумма проекта (расчет по функции БЗ)

Сумма проекта (расчет по формуле)

Сумма проекта (расчет по функции БЗ)

1

?

?

?

?

2

?

?

?

?

3

?

?

?

?

Порядок работы

Постройте сравнительную диаграмму по результатам расчетов для двух, вариантов инвестирования. Выясните, какую сумму надо вносить ежегодно по каждому варианту инвестирования, чтобы общая сумма проекта составила

2000000 р.

Сравните полученный результат с правильным ответом:

для n = 3 сумма проекта по 1-му варианту — 1889664,00 р.; по 2-му варианту — 1719800,00 р.

Краткая с п р а в к а. Формулы для расчета:

1-й вариант: Сумма проекта = D * ((1 + i))^ n — 1) * (1 +i)/i;

2-й вариант: Сумма проекта = D * ((1 + i)^ n — 1)/i.

Задание 6. Создать по образцу бланк счета для аренды автомобиля в MS Ехсе1.

Автомобиль использовался с 12.10.04 00:00 до 14.10.04 16:40.

Тарифная ставка = 120 р./ч.

Краткая справка. Для ввода даты используйте функции: «Сегодня». При вводе периода аренды автомобиля используйте формат «Дата», в котором присутствуют дата и время.

Значение даты и времени представляют собой так называемые серийные числа, поэтому с ними можно работать как с обычными числами, например вычитать одну дату из другой, чтобы получить разность в днях.

Порядок работы

Для подсчета количества часов аренды автомобиля установите в ячейке «Итого» числовой формат, рассчитайте разницу дат пользования (Дата по: — Дата с:). Вы получите количество дней пользования автомобилем. Для перевода количества дней пользования автомобилем в часы произведите умножение на 24 .

Расчет суммы счета сделайте по следующей формуле

Всего = «Тариф за час» * Итого.

СПИСОК ЛИТЕРАТУРЫ

  1. Основы современных компьютерных знаний. А.Д.Хомоненко «КОРОНА»,2012
  2. В.П. Попов Основы  компьютерных технологий. – М.:  Финансы и статистика 2002
  3. В.С. Мишкина и др. Лабораторный практикум по информатике. – М.: Высш. Шк.,2003А.В.
  4. А.В. Могилев и др. Информатика Под редакцией Е.К. Хеннера. – М.: Издательский центр «Академия»,2003
Источник

Тема: 
Решение задач с помощью уравнений средствами табличного процессора Microsoft Excel

Эпиграф
урока:

«Сосредотачивая
на задаче свое внимание, вы подготавливаете свою память к тому, чтобы извлечь
из нее все, что может принести вам пользу»

Пойа
Д.

 Оборудование: цветные карточки
«Светофор», карточки с заданиями (уравнения, задачи), компьютер с проектором,
ноутбуки для учащихся 4-5 шт.

                          Ход урока.

1.   Этап.
Организационный момент.

Приветствие.

2. Этап. Актуализация знаний.

Повторение. Решение уравнений.

1. Устный счет (Работа в парах). Диктант:   /учащиеся записывают + или — /

а)     Корни
уравнения изменяются, если обе части уравнения  умножить на число (-10) (Нет)

б)    Может
ли разность двух отрицательных чисел быть целым положительным числом? (Да)

в)     Корни
уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части
уравнения в другую, изменив при этом его знак (Да)

г)     Если
перед скобками стоит знак «–», то нужно раскрыть скобки, сохранив знаки
слагаемых (Нет)

д)    На
ноль делить можно (Нет)

е)     Чтобы
сложить подобные слагаемые, надо сложить их коэффициенты и результат умножить
на общую буквенную часть (Да)

ж)   Если
перед скобками стоит знак «+», то можно опустить скобки, сохранив знаки
слагаемых (Да)

з)     Чтобы
перемножить два числа с разными знаками, надо перемножить модули этих чисел «–»
(Нет)

и)    Произведение
может быть равно нулю, когда хотя бы один из множителей равен нулю (Да)

к)     Может
ли сумма двух целых положительных чисел быть равной 0?(Нет)

Учащиеся обмениваются тетрадями. Проверка:
– + + – – + + – + –

 Оценивание работы на полях: “5” – 10-9
верных знаков, “4” – 7-8 знаков, “3” – 6-5 знака.

2.
Решение уравнений.

При решении
уравнений были допущены ошибки. Найдите и исправьте их.

а)     х+2,7=3                          (х+2,7=3  
х=3-2,7   х=0,3)

х=3+2,7

х=5,7

б)    3х-1=2(х-2)                     (3х-1=2х-4 
3х-2х=1-4   х=-3)

3х-1=2х-4

3х+2х=1+4

5х=5

х=1

в)     25-4х=12-5х                   (5х-4х=12-25 
х=-13)

5х-4х=12+25

х=37

г)     2х+7=х+5,5                     (2х-х=5,5-7 
х=-1,5)

2х-х=5,5-7

х=4,8

д)    7х+3=7х+5                     (0х=2,
уравнение не имеет корней)

7х-7х=5-3

х=2

е)     3х+х-7=4х-7                   (0х=0,
х — любое число)

4х-4х=7-7

х=0

3.
Упрощение выражений.

Докажите, что
значение выражения 5(а+1)-(5а-4) не зависит от значения переменной.

Доказательство:

5(а+1)-(5а-4)=5а+5-5а+4=9

Следовательно,
значение выражения 5(а+1)-(5а-4) не зависит от значения переменной.

3.
Этап. Закрепление.

Решение задач с помощью табличного
процессора Microsoft Excel.
(Учащиеся работают на компьютерах)

Задача№1

Сейчас отцу 34 года, а сыну 11 лет. Через
сколько лет возраст отца будет в 2 раза больше возраста сына?

На экранах компьютеров учащиеся видят
таблицу:

Необходимо
составить уравнение к задаче по данной таблице и решить его:

Составим
уравнение: 34+х=2(11+х)

Решаем уравнение:

34+х=22+2х;

2х-х=34-22;

х=12.

Ответ: через 12 лет возраст отца будет в 2
раза больше возраста сына.

Проверка:

Учащиеся вводят в таблицу полученный
результат и формулы:

При условии, что в ячейке D2
получается значение 2, задача решена верно.

Задача№2

2.Расстояние от
пристани А до пристани В катер проплыл за 6 ч., а от пристани В до пристани А –
за 7 ч. Скорость течения реки 2км/ч. Найти собственную скорость катера.

На экранах компьютеров учащиеся видят
таблицу:

х км/ч.- собственная скорость катера

Необходимо
составить уравнение к задаче по данной таблице и решить его:

Составим
уравнение: 6(х+2)= 7(х-2)

Решаем уравнение:

6х+12=7х-14;

6х-7х=-14-12;

-х=-26;

х=26.

Ответ: собственная скорость катера 26
км/ч.

Проверка:

Учащиеся вводят в таблицу полученный
результат и формулы:

При условии, что в ячейках E2
и E3 получаются равные
значения, задача решена верно.

Физминутка для глаз.

4. Этап. Самостоятельная работа

1.На первой стоянке в 4 раза меньше
автомашин, чем на второй. После того как на первую приехали 35 автомашин, а со
второй уехали 25 автомашин, автомашин на стоянках стало поровну. Сколько
автомашин было на каждой стоянке первоначально.

На экранах компьютеров учащиеся видят
таблицу:

Необходимо
составить уравнение к задаче по данной таблице, решить его и выполнить проверку
средствами табличного процессора Microsoft Excel:

Составим
уравнение: х+35=4х-25

Решаем
уравнение:

х-4х=-25-35

-3х=-60

х=20 (машин)

4*20=80 (машин)

Ответ: на каждой стоянке
первоначально было 20 машин и 80 машин соответственно.

5. Этап. Домашнее  задание 

Уровень “3” —
№606 из учебника

Уровень “4” —
№611 из учебника

Уровень “5” –
составить 3 задачи, одну из них решить

6. Этап. Рефлексия.

Учащиеся оценивают
свою деятельность на уроке с помощью «Светофора»: Зелёная карточка – мне все
понятно

Желтая
карточка – у меня возникли затруднения

Красная
карточка – много непонятного

Источник

Цифровые образовательные ресурсы в профессиональной деятельности Презентации Решение задач в электронных таблицах Microsoft Excel Автор: Пивнева Н. Ю. учитель информатики и ИКТ МКОУ Дроздовская СОШ Воронежской области, Ольховатского района

Цифровые образовательные ресурсы в профессиональной деятельности

Презентации

Решение задач в электронных

таблицах Microsoft Excel

Автор: Пивнева Н. Ю.

учитель информатики и ИКТ

МКОУ Дроздовская СОШ

Воронежской области, Ольховатского района

Цели работы: В последнее время интерес к решению задач с использованием электронных таблиц стремительно растет не только у преподавателей информатики, но и у учителей других дисциплин: математика, физика, биология, география. Тем не менее основная нагрузка в изучении электронных таблиц приходится на уроки информатики. Я показала в данной работе, как с помощью электронных таблиц эффективно решаются задачи из разных сфер жизни: Решение задачи моделирования жизненной ситуации Решение статистической задачи Решение задачи по результатам исследований

Цели работы:

В последнее время интерес к решению задач с использованием электронных таблиц стремительно растет не только у преподавателей информатики, но и у учителей других дисциплин: математика, физика, биология, география. Тем не менее основная нагрузка в изучении электронных таблиц приходится на уроки информатики.

Я показала в данной работе, как с помощью электронных таблиц эффективно решаются задачи из разных сфер жизни:

  • Решение задачи моделирования жизненной ситуации
  • Решение статистической задачи
  • Решение задачи по результатам исследований

ВВЕДЕНИЕ В повседневной жизни людям приходится делать постоянные расчеты, поскольку постоянно возрастает объем информации и практически каждый день нам приходится выполнять финансовые, научные, личные расчеты разной степени сложности. Огромные возможности для этого несет в себе среда электронной таблицы. Это объясняется тем, что она: Одна из самых распространенных программ общего назначения и владение технологий работы в ней является одним из показателей информационной культуры человека. Позволяет обрабатывать большие массивы числовых данных, например статистические данные, результаты экспериментов и многое другое. Позволяет достаточно просто решить большое разнообразие задач (Самое главное-это связать параметры, описывающие объект, явление или процесс, некоторыми математическими соотношениями). Позволяет получить результаты моделирования практически мгновенно, с использованием простых технологий

ВВЕДЕНИЕ

В повседневной жизни людям приходится делать постоянные расчеты, поскольку постоянно возрастает объем информации и практически каждый день нам приходится выполнять финансовые, научные, личные расчеты разной степени сложности.

Огромные возможности для этого несет в себе среда электронной таблицы. Это объясняется тем, что она:

  • Одна из самых распространенных программ общего назначения и владение технологий работы в ней является одним из показателей информационной культуры человека.
  • Позволяет обрабатывать большие массивы числовых данных, например статистические данные, результаты экспериментов и многое другое.
  • Позволяет достаточно просто решить большое разнообразие задач (Самое главное-это связать параметры, описывающие объект, явление или процесс, некоторыми математическими соотношениями).
  • Позволяет получить результаты моделирования практически мгновенно, с использованием простых технологий

Достоинства электронных таблиц Поставленные задачи обычно решают с помощью языков программирования или другими средствами, хотя эти задачи можно легко и эффективно решать средствами Excel.

Достоинства электронных таблиц

Поставленные задачи обычно

решают с помощью языков

программирования или

другими средствами, хотя эти

задачи можно легко и

эффективно

решать средствами Excel.

Этапы решения задач(эл. табл.) Постановка задачи(выяснение условий, оформление решения разделов «дано» и «найти», заполнение таблицы данными, которые содержит в себе задача). Составление математической модели. Составление алгоритма решения. Оформление решения формул в виде текста в разделе «математическая модель». Создание сетки вычислений в разделе «решение». Анализ полученных результатов.

Этапы решения задач(эл. табл.)

  • Постановка задачи(выяснение условий, оформление решения разделов «дано» и «найти», заполнение таблицы данными, которые содержит в себе задача).
  • Составление математической модели.
  • Составление алгоритма решения.
  • Оформление решения формул в виде текста в разделе «математическая модель».
  • Создание сетки вычислений в разделе «решение».
  • Анализ полученных результатов.

Пяточок-сексот ЛНИ... Донос Пяточка в лесную налоговую инспекцию:

Пяточок-сексот ЛНИ…

  • Донос Пяточка в лесную налоговую инспекцию:

«Хорошо живет на свете Винни Пух..»

  • Какой подоходный налог должен заплатить Пух лесному государству, если его ежегодный доход с продажи «липового» меда, сделанного из сахара, крахмала, химических красителей и ароматизаторов, составляет 2400 баксов?
  • Государственный лесной налог в этом финансовом году, по Лесному налоговому кодексу, составляет 20% от выручки в рублях.
  • Винни Пух не растерялся и сказал рассудительному Кролику: — Ты будешь у нас адвокатом, реши задачу с помощью электронных таблиц Excel , используя текущий курс рубля относительно доллара.
  • — И не забудь посчитать еще 5% от суммы налога за то, что Пух скрывался от ЛНИ два месяца — не унимался Пятачок.
  • Так сколько денег всего задолжал Винни Пух налоговой инспекции в этом году? Сколько Винни Пух задолжал за прошлый год, если Государственный лесной налог в прошлом финансовом году, по Лесному налоговому кодексу, составлял 35% от выручки в рублях.

Дано: Доход Пятачка$ Найти: 2400 Подоходный Налог по НЛК % 20 Штраф % Сумма долга Пятачка руб.   5 Курс $ 30     Постановка задачи Алгоритм решения Перевести доход Пяточка из $ в рубли Вычислить подоходный налог по НЛК в рублях. Вычислить штраф за 2 месяца в рублях.

Дано:

Доход Пятачка$

Найти:

2400

Подоходный Налог по НЛК %

20

Штраф %

Сумма долга Пятачка руб.

5

Курс $

30

Постановка задачи

Алгоритм решения

  • Перевести доход Пяточка из $ в рубли
  • Вычислить подоходный налог по НЛК в рублях.
  • Вычислить штраф за 2 месяца в рублях.

Дано: Доход Пятачка$ 2400 Подоходный Налог по НЛК % Найти: 20 Сумма долга Пятачка руб. Штраф % Курс $ 5   30   Решение:   Подоходный налог руб.   Штраф руб. Ответ:       Ввод формул 15120 B7+B8 Решение задачи 14400 15120 =B2*B5/100*B3 720 B7/100*B4

Дано:

Доход Пятачка$

2400

Подоходный Налог по НЛК %

Найти:

20

Сумма долга Пятачка руб.

Штраф %

Курс $

5

30

Решение:

Подоходный налог руб.

Штраф руб.

Ответ:

Ввод формул

15120

B7+B8

Решение задачи

14400

15120

=B2*B5/100*B3

720

B7/100*B4

Статистика Подсчитайте суммарное количество осадков за каждый год (СУММ). Найдите минимальное количество осадков за каждый год. Найдите максимальное количество осадков за каждый год. Постройте диаграмму.

Статистика

  • Подсчитайте суммарное количество осадков за каждый год (СУММ).
  • Найдите минимальное количество осадков за каждый год.
  • Найдите максимальное количество осадков за каждый год.
  • Постройте диаграмму.

Количество осадков 606 454,7 657,7 =СУММ(B3:B14) 8,7 14,5 9,4 =МИН(B3:B14) 145,2 129,1 152,6 =МАКС(B3:B14)

Количество осадков

606

454,7

657,7

=СУММ(B3:B14)

8,7

14,5

9,4

=МИН(B3:B14)

145,2

129,1

152,6

=МАКС(B3:B14)

Задача для самостоятельного выполнения

Задача для

самостоятельного

выполнения

Биоритмы человека Существует легенда о том, что в древнем Китае монахи день за днем вели наблюдения за человеком. В результате они пришли к выводу, что период для физической активности составляет 23 дня, эмоциональной - 28 дней и интеллектуальной - 33 дня. Функции состояния человека в момент его рождения равны нулю, затем начинают возрастать, каждая за свой период принимает одно положительное максимальное и одно отрицательное минимальное значение. Указанные циклы можно описать приведенными ниже выражениями, в которых переменная х соответствует возрасту человека в днях:

Биоритмы человека

Существует легенда о том, что в древнем Китае монахи день за днем вели наблюдения за человеком. В результате они пришли к выводу, что период для физической активности составляет 23 дня, эмоциональной — 28 дней и интеллектуальной — 33 дня.

Функции состояния человека в момент его рождения равны нулю, затем начинают возрастать, каждая за свой период принимает одно положительное максимальное и одно отрицательное минимальное значение.

Указанные циклы можно описать приведенными ниже выражениями, в которых переменная х соответствует возрасту человека в днях:

Алгоритм решения задачи В среде MS Excel создать таблицу Биоритмы человека Периоды активности физическая эмоциональная 23 28 интеллектуальная Дата рождения   33 Порядковый день ввести дату отсчета заполнить вниз с шагом 1 день Физичес-кая Эмоциона- Интеллек- льная туальная Ввести в таблицу свою дату рождения Заполнить столбец Порядковый день Дата заполняется по формату 00.00.00. Признаком правильного набора даты является правое выравнивание в ячейке. Ввести расчетные формулы. При записи формул использовать стандартные функции SIN(...) и ПИ(...). Значение х вычисляется как разность между датой рождения (абсолютная ссылка) и датой порядкового дня. Скопировать расчетные формулы в тридцать строк Выделить столбцы с биоритмами Построить диаграмму: Вставка - График.

Алгоритм решения задачи

  • В среде MS Excel создать таблицу

Биоритмы человека

Периоды активности

физическая

эмоциональная

23

28

интеллектуальная

Дата рождения

33

Порядковый день

ввести дату отсчета заполнить вниз с шагом 1 день

Физичес-кая

Эмоциона-

Интеллек-

льная

туальная

  • Ввести в таблицу свою дату рождения
  • Заполнить столбец Порядковый день

Дата заполняется по формату 00.00.00. Признаком правильного набора даты является

правое выравнивание в ячейке.

  • Ввести расчетные формулы. При записи формул использовать стандартные функции
  • SIN(…) и ПИ(…). Значение х вычисляется как разность между датой рождения
  • (абсолютная ссылка) и датой порядкового дня.
  • Скопировать расчетные формулы в тридцать строк
  • Выделить столбцы с биоритмами
  • Построить диаграмму: Вставка — График.

Решение занимательных задач при изучении MS Excel на уроках информатики развивает у детей интерес к самостоятельной работе в этой программе и на других уроках (математика, физика, химия и др.)

Решение занимательных задач при изучении MS Excel на уроках информатики развивает у детей интерес к самостоятельной работе в этой программе и на других уроках (математика, физика, химия и др.)

Источник

Решение типовых задач линейного программирования в табличном процессоре MS Excel

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

. СУЩНОСТЬ ЗАДАЧИ ОПТИМИЗАЦИИ

.1 Немного истории

.2 Основные понятия

.3 Постановка задачи линейного
программирования

. ТИПОВЫЕ ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ

.1 Задача о рационе питания (задача
о диете)

.2 Задача о составлении плана
производства

.3 Задача о раскрое материалов

.4 Транспортная задача

. ПРИКЛАДНЫЕ ЗАДАЧИ ОПТИМАЛЬНОГО
РАСПРЕДЕЛЕНИЯ РЕСУРСОВ

.1 Характеристика программного
средства

.2 Решение задачи о рационе питания
в среде MS Excel

.3 Решение задачи о плане
производства в среде MS Excel

.4 Решение задачи о раскрое в среде
MS Excel

.5 Решение транспортной задачи в
среде MS Excel

ЗАКЛЮЧЕНИЕ

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

ВВЕДЕНИЕ

Линейное программирование часть математического
программирования, посвященная теории и методам решения экстремальных задач,
нахождения минимума или максимума функции цели, характеризующихся линейной
зависимостью между неизвестными переменными.

Применение методов линейного программирования
актуально в настоящее время, так как использование математических моделей
является важным направлением совершенствования планирования и анализа
деятельности фирм. Формулировка задачи в виде математической модели позволяет
конкретизировать информацию, сделать задачу более наглядной, создавать и
моделировать варианты, выбирать оптимальные, наиболее рациональные решения из
возможных альтернатив.

Актуальность курсовой работы связана с тем, что
линейное программирование широко используется в решении оптимизационных,
управленческих, логистических, распределительных и некоторых других видах
задач, в которых выявляется линейная зависимость между переменными. К тому же
линейное программирование — это наиболее разработанный раздел математического
программирования, а значит один из наиболее востребованных, в настоящее время.

Целью курсовой работы является разработка
практических рекомендаций по решению некоторых типовых задач линейного
программирования в табличном процессоре.

Для достижения поставленной цели необходимо
решить следующие задачи:

—       изучить и раскрыть необходимый
теоретический материал;

—       провести анализ некоторых типовых
задач линейного программирования;

—       проанализировать информационные
технологии, подходящие для расчета необходимых показателей;

—       на примере некоторых задач
сформулировать экономико-математические модели;

—       найти оптимальное решение задач с
помощью средств табличного процессора.

В работе применяются методы анализа данных по
тематике, обобщение и классификация изученного материала.

Теоретическая значимость работы выражается в
системном представлении классических задач линейного программирования.

Практическая значимость выражается в
рекомендациях по решению задач линейного программирования посредством
информационных технологий.

Структура курсовой работы включает в себя
введение, три параграфа, заключение и список использованных источников.

1. СУЩНОСТЬ ЗАДАЧИ ОПТИМИЗАЦИИ

1.1 Немного истории

Большинство задач, которые приходится решать
человеку, в процессе своей практической деятельности, являются
многовариантными, то есть предполагают наличие нескольких вариантов решения.
Всю свою жизнь человечество стремится отыскать наилучшее решение при имеющихся
ограничениях возможностей и ресурсов. Долгое время при этом он руководствовался
лишь здравым смыслом, опытом, интуицией.

На этапе индустриализации произошло резкое
увеличение масштабов производства, появилась необходимость решать задачи
управления, планирования, анализа альтернативных вариантов, выработки прогнозов
на будущее и многие другие. Очевидно, что увеличился объем обрабатываемой
информации, данных которые необходимо учитывать при решении задач такого рода.
Также нужно учитывать взаимосвязь между, казалось бы, отдельными, не связанными
между собой явлениями (загрязнение окружающей среды и промышленное
производство; характер взаимоотношений в коллективе и производственные
показатели, выполнение плана; химизация продуктов питания и уровень
онкологических заболеваний у населения и др.).

Однако, с развитием компьютерной и
вычислительной техники появилась возможность решать задачи, требующие большого объема
арифметических вычислений. Стало возможным привлечение математического
аппарата, к решению задач, решаемых ранее интуитивно и приблизительно. Стали
создаваться принципиально новые способы решения задач.

Таким образом, в 30-е годы XX в., появилась новая
математическая дисциплина — математическое программирование.

Математическое программирование — это раздел
математики, занимающийся анализом многомерных экстремальных задач управления и
планирования и разработкой теории и численных методов их решения [8].

Линейное программирование является наиболее
изученным разделом математического программирования. Термин линейного
программирования появился в работах Т. Купманса и Дж. Данцига в 1951 г[4].

1.2 Основные понятия

Математическое программирование — раздел математики,
разрабатывающий теоретическое обоснование и способы решения многомерных
экстремальных задач с ограничениями, т. е. задач на экстремум функции
нескольких переменных с ограничениями на область допустимых значений
неизвестных переменных.

Имеющиеся ресурсы представляются в виде системы
ограничений. Функцию, экстремальное значение которой нужно найти называют
целевой, показателем эффективности или критерием оптимальности. Именно эти две
составляющие являются необходимыми компонентами математической модели задачи.

В большинстве случаев модель в некотором роде
заменяет сам исследуемый объект, то есть оригинал. При решении задач вместо
исходного объекта (оригинала, словесного описания) используется его модель, в
частности математическая. Модель являлась представлением объекта в некоторой
форме, отличной от формы его реального существования.

Математическая модель задачи — это отображение
исследуемого объекта в виде систем неравенств и уравнений, функций и т. д.

Модель задачи математического программирования
включает в себя:

—       совокупность неизвестных переменных,
оказывая влияние на которые, систему можно оптимизировать. Это так называемый
вектор управления, план задачи или, проще говоря, вектор решения;

—       функцию цели, в некоторых источниках
она может иметь название целевой функции, показателя эффективности или же
критерия оптимальности. С помощью данного показателя эффективности
представляется возможным нахождения оптимального варианта решения задачи из
нескольких возможных решений. Наилучший план решения задачи доставляет функции
цели минимальное, либо максимальное значение. Это могут быть затраты на
грузоперевозки, количество единиц материала, доход от продажи товаров,
количество выпущенной продукции и многое другое.

Любые имеющиеся ресурсы, так или иначе ограничены,
к тому же в процессе производства, потребность в этих ресурсах сохраняется.
Именно из этого условия следуют вышеперечисленные компоненты задачи
математического программирования.

Ресурсы могут быть не только материальными или
финансовыми, но и трудовыми, техническими либо, же в качестве ресурса может
выступать научный и технологический потенциал.

Математически ограничения в ресурсах выражаются
с помощью систем уравнений или неравенств. Данная система неравенств образует
область экономических возможностей или так называемую область допустимых
решений. План, удовлетворяющий системе ограничений задачи, называется
допустимым. Допустимый план, доставляющий функции цели экстремальное значение,
называется оптимальным[13].

Модели линейного программирования широко
используются при оптимизации процессов практически во всех отраслях:

—    при составлении плана производства;

—       при разделении заданий и отдельных
технологических процессов по исполнителям;

—       при нахождении оптимального набора
изготавливаемой продукции;

—       при распределении работ по временным
промежуткам;

—       при определении маршрутов
грузопотоков между потребителями и поставщиками;

—       при составлении плана товарооборота
и порядка его распределении и т. д.

Наибольшее распространение методы и модели
линейного программирования получили при решении задач экономии ресурсов
(определение рациона питания, раскрой материалов, назначения), транспортных и
производственных задач.

1.3   Постановка задачи линейного
программирования

Линейное программирование — метод математического
программирования, отыскания экстремума функции, с определенными ограничениями,
выраженных в виде системы линейных неравенств или уравнений. Здесь линейность
заключается в том, что если изображать все ограничения и целевую функцию на
системе координат, то графически они будут представлены в виде прямых линий
[10].

Суть решения задачи линейного программирования
включает необходимость нахождения таких условий, которые будут приводить
функцию цели к минимуму или максимуму, то есть к экстремуму.

Условия задачи представлены в виде системы
линейных уравнений, показывающих ограничения имеющихся в наличии ресурсов:

(1.1)

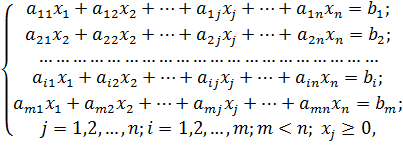
где xj— неизвестные переменные,
содержащие решение поставленной задачи;ij и bj—
известные постоянные величины, характеризующие условия задачи.

Целевая функция задается в виде:

(1.2)

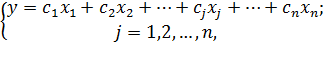
где cj—
постоянные коэффициенты стоимости.

Ограничения могут быть, заданы не только в виде
уравнений, но и в виде системы неравенств. В данном случае, для того чтобы
привести систему неравенств к виду (1.1), нужно в каждое линейное ограничение
ввести добавочные неотрицательные неизвестные: xn+1,
xn+2,
…,xn+m.

Общая математическая формулировка задачи
соответствует условиям (1.1) и (1.2).

Первая строка системы уравнений (1.1)
соответствует выражению:

,

где a11
—
количество единиц ресурсов вида 1 на первом предприятии; a12
—
количество единиц ресурсов вида 1 на втором предприятии и т.п.;b1 —
общий объем ресурсов вида 1(для всех предприятий); x1, x2
и т.д. — искомое количество предприятий типов 1, 2 и т.д.

Вторая строка системы уравнений (1.1) содержит
аналогичные величины для ресурсов вида 2 и т.д. Функция цели соответствует
формуле (1.2). Требуется обратить в минимум величину

,

где cj— показатель, характеризующий
издержки предприятий.

Пусть m — суммарное число разных типов ресурсов,
которые есть у собственника, а n — число видов предприятий, между которыми эти
ресурсы распределены. При этом известно, какое количество однородных ресурсов
различного вида (i=1, 2, …,m)
может быть реализовано на каждом из предприятий данного типа (j=1,2,…,n),
а также общее количество ресурсов данного вида (bi).
Известно также относительное значение издержек на каждом из предприятий(cj).

Задача заключается в том, чтобы наилучшим
образом разделить имеющиеся ресурсы по предприятиям, то есть найти неизвестные
величины xj.

Таким образом, особенностями линейного
программирования являются:

—       линейная зависимость функции цели;

—       область допустимых значений
устанавливает система линейных уравнений или неравенств.

2. ТИПОВЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Чтобы понять, откуда берутся задачи линейного
программирования, проанализируем некоторые, уже ставшие классическими, модели
подобных задач.

Основные виды задач линейного программирования:

—       задача об ассортименте;

—       задача о диете (рационе питания, о
смесях);

—       транспортная задача;

—       задача об оптимальном использовании
имеющихся мощностей;

—       задача о назначениях и др.

Обязательным условием для решения задачи
линейного программирования является построение экономико-математической модели
исследуемой экономической ситуации.

.1 Задача о рационе питания (задача о диете)

Задача о смесях появляется при составлении
рациона питания животных, удовлетворяющего конкретным медицинским требованиям
так, чтобы затраты на «меню» были сведены к минимуму [13].

Допустим, что у нас в наличии есть  продуктов
питания (зерно, комбикорм, сено и др.). Обозначим данные продукты с помощью.
Пусть, —
это стоимость единицы веса (например, цена килограмма) продукта Fi.
Правильная диета обязана приносить животному пользу, то есть обеспечивать его
необходимыми элементами, такими как белки, углеводы, кальций, калий, магний,
фосфор и др. Обозначим данные элементы через .
Тогда можно составить таблицу 1 указывающую, на то, какой объем каждого элемента
имеется в единице веса любого продукта.

Таблица 1 — Содержание нужных веществ в каждом
виде продукта

Получается, что величина aij
это количество i-го элемента, присутствующего в единице веса j-го продукта.
Матрица  называется
матрицей питательности.

Вектор решения для рациона питания должен
показать, какое количество xi
i-го продукта должно содержаться в меню«исследуемого» животного за день (месяц,
квартал, год). Он означает, что за определенный промежуток времени животное
должно быть обеспеченоx1единиц
первого продукта, x2
единиц второго, …, xn единиц n-го
продукта.

Какие же требования могут быть предъявлены к
рациону? Выполнение конкретных медицинских требований. Они состоят в том, что
за определенный срок животное должно получить не менее необходимого количества
каждого элемента. Обозначим через bj, то минимально необходимое
количество j-го элемента, которое должно получить животное. В таком случае,
рацион питания должен соответствовать полученным ограничениям (2.1).

(2.1)

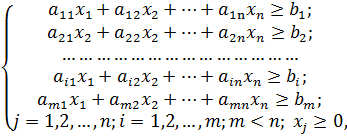
Тогда стоимость всей диеты будет составлять:

(2.2)

где  —
цена единицы веса i-го продукта.

Очевидно, что затраты должны быть как можно
меньше. Поэтому задача приобретает такой вид: найти рацион (2.2) минимальной
стоимости при выполнении всех ограничений (2.1). Математически это выглядит
так:

(2.3)

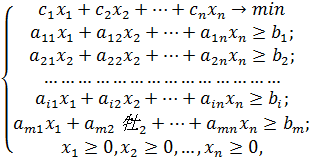
Таким образом, очевидно что:

—       реальная задача приобрела строгую
математическую форму;

—       функция цели (стоимость питания)
является линейной функцией;

—       ограничения на значения переменных x1,
x2,
…, xn имеют вид системы
линейных неравенств.

.2 Задача о составлении плана производства

Проанализируем производственную деятельность
некоторой структурной единицы (филиал, отдел, подразделение и др.).
Предположим, что конкретная производственная единица может выпускать некоторые
продукты

Для выпуска данных товаров необходимо
использовать различные материальные ресурсы. Пусть количество этих ресурсов
будет m; обозначим их через

Технологией производства товара назовем
набор чисел  показывающий,
какое количество-го ресурса необходимо для производства единицы товара .
Данные можно представить в виде таблицы 2 — технологической матрицы, которая
полностью описывает технологические потребности производства и элементами
которой являются числа aij.

Таблица 2 — Технологическая матрица

Предположим, в наличии есть
запасов каждого ресурса и планируется произвести единиц
-го ресурса. Так как невозможно превысить имеющийся лимит ресурсов, то план
производства  должен
удовлетворять ограничениям:

(2.4)

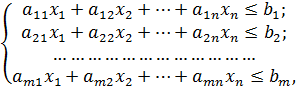
Обязательно должно соблюдаться условие
неотрицательности переменных : Очевидно,
что прибыль, должна быть, как можно больше. Поэтому стоящая задача составления
плана производства приобретает вид:

(2.5)

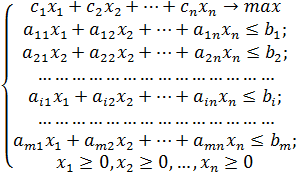
В итоге, снова получилась линейная функция цели,
и ограничения имеющихся ресурсов так же имеют характер линейных неравенств, то
есть, опять имеем дело с задачей линейного программирования.

.3 Задача о раскрое материалов

В нахождении наиболее рационального способа
раскроя имеющегося материала, (металлические стержни, бумажное полотно, ткань и
др.) состоит задача оптимального раскроя.

Нередко поиск оптимального способа раскроя
осуществляется в два этапа.

На начальном этапе находятся всевозможные
рациональные способы раскроя материала.

На II
этапе решаются задачи рациональных способов раскроя.

—       Нахождение рациональных способов
раскроя материала

В задачах данного вида рассматриваются так
называемые рациональные (оптимальные по Парето) способы раскроя. Пусть, из
единицы материала можно изготовить заготовки нескольких типов.

При увеличении числа заготовок одного вида за
счет сокращения числа заготовок другого вида, способ раскроя называется
рациональным.

Пусть—
индекс типа заготовки ();

 — номер способа
раскроя единицы материала ();

 — количество
заготовок вида , полученных при
раскрое единицы материала -м способом.

Математически представить определение
рационального способа раскроя материала можно в таком виде: способ раскроя  называется
рациональным, если для любого другого способа раскроя  из
соотношений , следуют
соотношения  [5].

—       Определение интенсивности
использования рациональных способов раскроя.

Обозначения:

 — индекс материала
();

 — номер типа
заготовки ();

 — индекс способа
раскроя единицы материала();

 — количество
заготовок вида , полученных при
раскрое единицы -го материала -м способом;

 — количество
заготовок вида  в комплекте,
отправляемому заказчику;

 — количество
материала-го вида;

— количество
единицу-го материала, раскраиваемых по -му способу
(интенсивность использования способа раскроя);

— величина отхода,
полученного при раскрое единицы -го материала по -му
способу;

— число комплектов
заготовок различного вида.

Имеется несколько типов моделей задач о раскрое
материала:

—       Модель I(раскрой,
с минимальным расходом материалов):

 

 

 

где (2.6) — функция цели (минимум количества
используемых материалов);

(2.7) — система ограничений, определяющих
количество заготовок, необходимое для выполнения работы;

(2.8) — условия неотрицательности переменных.

Модель II
(раскрой, с минимальными отходами материалов):

 

 

 

где (2.9) — функция цели (минимум отходов при
раскрое материалов);

(2.10) — система ограничений, определяющих
количество заготовок, необходимое для выполнения заказа;

(2.11) — условия неотрицательности переменных.

—       Модель III
(раскроя материала с учетом комплектации):

 

 

 

 

где (2.12) — функция цели (максимум комплектов,
включающих заготовки различных видов);

(2.13) — ограничения по количеству материалов;

(2.14) — система ограничений, определяющих количество
заготовок, необходимое для формирования комплектов;

(2.15) — условия неотрицательности переменных.

Рассмотрим несколько подробнее задачу о раскрое
материала в общем виде.

Пусть на обработку поступает a единиц сырьевого
материала одного вида (например, a листов картона одинаковых размеров). Из них
необходимо изготовить комплекты, в каждый из которых входит n видов изделий в
количестве, пропорциональном числам  Имеется
m способов обработки данного материала, то есть известны величины  определяющие
количество единиц j-х заготовок при i-м
способе раскроя [18].

Установить план раскроя, при котором количество
комплектов будет максимально. Согласно условиям задачи имеем, таблицу 3:

Таблица 3 -Способы раскроя

Вид
изделия Способ раскроя

m

Пусть xi—
количество единиц сырьевого материала, раскраиваемого i-м вариантом

Тогда количество изделий 1-го вида равно:

Принимая во внимание условие комплектности,
имеем:

 

где y — количество комплектов.

Аналогичные равенства можно записать и для всех
остальных типов изделий, то есть условие комплектности приводит к системе
ограничений:

.

Очевидно,  (на
раскрой поступает a единиц сырьевого материала), а также

Цель задачи — максимизировать количество
комплектов:

Итак, приходим к математической модели задачи о
раскрое:

 

 

 

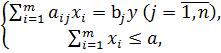
Чтобы выразить целевую функцию через переменные  достаточно
воспользоваться любым из соотношений:

 

.4 Транспортная задача

Проанализируем задачу, в которой речь идет о
рациональной перевозке некоторого однородного продукта от производителей к
потребителям, то есть транспортную задачу.

Пусть имеется m пунктов производства однородного
продукта (добыча руды в карьерах, сборка бытовой техники, изготовление
кондитерских изделий и др.) и n пунктов потребления этого продукта. Мощности
пунктов производства составляют  единиц однородного
продукта, а потребности каждого j-го пункта потребления равны  единиц.
Известны затраты на перевозку едиицы
продукта от i-го поставщика j-му потребителю. Составить такой план перевозок,
при котором суммарные затраты на все перевозки были бы наименьшими. Пусть спрос
и предложение совпадают, то есть

 

Данную транспортную задачу называют закрытой или
сбалансированной. При этом предполагается, что вся продукция от поставщиков
будет вывезена и спрос каждого из потребителей будет удовлетворен.

Составим математическую модель задачи. Обозначим
через  —
количество продукта, перевозимого из i-го пункта производства в j-й
пункт потребления. Тогда матрица:  —
план перевозок.

Матрицу  называют
матрицей затрат (тарифов).

Составим таблицу 4, в которую внесем все
исходные данные и перевозки xij.

Таблица 4 — Транспортная таблица

 

 

 

 

 

 

 

 

 

 c2n

 

 

 

Предположим, что транспортные затраты прямо
пропорциональны количеству перевозимого продукта. Тогда суммарные затраты
выразятся функцией цели:

 

которую необходимо минимизировать при
ограничениях: (весь продукт из
каждого i-го () пункта должен
быть, вывезен полностью),(спрос каждого j-го
()
потребителя должен быть, полностью удовлетворен).

Из условия задачи следует, что все .

Итак, математическая модель сбалансированной
транспортной задачи имеет вид:

 

 

 

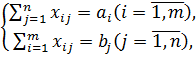
3. ПРИКЛАДНЫЕ ЗАДАЧИ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
РЕСУРСОВ

На основе, рассмотренной теоретической части,
необходимо составить математические модели некоторых задач линейного
программирования и найти оптимальное решение для каждой из них, с помощью
приложения MS Excel
2007.

.1 Характеристика программного средства

Для решения поставленных задач и наглядного
представления их решений была важна возможность использования математических
формул и непосредственно функции «Поиск решения».

Надстройка «Поиск решения» позволяет
найти оптимальное (максимальное или минимальное) значение для формулы
<javascript:AppendPopup(this,’xldefFormula_2_2′)>, содержащейся в целевой
ячейке. Поиск решения» работает с диапазоном ячеек, связанных с формулой в
целевой ячейке. Чтобы получить оптимальный результат по формуле из целевой
ячейки, «Поиск решения» изменяет значения в ячейках, выбранных как изменяемые.
Для конкретизации значений применяются ограничения (система неравенств),
которые могут ссылаться на другие ячейки (группы ячеек), влияющие на формулу
для ячейки с записанной целевой функцией[3].

Именно этими возможностями обладают
известные табличные процессоры Microsoft Office Excel 2007 и Open
Office Calc. В отличие от Open Office Calc MS Excel является более
распространенным и привычным для обычного пользователя, имеет более широкий
спектр поддерживаемых форматов файлов. При использовании MS Excel возникновение
несовместимости с другими программы в разы меньше, чем у Open Office. Так же в
MS Excel есть встроенный язык программирования — Visual Basic for Applications. Плюс ко
всему вышеперечисленному данное программное средство обладает более
функциональным и интуитивно понятным интерфейсом.

Надстройка «Поиск решения» в Open
Office Calc немногим отличается от похожей надстройки в MS Excel. В
последнее время эти два табличных редактора уже стали практически идентичны по
функциональному набору. Хотя стоит признать, что Calc все же уступает
конкуренту именно в наборе «Пакета анализа»[19].

Таким образом, для решения
поставленных задач использовалось программное средство Microsoft Office Excel 2007 из
пакета прикладных программ Microsoft Office.

.2 Решение задачи о рационе питания
в среде MS Excel

линейное программирование табличный
процессор

Постановка задачи:

Необходимо составить наименее затратный рацион
питания поросят, содержащий необходимое количество витаминов А, C и D.
Пищевая ценность рациона питания (в калориях) должна быть не менее необходимой.
Данная смесь изготавливается из двух видов кормов — К1 и К2.
Причем, корма вида K1 в рационе не должно быть использовано более
0,5 кг. Аналогично для корма K2
— не более 0,85 кг. Исходные данные для дальнейших расчетов приведены в таблице
5.

Таблица 5 — Содержание витаминов в кормах

Содержание
в 100 г К1, мг

Содержание
в  100 г К2, мг

Потребность, 
мг

Витамин
А

10

10

60

Витамин
D

40

10

100

Витамин
С

20

10

80

Энергетическая
ценность, калории

100

200

800

Стоимость
100 г, ден. ед.

5

7

Решение:

Построим математическую модель. За  обозначим
количество корма К1, аналогично за  —
объем К2.Исходя из условия задачи  и
 —
неотрицательные значения. Целевая функция будет стремиться к минимуму т.к.
расходы, с учетом всех необходимых условий, должны быть как можно меньше.

На основании исходных данных необходимо
составить систему ограничений. Для простоты восприятия почти все неравенства
можно сократить на положительное число, эти математические действия никак не
повлияют на конечный результат.

Из названий столбцов таблицы 5 ясно, что порции
кормов составляют по 100 грамм, а ограничение по количеству в условии задачи
дано в килограммах. Следовательно, необходимо их привести в ту же систему, что
и остальные неравенства. 0,5 кг это 500 г, а 0,85 кг — 850 г. Таким образом, .

Итак, если рассматривать всю совокупность
ограничений и целевую функцию, то математическая модель исходной задачи, примет
вид:

 

 

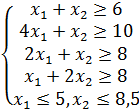
Задачу линейного программирования можно решить
как графически, так и симплекс-методом. В данном случае, воспользуемся пакетом
прикладных программ Microsoft Office, в частности MS
Excel, надстройкой
«Поиск решения».

Создадим форму для ввода данных, так решение
задачи будет представлено более наглядно, рисунок 1.

Рисунок 1 — Форма ввода данных в задаче о диете

Ячейки B3 и C3 отведены для переменных ,
пока они обнулены, но в дальнейшем они будут являться изменяемыми ячейками т.к.
именно эти значения влияют на функцию цели. В ячейку E3 введена формула для
целевой функции, которая будет стремиться к минимальному значению. В диапазоне
ячеек F7:F12 можно применить математическую функцию «Сумму произведений»
(СУММПРОИЗВ). Первый массив для всех неравенств, следовательно, его нужно
отметить знаком «$», как абсолютную ссылку, чтобы при копировании в другие
ячейки адрес этих ячеек не изменялся. Использование данной функции представлено
на рисунке 2.

Рисунок 2 — Введение формул

Далее, используем надстройку «Поиск решения».
Вызвать ее можно выбрав вкладку «Данные», закладку «Анализ». В диалоговом окне
«Поиска решения», рисунок 3, вводим ячейку цели функции, изменяемые ячейки и
все ограничения в виде неравенств, так же отмечаем маркером, что целевая
функция принимается равной минимальному значению.

Рисунок 3 — Диалоговое окно надстройки «Поиск
решения»

После нажатия кнопки «Выполнить» на экране
появляется решение задачи линейного программирования, рисунок 4.

Рисунок 4 — Результат работы «Поиска решения»

Таким образом, минимальное значение функции цели
,
то есть для составления оптимального суточного рациона питания, с минимальными
затратами и содержанием всех витаминов в полном объеме, нужно взять 400 грамм
корма К1и 200 грамм корма К2. При этом стоимость данных
витаминных добавок будет составлять 34 денежные единицы.

.3 Решение задачи о плане производства в среде
MS Excel

Постановка задачи:

Необходимо произвести изделия двух типов. Для их
изготовления имеется 120 кг алюминия. На изделиеI
типа расходуется 4 кг алюминия, а на изделиеII
типа — 2 кг. Составить план выпуска изделий, обеспечивающий получение
наибольшей прибыли от продажи изделий. Стоимость изделия I
типа установлена 4условные денежные единицы, а изделия II
типа — 5условных денежных единиц, причем изделий I
типа требуется изготовить не более 35, а изделий II
типа — не более 10.

Решение:

Обозначим количество изделийI
типа как ,
а количество, производимых по плану, изделий II
типа —.

Логично предположить, что Прибыль
от продажи изделий составит

Необходимо подобрать такой план производства,
при котором прибыль будет максимальна, то есть.

Также при составлении оптимального плана
производства нельзя не учитывать ограничения по имеющемуся ресурсу. При
производстве изделий I
типа расходуется  (кг). В то время,
на производство изделий II типа используется  (кг)
алюминия.Таким образом, суммарный расход алюминия составляет(кг).
Данная величина не должна превышать запасы алюминия в количестве 120 кг. В
итоге получаем неравенство:

Изделий I
типа в плане выпуска продукции должно быть не более 35 штук, то есть.
Аналогично для изделий II
типа: ,
так как по условию этих изделий должно быть не более 10.

Таким образом, математическая модель задачи
состоит из целевой функции и системы ограничений:

 

 

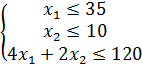
Решим задачу линейного программирования с
помощью программы MSExcel.

Для этого необходимо выполнить следующие шаги:

) создать форму для ввода исходных данных
задачи, изображенную на рисунке 5:

Рисунок 5 — Форма для ввода данных

Текст в данной форме непосредственно на ход
решения задачи не оказывает никакого влияния. Данные комментарии делают решение
задачи более понятной. Для неизвестных
и  зарезервированы
ячейкиВ10
и С10.
В них после решения задачи будут внесены полученные значения. Значение функции
цели Z будет зафиксировано в ячейке G9;

2) ввести исходные данные. В диапазон В4:С6
вводим коэффициенты при переменных в системе ограничений: «Первое» —
коэффициенты 1 и 0,«Второе» — 0 и 1,«Третье» — 4 и 2.В диапазоне ячеек D4:D6 и
Н4:Н6 заносим значения свободных членов системы ограничений: 35, 10 и 120. В
диапазон ячеек В11:С11 — коэффициенты целевой функции Z, то есть 4 и 5;

3) ввести формулы для расчета целевой функции и
системы ограничений. Для вычисления значений функции цели в
ячейкуG9необходимо ввести формулу = В11*В10 + С11*С10.Здесь вместо
коэффициентов 4 и 5 записаны их адреса В11 иС11, а вместо переменных  и
соответствующие
адреса В10
иС10.

Рисунок 6 — Заполненная форма

) выделить ячейку функции цели для запуска
команды «Поиск решения»;

) выбрать вкладку «Данные», в ней выбрать
закладку «Анализ», затем команду «Поиск решения»;

) в открывшемся диалоговом окне, представленном
на рисунке 7,
установить:

Рисунок 7 — Диалоговое окно команды «Поиск
решения»

—       в группе «Равной»переключатель на
максимальное значение;

—       в поле «Установить целевую
ячейку»ввести адрес ячейки G9,уже
содержащей формулу для расчета значения функции цели;

—       в поле «Изменения ячейки»указать
ссылки на изменяемые ячейки В10
и С10,
содержащие неизвестные  и ;

—       в поле «Ограничения»нужно задать
необходимые ограничения, для этого необходимо нажать кнопку «Добавить»;

) в результате открывается диалоговое окно,
рисунок 8, «Добавление ограничения»:

Рисунок 8- Диалоговое окно «Добавление
ограничения»

—       в поле «Ссылка на ячейку»указать
адрес левой части первого ограничения F4. Из списка выбрать нужный оператор,
означающий «не более» (<=);

—       в поле «Ограничения»указать адрес
правой части первого ограничения Н4. Нажать кнопку «ОК»,

—       следующие ограничения вводить
аналогично первому, нажав кнопку «Добавить».

Диалоговое окно «Поиск решения», рисунок 9, после ввода
исходных данных имеет вид:

Рисунок 9 — Форма после ввода исходных данных

) для поиска оптимального решения нажать кнопку
«Выполнить». Если задача линейного программирования имеет решение, то на экране
появятся результат работы команды «Поиск решения», как на рисунке 10.

Рисунок 10 — Результаты работы команды «Поиск
решения»

Максимальное значение целевой функции .
Оно достигается при плане производства.

Причем сырье (120 кг алюминия) используется
полностью (левая и правая части третьего ограничения равны между собой).

.4 Решение задачи о раскрое в среде MS Excel

Постановка задачи:

Для изготовления металлоконструкций используется
заготовки длиной 70, 100 и 120 см. Заготовки производят из металлических
стержней длиной 220 см. Для выполнения всего заказа требуется изготовить 102
стержня длиной 70 см, 120 стержней длиной 100 см и 80 стержней длиной 120
см.Какое минимальное количество материала необходимо использовать, чтобы
выполнить заказ?

Решение:

Сначала нужно определить все возможные способы
раскроя материала. Для наглядности представим эти данные в таблице 6:

Таблица 6 — Способы раскроя материала

Виды
заготовок

Способы
раскроя из стержня 220 см

I

II

III

IV

V

70 см

0

1

0

1

3

100
см

1

0

2

1

0

120 см

1

1

0

0

0

Отходы,
см

0

30

20

50

10

Таким образом, получаем пять различных способов
раскроя материала.

Обозначим через  —
количество единиц материала, раскраиваемых по -му способу (интенсивность
использования способа раскроя), то есть  —
количество материала, раскраиваемого по способу 1 и так далее до .

Зададим математическую модель нахождения общего
количества металлических стержней длиной 220 см. Его минимизация является целью
решения задачи. Следовательно, целевая функция будет иметь вид:

 

Система ограничений примет вид:

 

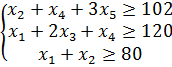
Очевидно, что количество заготовок ()
должно быть целым числом и не может быть отрицательным.

Следующим шагом будет решение задачи в MS Excel
с помощью надстройки «Поиск решения». На рисунке 11 изображено, какую
необходимо создать форму для ввода данных с занесенными в неё известными
значения.

Рисунок 11 -Форма для ввода данных

Ячейка G7 зарезервирована под функцию цели,
позже в нее будет записана формула для нахождения минимального количество
стержней длиной 220 см. В ячейках диапазона B3:F5, размещена таблица
рациональных способов раскроя материала, в диапазоне ячеек B6:F6 — величина
отходов для каждого способа раскроя, а в G3:G5 — требуемое количество стержней
заготовок различной длины. Ячейки B7:F7 заполнятся автоматически после
выполнения команды «Поиск решения», и будут равны количеству заготовок
получаемых при каждом способе раскроя.

В ячейках H3:H5необходимо указать формулы для
расчета фактического количества стержней разной длины. В ячейке H3 формула
будет иметь вид =$B$7*B3+$C$7*C3+$D$7*D3+$E$7*E3+$F$7*F3, ячейки H4 и H5
заполняются аналогично (для этого можно использовать автозаполнение т.к. в
формуле использованы абсолютные ссылки).

В ячейку G7 нужно занести целевую функцию,
вычисляющую суммарное количество единиц материала, то есть необходимое
количество стержней длиной 220 см. Таким образом, в данной ячейке будет введена
формула: =B7+C7+D7+E7+F7.

Необходимо воспользоваться надстройкой «Поиск
решения». Вызвать ее можно выбрав вкладку «Данные», закладку «Анализ». В
диалоговом окне «Поиска решения», рисунок 12, вводим ячейку целевой функции $G$7,
диапазон изменяемых ячеек:$B$7:$F$7, устанавливаем переключатель «Равной
минимальному значению».

Рисунок 12 — Диалоговое окно надстройки «Поиск
решения»

В поле «Изменяя ячейки» задается диапазон
подбираемых параметров — $B$7:$F$7.

Также нужно добавить ограничения:

—       количество заготовок должно быть
целым числом ($B$7:$F$7=целое);

—       количество не должно быть
отрицательным числом ($B$7:$F$7>=0);

—       фактическое количество стержней
различной длины, требуемое для выполнения заказа, должно быть не менее
необходимого количества ($H$3:$F$5>=$G$3:$G$5).

В результате выполнения надстройки «Поиск
решения» получаем минимальное количество материала необходимое для выполнения
заказа в ячейке G7 — 134
единицы материала, рисунок 13:

Рисунок 13 — Результат выполнения надстройки
«Поиск решения»

Так же на рисунке 13 видно, что для этого
используются только 3 способа раскроя материала(1 способ — 80 единиц, 3 способ
— 20 единиц и 5 способ — 34 единицы).

.5 Решение транспортной задачи в среде MS Excel

Решение транспортной задачи позволяет вычислить
наиболее эффективный вариант распределения продукции. На основании, данных о
запасах и заявках, а так же о стоимости доставки 1 единиц товара, производится
поиск оптимального решения транспортной задачи.

Постановка задачи:

Существует четыре пункта производства продукта A1,
A2, A3,
A4производственные мощности которых составляют 30, 40, 50 и 30
единиц. Данный товар востребован в трех пунктах потребления B1, B2,
B3, потребности которых составляют 40, 60 и 50 единиц. Затраты на
поставку единицы товара (у.д.е.) от пунктов производства до пунктов назначения
заданы матрицей:

 

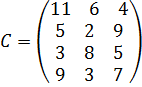
Необходимо определить план перевозок, с
минимальными транспортными затратами.

Решение:

Обозначим через  количество
единиц товара перевозимых от i-го поставщика к j-му потребителю. Тогда —
план перевозок. Суммарная стоимость перевозок выразится целевой функцией,
которую необходимо будет минимизировать:

 

Система ограничений примет вид:

 

 

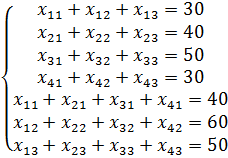
По аналогии с предыдущими задачами, создаем
форму ввода и заполняем ее исходными данными, рисунок 14:

Рисунок 14 — Форма для ввода данных к решению
транспортной задачи

Для функции цели зарезервирована ячейка H9,
для переменных  — ячейки B4:B7,
D4:D7, F4:F7, в них будут занесены результаты решения задачи. В ячейки B9, D9,
F9 необходимо ввести формулы для вычисления левых частей уравнений-ограничений
по заявкам. Для потребителя B1 ограничение имеет вид уравнения:

.

Следовательно, в ячейку B9 нужно записать
формулу: =СУММ(В4:В7).

Формулы в ячейках D9 и F9 задаются таким же
образом. В ячейки I4:I7 введем формулы для вычисления левых частей уравнений по
запасам.

Для поставщика A1 уравнение имеет
следующий вид:

,

что соответствует формуле в ячейке I4:= B4 + D4
+ F4. Аналогично задаются формулы для ячеек I5, I6 и I7.

Для вычисления значения целевой функции

 

В ячейку H9
запишем формулу: = СУММПРОИЗВ(C4:C7;
B4:B7)
+ +СУММПРОИЗВ(E4:E7;D4:D7)+СУММПРОИЗВ(G4:G7;
F4:F7).

Необходимо воспользоваться надстройкой «Поиск
решения». Вызвать ее можно выбрав вкладку «Данные», закладку «Анализ». В
диалоговом окне «Поиска решения», рисунок 15, вводим ячейку цели функции $H$9,
диапазон изменяемых ячеек: $B$4:$B$7;$D$4:$D$7;$F$4:$F$7.

Рисунок 15 — Ввод уравнений-ограничений для
транспортной задачи

Целевая функция считается равной минимальному
значению. Введем уравнения-ограничения по заявкам:B9=B8; D9=D8; F9=F8; по
запасам:I4:I6=H4:H6. Так же нужно указать неотрицательность
переменных:В4:B7>=0;D4:D7>=0;F4:F7>=0.

В результате выполнения программы «Поиск
решения»получим на экране в ячейках B4:B6; D4:D6; F4:F6 оптимальный план
перевозок, а в ячейке Н9 — минимальную общую стоимость за все перевозки,
рисунок 16:

Рисунок 16 — Результат работы надстройки «Поиск
решения»

Таким образом, 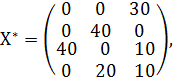в
то время как .

ЗАКЛЮЧЕНИЕ

Большинство задач, которые приходится решать
человеку, в процессе своей практической деятельности, являются
многовариантными, то есть предполагают наличие нескольких вариантов решения.
Всю свою жизнь человечество стремится отыскать наилучшее решение при имеющихся
ограничениях возможностей и ресурсов. Долгое время при этом он руководствовался
лишь здравым смыслом, опытом, интуицией.

Однако, впоследствии с развитием промышленности,
увеличением обрабатываемой информации возникла потребность использования
математических методов практически во всех сферах жизни (решение задач
управления и планирования производства, задач из области логистики,
распределение и экономия ресурсов и т.д.). Многие из таких задач относятся к
одной из областей математического программирования, а именно к линейному
программированию. Для математических моделей задач, при этом должно соблюдаться
условие линейной зависимости переменных как для системы ограничений, так и для
критерия оптимальности.

Основными используемыми способами решения задач
линейного программирования являются графический и симплекс-метод. Также для
задач подобного рода найти решение можно с помощью надстройки «Поиск решения»
табличного процессора Excel2007
из пакета прикладных программ Microsoft
Office.

В данной курсовой работе в
соответствии с ее целью и задачами, была собрана и систематизирована информация
по теоретическому обоснованию моделей, приводящих к задаче линейного
программирования. На основе анализа типовых задач линейного программирования,
были сформулированы условия задач каждого вида. Решение задач осуществлялось в
табличном процессореMS
Excel 2007. К
достоинствам, решения задач таким способом, можно отнести простоту
использования, минимум вычислений. В то же время следует отметить и недостаток
данного способа, к нему относится потеря некоторых решений, в том случае если
предполагается множество решений, этого можно избежать при решении графическим
методом.

Таким образом, применение методов линейного
программирования актуально в наши дни, так как использование математических
моделей является важным направлением совершенствования планирования
производства, анализа деятельности фирм, экономии ресурсов, разработки
оптимального плана грузопотоков и многого другого. Представление условия задачи
в виде математической модели помогает структурировать информацию, моделировать
альтернативные варианты, находить рациональные решения задачи.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.     Бродецкий,
Г.Л. Экономико-математические методы и модели в логистике. Процедуры
оптимизации: учебник / Г.Л. Бродецкий, Д.А. Гусев. — М.: Академия, 2012. — 281
с.

2.      Васильев,
А.Н. Финансовое моделирование и оптимизация средствами Excel 2007: учеб.
пособие.-СПб.: Питер, 2009.- 319 с.

.        Введение
в анализ «что если» [Электронный ресурс]. — Режим
доступа:http://office.microsoft.com/ru-ru/excel-help/HA010342628.aspx (дата
обращения 20.04.2014)

.        Введение
в исследование операций [Электронный ресурс]. —
http://ru.convdocs.org/docs/index-159945.html?page=9 (дата обращения
18.04.2014)

.        Задача
о раскрое материалов[Электронный ресурс]. — Режим доступа:
http://edu.nstu.ru/courses/mo_tpr/files/3.1.6.html (дата обращения 18.04.2014)

.        Задачи
оптимизации в Excel[Электронный
ресурс]. — Режим доступа: http://exsolver.narod.ru/LM/LM_material.html (дата
обращения 19.04.2014)

.        Змеев,
О.А. Исследование операций [Электронный ресурс]. — Режим доступа:
http://abc.vvsu.ru/Books/ebooks_iskt/%D0%AD%D0%BB%D0%B5%
D0%BA%D1%82%D1%80%D0%BE%D0%BD%D0%BD%D1%8B%D0%B5%D1%83%D1%87%D0%B5%D0%B1%D0%BD%D0%B8%D0%BA%D0%B8/%D0%98%D1%81%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5%20%D0%BE%D0%BF%D0%B5%D1%80%D0%B0%D1%86%D0%B8%D0%B9/fmi.asf.ru/vavilov/index.htm
(дата обращения 20.04.2014)

.        Интерактивный
обучающий курс. Математика [Электронный ресурс]. — Режим доступа:
http://math.immf.ru (дата обращения 18.04.2014)

.        Косарева,
А.С., Ляпина, Е.А. Использование метода линейного программирования в процессе
финансового планирования и бюджетирования // Современная наука: актуальные
проблемы теории и практики. — 2013. -№3-4. — С.20-23.

.        Красс,
М.С. Математические методы и модели для магистрантов экономики: учеб. пособие.
2-е изд., дополненное / М.С. Красс, Б.П. Чупрынов — СПб.: Питер, 2013.- 486 с.

.        Линейное
программирование [Электронный ресурс]. — Режим доступа: http://ecnmx.ru/article/a-27.html
(дата обращения 20.04.2014)

.        Макаров,
В.И. Экономико-математические методы и модели. Задачник : учеб. пособие. — М.:
КноРус, 2009. — 208 с.

.        Методы
линейного программирования [Электронный ресурс]. — Режим доступа: http://math.immf.ru/lections/302.html
(дата обращения 18.04.2014)

.        Орлова,
И.В. Экономико-математические методы и модели: компьютерное моделирование :
учебное пособие для вузов/ И. В. Орлова, В. А. Половников. -2-е изд., испр.
-М.: Вузовский учебник, 2010.-365 с.

.        Примеры
решения задач симплексным методом в Excel[Электронный
ресурс]. — Режим доступа: http://math.semestr.ru/simplex/excel.php
(дата обращения 18.04.2014).

.        Просветов
Г.И. Математические методы в логистике: задачи и решения: учебно-практическое
пособие. — 2-е изд., доп. -М.: Альфа-Пресс, 2009. -303с.

.        Решение
задач линейного программирования в Excel [Электронный ресурс]. — Режим доступа:
http://www.matburo.ru/ex_mp.php?p1=mpexcel
(дата обращения 20.04.2014)

.        Решение
задач оптимизации в среде MS Excel[Электронный ресурс]. — Режим доступа:
http://ieu.udsu.ru/moodle/pluginfile.php/249/mod_resource/ content
/2/OptRas.htm (дата обращения 18.04.2014)

.        Свободный
поиск. Поиск решения в OpenOffice.org Calc[Электронный ресурс]. — Режим
доступа: http://mxl4.net/blog/2009/01/svobodnyj-poisk.html(дата обращения
18.04.2014).

Источник

Понравилась статья? Поделить с друзьями:
  • Решение задач в таблице word
  • Решение задач в microsoft word excel
  • Решение задач в excel через подбор параметра
  • Решение задач в excel цена
  • Решение задач в excel функция впр в excel