Решение задач в excel по замене оборудования

Содержание

  1. Задача замены оборудования excel
  2. Задача замены оборудования excel
  3. Тема: Решение задач замены оборудования средствами ЭТ Excel

Задача замены оборудования excel

На этом шаге мы рассмотрим применение задачи замены оборудования .

Компания планирует определить оптимальную политику замены используемого в настоящее время трехлетнего механизма на протяжении следующих 4 лет ( n = 4), т.е. вплоть до начала пятого года. Таблица 1 содержит относящиеся к задаче данные. Компания требует обязательной замены механизма, который находится в эксплуатации 6 лет. Стоимость нового механизма равна 100 000 долл.

Возраст t (года) Прибыль r(t) (долл.) Стоимость обслуживания c(t) (долл.) Остаточная стоимость s(t) (долл.)
0 20000 200 —
1 19000 600 80000
2 18500 1200 60000
3 17200 1500 50000
4 15500 1700 30000
5 14000 1800 10000
6 12200 2200 5000

Таблица 1. Данные к задаче замены оборудования

Определение допустимых значений возраста механизма на каждом этапе является нетривиальной задачей. На рис. 1 представлена рассматриваемая задача замены оборудования в виде сети. В начале первого года имеется механизм, эксплуатирующийся 3 года (на графике рис. 1 по оси Y откладывается возраст механизма). Мы можем либо заменить его (З) , либо эксплуатировать (С) на протяжении следующего года. Если механизм заменили, то в начале второго года его возраст будет равен одному году, в противном случае его возраст будет 4 года. Такой же подход используется в начале каждого года, начиная со второго по четвертый.

Рис. 1. Схема возможной замены механизма

Если однолетний механизм заменяется в начале второго или третьего года, то заменивший его механизм к началу следующего года также будет однолетним. К тому же, в начале 4-го года 6-летний механизм обязательно должен быть заменен, если он еще эксплуатируется; в конце 4-го года все механизмы продаются (П) в обязательном порядке. На схеме сети также видно, что в начале второго года возможны только механизмы со сроком эксплуатации 1 или 4 года. В начале третьего года механизм может иметь возраст 1, 2 или 5 лет, а в начале четвертого — 1, 2, 3 или 6 лет.

Решение данной задачи эквивалентно поиску маршрута максимальной длины (т.е. приносящего максимальную прибыль) от начала первого года к концу четвертого в сети, показанной на рис. 1. При решении этой задачи используем табличную форму записи. (Числовые данные в таблице кратны тысячам долларов.)

. C З Оптимум
t r(t) + s(t + 1) — c(t) r(0) + s(t) + s(1) — c(0) — I f 4 (t) Решение
1 19,0 + 60 — 0,6 = 78,4 20 + 80 + 80 — 0,2 — 100 = 79,8 79,8 З
2 18,5 + 50 — 1,2 = 67,3 20 + 60 + 80 — 0,2 — 100 = 59,8 67,3 С
3 17,2 + 30 — 1,5 = 45,7 20 + 50 + 80 — 0,2 — 100 = 4,8 49,8 З
4 Необходима замена 20 + 5 + 80 — 0,2 — 100 = 4,8 4,8 З

Таблица 2. Результаты, полученные на этапе 4

. C З Оптимум
t r(t) — c(t) + f 4 (t + 1) r(0) + s(t) — c(0) — I + f 4 (1) f 3 (t) Решение
1 19,0 — 0,6 + 67,3 = 85,7 20 + 80 — 0,2 — 100 + 79,8 = 79,6 85,7 С
2 18,5 — 1,2 + 49,8 = 67,1 20 + 60 — 0,2 — 100 + 79,8 = 59,6 67,1 С
5 14,0 — 1,8 + 4,8 = 17,0 20 + 10 — 0,2 — 100 + 79,8 = 9,6 17,0 З

Таблица 3. Результаты, полученные на этапе 3

. C З Оптимум
t r(t) — c(t) + f 3 (t + 1) r(0) + s(t) — c(0) — I + f 3 (1) f 2 (t) Решение
1 19,0 — 0,6 + 67,1 = 85,5 20 + 80 — 0,2 — 100 + 85,7 = 85,5 85,5 С или З
4 15,5 — 1,7 + 19,6 = 33,4 20 + 30 — 0,2 — 100 + 85,7 = 35,5 35,5 З

Таблица 4. Результаты, полученные на этапе 2

. C З Оптимум
t r(t) — c(t) + f 2 (t + 1) r(0) + s(t) — c(0) — I + f 2 (1) f 1 (t) Решение
1 17,2 — 1,5 + 35,5 = 51,2 20 + 50 — 0,2 — 100 + 85,5 = 55,3 55,3 З

Таблица 5. Результаты, полученные на этапе 1

На рис. 2 показана последовательность получения оптимального решения. В начале первого года оптимальным решением при t = 1 является замена механизма. Следовательно, новый механизм к началу второго года будет находиться в эксплуатации 1 год. При t = 1 в начале второго года оптимальным решением будет либо использование, либо замена механизма. Если он заменяется, то новый к началу третьего года будет находиться в эксплуатации 1 год, иначе механизм будет иметь возраст 2 года. Описанный процесс продолжается до тех пор, пока не будет определено оптимальное решение для четвертого года.

Рис.2. Решение примера

Следовательно, начиная с первого года эксплуатации механизма, альтернативными оптимальными стратегиями относительно замены механизма будут (З, С, С, 3) и (З, 3, С, С) . Общая прибыль составит 55 300 долл.

На следующем шаге мы рассмотрим решение задачи .

Источник

Задача замены оборудования excel

На этом шаге мы рассмотрим задачу замены оборудования .

Чем дольше механизм эксплуатируется, тем выше затраты на его обслуживание и ниже его производительность. Когда срок эксплуатации механизма достигает определенного уровня, может оказаться более выгодной его замена. Задача замены оборудования, таким образом, сводится к определению оптимального срока эксплуатации механизма.

Предположим, что мы занимаемся заменой механизмов на протяжении n лет. В начале каждого года принимается решение либо об эксплуатации механизма еще один год, либо о замене его новым. Обозначим через r(t) и c(t) прибыль от эксплуатации t -летнего механизма на протяжении года и затраты на его обслуживание за этот же период. Далее пусть s(t) — стоимость продажи механизма, который эксплуатировался t лет. Стоимость приобретения нового механизма остается неизменной на протяжении всех лет и равна I .

Элементы модели динамического программирования таковы.

  1. Этап i представляется порядковым номером года i, i = 1, 2, . n .
  2. Вариантами решения на i -м этапе (т.е. для i -го года) являются альтернативы: продолжить эксплуатацию или заменить механизм в начале i -го года.
  3. Состоянием на i -м этапе является срок эксплуатации t (возраст) механизма к началу i -го года.

Пусть f i (t) — максимальная прибыль, получаемая за годы от i до n при условии, что в начале i -го года имеется механизм t -летнего возраста.

Рекуррентное уравнение имеет следующий вид.

На следующем шаге рассмотрим применение задачи замены оборудования .

Источник

Тема: Решение задач замены оборудования средствами ЭТ Excel

Цель:

1. Ознакомиться с основными понятиями

2. Освоить порядок определения оптимальных сроков замены оборудования

3. Научиться оценивать полученные результаты

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1.1 Классификация задач замены оборудования

Задачи замены оборудования по наличию того или иного признака можно разделить следующим образом.

1. По характеру замены оборудования на три типа:

— по замене оборудования длительного использования из-за неуклонно возрастающих с увеличением срока службы эксплуатационных затрат. В этих задачах определяется оптимальный срок службы оборудования, минимизирующий эксплуатационные затраты;

— по замене оборудования с целью предупреждения отказов (поломки). Требуется найти такое время замены оборудования, чтобы суммарные издержки были минимальными.

— по выбору оптимального плана предупредительного ремонта и профилактического обслуживания оборудования для уменьшения вероятности отказа.

2. По характеру учета затрат на оборудование на дискретные и непрерывные. Если расходы по ремонту и уходу за оборудованием производятся через некоторые интервалы времени, то задача дискретная, в противном случае – непрерывная.

3. По выходу из строя оборудования на детерминированные и случайные. Если расходы по ремонту и уходу за оборудованием являются постоянными или известными функциями от времени, то мы имеем детерминированную задачу замены оборудования.

4. По стратегии замены оборудования на плановые и смешанные. Если замена оборудования производится строго по плану с учетом соотношения затрат на ремонт и уход за оборудованием, то имеем задачу с плановой стратегией замены оборудования. Смешанные задачи замены оборудования ¾ это задачи, в которых придерживаются плановой стратегии замены оборудования, но если оборудование вышло из строя раньше запланированного времени, то оно заменяется.

5. По времени учета затрат на оборудование с приведением затрат и без приведения затрат. Если затраты на эксплуатацию оборудования осуществляются в разные сроки или они изменяются во времени, то следует привести затраты более поздних лет к расчетному, в этом случае имеем задачу замены оборудования с приведением затрат, в противном случае ¾ без приведения затрат.

1.2 Задача замены оборудования длительного

Пусть в эксплуатации находится некоторое оборудование. Покупная цена оборудования S. Известны затраты на эксплуатацию оборудования (уход за ним, ремонт т.д.), производимые в начале (1,2, …, t,… n) периодов. Предположим, что периоды равны году. Обозначим затраты, производимые в t – й период, через Ct . В результате старения балансовая цена оборудования непрерывно падает и зависит от периода списания, обозначим ее St. Требуется определить период списания оборудования, чтобы затраты на единицу времени были минимальны.

1. Дискретную, в которой известны C1, C2 … Ct (где Сt+1 > Ct), а также значения S1, S2 … St (где St+1 Y(t) Ct и St+1 t A=A/(1+Енп) t тенге в период t. Обозначим через Yt размер затрат, приведенных к текущему моменту времени, за все будущее время.

(7.11)

Чтобы затраты при замене оборудования были наименьшими должно выполняться условие (7.6) . Подставив (t+1) вместо t в целевую функцию Yt и выполнив ряд преобразований, получаем:

(7.12)

Аналогично, подставив (t-1) вместо t в целевую функцию Yt и выполнив ряд преобразований, находим:

(7.13)

Если теперь вместо Yt подставить его математическое выражение через искомый параметр, получим:

(7.14)

Из этого неравенства вытекают следующие правила замены оборудования:

1) если затраты на эксплуатацию оборудования в очередном периоде меньше средневзвешенных затрат за все предыдущие периоды, то оборудование не следует заменять;

2) если же затраты на эксплуатацию оборудования в очередном периоде превосходят средневзвешенные затраты за все предыдущие периоды, то оборудование следует заменять.

2 ПРИМЕР Выполнения лабораторной работы

2.1 постановка задачи

Для приведенных исходных данных определите оптимальный срок списания оборудования:

Покупная цена оборудования S=1500 у. е .

Затраты на эксплуатацию оборудования Ct= 30 *t

Норматив для приведения разновременных затрат Eнп=0,08

2.2 РЕШЕНИЕ ЗАДАЧИ

Решение задачи проводится по приведенному алгоритму.

Алгоритм 7.1. Решение задачи замены оборудования с учетом приведения затрат к текущему моменту времени.

1. Создание формы для ввода условий задачи.

Ø Откройте рабочий лист ЭТ Excel

Ø Сделать форму для ввода условий задачи (рисунок 7.1)

Весь текст на рисунке 7.1 и в дальнейшем является комментарием и на решение задачи не влияет.

2. Ввод исходных данных.

Ø В ячейки G2:G5 введите исходные данные S, Енп, А1, А2

Ø В ячейки А11:А25 введите значения t от 1 до 20, используя автозаполнение. На экране: Рисунок 7.2

3. Ввод зависимостей из математической модели (Рисунок 7.3)

3.1. Присвойте имена ячейкам G2:G5:

Ø М1

Ø Вставка, Имя, Присвоить…

На экране: диалоговое окно Присвоение имени

Ø Добавить

Ø Ок

Повторите действия для ячеек G3, G4, G5.

3.2. Заполните ячейку В8:

Ø В ячейку В8 введите формулу: = 1/(1+E).

Ø М1

Ø Формат, Ячейки…

На экране диалоговое окно Формат ячейки

Ø Курсор в окно Число десятичных знаков

Ø М1

Ø Введите: 3

Ø Ок

3.3. Заполните интервал В11:В25

Ø В ячейку В11 введите формулу: = A*A11+B*A11^2

Распространите формулу до ячейки B25

Ø Курсор в ячейку B11

Ø М1

Ø Курсор на правый нижний угол ячейки

Ø МН до В25

3.4. Заполните интервал С11:С25

Ø В ячейку С11 введите формулу: =$B$8^(A11-1)

Ø Распространите формулу до ячейки С25

3.5. Заполните интервал D11:D25

Ø В ячейку D11 введите формулу, для вычисления Y(t):

Распространите формулу до ячейки D25

3.6. Заполните интервал E11:E25

Ø В ячейку E11 введите формулу: = B11/(1-$B$8)

Ø Распространите формулу до ячейки E25

3.7. Заполните интервал F11:F24

Ø В ячейку F11 введите формулу:

Ø =ЕСЛИ(И(D11 2 +50*t; норматив для приведения разновременных затрат Eнп=0,08

Требования к отчету по лабораторной работе

Отчет должен содержать:

1. Условие задачи.

2. Результаты решения задачи.

3. Выводы по решению задачи.

Лабораторная работа N8

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Источник

Источник

Динамическое
программирование: замена оборудования,
подверженного старению

Цель работы:

Решение задачи замены оборудования с
помощью метода динамического
программирования, который заключается
в поэтапном планировании многошагового
процесса, где на каждом этапе оптимизируется
только один шаг. Управление на каждом
шаге должно выбираться с учетом всех
его последствий в будущем.

Задача замены оборудования, таким
образом, сводится к определению
оптимального срока его эксплуатации.

Ход
работы:

Самостоятельное задание №10.

Решить задачу
замены оборудования с помощью формул
в Excel.

Исходные данные:

Время
использования оборудования (t)

0

1

2

3

4

5

Прибыль
r(t)

90

85

81

77

70

68

Затраты
c(t)

21

28

31

33

42

51

Замена
s(t)

46

46

51

57

59

Решение.

Задача состоит
в том, чтобы найти такую стратегию
управления, определенной решениями,
принимаемыми к началу каждого года,
чтобы общая прибыль предприятия за весь
период является максимальной. В качестве
управлений выступают решения о замене
и сохранении оборудования, принимаемые
в начале каждого года:

Uс
– решение о
сохранении оборудования;

Uз
– решение о
замене оборудования.

Решение найдем
с помощью алгоритма решения задач
динамического программирования,
включающего в себя 2 этапа:

  1. при
    движении от начала 6-го года к началу
    1-го года для каждого допустимого
    состояния оборудования находим условное
    оптимальное управление;

  2. при
    движении от начала 1-го года к началу
    6-го года из условных оптимальных решений
    составляем для каждого года оптимальный
    план замены оборудования.

Пусть в начале
k-го года (k = 1…6) возраст оборудования
составляет tk
лет. Тогда прибыль предприятия Wk
за k-й год составит:

Чтобы найти
возраст оборудования в начале следующего
(k+1)-го года, используем уравнение
оптимальности:

Найдем сначала
условно оптимальное решение для 6-го
года. Так как в начальный момент мы имеем
новое оборудование (t0
= 0), то
возраст оборудования к началу 6-го года
может составлять от 1 до 5 лет. Для каждого
из этих возрастов найдем условно
оптимальное решение и соответствующее
значение функции W6(t6).

Таблица
1.
Условно-оптимальное решение на начало
6-ого года

Возраст
оборудования,
t

W6(t)

Усл-оптим.
решение

1

57

Uс

2

50

Uс

3

44

Uс

4

28

Uс

5

17

Uс

Аналогично
находим условно-оптимальные решения
для 5,4,3,2,1 годов.

Таблица
2.
Условно-оптимальное решение на начало
5-ого года

Возраст
оборудования,
t

W6(t)

Усл-оптим.
решение

1

107

Uс

2

94

Uс

3

75

Uз

4

69

Uз

Таблица
3.
Условно-оптимальное решение на начало
4-ого года

Возраст
оборудования,
t

W6(t)

Усл-оптим.
решение

1

151

Uс

2

130

Uз

3

125

Uз

Таблица
4.
Условно-оптимальное решение на начало
3-ого года

Возраст
оборудования,
t

W6(t)

Усл-оптим.
решение

1

187

Uс

2

175

Uс

Таблица
5.
Условно-оптимальное решение на начало
2-ого года

Возраст
оборудования,
t

W6(t)

Усл-оптим.
решение

1

232

Uс

Для 1-го годаэксплуатации
оборудования решение единственно —сохранить
оборудование.

Значит,
возраст оборудования к началу 2-го года
равен одному году. По полученным данным
таблицы 5 для 2-го
года
решение будет сохранить
оборудование.

Тогда возраст
оборудования к началу 3-го года становится
равным двум годам. По таблице 4 вначале
3-го
года
оборудование также следует сохранить.

Тогда возраст
оборудования к началу 4-го года становится
равным трем годам. При таком возрасте
оборудование на 4-м
году
по таблице 3 следует
заменить.

После замены
оборудования его возраст к началу 5-го
года
составит 1 год. По данным таблицы 2 при
таком возрасте оборудование менять
не следует.

Поэтому
возраст оборудования к началу 6-го
года
составит 2 года, это значит, что по
таблице 1 менять
его
не надо.

Вывод:

Значит, оптимальный
план замены оборудования будет выглядеть
следующим образом:

Таблица
6. Оптимальный
план замены оборудования.

Годы

1

2

3

4

5

6

Оптимальное
решение

Сохранить

Сохранить

Сохранить

Заменить

Сохранить

Сохранить

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Известно, что оборудование со временем изнашивается, физически и морально стареет. В процессе эксплуатации падает производительность, и растут эксплуатационные расходы на текущий ремонт. Со временем возникает необходимость замены оборудования, так как его дальнейшая эксплуатация обходится дороже, чем замена. Отсюда задача о замене оборудования может быть сформулирована следующим образом.

Разработать оптимальную стратегию замены оборудования возраста лет в плановом периоде продолжительностью лет, если известны:

– стоимость продукции, производимой в течение года на оборудовании возраста лет ();

– ежегодные расходы, связанные с эксплуатацией оборудования возраста лет ();

– остаточная стоимость оборудования возраста лет;

– стоимость нового оборудования и расходы, связанные с установкой, наладкой и запуском.

В начале каждого года имеется две возможности: сохранить оборудование и получить прибыль или заменить его и получить прибыль . Прибыль от использования оборудования в последнем -м году планового периода запишется в следующем виде:

(4.5)

А прибыль от использования оборудования в период с -го по-й год –

(4.6)

Где – прибыль от использования оборудования в период с -го по -й год.

В случае, если оба управления («сохранение» и «замена») приводят к одной и той же прибыли, то целесообразно выбрать управление «сохранение».

Пример 10

Найти оптимальную стратегию замены оборудования возраста 3 года на период продолжительностью 10 лет, если для каждого года планового периода известны стоимость продукции, производимой с использованием этого оборудования, и эксплутационные расходы (таблица 24). Известны также остаточная стоимость, не зависящая от возраста оборудования и составляющая 4 ден. ед., и стоимость нового оборудования, равная 18 ден. ед., не меняющаяся в плановом периоде.

Таблица 24

0

1

2

3

4

5

6

7

8

9

10

31

30

28

28

27

26

26

25

24

24

23

8

9

9

10

10

10

11

12

14

16

18

Решение

I этап. Условная оптимизация

1-й шаг. . Начнем процедуру условной оптимизации с последнего, десятого года планового периода. Для этого шага состояние системы: = 0, 1, 2, …, 9, 10. Функциональное уравнение (4.5) с учетом числовых данных примера принимает вид

Тогда

;

;

;

;

;

;

;

;

;

;

.

Полученные результаты занесем в таблицу (первая строка таблицы 25).

2-й шаг. . Проанализируем девятый год планового периода. Для второго шага возможны состояния системы  = 0, 1, 2, …, 9, 10. Функциональное уравнение (4.6) с учетом числовых данных примера принимает вид

Тогда

;

;

;

;

;

;

;

;

.

Полученные результаты занесем в таблицу (вторая строка таблицы 25).

Продолжая вычисления описанным способом, постепенно заполняем всю таблицу (см. таблица 25).

Таблица 25

0

1

2

3

4

5

6

7

8

9

10

23

21

19

18

17

16

15

13

10

9

9

44

40

37

35

33

31

30

30

30

30

30

63

58

54

51

49

49

49

49

49

49

49

81

75

70

67

67

67

67

67

67

67

67

98

91

86

85

84

84

84

84

84

84

84

114

107

104

102

101

100

100

100

100

100

100

130

125

121

119

117

116

116

116

116

116

116

148

142

138

135

134

134

134

134

134

134

134

165

159

154

152

151

151

151

151

151

151

151

182

175

171

169

168

168

168

168

168

168

168

II этап. Безусловная оптимизация

В начале исследуемого десятилетнего периода возраст оборудования составляет 3 года. Находим в таблице на пересечении строки и столбца  = 3 значение максимальной прибыли —  = 169. Найдем теперь оптимальную политику, обеспечивающую эту прибыль. Значение 169 записано слева от жирной черты в области «политик сохранения». Это означает, что в начале первого года принимается решение о сохранении оборудования. К началу второго года возраст оборудования 3 + 1 = 4 года. Расположенная на пересечении строки и столбца  = 4 клетка находится слева от жирной черты, следовательно, и второй год нужно работать на имеющемся оборудовании. К началу третьего года возраст оборудования 4 + 1 = 5 лет. Расположенная на пересечении строки и столбца  = 5 клетка находится справа от черты, в области «политик замены», следовательно, в начале третьего года следует заменить оборудование. К началу четвертого года возраст оборудования составит один год. Расположенная на пересечении строки и столбца  = 1 клетка находится слева от черты, следовательно, четвертый год следует работать на имеющемся оборудовании. Продолжая рассуждать таким образом, последовательно находим  = 104,  = 85,  = 67,  = 58,  = 37,  = 18.

Цепь решений безусловной оптимизации можно изобразить символически следующим образом:

.

Итак, на оборудовании возраста 3 года следует работать
2 года, затем произвести замену оборудования, на новом оборудовании работать 3-й, 4-й, 5-й и 6-й годы, после чего произвести замену оборудования и на следующем оборудовании работать 7-й, 8-й, 9-й и 10-й годы планового периода. При этом прибыль будет максимальной и составит  = 169 ден. ед.

< Предыдущая   Следующая >
Источник


Создадим модель для нахождения наилучшего распределения ресурсов, при котором минимизируются затраты (Allocation Problem). Расчет будем проводить с помощью надстройки Поиск решения.

Задача оптимального распределения ресурсов (распределительная задача) заключается в отыскании наилучшего распределения ресурсов, при котором либо максимизируется результат, либо минимизируются затраты. Решим задачу, в которой минимизируются затраты, на основе примера с сайта

www.solver.com

.

Вводная статья про

Поиск решения

в MS EXCEL 2010

находится здесь

.

Задача

Предприятие выпускает продукт (только один вид изделия и ничего более) и ему необходимо выполнить заказ клиента. На предприятии 3 типа оборудования. Все типы оборудования выпускают один и тот же продукт. Производительность каждого типа оборудования разная. Каждый тип оборудования имеет постоянную и переменную часть расходов. Переменная часть расходов пропорциональна количеству произведенных изделий. Имеется ограниченное количество единиц оборудования каждого типа (но общее количество оборудования избыточно для выполнения заказа). Требуется минимизировать расходы на оборудование при условии выполнения заказа.

Создание модели

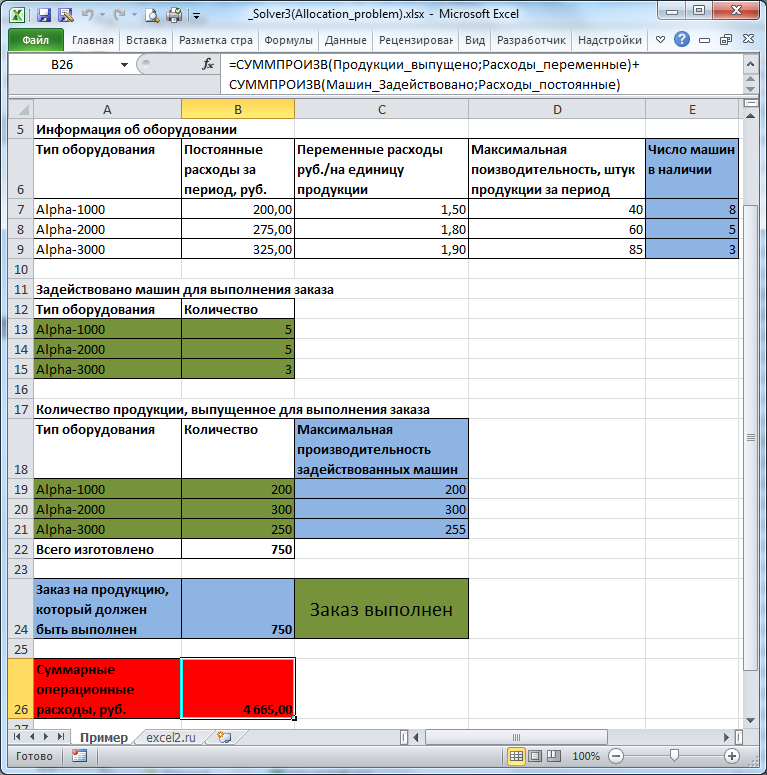
На рисунке ниже приведена модель, созданная для решения задачи (см.

файл примера

).

Предприятие несет расходы в зависимости от типа оборудования: использование оборудования типа Alpha-3000 самое дорогое в эксплуатации, но оно и самое производительное. Оборудование типа Alpha-1000 самое дешевое в эксплуатации, но оно и менее производительное. Задача

Поиска решения

выбрать наиболее дешевое оборудование, так чтобы заказ был выполнен (мощностей Alpha-1000 не хватит для выполнения заказа). Казалось бы, решение очевидно (взять по максимуму дешевое оборудование, остальную производительность обеспечить более дорогим). Однако, если учесть, что из-за низкой производительности дешевых машин приходится их брать больше, неся существенные постоянные расходы, то решение уже не кажется очевидным.


Переменные (выделено зеленым)

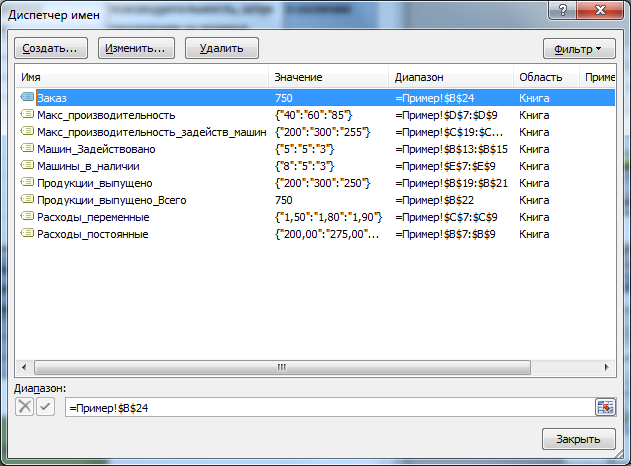
. В качестве переменных модели следует взять количество задействованных единиц оборудования каждого типа и суммарное количество продукции, выпущенное на каждом типе оборудования (производительность задается не для каждой единицы, а для типа в целом). Переменные выделены зеленым. Для наглядности диапазонам ячеек, содержащих переменные, присвоены

имена

Машин_Задействовано

и

Продукции_выпущено.


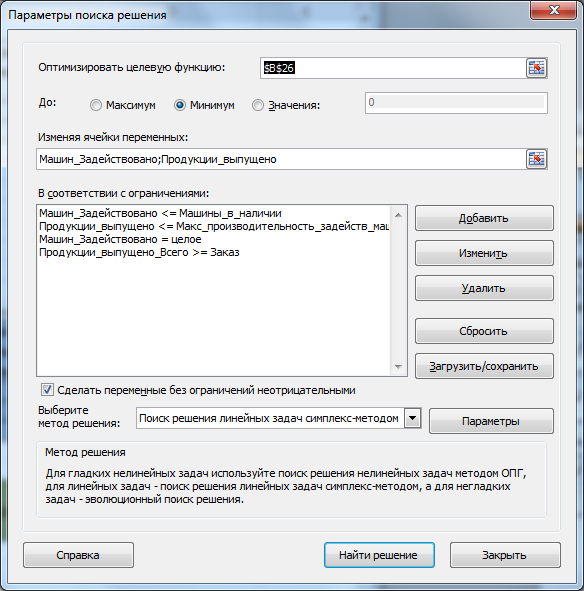
Ограничения (выделено синим)

. Количество задействованных машин должно быть целым числом. Количество задействованных машин каждого типа должно быть не больше, чем имеется в наличии. Всего должно быть выпущено продукции не меньше чем величина заказа. Также необходимо ограничить производительность задействованного оборудования. Производительность задается не для каждой единицы, а для типа в целом. Максимальная производительность задействованного оборудования рассчитывается

формулой массива

=

Машин_Задействовано* Макс_производительность

Макс_производительность

– это

именованный диапазон

. Ограничения выделены синим цветом.


Целевая функция (выделено красным)

. Целевая функция задается формулой =

СУММПРОИЗВ(Продукции_выпущено_По_типу; Расходы_переменные)+ СУММПРОИЗВ(Машин_Задействовано; Расходы_постоянные)

Это просто суммарные операционные расходы (переменная и постоянные части). Результат вычисления этой формулы должен быть минимизирован (выделено красным).

Убедитесь, что метод решения соответствует линейной задаче. Теперь в диалоговом окне можно нажать кнопку

Найти решение

.

Результаты расчетов


Поиск решения

найдет оптимальный набор единиц оборудования по типам и их производительность, при котором операционные расходы будут минимальные, а заказ выполнен. Обратите внимание, что значение переменных (количество продукции, выпущенное на каждом типе оборудования) – целые числа, хотя в ограничениях этого прописано не было. Изменив значения максимальной производительности с 40 на, например, 40,3 (ячейка

D

7

) и пересчитав еще раз, получим нецелые значения выпущенной продукции. Т.е. Поиск решения сам «догадался», что нам требуются целые значения переменной, т.к. в качестве ограничения были указаны значения без дробной части. Двигаемся дальше. В условии задачи предполагается, что выпуск продукции осуществляется лишь в течение одного периода. В статье

Поиск решения MS EXCEL (1.3). Распределение ресурсов (ограничение по количеству оборудования, несколько периодов)

решим задачу определения наилучшего распределения ресурсов в случае нескольких периодов.

Источник

Изучив алгоритмы «ручного» решения задач линейного программирования, полезно познакомиться и со способом упростить этот процесс. Ясно, что чем сложнее задача, чем больше в ней переменных и условий, тем утомительнее и дольше ее решать. В таких случаях удобно использовать специальные математические пакеты, или доступную многим программу MS Excel (версии 2003, 2007, 2010, 2013 и др.).

Решить задачи линейного программирования в Excel достаточно просто:

  • составить математическую модель задачи,
  • внести исходные данные задачи и ограничения,
  • выделить место под ячейки решения и целевую функцию, ввести ее формулу,
  • запустить надстройку Поиск решения,
  • установить нужные параметры решения и запустить выполнение.

Программа подберёт оптимальное решение и покажет его в нужных ячейках, вычислит значение целевой функции. При необходимости можно построить отчеты для анализа решения задачи.

Подробнее все эти этапы с пояснениями и скриншотами разобраны ниже в примерах на разных задачах линейного программирования — изучайте, ищите похожие, решайте.

Помогаем студентам: Работы по линейному программированию на заказ

Спасибо за ваши закладки и рекомендации

Линейное программирование: примеры в Excel

Задача 1. Построить математическую модель задачи и решить её средствами Excel. Записать сопряжённую задачу. Провести анализ и сделать выводы по полученным результатам.
Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
Определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.

Задача 2. Цех производит 8 различных видов деталей для двигателей A, B, C1, C2, C3, D, E6, F имея в своем распоряжении перечисленный ниже парк из 7 видов универсальных станков: 2 шт. -ADF, 3 шт. -SHG, 3 шт. -BSD, 1 шт. -AVP, 1 шт. -BFG, 3 шт. -ABM, 2 шт. -RL.
Время, требуемое для обработки единицы каждого продукта на каждом станке, вклад в прибыль от производства единицы каждого продукта и рыночный спрос на каждый продукт за месяц даны в таблице.
Цех работает 12 часов в день. Каждый месяц содержит 26 рабочих дней. Для упрощения задачи считаем, что возможен произвольный порядок обработки деталей на различных станках.
Составьте оптимальный план производства.
Определите, производство каких продуктов лимитировано рынком, и каких – техническими возможностями цеха. Какие машинные ресурсы должны быть увеличены в первую очередь, чтобы добиться максимального увеличения прибыли (при заданных потребностях рынка)?
Есть ли продукт, который невыгодно производить? Почему? Что нужно изменить, чтобы все продукты стало выгодно производить?

Может пригодиться: транспортные задачи в Excel

Задача 3. Необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ тиамина Т и ниацина Н. Пищевая ценность рациона (в калориях) должна быть не менее заданной. Смесь для цыплят изготавливается из двух продуктов — К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в таблице.

Задача 4. Фирма «Компьютер-сервис» поставляет компьютеры под ключ четырех базовых комплектаций: «домашний», «игровой», «офисный» и «экстрим». Известны средние затраты времени на сборку, проверку и подключение компьютеров. Каждый компьютер приносит определенный уровень прибыли, но спрос ограничен. Кроме того, в плановом периоде ограничен ресурс человеко-часов, отведенных на выполнение каждой производственной операции. Определить, сколько компьютеров каждого типа необходимо произвести в плановом периоде, имея целью максимизировать прибыль.

Задача 5. На лесопилку поступают доски длиной 10 м. По контракту лесопилка должна поставить клиенту не менее 100 досок длиной 5 м, не менее 200 досок длиной 4 м и не менее 300 досок длиной 3 м. Как работникам лесопилки выполнить условия контракта, разрезав наименьшее количество досок?

Помогаем с контрольными по линейному программированию

Задача 6. Компания «Евростройтур» организует экскурсионные автобусные туры по странам Европы. Компания получила 4 новых автобуса и предполагает направить их на маршруты во Францию, Италию, Чехию и Испанию.
Каждый автобус обслуживают 2 водителя. Компанией приглашены 8 водителей, в различной степени знакомых с дорогами европейских стран (в % от экскурсионного маршрута).

Необходимо распределить водителей так, чтобы общий показатель освоения маршрутов был максимальным.

Задача 7. Решить задачу методом ветвей и границ, решая отдельные задачи линейного нецелочисленного программирования с помощью функции «Поиск решения» в Microsoft Excel (в случае, если первая же задача ЛП выдает целочисленное решение, не позволяя ветвить задачу, немного изменить начальные условия).

Состав еды рядовых регламентируется верховной ставкой главнокомандующего, которая устанавливает нижние нормы питания в сутки по основным компонентам: 1500 килокалорий, 100 г белков, 280 г углеводов, 90 г жиров, 1 кг воды. На складах есть 4 вида продуктов, которые выдают защитникам Родины сухим пайком: лимонад, тушенка в маленьких банках, унифицированные наборы горбушек и пирожки с ежевикой. Стоимость этих четырех продуктов соответственно 12 руб., 34 руб., 3 руб. и 20 руб. Какова минимальная сумма, которую должен затратить прапорщик на питание одного солдата?

Задача 8. Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить a11 кг сырья первого типа, a21 кг сырья второго типа, a31 кг сырья третьего типа.
На изготовление единицы Изделия 2 требуется затратить a12 кг сырья первого типа, a22 кг сырья второго типа, a32 кг сырья третьего типа.
Производство обеспечено сырьем каждого типа в количестве b1 кг, b2 кг, b3 кг соответственно.
Рыночная цена единицы Изделия 1 составляет c1 тыс. руб., а единицы Изделия 2 — c2 тыс.руб.
Требуется:
1) построить экономико – математическую модель задачи;
2) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи графического метода решения задачи линейного программирования.
3) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи табличного симплекс – метода решения задачи линейного программирования.
4) составить план производства изделий, обеспечивающий максимальную выручку от их реализации, используя надстройку «Поиск решения» в среде MS EXCEL.

Полезные ссылки

  • Графическое решение ЗЛП
  • Симплекс-метод решения ЗЛП
  • Решенные контрольные по ЛП
  • Онлайн учебник по оптимальным решениям
Источник

Понравилась статья? Поделить с друзьями:
  • Рецепты в microsoft word
  • Решение задач в excel на поиск подбора параметров
  • Решение задач excel платно
  • Рецептурный бланк 148 1 у 88 скачать word
  • Решение задач в excel матрицы