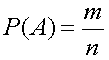Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
- ДИСП;
- ГИПЕРГЕОМ.РАСП;
- СРЗНАЧ и другие.
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
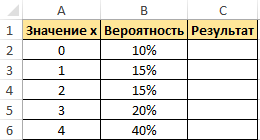
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
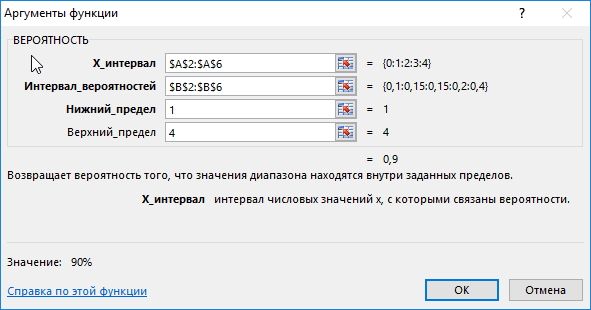
Для этого введем функцию со следующими аргументами:
тут:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
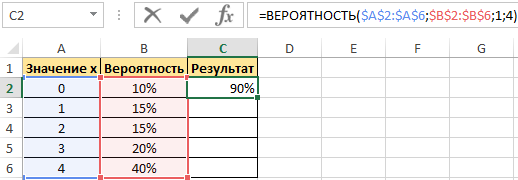
В результате выполненных вычислений получим:
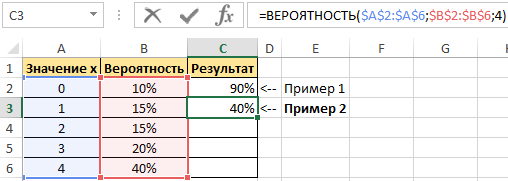
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
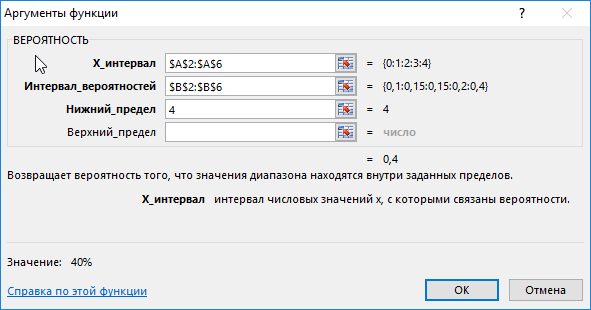
Введем в ячейку С3 введем функцию с такими аргументами:
тут:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Получим:
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Введем формулу:
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Скачать примеры функции ВЕРОЯТНОСТЬ в Excel
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
Содержание
- Формула Бернулли в Excel
- Схема независимых испытаний
- Формула Бернулли в Эксель
- Примеры решений задач
- Функция ВЕРОЯТНОСТЬ для расчета вероятности событий в Excel
- Примеры использования функции вероятность для расчетов в Excel
- Вычисление процента вероятности события в Excel
- Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
- Решение задач на вычисление вероятности в Excel
Формула Бернулли в Excel
В этой статье я расскажу о том, как решать задачи на применение формулы Бернулли в Эксель. Разберем формулу, типовые задачи — решим их вручную и в Excel. Вы разберетесь со схемой независимых ипытаний и сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Схема независимых испытаний
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) — соответственно $q=1-p$. Найти вероятность, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Эта вероятность вычисляется по формуле Бернулли:
$$ P_n(k)=C_n^k cdot p^k cdot (1-p)^=C_n^k cdot p^k cdot q^. qquad(1) $$
Данная схема описывает большой пласт задач по теории вероятностей (от игры в лотерею до испытания приборов на надежность), главное, выделить несколько характерных моментов:
- Опыт повторяется в одинаковых условиях несколько раз. Например, кубик кидается 5 раз, монета подбрасывается 10 раз, проверяется 20 деталей из одной партии, покупается 8 однотипных лотерейных билетов.
- Вероятность наступления события в каждом опыте одинакова. Этот пункт связан с предыдущим, рассматриваются детали, которые могут оказаться с одинаковой вероятностью бракованными или билеты, которые выигрывают с одной и той же вероятностью.
- События в каждом опыте наступают или нет независимо от результатов предыдущих опытов. Кубик падает случайно вне зависимости от того, как упал предыдущий и т.п.
Если эти условия выполнены — мы в условиях схемы Бернулли и можем применять одноименную формулу. Если нет — ищем дальше, ведь классов задач в теории вероятностей существенно больше (и о решении некоторых написано тут): классическая и геометрическая вероятность, формула полной вероятности, сложение и умножение вероятностей, условная вероятность и т.д.
Подробнее про формулу Бернулли и примеры ее применения можно почитать в онлайн-учебнике. Мы же перейдем к вычислению с помощью программы MS Excel.
Формула Бернулли в Эксель
Для вычислений с помощью формулы Бернулли в Excel есть специальная функция =БИНОМ.РАСП() , выдающая определенную вероятность биномиального распределения.
Чтобы найти вероятность $P_n(k)$ в формуле (1) используйте следующий текст =БИНОМ.РАСП($k$;$n$;$p$;0) .
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, k, p$ и получить искомую вероятность (текст полностью виден в строке формул вверху).
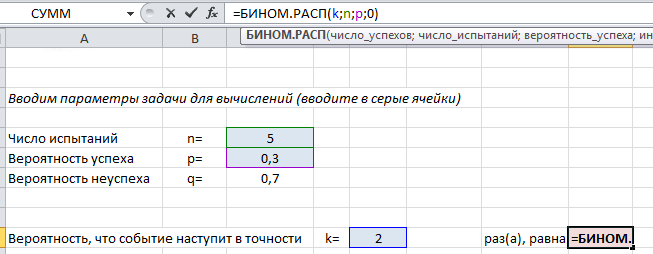
Пример применения формулы на конкретных задачах мы рассмотрим ниже, а пока введем в лист Excel другие нужные формулы, которые пригодятся в решении:
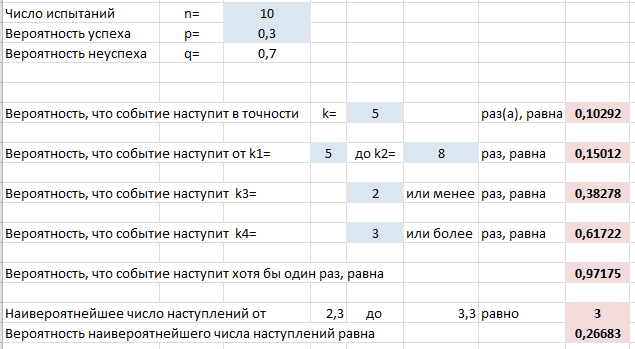
Выше на скриншоте введены формулы для вычисления следующих вероятностей (помимо самих формул для Excel ниже записаны и исходные формулы теории вероятностей):
- Событие произойдет в точности $k$ раз из $n$:
=БИНОМ.РАСП(k;n;p;0)
$$P_n(k)=C_n^k cdot p^k cdot q^$$ - Событие произойдет от $k_1$ до $k_2$ раз:
=БИНОМ.РАСП(k_2;n;p;1) — БИНОМ.РАСП(k_1;n;p;1) + БИНОМ.РАСП(k_1;n;p;0)
$$P_n(k_1le X le k_2)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не более $k_3$ раз:
=БИНОМ.РАСП(k_3;n;p;1)
$$P_n(0le X le k_3)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет не менее $k_4$ раз:
=1 — БИНОМ.РАСП(k_4;n;p;1) + БИНОМ.РАСП(k_4;n;p;0)
$$P_n(k_4le X le n)=sum_^ C_n^i cdot p^i cdot q^$$ - Событие произойдет хотя бы один раз:
=1-БИНОМ.РАСП(0;n;p;0)
$$P_n( X ge 1)=1-P_n(0)=1-q^$$ - Наивероятнейшее число наступлений события $m$:
=ОКРУГЛВВЕРХ(n*p-q;0)
$$np-q le m le np+p$$
Вы видите, что в задачах, где нужно складывать несколько вероятностей, мы уже используем функцию вида =БИНОМ.РАСП(k;n;p;1) — так называемая интегральная функция вероятности, которая дает сумму всех вероятностей от 0 до $k$ включительно.
Примеры решений задач
Рассмотрим решение типовых задач.
Пример 1. Произвели 7 выстрелов. Вероятность попадания при одном выстреле равна 0,75. Найти вероятность того, что при этом будет ровно 5 попаданий; от 6 до 7 попаданий в цель.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=7$, вероятность попадания при каждом одинакова и равна $p=0,75$, вероятность промаха $q=1-p=1-0,75=0,25$. Нужно найти, что будет ровно $k=5$ попаданий. Подставляем все в формулу (1) и получаем:
$$ P_7(5)=C_<7>^5 cdot 0,75^5 cdot 0,25^2 = 21cdot 0,75^5 cdot 0,25^2= 0,31146. $$
Для вероятности 6 или 7 попаданий суммируем:
$$ P_7(6)+P_7(7)=C_<7>^6 cdot 0,75^6 cdot 0,25^1+C_<7>^7 cdot 0,75^7 cdot 0,25^0= \ = 7cdot 0,75^6 cdot 0,25+0,75^7=0,44495. $$
А вот это решение в файле эксель:

Пример 2. В семье десять детей. Считая вероятности рождения мальчика и девочки равными между собой, определить вероятность того, что в данной семье:
1. Ровно 2 мальчика
2. От 4 до 5 мальчиков
3. Не более 2 мальчиков
4. Не менее 7 мальчиков
5. Хотя бы один мальчик
Каково наиболее вероятное число мальчиков и девочек в семье?
Решение. Сначала запишем данные задачи: $n=10$ (число детей), $p=0,5$ (вероятность рождения мальчика). Формула Бернулли принимает вид: $$P_<10>(k)=C_<10>^k cdot 0,5^kcdot 0,5^<10-k>=C_<10>^k cdot 0,5^<10>$$ Приступим к вычислениям:
$$1. P_<10>(2)=C_<10>^2 cdot 0,5^ <10>= frac<10!><2!8!>cdot 0,5^ <10>approx 0,044.$$ $$2. P_<10>(4)+P_<10>(5)=C_<10>^4 cdot 0,5^ <10>+ C_<10>^5 cdot 0,5^<10>=left( frac<10!> <4!6!>+ frac<10!> <5!5!>right)cdot 0,5^ <10>approx 0,451.$$ $$3. P_<10>(0)+P_<10>(1)+P_<10>(2)=C_<10>^0 cdot 0,5^ <10>+ C_<10>^1 cdot 0,5^<10>+ C_<10>^2 cdot 0,5^<10>=left( 1+10+ frac<10!> <2!8!>right)cdot 0,5^ <10>approx 0,055.$$ $$4. P_<10>(7)+P_<10>(8)+P_<10>(9)+P_<10>(10)=\ = C_<10>^7 cdot 0,5^ <10>+ C_<10>^8 cdot 0,5^<10>+ C_<10>^9 cdot 0,5^<10>+ C_<10>^10 cdot 0,5^ <10>=\=left(frac<10!><3!7!>+ frac<10!> <2!8!>+ 10 +1right)cdot 0,5^ <10>approx 0,172.$$ $$5. P_<10>(ge 1)=1-P_<10>(0)=1-C_<10>^0 cdot 0,5^ <10>= 1- 0,5^ <10>approx 0,999.$$
Наивероятнейшее число мальчиков найдем из неравенства:
$$ 10 cdot 0,5 — 0,5 le m le 10 cdot 0,5 + 0,5, \ 4,5 le m le 5,5,\ m=5. $$
Наивероятнейшее число — это 5 мальчиков и соответственно 5 девочек (что очевидно и по здравому смыслу, раз их рождения вероятность одинакова).
Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Вероятность выигрыша по одному лотерейному билету равна 0,3. Куплено 8 билетов. Найти вероятность того, что а) хотя бы один билет выигрышный; б) менее трех билетов выигрышные. Какое наиболее вероятное число выигрышных билетов?
Решение. Полное решение этой задачи можно найти тут, а мы сразу введем данные в Эксель и получим ответы: а) 0,94235; б) 0,55177; в) 2 билета. И они совпадут (с точностью до округления) с ответами ручного решения.

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Источник
Функция ВЕРОЯТНОСТЬ для расчета вероятности событий в Excel
Очень часто при работе в Excel необходимо использовать вычисления вероятности появления некоторого события. Для этого используется статистическая функция ВЕРОЯТНОСТЬ.
Примеры использования функции вероятность для расчетов в Excel
Стоит отметить, что используются часто в Excel и другие статистические функции, к примеру:
Функция выполняет вычисление вероятности того, что значения с интервала находятся в заданных пределах. В случае, если верхний предел не будет задан, то будет возвращена вероятность того, что значения аргумента x_интервал будет равно значению аргумента под названием нижний_предел.
Вычисление процента вероятности события в Excel
Пример 1. Дана таблица диапазона числовых значений, а также вероятностей, которые им соответствуют:
Необходимо при использовании данной статистической функции вычислить вероятность события, что значение с указанного интервала входит в интервал [1;4].
Для этого введем функцию со следующими аргументами:
- х_интервал – это начальные данные (0, …, 4);
- интервал вероятностей является множеством вероятностей для начальных данных (0,15; 0,1; 0,15; 0,2; 0,4);
- нижний предел равен значению 1;
- верхний предел равен 4.
В результате выполненных вычислений получим:
Пример 2. В условии предыдущего примера нужно вычислить вероятность события «значение х равно 4».
Введем в ячейку С3 введем функцию с такими аргументами:
- х_интервал – начальные параметры (0, …, 4);
- интервал вероятностей – совокупность вероятностей для параметров (0,1; 0,15; 0,2; 0,15; 0,4);
- нижний предел – 4;
В данном примере верхний предел не указан, поскольку необходимо конкретное значение вероятности, а именно для значения 4.
Функция ВЕРОЯТНОСТЬ при нескольких условиях интервалов
Пример 3. В условии примера 1 нужно вычислить вероятность того, что значения интервала [0; 4] будут находится находятся внутри интервалов [0;1] и [3;4].
Описание формул аналогичные предыдущим примерам.
В результате выполненных вычислений получим:
Таким образом составив формулу можно с помощью данной функции вычислить процент вероятности при нескольких условиях.
Источник
Решение задач на вычисление вероятности в Excel
Пример 4. В партии 20 изделий, из них 5 бракованных. Найти вероятность того, что в выборке из 4 изделий ровно одно бракованное.
Решение. В данной задаче, прежде всего, определим значения параметров: число_успехов_ в_ выборке = 1; размер_ выборки = 4; число_ успехов_ в_ совокупности = 5; размер_ совокупности = 20.
Искомую вероятность можно рассчитать с помощью функции = ГИПЕРГЕОМЕТ (1; 4; 5; 20), которая дает значение 0,4696.
Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность события А в каждом испытании одна и та же, а именно равна р. Следовательно, вероятность ненаступления события А в каждом испытании также постоянна и равна q = 1 – р.
Вероятность того, что при n повторных независимых испытаниях событие А осуществится ровно k раз вычисляется по формуле Бернулли: 
Для нахождения наиболее вероятного числа успехов k 0 по заданным n и р можно воспользоваться неравенствами np – q £ k 0£ np + p или правилом: если число np + p не целое, то k 0 равно целой части этого числа.
В случае, если n велико, р мало, а 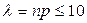

Пример 5. Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна р = 0,75. Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии на протяжении каждых из 6 суток постоянна и равна p = 0,75. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна q = 1- р = 1 — 0,75 = 0,25. Искомая вероятность по формуле Бернулли равна 
Пример 6. Телефонная станция обслуживает 400 абонентов. Для каждого абонента вероятность того, что в течение часа он позвонит на станцию, равна 0,01. Найти вероятность, что в течение часа ровно 5 абонентов позвонят на станцию.
Решение. Так как р = 0,01 мало и n = 400 велико, то будем пользоваться приближенной формулой Пуассона при l = 400 × 0,01 = 4. Тогда Р 400(5)» 
В случае, когда число повторных испытаний большое и формула Бернулли неприменима, используют формулы Лапласа.
Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 


Имеются таблицы, в которых помещены значения функции 
Интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 


При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами для интеграла 

Пример 7. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение. По условию n = 400; k = 80; р = 0,2; q = 0,8. Воспользуемся асимптотической формулой Лапласа: 


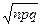

Пример 8. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение. Воспользуемся интегральной формулой Лапласа: n = 400; k 1 = 70; k 2 = 100; р = 0,2; q = 0,8; 

Для вычисления в Excel используем формулу нормального распределения = НОРМРАСП(100; 80; 8; 1) — НОРМРАСП(70; 80; 8; 1), которая дает значение 0,8882. При этом параметр интегральная = 1, остальные значения параметров определяются аналогично примеру, рассмотренному выше.
Источник
Цели и задачи:
Образовательные: закрепить такие
понятия теории вероятности как: среднее
арифметическое, размах, мода и медиана рядов
чисел; систематизировать знания по пройденной
теме, формировать умение учащихся применять
знания к решению практических задач, контроль,
оценка и проверка знаний учащихся, закрепить
знание способов ввода данных в ячейки и порядок
создания формул с использованием встроенных
функций в табличном процессоре MS Excel. Показать
важность межпредметных связей
Развивающие: развитие
познавательной активности, творческих
способностей учащихся, умения сопоставлять,
анализировать, развить навыки ввода данных в
ячейки с использованием автозаполнения и
вычисления итоговых значений с помощью
статистических функций табличного процессора MS
Excel;
Воспитательные: способствовать
воспитанию у учащихся аккуратности, усидчивости,
навыков учебного труда, интереса к предмету.
Ход урока
-
Организационный момент.
-
Актуализация опорных знаний. Опрос.
- Как определить среднее арифметическое ряда?
- Что называется модой ряда?
- Как определить размах ряда?
- Что называется медианой ряда?
- Что такое адрес ячейки и из чего он состоит?
- Чем абсолютный адрес отличается от
относительного? - Что такое автозаполнение и как им пользоваться?
- Что такое функция Excel?
-
Решить задачу:
- Администрация школы решила проверить
математическую подготовку учащихся 8 класса. С
этой целью был составлен тест, содержащий 9
заданий. Работу выполняли 40 учащихся школы. При
проверке каждой работы учитель отмечал число
верно выполненных заданий. В результате был
составлен такой ряд чисел:
- Определить сколько заданий в среднем выполнил
каждый ученик верно? - Найти разницу в числе верно выполненных заданий
между учащимися. - Чему равна мода и медиана данного ряда?
-
Закрепление материала
6,5,4,0,4,5,7,9,1,6,8,7,9,5,8,6,7,2,5,7,6,3,4,4,5,6,8,6.7,7,4,3.5,9,6,7,8,6,9,8.
Задача разбирается вместе с учителем
для постановки проблемной ситуации, в разрешении
которой помогает использование электронных
таблиц.
Чтобы ответить на вопросы задачи
необходимо упорядочить ряд данных, а при
нахождении статистических характеристик ряда
нам помогут на доске записанные статистические
функции Excel, которые используются для нахождения
среднего арифметического, размаха, моды и
медианы рядов чисел:
=МЕДИАНА(аргументы) – медиана
ряда;
=СРЗНАЧ(аргументы) – среднее
арифметическое ряда;
=МОДА(аргументы) – мода ряда;
=МАКС(аргументы)-МИН(аргументы)
– размах ряда.
Учащиеся получают листки с задачами,
рассаживаются за компьютеры и решают их с
помощью Excel. Для решения задач необходим файл
(Приложение1)
Задачи для закрепления
- Найдите среднее арифметическое, размах, моду и
медиану рядов чисел; - За четверть Люда получила по алгебре пять двоек,
четыре четверки и две пятерки. Ее мама считает,
что за четверть Люде надо ставить двойку, папа
считает, что надо ставить тройку, а сама Люда
считает, что надо ставить четверку. Попробуйте
привести аргументы в пользу каждой точки зрения
(какие статистические характеристики вычисляет
каждый член семьи?). Какую бы оценку вы поставили
Люде? - В таблице представлены результаты опроса 100
человек. - Света, Люда и Женя договорились в течение трех
дней по-очереди поливать в классе цветы. Сколько
у них есть способов установить порядок
дежурства? - 8 детей делят пирожки. Все пирожки имеют разную
начинку. Один из них с морковью. Сколько
существует способов разделить пирожки (каждому
по штуке) так, чтобы пирожок с морковью не
достался ребенку, который не любит такую начинку?
| Количество опрошенных | Зарплата |
| 10 | 500 |
| 30 | 1000 |
| 50 | 1500 |
| 10 | 3000 |
а) сколько денег, в среднем, получает один
человек из этой группы (найдите среднее
арифметическое ряда данных)?
б) сколько денег получает ежемесячно
“средний” человек из этой группы (найдите
медиану этих данных)?
в) какой заработок наиболее распространен у
членов этой группы (найдите моду этих данных)?
-
Подведение итогов (выставление оценок)
Приложение
17 авг. 2022 г.
читать 2 мин
Вероятность описывает вероятность того, что некоторое событие произойдет.
Мы можем рассчитать вероятности в Excel, используя функцию PROB , которая использует следующий синтаксис:
ПРОБ(x_диапазон, вероятностный_диапазон, нижний_предел, [верхний_предел])
куда:
- x_range: диапазон числовых значений x.
- prob_range: диапазон вероятностей, связанных с каждым значением x.
- нижний_предел: нижний предел значения, для которого вы хотите получить вероятность.
- upper_limit: Верхний предел значения, для которого вы хотите получить вероятность. По желанию.
В этом руководстве представлено несколько примеров использования этой функции на практике.
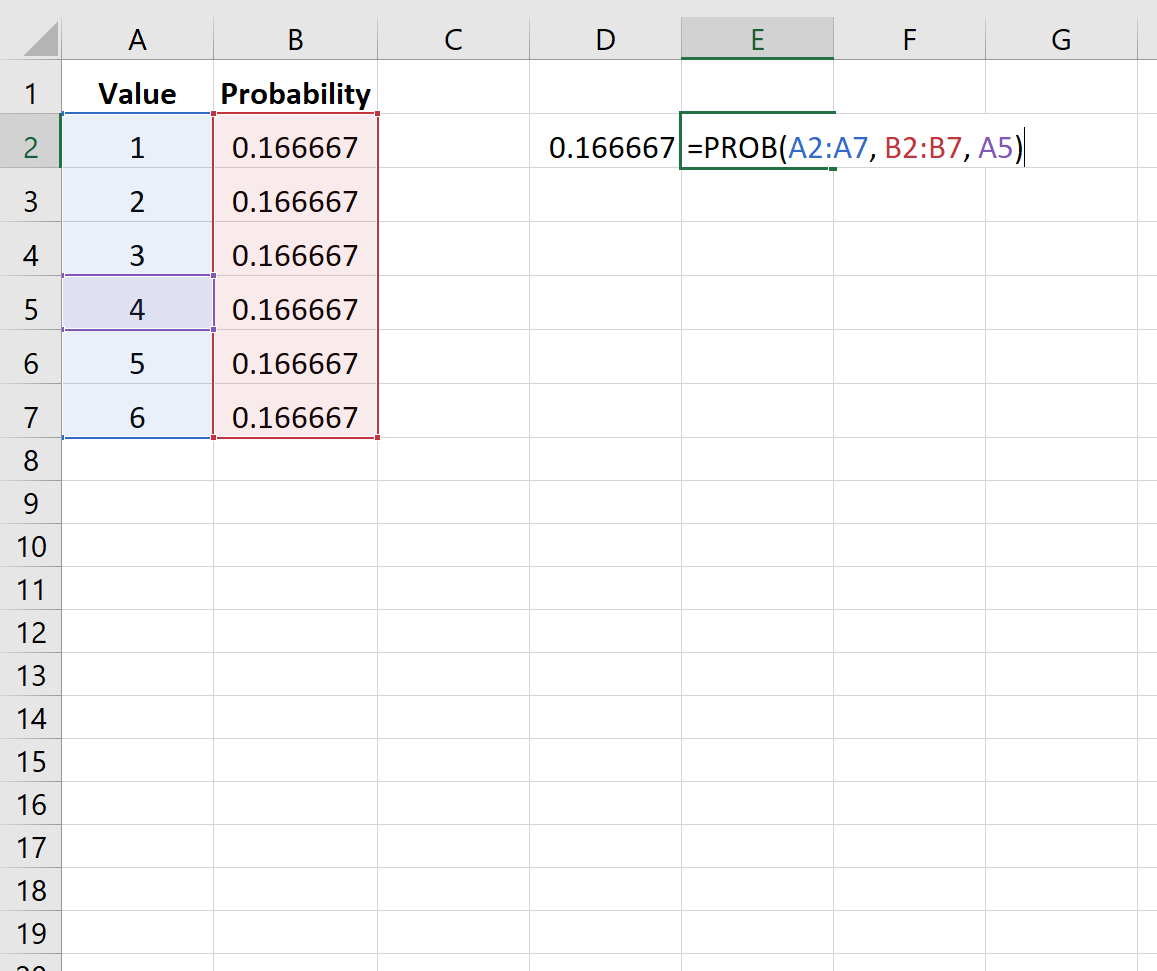
Пример 1: Вероятность игры в кости
На следующем изображении показана вероятность выпадения кубика с определенным значением при данном броске:
Поскольку кости с одинаковой вероятностью выпадут на каждом значении, вероятность одинакова для каждого значения.
На следующем рисунке показано, как найти вероятность того, что кубик выпадет на число от 3 до 6:
Вероятность оказывается равной 0,5 .
Обратите внимание, что аргумент верхнего предела является необязательным. Таким образом, мы могли бы использовать следующий синтаксис, чтобы найти вероятность того, что кости приземлятся только на 4:
Вероятность оказывается равной 0,166667 .
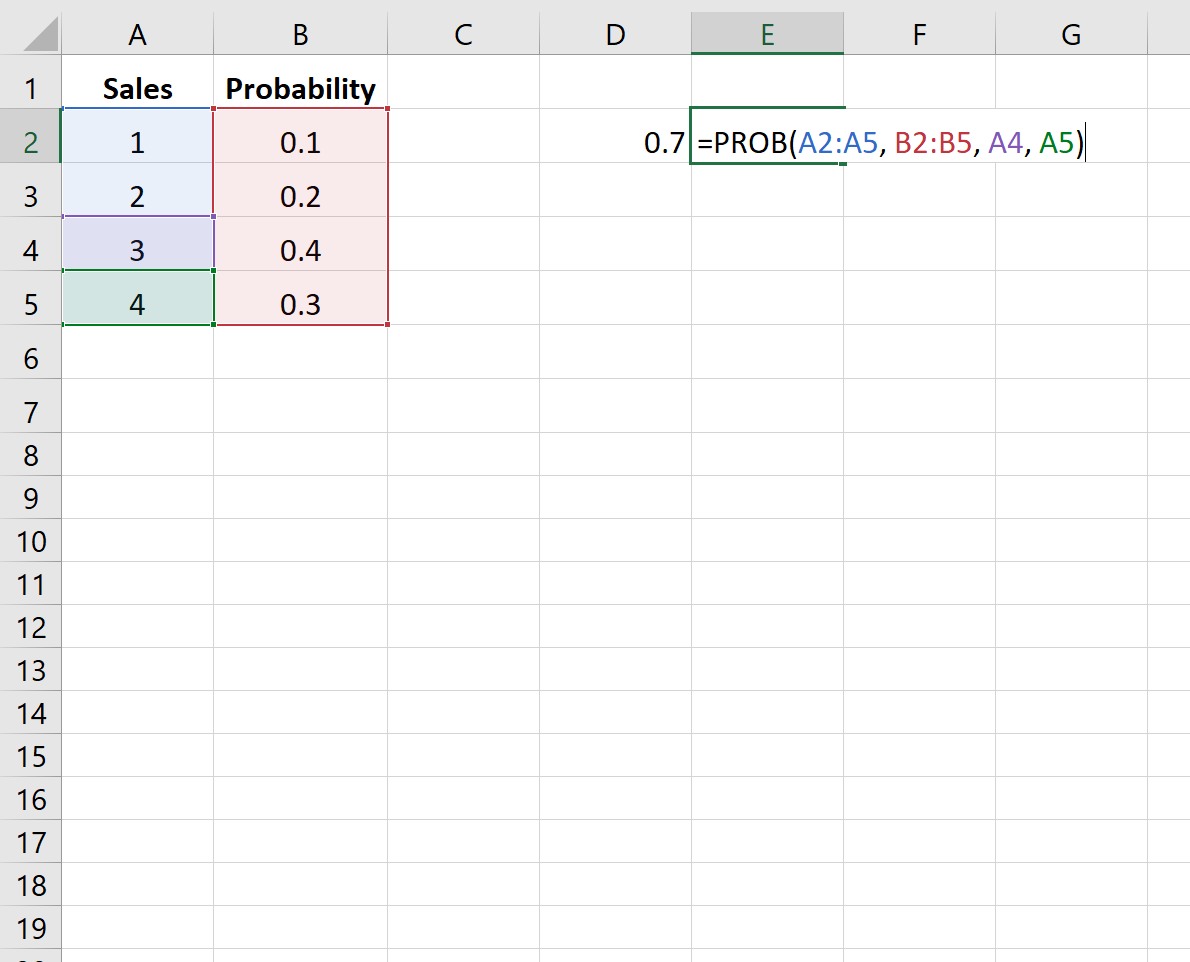
Пример 2: Вероятность продаж
На следующем изображении показана вероятность того, что компания продаст определенное количество товаров в предстоящем квартале:
На следующем рисунке показано, как найти вероятность того, что компания совершит 3 или 4 продажи:
Вероятность оказывается равной 0,7 .
Дополнительные ресурсы
Как рассчитать относительную частоту в Excel
Как рассчитать кумулятивную частоту в Excel
Как создать частотное распределение в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
«КАРСУНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ
ИМЕНИ В.В.ТИХОМИРОВА»
Методическая
разработка
интегрированного
урока
по
ОУД.03. МАТЕМАТИКА и ОУД.07. ИНФОРМАТИКА
Специальности:
34.02.01. Сестринское дело,
медицинская сестра/медицинский брат
Тема:
Решение задач по теме: «Элементы теории вероятности с помощью электронной
таблицы MS Excel».
Составила:
Преподаватель
математики и информатики:
Тимохина Л.Н.
р.п.
Карсун – 2020-21 уч.год
Пояснительная записка.
Вашему вниманию представляется интегрированный
урок информатики и математики. Проведению интегрированных уроков в учебном
процессе способствует развитию межпредметные связи, где информатика выступает в
роли интегрирующей дисциплины. При использовании компьютера в учебном процессе
учащийся становится полноправным его участником. Педагог не дает готовых
знаний, но побуждает учеников к самостоятельному поиску.
Компьютерные средства позволяют обеспечить наилучшую реализацию принципа
наглядности, которому принадлежит ведущее место в образовательных технологиях.
Широкое использование графических возможностей компьютера имеют большую
прикладную направленность.
На интегрированном уроке математики и информатики в на 1 курсе по теме «Решение задач по теме: «Элементы теории вероятности»» для моделирования использовался табличный
процессор Excel. Актуальность данного
метода: необходимость подготовки специалистов современного уровня, хорошо
знающих математику, и умеющих применять математические методы на компьютере.
Интегрированный урок математики и
информатики
Тип урока
– Урок применения знаний и умений.
Вид
– урок-практикум
Форма проведения урока: беседа,
работа в группах, индивидуальная работа.
Оборудование: проектор, экран, компьютер, презентация, карточки с заданиями.
Время проведения урока: 45 мин
Цели:
1. Закрепить
основные понятия комбинаторики с помощью решения задач, показать применение
комбинаторики в практических целях и в жизни человека.
2.Формирование умений и
навыков создания, редактирования, форматирования и записи
формул в электронных таблицах Excel
3. Формирование информационной компетентности учащихся через решение
задач с помощью MS Excel.
Задачи:
Образовательные:
— продолжить
формировать у учащихся представления о комбинаторике и ее применении в жизни
человека;
— расширить
представление учащихся о возможных сферах применения электронных таблиц;
— отработка навыков решения задач с использованием электронной
таблицы Excel.
Развивающие:
— развитие комбинаторного мышления учащихся;
— формирование интеллектуальных умений: анализировать, выделять
главное при работе с текстом задачи;
— развитие умений применять знания для решения задач различного
рода с помощью электронных таблиц.
— развивать опыт общения при работе в группах
Воспитательные:
— воспитывать коммуникативные компетенции;
— продолжить формирование
общей и математической культуры учащихся;
— воспитывать понимание
значимости ведущей роли математики в развитии современного научно-технического
общества;
— воспитывать
самоконтроль и взаимоконтроль
Формируемые
общие и профессиональные компетенции, определенные стандартом (ФГОС):
–
сформированность представлений о процессах и явлениях, имеющих вероятностный
характер, статистических закономерностях в реальном мире, основных понятиях
элементарной теории вероятностей; умений находить и оценивать вероятности
наступления событий в простейших практических ситуациях и основные
характеристики случайных величин;
– владение навыками использования готовых
компьютерных программ при решении задач.
Ход
урока
Здравствуйте ребята!
Садитесь. Сегодня у нас необычный урок. Раньше мы на уроках информатики
применяли знания, полученные на уроках математики, а сегодня будем использовать
знания информатики в решении математических задач. Девиз урока: «Человек думает
,а компьютер решает».
Мы с вами
находимся в компьютерном классе, поэтому повторим правила поведения при работе
с компьютером. Каждый называет по одному правилу, повторяться нельзя.
Примерный план ответа:
— без разрешения учителя в класс не входить;
— на перемене всем выходить из кабинета;
— с едой в класс не входить;
— садиться на строго отведенное место;
— запрещается трогать руками разъемы, экран и тыльную сторону ПК;
— приступать к работе с компьютером только с разрешения учителя;
— не ремонтировать ПК самостоятельно;
— немедленно прекратить работу при поломке ПК;
— сидеть на расстоянии от экрана не менее 60-70 см .
Слайд 1- высказывание
Автор высказывания
на слайде является автором так называемого классического определения
вероятности, пришедшего из области азартных игр, где теория вероятностей
применялась для определения перспективы выигрыша.
Слайд
2 с формулой.
—
Что такое вероятность? (Вероятностью Р наступления случайного события А
называется отношение m к n, где n – это число всех возможных исходов
эксперимента, а m – это число всех благоприятных исходов).
Вероятность
события = Число благоприятных исходов / число всех равновозможных исходов.
— Какие темы
мы с вами изучили на последних уроках алгебры? (перестановки, размещения,
сочетания)
— Что нам
необходимо сделать, чтобы закрепить изученные темы? (применить теорию на
практике, решать задачи по данной теме)
— Как вы
считаете, какова тема и цель сегодняшнего урока? (закрепить основные понятия
комбинаторики с помощью решения задач) (СЛАЙДЫ 3,4)
Повторение
А теперь давайте вспомним все то, что мы изучали на прошлых уроках:
1)
Что
означает слово «комбинаторика» (соединять, сочетать)
2)
Какие
задачи называются комбинаторными?
(Комбинаторная задача – задача, в которой идет речь о тех или
иных комбинациях объектов)
3)
В каких сферах жизни применяется комбинаторика?
-учебные заведения (составление расписаний)
-сфера общественного питания (составление меню)
-лингвистика (рассмотрение вариантов комбинаций букв)
-география (раскраска карт)
-биология (расшифровка кода ДНК)
-химия (анализ возможных связей между химическими элементами)
-экономика (анализ вариантов купли-продажи акций)
-азартные игры (подсчёт частоты выигрышей)
-криптография (разработка методов шифрования)
-доставка почты (рассмотрение вариантов пересылки)
-спортивные соревнования (расчёт количества игр между участниками)
4) Что такое
перестановка?
5) Что
такое размещение?
6) Что такое
сочетание?
Слайды 5,6,7
Устная работа
1)
Вычислите
устно: 2! (2),3!(6), 4!(24),5!(120), 6! (720)
2)
5!:0!
(120), 10!:8! (90), 100!:99! (100), 11!:8! (720)
3)
Заполните
пропуски в формулах:
4)
(28)
, (24)
5)Сколькими способами
можно поставить на полке 5 разных книг? (перестановка-120)
6)Имеется 6 разных
цветов. Сколькими способами можно составить букет из трех цветов? (сочетания — 20)
7) Сколько двузначных
чисел можно составить из чисел 1,2,3,4 ,используя в записи числа каждую из них
не более одного раза? (размещения -12 чисел)

На книжной полке стоят 20 книг, из них 3 справочника. Какова вероятность, что
взятая с полки книга не окажется справочником? (Р =17 / 20 = 0,85).
Какими
способами можно решать комбинаторные задачи? (СЛАЙД 
—
перебор возможных вариантов,
—
дерево возможных вариантов;
—
комбинаторное правило умножения;
—
составление таблицы;
—
с помощью графов;
—
формул перестановок, размещений и сочетаний.
При
решении комбинаторных задач важно понять, к какому типу относится задача.
Вспомним,
какие комбинации встречаются: перестановки, размещения, сочетания. Как же
различить их друг от друга и выбрать правильную формулу для решения?
Слайд 9
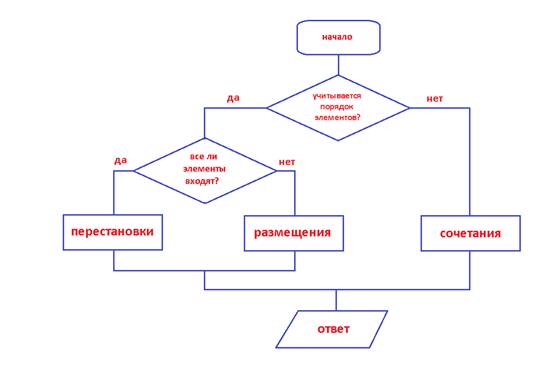
Посмотрите
на слайд: Как называется данная схема? (блок-схема) К какому типу она
относится? (разветвляющийся)
Слайд 10
Посмотрите на таблицу (простейшие комбинации)
Итак,
после определения типа задачи мы можем использовать соответствующую формулу. Но
вычисление по формуле – иногда очень трудоемкий процесс. В этом нам поможет
электронная таблица Excel.
Практическая Часть (слайды №11-18)
Учитель информатики показывает примеры
задач, решаемых с помощью EXCEL.
Самостоятельная
работа в группах.
Каждая
группа получила 4 задачи. Вам нужно выяснить к какому типу относится каждая задача
и применить полученные сейчас знания для их решения.
Задача
№1.
В группе 7 человек успешно занимаются математикой. Сколькими способами можно выбрать
из них двоих для участия в математической олимпиаде?(21 способ.)
Имеется
2 красных и 5 желтых тюльпанов. Сколько различных вариантов составления букета
из 3-х цветков? (35)
Задача
№2.
Сколько существует шестизначных чисел (без повторения цифр), у которых цифра 5
является последней? (Фиксируем цифру 5 на последнем месте, на остальные пять
перед ней выбираем любые пять цифр из 9 оставшихся (с учетом порядка выбора).
Количество
вариантов = 5 · 6
· 7 · 8 · 9 = 15120 чисел. Но мы знаем, что цифра 0 не может стоять на первом
месте. Мы должны «отбросить» из этих чисел те, у которых 0 на первом месте (и 5
на последнем).
Таких чисел = 5 · 6 · 7 · 8 = 1680
чисел.
Значит, всего
15120 – 1680 = 13440 вариантов.
О т в е т: 13440.
В
группе 5 девушек и 8 юношей. Для представительства этой группы на конференции
выбирают 4 человека, которым присваиваются номера для выступления на данной
конференции. Сколько различных вариантов составления такой группы можно
построить? (17160)
Задача № 3. У
Вовы на обед первое, второе, третье блюда и салат. Он обязательно начнет с
салата, а остальное съест в произвольном порядке. Найдите число возможных
вариантов обеда.( После салата Вова может выбрать любое из
трех блюд, затем – из двух, а закончить оставшимся. Общее число вариантов: Р3
= 3! = 6.)
Сколько
существует перестановок букв слова «конус», в которых буквы «к», «о», «н»
стоят рядом в указанном порядке?( Буквы
«к», «о», «н» стоят рядом в указанном порядке, поэтому конструкцию «кон» можно
считать одной буквой. Значит нужно найти количество перестановок из трех
элементов: Р = 3! = 6)
Задача
№ 4.
В случайном эксперименте бросают две игральные кости. Найдите вероятность
того, что сумма выпавших очков равна 6. Ответ округлите до сотых.( Р(А) = 5/36
= 0,14)
Люда
дважды бросает игральный кубик. В сумме у неё выпало 9 очков. Найдите
вероятность того, что при одном из бросков выпало 5 очков. (Множество
элементарных исходов удобно представить таблицей. Строки соответствуют
результату первого броска, столбцы – результату второго броска.
Всего
элементарных событий, при которых сумма очков 9 будет п = 4.
Значит,
событию А = {при одном из бросков выпало 5 очков} благоприятствует 2
элементарных исхода. Следовательно, т = 2. Поэтому, Р(А) = 2/4 = 0,5.)
Отчет
каждой группы о проделанной работе.
Лидер
группы предлагается сказать «благодарю» кому-то одному из участников группы,
чей вклад в работу группы был наиболее ценен.
Домашнее
задание: Собрать информацию об ученых,
занимавшихся изучением комбинаторики, составить доклад.
Итог урока. Рефлексия (СЛАЙД 19)
Выберите каждый начало предложения и закончите его.
•
Сегодня я узнал…
•
Было интересно…
•
Было трудно…
•
Я выполнял задания…
•
Я понял, что…
•
Теперь я могу…
•
Я научился…
•
У меня получилось…
•
Я смог…
•
Я попробую…
•
Урок дал мне для жизни…
•
Мне захотелось …
«ТРИ
М». Учащимся предлагается назвать три момента, которые продемонстрировали им
преимущество использования электронных таблиц в решении комбинаторных задач.
-Был
ли полезен вам опыт, приобретенный на этом уроке? Как вы думаете, при решении
каких математических задач так же можно использовать электронные таблицы?
СЛАЙД
20 (домашнее задание)
Вывод:
На данном уроке мы отработали навыки
решения задач по теме Решение задач по теме: «Элементы теории вероятности с
помощью электронной таблицы MS Excel». , а так же отработали навыки
составления таблиц в электронных таблицах Excel, правила написания
расчетных формул. А так же мы увидели, как перекликаются и связаны такие
предметы как математика и информатика.
Мы
видим, что интегрированные уроки дают ученику достаточно широкое и яркое
представление о мире, в котором он живёт, о взаимосвязи явлений и предметов,
решают множество отдельных задач и их совокупность. Формы урока могут быть
различны, но в каждом должно быть достаточно материала для упражнения
«деятельных сил» (И.Г. Песталоцци) ребёнка, данных ему от природы.
Интегрированные
уроки способствуют повышению интереса учащихся к знаниям, уровня мотивации.
Учитель
должен сочетать наиболее приемлемые для интеграции учебные предметы, отказаться
от традиционных шаблонных форм организации урока, уметь свободно строить
учебный процесс, но все же придерживаться установленных требований проведения
урока.
Литература, использованная при подготовке к уроку:
1.
Математика. 10-11
классы: элективный курс «В мире случайных закономерностей» / ав.-сост. В.Н.
Студенецкая и др. – Волгоград: Учитель, 2007. – 126 с.
2.
Задачник-практикум по
теории вероятностей с элементами комбинаторики и математической статистики:
Учебное пособие для студентов-заочников IV курса
физико-математических факультетов педагогических институтов / Н.Я. Виленкин,
В.Г. Потапов. – Москва: Просвещение, 1979. – 112 с.
3. Демоверсии ЕГЭ по математике – 2015, 2016.
4. http://mathege.ru/ — открытый банк заданий
по математике.
5. Алгебра и начала анализа. 11 кл.: Учеб.
для общеобразоват. Учреждений: базовый и профил. уровни / Ю. М. Колягин, М. В.
Ткачева, Н. Е. Федорова, М. И. Шабунин./под редакцией А.Б.Жижченко– М.
:Просвещение, 2009- 336 с.
Скачано с www.znanio.ru