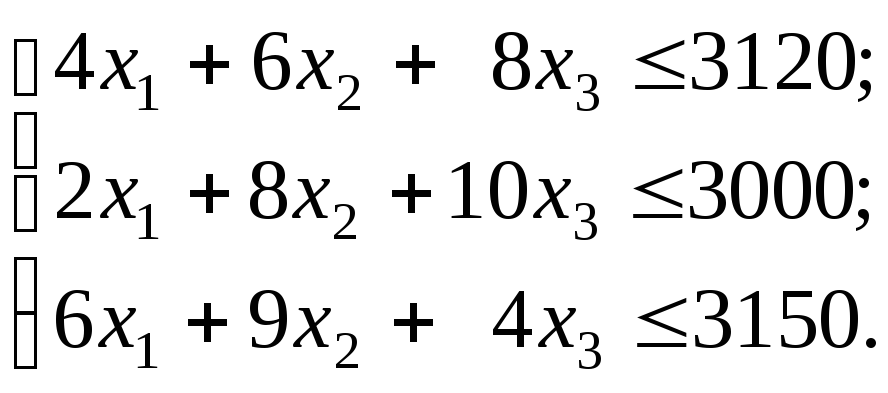Содержание
- Использование табулирования
- Создание таблицы
- Построение графика
- Вопросы и ответы
Табулирование функции представляет собой вычисление значения функции для каждого соответствующего аргумента, заданного с определенным шагом, в четко установленных границах. Эта процедура является инструментом для решения целого ряда задач. С её помощью можно локализовать корни уравнения, найти максимумы и минимумы, решать другие задачи. С помощью программы Excel выполнять табулирование намного проще, чем используя бумагу, ручку и калькулятор. Давайте выясним, как это делается в данном приложении.
Использование табулирования
Табулирование применяется путем создания таблицы, в которой в одной колонке будет записано значение аргумента с выбранным шагом, а во второй — соответствующее ему значение функции. Затем на основе расчета можно построить график. Рассмотрим, как это делается на конкретном примере.
Создание таблицы
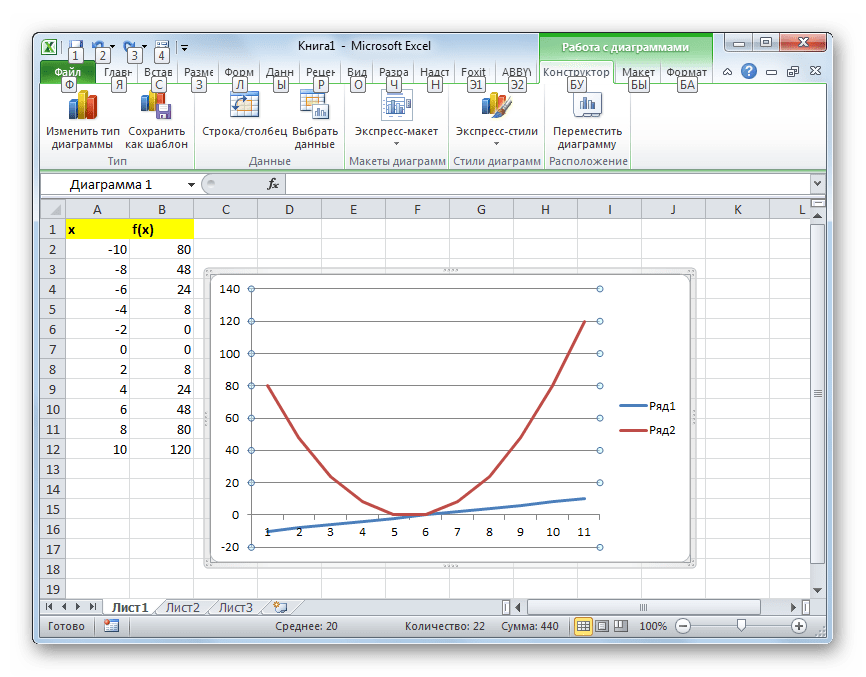
Создаем шапку таблицы с колонками x, в которой будет указано значение аргумента, и f(x), где отобразится соответствующее значение функции. Для примера возьмем функцию f(x)=x^2+2x, хотя для процедуры табулирования может использоваться функция любого вида. Устанавливаем шаг (h) в размере 2. Граница от -10 до 10. Теперь нам нужно заполнить столбец аргументов, придерживаясь шага 2 в заданных границах.
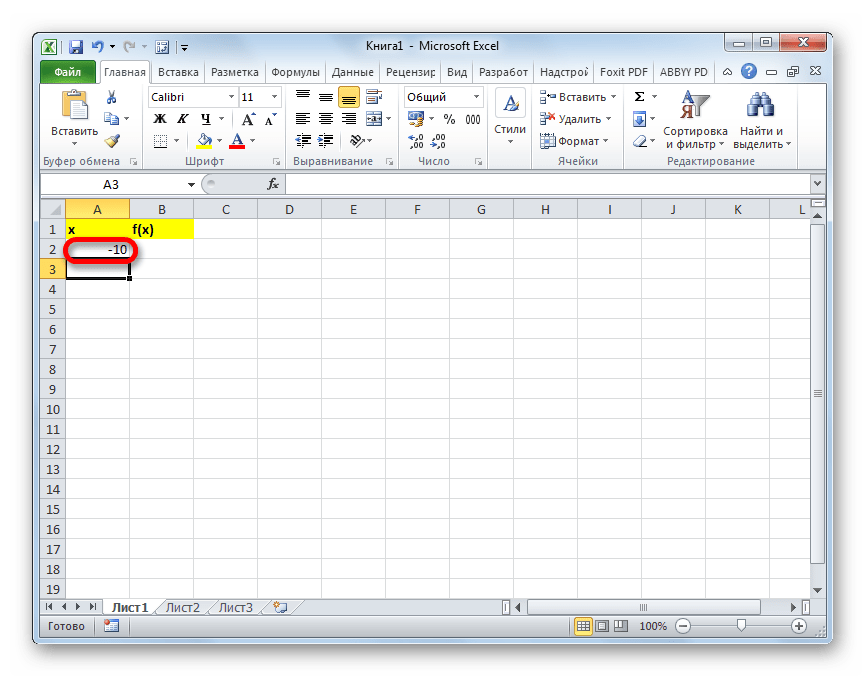
- В первую ячейку столбца «x» вписываем значение «-10». Сразу после этого жмем на кнопку Enter. Это очень важно, так как если вы попытаетесь произвести манипуляцию мышкой, то значение в ячейке превратится в формулу, а в данном случае это не нужно.
- Все дальнейшие значения можно заполнить вручную, придерживаясь шага 2, но удобнее это сделать с помощью инструмента автозаполнения. Особенно этот вариант актуален, если диапазон аргументов большой, а шаг — относительно маленький.
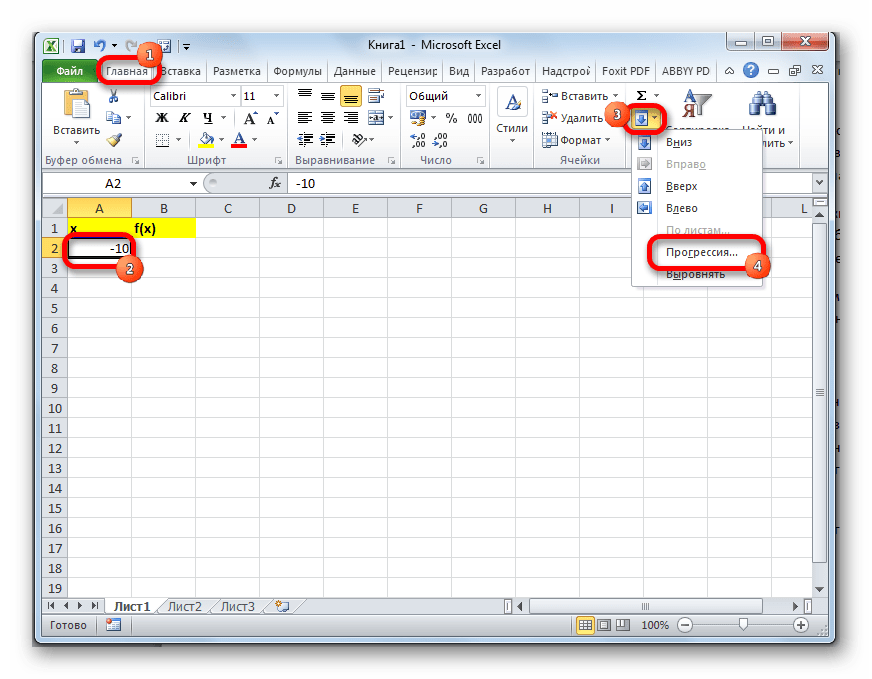
Выделяем ячейку, в которой содержится значение первого аргумента. Находясь во вкладке «Главная», кликаем по кнопке «Заполнить», которая размещена на ленте в блоке настроек «Редактирование». В появившемся списке действий выбираем пункт «Прогрессия…».
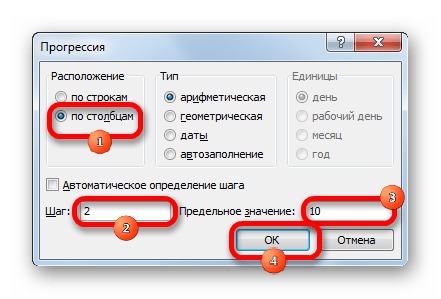
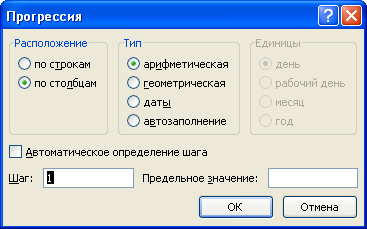
- Открывается окошко настройки прогрессии. В параметре «Расположение» устанавливаем переключатель в позицию «По столбцам», так как в нашем случае значения аргумента будут размещаться именно в колонке, а не в строке. В поле «Шаг» устанавливаем значение 2. В поле «Предельное значение» вписываем число 10. Для того чтобы запустить прогрессию, жмем на кнопку «OK».
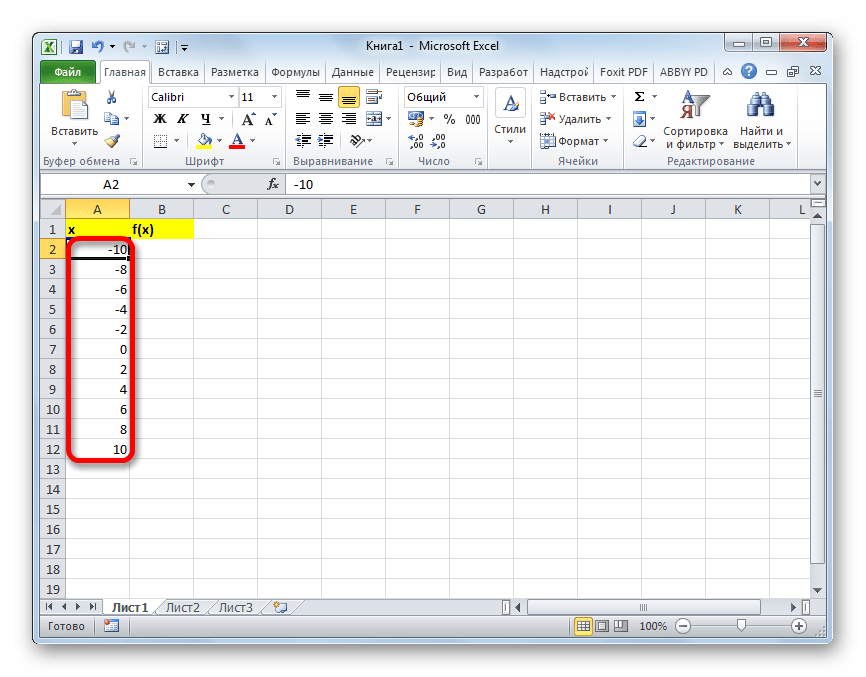
- Как видим, столбец заполнен значениями с установленными шагом и границами.
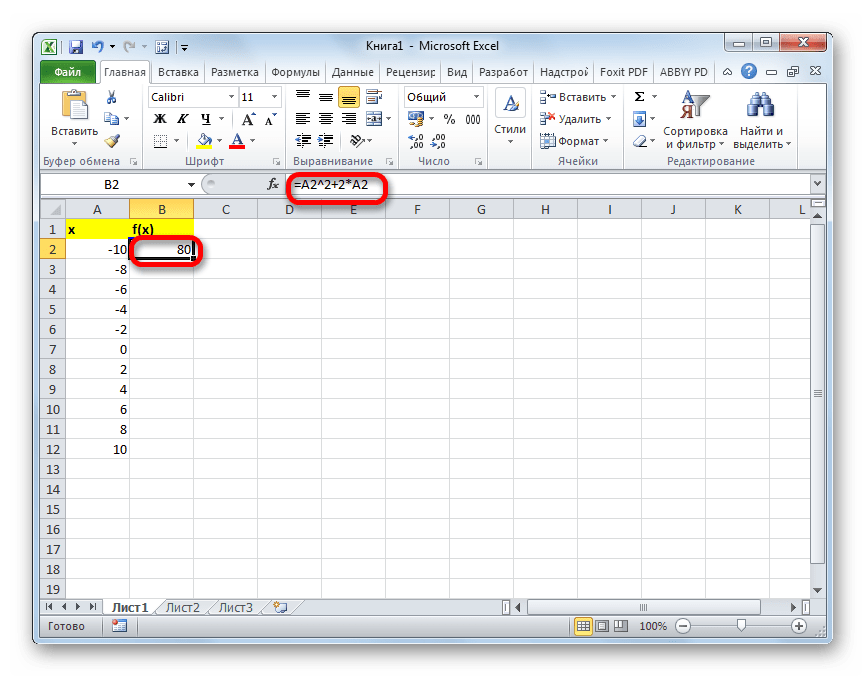
- Теперь нужно заполнить столбец функции f(x)=x^2+2x. Для этого в первую ячейку соответствующей колонки записываем выражение по следующему шаблону:
=x^2+2*xПри этом, вместо значения x подставляем координаты первой ячейки из столбца с аргументами. Жмем на кнопку Enter, чтобы вывести результат вычислений на экран.
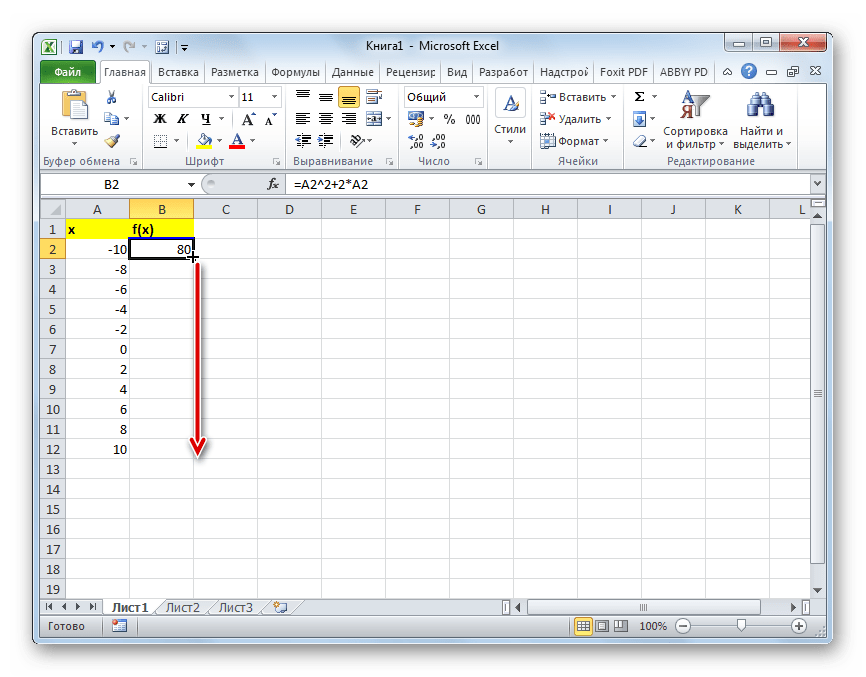
- Для того, чтобы произвести вычисление функции и в других строках, снова воспользуемся технологией автозаполнения, но в данном случае применим маркер заполнения. Устанавливаем курсор в нижний правый угол ячейки, в которой уже содержится формула. Появляется маркер заполнения, представленный в виде небольшого по размеру крестика. Зажимаем левую кнопку мыши и протягиваем курсор вдоль всего заполняемого столбца.
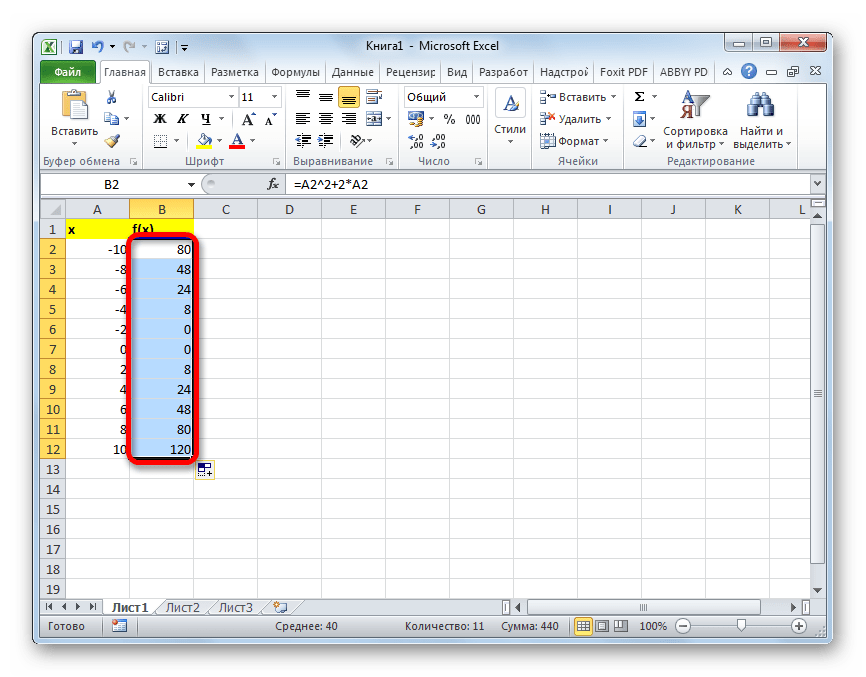
- После этого действия вся колонка со значениями функции будет автоматически заполнена.
Таким образом, табуляция функции была проведена. На её основе мы можем выяснить, например, что минимум функции (0) достигается при значениях аргумента -2 и 0. Максимум функции в границах вариации аргумента от -10 до 10 достигается в точке, соответствующей аргументу 10, и составляет 120.
Урок: Как сделать автозаполнение в Эксель
Построение графика
На основе произведенной табуляции в таблице можно построить график функции.
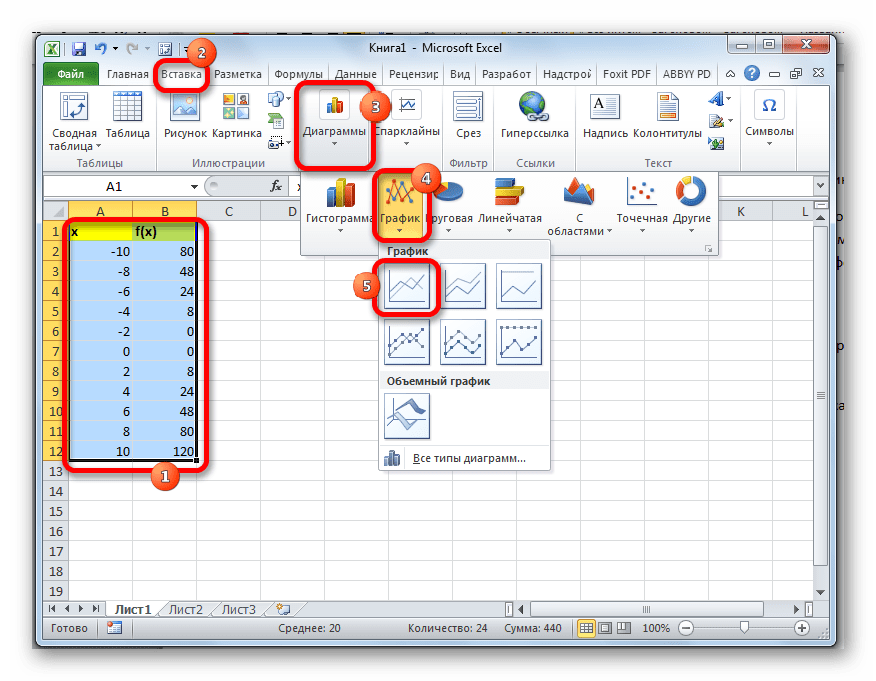
- Выделяем все значения в таблице курсором с зажатой левой кнопкой мыши. Перейдем во вкладку «Вставка», в блоке инструментов «Диаграммы» на ленте жмем на кнопку «Графики». Открывается список доступных вариантов оформления графика. Выбираем тот вид, который считаем наиболее подходящим. В нашем случае отлично подойдет, например, простой график.
- После этого на листе программа выполняет процедуру построения графика на основе выделенного табличного диапазона.
Далее по желанию пользователь может отредактировать график так, как считает нужным, используя для этих целей инструменты Excel. Можно добавить названия осей координат и графика в целом, убрать или переименовать легенду, удалить линию аргументов, и т.д.
Урок: Как построить график в Эксель
Как видим, табулирование функции, в общем, процесс несложный. Правда, вычисления могут занять довольно большое время. Особенно, если границы аргументов очень широкие, а шаг маленький. Значительно сэкономить время помогут инструменты автозаполнения Excel. Кроме того, в этой же программе на основе полученного результата можно построить график для наглядного представления.
Еще статьи по данной теме:
Помогла ли Вам статья?
Решение уравнения с помощью инструмента «Поиск решения».
Практическая работа № 17.
Тема: Решение линейных и нелинейных уравнений с помощью MS Excel.
Цель: научиться решать линейные и нелинейные уравнения различными способами.
Теоретические сведения и задания:
Графический метод решения уравнения.
Известно, что графическим решением уравнения f(x)=0 является точка пересечения графика функции f(x) с осью абсцисс, т.е. такое значение x, при котором функция обращается в ноль.
Разберем графический метод решения уравнения на примере: пусть необходимо решить уравнение x 3 — 0,01x 2 — 0,7044x + 0,139104 = 0.
На листе 1 проведем табулирование нашей функции на интервале от -1 до 1 с шагом 0,2, для этого построим таблицу значений. Затем по таблице построим точечную диаграмму. Результаты вычислений приведены на рисунке, где в ячейку В2 была введена формула: = A2^3 — 0,01*A2^2 — 0,7044*A2 + 0,139104. На графике видно, что функция три раза пересекает ось Оx, а так как полином третьей степени имеет не более трех вещественных корней, то графическое решение поставленной задачи найдено. Иначе говоря, была проведена локализация корней, т.е. определены интервалы, на которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8] (можно получить более точное решение если выбрать шаг 0,1).
Лист 1 переименовать в Задание1 и сохранить работу в своей папке с именем Фамилия пр17.xls
Решение уравнения с помощью инструмента «Подбор параметра».
Перейти на лист 2.
Чтобы решить нелинейное уравнение можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.
Возьмем в качестве примера квадратное уравнение х 2 -5х+6=0. Для нахождения корней уравнения выполним следующие действия:
В ячейку С3 введем формулу для вычисления значения функции, стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.
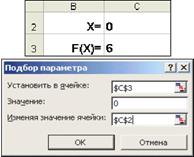
· В окне диалога Подбор параметра в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
· После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.
При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка Продолжить — для возврата в обычный режим подбора параметра.
Вернемся к примеру. Возникает вопрос: как получить второй корень? Для того чтобы найти второй корень, достаточно в качестве начального приближения в ячейку C2 поместить константу 5 и после этого запустить процесс Подбор параметра.
Лист 2 переименовать в Задание2.
Решение уравнения с помощью инструмента «Поиск решения».
Команда Подбор параметра является удобной для решения простых уравнений. Для более сложных задач следует использовать команду Поиск решения, доступ к которой реализован через пункт меню Сервис/Поиск решения. При решении уравнений с помощью Поиска решений можно учитывать различные дополнительные ограничения, например, ОДЗ (область допустимых значений).
Перейти на лист 3.
Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.
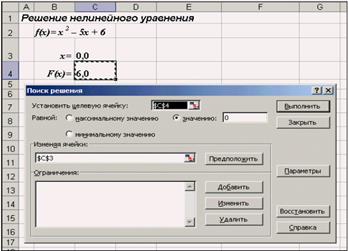
После открытия диалога Поиск решения необходимо выполнить следующие действия:
1. в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
2. для максимизации значения целевой ячейки, установить переключатель максимальному значению, для минимизации используется переключатель минимальному значению, в нашем случае устанавливаем переключатель в положение значению и вводим значение 0;
3. в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции (С3), разделяя их знаком «;» (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического поиска всех влияющих на решение ячеек используется кнопка Предположить;
4. в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
5. для запуска процесса поиска решения нажать кнопку Выполнить.

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, как на рисунке. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
Задание: Используя метода Подбор параметров, найти корни уравнения 
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Квадратное уравнение в Excel
В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.
Ход решения
Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.
Получим формулу вида ax 2 +bx+c=0
В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).
Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x1= C4 x2=. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2
Перейдем к вводу формул для решения
Дискриминант квадратного трехчлена равен b 2 -4ac
В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:
Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x1
Для расчета x2 введем похожую формулу, но со знаком плюс
Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x1 и x2.
Защита листа в Excel
Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.
Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.
Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.
Так же вас может заинтересовать материал как закрепить область в Экселе.
источники:
http://urok.1sept.ru/articles/564361
http://abuzov.ru/kvadratnoe-uravnenie-v-excel-reseno/
Содержание
- Числовые последовательности в EXCEL (порядковые номера 1,2,3. и др.)
- Используем формулы
- Используем клавишу CTRL
- Используем правую клавишу мыши
- Используем начало последовательности
- Использование инструмента Прогрессия
- Как сделать ряд чисел в excel?
- Функция случайного числа в Excel
- Выборка случайных чисел с помощью СЛЧИС
- Функция СЛУЧМЕЖДУ
- Как сделать генератор случайных чисел в Excel
- Генератор случайных чисел нормального распределения
- Про аргументы функции РЯД
- Применение именованных диапазонов в функции РЯД
Числовые последовательности в EXCEL (порядковые номера 1,2,3. и др.)
history 10 апреля 2013 г.
Создадим числовые последовательности различных видов: 1, 2, 3, . 1, 3, 5, 7, . I, II, III, IV, . 100, 200, 300. 00-01 , 00-02, . 1, 1, 1, 2, 2, 2. и пр.
Используем формулы
Сформируем последовательность 1, 2, 3, . Пусть в ячейке A2 введен первый элемент последовательности — значение 1 . В ячейку А3 , вводим формулу =А2+1 и копируем ее в ячейки ниже (см. файл примера ).
Так как в формуле мы сослались на ячейку выше с помощью относительной ссылки , то EXCEL при копировании вниз модифицирует вышеуказанную формулу в =А3+1 , затем в =А4+1 и т.д., тем самым формируя числовую последовательность 2, 3, 4, .
Если последовательность нужно сформировать в строке, то формулу нужно вводить в ячейку B2 и копировать ее нужно не вниз, а вправо.
Чтобы сформировать последовательность нечетных чисел вида 1, 3, 7, . необходимо изменить формулу в ячейке А3 на =А2+2 . Чтобы сформировать последовательность 100, 200, 300, . необходимо изменить формулу на =А2+100 , а в ячейку А2 ввести 100.
Другим вариантом создания последовательности 1, 2, 3, . является использование формулы =СТРОКА()-СТРОКА($A$1) (если первый элемент последовательности располагается в строке 2 ). Формула =СТРОКА(A2)-СТРОКА($A$1) позволяет создать вертикальную последовательность, в случае если ее первый элемент последовательности располагается в любой строке. Тот же результат дают формулы =ЧСТРОК($A$1:A1) , =СТРОКА(A1) и =СТРОКА(H1) . Формула =СТОЛБЕЦ(B1)-СТОЛБЕЦ($A$1) создает последовательность, размещенную горизонтально. Тот же результат дают формулы =ЧИСЛСТОЛБ($A$1:A1) , =СТОЛБЕЦ(A1) .
Чтобы сформировать последовательность I, II, III, IV , . начиная с ячейки А2 , введем в А2 формулу =РИМСКОЕ(СТРОКА()-СТРОКА($A$1))
Сформированная последовательность, строго говоря, не является числовой, т.к. функция РИМСКОЕ() возвращает текст. Таким образом, сложить, например, числа I+IV в прямую не получится.
Другим видом числовой последовательности в текстовом формате является, например, последовательность вида 00-01 , 00-02, . Чтобы начать нумерованный список с кода 00-01 , введите формулу =ТЕКСТ(СТРОКА(A1);»00-00″) в первую ячейку диапазона и перетащите маркер заполнения в конец диапазона.
Выше были приведены примеры арифметических последовательностей. Некоторые другие виды последовательностей можно также сформировать формулами. Например, последовательность n2+1 ((n в степени 2) +1) создадим формулой =(СТРОКА()-СТРОКА($A$1))^2+1 начиная с ячейки А2 .
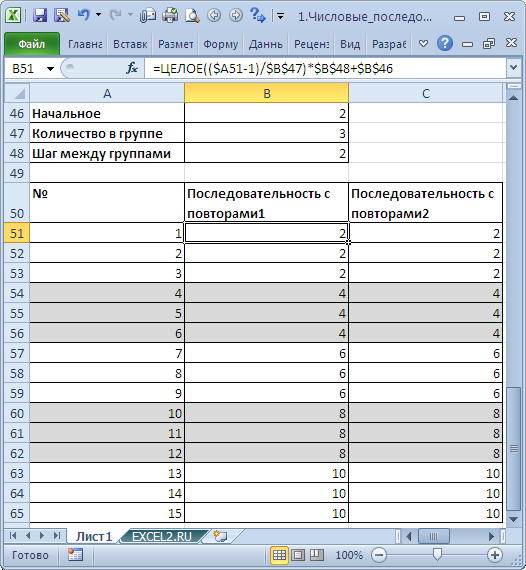
Создадим последовательность с повторами вида 1, 1, 1, 2, 2, 2. Это можно сделать формулой =ЦЕЛОЕ((ЧСТРОК(A$2:A2)-1)/3+1) . С помощью формулы =ЦЕЛОЕ((ЧСТРОК(A$2:A2)-1)/4+1)*2 получим последовательность 2, 2, 2, 2, 4, 4, 4, 4. , т.е. последовательность из четных чисел. Формула =ЦЕЛОЕ((ЧСТРОК(A$2:A2)-1)/4+1)*2-1 даст последовательность 1, 1, 1, 1, 3, 3, 3, 3, .
Примечание . Для выделения повторов использовано Условное форматирование .
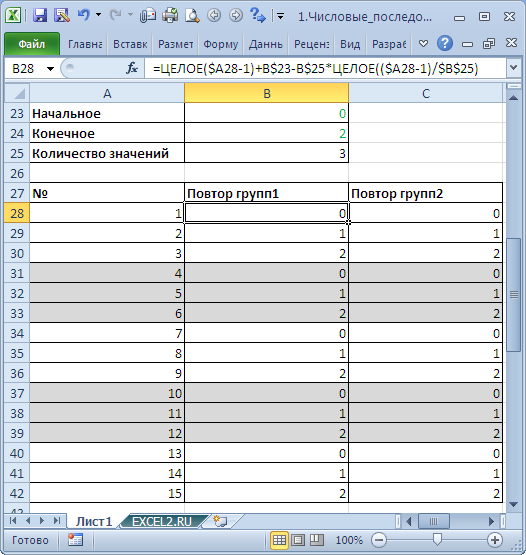
Формула =ОСТАТ(ЧСТРОК(A$2:A2)-1;4)+1 даст последовательность 1, 2, 3, 4, 1, 2, 3, 4, . Это пример последовательности с периодически повторяющимися элементами.
Используем клавишу CTRL
Пусть, как и в предыдущем примере, в ячейку A2 введено значение 1 . Выделим ячейку A2 . Удерживая клавишу CTRL , скопируем Маркером заполнения (при этом над курсором появится маленький плюсик), значение из A 2 в ячейки ниже. Получим последовательность чисел 1, 2, 3, 4 …
ВНИМАНИЕ! Если на листе часть строк скрыта с помощью фильтра , то этот подход и остальные, приведенные ниже, работать не будут. Чтобы разрешить нумерацию строк с использованием клавиши CTRL , выделите любую ячейку с заголовком фильтра и дважды нажмите CTRL + SHIFT + L (сбросьте фильтр).
Используем правую клавишу мыши
Пусть в ячейку A2 введено значение 1 . Выделим ячейку A2 . Удерживая правую клавишу мыши, скопируем Маркером заполнения , значение из A2 в ячейки ниже. После того, как отпустим правую клавишу мыши появится контекстное меню, в котором нужно выбрать пункт Заполнить . Получим последовательность чисел 1, 2, 3, 4 …
Используем начало последовательности
Если начало последовательности уже задано (т.е. задан первый элемент и шаг последовательности), то создать последовательность 1, 2, 3, . можно следующим образом:
- пусть в ячейке А2 введено значение 1 , а в ячейке А3 значение 2 ;
- выделяем ячейки A2 и A3 ;
- беремся за правый нижний угол и Маркером заполнения протягиваем вниз.
Получаем результат как в предыдущем случае. Если в ячейке А3 введено значение 3 , т.е. задан шаг последовательности равный 2, то мы получим последовательность нечетных чисел.
Создадим последовательность вида 1, 2, 3, 1, 2, 3. для этого введем в первые три ячейки значения 1, 2, 3, затем маркером заполнения , удерживая клавишу CTRL , скопируем значения вниз.
Использование инструмента Прогрессия
Воспользуемся стандартным средством EXCEL для создания прогрессий, в то числе и арифметических.
- вводим в ячейку А2 значение 1 ;
- выделяем диапазон A2:А6 , в котором будут содержаться элементы последовательности;
- вызываем инструмент Прогрессия ( Главная/ Редактирование/ Заполнить/ Прогрессия. ), в появившемся окне нажимаем ОК.
Использование в работе : Подходы для создания числовых последовательностей можно использовать для нумерации строк , сортировки списка с числами , разнесения значений по столбцам и строкам .
СОВЕТ: О текстовых последовательностях вида первый, второй, . 1), 2), 3), . можно прочитать в статье Текстовые последовательности . О последовательностях значений в формате дат (и времени) вида 01.01.09, 01.02.09, 01.03.09, . янв, апр, июл, . пн, вт, ср, . можно прочитать в статье Последовательности дат и времен . О массивах значений, содержащих последовательности конечной длины, используемых в формулах массива , читайте в статье Массив значений (или константа массива или массив констант) .
Источник
Как сделать ряд чисел в excel?
Перед многими пользователями встает задача оформить в табличном виде какую-либо последовательность данных, подчиняющихся стандартным правилам. Примером может служить нумерация строк (последовательность натуральных чисел), последовательность дат в графике работы, инвентарные номера в ведомости учета и так далее. Статья поможет вам использовать возможности Excel для автоматизации процесса создания таких последовательностей.
Ввод каких данных может быть автоматизирован?
- последовательность чисел;
- последовательность дат;
- последовательность текстовых данных;
- последовательность формул.
Справиться с поставленной задачей могут помочь:
Рассмотрим решение задачи формирования последовательности чисел. Здесь возможно несколько вариантов:
- нужно получить ряд натуральных чисел (пронумеровать строки);
- нужно получить ряд чисел, в котором последующее число отличается от предыдущего на определенный шаг (четные, нечетные, арифметическая прогрессия);
Для создания таких последовательностей нужно:
- ввести первое и последующее значения (разница между значениями задает шаг изменения значений ряда);
- выделить обе ячейки;
- навести курсор мыши на маркер заполнения (правый нижний угол выделенного диапазона) и с нажатой левой кнопкой мыши протянуть маркер до формирования нужного количества значений (если тянуть маркер в направлении второго выделенного числа, то получаем ряд последующих чисел, если в направлении первого выделенного числа, то получаем ряд предыдущих чисел).
- ввести первое значение;
- в группе «Редактирование» на вкладке «Главная» открыть список у пункта «Заполнить» и выбрать вариант «Прогрессия» (обратите внимание, что при этом должна быть выделена ячейка с начальным значением);
- заполнить поля формы нужными данными (в рассматриваемом примере формируется ряд четных чисел, расположение сверху вниз (по столбцам), предельное значение 10, шаг 2).
Для создания последовательности дат (если нужны все даты определенного диапазона) достаточно ввести только начальное значение и воспользоваться маркером заполнения. Если нужны некоторые даты (в случае составления графика работы, например), то необходимо ввести начальную и последующую даты, далее выполнить такой же алгоритм, как для последовательности чисел. Команда
«Прогрессия» дает возможность выбрать варианты формирования ряда (например, нужны только рабочие дни).
Последовательность текстовых данных может быть получена для дней недели, месяцев, для любого текста с цифрой (цифрами) в конце (например, ИНВ01). Для ее формирования достаточно начального значения.
Можно создавать свои списки. На рисунке приведен пример списка сотрудников. Этот список необходимо импортировать с помощью команды
«Файл».
Стоит отметить, что встроенные последовательности существуют и в более ранних версиях Excel.
У нас есть последовательность чисел, состоящая из практически независимых элементов, которые подчиняются заданному распределению. Как правило, равномерному распределению.
Сгенерировать случайные числа в Excel можно разными путями и способами. Рассмотрим только лучше из них.
Функция случайного числа в Excel
- Функция СЛЧИС возвращает случайное равномерно распределенное вещественное число. Оно будет меньше 1, больше или равно 0.
- Функция СЛУЧМЕЖДУ возвращает случайное целое число.
Рассмотрим их использование на примерах.
Выборка случайных чисел с помощью СЛЧИС
Данная функция аргументов не требует (СЛЧИС()).
Чтобы сгенерировать случайное вещественное число в диапазоне от 1 до 5, например, применяем следующую формулу: =СЛЧИС()*(5-1)+1.
Возвращаемое случайное число распределено равномерно на интервале .
При каждом вычислении листа или при изменении значения в любой ячейке листа возвращается новое случайное число. Если нужно сохранить сгенерированную совокупность, можно заменить формулу на ее значение.
- Щелкаем по ячейке со случайным числом.
- В строке формул выделяем формулу.
- Нажимаем F9. И ВВОД.
Проверим равномерность распределения случайных чисел из первой выборки с помощью гистограммы распределения.
- Сформируем «карманы». Диапазоны, в пределах которых будут находиться значения. Первый такой диапазон – 0-0,1. Для следующих – формула =C2+$C$2.
- Определим частоту для случайных чисел в каждом диапазоне. Используем формулу массива <=ЧАСТОТА(A2:A201;C2:C11)>.
- Сформируем диапазоны с помощью знака «сцепления» (=»»).
- Строим гистограмму распределения 200 значений, полученных с помощью функции СЛЧИС ().
Диапазон вертикальных значений – частота. Горизонтальных – «карманы».
Функция СЛУЧМЕЖДУ
Синтаксис функции СЛУЧМЕЖДУ – (нижняя граница; верхняя граница). Первый аргумент должен быть меньше второго. В противном случае функция выдаст ошибку. Предполагается, что границы – целые числа. Дробную часть формула отбрасывает.
Пример использования функции:
Случайные числа с точностью 0,1 и 0,01:
Как сделать генератор случайных чисел в Excel
Сделаем генератор случайных чисел с генерацией значения из определенного диапазона. Используем формулу вида: =ИНДЕКС(A1:A10;ЦЕЛОЕ(СЛЧИС()*10)+1).
Сделаем генератор случайных чисел в диапазоне от 0 до 100 с шагом 10.
Из списка текстовых значений нужно выбрать 2 случайных. С помощью функции СЛЧИС сопоставим текстовые значения в диапазоне А1:А7 со случайными числами.
Воспользуемся функцией ИНДЕКС для выбора двух случайных текстовых значений из исходного списка.
Чтобы выбрать одно случайное значение из списка, применим такую формулу: =ИНДЕКС(A1:A7;СЛУЧМЕЖДУ(1;СЧЁТЗ(A1:A7))).
Генератор случайных чисел нормального распределения
Функции СЛЧИС и СЛУЧМЕЖДУ выдают случайные числа с единым распределением. Любое значение с одинаковой долей вероятности может попасть в нижнюю границу запрашиваемого диапазона и в верхнюю. Получается огромный разброс от целевого значения.
Нормальное распределение подразумевает близкое положение большей части сгенерированных чисел к целевому. Подкорректируем формулу СЛУЧМЕЖДУ и создадим массив данных с нормальным распределением.
Себестоимость товара Х – 100 рублей. Вся произведенная партия подчиняется нормальному распределению. Случайная переменная тоже подчиняется нормальному распределению вероятностей.
При таких условиях среднее значение диапазона – 100 рублей. Сгенерируем массив и построим график с нормальным распределением при стандартном отклонении 1,5 рубля.


Используем функцию: =НОРМОБР(СЛЧИС();100;1,5).
Программа Excel посчитала, какие значения находятся в диапазоне вероятностей. Так как вероятность производства товара с себестоимостью 100 рублей максимальная, формула показывает значения близкие к 100 чаще, чем остальные.
Перейдем к построению графика. Сначала нужно составить таблицу с категориями. Для этого разобьем массив на периоды:
- Определим минимальное и максимальное значение в диапазоне с помощью функций МИН и МАКС.
- Укажем величину каждого периода либо шаг. В нашем примере – 1.
- Количество категорий – 10.
- Нижняя граница таблицы с категориями – округленное вниз ближайшее кратное число. В ячейку Н1 вводим формулу =ОКРВНИЗ(E1;E5).
- В ячейке Н2 и последующих формула будет выглядеть следующим образом: =ЕСЛИ(G2;H1+$E$5;»»). То есть каждое последующее значение будет увеличено на величину шага.
- Посчитаем количество переменных в заданном промежутке. Используем функцию ЧАСТОТА. Формула будет выглядеть так:
На основе полученных данных сможем сформировать диаграмму с нормальным распределением. Ось значений – число переменных в промежутке, ось категорий – периоды.
График с нормальным распределением готов. Как и должно быть, по форме он напоминает колокол.
Сделать то же самое можно гораздо проще. С помощью пакета «Анализ данных». Выбираем «Генерацию случайных чисел».
О том как подключить стандартную настройку «Анализ данных» читайте здесь.
Заполняем параметры для генерации. Распределение – «нормальное».
Жмем ОК. Получаем набор случайных чисел. Снова вызываем инструмент «Анализ данных». Выбираем «Гистограмма». Настраиваем параметры. Обязательно ставим галочку «Вывод графика».
Скачать генератор случайных чисел в Excel
График с нормальным распределением в Excel построен.
Если вы выберите ряд данных какой-нибудь диаграммы и взгляните на строку формул, вы увидите, что ряд данных генерируется с помощью функции РЯД. РЯД – это специальный вид функции, который используется только в контексте создания диаграммы и определяет значения рядов данных. Вы не сможете использовать ее на рабочем листе Excel и не сможете включить стандартные функции в ее аргументы.
Про аргументы функции РЯД
Для всех видов диаграмм, кроме пузырьковой, функция РЯД имеет список аргументов, представленных ниже. Для пузырьковой диаграммы, требуется дополнительный аргумент, который определяет размер пузыря.
| АРГУМЕНТ | ОБЯЗАТЕЛЬНЫЙ/ НЕ ОБЯЗАТЕЛЬНЫЙ | ОПРЕДЕЛЕНИЕ |
| Имя | Не обязательный | Имя ряда данных, которое отображается в легенде |
| Подписи_категорий | Не обязательный | Подписи, которые появляются на оси категорий (если не указано, Excel использует последовательные целые числа в качестве меток) |
| Значения | Обязательный | Значения, используемые для построения диаграммы |
| Порядок | Обязательный | Порядок ряда данных |
Каждый из этих аргументов соответствует конкретным данным в полях диалогового окна Выбор источника данных (Правый щелчок мыши по ряду данных, во всплывающем меню выбрать Выбор данных).
В строке формул Excel вы можете увидеть примерно такую формулу:
Аргументами функции РЯД являются данные, которые можно найти в диалоговом окне Выбор источника данных:
Имя – аргумент Diag!$B$1 можно найти, если щелкнуть по кнопке Изменить, во вкладке Элементы легенды (ряды) диалогового окна Выбор источника данных. Так как ячейка B1 имеет подпись Значение, ряд данных будет называться соответственно.
Подпись_категорий – аргумент Diag!$A$2:$A$100 находится в поле Подписи горизонтальной оси (категории).
Значения – аргумент значений ряда данных Diag!$B$2:$B$100 находится там же, где мы указали имя ряда.
Порядок – так как наша диаграмма имеет всего один ряд данных, то и порядок будет равен 1. Порядок рядов данных отражается в списке поля Элементы легенды (ряды)
Применение именованных диапазонов в функции РЯД
Прелесть использования функции РЯД заключается в возможности использования именованных диапазонов в ее аргументах. Используя именованные диапазоны, вы можете легко переключаться между данными одного ряда данных. Что более важно, используя именованные диапазоны в качестве аргументов функции РЯД, можно создавать динамические диаграммы. Вообще, все диаграммы динамические, в том смысле, что при изменении данных, диаграммы меняют свой внешний вид. Но используя именованные диапазоны вы можете сделать так, чтобы график автоматически обновлялся при добавлении новых данных в книгу или выбирал какое-нибудь подмножество данных, например, последние 30 значений.
Методика создания динамических диаграмм на основе именованных диапазонов была описана мной в одной из предыдущих статей.
Источник
|
0 / 0 / 0 Регистрация: 17.08.2017 Сообщений: 2 |
|
|
1 |
|
Как протянуть формулу с определенным шагом?18.08.2017, 14:51. Показов 30855. Ответов 8
Здравствуйте, уважаемые гуру экселя! Помогите пожалуйста решить проблему: есть карточки объектов на листе «24», по ним суммы затрат выведены в отдельный столбец: для объекта 1 это W6, для объекта 2 это AU6, для объекта 3 это W23, для объекта 4 это AU23 и т.д. Мне нужно на листе «факт недельный» рядом с каждым объектом в графе «24 расход» вывести эти цифры. И так как объектов 200, надо эту формулу протянуть, а не писать вручную. Т.е. на листе «факт недельный» в ячейке C4 должно быть значение с листа «24» W6, в ячейке C5 должно быть значение с листа «24» AU6, в ячейке C6 должно быть значение с листа «24» W23, в ячейке C7 должно быть значение с листа «24» AU23 и т.д. Помогите пожалуйста! Заранее благодарен))
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
18.08.2017, 14:51 |
|
8 |
|
1237 / 673 / 240 Регистрация: 22.12.2015 Сообщений: 2,094 |
|
|
18.08.2017, 15:24 |
2 |
|
Решениеspbdab, по сути это задача для базы данных, а не для экселя. Код =СМЕЩ('24'!$P$5;17*([@№]-1);0)
Если компоновку менять не будете, то нужно будет вместо нуля учесть смещение по столбцам:
0 |
|
0 / 0 / 0 Регистрация: 17.08.2017 Сообщений: 2 |
|
|
18.08.2017, 18:37 [ТС] |
3 |
|
Спасибо вам огромное, вы очень меня выручили! )))) Карточки объектов поменял))
0 |
|
0 / 0 / 0 Регистрация: 14.06.2021 Сообщений: 2 |
|
|
14.06.2021, 16:37 |
4 |
|
Добрый день уважаемые форумчане! Подскажите пожалуйста как реализовать некоторые операции в excel. В приложенном файле «Накопительная ведомость» есть три листа: 1й- ОМЗ, 2й- СТС, 3й- Сводная ( в котором ссылки на 1й и 2й лист), так вот вопрос в том как протянуть-скопировать эти ячейки со ссылками на предыдущие листы, что бы данные отображались корректно, а именно, если выделить диапазон ячеек F9:J9 (1е число месяца) и протянуть на K9:O9 (2е число месяца), то excel вставляет данные с шагом в 6 ячеек вправо, а нужно что бы брал данные из следующей ячейки, т.е последовательно, что бы данные по датам совпадали. Очень нужна ваша помощь.
0 |
|
3827 / 2254 / 751 Регистрация: 02.11.2012 Сообщений: 5,930 |
|
|
14.06.2021, 16:58 |
5 |
|
вариант, формула для F9 Код =ИНДЕКС('ООО "ОМЗ"'!$G$9:$Z$9;;ПОИСКПОЗ(ДЕНЬ(F7);'ООО "ОМЗ"'!$G$6:$Z$6;))
в G9 по аналогии. П.С. в эксель объединение — ЗЛО.
1 |
|
0 / 0 / 0 Регистрация: 14.06.2021 Сообщений: 2 |
|
|
14.06.2021, 23:19 |
6 |
|
Выражаю просто мега огромную благодарность!!! Так оперативно ответили, выручили очень сильно!!!!
0 |
|
0 / 0 / 0 Регистрация: 25.06.2021 Сообщений: 2 |
|
|
30.06.2021, 13:06 |
7 |
|
Добрый день! Нужна помощь от опытных пользователей excel по составлению формулы для протягивания ячеек. Дано: на листе «Сводка» некоторые данные берутся с листа «Промо» (почти все данные из столбцов с A по L). При выделении диапазона A7:G9 на листе «Сводка» и протягивании вниз excel вставляет данные с шагом в 2 ячейки вниз, а нужно последовательно (как пример для одной ячейки: в «Сводке» ячейка A7 данные берет с листа «Промо» ячейки А3, а при протягивании в «Сводке» А10 данные берет с А6 «Промо», но должны быть с А4).
0 |
|
1237 / 673 / 240 Регистрация: 22.12.2015 Сообщений: 2,094 |
|
|
30.06.2021, 16:24 |
8 |
|
При выделении диапазона A7:G9
а при протягивании в «Сводке» А10 данные берет с А6 «Промо», но должны быть с А4). В А10 вбейте =ИНДЕКС(Промо!$A$3:$A$8;(СТРОКА()-СТРОКА($A$7))/3+1)
1 |
|
0 / 0 / 0 Регистрация: 25.06.2021 Сообщений: 2 |
|
|
30.06.2021, 21:24 |
9 |
|
Большое вам спасибо! Вы очень помогли!
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
30.06.2021, 21:24 |
|
9 |
15
Лабораторная
работа № 1
Цель работы:изучение современных программных
средств решения задачи линейного
программирования; практическое решение
задач линейного программирования
графическим методом, симплекс-методом
и средствами программыMicrosoftExcel; программная реализация
симплекс-метода на языке программирования
высокого уровня.
1. Теоретическая часть
Для решения задач
линейного программирования в программе
Microsoft
Excel
имеется надстройка Поиск
решения,
обращение
к которой производится из меню Сервис.
Если команда
Поиск решения
отсутствует в меню Сервис,
то требуется установить надстройку
«Поиск решения». Для этого в меню Сервис
выбирается команда Надстройки,
которая открывает диалоговое окно,
показанное на рис. 1.
Рис. 1
Далее в этом окне
устанавливается флажок той надстройки,
которую необходимо загрузить, и нажимается
кнопка OK.
Покажем использование
надстройки
«Поиск решения» на примере решения
следующей задачи.
Постановка задачи
Предприятие
изготавливает и реализует три вида
продукции – P1,
Р2
и Р3.
Для производства продукции используются
три вида ресурсов – комплектующие
изделия, сырье и материалы. Запасы
ресурсов и их расход на изготовление
единицы продукции каждого вида приведены
в табл. 1.
Таблица 1
|
Виды |
Расходы |
Запасы ресурсов, |
||
|
P1 |
P2 |
P3 |
||
|
Комплектующие |
4 |
6 |
8 |
3120 |
|
Сырье |
2 |
8 |
10 |
3000 |
|
Материалы |
6 |
9 |
4 |
3150 |
Прибыль от реализации
единицы продукции каждого вида составляет
240, 210 и 180 денежных единиц для P1,
Р2
и Р3
соответственно.
Требуется определить
производственную программу предприятия
таким образом, чтобы прибыль от реализации
продукции была максимальной.
Математическая модель задачи
Обозначим переменными
x1,
x2
и x3
искомые объемы производства продукции
видов P1,
Р2
и Р2,
а через F
– прибыль предприятия. Тогда математическая
постановка представленной задачи
принимает следующий вид.
Определить значения
переменных x1,
x2
и x3,
для которых достигается максимум целевой
функции
F
=
240 x1
+ 210 х2
+ 180 x3
при ограничениях:
Целевая функция
описывает суммарную прибыль от реализации
произведенной продукции всех трех
видов. Ограничения (1), (2) и (3) учитывают
расход и запасы комплектующих изделий,
сырья и материалов соответственно.
Поскольку объемы производства продукции
не могут быть отрицательными, добавляются
условия
x1
≥ 0; x2
≥ 0; x3
≥ 0.
Порядок оптимального решения задачи
Примерные действия,
необходимые для решения задачи линейного
программирования средствами программы
Excel,
представим в виде последовательности
шагов.
Шаг 1.
Исходные данные задачи записываются
на рабочем листе электронной таблицы.
Один из вариантов показан на рис. 2.
Рис. 2
Замечание.
Если известно исходное допустимое
базисное решение, то можно несколько
ускорить процесс поиска оптимального
решения. Для этого начальные значения
некоторых или всех переменных могут
быть заданы вручную. В данном примере
для их хранения используются ячейки
$B$2,
$C$2
и $D$2.
Если допустимое базисное решение не
задано, то программа Excel
автоматически определяет начальные
значения переменных задачи.
Шаг 2.
В ячейку E3
вводится формула
=СУММПРОИЗВ(В3:D3;
$B$2:$D$2)
для вычисления
текущего значения целевой функции,
которая находит сумму попарных
произведений ячеек (В3:D3)
с коэффициентами при переменных в
выражении целевой функции на ячейки
($B$2:$D$2)
с текущими значениями переменных.
Шаг 3.
Чтобы задать ограничения решаемой
задачи, в ячейки E5,
E6
и E7
копируется формула из ячейки E3.
После этого в указанных ячейках должны
быть получены формулы, представленные
в табл. 2.
Таблица
2
-
Ячейка
Содержание
(формула)E5
=СУММПРОИЗВ(В5:D5;
$B$2:$D$2)E6
=СУММПРОИЗВ(В6:D6;
$B$2:$D$2)E7
=СУММПРОИЗВ(В7:D7;
$B$2:$D$2)
Шаг 4.
После создания таблицы с исходными
данными курсор устанавливается в ячейку
E3,
содержащую формулу для вычисления
целевой функции. Далее в меню Сервис
выбирается
команда Поиск
решения,
которая открывает диалоговое окно,
приведенное на рис. 3.
Рис. 3
В поле Установить
целевую ячейку
окна «Поиск решения», показанного на
рис. 3, должен
появиться адрес ячейки с формулой
целевой функции (в данном примере это
ячейка $E$3).
Затем в этом окне
(рис. 3) заполняются следующие поля этого
окна:
— в поле Равной
переключатель вида экстремума целевой
функции устанавливается в положение
максимальное
значение
(или минимальное
значение
при
соответствующей постановке задачи);
— в поле Изменяя
ячейки
указывается
диапазон ячеек со значениями переменных
задачи, выделяемый на рабочем листе
электронной таблицы (в примере это
ячейки $B$2:$D$2);
— в поле Ограничения
задаются
ограничения исходной задачи. Для этого
курсор устанавливается в поле ввода
ограничений и нажимается кнопка Добавить.
В результате
выводится диалоговое окно «Добавление
ограничения», показанное на рис. 4.
Рис. 4
В этом окне в поле
Ссылка на
ячейку
вводится
адрес ячейки
с формулой соответствующего ограничения
(например, для ограничения (1) это будет
ячейка E5),
а в поле Ограничение
указывается
предельное значение, которое может
принимать выбранное ограничение (в
данном примере правая часть ограничения
(1) находится в ячейке G5).
Следует заметить,
что заполнение полей Ссылка
на ячейку
и Ограничение
в окне «Добавление
ограничения» можно выполнить выделением
соответствующих ячеек рабочего листа
электронной таблицы.
Затем выбирается
вид отношения, связывающего левую и
правую части ограничения, что показано
на рис. 5.
Рис. 5
После нажатия
кнопки Добавить
в окне
«Добавление ограничения»
(или кнопки
ОК
для ввода
последнего ограничения) данное ограничение
попадает в список ограничений решаемой
задачи. С помощью кнопок Удалить
и Изменить
можно удалять
выделенные в списке ограничения или
вносить в них исправления.
Замечание.
В окне «Добавление
ограничения» можно указать, что все или
некоторые переменные должны принимать
только целые значения (рис. 5). Это
позволяет получать решения задач
целочисленного линейного программирования
(полностью или частично целочисленных).
Шаг 5.
После заполнения всех полей окна «Поиск
решения» нажимается кнопка Параметры
(рис. 3),
которая открывает диалоговое окно
«Параметры поиска решения», показанное
на рис. 6.
Рис. 6
В этом окне требуется
установить флажки Линейная
модель
для решения
задачи линейного программирования и
Неотрицательные
значения,
если такое
условие накладываются на все переменные
задачи.
Здесь (рис. 6) также
можно определить параметры процесса
решения: предельное время поиска решения,
максимальное количество итераций,
точность и т.п. Флажок Показывать
результаты
итераций
позволяет по шагам следить за поиском
решения. Флажок Автоматическое
масштабирование
включается
в том случае, когда разброс значений
переменных очень велик.
Шаг 6.
Задав необходимые параметры в окне
«Параметры
поиска решения»,
следует нажать на кнопку Выполнить
для поиска
решения задачи (рис. 3) в
окне «Поиск решения».
Если решение найдено, то на экран
выводится окно с соответствующим
сообщением (рис. 7).
Рис. 7
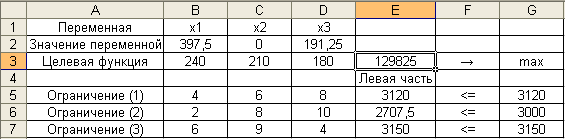
Полученные
результаты отображаются на рабочем
листе электронной таблицы, как это
показано на рис. 8. В частности, значения
переменных — в ячейках $B$2:$D$2,
значение целевой функции – в ячейке
E3.
Рис. 8
Таким образом,
получено оптимальное решение исходной
задачи в виде вектора
,
где,
и
,
для которого значение целевой функцииF
максимально и составляет F*
= 129825.
Результаты решения
задачи линейного программирования
также можно сохранить в виде отдельных
рабочих листов с именами Отчет
по результатам,
Отчет
по устойчивости
и Отчет
по пределам.
Для сохранения
результатов в виде отчетов необходимо
предварительно в поле Тип
отчета
выделить
требуемые типы отчетов (рис. 7). В этом
же окне можно отказаться от полученных
решений и восстановить исходные значения
переменных.
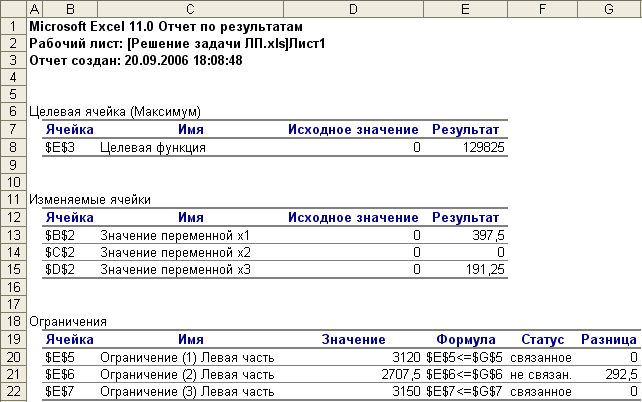
Отчет по результатам
для рассмотренной задачи показан
на рис. 9.
Рис. 9
В данном отчете
представлены оптимальное решение задачи
линейного программирования и его
расположение в области допустимых
решений. В графах Результат
выводятся
оптимальные значения целевой функции
F*
и переменных задачи
,
а также их значения для исходного
базисного решения, с которого начинался
поиск оптимального решения (графаИсходное
значение).
Состояние
ограничений (графа Статус)
характеризует расположение точки
в области допустимых решений. ГрафаРазница
показывает разности между значениями
левых и правых частей ограничений
(невязки). Для связанного ограничения
невязка равна нулю, что свидетельствует
о расположение точки
на границе области допустимых решений,
которая задается этим ограничением.
Если ограничение являются не связанным,
то оно не влияет на оптимальное решение.
Замечание.
В экономической интерпретации связанные
ограничения соответствуют дефицитным
ресурсам. Для не связанных ограничений
графа Разница
показывает оставшиеся объемы
неиспользованных не дефицитных ресурсов.
В рассмотренной задаче ограничения (1)
и (3) соответствуют комплектующим изделиям
и материалам, которые являются дефицитными
ресурсами. Ограничение (2) является не
связанным, т.е. не влияет на оптимальный
план производства продукции по критерию
максимальной прибыли. Это означает, что
второй ресурс (сырье) не использован в
объеме 292,5 ед.
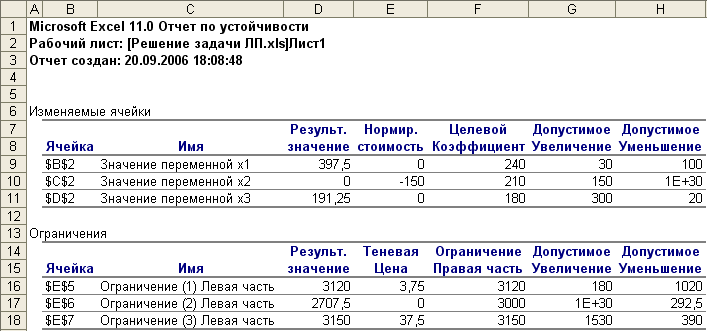
В
отчете по устойчивости (рис.
10) приведены
границы устойчивости переменных задачи
(графы Допустимое
увеличение
и Допустимое
уменьшение
коэффициентов целевой функции), а также
границы устойчивости теневых цен (т.е.
переменных двойственной задачи), в
пределах которых оптимальное решение
не изменяется. Большие
значения пределов (1Е+30)
означают фактическое
отсутствие соответствующих границ,
т.е. переменная может изменяться до
бесконечности.
Рис. 10
В графе Нормированная
стоимость
элемент во второй строке
(-150) показывает,
на сколько уменьшится значение функции,
если в решении переменную x2
увеличить на единицу. С другой стороны,
при допустимом увеличении коэффициента
функции при неизвестной x2
на 150 единиц значение этой переменной
не изменится, т.е. неизвестная x2
будет равна нулю, а если выйти за пределы
допустимого увеличения (коэффициент
при x2
увеличить более чем на 150), то неизвестная
x2
в решении будет больше нуля.
В
отчете
по пределам
(рис. 11) показаны нижние и верхние пределы
возможного изменения переменных (в
пределах области допустимых решений)
и соответствующие значения целевой
функции (графа Целевой
результат)
при этих изменениях. В частности, если
x1
= 0, а x2
и x3
остаются без изменений, то F
= 2400
+ 2100
+ 180191,25
= 34425; при x3
= 0 и неизменных x1
и x2
получим F
= 240397,5
+ 2100
+ 1800
= 95400.
Рис. 11
Соседние файлы в папке 3922
- #
- #
- #
- #
- #
- #



















 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):















 Сообщение было отмечено spbdab как решение
Сообщение было отмечено spbdab как решение