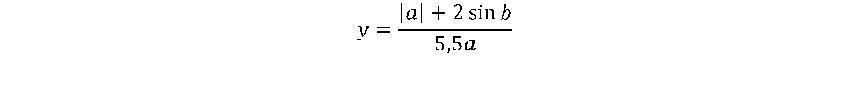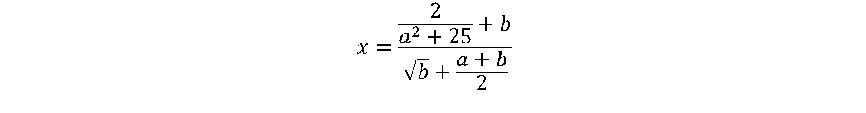Решение задач с помощью математических функции в excel

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.



Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Решение различных
математических задач, используя надстройки
«Подбор параметра» и «Поиск решения» в MS Excel.

Цель работы. Изучить:

·      надстройку «Подбор параметра» для нахождения корней нелинейных
уравнений;

·      надстройку «Поиск решения» для нахождения корней систем уравнений.

Пользуясь приемами выполнения простейших
расчетов и построения графиков функций в Excel, можно
находить решение различных математических задач. Рассмотрим это на примере
наиболее часто встречающихся задач нахождения корней нелинейных уравнений и
решения систем линейных уравнений. Указанные математические задачи легко
решаются с помощью надстроек Excel Поиск решения и Подбор параметра.

Подбор параметра

Надстройка Microsoft Excel Подбор параметра служит для нахождения
оптимального желаемого решения за счет изменения одного из параметров. С
формальной точки зрения такие задачи описываются уравнением с одной переменной,
которое в общем случае можно представить в следующем каноническом виде:

F(x) = 0,

где функция F(x) определена и непрерывна на интервале [a, b]. Таким образом, можно сказать, что
инструмент Подбор параметра служит для нахождения корня уравнения x. В этой надстройке реализован алгоритм метода
половинного деления.

Пример 1. Решим
уравнение x² – 3 =
0, используя надстройку Подбор параметра.

В ячейку А1 вводится начальное приближение
для поиска одного из корней уравнения. Лучше найти его графически, хотя можно подставить и произвольное значение (например,
ноль). В ячейку В2 записывается в виде формулы левая часть решаемого уравнения.
Диалоговое окно данного инструмента вызывается через меню Данные
/ Что-если / Подбор параметра и имеет
следующий вид (рис. 2.7.1, 2.7.2):

Рис. 2.7.1. Надстройка Подбор параметра

В поле Установить в ячейке вводится
ссылка на ячейку, содержащую левую часть уравнения. В поле Значение
непосредственно (т.е. без ссылок на ячейки) вводится правая часть уравнения.
Причем правая часть уравнения должна обязательно представлять собой конкретное
числовое значение. Если правая часть уравнения содержит переменную или
какое-либо выражение, то такое уравнение должно быть предварительно
преобразовано к равносильному виду (в общем случае, к каноническому виду F(x) = 0). Нажав кнопку ОК, получаем в
ячейке А1 значение искомого корня: 1,731856.

Рис. 2.7.2. Надстройка Подбор параметра

Поиск решения

Нелинейные
уравнения также можно решать, используя надстройку Поиск решения. Для
того чтобы ее подключить, следует в меню Office (рис. 2.7.3) выбрать пункт Параметры Excel (рис. 2.7.4) и в раскрывшемся списке войти в меню Надстройки,
далее активировать Поиск решения, установив флажок против пункта Поиск
решения (рис. 2.7.5).

Рис. 2.7.3 Кнопка Office

Рис. 2.7.4. Меню Office

Рис. 2.7.5. Надстройки

После нажатия кнопки ОК
соответствующий значок появится во вкладке Данные (рис. 2.7.6).

Рис. 2.7.6. значок Поиск решения

Пример 2. Решим
уравнение x² – 3 =
0, используя надстройку Поиск решения.

В ячейку А1
заносится начальное приближение корня, в ячейку В1 – левая
часть уравнения в виде формулы. Для предыдущего примера она имеет вид =А1*А1-3.

Далее из вкладки меню Данные
запускается надстройка Поиск решения.

В открывшемся диалоговом окне Поиск
решения устанавливается целевая ячейка $B$1, равная
нулевому значению. В текстовом поле Изменяя ячейки устанавливается адрес
$А$1 и нажимается кнопка Выполнить (рис. 2.7.7).

Рис. 2.7.7. Надстройка Поиск
решения

В ячейке А1 получается значение корня
1,732051 (рис. 2.7.8).

Рис. 2.7.8. Результаты работы
надстройки Поиск решения

Как видим, оно совпало с точностью до 0,001
с найденным ранее значением.

Обращает на
себя внимание неточность решения. Мы получаем очень близко приближающиеся к
точным, но все же неточные корни уравнения. Это происходит потому, что решение
уравнений на вычислительной технике происходит не аналитическими методами, как
это делает человек, а специально разработанными методами, получившими название
численных. В отличие от аналитических (точных) методов численные методы
обладают определенной погрешностью. В Excel с целью повышения точности решения
пользователь может уменьшить погрешность вычислений, но при этом может
потребоваться увеличение количества итераций. При этом надо помнить, что тем
самым увеличивается время на поиск решения. Установленные по умолчанию значения подходят для большинства практических задач, относительная
погрешность вычислений составляет 0,001 (рис. 2.7.9).

Рис. 2.7.9. Изменение
погрешности

Следует отметить, что найден только один из
двух корней данного уравнения. Для нахождения второго корня, следует в ячейку
А1 ввести новое приближение, близкое ко второму корню, и повторить поиск
решения.

Пример 3. Решим
систему уравнений, используя надстройку Поиск решения.

Для того, чтобы использовать рассматриваемую
надстройку Поиск решения для нахождения решения системы линейных
алгебраических уравнений, следует ввести в
столбец А начальное приближение для значений всех неизвестных. Пусть это будут
нули. В столбец В ввести формулы, описывающие левые части уравнений. В столбец
С вводят значения правых частей уравнений. Курсор ставят на ячейку В1 и
запускают надстройку Поиск решения. Значение целевой ячейки $B$1устанавливают равным значению ячейки С1. Изменяют значения ячеек
столбца А. К ограничениям добавляют все уравнения, кроме первого. Для системы
уравнений:

настроенный на
показ формул лист Excel с диалоговым окном Поиск решения
будут выглядеть так, как это показано на рисунках 2.7.10, 2.7.11.

Рис. 2.7.10. добавление ограничения

Рис. 2.7.11. Поиск решения
системы уравнений

Нажав кнопку Выполнить, получается в
столбце А значение неизвестных (рис. 2.7.12):

Как видно, надстройка Поиск решения
очень удобна для решения рассмотренных задач. Однако следует помнить, что
алгоритмы, реализованные в ней, предназначались не для них, а для решения задач
оптимизации. Поэтому возможны сбои в работе надстройки, и к полученным
результатам необходимо подходить критически.

.

Рис. 2.7.12. Результаты
работы с надстройкой Поиск решения

Задания для выполнения

Варианты заданий для работы приведены в
таблице 2.7.1, 2.7.2.

Задание1.

1.                 
Используя надстройку «Подбор параметра», найти все
корни уравнения (по вариантам) на отрезке [-2; +2] (табл. 2.7.1).

Таблица 2.7.1

Варианты заданий

Задание 2.

1.                 
Используя надстройку «Поиск решения», решить
систему линейных уравнений AX = B (по вариантам) (табл. 2.7.2)
и проверить правильность решения в Excel, подставив найденные значения неизвестных в систему уравнений. A – матрица коэффициентов при x1, x2, x3, x4. В- матрица свободных членов уравнений.

 Таблица 2.7.2

Варианты заданий

Чаще всего среди доступных групп функций пользователи Экселя обращаются к математическим. С помощью них можно производить различные арифметические и алгебраические действия. Их часто используют при планировании и научных вычислениях. Узнаем, что представляет собой данная группа операторов в целом, и более подробно остановимся на самых популярных из них.

Применение математических функций

С помощью математических функций можно проводить различные расчеты. Они будут полезны студентам и школьникам, инженерам, ученым, бухгалтерам, планировщикам. В эту группу входят около 80 операторов. Мы же подробно остановимся на десяти самых популярных из них.

Открыть список математических формул можно несколькими путями. Проще всего запустить Мастер функций, нажав на кнопку «Вставить функцию», которая размещена слева от строки формул. При этом нужно предварительно выделить ячейку, куда будет выводиться результат обработки данных. Этот метод хорош тем, что его можно реализовать, находясь в любой вкладке.

Также можно запустить Мастер функций, перейдя во вкладку «Формулы». Там нужно нажать на кнопку «Вставить функцию», расположенную на самом левом краю ленты в блоке инструментов «Библиотека функций».

Существует и третий способ активации Мастера функций. Он осуществляется с помощью нажатия комбинации клавиш на клавиатуре Shift+F3.

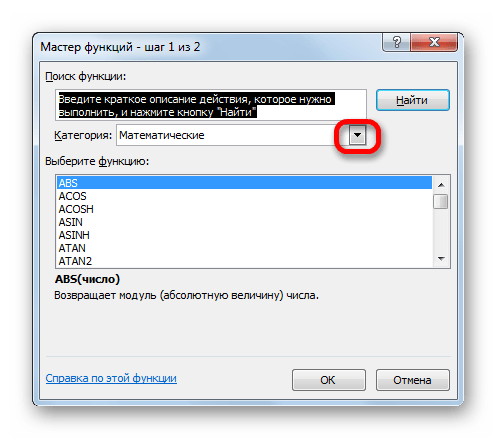
После того, как пользователь произвел любое из вышеуказанных действий, открывается Мастер функций. Кликаем по окну в поле «Категория».

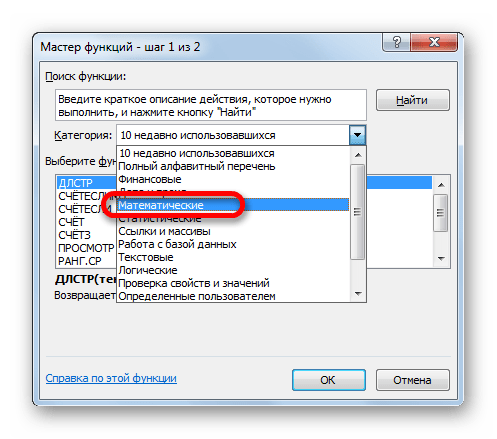
Открывается выпадающий список. Выбираем в нем позицию «Математические».

После этого в окне появляется список всех математических функций в Excel. Чтобы перейти к введению аргументов, выделяем конкретную из них и жмем на кнопку «OK».

Существует также способ выбора конкретного математического оператора без открытия главного окна Мастера функций. Для этого переходим в уже знакомую для нас вкладку «Формулы» и жмем на кнопку «Математические», расположенную на ленте в группе инструментов «Библиотека функций». Открывается список, из которого нужно выбрать требуемую формулу для решения конкретной задачи, после чего откроется окно её аргументов.

Правда, нужно заметить, что в этом списке представлены не все формулы математической группы, хотя и большинство из них. Если вы не найдете нужного оператора, то следует кликнуть по пункту «Вставить функцию…» в самом низу списка, после чего откроется уже знакомый нам Мастер функций.

Урок: Мастер функций в Excel

СУММ

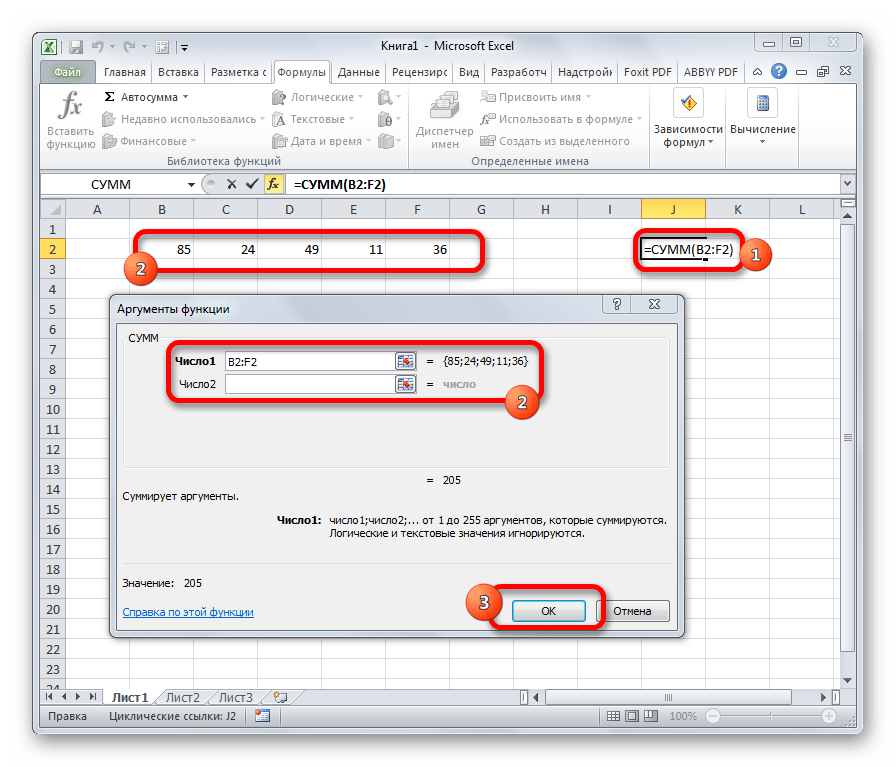
Наиболее часто используется функция СУММ. Этот оператор предназначен для сложения данных в нескольких ячейках. Хотя его можно использовать и для обычного суммирования чисел. Синтаксис, который можно применять при ручном вводе, выглядит следующим образом:

=СУММ(число1;число2;…)

В окне аргументов в поля следует вводить ссылки на ячейки с данными или на диапазоны. Оператор складывает содержимое и выводит общую сумму в отдельную ячейку.

Урок: Как посчитать сумму в Экселе

СУММЕСЛИ

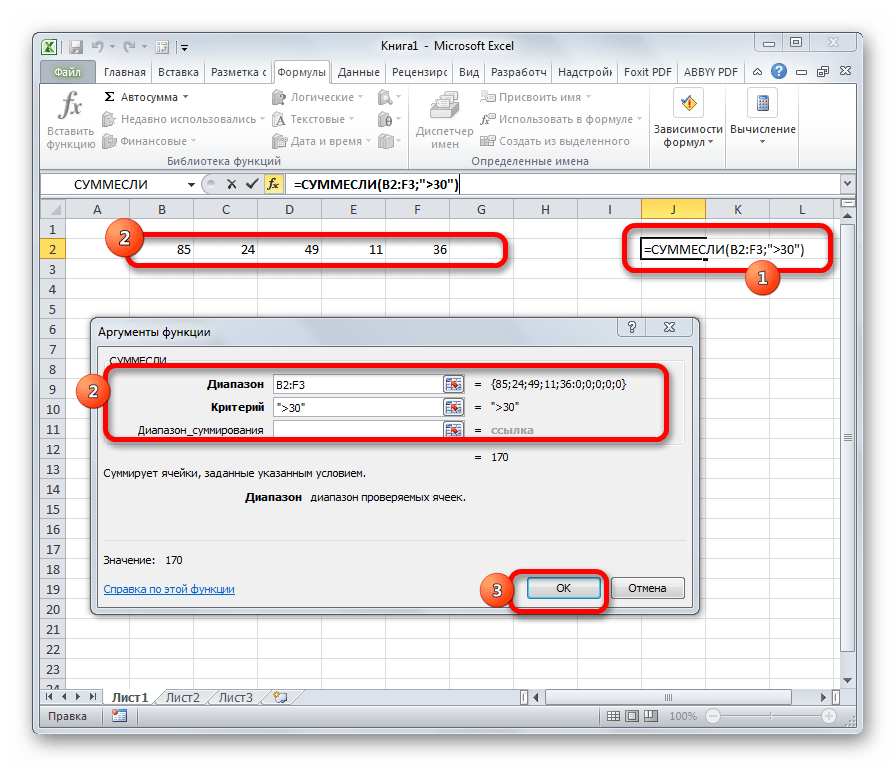
Оператор СУММЕСЛИ также подсчитывает общую сумму чисел в ячейках. Но, в отличие от предыдущей функции, в данном операторе можно задать условие, которое будет определять, какие именно значения участвуют в расчете, а какие нет. При указании условия можно использовать знаки «>» («больше»), «<» («меньше»), «< >» («не равно»). То есть, число, которое не соответствует заданному условию, во втором аргументе при подсчете суммы в расчет не берется. Кроме того, существует дополнительный аргумент «Диапазон суммирования», но он не является обязательным. Данная операция имеет следующий синтаксис:

=СУММЕСЛИ(Диапазон;Критерий;Диапазон_суммирования)

ОКРУГЛ

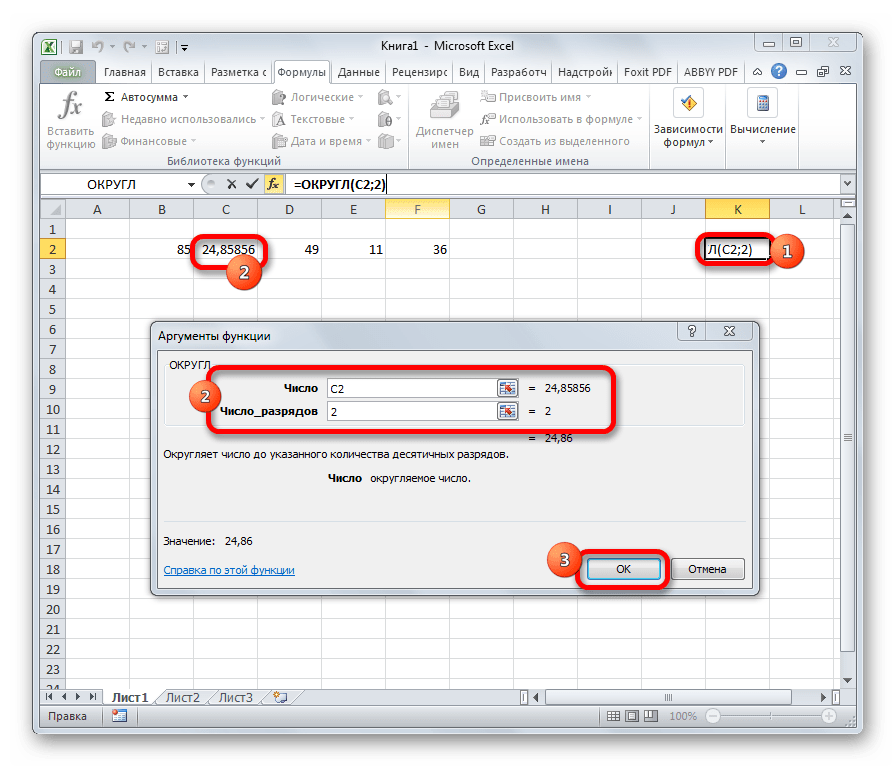
Как можно понять из названия функции ОКРУГЛ, служит она для округления чисел. Первым аргументом данного оператора является число или ссылка на ячейку, в которой содержится числовой элемент. В отличие от большинства других функций, у этой диапазон значением выступать не может. Вторым аргументом является количество десятичных знаков, до которых нужно произвести округление. Округления проводится по общематематическим правилам, то есть, к ближайшему по модулю числу. Синтаксис у этой формулы такой:

=ОКРУГЛ(число;число_разрядов)

Кроме того, в Экселе существуют такие функции, как ОКРУГЛВВЕРХ и ОКРУГЛВНИЗ, которые соответственно округляют числа до ближайшего большего и меньшего по модулю.

Урок: Округление чисел в Excel

ПРОИЗВЕД

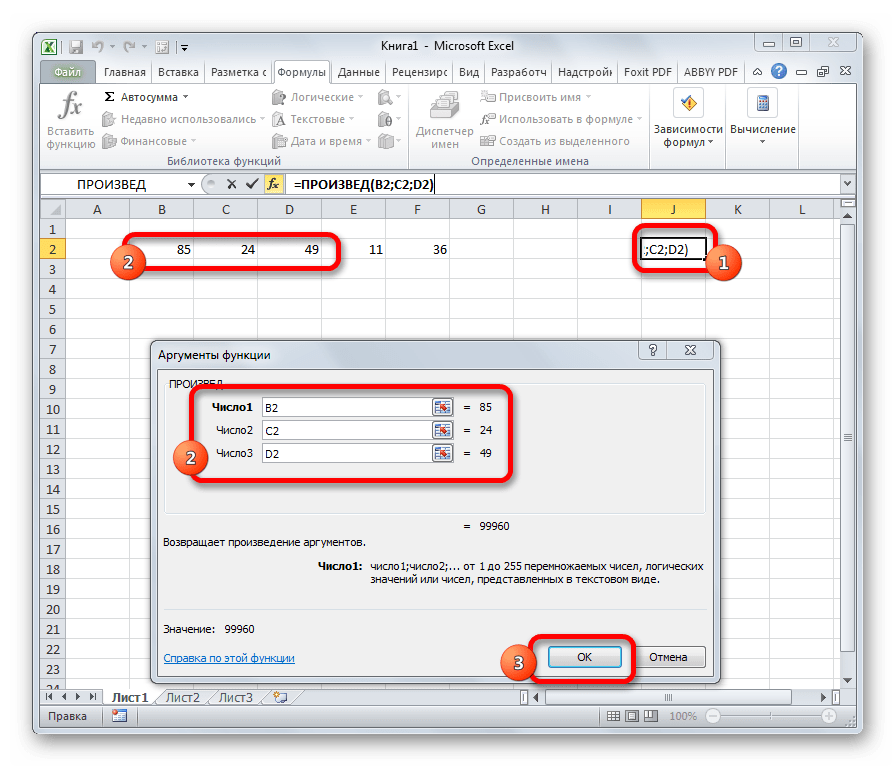
Задачей оператора ПРИЗВЕД является умножение отдельных чисел или тех, которые расположены в ячейках листа. Аргументами этой функции являются ссылки на ячейки, в которых содержатся данные для перемножения. Всего может быть использовано до 255 таких ссылок. Результат умножения выводится в отдельную ячейку. Синтаксис данного оператора выглядит так:

=ПРОИЗВЕД(число;число;…)

Урок: Как правильно умножать в Excel

ABS

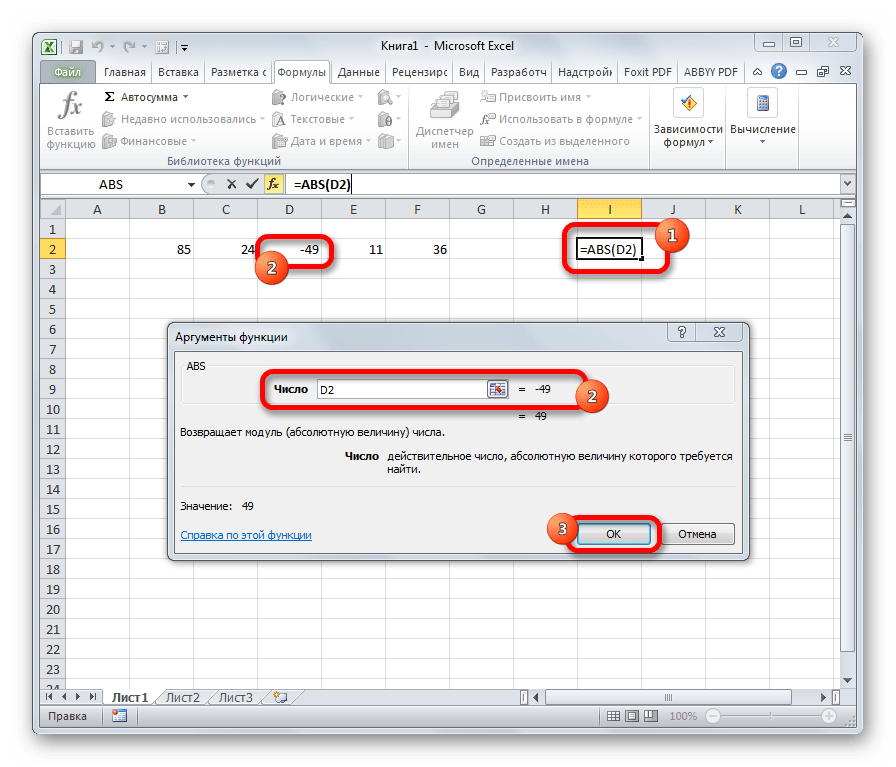
С помощью математической формулы ABS производится расчет числа по модулю. У этого оператора один аргумент – «Число», то есть, ссылка на ячейку, содержащую числовые данные. Диапазон в роли аргумента выступать не может. Синтаксис имеет следующий вид:

=ABS(число)

Урок: Функция модуля в Excel

СТЕПЕНЬ

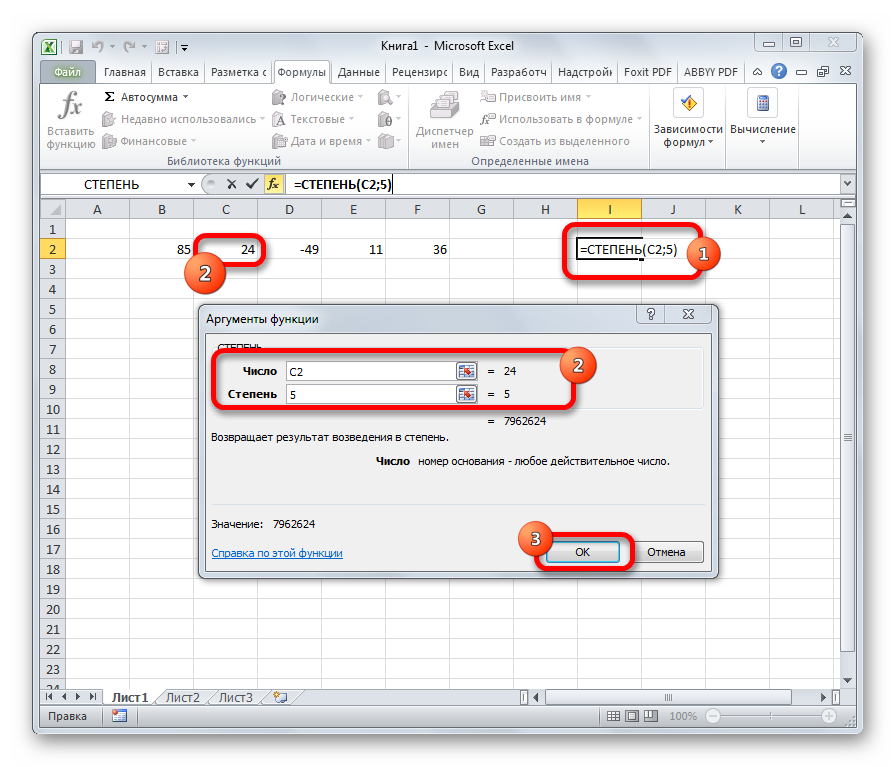
Из названия понятно, что задачей оператора СТЕПЕНЬ является возведение числа в заданную степень. У данной функции два аргумента: «Число» и «Степень». Первый из них может быть указан в виде ссылки на ячейку, содержащую числовую величину. Второй аргумент указывается степень возведения. Из всего вышесказанного следует, что синтаксис этого оператора имеет следующий вид:

=СТЕПЕНЬ(число;степень)

Урок: Как возводить в степень в Экселе

КОРЕНЬ

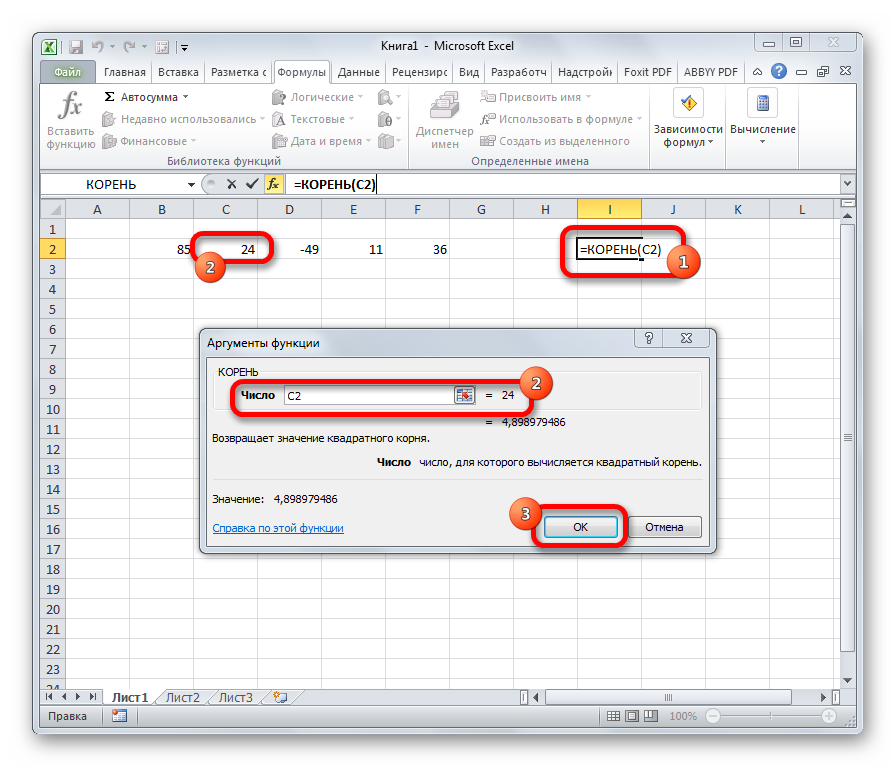
Задачей функции КОРЕНЬ является извлечение квадратного корня. Данный оператор имеет только один аргумент – «Число». В его роли может выступать ссылка на ячейку, содержащую данные. Синтаксис принимает такую форму:

=КОРЕНЬ(число)

Урок: Как посчитать корень в Экселе

СЛУЧМЕЖДУ

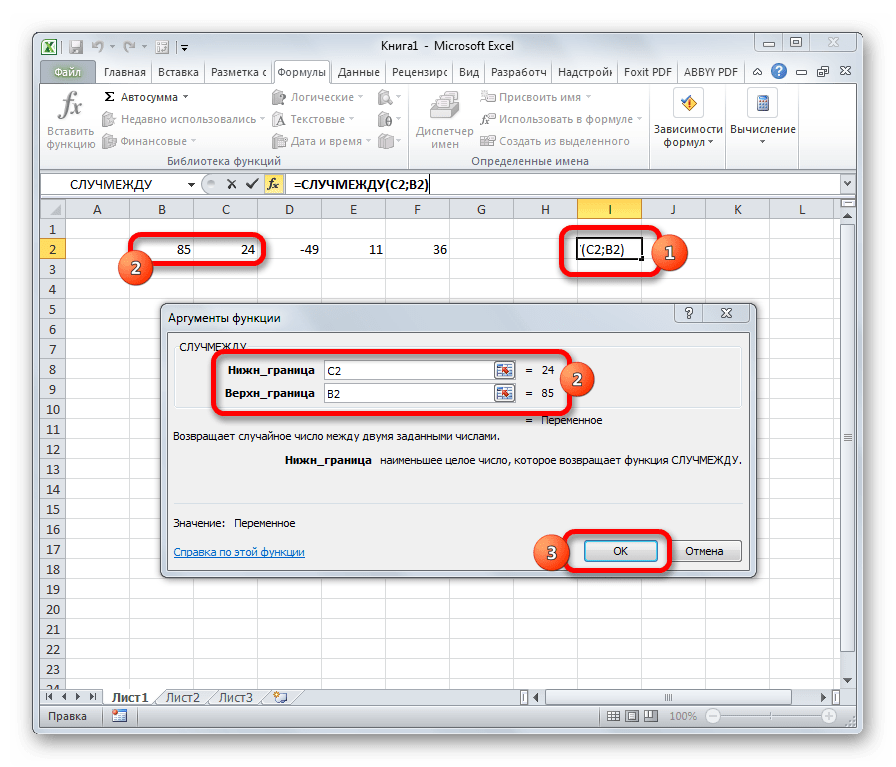
Довольно специфическая задача у формулы СЛУЧМЕЖДУ. Она состоит в том, чтобы выводить в указанную ячейку любое случайное число, находящееся между двумя заданными числами. Из описания функционала данного оператора понятно, что его аргументами является верхняя и нижняя границы интервала. Синтаксис у него такой:

=СЛУЧМЕЖДУ(Нижн_граница;Верхн_граница)

ЧАСТНОЕ

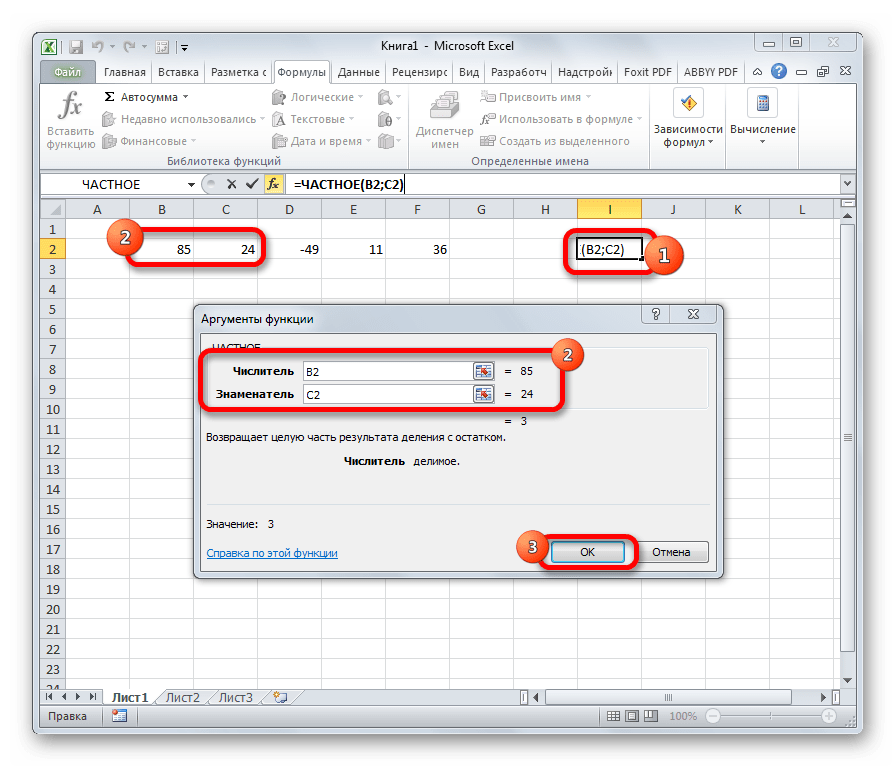
Оператор ЧАСТНОЕ применяется для деления чисел. Но в результатах деления он выводит только четное число, округленное к меньшему по модулю. Аргументами этой формулы являются ссылки на ячейки, содержащие делимое и делитель. Синтаксис следующий:

=ЧАСТНОЕ(Числитель;Знаменатель)

Урок: Формула деления в Экселе

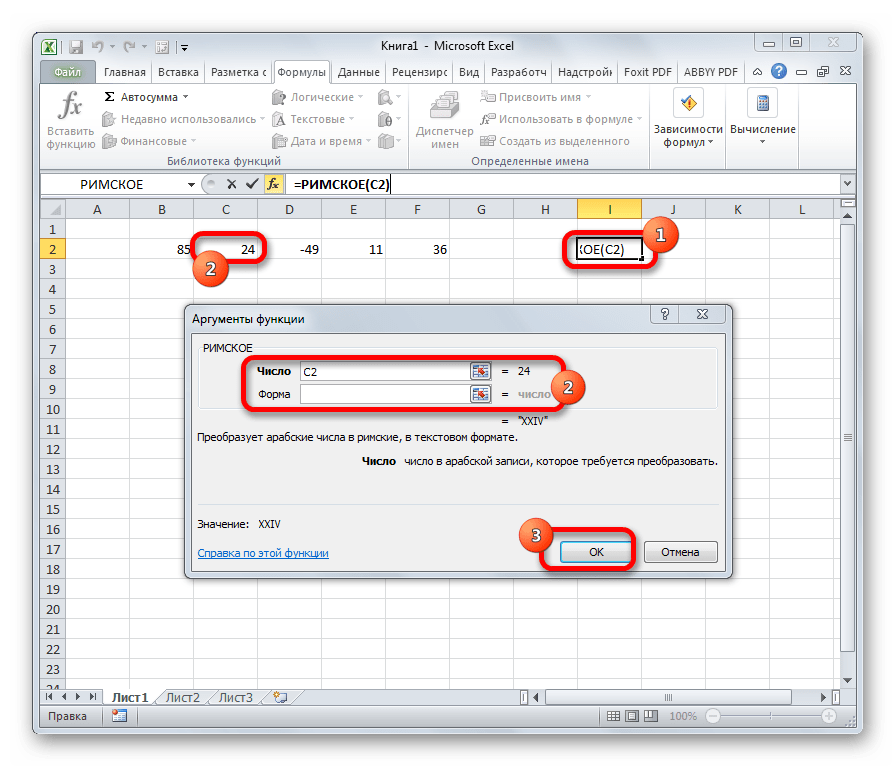
РИМСКОЕ

Данная функция позволяет преобразовать арабские числа, которыми по умолчанию оперирует Excel, в римские. У этого оператора два аргумента: ссылка на ячейку с преобразуемым числом и форма. Второй аргумент не является обязательным. Синтаксис имеет следующий вид:

=РИМСКОЕ(Число;Форма)

Выше были описаны только наиболее популярные математические функции Эксель. Они помогают в значительной мере упростить различные вычисления в данной программе. При помощи этих формул можно выполнять как простейшие арифметические действия, так и более сложные вычисления. Особенно они помогают в тех случаях, когда нужно производить массовые расчеты.

Задачи на использование математических функций

Операцию возведения в степень не использовать

1. Известна сторона квадрата. Подготовить лист для расчета его площади.

1. Известна площадь квадрата. Оформить лист для расчета его стороны.

2. Известна площадь круга. Оформить лист для определения его диаметра.

3. Даны катеты прямоугольного треугольника. Подготовить лист для расчета его гипотенузы. Решение оформить в виде:

1. Даны стороны прямоугольника. Оформить лист для расчета его диагонали.

2. Известна длина стороны равностороннего треугольника. Оформить лист для определения его высоты.

3. Оформить лист для расчета среднего геометрического двух заданных целых чисел.

4. Даны стороны прямоугольного параллелепипеда. Оформить лист для определения его диагонали.

5. Считая, что Земля – идеальная сфера с радиусом R≈6350 км, определить расстояние от точки, с заданной высотой над Землей до линии горизонта.

6. Оформить лист для расчета периметра прямоугольного треугольника по известным катетам.

7. Известна площадь квадрата. Оформить лист для расчета его диагонали.

8. Даны стороны треугольника. Оформить лист для определения его площади.

9. Известны координаты двух точек на плоскости. Оформить лист для вычисления расстояния между ними.

10. Даны основания и высота равнобедренной трапеции. Подготовить лист для вычисления ее периметра.

11. Треугольник задан координатами своих вершин. Подготовить лист для вычисления его периметра и площади.

12. Подготовить лист для расчета синуса, косинуса, тангенса и котангенса угла, значение которого будет вводиться в одну из ячеек. Рассмотреть 2 варианта:

    1. значение угла указывается в радианах;

    2. значение угла указывается в градусах.

13. Подготовить лист для определения абсолютной величины числа, значение которого будет вводиться в одну из ячеек.

14. Известна диагональ квадрата. Оформить лист для расчета его площади и периметра.

15. Подготовить лист для определения площади ромба по известной длине его стороны и значению внутреннего угла в градусах.

16. Даны стороны параллелограмма и значение одного из внутренних углов (в градусах). Подготовить лист для определения площади параллелограмма.

17. Даны стороны треугольника и угол между ними (в градусах). Подготовить лист для определения площади треугольника.

18. Дано основание равнобедренного треугольника, а также угол при основании. Подготовить лист для определения периметра треугольника. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.

19. Известны размеры большего основания и боковой стороны равнобедренной трапеции, а также угол при большем основании. Подготовить лист для определения периметра трапеции. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.

20. Дано основание равнобедренного треугольника, а также угол при основании. Подготовить лист для вычисления площади треугольника.

21. Подготовить лист для определения угла по известному значению его:

    1. Синуса;

    2. Косинуса;

    3. Тангенса;

    4. Котангенса.

Во всех случаях определить величину угла в радианах и градусах.

1. Известны длины сторон равнобедренного треугольника. Подготовить лист для вычисления его внутренних углов (в градусах).

2. Известны размеры оснований и боковой стороны равнобедренной трапеции. Подготовить лист для вычисления угла (в градусах) при большем основании.

3. Даны стороны a, b, c треугольника. Подготовить лист для вычисления его углов (в градусах) по теореме косинусов:

A=arcos(b² + c² – a²)/2bc

1. Даны катеты прямоугольного треугольника. Подготовить лист для вычисления острых углов треугольника (в градусах).

2. Даны основание и высота равнобедренного треугольника. Подготовить лист для вычисления угла (в градусах) при основании.

3. Известны размеры диагоналей ромба. Подготовить лист для вычисления его внутренних углов (в градусах).

4. Даны координаты на плоскости двух точек. Подготовить лист для вычисления угла наклона к оси абсцисс прямой, соединяющей эти точки.

5. Подготовить лист для нахождения десятичного логарифма числа, которое будет указываться в одной из ячеек.

6. Подготовить лист для нахождения натурального логарифма числа, которое будет указываться водной из ячеек.

7. Подготовить лист для вычисления значений e^π и π^e.

8. Дана гипотенуза прямоугольного треугольника, а также один из его острых углов (в градусах). Подготовить лист для вычисления катетов этого треугольника.

9. Известна длина диагонали прямоугольника, а также угол ее наклона к большей стороне прямоугольника. Оформить лист для расчета площади и периметра прямоугольника.

10. Известны размеры большего основания и боковой поверхности равнобедренной трапеции, а также угол при большем основании. Подготовить лист для вычисления периметра и площади трапеции. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.

11. Оформить лист для расчета значения функций

при данных значениях a и b

1. Считая, что Земля – идеальная сфера с радиусом R ≈ 6350 км, подготовить лист для определения расстояния до линии горизонта от точки с высотой над Землей, равной 1, 2, …, 10 км.

2. Получить на листе 10 первых чисел Евклида. Числа Евклида вычисляются по формуле:

E_k = 2^k-1(2k-1), k = 1, 2, 3, …

1. Получить на листе 8 первых чисел ферма. Числа Ферма вычисляются следующим образом:

F_k = 2^A+1, A = 2^k+1, k = 1, 2, 3, …

1. Подготовить на листе таблицу значений функции y = sin(x), где х меняется от 0 до 6,5 радиан с шагом 0,5.

2. Получить на листе таблицу значений sin2, sin3, …, sin20 (значения углов указаны в радианах.

3. Получить на листе таблицу значений tg5, tg6, …, tg15 (значения углов указаны в радианах).

4. Получить на листе таблицу значений тригонометрических функций y = sin(x/2),

y = sin(2x), y = cosx для x, равного 0⁰, 20⁰, 40⁰, …, 720⁰.

1. Пусть функция y(x) задана таблицей:

Значения аргумента х расположены в порядке возрастания, но не обязательно равномерно. Предположим, что точки (х_i, уi) последовательно соединены отрезками прямых линий. Угловым коэффициентом каждого отрезка называется дробь:

(y_i-1 — y_i)/ (x_i-1 — x_i)

Оформить лист, на котором для каждого отрезка определить:

• Его угловой коэффициент;

• Угол наклона к горизонтали (в градусах).

1. Около стены наклонно стоит палка длиной 4,5 м. Один ее конец находится на расстоянии 3 м от стены. Нижний коней палки начинает скользить в плоскости, перпендикулярной стене. Оформить на листе таблицу для определения значения угла между палкой и полом (в градусах) с момента начала скольжения до падения палки через каждые 0,2 м.

2. Плотность воздуха убывает с высотой по закону p=p₀e^—bz, где p – плотность на высоте b метров, p₀ =1,29 кг/м³, z=1,25*10^-4. Получить на листе таблицу зависимости плотности от высоты для значений от 0 до 1000 м через каждые 100 м.

3. Получить на листе значения sin1, sin1+sin2, sin1+ sin2+sin3, …, sin1+sin2+…+ sin10. Значения получить в ячейках B2:B11, введя формулу только в одну ячейку и распространив (скопировав) ее на остальные ячейки диапазона.

   	A	B	C
   1
   2	1	0,841471
   3	2	1,750768
   4	3	1,891888
   5	4	1,135086
   6	5	0,176162
   7	6	-0,10325
   8	7	0,553733
   9	8	1,543091
   10	9	1,955209
   11	10	1,411188
   12

4. Получить на листе значения 1/ sin1, 1/( sin1+sin2), …, 1/(sin1+sin2+…+ sin10).

5. Значения получить С2:С11, введя формулу только в ячейки В2 и С2 и распространив (скопировав) их на остальные ячейки диапазона В2:С11.

1. Получить на листе значения cos1/sin1, (cos1+ cos2, )/ (sin1+sin2), …,( cos1+…+ cos15)/( sin1+…+ sin15).

Значения получить в ячейках F2:F11, введя формулы только в ячейки второй строки и распространив (скопировав) их на остальные ячейки диапазона В2: F11.

Литература:

Д.М. Златопольский. Задачник по Excel, 2002, №24. Информатика