Содержание
- Примеры по финансовой математике в Excel
- Решение финансовой математики в Excel
- 10 популярных финансовых функций в Microsoft Excel
- Выполнение расчетов с помощью финансовых функций
- ДОХОД
- ПРПЛТ
- СТАВКА
- ЭФФЕКТ
- Раздел 2. Финансовые вычисления с использованием Excel Задание 1. Решение задачи с помощью функции бз
- Методические указания для решения задания 1
- Задание 2. Решение задачи с помощью функции пз
- Методические указания для решения задания 2
- Задание 3. Решение задачи с помощью функции норма
Примеры по финансовой математике в Excel
В этом разделе вы найдете примеры задач c решением по финансовой математике, выполненные с помощью пакета Excel. Другие примеры с решениями вручную вы найдете здесь.
Для решения финансовых задач в Эксель используются как встроенные финанансовые функции (например, ПЛТ, СТАВКА, КПЕР, ПС, БС, ПОЛУЧЕНО и т.д), так и формулы, вводимые вручную, чтобы получить ответ согласно некоторой сложной формуле (для которой нет встроенной функции). Иногда используются также функции подбора параметра и поиска решения.
Решение финансовой математики в Excel
Задача 1. Вас просят дать в долг 03.03.2012 г. 20000 р. и обещают вернуть 18.08.2012 г. 4800 р., 13.11. 2012 г. – 5400 р., 07.03.2013 г. – 5700 р. и 31.05.2013 г. – 6200 р. Оценить выгодность предложения, если существует возможность положить деньги в банк под 13% годовых.
Задача 2. Вы заняли на 4 года 10000 руб. под 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определить величину годового платежа.
Задача 3. Предприятие рассматривает целесообразность принятия новой технологической линии. На рынке имеются две модели со следующими параметрами:
П1 П2
Цена. 9500 13000
Генерируемый годовой доход. 2100 2250
Срок эксплуатации. 8 лет 12 лет
Ликвидационная стоимость. 500 800
Требуемая норма прибыли. 11% 11%
Обоснуйте целесообразность приобретения той или иной технологической линии.
Задача 4. Вы открываете счёт и собираетесь вкладывать по 1400 р. в начале каждого года в течении 8 лет при годовой ставке 3,5%. Сколько денег будет на счете через 8 лет?
Задача 5. Контракт между фирмой и банком предусматривает в течение 3 лет фирме ежегодными платежами в размере 24 тыс. руб. в начале каждого года под ставку 14% годовых. Фирма возвращает долг, выплачивая последовательно в конце 3,4,5 годов. Какова чистая современная величина NPV для банка?
Задача 6. Годовая процентная ставка составляет 9% и остается неизменной в течение всего периода, а годовая купонная ставка по облигации с номиналом 1400 руб. со сроком обращения 10 лет установлена в размере 14%. Сколько стоит эта облигация при эмиссии? Сколько будет стоить эта облигация через 5 лет. Какова доходность облигации за 10 лет.
Задача 7. Кредит в размере 500 млн. руб. выдан на 5 лет под 17 % годовых с начислением процентов и выплатой в конце каждого года. Выплаты основного долга должны уменьшаться ежегодно на 8 млн. руб. Составить план погашения кредита.
Задача 8. На вклад начисляются сложные проценты: а) каждые полгода; б) ежеквартально; в) ежемесячно. Вычислить годовую номинальную процентную ставку, при которой происходит реальное наращение капитала, если ежеквартальный темп инфляции составляет 2%. Известно:
h = 2%; m1 = 2; m2 = 4; m3 = 12.
Найти: i1 — ? i2 — ? i3 — ?
Задача 9. Предприниматель получил ссуду в банке в размере 20 млн. руб. сроком на 5 лет на следующих условиях: для первых двух лет процентная ставка равна 25% годовых, на оставшиеся 3 года ставка равна 23% годовых. Найдите доход банка за 5 лет, если сложные ссудные проценты начисляются ежеквартально.
Известно: Р = 20 000 000 руб.; i1 = 0,25 или 25% n1 = 2 года i2 = 0,23 или 23% n2 = 3 года m = 4
Найти: I — ?
Задача 10. Определить годовую процентную ставку банка, если вкладчик внес 3297 д.е. на 6 лет, сумма на счете в конце срока составила 12934 д.е. В первую треть срока начислялись простые проценты, а в оставшийся – сложные, 5 раз в год.
Источник
10 популярных финансовых функций в Microsoft Excel
Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.
Выполнение расчетов с помощью финансовых функций
В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.
Переход к данному набору инструментов легче всего совершить через Мастер функций.
- Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.
В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.
ДОХОД
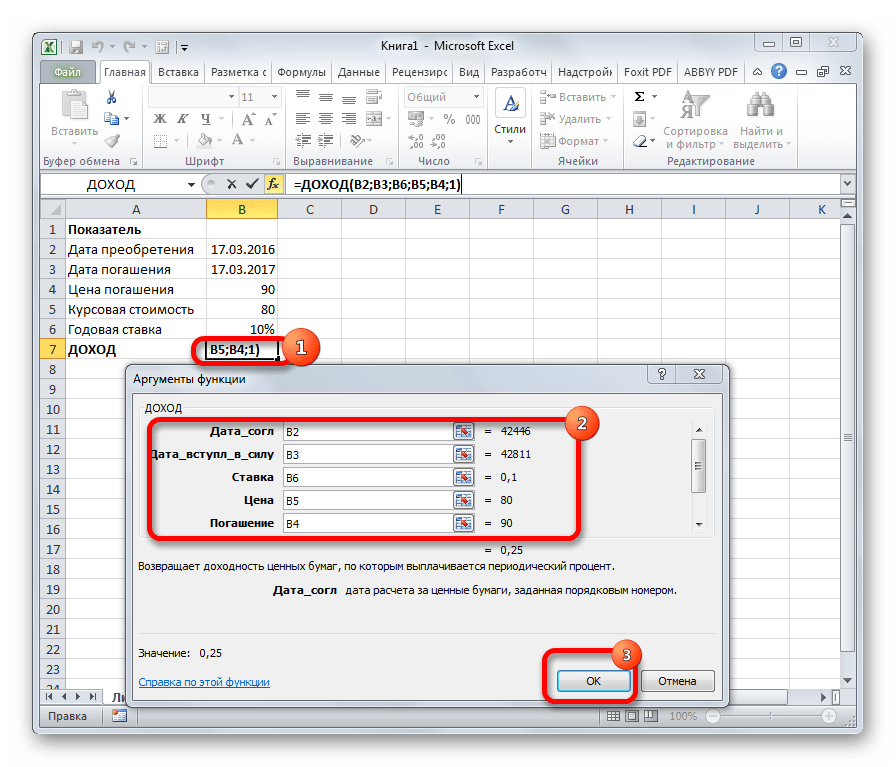
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:
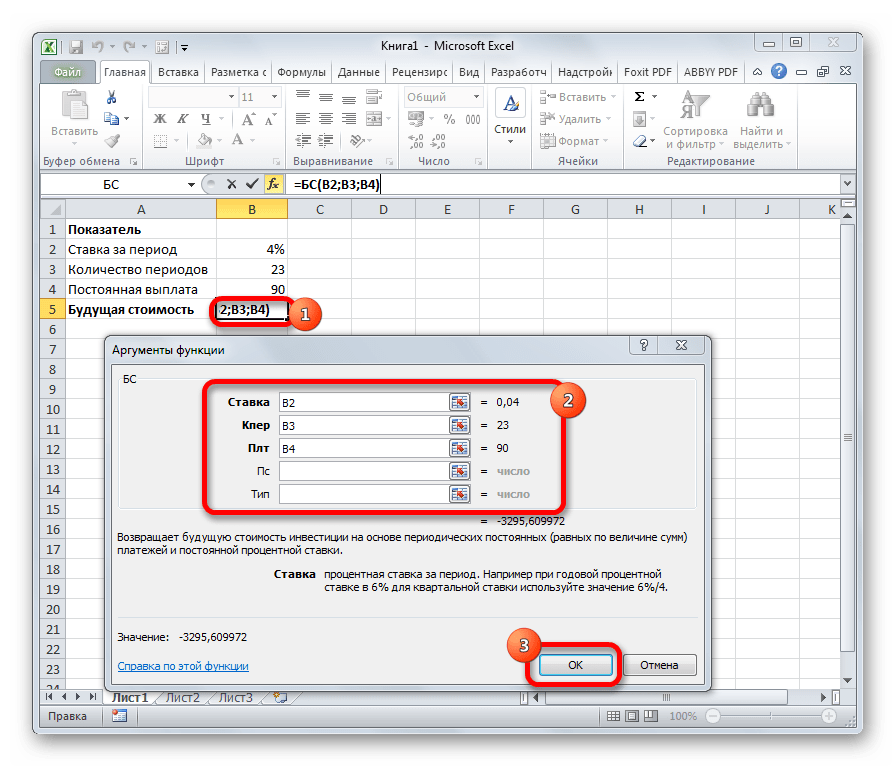
Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:
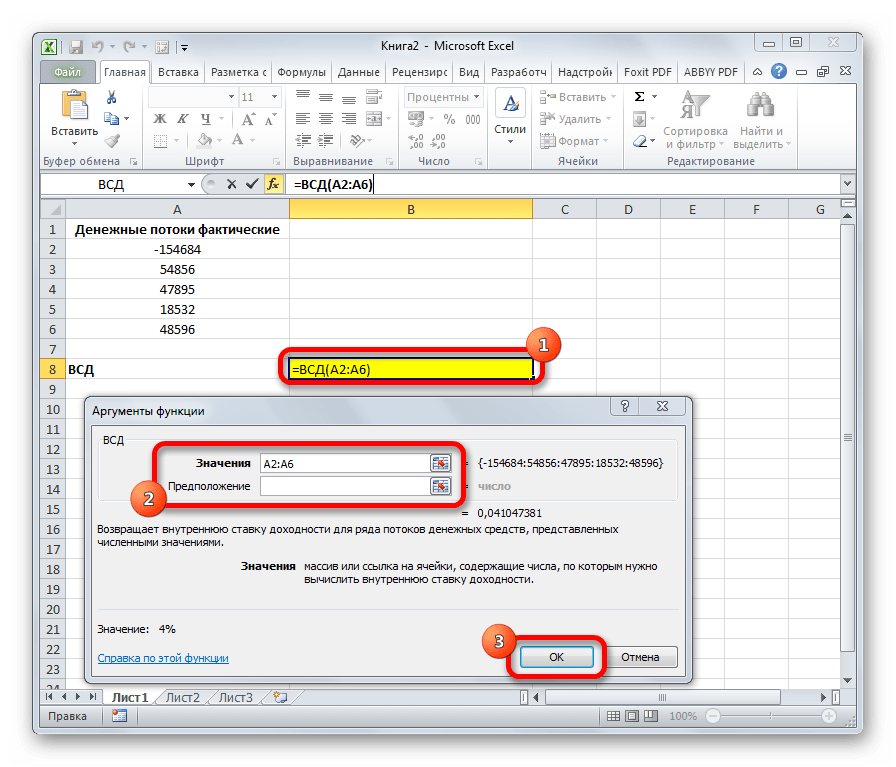
Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:
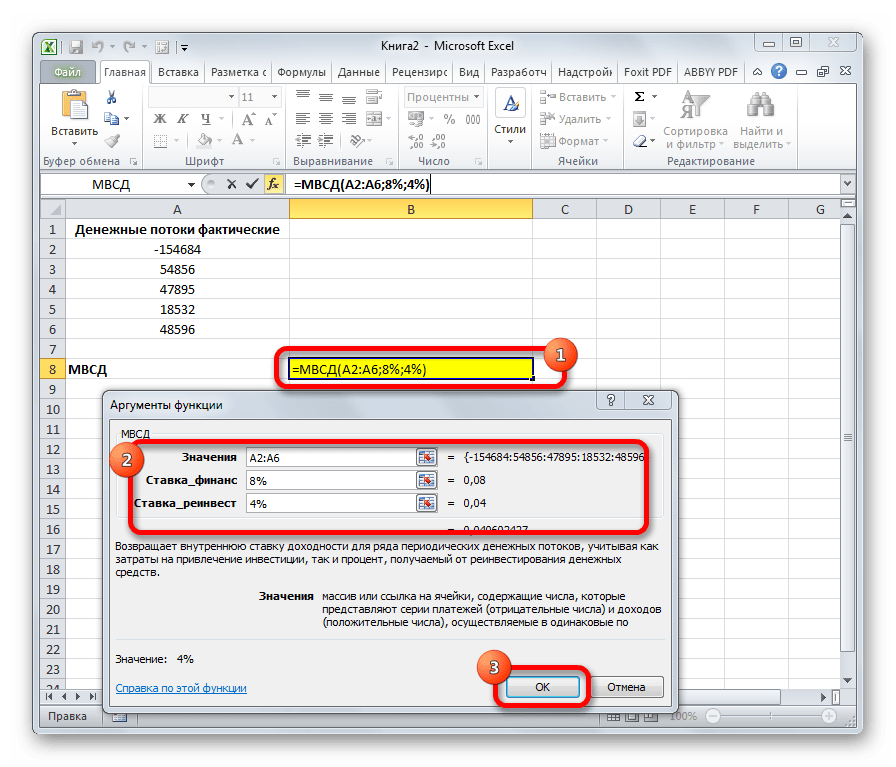
Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:
ПРПЛТ
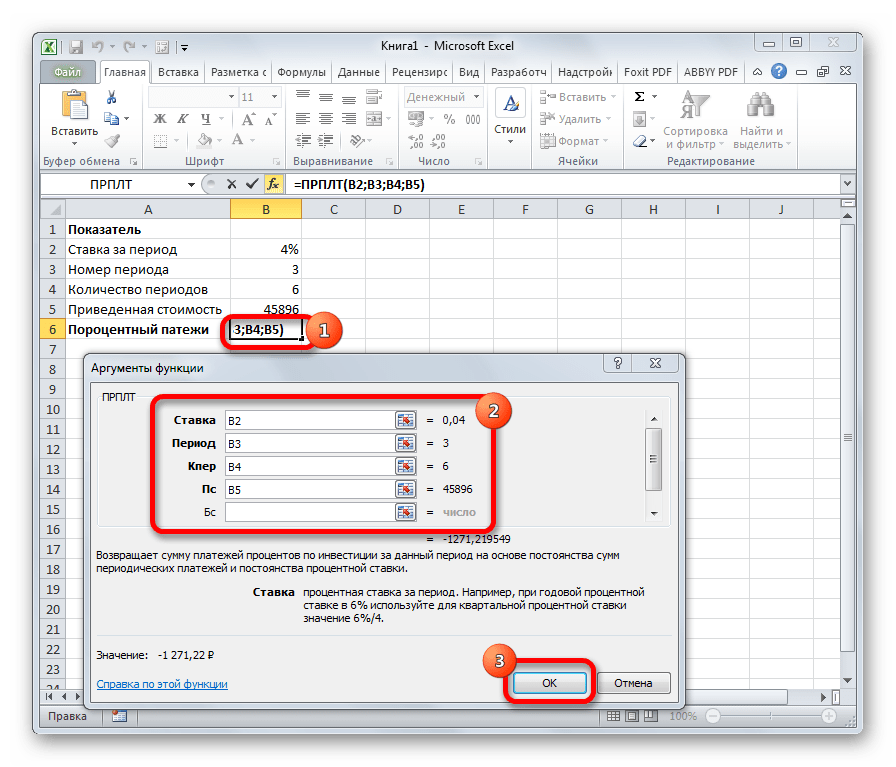
Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:
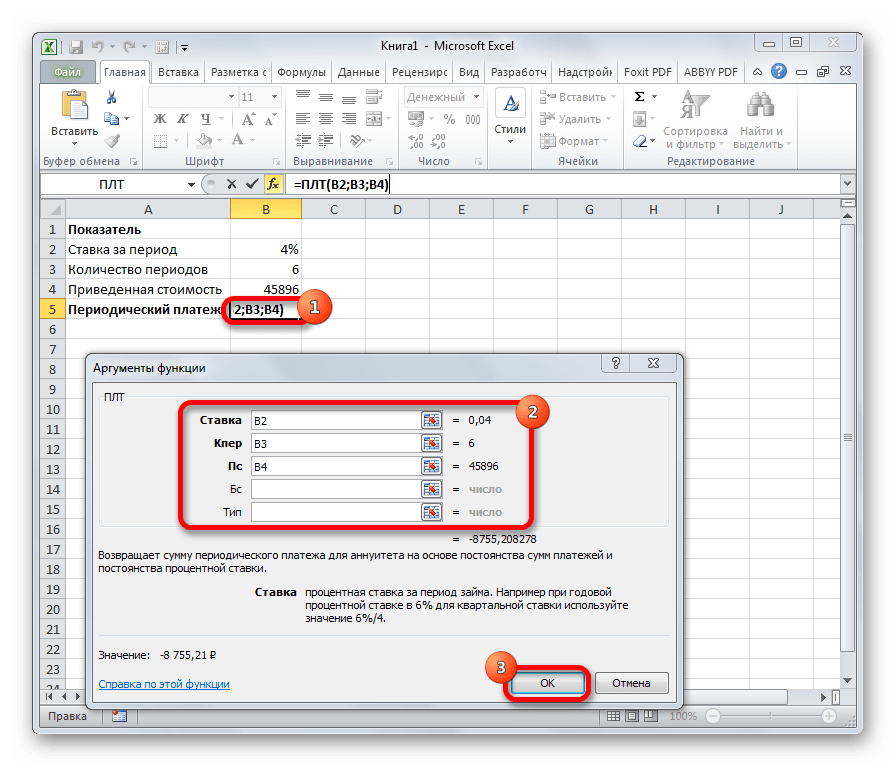
Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:
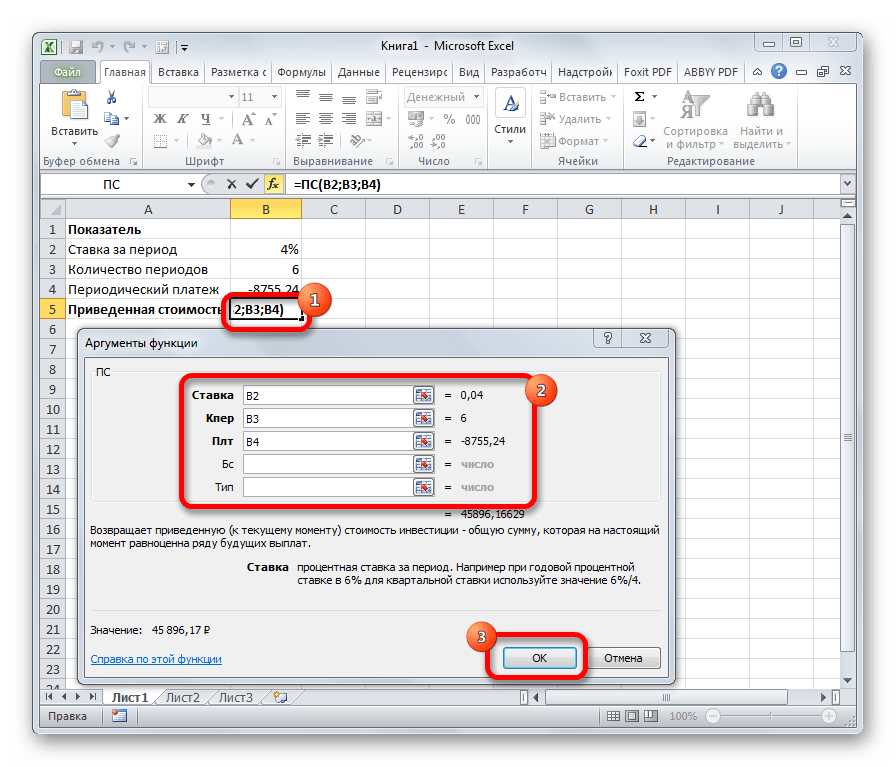
Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:
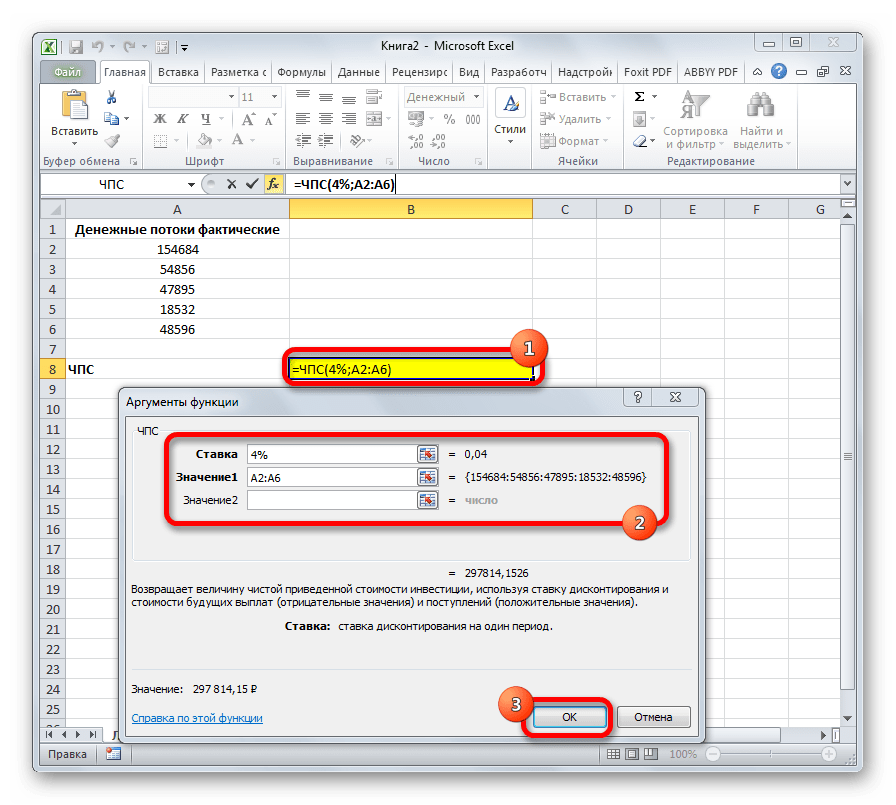
Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:
СТАВКА
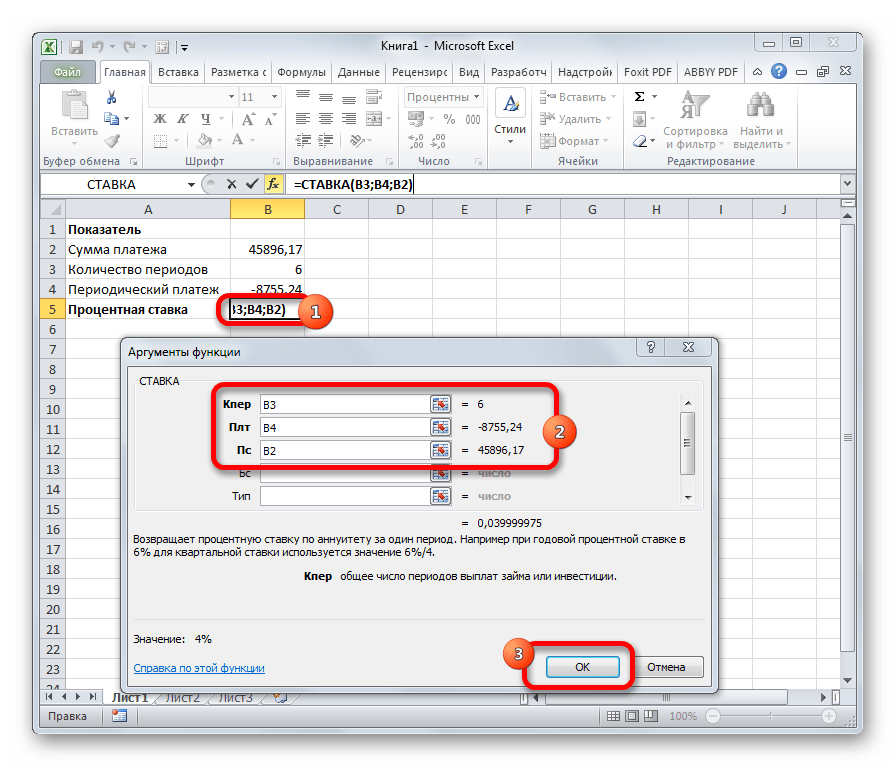
Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:
ЭФФЕКТ
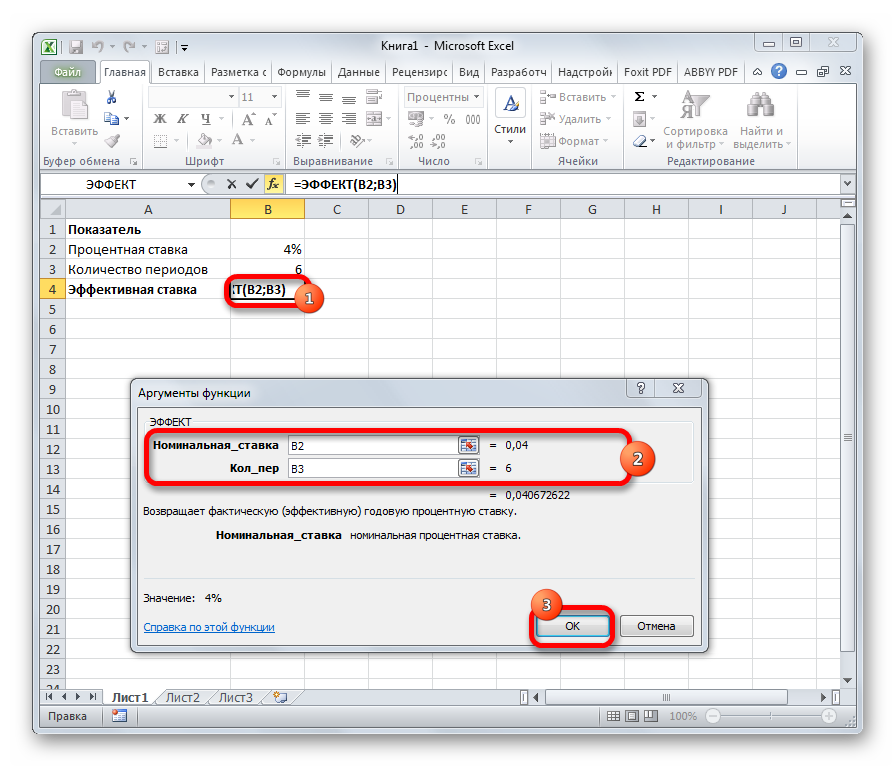
Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:
Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.
Источник
Раздел 2. Финансовые вычисления с использованием Excel Задание 1. Решение задачи с помощью функции бз
1. В табличном процессоре MS Excel сформировать расчетную таблицу для следующего условия:
Сумма в 10 000 рублей помещена в банк на депозит сроком на десять лет. Ставка по депозиту 20% годовых. Проценты начисляются один раз в год. Какая сумма будет находиться на счете в конце срока?
2. С помощью финансовой функции БЗ решить задачу.
3. Сохраните выполненное задание.
4. Представьте результат решения на проверку преподавателю.
Методические указания для решения задания 1
1. Откройте табличный процессор MS Excel. Увеличьте ширину столбца А. Объедините ячейки А1 и В1. 2. Сформируйте таблицу по образцу. Сделайте рамку на таблице. Выделите ее и в раскрывающемся меню кнопки «Граница» на панели инструментов выберите кнопку «все границы»
и нажмите ее. Обратите внимание, что в ячейке В3 необходимо установить денежный формат (рубли), а в ячейке В4 – процентный формат.
3. Выделите ячейку В7 и на панели инструментов нажмите кнопку «Вставка функции». В окне «Мастер функций» выберите категорию «Финансовые» и в окне «Функция» — БЗ.
Выполните команду ОК.
4. В открывшемся окне БЗ необходимо заполнить все ячейки.




Выполните команду ОК.
Задание 2. Решение задачи с помощью функции пз
1. В табличном процессоре MS Excel сформировать расчетную таблицу для следующего условия:
Выплаченная по 4-летнему депозиту сумма составила 14 641руб. Определить первоначальную величину вклада, если ставка по депозиту равна 10% годовых.
2. С помощью финансовой функции ПЗ решить задачу.
3. Сохраните выполненное задание.
4. Представьте результат решения на проверку преподавателю.
Методические указания для решения задания 2
1. Откройте табличный процессор MS Excel. Увеличьте ширину столбца А. Объедините ячейки А1 и В1. 2. Сформируйте таблицу по образцу. Обратите внимание, что в ячейке В4 необходимо установить процентный формат, а в ячейке В7 –денежный формат (рубли).
3. Выделите ячейку В3 и на панели инструментов нажмите кнопку «Вставка функции». В окне «Мастер функций» выберите категорию «Финансовые» и в окне «Функция» — ПЗ.
Выполните команду ОК.
4. В открывшемся окне ПЗ необходимо заполнить все ячейки.




Выполните команду ОК.
Задание 3. Решение задачи с помощью функции норма
1. В табличном процессоре MS Excel сформировать расчетную таблицу для следующего условия:
Страховая компания реализует полисы стоимостью 2000 денежных единиц. Определить годовую доходность данной операции, если по условиям договора предполагается выплата 10000 денежных единиц по истечении 5 лет. Банковская практика предполагает ежеквартальное начисление процентов.
2. С помощью финансовой функции НОРМА решить задачу.
3. Сохраните выполненное задание.
4. Представьте результат решения на проверку преподавателю.
Источник
В этом разделе вы найдете примеры задач c решением по финансовой математике, выполненные с помощью пакета Excel. Другие примеры с решениями вручную вы найдете здесь.
Для решения финансовых задач в Эксель используются как встроенные финанансовые функции (например, ПЛТ, СТАВКА, КПЕР, ПС, БС, ПОЛУЧЕНО и т.д), так и формулы, вводимые вручную, чтобы получить ответ согласно некоторой сложной формуле (для которой нет встроенной функции). Иногда используются также функции подбора параметра и поиска решения.
Поможем с Excel, финансами и математикой 
Решение финансовой математики в Excel
Задача 1. Вас просят дать в долг 03.03.2012 г. 20000 р. и обещают вернуть 18.08.2012 г. 4800 р., 13.11. 2012 г. – 5400 р., 07.03.2013 г. – 5700 р. и 31.05.2013 г. – 6200 р. Оценить выгодность предложения, если существует возможность положить деньги в банк под 13% годовых.
Задача 2. Вы заняли на 4 года 10000 руб. под 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определить величину годового платежа.
Задача 3. Предприятие рассматривает целесообразность принятия новой технологической линии. На рынке имеются две модели со следующими параметрами:
П1 П2
Цена……………………………………….. 9500 13000
Генерируемый годовой доход…….2100 2250
Срок эксплуатации……………………. 8 лет 12 лет
Ликвидационная стоимость………..500 800
Требуемая норма прибыли…………..11% 11%
Обоснуйте целесообразность приобретения той или иной технологической линии.
Задача 4. Вы открываете счёт и собираетесь вкладывать по 1400 р. в начале каждого года в течении 8 лет при годовой ставке 3,5%. Сколько денег будет на счете через 8 лет?
Задача 5. Контракт между фирмой и банком предусматривает в течение 3 лет фирме ежегодными платежами в размере 24 тыс. руб. в начале каждого года под ставку 14% годовых. Фирма возвращает долг, выплачивая последовательно в конце 3,4,5 годов. Какова чистая современная величина NPV для банка?
Задача 6. Годовая процентная ставка составляет 9% и остается неизменной в течение всего периода, а годовая купонная ставка по облигации с номиналом 1400 руб. со сроком обращения 10 лет установлена в размере 14%. Сколько стоит эта облигация при эмиссии? Сколько будет стоить эта облигация через 5 лет. Какова доходность облигации за 10 лет.
Задача 7. Кредит в размере 500 млн. руб. выдан на 5 лет под 17 % годовых с начислением процентов и выплатой в конце каждого года. Выплаты основного долга должны уменьшаться ежегодно на 8 млн. руб. Составить план погашения кредита.
Задача 8. На вклад начисляются сложные проценты: а) каждые полгода; б) ежеквартально; в) ежемесячно. Вычислить годовую номинальную процентную ставку, при которой происходит реальное наращение капитала, если ежеквартальный темп инфляции составляет 2%. Известно:
h = 2%; m1 = 2; m2 = 4; m3 = 12.
Найти: i1 — ? i2 — ? i3 — ?
Задача 9. Предприниматель получил ссуду в банке в размере 20 млн. руб. сроком на 5 лет на следующих условиях: для первых двух лет процентная ставка равна 25% годовых, на оставшиеся 3 года ставка равна 23% годовых. Найдите доход банка за 5 лет, если сложные ссудные проценты начисляются ежеквартально.
Известно: Р = 20 000 000 руб.; i1 = 0,25 или 25% n1 = 2 года i2 = 0,23 или 23% n2 = 3 года m = 4
Найти: I — ?
Задача 10. Определить годовую процентную ставку банка, если вкладчик внес 3297 д.е. на 6 лет, сумма на счете в конце срока составила 12934 д.е. В первую треть срока начислялись простые проценты, а в оставшийся – сложные, 5 раз в год.
Помогаем с решением задач по финансовой математике
Может быть интересно:
|
|
Содержание
- Выполнение расчетов с помощью финансовых функций
- ДОХОД
- БС
- ВСД
- МВСД
- ПРПЛТ
- ПЛТ
- ПС
- ЧПС
- СТАВКА
- ЭФФЕКТ
- Вопросы и ответы
Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.
Выполнение расчетов с помощью финансовых функций
В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.
Переход к данному набору инструментов легче всего совершить через Мастер функций.
- Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.
- Запускается Мастер функций. Выполняем клик по полю «Категории».
- Открывается список доступных групп операторов. Выбираем из него наименование «Финансовые».
- Запускается перечень нужных нам инструментов. Выбираем конкретную функцию для выполнения поставленной задачи и жмем на кнопку «OK». После чего открывается окно аргументов выбранного оператора.
В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.
Урок: Мастер функций в Excel
ДОХОД
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:
=ДОХОД(Дата_сог;Дата_вступ_в_силу;Ставка;Цена;Погашение»Частота;[Базис])
БС
Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:
=БС(Ставка;Кол_пер;Плт;[Пс];[Тип])
ВСД
Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:
=ВСД(Значения;[Предположения])
МВСД
Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:
=МВСД(Значения;Ставка_финансир;Ставка_реинвестир)
ПРПЛТ
Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:
=ПРПЛТ(Ставка;Период;Кол_пер;Пс;[Бс])
ПЛТ
Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:
=ПЛТ(Ставка;Кол_пер;Пс;[Бс];[Тип])
ПС
Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:
=ПС(Ставка;Кол_пер;Плт;[Бс];[Тип])
ЧПС
Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:
=ЧПС(Ставка;Значение1;Значение2;…)
СТАВКА
Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:
=СТАВКА(Кол_пер;Плт;Пс[Бс];[Тип])
ЭФФЕКТ
Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:
=ЭФФЕКТ(Ном_ставка;Кол_пер)
Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.
2.4.1 Общие рекомендации
В пакете Excel
существует группа функций, предназначенных
для расчета финансовых операций по
кредитам, ссудам, займам. Эти расчеты
основаны на концепции временной стоимости
денег и предполагают неравноценность
денег, относящихся к разным моментам
времени. Эта группа функций охватывает
следующие расчеты:
-
определение
наращенной суммы (будущей стоимости), -
определение
начального значения (текущей стоимости), -
определение срока
платежа и процентной ставки, -
расчет периодических
платежей, связанных с погашением займов.
Для
расчетов Excel
использует приведенную выше формулу
(22)
Эти
формулы используют встроенные функции
БC,
КПЕР, ПC,
ПЛТ, ЭФФЕКТ и
другие.
В
финансовых функциях Excel
необходимо строго учитывать знаки
величин PV,
FV
и С. Когда мы отдаем какую – либо величину,
ставим перед ней знак минус, если получаем
– плюс.
Работать
с финансовыми функциями удобно с помощью
Мастера функций
Когда
появляется окно выбранной функции, в
его поля нужно ввести заданные значения.
Если какое – либо значение равно нулю,
это поле можно не заполнять. Если рента
постнумерандо, поле Тип
тоже можно не заполнять.
Не
забывайте в поле Норма
вводить величину процентной ставки за
период r/m,
а в поле Число
– периодов
– число периодов выплат или начисления
процентов n=k·m.
2.4.2 Вычисление будущего значения
В
Excel
будущему значению FV
соответствует функция БС.
БС
— стоимость
постоянных платежей в определенные
периоды на основе постоянной процентной
ставки.
Позволяет рассчитать
объем вклада через определенный
промежуток времени на основе периодических
постоянных платежей и постоянной
процентной ставки.
Синтаксис
БС(ставка;кпер;плт;пс;тип)
ставка
— процентная
ставка за период.
кпер
— количество
периодов, в которые производится выплата
годовых процентов.
плт
-выплата—
размер выплаты, производимой в каждом
периоде; это значение постоянно в течение
всего времени выплат. Обычно плата
состоит из основного платежа и платежа
по процентам без учета других налогов
и сборов.
пс
— общая сумма
всех будущих платежей с настоящего
момента. Если аргумент пс
опущен,
то он полагается равным 0.
тип
— число,
определяющее когда должна производиться
выплата. Может принимать значения 0 или
1: 0 — выплата в конце периода, 1 — выплата
в начале периода.
Единицы
измерения для аргументов ставка
и кпер
должны быть согласованы. Если производятся
ежемесячные платежи по четырехгодичному
займу из расчета 12% годовых, то норма
должна быть 12%/12, а кпер
должно быть 4*12. Если производятся
ежегодные платежи по тому же займу, то
ставка
должна быть
12%, а кпер
должно быть 4.
Ваш вклад
представляется отрицательным числом,
а деньги, которые вы получите, представляются
положительным числом.
В
принятых в данной работе обозначениях
FV=БС(r/m;
k·m;
С; PV;
тип).
Пример
15 Определим,
сколько денег будет на счету через год,
если вы собираетесь вложить 1000 рублей
под 6% годовых (что составит в месяц
6%/12 или 0,5%). Причем вы собираетесь
вкладывать по 100 рублей в начале каждого
следующего месяца в течение года.
Через год на счете
будет:
БС
(0,5%;12;-100;-1000;1)=2301,40 р.
Определение будущей
стоимости на основе постоянной процентной
ставки.
Пример
16 Определить
сумму вклада на банковском счете, если
положить 37 тыс. руб. на 3 года под 11,5%
годовых. Проценты начисляются каждые
полгода.
Алгоритм решения
задачи:
Поскольку
необходимо рассчитать единую сумму
вклада на основе постоянной процентной
ставки, то используем функцию БС(). В
связи с тем, что проценты начисляются
каждые полгода, аргумент ставка равен
11,5%/2. Общее число периодов начисления
равно 3*2 (аргумент кпер). По условию
аргумент пс
(начальное значение) равен 37000 руб. и
задается в виде отрицательной величины
(- 37 000), т.к. с точки зрения вкладчика это
отток его денежных средств (вложение
средств). Аргумент платеж отсутствует,
т.к. вклад не пополняется, аргумент тип
равен 0, т.к. в подобных операциях проценты
начисляются в конце каждого периода
(задается по умолчанию). Тогда к концу
3-го года на банковском счете имеем:
= БС(11,5%/2;3*2;;-37000) =
51746,86 руб.
Отметим, что по
условию задачи указаны годовой процент
и число лет. Если процент начисляется
несколько раз в год, то следует рассчитать
общее число периодов начисления процентов
и ставку процента за период начисления.
Для наиболее распространенных методов
внутригодового учета процента можно
привести следующую таблицу расчета
основных величин.
Расчет процентной
ставки для различной периодичности
начислений
|
Метод начисления |
Общее число |
Ставка процента |
|
Ежегодный |
N |
K |
|
Полугодовой |
N*2 |
K/2 |
|
Квартальный |
N*4 |
K/4 |
|
Месячный |
N*12 |
K/12 |
|
Ежедневный |
N*365 |
K/365 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.