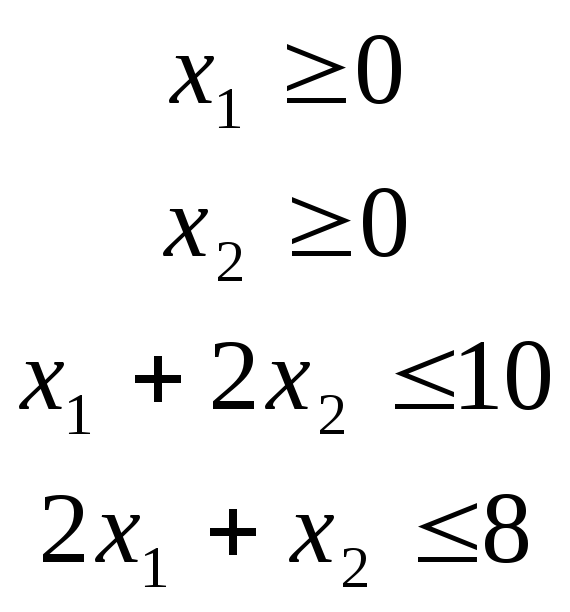Решение задач по оптимизации с использованием ms excel

На этой странице вы найдете примеры решений различных оптимизационных задач с использованием пакета электронных таблиц MS Excel (используется как надстройка Поиск решения, так и ручные вычисления).

Задачи оптимизации и Excel

Задачи оптимизации имеют огромное прикладное значение и возникают в самых разных разделах экономики, техники, военного дела и т.п. В таких задачах нас интересуют поиск некоторого оптимального решения (минимизующего или максимизирующего целевую функцию: прибыль, затраты, калорийность и т.п.) в условиях ограничений (наличия ресурсов, дорог, времени, продуктов и т.п.).

Вот некоторые примеры экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация калорийности и стоимости рациона (как для людей, так и для животных), минимизация расходов на перевозку грузов по маршрутам, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.

Часто эти задачи (даже учебные, даже в случае линейности) содержат более десяти переменных(а в случае, например, транспортных задач, и вовсе десятки), что делает ручные расчеты нерациональными. В то же время привычная для всех программа Excel прекрасно подходит для поиска решения.

Алгоритм решения с помощью надстройки «Поиск решения» следующий:

• составить математическую модель задачи: выделить и обозначить переменные, ограничения на них в виде равенств и неравенств (естественные, например, неотрицательность количества, и дополнительные, например, «запасов железной руды не более 10 т»), целевую функцию (то, что нужно оптимизировать) выразить через переменные.
• выделить место под переменные задачи; внести ограничения (левые части — в виде формул от переменных, правые — в виде констант) в файл электронной таблицы Excel,
• внести в ячейку формулу для целевой функции,
• запустить надстройку Поиск решения,
• установить нужные параметры решения (ограничения в листе, ограничения неотрицательности, условие линейности при необходимости и т.п.) и запустить выполнение.

Excel вычислит оптимальные значения переменных и покажет их в ячейках, а также значение целевой функции. Дополнительно можно построить отчеты для анализа решения задачи.

Некоторые задачи оптимизации решаются не с помощью надстройки Поиск решения, а путем подбора параметра или ручных расчетов. Ниже вы найдете примеры разных задач, а также ссылки на другие разделы со сходными заданиями.

Задачи оптимизации: примеры в Excel

Задача 1. Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля $R_j$. Определена экономическая эффективность $К$ — каждого проекта в зависимости от рентабельности производства. По истечении трех сроков $S_i$ рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д. е.):


Выберите оптимальное решение в соответствии с критериями Лапласа, Вальда, Сэвиджа и Гурвица (при $а = 0,5$).

Задача 2. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода каждого вида сырья на изготовление единицы продукции данного вида в таблице 6. В ней же указаны прибыль от реализации единицы изделия каждого вида и общее количество сырья данного, которое может быть использовано предприятием.
Требуется такой составить такой план производства изделий А и В, при котором прибыль от реализации будет максимальной?

Задача 3. Фирма N, имеющая филиалы (k), производит продукцию. Каждый филиал фирмы выпускает четыре вида продукции из пяти (i=1-5). Данные, характеризующие производство филиалов $b_{ki}$, приведены в табл.1.
Филиалы фирмы закупают сырье, из которого производят продукцию, у семи АО (j =1-7). Выход готового продукта из 1 тонны сырья $a_{ij}$ показан в табл.2.
Прибыль филиалов фирмы при закупке 1тн сырья у разных АО, $С_{kj}$ , показана в табл.3.
В разделе 1 работы требуется:
1.1.Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, ($x_j$), максимизируя прибыль филиала. Далее, студент формулирует экономико-математическую модель общей задачи линейного программирования (ОЗЛП).
1.2.С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции.

Задача 4. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки?
Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5.
Для решения задачи используется ППП Excel.

Задача 5. Менеджер проекта по строительству нового торгового гипермаркета компании Наше дело надеется завершить проект за пару недель до Рождества.
После обзора оценок времени выполнения отдельных стадий выяснилось, что потребуются дополнительные инвестиции, чтобы сократить длительность проекта так, чтобы он действительно завершился вовремя. В таблице приведены оценки длительностей стадий и стоимость их сокращения на 1 и на 2 недели.
a. Нарисуйте сетевую диаграмму проекта и найдите критический путь.
b. Определите минимальную стоимость сокращения проекта на 5 недель.

Полезные ссылки

Методички

• Решение оптимизационных задач в среде MS Excel 2013 Методические указания небольшого объема. Разобраны стандартные задачи: ЛП, транспортная, нелинейная, приведены скриншоты решения и пояснения.
• Решение задач оптимизации в Microsoft Excel 2010 Учебное пособие ТОГУ, 101 страница, более увесистый и подробный документ. Разбирается надстройка Поиск решения, решение задач линейного и нелинейного программирования и СЛАУ.

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.



Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Решение
задач оптимизации с использованием MS
Excel

С помощью
инструмента «Поиск решения» решаются
задачи оптимизации следующих типов.

1. Имеется
функция одной или нескольких переменных
и необходимо найти значения переменных,
при которых функция равна либо минимуму
или максимуму.

2. Имеется
функция одной или нескольких переменных
и необходимо найти значения переменных,
при которых функция равна либо минимуму
либо максимуму с учётом дополнительных
ограничений.

Функция,
значение которой отыскивается с помощью
инструмента «Поиск решения» называется
целевой функцией, а ячейка, где содержится
формула для вычисления значений функции,
называется целевой ячейкой.

Ограничение
состоит из левой части, в которой
содержится формула для вычисления
некоторой величины, и правой части, в
которой указывается величина ограничения.
Левая и правая части соединяются либо
знаком равенства, либо знаком неравенства.

Пример
1. Надо найти максимум
функции

при следующих ограничениях:

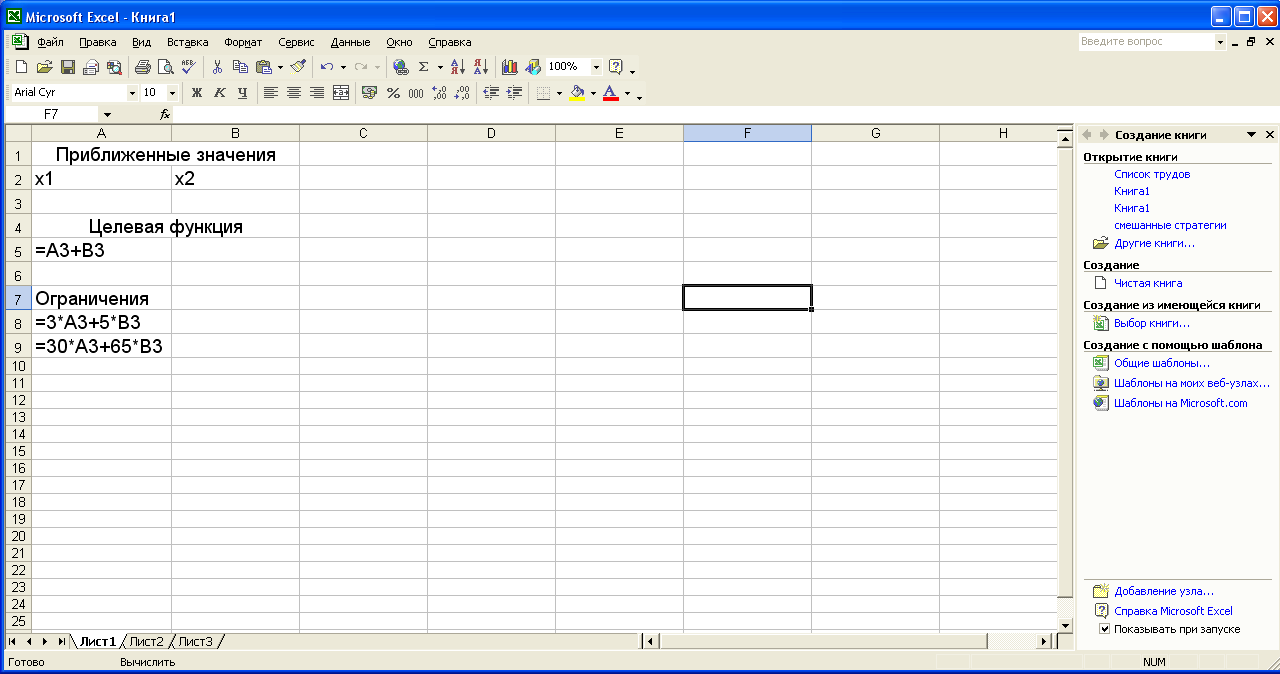
Эти данные
можно внести на лист следующим образом:

	А	В
1	Переменные
2	Х1	Х2
3	0	0
4	Целевая функция
5	=300*А3+200*В3
6	Ограничения
7	=А3+2*В3	10
8	=2*А3+В3	8

После
внесения исходных данных надо сделать
активной целевую ячейку и вызвать «Поиск
решения» через меню «СервисПоиск
решения».

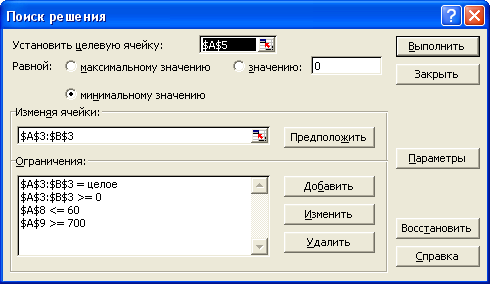
В
появившемся диалоговом окне надо
заполнить ряд полей.

Поле «Установить
целевую ячейку» должно содержать адрес
целевой ячейки. В нашем случае это адрес
А5.

Затем
установить переключатель «Равной» в
положение «Максимальному значению».

Поле
«Изменяя ячейки» должно содержать
диапазон ячеек, содержащих независимые
переменные. В нашем случае это А3:В3.

П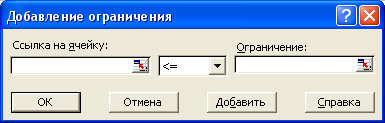оле
«Ограничения» должно содержать все
ограничения, если они имеются. В нашем
случае, по условию задачи имеются четыре
ограничения. Чтобы внести в это поле
ограничения надо щелкнуть по кнопке
«Добавить».

Появится
диалоговое окно с тремя полями
расположенными в ряд. Самое левое поле
«Ссылка на ячейку», среднее поле со
списком, и правое поле «Ограничение».

Поле
«Ссылка на ячейку» должно содержать
адрес ячейки с формулой ограничения. В
поле со списком выбирается знак
ограничения. Поле «Ограничение» содержит
либо величину ограничения, либо адрес
ячейки, где эта величина содержится.

В
нашем случае, формула первого ограничения
представляет собой просто переменную
х1, поэтому указываем адрес А3, затем
выбираем из списка неравенство больше
или равно и величину ограничения
указываем равной нулю. Чтобы добавить
следующее ограничение надо в этом же
окне щелкнуть по кнопке «Добавить» и
внести новые данные. И так, до тех пор,
пока не будут набраны данные по всем
ограничениям. После внесения данных по
последнему ограничению надо щелкнуть
по кнопке ОК.

После
этого можно щелкнуть по кнопке «Выполнить».

Через
некоторое время появиться окно с
результатом поиска решения. Возможны
два варианта.

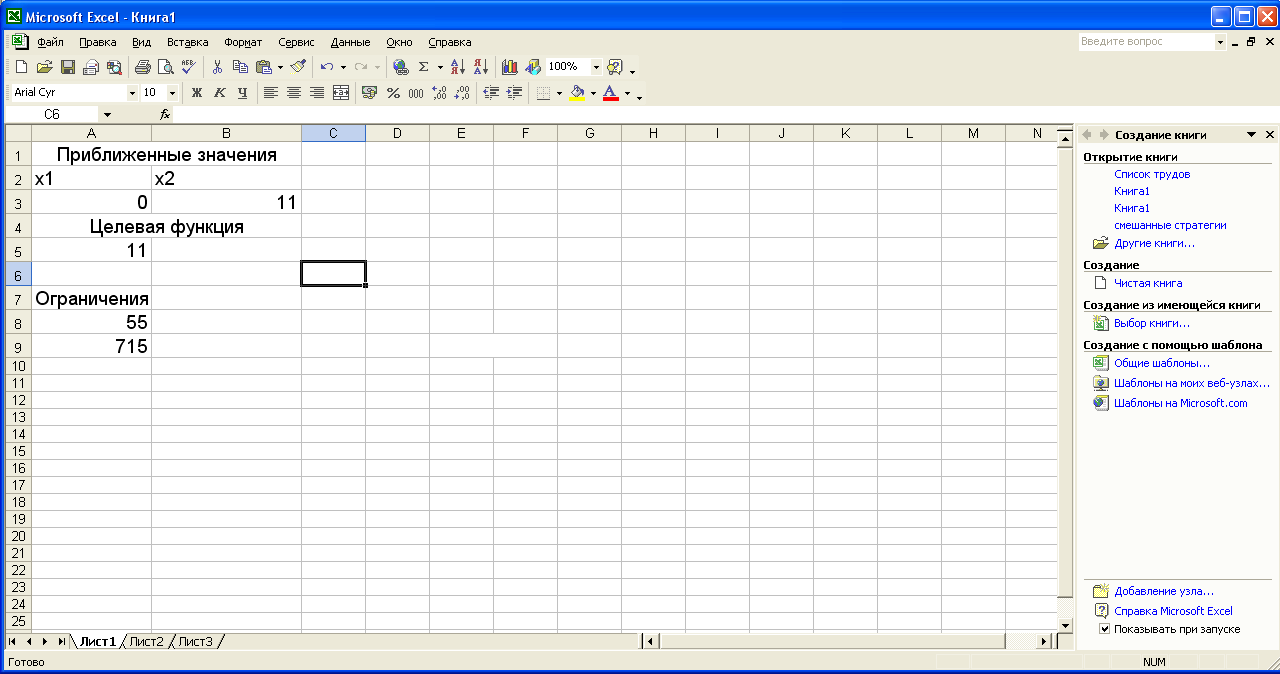
Если в
окне будет сообщение «Решение найдено»,
то можно нажимать на кнопку ОК и в ячейках
на листе будут содержаться найденные
значения.

В нашем
случае ячейки должны содержать: А3=2,
В3=4, А5=1400, А8=10, А9=8.

Если
появится сообщение «Процесс не сходится»,
то это означает, что решения не существует
или оно не найдено при установленных
параметрах поиска. Эти параметры можно
изменить, если до щелчка по кнопке
«Выполнить» нажать кнопку «Параметры».
Можно попробовать изменить параметры
«Максимальное время», «Предельное число
итераций», «относительная погрешность»
и «Допустимое отклонение».

Пример
2.

Авиакомпания
М* по заказу армии должна перевезти на
некотором участке 700 человек. В распоряжении
компании имеется два типа самолетов,
которые можно использовать для перевозки.
Самолет первого типа перевозит 30
пассажиров и имеет экипаж 3 человека,
второго типа – 65 и 5 соответственно.

Эксплуатация
1 самолета первого типа обойдется 5000$,
а второго 9000$. Сколько надо использовать
самолетов каждого типа, если для
формирования экипажей имеется не более
60 человек.

Для начала,
обозначим переменные: пусть X₁
– это оптимальное количество самолетов
первого типа, X₂
– оптимальное количества самолетов
второго типа. Очевидно, что стоимость
эксплуатации самолетов должна быть
минимальной. Следовательно,

5000X₁
+ 9000X₂→min

Теперь определим
ограничения. Для формирования экипажей
имеется не более 60 человек, следовательно:

3X₁+5X₂<=60

Пассажиров надо
перевезти не менее 700 человек,
следовательно:

30X₁+65X₂>=700

Сформируем страницу
электронной таблицы и постановку задачи
линейного программирования в диалоговом
окне:

После выполнения
поставленной задачи получаем следующие
значения переменных. Как показано на
рисунке

Т.е. нам
необходимо (X₁=0)
0 самолётов первого класса и (X₂=11)
11 самолётов второго класса, для перевозки
пассажиров.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В данной статье рассматривается расчет инструмента Excel «Поиск решений». Освоение работы с надстройкой «Поиск решений» даст преимущество в решении многих экономических задач: минимизация расходов при формировании состава сырья и штатного расписания, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы.

Зачастую экономисты в своей практике встречаются с вопросами оптимизации расходов.

Рассмотрим пример оптимизации транспортных расходов с помощью инструмента Excel «Поиск решений».

Пример 1

На предприятии X осуществляются транспортные перевозки с помощью четырех компаний до пяти населенных пунктов. Руководство компании решило распределить все количество перевозок между поставщиками транспортных услуг (транспортными компаниями) в определенной пропорции, выраженной в процентном соотношении — удельный вес в общем количестве перевозок. Известны также тарифы транспортных компаний за одну ездку и количество плановых перевозок до каждого населенного пункта в планируемом периоде .

Необходимо оптимально распределить ездки в населенные пункты между транспортными компаниями таким образом, чтобы транспортные расходы были минимальными.

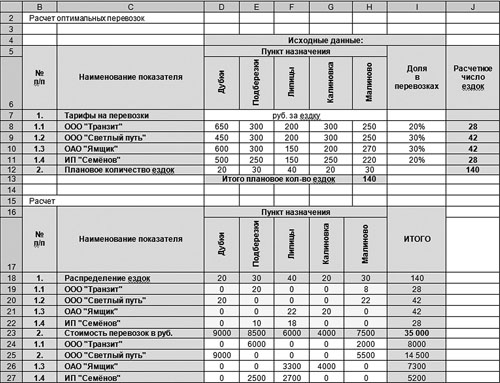
Для успешного решения этой задачи необходимо выбрать минимизируемую ячейку, определить ограничения, а также правильно сформировать таблицы с исходными и расчетными данными (рис. 1). 

 

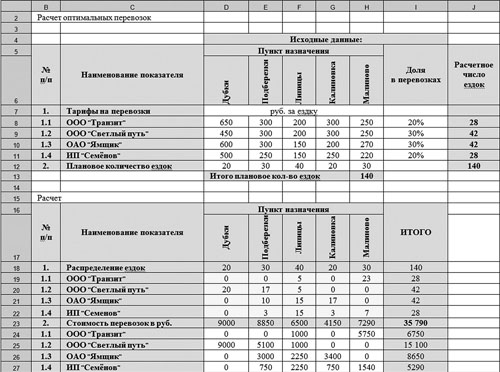
 Рис. 1. Расчет оптимальных перевозок

На рис. 1 расположены две таблицы: с исходными данными и расчетными данными. В ячейках D8:H11 расположены тарифы за 1 ездку в разрезе транспортных компаний до пунктов назначения, в ячейках D12:H12 — плановое количество ездок за период до пунктов назначения, в ячейках I8:I11 — удельный вес перевозок каждой транспортной компании в общем количестве планируемых перевозок за период. Эти ячейки для удобства не раскрашены. В ячейках J8:J12 и Н13 рассчитано число ездок по каждой транспортной компании и в целом за период. Формулы в этих ячейках выглядят следующим образом:

Ячейка Н13: =СУММ(D12:H12),

Ячейка J8: =I8*$H$13.

Данную формулу из ячейки J8 протаскиваем (копируем) в ячейки J9, J10, J11.

Ячейка J12: =СУММ(J8:J11).

Следующая таблица на листе посвящена расчету и называется «Расчет». Ячейки D19:Н22 предназначены для распределения количества ездок до пунктов назначения между транспортными компаниями. На рис. 1 в ячейках дано такое распределение, заполненное вручную. В ячейках D23:I27 рассчитаны суммы расходов на транспортные перевозки в разрезе транспортных компаний, оказывающих транспортные услуги, и пунктов назначений, а также итоги.

Приведем формулы, представленные в этих ячейках.

Значения в ячейках D24:Н27 получены перемножением количества ездок (ячейки D19:Н22) на тарифы (ячейки D8:Н12). В ячейку D24 запишем формулу:

=D19*D8.

Протащим (скопируем) формулу в ячейки D25:D27 и E24:Н27.

В ячейках D23:I23 формируются итоговые суммы транспортных услуг в разрезе пунктов назначения. Запишем в ячейку D23 формулу:

=СУММ(D24:D27).

Протащим (скопируем) эту формулу в ячейки Е23:I23.

В ячейках I24:I27 формируются итоговые суммы транспортных услуг в разрезе компаний, оказывающих эти услуги. Запишем в ячейку I24 формулу:

=СУММ(D24:H24).

Протащим (скопируем) ее в ячейки I25:I27.

Таким образом, стоимость транспортных расходов по компании в целом формируется в ячейке I23. В первоначальном расчете, представленном на рис. 1, данная сумма равна 35 790 руб.

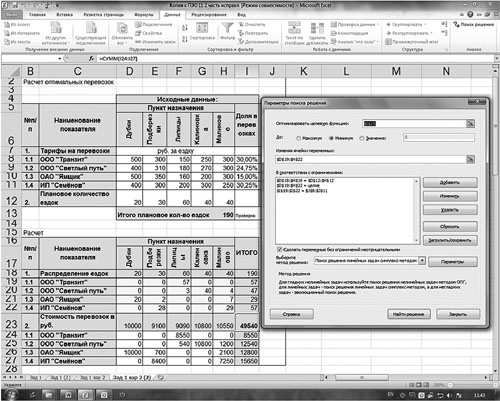
Скопируем данный лист в эту же книгу. Далее необходимо приступить непосредственно к оптимизации. Задача — подобрать в ячейках D19:Н22 такие значения, чтобы в ячейке I23 была рассчитана минимальная сумма расходов на транспорт. Для этого воспользуемся инструментом «Поиск решений».

Для начала надо выбрать оптимизируемую ячейку (I23). Затем вызовем диалоговое окно «Поиск решений», представленное на рис. 2.

Это важно. Надстройку «Поиск решений» не всегда можно обнаружить в меню рабочего стола компьютера, так как она может быть не подключена. Для ее подключения необходимо выполнить ряд действий, которые аналогичны во всех версиях MS Office: «Сервис — Надстройки — Поиск решений (установить флажок)». Теперь данный инструмент можно будет найти на панели инструментов рабочего стола.

 

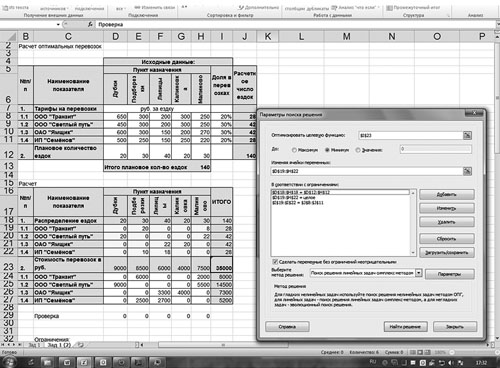
Рис. 2. Использование надстройки «Поиск решений»

В строке «Оптимизировать целевую функцию» будет стоять адрес оптимизируемой ячейки, в данном случае — $I$23. Выберем цель, поставив флажок «Минимум». В строке «Изменяя ячейки переменных» помещаются адреса ячеек, которые необходимо будет подобрать для достижения желаемого результата ($D$19:$Н$22).

В поле запишем ограничения в соответствии с ограничениями. Для этого воспользуемся кнопкой «Добавить», которая откроет окно «Добавить ограничения». Введем одно из ограничений:

$D$19:$H$22 = целое,

$D$12:$H$12 = $D$18:$H$18,

$J$8:$J$11 = $I$19:$I22.

Чтобы добавить следующее ограничение, в этом же окне нажмите на кнопку «Добавить». Результатом этого действия будет добавление текущего ограничения в список ограничений, а поля окна «Добавить ограничения» будут очищены для ввода следующего ограничения. После того как введено последнее из ограничений, необходимо нажать на кнопку «ОК».

Порядок ввода ограничений не имеет значения. Главное — не забыть ни одно из ограничений.

В данном примере все ограничения представлены в виде равенств. Но существуют задачи, в которых требуются ввести ограничения в виде неравенств. Например, в транспортных компаниях объем перевозимого груза не может превышать грузоподъемности автомобиля (или время работы автотранспортного средства не может превышать количества часов в сутки за вычетом нормативных простоев).

Очень важно правильно сформулировать ограничения. Для того чтобы не забыть ни одно из ограничений, необходимо правильно поставить задачу и определить ее цели. Не бывает мелочей в постановке задачи. В задаче о поставке деталей необходимо учесть, что количество деталей на складе на начало периода плюс количество поступивших за планируемый период деталей должно равняться сумме их остатка на складе на конец периода плюс количество отгруженных деталей за планируемый период. Или, например, количество деталей на начало планируемого периода должно равняться количеству деталей на конец периода, предшествующему планируемому.

Необходимо также помнить о том, что некоторые показатели могут быть только положительными значениями (например, сумма поступления от покупателя на расчетный счет поставщик). В данном случае в ограничениях целесообразно указать, что эта величина не может быть отрицательной, иначе надстройка «Поиск решений», вполне возможно, предложит в качестве решения отрицательное число.

Далее следует выбрать метод решения. Для этого необходимо определить, является модель линейной или нелинейной. Напомним, что линейной моделью является такая модель, связи в которой между данными для расчета и результирующим показателем можно описать линейными функциями. Линейная функция имеет следующий вид:

F(x) = a1 × x1 + а2 × x2 + … + аn × xn,

где a1, а2, …, аn — константы;

x1, x2, …, xn — переменные.

Данная модель является линейной.

Примером нелинейной модели является оптимизация перевозок с целью минимизации расходов, когда тарифы на перевозки распределены по интервалам:

• от 0 до 10 км — стоимость перевозки 200 руб.;
• от 11 до 20 км — стоимость перевозки 250 руб.;
• от 21 до 50 км — стоимость перевозки 500 руб. и т. д.

Вернемся к диалоговому окну «Параметры поиска решений». Далее нажимаем кнопку «Найти решение», в результате чего появится окно с результатом поиска решения. Так как нам необходимо сохранить найденный результат, то ставим флажок «Сохранить найденное решение», в результате чего на нашем листе сохранится найденное решение. Нажмем кнопку «ОК».

В ячейках $D$19:$Н$22 появляются подобранные системой значения, при которых в ячейке I23 формируется минимальное значение стоимости транспортных услуг — 35 000 руб.

В данном случае отклонения от подобранного нами вручную результата составляют лишь 2,2 %, или 790 руб., но это означает лишь то, что мы вручную удачно подобрали решение.

На рис. 3 представлены полученные при оптимизации данные.

Рис. 3. Результаты оптимизации

Для того чтобы использовать ссылки на ячейки в составе сценария, необходимо сохранить этот сценарий, нажав на кнопку «Сохранить сценарий» в окне «Результат поиска решения», введя имя сценария и нажав кнопку «ОК». При этом исходные данные сохраняются.

Таким образом, предоставлена возможность сохранить все варианты решений при изменении исходных данных. Затем можно создавать отчеты, по которым можно сравнивать влияние изменений исходных данных и ограничений на результат решения.

Существует одна важная деталь: при расчетах количества ездок лучше всего в ячейках J8:J11 использовать функцию округления, чтобы значения были целыми числами.

По этому случаю рассмотрим пример с другими исходными данными.

Пример 2

В ячейках J8:J11 запишем формулу, позволяющую округлить вычисляемые значения до целого числа, которая имеет вид:

Ячейка J8: =ОКРУГЛ(I8*$H$13;0).

Протащим (скопируем) эту формулу в ячейки J9:J11.

Как видим (рис. 4) плановое количество ездок в ячейке Н13 отличается от суммы в ячейках J8:J11, записанной в ячейке J12: значение в ячейке J12, полученное в результате суммирования округленных результатов расчетов числа ездок в ячейках J8:J11, не равно значению в ячейке Н13, полученному суммированием планового числа ездок до пунктов назначения. Это издержки примененной функции округления. Для того чтобы избежать данной ошибки, проделаем следующую процедуру. Для контроля и удобства вычислений введем проверочную ячейку J13. Формула в этой ячейке будет представлять собой разницу полученных значений в ячейках J12 и H13. Ячейка понадобится нам для коррекции вычислений.

 

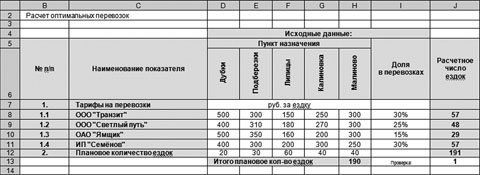
Рис. 4. Пример с функцией округления расчетного числа ездок до целого числа

Используем для коррекции инструмент «Подбор параметра». Процедура подбора иллюстрируется на рис. 5.

 

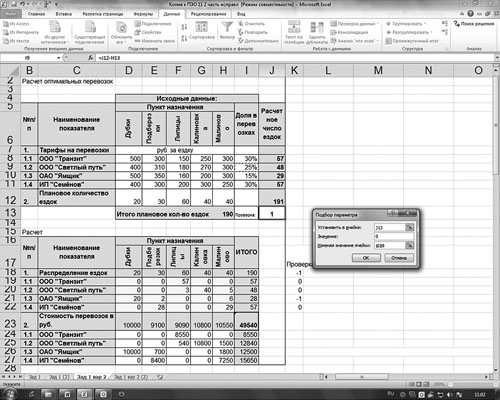
Рис. 5. Использование инструмента «Подбор параметра»

Здесь необходимо применить следующую схему: подобрать в ячейке J13 значение равное 0, изменяя значение в ячейке I9 (доля в перевозках). Предварительно в ячейку I11 целесообразно ввести следующую формулу:

=100 % – I8 – I9 – I10.

Тогда при изменении значения в ячейке I9 в результате применения инструмента «Подбор параметра» автоматически изменится и значение в ячейке I11.

Так как в ячейках I8:I11 применено округление до целого значения, изменения в ячейках I9 и I11 на 0,25 % не обнаруживаются. Эти изменения будут видны, если мы добавим знаки после запятой.

Результат применения инструмента «Подбор параметра» приведен на рис. 6 (на с. …).

Необходимо проделать процедуры, что и в предыдущем примере (см. рис. 1, 2, 3). В ячейках D19:H22 распределим количество ездок для каждой транспортной компании до каждого пункта назначения, используя следующие ограничения:

D19:H22 = целое,

D12:H12 = D18:H18,

J8:J11 = I19:I22.

Сумма транспортных расходов в ячейке I23 на рис. 6 рассчиталась равной 49 540 руб., а наша задача — минимизировать ее.

 

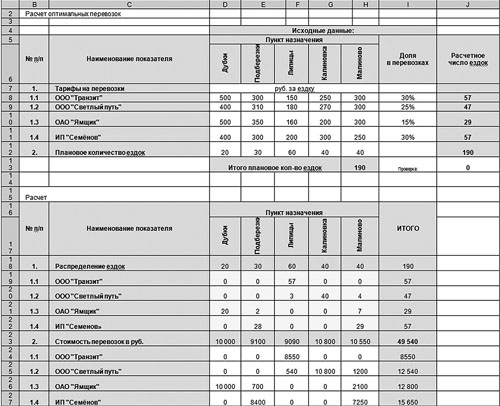
Рис. 6. Скорректированный вариант

На рис. 7 представлена демонстрация использования инструмента «Поиск решений» для оптимизации результата.

 

Рис. 7. Минимизация значения в ячейке I23 с помощью надстройки «Поиск решения»

На рис. 8 в ячейках D19:Н22 представлены данные, полученные в ходе оптимизации с помощью инструмента «Поиск решений». В результате минимизации в ячейке I23 получено значение 44 990 руб. Отклонения от достигнутого при первоначальном распределении результата составило 9 %, или 4550 руб.

Возможно, имеет право на существование такой вопрос: «Для чего нужна табличная часть со стоимостями перевозок в разрезе транспортных компаний и пунктов назначений?». Ведь можно было бы просто в итоговую ячейку I23 ввести формулу:

=СУММПРОИЗВ(D8:D11;D19:D22)+СУММПРОИЗВ(E8:E11;E19:E22)+СУММПРОИЗВ(F8:F11;F19:F22)+СУММПРОИЗВ(G8:G11;G19:G22)+СУММПРОИЗВ(H8:H11;H19:H22).

Следует помнить следующее:

• строк и столбцов может быть достаточно большое количество. Это значит, что написание самой формулы в ячейках будет слишком трудоемкой задачей;
• потеряется возможность анализа данных по компаниям и пунктам назначения. Значит, целесообразнее использовать вспомогательную таблицу (в нашем примере это ячейки B23:I27), которая содержала бы множество простых формул. Эти формулы записываются всего в два мгновения: запись в одной из ячеек и копирование или протаскивание в остальные ячейки. Такая таблица несет в себе полезную для анализа информацию о стоимости транспортных услуг в разрезе перевозчиков и пунктов назначения.

 

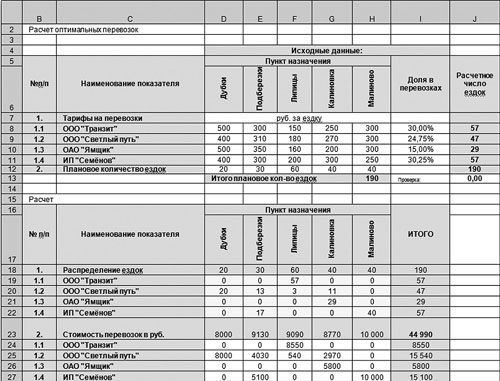
Рис. 8. Результат оптимизации примера с округлением

Заключение

В данной статье рассмотрена простейшая задача, цель статьи — побудить экономистов использовать в расчетах инструмент Excel «Поиск решений», который удобен и прост в применении. Освоив и поняв данный инструмент, можно будет переходить к более сложным задачам.

Освоение работы с надстройкой «Поиск решений» даст преимущество в решении многих экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.

Конспект урока

Решение задач оптимизации с помощью
электронных таблиц Excel

    Учитель информатики и ИКТ

Кабанова Татьяна Витальевна

ГБОУ школа №58

Приморского района Санкт-Петербурга

Тема. Решение
задач оптимизации в  Excel.

Тип
урока: обобщение и систематизация
знаний.

Цели урока:

образовательные —
обобщение и систематизация знаний по теме «Обработка числовой информации»

Задачи:

1.           
закрепление знаний об общих
принципах работы табличного процессора Microsoft Excel;

2.           
практическое применение изученного
материала, приобретение навыков в составлении таблиц разного типа;

3.           
развитие умения выбирать
наиболее оптимальную структуру таблицы, создать и оформить таблицу;

4.           
формирование представления о
вычислениях в электронной таблице как наиболее важных в изучении информатики и
широко применяемых на практике.

развивающие — продолжить
развитие логического мышления, глубины и гибкости ума.

Задачи:

1.           
развитие познавательного
интереса, речи и внимания учащихся;

2.           
развитие способности логически
рассуждать;

3.           
формирование информационной
культуры и потребности приобретения знаний;

4.           
развитие умения применять
полученные знания для решения задач различных предметных областей.

5.           
развивать
у школьников теоретическое мышление, формирование операционного мышления,
направленного на выбор оптимальных решений.

воспитательные — продолжать
воспитывать информационную культуру, общечеловеческие качества личности
школьника

Задачи:

1.           
воспитание творческого подхода
к работе, желания экспериментировать;

2.           
воспитание трудолюбия, чувства
уважения к науке;

3.           
продолжить воспитывать культуру
общения;

4.           
продолжить формировать чувство
долга, настойчивости, дисциплинированность; продолжить формирование творческих,
исследовательских качеств учащихся;

5.           
продолжить воспитывать
эстетический вкус.

Ход урока:

I.                     
Организационный этап. (Цель: настроить учащихся на работу на уроке)

Сегодня мы продолжаем изучение темы «Обработка числовой
информации». На предыдущих занятиях мы узнали основные информационные единицы
электронной таблицы, типы и форматы данных, используемых в Excel, основные функций, используемых при записи формул, общие правила
подготовки электронной таблицы, а так же графические возможности табличного
процессора, учились решать задачи с использованием ЭТ.

Сегодня цель нашего урока: закрепить и обобщить знания,
полученные по этой теме, развивать умение применять полученные знания для
решения задач из различных предметных областей.

II. Актуализация знаний и фронтальный
опрос

– Итак, что мы с вами знаем и умеем делать: создавать
редактировать и формировать табличный документ, выполнять вычисления по
формулам, применять относительные и абсолютные ссылки, использовать  функции.
Давайте вспомним и повторим то, что нам уже знакомо.

Таким образом, можно сделать вывод:
области применения электронных таблиц очень разнообразны, без них не может обойтись практически ни один современный специалист.

III.
Изложение нового материала

Человек,
совершая те или иные деяния, стремился вести себя таким образом, чтобы
результат, достигаемый как следствие некоторого поступка, оказался в
определенном смысле наилучшим. Двигаясь из одного пункта в другой, он стремился
найти кратчайший среди возможных путь. Строя жилище, он искал такую его
геометрию, которая при наименьшем расходе топлива, обеспечивала приемлемо
комфортные условия существования. Занимаясь строительством кораблей, он пытался
придать им такую форму, при которой вода оказывала бы наименьшее сопротивление.
Можно легко продолжить перечень подобных примеров.

Задачи
на отыскание оптимального решения называются задачами оптимизации.
Применяемые в процессе оптимизации методы получили название методов
оптимизации. При постановке и решении задач оптимизации возникают два
вопроса: что и как оптимизировать?

Ответ
на первый вопрос получается как результат глубокого изучения проблемы, которую
предстоит решить. Выявляется тот параметр, который определяет степень
совершенства решения возникшей проблемы. Этот параметр обычно называют целевой
функцией или критерием качества. Далее устанавливается совокупность
величин, которые определяют целевую функцию. Наконец, формулируются все
ограничения, которые должны учитываться при решении задачи. После этого
строится математическая модель, заключающаяся в установлении аналитической
зависимости целевой функции от всех аргументов и аналитической формулировки
сопутствующих задаче ограничений. Далее приступают к поиску ответа на второй
вопрос.

Понятие
«наилучший, оптимальный» может быть выражено количественными критериями – минимум
затрат, минимум времени, максимум прибыли и т.д. Для решения таких задач в ЭТ
используется надстройка Поиск решения.

При решении задач оптимизации с помощью MS Excel применяют алгоритм:

1)     
разбор условия задачи;

2)     
построение математической модели;

3)     
выбор изменяемых данных (параметров);

4)     
задание ограничений;

5)     
выбор целевой функции;

6)     
решение задачи на компьютере;

7)     
анализ  полученных результатов.

Виды задач, которые могут быть решены с помощью Поиска решения:

:
Составление оптимального плана производства;

:
Решение системы линейных уравнений;

:
Транспортная задача;

:
Задача о назначениях;

:
Решение уравнения регрессии

Предлагаю
для рассмотрения одну из таких задач.

            На участке работает 20 человек; каждый из них в среднем
работает 1800 ч в год. Выделенные ресурсы: 32 т металла, 54 тыс. кВт∙ч
электроэнергии. План реализации: не менее 2 тыс. изделий А и не менее 3 тыс.
изделий Б. На выпуск 1 тыс. изделий А затрачивается 3 т металла, 3 тыс. кВт∙ч
электроэнергии и 3 тыс. ч рабочего времени. На выпуск 1 тыс. изделий Б
затрачивается 1 т металла, 6 тыс. кВт∙ч электроэнергии и 3 тыс. ч рабочего
времени. От реализации 1 тыс. изделий А завод получает прибыль 500 тыс. р., от
реализации 1 тыс. изделий Б – 700 тыс. р. Выпуск каждого количества изделий А и
Б (в тыс. штук) надо запланировать, чтобы прибыль от их реализации была
наибольшей. Составить модель и решить задачу.

Построим математическую модель:

Пусть
х(тыс. шт.) – искомое количество изделий А.

          
у(тыс.шт.) – искомое количество изделий Б.

Для
изготовления 1 тыс. изделий А и 1 тыс. изделий Б используется металла: 3∙х+1∙у.

Для
изготовления 1 тыс. изделий А и 1 тыс. изделий Б затрачивается электроэнергии:
3∙х+6∙у (тыс.кВт∙ч) 

Для
изготовления 1 тыс. изделий А и 1 тыс. изделий Б затрачивается рабочего
времени: 3∙х+3∙у (тыс.кВт∙ч)

Прибыль
от реализации 1 тыс. изделий А и 1 тыс. изделий Б: х∙500+у∙700 (тыс.р.)

Зададим ограничения:

Использование
металла: (3∙х+1∙у)≤32.

Затрата
электроэнергии: (3∙х+6∙у)≤54.

Затрата
рабочего времени: (3∙х+3∙у)≤36 (т.к. 20 рабочих по 1800 часов в год, получается
20∙1800=36000. Поэтому ставим число 36 тыс. часов).

Прибыль
должна быть максимальной, то есть х∙500+у∙700 = max

Решение задачи на компьютере:

Внести данные в таблицу

Найдём
оптимальное решение, для этого:

Выделим
целевую ячейку

Выбрать
Данные→Поиск решения

Установим
целевую ячейку, равную максимальному значению;

Укажем
изменяемые ячейки (количество изделий А и изделий В)

Добавить
записи ограничений (затраты на использование металла, расход на электроэнергию
и затраты рабочего времени)

Таким
образом, с помощью электронной таблицы найдено оптимальное решение для
максимизации дохода данного кооператива.

Работа
с данной надстройкой вызывает наибольшее затруднение, так как для того, чтобы
Excel смоделировал «осмысленное» значение, необходимо правильно отобрать
входные данные и определить все ограничения. Другими словами, правильно
построить математическую модель. Основные проблемы, с которыми сталкиваются при
решении задач на оптимизацию, это определение изменяемых ячеек и указание
ограничений. Необходимо обратить внимание на то, что параметры должны быть
прямо, или косвенно связаны с целевой ячейкой формулой.

Рассмотренные
задачи позволяют сделать акцент на практическую значимость  формализации
задачи,  способов решения задач с помощью электронных таблиц.

III. Оперирование знаниям. (Практическая самостоятельная работа).

(Цель: проверить умение применения знаний при решении практической
задачи)

В
оставшееся время мы выполним практическую самостоятельную работу. Скопировать
задачу на Лист2 и решить задачу: Кооператив из 20 человек выпускает А и Б.
Кооператив намерен получать прибыль не менее 6,5 млн.р. в год. Ему выделили 54
тыс. кВт∙ч электроэнергии. Какое минимальное количество металла потребуется
кооперативу, чтобы обеспечить нужную прибыль?

‑
Сохраните свои работы в личных папках

IV. Подведение итогов.

Итак, сегодня на уроке мы в очередной раз
убедились в многофункциональности возможностей компьютерной техники. А именно,
в возможностях электронных таблиц Excel. Мы увидели, что с помощью этой
программы можно решить оптимизационные задачи, вспомнили, как выбирается
оптимальная структура таблицы, как используются различные виды ссылок. Т.е.
цель нашего урока полностью достигнута.

В качестве домашнего задания я предлагаю вам
выбрать любую дисциплину и составить задачу оптимизации с использованием
программы MS Excel.