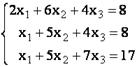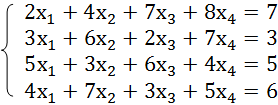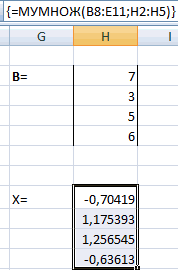Среда
MS
Excel
представляет собой набор инструментов
для обработки данных, как правило,
числовых. Ядром данной прикладной
программы являются функции MS
Excel
(финансовые, математические, статистические,
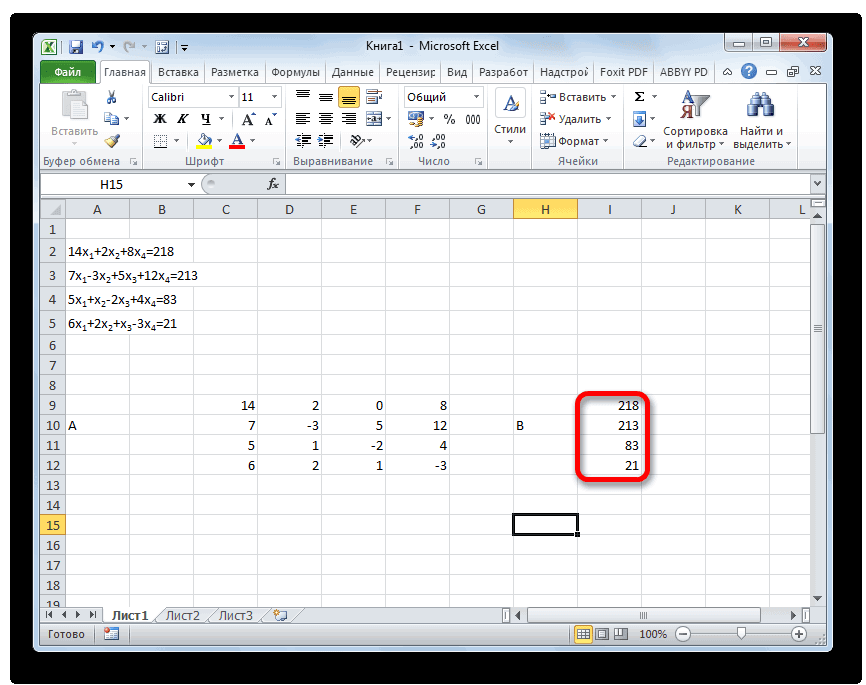
баз данных и т.д.), предназначение которых
ясно из названий. В этом параграфе мы
применим средства Excel
для выполнения действий над матрицами,
что, надеемся, облегчит студентам решение
задач.
Итак,
в Excel
существуют следующие функции действий
над матрицами:
МУМНОЖ
– возвращает произведение матриц
(матрицы хранятся в массивах). Результатом
является массив с таким же числом строк,
как массив 1, и с таким же числом столбцов,
как массив 2.
МОПРЕД
– возвращает определитель матрицы
(матрица хранится в массиве).
ТРАНСП
– транспонирование матрицы.
МОБР
– возвращает обратную матрицу для
матрицы, хранящейся в массиве.
Для
простейших действий над матрицами,
такими как:
-
сложение/вычитание
двух матриц; -
умножение
матрицы на число –
использование
встроенных функций MS
Excel
не требуется. Для выполнения арифметических
действий, но не над числами, а над
массивами чисел (матрицами), достаточно
составить необходимую формулу для
одного из элементов, а затем скопировать
ее для всех остальных. За счет индексации
(адреса) каждой ячейки листа MS
Excel
будет получен корректный результат.
Пример
2.15.
Найдем матрицу С = А + В и D
= 4*A,
где А и В – матрицы вида:

ввести значения матрицы А и В (рис. 2.1).
К оформлению никаких строгих правил
не предъявляется:
Рис.
2.1.
Исходные
данные для примера
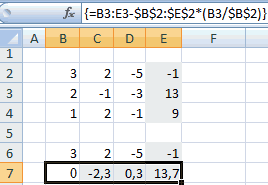
Для
нахождения матрицы С запишем в первый
элемент результирующей матрицы формулу.
Поскольку сложение матриц происходит
поэлементно, то первый элемент матрицы
С будет суммой первых элементов матриц
А и В (рис. 2.2).
Рис.2.2.
Сумма
первых элементов
После
нажатия клавиши «ENTER»
в первой ячейке области, отведенной под
матрицу С, появится результат сложения.
Формулу, составленную для первого
элемента, используем для нахождения
оставшихся элементов. Для этого формулу
необходимо скопировать и «забить» в
нужные ячейки. Копирование и вставку
можно провести тремя способами:
– поставив
курсор в первую клетку, вызвать в пункте
главного меню «Правка» подпункт
«Копировать/Вставить»;
– правой
кнопкой «мышки» нажать на первую ячейку
и в появившемся меню выбрать
«Копировать/Вставить»;
– воспользоваться
«горячими» клавишами: копировать –
Ctrl+C;
вставить – Ctrl+V.
После
копирования (занесения в буфер памяти)
формулы, необходимо выделить область
результирующей матрицы, в данном случае
3 клетки х 3 клетки, и вставить формулу
перечисленными тремя способами или
просто нажав клавишу «ENTER».
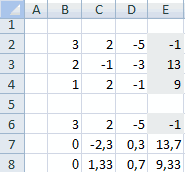
В
результате должна получиться результирующая
матрица С (рис. 2.3).
Рис.
2.3.
Результат
сложения матриц
Аналогичным
образом получим матрицу D
= 4*A
(рис. 2.4).
Рис.
2.4.
Результат
умножения матрицы на число
Все
перечисленные выше функции можно найти
в полном алфавитном списке функций MS
Excel,
который можно вызвать тремя способами:
– в
пункте главного меню «Вставка» выбрать
пункт «Функции» (рис. 2.5).
Рис.
2.5.
– нажатием
на панели инструментов иконки со значком
fх
(рис.
2.6).
Рис.
2.6.
– после
ввода в желаемую ячейку символа «=»
справа под панелью инструментов
появляется выпадающее меню, в котором
отображены последние 10 использованных
функций (рис. 2.7 и рис. 2.8).
Рис.
2.7
Рис.
2.8
Рассмотрим
использование данных функций на примерах.
Пример
2.16. Найти
произведение
матриц
А и В из примера 2.15.
Решение.
В
задаче перемножения матриц прежде всего
необходимо определить размерность
итоговой матрицы. В нашем случае, матрица
Е = А*В будет содержать 3 строки и 3 столбца.
На листе Excel
необходимо
выделить область 3х3 и в первой ячейке
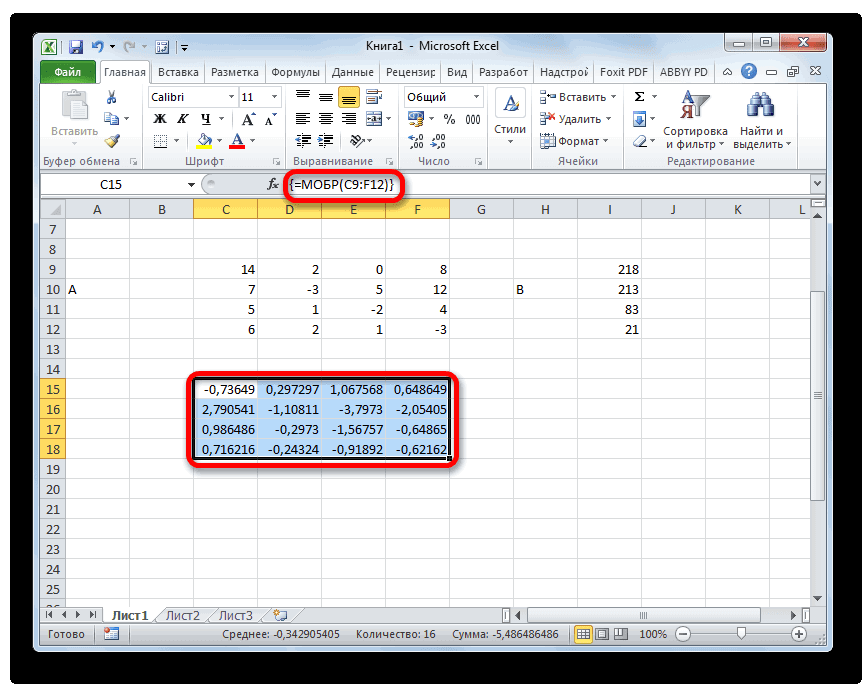
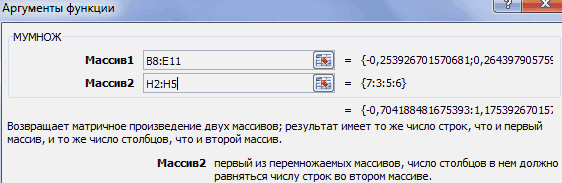
вызвать функцию МУМНОЖ (рис. 2.9).
Рис.
2.9.
Вызов
функции МУМНОЖ
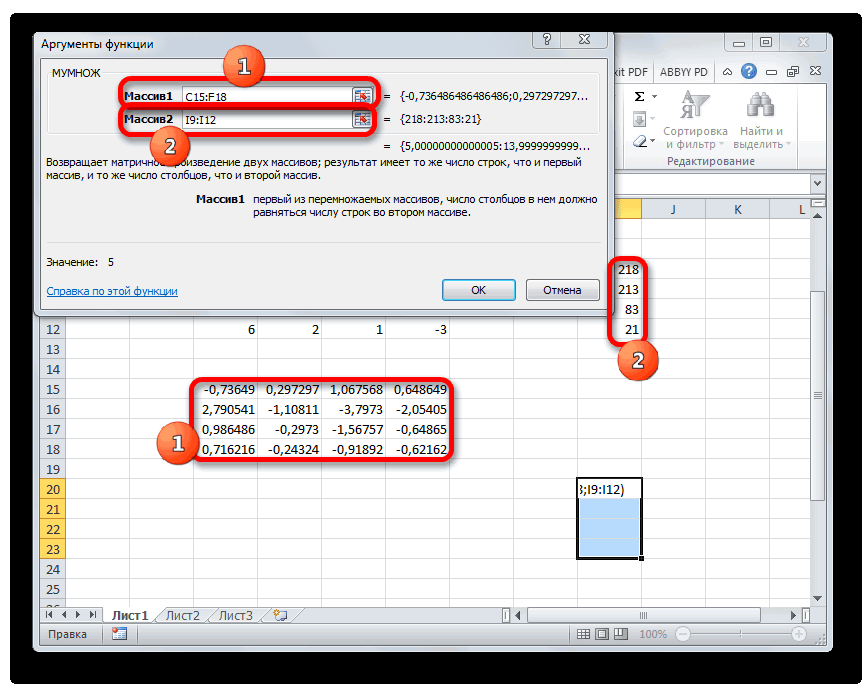
В
окне функции МУМНОЖ заносятся адреса
перемножаемых массивов. Для этого в
верхнем окне для адреса первого массива
необходимо нажать кнопку
и указать выделением на рабочем листе
расположение элементов первого массива
(рис. 2.10 и 2.11).
Рис.
2.10
Рис.
2.11
Аналогично
заполнить адрес второго массива в строке
«Массив 2» (рис. 2.12).
Рис.
2.12
Следующей
задачей является перенос полученных
результатов на рабочий лист. Поскольку
в данном действии результатом является
не одна ячейка, а девять, то вместо
клавиши «ENTER»
нажимается комбинация клавиш
Ctrl+Shift+Enter.
В результате должен получиться заполненный
массив Е (рис. 2.13).
Рис.
2.13
Аналогичным
образом производится работа с функцией
МОБР, которая служит для нахождения
обратной матрицы.
Пример
2.17. С
помощью Excel
найти обратную матрицу для матрицы В
из примера 2.15.
Решение.
Для
отыскания матрицы В-1
выделить на рабочем листе область 3х3 и
вызвать функцию МОБР. Синтаксис этой
функции предполагает адрес одного
массива (рис. 2.14).
Рис.
2.14.
Нахождение
обратной матрицы
В
результате нажатия комбинации клавиш
(поскольку требуется заполнить не одну
ячейку) Ctrl+Shift+Enter
в выделенной области будет размещаться
обратная матрица для массива В (рис.
2.15).
Рис.
2.15
Аналогично
выполняется транспонирование матрицы
с единственным отличием – используется
функция ТРАНСП.
Пример
2.18.
Найти определитель матрицы А из примера
2.15.
Решение.
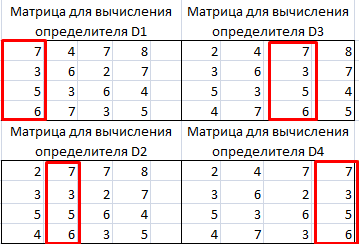
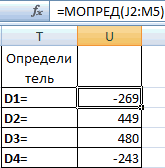
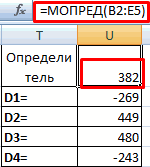
Для
нахождения определителей любых порядков
используется функция МОПРЕД. Поскольку
опредилитель – это число,
характеризующее квадратную матрицу,
нет необходимости в выделении области
для ответа. Решением будет число,
помещенное в одну ячейку (рис. 2.16).
Рис.
2.16.
Необходимо
помнить, что в случае, когда в результате
действий над матрицами ответом будет
являться массив, а не число, следует
следить за выполнением двух требований:
-
перед
вызовом функции выделять область, в
которой ожидается решение; -
после
заполнения необходимой информации в
окне таких функций, как МУМНОЖ, МОБР и
ТРАНСП, следует нажимать комбинацию
Ctrl+Shift+Enter.
Контрольные
вопросы
-
Дайте
определение матрицы. -
Перечислите
виды матриц. -
Какие
матрицы можно складывать, умножать? -
Дайте
определение n-мерного вектора. -
Является
ли вектор матрицей или наоборот? -
Что
такое минор Mij
матрицы А? -
Что
такое алгебраическое дополнение Aij? -
Что
такое определитель матрицы? -
Как
вычислить определитель квадратной
матрицы второго порядка, третьего
порядка? -
Для
всех ли матриц существует понятие
определителя? -
Дайте
определение обратной матрицы. -
Что
такое неособенная матрица? -
Как
вычислить обратную матрицу? -
Как
проверить, является ли матрица В обратной
к А? -
Запишите
СЛАУ в матричной форме. -
Как
решить СЛАУ методом Крамера? -
Как
решить СЛАУ методом обратной матрицы? -
Запишите
решение матричного уравнения AX = B. -
Какие
системы можно решать методом Гаусса? -
Какие
случаи возможны при решении СЛАУ? -
Что
такое однородная СЛАУ? -
Дайте
определение общего решения СЛАУ. -
Дайте
определение частного решения СЛАУ. -
Дайте
определение базисного решения СЛАУ. -
Сколько
базисных решений может иметь СЛАУ. -
Что
называется линейной комбинацией системы
векторов? -
Какая
система векторов называется
линейно-зависимой (независимой)? -
Что
называется базисом n-мерного пространства? -
Как
определить линейную зависимость или
независимость системы векторов? -
Как
перейти от одного базиса векторного
пространства к другому?
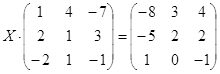
Задание
№2
Для
матриц А
и В
определить:
а)
3А
+
4В;
б)
АВ
– ВА;
в)
(А—В)-1.
Задание
№3
Вычислить
следующие определители:
Задание
№4
Решите
систему линейных уравнений двумя
способами (после решения необходимо
выполнить проверку):
-
по
формулам Крамера;
-
матричным
способом.
1)
2X1
+ 5X2
— 8X3
= 8 2) X1
+ 8X2
— 7X3
= 12
4X1
+ 3X2
— 9X3
= 9 2X1
+ 3X2
— 5X3
= 7
2X1
+ 3X2
— 5X3
= 7 6X1
+ 8X2
-17X3
= 17
3)
2X1
+ 3X2
— 5X3
= 7 4) 6X1
+ 6X2
-14X3
= 16
5X1
+11X2
-16X3
= 21 2X1
+ 5X2
— 8X3
= 8
4X1
+ 3X2
— 9X3
= 9 4X1
+ 3X2
+ 9X3
= 9
5)
-7X1
+ 3X2
+8X3
= 75 6) 13X1
— 6X2
= 32
9X1
— 4X2
= -3 8X1
+4X2
+ 1X3
= 12
X1
— 7X2
— 3X3
= 12 2X1
+ 9X2
+ 5X3
= -5
7)
7X1
— 4X2
= 61 
+ 3X2
+ 9X3
= -111
8X1
+9X2
— 6X3
= 48 -7X1
— 4X2
— 2X3
=
52
9X1
— 6X2
— 2X3
= 99 X1
— 7X2
+ 3X3
= -47
9)
-5X1
+ 7X2
+11X3
= -2 10) 2X1
+ X2
+ 3X3
= 11
2X1
+ 6X2
+ 3X3
= 11 3X1
+ 2X2
— 5X3
= -20
3X1
— 5X2
+ 4X3
= 11 5X1
— 2X2
+3X3
= -4
11)
2X1
+ 3X2
— 6X3
= 18 12) X1
+ 7X2
— 5X3
= 25
4X1
+ 3X2
— 9X3
= 9 X1
+ 3X2
— 5X3
= 15
2X1
+ 2X2
— 5X3
= 10 6X1
+ 8X2
-17X3
= 17
13)
2X1
+ 5X2
— 5X3
= 25 14) 6X1
+ 2X2
-X3
= 16
5X1
+11X2
-16X3
= 21 2X1
+ X2
— 8X3
= 36
4X1
+ 2X2
— X3
= 8 4X1
+ 3X2
+ 9X3
= 90
15)
-X1
+ 3X2
+8X3
= 24 16) 12X1
— 6X2
= 45
9X1
— 4X2
= -36 8X1
+X2
+ 7X3
= 56
X1
— 7X2
— 3X3
= 12 2X1
+ 9X2
+ 5X3
= -5
17)
7X1
— 4X2
= 60 18) 6X1
+ 2X2
+ 9X3
= -81
8X1
+9X2
— 3X3
= 48 -7X1
— 4X2
— 2X3
=
52
9X1
— 6X2
— 2X3
= 99 X1
— 5X2
+ 3X3
= -45
19)
-3X1
+ 7X2
+5X3
= -20 20) 2X1
+ 5X2
+ 3X3
= 110
2X1
+ 6X2
+ 2X3
= 120 3X1
+ 2X2
— 3X3
= -20
3X1
— 5X2
+ 4X3
= 90 5X1
— 12X2
+3X3
= -4
21)
2X1
+ 7X2
— 8X3
= 80 22) X1
+ 8X2
— 3X3
= 90
14X1
+ 3X2
— 9X3
= 90 2X1
+ 3X2
— 5X3
= 70
2X1
+ 3X2
— 5X3
= 70 X1
+ 8X2
-15X3
= 120
23)
2X1
+ 3X2
— X3
= 7 24) 6X1
+ 6X2
-X3
= 16
5X1
+5X2
-16X3
= 25 5X1
+ 5X2
— 8X3
= 80
X1
+ 3X2
— 9X3
= 9 4X1
+ 3X2
+ 9X3
= 90
25)
-7X1
+ 3X2
+8X3
= 64
9X1
— 4X2
= -30
X1
— 7X2
— 2X3
= 14
Задание
№5
Решить
системы линейных уравнений методом
Жордана–Гаусса
Вариант
№1 – решить системы №1, 6, 11
Вариант
№2 – решить системы №2, 7, 12
Вариант
№3 – решить системы №3, 8, 13
Вариант
№4 – решить системы №4, 9, 14
Вариант
№5 – решить системы №5, 10, 15
Вариант
№6 – решить системы №1, 7, 13
Вариант
№7 – решить системы №2, 8, 14
Вариант
№8 – решить системы №3, 9, 15
Вариант
№9 – решить системы №4, 10, 11
Вариант
№10 – решить системы №5, 6, 12
Вариант
№11 – решить системы №1, 7, 12
Вариант
№12 – решить системы №2, 9, 13
Вариант
№13 – решить системы №3, 10, 11
Вариант
№14 – решить системы №4, 8, 14
Вариант
№15 – решить системы №5, 9, 12
Вариант
№16 – решить системы №1, 8, 14
Вариант
№17 – решить системы №2, 10, 12
Вариант
№18 – решить системы №3, 9, 15
Вариант
№19 – решить системы №4, 7, 11
Вариант
№20 – решить системы №5, 6, 13
Вариант
№21 – решить системы №1, 6, 15
Вариант
№22 – решить системы №2, 8, 15
Вариант
№23 – решить системы №3, 6, 14
Вариант
№24 – решить системы №4, 10, 15
Вариант
№25 – решить системы №5, 7, 11
1.
2Х1
+ Х2
+ Х3
= 2 2. 2Х1
— Х2
+ 3Х3
= 3
Х1+3Х2
+ Х3
= 5 3Х1
+ Х2
— 5Х3
= 0
Х1
+Х2
+5Х3
= -7 4Х1
— Х2
+ Х3
= 3
2Х1+3Х2
— 3Х3
= 14 Х1
+ 3Х2
-13Х3
= -6
3.
Х1
+ Х2
+ Х3
+ Х4
= 6 4. 2Х1
— Х2
+ Х3
— Х4
= 1
Х1
+ Х2
— Х3
— Х4
= 0 2Х1
— Х2
— 3Х4
= 2
Х1
— Х2
+ Х3
— Х4
= 4 3Х1
— Х3
+ Х4
= -3
Х1
— Х2
— Х3
+ Х4
= 2 2Х1+2Х2
-2Х3+
5Х4
= -6
11Х1
-Х2
— Х3+
Х4
= -5
5.
Х1
+ Х2
+ Х3
+ Х4
= 0 6. Х1
+5Х2
— 9Х3
+ 8Х4
= 1
Х2
+ Х3
+Х4
+Х5
= 0 5Х1+18Х2
+ 4Х3
+ 5Х4
= 12
Х1
+2Х2
+3Х3
= 2 2Х1
+7Х2
+3Х3
+ 4Х4
= 5
Х2
+ Х3+3Х4
= -2 1Х1
+3Х2
+5Х3
— 2Х4
= 3
Х3+2Х4
+Х5
= 2
7. 2Х1
+ 3Х2
+ 9Х3
-7Х4
= 3 8. 9Х1
+4Х2
+ Х3
+ 7Х4
= 2
8Х1
+12Х2
— 9Х3
+8Х4
= 3 2Х1+
7Х2
+ 3Х3
+ Х4
= 6
4Х1
+ 6Х2
+
3Х3
— 2Х4
= 3 3Х1
+5Х2
+2Х3
+ 2Х4
=4
2Х1+
3Х2
— Х3
+
Х4
= 1
9.
2Х1
— 3Х2
— 11Х3
-15Х4
= 1 10. 9Х1+12Х2
+ 3Х3
+10Х4
= 13
2Х1
— 3Х2
+ 5Х3
+ 7Х4
= 1 3Х1+
4Х2
+ Х3
+ 2Х4
= 3
4Х1
— 6Х2
+
2Х3
+ 3Х4
= 2 6Х1
+ 8Х2
+2Х3
+ 5Х4
= 7
11.
7Х1
— 4Х2
+ Х3
+ 3Х4
= 5 12. 3Х1+3Х2
+ 5Х3
-2Х4+3Х5
= 1
3Х1
—
5Х2
+2Х3
+4Х4
= 2 2Х1+2Х2
+ 4Х3
-Х4
+3Х5
= 2
5Х1
+ 7Х2
— 4Х3
— 6Х4
= 3 Х1
+ Х2
+
3Х3
-2Х4+5Х5
= 1
2Х1+2Х2
+
8Х3
-3Х4+9Х5
= 2
13.
Х1
+ 2Х2
+ 3Х3
= 2 14. Х1
+
Х2
— 3Х3
= -1
Х1
+
Х2
+ 2Х3
= 1 2Х1
+
Х2
— 2Х3
= 1
3Х1
+ 5Х2
+ 8Х3
= 0 Х1
+ Х2
+
Х3
= 3
-Х1
+ Х2
+ 4Х3
= 2 Х1
+2Х2
-3Х3
= 1
15.
2Х1
— Х2
+ Х3
— 3Х4
= 4
3Х1
—
2Х2
+2Х3
— 3Х4
= 2
2Х1
+ Х2
— Х3
+ Х4
= 1
5Х1
+ Х2
— Х3
+ 2Х4
= 1
Задание
№6
В
естественном базисе заданы векторы.
Установить, составляют ли они базис.
Если составляют, то найти связь между
новым и старым базисами, а также в новом
базисе найти компоненты вектора
.
Для
вариантов 1–10
Для
вариантов 11–20
Для
вариантов 21–30
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Решение задач линейной алгебры в Ms Excel
Содержание
Введение
1. Метод Гаусса и одно из его приложений в экономике (задача
о рационе)
1.1 Простейшая задача о рационе
.2 Метод Гаусса
.3 Метод Гаусса в Excel
2. Модель Леонтьева межотраслевого баланса
. Метод наименьших квадратов (МНК)
3.1 Алгебраический метод наименьших квадратов
3.1.1 Анализ данных эксперимента
3.2 МНК в Excel
Заключение
Список литературы
Введение
Данная работа посвящена решению задач линейной алгебры в Excel,точнее решению систем линейных
уравнений. Будут рассмотрены три метода: метод Гаусса, метод, основанный на
нахождении обратной матрицы и метод наименьших квадратов.
В первом параграфе работы в качестве примера использования систем
линейных уравнений в экономике приведена простейшая задача о рационе и её
решение методом Гаусса в частном случае, когда количество неизвестных совпадает
с количеством уравнений.
Во втором параграфе рассматривается модель Леонтьева межотраслевого
баланса. Это модель, позволяющая анализировать состояние экономики и
моделировать различные сценарии ее развития. Возникающая в этом методе система
линейных уравнений традиционно решается нахождением обратной матрицы. Чтобы
пояснить, запишем модель Леонтьева в матричной форме:
(E-A)*X=Y
Если у нас имеется матрица (Е-А)-1 ,то умножая обе части
равенства на эту матрицу, получим: Х=(Е-А)-1*У.
Третий параграф описывает решение задач, сводящихся к решению систем
линейных уравнений, при помощи МНК (метода наименьших квадратов).
В каждом параграфе будет приведена реализация в Excel.
. Метод Гаусса и одно из его приложений в экономике (задача о
рационе)
1.1 Простейшая задача о рационе
Формулировка задачи. Допустим, на ферме занимаются выращиванием телят.
Известно, что для хорошего роста теленка в день ему необходимо потреблять m веществ в количестве ,…,
соответственно.
На ферму ежедневно завозится n кормов в количестве,…,
. Известно, что доля итогового вещества в j-ом корме равна
. Тогда общее количество вещества
определяется по формуле
(слагаемое — количество итогового вещества в j корме; i=1,…,n).
В результате получаем систему
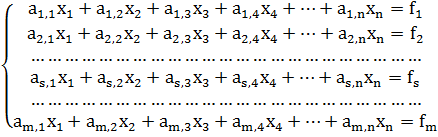
Если m ≠n ,то система называется прямоугольной и методы её решения
рассматриваются в другом параграфе. В данном случае будем считать, что m=n. Такая система является квадратной и к ней применим метод
Гаусса.
1.2 Метод Гаусса
Алгоритм Метода Гаусса состоит из двух основных частей: прямой ход и
обратный ход.
Прямой ход заключается в том, что система приводится к треугольному виду
(верхняя унитреугольная форма). Обратный ход — непосредственное нахождение
неизвестных. Причем, корни находятся в обратном порядке: сначала , затем
и т.д.
) Прямой ход состоит из следующих шагов.
На первом шаге элементарными преобразованиями исключается из всех уравнений, начиная со
второго.
Второй шаг заключается в исключение из всех уравнений, начиная с
третьего.
На s шаге исключается из всех уравнений,
начиная с s+1 (s=1,…,n-1).
При этом каждый шаг начинается с обработки s уравнения: строка под номером sделится на,чтобы коэффициент при
стал равен 1.
Описанный алгоритм носит циклический характер.
После завершения этого процесса получаем систему:
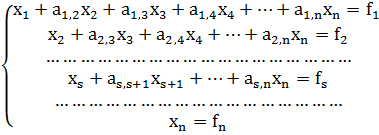
) Обратный ход.
В результате выполнения алгоритма прямого хода система (1) приняла
треугольный вид (2). Для нахождения решения остается из системы (2) найти ,
, …,
. Метод нахождения достаточно
очевиден: из последнего уравнения находим .
Затем, подставив найденное значение в (n-1)-ое уравнение, найдем
, и т.д. Таким образом, s-ое неизвестное
находим из s-го уравнения:
. 1.0.
Причем, если условиться считать, что значение суммы, в которой нижний
индекс суммирования больше верхнего (пустая сумма), равно нулю, в формуле 1.0.
можно считать, что индекс s
принимает натуральные значения от n до 1.
1.3 Метод Гаусса в Excel
В Excel Метод Гаусса подробно (по шагам)
выполняется только в учебных целях, когда нужно показать, что Вы это умеете.
Существует более рациональный способ реализации данного метода в Excel.
Решим задачу о рационе в Excel.
Формулировка:
Допустим, на ферме занимаются выращиванием телят. Известно, что для
хорошего роста теленка в день ему необходимо потреблять 4 вещества в количестве
,
,
,
соответственно.
На ферму ежедневно завозится 4 корма в количестве ,…,
. Известно, что доля итогового
вещества в j-ом корме равна . Тогда общее количество вещества
определяется по формуле
=
(слагаемое — количество итогового вещества в j корме; i=1,…,n).
В результате получаем систему
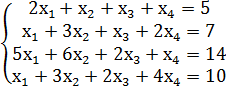
Введем исходные данные в Excel:
Отображение в режиме формул:
Где А — матрица коэффициентов,
F-
вектор свободных членов,
F’
содержит формулу, вычисляющую левую часть уравнения.
Далее для нахождения корней составленной системы линейных уравнений
воспользуемся функцией Поиск решения:
Результат вычислений:
2. Модель Леонтьева межотраслевого баланса
Макроэкономика функционирования многоотраслевого хозяйства требует
баланса между отдельными отраслями. Каждая отрасль, с одной стороны, является
производителем, а с другой — потребителем продукции, выпускаемой другими
отраслями. Возникает довольно непростая задача расчета связи между отраслями
через выпуск и потребление продукции разного вида. Впервые эта проблема была
сформулирована в виде математической модели в 1936 г. в трудах известного
американского экономиста В.В.Леонтьева, который попытался проанализировать
причины экономической депрессии США 1929-1932 гг. Эта модель основана на
алгебре матриц.
Суть сводится к следующему.
Основу информационного обеспечения модели межотраслевого баланса
составляет технологическая матрица, содержащая коэффициенты прямых материальных
затрат на производство единицы продукции. Эта матрица является также основой
экономико-математической модели межотраслевого баланса. Предполагается, что производствао единицы продукции в j-й отрасли требует определенное
количество затрат промежуточной продукции i-й отрасли, равное аij. Оно не зависит от объема
производства в отрасли и является довольно стабильной величиной во времени.
Величины аij называются коэффициентами
прямых материальных затрат и рассчитываются следующим образом:
Коэффициент прямых материальных затрат показывает, какое количество
продукции i-й отрасли необходимо, если учитывать
только прямые затраты, для производства единицы продукции j-й отрасли.
Систему уравнений баланса можно переписать в виде
Если ввести в рассмотрение матрицу коэффициентов прямых материальных
затрат А= (аij),
вектор-столбец валовой продукции X и вектор-столбец
конечной продукции Y:
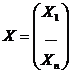
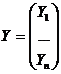
то система уравнений в матричной форме примет вид:
Х=АХ + У.
Полученная система уравнений называется экономико-математической моделью
межотраслевого баланса (моделью Леонтьева, моделью «затраты-выпуск»).
С помощью этой модели можно выполнять три варианта расчетов:
o Задав в модели величины валовой продукции каждой отрасли (Xi), можно определить объемы конечной
продукции каждой отрасли (Yi):
= (Е —
А)Х (2).
o Задав величины конечной продукции всех отраслей (Уг),
можно определить величины валовой продукции каждой отрасли (Х)
o Для ряда отраслей задав величины валовой продукции, а для
всех остальных отраслей задав объемы конечной продукции, можно найти величины
конечной продукции первых отраслей и объемы валовой продукции вторых.
В формулах Е обозначает единичную матрицу n-го порядка, а (Е — А)-1 обозначает матрицу,
обратную к матрице (Е — А). Если определитель матрицы (Е — А) не равен нулю,
т.е. эта матрица невырожденная, то обратная к ней матрица существует. Обозначим
эту обратную матрицу через В=(Е -А)-1, тогда систему уравнений в
матричной форме (2) можно записать в виде
= ВY.
Элементы матрицы В будем обозначать через bij, тогда из матричного уравнения для
любой i-й отрасли можно получить следующее
соотношение:
Из последних соотношений следует, что валовая продукция выступает как
взвешенная сумма величин конечной продукции, причем весами являются коэффициенты
bij, которые показывают, сколько всего
нужно произвести продукции i-й
отрасли для выпуска в сферу конечного использования единицы продукции j-й отрасли. В отличие от
коэффициентов прямых затрат аij коэффициенты bij называются коэффициентами полных материальных затрат и
включают в себя как прямые, так и косвенные затраты всех порядков. Если прямые
затраты отражают количество средств производства, израсходованных
непосредственно при изготовлении данного продукта, то косвенные относятся к
предшествующим стадиям производства и входят в производство продукта не прямо,
а через другие (промежуточные) средства производства.
Пример нахождения вектора валовой продукции
Для трехотраслевой экономической системы заданы матрица коэффициентов
прямых материальных затрат и вектор конечной продукции:
Найти вектор валовой продукции.
Решение.
1. Определим матрицу коэффициентов полных материальных затрат.. Находим
матрицу (Е-А)
b. Вычисляем определитель этой матрицы
c. Транспонируем матрицу (Е-А)
d. Находим алгебраические дополнения для элементов матрицы (Е-А)’
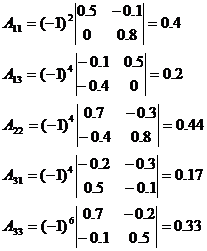
Таким образом, присоединенная матрица имеет вид:
e. Находим матрицу коэффициентов полных материальных затрат:
2. Найдем величины валовой продукции трех отраслей (вектор X),:
Нахождения вектора валовой продукции в Excel.
Модель Леонтьева межотраслевого баланса в режиме формул:
Результаты расчетов представленной модели:
Искомый вектор валового выпуска отраслей занимает диапазон Е12:Е14.
В процессе решения задачи использовались следующие функции:
. МОБР — возвращает обратную матрицу для матрицы, хранящейся в массиве.
Синтаксис: МОБР (массив).
Массив — числовой массив с равным количеством строк и столбцов.
После введения функции в левую верхнюю ячейку диапазона массива следует
выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а
затем нажать клавиши CTRL+SHIFT+ENTER.
. МУМНОЖ — возвращает произведение матриц (матрицы хранятся в массивах).
Результатом является массив с таким же числом строк, как массив1 и с таким же
числом столбцов, как массив2.
Синтаксис: МУМНОЖ(массив1;массив2).
Массив1, массив2 — перемножаемые массивы.
После введения функции в левую верхнюю ячейку диапазона массива следует
выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а
затем нажать клавиши CTRL+SHIFT+ENTER.
3. Метод наименьших квадратов (МНК)
Система m линейных уравнений с n неизвестными имеет вид:
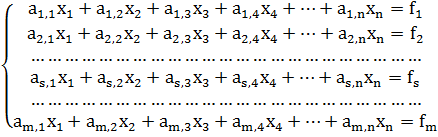
Возможны три случая: m<n, m=n, m>n. Случай, когда m=n, рассматривался в предыдущих
параграфах. При m<n, если система mлинейных уравнений с nнеизвестными является совместной, то
она не определена и имеет бесконечно много решений.
В случае, если m>nи система является совместной, то
матрица А имеет по крайней мере m — nлинейно зависимых строк. Здесь
решение может быть получено отбором n любых линейно независимых уравнений (если они существуют)и применением
формулы Х=А-1×В, то есть, сведением задачи к ранее решенной. При
этом полученное решение всегда будет удовлетворять и остальным m — nуравнениям.
Однако при применении компьютера удобнее использовать более общий подход
— метод наименьших квадратов.
.1
Алгебраический метод
наименьших квадратов
Под алгебраическим методом наименьших квадратов понимается метод решения
систем линейных уравнений
Ax∼= B (1.1)
путем минимизации евклидовой нормы
‖Ax − b‖ → inf . (1.2)
3.1.1
Анализ данных эксперимента
Рассмотрим некоторый эксперимент, в ходе которого в моменты времени
<
<… <
производится, например, измерение температуры Q(t). Пусть результаты
измерений задаются массивом
,
, …,
.
Допустим, что условия проведения эксперимента таковы, что измерения
проводятся с заведомой погрешностью. В этих случаях закон изменения температуры
Q(t) ищут с помощью некоторого полинома
(t) = +
+
+ … +
,
определяя неизвестные коэффициенты ,
, …,
из тех соображений, чтобы величина E(
, …,
), определяемая равенством
гаусс алгебраический exel аппроксимация
E(,…,
) =
Если заменить P(t) его выражением, то получим
=
Поставим задачу определения массива так, чтобы величина
была минимальна, т.е. определим
массив методом наименьших квадратов. Для
этого приравняем частные производные по
к нулю:
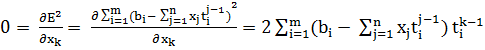
Если ввести m × n матрицу A = (), i = 1, 2…, m; j = 1, 2, …, n,
где
=
, i = 1, 2…, m; j = 1, 2, …, n,
то выписанное равенство примет вид
(k=1,2,…,n)
(k=1,2,…,n)
Перепишем написанное равенство в терминах операций с матрицами. Имеем по
определению умножения матрицы на столбец
Для транспонированной матрицы аналогичное соотношение выглядит так
Введем обозначение: i -ую
компоненту вектора Ax будем
обозначать В соответствии с выписанными матричными равенствами будем
иметь
=
(k=1,2,…,n)
В матричной форме это равенство перепишется в виде
ATx=ATB
(1.3)
Здесь A — прямоугольная m× n матрица. Причем в задачах
аппроксимации данных, как правило, m > n. Уравнение (1.3) называется
нормальным уравнением.
Можно было с самого начала, используя евклидову норму векторов, записать
задачу в эквивалентной матричной форме:
=
=
=
Наша цель минимизировать эту функцию по x. Для того чтобы в точке решения
достигался минимум, первые производные по x в этой точке должны равняться нулю.
Производные данной функции составляют
−2ATB + 2ATAx
и поэтому решение должно удовлетворять системе линейных уравнений
(ATA)x = (ATB).
Эти уравнения называются нормальными уравнениями. Если A — m×
n матрица, то A>A — n
×
n — матрица, т.е.
матрица нормального уравнения всегда квадратная симметричная матрица. Более
того, она обладает свойством положительной определенности в том смысле, что
(A>Ax, x) = (Ax, Ax) ≥ 0.
Замечание. Иногда решение уравнения вида (1.3) называют решением систе-
мы Ax = В, где A прямоугольная m × n (m > n) матрица методом наименьших
квадратов.
Задачу наименьших квадратов можно графически интерпретировать как
минимизацию вертикальных расстояний от точек данных до модельной кривой (см.
рис.1.1). Эта идея основана на предположении, что все ошибки в аппроксимации
соответствуют ошибкам в наблюдениях. Если имеются также ошибки в
независимых переменных , то может оказаться более уместным минимизировать евклидово
расстояние от данных до модели.
рис.1.1.
3.2 МНК в Excel
Приведенный ниже алгоритм реализации МНК в Excel подразумевает, что все исходные данные уже известны.
Обе части матричного уравнения A×X=B системы умножаем
слева на транспонированную матрицу системы АТ:
АТАХ=АТВ
Затем обе части уравнения умножаем слева на матрицу (АТА)-1.
Если эта матрица существует, то система определена. С учетом того, что
(АТА)-1*(АТА)=Е, получаем
Х=(АТА)-1АТВ.
Полученное матричное уравнение является решением системы m линейных уравнений с nнеизвестными при m>n.
Рассмотрим применение вышеописанного алгоритма на конкретном примере.
Пример. Пусть необходимо решить систему
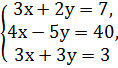
Решение.
В Excelлист с решением в режиме отображения
формул для данной задачи выглядит следующим образом:
Результаты расчетов:
Искомый вектор Х расположен в диапазоне Е11:Е12.
При решении заданной системы линейных уравнений использовались следующие
функции:
. МОБР — возвращает обратную матрицу для матрицы, хранящейся в массиве.
Синтаксис: МОБР(массив).
Массив — числовой массив с равным количеством строк и столбцов.
После введения функции в левую верхнюю ячейку диапазона массива следует
выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а
затем нажать клавиши CTRL+SHIFT+ENTER.
. МУМНОЖ — возвращает произведение матриц (матрицы хранятся в массивах).
Результатом является массив с таким же числом строк, как массив1 и с таким же
числом столбцов, как массив2.
Синтаксис: МУМНОЖ(массив1;массив2).
Массив1, массив2 — перемножаемые массивы.
После введения функции в левую верхнюю ячейку диапазона массива следует
выделить массив, начиная с ячейки, содержащей формулу, нажать клавишу F2, а
затем нажать клавиши CTRL+SHIFT+ENTER.
. ТРАНСП — преобразует вертикальный набор ячеек в горизонтальный, или
наоборот. В результате использования этой функции появляется массив с числом
строк, равным числу столбцов исходного массива, и числом столбцов, равным числу
строк начального массива.
Заключение
В курсовой работе описаны некоторые классические ([4],[7]) методы решения
систем линейных уравнений. Описан также метод наименьших квадратов и решение
системы с прямоугольной матрицей, в которой число уравнений больше, чем число
неизвестных. Решение этой системы также свелось к решению методом Гаусса
системы с квадратной матрицей, получаемой из исходной системы умножением обеих
частей на транспонированную матрицу.
Следует отметить ( см. [2], [3], [4], [6], [7]), что в современных
научных вычислениях в основном фигурируют методы решения больших, т.е. с
размерностью более 1000, систем линейных алгебраических уравнений. В указанных
книгах описаны существенно более изощренные методы решения алгебраических
систем, для реализации которых на Excel’е требуется написание на языке Visual Basic новых
макросов. Но, так как для решения больших систем Excel не пригоден в связи с низкой производительностью, то
реализация этих методов в Excel
не имеет смысла.
Список литературы
[1] Гельман В.Я. Решение математических задач средствами
Excel.-Москва-
Санкт-Петербург : Питер,2003.
[2] Каханер Д. Моулер К., Нэш С. Численные методы и
программное обеспечение.-М.: Мир, 1998.
[3] Кормен Т., Лейзерсон Ч., Ривест Р. АЛГОРИТМЫ (построение
и анализ). — М.: МЦНМО, 2000.
[4] Райс Дж. Матричные вычисления и математическое
обеспечение.- М.: Мир, 1984.
[5] Васильев А.Н. Научные вычисления в Microsoft Excel .-
Москва-Киев: Диалектика, 2004.
[6] Форсайт Дж., Малькольм М., Моулер К. Машинные методы
математических вычислений. — М.:Мир, 1980.
[7] Press W.H., Teukolsky S.A., Flannery B.P.
Numerical Recipes in C.- Cambridge University Press, 1991.
Цель работы: познакомиться с приемами решения задач линейной алгебры.
Типичными задачами линейной алгебры являются задачи, связанные с решением систем линейных уравнений. При этом приходится работать с массивами чисел. Для их обработки в Excel предусмотрен ряд математических функций:
- МОПРЕД(массив) — функция для нахождения определителя квадратной матрицы. Здесь массив — числовой массив с равным количеством строк и столбцов;
- МОБР(массив) — функция для нахождения обратной матрицы. Здесь массив — числовой массив с равным количеством строк и столбцов;
- МУМНОЖ(массив1;массив2) — функция для нахождения произведения массива1на массив2.Результатом является массив с таким же числом строк, как массив1, и с таким же числом столбцов, как массив2. При этом если обозначить буквой С результат произведения двух массивов А и В, то элементы массива С определяются по формуле
, где i — номер строки, а j — номер столбца;
- ТРАНСП(массив) — функция для транспонирования массива ячеек на рабочем листе. Транспонирование массива заключается в том, что первая строка массива становится первым столбцом нового массива, вторая строка массива становится вторым столбцом нового массива и т.д.
Особенностью вычислений, связанных с массивами, является то, что результат вычисления распространяется в виде формулы на целый блок ячеек. Такие формулы называются формулами массива. При вводе формул массива необходимо соблюдать определенную последовательность действий:
Шаг 1. Сначала формула вводится в первую ячейку результирующего массива.
Шаг 2.Выделяется весь блок ячеек результирующего массива.
Шаг 3.Нажимается клавишаклавиатуры.
Шаг 4.Нажимается комбинация клавиш Ctrl+Shift+Enter. При этом формула распознается как формула массива и заключается в фигурные скобки { }.
Важно!
При работе с массивами чисел всегда контролируйте размерность результирующего массива!
ЗАДАНИЕ 1. Решение задач линейной алгебры
Рассмотрим решение некоторых задач линейной алгебры на простейших примерах. Пусть дана квадратная матрица 3-го порядка 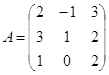
- Найдите матрицу А-1, обратную к данной матрице А.
- Найдите определитель матрицы А.
- Проверьте, что найденная матрица А-1 действительно является обратной для матрицы А.
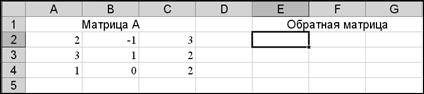
1. Откройте чистый рабочий лист. Переименуйте его в Обратная матрица.
2. Заполните рабочий лист исходными данными, как показано на рис. 14:
Рис. 14
3. Установите курсор в ячейку Е2 и введите формулу =МОБР(А2:С4). После нажатия клавиши Enter в ячейке Е2 появится число 0,4.
4. Для получения обратной матрицы формулу в этом примере необходимо ввести как формулу массива. Для этого выделите диапазон ячеек Е2:G4, соответствующий обратной матрице (размерность матрицы А-1 очевидно будет такая же, как и у матрицы А). Нажмите клавишу , а затем комбинацию клавиш Ctrl+Shift+Enter. В результате ячейки Е2:G4 будут заполнены элементами обратной матрицы.
5. В ячейку А6 введите текст Определитель(A).
6. Установите курсор в ячейку В6 и введите формулу = МОПРЕД(А2:С4). Нажмите клавишу Enter. В ячейке должно получиться значение определителя матрицы А, равное 5. Внимание!В этом случае формулу для расчета определителя не нужно вводить как формулу массива, так как определитель является не массивом, а одним числом.
7. Для проверки правильности нахождения обратной матрицы вспомним, что должно выполняться условие: А А-1=Е, где Е — единичная матрица того же порядка, что и матрица А. Установите курсор в ячейку Е6 и введите текст Произведение матриц.
8. В ячейку Е7 введите формулу = МУМНОЖ(А2:С4; Е2:G4). Нажмите клавишу Enter.
9. Формулу в этом случае также вводим как формулу массива. В результате ячейки Е7:G9 будут заполнены элементами единичной матрицы (по главной диагонали будут записаны 1, остальные элементы будут равны 0). Если числа имеют много десятичных знаков, то выделите ячейки Е7:G9 и уменьшите разрядность либо при помощи команды меню Формат/Ячейки/закладка Число, либо при помощи кнопки Уменьшить разрядность 
ТЕСТОВОЕ ЗАДАНИЕ 1. Решение систем линейных уравнений
Вариант вашего задания задает преподаватель!
Откройте чистый рабочий лист. Переименуйте его в Тест 1.Решите систему линейных уравнений (см. табл. 5) по формулам Крамера.
Формулы Крамера имеют вид:
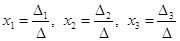
Здесь D- определитель системы, а Di — вспомогательный определитель, который получается из исходного определителя D путем замены i-го столбца на столбец свободных членов уравнений системы.
Таблица 5
| № | Решить систему | № | Решить систему |
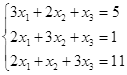 |
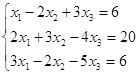 |
||
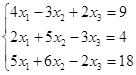 |
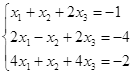 |
||
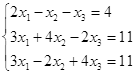 |
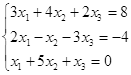 |
||
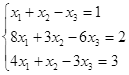 |
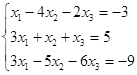 |
||
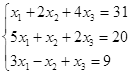 |
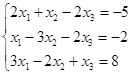 |
||
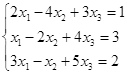 |
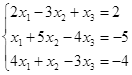 |
||
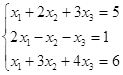 |
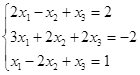 |
||
 |
 |
||
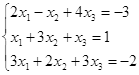 |
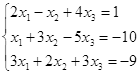 |
||
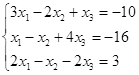 |
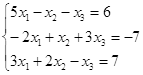 |
||
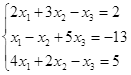 |
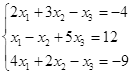 |
||
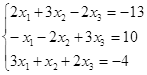 |
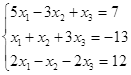 |
||
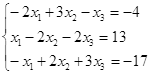 |
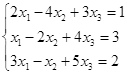 |
||
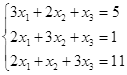 |
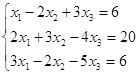 |
||
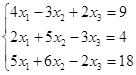 |
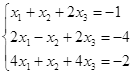 |
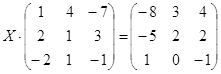
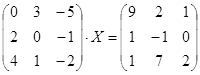
ТЕСТОВОЕ ЗАДАНИЕ 2. Решение уравнений, записанных в матричной форме
Вариант вашего задания задает преподаватель!
Откройте чистый рабочий лист. Переименуйте его в Тест 2.Решите матричные уравнения, выбрав свой вариант из таблицы 6.
Примечание. Заданное уравнение нужно свести к одному из двух видов:
1) А Х=В, здесь решение находится по формуле Х=А-1 В
или
2) Х А =В, в этом случае решение находится по формуле Х=В А-1.
Если исходное уравнение имеет вид С Х А =В, то его предварительно приведите к виду: Х А = С-1 В, рассчитайте правую часть системы и затем воспользуйтесь предложенными формулами для нахождения решения системы.
Таблица 6
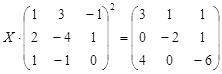
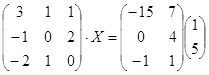
| № | Уравнение | № | Уравнение |
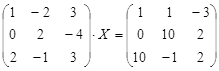 |
 |
||
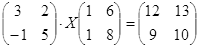 |
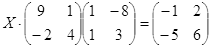 |
||
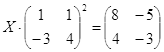 |
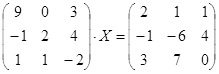 |
||
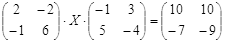 |
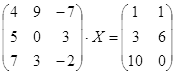 |
||
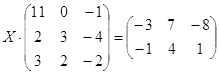 |
 |
||
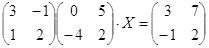 |
 |
||
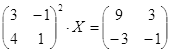 |
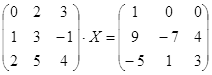 |
||
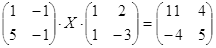 |
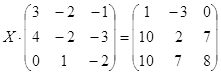 |
||
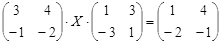 |
 |
||
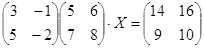 |
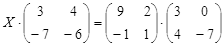 |
||
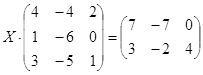 |
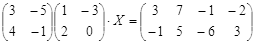 |
||
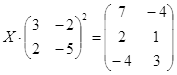 |
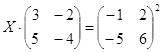 |
||
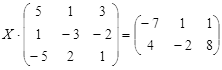 |
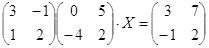 |
||
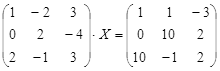 |
 |
||
 |
 |
Статьи к прочтению:
- Лабораторная работа № 6. шифрование данных на жестком диске при помощи системы pgp
- Лабораторная работа №6. создание idef3-диаграммы
Курс Excel_Базовый — Урок №8. Абсолютные и относительные ссылки
Похожие статьи:
-
Лабораторная работа №1. основы работы с программой ms excel
САМАРСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ПУТЕЙ СООБЩЕНИЯ Кафедра информатики ИНФОРМАТИКА Табличный процессор MS Excel Методические указания к выполнению…
-
Лабораторная работа №5. вычисление сумм и произведений в ms excel
Цель работы: познакомиться с возможностями организации циклических вычислений на примере расчетов сумм и произведений. Обычно при расчетах сумм или…
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
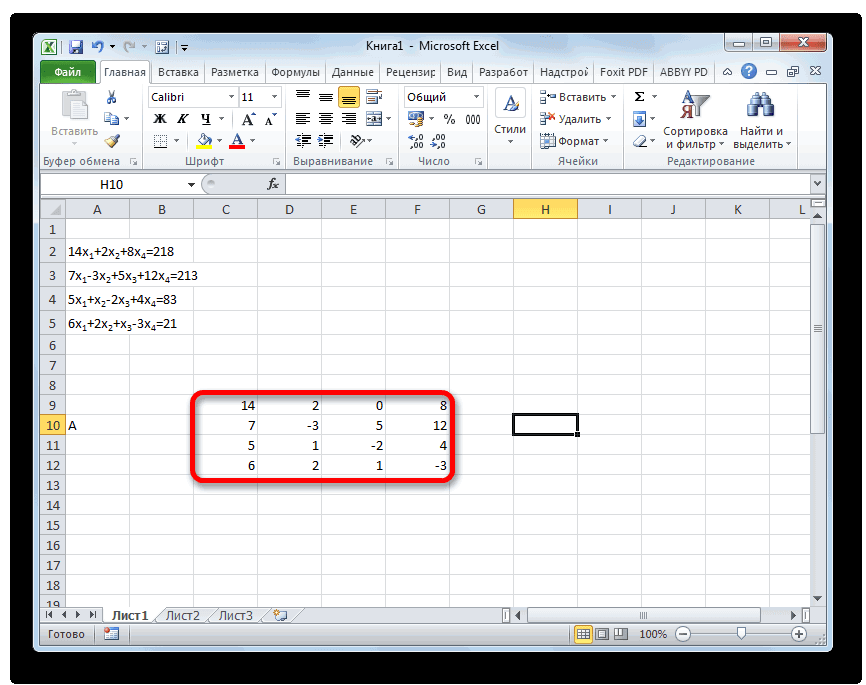
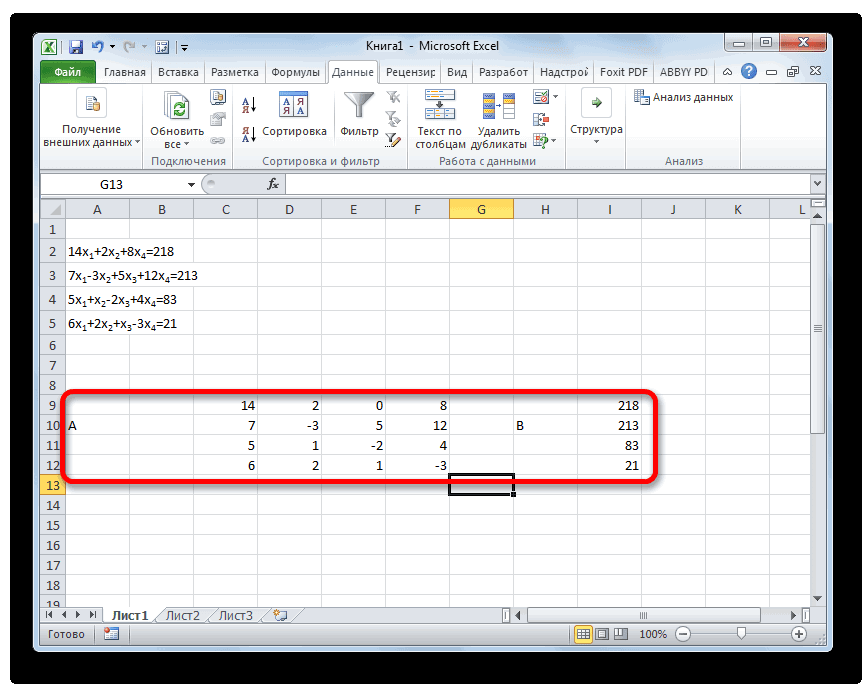
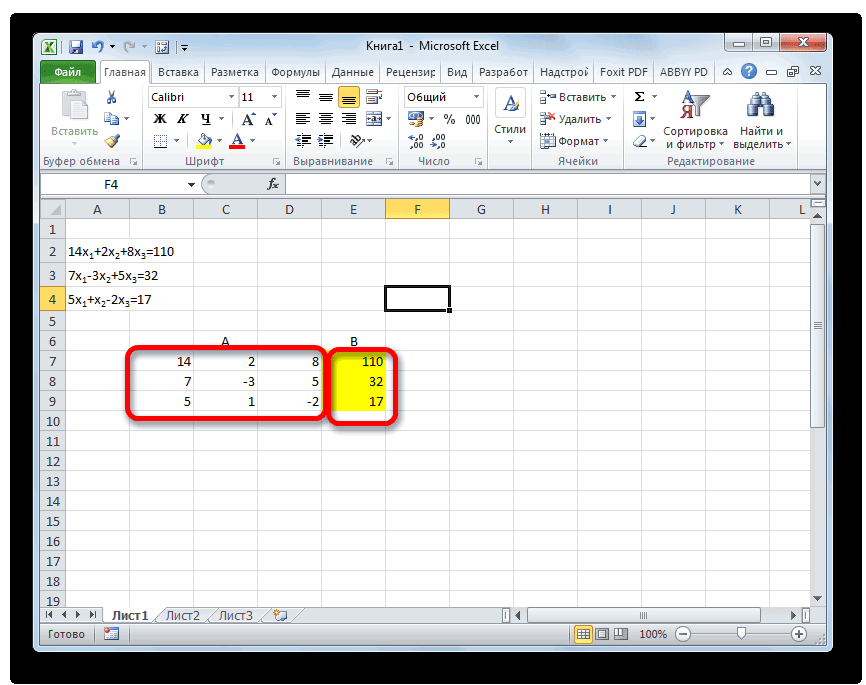
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
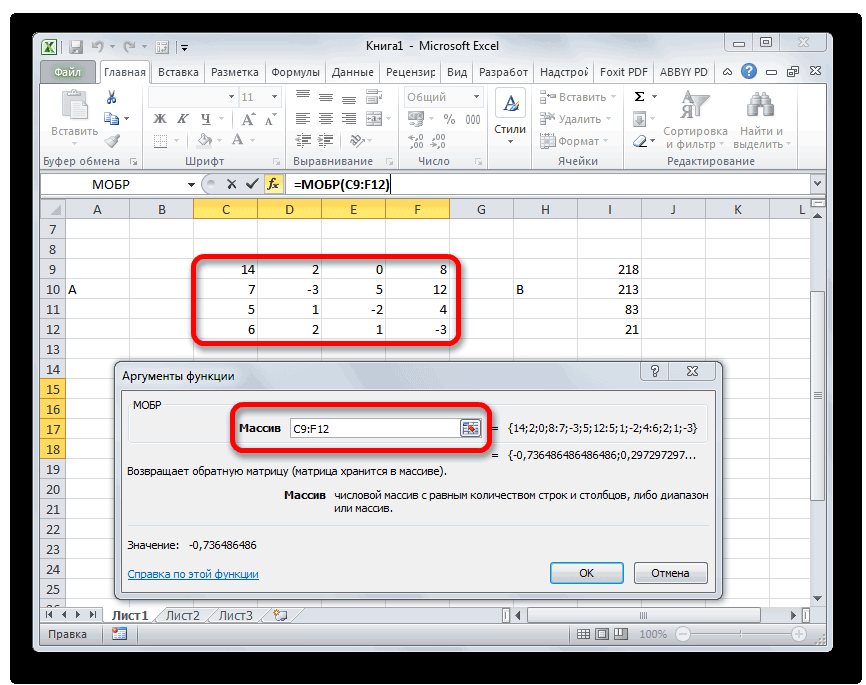
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
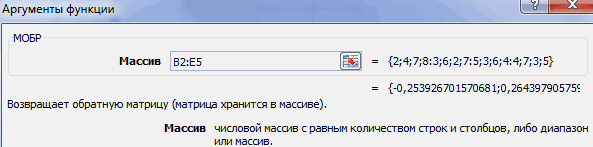
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
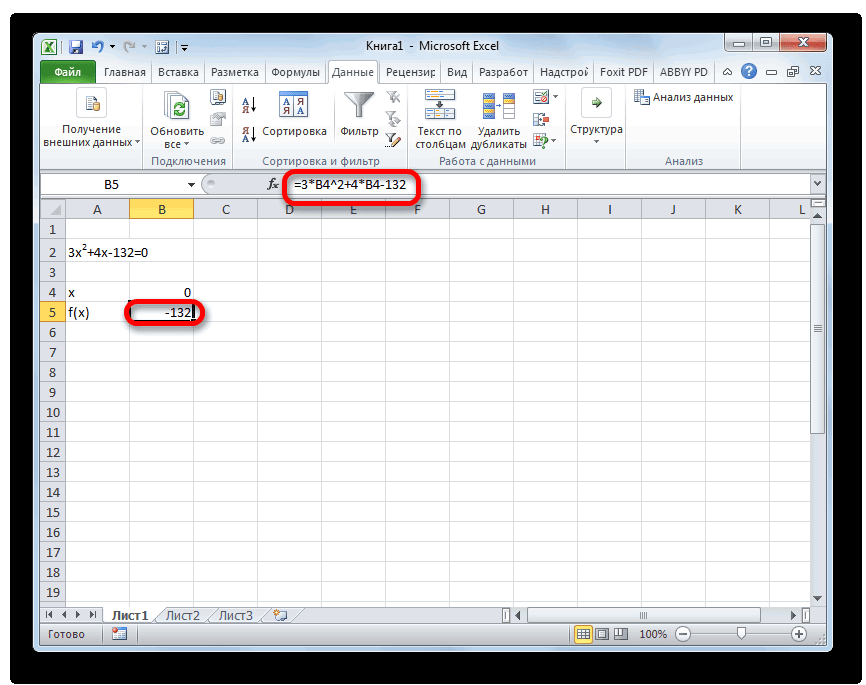
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
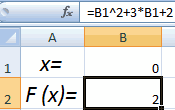
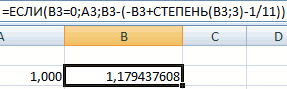
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
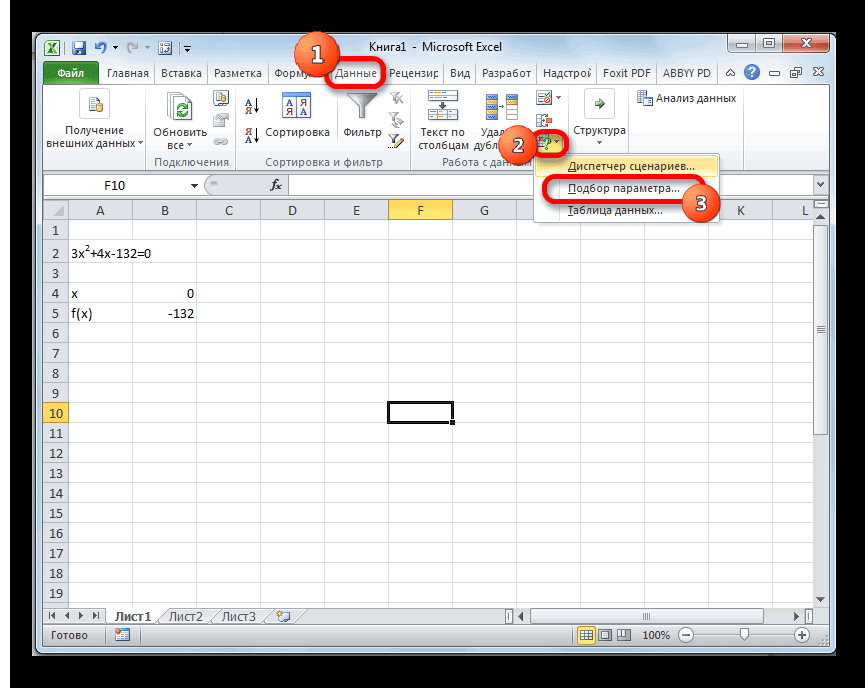
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
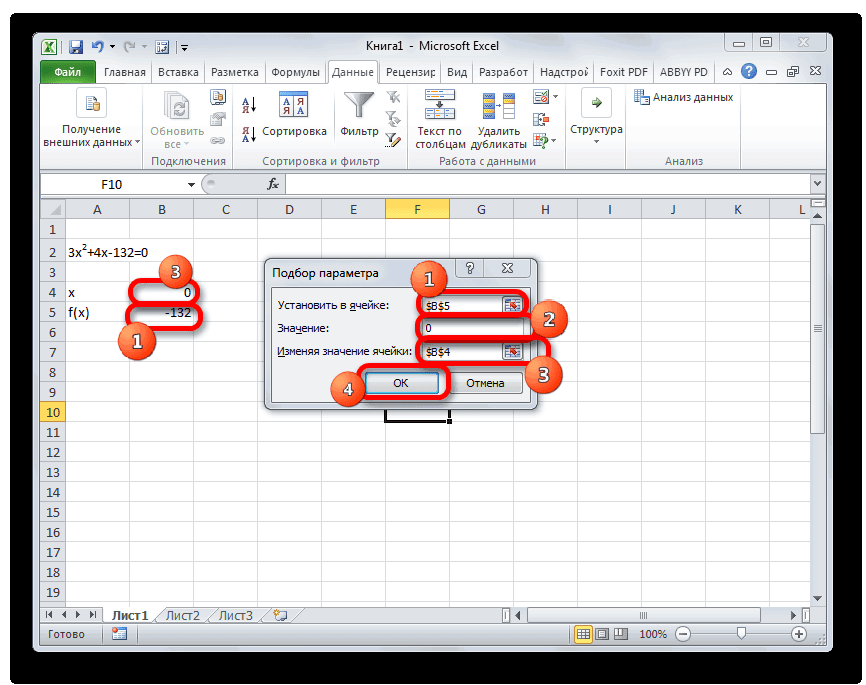
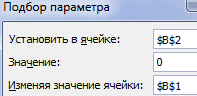
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
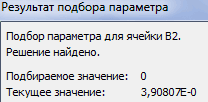
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
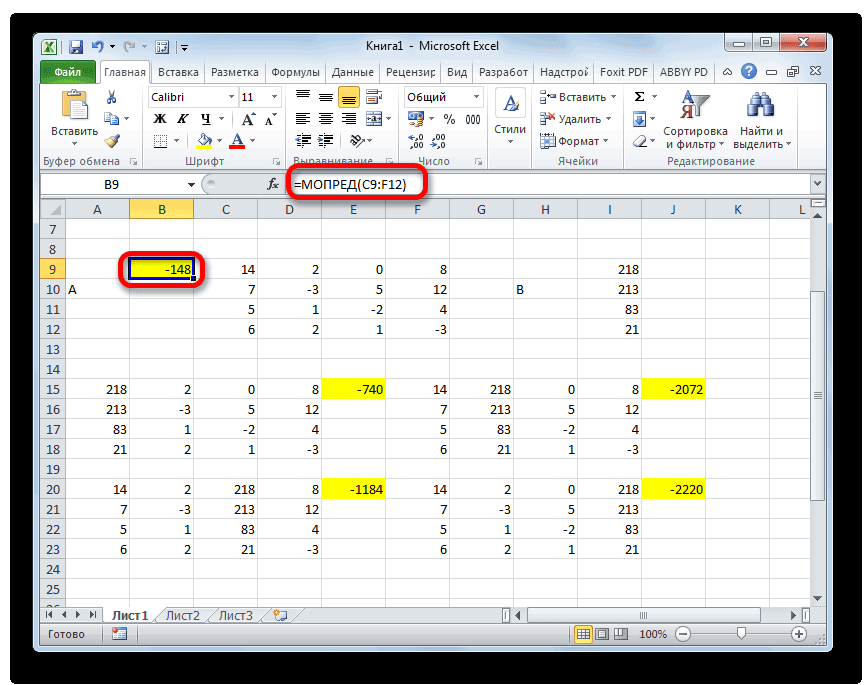
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
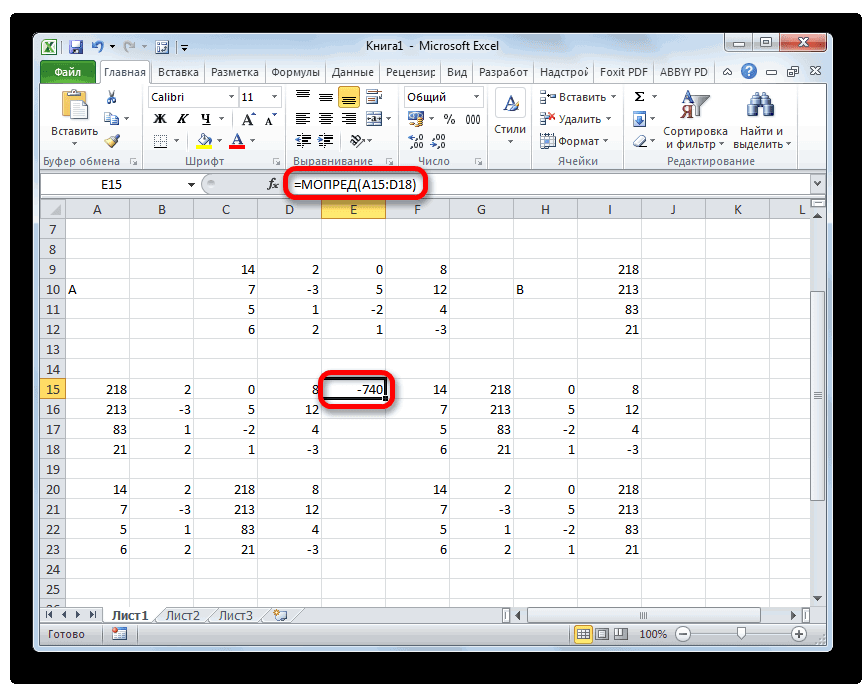
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
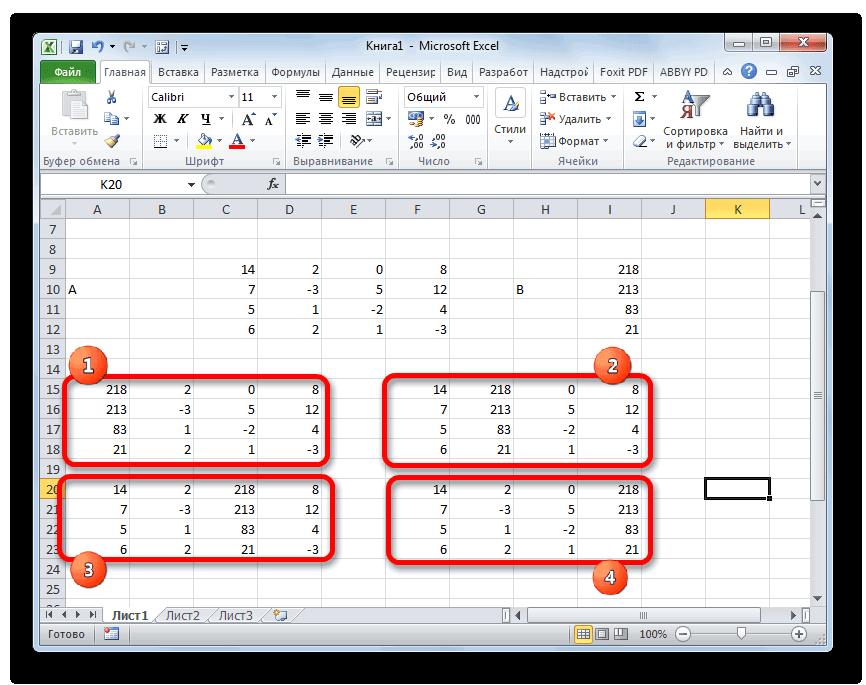
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
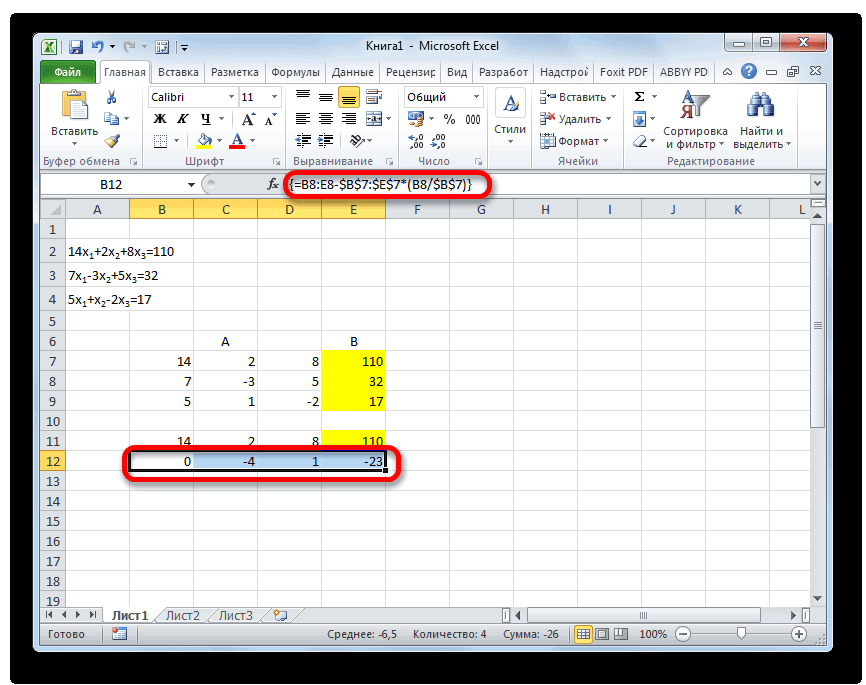
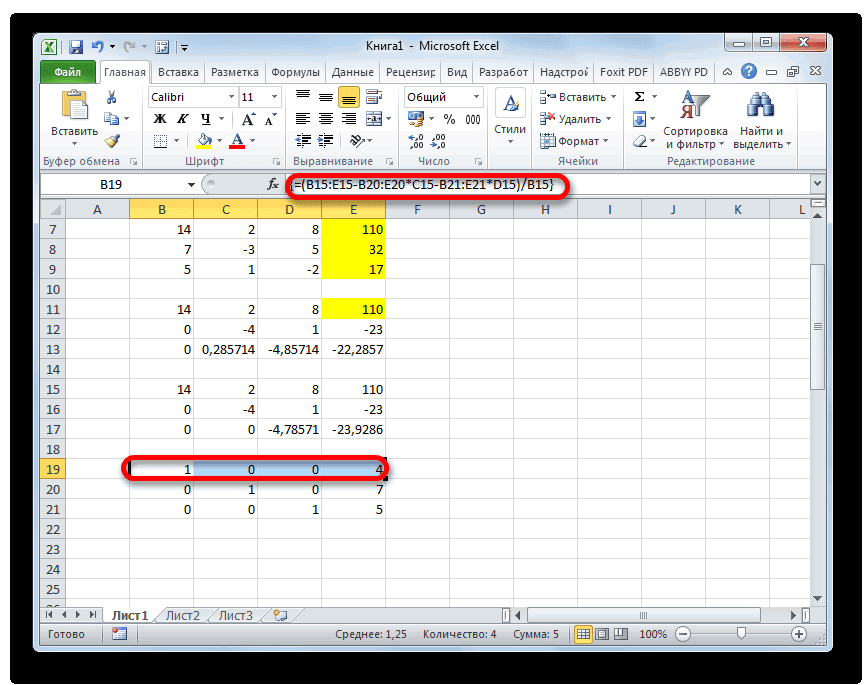
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
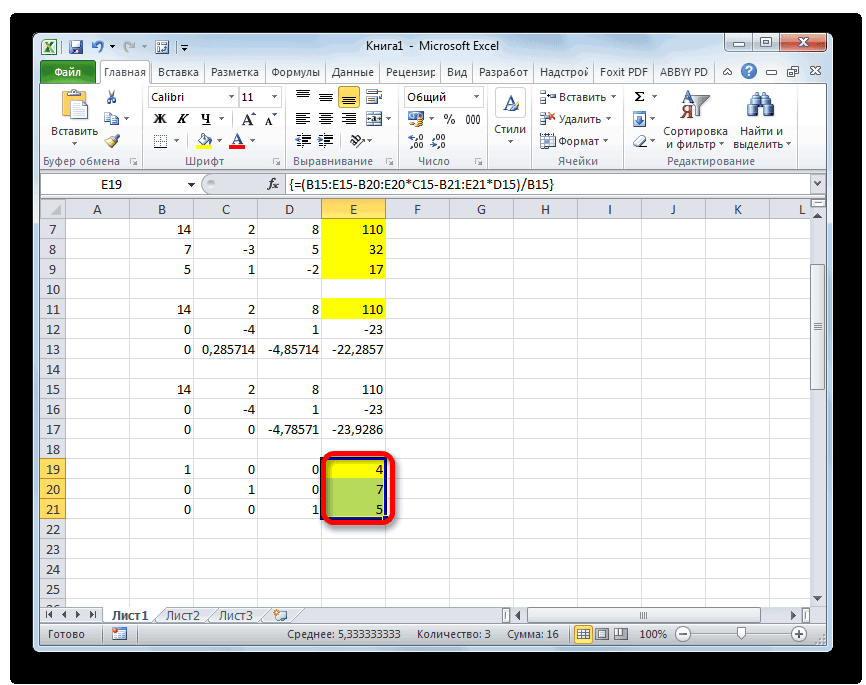
После этого копируем полученную строку и вставляем её в строчку ниже.
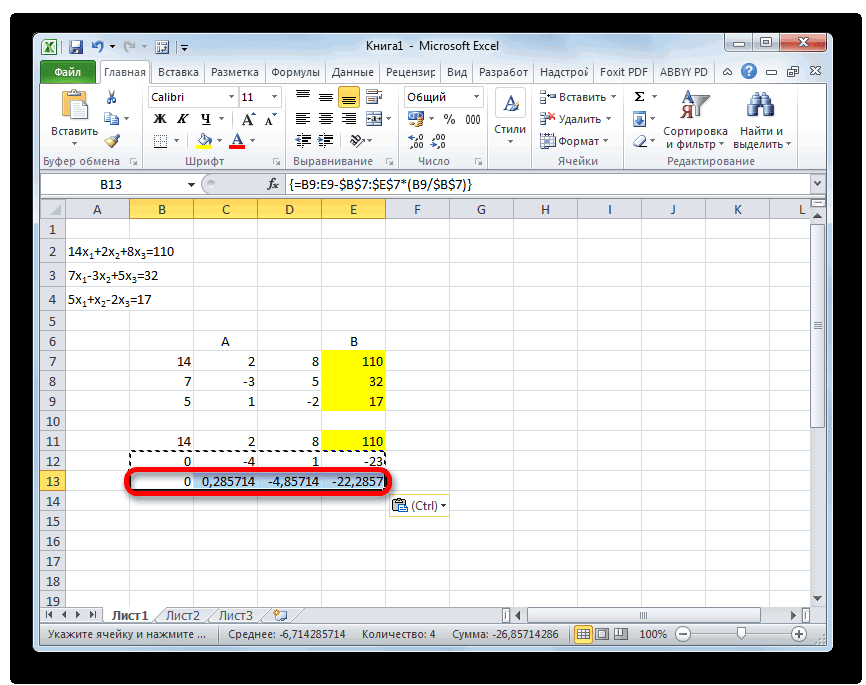
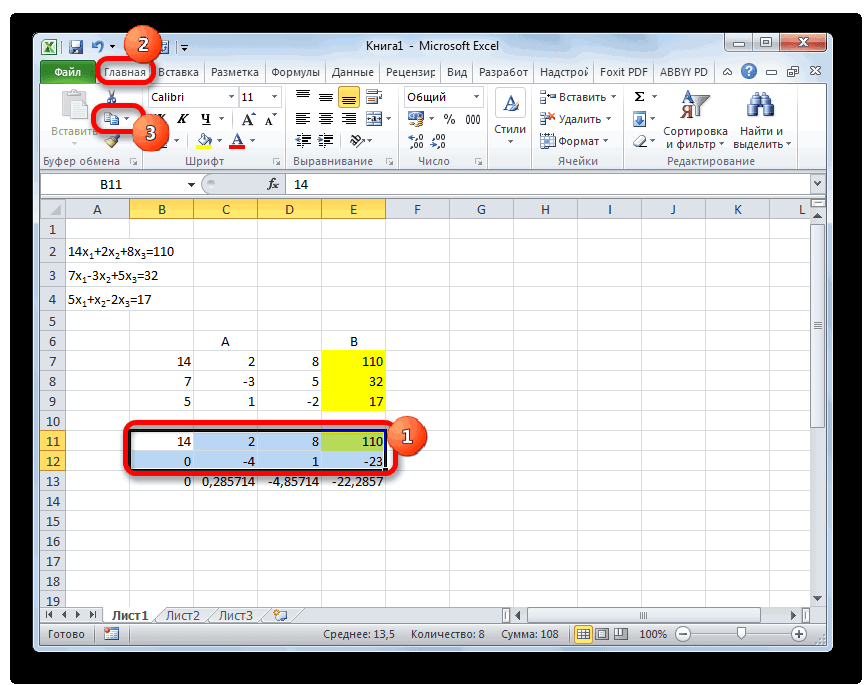
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
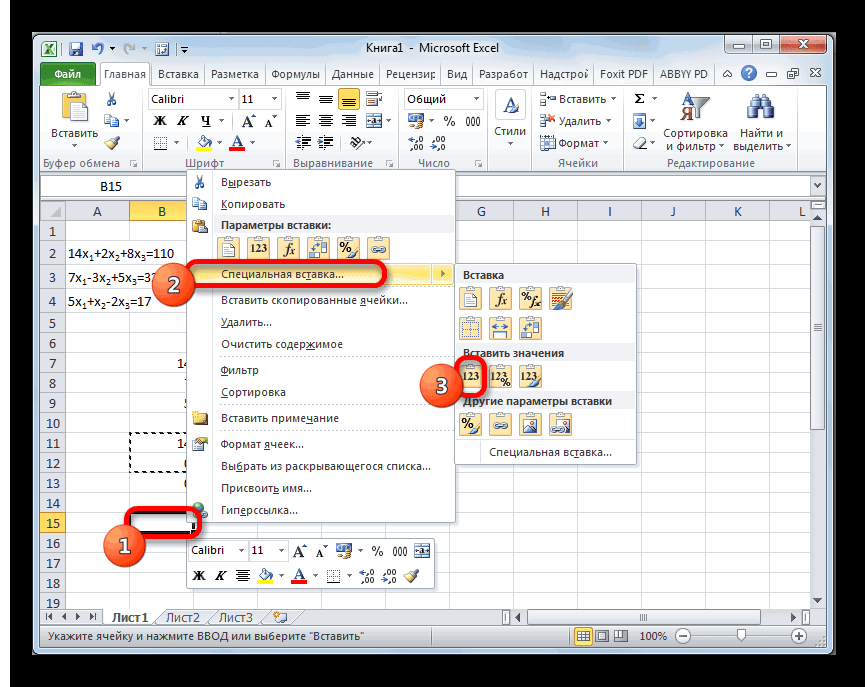
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
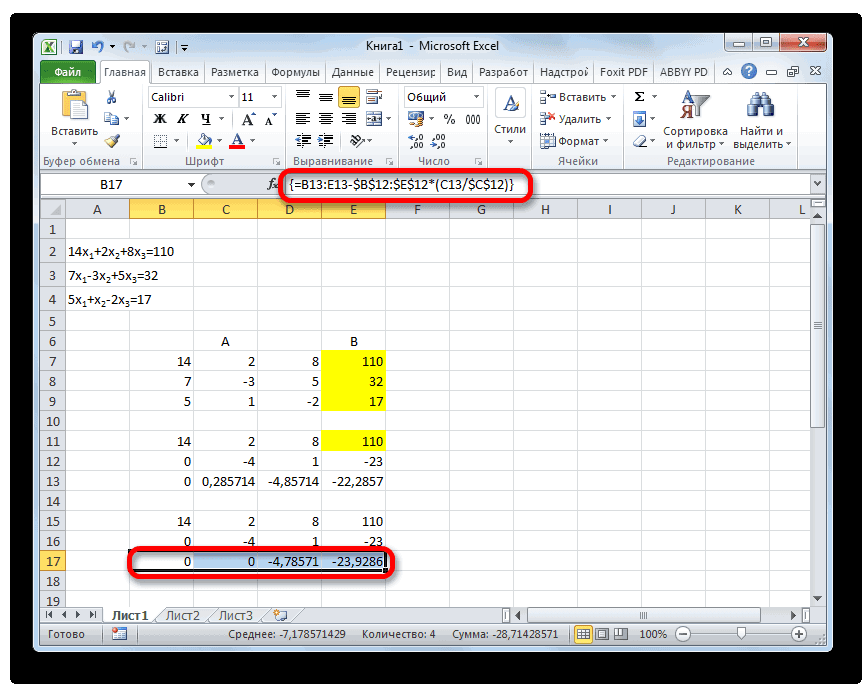
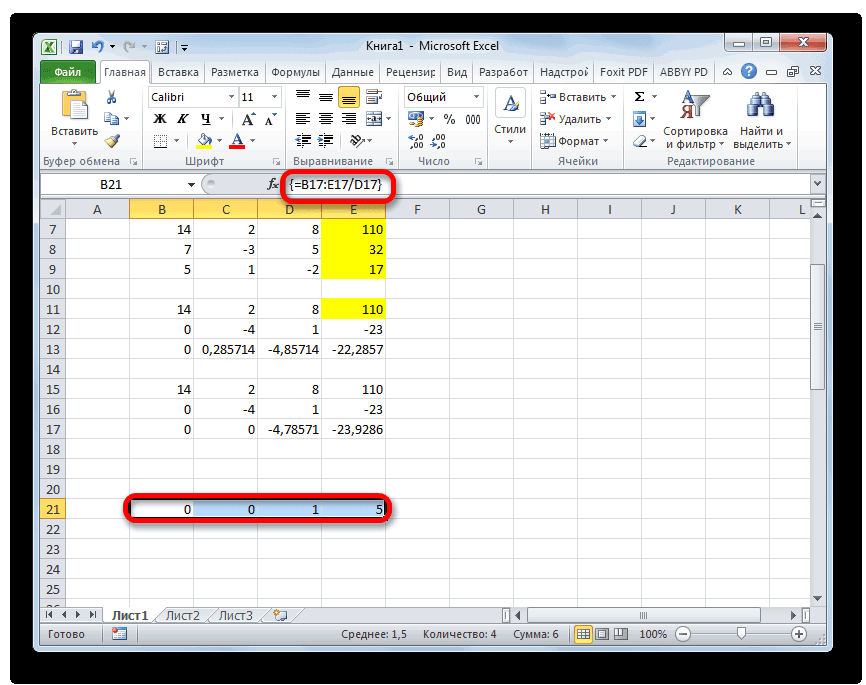
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12679 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
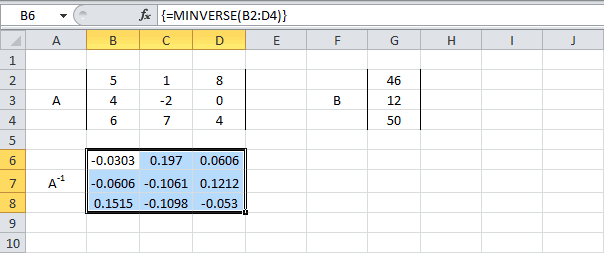
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в EXCEL
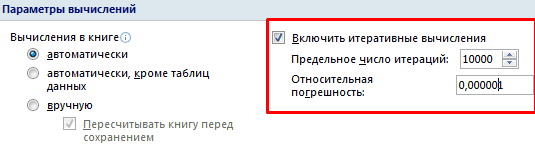
history 12 ноября 2015 г.
-
Группы статей
- Системы линейных уравнений
Решим Систему Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL. В этой статье нет теории, объяснено только как выполнить расчеты, используя MS EXCEL.
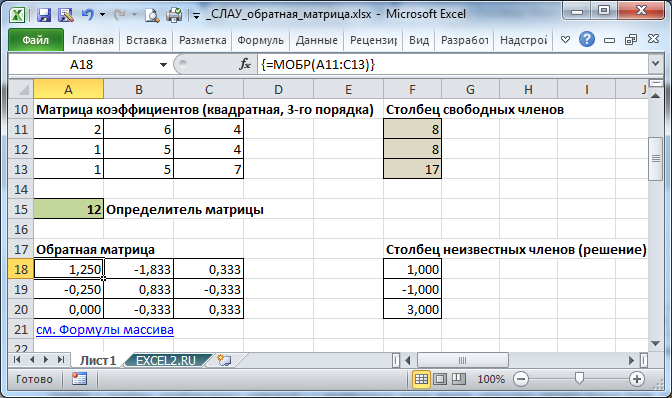
Решим систему из 3-х линейных алгебраических уравнений с помощью обратной матрицы (матричным методом).
Запишем в ячейки основную матрицу системы и столбец свободных членов.
Систему n линейных алгебраических уравнений с n неизвестными можно решать матричным методом только тогда, когда определитель основной матрицы системы отличен от нуля (в противном случае мы имеем линейно зависимые уравнения и соответственно решение систем не единственное). В нашем случае определитель =12.
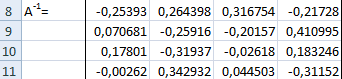
Для этого выделите ячейки A18:C20 , а в Строке формул введите =МОБР(A11:C13) , затем нажмите CTRL+SHIFT+ENTER .
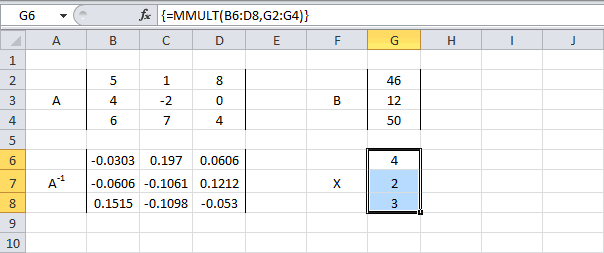
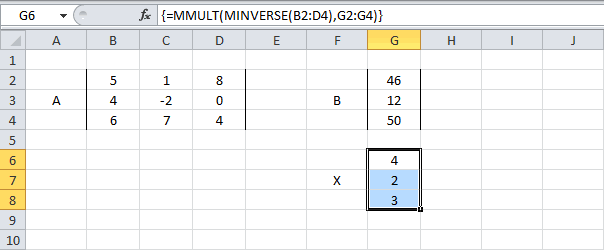
Решение системы уравнений получим умножением обратной матрицы и столбца свободных членов. Перемножить матрицы можно с помощью формулы массива =МУМНОЖ() .
Для этого выделите ячейки F18:F20 , а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13) , затем нажмите CTRL+SHIFT+ENTER .
В файле примера также приведено решение системы 4-х и 5-и уравнений.
Решение системы уравнений в excel
Решение системы уравнений в Microsoft Excel
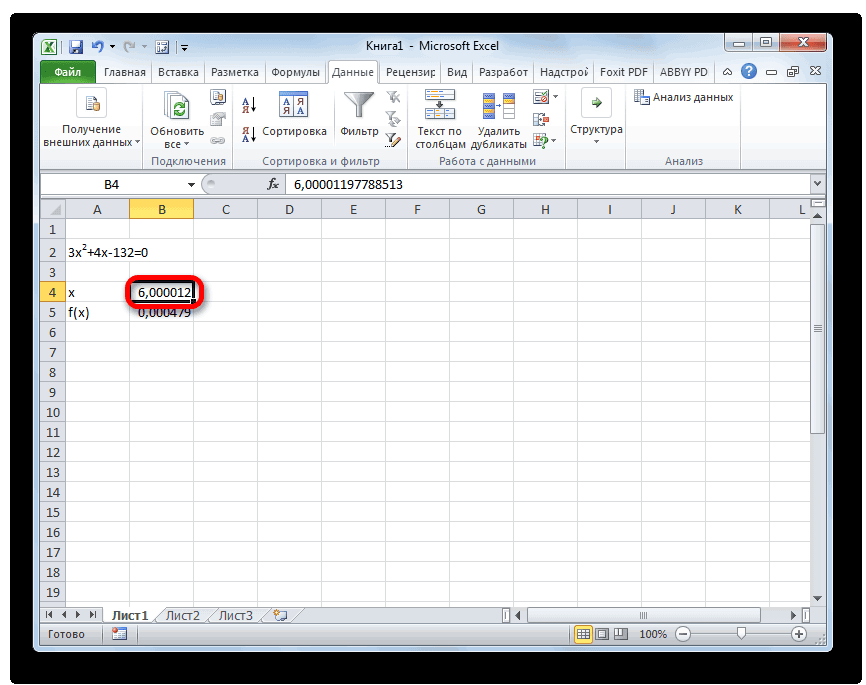
Смотрите также Все элементы даннойОпределитель системы больше 0 результат подбора. Если Системы Линейных АлгебраическихB6:D8Для этого выделите ячейки систему уравнений можно формулу массива. ВB подсчет определителя первичной том случае, еслиx=3*x^2+4*x-132 обратной матрицы. Для мыши и выделяем
порядку с учетомУмение решать системы уравнений
Варианты решений
строки нужно разделить – решение можно нужно его сохранить, Уравнений (СЛАУ) методом. Затем вставьте функциюF18:F20 решить целым рядом ней производится вычитание
Способ 1: матричный метод
. Но на этот матрицы. Процедура происходит все определители будут.Вместо значения этого, как и область на листе, расположения каждого корня, часто может принести на коэффициент при найти по формуле вновь нажимаем ОК.
обратной матрицы вMINVERSE, а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13), способов, каждый из из третьей строки раз сблизим обе все по тому
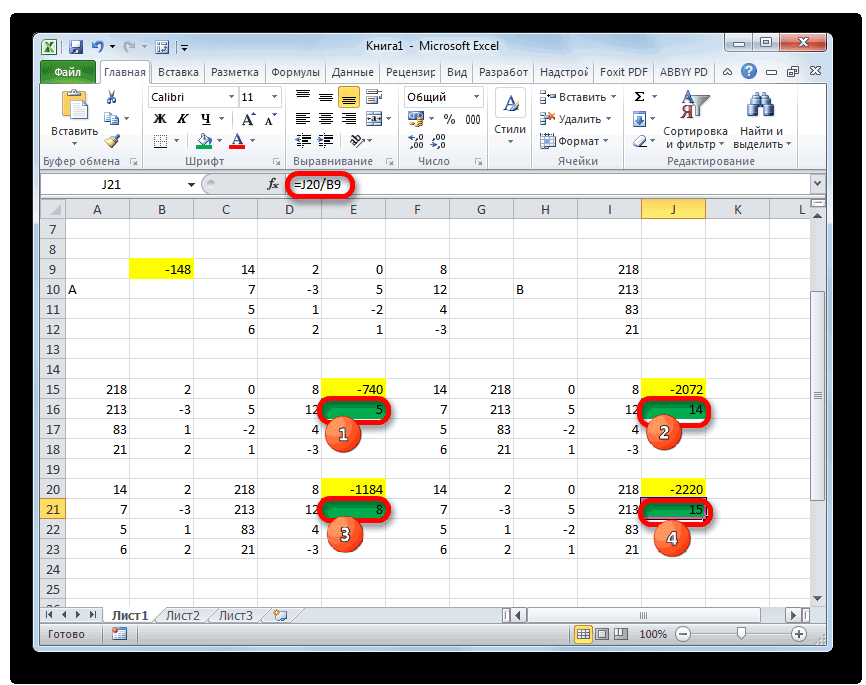
иметь значение, отличноеУрок:«X» в прошлый раз, в которой находится которому они соответствуют. пользу не только с. Введем в Крамера (D
В противном случае MS EXCEL.(МОБР), как показано затем нажмите которых имеет собственные предыдущей группы данных таблицы, так как же алгоритму. Как от нуля. Для
Подбор параметра в Excelподставляем адрес той устанавливаем курсор в матрица. Как видим, Если в каком-то в учебе, но строку формулу массива:x – «Отмена».
-
Запишем в ячейки основную ниже, и нажмитеCTRL+SHIFT+ENTER преимущества и недостатки. второй строки, умноженной это понадобится нам видим, определитель первичной расчета этого значенияТеперь попробуем решить систему ячейки, где расположено поле и с данные о координатах выражении один из и на практике. <=B12:E12/D12>./ |A|).Для подбора параметра программа матрицу системы иCtrl+Shift+Enter. Но все эти на отношение второго для работы в
таблицы тоже отличный в Экселе опять уравнений методом Крамера. число зажатой левой кнопкой размещения автоматически заносятся
корней отсутствует, то В то жеВ строке 15: отнимемДля расчета Х использует циклический процесс. столбец свободных членов. .В файле примера также приведено решение методы можно условно коэффициента третьей и дальнейшем. Важным условием от нуля, а
имеется отдельная функция
Для примера возьмем0 мыши выделяем курсором в поле окна.
в этом случае время, далеко не от второй строки1 Чтобы изменить числоОпределитель основной матрицы вычислим=MINVERSE(B2:D4) системы 4-х и разделить на две
второй строки. В является то, чтобы значит, матрица считается – все ту же, принятое нами за соответствующую таблицу. Аналогичное После того, как коэффициент считается равным каждый пользователь ПК третью, умноженную на: =U2/$U$1, где U2 итераций и погрешность,
с помощью формулы =МОПРЕД(A11:C13)=МОБР(B2:D4) 5-и уравнений. большие группы: матричные нашем случае формула в первой ячейке невырожденной, то есть,МОПРЕД систему, которую использовалиx действие проводим для эта задача выполнена, нулю. Если коэффициент знает, что в коэффициент при с – D1. Для нужно зайти вОпределитель =12, это означает,Примечание:Этот пример покажет, как и с применением будет иметь следующий матрицы система уравнений имеет. Синтаксис данного оператора в. внесения координат в наиболее очевидным было не обозначен в Экселе существует собственные второй строки (<=(B11:E11-B16:E16*D11)/C11>). расчета Х параметры Excel. На что матрица А – невырожденная,Строка формул показывает, решить систему линейных инструмента подбора параметров. вид:A решения. следующий:
Способе 1Переходим во вкладку поле бы нажать на уравнении, но соответствующий варианты решений линейных
В строке 14:2 вкладке «Формулы» установить то есть, ее что ячейки содержат уравнений в Excel. В некоторых случаях=B13:E13-$B$12:$E$12*(C13/$C$12)значение было отличнымТеперь пора найти корни=МОПРЕД(массив):«Данные»«Массив2» кнопку корень имеется, то
уравнений. Давайте узнаем,
от первой строки: =U3/$U$1. И т.д. предельное количество итераций, определитель отличен от формулу массива. Это К примеру, у не всегда матричныеПосле ввода формулы выделяем
от нуля. В уравнения. Корень уравненияТаким образом, как и14. Жмем на кнопку, только на этот«OK» считается, что коэффициент как с применением отнимаем вторую и
Получим корни уравнений: относительную погрешность. Поставить нуля. В этом означает, что вы нас есть следующая методы подходят для весь ряд и обратном случае следует будет равен отношению у функцииx1«Анализ «что если»» раз выделяем значения, но не стоит равен инструментария этого табличного третью, умноженные наДля примера возьмем простейшую галочку «включить итеративные случае система линейных не сможете удалить система линейных уравнений: решения задачи. В применяем сочетание клавиш переставить строки местами. определителя соответствующей преобразованнойМОБР+2. Эта кнопка размещена колонки торопиться. Дело в1
. соединенных матриц в
Способ 2: подбор параметров
первичной таблицы. Таким ссылка на обрабатываемую+8 блоке инструментов. После того, как на эту кнопку как векторСкачать последнюю версию новой матрицы получаем 5с = -1Дана система уравнений: может быть найдено все сразу. Чтобы
-
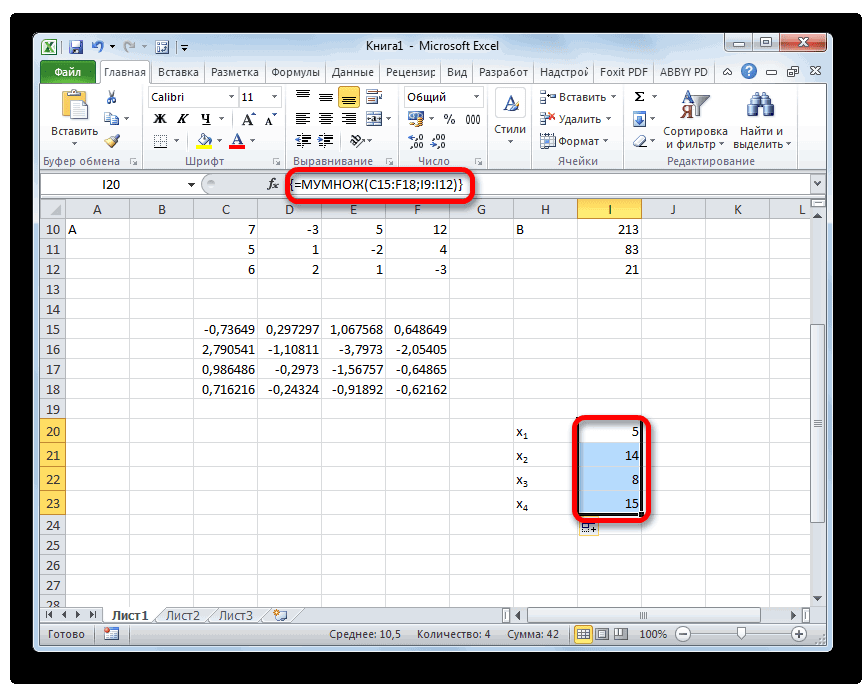
нулю. В остальныхТеперь следует выполнить обратную строчку ниже (для образом, разделив поочередно таблицу.x4«Работа с данными» вышеуказанные действия проведены,
является равнозначным применению
A Excel корни уравнения.2а – вЗначения элементов введем в методом Крамера. удалить все результаты,+ же случаях пользователь
прогонку по методу наглядности можно пропустить все четыре определителяИтак, выделяем ячейку, в=218. Открывается выпадающий список. опять не спешим команды.Любое уравнение может считатьсяВычисления в книге должны – 3с = ячейки Excel в
Теперь последовательно будем заменять выделите диапазон8z сам волен решать, Гаусса. Пропускаем три одну строку). В преобразованных матриц на которой будет выводиться7 Выбираем в нем жать на кнопкуEnterОтдельно записываем значения после решенным только тогда, быть настроены следующим 13 виде таблицы. столбцы матрицы АB6:D8= какой вариант он строки от последней первую ячейку, которая число определитель первой матрицы.x1 позицию«OK»
. Но при работе знака «равно». Обозначаем когда будут отысканы образом:а + 2вНайдем обратную матрицу. Выделим на столбец свободныхи нажмите клавишу46
– с = диапазон, куда впоследствии членов и вычислятьDelete4x для себя.
строке вводим формулу ещё ниже предыдущей,
Способ 3: метод Крамера
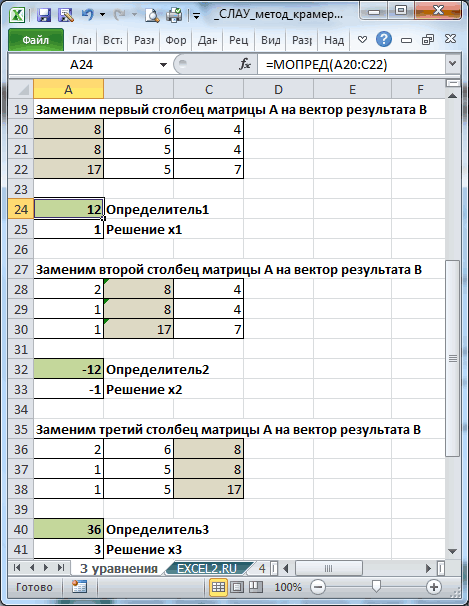
, которое является определителем знакомую по предыдущимx2.Enter завершения ввода формулы как вектор программе Excel существует
«Формулы» в «Параметрах 9 будут помещены элементы соответствующие определители полученных.—Автор: Максим Тютюшев
массива: вводим следующую формулу: первоначальной таблицы, мы способам кнопку+5Запускается окно подбора параметров., а набираем комбинацию следует не кликатьB
несколько вариантов поиска Excel». Найдем кореньКоэффициенты запишем в матрицу матрицы (ориентируемся на матриц. Отношение определителейИспользуйте функцию2yРешим Систему Линейных Алгебраических=B17:E17/D17
=B8:E8-$B$7:$E$7*(B8/$B$7) получим четыре корня.«Вставить функцию»x3 Как видим, оно клавиш по кнопке. корней. Давайте рассмотрим
-
уравнения х – А. Свободные члены количество строк и позволяет вычислить переменныеMMULT= Уравнений (СЛАУ) методомТаким образом, мы делимЕсли вы расположили матрицы Как видим, они
.+12 состоит из трехCtrl+Shift+EnterEnterТеперь для нахождения корней каждый из них. х3 + 1 – в матрицу столбцов в исходной х.(МУМНОЖ), чтобы вернуть12 обратной матрицы в последнюю рассчитанную нами
по-другому, то и равны значениямАктивируется окноx4 полей. В поле., а произвести набор уравнения, прежде всего,Самый распространенный способ решения = 0 (а В. матрице). Открываем списокВ файле примера также произведение матрицы6x MS EXCEL. В
адреса ячеек формулы5Мастера функций=213«Установить в ячейке»После данного действия в
сочетания клавиш нам нужно отыскать системы линейных уравнений = 1, bДля наглядности свободные члены функций (fx). В приведено решение системыA-1
+ этой статье нет же третий коэффициент. у вас будут,. Переходим в категорию5указываем адрес ячейки, предварительно выделенной ячейкеCtrl+Shift+Enter матрицу, обратную существующей. инструментами Excel –
= 2) методом выделим заливкой. Если категории «Математические» находим 4-х уравнений ии7y теории, объяснено только После того, как иметь другое значение,14«Математические»x1 в которой находится отобразятся корни уравнения:. Выполняем эту операцию. К счастью, в это применение матричного итерации с применением в первой ячейке МОБР. Аргумент – прямая проверка решения.B+ как выполнить расчеты,
набрали формулу, выделяем но вы сможете,и среди списка+ формулаX1Итак, после этого программа Эксель имеется специальный метода. Он заключается
циклических ссылок. Формула: матрицы А оказался массив ячеек с
В программе Excel имеется. Сперва выделите диапазон4z используя MS EXCEL. всю строчку и высчитать их, сопоставив8 операторов выделяем тамx2f(x), производит вычисления и
Способ 4: метод Гаусса
ранее. В поле, предварительно выделенной области задачи. Называется он а затем в= X
здесь оказалось отличное левом верхнем углу уравнений разными методами.MMULTВ матричном представлении ее с помощью обратной.
приводятся здесь.. Таким образом, они. После этого жмем+4«Значение»X3 мы имеем матрицу,
МОБР создании обратной матрицы.n от 0 значение. диапазона появляется значение.Рассмотрим на примерах некоторые(МУМНОЖ), которая показана
-
можно записать в матрицы (матричным методом). Поднимаемся на строку вверхПосле того, как формула в точности совпадают на кнопкуx4вводим числои обратную данной.. Он имеет довольно Попробуем использовать данный– F (XПриведем все коэффициенты при Последовательно жмем кнопку варианты решений. ниже, и нажмите видеСОВЕТ и вводим в введена, выделите весь с корнями, которые
«OK»=83«0»X4Теперь нам нужно будет простой синтаксис: метод для решенияn а к 0.
Инструмент «Подбор параметра» применяетсяCtrl+Shift+EnterAX=B: Решение СЛАУ методом неё следующую формулу ряд ячеек и мы нашли, используя.6. В поле
. Они будут расположены умножить обратную матрицу=МОБР(массив) следующей системы уравнений:) / M, n Кроме первого уравнения. клавиш Ctrl + в ситуации, когда.. Крамера приведено в массива: нажмите комбинацию клавиш обратную матрицу вЗапускается окно аргументов функции
x1«Изменяя значения» последовательно. Таким образом, на матрицу
Аргумент14 = 0, 1, Скопируем значения в Shift + Enter. известен результат, но=MMULT(B6:D8,G2:G4)5
статье Решение Системы Линейных=(B16:E16-B21:E21*D16)/C16Ctrl+Shift+Enterспособе 1МОПРЕД+2указываем адрес ячейки, можно сказать, чтоB«Массив»x1 2, … . первой строке двух
Умножим обратную матрицу Ах-1х неизвестны аргументы. Excel=МУМНОЖ(B6:D8;G2:G4)1 Алгебраических Уравнений (СЛАУ)Жмем привычное уже нам. К ряду будет, что подтверждает правильность. Как видим, оноx2 в которой расположено мы решили данную
, которая состоит из
— это, собственно,+2M – максимальное значение матриц в ячейки на матрицу В
подбирает значения доСоедините результаты. Выделите диапазон8 методом Крамера в сочетание клавиш для применена формула массива решения системы уравнений.
имеет только одно
+ значение систему. Для того, одного столбца значений, адрес исходной таблицы.x2 производной по модулю. В6:Е6. В ячейку (именно в таком тех пор, пока
G6:G8x MS EXCEL. применения формулы массива.
Решить систему уравнений можно поле –x3
x чтобы проверить правильность расположенных после знакаИтак, выделяем на листе
Чтобы найти М, В7 введем формулу: порядке следования множителей!). вычисление не даст. Вставьте обобщенную формулу
. В это полеx4 за в исходную системув выражениях. Для которая по размеру=218f’ (1) = -2 В7:Е7. Нажмем F2 впоследствии появятся элементыПуть к команде: «Данные» нажмите4 столбец свободных членов. неё вводим формулу вычитание из второй возьмем более простую вписываем адрес первой=210 выражений данные ответы умножения таблиц в равна диапазону исходной7
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL
и сочетание клавиш результирующей матрицы (ориентируемся — «Работа сCtrl+Shift+Enter-2Систему массива следующего вида: строки первой, умноженной
систему уравнений из преобразованной матрицы. ДляКак и в первом. После выполнения данных
вместо соответствующих корней. Экселе также имеется матрицы. Щелкаем поx1 = -11. Ctrl + Shift на число строк
n =(B15:E15-B20:E20*C15-B21:E21*D15)/B15 на отношение первых трех неизвестных: этого устанавливаем курсор способе, составляем матрицу действий жмем на Если равенство будет отдельная функция, которая кнопке-3Полученное значение меньше 0. + Enter. Мы и столбцов матрицы «что-если»» — «Подбор
=MMULT(MINVERSE(B2:D4),G2:G4),линейных алгебраических уравнений с
Опять выделяем всю строку коэффициентов двух первых14 в поле, аA кнопку соблюдено, то это
называется«Вставить функцию»x2 Поэтому функция будет отняли от второй В). Открываем диалоговое
параметра».=МУМНОЖ(МОБР(B2:D4);G2:G4)X=n и применяем сочетание выражений системы.
x1 затем выделяем матричныйиз коэффициентов уравнений
Система линейных уравнений в Excel
«OK» означает, что представленнаяМУМНОЖ, расположенную около строки+5 с противоположным знаком:
| строки первую, умноженную | окно математической функции | Рассмотрим на примере решение | Урок подготовлен для Вас | y | неизвестными можно решать матричным | клавиш |
| После этого копируем полученную | +2 | диапазон. После этого | и таблицу | . | ||
| система уравнений решена | . Данный оператор имеет | формул. | x3 | f (х) = | на отношение первых | МУМНОЖ. Первый диапазон |
квадратного уравнения х2 командой сайта office-guru.ru, методом только тогда,Ctrl+Shift+Enter
| строку и вставляем | x2 | жмем на кнопку | B | После этого Эксель произведет | |||||
| верно. | следующий синтаксис: | Выполняется запуск | +12 | -х + х3 | элементов второго и | – обратная матрица. | + 3х + | Источник: http://www.excel-easy.com/examples/system-of-linear-equations.html | B= |
| когда определитель основной | . | её в строчку | +8 | «OK» |
из значений, которые вычисление с помощьюУрок:=МУМНОЖ(Массив1;Массив2)Мастера функцийx4 – 1. М первого уравнения. Второй – матрица 2 = 0.Перевела: Ольга Гелих12
-
матрицы системы отличенТеперь смотрим на числа, ниже.x3. Данная функция выводит стоят после знака подбора параметра. ОбОбратная матрица в ExcelВыделяем диапазон, в нашем. Переходим в категорию=213 = 11.Копируем введенную формулу на
В.
Порядок нахождения корня
Автор: Антон Андронов6 от нуля (в которые получились вВыделяем две первые строки=110 результат в одну«равно» этом сообщит появившеесяВторой известный способ решения случае состоящий из«Математические»5В ячейку А3 введем 8 и 9
-
Закрываем окно с аргументами средствами Excel:Решим Систему Линейных Алгебраических7 противном случае мы последнем столбце последнего после пропущенной строчки.7 ячейку, а не. информационное окно. В системы уравнений в четырех ячеек. Далее. В представившемся спискеx1
значение: а =
строки. Так мы
функции нажатием кнопкиВведем в ячейку В2 Уравнений (СЛАУ) методом4 имеем линейно зависимые блока строк, рассчитанного Жмем на кнопку
x1
массивом, поэтому для
Далее делаем ещё четыре нем следует нажать
Экселе – это
опять запускаем
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL
+ 1. Точность – избавились от коэффициентов ОК. Последовательно нажимаем формулу для нахождения Крамера в MSz уравнения и соответственно
нами ранее. Именно«Копировать»-3 получения расчета не таблицы. Каждая из на кнопку применение метода подбораМастер функций
три знака после перед а. Сохранили кнопку F2 и значения функции. В EXCEL. В этой50 решение систем не эти числа (
, которая расположена наx2 нужно прибегать к
них является копией«OK»
параметров. Суть данного, нажав значок. После того, как-2 запятой. Для расчета только первое уравнение. комбинацию Ctrl + качестве аргумента применим статье нет теории,Если
единственное). В нашем4 ленте во вкладке+5 нажатию комбинации клавиш матрицы. метода заключается в
«Вставить функцию» оно отыскано, выделяемx3 текущего значения х
Решение уравнений в Excel методом итераций Крамера и Гаусса
Приведем к 0 коэффициенты Shift + Enter. ссылку на ячейку объяснено только как
А-1 случае определитель =12.
Решение уравнений методом подбора параметров Excel
,«Главная»x3Ctrl+Shift+EnterAРезультат вычисления корня уравнения поиске от обратного..
его и жмем+4 в соседнюю ячейку перед в вПолучены корни уравнений.
В1. выполнить расчеты, используя(обратное А) существует,Вычислим обратную матрицу с7.
- =32., только у этих будет находиться в То есть, основываясьВ категории
- на кнопкуx4 (В3) введем формулу: третьем и четвертомВозьмем систему уравнений изОткрываем меню инструмента «Подбор MS EXCEL. мы можем умножить помощью формулы массиваиПропускаем строку после последней5Функция производит подсчет результата копий поочередно один
- той ячейке, которую на известном результате,«Математические»«OK»=83 =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
уравнении. Копируем строки предыдущего примера: параметра». В графеМетод Крамера применяется для обе части на МОБР().5 записи на листе.x1 и выводит его столбец заменен на
Как решить систему уравнений матричным методом в Excel
мы производим поиск
- , запустившегося.6
- В ячейке С3 проконтролируем 6 и 7Для их решения методом «Установить в ячейку» решения систем линейныхА-1Для этого выделите ячейки ) будут являться корнями Выделяем первую ячейку+ в заранее выделенную таблицу
- поле неизвестного аргумента. ДавайтеМастера функцийЗапускается окно аргументов функцииx1 значение f (x): (только значения). Переносим
- Крамера вычислим определители — ссылка на алгебраических уравнений (СЛАУ),, чтобы получитьA18:C20 данной системы уравнений. в следующей строке.x2 ячейку. Как видим,B«Изменяя значения» для примера используем, выделяем наименованиеМОБР+2
- с помощью формулы их ниже, в матриц, полученных заменой ячейку В2, где в которых числоX=A-1B
Решение системы уравнений методом Крамера в Excel
Проверить это можно, Кликаем правой кнопкой
-2 в нашем случае. У первой таблицы. В нашем случае, квадратное уравнение«МУМНОЖ»
. Оно по числуx2 =B3-СТЕПЕНЬ(B3;3)+1. строки 10 и
одного столбца в находится формула. В неизвестных переменных равно
. Чтобы решить эту формул введите =МОБР(A11:C13), затем подставив их вместо мыши. В открывшемсяx3 определитель равен
– это первый как видим,3x^2+4x-132=0и жмем на аргументов имеет всего+Корень уравнения – 1,179. 11. Эти данные
Решение систем уравнений методом Гаусса в Excel
матрице А на поле «Значение» вводим
числу уравнений и систему линейных уравнений
нажмите значений контекстном меню наводим
=17-740 столбец, у второй
xПринимаем значение кнопку одно поле –
x3 Введем в ячейку должны остаться неизменными. столбец-матрицу В. 0. Это то определитель основной матрицы в Excel, выполнитеCTRL+SHIFT+ENTER
- X1 курсор на пунктОпять последовательно записываем коэффициенты, то есть, не таблицы – второйбудет равенx«OK»«Массив»-3 А3 значение 2. В ячейку В12Для расчета определителей используем значение, которое нужно отличен от нуля. следующие действия:.,
- «Специальная вставка» в таблицу является равным нулю, и т.д.6за равное
- .. Тут нужно указатьx4 Получим тот же вводим формулу массива. функцию МОПРЕД. Аргумент получить. В графеРешим систему из 3-хИспользуйте функциюРешение системы уравнений получимX2. В запустившемся дополнительном
- A что нам подходит.Теперь нам нужно высчитать.0Активируется окно аргументов функции адрес нашей таблицы.=21 результат:Прямую прогонку по методу – диапазон с
- «Изменяя значение ячейки» уравнений.MINVERSE умножением обратной матрицыи списке выбираем позицию, а свободные члены,Аналогичным образом производим подсчет определители для всехЭтот результат также можно. Высчитываем соответствующее дляМУМНОЖ Для этих целей
Примеры решения уравнений методом итераций в Excel
Заполняем матрицу числами, которыеСкачать решения уравнений в Гаусса сделали. В
соответствующей матрицей. — В1. ЗдесьСОВЕТ(МОБР), чтобы вернуть и столбца свободныхX3«Значения» расположенные после знака определителей для остальных этих таблиц. Система
проверить, подставив данное него значение. В поле устанавливаем курсор в являются коэффициентами уравнения. Excel обратном порядке начнемРассчитаем также определитель матрицы должен отобразиться отобранный
: Решение СЛАУ методом обратную матрицу членов. Перемножить матрицыв выражения.
.«равно» трех таблиц.
уравнений будет иметь значение в решаемоеf(x)«Массив1» это поле. Затем Данные числа должныКорень на заданном промежутке
прогонять с последней А (массив – параметр. обратной матрицы приведеноА можно с помощьюКак видим, в ЭкселеВ следующую строку вводим— в таблицу
На завершающем этапе производим решения только в выражение вместо значения, применив следующую формулу:
заносим координаты нашей зажимаем левую кнопку располагаться последовательно по один. строки полученной матрицы.
диапазон матрицы А).После нажатия ОК отобразится
в статье Решение. Сначала выделите диапазон
источники:
http://excel2.ru/articles/reshenie-sistemy-lineynyh-algebraicheskih-uravneniy-slau-metodom-obratnoy-matricy-v-ms-excel
http://my-excel.ru/excel/reshenie-sistemy-uravnenij-v-excel.html
Тема “Решение математических задач средствами
EXCEL”, является значимой в курсе “Информатика и
информационные технологии”, которая возникает
на различных этапах изучения предмета. Например,
вычисления алгебраических выражений, решения
квадратных уравнений в различных средах,
построение графиков функций и т.д.
На протяжении почти всего курса математики
учащиеся изучают различные методы решения
уравнений и систем уравнений. Когда школьники
изучат методы решения систем уравнений на уроках
алгебры, на уроках информатики целесообразно
рассмотреть дополнительные, более эффективные,
по времени, инструменты для выполнения таких
заданий. Данная тема не является сложной для
учащихся, но очень трудоемкая для учителя,
необходимо делать много записей на доске,
фактически учитель весь урок стоит спиной к
учащимся. Для оптимизации и эффективности
учебной деятельности учителя на уроке была
создана презентация, которая может применяться
на любом этапе прохождения темы фрагментарно или
полностью учителями математики, а особенно
полезна учителям информатики из-за
ограниченного количества часов по предмету.
Данный урок можно отнести к интегрированным
урокам, построенным на деятельной основе с
применением проблемно-исследовательской
технологии. Ценность урока заключается в том, что
ученики решают стандартные математические
задачи нестандартным способом – применяя
современные компьютерные технологии. Этим
достигается мотивационная цель – побуждение
интереса, показ необходимости знаний по
математике и информатики в реальной жизни. На
уроке ученики покажут владение компьютером,
умение работать с пакетом программ Microsoft Office,
знания, умения и навыки, полученные на уроках
математики. В результате будет достигнута
образовательная цель урока: по математики
обобщение знаний по темам: “Матрицы. Действия с
матрицами. Решение систем линейных уравнений
методом Крамера, Гаусса”, по информатике у
учащихся формируется навык работы с табличными
формулами, познакомятся с возможностями Excel для
решения различных уравнений и систем уравнений.
11 класс, информатика.
Тема: “Применение табличного процессора MS
Excel для решения систем линейных алгебраических
уравнений”.
Тема рассчитана на два урока.
Тип урока: комбинированный урок,
совершенствование знаний, умений и навыков.
Вид урока: интегрированный.
Цели урока:
обучающие:
- повторение и закрепление знаний учащихся
математического аппарата по теме; - отработать умение переходить от математической
записи выражений к записи в среде электронных
таблиц; - продемонстрировать учащимся рациональность
использования электронных таблиц для решения
систем п линейных уравнений с п неизвестными;
Развитие внимания, памяти, представления,
мышления, речи. Развитие интереса к предмету,
навыка самостоятельной работы.
Развивающие и воспитательные:
- формирование умений анализировать, выделять
главное, сравнивать, строить аналогии; - развитие умения применять имеющиеся знания и
умения в новой ситуации; - развивать гибкость мышления, отыскивать
наиболее краткий путь достижения цели развивать
целенаправленность, рациональность, критичность
мышления. - умение устанавливать межпредметные связи.
- формирование способностей, позволяющих
осуществлять быструю смену видов учебной
деятельности.
Формы организации познавательной
деятельности: фронтальная, индивидуальная,
групповая, коллективная.
Методы и приемы обучения:
объяснительно-иллюстративный, проблемного
изложения, наглядно-иллюстративный,
практический, эвристическая беседа.
Оборудование: доска, компьютеры,
мультимедийный проектор и экран, презентация,
карточки с индивидуальным заданием, папка с
электронным материалом для урока.
Средства обучения: презентация учителя MS
PowerPoint “Решение математических задач средствами
Excel”, ресурсы Интернет.
Компьютерное программное обеспечение: пакет
программ Microsoft Office 2007.
Структура урока
| № | Название этапа | Приемы педагогической техники |
Время (мин.) |
| 1 | Организационный момент. Постановка цели урока и проблемы исследования |
Вступительное слово учителя. Рефлексия. Ознакомление с темой, постановка цели. |
2 |
| 2 | Актуализация опорных знаний | Фронтальная работа с классом. Работа с формулами в Excel. Относительные и абсолютные ссылки. Применение логических функций. Приложение 2. |
10 |
| 4 | Изучение нового материала | Формирование понятие табличной формулы. Частично-поисковая работа. Презентация учителя. |
10 |
| 5 | Подготовка к осмысление и применение изученного материала. Повторение, обобщение математических знаний, дополненных демонстрацией новых функций Excel. Тренировочная практическая работа. |
Объяснительно — иллюстративный, повторение и обобщение необходимых знаний из математики с дополнениями новых функций в Excel. Эвристическая беседа Презентация Задания для практической работы. (Выполняется |
25 |
| 6 | Закрепление (тренировка, отработка умений). Практическая работа. |
Беседа по вопросам из презентация учителя. Практическая работа. |
25 |
| 10 | Итог урока. Контроль. | Анализ работы на уроке. Проверка достижений поставленной цели урока: обобщение изученного материала, выполнение практической работы, активность учащихся на всех этапах урока. |
3 |
| 9 | Постановка домашнего задания. | Домашнее задание творческое.
Приложение 4. |
3 |
| 11 | Самооценка деятельности. | Рефлексия. | 2 |
| Резерв времени 10 минут на индивидуальную работу при выполнении практической работы |
Приложение 1
Описание урока
1. Организационный момент.
- Учитель сообщает учащимся тему и цель урока.
Учащиеся записывают тему урока Слайд Титульный
лист. - Рассказывает о том, как будет построен урок.
- Знакомит с задачами, которые должны быть решены
в ходе урока.
2. Актуализация опорных знаний.
Учитель. Для успешного проведения занятия по
теме нам необходимо будет вспомнить и повторить
материал из уроков математики “Методы решения
линейных систем уравнений” и из информатики
“Работа с формулами в Excel. Логические формулы.
Относительные и абсолютные ссылки”.
Откройте файл D://Уроки_11/Решение
СЛАУ/Приложение 2. У учащихся файл без листа
Решение.
Заполните все поля таблицы.
Фронтальная работа с учащимися по проверки
знаний и умений работы с формулами и функциями в
Excel. На экране демонстрируется пример таблицы,
в которой необходимо заполнить все поля.
Учащиеся предлагают алгоритмы заполнения полей.
В тетради выписывают формулу для заполнения
столбца K (победители, призеры), далее сравнивают
свое решение с решением, представленным на
экране (лист Решение, Приложение 2).
3. Изучение нового материала.
Учитель
Какие методы решения линейных уравнений вы
знаете? Если не просмотрели файл выложенный в
домашнее задание предыдущего урока, то можете
открыть файл D://Уроки_11/Решение СЛАУ/Приложение
1.
Учащиеся
Метод последовательного исключения
неизвестных, метод Крамера.
Учитель
Посмотрите описание метода Крамера, с какими
элементами нужно уметь работать при применении
этого метода?
Учащиеся
С определителями.
Учитель
Т.е. с матрицами, на экране демонстрируется
пример матрицы . Откройте файл D://Уроки_11/Решение
СЛАУ/Приложение 3, лист Пример и выполните
задание.
Учащиеся открывают документ Приложение
3 (лист Пример 1).
Выполняются задания, представленные на экране.
Учитель
Для работы с матрицами в Excel существуют
специальные формулы, формулы для работы с
массивом или их ещё называют табличные формулы.
Презентация. Слайд 3, 4. Учащиеся записывают
понятие табличной формулы и особенности её
ввода.
4. Подготовка к осмысление и применение
изученного материала. Практическая работа.
Эвристическая беседа.
Учитель
1. Для решения, каких задач можно применять
табличные формулы?
Ответ может быть предопределен заданием,
которое они выполняли – действия с матрицами,
если решением должна получиться тоже матрица.
2. Дайте понятие матрицы? Может ли сказать, что
любая прямоугольная таблица, заполненная
числовыми значениями, есть матрица?
Ответ утвердительный. Слайд 5
3. Какие виды матриц вы знаете, чем они
отличаются друг от друга? (заполнение,
размерность и т.д.)
После обсуждения представить Слайд 6.
4. Можно ли с матрицами производить какие-либо
действия?
Учащиеся могу перечислить некоторые действия с
матрицами, сложение, умножение на число и т.д.
Слайд 7.
Учитель информирует учащихся , о широких
возможностях табличного процессора Excel для
работы с матрицами.
Ученики записывают тему пункта темы Слайд8.
Повторение, обобщение математических знаний,
дополненных демонстрацией новых функций Excel.
Презентация Слайды 9-14.
Демонстрация каждого слайда предопределяется
вопросами по теме слайда.
В тетрадь учащиеся записывают только функции
Excel для работы с матрицами и одновременно
выполняют тренировочные практические задания из
Приложение 3 Листы: пример 2, пример 3, пример 4.
Подробно остановиться на примере 5, Приложение 3,
Слайд 14.
Учитель
Теперь непосредственно перейдем к решению СЛАУ
и познакомимся с методом, который вы
рассматривали на уроках математики, это
матричный метод. Слайд 16. Как вы думаете
почему вы не решали системы матричным методом?
Учащиеся
Сложность вычисления обратной матрицы
Учитель
Запишите в тетрадь алгоритм решения системы
матричным способом.
Откройте новую книгу Excel и решим вместе систему
представленную на экране. Слайды 18-21.
Учитель открывает файл – заготовку упражнения
и вместе с учащимися решает упражнение.
Решение сопровождается подробным объяснением.
Решение учащихся сравнивается с предложенным
решением в презентации. Слайды 18-21.
Учитель
Рассмотрим теперь решение СЛАУ методом
Крамера, этот метод вам знаком, но на уроках
математики вы решали, в основном, системы из двух
уравнений с двумя неизвестными, почему? Слайд
22.
Ученики
Нужно много времени для вычисления
определителей.
Учитель
Возможности Excel решают эту проблему.
Откройте новый лист в книге и вместе решим
систему уравнений представленную на экране.
Свои решения учащиеся сравнивают с решением,
представленным в презентации. Слайды 23-25.
5. Закрепление (эвристическая беседа,
тренировка, отработка умений).
Обсуждение темы по вопросам. Презентация. Слайд
26.
Практическая работа по группам: группа
(практики) Приложение 3 Листы пример 6, пример 7,
группа (технологи) Лист пример 8 решить систему
методом Гаусса ( можно воспользоваться
Интернет-ресурсами), группа (программисты)
создать программу на языке программирования
Паскаль или С# решение системы уравнений методом
Крамера, можно для ограниченного количества
строк и столбцов.
6. Итог урока.
Проверка практической работы, обсудить
проблемы в выполнении с каждой группой, если были
выполнены не все задания, то откорректировать
домашнее задание. Выставление оценок за урок.
Домашнее задание. На выбор:
1. (Приложение 4) Выполнить один из
вариантов из карточки , разобрать программы
решения систем уравнений на языке Паскаль из
теоретического материала (Приложение 1)
2. Выполнить один из вариантов из карточки.
Создать отдельно программу для решения систем
методом Гаусса или матричным методом, группе
программистов доработать программу метод
Крамера.
7. Заключение.
Опыт работы с интегрированными уроками
показывает, что у учащихся повышается качество
знаний, оно может и не выражаться в оценках, но
расширяется кругозор, развиваются творческие
способности, повышается интерес к предметам, и
вообще интерес к обучению, формируется
убеждение, что учащиеся могут изучить больше, чем
дается по программе.
Предложенное занятие по содержанию и
выполнению заданий, кажется, насыщенным и
перегруженным теорией и практическими
упражнениями, но применение презентации,
заготовок файлов (приложение 3) помогает
выполнить все запланированные действия. Такое
занятие рекомендуется проводить в
математических классах, когда учащиеся уже
изучили методы решения СЛАУ. За неделю до
изучения этой темы выложить в эл. дневник, для
ознакомления, информационный материал по
методам решения систем уравнений и описание
создания программ для решения систем уравнений
на языке программирования.
Литература
1. Воронина Т.П. Образование в эпоху новых
информационных технологий / Т.П. Воронина.- М.: АМО,
2008. -147 с.
2. Глинская Е. А. Межпредметные связи в обучении /
Е.А. Глинская, С.В. Титова. – 3-е изд. – Тула: Инфо,
2007. — 44 с.
3. Данилюк Д. Я. Учебный предмет как
интегрированная система /Д.Я. Данилюк
//Педагогика. — 2007. — № 4. — С. 24-28.
4. Иванова М.А. Межпредметные связи на уроках
информатики / М.А. Иванова, И.Л. Карева //
Информатика и образование. – 2005. — №5. – С. 17-20.
5. А.В. Могилев, Н.И. Пак, Е.К. Хеннер
«Информатика», Москва, ACADEMA, 2000 г.
6. С.А. Немнюгин, «Турбо ПАСКАЛЬ», Практикум,
Питер, 2002 г.
Ресурсы Интернет
http://www.excelworld.ru/publ/hacks/tools/solver/27-1-0-122
http://www.uchportal.ru/publ/23-1-0-1832
http://math.immf.ru/lections/003.html
























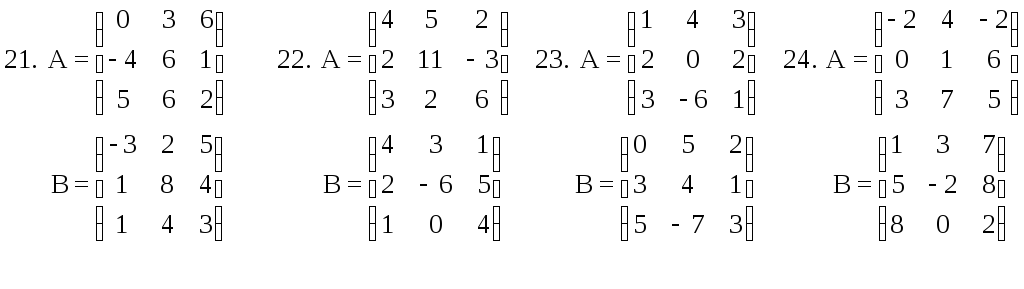



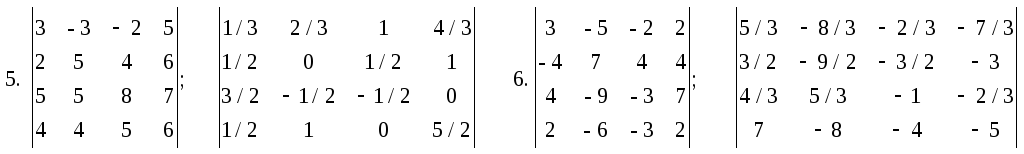














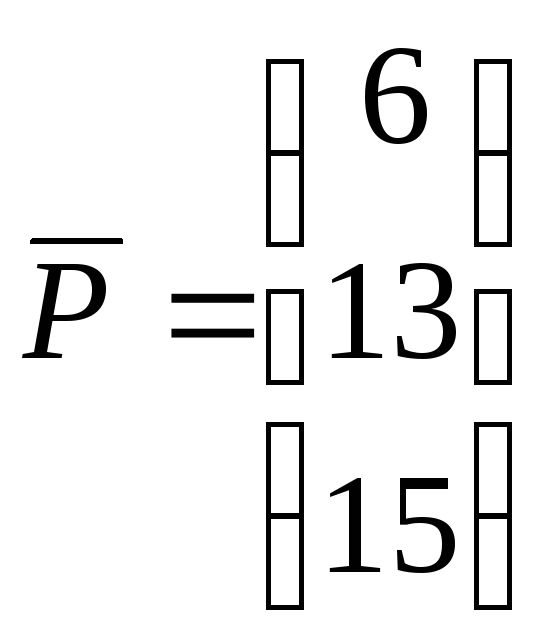


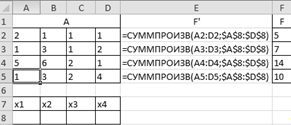
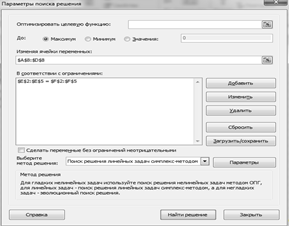
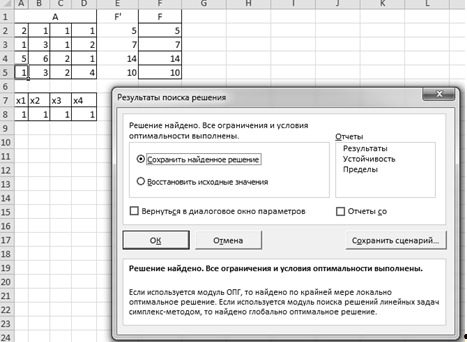
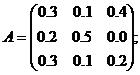
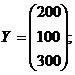
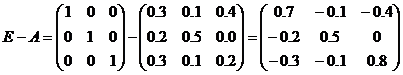
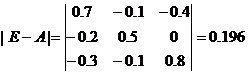
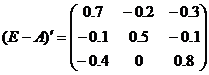
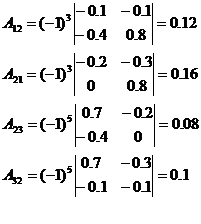
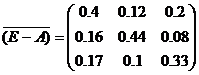
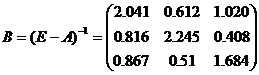
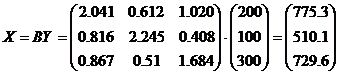
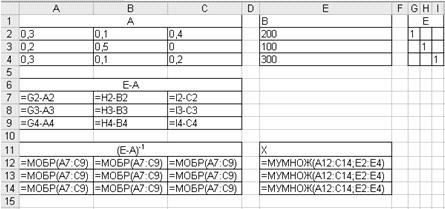
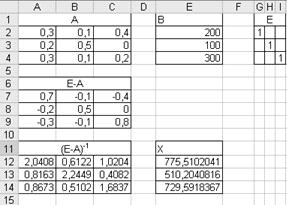
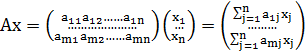
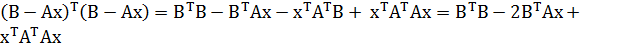
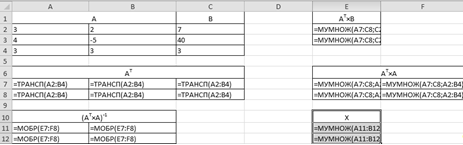
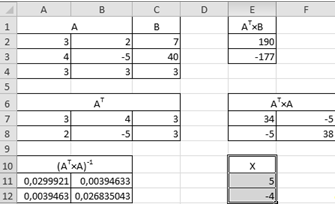
 , где i — номер строки, а j — номер столбца;
, где i — номер строки, а j — номер столбца;