В этом разделе вы найдете примеры задач c решением по финансовой математике, выполненные с помощью пакета Excel. Другие примеры с решениями вручную вы найдете здесь.
Для решения финансовых задач в Эксель используются как встроенные финанансовые функции (например, ПЛТ, СТАВКА, КПЕР, ПС, БС, ПОЛУЧЕНО и т.д), так и формулы, вводимые вручную, чтобы получить ответ согласно некоторой сложной формуле (для которой нет встроенной функции). Иногда используются также функции подбора параметра и поиска решения.
Поможем с Excel, финансами и математикой 
Решение финансовой математики в Excel
Задача 1. Вас просят дать в долг 03.03.2012 г. 20000 р. и обещают вернуть 18.08.2012 г. 4800 р., 13.11. 2012 г. – 5400 р., 07.03.2013 г. – 5700 р. и 31.05.2013 г. – 6200 р. Оценить выгодность предложения, если существует возможность положить деньги в банк под 13% годовых.
Задача 2. Вы заняли на 4 года 10000 руб. под 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определить величину годового платежа.
Задача 3. Предприятие рассматривает целесообразность принятия новой технологической линии. На рынке имеются две модели со следующими параметрами:
П1 П2
Цена……………………………………….. 9500 13000
Генерируемый годовой доход…….2100 2250
Срок эксплуатации……………………. 8 лет 12 лет
Ликвидационная стоимость………..500 800
Требуемая норма прибыли…………..11% 11%
Обоснуйте целесообразность приобретения той или иной технологической линии.
Задача 4. Вы открываете счёт и собираетесь вкладывать по 1400 р. в начале каждого года в течении 8 лет при годовой ставке 3,5%. Сколько денег будет на счете через 8 лет?
Задача 5. Контракт между фирмой и банком предусматривает в течение 3 лет фирме ежегодными платежами в размере 24 тыс. руб. в начале каждого года под ставку 14% годовых. Фирма возвращает долг, выплачивая последовательно в конце 3,4,5 годов. Какова чистая современная величина NPV для банка?
Задача 6. Годовая процентная ставка составляет 9% и остается неизменной в течение всего периода, а годовая купонная ставка по облигации с номиналом 1400 руб. со сроком обращения 10 лет установлена в размере 14%. Сколько стоит эта облигация при эмиссии? Сколько будет стоить эта облигация через 5 лет. Какова доходность облигации за 10 лет.
Задача 7. Кредит в размере 500 млн. руб. выдан на 5 лет под 17 % годовых с начислением процентов и выплатой в конце каждого года. Выплаты основного долга должны уменьшаться ежегодно на 8 млн. руб. Составить план погашения кредита.
Задача 8. На вклад начисляются сложные проценты: а) каждые полгода; б) ежеквартально; в) ежемесячно. Вычислить годовую номинальную процентную ставку, при которой происходит реальное наращение капитала, если ежеквартальный темп инфляции составляет 2%. Известно:
h = 2%; m1 = 2; m2 = 4; m3 = 12.
Найти: i1 — ? i2 — ? i3 — ?
Задача 9. Предприниматель получил ссуду в банке в размере 20 млн. руб. сроком на 5 лет на следующих условиях: для первых двух лет процентная ставка равна 25% годовых, на оставшиеся 3 года ставка равна 23% годовых. Найдите доход банка за 5 лет, если сложные ссудные проценты начисляются ежеквартально.
Известно: Р = 20 000 000 руб.; i1 = 0,25 или 25% n1 = 2 года i2 = 0,23 или 23% n2 = 3 года m = 4
Найти: I — ?
Задача 10. Определить годовую процентную ставку банка, если вкладчик внес 3297 д.е. на 6 лет, сумма на счете в конце срока составила 12934 д.е. В первую треть срока начислялись простые проценты, а в оставшийся – сложные, 5 раз в год.
Помогаем с решением задач по финансовой математике
Может быть интересно:
|
|
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
|
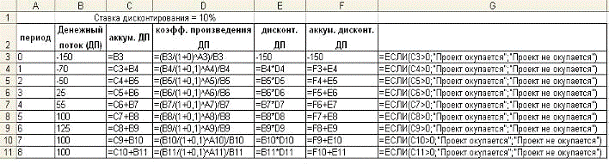
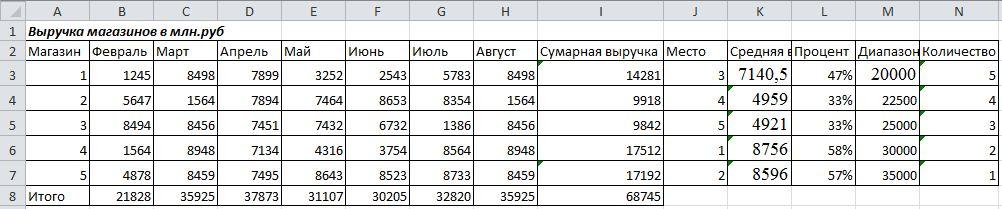
Задача 1 Ожидается, что проект, требующий инвестиций в размере 100 тыс.долл., будет генерировать доход в течении 8 лет в сумме 30 тыс.долл. ежегодно. Приемлемая ставка дисконтирования равна 10%. Рассматриваются два варианта: без учета риска и с учетом риска. В первом случае анализ проводится без какой-либо корректировки исходных данных. Во втором случае для последних трех лет вводится понижающий коэффициент 0,9, а так же поправка на риск к ставке дисконтирования в размере трех процентных пунктов. Стоит ли принять этот проект в каждом из приведенных вариантов? А) без учета риска. Формула дисконтирования выглядит следующим образом: где PVk – приведенная (текущая) стоимость денежного потока k-го периода проекта NCFk – чистый денежный поток k-го периода проекта k – период проекта r – ставка дисконтирования (в десятичном выражении) Ставка дисконтирования нашего проекта составляет 10%, то есть r = 0.1. Дисконтируем чистый денежный поток (NCF) 1-8 периодов. Подставляя в формулу дисконтирования соответствующие значения, получаем: Теперь рассчитаем первый показатель эффективности инвестиционного проекта – NPV (Net Present Value) – чистая приведенная стоимость проекта. Классическая формула для расчета NPV выглядит следующим образом: где NPV – чистый приведенный денежный поток NCF – чистый денежный поток соответствующего периода проекта n – горизонт исследования, выраженный в интервалах планирования (срок проекта) k – период проекта r – ставка дисконтирования (в десятичном выражении) Показатель NPV заключается в суммировании дисконтированных чистых денежных потоков (PV) c 1 по n-ый период проекта и прибавлении к нему отрицательного денежного потока 0-го периода (инвестиций). То есть за счет положительного, либо отрицательного знака чистого денежного потока каждого периода при расчете NPV у нас осуществляется сложение, либо вычитание соответственно дисконтированного денежного потока каждого следующего периода. NPV = PV1период PV2период … PV8период NCF0 = 27,27 24,78 22,54 20,49 18,63 16,94 15,39 13,99 – 100 = 60,03 тыс. дол. Если NPV > 0, это значит, что проект в рассматриваемый период обеспечит даже min доход, равный доходу от безрисковых вложений, заложенный в ставке дисконтирования, а, возможно, покроет даже инвестиции и текущие затраты. Б) с учетом риска Другим важным фактором, влияющим на оценку эффективности инвестиционного проекта, является фактор риска. Поскольку риск в инвестиционном процессе независимо от его конкретных форм, в конечном счете, предстает в виде возможного уменьшения реальной отдачи от капитала по сравнению с ожидаемой, то для учета риска часто вводят поправку к уровню процентной ставки, которая характеризует доходность по безрисковым вложениям (например, по сравнению с банковскими депозитами или краткосрочными государственными ценными бумагами). Ставка дисконтирования проекта составляет 10%, то есть r = 0.1. в первые 5 лет, а в следующие 3 года r = 0,13. Дисконтируем чистый денежный поток (NCF) 1-8 периодов. Подставляя в формулу дисконтирования соответствующие значения, получаем: NPV = PV1период PV2период … PV8период NCF0 = 27,27 24,78 22,54 20,49 18,63 16,02 14,17 12,54 – 100 = 56,44 тыс. дол. Как и в первом случае NPV > 0, это значит, что проект в рассматриваемый период обеспечит доход 56,44 тыс. долл. Ответ: В обоих случаях этот проект стоит принять т.к. он обеспечивает доход и покрывает инвестиционные и текущие затраты. Задача 2 По имеющимся данным о выпуске и себестоимости однородной продукции за год определите структуру затрат: а) методом максимальной и минимальной точки; б) методом регрессионного анализа. Методику определения структуры затрат см. в источниках [7, 11]. Данные о выпуске продукции и затратах на производство
|
Существует три основных метода дифференциации издержек:
1. Метод максимальной и минимальной точки
2. Графический (статистический) метод
3. Метод наименьших квадратов.
При методе дифференциации издержек методом максимальной и минимальной точки из всей совокупности данных выбираются два периода с наибольшим и наименьшим объёмом производства. Определяется ставка переменных издержек – это средние переменные расходы в себестоимости единицы продукции.
Ставка переменных издержек = [(Максимальная общая сумма издержек – минимальная общая сумма издержек]: , (34)
Определяется общая сумма постоянных издержек:
Постоянные издержки = Максимальная общая сумма издержек – ставка переменных издержек (35)
2. Дифференциация издержек графическим (статистическим) методом.
Как известно, линия общих издержек определяется уравнением первой степени:
Y = a b x,
где Y – общие издержки;
a – уровень постоянных издержек;
b – ставка переменных издержек;
x – объём производства, физических единиц.
Статистический метод основан на использовании коррекционного анализа, хотя сами коэффициенты коррекции не определяются.
Ставка переменных издержек = (совокупные издержки – постоянные издержки)/объём производства
3. Дифференциация затрат методом наименьших квадратов является наиболее точной, так как в ней используются все данные о совокупных издержках и определяются коэффициенты a и b.
Ставка переменных издержек b равна
А) Дифференциация издержек методом максимальной и минимальной точки.
Из всей совокупности данных выбираются два периода с наибольшим и наименьшим объемом производства – август и февраль. В августе сумма переменных издержек будет максимальной, а постоянных – минимальной. В феврале – соответственно наоборот.
|
Показатель |
Объем производства |
Разность между max и min величинами |
|
|
максимальный |
минимальный |
||
|
1. Объем производства, тыс.шт. |
590 |
230 |
360 |
|
% |
100 |
38,9 |
61,1 |
|
2. Выручка, тыс.руб. |
350 000 |
215 000 |
135 000 |
|
3. Затраты, тыс.руб. |
250 000 |
190 000 |
60 000 |
Ставка переменных издержек = [(250 000-190 000)]х ]:590 = 166,4 руб/шт
Определяется общая сумма постоянных издержек:
Постоянные издержки = 250 000-166,4 руб/шт х 590 тыс.шт. = 151 824 тыс.руб.
Б) По методу максимальной и минимальной точки:
Y=151 824 166,4 х
Алгоритм определения коэффициентов и результаты расчетов представлены в таблице
|
Месяц |
Объем производства Х (тыс.шт.) |
, (тыс.шт.) |
Суммарные издержки Y (тыс.руб.) |
, (тыс.руб.) |
||
|
январь |
260 |
-125 |
195 000 |
-18 750 |
15 625 |
2 343 750 |
|
февраль |
230 |
-155 |
190 000 |
-23 750 |
24 025 |
3 681 250 |
|
март |
310 |
-75 |
200 000 |
-13 750 |
5 625 |
1 031 250 |
|
апрель |
280 |
-105 |
200 000 |
-13 750 |
11 025 |
1 443 750 |
|
май |
350 |
-35 |
205 000 |
-8 750 |
1 225 |
306 250 |
|
июнь |
410 |
25 |
215 000 |
1 250 |
625 |
31 250 |
|
июль |
520 |
135 |
240 000 |
26 250 |
18 225 |
3 543 750 |
|
август |
590 |
205 |
250 000 |
36 250 |
42 025 |
7 431 250 |
|
сентябрь |
370 |
-15 |
210 000 |
-3 750 |
225 |
56 250 |
|
октябрь |
490 |
105 |
230 000 |
16 250 |
11 025 |
1 706 250 |
|
ноябрь |
450 |
65 |
225 000 |
11 250 |
4 225 |
731 250 |
|
декабрь |
360 |
-25 |
205 000 |
-8750 |
625 |
218 750 |
|
Итого |
4620 |
2 565 000 |
134 500 |
22 525 000 |
||
|
среднее |
385 |
213 750 |
Ставка переменных издержек равна:
Переменные издержки в расчете на среднемесячный объем производства составляют 385 тыс.шт.х167,47 руб/шт=64 475,95 тыс.руб. Тогда постоянные издержки составляют 213 750-64 475,95= 149 274,1 тыс.руб.
По методу регрессионного анализа:
Y=149 274,1 167,47 х
Задача 3
Компания осуществляет закупки на условиях 2/20 брутто 45, не пользуется скидкой и производит оплату на 90-й день. С течением времени поставщик стал требовать строго соблюдения сроков оплаты. Компания может получить банковский кредит сроком на год на условиях: ставка кредита 20% простых в год, компенсационный остаток – 25%.
Отчетный баланс компании, млн.руб.
|
АКТИВ |
Значение |
ПАССИВ |
Значение |
|
Денежные средства |
10 |
КЗ |
60 |
|
Дебиторская задолженность |
25 |
Веселя к оплате |
10 |
|
Запасы |
80 |
Начисления |
10 |
|
Основные средства |
60 |
Долгосрочные пассивы |
25 |
|
Обыкновенные акции |
70 |
||
|
Баланс |
175 |
Баланс |
175 |
Определите цену нового торгового кредита, сравните с банковским кредитом. Постройте новый баланс фирмы.
Если компания осуществляет закупки на условиях 2/20 брутто 45, это значит, что фирма готова предоставить скидку 2% если оплата будет осуществлена в течение 20 дней со дня, обозначенного в счете-фактуре. Минимальный срок, в течение которого должна быть произведена оплата без предоставления скидки, составляет 45 дней.
Если компания производит закупки ежегодно на сумму 60 млн рублей ( эта сумма отражена в балансе по строке «кредиторская задолженность»), то ежедневно ее закупки составят сумму в: 60/360 = 0,166 млн.рублей в день
Если бы компания пользовалась скидкой, производя оплату на 20 день, ее кредиторская задолженность составит в среднем: 20х0,166= 3,32 млн.рублей
Т.к. компания решила отказаться от скидки и производить оплату на 90 день, то ее кредиторская задолженность увеличится и составит:
45*0,166=7,47 млн.рублей
Таким образом, дополнительный кредит составит:
7,47-3,32 = 4,15 млн.рублей и может быть использован на осуществление закупок.
Компания отказалась от скидки в 2% на 60 млн.рублей закупок, то есть в год дополнительные затраты составляют 0,02х60 =1,2 млн.рублей.
Тогда цена торгового кредита составит
Цкр=1,2 /4,5 = 28,9 %
Эффективная годовая ставка по торговому кредиту
Ставка процента за кредит за период:
0,02/0,98= 0,0204
Дополнительный срок пользования кредитом составляет 45-20= 25 дней, в году таких периодов 360/25=14,4. Эта ставка начисляется 14,4 раза в год, таким образом, цена торгового кредита, рассчитанная как эффективная годовая ставка, составит:
(1,0 0,0204)14,4-1,0=0,338 или 33,8%
Рассчитаем эффективную ставку банковского кредита.
Если банк требует что на счету у компании оставался компенсационный остаток в размере 25% от суммы кредита, то значит компания вынуждена увеличить сумму кредита до 60 0,25х60=75 млн.рублей
Если ставка за кредит равна 20%, то общая сумма процентов составит 75*0,2= 15 млн.рублей.
Поскольку со счета можно снять только 60 млн.рублей, то фактически эффективная ставка процента равна 15/60=0,25 или 25%.
Если фирма решила воспользоваться скидкой и отказаться от торгового кредита, ей придется привлекать дополнительные средства из банка. Ежедневно она приобретает товар на сумму 0,166 млн.рублей, и спустя 20 дней, ее кредиторская задолженность будет равна 3,32 млн.рублей
При составлении прогнозного баланса предполагается, что величина активов, начислений и акционерного капитала не меняются и не зависят от выбора того или иного подхода. Балансы отличаются лишь суммами по статьям «кредиторская задолженность» и «векселя к оплате». Также нужно учесть, что, на сколько снижается кредиторская задолженность в пассиве баланса, на столько увеличиваются денежные средства и снижаются товарно-материальные запасы в активе баланса.
Прогнозный баланс компании, млн.руб.
|
АКТИВ |
Значение |
ПАССИВ |
Значение |
|
Денежные средства |
25 |
КЗ |
45 |
|
Дебиторская задолженность |
25 |
Веселя к оплате |
25 |
|
Запасы |
65 |
Начисления |
10 |
|
Основные средства |
60 |
Долгосрочные пассивы |
25 |
|
Обыкновенные акции |
70 |
||
|
Баланс |
175 |
Баланс |
175 |
Если компания отказывается от скидки, то расходы по выплате процентов по кредиту равны нулю, но в то же время увеличатся затраты на величину возможной скидки, что составляет 1,2 млн.рублей. С другой стороны, если фирма решает воспользоваться скидкой, то ей придется нести дополнительные расходы по выплате процентов за привлеченный кредит
Таким образом, сравнивая дополнительные расходы и выгоды, можно сделать вывод, что сумма упущенной выгоды ниже, чем расходы по выплате процентов.
Задача 4
По приведенным данным рассчитать среднюю продолжительность оборота (погашения) дебиторской задолженности покупателей и кредиторской задолженности поставщикам в отчетном и базисных годах. Определить влияние отдельных факторов на ускорение (замедление) оборачиваемости дебиторской и кредиторской задолженности в отчетном году по сравнению с базисным годом. Оценить эффективность отвлечения средств в дебиторскую задолженность и обоснованность привлечения заемных средств в виде товарного кредита.
|
Показатель |
Условн. обознач. |
Предыд. год |
Отчетн. год |
|
1. Выручка от продаж, тыс. руб. |
В |
29 670 |
33 304 |
|
2. Себестоимость проданной продукции, тыс. руб. |
Sпр |
21 670 |
22 280 |
|
3. Среднегод. балансовая величина дебитор. задолж., тыс. руб. |
2318 |
2555 |
|
|
4. Среднегод. балансовая величина кредитор. задолж., тыс.руб |
2022 |
1911 |
|
|
5. Средняя продолжительность оборота (погашения) ДЗ, дни |
Lдз |
||
|
6. Средняя продолж-ть оборота (погашения) КЗ поставщикам., дни |
Lкзп |
Влияние факторов на коэффициенты оборачиваемости анализируется по модели:
,
где Кобi – коэффициент оборачиваемости i-го вида оборотных средств;
В – выручка от реализации;
средние остатки i-го вида оборотных средств.
Средняя продолжительность 1 оборота в днях вычисляется по формуле

Показатель |
Условн. обознач. |
Предыд. год |
Отчетн. год |
|
1. Выручка от продаж, тыс. руб. |
В |
29 670 |
33 304 |
|
2. Себестоимость проданной продукции, тыс. руб. |
Sпр |
21 670 |
22 280 |
|
3. Среднегод. балансовая величина дебитор. задолж., тыс. руб. |
2318 |
2555 |
|
|
4. Среднегод. балансовая величина кредитор. задолж., тыс.руб |
2022 |
1911 |
|
|
5. Коэффициент оборачиваемости ДЗ, об |
Коб дз |
12,8 |
13,03 |
|
6. Коэффициент оборачиваемости КЗ, об |
Коб кз |
14,75 |
17,43 |
|
7. Средняя продолжительность оборота (погашения) ДЗ, дни |
Lдз |
28,125 |
27,628 |
|
8. Средняя продолж-ть оборота (погашения) КЗ поставщикам., дни |
Lкзп |
24,41 |
20,65 |
Проанализируем влияние факторов на коэффициент оборачиваемости дебиторской задолженности. Общее отклонение коэффициента оборачиваемости дебиторской задолженности:
В том числе за счет изменения отдельных факторов:
за счет изменения выручки от реализации:
за счет изменения среднего остатка готовой продукции:

Коэффициенты оборачиваемости |
Базисный год |
Отчетный год |
Изменение |
||
|
всего |
в т.ч. за счет изменений |
||||
|
объема реализации |
средних остатков средств |
||||
|
1. Дебиторской задолженности |
12,8 |
13,03 |
0,23 |
-954,52 |
-2388,75 |
|
2 Кредиторской задолженности |
14,75 |
17,43 |
2,68 |
-1099,70 |
1568,05 |
Экономический эффект в результате ускорения оборачиваемости выражается в относительном высвобождении средств из оборота, а также в увеличении суммы выручки и прибыли. Сумма высвобождаемых средств из оборота в связи с ускорением (-Э) или дополнительно привлеченных средств в оборот ( Э) при замедлении оборачиваемости определяется по формуле:

Оборотные активы |
Оборачиваемость, в днях |
Влияние на размер оборотных активов, тыс.руб. |
|||
|
базисный год |
отчетный год |
изменения ( , -), ДПобi |
высвобождение средств |
дополнительное привлечение средств |
|
|
1. Дебиторская задолженность |
28,125 |
27,628 |
-0,497 |
-15,2 |
x |
|
2 Кредиторская задолженность |
24,41 |
20,65 |
-3,74 |
-114,9 |
x |
Задача 5
Выручка от реализации в компании АА в январе составила 50 000 долл.; в последующие месяцы ожидается прирост с темпом 1% в месяц. Оплата за поставленную клиентам продукцию осуществляется на следующих условиях: 20% месячного объема реализации составляет выручка за наличный расчет; 40% продается в кредит с оплатой в течение месяца и предоставляемой клиентам скидкой в размере 3%; оставшаяся часть продукции оплачивается в течении двух месяцев, при этом 5 % этой суммы составляют безнадежные долги.
Рассчитайте величину денежных поступлений в июне.
При планировании поступлений денежных средств проводится расчет предполагаемых поступлений денежных средств на основании имеющихся плановых данных по доходам за данный период и возможным погашением дебиторской задолженности покупателями (Поступления)
Расчет поступлений выполняется с учетом сложившейся практики взаимоотношений с покупателями. Для этого с помощью, например, статистических методов проводится анализ текущей деятельности предприятия и определяются следующие показатели:
сроки погашения дебиторской задолженности;
процент поступающих авансов от общей суммы, реализуемой продукции (товара);
сроки от получения авансов до исполнения предприятием соответствующих обязательств;
процент «безнадежных» долгов в общей доле предъявленных покупателям счетов.
Расчет этих показателей производится по каждому виду деятельности в разрезе групп контрагентов. Для этого можно использовать бухгалтерскую базу предприятия.
|
Показатель |
Январь |
Февраль |
Март |
Апрель |
Май |
Июнь |
|
Выручка от реализации |
50000 |
50500 |
51005 |
51515,05 |
52030,2 |
52550,5 |
|
В т.ч. реализация в кредит |
40000 |
40400 |
40804 |
41212,04 |
41624,16 |
42040,4 |
|
Поступление денежных средств-всего, в том числе: |
10000 |
25620 |
47876,2 |
48354,96 |
48838,51 |
49326,9 |
|
20%-выручка за наличный расчет |
10000 |
10100 |
10201 |
10303,01 |
10406,04 |
10510,1 |
|
40% реализации в кредит прошлого месяца (3%-скидка) |
– |
15520 |
15675,2 |
15831,95 |
15990,27 |
16150,17 |
|
55% реализации в кредит позапрошлого месяца |
– |
– |
22000 |
22220 |
22442,2 |
22666,62 |
Величина денежных поступлений в июне составила 49 326, 9 тыс.рублей.
Задача 6
Планируемая годовая потребность в материалах составляет 180 тыс.ед. Если заказывается партия объемом менее 50 тыс.ед., то себестоимость материалов будет 20 руб. за единицу, если объем заказа выше, то можно получить скидку в размере 5%. Анализируются две альтернативы: а) делать два заказа по 90 тыс.ед. в каждом; б) делать ежемесячный заказ по 15000 ед.
Требуется: а) определить, какая из этих альтернатив является более дорогостоящей для компании; б) найти, во что обходится компании выбор более дорогостоящего варианта, если высвобожденные деньги можно было бы вложить в банк под 8% годовых.
А) определить, какая из этих альтернатив является более дорогостоящей для компании
а) (90000 ед. * (20 руб. * 5 %)) * 2 = 3 420 000 руб.
б) 15000 ед. * 20 руб. * 12 мес. = 3 600 000 руб.
Таким образом, второй вариант является более дорогостоящим.
Б) FV = (3600000-3420000) * (1 0.08) = 180000*1.08 = 194400
Доход составил бы 14400 руб.
Задача 7
Компания АВ делает заказ сырья по цене 4 долл. за единицу партиями в объеме 200 единиц каждая. Потребность в сырье постоянна и равна 10 единиц в день в течении 250 рабочих дней. Стоимость исполнения одного заказа 25 долл., а затраты по хранению составляют 12,5 % стоимости сырья.
1. Рассчитайте оптимальный размер заказа EOQ и эффект от перехода от текущей политики заказа сырья к политике, основанной на EOQ.
2. Поставщик соглашается снизить цену сырья, если заказ будут делать большими партиями. Условия таковы: при объеме заказа до 599 ед., скидка не предоставляется; при объеме заказа от 600 до 999 ед., скидка составит 10%; при объеме заказа более 1000 ед., скидка – 15%. Рассчитайте EOQ в этих условиях.
1) Величина оптимального заказа (EOQ) определяется по формуле (модель Уилсона):
,
Где F – постоянные затраты по размещению и выполнению одного заказа, $.;
Z – общая годовая потребность в запасах, ед.;
С – годовые затраты по хранению, в долях ед.;
Р – цена приобретения единицы запасов, $.
ед.
Рассчитаем эффект (Э) от перехода от текущей политики заказа сырья к политике, основанной на EOQ, для этого рассчитаем затраты для текущей политики (размер партии 200 шт.) и затраты для оптимального заказа (размер партии 500 шт.)
,
где ; – затраты на транспортировку, – затраты на хранение
; – объем партии
При скидке 10 % при объеме заказа от 600 до 999 ед:
При скидке 15 % при объеме заказа более 1000 ед:

Финансовые задачи в Excel
Экономический
факультет
Кафедра
Информационных технологий
Информационные
системы в экономике
Финансовые
задачи в Excel
Содержание
Раздел 1 Технология работы с
финансовыми Функциями Еxcel. Основные понятия финансовых методов расчета 4
.1 Операции наращения.
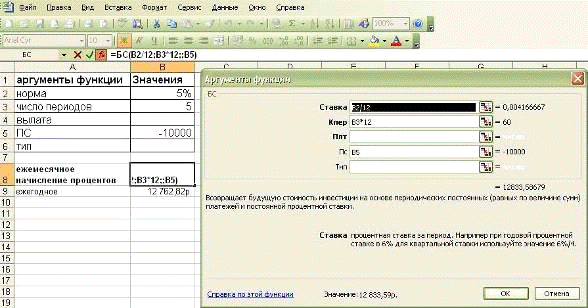
Функция бс(). 11
.2 Операции дисконтирования 16
.3 Определение срока
финансовой операции 17
.4 Определение процентной
ставки 18
.5 Расчет эффективной и
номинальной ставки процентов 19
.6 Начисление процентов по
плавающей ставке 20
Раздел 2. Потоки платежей и
финансовые ренты 22
.1 Определение будущей
(наращенной) стоимости потока платежей. Функция бс() 23
.2 Современная (текущая)
величина аннуитета. Функция пс() 25
.3 Расчет периодических
платежей 27
Раздел 3. Оценка
инвестиционных процессов 36
.1.Чистый приведенный доход.
Функция чпс 37
.2 Срок окупаемости 41
.3 Индекс рентабельности 43
.4 Внутренняя норма
доходности.Функция чиствндох 45
.5 Модифицированная
внутренняя норма доходности.Функция мсвд 46
.6 Денежный поток
инвестиционного проекта с произвольными периодами поступления платежей 49
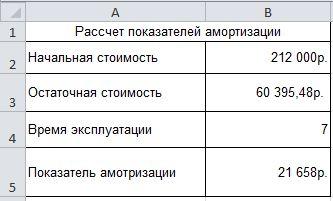
Раздел 4. Функции excel для
расчета амортизации 51
Аргументы функций excel для
расчета амортизации 51
Контрольные работы 55
Раздел 1. Технология работы с финансовыми функциями Еxcel. Основные понятия финансовых методов расчета
финансовый программа функция
Рассмотрим процесс наращения (accumulation), т.е. определения денежной сумм
будущем, исходя из заданной суммы сейчас.
Экономический смысл операции наращения состоит в
определении величины той суммы, которой будет или желает располагать инвестор
по окончании этой операции. Здесь идет движение денежного потока от настоящего
к будущему.
Существуют различные способы начисления процентов и
соответствующие процентных ставок
Величина FV показывает будущую стоимость «сегодняшней» величины инвестиции PV при заданном уровне интенсивности
начисления процентов r
Простая процентная ставка — применяется к одной и той же первоначальной сумме
долга на протяжении всего срока ссуд исходная база (денежная сумма) всегда одна
же.
Сложная процентная ставка — применяется к наращенной сумме долга, т.е сумме,
увеличенной на величину начисленных предыдущий период процентов, — таким
образом исходная база постоянно увеличивается.
Фиксированная процентная ставка — ставка, зафиксированная в виде
определенного числа (сумы) в финансовых контрактах.
Плавающая процентная ставка — привязанная к определенной величине, изменяющейся
во времени, включая надбавку к ней (маржу), которая определяется целым рядом
условий (сроком операции и т.п.).
Постоянная процентная ставка — неизменная на протяжении всего
периода ссуды.
Переменная процентная ставка — дискретно изменяющаяся во времени,
но имеющая конкретную числовую характеристику.
В любой простейшей финансовой операции всегда
присутствуют четыре величины:
время (n)
современная величина (PV),
— наращенная или будущая величина (FV),
— процентная ставка (r)
n — Срок погашения долга (англ. number of periods) — интервал времени, по истечении которого сумму
долга и проценты нужно вернуть. Срок измеряется числом расчетных периодов —
обычно равных по длине подинтервалов времени, в конце (или начале) которых
начисляются проценты.
Если начисление процентов будет производиться m раз в год, а срок погашения
долга — n лет, то общее количество периодов начисления за весь
срок финансовой операции составит
PV—
текущая стоимость (англ. present value) — исходная сумма или
оценка современной величины денежной суммы, поступление которой ожидается в
будущем, в пересчете на более ранний момент времени;
FV—
будущая стоимость (англ. future value) — наращенная сумма или
будущая стоимость, т.е. первоначальная сумма долга с начисленными на нее
процентами к концу срока ссуды;
I— Процентные деньги (англ. interest
money), называемые часто коротко «проценты», представляют
собой абсолютный доход от предоставления долга.
I=FV—PV
Оценка
эффективности финансовых операций по величине процентных денег на практике
используется достаточно редко, так сама их величина, не учитывающая фактор
времени, мало что может сказать о реальной доходности операции. Необходимо
иметь возможность сопоставить ее с темпом обесценивания денег (инфляции) или
результатами другой финансовой операции. Поэтому в финансово-экономических
расчетах наиболее широко пользуются относительные показатели:
г
— процентная ставка (rate of interest), характеризующая
интенсивность начисления процентов за единицу времени,- отношение суммы
процентных денег, выплачивающихся за определенный период времени, к величине
ссуды. Этот показатель выражается либо в долях единицы, либо в процентах.
На
рабочем листе в отдельных ячейках осуществляется подготовка значений основных
аргументов функции.
Для
расчета результата финансовой функции Excel курсор устанавливается в
новую ячейку для ввода формулы, использующей встроенную финансовую функцию.
Осуществляется
вызов «Мастера функций»
На
основной панели инструментов имеются кнопки «Мастер функций», с
помощью которой открывается диалоговое окно Диспетчера функций.
Диалоговое
окно «Диспетчер функций» организовано по тематическому принципу.
После выбора в левом списке «Категории» тематической группы «Финансовые»,
на экран будет выведено диалоговое окно с полным перечнем списка имен
функций, содержащихся в данной группе.
Поиск
необходимой финансовой функции осуществляется путем последовательного просмотра
списка.
Для
выбора функции курсор устанавливается на имя функции.
Рис.1-3.
Последовательность действий при выборе необходимой финансовой функции
В
результате выполненных действий на экране откроется диалоговое окно выбранной
функции.
В
поля диалогового окна функции:
можно
вводить как сами значения аргументов, так и ссылки на адреса ячеек, содержащие
необходимые значения;
все
расходы денежных средств (платежи) представляются отрицательными числами, а все
поступления денежных средств — положительными числами;
процентная
ставка вводится в виде десятичной дроби, либо с использованием знаке %;
Для
исчисления характеристик финансовых операций с наращением и дисконтированием
вложенных сумм удобно использовать функции БС, IIC, KIIEP,
СТАВКА, БЗРАСПИС, НОМИНАЛ, ЭФФЕКТ. ПРПЛТ, ОБЩПЛАТ, ОСППЛАТ, ОБЩДОХОД.
Таблица
1.
Функции
рабочего листа Excel для оценки разовых и периодических (потоков)
|
Наименование функции |
Формат функции |
Назначение функции |
|
БС |
БС(ставка ;кпер;плт;пс;тип) |
рассчитывает будущую |
|
ПС |
ПС(ставка ;кпер;плт;бс;тип) |
предназначена для расчета |
|
КПЕР |
КПЕР(ставка ;плт;пс;бс;тип) |
вычисляет количество |
|
СТАВКА |
СТАВКА(кпер;плт;пс;бс;тип) |
вычисляет процентную |
|
БЗРАСПИС |
БЗРАСПИС (сумма; массив |
удобно использовать для |
|
НОМИНАЛ |
НОМИНАЛ (эф_ставка;кол_пер) |
Возвращает номинальную |
|
ЭФФЕКТ |
ЭФФЕКТ (ном_ставка; |
Возвращает фактическую |
|
ПРПЛТ |
ПРПЛТ(ставка;период;кпер;пс |
Возвращает сумму платежей |
|
ОСПЛТ |
ОСПЛТ(ставка |
Возвращает величину платежа |
|
ОБЩДОХОД |
ОБДОХОД |
Вычисляет сумму основных |
|
ПЛТ |
ПЛТ(ставка;кпер;нз;бс; тип) |
позволяет рассчитать сумму |
|
ЧПС |
ЧПС (ставка;значение 1; |
Возвращает величину чистой |
|
ЧИСТВНДОХ |
ЧИСТВНДОХ |
Возвращает внутреннюю сумму |
|
ЧИСТНЗ |
ЧИСТНЗ |
Возвращает чистую текущую |
|
МСВД |
МСВД |
Возвращает модифицированную |
|
ВСД |
ВСД(значения;предположение) |
Возвращает внутреннюю |
|
АПЛ |
АПЛ(нач_стоимость;ост_стоимость;время_эксплуатации) |
Возвращает величину |
|
АСЧ |
АСЧ(нач_стоимость;ост_стоимость; |
Возвращает величину |
|
ДДОБ |
ДДОБ(нач_стоимость;ост_стоимость;время_эксплуатации;период; |
Возвращает значение |
|
ФУО |
ФУО(нач_стоимость;ост_стоимость; |
Возвращает величину |
Как видно из приведенной таблицы, большинство
финансовых функций имеет одинаковый набор базовых аргументов:
ставка — процентная ставка за период (норма
доходности или цена заемных средств — r)
Например, если получена ссуда на автомобиль под 10
процентов годовых и делаются ежемесячные выплаты, то процентная ставка за месяц
составит 10%/12 или 0,83%. В качестве значения аргумента ставка нужно ввести в
формулу 10%/12 или 0,83% или 0,0083
кпер — срок (число периодов N) проведения операции. Например, если получена ссуда на
4 года под приобретение автомобиля и делаются ежемесячные платежи, то ссуда
имеет 4* 12 (или 48) периодов. В качестве значения аргумента кпер в
формулу нужно ввести число 48.
Плт — выплата, производимая в каждый период и не
меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи
и платежи по процентам, но не включают других сборов или налогов. Например,
ежемесячная выплата по четырехгодичному займу в 10 000 руб. под 12 процентов
годовых составит 263,33 руб. В качестве значения аргумента выплата нужно ввести
в формулу число -263,33.
Пс — это приведенная к текущему моменту стоимость
(величина PV) или общая сумма, которая на текущий момент равноценна
ряду будущих платежей. Если аргумент ПС опущен, то он полагается равным
0. В этом случае должно быть указано значение аргумента Плт.;
Бс — требуемое значение будущей стоимости (FV) или остатка средств после последней выплаты. Если
аргумент опущен, он полагается равным 0 (будущая стоимость займа, например,
равна 0). Например, если предполагается накопить 50000 руб. для оплаты
специального проекта в течение 18 лет, то 50 000 руб. это и есть будущая
стоимость
[тип] — число 0 или 1, обозначающее, когда
должна производиться выплата, 1 — начало периода (обычная рента или
пренумерандо), 0 — конец периода (постнумерандо).
1.1
Операции наращения. Функция БС().
Функции, обслуживающие расчеты по операциям наращения
позволяют рассчитать будущую стоимость разовой суммы по простым и сложным
процентам, а также будущее значение потока платежей, как на основе постоянной
процентной ставки, так и на основе переменной процентной ставки.
Функция БС() — будущее значение — рассчитывает
наращенную величину разовой денежной суммы или периодических постоянных
платежей на основе постоянной процентной ставки.
Простые проценты. Для решения задач наращения по схеме
простых процентов функция БС() в качестве аргументов использует только
аргументы: норма; число периодов; ПС.
Остальные аргументы не используются.
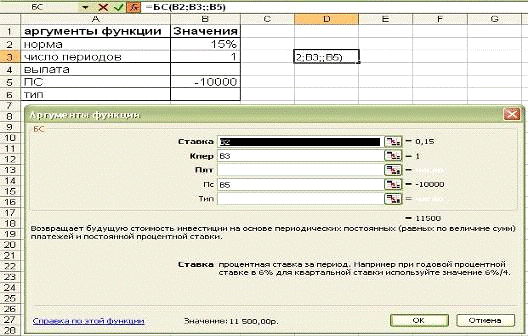
Пример 1-1
Определить наращенную сумму для
вклада в размере 10000 руб., размещенного под 15% годовых на один год.
Рис. 1-4 Решение примера 1-1.
Таким образом, через год наращенная
сумма составит 11500 руб.
В приведенном примере, в качестве аргумента функции Кпер
было указано целое число (1 год).
Если продолжительность финансовой операции
представлена в днях, то необходимо ввести корректировку в процентную ставку,
т.е. аргумент норма должен быть представлен как t/ T *r%.
Если время финансовой операции выражено в днях, то
расчет простых процентов может быть произведен одним из трех возможных
способов:
Обыкновенные проценты с приближенным числом дней
ссуды, или, как часто называют «германская практика расчета», когда
продолжительность года условно принимается за 360 дней, а целого месяца — 30
дней.
1.
Обыкновенные
проценты с точным числом дней ссуды, или «английская практика расчета», когда
продолжительность года условно принимается за 360 дней, а продолжительность
суды рассчитывается точно по календарю.
2.
Точные проценты с
точным числом дней ссуды, или «английская практика расчета», когда
продолжительность года и продолжительность ссуды берутся точно по календарю
Пример 1-2
Вклад размером в 2000 руб. положен с
06.06 по 17.09 невисокосного года под 30% годовых. Найти величину капитала на
17.09 по различной практике начисления процентов.
Решение
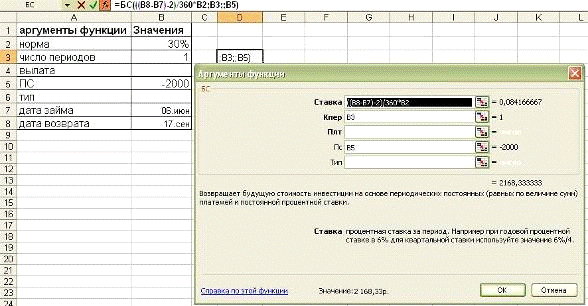
Германская практика расчета
В соответствии с германской практикой
расчета период накопления составляет 101 день.
БС(((В8-В7)-2)/360*В2;ВЗ;;В5) =2168,3
руб.
Рис. 1-5 Решение примера 1-2
(Германская практика расчета).
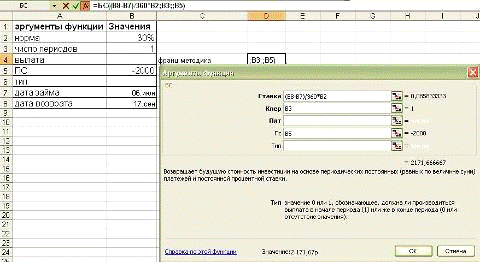
Французская система расчета
В соответствии с германской практикой
расчета период накопления составляет 103 дня.
БС(((В8-В7))/360*В2;ВЗ;;В5) = 2171,7
руб.
Рис. 1-6 Решение примера 1-2
(Французская система расчета).
Таким образом, начисление процентов
по германской практике приведет к получению суммы в размере 2168,33 руб., по
французской практике — 2171,7 руб.
Сложные проценты
При использовании сложных процентов используются те же
аргументы, что и в простых процентах, с использованием годовой процентной
ставки и целого числа лет.
Пример 1-3
Определить будущую величину вклада в
10000 руб. помещенного в банк на 5 лет под 5% годовых, если начисление
процентов осуществляется:
а) раз в году;
б) раз в месяц.
Решение
Рис. 1-7 Решение примера 1-3 при
ежемесячном начислении процентов
а) 12762,83 руб.
б) 12833,59 руб.
Обратите внимание, что если же период начисления
процентов будет меньше года, то необходимо модифицировать аргументы ставка
и число периодов:
ставка — берется ставка процентов за период
начисления, т.е. используется номинальная годовая ставка процентов,
скорректированная на число раз (т) начисления процентов в течение года r% / т;
число периодов — указывается общее число раз
начисления процентов за весь срок финансовой операции п • т.
1.2
Операции дисконтирования
Для расчета приведенной к конкретному моменту времени
наращенной суммы Excel предлагает
использование встроенной финансовой функции ПС().
Расчет с использованием функции ПС() является
обратным к определению наращенной суммы при помощи функции БС, поэтому
сущность используемых аргументов в этих функциях аналогична. Вместе с тем,
аргумент ПС заменяется на аргумент БС — будущая стоимость или
будущее значение денежной суммы (FV).
Функция ПС() быть использована для расчета по простым
и сложным процентам.
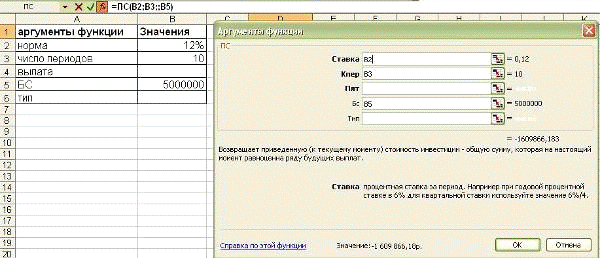
Пример 1-4
Фирме потребуется 5000 тыс. руб.
через 10 лет. В настоящее время располагает деньгами и готова положить их на
депозит единым вкладом с тем, чтобы через 10 лет получить необходимую сумму.
Определить необходимую сумму текущего вклада
если ставка процента по нему составляет 12% в год.
Решение.
ПС(В2;ВЗ;;В5) = -1609866,18 руб.
Рис. 1-8 Решение примера 1-4
Обратите внимание, что результат получился
отрицательным, так как это сумма, которую фирма должна положить на депозит, с
тем, чтобы через 10 лет получить необходимую сумму.
1.3
Определение срока финансовой операции
Для определения срока финансовой операции используется
функция КПЕР0, которая вычисляет общее число периодов начисления
процентов на основе постоянной процентной ставки. Данная функция используется
как для единого платежа, так и для платежей, распределенных во времени.
Синтаксис КПЕР (норма, выплата, нз, бс, тип).
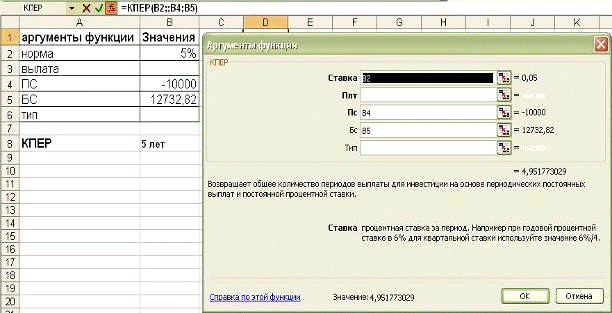
Пример 1-5
По вкладу в 10000,00, помещенному в
банк под 5% годовых, начисляемых ежегодно, была выплачена сумма 12762,82.
Определить срок проведения операции (количество периодов начисления).
Решение.
КПЕР(В2;;В5;В6) = 5 лет
Следует обратить особое внимание на то, что
результатом применения функции является число периодов (а не число лет),
необходимое для проведения операции.
Если платежи производятся несколько раз в год, то
значение функции означает общее число периодов начисления процентов.
Если необходимо срок платежа выразить в годах, то
полученное значение необходимо разделить на число начислений процентов в году
Рис. 1-9 Решение примера 1-5
Пример 1-6
Через сколько лет вклад размером 500
руб. достигнет величины 1000 руб. при ставке процентов 10% с ежемесячным
начислением процентов?
Решение. КПЕР(10%/12;;-500;1000)
=83,5 мес. =83,5 мес./12мес. = 7 лет.
1.4
Определение процентной ставки
Для определения величины процентной ставки при
известных величинах вложенных и наращенных сумм и количестве периодов
начисления процентов Excel
предлагает использование финансовой функции «Ставка».
Аргументы функции:
ПС — вложенная сумм
БС — наращенная сумма;
Кпер — количество периодов начисления
процентов.
Пример 1-7
Фирме через 2 года потребуется 100000
руб. Для достижения этой цели фирма готова положить на депозит 25000 руб. Каким
должен быть процент на инвестированные средства с тем, чтобы к концу второго
года была получена необходимая сумма?
Решение
СТАВКА(2*12;;-25000;100000)=6%
1.5 Расчет
эффективной и номинальной ставки процентов
Для расчета эффективной и номинальной ставки процентов
Excel предлагает использование функций ЭФФЕКТ()
и НОМИНАЛ().
Функция ЭФФЕКТ()
Функция вычисляет действующие (эффективные) ежегодные
процентные ставки, если задана номинальная годовая процентная ставка и
количество периодов начисления в году.
Синтаксис ЭФФЕКТ (номинальная ставка, кол_пер).
Пример 1-8
Номинальная ставка составляет 11%. Рассчитайте
эффективную процентную ставку при следующих вариантах начисления процентов:
полугодовом; квартальном; ежемесячном.
Решение
ЭФФЕКТ =
11,3% — при полугодовом начислении
процентов
,46% — при квартальном начислении
процентов
,57% — при ежемесячном начислении
процентов
Функция НОМИНАЛ()
Функция вычисляет номинальную годовую процентную
ставку, если известны эффективная ставка и число периодов начисления в год.
Синтаксис НОМИНАЛ (эффект_ставка, кол_пер).
Пример 1-9
Эффективная ставка составляет 28%, а
начисление процентов производится ежемесячно. Необходимо рассчитать номинальную
ставку
Решение: Номинальная ежемесячная процентная
ставка будет равна:
НОМИНАЛ (28%,12) = 0,2494 или 29,14%
1.6
Начисление процентов по плавающей ставке
Для расчета будущей величины разовой инвестиции в
случае, если начисление процентов осуществляется по плавающей ставке используется
функция БЗРАСПИС(). Подобные операции широко распространены в
отечественной финансовой и банковской практике. В частности, доходы по
облигациям государственного сберегательного займа (ОГСЗ), начисляются раз в
квартал по плавающей купонной ставке
Пример 1-10
Ставка банка по срочным валютным
депозитам на начало года составляет 20% годовых, начисляемых раз в квартал.
Первоначальная сумма вклада — $1000. В течении года ожидается снижение ставок
раз в квартал на 2, 3 и 5 процентов соответственно. Определить величину
депозита к концу года
Решение
Введем ожидаемые значения процентных
ставок в блок ячеек электронной таблицы, например: 20%/4 в ячейку В2, 18%/4 в
ячейку ВЗ, 17%/4 в ячейку В4 и 15%/4 в ячейку В5. Тогда функция будет иметь
следующий вид: =БЗРАСПИС(1000; С2:С5) = 1166,86$
Раздел
2. Потоки платежей и финансовые ренты
Проведение практически любой финансовой операции порождает движение
денежных средств. Такое движение может характеризоваться возникновением
отдельных платежей, или множеством выплат и поступлений, распределенных во
времени. В финансовой практике широко распространены контракты, предусматривающие
не разовое, а систематическое движение средств — выплаты/поступления по
заданному графику происходят регулярно.
В процессе количественного анализа финансовых операций, удобно
абстрагироваться от их конкретного экономического содержания и рассматривать
порождаемые ими движения денежных средств как численный ряд, состоящий из
последовательности распределенных во времени платежей CF1, CF2, …, CFn. Для
обозначения подобного ряда в мировой практике широко используется термин
«поток платежей» или «денежный поток» {cashflow — CF).
Каждый отдельный элемент такого численного ряда CF представляет собой разность между
всеми поступлениями (притоками) денежных средств и их расходованием (оттоками)
на конкретном временном отрезке проведения финансовой операции. Таким образом,
величина CFt может иметь как положительный, так и
отрицательный знак.
Количественный анализ денежных потоков, генерируемых
за определенный период времени в результате реализации финансовой операции, или
функционирования каких-либо активов, в общем случае сводится к исчислению
следующих характеристик:
— будущей стоимости потока за п периодов;
— современной стоимости потока за я периодов.
Часто возникает необходимость определения и ряда
других параметров финансовых операций, важнейшими из которых являются:
— величина потока платежей в периоде t;
r
— процентная ставка;
п
— срок (количество периодов)
проведения операции.
Поток платежей, все члены которого имеют одинаковое
направление (знак), а временные интервалы между последовательными платежами
постоянны, называется финансовой рентой или аннуитетом (англ.
annuity).
При рассмотрении финансовой ренты используются
основные категории:
член ренты (CFt) — величина каждого отдельного платежа;
период ренты (t) — временной интервал между членами ренты;
срок ренты (n) — время от начала финансовой ренты до конца последнего
ее периода;
процентная ставка (r) — ставка, используемая при наращении платежей, из которых
состоит рента.
В отличие от разовых платежей, рассмотренных
нами в предыдущем разделе, для количественного анализа аннуитетов нам
понадобятся все выделенные ранее характеристики денежных потоков: FV, PV, CF, r и n
( и соответственно, все аргументы рассмотренных ранее финансовых функций Excel, (функции: БС(); IIC(); КПЕР(); СТАВКА(); ПЛТ();
БЗРАСПИС(); НОМИНАЛ(); ЭФФЕКТ()) и др.)
2.1 Определение будущей (наращенной стоимости
потока платежей. Функция БС()
Наращенная сумма — сумма всех платежей с начисленными
на них процентами к концу срока ренты. Это может быть обобщенная сумма
задолженности, итоговый объем инвестиций и т.п.
Пример 2-1
На счет в банке в течении пяти лет в
конце каждого года будут вноситься суммы в размере 500 руб., на которые будут
начисляться проценты по ставке 30%. Определить сумму, которую банк выплатит
владельцу счета.
Решение:
БС(30%;5;-500;;0)=4521,55
сумма всех взносов с начисленными
процентами будет равна 4521,55 руб.
Пример 2-2
Предположим, что каждый год ежемесячно
в банк помещается сумма в 1000. Ставка равна 12% годовых, начисляемых в конце
каждого месяца. Какова будет величина вклада к концу 4-го года?
Общее количество платежей за 4 года
равно: 4* 12 = 48. Ежемесячная процентная ставка составит: 12% /12 = 1%.
Решение:
БС(12%/12;4*12;-1000)= 61222,61
2.2 Современная (текущая) величина
аннуитета. Функция ПС()
Современная (текущая) величина потока
платежей (капитализированная
или приведенная величина) — это сумма платежей, дисконтированных на момент
начала ренты по ставке начисляемых сложных процентов.
Пример 2-3
Предположим, что мы хотим получать
доход, равный $1000 в год, на протяжении 4-х лет. Какая сумма обеспечит
получение такого дохода, если ставка по срочным депозитам равна 10% годовых?
Решение.
PV = 1000*(1-(1+10%)-4)/10%= 3169,87.
При использовании финансовой функции Excel
=ПС(10%;4;-1000)=3169,87
Таким образом, для получения в течение четырех лет
ежегодного дохода в $1000 необходимо сегодня положить в банк $3169,87.
Пример 2-4
Рассматриваются два варианта
приобретения дома стоимостью 100 мл. руб.:
А) единовременный платеж.
Б) ежемесячно в течение 15 лет
вносить в банк по 1 млн., руб.
Определить какой из вариантов
приобретения дома предпочтительнее, если ставка процента — 8% годовых, а
проценты начисляются ежемесячно?
Решение.
Для ответа на поставленный вопрос нам
необходимо сравнить, что выгоднее: заплатить сегодня всю суммы полностью или
растянуть платежи на 15 лет.
Для сравнения необходимо привести эти
денежные потоки к одному периоду времени, т.е. рассчитать текущую стоимость
будущих фиксированных периодических выплат.
Таким образом, текущая стоимость
будущих периодических платежей больше запрашиваемой стоимости дома (104,64 млн.
руб. > 100 млн. руб.), следовательно, выгоднее покупать дом сразу.
2.3 Расчет периодических платежей
Функции Excel
помимо расчета наращенной и приведенной стоимости позволяют выполнить основные
расчеты, связанные с оценкой периодических платежей:
) периодические постоянные по величине платежи,
осуществляемые на основе постоянной процентной ставки (функция ПЛТ);
2) платежи по процентам за конкретный период (функция ПРПЛТ);
3) сумму платежей по процентам за несколько периодов,
идущих подряд друг за другом (функция ОБЩПЛАТ);
4) основные платежи по займу (за вычетом процентов) за
конкретный период (функция ОСПЛТ);
) сумму основных платежей за несколько периодов,
идущих подряд (функция ОБЩДОХОД).
Наиболее часто все эти величины используются при
составлении плана (схемы) равномерного погашения займа. Если заем погашается
равными платежами в конце (начале) каждого периода, то будущая стоимость этих
платежей ( при его полном погашении) будет равна сумме займа с начисленными
процентами к концу последнего расчетного периода. В тоже время текущая
стоимость выплат по займу должна быть равна настоящей сумме займа.
Если известна величина займа, срок на который он был
выдан и процентная ставка, то можно легко, используя функцию ПЛТ, определить
величину периодических платежей, необходимых для равномерного погашения займа.
Вычисленные платежи включают в себя сумму процентов по
непогашенной части займа и основную выплату по нему. Эти величины зависят от
номера периода и могут быть рассчитаны с помощью функций ПРПЛТ, ОСПЛАТ. Накопленные
суммы могут быть определены с помощью функций ОБЩПЛАТ и ОБЩДОХОД.
2.3.1
Определение величины периодического платежа. Функция ПЛТ().
Функция вычисляет величину выплаты за один период на
основе фиксированных периодических выплат и постоянной процентной ставки.
Выплаты, рассчитанные функцией ПЛТ, включают основные платежи и платежи по
процентам.
Синтаксис ПЛТ (норма, кпер, нз, бс, тип).
Функция ПЛТ применяется в следующих расчетах.
1.
Допустим,
известна будущая стоимость фиксированных периодических выплат, производимых в
начале или в конце каждого расчетного периода. Требуется рассчитать размер этих
выплат.
Соответствующая запись в EXCEL имеет вид:
ПЛТ (норма, кпер,, бс, тип).
2.
Предположим,
рассчитываются равные периодические платежи по займу величиной нз, необходимые
для полного погашения этого займа через кпер число периодов. Текущая
стоимость этих выплат должна равняться текущей сумме займе.
Соответствующий расчет в EXCEL выполняется по формуле:
ПЛТ (норма, кпер, нз, ,тип).
Пример 2-6
Предположим, что необходимо накопить
4000 руб. за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой
должна быть эта сумма, если норма процента по вкладу составляет 12% годовых.
Решение.
Определим общее число периодов
начисления процентов и ставку процента за период по таблице 2. Эти величины
составят соответственно 3*12 (аргумент кпер) и 12%/12 (аргумент норма).
Аргумент тип = 0, т.к. по условию это вклады постнумерандо. Рассчитаем величину
ежемесячных выплат: ПЛТ(12%/12,12-3„4000) = -92,86 руб.
Пример 2-7
Допустим, банк выдал ссуду 200 тыс.
руб. на 4 года под 18% годовых. Ссуда выдана в начале года, а погашение
начинается в конце года одинаковыми платежами. Определите размер ежегодного
погашения ссуды.
Решение
Ежегодные платежи составят
ПЛТ (18%,4,200000,,) = -74,3 тыс.
руб.
2.3.2
Расчет платежей по процентам. Функция ПРПЛТ
Функция
позволят определить сумму платежей процентов по инвестиции за данный период на
основе постоянства сумм периодических платежей и постоянства процентной ставки.
Синтаксис
ПРПЛТ (норма, период, кпер, пс,
бс, тип).
Функция
предназначена для следующих расчетов.
1.
При равномерном
погашении займа постоянная периодическая выплата включает в себя платежи по
процентам по непогашенной части займа и выплату задолженности. Так как
непогашенная часть займа уменьшается по мерс его погашения, то уменьшается и
доля платежей по процентам в общей сумме выплаты, и увеличивается доля выплаты
задолженности. Чтобы найти размер платежа по процентам на конкретный период,
следует использовать формулу:
ПРПЛТ (норма, период, кпер, пс), если погашение займа производится равными
платежами в конце каждого расчетного периода.
2.
Допустим,
необходимо вычислить доход, который приносят постоянные периодические выплаты
за конкретный период. Этот доход представляет собой сумму процентов,
начисленных на накопленную (с процентами) к данному моменту совокупную величину
вложений. Расчет ведется по формуле:
ПРПЛТ (норма, период, кпер,, бс, тип).
Пример 2-8
Необходимо определить величину
платежей по процентам за первый месяц трехгодичного займа в 800тыс.руб. Ставка
банка 10%.
Решение.
ПРПЛТ(10%/12;1;3*12;-800) = 6666,67
руб.
·
В поле «Ставка»
диалогового окна заносится величина месячной процентной ставки;
·
в поле «Период»
заносится номер периода для которого мы хотим определить величину платежей
по процентам;
·
в поле
«Кпер»заносится количество периодов начисления процентов ( в нашем примере
3*12);
·
в поле «Пс»
заносится величина займа.
После нажатия кнопки «ОК» мы получим, что платежи по
процентам за первый месяц составили -6666,67 руб.
За счет ежегодных отчислений в течении
6 лет был создан фонд в 5 млн. руб. Необходимо определить какой доход принесли
вложения за последний год, если ставка банка составляла 12%
Решение
Доход за последний год (6 период)
составил:
ПРПЛТ(12%;6;6;;5) =0,469 млн. руб.
.3.3 Расчет суммы платежей по
процентам по займу
Функция
ОБШПЛАТ
Функция
позволяет вычислить накопленный доход (сумму платежей по процентам) по
займу, который погашается равными платежами в конце или начале каждого
расчетного периода, между двумя периодами выплат.
Синтаксис
функции: ОБЩПЛАТ
(ставка;
Кол_пер; Нз ; нач_период; кон_период;тип)
Пример
2-10
Для
приобретения недвижимости была взята ссуда 12000 тыс. руб. Условия ссуды:
Процентная
ставка — 9%;
Срок
— 25 лет
Проценты
начисляются ежемесячно
Необходимо
найти сумму выплат за 2-й год и за 1 -й месяц займа
Решение
В диалоговом окне функции ОБЩПЛАТ() :
·
В строке «Ставка» заносится
величина процентной ставки, начислямой за период (9%/12);
·
в строке «Кол_пер»
записывается количество периодов начисления платежей (25*12);
·
в строке «Нз»
записывается величина займа;
·
в строках «Нач_период»
и «Кон_период» записываются начальный и конечный периоды, для
которых вычисляется сумма выплат по процентам (13 и 24), соответственно;
После щелчка на кнопке «ОК» будет
рассчитана сумма платежей по процентам за второй год:
=ОБЩПЛАТ(9%/12;25*12;12000;13;24;0)
=-1062 тыс. руб.
Аналогичным образом может быть
вычислена сумма выплат по
процентам за первый месяц займа:
=ОБЩПЛАТ(9%/12;25*1;12000;1;1;0)= -90
тыс. руб.
2.3.4
Расчет величины основных платежей по займу. Функция ОСПЛT
Функция позволяет вычислить величину основного платежа
(выплаты) по займу, который погашается равными платежами в конце или начале
расчетного периода, на расчетный период.
Пример 2-11
Была взята ссуда в размере 70000тыс. руб. сроком на 3
года под 17% годовых. Необходимо рассчитать величины основных платежей для
каждого года займа.
Решение
Напомним, что сумма основного платежа по займу
получается как разность между фиксированной периодической выплатой и процентами
по непогашенной части долга.
Размер основных выплат по займу, определяемый с
помощью функции ОСПЛТ может быть определен как:
|
Период |
Формула |
Основной платеж |
|
1-й год |
=ОСПЛТ(17%;1;3;70000) |
-19 780.16р. |
|
2-й год |
=ОСПЛТ(17%;2;3;70000) |
-23 142.78р. |
|
3-й год |
ОСПЛТ(17%;3;3;70000) |
-27 077.06р. |
|
ИТОГО |
-70 000.00р. |
2.3.5 Расчет суммы основных платежей
по займу. Функция ОБЩДОХОД
Функция позволяет вычислить сумму основных платежей по
займу, который погашается равными платежами в конце или начале каждого
расчетного периода, между двумя периодами.
Пример 2-12
Выдана ссуда в размере 1000 тыс. руб.
сроком на 6 лет под 15% годовых, начисляемых ежеквартально. Определить величину
основных выплат за 5-й год.
Решение
Периоды платежей за 5-й год будут
иметь номера 17 и 20, соответственно. Так как ссуда погашается равными
платежами в конце каждого периода (квартала), то размер выплаты за пятый год
составит:
=ОБЩДОХОД(15%/4;6*4;1000;17;20;0)=201,43
тыс. руб.
Раздел
3. Оценка инвестиционных процессов
Инвестиции — это долгосрочные финансовые
вложения экономических ресурсов с целью создания и получения выгоды в будущем,
которая должна быть выше начальной величины вложений.
Инвестиционный процесс — это последовательность связанных
инвестиций, растянутых во времени, отдача от которых также распределена во
времени. Этот процесс характеризуется двусторонним потоком платежей, где
отрицательные члены потока являются вложениями денежных средств в
инвестиционный проект, а положительные члены потока — доходы от инвестированных
средств.
Методы измерения доходности инвестиционных проектов
основаны на анализе равномерного денежного потока. Ожидаемые значения
элементов денежного потока, соответствующие будущим периодам, являются
результатом сальдирования всех статей доходов и расходов, связанных с
осуществлением проекта.
Для приведения значений элементов денежного потока к
сопоставимому во времени виду по выбранной норме дисконтирования оценивается
суммарная текущая стоимость на момент принятия решения о вложении капитала,
предшествующий началу движения средств. Уровень процентной ставки, применяемой
в качестве нормы дисконтирования, должен соответствовать длине периода,
разделяющего элементы денежного потока.
В качестве показателей эффективности инвестиционных
проектов обычно используются:
·
чистый
приведенный доход —
текущая стоимость всех доходов и расходов по проекту;
·
срок
окупаемости —
характеризует срок окупаемости средств, вложенных (инвестированных) в проект;
·
внутренняя
норма доходности —
это ставка дисконтирования, приравнивающая сумму приведенных доходов от
инвестиционного проекта к величине инвестиций, т.е. вложения окупаются, но не
приносят прибыль.
3.1 Чистый приведенный доход. Функция
ЧПС
При оценке инвестиционных проектов используется метод
расчета чистого приведенного дохода, который предусматривает
дисконтирование денежных потоков: все доходы и затраты приводятся к одному
моменту времени.
Центральным показателем в рассматриваемом методе
является показатель NPV (net present value) — текущая стоимость денежных потоков за вычетом
текущей стоимости денежных оттоков. Это обобщенный конечный результат
инвестиционной деятельности в абсолютном измерении.
Показатель NPV характеризует абсолютный прирост, поскольку оценивает,
на сколько приведенный доход перекрывает приведенные затраты:
·
при NPV > 0 проект может быть принят;
·
при NPV < 0 проект не принимается,
·
при NPV= 0 проект не имеет ни прибыли, ни убытков
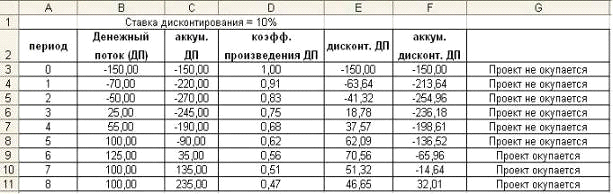
Пример 3-1
Найти чистый дисконтированный доход
проекта, требующего стартовых инвестиций в объеме 150 тыс. руб., денежный поток
которого задан рис.6-1, по ставке дисконтирования 10% годовых.
Решение
На листе Excel создадим таблицу, подобную
приведенной на Рис. 3-1.
Рис. 3-1. Фрагмент рабочего листа MS Excel с вычислением величины чистого
дисконтированного потока
Рис. 3-2 Фрагмент рабочего листа MS Excel в режиме отображения формул с
вычислением величины чистого дисконтированного потока
В ячейках столбца:
·
«А»
размещены периоды поступления (оттока) денежных средств;
·
«В»
размещаются величины денежных потоков в соответствующие периоды;
·
«С»
размещены аккумулированные значения денежных потоков в данном периоде.
Например, в ячейке «С4» может быть записано: =СЗ+В4;
·
«D» размещаются формулы расчета величины
коэффициента дисконтирования денежных потоков. Например, в ячейке «D3» записывается: =(ВЗ/(1+0,1)^А3)/ВЗ;
в ячейке «D4» записывается: =(В4/(1+0,1)^А4)/В4 и т.д.;
^ — обозначение возведения в степень
·
«Е»
значения дисконтированных денежных потоков. Например, в ячейке «Е4»
записывается: =B4*D4
·
«F» записываются формулы расчеты
аккумулированных дисконтированных денежных потоков в соответствующий период
времени. Например, в ячейке «F3» записывается величина
денежного потока в начальный период (начальные инвестиции): =D3; в ячейке «F4» записывается: =F3+E4 и т.д.
·
«G» записывается логическая функция
анализа окупаемости проекта. Например, в ячейке «G3» записывается формула: =ЕСЛИ(СЗ>0;
«Проект окупается»;»Проект не окупается»), которая
копируется в ячейки G4:G11 таблицы.
Таким образом, в результате
выполненных вычислений получаем:
Чистый дисконтированный доход = 32,01
Дисконтированный доход =
-(-150)+32,01 = 182,01
Готовый результат 182,01 в
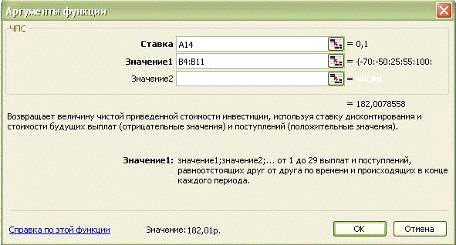
одной клетке дает табличная формула =NPV(10%;B4:B11), вызывающая специальную финансовую
функцию со ссылкой на норму дисконтирования («Ставка») и табличные
координаты блока значений («Значения1».,..)элементов денежного
потока, расположенных в хронологическом порядке.
В русских версиях MS Excel функция NPV имеет название ЧПС.
Рис. 3-4. Диалоговое окно функции ЧПС
Пояснения.
Функция ЧПС() возвращает величину чистой приведенной
стоимости инвестиции, используя ставку дисконтирования, а также стоимости
будущих выплат (отрицательные значения) и поступлений (положительные значения).
Синтаксис функции: ЧПС(ставка;значение1;значение2;…)
Ставка — ставка дисконтирования за один период.
Значение1, значение2,… — от 1 до 29 аргументов,
представляющих расходы и доходы.
Значение1, значение2,… должны быть равномерно
распределены во времени, выплаты должны осуществляться в конце каждого периода.
Значение1, значение2,… могут вводится либо в
отдельные окна либо списком (при этом, порядок ввода значений (либо значений в
списке) определяется порядком поступлений и платежей)
Для вычисления чистого дисконтированного дохода к
выражению =NPV(10%;C4:C11) необходимо добавить отрицательную величину инвестиционных
затрат нулевого периода, записанное в таблице в ячейке ВЗ=ЧПС(10%;В4:В11)+В3 =
32,01
Метод определения чистой текущей
стоимости часто используется при оценке эффективности инвестиций. Он позволяет
определить нижнюю границу прибыльности и использовать ее в качестве критерия
при выборе наиболее эффективного проекта.
Положительное значение NPV является показателем того, что
проект приносит чистую прибыль, после покрытия всех связанных с ним расходов
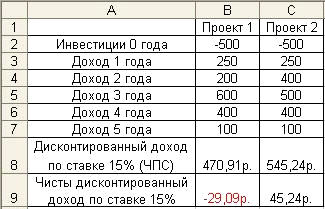
Пример 3-2
Сравним два проекта, денежные потоки
которых представлены на рис. 3-5 , при значениях ставки дисконтирования 15%
Рис. 3-5 Исходные данные и решение
Примера 3-2
В ячейках «В9» и «С9» вычисляется
значения чистого дисконтированного дохода для Проектов 1 и 2.
Выполненные расчеты показывают целесообразность
принятия Проекта 2, не смотря на то, что величины денежных потоков обоих
проектов различаются несущественно
3.2
Срок окупаемости
Для анализа эффективности инвестиций часто
используется такой показатель, как срок окупаемости — продолжительность
времени, в течение которого дисконтированные на момент завершения инвестиций
прогнозируемые денежные поступления равны сумме инвестиций. Иными словами — это
количество лет, необходимых для компенсации стартовых инвестиций.
Пример 3-3
Рассчитать срок окупаемости проекта,
для которого размер инвестиций составляет 1 млн. руб., а денежные поступления в
течение 5 лет будут составлять: 250; 400; 800; 900; 900 тыс. руб.
соответственно. Ставка дисконтирования 15%.
Решение.
На листе Excel создадим таблицу, подобную
приведенной на рис.3-7
Рис. 3-7. Фрагмент рабочего листа Excel с исходными данными и решением
примера 3-3
Рис. 3-8. Фрагмент рабочего листа Excel в режиме отображения формул
исходными данными и решением примера 3-3
В ячейках:
·
CI :G1 размещены номера периодов
поступления денежных средств;
·
C2:G2 размещены величины поступления
денежных средств;
·
C3:G3 размещены формулы дисконтирования
поступающих денежных средств. Например, в ячейке СЗ записана формула
=С2/((1+15%)^С1),
соответствующая левой части формулы 6-3;
·
C4:G4 записаны формулы вычисления
накопленного в данный период дисконтированного денежного потока. Например, в
ячейке С4 записана формула =В4+С3 (сумма величины инвестиции и
поступивших в этот период (1) денежных средств), а в ячейке D4 записывается формула =C4+D3 (сумма величины накопленного
дисконтированного потока и поступивших в этот период (2) денежных средств) и
т.д.
Анализируя построенную таблицу легко
видеть, что инвестиции полностью окупаются в интервале между 2 и 3 периодами.
Следовательно, период окупаемости может быть найден как:
=Dl+(-D4/E3) =2+480,15/526,01 =2,91 года
Таким образом, период, реально
необходимый для возмещения инвестированной сумы, составит 2,91 года или 2 года
и 332 дня.
Период окупаемости может быть также
определен, если в ячейку С5 записать формулу: =ЕСЛИ(С4>0;С1-(В4+С3)/С3;0)
и скопировать ее в остальные ячейки строки.
3.3
Индекс рентабельности
Индекс рентабельности (PI) показывает, сколько единиц современной величины
денежного потока приходится на единицу предполагаемых первоначальных затрат.
Если величина критерия РI> 1, то современная стоимость денежного
потока проекта превышает первоначальные инвестиции, обеспечивая тем самым
наличие положительной величины NPV. При
этом норма рентабельности превышает заданную и проект следует принять.
При РI=1 величина NPV= 0 и инвестиции не приносят дохода.
В случае, если PI < 1, проект не обеспечивает заданного
уровня рентабельности и его следует отклонить
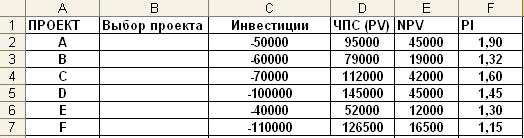
Пример 3-4
Фирма рассматривает возможность
участия в финансировании шести проектов, предполагаемые условия реализации
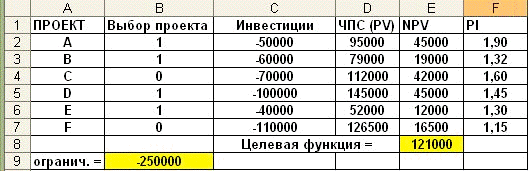
которых приведены в таблице рис. 3-8. Инвестиционный бюджет фирмы равен 250000.
Рис. 3-9 Фрагмент рабочего листа Excel с исходными данными и решением
примера 3-4
Как следует из таблицы (столбец
«Е»), чистая приведенная стоимость всех проектов (NPV) больше нуля, а индекс
рентабельность (PI) больше 1. И, если бы инвестиционный бюджет фирмы не был ограничен
суммой в 250000 то все проекты следовало бы принять. Однако из-за
ограниченности бюджета может быть реализован только тот набор (портфель)
проектов, при котором суммарные инвестиции не превышают 250000.
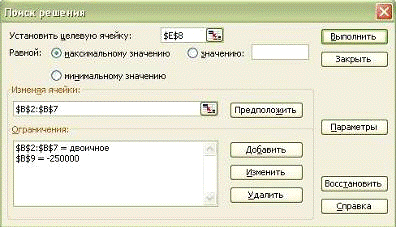
Для выбора наиболее привлекательных
проектов воспользуемся операцией «Поиск решения».
В ячейке «Е8″запишем целевую
функцию: =СУММПРОИЗВ(В2:В7;Е2:Е7);
Примечание: в ячейках столбца «В»
размещаются результаты выбора проекта: «1» -проект выбран;
«0» — проект отклонен.
в ячейке «В9» запишем
формулу ограничений:
=СУММПРОИЗВ(В2:В7;С2:С7);
в диалоговом окне «Поиск
решения» выполним необходимые установки:
Рис. 3-10 Диалоговое окно «Поиск
решения»
В результате выполнения процедуры «Поиск
решения» оказывается оптимальным инвестирование четырех
проектов:»А», «И», «D» и «Е», при этом
суммарная величина NPV составит 121000 (см. рис. 3-11)
Рис. 3-11 Выбор проектов для инвестирования
3.4
Внутренняя норма доходности. Функция ЧИСТВНДОХ
Под внутренней нормой доходности понимают процентную
ставку, при которой чистая современная стоимость инвестиционного проекта равна
нулю.
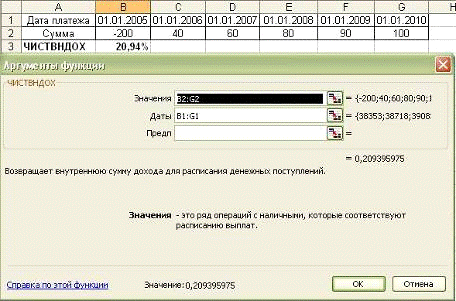
Функция ЧИСТВНДОХ возвращает внутреннюю сумму дохода
для расписания денежных поступлений
Пример 3-5
Фирма намерена 1 января 2005 г.
инвестировать 200 млн. руб. в проект, ожидаемые доходы по которому в
последующие 5 лет составят 40, 60, 80, 90 и 100 млн. руб.
Определите внутреннюю норму дохода по проекту,
если поступление доходов будет производится 1 января каждого года
Решение
Рис.3-12 Решение примера 3-5
Таким образом, при рыночной ставке дисконта менее 20,94%
инвестирование проекта — целесообразно.
3.5 Модифицированная внутренняя норма доходности.
Функция МСВД
Функция возвращает модифицированную внутреннюю
скорость оборота средств для ряда периодических поступлений и выплат переменной
величины.
При этом учитывается как стоимость инвестиции, так и
доход, получаемый от реинвестирования.
Синтаксис МВСД (значения, финансовая норма,
реинвест_норма).
Значения — это массив или ссылка на ячейки,
содержащие числовые величины. Эти числа представляют ряд денежных выплат
(отрицательные значения) и поступлений (положительные значения), происходящие в
регулярные периоды времени.
Аргумент значения должен содержать по крайней мере
одно положительное и одно отрицательное значение для того, чтобы можно было
вычислить модифицированную внутреннюю скорость оборота. В противном случае
функция МВСД возвращает значение ошибки #ДЕЛУ0!.
Если аргумент, который является массивом или ссылкой,
содержит тексты, логические значения или пустые ячейки, то такие значения
игнорируются; однако, ячейки, которые содержат нулевые значения, учитываются.
Финансовая норма — это норма прибыли, выплачиваемой за
деньги, находящиеся в наличном обороте.
Реинвест_норма — это норма прибыли, получаемой за
деньги, находящиеся в наличном обороте при реинвестировании.
Замечания
МВСД использует порядок расположения чисел в аргументе
значения для определения порядка выплат и поступлений. Убедитесь, что значения
выплат и поступлений введены в нужной последовательности и с правильными
знаками (положительные зна чения для получаемых денег и отрицательные значения
для выплачиваемых).
Пример 3-6
Предположим, что Вы занимаетесь
рыболовным промыслом и только что завершили пятый год работы. Пять лет назад вы
взяли 120 000 руб. под 10 процентов годовых для покупки лодки.
Ваши годовые уловы принесли прибыль в
39 000 руб., 30 000 руб., 21 000 руб., 37 000 руб. и 46 000 руб.
соответственно. За эти годы Вы реинвестировали получаемую прибыль под 12%
процентов годовых. Пусть на рабочем листе Ваш заем введен как -120 000 в ячейку
В1 и в ячейки В2:В6 введены значения Вашей прибыли за каждый год.
Решение
Тогда модифицированная внутренняя
скорость оборота за пять лет вычисляется следующим образом:
МВСД(В1:В6; 10%; 12%) равняется 12,61
процентам
Модифицированная внутренняя скорость
оборота за три года вычисляется следующим образом:
МВСД(В1 :В4; 10%; 12%) равняется
-4,80 процентам
Модифицированная внутренняя скорость
оборота за пять лет, если значение аргумента реинвест_норма равно 14%,
вычисляется следующим образом:
МВСД(В1:В6; 10%; 14%) равняется 13,48
процентам
Примеры 3-7
Предположим, пять лет назад была взята ссуда в размере 1 млн.
руб. под 10% годовых для финансирования проекта, прибыль по которому за эти
годы составила: 100, 270, 450, 340 и 300 тыс. руб. Эти деньги были
реинвестированы под 12% годовых. Найти модифицированную внутреннюю скорость
оборота инвестиции.
Решение
Пусть на рабочем листе заем введен
как -1000 в ячейку В1, и в ячейки В2.В6 введены значения прибыли за каждый год.
Тогда модифицированная внутренняя скорость оборота за пять лет вычисляется
следующим образом:
МВСД(В1:В6,10%,12%)= 12.25%.
Модифицированная внутренняя скорость
оборота за пять лет, если бы ставка реинвестирования составляла 14%,
вычисляется следующим образом:
МВСД(В1:В6,10%14%)= 12.99%.
3.6 Денежный поток инвестиционного проекта с произвольными периодами
поступления платежей
Функции ЧИСТНЗ
В том случае, если поступления (оттоки) денежных
средств происходят в произвольные периоды времени), то для расчета величины
чистого дисконтированного дохода может быть использована функция Excel ЧИСТНЗ
|
Ставка |
это ставка |
|
Значения |
это ряд денежных потоков, |
|
Даты |
это расписание дат |
Пример 3-7
июля 2003 года была сделана инвестиция в проект
в размере 10000 тыс. рублей
В результате реализации проекта
ожидается получение прибыли: 15 сентября 200: — 2750 тыс. руб.; 1 ноября 2003г.
-4250 тыс. руб. и 1 января 2004г. — 5250 тыс. руб.
Норма дисконтирования 9%
Необходимо определить чистую текущую
стоимость инвестиции на 1 июля 2003 на 1 июля 2002г
Решение.
На листе Excel создайте таблицу, подобную
приведенной на рисунке.
Рис. 3-13 Исходные данные примера
Вызовите функцию ЧИСТНЗ, расположенную
в категории функций «Финансовые» и введите в диалоговое окно этой функции
необходимые аргументы:
Рис. 3-13 Диалоговое окно Функции ЧИСТНЗ
Чистая текущая стоимость инвестиции
на 1 июля 2003 составит = 1856,25 тыс. руб.
на 1 июля 2002 = 1702,98 тыс. руб.,
при этом формула будет иметь вид: =ЧИСТНЗ(9%;А2:Е2;А1:Е1).
Раздел 4. Функции Excel для расчета
амортизации
Группа функций для расчета амортизации основных фондов позволяет
рассчитать амортизационные отчисления следующими методами:
) равномерным, функция АПЛ;
) суммы чисел (лет), функция АСЧ;
) фиксированного уменьшения остатка с использ. функции ФУО;
) уменьшающегося остатка или двойного процента, функция ДДОБ.
Аргументы функций Excel для расчета амортизации
|
Аргумент |
Значение аргумента |
|
без_переключения |
Логическое значение, |
|
время_ амортизации |
Срок эксплуатации имущества |
|
время_полн_аморт |
|
|
время_эксплуатации |
|
|
кон_период |
Конечный период для |
|
коэффициент |
Коэффициент ускоренной |
|
месяц |
Число месяцев в первом году |
|
нач_период |
Начальный период для |
|
остаточная_ стоимость |
Остаточная стоимость |
|
ост_стоим |
|
|
ликвидная_стоимость |
|
|
период |
Период, для которого |
|
стоимость |
Первоначальная стоимость |
|
ликв_стоимость |
Пример 3-1.
Определить величину ежегодной амортизации оборудования
начальной стоимостью 400 тыс. руб., если срок эксплуатации оборудования 10 лет,
остаточная стоимость 250 тыс. руб., используя различные методы расчета и
функции Excel. Результаты представить в виде табл. 2.
Таблица 5. Расчет амортизации различными методами.
|
год |
АПЛ |
АСЧ |
ФУО |
ДДОБ |
|
1 |
375,00 |
681,82 |
968,00 |
800,00 |
|
2 |
375,00 |
613,64 |
733,74 |
640,00 |
|
3 |
375,00 |
545,45 |
556,18 |
512,00 |
|
4 |
375,00 |
477,27 |
421,58 |
409,60 |
|
5 |
375,00 |
409,09 |
319,56 |
327,68 |
|
6 |
375,00 |
340,91 |
242,23 |
262,14 |
|
7 |
375,00 |
272,73 |
183,61 |
209,72 |
|
8 |
375,00 |
204,55 |
139,17 |
167,77 |
|
9 |
375,00 |
136,36 |
105,49 |
134,22 |
|
10 |
375,00 |
68,18 |
79,96 |
107,37 |
|
итого |
3750,0 |
3750,0 |
3749,5 |
3570,5 |
Функция AПЛ
Функция АПЛ вычисляет амортизацию имущества за один
период равномерным методом. При использовании равномерного метода для каждого
периода величина амортизационных отчислений одинакова, а совокупная величина
отчислений к концу последнего периода равна стоимости амортизируемого
имущества.
Синтаксис AПЛ (нач_стоимость, остат_стоимость,
время_эксплуатации).
При равномерном методе расчета за
каждый год амортизация составит:
АПЛ(4000,250,10) = 375 тыс. руб.
Функция АСЧ
Функция АМГД позволяет рассчитать амортизационные
отчисления за заданный период методом суммы чисел. Этот метод характеризуется
постоянным понижением амортизационных отчислений и обеспечивает полное
возмещение амортизируемой стоимости имущества.
Синтаксис АСЧ (нач_стоимость, ост_стоимость,
время_эксплуатации, период).
Определим величину амортизации за
первый и третий годы эксплуатации методом суммы чисел. За первый год
амортизация составит:
АСЧ(8000,500,10,1) = 681,82 тыс.
руб.,
за третий год величина
амортизационных отчислений составит:
АСЧ (8000,500,10,3)= 545,45 тыс.руб.
Функция ФУО
Функция ФУО вычисляет величину амортизации имущества
для заданного периода с использованием метода постоянного учета амортизации.
Данный метод использует фиксированную норму амортизации.
Синтаксис ФУО (нач_стоимость, ост_стоимость,
время_эксплуатации, период, месяцы).
Рассчитаем величину амортизации за
первый, третий и последний годы эксплуатации этим методом. За первый год
амортизация
составит:
ФУО(4000,250,10,1) = 968 тыс. руб.,
за третий год амортизация составит:
ФУО (4000,250,10,3) = 566,18 тыс.
руб.,
а в последнем году амортизационные
отчисления составят: ФУО (4000,250,10,10)= 79,96 тыс. руб.
Функция ДДОБ
Функция ДДОБ позволяет рассчитать сумму амортизации
для заданного периода методом уменьшающегося остатка. При этом можно задать
коэффициент ускоренной амортизации, по умолчанию равный двум.
Синтаксис ДДОБ (нач_стоимость, ост_стоимость,
время эксплуатации, период, коэффициент).
Амортизационные отчисления при использовании метода
двукратного учета амортизации (аргумент коэффициент = 2) постоянно
уменьшаются на протяжении срока эксплуатации, но их суммарная величина в итоге
полностью не возмещает амортизируемую стоимость имущества.
Рассчитаем величину амортизации за
первый и третий годы эксплуатации методом двукратного учета амортизации. За
первый год амортизация составит:
ДДОБ(4000,250,10,1) = 800 тыс. руб.,
за третий год:
ДДОБ(4000,250,10,3) = 512 тыс. руб.
Вариант 1
|
1. Рассчитать какая сумма |
БС |
|
2. Срок ссуды — 5 лет, |
БЗРАСПИС |
|
3. Компании X потребуется 100000 |
СТАВКА |
|
4. Определить эффективную |
(ЭФФЕКТ) |
|
5. Банк выдал ссуду 150 |
(ПЛТ) |
|
6. Определите эффективность |
(ЧПС) |
|
7. Определить величину |
(АПЛ) |
Вариант 2
|
1. У Вас есть возможность ежегодно в течение 4 лет |
(БС) |
|
2. По вкладу в 10000 |
(КПЕР) |
|
3. Определить величину |
(ДДОБ) |
|
4. Пять лет назад была |
(МСВД) |
|
5. Определите сумму |
(ОБЩДОХОД) |
|
6. Определите номинальную |
(НОМИНАЛ) |
|
7. Рассмотрим инвестиции, |
(ЧПС) |
Вариант 3
|
1. Вы решили приобрести |
(ПС) |
|
2. Для обеспечения будущих |
(КПЕР) |
|
3. Ставка банка по срочным |
(ЭФФЕКТ) |
|
4. Вычислить 10 годичную |
(ПЛТ) |
|
5. Определите чистую |
(ЧИСТНЗ) |
|
6. Определить величину |
(АСЧ) |
|
7. Пусть в долг на полтора |
(СТАВКА) |
Вариант 4
|
1. Предположим, что |
(ПС) |
|
2. Рассчитайте внутреннюю |
(ЧИСТВНДОХ) |
|
3. Определить величину |
(ДДОБ) |
|
4. Какую сумму |
(ПЛТ) |
|
5. Чему равна эффективная |
(ЭФФЕКТ) |
|
6. Рассчитайте процентную |
(СТАВКА) |
|
7. Ссуда 63200 руб., |
(КПЕР) |
Вариант 5
|
1. Вы хотите |
(БС) |
|
2. Ставка банка по срочным |
(БЗРАСПИС) |
|
3. Определить величину |
(ФУО) |
|
4. За какой срок в годах |
(КПЕР) |
|
5. Выдан кредит 200 000 |
(СТАВКА) |
|
6. Эффективная ставка |
(НОМИНАЛ) |
|
7. Определите платежи по |
(ПРПЛТ) |
Вариант 6
|
1. Рассматриваются два |
(ПС) |
|
2. Была выдана ссуда в |
(ОБЩДОХОД) |
|
3. Заем в 144 тыс. руб. |
(СТАВКА) |
|
4. Чему равна эффективная |
(ЭФФЕКТ) |
|
5. Найдите сумму выплат за |
(ОБЩПЛАТ) |
|
6. Определите |
(ВСД) |
|
7. Определить величину |
(ФУО) |
Вариант 7
|
1. Фирма создает фонд для |
(БС) |
|
2. Рассчитайте, через |
(КПЕР) |
|
3. В долг на 2 года дана |
(СТАВКА) |
|
4. Чему равна номинальная |
(НОМНАЛ) |
|
5. Определите основные |
(ОСПЛТ) |
|
6. Для приобретения |
(МСВД) |
|
7. Определить величину |
(АПЛ) |
Вариант 8
|
1. Ссуда в 20 000 руб. дана |
(БС) |
|
2. Ссуда 87000 руб., |
(КПЕР) |
|
3. Какой должна быть |
(СТАВКА) |
|
4. Чему равна эффективная |
(ЭФФЕКТ) |
|
5. Определите ежемесячные |
(ПЛТ) |
|
6. Затраты по проекту в |
(ЧПС) |
|
7. Определить величину |
(ДДОБ) |
Вариант 9
|
1. Вексель на 3 000 000 |
(ПС) |
|
2. Ссуда размером 61000 |
(КПЕР) |
|
3. Рассчитайте годовую |
(СТАВКА) |
|
4. Ставка банка по срочным |
(ЭФФЕКТ) |
|
5. Для приобретения |
(ОБЩПЛАТ) |
|
6. Определите чистую |
(ЧИСТНЗ) |
|
7. Определить величину |
(АПЛ) |
Вариант 10
|
1. Рассматриваются две |
(БС) |
|
2. Физическому лицу выдан |
(СТАВКА) |
|
3. Определите величину |
(ПРПЛТ) |
|
4. Сравните два проекта, |
(ЧПС) |
|
5. Определите чистую |
(ЧИСТНЗ) |
|
6. Определить величину |
(АСЧ) |
|
7. Ожидается, что ежегодные |
(КПЕР) |
Задача
1
Требуется
рассчитать 10-летнею ипотечную ссуду со
ставкой 14% годовых при начальном взносе
25% суммы и ежемесячной (ежегодной)
выплате.
Решение
задачи
Для
решения задачи используется функция
ПЛТ.
Функция
вычисляет величину выплаты за один
период годовой ренты (например, регулярных
платежей по займу) при постоянной
процентной ставке. ПЛТ(ставка;кпер;пс;бс;тип),
Ставка — процентная ставка по ссуде,
Кпер — общее число выплат по ссуде.
Пс —
приведенная к текущему моменту стоимость,
или общая сумма, которая на текущий
момент равноценна ряду будущих платежей,
называемая также основной суммой.
Бс —
требуемое значение будущей стоимости,
или остатка средств после последней
выплаты. Если аргумент бс опущен, то он
полагается равным 0 (нулю), т. е. для займа,
например, значение бс равно 0.
Тип —
число 0 (нуль) или 1, обозначающее, когда
должна производиться выплата.
Исходные
данные для решения задачи представлены
на рис.1.
Рис.1
Исходные данные.
Формулы
для решения задачи представлены на
рис.2
Рис.2
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.3.
Рис.3
Результаты решения задачи.
Вывод
При расчёте 10-летней ипотечной ссуды
со ставкой 14% годовых при начальном
взносе 25% суммы и ежемесячной (ежегодной)
выплате. Общая сумма выплат составит
41580000р.
Задача
2
Рассмотреть
возможность инвестиций 36 000 руб. Возврат
10 000 руб. через год, 15 000 руб. через два
года и т. д. 21 000 руб. — через 3 лет.
Решение
задачи
ЧПС
– Возвращает величину чистой приведенной
стоимости инвестиции, используя ставку
дисконтирования, а также стоимости
будущих выплат (отрицательные значения)
и поступлений (положительные значения).
Подбор
параметров,
выбрав
команду Подбор
параметров в
меню Сервис.
При подборе параметра Excel изменяет
значение в одной конкретной ячейке до
тех пор, пока вычисления по формуле,
ссылающейся на эту ячейку, не дадут
нужного результата.
Исходные
данные для решения задачи представлены
на рис.4.
Рис.4
Исходные данные.
Формулы
для решения задачи представлены на
рис.5.
Рис.5
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.6.
Рис.6
Результаты решения.
Вывод
При
расчёте инвестиций на 3 лет, с возвратом
по
10000,
15000,
21000 рублей
с процентной ставкой более 1% не имеет
смысл.
Задача
3
Рассмотреть
возможность инвестиций 360000
руб. Возврат по 41000 руб. в течение 11 лет.
При какой годовой процентной ставке
это имеет смысл?
Решение
задачи
ПС(
ставка; кпер; выплата; бз; тип)
ставка
— процентная ставка за период;
кпер
— общее число периодов выплат;
выплата
— величина постоянных периодических
платежей;
бз
— будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты. Если параметр бз опущен, то его
значение полагается равным о (будущая
стоимость займа, например, равна о);
Тип
— число, равное 0 или 1, обозначающее,
когда должна производиться выплата.
Если значение параметра тип равно 0 или
он опущен, то оплата производится в
конце периода, если же его значение
равно 1, то в начале периода.
Подбор
параметров,
выбрав
команду Подбор
параметров в
меню Сервис.
При подборе параметра Excel изменяет
значение в одной конкретной ячейке до
тех пор, пока вычисления по формуле,
ссылающейся на эту ячейку, не дадут
нужного результата.
Исходные
данные для решения задачи представлены
на рис.7.
Рис.7
Исходные данные.
Формулы
для решения задачи представлены на
рис.8.
Рис.8
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.9.
Рис.9
Результаты решения.
Вывод
При
рассмотрении возможности инвестиций
360000 руб на 11 лет. С ежегодным возвращением
по 41 000 руб . С процентной ставкой более
1% , выгодна.
Задача
4
Вычислить
основные платежи, плату по процентам,
общую ежегодную выплату и остаток долга
на примере ссуды 300000 руб. под годовую
ставку8% на срок 10 лет.
Решение
задачи
Присвойте
ячейкам следующие имена:
Для
ссылки на ячейки в столбцах и строках
можно использовать заголовки этих
столбцов и строк листа. Также для
представления ячеек, диапазонов ячеек,
формул или констант
можно
создавать имена.
Заголовки можно использовать в формулах,
содержащих ссылки на данные на том же
листе; для представления группы ячеек,
находящейся на другом листе, этой группе
следует присвоить имя.
Ячейка
Имя
B1
Процент
B2
Срок
B3
Ежегодная_плата
B4
Размер_ссуды
Кроме
того, в ячейки введите формулы:
Ячейка
Формула
Описание
ВЗ
=ПЛТ(Процент;Срок;–Размер_ссуды)
Ежегодная плата
D6
=Размер_ссуды
Начальный остаток долга
А7
=A6+1
Номер года
В7
=D6*Процент
Плата по процентам
С7
=Ежегодная_плата-В7
Основная плата за первый год
D7
=ЕСЛИ(D6-С7<>0;D6-С7) Остаток
долга за первый год
Исходные
данные для решения задачи представлены
на рис.10.
Рис.10
Исходные данные.
Формулы
для решения задачи представлены на
рис.11.
Рис.11
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.12.
Рис.12
Результаты решения.
Вывод
Были
вычислены основные платежи, плата по
процентам , общая ежегодная выплата.
Задача
5
Рассмотреть
возможность инвестиций 360000 руб. под
годовую ставку 5%. Возможна выплата по
41000 руб. в год. Сколько лет займут эти
выплаты?
Решение
задачи
КПЕР
(ставка; выплата; нз; бз; тип)
ставка
— процентная ставка за период;
выплата
— величина постоянных периодических
платежей;
нз
— текущее значение, т. е. общая сумма,
которую составят будущие платежи;
бз
— будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты. Если параметр бз опущен, то его
значение полагается равным 0 (будущая
стоимость займа, например, равна 0);
тип—
число, равное 0 или 1, обозначающее, когда
должна производиться выплата. Если
значение параметра тип равно 0 или он
опущен, то оплата производится в конце
периода, если его значение равно 1, то в
начале периода.
Исходные
данные для решения задачи представлены
на рис.13.
Рис.13
Исходные данные.
Формулы
для решения задачи представлены на
рис.14.
Рис.14
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.15.
Рис.15
Результаты решения.
Вывод
При
расмотрении инвестиций на сумма 360000
руб. под годовую ставу 5% и возможных
выплат по 41000 руб. Выплаты зайдут 12 лет.
Задача
6
Рассмотреть
возможность инвестиций 22000 руб. С
выплатами в определенные дниИмеет ли
смысл это при годовой ставке 1 % (Сумма
выплат из задания 2).
Решение
задачи
ЧПС
(ставка; 1-е значение; 2-е значение;
…)
ставка
— процентная ставка за период;
1-е
значение, 2-е значение, … — от 1 до 29
аргументов, представляющих расходы и
доходы. 1-е значение, 2-е значение, …
должны быть равномерно распределены
по времени и осуществляться в конце
каждого периода. НПЗ использует
порядок аргументов 1-е значение, 2-е
значение,…для определения порядка
поступлений и платежей.
Исходные
данные для решения задачи представлены
на рис.16.
Рис.16
Исходные данные.
Формулы
для решения задачи представлены на
рис.17.
Рис.17
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.18.
Рис.18
Результаты решения.
Вывод
Рассмотрев
возможность инвестиций 22000 руб. С
выплатами в определенные дни Не имеет
смысл это при годовой ставке 15 %.
Задача
7
Составить
отчетную ведомость реализации товаров
6
магазинами с
февраль
по август.
Решение
задачи
В
этой отчетной ведомости надо определить:
суммарную
и среднюю выручку каждого из магазинов
за отчетный период;
суммарную
выручку всех магазинов за каждый месяц
отчетного периода;
место,
которое занимает каждый из магазинов
в суммарном объеме выручки;
долю
каждого из магазинов в суммарном объеме
выручки;
количество
магазинов, имеющих суммарную выручку
до 1000 млн руб., от 1000 млн руб. до 1500 млн
руб., от 1500 млн руб. до 2000 млн руб. и свыше
2000 млн руб.
Исходные
данные для решения задачи представлены
на рис.19.
Рис.19
Исходные данные.
Формулы
для решения задачи представлены на
рис.20,1/20,2.
Рис.20,1
Формулы для решения задачи.
Рис.20,2
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.21.
Рис.21
Результаты решения.
Вывод
Составлена
отчетная ведомость реализации товаров
6 магазинами с
февраль
по август.
Задача
8
Рассмотреть
возможность инвестиций 8138
руб. под годовую ставку 7% и собираетесь
отдавать по 711
руб. в год.
Сколько лет займут выплаты?
Решение
задачи
КПЕР
(ставка; выплата; нз; бз; тип)
ставка
— процентная ставка за период;
выплата
— величина постоянных периодических
платежей;
нз
— текущее значение, т. е. общая сумма,
которую составят будущие платежи;
бз
— будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты. Если параметр бз опущен, то его
значение полагается равным 0 (будущая
стоимость займа, например, равна 0);
тип—
число, равное 0 или 1, обозначающее, когда
должна производиться выплата. Если
значение параметра тип равно 0 или он
опущен, то оплата производится в конце
периода, если его значение равно 1, то в
начале периода.
Исходные
данные для решения задачи представлены
на рис.22.
Рис.22
Исходные данные
Формулы
для решения задачи представлены на
рис.23.

Формулы для решения задачи.
Результаты
решения задачи представлены на рис.24.
Рис.24
Результат решения.
Вывод
Рассмотрели
возможность инвестиций 8138 руб. под
годовую ставку 7% с выплатами по 711 руб.
выплаты займут 23,9 лет.
Задача
9
Рассмотреть
возможность вкладывать по 711 руб. в
течение 12 лет при годовой ставке 7%.
Сколько денег будет на счету через 12
лет?
Решение
задачи
БС(ставка;кпер;плт;пс;тип)
Ставка —
это процентная ставка за период.
Кпер —
это общее число периодов платежей по
аннуитету.
Плт —
это выплата, производимая в каждый
период; это значение не может меняться
в течение всего периода выплат. Обычно
плт состоит из основного платежа и
платежа по процентам, но не включает
других налогов и сборов. Если аргумент
опущен, должно быть указано значение
аргумента пс.
Пс —
это приведенная к текущему моменту
стоимость или общая сумма, которая на
текущий момент равноценна ряду будущих
платежей. Если аргумент нз опущен, то
он полагается равным 0. В этом случае
должно быть указано значение аргумента
плт.
Тип —
это число 0 или 1, обозначающее, когда
должна производиться выплата. Если этот
аргумент опущен, то он полагается равным
0.
Исходные
данные для решения задачи представлены
на рис.25.
Рис.25
Исходные данные.
Формулы
для решения задачи представлены на
рис.26.
Рис.26
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.27.
Рис.27
Результат решения.
Вывод
При
рассмотрении возможности вкладывать
по 711 руб. в течение 12 лет при годовой
ставке 7%. Денег будет через 17 лет
5647,25руб.
Задача
10
Определить
процентную ставку для 7 летнего займа
в 8138
руб. с ежегодной выплатой в 711
руб.
Решение
задачи
СТАВКА(кпер;плт;пс;бс;тип;предположение)
Кпер —
общее число периодов платежей по
аннуитету.
Плт —
регулярный платеж (один раз в период),
величина которого остается постоянной
в течение всего срока аннуитета. Обычно
плт состоит из платежа основной суммы
и платежа процентов, но не включает
других сборов или налогов. Если аргумент
опущен, должно быть указано значение
аргумента бс
Пс —
приведенная к текущему моменту стоимость
или общая сумма, которая на текущий
момент равноценна ряду будущих платежей.
Бс —
требуемое значение будущей стоимости
или остатка средств после последней
выплаты. Если аргумент бс опущен, то он
полагается равным 0 (например, бзс для
займа равно 0).
Тип —
число 0 или 1, обозначающее, когда должна
производиться выплата.
Исходные
данные для решения задачи представлены
на рис.28.
Рис.28
Исходные данные.
Результаты
решения задачи представлены на рис.29.
Рис.29
Решения задачи.
Вывод
Определена
процентная ставку для 7 летнего займа
в 8138 руб. с ежегодной выплатой в 711руб.
Задача
11
Составить
таблицу начисления премии по итогам
работы сети n магазинов с августа
по февраль
по следующему правилу:
если
продукции продано не меньше чем на
212000
руб., то комиссионные составляют 10%;
за
первое место дополнительно начисляется
7%, за второе место – 3,5% ,за четвёртое
место –6%.
Решение
задачи
Cрзнач
находит среднее арифметическое значение
из указанного диапазона ячеек.
Синтаксис:
СРЗНАЧ
(число1; число2; …)
Функция
ранг возвращает ранг числа в списке
чисел. Ранг числа — это его величина
относительно других значений в списке.
(Если список отсортировать, то ранг
числа будет его позицией.)
Синтаксис:
РАНГ(число;
ссылка; порядок)
число
— число, для которого определяется
ранг;
ссылка
— массив или ссылка на список чисел.
Нечисловые значения в ссылке игнорируются;
порядок
— число, определяющее способ упорядочения.
Если значение параметра порядок равно
0 или он опущен, то MS Excel определяет ранг
числа так, как если бы ссылка была
списком, отсортированным в порядке
убывания. Если значение параметра
порядок является любым ненулевым
числом, то MS Excel определяет ранг числа
так, как если бы ссылка была списком,
отсортированным в порядке возрастания.
Функция
ранг присваивает одинаковым числам
одинаковый ранг.
Функция
частота возвращает распределение частот
в виде вертикального массива. Для данного
множества значений и данного множества
карманов (т.е. интервалов в математическом
смысле) частотное распределение
подсчитывает, сколько исходных значений
попадает в каждый интервал.
Синтаксис:
ЧАСТОТА
(массив_данных; двоичный__массив)
массив_данных
— массив или ссылка на множество данных,
для которых вычисляются частоты; если
массив_данных не содержит значений, то
функция частота возвращает массив
нулей;
двоичный_массив
— массив или ссылка на множество
интервалов, в которые группируются
значения аргумента массив_данных.
ЕСЛИ двоичный_массив не содержит
значений, то функция частота возвращает
количество элементов в аргументе
двоичный_массив.
Исходные
данные для решения задачи представлены
на рис.30.
Рис.30
Исходные данные.
Формулы
для решения задачи представлены на
рис.31,1/31,2.
Рис.31,1
Формулы для решения задачи.
Рис.31,2
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.32.
Рис.32
Решения задачи.
Задача
12
Предприятие
владеет основными средствами 212000
руб. Рассчитать показатели амортизации
за 7лет.
Решение
задачи
АПЛ
Возвращает величину амортизации актива
за один период, рассчитанную линейным
методом.
АПЛ(нач_стоимость;ост_стоимость;время_эксплуатации)
Нач_стоимость —
затраты на приобретение актива.
Ост_стоимость —
стоимость в конце периода амортизации
(иногда называется остаточной стоимостью
имущества).
Время_эксплуатации —
количество периодов, за которые
собственность амортизируется (иногда
называется периодом амортизации).
Исходные
данные для решения задачи представлены
на рис.33.
Рис.33
Исходные данные.
Формулы
для решения задачи представлены на
рис.34.
Рис.34
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.35.
Рис.35
Результаты решения.
Вывод
Предприятие
владеет основными средствами 212000
руб. Рассчитали показатели амортизации
за 7 лет. Результат амортизации 21658 руб.
Задача
13
Предприятие
владеет основными средствами. Рассчитать
показатели амортизации за период при
следующих условиях. Дополнительные
условия: Амортизация за первый год.
Решение
задачи
ДДОБ
(стоимость; остаточная_стоимость;
время__эксплуатации; период;коэффициент)
стоимость
— начальная стоимость имущества;
остаточная_стоимость
— остаточная стоимость в конце периода;
время__эксплуатации
— количество периодов, за которые
собственность амортизируется (иногда
называется временем полной амортизации);
время_эксплуатации
— количество периодов, за которые
амортизируется имущество (иногда
называется временем полной амортизации);
коэффициент
— норма снижения балансовой стоимости
(амортизации).Если коэффициент опущен,
то предполагается, что он равен 2 ( метод
двукратного учета амортизации).
Исходные
данные для решения задачи представлены
на рис.36.
Рис.36
Исходные данные.
Формулы
для решения задачи представлены на
рис.37.
Рис.37
Формулы для решения задачи.
Результаты
решения задачи представлены на рис.38.
Рис.38
Результаты решения.
Вывод
Предприятие
владеет основными средствами 212000руб.
Рассчитать показатели амортизации за
период 7 лет . при дополнительном условии:
вычислении амортизации за первый год
равной 11459,54р.