Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
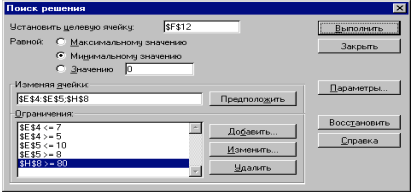
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
. РЕШЕНИЕ
ЭКОНОМИЧЕСКИХ ЗАДАЧ В MS Excel
5.1.
Моделирование как метод познания
Моделирование — исследование каких-либо явлений, процессов
или систем объектов путем построения и изучения их моделей; использование
моделей для определения или уточнения характеристик и рационализации способов
построения вновь конструируемых объектов. На идее моделирования базируется
любой метод научного исследования — как теоретический (при котором используются
различного рода знаковые, абстрактные модели), так и экспериментальный
(использующий предметные модели).
В исследуемой сложной системе выделяются наиболее существенные
признаки, свойства, связи, а несущественные, с точки зрения исследователя,
признаки, свойства, связи не учитываются. Такой подход позволяет построить
упрощенную модель сложной системы и приступить к ее изучению. Модель, в широком
смысле слова, любой аналог (изображение, описание, схема, чертеж, график, план,
карта и т. п.) какого-либо объекта, процесса или явления, используемый для
изучения или исследования.
На рисунке 3.1. в виде представлены этапы моделирования, которые, в
зависимости от возраста и рода деятельности может применять человек в процессе
познания мира и практической деятельности.
Рисунок 3.1. — Этапы познания мира
Прикладное моделирование. В процессе своей повседневной деятельности люди
используют различные модели. Появились целые отрасли, в которых моделирование
играет ведущую роль. Художники-модельеры конструируют одежду. Дизайнеры создают
проекты, предназначенные для формирования эстетических и функциональных качеств
окружающего пространства или предметов. Внедрение компьютерных технологий
многократно умножило созидательный потенциал творческих людей, позволяя
оперативно решать задачи, на которые в недавнем прошлом уходили значительные
временные ресурсы.
Научное моделирование призвано подтвердить или опровергнуть научную
гипотезу. Гипотеза часто выступает как теоретическое утверждение, которое на
данный момент времени еще не доказано экспериментально или имеющимися
средствами не может быть доказано в принципе. В научном моделировании можно
выделить два базовых направления: материальное моделирование и абстрактное
моделирование. Материальное (предметное или физическое) моделирование в
качестве моделей использует материальные предметы, абстрактное — математические
модели, мысленный эксперимент, образное мышление.
Физическое (экспериментальное) моделирование — замена изучения некоторого объекта или
явления экспериментальным исследованием его модели, имеющей ту же физическую
природу.
Математическое моделирование — замена изучения некоторого объекта или явления теоретическим
исследованием его модели, в основу которой положены подтвержденные практикой
теоретические законы.
Модели по области использования классифицируются на:
игровые модели (стратегические, ролевые, имитационные — симуляторы,
тренажеры, спортивные);
учебные модели (наглядные пособия, имитационные – тренажеры, обучающие
программы);
научно-технические модели (модели объектов, явлений, связей, модели
технологических процессов, имитационные — испытательные стенды).
По способу представления модели классифицируются на:
материальные модели (детские игрушки, наглядные пособия,
экспериментальные лабораторные установки и модели);
информационные (абстрактные) модели (вербальные[1], знаковые — книги, карты,
схемы, рисунки, компьютерное моделирование).
В процессе моделирования на языке программирования Microsoft
Excel можно выделить несколько этапов: постановка задачи;
формализация; составление алгоритма; программирование; тестирование; отладка;
оформление; прогнозирование.
В зависимости от сложности поставленной задачи некоторые этапы
моделирования могут менять очередность, объединяться или исключаться, в силу
отсутствия в них необходимости и/или очевидности решения.
Постановка задачи
1. Ознакомление с условием задачи.
2. Сбор необходимых дополнительных сведений.
3. Определение необходимости использования
универсальных констант.
4. Перевод величин в единую систему измерений,
например, СИ, СГС.
5. Определение математических или физических
законов, описывающих явления, изображаемые в условии задачи.
3.2. Пример моделирования в среде Microsoft Excel
Построить компьютерную модель электрических нагрузок двухкомнатной
квартиры. При превышении суммарных нагрузок более 5 000 Вт выдавать
сигнал опасности.
Как показывает статистика возникновения пожаров, более половины пожаров
возникает из-за неисправности в электрооборудовании и короткого замыкания в
проводке. Плавкие предохранители, которые применяются в большинстве
электрических приборов, не являются панацеей. Специалисты указывают на два
существенных недостатка плавких предохранителей:
1. Инертность (замедленное срабатывание). Пока
плавкий предохранитель перегорит, объект охраны уже сгорел.
2. Статистический разброс параметров. Плавкий
предохранитель, промаркированный на определенный номинал, может выдержать
превышение нагрузки в 15–20 раз. Если рабочая нагрузка в 3–5 раз превышает
номинальную, то плавкий предохранитель не сгорит, а сгорит объект охраны.
Снизить пожарную опасность объектов можно только внедрением в систему
охраны электронных предохранителей, которые отличаются повышенным
быстродействием и способны отключить объект охраны при превышении нагрузки на
0,1% и менее.
Дополнительные сведения задачи — список электроприборов обычной
двухкомнатной квартиры. В таблице 3.1. представлен список электрических
приборов. Нумерация приборов произведена в соответствии с номером строки
таблицы (2, 3, … 15).
Таблица 3.1. Список электрических
приборов
|
Электроприбор |
Мощность, Вт |
|
|
2. Лампы (зал) |
180 |
|
|
3. Лампа (кухня) |
100 |
|
|
4. Лампа (спальня) |
100 |
|
|
4. Лампа (ванная) |
60 |
|
|
6. Лампа (туалет) |
60 |
|
|
7. Лампа (прихожая) |
60 |
|
|
8. Телевизор |
300 |
|
|
9. Холодильник |
600 |
|
|
10.Стиральная |
1 000 |
|
|
11. Электрическая |
1 500 |
|
|
12. Пылесос |
600 |
|
|
13. Компьютер |
150 |
|
|
14. Утюг |
800 |
|
|
15. Тостер |
100 |
На рисунке 3.2. представлена схема контроля электрических нагрузок. На
схеме присутствуют:
A2:A15 — электрические приборы;
B2:B15 — селективные переключатели;
С2:С15 — цифровые индикаторы потребляемой мощности;
S — программный сумматор электрических нагрузок.
E4 — цифровой индикатор суммарной мощности;
D6 — излучатель сигнала тревоги.
Вот такую функциональную схему необходимо запрограммировать в среде Microsoft
Excel.
Рисунок 2. — Схема электрических нагрузок
Формализация, алгоритмизация и
программирование
1. Распределение, именование ячеек памяти (ячеек
таблицы).
2. Определение направления потоков данных:
входные (ввод) и выходные (вывод).
3. Определение и задание формата данных.
4. Составление математического закона (формулы),
описывающего алгоритм решения задачи.
5. Составление программы на языке
программирования.
В таблице 3.2. и на рисунке 3.3. представлено распределение ячеек
рабочего листа.
Таблица 3.2. — Распределение
ресурсов рабочего листа Microsoft Excel
|
Ячейка |
Направление потока |
Имя ячейки (Заголовок) |
Величина |
|
A2:A15 |
(Электроприбор) |
Названия |
|
|
В2:B15 |
Ввод |
(Состояние) |
Селективный 0 — 1 — включено. |
|
С2:C15 |
Вывод |
Мощность |
Цифровые 0 — Pi — если Состояниеi = 1. |
|
E4 |
Вывод |
Цифровой |
|
|
D6 |
Вывод |
Излучатель «Норма», «Пожар», |
Ячейки A1, B1, C1 содержат заголовки списка.
В ячейки A2:A15 внесены названия электрических приборов.
Ячейки B2:B15, будут работать в режиме селективного переключателя с
двумя возможными состояниями: 0 — выключено; 1— включено.
Ячейки C2:C15 отображают мощность включенного прибора Pi, где Pi — мощность отдельного прибора, i —
номер строки таблицы (i = 2, 3,
…, 15).
Ячейка E4 получена путем объединения четырех ячеек диапазона E4:F5.
Ячейка D6 получена путем объединения двадцати ячеек диапазона D6:G10.
Рисунок 3.3. — Распределение ячеек рабочего листа
Объединение
ячеек
Для объединения диапазона ячеек в одну ячейку необходимо выделить
требуемый диапазон ячеек и нажать кнопку Объединить и поместить в центре панели
инструментов Форматирование.
Селективные
переключатели
Ячейки B2:B15 должны
работать в режиме селективных переключателей с двумя состояниями: 0 —
выключено; 1 — включено.
Для того чтобы для ячеек B2:B15 запрограммировать два возможных состояния, необходимо
их выделить и командой Формат4Условное
форматирование открыть окно
диалога Условное форматирование (рисунок 3.4.).
Условие 1 имеет три поля кнопку Формат:
Раскрывающийся список типов условных форматов, применяется для выделенной ячейки или их
диапазона. Для форматирования ячейки на основе ее значения или содержимого
используется параметр значение. Для форматирования ячейки на основе указанной пользователем формулы
используется параметр формула. Значение формулы должно быть истинно или ложно.
Раскрывающийся список операторов, используется при задании условия для
выделенного диапазона ячеек. При выборе значений между или вне
необходимо указать верхнее и нижнее значения для условия форматирования.
Рисунок 3.4. — Окно диалога Условное форматирование
Поле ввода значения или формулы для применения условия форматирования к
выделенному диапазону ячеек. При выборе значений между или вне
необходимо указать верхнее и нижнее значения для условия форматирования.
Кнопка Формат предназначена для выбора
элементов отображения содержимого ячейки (диапазона ячеек) при условном
форматировании. В каждой операции форматирования к ячейке применяется только
один условный формат. В данной задаче для диапазона ячеек B2:B15 выбраны следующие параметры условного
форматирования:
если значение ячейки равно 1 , то ее
содержимое отображается черными буквами на зеленом фоне (условие 1);
если значение ячейки равно 0 , то ее
содержимое отображается белыми буквами на красном фоне (условие 2).
Цвета букв и фона в каждом условии форматирования задается в окне
диалога Формат ячеек, которое открывается нажатием на соответствующую
кнопку Формат.
После применения условного форматирования к диапазону ячеек B2:B15 любая выделенная ячейка принимает форму
раскрывающегося списка с двумя возможными значениями 0 и 1 (рисунок
3.5.).
Рисунок 3.5. — Ячейки B2:B15 после применения условного форматирования
Для того чтобы исключить ввод в ячейки B2:B15 любых чисел, кроме 0 и 1, необходимо выделить этот диапазон ячеек и
командой Данные 4Проверка4 Параметры открыть вкладку Параметры
окна диалога Проверка вводимых значений (рисунок 3.6). В
раскрывающемся списке Тип данных установить параметр Список. В поле Источник набрать список из
двух чисел: 0;
1.
Рисунок 3.6. — Вкладка Параметры окна диалога Проверка
вводимых значений
Цифровые
индикаторы
Ячейки C2:C15 играют роль цифровых индикаторов потребляемой
мощности каждой нагрузкой. Например, если переключатель B2 выключен (0), то индикатор C2 отображает 0. Если переключатель B2 включен (1), то индикатор C2 отображает номинальную мощность, в
соответствии с таблицей 3.1.
Для ячейки C2, расчетная формула примет вид: =ЕСЛИ(B2=1;180;0).
Для ячейки C3: =ЕСЛИ(B3=1;100;0).
Аналогично заполняются ячейки C4:C15. На рисунке 3.7 показан внешний вид рабочего листа
после заполнения ячеек A1:A15; B1:B15; C1:C15.
Рисунок 3.7. — Функционирование переключателей и
цифровых индикаторов
К диапазону ячеек C2:C15 можно применить условное форматирование, показанное
на рисунке 3.8, а именно: значение включенной нагрузки (значение нагрузки
больше 0) отображать красным цветом.
Для большего цветового контраста рекомендуется выделить ячейки C2:C15 и установить желтый цвет шрифта кнопкой Цвет шрифта
панели инструментов Стандартная. Тогда все нулевые значения нагрузок
будут отображаться желтым цветом, а ненулевые (включенные) — красным.
Рисунок 3.8. — Параметры условного
форматирования ячеек C2:C15
Цифровой
индикатор суммарной мощности
Ячейка E4 играет роль
цифрового индикатора суммарной мощности. В ней должна отображаться сумма ячеек C2:C15. Для повышения наглядности формулы присвоим
диапазону ячеек C2:C15 имя
Мощность. Напомним, что для этого необходимо выделить
диапазон ячеек C2:C15 и
командой Вставка4Имя4Создать
присвоить диапазону имя Мощность.
Для расчета суммарной мощности необходимо в ячейке E4 набрать формулу: =СЦЕПИТЬ(СУММ(Мощность);»
Вт»).
В этой формуле применена функция СЦЕПИТЬ категории Текстовые функции (см. таблицу 3.3),
имеющая формат:
Таблица 3.3.
|
СЦЕПИТЬ(текст_1;текст_2;…) |
|
|
текст_1, текст_2, … |
от 1 до 30 элементов текста, объединяемых |
Внимание! Вместо функции
СЦЕПИТЬ для объединения текстов можно использовать оператор конкатенации
«&».
Излучатель
сигнала тревоги
Ячейка D6 играет роль
излучателя сигнала тревоги, который работает по алгоритму:
Этот алгоритм можно запрограммировать, если в ячейке D6 набрать формулу: =ЕСЛИ(СУММ(Мощность)>=5000;»Пожар»;»Норма»).
Тестирование и отладка
1. Запуск программы в работу.
2. Проверка правильности записи операторов и
формул.
3. Проверка соответствия ссылок именам ячеек.
4. Оценка истинности результата.
На рисунке 3.9 показан момент подачи сигнала тревоги при превышении
заданного порога суммарных нагрузок.
Рисунок 3.9. — Тестирование модели электрических
нагрузок
Оформление
1. Сопровождение программы комментариями.
2. Создание дружелюбного интерфейса пользователя.
3. Ограничение доступа пользователя к содержимому
ячеек.
Применяя условное форматирование для ячеек E4, D6 в совокупности с изменением размера шрифта можно изменить внешний вид
и цифрового индикатора суммарной мощности, и излучателя сигнала тревоги
(рисунок 3.10).
Рисунок 3.10. — Оформление рабочего листа
Границы
и заливка ячеек
Команда Формат4Ячейки4Вид
позволяет изменять цвета заливки и границы ячеек или диапазонов ячеек по
усмотрению пользователя без ущерба для условного форматирования.
Сокрытие
сетки
Команда Сервис4Параметры4Вид
открывает вкладку Вид окна диалога Параметры. Для сокрытия сетки
необходимо выключить переключатель с флажком Сетка.
О
защите ячеек
Защита ячеек предназначена для ограничения доступа пользователя к
содержимому ячеек. По умолчанию все ячейки рабочего листа защищены. Но защита
ячеек включается после установки защиты рабочего листа или книги. Перед
установкой защиты рабочего листа необходимо разрешить доступ к ячейкам B2:B15, в которые будет осуществляться ввод
информации.
Для снятия защиты ячеек необходимо:
выделить диапазон ячеек B2:B15 и командой Формат 4Ячейки 4Защита открыть вкладку Защита окна диалога Формат
ячеек;
выключить переключатель с флажком Защищаемая ячейка.
Для установки защиты рабочего листа необходимо:
командой Сервис4Защита4Защитить лист.. открыть окно диалога Защита
листа;
в списке Разрешить всем пользователям этого листа
установить необходимые переключатели с флажками;
в поле Пароль для отключения защиты листа, если
есть необходимость, то можно набрать пароль. В этом случая снять защиту листа
сможет только пользователь, который знает пароль.
Прогнозирование
Варьирование в допустимых пределах значениями
переменных с целью изучения их влияния на результат вычислений.
Выдача прогноза о возможностях совершенствования
производственного процесса, условий эксперимента и т.п.
Задание.
По итогам моделирования сделайте выводы о необходимости:
ограничения суммарной нагрузки;
модернизации охранных устройств.
Дополните таблицу 3.1. Список электрических приборов следующими бытовыми электроприборами:
малогабаритный телевизор;
радиоприемник, магнитофон;
настольная лампа;
торшер;
люстра на пять ламп (5 ´ 60 Вт);
музыкальный центр;
микроволновая печь;
кофеварка;
соковыжималка;
электрическая мясорубка;
кухонный комбайн.
Решение задач экономико-математического моделирования с помощью программы Excel
Решение задач
экономико-математического моделирования с помощью программы Excel
Определить оптимальное сочетание
трех зерновых культур: пшеницы, ячменя и овса
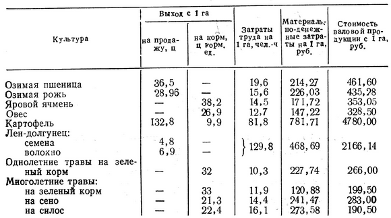
Производство культур характеризуется
показатели таблицы.
|
Показатели |
Озимая пшеница |
Яровой ячмень |
Овес |
|
Урожайность с 1 га, ц. |
40 |
35 |
30 |
|
Затраты труда на 1 га, чел.-ч. |
20 |
15 |
13 |
|
Затраты удобрений на 1 га, руб. |
80 |
50 |
40 |
Производственные ресурсы: пашня-1600
га, труд — 27000 чел.-ч., удобрения — 99000 руб.
В структуре посевов площадь под оз.
пшеницы должна составлять не менее 50 %. Критерий оптимальности максимальное
производство зерна.
Решение.
Обозначим через:
х1-площадь оз. пшеницы, га.
х2-площадь яр. ячмень, га.
х3-площадь овса, га.
Запишем условие задач в виде системы
ограничений (уравнений и неравенств).
) По уборки площади посевов
трех зерновых, га
Х1+х2+х3=1600
) По использовании ресурсов
труда
*х1+15*х2+13*х3≤27000
) По затратам удобрений, руб.
*х1+50*х2+40*х3≤99000
) По структуре посевной
площади
х1≥0,5(х1+х2+х3)
х1≥0,5*х1+0,5*х2+0,5*х3
,5х1-0,5х2-0,5х3≥0
ЦФ= критерий max производства зерна.
ЦФ=40*х1+35*х2+30*х3→max
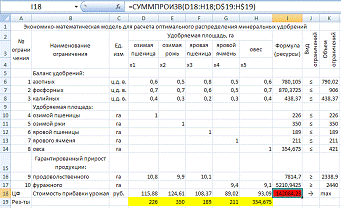
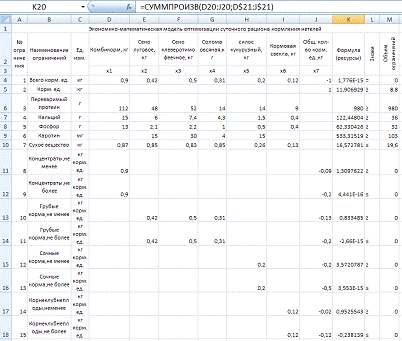
Решение задачи в Excel
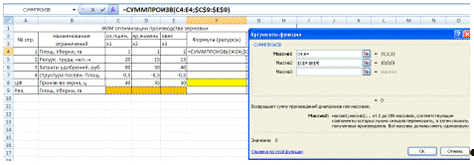
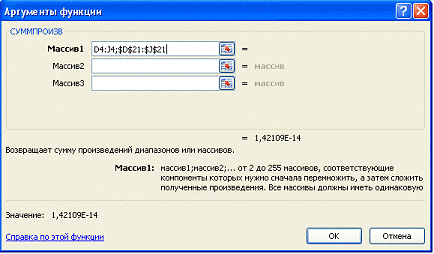
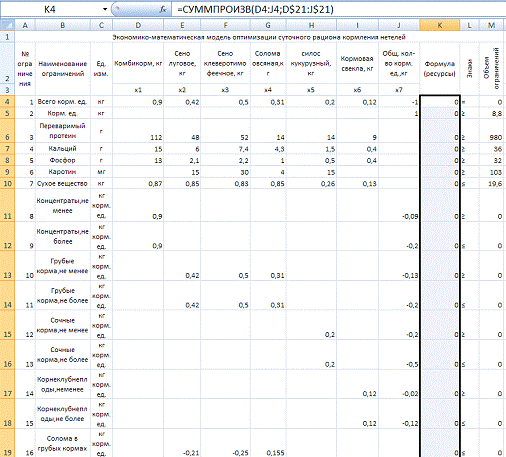
В ячейку F4 вставим формулу «
=СУММПРОИЗВ(С4:Е4;$C$9:$E$9)», затем растянем форму до целевой ячейки
включительно.
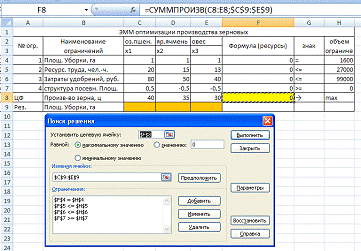
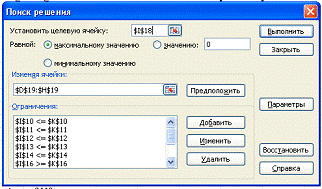
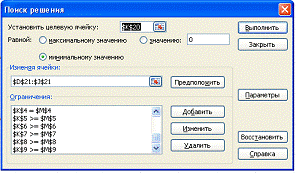
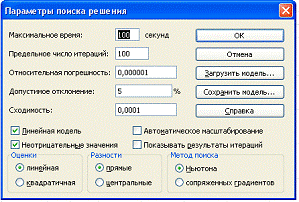
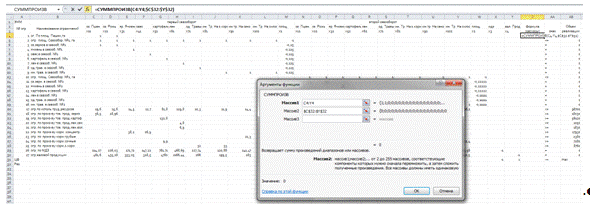
Затем находим решение задачи с
помощью «поиска решения». Находим: Данные→Анализ→Поиск решения. Как
видно на рисунке: устанавливаем целевую ячейку; равный- max значению; изменяя
ячейки и ограничение.
программирование excel оптимальный
модель
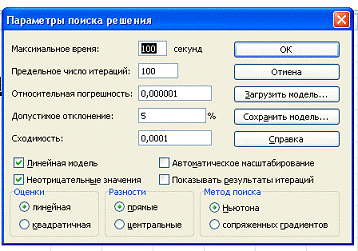
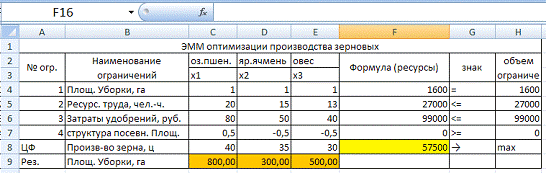
После выполненных операций нажимаем,
на «выполнить» и получаем возможное решение задачи:
Вывод: Оптимальное сочетание трех
зерновых культур, максимальное производства зерна будет при площади уборки: оз.
пшеницы — 800 га, яр. ячмень — 300 га, овес — 500 га.
Экономико-математические модели для
расчета оптимального распределения минеральных удобрений
Рассчитать план распределения
минеральных удобрений, при котором достигается максимум стоимости прибавки
урожая. При этом по плану необходимо получить не менее 23 000 ц
продовольственного и 17 000 ц фуражного зерна. Площадь посева культур,
рекомендуемые дозы внесения удобрений и прибавка урожая показаны в табл.7.1.
Сведения о количестве, качестве и стоимости минеральных удобрений приведены в
табл.7.2.
Таблица 7.1
|
Показатели |
Озимая пшеница |
Озимая рожь |
Яровая пшеница |
Яровой ячмень |
Овес |
|||||
|
Площадь посева, га |
226 |
350 |
189 |
211 |
421 |
|||||
|
Урожайность без внесения удобрений с 1 га, ц |
29,7 |
26,3 |
25,1 |
28,9 |
20,1 |
|||||
|
Азотных |
0,6 |
0,5 |
0,8 |
0,5 |
0,6 |
|||||
|
Фосфорных |
0,7 |
0,7 |
0,6 |
0,5 |
0,7 |
|||||
|
Калийных |
0,4 |
0,3 |
0,2 |
0,3 |
0,4 |
|||||
|
Прибавка урожая за счет внесения удобрений с 1 га: |
||||||||||
|
ц |
10,8 |
9,9 |
10,1 |
9,4 |
9,1 |
|||||
|
руб |
115,88 |
124,61 |
108,37 |
89,02 |
93,09 |
Таблица 7.2
|
показатели |
Сульфат аммония N |
Суперфосфат Р2О5 |
Хлористый калий К2О |
|
Количество, ц |
3762 |
4530 |
743 |
|
Содержание действующего вещества, % |
21 |
20 |
59 |
|
Цена 1 ц, руб |
4,00 |
2,39 |
1,10 |
|
Стоимость внесения 1 ц, руб |
0,25 |
0,19 |
0,26 |
Решение:
ЭММ для расчета оптимальных рационов
кормления с/х животных
Рассчитать оптимальный суточный
рацион кормления нетелей средней живой массой 480 кг. В рационе должно
содержаться не менее 8,8 кг кормовых единиц, 980 г переваримого протеина, 36 г
кальция, 32 г фосфора, 103 мг каротина и не более 19,6 кг сухого вещества.
Рацион составляется из комбикорма,
сена лугового, сена клеверотимофеечного, соломы овсяной, силоса кукурузного и
кормовой свеклы. Содержание питательных веществ в кормах и их себестоимость
представлены в таблице 9.5.
В соответствии с зоотехническими
требованиями отдельные группы кормов в рационе могут изменяться в следующих
пределах, % к общему количеству кормовых единиц: концентрированные — от 9 до
20, грубые — от 13 до 20, сочные — от 20 до 50 и корнеклубнеплоды — от 2 до 12.
Удельный вес соломы в грубых кормах должен составлять не менее 50%.
Таблица 9.5
|
Корма |
Содержание в 1 кг корма |
Себестоимость 1 кг корма, коп |
|||||
|
Кормовых единиц, кг |
Переваримого протеина, г |
Кальция, г |
Фосфора, г |
Каротина, мг |
|||
|
Комбикорм |
0,9 |
112 |
15 |
13 |
— |
0,87 |
14,5 |
|
Сено луговое |
0,42 |
48 |
6 |
2,1 |
15 |
0,85 |
3,4 |
|
Сено клеверотимофеечное |
0,5 |
52 |
7,4 |
2,2 |
30 |
0,83 |
2,1 |
|
Солома овсяная |
0,31 |
14 |
4,3 |
1 |
4 |
0,85 |
0,2 |
|
Силос кукурузный |
0,2 |
14 |
1,5 |
0,5 |
15 |
0,23 |
0,6 |
|
Кормовая свекла |
0,12 |
9 |
0,4 |
0,4 |
— |
0,13 |
2,1 |
Решение:
Определим перечень переменных.
Количество кормов, которая может войти в рацион нетелей, обозначим через:
Х1-количество комбикорма в рационе,
кг
Х2-количество сена лугового в
рационе, кг
Х3-количество сена
клеверотимофеечного в рационе, кг
Х4-количество соломы овсяной в
рационе, кг
Х5-количество силоса кукурузного в
рационе, кг
Х6-количество кормовой свеклы в рационе,
кг
Х7-общее количество кормовых единиц
в рационе, кг
Запишем систему ограничений в
развернутом виде.
. Ограничения по балансу питательных
веществ в рационе:
) общее количество кормовых единиц
,9х1+0,42х2+0,5х3+0,31х4+0,2х5+0,12х6=х7
или после преобразования
,9х1+0,42х2+0,5х3+0,31х4+0,2х5+0,12х6-х7=0
) кормовые единицы не менее
Х7 ≥ 8,8
) переваримого протеина не менее
х1+48х2+52х3+14х4+14х5+9х6 ≥
980
) кальция не менее
х1+6х2+7,4х3+4,3х4+1,5х5+0,4х6 ≥
36
) фосфора не менее
) каротина не менее
х2+30х3+4х4+15х5 ≥ 103
. Ограничения по содержанию сухого
вещества в рационе:
)
0,87х1+0,85х2+0,83х3+0,85х4+0,26х5+0,13х6 ≤ 19,6
. Ограничения по содержанию
отдельных групп кормов в рационе:
) концентрированных не менее
,9х1 ≥ 0,09х7
или после преобразований
,9х1-0,2х7 ≥ 0
) концентрированных не более
,9х1 ≤ 0,2х7
или после преобразований
,9х1-0,2х7 ≤ 0
) грубых не менее
,42х2+0,5х3+0,31х4 ≥ 0,13х7
или после преобразований
,42х2+0,5х3+0,31х4-0,13х7 ≥ 0
) грубых не более
,42х2+0,5х3+0,31х4 ≤ 0,2х7
или после преобразований
,42х2+0,5х3+0,31х4-0,2х7 ≤ 0
) сочных не менее
,2х5≥0,2х7
или 0,2х5-0,2х7≥0
) сочных не более
,2х5≤0,5х7
или 0,2х5-0,5х7≤0
) корнеклубнеплодов не менее
,12х6≥0,02х7
или 0,2х6-0,02х7≥0
)корнеклубнеплодов не более
,12х6≤0,12х7
или 0,12х6-0,12х7≤0
. ограничения по содержанию
отдельных видов кормов
) удельный вес соломы в группе
грубых
,31х4≥0,5*(0,42х2+0,5х3+0,31х4)
или после преобразований
,21х2-0,25х3+0,155х4≥0
Целевая функция — минимальная
себестоимость рациона=14,5х1+3,4х2+2,1х3+0,2х4+0,6х5+2,1х6→min
Определить оптимальную структуру
посевных площадей, обеспечивающую получение максимума валовой продукции. В
хозяйстве имеется 2377 га пашни. Ресурсы труда — 98700 чел.-ч.
Данные при возделывании культур
представлены в таблице:
Сельскохозяйственные культуры могут
размещаться по двум вариантам севооборотов:
Севооборот №1
. однолетние травы
. озимые зерновые
. картофель
. ячмень с подсевом многолетних трав
. многолетние травы
. озимые зерновые
. лен
. овес
Севооборот №2
. однолетние травы
. озимые зерновые с подсевом
многолетних трав
. многолетние травы
. лен
. картофель
. ячмень
. озимые зерновые
. картофель
. ячмень
Плановое задание по продажи
продукции государству, ц:
) картофель 56120
) льносемена 1050
) льноволокно 1830
Для обеспечения животноводства
кормами необходимо произвести следующее количество кормов, ц корм.ед.:
концентрированных 17930
грубых 2380
сочных 7280
зеленых 8760
Основные переменные:
В севообороте №1:
х11 — озимая пшеница
х21 — озимая рожь
х31 — яровой ячмень
х41 — овес
х51 — картофель
х61 — лен
х71 — однолетние травы
х81 — многолетние травы на зеленый
корм
х91 — многолетние травы на сено
х101 — многолетние травы на силос
х1 — площадь севооборота №1
В севообороте №2
х12 — озимая пшеница
х22 — озимая рожь
х32 — яровой ячмень
х52 — картофель
х62 — лен
х72- однолетние травы
х82 — многолетние травы на зеленый
корм
х92 — многолетние травы на сено
х102 — многолетние травы на силос
х2 — площадь севооборота №2
х3 — материально-денежные затраты,
руб.
х4 — Валовая продукция, руб.
Система ограничений:
. По площади пашни:
) х1+х2<=2377
. По площади севооборота №1:
)
х11+х21+х31+х41+х51+х61+х71+х81+х91+х101-х1<=0
. По площади отдельных
сельскохозяйственных культур внутри севооборота №1:
) озимые зерновые в севообороте
№1+x21=0,25×1
) ячмень-0,125×1=0
) овес-0,125×1=0
) картофель-0,125×1=0
) лен-0,125×1=0
) однолетние травы-0,125×1=0
) многолетние
травы+x91+x101-0,125×1=0
. По площади севооборота №2:
) x12+x22+x32+x52+x62+x72+x82+x92+x102-x2<=0
. По площади отдельных
сельскохозяйственных культур внутри севооборота №2:
) озимые зерновые+x22-0,22×2=0
) ячмень-0,22×2=0
) картофель-0,22×2=0
) лен-0,11×2=0
) однолетние травы-0,11×2=0
) многолетние
травы+x92+x102-0,11×2=0
. По использованию трудовых
ресурсов:
)
19,6×11+15,6×21+14,5×31+12,7×41+81,8×51+ 129,8×61+
10,37×71+11,9×81+14,4×91+16,1×10,1+19,6×12+15,6×22+14,5×32+81,8×52+129,8×62+10,37×72+11,9×82+14,4×92+16,1×10,2<=98700
. На продажу:
) зерно, ц+x21+x12+x22>=18030
) картофель, ц+x52>=56120
) льносемена
,8×6,1+4,8×6,2>=1050
) льноволокно
,9×61+6,9×62>=1830
. По производству кормов:
) концентрированные корма,
ц.корм.ед.
,2×3+26,9×41+38,2×32>=17930
) грубые корма
,3×91+21,3×92>=2380
,9×51+22,4×101+9,9×52+22,4×102>=7280
) зеленый корм
x71+33×81+32×72+33×82>=8760
. Материально-денежные затраты, руб.
)
214,27×11+226,03×21+171,72×31+147,22×41+781,71×51+468,69×61
+227,74×71+120,88×81+241,47×91+273,58×101+214,27×12+226,03×22+171,72×32+781,71×52+468,69×62+227,74×72+120,88×82+241,47×92+273,58×102-x3=0
. Валовая продукция, руб.
)
461,6×11+435,28×21+…+190,5×10,1+461,6×12+…+190,5×10,2-x4=0
ЦЕЛЕВАЯ ФУНКЦИЯ: х4 стремится к
максимуму
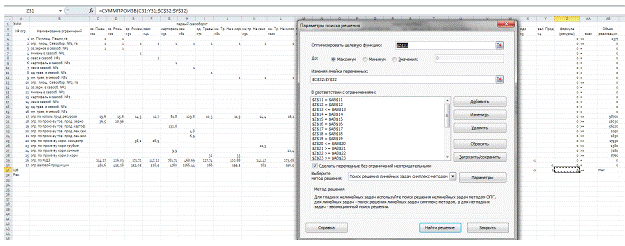
Решение задачи:
В ячейку Z4 вставим формулу «
=СУММПРОИЗВ(С4:Y4;$C$31:$Y$31)», затем растянем форму до целевой ячейки
включительно.
Затем находим решение задачи с помощью «поиска решения». Находим:
Данные→Анализ→Поиск решения. Как видно на рисунке: устанавливаем
целевую ячейку; равный- max значению; изменяя ячейки и ограничение.
На сегодняшний день разработано большое количество специализированных программных продуктов для проведения экономических расчетов, однако сотрудники финансово-экономических служб чаще всего пользуются табличным редактором Excel. Причина популярности данного инструмента — обширный функционал Excel и постоянное его развитие практически в каждой новой версии табличного редактора.
В рамках одной статьи невозможно рассмотреть все достоинства Excel, которые экономисты могут применить в своей работе, поэтому остановимся на анализе лучших функций редактора, используемых для решения экономических задач.
Для удобства восприятия материала сгруппируем эти функции в три блока:
1. Функционал расчетных формул в Excel.
2. Функционал Excel для обработки табличных данных.
3. Инструменты Excel для моделирования и анализа экономических данных.
ФУНКЦИОНАЛ РАСЧЕТНЫХ ФОРМУЛ В EXCEL
Расчетные формулы являются изначальным и основополагающим функционалом табличного редактора Excel, поэтому рассмотрим их в первую очередь.
Пакет встроенных расчетных формул включает в себя десятки наименований, но самыми востребованными в работе экономистов являются следующие формулы: ЕСЛИ, СУММЕСЛИ и СУММЕСЛИМН, ВПР и ГПР, СУММПРОИЗВ, СЧЕТЕСЛИ.
Решение экономической задачи с помощью формулы ЕСЛИ
Формула ЕСЛИ — расчетная функция Excel, которую наиболее часто используют для решения несложных экономических расчетов. Она относится к группе логических формул и позволяет рассчитать необходимые данные по условиям, заданным пользователями.
С помощью формулы ЕСЛИ можно сравнить числовые или текстовые значения по прописанным в формуле условиям.
Запись расчетной формулы в заданной ячейке в общем виде выглядит так:
=ЕСЛИ(логическое_выражение;[значение_если_истина];[значение_если_ложь]),
где логическое выражение — данные, которые нужно проверить/сравнить (числовые или текстовые значения в ячейках);
значение_если_истина — результат, который появится в расчетной ячейке, если значение будет верным;
значение_если_ложь — результат, который появится в расчетной ячейке при неверном значении.
Задача № 1. Предприятие реализует три номенклатурные группы продукции: лимонад, минеральная вода и пиво. С 01.09.2020 запланировано установить скидку в размере 15 % на пиво.
Чтобы сформировать новый прайс на продукцию, сохраняем ее перечень в виде таблицы Excel. В первом столбце таблицы отражена номенклатура всей продукции в алфавитном порядке, во втором — признак группы продукции.
Для решения задачи создаем в таблице третий столбец и прописываем в первой ячейке номенклатуры формулу: =ЕСЛИ(C4=»пиво»;15%;0).
Эту формулу продлеваем до конца перечня номенклатуры продукции. В итоге получаем сведения о продукции, на которую с сентября снизится цена (табл. 1).
В данном примере показано использование формулы ЕСЛИ для обработки текстовых значений в исходных данных.
Решение экономической задачи с помощью формулы СУММЕСЛИ
Формулы СУММЕСЛИ и СУММЕСЛИМН также используют для экономических расчетов, но они обладают более широкими возможностями для выборки и обработки данных. Можно задать не одно, а несколько условий отборов и диапазонов.
Задача № 2. На основе ведомости начисления заработной платы сотрудникам магазина нужно определить общую сумму зарплаты продавцов.
Чтобы решить эту задачу, сохраняем ведомость из учетной базы данных в виде таблицы Excel. В данном случае нам нужно не просто произвести выборку значений, но и суммировать их результат. Поэтому будем использовать более сложную разновидность формулы ЕСЛИ — СУММЕСЛИ.
Для решения задачи добавим внизу таблицы еще одну строку «Всего продавцы». В ее ячейке под суммой зарплаты, начисленной сотрудникам магазина, пропишем следующую формулу:=СУММЕСЛИ(C4:C13;»продавец»;D4:D13).
Таким образом мы задали условие, при котором табличный редактор обращается к столбцу с наименованием должностей (столбец С), выбирает в нем значение «Продавец» и суммирует данные ячеек с начисленной заработной платой из столбца D в привязке к этой должности.
Результат решения задачи — в табл. 2.
Решение экономической задачи с помощью формул ВПР и ГПР
Формулы ВПР и ГПР используют для решения более сложных экономических задач. Они популярны среди экономистов, так как существенно облегчают поиск необходимых значений в больших массивах данных. Разница между формулами:
- ВПР предназначена для поиска значений в вертикальных списках (по строкам) исходных данных;
- ГПР используют для поиска значений в горизонтальных списках (по столбцам) исходных данных.
Формулы прописывают в общем виде следующим образом:
=ВПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер столбца, из которого будут подставлены данные; [интервал просмотра данных]);
=ГПР(искомое значение, которое требуется найти; таблица и диапазон ячеек для выборки данных; номер строки, из которой будут подставлены данные; [интервал просмотра данных]).
Указанные формулы имеют ценность при решении задач, связанных с консолидацией данных, которые разбросаны на разных листах одной книги Excel, находятся в различных рабочих книгах Excel, и размещении их в одном месте для создания экономических отчетов и подсчета итогов.
Задача № 3. У экономиста есть данные в виде таблицы Excel о реализации продукции за сентябрь в натуральном измерении (декалитрах) и данные о реализации продукции в сумме (рублях) в другой таблице Excel. Экономисту нужно предоставить руководству отчет о реализации продукции с тремя параметрами:
- продажи в натуральном измерении;
- продажи в суммовом измерении;
- средняя цена реализации единицы продукции в рублях.
Для решения этой задачи с помощью формулы ВПР нужно последовательно выполнить следующие действия.
Шаг 1. Добавляем к таблице с данными о продажах в натуральном измерении два новых столбца. Первый — для показателя продаж в рублях, второй — для показателя цены реализации единицы продукции.
Шаг 2. В первой ячейке столбца с данными о продажах в рублях прописываем расчетную формулу: =ВПР(B4:B13;Табл.4!B4:D13;3;ЛОЖЬ).
Пояснения к формуле:
В4:В13 — диапазон поиска значений по номенклатуре продукции в создаваемом отчете;
Табл.4!B4:D13 — диапазон ячеек, где будет производиться поиск, с наименованием таблицы, в которой будет организован поиск;
3 — номер столбца, по которому нужно выбрать данные;
ЛОЖЬ — значение критерия поиска, которое означает необходимость строгого соответствия отбора наименований номенклатуры таблицы с суммовыми данными наименованиям номенклатуры в таблице с натуральными показателями.
Шаг 3. Продлеваем формулу первой ячейки до конца списка номенклатуры в создаваемом нами отчете.
Шаг 4. В первой ячейке столбца с данными о цене реализации единицы продукции прописываем простую формулу деления значения ячейки столбца с суммой продаж на значение ячейки столбца с объемом продаж (=E4/D4).
Шаг 5. Продлим формулу с расчетом цены реализации до конца списка номенклатуры в создаваемом нами отчете.
В результате выполненных действий появился искомый отчет о продажах (табл. 3).
На небольшом количестве условных данных эффективность формулы ВПР выглядит не столь внушительно. Однако представьте, что такой отчет нужно сделать не из заранее сгруппированных данных по номенклатуре продукции, а на основе реестра ежедневных продаж с общим количеством записей в несколько тысяч.
Тогда эта формула обеспечит такую скорость и точность выборки нужных данных, которой трудно добиться другими функциями Excel.
Решение экономической задачи с помощью формулы СУММПРОИЗВ
Формула СУММПРОИЗВ позволяет экономистам справиться практически с любой экономической задачей, для решения которой нужно работать с несколькими массивами данных. Она обладает всеми возможностями рассмотренных выше формул, умеет суммировать произведения данных из списка до 255 источников (массивов).
Задача № 4. Есть реестр продаж различной номенклатуры продукции за сентябрь 2020 г. Нужно рассчитать из общего реестра данные о суммах реализации по основным номенклатурным группам продукции.
Чтобы выполнить задачу, добавим внизу реестра три новые строки с указанием групп продукции и пропишем в ячейке с будущими данными о продажах первой группы (пиво) следующую формулу: =СУММПРОИЗВ(((C4:C13=C16)*D4:D13)). Здесь указано, что в ячейке должно быть выполнено суммирование произведений значений диапазона ячеек столбца с наименованием групп продукции (C4:C13) с условием отбора наименования группы «Пиво» (С16) на значения ячеек столбца с суммами продаж (D4:D13).
Далее копируем эту формулу на оставшиеся две ячейки, заменив в них условия отбора на группу «Лимонад» (С17) и группу «Минеральная вода» (С18).
Выполнив указанные действия, получим искомое решение задачи в табл. 4.
Решение экономической задачи с помощью формулы СЧЕТЕСЛИ
Формула СЧЕТЕСЛИ используется не так широко, как предыдущие, но она выручает экономистов, если нужно минимизировать ошибки при работе с таблицами Excel. Эта формула удобна для проверки корректности вводимых данных и установке различного рода запретов, что особенно важно, если с данными работает несколько пользователей.
Задача № 5. Экономисту поручили провести корректировку справочника номенклатуры ТМЦ в учетной базе данных компании. Справочник долгое время не проверяли, данные в него вносили порядка 10 человек, поэтому появилось много некорректных и дублирующих наименований.
Чтобы повысить качество работы, приняли решение создать обновленный справочник в книге Excel, а затем сопоставить его с данными в учетной базе и исправить их. Проблема заключалась в том, что перечень номенклатуры составляет порядка 3000 наименований. Вносить его в книгу будут шесть человек, а это создает риск дублирования позиций.
Экономист может решить эту проблему с помощью формулы СЧЕТЕСЛИ. Нужно выполнить следующие действия:
- выбираем диапазон ячеек, куда будут вноситься наименования номенклатуры (В5:В3005);
- в меню редактора выбираем путь: Данные → Проверка данных;
- в появившемся диалоговом окне выбираем вкладку Параметры и указываем в выпадающем списке Тип данных вариант Другой;
- в строке Формула указываем: =СЧЕТЕСЛИ($В$5:$В$3005;В5)<=1;
- в диалоговом окне на вкладке Сообщение об ошибке вводим текст сообщения и нажимаем кнопку «ОК».
Если кто-либо из сотрудников будет пытаться ввести в указанный диапазон ячеек наименование ТМЦ, которое уже есть в диапазоне, у него это не получится. Excel выдаст сообщение в таком виде (рис. 1).
ФУНКЦИОНАЛ EXCEL ДЛЯ ОБРАБОТКИ ТАБЛИЧНЫХ ДАННЫХ
Помимо расчетных формул в табличном редакторе Excel присутствует набор инструментов, значительно облегчающих жизнь экономистам, которые работают с большими объемами данных. К наиболее популярным из них можно отнести функцию сортировки данных, функцию фильтрации данных, функцию консолидации данных и функцию создания сводных таблиц.
Решение экономической задачи с применением функции сортировки данных
Функционал сортировки данных позволяет изменить расположение данных в таблице и выстроить их в новой последовательности. Это удобно, когда экономист консолидирует данные нескольких таблиц и ему нужно, чтобы во всех исходных таблицах данные располагались в одинаковой последовательности.
Другой пример целесообразности сортировки данных — подготовка отчетности руководству компании. С помощью функционала сортировки из одной таблицы с данными можно быстро сделать несколько аналитических отчетов.
Сортировку данных выполнить просто:
- выделяем курсором столбцы таблицы;
- заходим в меню редактора: Данные → Сортировка;
- выбираем нужные параметры сортировки и получаем новый вид табличных данных.
Задача № 6. Экономист должен подготовить отчет о заработной плате, начисленной сотрудникам магазина, с последовательностью от самой высокой до самой низкой зарплаты.
Для решения этой задачи берем табл. 2 в качестве исходных данных. Выделяем в ней диапазон ячеек с показателями начисления зарплат (B4:D13).
Далее в меню редактора вызываем сортировку данных и в появившемся окне указываем, что сортировка нужна по значениям столбца D (суммы начисленной зарплаты) в порядке убывания значений.
Нажимаем кнопку «ОК», и табл. 2 преобразуется в новую табл. 5, где в первой строке идут данные о зарплате директора в 50 000 руб., в последней — данные о зарплате грузчика в 18 000 руб.
Решение экономической задачи с использованием функционала Автофильтр
Функционал фильтрации данных выручает при решении задач по анализу данных, особенно если возникает необходимость проанализировать часть исходной таблицы, данные которой отвечают определенным условиям.
В табличном редакторе Excel есть два вида фильтров:
- автофильтр — используют для фильтрации данных по простым критериям;
- расширенный фильтр — применяют при фильтрации данных по нескольким заданным параметрам.
Автофильтр работает следующим образом:
- выделяем курсором диапазон таблицы, данные которого собираемся отфильтровать;
- заходим в меню редактора: Данные → Фильтр → Автофильтр;
- выбираем в таблице появившиеся значения автофильтра и получаем отфильтрованные данные.
Задача № 7. Из общих данных о реализации продукции за сентябрь 2020 г. (см. табл. 4) нужно выделить суммы продаж только по группе лимонадов.
Для решения этой задачи выделяем в таблице ячейки с данными по реализации продукции. Устанавливаем автофильтр из меню: Данные → Фильтр → Автофильтр. В появившемся меню столбца с группой продукции выбираем значение «Лимонад». В итоге в табл. 6 автоматически остаются значения продаж лимонадов, а данные по группам «Пиво» и «Минеральная вода» скрываются.
Для применения расширенного фильтра нужно предварительно подготовить «Диапазон условий» и «Диапазон, в который будут помещены результаты».
Чтобы организовать «Диапазон условий», следует выполнить следующие действия:
- в свободную строку вне таблицы копируем заголовки столбцов, на данные которых будут наложены ограничения (заголовки несмежных столбцов могут оказаться рядом);
- под каждым из заголовков задаем условие отбора данных.
Строка копий заголовков вместе с условиями отбора образуют «Диапазон условий».
Порядок работы с функционалом консолидации данных
Функционал консолидации данных помогает экономистам в решении задач по объединению данных из нескольких источников в одну общую таблицу. Например, экономисты холдинговых компаний часто создают однотипные таблицы с данными по разным компаниям холдинга и им требуется предоставить руководству сводные данные о работе всей группы компаний. Для упрощения формирования сводных показателей как раз и подходит функционал консолидации данных.
Консолидация работает только с идентичными таблицами Excel, поэтому для успеха все объединяемые таблицы должны отвечать следующим требованиям:
- макеты всех консолидируемых таблиц одинаковые;
- названия столбцов во всех консолидируемых таблицах идентичные;
- в консолидируемых таблицах нет пустых столбцов и строк.
Работа с функционалом консолидации включает ряд последовательных действий:
1) открываем файлы со всеми таблицами, из которых собираемся консолидировать данные;
2) в отдельном файле, где будет находиться консолидированный отчет, ставим курсор на первую ячейку диапазона консолидированной таблицы;
3) в меню Excel открываем вкладки: Данные → Работа с данными → Консолидация;
4) в открывшемся диалоговом окне выбираем функцию консолидации (как правило, это «сумма», потому что нам требуется суммировать значения нескольких таблиц);
5) в диалоговом окне консолидации указываем ссылки на диапазоны объединяемых таблиц (диапазоны должны быть одинаковые);
6) если требуется автоматическое обновление данных консолидированной таблицы при изменении данных исходных таблиц, ставим галочку напротив «Создавать связи с исходными данными»;
7) завершаем консолидацию нажатием кнопки «ОК». В итоге получаем сводную структурированную таблицу, объединяющую данные всех исходных таблиц.
Решение экономической задачи с использованием функционала сводной таблицы для создания нового отчета
Функционал сводных таблиц позволяет сформировать различного рода отчеты из одного или нескольких массивов данных с возможностью обновления отчетных данных в случае изменения информации в исходных массивах. Используя сводные таблицы, можно быстро перенастроить параметры отчета.
Для создания сводной таблицы нужно зайти в меню Excel и вызвать Мастера сводных таблиц. В моей версии редактора это выполняется через Вставка → Сводная таблица, в некоторых версиях нужно выбрать Данные → Сводная таблица.
В появившемся диалоговом окне формируем параметры будущей таблицы:
- указываем исходную таблицу или диапазон ячеек Excel, откуда будут взяты данные для сводной таблицы. В последних версиях Excel также можно выбрать вариант обработки данных из внешних источников;
- указываем место, куда размещать создаваемый отчет сводной таблицы (новый лист, ячейки открытого листа);
- в открывшемся конструкторе отчета указываем, какие исходные данные будут выведены в строки и столбцы отчета, при необходимости настраиваем фильтры для показателей сводной таблицы и создаем новый отчет.
Задача № 8. Экономисту нужно создать отчет на основе реестра данных о реализации продукции за сентябрь 2020 г. В отчете должно быть два уровня группировки данных. На первом уровне нужно вывести итоги по группам продукции, на втором уровне — по ее номенклатурным позициям. Чтобы решить эту задачу, вызываем Мастера сводных таблиц. Указываем, что данные берем из ячеек табл. 4, а отчет будем размещать на новом листе книги Excel. В конструкторе отчета указываем, что в первой колонке отчета будут показатели групп и номенклатурных единиц продукции, во второй — данные о суммах реализации. После этого даем команду создать сводную таблицу. Результат — в табл. 7.
ИНСТРУМЕНТЫ EXCEL ДЛЯ МОДЕЛИРОВАНИЯ И АНАЛИЗА ЭКОНОМИЧЕСКИХ ДАННЫХ
Постоянное развитие функционала табличного редактора Excel привело к тому, что появилось много новых инструментов, которые могут помочь экономистам в решении выполняемых ими задач. К числу наиболее значимых можно отнести функцию «Поиск решения», пакет расширенного анализа данных и специализированные надстройки.
Решение экономической задачи с помощью надстройки «Поиск решения»
Функция «Поиск решения» позволяет найти наиболее рациональный способ решения экономической задачи математическими методами. Она может автоматически выполнить расчеты для задач с несколькими вводными данными при условии накладывания определенных ограничений на искомое решение.
Такими экономическими задачами могут быть:
- расчет оптимального объема выпуска продукции при ограниченности сырья;
- минимизация транспортных расходов на доставку продукции покупателям;
- решение по оптимизации фонда оплаты труда.
Функция поиска решения является дополнительной надстройкой, поэтому в стандартном меню Excel мы ее не найдем. Чтобы использовать в своей работе функцию «Поиск решения», экономисту нужно сделать следующее:
- в меню Excel выбрать путь: Файл → Параметры → Надстройки;
- в появившемся списке надстроек выбрать «Поиск решения» и активировать эту надстройку;
- вернуться в меню Excel и выбрать: Данные → Поиск решения.
Задача № 9. Туристической компании необходимо организовать доставку 45 туристов в четыре гостиницы города с трех пунктов прибытия при минимально возможной сумме затрат. Для решения задачи составляем таблицу с исходными данными:
1. Количество прибывающих с каждого пункта — железнодорожный вокзал, аэропорт и автовокзал (ячейки Н6:Н8).
2. Количество забронированных для туристов мест в каждой из четырех гостиниц (ячейки D9:G9).
3. Стоимость доставки одного туриста с каждого пункта прибытия до каждой гостиницы размещения (диапазон ячеек D6:G8).
Исходные данные, размещенные таким образом, показаны в табл. 8.1.
Далее приступаем к подготовке поиска решения.
1. Создаем внизу исходной таблицы такую же таблицу для расчета оптимального количества доставки туристов при условии минимизации затрат на доставку с диапазоном ячеек D15:G17.
2. Выбираем на листе ячейку для расчета искомой функции минимизации затрат (J4) и прописываем в ячейке расчетную формулу: =СУММПРОИЗВ(D6:G8;D15:G17).
3. Заходим в меню Excel, вызываем диалоговое окно надстройки «Поиск решения» и указываем там требуемые параметры и ограничения (рис. 2):
- оптимизировать целевую функцию — ячейка J4;
- цель оптимизации — до минимума;
- изменения ячейки переменных — диапазон ячеек второй таблицы D15:G17;
- ограничения поиска решения:
– в диапазоне ячеек второй таблицы D15:G17 должны быть только целые значения (D15:G17=целое);
– значения диапазона ячеек второй таблицы D15:G17 должны быть только положительными (D15:G17>=0);
– количество мест для туристов в каждой гостинице таблицы для поиска решения должно быть равно количеству мест в исходной таблице (D18:G18 = D9:G9);
– количество туристов, прибывающих с каждого пункта, в таблице для поиска решения должно быть равно количеству туристов в исходной таблице (Н15:Н17 = Н6:Н8).
Далее даем команду найти решение, и надстройка рассчитывает нам результат оптимальной доставки туристов (табл. 8.2).
При такой схеме доставки целевое значение общей суммы расходов действительно минимальное и составляет 1750 руб.
Пакет расширенного анализа данных
Пакет расширенного анализа данных применяют, если нужно исследовать различного рода статистические анализы, ряды данных, спрогнозировать тренды и т. д.
Пакет является надстройкой к Excel, устанавливается в основное меню аналогично функции поиска решений (Файл → Параметры → Надстройки → Пакет анализа). Вызвать его можно командой Данные → Анализ данных через диалоговое окно, в котором отражены все заложенные в надстройке виды анализа (рис. 3).
Специализированные надстройки для финансово-экономической работы
В последние годы значительно расширился перечень специализированных надстроек к табличному редактору Excel, которые могут использовать в своей работе экономисты. Практически все они бесплатные, легко устанавливаются самим пользователем.
Не будем останавливаться на таких надстройках, как Power Query, Power Pivot, Power Quick, так как они в большей степени используются в целях бизнес-аналитики, чем для решения экономических задач.
Есть и другие надстройки к Excel, которые могут облегчить работу специалистов финансово-экономических служб. Интерес представляют две бесплатные надстройки — «Финансист» и PowerFin.
Надстройку «Финансист» можно установить на свою версию Excel как в автоматическом, так и ручном режиме. В надстройке собрано много полезных для экономистов функций. Достаточно перечислить основные блоки данной надстройки:
- финансовые функции (ликвидность, платежеспособность, финансовая устойчивость, рентабельность, оборачиваемость, безубыточность продаж, отсрочка платежа, налоги и т. д.);
- работа с формулами;
- работа с текстом;
- работа с книгами и листами Excel;
- работа с ячейками Excel;
- поиск дубликатов и сравнение диапазонов данных;
- вставка дат и примечаний к диапазонам данных;
- загрузка курсов валют;
- создание выпадающих списков.
Надстройка PowerFin будет полезна прежде всего экономистам, которые работают с кредитами и инвестициями. Она без проблем устанавливается в меню надстроек Excel и имеет следующие функции:
- кредитный калькулятор (с функцией выведения калькулятора на лист, в том числе с возможностью автоматического формирования графика платежей);
- депозитный калькулятор для вычисления основных параметров инвестиций (с функцией выведения калькулятора на лист);
- вычисление требуемой процентной ставки исходя из первоначальной и будущей стоимости инвестиций;
- набор основных формул для расчета эффективности проекта: дисконтированного денежного потока, чистого денежного дохода, внутренней нормы доходности, срока окупаемости.
Статья опубликована в журнале «Планово-экономический отдел» № 10, 2020.
Цели урока:
1. Образовательные:
— формирование умений применять имеющиеся
математические знания и знания из курса
информатики к решению практических задач;
— ознакомление с задачами оптимизации и
способами их решения с помощью ms Excel;
2. Развивающие:
– развитие внимания, познавательной
активности, творческих способностей,
логического мышления.
3. Воспитательные:
– воспитание интереса к предмету;
– самостоятельности в принятии решения;
– формирование культуры общения.
Методы обучения:
– частично-поисковый;
– проблемный.
Тип урока: Комбинированный.
Дидактическое и методическое оснащение урока:
– план выполнения работы в ms Excel, инструкции по
выполнению практической работы.
1. Организация начала урока.
В нашей стране сейчас очень много внимания
уделяется развитию бизнеса и
предпринимательства. И кто знает, может среди
многие из вас свяжут свою жизнь с экономикой,
станут предпринимателями, директорами,
бухгалтерами, менеджерами, и уже сейчас вы должны
понимать суть выполняемой работы на той или иной
должности и меру ответственности перед людьми и
предприятием. Мы убедимся с вами на сегодняшнем
уроке, насколько необходимо успешному
бизнесмену знать возможности информационных
технологий и уметь применять их в своей
деятельности.
На предыдущих уроках мы рассмотрели основные
понятия электронных таблиц. Сегодня вы должны
показать, насколько хорошо владеете понятиями:
ячейка, абсолютный и относительный адрес, умеете
решать различные задачи в электронных таблицах.
Подготовительный этап.
— С какой целью используют Excel? (Электронные
таблицы позволяют сформировать данные в виде
таблицы, рассчитать содержимое ячейки с помощью
формулы, представить числовую информацию в
графическом виде).
Электронные таблицы – это мощная программа по
обработке числовых данных. Excel позволяет не
только производить расчеты, но и решать сложные
задачи в различных сферах деятельности, такие
как задачи оптимизации, прогнозирования.
Часто при решении практических задач возникают
ситуации, когда необходимо достичь какой-то
конкретной цели. Например, необходимо чтобы
себестоимость продукции составляла 20 рублей.
Специфика таких задач состоит в том, что в Вашем
распоряжении есть математическая модель
исследуемого процесса, например, закон
ценообразования, но Вы не знаете, при каком
значении входящего в нее параметров можно
достичь поставленную цель. Решение таких задач
можно искать методом перебора. Однако в лучшем
случае на это уходит много времени. Можно
предложить другие способы решения. В Excel они
реализованы как поиск значения параметра
формулы, удовлетворяющего ее конкретному
значению.
Процедуру “Поиск значения параметра”
используют для поиска такого значения ячейки,
при котором значение другой ячейки, вычисляемое
по формуле, заранее задано. В формуле должна быть
ссылка на ячейку, значения которой ищут.
Ограничения на искомое значение ячейки не
налагают.
Познакомимся с этой процедурой на примере
составления штатного расписания предприятия.
2. Изучение нового материала.
a. Использование надстройки “Поиск решения”
при решении прикладных задач.
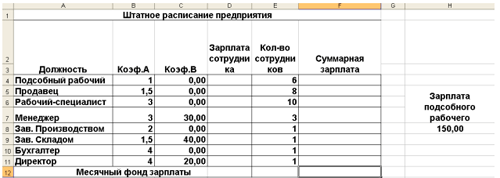
Пусть известно, что в штате вашего предприятия
должно состоять 6 подсобных рабочих, 8 продавцов,
10 рабочих-специалистов, 3 менеджера, зав.
производством, заведующая складом, бухгалтер и
директор. Общий месячный фонд зарплаты
составляет 10 000 у.е. Необходимо определить, какими
должны быть оклады сотрудников предприятия.
- Продавец получает в 1,5 раза больше подсобного
рабочего (А2=1,5; В2=0); - Рабочий-специалист – в 3 раза больше подсобного
рабочего (А3=0;В3=0); - Менеджер — на 30 у.е. больше, чем
рабочий-специалист(А4=3; B4=30); - Заведующий производством — в 2 раза больше
грузчика(А5=2; В5=0); - Зав. складом — на 40 у.е. больше продавца (А6=1,5;
В6=40); - Бухгалтер — в 4 раза больше подсобного рабочего
(А7=4; В7=0); - Директор — на 20у.е. больше бухгалтера (А8=4; В8=20);
Построим модель решения этой задачи
— Как вы думаете, что мы возьмем за основу для
расчета зарплаты работников предприятия? (оклад
подсобного рабочего) Почему? (Все другие оклады
рассчитываются исходя из оклада подсобного
рабочего). За основу возьмем оклад подсобного
рабочего, а остальные оклады будем вычислять,
исходя из него: во столько-то раз или на
столько-то больше.
Введем обозначения коэффициентов: А –
показывает, во сколько раз оклад по должности
больше оклада подсобного рабочего; А1—для
подсобного рабочего, А2— для продавца и т.д.
В – коэффициент, который показывает, на сколько
больше. В1, В2 и т.д.
— Что еще известно в задаче? (количество
работников каждой должности) Обозначим
количество работников через N: N1,N2,…N8
— Чтобы рассчитать зарплату для каждой должности,
мы должны знать оклад подсобного рабочего.
Обозначим его С.
Мы знаем количество человек на каждой
должности, коэффициенты и то, что фонд заработной
платы =10000 у.е. Каким образом мы можем записать
математическую модель решения этой задачи? Нашу
модель можно записать как уравнение
N1*A1*C+N2*(A2*C+B2)+…+N8*(A8*C+B8)
= 10000, проверим по таблице
В этом уравнении нам известны A1…A8, B1…B8
и N1… N8, а С неизвестно.
Анализ уравнения показывает, что задача
составления расписания свелась к решению
линейного уравнения относительно С. Решим его.
Технология работы:
Предположим, что оклад подсобного рабочего
равен 150 у.е.
— Сколько столбцов нам необходимо построить?
Введем исходные данные в рабочий лист
электронной таблицы, как показано:
В столбце D вычислим заработную плату для
каждой должности.
Вспомните правила набора формулы в строке
формул.
Записываем формула, начиная со знака “=”. Какую
формулу мы должны ввести, чтобы рассчитать
зарплату подсобного рабочего? (Для ячейки D4
формула расчета имеет вид =B4*$H$8+C4). Почему нам
необходима абсолютная ссылка на ячейку H8? (
параметры этой ячейки не должны изменяться)
Нужно ли вводить формулы в каждую ячейку
столбца D? (Можно воспользоваться
автозаполнением).
В столбце F вычислите заработную плату всех
рабочих данной должности. Какую формулу введем в
ячейку F4 (формула расчета имеет вид =D4*E4).
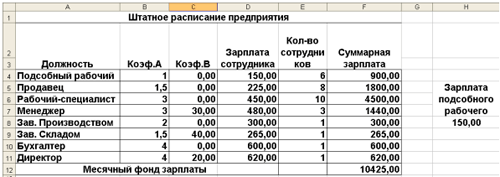
В ячейке F12 вычислите суммарный фонд заработной
платы предприятия. Какой функцией воспользуемся?
(СУММ или пиктограммой “Автосумма”). Рабочий
лист электронной таблицы будет выглядеть, как
показано ниже.
Что же получилось? Взяв оклад подсобного
рабочего за 150 у.е., мы превысили месячный фонд
зарплаты. Определим оклад подсобного рабочего
так, чтобы расчетный фонд был равен заданному.
Как решить поставленную задачу? (уменьшить оклад
подсобного рабочего, скажем, до 120 у.е.). Для
решения этой задачи воспользуемся процедурой
“Подбор параметра”.
- активизируем команду Подбор параметра из
меню Сервис; - в поле «Установить в ячейке» появившегося
окна введем ссылку на ячейку F12, содержащую
формулу; - в поле «Значение» наберем искомый
результат 10000; - в поле «изменяя значение ячейки» введем
ссылку на изменяемую ячейку H8 и щелкните на
кнопке ОК.
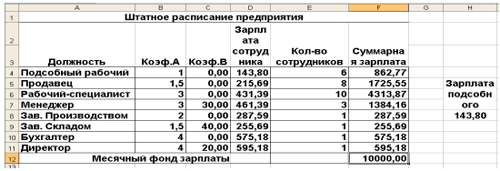
Как видите, программа нашла оптимальное
решение.
Анализ задачи показывает, что с помощью Excel
можно решать линейные уравнения. Конечно, такое
уравнение может решить любой школьник. Однако,
благодаря этому простому примеру стало,
очевидным, что поиск значения параметра формулы,
удовлетворяющего ее конкретному значению, — это
не что иное, как численное решение уравнений.
Другими словами, используя Excel, можно решать
любые уравнения с одной переменной.
— Для чего используется процедура “Подбор
параметров”?
b. Задачи оптимизации.
В предыдущей задаче мы рассмотрели поиск
значения параметра, позволяющего достичь
конкретной цели.
Решаемые задачи могут быть более сложными.
Например, поиск нескольких параметров,
обеспечивающих некоторый наперед заданный
результат.
Кроме того, иногда интересует не конкретный
результат, а минимально или максимально
возможный. Например, как минимизировать затраты
на содержание персонала или максимизировать
прибыли от реализации продукции?
Такие задачи в Excel решают с помощью Поиска
решения.
Познакомимся с решением этих задач на
следующем примере.
Составление штатного расписания
Усложним рассмотренную задачу. Пусть известно,
что для нормальной работы предприятия
необходимо 5-7 подсобных рабочих, 8-10продавцов, 10
рабочих-специалистов, 3 менеджера, зав.
производством, зав. складом, бухгалтер и
директор. Общий месячный фонд зарплаты должен
быть минимален. Необходимо определить, какими
должны быть оклады сотрудников, при условии, что
оклад подсобного рабочего не должен быть меньше
прожиточного минимума 80у.е.
В качестве модели решения этой задачи возьмем,
как и в первой главе, линейную.
Нужно ли менять уравнение, составленное нами
для решения предыдущей задачи? Запишем ее так:
N1*A1*C+N2*(A2*C+B2)+…+N8*(A8*C+B8)
= Минимум.
В этом уравнении нам не известно число
подсобных рабочих (N1), продавцов (N2), и оклад
подсобного рабочего(С).
Используя Поиск решения, найдем их. В меню Сервис
активизируем команду Поиск решения. В окне Установить
целевую ячейку укажем ячейку F12, содержащую
модель. Поскольку необходимо минимизировать
общий месячный фонд зарплаты, то активизируем
радиокнопку Минимальному значению.
Используя кнопку Добавить, опишем
ограничения задачи. Какие ограничения следует
добавить?Окончательно окно Поиска решения
будет выглядеть так:
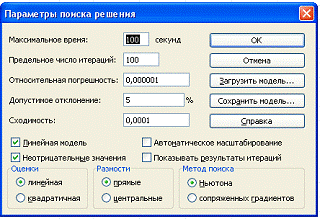
Опишем Параметры поиска. Щелкнем на кнопке
ОК, а затем — Выполнить.
Решение приведено на рис. Оно тривиально: чем
меньше сотрудников и чем меньше их оклад, тем
меньше месячный фонд заработной платы.
Задачи, в которых необходимо найти оптимальное
значение параметров, называются задачами
оптимизации.
Для закрепления пройденного материала решим
следующую задачу.
3. Закрепление. Практическая работа.
Решим подобную задачу самостоятельно.
Прочитайте условия задачи.
План выгодного производства
Предположим, что мы решили производить
несколько видов конфет. Назовем их условно
«A», «B» и «C». Известно, что
реализация 10-и килограмм конфет «А» дает
прибыль 9 у.е.., «В» — 10 у.е. и «С» — 16 у.е.
Конфеты можно производить в любых количествах
(сбыт обеспечен), но запасы сырья ограничены.
Необходимо определить, каких конфет и сколько
десятков килограмм необходимо произвести, чтобы
общая прибыль от реализации была максимальной.
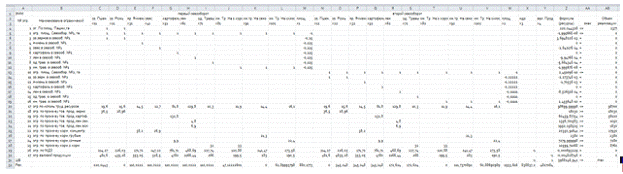
Нормы расхода сырья на производство 10 кг конфет
каждого вида приведены ниже.
| Сырье | Нормы расхода сырья | Запас сырья | ||
| А | В | С | ||
| Какао | 18 | 15 | 12 | 360 |
| Сахар | 6 | 4 | 8 | 192 |
| Наполнитель | 5 | 3 | 3 | 180 |
| Прибыль | 9 | 10 | 16 |
Какие формулы нам нужно будет ввести, чтобы
рассчитать общую прибыль от производства? Чтобы
рассчитать прибыль от производства каждого
сорта конфет (Количество нужно умножить на
прибыль от производства 10 кг конфет). Как
рассчитать расход каждого вида сырья?
(количество выпускаемых конфет умножить на нормы
расхода каждого вида сырья). Какая ячейка будет
содержать математическую модель?
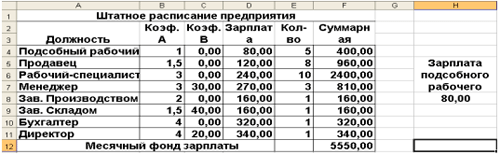
Из решения видно, что оптимальный план выпуска
предусматривает изготовление 80 кг конфет
«В» и 20 кг конфет «С». Конфеты «А»
производить не стоит. Полученная Вами прибыль
составит 400 у.е.
4. Рефлексия.
— Что вы можете сказать о сегодняшнем уроке?
— Как вы считаете, полезны ли для вас знания и
умения, которые вы получили сегодня на уроке?
— Владея технологией работы в электронных
таблицах, вы сможете не только грамотно
организовать предприятия, но и оптимизировать
его производство.