Решение задач оптимизации в excel лабораторные работы

Цель
работы: Научиться решать задачи
оптимизации различных типов

средствами
MS Excel.

Требования к содержанию, оформлению и порядку выполнения

Для выполнения
лабораторной работы необходимо создать
новую рабочую книгу Excel
под именем «Ваша фамилия, Лабораторная
работа №2, (например: «Иванов И.П.
Лабораторная работа №2»).

Перед выполнением
лабораторной работы изучите теоретическую
часть.

Рабочие листы
рабочей книги должны быть именованы
Задание1, Задание2, Задание3. Результаты
решения задач поместите в файл отчета.

После выполнения
лабораторной работы ответьте на
контрольные вопросы. Ответы на контрольные
вопросы поместите в файл отчета. Свою
рабочую книгу вместе с ответами на
контрольные вопросы необходимо
предоставить преподавателю на дискете,
подписав ее вышеуказанным образом.

Теоретическая часть

Оптимизации
занимают очень важное место в экономике
организаций и предприятий. Задачи по
поиску наилучшего
(оптимального)
решения из множества допустимых решений
называются оптимизационными
задачами (экстремальными
задачами, задачами линейного
программирования). Решение любой
оптимизационной задачи сводится к
нахождению некоторого набора условий,
при которых интересуемая величина будет
минимальной или максимальной. Целями
решения оптимизационных задач в экономике
могут быть увеличение прибыли, снижение
затрат, повышение производительности
труда, рациональное использование
оборудования, повышение эффективности
инвестиций и многие другие.

Все оптимизационные
задачи имеют три свой­ства:

• имеется единственная
  максимизируемая или минимизируемая
  цель (прибыль, производительность,
  ре­сурсы и т.д.);

• имеются ограничения,
  выражающиеся, как правило, в виде
  неравенств (напри­мер, объем
  используемого сырья не может превышать
  объем имеющегося сы­рья на складе,
  или время работы станка за сутки не
  должно быть больше 24 часов минус время
  на обслуживание);

• имеется набор
  входных значений-переменных, прямо или
  косвенно влияющих на ограничения и на
  оптимизируемые величины.

Для решения
оптимизационной задачи необходимо
описать заданную цель (например, получение
максимальной прибыли), а также запас
имеющихся ресурсов и условия их
использования для достижения цели. При
таком описании выделяют следующие два
понятия:

• Математическую
  модель;

• Целевую функцию.

Математическая
модель задачи оптимизации задает
множество допустимых решений X
. Множество X
определяется имеющимися запасами
ресурсов и условиями их использования
для достижения цели. Множество допустимых
решений называют также ограничениями
задачи. Т.о. формулировка таких задач
представляет собой систему уравнений
с не­сколькими неизвестными и набор
ограничений на решения.

Целевая функция
f(x) представляет собой числовую
характеристику, максимальному или
минимальному значению которой
соответствует оптимальное решение.

Примерами задач
оптимизации в экономике могут служить
задачи максимизации прибыли предприятия
в условиях ограниченных ресурсов;
транспортные задачи (минимизация
расходов на перевозку); планирование
штатного расписания; оптимальный
раскрой материалов, получение заданного
качества смеси при наименьших рас­ходах
и т.д.

Рассмотрим подробнее
на примере задачи максимизации
прибыли предприятия в условиях
ограниченных ресурсов
процесс описания математической модели
и целевой функции.

Предприятие может
выпускать n
видов продукции, используя для этого m
видов ресурсов. Пусть для производства
одной единицы продукции

-го
вида используется

единиц ресурса

-го
вида. Прибыль от реализации одной единицы
продукции

-го
вида обозначим через

,

рублей. Требуется определить такой
объем выпуска продукции, который
обеспечивает предприятию наибольшую
прибыль.

Обозначим через

,

объем продукции j
— го вида, выпускаемой в соответствии с
некоторым планом. Тогда математическую
модель задачи можно записать в следующем
виде

(1)

Эта модель
определяется ограничениями на выпуск
продукции, обусловленными имеющимися
запасами ресурсов. Целевую функцию
задачи можно записать следующим образом

(2)

После построения
математической модели и записи целевой
функции задача определения объема
выпуска продукции, обеспечивающего
предприятию наибольшую прибыль, может
быть сформулирована как задача

Найти
(3)

при условии (1) и

(4)

Условие (4), указывает
на неотрицательность выпуска продукции.

В (3), (1), (4) отсутствуют
ограничения по спросу на продукцию,
которым в рыночной экономике принадлежит
важная роль. Введем эти ограничения в
задачу следующим образом. Обозначим
через

,

верхнее ограничение по спросу на
продукцию

-го
вида, а через

нижнее ограничение по спросу на продукцию

-го
вида, тогда задача примет следующий
вид

Найти
(5)

при условии

(6)

(7)

(8)

В общем случае
прибыль с ростом объема производства
может начать уменьшаться из-за
дополнительных затрат, связанных,
например, с реализацией продукции.

Обозначим через

степень влияния на прибыль объема
выпуска j-го
изделия. Тогда целевая функция задачи
может быть записана в следующем виде:

(9)

а сама задача
примет вид

(10)

при условиях (6),
(7), (8).

Заметим, что если

,
то прибыль не зависит от объема выпуска
j-го
изделия.

Для решения задач
оптимизации в Excel имеется специальная
надстройка «Поиск
решения» (Solver).
Поскольку пакет Поиск
решения
является надстройкой, то перед началом
работы необходимо установить ее. Для
этого выберите в меню пункт Сервис/Надстройки.
В диалоговом окне найдите в списке
надстроек Поиск
решения,
установите слева от него флажок и
щелкните на кнопке ОК (если будет выдано
сообщение, что данный компонент не
установлен, Вам придется сначала его
установить). В дальнейшем при запуске
Excel Solver
будет загружаться ав­томатически,
пока Вы не снимите флажок в окне Надстройки
и запустить этот пакет можно выбрав в
меню Сервис
пункт Поиск
ре­шения.

В целом решение
задач оптимизации с помощью пакета
Поиск решения состоит из следующих
этапов:

• Оформление рабочего
  листа (ввод на рабочий лист исходных
  данных и формул);

• Вызов диалогового
  окна Поиск решения.

• Указание целевой
  ячейки (ячейки в которой хранится
  целевая функция);

• Указание изменяемых
  значений;

• Указание условий
  (ограничений);

• Изменение настроек
  поиска решения (при необходимости);

На этапе
оформления
необходимо:

1.Ввести исходные
данные в ячейки рабочего листа Excel;

2.Разметить блоки
ячеек, необходимые для формирования
элементов математической модели и
целевой функции;

3.Сформировать на
рабочем листе EXCEL элементы математической
модели и целевую функцию.

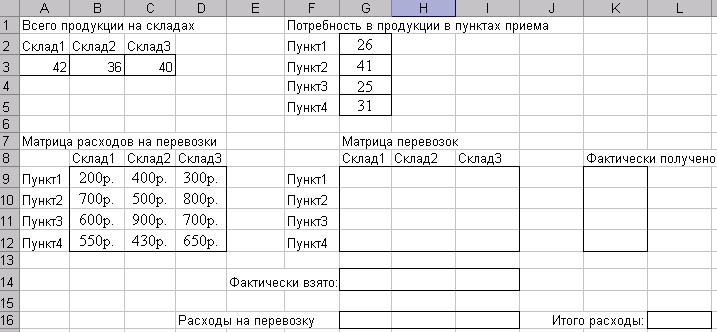
Рис.1. Пример
оформления рабочего листа для решения
задачи оптимизации связанной с
минимизацией расходов на перевозки
(транспортная задача).

Когда рабочий лист
будет оформлен, нужно активизировать
компонент Поиск
решения. В
результате откроется диалоговое окно
Поиск решения
(рис.2).

Рис.2. Вид диалогового
окна Поиск решения.

Для указания
целевой ячейки, необходимо ввести ее
адрес в поле
Установить целевую ячейку
или выбрать адрес ячейки щелкнув на ней
мышкой (предварительно установив курсор
в вышеописанное поле).

Затем в зависимости
от того хотим ли мы максимизировать и
минимизировать целевую функцию выбрать
с помощью переключателя необходимый
параметр максимальному
значению или
минимальному значению.

В поле Изменяя
ячейки
вводится адрес интервала ячеек, значения
которых будут изменяться в ходе поиска
оптимального решения.

С помощью кнопки
Добавить
можно
добавлять
ограничения, а с помощью двух других
можно изменять имеющиеся ограничения
или удалять. После нажатия на кнопку
Добавить
открывается диалоговое окно Добавление
ограничения
(рис.3).

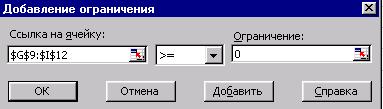
Рис.3. Вид диалогового
окна Добавление ограничения.

В этом окне в поле
Ссылка на
ячейку выбирается
адрес ячейки или интервала ячеек, на
значение которых накладывается
ограничение, далее в следующем поле
выбирается отношение (равно, больше или
равно, меньше или равно и т.д.) и в поле
ограничение вводится некое число или
адрес ячеек. С помощью кнопки Добавить
можно добавить описанное ограничение
и прейти к следующему. После закрытия
этого окна осуществляется возврат к
предыдущему окну Поиск
решения.

После того как
будут определены основные поля можно
приступать к поиску оптимального решения
для этого предназначена кнопка Выполнить.
Через некоторое время после нажатия на
эту кнопку откроется диалоговое окно
Результаты
поиска решения (рис.4.),
в котором можно выбрать сохранять
найденное решение (по месту изменяемых
ячеек) или восстановить их исходные
значения и далее ОК.

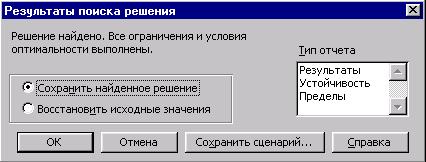
Рис.4. Вид диалогового
окна Результаты поиска решения.

После решения
задачи можно выбрать одну из следующих
возможностей:

• Сохранить найденное
  решение на место изменяемых ячеек;

• Восстановить
  исходные значения в изменяемых ячейках;

• Создать несколько
  отчетов по процедуре поиска. Причем
  можно выбрать три типа отчетов (используя
  клавишу Ctrl
  или Shift):

  • Результаты.   
    Используется для создания отчета,
    состоящего из целевой ячейки и списка
    влияющих ячеек модели, их исходных и
    конечных значений, а также формул
    ограничений и дополнительных сведений
    о наложенных ограничениях.

  • Устойчивость.   
    Используется для создания отчета,
    содержащего сведения о чувствительности
    решения к малым изменениям в формуле
    (поле Установить целевую ячейку,
    диалоговое окно Поиск решения) или в
    формулах ограничений.

  • Ограничения.   
    Используется для создания отчета,
    состоящего из целевой ячейки и списка
    влияющих ячеек модели, их значений, а
    также нижних и верхних границ. Такой
    отчет не создается для моделей, значения
    в которых ограничены множеством целых
    чисел.

• Сохранить сценарий.
  Для сохранения решения в виде сценария,
  который можно будет использовать в с
  помощью диспетчера сценариев Microsoft
  Excel.

С помощью кнопки
Параметры
диалогового окна Поиск
решения
(рис.2) можно вызвать диалоговое окно
Параметры
поиска решения
(рис.5) и с помощью его элементов изменить
параметры работы инструмента Поиск
решения.

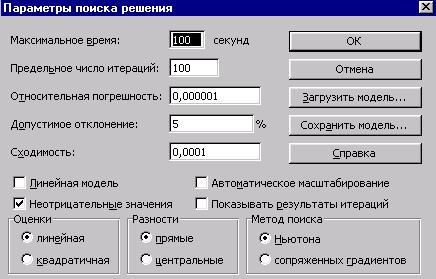
Рис.5. Вид диалогового
окна Параметры поиска решения.

Если решение в
ходе выполнения процедуры Поиска решения
не было найдено, зачастую его можно
найти, изменив параметры и повторно
запустив Поиск решения.

С помощью элементов
диалогового окна Параметры поиска
решения можно изменить следующее:

• Максимальное
  время. Если
  появится сообщение о том, что время на
  поиск решение истекло, то нужно добавить
  время на поиск решения;

• Предельное число
  итераций.
  Ограничивает число промежуточных
  решений, допускаемых при поиске решения;

• Относительная
  погрешность.
  Служит для задания точности, с которой
  определяется соответствие ячейки
  целевому значению или приближение к
  указанным границам;

• Допустимое
  отклонение.
  Позволяет установить максимальное
  отклонение в % для целочисленных
  итераций.

• Сходимость.
  Когда относительное изменение значения
  в целевой ячейке за последние пять
  итераций становится меньше числа,
  указанного в поле Сходимость,
  поиск прекращается. Сходимость
  применяется только к нелинейным задачам.

• Линейная модель.
  Служит для ускорения поиска решения
  линейной задачи оптимизации. Можно
  использовать, если все зависимости в
  модели линейные. Нельзя использовать
  эту опцию, если изменяемые ячейки
  умножаются или делятся или в задаче
  используется возведение в степень.

• Неотрицательные
  значения.
  Позволяет установить нулевую нижнюю
  границу для тех влияющих ячеек, для
  которых не были установлены ограничения.

• Автоматическое
  масштабирование.
  Служит для включения автоматической
  нормализации входных и выходных
  значений, качественно различающихся
  по величине — например, максимизация
  прибыли в процентах по отношению к
  вложениям, исчисляемым в миллионах
  рублей.

• Показывать
  результаты итераций.
  Позволяет просматривать результаты
  отдельных итераций.

• Разделы
  Оценка, Разности и Методы поиска.
  Позволяют контролировать некоторые
  технические аспекты решения задач. В
  большинстве случаем нет необходимости
  изменять их установки.

• Сохранить модель.
  Служит для отображения на экране
  диалогового окна, в котором можно задать
  ссылку на область ячеек, предназначенную
  для хранения модели оптимизации. Данный
  вариант предусмотрен для хранения на
  листе более одной модели оптимизации –
  первая модель сохраняется автоматически.

• Загрузить модель.
  Служит для отображения на экране
  диалогового окна, в котором можно задать
  ссылку на область ячеек, содержащих
  загружаемую модель.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Практическая работа №11

Тема: Задачи оптимизации (поиск решения) в MS Excel.

Цель: — изучение технологии поиска решения для задач
оптимизации (минимизации, максимизации).

Вид
работы: фронтальный

Время
выполнения: 2 часа

Задания к практической работе

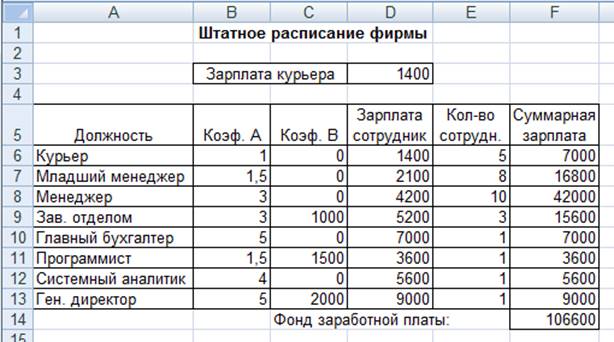
Задание
1. Минимизация фонда заработной платы
фирмы.

Пусть известно, что для нормальной работы фирмы
требуется 5…7 курьеров, 8…10 младших менеджеров, 10 менеджеров, 3 заведующих
отделами, главный бухгалтер, программист, системный аналитик, генеральный
директор фирмы.

Общий месячный фонд зарплаты должен быть минимален.
Необходимо определить, какими должны быть оклады сотрудников фирмы, при
условии, что оклад курьера не должен быть меньше 1400 р.

В качестве модели решения этой задачи возьмем линейную
модель. Тогда условие задачи имеет вид N₁*A₁*x+N₂*(A₂*x+B₂)+…+N₈*(A₈*x+B₈)
= Минимум, где N_i – количество работников данной специальности; x
– зарплата курьера; A_i и B_i – коэффициенты заработной
платы сотрудников фирмы.

Ход работы

1.  
Запустите редактор электронных
таблиц Microsoft Excel и откройте созданный в Практической работе 4 файл
«Штатное расписание».

Скопируйте содержимое листа «Штатное расписание 1» на
новый лист и присвойте копии листа имя «Штатное расписание 2».

2.  
В меню Данные – Анализ «что –
если» активизируйте команду Поиск решения (рис. 1).

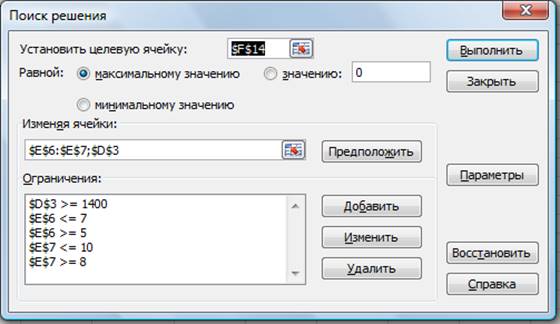
3.  
В окне Установить целевую
ячейку укажите ячейку F14, содержащую модель – суммарный фонд заработной
платы.

Рисунок 1 — Задание условий для минимизации фонда заработной
платы

Поскольку необходимо минимизировать общий месячный
фонд зарплаты, активизируйте кнопку равный – Минимальному значению.

В окне Изменяя ячейки укажите адреса ячеек, в
которых будет отражено количество курьеров и младших менеджеров, а также
зарплата курьера — $E$6:$E$7:$D$3 (при задании ячеек E6, E7 и D3 держите
нажатой клавишу [Ctrl]).

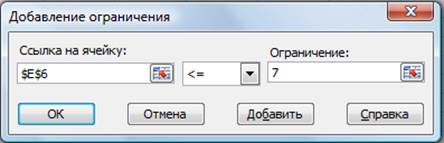
Используя кнопку Добавить в окнах Поиск
решения и Добавление ограничений, опишите все ограничения задачи:
количество курьеров изменяется от 5 до 7, младших менеджеров од 8 до 10, а
зарплата курьера >1400 (рис.2).

Рисунок
2 — Добавление ограничений для минимизации фонда заработной платы

Ограничения наберите в виде

$D$3>=1400

$E$6>5

$E$6<7

$E$7>=8

$E$7 <=10.

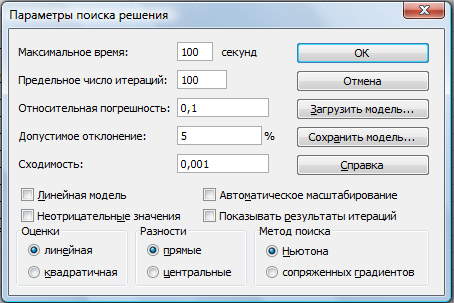
Активизируйте кнопку Параметры, введите
параметры поиска, как показано на рис. 3.

Рисунок
3 — Задание параметров поиска решения по минимизации фонда заработной платы.

Окончательный вид окна Поиск решения приведен
на рис. 1.

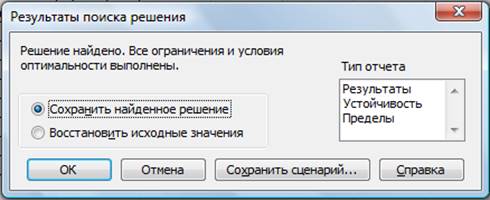
Запустите процесс поиска решения нажатием кнопки Выполнить.
В открывшемся диалоговом окне Результаты поиска решения задайте
опцию Сохранить найденное решение (рис. 4).

Рисунок
4 — Сохранение найденного при поиске решения

Решение задачи приведено на рис. 5. Оно тривиально:
чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд
заработной платы.

Рисунок
5 — Минимизация фонда заработной платы

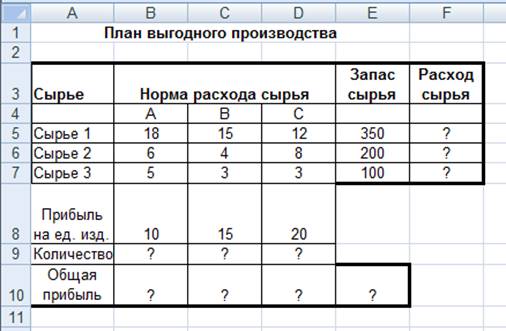
Задание
2. Составление плана выгодного
производства.

Фирма производит несколько видов продукции из одного и
того же сырья – А, В и С. Реализация продукции А дает прибыль 10 р., В – 15 р.
и С – 20 р. на единицу изделия.

Продукцию можно производить в любых количествах,
поскольку известно, что сбыт обеспечен, но ограничены запасы сырья. Необходимо
определить, какой продукции и сколько надо произвести, чтобы общая прибыль от
реализации была максимальной.

Нормы расхода сырья на производство продукции каждого
вида приведены в табл. 1.

Таблица 1

Сырье	Нормы расхода сырья	Запас сырья
А	В	С
Сырье 1	18	15	12	350
Сырье 2	6	4	8	200
Сырье 3	5	3	3	100
Прибыль	10	15	20

Ход работы

1.  
Запустите редактор электронных таблиц
Microsoft Excel и создайте новую электронную книгу.

2.  
Создайте расчетную таблицу как на
рис. 6. Введите исходные данные и формулы в электронную таблицу. Расчетные
формулы имеют такой вид:

Расход сырья 1=(количество сырья 1) * (норма расхода
сырья А) + (количество сырья 1) * (норма расхода сырья В) + (количество сырья
1) * (норма расхода сырья С).

Значит, в ячейку F5 нужно ввести формулу =
B5*$B$9+C5*$C$9+D5*$D$9.

Обратите внимание, что значения количества сырья
каждого вида пока не известны и будут подобраны в процессе решения задания
(ячейки В9:D9 пока пустые).

(Общая прибыль по А) = (прибыль на ед.
изделий А) * (количество А),

Следовательно в ячейку В10 следует
ввести формулу = В8 * В9.

Итоговая общая прибыль = (Общая прибыль
по А) + (Общая прибыль по В) + (Общая прибыль по С),

значит в ячейку Е10 следует ввести
формулу = СУММ(В10:D10).

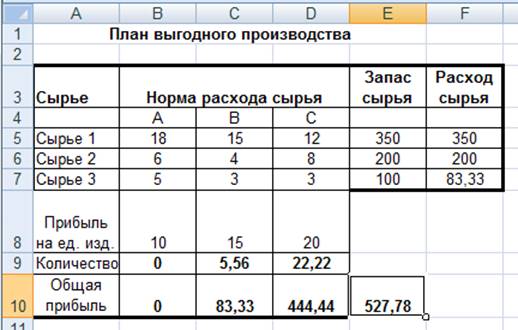
Рисунок 6 — Исходные
данные для Задания 2

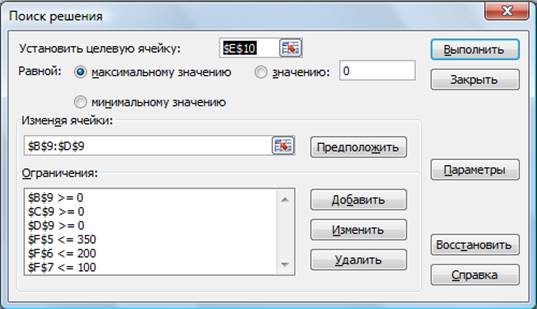
3.  
В меню Данные активизируйте
команду Поиск решения и введите параметры поиска, как указано на рис 7.

Рисунок 7 — Задание
условий и ограничений для поиска решений

В качестве целевой ячейки укажите ячейку «Итоговая
общая прибыль» (Е10), в качестве изменяемых ячеек – ячейки количества сырья –
(В9:D9).

Не забудьте задать максимальное значение суммарной
прибыли и указать ограничения на запас сырья:

расход сырья 1<=350; расход сырья 2<=200; расход
сырья 3<=100, а также положительные значения количества сырья А,  В, С
>=0.

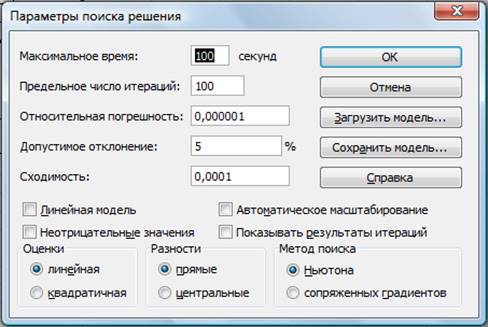
Установите параметры поиска решения (рис. 8). Для
этого кнопкой Параметры откройте диалоговое окно Параметры поиска
решения, установите параметры по образцу, задайте линейную модель расчета (Линейность
модели).

Рисунок 8 — Задание
параметров поиска решения

4.  
Кнопкой Выполнить запустите
Поиск решения. Если вы сделали все верно, то решение будет как на рис.
9.

Рисунок 9 — Найденное
решение максимизации прибыли при заданных ограничениях

5.  
Сохраните созданный документ под
именем «План производства».

Вывод. Из решения видно, что оптимальный план выпуска предусматривает
изготовление 5,56 кг продукции В и 22,22
кг продукции С. Продукцию А производить не стоит. Полученная прибыль при этом
состоит 527,78 р.

Задание
3. Используя файл «План производства»
(см.задание 2), определить план выгодного производства, т. е. какой продукции и
сколько необходимо произвести, чтобы общая прибыль от реализации была
максимальной.

Выберите нормы расхода сырья на производство продукции
каждого вида и ограничения по запасам сырья из таблицы соответствующего
варианта (5 вариантов):

Вариант 1

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	25	17	11	500
Сырье 2	9	7	10	400
Сырье 3	15	8	5	300
Прибыль на ед. изделия	5	10	12
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Вариант 2

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	12	11	8	3500
Сырье 2	14	15	2	280
Сырье 3	8	9	10	711
Прибыль на ед. изделия	10	9	8
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Вариант 3

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	10	20	15	2700
Сырье 2	16	25	13	3800
Сырье 3	8	9	10	1200
Прибыль на ед. изделия	7	8	6
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Вариант 4

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	14	15	19	460
Сырье 2	7	8	12	820
Сырье 3	17	24	6	214
Прибыль на ед. изделия	15	10	25
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Вариант 5

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	12	18	3	625
Сырье 2	16	25	13	227
Сырье 3	8	9	10	176
Прибыль на ед. изделия	18	15	9
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Рекомендуемая
литература: 1, 2, 3, 4

На этой странице вы найдете примеры решений различных оптимизационных задач с использованием пакета электронных таблиц MS Excel (используется как надстройка Поиск решения, так и ручные вычисления).

Задачи оптимизации и Excel

Задачи оптимизации имеют огромное прикладное значение и возникают в самых разных разделах экономики, техники, военного дела и т.п. В таких задачах нас интересуют поиск некоторого оптимального решения (минимизующего или максимизирующего целевую функцию: прибыль, затраты, калорийность и т.п.) в условиях ограничений (наличия ресурсов, дорог, времени, продуктов и т.п.).

Вот некоторые примеры экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация калорийности и стоимости рациона (как для людей, так и для животных), минимизация расходов на перевозку грузов по маршрутам, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.

Часто эти задачи (даже учебные, даже в случае линейности) содержат более десяти переменных(а в случае, например, транспортных задач, и вовсе десятки), что делает ручные расчеты нерациональными. В то же время привычная для всех программа Excel прекрасно подходит для поиска решения.

Алгоритм решения с помощью надстройки «Поиск решения» следующий:

• составить математическую модель задачи: выделить и обозначить переменные, ограничения на них в виде равенств и неравенств (естественные, например, неотрицательность количества, и дополнительные, например, «запасов железной руды не более 10 т»), целевую функцию (то, что нужно оптимизировать) выразить через переменные.
• выделить место под переменные задачи; внести ограничения (левые части — в виде формул от переменных, правые — в виде констант) в файл электронной таблицы Excel,
• внести в ячейку формулу для целевой функции,
• запустить надстройку Поиск решения,
• установить нужные параметры решения (ограничения в листе, ограничения неотрицательности, условие линейности при необходимости и т.п.) и запустить выполнение.

Excel вычислит оптимальные значения переменных и покажет их в ячейках, а также значение целевой функции. Дополнительно можно построить отчеты для анализа решения задачи.

Некоторые задачи оптимизации решаются не с помощью надстройки Поиск решения, а путем подбора параметра или ручных расчетов. Ниже вы найдете примеры разных задач, а также ссылки на другие разделы со сходными заданиями.

Задачи оптимизации: примеры в Excel

Задача 1. Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля $R_j$. Определена экономическая эффективность $К$ — каждого проекта в зависимости от рентабельности производства. По истечении трех сроков $S_i$ рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д. е.):


Выберите оптимальное решение в соответствии с критериями Лапласа, Вальда, Сэвиджа и Гурвица (при $а = 0,5$).

Задача 2. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода каждого вида сырья на изготовление единицы продукции данного вида в таблице 6. В ней же указаны прибыль от реализации единицы изделия каждого вида и общее количество сырья данного, которое может быть использовано предприятием.
Требуется такой составить такой план производства изделий А и В, при котором прибыль от реализации будет максимальной?

Задача 3. Фирма N, имеющая филиалы (k), производит продукцию. Каждый филиал фирмы выпускает четыре вида продукции из пяти (i=1-5). Данные, характеризующие производство филиалов $b_{ki}$, приведены в табл.1.
Филиалы фирмы закупают сырье, из которого производят продукцию, у семи АО (j =1-7). Выход готового продукта из 1 тонны сырья $a_{ij}$ показан в табл.2.
Прибыль филиалов фирмы при закупке 1тн сырья у разных АО, $С_{kj}$ , показана в табл.3.
В разделе 1 работы требуется:
1.1.Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, ($x_j$), максимизируя прибыль филиала. Далее, студент формулирует экономико-математическую модель общей задачи линейного программирования (ОЗЛП).
1.2.С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции.

Задача 4. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки?
Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5.
Для решения задачи используется ППП Excel.

Задача 5. Менеджер проекта по строительству нового торгового гипермаркета компании Наше дело надеется завершить проект за пару недель до Рождества.
После обзора оценок времени выполнения отдельных стадий выяснилось, что потребуются дополнительные инвестиции, чтобы сократить длительность проекта так, чтобы он действительно завершился вовремя. В таблице приведены оценки длительностей стадий и стоимость их сокращения на 1 и на 2 недели.
a. Нарисуйте сетевую диаграмму проекта и найдите критический путь.
b. Определите минимальную стоимость сокращения проекта на 5 недель.

Полезные ссылки

Методички

• Решение оптимизационных задач в среде MS Excel 2013 Методические указания небольшого объема. Разобраны стандартные задачи: ЛП, транспортная, нелинейная, приведены скриншоты решения и пояснения.
• Решение задач оптимизации в Microsoft Excel 2010 Учебное пособие ТОГУ, 101 страница, более увесистый и подробный документ. Разбирается надстройка Поиск решения, решение задач линейного и нелинейного программирования и СЛАУ.

Skip to document

Решение задач оптимизации в Excel

Построение математической модели

Фирма рекламирует свою продукцию с использованием четырех средств: телевизора, радио, газет и рекламных плакатов. Маркетинговые исследования показали, что эти средства приводят к увеличению прибыли соответственно на 10, 5, 7 и 4 доллара в расчете на 1 доллар, затраченный на рекламу. Распределение рекламного бюджета по различным видам рекламы подчинено следующим ограничениям:

а) Полный бюджет составляет 500000 долларов;

b) Следует расходовать не более 40% бюджета на телевидение и не более 20% бюджета на рекламные щиты;

с) Вследствие привлекательности для молодежной части населения различных музыкальных каналов на радио по этой позиции следует расходовать по крайней мере половину того, что планируется на телевидение.

Необходимо:

1. Сформулировать и решить задачу распределения средств по различным источникам для получения максимальной прибыли от рекламы;

2. Объяснить смысл данных отчета по устойчивости;

3. Определить изменится ли оптимальный план распределения средств, если увеличение прибыли от газетной рекламы снизится до 5 долларов в расчете на 1 доллар, затраченный на рекламу;

4. Определить, в какой вид рекламы будет выгоднее вложить дополнительные средства в случае увеличения бюджета фирмы.

Составим математическую модель задачи, выбрав в качестве переменных , х4 — количество средств, затраченных на телевидение, рекламные плакаты, радио и газеты соответственно. Тогда ожидаемая прибыль от рекламы может быть подсчитана по формуле

(1)

Переменные задачи удовлетворяют ограничениям

(2)

в левых частях которых вычислены затраты денежных ресурсов на телевидение, радио, газеты и рекламные плакаты, а в правых частях записаны максимально возможные запасы средств на эти ресурсы. Учитывая, что переменные задачи по своему экономическому смыслу не могут принимать отрицательные значения, получаем математическую модель задачи оптимального распределения денежных ресурсов с целью получения максимального дохода от рекламы.

.

Очевидно, что построенная модель имеет линейную структуру и, следовательно, является задачей линейного программирования.

Создание электронной модели

Чтобы привлечь компьютер к решению этой задачи необходимо ввести исходные данные на лист Excel.

Сначала заносим в таблицу неизменяемые данные, а затем заполняем изменяемые ячейки, в которых расположены компоненты плана . На этапе ввода исходных данных сюда заносятся любые числа, например, единицы. После решения в этих ячейках будут находиться оптимальные значения переменных. Целевая функция (суммарный доход) и левые части ограничений (Затраты по видам реклам) подсчитываются в соответствие с составленной моделью по формуле (1) и левым частям (2).

Вид рекламы	Х1	Х2	Х3	Х4	Суммарный доход
План запуска рекламы	1	1	1	1
Прибыль от 1 затраченного $	10	4	5	7	26

Затраты по видам реклам	Затраты по видам реклам	Прибыль от вида рекламы	Запасы денежных ресурсов (тыс. $)
Х1	Х2	Х3	Х4
На телевидение	1	1	200
На рекламные щиты	1	1	100
На радио	1	1	100
На газеты	1	1	100
Общие затраты на все виды реклам	1	1	1	1	4	500

Отчет по результатам

Отчет состоит из трех таблиц, расположенных на одном листе книги Excel.

Целевая ячейка (Максимум)
Ячейка	Имя	Исходное значение	Результат
$F$3	Прибыль от 1 затраченного $ Сумм-ый доход	26	3700
Изменяемые ячейки
Ячейка	Имя	Исходное значение	Результат
$B$2	План запуска рекламы Х1	1	200
$C$2	План запуска рекламы Х2	1
$D$2	План запуска рекламы Х3	1	200
$E$2	План запуска рекламы Х4	1	100
Ограничения
Ячейка	Имя	Значение	Формула	Статус	Разница
$F$43	Бюджет затрачиваемый на рекламу	500	$F$43<=$G$12	связанное
$B$2	План запуска рекламы Х1	200	$B$2<=$G$8	связанное
$C$2	План запуска рекламы Х2	$C$2<=$G$9	не связан.	100
$D$2	План запуска рекламы Х3	200	$D$2>=$G$10	не связан.	100
$E$2	План запуска рекламы Х4	100	$E$2<=$G$11	связанное

В первой таблице выводятся сведения о целевой функции. В столбце Исходное значение приведено значение целевой функции до начала вычислений, в столбце Результат — после оптимизации.

Следующая таблица содержит значения искомых переменных (изменяемых ячеек) до и после решения задачи.

оптимизация математическая электронная модель

Последняя таблица показывает значения левых частей ограничений на оптимальном решении задачи. В столбце Формула приведены зависимости, которые были введены в диалоговом окне Поиск решения, в столбце Разница показано количество неиспользованного ресурса. Если ресурс дефицитен, т.е. используется полностью, то в столбце Статус указывается связанное (соответствующее ограничение активно); при неполном использовании ресурса в этом столбце указывается не связанное (ограничение не активно).

Из отчета по результатам применительно к данной задаче видим, что оптимальный план распределения средств состоит в еженедельных затратах на телевидение в размере 200 000$, на газеты в размере 100 000$ и на радио в размере 200 000$, а вкладывать денежные средства в рекламные щиты не выгодно. Таким образом , и максимальный суммарный доход 000$. При этом полный бюджет на рекламу продукции используются полностью, т.е. является дефицитным, а также денежные средства отпущенные на телевидение и газеты расходуется полностью и также являются дефицитными, а денежные средства на рекламные щиты расходовать нецелесообразно.

Отчет по устойчивости

Отчет по устойчивости содержит информацию, позволяющую провести постоптимальный анализ решения задачи. Цель анализа заключается в определении таких границ изменения исходных данных задачи (коэффициентов целевой функции и правых частей ограничений), при которых ранее найденный оптимальный план сохраняет свою оптимальность и в изменившихся условиях.

Изменяемые ячейки
Результ.	Нормир.	Целевой	Допустимое	Допустимое
Ячейка	Имя	значение	стоимость	Коэффициент	Увеличение	Уменьшение
$B$2	План запуска рекламы Х1	200	5	10	1E+30	5
$C$2	План запуска рекламы Х2	-1	4	1	1E+30
$D$2	План запуска рекламы Х3	200	5	2	1
$E$2	План запуска рекламы Х4	100	2	7	1E+30	2
Ограничения
Результ.	Теневая	Ограничение	Допустимое	Допустимое
Ячейка	Имя	значение	Цена	Правая часть	Увеличение	Уменьшение
$F$43	Бюджет затрачиваемый на рекламу	500	5	500	1E+30	100

Отчет состоит из двух таблиц, расположенных на одном листе книги Excel.

В первой таблице (Изменяемые ячейки) приводится следующая информация о переменных:

· результирующее значение — оптимальные значения переменных;

· нормированная стоимость — ее величина равна значению соответствующей симплексной оценки с противоположным знаком. Для невыпускаемой продукции нормированная стоимость показывает, на сколько изменится целевая функция при принудительном включении единицы этой продукции в оптимальное решение;

· коэффициенты целевой функции;

· предельные значения приращения коэффициентов целевой функции, которые показывают на сколько можно увеличить и уменьшить каждый целевой коэффициент в отдельности, сохраняя при этом оптимальные значения переменных.

Во второй таблице (ограничения) приводятся аналогичные значения для ограничений задачи:

· величины использованных ресурсов (левые части ограничений) при оптимальном плане выпуска продукции;

· теневые цены, т.е. оптимальные значения двойственных переменных, которые показывают, как изменится целевая функция при изменении соответствующего запаса ресурса на единицу;

· исходные запасы ресурсов (правые части ограничений);

· предельные значения приращений ресурсов (их допустимое увеличение и уменьшение), при которых сохраняется оптимальный план двойственной задачи и базисный набор переменных, входящих в оптимальное решение исходной задачи (ассортимент выпускаемой продукции).

Используем результаты отчета по устойчивости для проведения постоптимального анализа в данной задаче:

Исследуем сначала влияние на оптимальный план изменений коэффициентов целевой функции — прибыль от 1 затраченного $ на рекламу определенного вида.

Из первой таблицы следует, что оптимальный план затрат на рекламу не изменится, если первоначальная прибыль долл. рекламы Х1 возрастет на 1Е+30 доллара или уменьшится на 5 доллара. Другими словами, условие сохранения оптимального плана при изменении прибыли от рекламы Х1 имеет вид: или .

Аналогично, условие сохранения оптимального плана при изменении прибыли рекламы Х3 имеет вид: или , и условие сохранения оптимального плана при изменении прибыли рекламы Х4 имеет вид: или .

Наконец, при изменении прибыли от рекламы Х2 ранее найденный план останется оптимальным, если исходная цена возрастет не более чем на 1 доллар. В то же время любое уменьшение цены не влияет на оптимальный план , так как число равно , т.е. практически является бесконечно большим числом. Таким образом, условие сохранения оптимальности плана при изменении цены примет вид . Это означает, что рекламу Х2 не выгодно запускать (), если прибыль от нее будет не выше 5 долларов. Если же прибыль превысит 5 долларов от использования рекламных щитов, то план перестанет быть оптимальным, и в новом оптимальном решении будет положительным т.е. использование рекламы в виде рекламных щитов станет выгодным.

Отчет по пределам

Третий отчет для данной задачи, называемый отчетом по пределам, состоит из двух таблиц.

Первая таблица в комментариях не нуждается.

Целевое
Ячейка	Имя	Значение
$F$3	Прибыль от 1 затраченного $ Сумм-ый доход	3700
Изменяемое	Нижний	Целевой	Верхний	Целевой
Ячейка	Имя	Значение	предел	результат	предел	результат
$B$2	План запуска рекламы Х1	200	1700	200	3700
$C$2	План запуска рекламы Х2	3700	-1,15597E-09	3700
$D$2	План запуска рекламы Х3	200	100	3200	200	3700
$E$2	План запуска рекламы Х4	100	3000	100	3700

Во второй таблице показано, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального плана выпуска:

· приводятся значения в оптимальном решении;

· приводятся нижние и верхние пределы изменения значений и значения целевой функции при выпуске данного типа продукции на нижнем и верхнем пределах.

Так например, если из оптимального плана исключить запуск рекламы Х1, положив и сохранить оптимальные значения остальных переменных, то доход от рекламы продукции будет равен

Значения целевой функции — дохода от рекламы продукции, вошедшей в оптимальное решение на верхних пределах везде равно максимальной величине 3700 долларов.

Рассмотренный пример показывает, как использование средства «Поиск решения» облегчает задачу принятия оптимальных решений в экономике.