Решение задач оптимального планирования в microsoft excel 11 класс

МБОУ «Учхозская средняя общеобразовательная школа» Краснослободского муниципального района Республики Мордовия

Конспект урока по информатике в 11 классе

«Решение задачи оптимального планирования в MS Excel»

Урок подготовил и провел: учитель информатики и ИКТ Бахарев Юрий Владимирович

п. Преображенский -2021

Цель урока: научить учащихся решать задачи оптимального планирования средствами MS Excel.

Задачи:

1. познакомить учащихся с особым видом экономических задач – задач оптимального планирования, способом их решения в среде MS Excel;

2. закрепить навыки работы с формулами в среде электронных таблиц;

3. развивать умение анализировать и обобщать материал, строить математическую модель задачи;

4. воспитывать самостоятельность и ответственность в принятии решения.

Оборудование:

1. Компьютер преподавателя

2. Компьютеры учащихся – 10 шт.

3. Локальная сеть

4. Программное обеспечение: MS PowerPoint, MS Excel

Продолжительность урока: 40 мин.

Ход урока

1. Организующее начало урока.

2. Выявление имеющихся знаний и умений.

1. а) Что такое корреляционная зависимость?

б) Что такое корреляционный анализ?

в) Какие типы задач можно решать с помощью корреляционного анализа?

г) Какая величина является количественной мерой корреляции? Какие значения она может принимать?

1. С помощью какого средства табличного процессора можно вычислить коэффициент корреляции?

2. а) Для данных из таблицы, представленной на рис. 2.18, постройте две линейные регрессионные модели.

б) Для этих же данных вычислите коэффициент корреляции. Сравните с приведенными на рис. 2.18 результатами.

3. Изучение нового материала.

Решение задачи оптимального планирования в MS Excel.

Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец, государства.

Постановка задачи планирования выглядит следующим образом:

• имеются некоторые плановые показатели: х, у и другие;

имеются некоторые ресурсы: R1, R2 и другие, за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены; имеется определенная стратегическая цель, зависящая от значений х, у и других плановых показателей, на которую следует ориентировать планирование.

Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.

Рассмотрим пример, из которого вы получите представление об одном из подходов к решению задачи оптимального планирования.

Пусть совхоз «Красная слобода!» занимается возделыванием только двух культур — зерновых и картофеля — и располагает следующими ресурсами: пашня — 5000 га, труд — 300 тыс. чел.-ч, возможный объем тракторных работ — 28 000 условных га.

Цель производства—получение максимального объема валовой продукции (в стоимостном выражении).

Найдите оптимальное сочетание посевных площадей культур.

Решение.

Этап I. Для составления математической модели воспользуемся нормативами затрат и выхода продукции для данного совхоза.

Таблица 10

Культуры	Затраты на 1 га посева	Стоимость валовой продукции с 1 га, р.
труда, чел.-ч	тракторных работ, усл. га
Зерновые Картофель	30 150	4 12	400 1000

Критерием оптимальности является максимум стоимости валовой продукции. Этот максимум должен достигаться в условиях использования ограниченных ресурсов пашни, труда и механизированных работ.

Задача является многовариантной, так как имеется множество допустимых вариантов сочетания посевных площадей двух культур, но не все они равнозначны с точки зрения требования оптимальности.

Допустим, что примем решение всю площадь засеять картофелем, который обеспечивает наибольший выход валовой продукции с 1 га. Но для возделывания картофеля на площади 5000 та потребуется 150·5000 = 750 000 Чел.-ч., а мы такими ресурсами не располагаем. Ясно, что такое решение не является приемлемым. Если же засеем всю площадь зерновыми, объем валовой продукции не окажется наибольшим, да и значительная часть трудовых ресурсов не будет использована.

Для поиска оптимального решения задачи обозначим через х₁ -га площадь, отводимую под зерновые, а через х₂ га — площадь, отводимую под картофель. Тогда стоимость зерновых составит 400 х₁ р., а стоимость картофеля — 1000 х₂ р. Отсюда стоимость всей валовой продукции составит ( 400 х₁ + 1000 х₂) р. Обозначим это выражение через у и назовем его целевой функцией:

у = 400 х₁ + 1000 х₂

Нам надо найти максимум этой целевой функции при соблюдении следующих условий:

а) общая площадь зерновых и картофеля не должна превышать 5000 га, т. е. х₁ + х₂≤5000;

б) общие затраты труда не должны превосходить 300 тыс. человеко-часов, т. е. 30 х₁ + 150 х₂≤ 300 000;

в) общий объем механизированных работ не должен превосходить 28 000 усл. га, т. е. 4 х₁ + 12 х₂≤28 000;

г) площади, отводимые под зерновые и картофель, могут принимать только неотрицательные значения: х₁≥0 и х₂ ≥0.

Таким образом, условия задачи выражаются следующей системой неравенств

Требуется найти такие значения х₁ и х₂, при которых целевая функция у = 400 х₁ + 1000 х₂ принимает наибольшее значение.

х₁≥0 и х₂ ≥0xi^O и х2^0.

Этап II. Решим задачу графически.

Построим прямую х₁ + х₂=5000. Координаты всех точек треугольника LOK удовлетворяют неравенству х₁ + х₂≤5000.

Построим прямую 30 х₁ + 150 х₂=300 000. Координаты всех точек треугольника АОС удовлетворяют неравенству 30 х₁ + 150 х₂≤ 300 000.

Построим прямую 4 х₁ + 12 х₂=28 000. Координаты всех точек треугольника BOD удовлетворяют неравенству 4 х₁ + 12 х₂≤28 000.

Неравенствам х₁≥0 и х₂ ≥0 удовлетворяют все точки I четверти координатной плоскости х₁0х₂ .

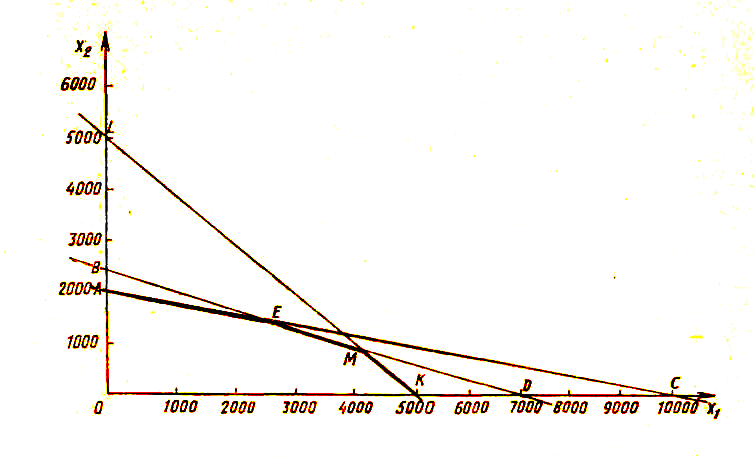
Любая точка многоугольник» АЕМКО удовлетворяет системе неравенств. Для нахождения наибольшего значения целевой функции найдем ее значения в вершинах многоугольника АЕМКО.

Таким образом, наибольшее значение целевой функции достигается в вершине М, что соответствует варианту плана, по которому под зерновые отводится 4000 га, а под картофель — 1000 га.

В связи с тем что введение понятия о линейном программировании в массовой школе не предусмотрено, такая задачу мы можем выполнить используя средство «Поиск решения» которая реализована в MS Ехsel.

1. Практическая работа 19.

«Решение задачи оптимального планирования в MS Excel»

Цели работы:

• получение представления о построении оптимального плана методом линейного программирования;

• практическое освоение раздела MS Excel «Поиск решения» для построения оптимального плана.

Средство, о котором идет речь, называется «Поиск решения». Соответствующая команда находится в меню Сервис. «Поиск решения» — одно из самых мощных средств ТП Excel, и мы не будем даже пытаться освоить все его возможности. Покажем на рассмотренном нами простейшем примере («зерно и картофель»), как воспользоваться указанным средством.

Вначале надо подготовить электронную таблицу к решению задачи оптимального планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки В5 и С5 зарезервированы соответственно для значений х₁ га (площадь отведенная для посевов зерна ) и х₂ га (площадь отведенная под картофель). Ниже этих ячеек представлена система неравенств (а), определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция (Р) занесена в ячейку В15.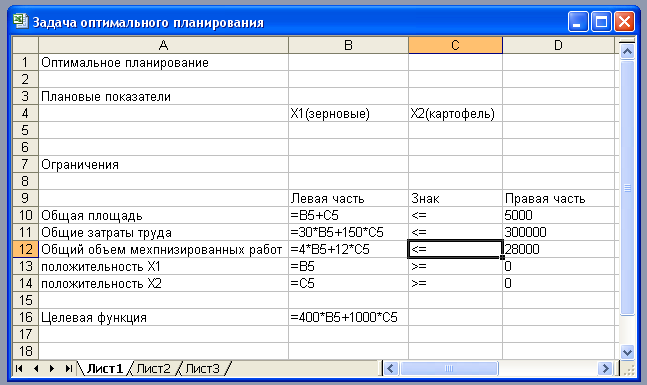

Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей, где расположены данные. Для этого надо выполнить команду = Сервис = Поиск решения. На экране откроется соответствующая форма (рис. 2)

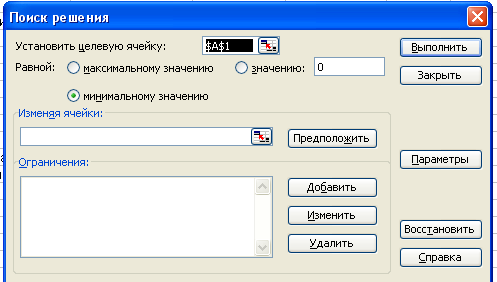
Далее надо выполнить следующий алгоритм:

1. Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически).

2. Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.

3. В поле «Изменяя ячейки» ввести В5:С5, то есть сообщить, какое место отведено под значения переменных -плановых показателей.

4. В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10D10; B1K=D11; B12=D12; B13=D13. Ограничения вводятся следующим образом:

= щелкнуть по кнопке «Добавить»;

в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку В10, выбрать из меню знак неравенства D10; снова щелкнуть по кнопке «добавить» и аналогично ввести второе ограничение B11D11 и так далее. В конце надо щелкнуть на кнопке ОК.

5. Закрыть диалоговое окно «Добавление ограничения».
Снова появится форма «Поиск решения» (рис. 3).

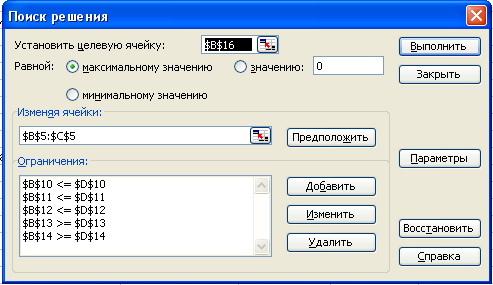
6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры» — появится форма «Параметры поиска решения» (рис. 4).

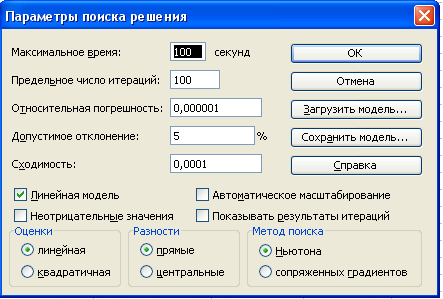
1. Надо выставить флажок на переключателе «Линейная модель» Остальная информация в форме «Параметры поиска решения» служебная, автоматически устанавливаемые значения нас устраивают и вникать в их смысл мы не будем. Следует щелкнуть по кнопке ОК, что возвратит нас в форму «Поиск решения».

Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение (числа 4000 и 1000), а также число 2600000 в ячейке В16 — максимальное значение целевой функции (рис. 5).

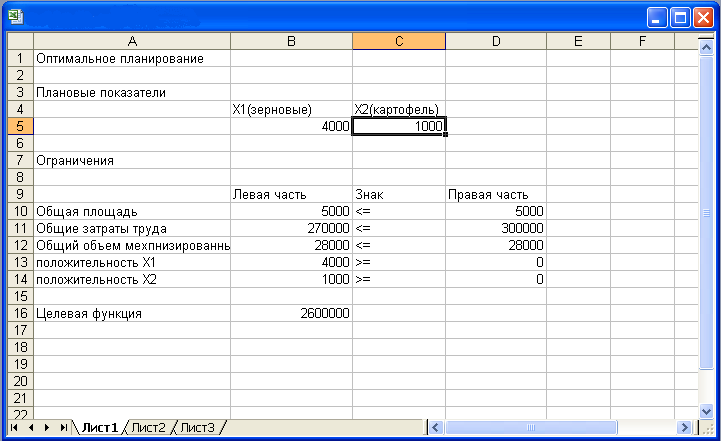
Этап III. Оптимальное сочетание посевных площадей культур: зерновые — 4000 га, картофель—1000 га. Существенно провести экономический анализ оптимального решения задачи.

При х₁=4000 и х₂=1000 х₁ + х₂=5000, а это значит, что пашня используется полностью.

4 х₁ + 12 х₂≤ 300 000= 4·4000+ 12·1000 = 28 000. Это означает, что ресурсы тракторного парка используются полностью.

30 х₁ + 150 х₂= 30·4000+150·1000 = 270 000. Мы выяснили, что трудовые ресурсы недоиспользованы на 30 000 чел.·ч. Полное использование трудовых ресурсов сдерживается ограниченностью пашни и мощностью тракторного парка. Как видим, для рассмотренного в задаче совхоза ресурсы имеют разную ценность: человеческих рук в избытке, а механизированный труд дефицитен.

5. Закрепление новой темы по вопросам:

1. В чем состоит задача оптимального планирования?

2. Что такое плановые показатели, ресурсы, стратегическая цель? Приведите примеры.

3. Попробуйте сформулировать содержание оптимального планирования своей учебной деятельности.

4. Что такое математическое программирование, линейное программирование?

6. Д/З § 38, читать конспект, составить математическую модель для решения 1 задачи

Список используемой литературы:

1. Семакин И.Г Учебник Информатика и ИКТ. Базовый уровень 10-11 класс.. М. Бином.

2. И.М. Шапиро. Использование задач с практическим содержанием в преподавании математики. М. Просвещение 1990 г.

Материал был опубликован на сайте «Педсовет» и «Педмир». Нарушены авторские права. материал должен быть удален!!!!!

МБОУ «Учхозская средняя общеобразовательная школа» Краснослободского муниципального района Республики Мордовия

Конспект  урока  по информатике в 11 классе

«Решение задачи оптимального планирования в MS Excel» 

Урок подготовил и провел: учитель информатики и ИКТ Бахарев Юрий Владимирович

        п. Преображенский -2013

Цель урока: научить учащихся решать задачи оптимального планирования средствами MS Excel.

Задачи:

1. познакомить учащихся с особым видом экономических задач – задач оптимального планирования, способом их решения в среде MS Excel;
2. закрепить навыки работы с формулами в среде электронных таблиц;
3. развивать умение анализировать и обобщать материал, строить математическую модель задачи;
4. воспитывать самостоятельность и ответственность в принятии решения.

Оборудование:

1. Компьютер преподавателя
2. Компьютеры учащихся – 10 шт.
3. Локальная сеть
4. Программное обеспечение: MS PowerPoint, MS Excel

Продолжительность урока: 40 мин.

Ход урока

1. Организующее начало урока.
2. Выявление имеющихся знаний и умений.

1.        а)  Что такое корреляционная зависимость?

б)         Что такое корреляционный анализ?

в)         Какие типы задач можно решать с помощью корреляционного анализа?

г)         Какая величина является количественной мерой корреляции? Какие значения она может принимать?

1. С помощью какого средства табличного процессора можно вычислить коэффициент корреляции?
2. а) Для данных из таблицы, представленной на рис. 2.18, постройте две линейные регрессионные модели.

б) Для этих же данных вычислите коэффициент корреляции. Сравните с приведенными на рис. 2.18 результатами.

3.  Изучение нового материала. 

Решение задачи оптимального планирования в MS Excel.

Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец, государства.

Постановка задачи планирования выглядит следующим образом:

• имеются некоторые плановые показатели: х, у и другие;

имеются некоторые ресурсы: R1, R2 и другие, за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены; имеется определенная стратегическая цель, зависящая от значений х, у и других плановых показателей, на которую следует ориентировать планирование.

Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.

Рассмотрим пример, из которого вы получите представление об одном из подходов к решению задачи оптимального планирования.

Пусть совхоз занимается возделыванием только двух культур — зерновых и картофеля — и располагает следующими ресурсами: пашня — 5000 га, труд — 300 тыс. чел.-ч, возможный объем тракторных работ — 28 000 условных га.

  Цель производства—получение максимального объема валовой продукции (в стоимостном выражении).

 Найдите оптимальное сочетание посевных площадей культур.

Решение.

Этап I. Для составления математической модели воспользуемся нормативами затрат и выхода продукции для данного совхоза.

Таблица   10

Культуры	Затраты на 1 га посева	Стоимость валовой продукции с 1 га, р.
труда, чел.-ч	тракторных работ, усл. га
Зерновые Картофель	30 150	4  12	400 1000

Критерием оптимальности является максимум стоимости валовой продукции. Этот максимум должен достигаться в условиях использования ограниченных ресурсов пашни, труда и механизированных работ.

Задача является многовариантной, так как имеется множество допустимых вариантов сочетания посевных площадей двух культур, но не все они равнозначны с точки зрения требования оптимальности.

Допустим, что примем решение всю площадь засеять картофелем, который обеспечивает наибольший выход валовой продукции с 1 га. Но для возделывания картофеля на площади 5000 та потребуется 150·5000 = 750 000 Чел.-ч., а мы такими ресурсами не располагаем. Ясно, что такое решение не является приемлемым. Если же засеем всю площадь зерновыми, объем валовой продукции не окажется наибольшим, да и значительная часть трудовых ресурсов не будет использована.

Для поиска оптимального решения задачи обозначим через х1 -га площадь, отводимую под зерновые, а через х2 га — площадь, отводимую под картофель. Тогда стоимость зерновых составит 400 х1 р., а стоимость картофеля — 1000 х2 р. Отсюда стоимость всей валовой продукции составит ( 400 х1 + 1000 х2) р. Обозначим это выражение через у и назовем его целевой функцией:

у = 400 х1 + 1000 х2

Нам надо найти максимум этой целевой функции при соблюдении следующих условий:

а)        общая площадь зерновых и картофеля не должна превышать 5000 га, т. е.  х1 +  х2≤5000;

б)        общие затраты труда не должны превосходить 300 тыс. человеко-часов, т. е. 30 х1 + 150 х2≤ 300 000;

в)        общий объем механизированных работ не должен превосходить 28 000 усл. га, т. е. 4 х1 + 12 х2≤28 000;

г)        площади, отводимые под зерновые и картофель, могут принимать только неотрицательные значения: х1≥0 и  х2 ≥0.

Таким образом, условия задачи выражаются следующей системой неравенств

Требуется найти такие значения х1 и х2, при которых целевая функция у = 400 х1 + 1000 х2 принимает наибольшее значение.

 х1≥0 и  х2 ≥0xi^O и х2^0.

Этап II. Решим задачу графически.

Построим прямую х1 +  х2=5000. Координаты всех точек треугольника LOK удовлетворяют неравенству х1 +  х2≤5000.

Построим прямую 30 х1 + 150 х2=300 000. Координаты всех точек треугольника АОС удовлетворяют неравенству 30 х1 + 150 х2≤ 300 000.

Построим прямую 4 х1 + 12 х2=28 000. Координаты всех точек треугольника BOD удовлетворяют неравенству 4 х1 + 12 х2≤28 000.

Неравенствам х1≥0 и  х2 ≥0 удовлетворяют все точки I четверти координатной плоскости х10х2 .

Любая точка многоугольник» АЕМКО удовлетворяет системе неравенств. Для нахождения наибольшего значения целевой функции найдем ее значения в вершинах многоугольника АЕМКО.

Таким образом, наибольшее значение целевой функции достигается в вершине М, что соответствует варианту плана, по которому под зерновые отводится 4000 га, а под картофель — 1000 га.

В связи с тем что введение понятия о линейном программировании в массовой школе не предусмотрено, такая задачу мы можем выполнить используя  средство «Поиск решения» которая реализована в MS Ехsel.

1. Практическая работа  19.

«Решение задачи оптимального планирования в MS Excel»

Цели работы:

•        получение   представления   о   построении   оптимального плана методом линейного программирования;

•        практическое освоение раздела MS Excel «Поиск решения» для построения оптимального плана.

Средство, о котором идет речь, называется «Поиск решения». Соответствующая команда находится в меню Сервис. «Поиск решения» — одно из самых мощных средств ТП Excel, и мы не будем даже пытаться освоить все его возможности. Покажем на рассмотренном нами простейшем примере («зерно и картофель»), как воспользоваться указанным средством.

Вначале надо подготовить электронную таблицу к решению задачи оптимального планирования. В режиме отображения формул таблица показана на рис. 2.20. Ячейки В5 и С5 зарезервированы соответственно для значений х1 га  (площадь отведенная для посевов зерна ) и х2 га (площадь отведенная под картофель). Ниже этих ячеек представлена система неравенств (а), определяющая ограничения на искомые решения. Неравенства разделены на левую часть (столбец В) и правую часть (столбец D). Знаки неравенств в столбце С имеют чисто оформительское значение. Целевая функция (Р) занесена в ячейку В15.

Теперь следует вызвать программу оптимизации «Поиск решения» и сообщить ей, где расположены данные. Для этого надо выполнить команду => Сервис => Поиск решения. На экране откроется соответствующая форма (рис. 2)

Далее надо выполнить следующий алгоритм:

1. Ввести координату ячейки с целевой функцией. В нашем случае это В15. (Заметим, что если перед этим установить курсор на ячейку В15, то ввод произойдет автоматически).
2. Поставить отметку «максимальному значению», то есть сообщить программе, что нас интересует нахождение максимума целевой функции.
3. В поле «Изменяя ячейки» ввести В5:С5, то есть сообщить, какое место отведено под значения переменных -плановых показателей.
4. В поле «Ограничения» надо ввести информацию о неравенствах-ограничениях, которые имеют вид B10<=D10; B1K=D11; B12>=D12; B13>=D13. Ограничения вводятся следующим образом:

=> щелкнуть по кнопке «Добавить»;

в появившемся диалоговом окне «Добавление ограничения» ввести ссылку на ячейку В10, выбрать из меню знак неравенства <= и ввести ссылку на ячейку D10; снова щелкнуть по кнопке «добавить» и аналогично ввести второе ограничение B11<=D11 и так далее. В конце надо щелкнуть на кнопке ОК.

5.        Закрыть диалоговое окно «Добавление ограничения».
Снова появится форма «Поиск решения» (рис. 3).

6. Теперь надо дать последние указания: задача является линейной (это многократно облегчит программе ее решение). Для этого следует щелкнуть по кнопке «Параметры» — появится форма «Параметры поиска решения» (рис. 4).

1. Надо выставить флажок на переключателе «Линейная модель» Остальная информация в форме «Параметры поиска решения» служебная, автоматически устанавливаемые значения нас устраивают и вникать в их смысл мы не будем. Следует щелкнуть по кнопке ОК, что возвратит нас в форму «Поиск решения».

Вся информация введена. Далее надо щелкнуть по кнопке «Выполнить» — мгновенно в ячейках В5 и С5 появится оптимальное решение (числа 4000 и 1000), а также число 2600000 в ячейке В16 — максимальное значение целевой функции (рис. 5).

Этап III. Оптимальное сочетание посевных площадей культур: зерновые — 4000 га, картофель—1000 га. Существенно провести экономический анализ оптимального решения задачи.

При х1=4000 и х2=1000 х1 +  х2=5000, а это значит, что пашня используется полностью.

4 х1 + 12 х2≤ 300 000= 4·4000+ 12·1000 = 28 000. Это означает, что ресурсы тракторного парка используются полностью.

30 х1 + 150 х2= 30·4000+150·1000 = 270 000. Мы выяснили, что трудовые ресурсы недоиспользованы на 30 000 чел.·ч. Полное использование трудовых ресурсов сдерживается ограниченностью пашни и мощностью тракторного парка. Как видим, для рассмотренного в задаче совхоза ресурсы имеют разную ценность: человеческих рук в избытке, а механизированный труд дефицитен.

5. Закрепление новой темы по вопросам:

1. В чем состоит задача оптимального планирования?
2. Что такое плановые показатели, ресурсы, стратегическая цель? Приведите примеры.
3. Попробуйте сформулировать содержание оптимального планирования своей учебной деятельности.
4. Что такое математическое программирование, линейное программирование?

6.       Д/З   § 38, читать конспект, составить математическую модель для решения 1 задачи

Список используемой литературы:

1. Семакин И.Г  Учебник  Информатика и ИКТ. Базовый уровень 10-11 класс..  М. Бином.

2. И.М. Шапиро.  Использование задач с практическим содержанием в преподавании математики. М. Просвещение 1990 г.

Конспект урока

Предмет: Информатика и ИКТ

Тип урока: Урок комплексного применения знаний, умений и навыков.

Тема: «Решение задач оптимального планирования в MS Excel»

Продолжительность: 45 минут

Класс: 11А

Технологии: информационно-коммуникационная

Урок подготовила и провела:

Голохвастова Наталья Сергеевна, учитель информатики и ИКТ высшей квалификационной категории

​​​​​​​ Аннотация.

Характеристика класса

В классе 14 учащихся, по итогам третьей четверти успевают все. Работают на творческом уровне -1 человек, на конструктивном — 8 человек. Уровень воспитанности – достаточный. Уровень сформированности ОУУН – достаточный. Темп и скорость обучения средние.

Характеристика темы

Данный урок является одним из заключительных в теме «Математическое моделирование в планировании и управлении». Учащиеся знают, что такое оптимальное планирование и какие возможности имеет MS Excel для решения задач оптимального планирования, знают как использовать сервис «Поиск решения» для решения задач оптимального планирования. На работу «Решение задач оптимального планирования» отводится 2 урока.

Система целей к уроку

Общедидактическая цель (ОДЦ): приобретение умений самостоятельно в комплексе применять полученные ранее знания, умения, навыки и осуществлять их перенос в новые условия.

Триединая дидактическая цель (ТРЦ)

Образовательный аспект: создать условия для получения представления о построении оптимального плана методом линейного программирования; создать условия для освоения раздела MS Excel «Поиск решения» для построения оптимального плана.

Воспитательный аспект: создать условия для поддержания благоприятного морально-психологического климата в классе, вовлечения учащихся в анализ учебных ситуаций и коллективного решения проблем.

Развивающий аспект: создать условия для развития логического мышления грамотного математического языка, привития навыков самостоятельной работы.

Структура урока, дидактические задачи этапов урока.

Содержание учебного материала (СУМ): понятие оптимального планирования, плановых показателей, ресурсов и их ограниченности, стратегической цели, сервиса MS Excel «Поиск решения».

Умения и навыки: применять полученные знания при решении задач оптимального планирования.

Творческая деятельность: самостоятельный перенос ранее усвоенных ЗУН в новую ситуацию умение самостоятельно видеть элементы объекта в их взаимосвязи.

Эмоционально-ценностное отношение к жизни: создание адаптивной среды на уроке для воспитания активной жизненной позиции ученика.

Формы организации познавательной деятельности (ФОПД)

Общеклассная

Индивидуальная

Парная

Методы обучения.

Репродуктивные

Объяснительно- иллюстративные

Частично поисковые

Формы реализации методов: беседа, самостоятельная мыслительная деятельность, практическая работа.

Средства обучения: наглядные, дидактический материал.

Система контроля на уроке за достижением промежуточных и конечных результатов сочетание контроля учителя, самоконтроля и взаимоконтроля, тестирующая оболочка MyTestStudent, MyTestServer.

Оборудование.

Компьютер преподавателя, компьютеры учащихся – 15 шт., локальная сеть, программное обеспечение: MS Excel, MyTestStudent, MyTestServer, MyTestEditor, WorkSpace; интерактивная доска, мультимедийный проектор.

Конспект урока

Организация начала занятия.

Тема урока (Слайд 1 презентации): Работа «Решение задач оптимального планирования в MS Excel». Ученики формулируют цель урока. (Слайд 2). Учитель озвучивает план урока (Слайд 3).

Выявление имеющихся знаний и умений.

Проверим, насколько хорошо вы владеете терминологией по теме. Пройдите за компьютеры и выполните Тест 1.

В чем состоит задача оптимального планирования? [В определении значений плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели]

Что такое плановые показатели? [Продукт, план выпуска которого требуется рассчитать]

Что такое ресурсы? [Это то, за счёт чего достигаются плановые показатели]

Что называется стратегической целью? [Это уравнение зависимости между плановыми показателями]

Как называется команда в MS Excel для решения задач оптимального планирования и в какой части меню она расположена? [Сервис Поиск решения]

Подведём итоги, выставим первую из трёх оценок за работу. (Тестовая оболочка сама выставляет оценку после прохождения теста учеником, учитель заносить её в журнал (бумажный и электронный)

Проверка домашнего задания.

Мы знаем, что такое оптимальное планирование, как использовать MS Excel для решения задач оптимального планирования. Дома вам необходимо было составить систему неравенств для решения задачи о школьном кондитерском цехе (Слайд 4) из задания 1 работы 16, заполнив пропуски на карточке (Приложение 1).

Проверим правильность выполненной работы. На Слайде 5 необходимо установить соответствие между пояснениями и выражениями.

(Один из учеников озвучивает неравенства, учитель использует возможности интерактивной доски для «перетаскивания» выражений). Слайд 6 Система неравенств для решения задания 1.

– 5. Применение знаний и способов действий. Контроль и самоконтроль.

А) Система неравенств нами получена. Ваша задача подготовить электронную таблицу к решению задачи и применить средство «Поиск решения». Если возникли затруднения, то можно воспользоваться информацией со Слайда 7.

(Учащиеся выполняют задание 1 работы и проверяют правильность в программе MyTestStudent, открыв файл Задание 1). При возникновении затруднений учащиеся обращаются к учителю или свободному консультанту.

Тестовая оболочка выставляет оценку за работу. Учитель корректирует её, учитывая степень самостоятельности работы учащихся. Учитель подводит итог, выставляет вторую из трёх оценок за работу.

Б) Выполним задание 2 (Слайд 8). Составить оптимальный план проведения экскурсионных поездок школьников во время каникул (текст на слайде). Задача не проста. Уточним условие задачи на примере Чукотского автономного округа. Составим оптимальный план проведения экскурсионных поездок школьников во время каникул. Посмотрите на карту на доске. Департамент образования, культуры и молодежной политики ЧАО может профинансировать поездки школьников из пяти районов (Билибинского, Чаунского, Анадырьского, Иультинского, Чукотского) в три места (Анадырь, Билибино, о. Врангеля). Слайд 9 (Текст на слайде).

Разберём математическую формулировку задачи (Слайд 10).

Плановые показатели: А1 – число учащихся из 1 района, которые поедут в город Анадырь и т.п.

Ограничения:

первое условие состоит в том, все учащиеся из каждого района поедут на экскурсию. Математически оно выражается следующими уравнениями:

А1+Б1+В1=300 и т.п.

второе условие: в каждый город поедут столько учащихся, сколько этот город в состоянии принять: А1+А2+А3+А4+А5=500 и т.п.

кроме того, искомые величины, разумеется, неотрицательны: А1≥0 и т.п.

Подведение итогов. Задание на дом.

Мы справились с одной довольно трудной задачей. Математическую модель второй задачи вам предстоит составить дома, используя обозначения плановых показателей: А1, А2, А3 и т.п.

Приложение 1

Задание. Используя текст задачи о школьном кондитерском цехе из задания 1 работы 16 (стр 136 учебника), заполните клетки со знаком «?»

Список используемой литературы:

1. Семакин И.Г Учебник Информатика и ИКТ. Базовый уровень 10-11 класс.. М. Бином.

2. И.М. Шапиро. Использование задач с практическим содержанием в преподавании математики. М. Просвещение 1990 г.

Гипермаркет знаний>>Информатика>>Информатика 11 класс>>Информатика: Компьютерный практикум: Работа 16. Решение задачи оптимального планирования в MS Excel

• получение представления о построении оптимального плана диет линейного программирование;

• практическое освоение раздела MS Excel «Поиск решения» для построения оптимального плана.

Решить задачу о школьном кондитерском цехе, рассмотренную в новой постановке. Пусть цех производит четыре вида продукции:

• пирожки ( максимально возможно произвести 2000 шт. в день, если ничего больше непроизводится);

• шанежки (максимальный выпуск 1500 штук в день);

• булочки (максимальный выпуск 1200 штук в день);

• пирожные (максимальный выпуск 700 штук в день). Соотношение стоимости изделий таково: пирожок/булочка — 2/1; пирожок/шанежка — 1/2; пирожок/пирожное — 1/4.

Емкость склада равна 1100 изделий независимо от их вида.

Составь оптимальный план выпуска продукции исходя из той же цели — достижения максимальной выручки цеха. При решении задачи использовать средство Excel «Поиск решения».

Задание 2

Составить оптимальный план проведения экскурсионных поездок школьников во время каникул в следующей ситуации. Областной департамент образования может профинансировать поездки школьников из пяти районов области (районы будем обозначать номерами) в три города (назовем эти города X, У и Z).

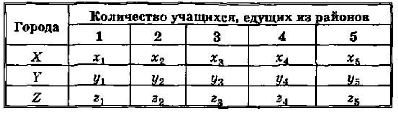
Количество учащихся, которых следует отправить в поездки, таково:

Экскурсионное бюро может в данные каникулы обеспечить поездку следующего числа учащихся в каждый из этих городов:

Стоимость (в рублях) поездки одного учащегося из районов в города приведена в следующей таблице:

Смысл чисел в таблице таков: если в ячейке Y2 стоит 600, то это значит, что поездка одного учащегося из района 2 в город У обходится в 600 рублей.

Необходимо составить такой план экскурсий, который:

• позволяет каждому из числа намеченных к поездке учащихся побывать на экскурсии;

• удовлетворяет условию, определяющему общее число экскурсантов, едущих в каждый из городов;

• обеспечивает максимально низкие суммарные расходы финансирующей стороны.

Первое условие (ограничение задачи) состоит в том, что все учащиеся из каждого района поедут на экскурсию. Математически оно выражается следующими уравнениями:

      x₁ + у₁ + z₁ = 300,

      х₂ + у₂ + z₂ = 250,                                                 (1)

      х₃ + у₃ + z₃ = 400, 

      х₄ + у₄+ z₄ = 350,

      х₅ + у₅+ z₅ = 200.

Второе условие: в каждый город поедут столько учащихся, сколько этот город в состоянии принять:

     х₁ + х₂ + хз + х₄ + х₅ = 400,

     у₁ + у₂ + у₃ + у₄ + у₅ = 500                                    (2)

    z1 + z₂ +z₃ + z₄ + z₅ = 600.

Кроме того, искомые величины, разумеется, неотрицательны:

     х₁ >= 0,…, х₅ >= 0, у_1>= 0,…, у₅ >= 0, z₁ >= 0,…, z₅ >= 0.                                     (3)

Теперь запишем общую стоимость расходов на экскурсии. Поскольку привезти, например, на экскурсию х₁ учащихся стоит хг · 500 рублей (см. таблицу стоимости поездки), то общие расходы составят:

      S = х₁ • 500 + х₂ • 700 + х₃ • 750 + х₄ • 1000 + х₅ • 1100 + у₁ • 700 + у₂ • 600 + у₃ • 400 +                       (4)

Это — весьма непростая задача. Однако ее вполне можно решить (как и существенно более сложные задачи) с помощью средств «Поиск решений» программы Excel, которым вам и надлежит воспользоваться.
Приведем результат решения этой задачи:

Итак, в город X поедут на экскурсию 300 учащихся из района №1 и 100 учащихся из района № 2, в город У — 100 учащихся из района № 2 и 400 из района № 3, в город Z — 50 учащихся из района № 2, 350 из района № 4 и 200 — из района № 5.

Семакин И.Г., Хеннер Е.К., Информатика и ИКТ, 11

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.

Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки

©  Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.

Разработка — Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: