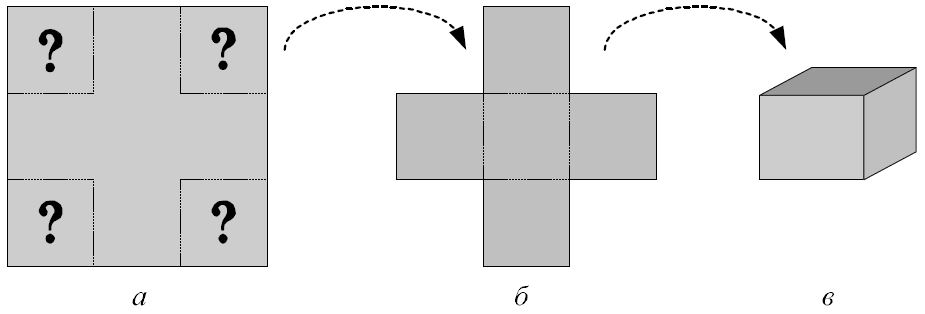
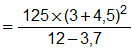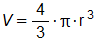Данная задача формулируется следующим образом. Имеется квадратная заготовка из некоторого гибкого материала, например, картона или жести, причем размеры этой заготовки фиксированы для конкретной ситуации (Рис. 1. а). Из этой заготовки следует вырезать четыре равных квадрата по её углам, а полученную фигуру (Рис. 1. б) согнуть так, чтобы получилась коробка без верхней крышки (Рис. 1. в). При этом необходимо так выбрать размер вырезаемых квадратов, чтобы получилась коробка максимального объема.
Рис. 1. Схема изготовления коробки из прямоугольной заготовки фиксированного размера
На примере данной задачи можно проиллюстрировать все элементы постановки задач оптимизации. Оценочной функцией в данной задаче служит объем изготовленной коробки. Проблема выбора заключается в выборе размера вырезаемых квадратов. Действительно, если размер вырезаемых квадратов будет слишком мал, то будет получена широкая коробка малой высоты, а значит, и ее объем окажется невелик. С другой стороны, если размер вырезаемых квадратов будет слишком большой, то будет получена узкая коробка большой высоты, а значит, и ее объем также окажется невелик.
В то же время на выбор размера вырезаемых квадратов оказывает влияние ограничение размера исходной заготовки. Действительно, если вырезать квадраты со стороной, равной половине стороны исходной заготовки, то задача теряет смысл. Сторона вырезаемых квадратов также не может превышать половину стороны исходной заготовки, поскольку это невозможно из практических соображений. Из этого следует, что в постановке данной задачи должны присутствовать некоторые ограничения.
Задача о коробке максимального объема имеет не только наглядную интерпретацию, но и достаточно простое аналитическое решение. Она относится к классу задач нелинейной оптимизации, методы решения которых подробно рассматриваются ниже.
Математическая постановка задачи о коробке максимального объема
Для математической постановки данной задачи необходимо ввести в рассмотрение некоторые параметры, характеризующие геометрические размеры коробки. С этой целью дополним содержательную постановку задачи соответствующими параметрами. С этой целью будем рассматривать квадратную заготовку из некоторого гибкого материала, которая имеет длину стороны L (Рис. 2). Из этой заготовки следует вырезать четыре равных квадрата со стороной r по ее углам, а полученную фигуру согнуть, так чтобы получилась коробка без верхней крышки. Задача состоит в таком выборе размера вырезаемых квадратов, чтобы в результате получилась коробка максимального объема.
Рис. 2. Схема изготовления коробки из прямоугольной заготовки с указанием ее размеров
Для математической постановки данной задачи необходимо определить переменные соответствующей задачи оптимизации, задать целевую функцию и специфицировать ограничения. В качестве переменной следует взять длину стороны вырезаемого квадрата r, которая в общем случае, исходя из содержательной постановки задачи, принимает непрерывные действительные значения.
Целевой функцией является объем полученной коробки. Поскольку длина стороны основания коробки равна: L — 2r, а высота коробки равна r, то ее объем находится по формуле: V(r) = (L — 2r)² * r. Исходя из физических соображений, значения переменной r не могут быть отрицательными и превышать величину половины размера исходной заготовки Z, т. е. 0,5 * L.
С целью унификации, обозначим переменную через х = r, что не оказывает влияния на характер решаемой задачи оптимизации. Тогда математическая постановка задачи о коробке максимального объема может быть записана в следующем виде: f(x) = x * (L - 2x)² → max, где Δβ = {X ∈ R¹ | 0 ≤ x ≤ 0,5 * L}.
Целевая функция данной задачи является нелинейной, поэтому задача о коробке максимального размера относится к классу задач нелинейного программирования или нелинейной оптимизации.
Решение задачи о коробке максимального объема с помощью программы MS Excel
Не уменьшая общности математической постановки задачи, предположим: L = 1. Для решения данной задачи с помощью программы MS Excel создадим новую книгу с именем Нелинейная Оптимизация и изменим имя ее первого листа на Задача о коробке. Сделаем необходимые надписи в ячейках А1:В2. После этого введем в ячейку С2 формулу: =C1*(1-2*C1)^2, которая представляет целевую функцию. Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи о коробке максимального объема имеет следующий вид (Рис. 3).
Рис. 3. Исходные данные для решения задачи о коробке максимального объема
При изображении исходных данных для решения задачи о коробке максимального объема (Рис. 3.) выбран режим отображения формул в ячейках рабочего листа, что оказывается весьма удобным для визуального контроля правильности задания выражений для соответствующих формул. Этот режим может быть установлен с помощью выполнения операции главного меню: Формулы → Показать формулы. С помощью удаления этой отметки можно вернуться к обычному режиму изображения ячеек рабочего листа.
Для дальнейшего решения задачи следует воспользоваться инструментом поиска решения программы MS Office Excel. С этой целью необходимо выполнить операцию меню: Данные → Поиск решения.
После вызова инструмента поиска решения появится диалоговое окно мастера задания параметров для нахождения решения (Рис. 4). Ввиду важности этого инструмента следует более подробно остановиться па элементах его диалоговых окон.
Рис. 4. Диалоговое окно Поиск решения
Первое диалоговое окно Поиск решения (Рис. 4) имеет следующие элементы:
- поле Оптимизировать целевую функцию — используется для задания ссылки на ячейку, в которой задана формула с выражением целевой функции решаемой задачи оптимизации;
- переключатели в группе До: — определяют характер решаемой задачи оптимизации. Для нахождения решения с максимальным значением целевой функции этот переключатель ставится в положение максимальному значению, для нахождения решения с минимальным значением — в положение минимальному значению. Наконец, для нахождения решения, при котором целевая функция принимает некоторое фиксированное значение, переключатель ставится в положение Значению, справа от которого можно ввести требуемое фиксированное значение;
- поле Изменяя ячейки переменных — служит для указания ячеек, которые должны изменяться в процессе поиска решения задачи. Именно в этих ячейках должны находиться переменные решаемой задачи оптимизации;
- в многострочном поле В соответствии с ограничениями отображаются ограничения решаемой задачи оптимизации;
- кнопка Добавить — служит для вызова дополнительного окна Добавление ограничения (Рис. 5);
- кнопка Изменить — служит для вызова дополнительного окна Добавление ограничения, в котором будет отображено ограничение, выбранное в многострочном поле Ограничения;
- кнопка Удалить — служит для удаления ограничения, выбранного в многострочном поле Ограничения;
- кнопка Выполнить — служит для запуска процесса нахождения оптимального решения после спецификации всех параметров поиска решения;
- кнопка Сбросить — служит для сброса всех параметров поиска решения;
- кнопка Загрузить / сохранить — служит для загрузки сохраненных условий ограничений или сохранения условий ограничения;
- кнопка Выполнить — служит для запуска процесса нахождения оптимального решения после спецификации всех параметров поиска решения;
- кнопка Параметры — служит для вызова дополнительного окна Параметры поиска решения (Рис. 3.5) для спецификации дополнительных параметров поиска решения, часть которых уже задана по умолчанию.
Рис. 5. Диалоговое окно Добавление ограничения
Диалоговое окно Добавление ограничения (Рис. 5) предназначено для задания одного ограничения и имеет следующие элементы:
- поле Ссылки на ячейки — служит для указания ячейки или диапазона ячеек, в которых содержится левая часть задаваемого ограничения;
- выпадающий список в центре окна — содержит перечень знаков неравенств ограничений, а также возможность спецификации требования целочисленности или двоичных значений переменных. Мастер поиска решений допускает спецификацию ограничений в виде равенств и неравенств;
- поле Ограничение — служит для указания ячейки, диапазона ячеек или конкретного числа, которое специфицирует правую часть задаваемого ограничения;
- кнопка ОК — служит для добавления ограничения к параметрам поиска решения и закрытия окна Добавление ограничения;
- кнопка Отмена — для закрытия окна Добавление ограничения без добавления ограничения к параметрам поиска решения;
- кнопка Добавить — для добавления ограничения к параметрам поиска решения без закрытия окна Добавление ограничения;
- кнопка Справка — служит для получения справочной информации об элементах диалогового окна Добавление ограничения.
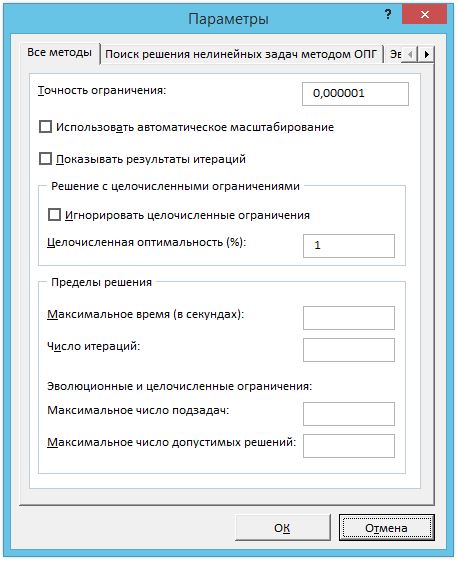
Рис. 6. Диалоговое окно Параметры поиска решения
Диалоговое окно Параметры поиска решения (Рис. 3.5) предназначено для спецификации дополнительных параметров нахождения решения или изменения уже заданных параметров. Следует заметить, что значения большинства этих параметров, используемых по умолчанию, подходят для решения типовых задач оптимизации. Диалоговое окно Параметры поиска решения имеет следующие элементы.
- Поле Максимальное время служит для ограничения времени, отпускаемого на поиск решения задачи. В это поле можно ввести время (в секундах), не превышающее 32 767. Установленное по умолчанию значение 100 подходит для решения рассматриваемых типовых задач.
- Поле Число итераций служит для ограничения времени решения задачи посредством задания некоторого предельного числа промежуточных вычислений. Установленное по умолчанию значение 100 подходит для решения рассматриваемых типовых задач.
- Флажок Показывать результаты итераций служит для приостановки поиска решения для просмотра результатов отдельных итераций.
- Флажок Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, — например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.
Продолжим решение задачи о коробке максимального объема. В первом окне мастера поиска решения следует в поле с именем Установить целевую ячейку указать ячейку $С$2, в которой содержится формула для расчета целевой функции задачи, а в поле е именем Изменяя ячейки ввести абсолютный адрес ячейки $C$1, в которую будет записано искомое решение задачи.
После этого следует добавить два ограничения на допустимые значения переменной. Для этого следует нажать кнопку Добавить, в результате чего появится дополнительное окно задания ограничений (Рис. 7). Для ввода адресов ячеек в левую часть ограничения предназначено поле е именем Ссылка на ячейку. Форма неравенства ограничения выбирается из вложенного списка в средней части окна.
Наконец, для задания правой части ограничений в поле ввода с именем Ограничение следует ввести с клавиатуры следующие числа: 0,5 — для первого ограничения и 0 — для второго. После спецификации каждого из ограничений их необходимо включить в модель расчета, для чего следует нажать кнопку Добавить или ОК. Для того чтобы закрыть дополнительное окно задания ограничений и вернуться в исходное окно мастера поиска решения, следует нажать кнопку Отмена или ОК.
Остальные параметры мастера поиска решения, для редактирования которых предназначено дополнительное второе окно этого мастера, можно оставить без изменения. Окончательный внешний вид диалогового окна мастера поиска решения после задания необходимой информации изображен на Рис. 7.
Рис. 7. Параметры мастера поиска решения для задачи о коробке
Для редактирования некоторого ограничения его следует выделить в многострочном поле с именем Ограничения и нажать кнопку с именем Изменить. В этом случае появится дополнительное окно, аналогичное изображенным на Рис. 7, в котором можно выполнить необходимые действия по редактированию выбранного ограничения.
После задания необходимых параметров поиска решения можно приступить к выполнению численных расчетов, для чего следует нажать кнопку Выполнить. После выполнения численных расчетов программой MS Excel практически мгновенно будет получено количественное решение, которое имеет следующий вид (Рис. 8).
Рис. 8. Результат количественного решения задачи о коробке максимального объема
Интерпретируя полученные количественные значения, можно прийти к следующему заключению. Результатом решения является оптимальное значение стороны вырезаемого квадрата: ropt = 0,166666693977061, при котором изготовленная коробка будет иметь максимальный объем: Vmax = 0,0740740740740726. Напомним, что это решение соответствует длине стороны исходной заготовки, равной 1.
Полученное решение имеет общий характер, поскольку в любом конкретном случае для получения решения рассматриваемой задачи оптимизации значение L следует умножить на найденное значение ropt. Например, если L = 2, то для получения коробки максимального объема следует вырезать по углам исходной заготовки квадраты со стороной 0,166666693977061 * 2 = = 0,333333387954122 м.
Таким образом, задача о коробке максимального объема в каждом конкретном случае может быть решена простой подстановкой в расчетную формулу ropt = 0,166666693977061 * L конкретного значения величины L. Допустимая точность решения задается в каждом конкретном случае, исходя из специфики задачи и соответствующей проблемной области.
Для анализа найденного решения можно построить график целевой функции и визуально оценить его корректность. С этой целью на отдельном рабочем листе е помощью операции автозаполнения ячеек зададим последовательный ряд чисел исходной переменной r в диапазоне от 0 до 1 с интервалом 0.01, которые запишем в ячейки с адресами А2:А52. Рядом в ячейки В2:В52 запишем соответствующие значения целевой функции. Для этого можно записать формулу: =A2*(1-2*A2)^2 в ячейку В2 и с помощью операции автозаполнения «протащить» содержание этой ячейки на диапазон В3:В52.
После этого для построения графика целевой функции для задачи о коробке следует воспользоваться мастером диаграмм. Построенный график целевой функции будет иметь следующий вид как на Рис. 9. Визуальный анализ этого графика показывает, что максимум целевой функции находится между значениями х = 0,16 и х = 0,17. Этот факт можно также проверить, сравнив значения в ячейках В18 и В19. Тем самым, можно сделать вывод о корректности полученного результата решения данной задачи оптимизации.
Рис. 9. График целевой функции в задаче о коробке максимального объема
Аналитическое решение задачи о коробке максимального объема
Поскольку задача о коробке максимального объема имеет достаточно простое аналитическое решение, оно приводится для дополнительной проверки правильности численных расчетов программы MS Excel.
Прежде всего, следует заметить, что целевая функция является непрерывной и дифференцируемой на всем интервале ее задания, включая множество допустимых альтернатив Δβ, которое, в свою очередь, является замкнутым. Как следует из курса математического анализа, непрерывная функция на замкнутом множестве достигает своих экстремальных значений, из которых нас интересуют точки максимума данной функции. Для нахождения экстремума аналитическим способом следует определить первую производную целевой функции и отыскать ее корни.
Первая производная функции: f(x) = x*(1-2x)² равна df(x)/dx = 12x²-8x+1. Соответствующее уравнение: 12x²-8x+1=0 является квадратным, которое имеет два корня: Х = 1/6 и х2 = 1/2. Анализ графика целевой функции (см. Рис. 3.5) показывает, что максимальному значению этой функции соответствует первый корень. Данное значение является допустимым и служит точным аналитическим решением задачи оптимизации о коробке максимального размера.
Таким образом, ropt = 1/6. Поскольку число 1/6 является иррациональным и представляет собой периодическую дробь 0.16(6), при желании можно получить его любое приближение произвольной точности. Сравнивая найденное ранее значение 0,166666693977061 с соответствующим округлением точного значения, можно получить относительную погрешность программы MS Excel. Это значение равно: 0.000016382137877% и свидетельствует о том, что решение задач оптимизации программой MS Excel с гладкой целевой функцией выполняется весьма эффективно.
Программа Excel является лучшим калькулятором. Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы. Все их возможности поддерживает программа Excel. Более того, он имеет неоспоримые преимущества.
В некоторых формулах можно выполнить только одно математическое вычисление при калькуляционных расчетах. В таких случаях, если меняются данные нужно изменить формулу. Но если все данные будут распределены по ячейкам, а формула будет только ссылаться на них, то при любых изменениях нет необходимости менять формулу. Одна формула может использоваться многократно. Чтобы понять, как это работает, лучше привести несколько практических примеров.
Как рассчитать объем и площадь в Excel
В ячейке A1 запишем формулу вычисления объема параллелепипеда: a = 6 см; b = 8 см; c = 12 см.
В ячейке A2 запишем формулу вычисления площади круга: r = 25 см.
В ячейке A3 формула содержит безаргументную функцию ПИ(), которая содержит в себе полное число ПИ (а не 3.14). Поэтому значения ячеек A2 и A3 немного отличаются.
Вычисление арифметических формул в Excel
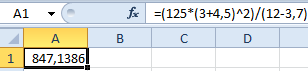
Допустим нам нужно в Excel вычислить формулу:
Чтобы получить результат вычисления ее нужно просто записать в одну строку: =(125*(3+4,5)^2)/(12-3,7).
Данная формула содержит 5 арифметических действий: суммирование, вычитание, умножение, деление и поднесение к степени (^). Если мы записываем все в одно строку, то нужно соблюдать правила арифметической последовательности. Для этого нужно использовать скобки.
Формула для вычисления объема сферы в Excel
Например, нам нужно регулярно вычислить объемы сфер с разными радиусами.
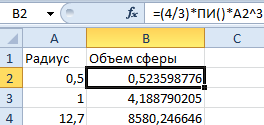
Формула вычисления объема сферы выгладит так:
Предыдущие примеры плохо подходят для решения данной задачи, так как они не используют переменных значений в формулах, а только константы. Из-за этого при смене радиуса нужно переписывать формулу. Но Excel позволяет нам использовать эффективное решение:
- В ячейку B2 запишем формулу вычисления объема сферы в одну строку: =(4/3)*ПИ()*A2^3 (A2 – это ссылка на ячейку).
- В ячейке A2 будем вводить разные радиусы и после каждого ввода в ячейке B2 будем получать результат вычисления объема сфер соответствующих своим радиусам.
Примечание. Если вы используете в Excel многократные вычисления или формулы содержащие ссылки на ячейки в качестве переменных значений, то всегда подписывайте каждую ячейку с входящими данными и формулами. Это позволит избежать ошибок и легко читать значения или результаты вычисления формул.
Excel 2013 makes several categories of math problems easier, among them calculating volumes in solid geometry. While keying numbers into a calculator can get you the right answer, Excel allows you to enter multiple dimensions for the solid you’re working from, change them, and then see the differences in volume. Entering in the classical volume formulas is merely a matter of knowing how to enter them in an Excel-friendly format.
Volume of an Ellipsoid
Enter the labels «Radius 1,» «Radius 2» and «Radius 3» in cells A1, B1 and C1, respectively.
Enter the following formula in cell D2:
=(4/3)_PI()_A2_B2_C2
Enter the three different radii for the ellipsoid whose volume you want to enter in cells A2, B2 and C2. Entering the same number for all three values gives you the volume of a sphere.
Volume of a Rectangular Solid
Enter the labels «Height,» «Width» and «Length» in cells A4, B4 and C4, respectively.
Enter the following formula in cell D5:
=A5_B5_C5
Enter the three different side dimensions for the rectangular solid whose volume you’re deriving in cells A5, B5 and C5. If you enter the same dimensions for all three values, you’re calculating the volume of a cube.
Volume of a Cylindrical Solid
Enter the labels «Radius» and «Height» in cells A7 and B7, respectively.
Enter the following formula in cell D8:
=PI()_A8^2_B8
Enter the radius and height of the cylinder in cells A8 and B8.
Volume of a Cone
Enter the labels «Radius» and «Height» in cells A10 and B10, respectively.
Enter the following formula in cell D11:
=PI()_A11^2_B11*(1/3)
Enter the radius and height of the cone in cells A11 and B11.
Volume of a Torus
Enter the labels «Outer Radius» and «Inner Radius in cells A13 and B13, respectively.
Enter the following formula in cell D14:
=(1/4)_PI()^2_A14+B14*(A14-B14)^2
Enter the inner and outer radius of the torus in cells A14 and B14.
Вычисление формулы объема и площади в Excel
Программа Excel является лучшим калькулятором. Мы привыкли использовать для расчетов традиционные бухгалтерские калькуляторы. Все их возможности поддерживает программа Excel. Более того, он имеет неоспоримые преимущества.
В некоторых формулах можно выполнить только одно математическое вычисление при калькуляционных расчетах. В таких случаях, если меняются данные нужно изменить формулу. Но если все данные будут распределены по ячейкам, а формула будет только ссылаться на них, то при любых изменениях нет необходимости менять формулу. Одна формула может использоваться многократно. Чтобы понять, как это работает, лучше привести несколько практических примеров.
Как рассчитать объем и площадь в Excel
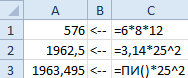
В ячейке A1 запишем формулу вычисления объема параллелепипеда: a = 6 см; b = 8 см; c = 12 см.
В ячейке A2 запишем формулу вычисления площади круга: r = 25 см.
В ячейке A3 формула содержит безаргументную функцию ПИ(), которая содержит в себе полное число ПИ (а не 3.14). Поэтому значения ячеек A2 и A3 немного отличаются.
Вычисление арифметических формул в Excel
Допустим нам нужно в Excel вычислить формулу:
Чтобы получить результат вычисления ее нужно просто записать в одну строку: =(125*(3+4,5)^2)/(12-3,7).
Данная формула содержит 5 арифметических действий: суммирование, вычитание, умножение, деление и поднесение к степени (^). Если мы записываем все в одно строку, то нужно соблюдать правила арифметической последовательности. Для этого нужно использовать скобки.
Формула для вычисления объема сферы в Excel
Например, нам нужно регулярно вычислить объемы сфер с разными радиусами.
Формула вычисления объема сферы выгладит так:
Предыдущие примеры плохо подходят для решения данной задачи, так как они не используют переменных значений в формулах, а только константы. Из-за этого при смене радиуса нужно переписывать формулу. Но Excel позволяет нам использовать эффективное решение:
- В ячейку B2 запишем формулу вычисления объема сферы в одну строку: =(4/3)*ПИ()*A2^3 (A2 – это ссылка на ячейку).
- В ячейке A2 будем вводить разные радиусы и после каждого ввода в ячейке B2 будем получать результат вычисления объема сфер соответствующих своим радиусам.
Примечание. Если вы используете в Excel многократные вычисления или формулы содержащие ссылки на ячейки в качестве переменных значений, то всегда подписывайте каждую ячейку с входящими данными и формулами. Это позволит избежать ошибок и легко читать значения или результаты вычисления формул.
Урок комбинированный по дисциплинам «Информатика» и «Математика». Вычисление площадей и объемов геометрических фигур в редакторе Excel
Цель урока: Усвоение новых знаний. Формирование знаний об использовании редактора электронных таблиц для решения задач математики. Вычисление площадей и объемов геометрических фигур. Освоение компетенций использования информационно-коммуникативных технологий.
ОКЗ. Решать проблемы, оценивать риски и принимать решения в нестандартных ситуациях.
ОК 4. Осуществлять поиск, анализ и оценку информации, необходимой для постановки и решения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии для совершенствования профессиональной деятельности.
ОК 6. Работать в коллективе и команде, обеспечивать ее сплочение, эффективно общаться с коллегами, руководством, потребителями
- формирование знаний об использовании редактора электронных таблиц для решения задач математики;
- вычисление площадей и объемов геометрических фигур.
- развивать логику мышления
- развивать положительные мотивы учебно-познавательной деятельности, интересов, творческой инициативы и активности.
- воспитывать интерес к изучаемой профессии.
- воспитывать такие качеств личности как дисциплины, самостоятельности, трудолюбия, и т.д.;
- воспитывать навыки организации рабочего места.
Оборудование: ПК, проектор, MS Excel 2010.
Тип урока: Комбинированный урок.
- Организационный момент (3 мин).
- Постановка темы и цели урока (3 мин).
- Систематизация знаний и умений по пройденному материалу.
- Опрос учащихся (18 мин).
- Изложение нового материала. Введение понятия математических функций в редакторе электронных таблиц. Вычисление площадей и объемов геометрических фигур. (25 мин.).
- Закрепление полученных знаний (15 мин.).
- Выполнение компьютерного теста (16 мин.)
- Постановка домашнего задания (5 мин.).
- Подведение итогов урока. Выставление оценок (5 мин.).
1. Организационный момент
Цель: Организовать группу, создать обстановку для естественного самовыражения студента.
Вместе с дежурным преподаватель проверяет готовность кабинета к занятию, отмечает отсутствующих.
2. Постановка темы и цели урока.
Цель: Ознакомление с темой урока, постановка проблемы, цели урока.
При постановке проблемы используется ПК для наглядности.
3. Систематизация знаний и умений по пройденному материалу.
Цель: Обобщение и систематизация знаний. Развитие логических умений: сравнивать, выделять главное.
Для подготовки студентов к усвоению нового материала повторяются и систематизируются их знания и умения в процессе устного опроса:
- Сформулируйте, как используется редактор электронных таблиц?
- Как построить таблицу?
- Как образуется адрес ячейки?
4. Изложение нового материала.
Цель: Усвоение новых знаний, создание положительного эмоционального настроя на работу всех студентов.
Преподаватель математики объясняет тему: Вычисление объемов и площадей геометрических фигур на примере цилиндра.
Расчет площади поверхности цилиндра
r- радиус основания
h- высота цилиндра
Формула площади боковой поверхности цилиндра, (Sбок):
Формула площади всей поверхности цилиндра:
Как вычислить объем цилиндра?
Объем цилиндра, (V):
- Создаем новый документ в редакторе электронных таблиц Excel.
- Создаем таблицу вычисления площади и объема цилиндра. Помним, что формула начинается со знака =
Не забываем, что программа использует адреса ячеек в формулах. - Формулы по столбцу распространяем автозаполнением.
- В столбцах D и E таблицы 2 раскрыты формулы редактора электронных таблиц Excel.
Задача. Заданы 3 цилиндра с высотой Н и радиусом основания R. Вычисляем объем фигуры V, площадь боковой поверхности Sб.п.
Таблица 1
Таблица 2
Задание 1: Самостоятельно заполнить столбец F, написать формулу для вычисления Sп.п.
Проверяется правильность выполнения задания с применением таблиц. Приложения 2.
Задание 2: Продолжить таблицу – добавить 3 строки: высота 10, а радиус равен номеру учащегося в журнале.
Задание для опережающих учащихся: по образцу на листе 3 в редакторе Excel создать таблицу вычисления объема и площади боковой поверхности шара (радиус 5 и 10условных единиц).
Закрепление полученных знаний.
Цель: Закрепление нового материала. Обобщение полученных знаний. Формирование умений. Освоение компетенций использования информационно-коммуникативных технологий. Развитие логического мышления. Формирование навыков самоконтроля. Воспитание воли, настойчивости и трудолюбия.
Для закрепления полученных знаний студенты выполняют тест в электронном виде на компьютере по теме “Редактор электронных таблиц Excel”. Приложение 1.
Фронтальным опросом вместе с учащимися подводятся итоги урока:
— сформулируйте, как вычислить объем цилиндра с помощью редактора электронных таблиц;
— сформулируйте, как вычислить площадь боковой поверхности цилиндра с помощью редактора электронных таблиц.
Постановка домашнего задания.
Цель: Закрепление знаний, применение знаний. Развитие умений и навыков. Воспитание воли, настойчивости, трудолюбия. Воспитание самоконтроля.
На дом задается прочитать объяснительный текст параграф 11.4 на странице 248. Учебник “Информатика” Е.В. Михеева. Составить таблицу для подсчета площадей геометрических фигур: треугольника и круга с выбранными произвольно размерами на плоскости в редакторе электронных таблиц, раскрыть формулы.
Подведение итогов урока.
Цель: Выставление оценок студентам, анализ ответов студентов, выяснить, что понравилось (не понравилось) и почему.
Обсудить с детьми, что узнали (чем овладели), что понравилось (не понравилось) и почему, что бы хотелось выполнить еще раз. Выставление оценок (поощрение) при опросе на уроке не только правильного ответа студента, но и анализ того, как студент рассуждал, какой способ использовал, почему и в чем ошибся. Отметка аргументируется по ряду параметров: правильности, самостоятельности, оригинальности.
Создание простой формулы
Создадим первую формулу. Допустим, вы хотите вычислить площадь круга. Конечно, можно взять в руки калькулятор и сделать это. А если вам требуется вычислить площадь круга сто раз при разных значениях радиуса? Представляете, сколько раз вам нужно нажать кнопки калькулятора, при этом записывая куда-то все результаты? Программа Excel может сделать это быстрее.
Итак, всем известно, что площадь круга равняется ?r2, где r – это радиус круга, а ? – константа.
1. Создайте новую книгу Excel или перейдите на чистый лист.
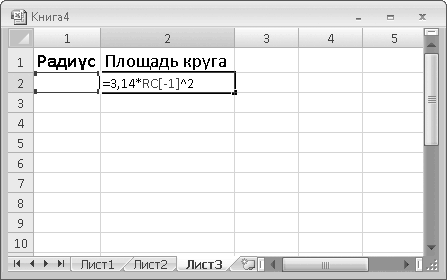
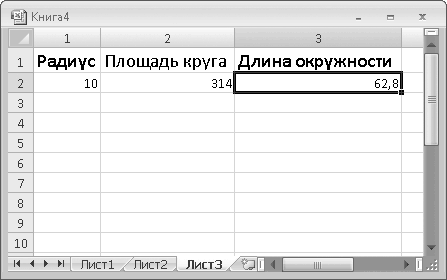
2. В ячейку R1C1 введите текст Радиус, а в ячейку R1C2 – Площадь круга.
3. Щелкните кнопкой мыши на ячейке R2C2. В этой ячейке мы создадим формулу.
4. Введите знак =. Это сообщает программе Excel, что в этой ячейке создается формула.
5. Введите число 3,14. Это число ?, округленное до двух знаков после запятой.
6. Введите знак *. В программе Excel это – знак умножения.
7. Щелкните кнопкой мыши на ячейке R2C1.
Вокруг этой ячейки появится «муравьиная дорожка», а относительный адрес этой ячейки отобразится в создаваемой формуле.
8. Введите знак ^. Это знак возведения числа в степень.
9. Введите число 2. Это степень, в которую нужно возвести число (рис. 6.1).
Рис. 6.1. Создание формулы для вычисления площади круга
ПРИМЕЧАНИЕ
Текст в ячейках R1C1 и R1C2 нам нужен только в качестве заголовков столбцов для наглядности. В столбец 1 мы будем вводить значение радиуса круга, а в столбце 2 получать результат (площадь).
ПРИМЕЧАНИЕ
Программа Excel содержит функцию автоматического добавления числа ?, с точностью пятнадцать знаков после запятой. Но о функциях мы поговорим позже.
10. Нажмите клавишу Enter. Формула будет создана, а в ячейке R2C2 появится значение 0.
Мы создали формулу в ячейке R2C2. Щелкните кнопкой мыши на этой ячейке и посмотрите на строку формул. Вы должны увидеть следующую формулу: =3,14*RC[-1]^2. В нашей формуле число 3,14 (?) умножается на значение ячейки, стоящей слева (в этой ячейке мы позже укажем радиус), которое, в свою очередь, возводится в квадрат. В данный момент результат вычисления равен нулю, так как ячейка R2C1 пуста (формула воспринимает это как 0).
Проверим результаты вычисления.
1. В ячейку R2C1 введите 10 и нажмите клавишу Enter. В ячейке R2C2 появится число 314.
2. В ячейку R2C1 введите число 15 и нажмите клавишу Enter. В ячейке R2C2 появится число 706,5.
Как видите, результат вычисления в ячейке R2C2 автоматически обновляется, как только вы вводите новое значение в ячейку R2C1. Иными словами, вы указываете только радиус, все остальное делает Excel по созданной вами формуле. И это, пожалуй, самый простой пример.
В столбце 3 создадим формулу вычисления длины окружности, которая также будет использовать значение радиуса из столбца 1. Формула длины окружности – 2?r.
1. В ячейку R1C3 введите текст Длина окружности.
2. Щелкните кнопкой мыши на ячейке R2C3.
4. Введите цифру 2.
5. Введите знак умножения (*).
6. Введите число ? (3,14).
7. Введите знак умножения (*).
8. Щелкните кнопкой мыши на ячейке R2C1. В формуле появится относительный адрес первой ячейки, в которой мы указываем радиус. У вас должна получиться формула следующего вида: =2*3,14*RC[-2].
9. Нажмите клавишу Enter. Если в ячейке R2C1 указано какое-либо число, вы немедленно получите результат вычисления длины окружности в ячейке R2C3.
10. Введите новое значение радиуса в ячейку R2C1 и нажмите клавишу Enter. Обратите внимание, что в ячейках R2C2 и R2C3 значения изменились одновременно. Сколько бы вы ни создали формул, использующих значение ячейки R2C1, результат их вычисления будет обновляться при изменении значения в этой ячейке (рис. 6.2).
Рис. 6.2. Формулы в ячейках R2C2 и R2C3 используют значение ячейки R2C1
Приведу арифметические операторы, которые вы можете использовать при создании формул:
+ – оператор сложения;
– – оператор вычитания;
* – оператор умножения;
/ – оператор деления;
^ – оператор возведения в степень. Этот оператор ставится после числа (или переменной), которое возводится в степень. После этого оператора указывается значение степени, которое может быть как числом, так и переменной (переменной в данном случае мы считаем ссылку на ячейку со значением);
% – оператор вычисления процента.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРес
Читайте также
Математические формулы
Математические формулы Кирпичи просто создавать, использовать, они понятны и просты, но на протяжении столетий возникло и сформировалось более тонкое понимание систем упорядочения. Эти открытия и нововведения развивали наше понимание сеток. Обращаясь к математике,
Формулы
Формулы Электронные таблицы не имели бы и сотой доли той популярности, которая есть у них на данный момент, если бы у них не было главного преимущества – возможности работать с формулами, на лету пересчитывая сотни и тысячи введенных значений, подводя промежуточные суммы
1.7. Формулы
1.7. Формулы Формулой считают любую последовательность не менее чем двух символов, которая не является словом (названием, аббревиатурой) в русском или каком-либо другом языке. Например, «MATLAB» является словом, «/(л:(0))» – нет.Формулы также нумеруются внутри одного раздела.
4.1. Математические формулы
4.1. Математические формулы В текстовом редакторе Word существует специальный инструмент для работы с формулами – редактор формул. С его помощью можно создавать сложные объекты, выбирая символы с панели инструментов и задавая переменные и числа. При этом размер шрифтов,
«Формулы в формулах»
«Формулы в формулах» При создании формул вы используете в качестве данных константы и адреса ячеек с данными. Вы можете также указать адреса ячеек, содержащих формулы. Допустим, в вашей таблице есть формула, возвращающая результат какого-то вычисления. Назовем ее
Создание простой графики
Создание простой графики Вы можете создавать простые графические объекты, используя простые геометрические фигуры, множество шаблонов которых представлено в галерее Фигуры. Можете изменять свойства каждой фигуры (форму, цвет, контур), а также добавлять к ним различные
Формулы
Формулы Разбить лист на ячейки и разрешить пользователям заполнять их – дело нехитрое. Но возможности Excel этим не ограничиваются. Следующая ступень мастерства – связать отдельные клетки с цифрами невидимыми связями с помощью математических формул. А это значит, что при
16.3. Формулы
16.3. Формулы Если вы никогда не работали в электронных таблицах с формулами, можете считать, что вы не использовали электронные таблицы вообще. Только хорошо освоив формулы, вы сможете понять всю гибкость и мощь электронных таблиц.Давайте разберемся с самыми простыми
1.7. Формулы
1.7. Формулы Формулой считают любую последовательность не менее чем двух символов, которая не является словом (названием, аббревиатурой) в русском или каком-либо другом языке. Например, MATLAB является словом, f(x(0)) – нет.Формулы также нумеруются внутри одного раздела. Номер
2.4. Формулы
2.4. Формулы 2.4.1. Формулы в документе, если их более одной, нумеруются арабскими цифрами, номер ставят с правой стороны страницы, в скобках, на уровне формулы.В пределах всего документа или ею частей, в случае деления документа на части, формулы имеют сквозную
14.8. Формулы
14.8. Формулы Ячейка может содержать не только статическое значение, но и формулу, т. е. значение ячейки будет вычисляться по заданной вами формуле. Давайте сразу перейдем к примерам формул — как говорится, лучше один раз увидеть, чем сто раз
5.2.6. Формулы
5.2.6. Формулы Формулой называется математическое выражение, начинающееся со знака равенства, которое содержит адреса ячеек, соединенные знаками арифметических операций. Также формула может содержать различные функции, аргументами которых являются как адреса ячеек, так
Формулы
Формулы Кроме тех типов данных, которые указаны в поле Числовые форматы диалогового окна Формат ячеек (см. рис. 4.23), существует еще один формат данных, который называется формулой и может храниться в ячейке. Этот формат указывает программе Excel, что прежде, чем поместить
Практическая работа 38. Создание простой таблицы
Практическая работа 38. Создание простой таблицы Задание. Создать таблицу, показанную на рис. 5.70, ввести в ячейки текст и отформатировать его. Рис. 5.70.Пример простой таблицыПоследовательность выполнения1. Создайте новый документ.2. Вставьте в документ таблицу 5 х 7 с помощью
Практическая работа 44. Создание простой таблицы с формулами
Практическая работа 44. Создание простой таблицы с формулами Задание. Составить таблицу расчета заработной платы для работников отдела, имея следующие исходные данные: фамилии сотрудников, их часовые ставки и количество отработанных часов.В таблице требуется вычислить:
Формула объема в таблице в Excel помогает быстро посчитать объем нужной фигуры, а сделать это можно при помощи инструкции выше.
- Параллелепипед;
- Сфера;
- Пирамида;
- Цилиндр;
- Конус.
Видеоинструкция
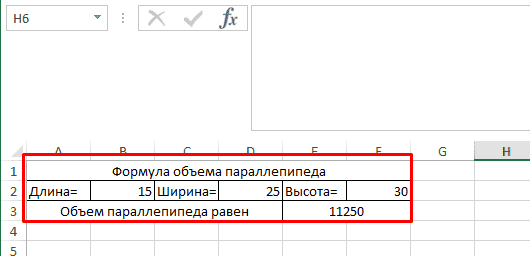
Формула объема параллелепипеда в Excel
Для этого потребуется использовать формулу:
=(Длина)*(Ширину)*(Высоту)
Пример можно скачать ниже:
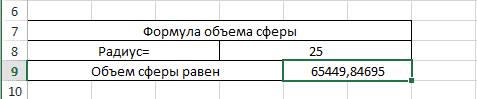
Сфера
Для шара можно воспользоваться конструкцией:
=(4/3)*ПИ()*(D8^3)
Пример:
Пирамида
В этом случае можно воспользоваться:
=((1/2)*B24*D24*SIN(F24))*(1/3)*H24
Пример:
Цилиндр
Задачу с данной фигурой можно решить через:
=ПИ()*C14*C14*F14
Пример:
Конус
В случае с конусом объем вычисляется через формулу:
=((1/2)*B24*D24*SIN(F24))*(1/3)*H24
Пример: