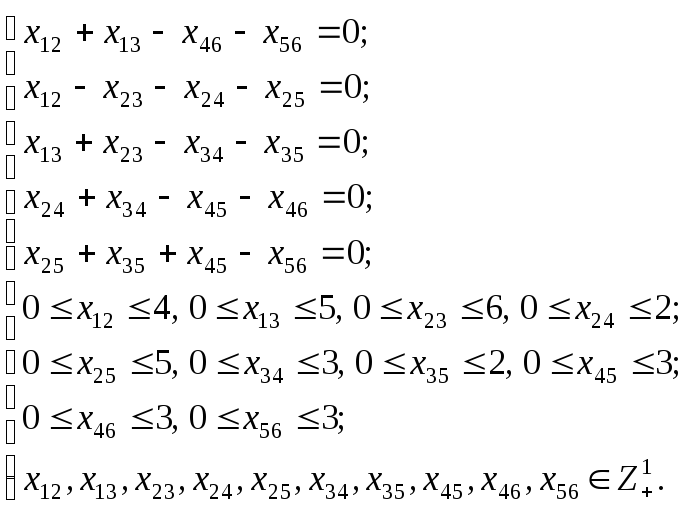Скачать материал
Скачать материал


- Сейчас обучается 121 человек из 40 регионов


- Сейчас обучается 36 человек из 26 регионов


- Сейчас обучается 122 человека из 48 регионов


Краткое описание документа:
Реализация в Excel
В качестве начального потока выбираем, например, поток, проходящий по ребрам 1-3-5-6. Максимальная величина потока, который можно пропустить по этим ребрам, равна 2.
На чистом рабочем листе заполняем форму решения задачи. В ячейки B3:G8 заносим данные о пропускных способностях ребер сети.
Ниже строим матрицу начального потока на сети.
Обратите внимание на то, что матрица начального потока должна быть антисимметрична. Поэтому сначала заполняем ее диагональные элементы, выделяя их каким-либо цветом, и ту часть матрицы, которая находится выше главной диагонали.
Для заполнения нижней части матрицы воспользуемся функцией ТРАНСП(массив).
Эта функция возвращает вертикальный диапазон ячеек в виде горизонтального и наоборот. Функция ТРАНСП должна быть введена как формула массива в интервал, который имеет столько же строк и столбцов, сколько столбцов и строк имеет аргумент массив.
Для заполнения столбца В13:В17 установите курсор в ячейку В13, введите формулу = — ТРАНСП(C12:G12) и нажмите клавишу <ENTER> (знак <–> перед формулой вводится для того, чтобы матрица получилась антисимметричной). В ячейке появится знак ошибки. Затем нужно выделить диапазон В13:В17, нажать клавишу , а затем клавиши . В результате будет сформирован первый столбец матрицы потока. Остальные столбцы под нижней диагональю заполняются аналогично.
Ниже матрицы потока строим матрицу ненасыщенности ребер.
Для этого в ячейку В21 вводим формулу:
=B3:G8-B12:G17
После чего выделяем диапазон В21: G26, нажимаем клавишу , а затем клавиши .
В результате третья матрица заполняется значениями, равными «недогрузке» ребер.
Находим ненасыщенные пути. Для этого в матрице ненасыщенности выбираем ненулевые элементы:
1|| 2, 3, 4
2|| 3, 4, 5
3|| —
4|| 5, 6
Таким образом, можно выбрать путь 1-2-4-6 с максимально возможным объемом дополнительного груза, равным 4.
Для удобства можно выписать процедуру поиска ненасыщенного пути справа от матрицы ненасыщенности ребер:
Выделяя потоки по выбранным ребрам каким-либо цветом, легко найти их минимум . Строим справа матрицу дополнительного потока по аналогии с матрицей начального потока.
Ниже строим матрицу нового потока №1 путем суммирования матриц начального и дополнительного потока (не забываем, что формулы вводятся как формулы массива). Снова находим матрицу ненасыщенных ребер для потока №1.
Процедуру повторяем до тех пор, пока не останется ненасыщенного пути из вершины 1 в вершину 6. Поток, найденный на этом шаге, будет максимальным.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 212 196 материалов в базе
-
Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Рейтинг:
2 из 5
- 23.06.2015
- 2623
- 24
- 23.06.2015
- 944
- 2

- 23.06.2015
- 1291
- 1

- 23.06.2015
- 935
- 3
- 23.06.2015
- 560
- 0
Необходимо найти кратчайший путь между 2-мя заданными городами. Построим линейную модель и с помощью надстройки Поиск решения решим задачу.
В статье
Поиск решения MS EXCEL (6.3). Задача коммивояжера (полный граф, линейная модель)
рассматривались модели, в которых коммивояжёру требуется посетить все имеющиеся города. В этой задаче посещение всех городов не требуется.
Задача
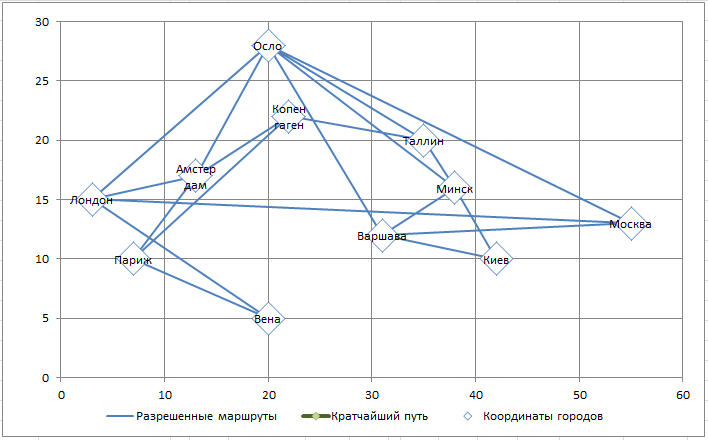
Имеется 11 городов, координаты которых известны. Маршруты проложены только между некоторыми городами (неполный граф). Найти кратчайший путь между 2-мя заданными городами. Построить Линейную модель.
Создание модели
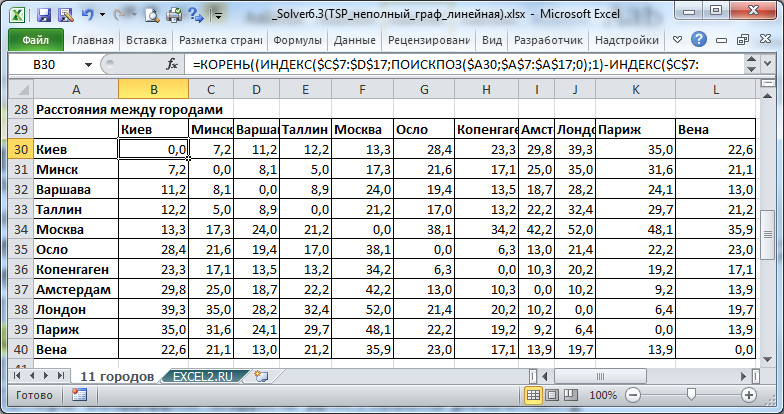
Так как даны координаты городов, то сначала найдем расстояния между ними (см.
файл примера
).
Расстояния рассчитаем с помощью формулы: =
КОРЕНЬ((ИНДЕКС($C$7:$D$17;ПОИСКПОЗ($A30;$A$7:$A$17;0);1)-ИНДЕКС($C$7:$D$17;ПОИСКПОЗ(B$29;$A$7:$A$17;0);1))^2 +(ИНДЕКС($C$7:$D$17;ПОИСКПОЗ($A30;$A$7:$A$17;0);2)-ИНДЕКС($C$7:$D$17;ПОИСКПОЗ(B$29;$A$7:$A$17;0);2))^2)
Теперь создадим линейную модель для решения задачи с помощью
Поиска решения
.
Совет
: Вводная статья про
Поиск решения
в MS EXCEL 2010
находится здесь
.
Обратите внимание, что не все города соединены сообщением (столбцы J:M), например нет прямого маршрута между Москвой и Парижем. Также для модели принципиально направление маршрута: Москва — Лондон, это не тоже самое, что Лондон-Москва (при необходимости список маршрутов можно расширить).
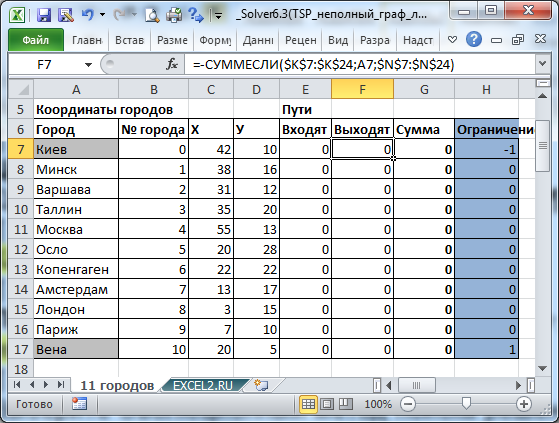
Переменные (выделено зеленым)
. В качестве переменных модели следует взять номера маршрутов между городами: если маршрут включен в кратчайший путь, то переменная =1, если нет, то =0.
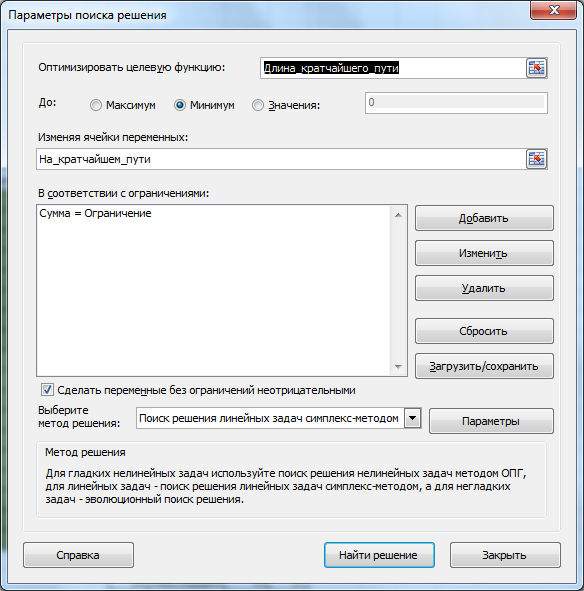
Ограничения (выделено синим)
. Необходимо, чтобы из каждого города, в котором побывал путешественник, был входящий и выходящий маршрут. Так как входящий маршрут обозначается 1, а исходящий -1, то их сумма, равная 0, будет означать, что в город вошли и вышли (включен в кратчайший путь). Исключение составляют город – начальная точка путешествия (сумма =-1) и город – конечная точка (сумма =1). Изменяя ограничение в синем столбце, можно задавать начальные и конечные пункты путешествия.
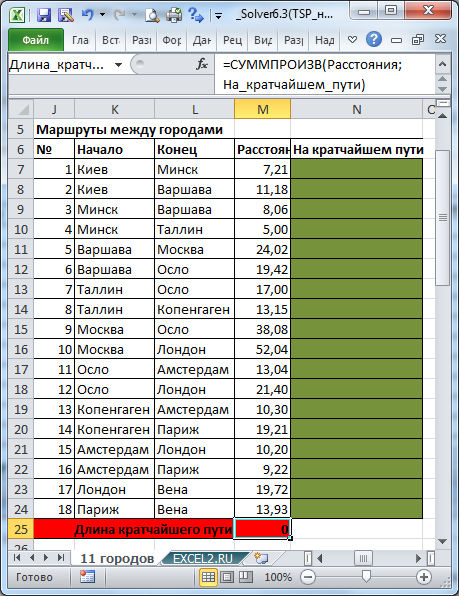
Целевая функция (выделено красным)
.
Длина маршрута должна быть минимальной.
Примечание
: для удобства настройки
Поиска решения
используются
именованные диапазоны
.
Выберите Линейный метод поиска решения, т.к. созданная модель является линейной.
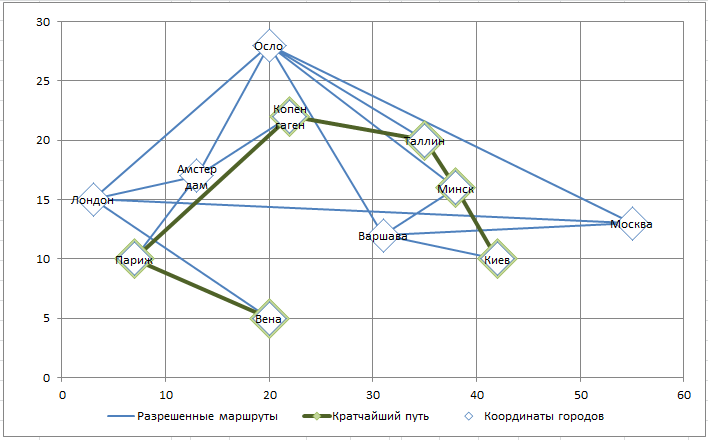
Найденное
Решение
Поиск решения
гарантировано найдет самый короткий маршрут, т.к. модель линейная.
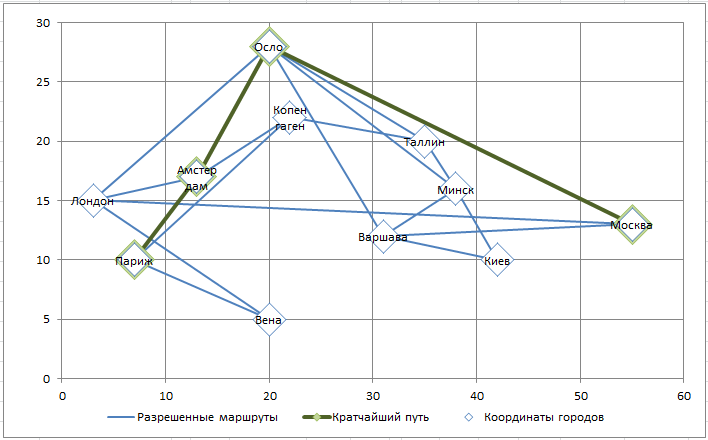
Изменив начальный и конечный пункт путешествия, и перезапустив
Поиск решения
, получим другой маршрут.
Будьте внимательны, не все пары конечных и начальных пунктов допустимы. Например, задав путешествие из Москвы в Копенгаген,
Поиск решения
не найдет маршрут, т.к. для этого потребуется «двигаться назад», а в маршрутах между городами обратные пути не прописаны (маршруты, конечно, можно добавить в столбцы J:M, но не забудьте изменить и другие формулы).
Рассмотрим задачу
нахождения максимального поток в сети,
которая представляет модель системы
магистральных трубопроводов, связывающих
источник добычи некоторого жидкого
продукта (нефти, сжиженного газа) с
предприятием по его промышленной
переработке. Данная модель может быть
представлена в виде схемы, формально
представляющая собой ориентированный
граф без циклов, состоящий из 6 вершин
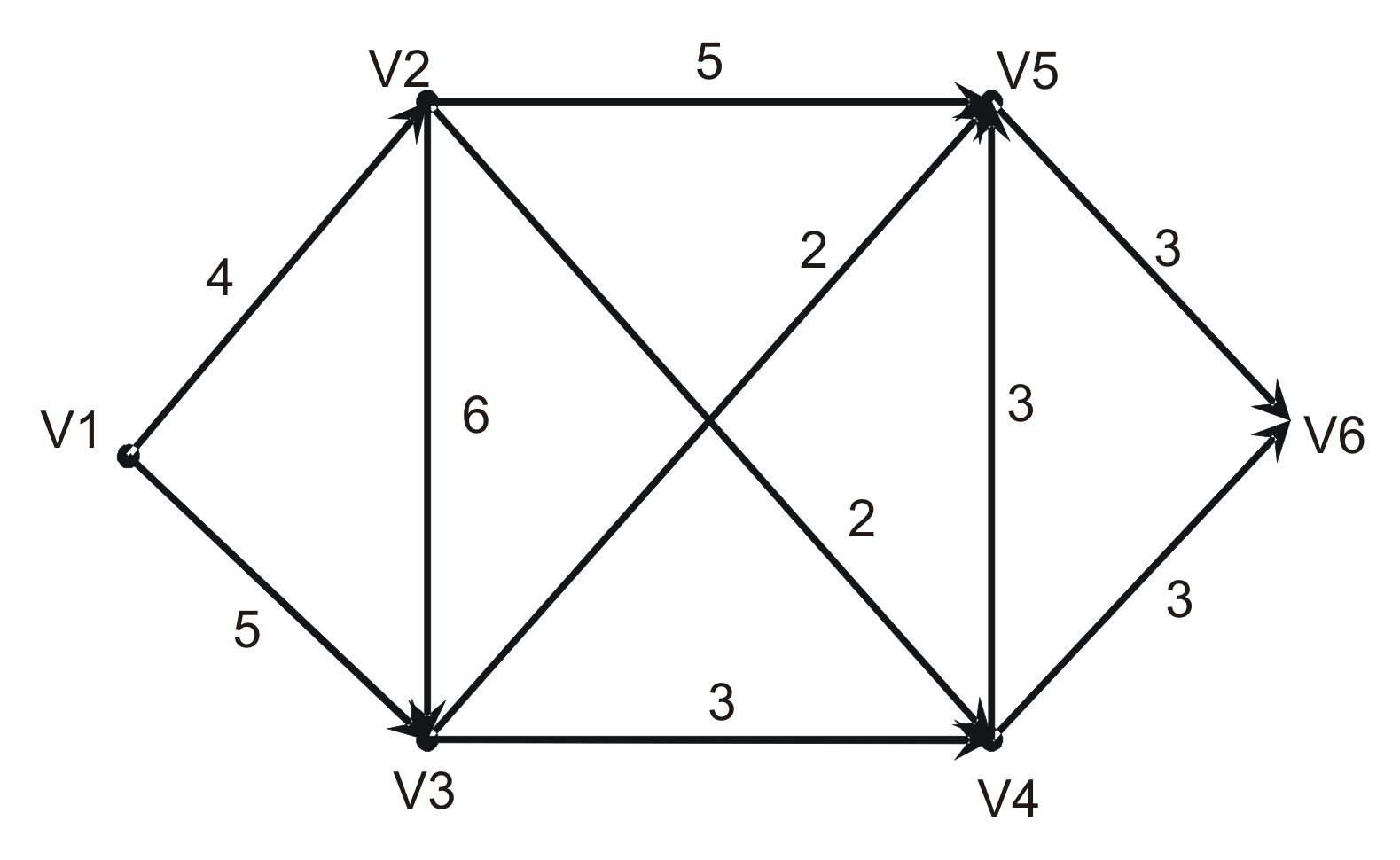
и 10 дуг (рис. 15.2). Предельные значения
пропускной способности каждого участка
рассматриваемой системы между двумя
соседними компрессорными станциями,
выраженные например в т/час,
равны значению весовой функции для
каждой дуги, которые указаны рядом с
изображением этой дуги в графе.
В предположении,
что источник, которому соответствует
вершина v1=vs,
обладает достаточными запасами продукта,
требуется определить количество
транспортируемого продукта по каждому
из участков трубопроводной системы до
стока, которому соответствует вершина
v6=vt,
так чтобы количество доставленного на
сток продукта было максимальным.
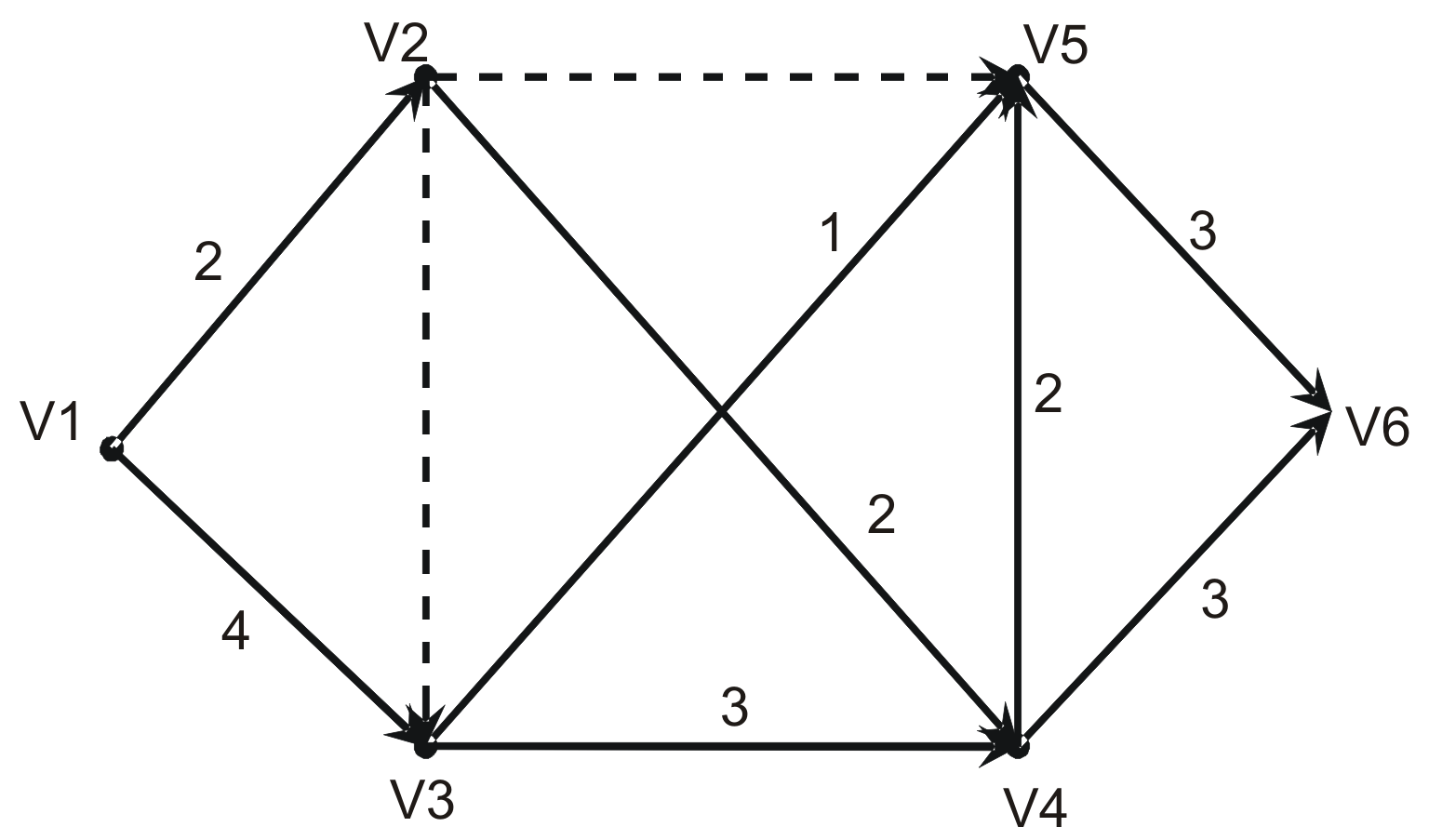
Рис.15.2. Исходный ориентированный граф
индивидуальной задачи о
максимальном потоке в сети
Переменными
математической модели данной индивидуальной
задачи о максимальном потоке в сети
являются 10 переменных: x12,
x13,
x23,
x24,
x25,
x34,
x35,
x45,
x46,
x56.
Каждая из этих переменных xij
может принимать неотрицательные
целочисленное значение, не превышающее
пропускной способности дуги cij
и
соответствующее величине потока
продукта, транспортируемого по отдельному
трубопроводу, связывающему компрессорные
станции – вершины сети. Тогда математическая
постановка рассматриваемой индивидуальной
задачи о максимальном потоке в сети
может быть записана в следующем виде:
(15.5)
где множество
допустимых альтернатив
формируется следующей системой
ограничений типа равенств и неравенств:
(15.6)
Заметим, что те
переменные xij,
для которых весовая функция дуг h
не определена или равна 0, не входят в
математическую постановку рассматриваемой
задачи (15.5) — (15.6).
Для решения
поставленной задачи воспользуемся
программой электронных таблиц MS
Excel
– компонентом офисного пакета MS
System
Office.
MS
Excel
позволяет выполнять быстрые расчеты и
содержит встроенные средства для решения
задач оптимизации. Также имеющиеся
возможности MS
Excel
могут быть расширены за счет использования
встроенного языка программирования
VBA
или вызова внешних функций из библиотек
динамической компоновки, разработанных
самим пользователем на таких языках
программирования как Borland
Delphi®
и MS
Visual
C++®.
Для решения
поставленной индивидуальной задачи
нахождения максимального потока в сети
с помощью программы MS
Excel
необходимо выполнить следующие действия.
-
Создать в книге
«Оптимизация на графах» новый рабочий
лист с именем «Максимальный поток». -
Ввести необходимые
надписи в ячейки A1:F1
(рис. 15.3). Конкретное содержание этих
надписей не оказывает влияния на решение
рассматриваемой задачи. -
В ячейки A2:A11
ввести индексы начальных вершин, а в
ячейки B2:B11
– индексы конечных вершин всех имеющихся
дуг исходного графа. -
В ячейки C2:C11
ввести значения пропускных способностей
дуг исходного графа. -
В ячейку F2
ввести формулу: =СУММ(D2:D3),
которая представляет целевую функцию
(15.5). -
В ячейку E2
ввести формулу: =СУММ(D2:D3)-СУММ(D10:D11),
которая представляет собой левую часть
первого ограничения (15.6). -
В ячейку E3
ввести значение левой части второго
ограничения: D2-СУММ(D4:
D6). -
В ячейку E4
ввести значение левой части третьего
ограничения: D3-СУММ(D7:
D8). -
В ячейку E5
ввести значение левой части четвертого
ограничения: СУММ(D5;
D7)-СУММ(D9:
D10). -
В ячейку E6
ввести значение левой части пятого
ограничения: СУММ(D6;
D8:D9)-D11.
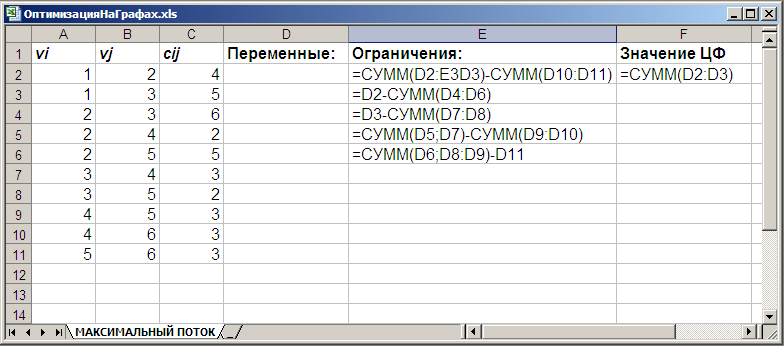
Внешний вид рабочего
листа с исходными данными для решения
задачи о минимальном пути в графе имеет
следующий вид (рис 15. 3).
Рис. 15.3. Исходные данные для решения
задачи о максимальном потоке в сети
Для дальнейшего
решения задачи следует вызвать мастер
поиска решений для чего необходимо
выполнить операцию главного меню: Сервис
| Поиск решения.
После появления
диалогового окна Поиск
решения
следует выполнить следующие действия:
-
В поле с именем
Установить
целевую ячейку:
ввести абсолютный адрес ячейки $F$2. -
Для группы Равной:
выбрать вариант поиска решения –
максимальному
значению. -
В поле с именем
Изменяя
ячейки:
ввести абсолютный адрес ячеек $D$2:$D$11. -
Задать первых 5
ограничений для рассматриваемой задачи.
С этой целью выполнить следующие
действия:
-
для задания этих
ограничений в исходном диалоговом
окне Поиск
решения
нажать кнопку с надписью Добавить; -
в появившемся
дополнительном окне выбрать диапазон
ячеек $E$2:$E$11,
который должен отобразиться в поле с
именем Ссылка
на ячейку; -
в качестве знака
ограничения из выпадающего списка
выбрать равенство «=»; -
в качестве значения
правой части ограничения ввести с
клавиатуры значение 0; -
для добавления
первого ограничения в дополнительном
окне нажать кнопку с надписью Добавить.
Задать первое из
10 ограничений на пропускные способности
дуг (15.6). С этой целью выполнить следующие
действия:
-
Для задания
ограничения в исходном диалоговом
окне Поиск
решения
нажать кнопку с надписью Добавить; -
В появившемся
дополнительном окне выбрать ячейку
$D$2,
которая должна отобразиться в поле с
именем Ссылка
на ячейку; -
В качестве знака
ограничения из выпадающего спуска
выбрать нестрогое неравенство «<=». -
В качестве значения
правой части ограничения в появившемся
дополнительном окне выбрать ячейку
$C$2,
которая должна отобразиться в поле с
именем Ссылка
на ячейку; -
Для добавления
первого ограничения в дополнительном
окне нажать кнопку с надписью Добавить.
Аналогичным
образом добавить остальные 9 ограничений
(15.6), используя в качестве исходных
ячеек $D$3:
$D$11
и $C$3:$C$11.
Задать ограничение
на целочисленные значения переменных.
С этой целью выполнить следующие
действия:
-
В исходном
диалоговом окне Поиск
решения
нажать кнопку с надписью Добавить; -
В появившемся
дополнительном окне выбрать диапазон
ячеек $D$2:$D$11,
который должен отобразиться в поле с
именем Ссылка
на ячейку; -
В качестве знака
ограничения из выпадающего списка
выбрать строку «цел»; -
В качестве значения
правой части ограничения в поле с
именем Ограничение:
оставить без изменения вставленное
программой значение «целочисленные»; -
Для добавления
первого ограничения в дополнительном
окне нажать кнопку с надписью Добавить.
В окне дополнительных
параметров поиска решения выбрать
отметки Линейная
модель и
Неотрицательные
значения.
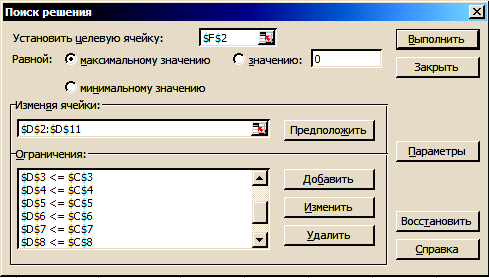
Общий вид диалогового
окна спецификации параметров мастера
поиска решения показан на рис. 15.4.
Рис. 15.4. Ограничения значений переменных
и параметры мастера поиска решения для
задачи о максимальном потоке в сети
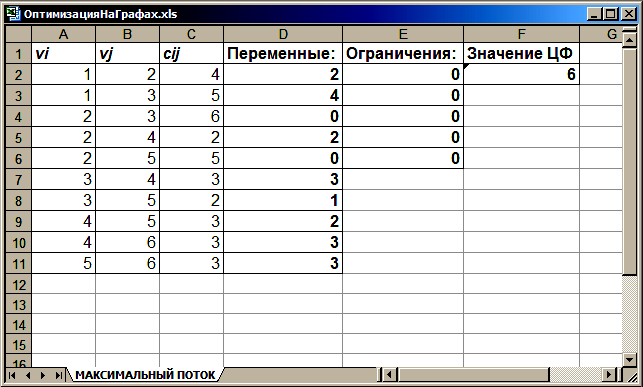
Рис. 15.5. Результат количественного
решения задачи о максимальном
потоке в сети
После задания
ограничений и целевой функции можно
приступить к поиску численного решения,
для чего следует нажать кнопку Выполнить.
После выполнения расчетов программой
MS
Excel
будет получено количественное решение,
которое имеет следующий вид (рис. 15.5).
Результатом решения
задачи о максимальном потоке в сети
являются найденные оптимальные значения
переменных:
,
,
,
,
,
,
,
,
остальные переменные равны 0. найденному
оптимальному решению соответствует
значение целевой функции:
.
Анализ найденного
решения показывает, что максимальный
поток в сети (рис. 15.2), проходящий из
вершины 1 в вершину 6, протекает по
следующим дугам: по дуге (1, 2) в количестве
2 т/час,
по дуге (1, 3) в количестве 4 т/час,
по дуге (2, 4) в количестве 2 т/час,
по дуге (3, 4) в количестве 3 т/час,
по дуге (3, 5) в количестве 1 т/час,
по дуге (4, 5) в количестве 2 т/час,
по дуге (4, 6) в количестве 3 т/час,
по дуге (5, 6) в количестве 3 т/час.
Тем самым найден
оптимальный план транспортировки
продукта от пункта добычи до пункта
переработки (рис. 15.6). При этом общая
величина потока транспортируемого
продукта для рассматриваемой сети будет
максимальна и равна 6 т/час.
Рис. 15.6. Минимальный поток в исходной
сети между вершинами 1 и 6.
Простейшая проверка
найденного решения может быть связана
с рассмотрением так называемых разрезов
графа сети (рис. 15.6). Разрезом
сети называется
множество,
которому принадлежит исток, и не
принадлежит сток. Т.е. разрез
— это минимальное (в смысле отношения
включения) множество дуг, удаление
которых “ разрывает” все пути, соединяющие
исток и сток.
Пропускной
способностью разреза называется
число, равное сумме пропускных способностей
дуг этого разреза. Разрез называется
минимальным,
если имеет наименьшую пропускную
способность.
Например,
применительно к найденному решению
задачи о максимальном потоке в сети
(рис. 15.6) множество дуг
удовлетворяет определению минимального
разреза и его пропускная способность
равна 6, что в точности равно величине
найденного максимального потока. Для
дополнительной проверки получаемых с
помощью программы MS
Excel
решений данной типовой задачи оптимизации
на графах можно воспользоваться
специальным алгоритмом
пометок Форда — Фалкерсона.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
Zhan_Klod Пользователь Сообщений: 11 |
Приветствую! |
|
Sanja Пользователь Сообщений: 14838 |
Кто-нибудь, что-нибудь понял? Согласие есть продукт при полном непротивлении сторон. |
|
IKor Пользователь Сообщений: 1167 |
#3 10.09.2018 15:08:42
В Вашем примере приведены несколько таблиц 5х5 с числовыми или текстовыми заголовками — откуда взялись связи длиной трех звеньев я не могу понять… В примере на «Лист1 (4)» у позиции «1» есть связь только с ней самой — таким образом, она выпадает из рассмотрения, что упрощает матрицу до 4х4. С учетом остальных связей путь от любой оставшейся позиции до любой другой не превышает двух звеньев… (каждая позиция соединяется с любая другой либо напрямую, либо через один промежуточный шаг). Более того, для ряда пар позиций существую разные промежуточные шаги. Также можно неограниченно долго шагать между позициями «3» и «4», составляя неоптимальный маршрут бесконечной длины… |
||
|
Zhan_Klod Пользователь Сообщений: 11 |
Задача для сыщиков |
|
StoTisteg Пользователь Сообщений: 441 |
Zhan_Klod, о правиле 6 рукопожатий слыхали? |
|
Sanja Пользователь Сообщений: 14838 |
StoTisteg, с языка снял Согласие есть продукт при полном непротивлении сторон. |
|
Андрей VG Пользователь Сообщений: 11878 Excel 2016, 365 |
#7 10.09.2018 15:32:01 Доброе время суток
Коллега, это задача на графах. Дана таблица связанности, судя по вопросу, нужно найти толи самый короткий путь от одного объекта до другого, толи самый длинный… матчасть для этого дела, правда на C++ |
||
|
Юрий М Модератор Сообщений: 60588 Контакты см. в профиле |
Про правило 6 рукопожатий: утверждается, что каждый человек опосредованно знаком с любым другим жителем планеты через цепочку общих знакомых. Но мне попадалась статья про некое племя, в котором здороваются потиранием носов (нос об нос). Получается, что эти люди выпали из нашего круга )) |
|
Zhan_Klod Пользователь Сообщений: 11 |
вот картинка таблицы Изменено: Zhan_Klod — 11.09.2018 06:52:00 |
|
bedvit Пользователь Сообщений: 2477 Виталий |
#10 11.09.2018 07:58:03
Андрей привет! Здорово. Положил себе в закрома. Может что-то и для Excel пригодится через .xll «Бритва Оккама» или «Принцип Калашникова»? |
||
|
Zhan_Klod Пользователь Сообщений: 11 |
#11 11.09.2018 08:10:11
Спасибо |
||
|
Zhan_Klod Пользователь Сообщений: 11 |
я по ссылке прошел. вот это место?: Алгоритм поиска компонент связности в графе |
|
Zhan_Klod Пользователь Сообщений: 11 |
Изменено: Zhan_Klod — 13.09.2018 08:55:15 |
|
Zhan_Klod Пользователь Сообщений: 11 |
#14 13.09.2018 11:27:23 А кто исправил название темы, добавил слова — (задача на графах). |