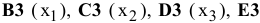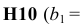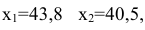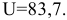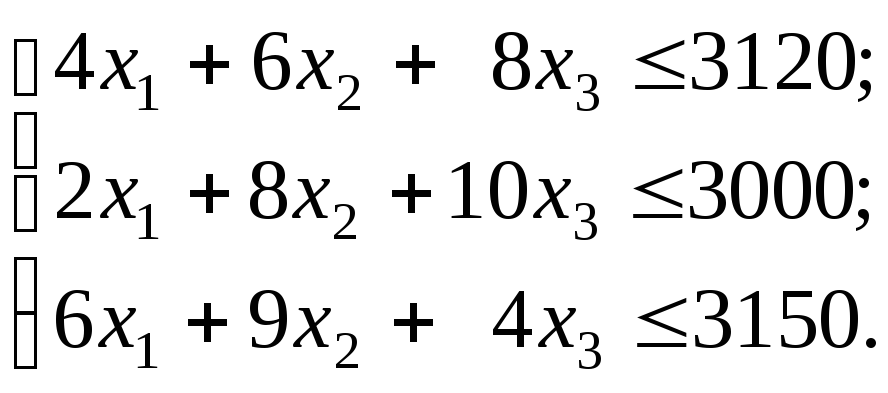Задачи линейного программирования относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе – это те задачи, в которых нужно найти наилучшее из всех возможных решений.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Линейное программирование
Линейное программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово «программирование» заимствовано из зарубежной литературы, где оно используется в смысле «планирование».
Решение задач линейного программирования с использованием microsoft excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.
Порядок выполнения работы
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить задачу линейного программирования в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.
Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- переменных,
- целевой функции (ЦФ),
- ограничений,
- граничных условий;
b) ввести исходные данные в экранную форму:
- коэффициенты ЦФ,
- коэффициенты при переменных в ограничениях,
- правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- формулу для расчета ЦФ,
- формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне «Поиск решения»):
- целевую ячейку,
- направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне «Поиск решения»):
- ячейки со значениями переменных,
- граничные условия для допустимых значений переменных,
- соотношения между правыми и левыми частями ограничений.
Решить задачу:
a) установить параметры решения задачи (в окне «Поиск решения»);
b) запустить задачу на решение (в окне «Поиск решения»);
с) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Возможно эта страница вам будет полезна:
Одноиндексные задачи линейного программирования
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
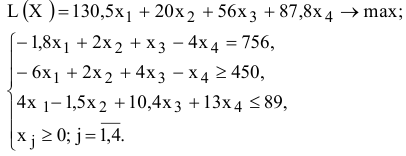
Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
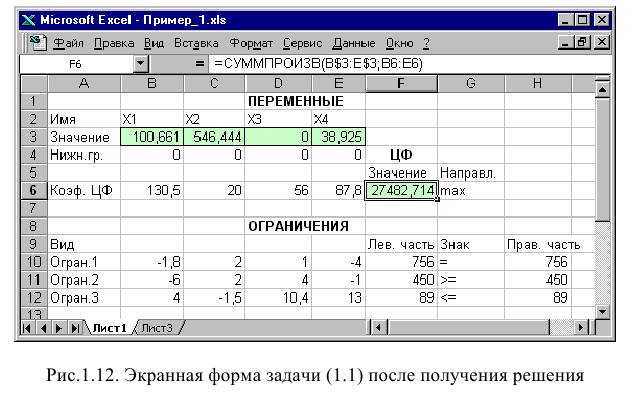
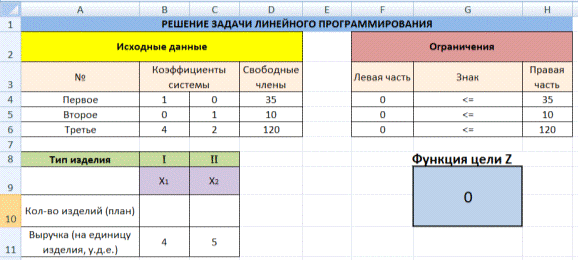
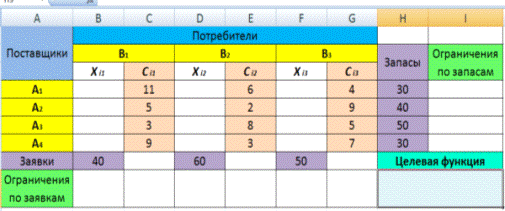
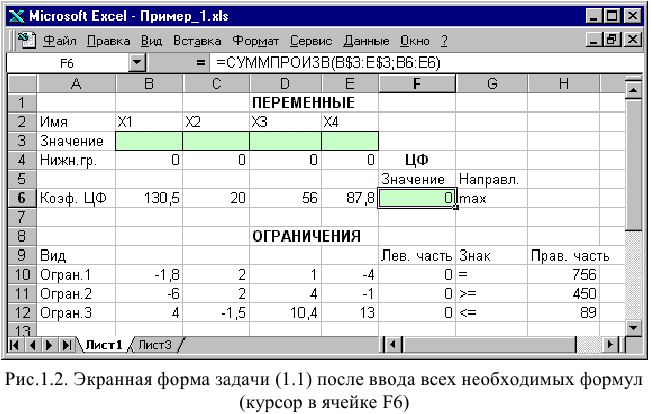
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис. 1.1.
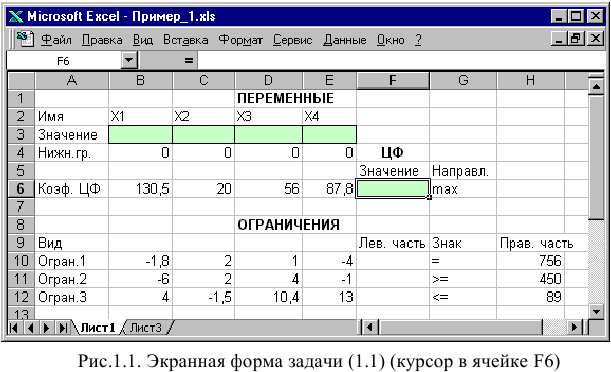
В экранной форме на рис. 1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи линейного программирования. Так, например, переменным задачи (1.1) соответствуют ячейки 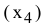
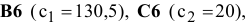
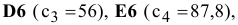
правым частям ограничений соответствуют ячейки
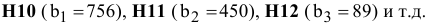
Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
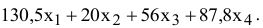
Используя обозначения соответствующих ячеек в Excel (см. рис. 1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6, Е6), то есть
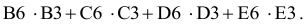
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу «Enter»
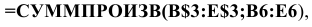
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;
символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись В6:Е6 указывает на ячейки В6, С6, D6 и Е6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима «Вставка функций», который можно вызвать из меню «Вставка» или при нажатии кнопки «
• курсор в поле F6;
• нажав кнопку «
• выберите в окне «Категория» категорию «Математические»;
• в окне «Функция» выберите функцию СУММПРОИЗВ;
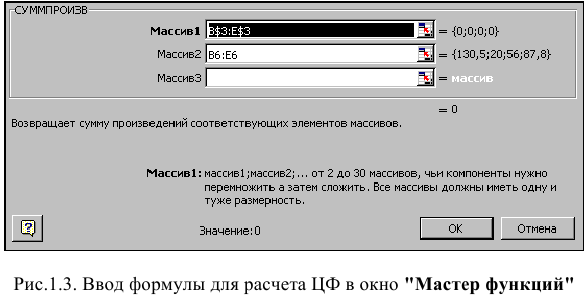
• в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение В$3:Е$3, а в строку «Массив 2» — выражение В6:Е6 (рис. 1.3);
• после ввода ячеек в строки «Массив 1» и «Массив 2» в окне «СУММПРОИЗВ» появятся числовые значения введенных массивов (см. рис. 1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Зависимости для левых частей ограничений
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (В 10, СЮ, D10, ЕЮ — 1-е ограничение; В11, С11, D11, El 1 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1.1.

Как видно из табл. 1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:
• поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами «Ctrl-Insert»);
• помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами «Shift-Insert») (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);
• на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис. 1.2).
Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис. 1.4 и 1.5).

Задание ЦФ
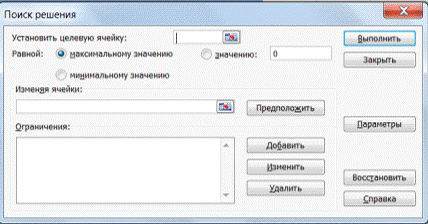
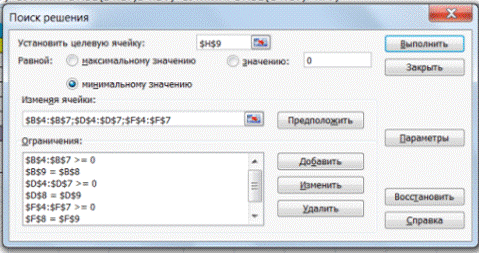
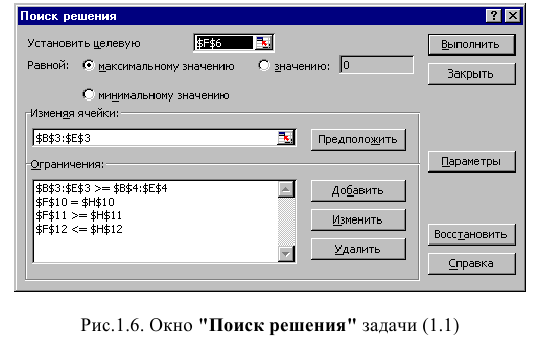
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис. 1.6):
• поставьте курсор в поле «Установить целевую ячейку»;
• введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме — это будет равносильно вводу адреса с клавиатуры;
• введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $BS3:$E$3. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1).
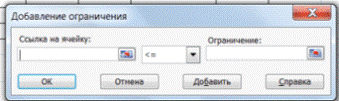
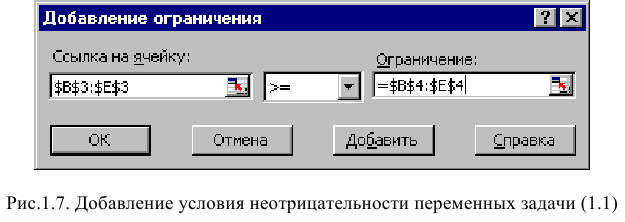
• Нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 1.7).
• В поле «Ссылка на ячейку» введите адреса ячеек переменных $BS3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.
• В поле знака откройте список предлагаемых знаков и выберите >.
• В поле «Ограничение» введите адреса ячеек нижней границы значений переменных, то есть $В$4:$Е$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.
Задание знаков ограничений <. >, =
• Нажмите кнопку «Добавить» в окне «Добавление ограничения».
• В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.
• В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =.
• В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $Н$10.
• Аналогично введите ограничения: $F$11>=$Н$11, $F$12<=$H$12.
• Подтвердите ввод всех перечисленных выше условий нажатием кнопки ОК.
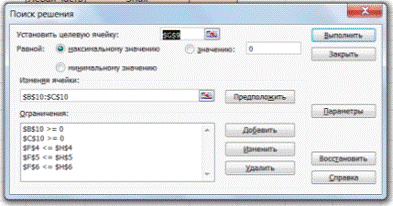
Окно «Поиск решения» после ввода всех необходимых данных задачи (1.1) представлено на рис. 1.6.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить» (см. рис. 1.6).
Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 1.8).
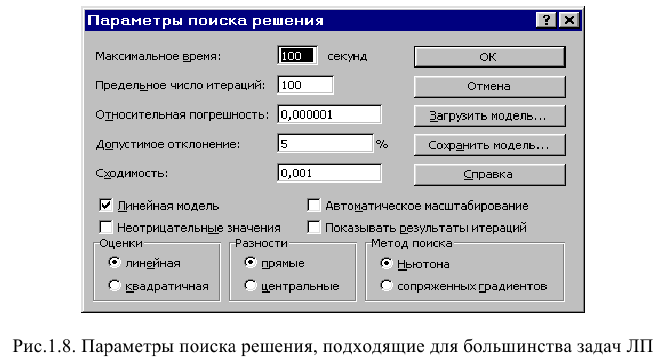
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость» применяется только при решении нелинейных задач.
Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки «ОК».
Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений, представленных на рис. 1.9, 1.10 и 1.11.

Иногда сообщения, представленные на рис. 1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис. 1.12).
Целочисленное программирование
Допустим, что к условию задачи (1.1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 1.13).
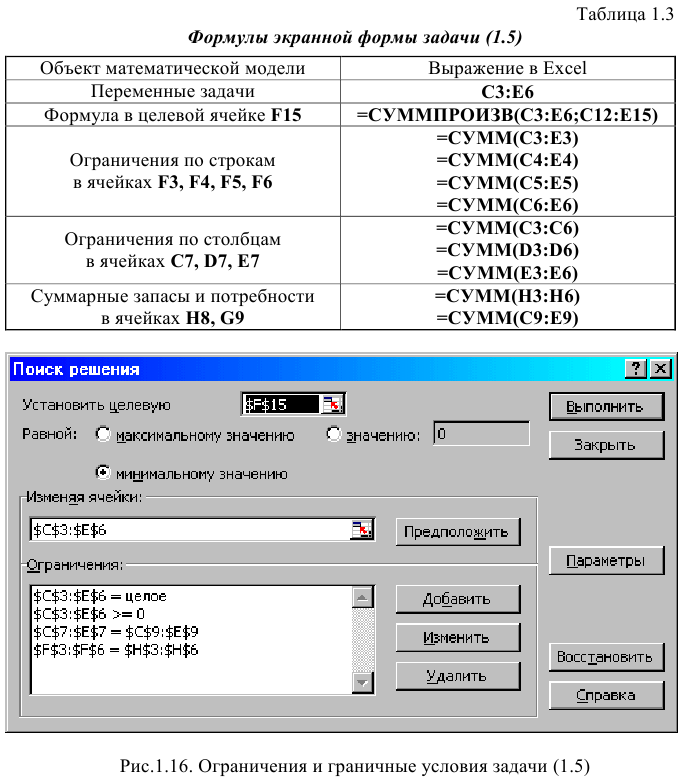
• В окне «Поиск решения» (меню «Сервис»—>»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения следующим образом (рис.1.14):
- в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $В$3:$Е$3;
- в поле ввода знака ограничения установите «целое»;
- подтвердите ввод ограничения нажатием кнопки «ОК».
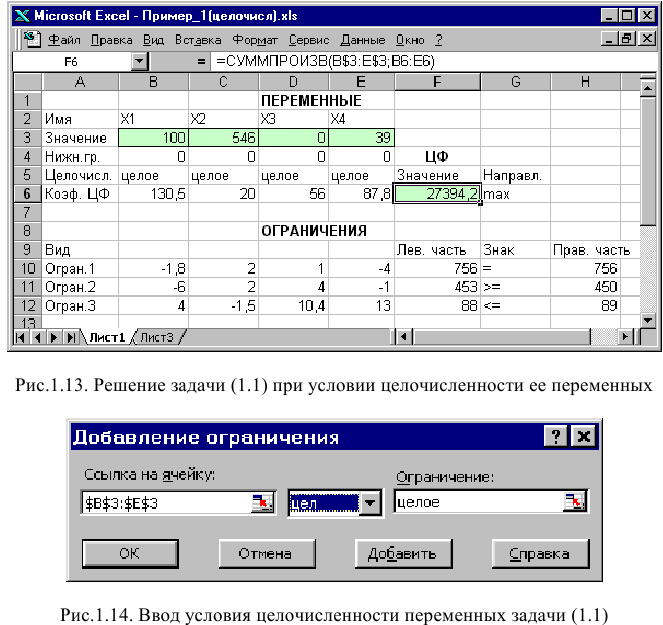
На рис. 1.13 представлено решение задачи (1.1), к ограничениям которой добавлено условие целочисленности значений ее переменных.
Двухиндексные задачи линейного программирования
Двухиндексные задачи линейного программирования вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.
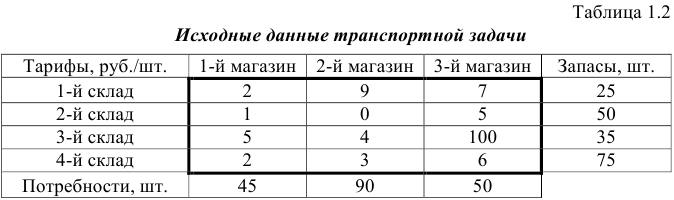
Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл. 1.2).
Целевая функция и ограничения данной задачи имеют вид
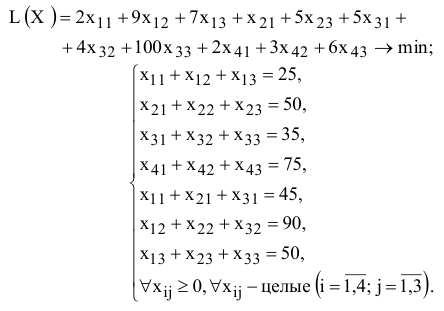
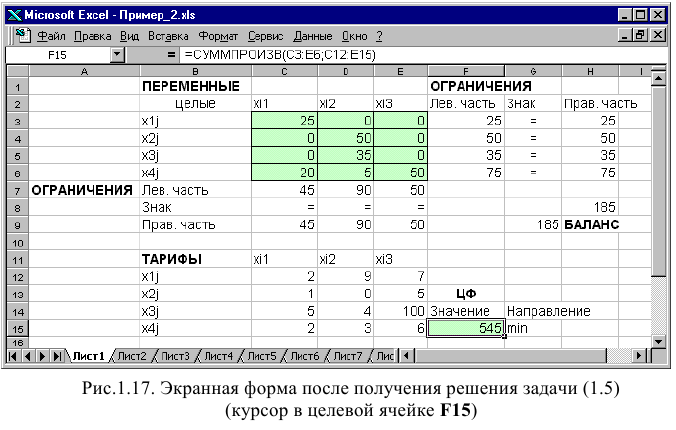
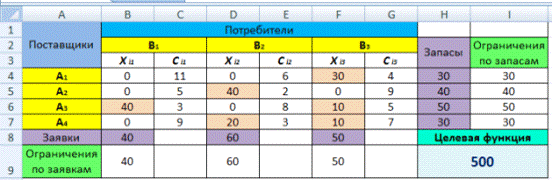
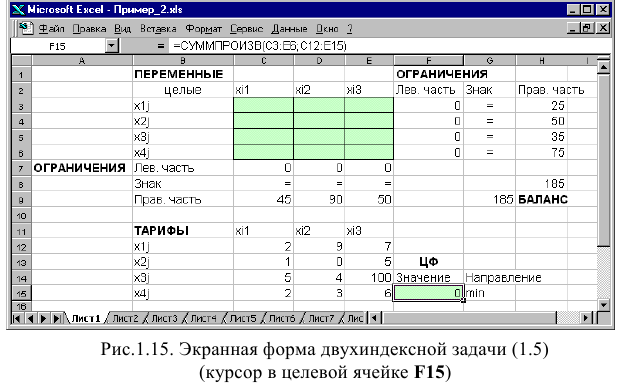
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис. 1.15, 1.16, 1.17 и в табл. 1.3.
Задачи с булевыми переменными
Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные 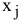
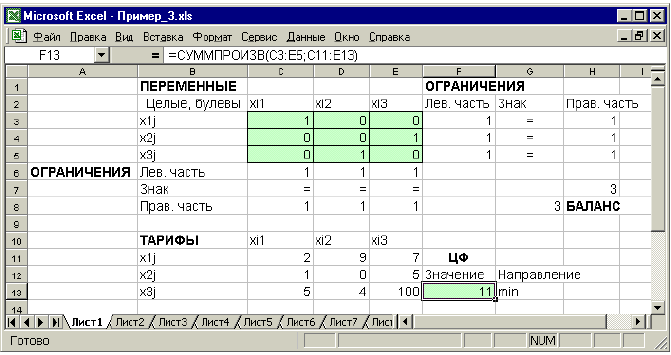
Рис. 1.18. Решение двухиндексной задачи с булевыми переменными
Помимо задания требования целочисленности (см. подразд.1.3.2) при вводе условия задач с булевыми переменными необходимо:
• для наглядности восприятия ввести в экранную форму слово «булевы» в качестве характеристики переменных (см. рис. 1.18);
• в окне «Поиск решения» добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис. 1.19).
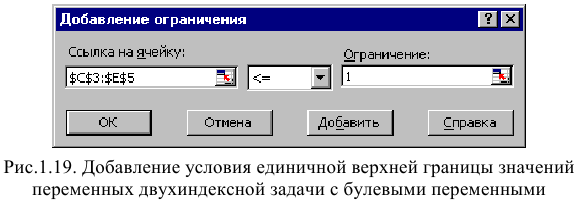
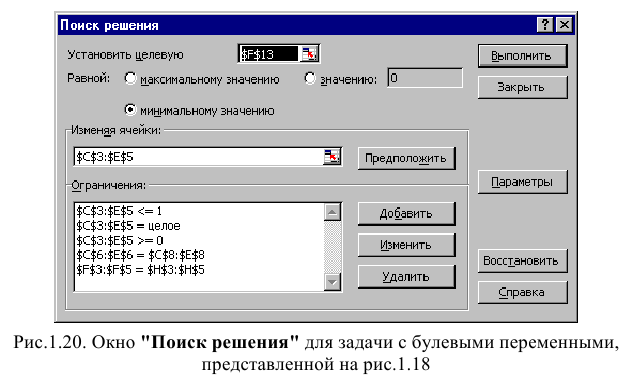
Вид окна «Поиск решения» для задачи с булевыми переменными, представленной на рис. 1.18, приведен на рис. 1.20.
Возможные ошибки при вводе условий задач линейного программирования
Если при решении задачи линейного программирования выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel.
Как решить задачу линейного программирования в excel
Цель работы
Приобретение навыков решения задач линейного программирования (ЗЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.
Инструкция по использованию microsoft excel для решения задач линейного программирования
Для того чтобы решить ЗЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
- • переменных,
- • целевой функции (ЦФ),
- • ограничений,
- • граничных условий;
b) ввести исходные данные в экранную форму:
- • коэффициенты ЦФ,
- • коэффициенты при переменных в ограничениях,
- • правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
- • формулу для расчета ЦФ,
- • формулы для расчета значений левых частей ограничений; с!) задать ЦФ (в окне «Поиск решения»):
- • целевую ячейку,
- • направление оптимизации ЦФ;
е) ввести ограничения и граничные условия (в окне «Поиск решения»):
- • ячейки со значениями переменных,
- • граничные условия для допустимых значений переменных,
- • соотношения между правыми и левыми частями ограничений. 2. Решить задачу:
a)установить параметры решения задачи (в окне «Поиск решения»,);
b) запустить задачу на решение (в окне «Поиск решения»,);
c) выбрать формат вывода решения (в окне «Результаты поиска решения»).
Одноиндексные ЗЛП
Рассмотрим пример нахождения решения для следующей одноиндексной ЗЛП:
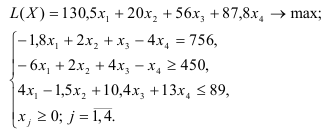
- Ввод исходных данных
Создание экранной формы и ввод в нее условия задачи
Экранная форма для ввода условий задачи (1) вместе с введенными в нее исходными данными представлена на рис.1.
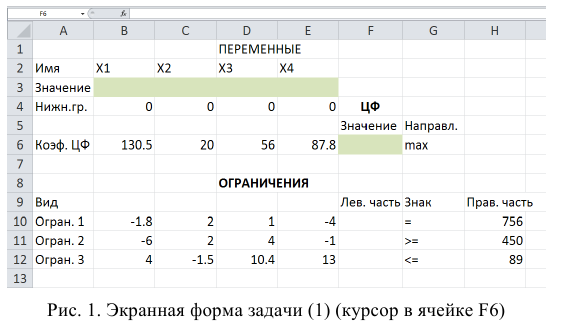
В экранной форме на рис. 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1) соответствуют ячейки
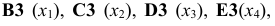
коэффициентам ЦФ соответствуют ячейки
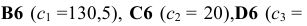
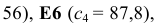
правым частям ограничений соответствуют ячейки
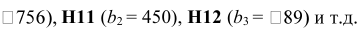
- Ввод зависимостей из математической модели в экранную форму
Зависимость для ЦФ.
В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1 (значение ЦФ определяется выражением
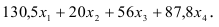
Используя обозначения соответствующих ячеек в Excel (см. рис. 1), формулу для расчета ЦФ (2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6,E6):
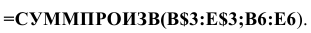
После этого в целевой ячейке появится 0 (нулевое значение) (рис. 2).
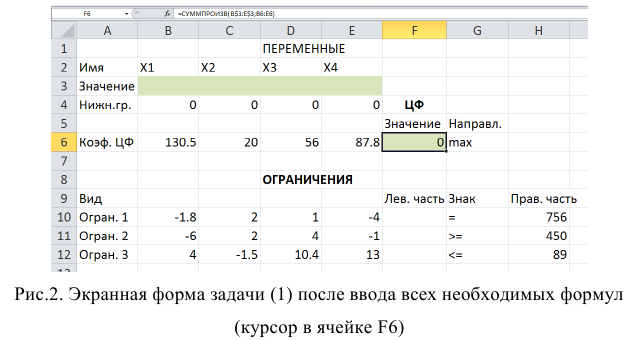
Зависимости для левых частей ограничений
Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи(ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, С10, D10, Е10 — 1-е ограничение; В11, C11,D11, Е11 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, записать самостоятельно. Проверка правильности введения формул
Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле. Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис». Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры»и заполнить некоторые поля окна «Параметры поиска решения».
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее32 767. Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр «Сходимость» применяется только при решении нелинейных задач. Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки «ОК». Запуск задачи на решение
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений:
• Сообщение об успешном решении задачи
• Сообщение при несовместной системе ограничений задачи
• Сообщение при неограниченности ЦФ в требуемом направлении Иногда второе и третье сообщения свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условийзадачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра»Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (будет рассмотрено позже). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис.3).
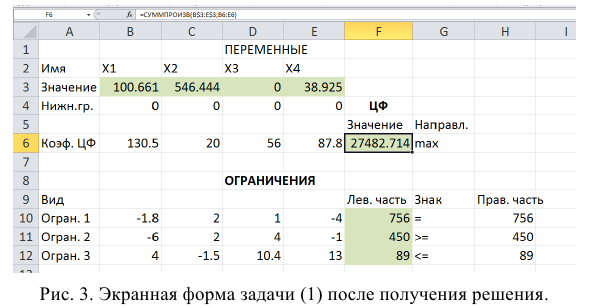
Целочисленное программирование
Допустим, что к условию задачи (1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 4).
• В окне «Поиск решения» (меню «Сервис»—►»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения целочисленности. Сравните результаты.
Получите у преподавателя индивидуальные задания.
Примеры решения экономических задач Задача 1.
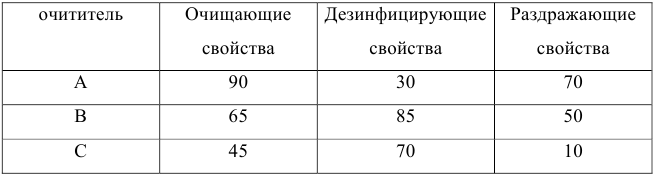
Средства очистки пола оценивают по следующим трем показателям:
- • очищающие свойства;
- • дезинфицирующие свойства;
- • раздражающее воздействие на кожу.
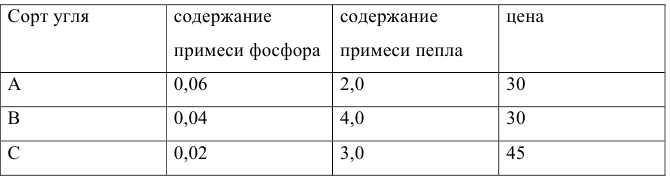
Каждый из этих показателей измеряется по линейной шкале от 0 до 100. Продукт на рынке должен иметь по крайней мере 60 ед. очищающих свойств и по крайней мере 60 ед. дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приведены в таблице.
Составим математическую модель задачи. Пусть 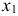
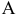
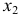
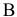
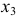
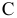
Целевая функция: 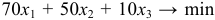
Ограничения:
Решение задачи с помощью MS Excel.
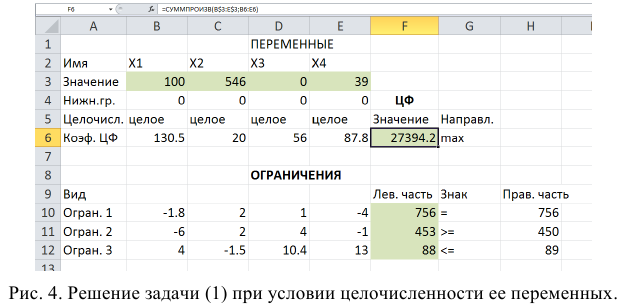
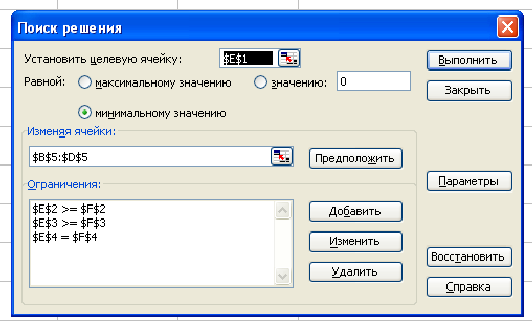
Заполним таблицу, содержащую исходные данные. Заполним диалоговое окно
«Поиск решения».
Щелкнув по кнопке ОК, мы получаем на месте исходной таблицы — таблицу с найденными оптимальными значениями. В результате в таблице получим значение целевой функции — 31,4 ед. раздражающего воздействия на кожу при
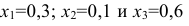
(т.е. очистители 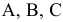
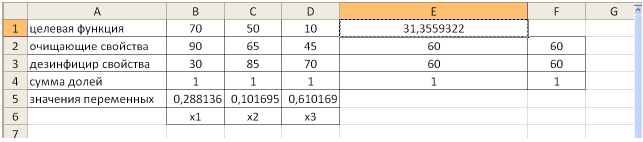
Задача 2.
Фирме требуется уголь с содержанием фосфора не более 0,03% и с примесью пепла не более 3,25%. Доступны 3 сорта угля 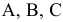
Как следует их смешать, чтобы удовлетворить ограничениям на примеси и минимизировать цену?
Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel
Задачи линейного программирования, целочисленного программирования и ряд задач нелинейного программирования могут быть решены с помощью стандартного прикладного программного обеспечения. Например, в ЭТ MS Excel для этого имеется модуль «Поиск решения», вызываемый командой меню «Сервис/Поиск решения». Для активизации данного модуля необходимо выполнить команду «Сервис/Надстройки» и установить флажок напротив строки меню «Поиск решения».
Рассмотрим пример применения «Поиска решения» на основе решения задачи оптимизации портфеля ценных бумаг — одной из классических задач управления финансовыми средствами.
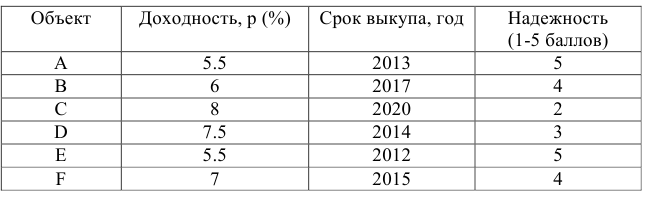
Постановка задачи. Перед инвестором стоит задача на основе информации, представленной в таблице 1, разместить имеющиеся средства так, чтобы получить максимальную прибыль за 1 период планирования (1 год), при этом должны быть выполнены следующие условия:
- Суммарный объем капитала составляет 100 000 $;
- доля средств, вложенная в один из объектов, не может превышать 25%;
- более 40% всех средств должны быть вложены в долгосрочные активы;
- доля высокорисковых активов не может превышать трети от суммарного объема.
Таблица 1 — Информация об объектах инвестирования
Построим экономико-математическую модель задачи.
Искомые переменные — объемы средств, вложенные в активы: 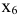
Прибыль, которую получит инвестор, задается целевой функцией:
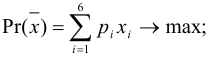
Сформируем ограничения:
Ограничения на суммарный объем активов —
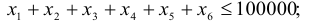
Ограничение на размер доли каждого актива
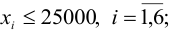
Необходимость долгосрочного инвестирования (например, более 3 лет)
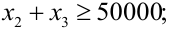
Учет необходимости снижения риска —
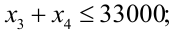
Естественное экономическое ограничение — неотрицательность искомых переменных —
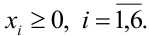
Для решения задачи выполним следующие шаги.
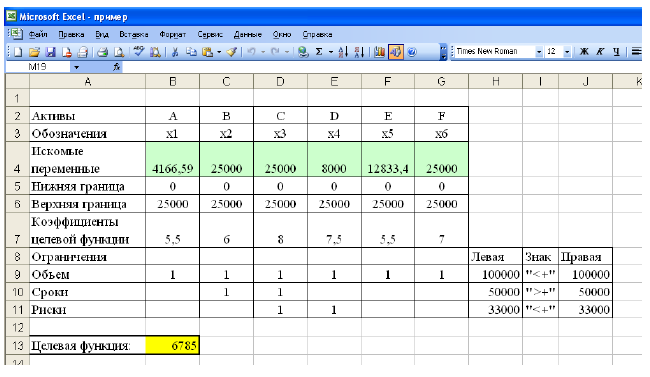
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 1.
Ячейки В13, Н9-Н11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Суммпроизв(…), аргументами которой являются диапазоны B4-G4 и диапазоны соответствующих параметров.
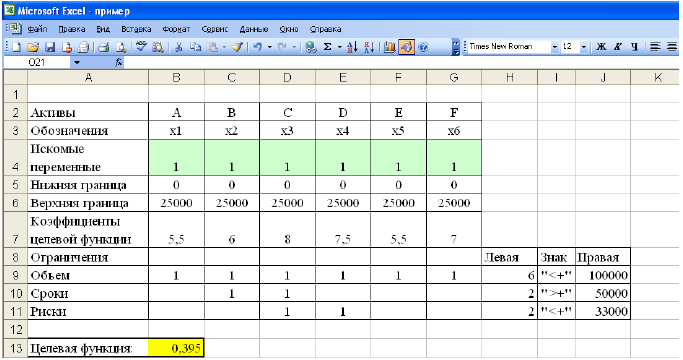
Рисунок 1 — Исходные данные для решения ЗЛП
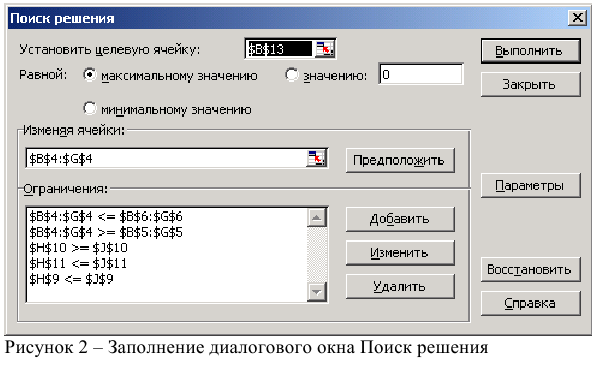
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 13), содержащей целевую функцию, указать тип целевой функции,
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В4 до G4).
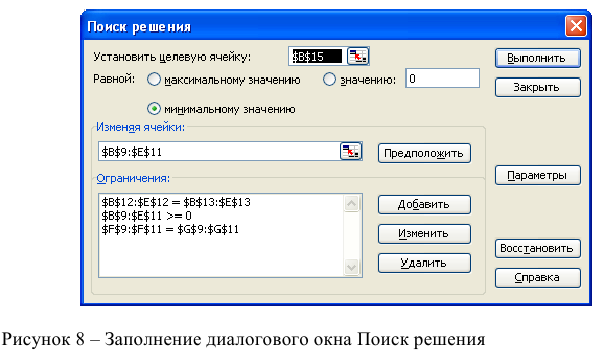
Затем последовательно заполнить все ограничения (Пример на рисунке 2.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить».
Далее, если это необходимо, устанавливаются особые значения параметров (кнопка «Параметры»).
Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 5.
Рисунок 5 — Результаты решения задачи
На рисунке 6 представлена структура инвестиционного портфеля.
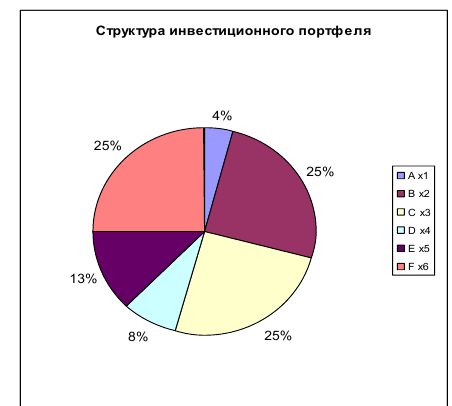
На основе решения проводится анализ, и принимаются соответствующие управленческие решения.
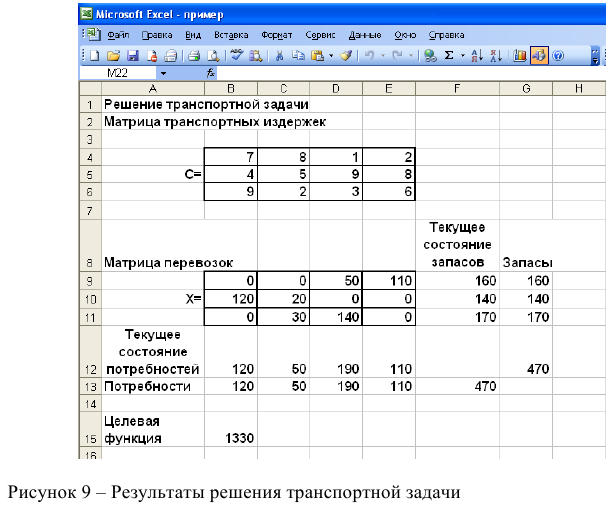
Технология решения транспортной задачи
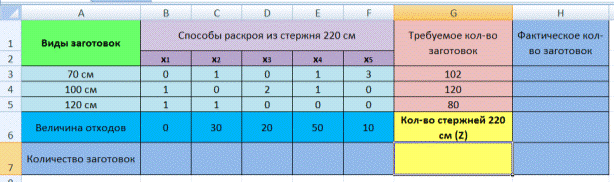
1. На рабочем листе представим необходимую для решения информацию, согласно рисунку 7.
Ячейки В15 содержит формулу Суммпроизв(…), аргументами которой являются диапазоны В4-Е6 и В9-Е11. Ячейки F9-F11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Сумм(…), аргументами которой являются диапазоны В9-Е9, В10-Е 10 и В11 -Е11. Аналогично определяются формулы в В12-Е 12.
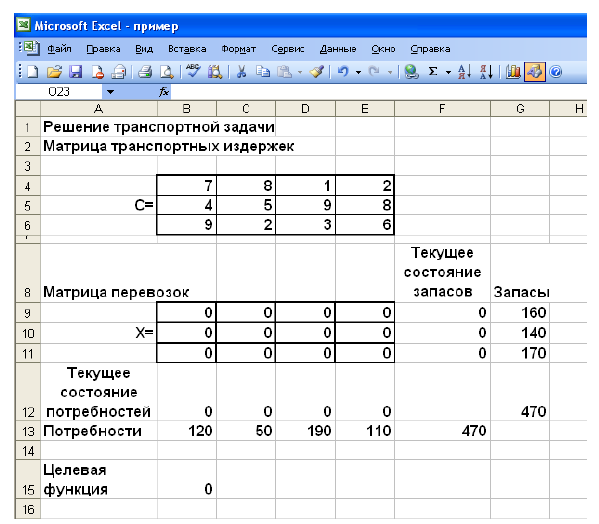
Рисунок 7 — Исходные данные для решения ЗЛП
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Указать адрес ячейки (В 15), содержащей целевую функцию, указать тип целевой функции (минимум),
В поле «изменяя ячейки» указать адреса всех искомых переменных (от В9 до Е11).
Затем последовательно заполнить все ограничения (Пример на рисунке 8.)
Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить». Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 9.
Технология решения задачи нелинейного программирования
Построить математическую модель и решить задачу потребительского выбора для заданной функции полезности 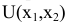
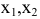
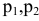
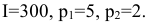
доходе I. Найти максимальное значение функции полезности.
Построим математическую модель задачи потребительского выбора:
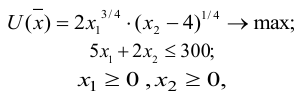
где 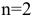
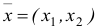
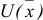
Набор, который является решением задачи потребительского выбора, называется оптимальным потребительским набором, или точкой локального рыночного равновесия потребителя. Поставленная задача — задача потребительского выбора — является задачей нелинейного программирования.
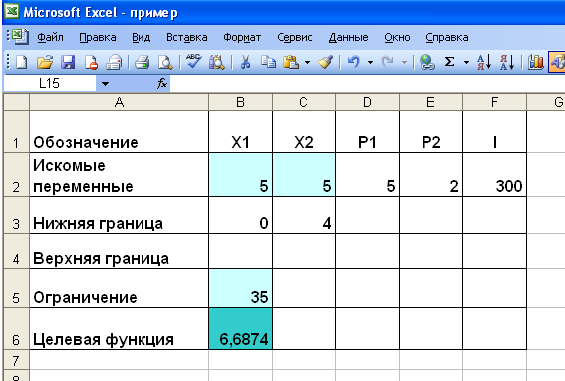
- На рабочем листе представим необходимую для решения информацию, согласно рисунку 10.
Ячейки В5, В6 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае ячейка В5 содержит формулу «=D2B2+E2C2», а ячейка В6 содержит формулу «=2В2Л(3/4)(С2-4)А(1/4)».
Рисунок 10 — Исходные данные для решения ЗНП
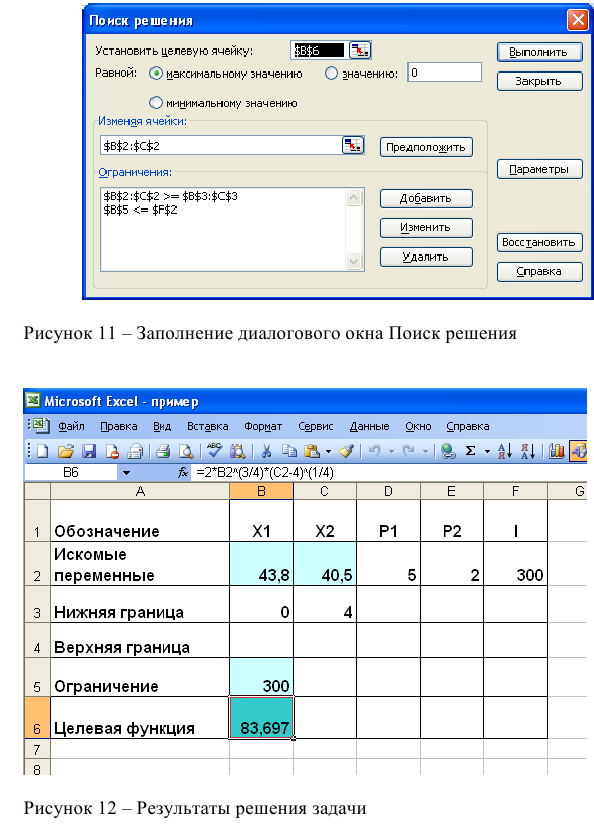
- Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:
Аналитическое решение задачи нелинейного программирования.
В рассматриваемом случае ограничение можно записать в виде строгого равенства, так как оптимальное решение достигается при полном использовании имеющихся средств.
Для решения классической задачи нелинейного программирования применим метод множителей Лагранжа, для этого составим функцию Лагранжа:
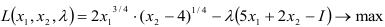
Найдем точки экстремума функции Лагранжа.
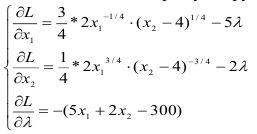
Приравняем каждое уравнение к 0:
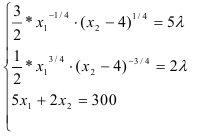
С помощью преобразований — разделим первое уравнение системы на второе, перейдем к системе:
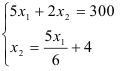
Подставим второе уравнение в первое и построим аналитические функции спроса:
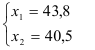
Максимальное значение функции полезности-
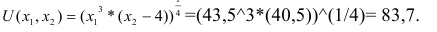
Решением задачи потребительского выбора будет набор
Возможно эти страницы вам будут полезны:
- Решение задач по математическому программированиюПримеры решения задач по математическому программированиюЗаказать работу по математическому программированиюПомощь по математическому программированиюЗадачи математического программированияЗадача линейного программированияРешение задач по линейному программированиюМетоды решения задач линейного программированияГрафическое решение задач линейного программированияГрафический метод решения задач линейного программированияЗаказать работу по линейному программированиюПомощь по линейному программированиюКонтрольная работа по линейному программированиюКурсовая работа по линейному программированию
15
Лабораторная
работа № 1
Цель работы:изучение современных программных
средств решения задачи линейного
программирования; практическое решение
задач линейного программирования
графическим методом, симплекс-методом
и средствами программыMicrosoftExcel; программная реализация
симплекс-метода на языке программирования
высокого уровня.
1. Теоретическая часть
Для решения задач
линейного программирования в программе
Microsoft
Excel
имеется надстройка Поиск
решения,
обращение
к которой производится из меню Сервис.
Если команда
Поиск решения
отсутствует в меню Сервис,
то требуется установить надстройку
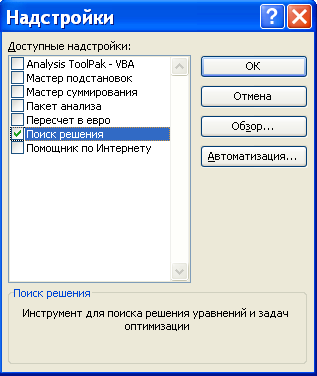
«Поиск решения». Для этого в меню Сервис
выбирается команда Надстройки,
которая открывает диалоговое окно,
показанное на рис. 1.
Рис. 1
Далее в этом окне
устанавливается флажок той надстройки,
которую необходимо загрузить, и нажимается
кнопка OK.
Покажем использование
надстройки
«Поиск решения» на примере решения
следующей задачи.
Постановка задачи
Предприятие
изготавливает и реализует три вида
продукции – P1,
Р2
и Р3.
Для производства продукции используются
три вида ресурсов – комплектующие
изделия, сырье и материалы. Запасы
ресурсов и их расход на изготовление
единицы продукции каждого вида приведены
в табл. 1.
Таблица 1
|
Виды |
Расходы |
Запасы ресурсов, |
||
|
P1 |
P2 |
P3 |
||
|
Комплектующие |
4 |
6 |
8 |
3120 |
|
Сырье |
2 |
8 |
10 |
3000 |
|
Материалы |
6 |
9 |
4 |
3150 |
Прибыль от реализации
единицы продукции каждого вида составляет
240, 210 и 180 денежных единиц для P1,
Р2
и Р3
соответственно.
Требуется определить
производственную программу предприятия
таким образом, чтобы прибыль от реализации
продукции была максимальной.
Математическая модель задачи
Обозначим переменными
x1,
x2
и x3
искомые объемы производства продукции
видов P1,
Р2
и Р2,
а через F
– прибыль предприятия. Тогда математическая
постановка представленной задачи
принимает следующий вид.
Определить значения
переменных x1,
x2
и x3,
для которых достигается максимум целевой
функции
F
=
240 x1
+ 210 х2
+ 180 x3
при ограничениях:
Целевая функция
описывает суммарную прибыль от реализации
произведенной продукции всех трех
видов. Ограничения (1), (2) и (3) учитывают
расход и запасы комплектующих изделий,
сырья и материалов соответственно.
Поскольку объемы производства продукции
не могут быть отрицательными, добавляются
условия
x1
≥ 0; x2
≥ 0; x3
≥ 0.
Порядок оптимального решения задачи
Примерные действия,
необходимые для решения задачи линейного
программирования средствами программы
Excel,
представим в виде последовательности
шагов.
Шаг 1.
Исходные данные задачи записываются
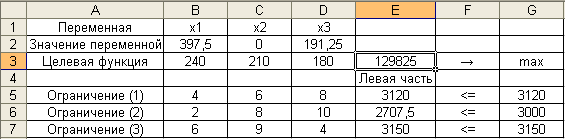
на рабочем листе электронной таблицы.
Один из вариантов показан на рис. 2.
Рис. 2
Замечание.
Если известно исходное допустимое
базисное решение, то можно несколько
ускорить процесс поиска оптимального
решения. Для этого начальные значения
некоторых или всех переменных могут
быть заданы вручную. В данном примере
для их хранения используются ячейки
$B$2,
$C$2
и $D$2.
Если допустимое базисное решение не
задано, то программа Excel
автоматически определяет начальные
значения переменных задачи.
Шаг 2.
В ячейку E3
вводится формула
=СУММПРОИЗВ(В3:D3;
$B$2:$D$2)
для вычисления
текущего значения целевой функции,
которая находит сумму попарных
произведений ячеек (В3:D3)
с коэффициентами при переменных в
выражении целевой функции на ячейки
($B$2:$D$2)
с текущими значениями переменных.
Шаг 3.
Чтобы задать ограничения решаемой
задачи, в ячейки E5,
E6
и E7
копируется формула из ячейки E3.
После этого в указанных ячейках должны
быть получены формулы, представленные
в табл. 2.
Таблица
2
-
Ячейка
Содержание
(формула)E5
=СУММПРОИЗВ(В5:D5;
$B$2:$D$2)E6
=СУММПРОИЗВ(В6:D6;
$B$2:$D$2)E7
=СУММПРОИЗВ(В7:D7;
$B$2:$D$2)
Шаг 4.
После создания таблицы с исходными
данными курсор устанавливается в ячейку
E3,
содержащую формулу для вычисления
целевой функции. Далее в меню Сервис
выбирается
команда Поиск
решения,
которая открывает диалоговое окно,
приведенное на рис. 3.
Рис. 3
В поле Установить
целевую ячейку
окна «Поиск решения», показанного на
рис. 3, должен
появиться адрес ячейки с формулой
целевой функции (в данном примере это
ячейка $E$3).
Затем в этом окне
(рис. 3) заполняются следующие поля этого
окна:
— в поле Равной
переключатель вида экстремума целевой
функции устанавливается в положение
максимальное
значение
(или минимальное
значение
при
соответствующей постановке задачи);
— в поле Изменяя
ячейки
указывается
диапазон ячеек со значениями переменных
задачи, выделяемый на рабочем листе
электронной таблицы (в примере это
ячейки $B$2:$D$2);
— в поле Ограничения
задаются
ограничения исходной задачи. Для этого
курсор устанавливается в поле ввода
ограничений и нажимается кнопка Добавить.
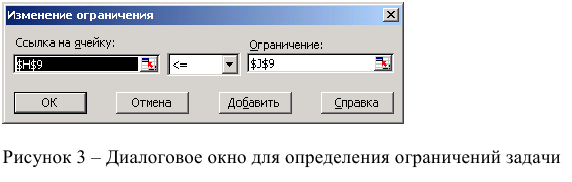
В результате
выводится диалоговое окно «Добавление
ограничения», показанное на рис. 4.
Рис. 4
В этом окне в поле
Ссылка на
ячейку
вводится
адрес ячейки
с формулой соответствующего ограничения
(например, для ограничения (1) это будет
ячейка E5),
а в поле Ограничение
указывается
предельное значение, которое может
принимать выбранное ограничение (в
данном примере правая часть ограничения
(1) находится в ячейке G5).
Следует заметить,
что заполнение полей Ссылка
на ячейку
и Ограничение
в окне «Добавление
ограничения» можно выполнить выделением
соответствующих ячеек рабочего листа
электронной таблицы.
Затем выбирается
вид отношения, связывающего левую и
правую части ограничения, что показано
на рис. 5.
Рис. 5
После нажатия
кнопки Добавить
в окне
«Добавление ограничения»
(или кнопки
ОК
для ввода
последнего ограничения) данное ограничение
попадает в список ограничений решаемой
задачи. С помощью кнопок Удалить
и Изменить
можно удалять
выделенные в списке ограничения или
вносить в них исправления.
Замечание.
В окне «Добавление
ограничения» можно указать, что все или
некоторые переменные должны принимать
только целые значения (рис. 5). Это
позволяет получать решения задач
целочисленного линейного программирования
(полностью или частично целочисленных).
Шаг 5.
После заполнения всех полей окна «Поиск
решения» нажимается кнопка Параметры
(рис. 3),
которая открывает диалоговое окно
«Параметры поиска решения», показанное
на рис. 6.
Рис. 6
В этом окне требуется
установить флажки Линейная
модель
для решения
задачи линейного программирования и
Неотрицательные
значения,
если такое
условие накладываются на все переменные
задачи.
Здесь (рис. 6) также
можно определить параметры процесса
решения: предельное время поиска решения,
максимальное количество итераций,
точность и т.п. Флажок Показывать
результаты
итераций
позволяет по шагам следить за поиском
решения. Флажок Автоматическое
масштабирование
включается
в том случае, когда разброс значений
переменных очень велик.
Шаг 6.
Задав необходимые параметры в окне
«Параметры
поиска решения»,
следует нажать на кнопку Выполнить
для поиска
решения задачи (рис. 3) в
окне «Поиск решения».
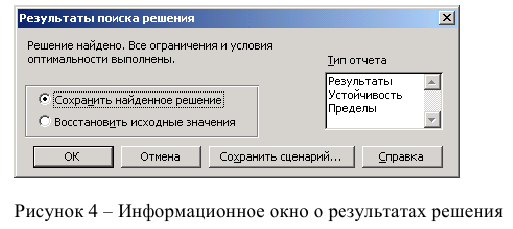
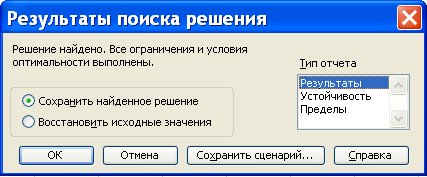
Если решение найдено, то на экран
выводится окно с соответствующим
сообщением (рис. 7).
Рис. 7
Полученные
результаты отображаются на рабочем
листе электронной таблицы, как это
показано на рис. 8. В частности, значения
переменных — в ячейках $B$2:$D$2,
значение целевой функции – в ячейке
E3.
Рис. 8
Таким образом,
получено оптимальное решение исходной
задачи в виде вектора
,
где,
и
,
для которого значение целевой функцииF
максимально и составляет F*
= 129825.
Результаты решения
задачи линейного программирования
также можно сохранить в виде отдельных
рабочих листов с именами Отчет
по результатам,
Отчет
по устойчивости
и Отчет
по пределам.
Для сохранения
результатов в виде отчетов необходимо
предварительно в поле Тип
отчета
выделить
требуемые типы отчетов (рис. 7). В этом
же окне можно отказаться от полученных
решений и восстановить исходные значения
переменных.
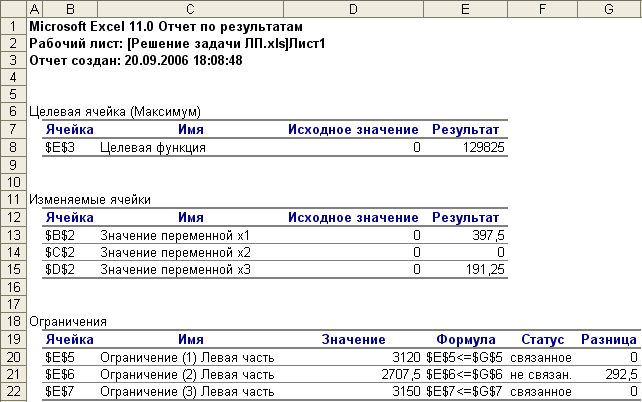
Отчет по результатам
для рассмотренной задачи показан
на рис. 9.
Рис. 9
В данном отчете
представлены оптимальное решение задачи
линейного программирования и его
расположение в области допустимых
решений. В графах Результат
выводятся
оптимальные значения целевой функции
F*
и переменных задачи
,
а также их значения для исходного
базисного решения, с которого начинался
поиск оптимального решения (графаИсходное
значение).
Состояние
ограничений (графа Статус)
характеризует расположение точки
в области допустимых решений. ГрафаРазница
показывает разности между значениями
левых и правых частей ограничений
(невязки). Для связанного ограничения
невязка равна нулю, что свидетельствует
о расположение точки
на границе области допустимых решений,
которая задается этим ограничением.
Если ограничение являются не связанным,
то оно не влияет на оптимальное решение.
Замечание.
В экономической интерпретации связанные
ограничения соответствуют дефицитным
ресурсам. Для не связанных ограничений
графа Разница
показывает оставшиеся объемы
неиспользованных не дефицитных ресурсов.
В рассмотренной задаче ограничения (1)
и (3) соответствуют комплектующим изделиям
и материалам, которые являются дефицитными
ресурсами. Ограничение (2) является не
связанным, т.е. не влияет на оптимальный
план производства продукции по критерию
максимальной прибыли. Это означает, что
второй ресурс (сырье) не использован в
объеме 292,5 ед.
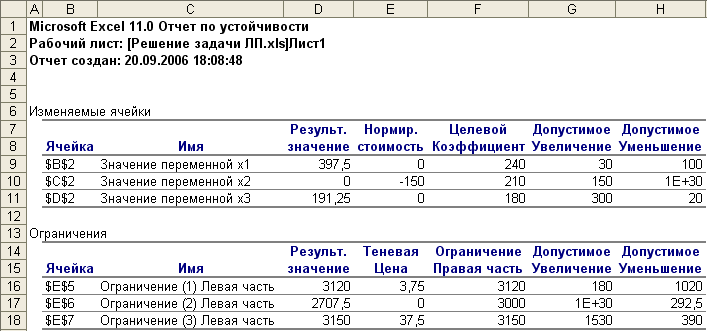
В
отчете по устойчивости (рис.
10) приведены
границы устойчивости переменных задачи
(графы Допустимое
увеличение
и Допустимое
уменьшение
коэффициентов целевой функции), а также
границы устойчивости теневых цен (т.е.
переменных двойственной задачи), в
пределах которых оптимальное решение
не изменяется. Большие
значения пределов (1Е+30)
означают фактическое
отсутствие соответствующих границ,
т.е. переменная может изменяться до
бесконечности.
Рис. 10
В графе Нормированная
стоимость
элемент во второй строке
(-150) показывает,
на сколько уменьшится значение функции,
если в решении переменную x2
увеличить на единицу. С другой стороны,
при допустимом увеличении коэффициента
функции при неизвестной x2
на 150 единиц значение этой переменной
не изменится, т.е. неизвестная x2
будет равна нулю, а если выйти за пределы
допустимого увеличения (коэффициент
при x2
увеличить более чем на 150), то неизвестная
x2
в решении будет больше нуля.
В
отчете
по пределам
(рис. 11) показаны нижние и верхние пределы
возможного изменения переменных (в
пределах области допустимых решений)
и соответствующие значения целевой
функции (графа Целевой
результат)
при этих изменениях. В частности, если
x1
= 0, а x2
и x3
остаются без изменений, то F
= 2400
+ 2100
+ 180191,25
= 34425; при x3
= 0 и неизменных x1
и x2
получим F
= 240397,5
+ 2100
+ 1800
= 95400.
Рис. 11
Соседние файлы в папке 3922
- #
- #
- #
- #
- #
- #
Ранее я писал, что для принятия решений с учетом ограничивающих факторов может использоваться линейное программирование. Напомню, что этот метод решает проблему распределения ограниченных ресурсов между конкурирующими видами деятельности с тем, чтобы максимизировать или минимизировать некоторые численные величины, такие как маржинальная прибыль или расходы.
При решении задач линейного программирования, во-первых, необходимо составить модель, то есть сформулировать условия на математическом языке. После этого решение может быть найдено графически (см., например, здесь), с использованием надстройки Excel «Поиск решения» (рассмотрено в настоящей заметке) или с помощью специализированных компьютерных программ (см., например, здесь).
Рассмотрим линейное программирование в Excel на примере задачи, ранее решенной графическим методом.
Задача. Николай Кузнецов управляет небольшим механическим заводом. В будущем месяце он планирует изготавливать два продукта (А и В), по которым удельная маржинальная прибыль оценивается в 2500 и 3500 руб., соответственно. Изготовление обоих продуктов требует затрат на машинную обработку, сырье и труд. На изготовление каждой единицы продукта А отводится 3 часа машинной обработки, 16 единиц сырья и 6 единиц труда. Соответствующие требования к единице продукта В составляют 10, 4 и 6. Николай прогнозирует, что в следующем месяце он может предоставить 330 часов машинной обработки, 400 единиц сырья и 240 единиц труда. Технология производственного процесса такова, что не менее 12 единиц продукта В необходимо изготавливать в каждый конкретный месяц. Необходимо определить количество единиц продуктов А и В, которые Николай доложен производить в следующем месяце для максимизации маржинальной прибыли.
Скачать заметку в формате Word, пример в формате Excel
1. Воспользуемся математической моделью построенной в упомянутой заметке. Вот эта модель:
Максимизировать: Z = 2500 * х1 + 3500 *х2
При условии, что: 3 * х1 + 10 * х2 ≤ 330
16 * х1 + 4 * х2 ≤ 400
6 * х1 + 6 * х2 ≤ 240
х2 ≥ 12
х1 ≥ 0
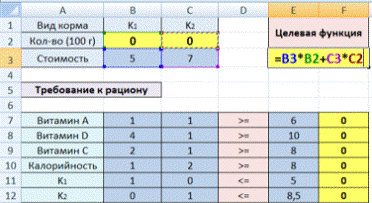
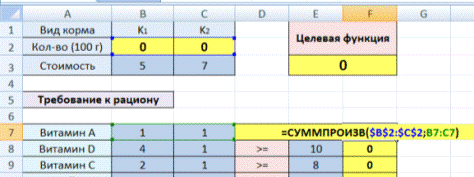
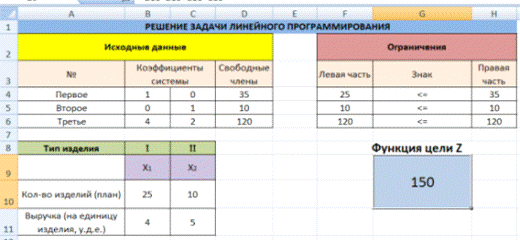
2. Создадим экранную форму и введем в нее исходные данные (рис. 1).
Рис. 1. Экранная форма для ввода данных задачи линейного программирования
Обратите внимание на формулу в ячейке С7. Это формула целевой функции. Аналогично, в ячейки С16:С18 введены формулы для расчета левой части ограничений.
3. Проверьте, если у вас установлена надстройка «Поиск решения» (рис. 2), пропустите этот пункт.
Рис. 2. Надстройка Поиск решения установлена; вкладка «Данные», группа «Анализ»
Если надстройки «Поиск решения» вы на ленте Excel не обнаружили, щелкните на кнопку Microsoft Office, а затем Параметры Excel (рис. 3).
Рис. 3. Параметры Excel
Выберите строку Надстройки, а затем в самом низу окна «Управление надстройками Microsoft Excel» выберите «Перейти» (рис. 4).
Рис. 4. Надстройки Excel
В окне «Надстройки» установите флажок «Поиск решения» и нажмите Ok (рис. 5). (Если «Поиск решения» отсутствует в списке поля «Надстройки», чтобы найти надстройку, нажмите кнопку Обзор. В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.)
Рис. 5. Активация надстройки «Поиск решения»
После загрузки надстройки для поиска решения в группе Анализ на вкладке Данные становится доступна команда Поиск решения (рис. 2).
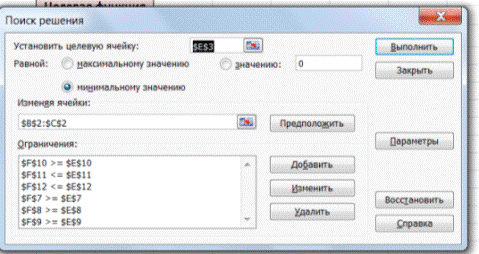
4. Следующим этапом заполняем окно Excel «Поиск решения» (рис. 6)
Рис. 6. Заполнение окна «Поиск решения»
В поле «Установить целевую ячейку» выбираем ячейку со значением целевой функции – $C$7. Выбираем, максимизировать или минимизировать целевую функцию. В поле «Изменяя ячейки» выбираем ячейки со значениями искомых переменных $C$4:$D$4 (пока в них нули или пусто). В области «Ограничения» с помощью кнопки «Добавить» размещаем все ограничения нашей модели. Жмем «Выполнить». В появившемся окне «Результат поиска решения» выбираем все три типа отчета (рис. 7) и жмем Ok. Эти отчеты нужны для анализа полученного решения. Подробнее о данных, представленных в отчетах, можно почитать здесь.
Рис. 7. Выбор типов отчета
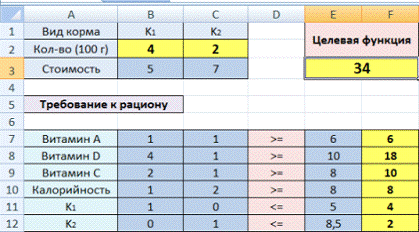
На основном листе появились значения максимизированной целевой функции – 130 000 руб. и изменяемых параметров х1 = 10 и х2 = 30. Таким образом, для максимизации маржинального дохода Николаю в следующем месяце следует произвести 10 единиц продукта А и 30 единиц продукта В.
Если вместо окна «Результат поиска решения» появилось что-то иное, Excel`ю найти решение не удалось. Проверьте правильность заполнения окна «Поиск решения». И еще одна маленькая хитрость. Попробуйте уменьшить точность поиска решения. Для этого в окне «Поиск решения» щелкните на Параметры (рис. 8.) и увеличьте погрешность вычисления, например, до 0,001. Иногда из-за высокой точности Excel не успевает за 100 итераций найти решение. Подробнее о параметрах поиска решения можно почитать здесь.
Рис. 8. Увеличение погрешности вычислений
Изучив алгоритмы «ручного» решения задач линейного программирования, полезно познакомиться и со способом упростить этот процесс. Ясно, что чем сложнее задача, чем больше в ней переменных и условий, тем утомительнее и дольше ее решать. В таких случаях удобно использовать специальные математические пакеты, или доступную многим программу MS Excel (версии 2003, 2007, 2010, 2013 и др.).
Решить задачи линейного программирования в Excel достаточно просто:
- составить математическую модель задачи,
- внести исходные данные задачи и ограничения,
- выделить место под ячейки решения и целевую функцию, ввести ее формулу,
- запустить надстройку Поиск решения,
- установить нужные параметры решения и запустить выполнение.
Программа подберёт оптимальное решение и покажет его в нужных ячейках, вычислит значение целевой функции. При необходимости можно построить отчеты для анализа решения задачи.
Подробнее все эти этапы с пояснениями и скриншотами разобраны ниже в примерах на разных задачах линейного программирования — изучайте, ищите похожие, решайте.
Помогаем студентам: Работы по линейному программированию на заказ
Лучшее спасибо — порекомендовать эту страницу
Линейное программирование: примеры в Excel
Задача 1. Построить математическую модель задачи и решить её средствами Excel. Записать сопряжённую задачу. Провести анализ и сделать выводы по полученным результатам.
Для производства столов и шкафов мебельная фабрика использует различные ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в таблице.
Определить, сколько столов и шкафов фабрике следует выпускать, чтобы прибыль от реализации была максимальной.
Задача 2. Цех производит 8 различных видов деталей для двигателей A, B, C1, C2, C3, D, E6, F имея в своем распоряжении перечисленный ниже парк из 7 видов универсальных станков: 2 шт. -ADF, 3 шт. -SHG, 3 шт. -BSD, 1 шт. -AVP, 1 шт. -BFG, 3 шт. -ABM, 2 шт. -RL.
Время, требуемое для обработки единицы каждого продукта на каждом станке, вклад в прибыль от производства единицы каждого продукта и рыночный спрос на каждый продукт за месяц даны в таблице.
Цех работает 12 часов в день. Каждый месяц содержит 26 рабочих дней. Для упрощения задачи считаем, что возможен произвольный порядок обработки деталей на различных станках.
Составьте оптимальный план производства.
Определите, производство каких продуктов лимитировано рынком, и каких – техническими возможностями цеха. Какие машинные ресурсы должны быть увеличены в первую очередь, чтобы добиться максимального увеличения прибыли (при заданных потребностях рынка)?
Есть ли продукт, который невыгодно производить? Почему? Что нужно изменить, чтобы все продукты стало выгодно производить?
Может пригодиться: транспортные задачи в Excel
Задача 3. Необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ тиамина Т и ниацина Н. Пищевая ценность рациона (в калориях) должна быть не менее заданной. Смесь для цыплят изготавливается из двух продуктов — К и С. Известно содержание тиамина и ниацина в этих продуктах, а также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в таблице.
Задача 4. Фирма «Компьютер-сервис» поставляет компьютеры под ключ четырех базовых комплектаций: «домашний», «игровой», «офисный» и «экстрим». Известны средние затраты времени на сборку, проверку и подключение компьютеров. Каждый компьютер приносит определенный уровень прибыли, но спрос ограничен. Кроме того, в плановом периоде ограничен ресурс человеко-часов, отведенных на выполнение каждой производственной операции. Определить, сколько компьютеров каждого типа необходимо произвести в плановом периоде, имея целью максимизировать прибыль.
Задача 5. На лесопилку поступают доски длиной 10 м. По контракту лесопилка должна поставить клиенту не менее 100 досок длиной 5 м, не менее 200 досок длиной 4 м и не менее 300 досок длиной 3 м. Как работникам лесопилки выполнить условия контракта, разрезав наименьшее количество досок?
Помогаем с контрольными по линейному программированию
Задача 6. Компания «Евростройтур» организует экскурсионные автобусные туры по странам Европы. Компания получила 4 новых автобуса и предполагает направить их на маршруты во Францию, Италию, Чехию и Испанию.
Каждый автобус обслуживают 2 водителя. Компанией приглашены 8 водителей, в различной степени знакомых с дорогами европейских стран (в % от экскурсионного маршрута).
Необходимо распределить водителей так, чтобы общий показатель освоения маршрутов был максимальным.
Задача 7. Решить задачу методом ветвей и границ, решая отдельные задачи линейного нецелочисленного программирования с помощью функции «Поиск решения» в Microsoft Excel (в случае, если первая же задача ЛП выдает целочисленное решение, не позволяя ветвить задачу, немного изменить начальные условия).
Состав еды рядовых регламентируется верховной ставкой главнокомандующего, которая устанавливает нижние нормы питания в сутки по основным компонентам: 1500 килокалорий, 100 г белков, 280 г углеводов, 90 г жиров, 1 кг воды. На складах есть 4 вида продуктов, которые выдают защитникам Родины сухим пайком: лимонад, тушенка в маленьких банках, унифицированные наборы горбушек и пирожки с ежевикой. Стоимость этих четырех продуктов соответственно 12 руб., 34 руб., 3 руб. и 20 руб. Какова минимальная сумма, которую должен затратить прапорщик на питание одного солдата?
Задача 8. Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить a11 кг сырья первого типа, a21 кг сырья второго типа, a31 кг сырья третьего типа.
На изготовление единицы Изделия 2 требуется затратить a12 кг сырья первого типа, a22 кг сырья второго типа, a32 кг сырья третьего типа.
Производство обеспечено сырьем каждого типа в количестве b1 кг, b2 кг, b3 кг соответственно.
Рыночная цена единицы Изделия 1 составляет c1 тыс. руб., а единицы Изделия 2 — c2 тыс.руб.
Требуется:
1) построить экономико – математическую модель задачи;
2) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи графического метода решения задачи линейного программирования.
3) составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи табличного симплекс – метода решения задачи линейного программирования.
4) составить план производства изделий, обеспечивающий максимальную выручку от их реализации, используя надстройку «Поиск решения» в среде MS EXCEL.
Полезные ссылки
|
|
Решение типовых задач линейного программирования в табличном процессоре MS Excel
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
. СУЩНОСТЬ ЗАДАЧИ ОПТИМИЗАЦИИ
.1 Немного истории
.2 Основные понятия
.3 Постановка задачи линейного
программирования
. ТИПОВЫЕ ЗАДАЧИ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
.1 Задача о рационе питания (задача
о диете)
.2 Задача о составлении плана
производства
.3 Задача о раскрое материалов
.4 Транспортная задача
. ПРИКЛАДНЫЕ ЗАДАЧИ ОПТИМАЛЬНОГО
РАСПРЕДЕЛЕНИЯ РЕСУРСОВ
.1 Характеристика программного
средства
.2 Решение задачи о рационе питания
в среде MS Excel
.3 Решение задачи о плане
производства в среде MS Excel
.4 Решение задачи о раскрое в среде
MS Excel
.5 Решение транспортной задачи в
среде MS Excel
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
ВВЕДЕНИЕ
Линейное программирование часть математического
программирования, посвященная теории и методам решения экстремальных задач,
нахождения минимума или максимума функции цели, характеризующихся линейной
зависимостью между неизвестными переменными.
Применение методов линейного программирования
актуально в настоящее время, так как использование математических моделей
является важным направлением совершенствования планирования и анализа
деятельности фирм. Формулировка задачи в виде математической модели позволяет
конкретизировать информацию, сделать задачу более наглядной, создавать и
моделировать варианты, выбирать оптимальные, наиболее рациональные решения из
возможных альтернатив.
Актуальность курсовой работы связана с тем, что
линейное программирование широко используется в решении оптимизационных,
управленческих, логистических, распределительных и некоторых других видах
задач, в которых выявляется линейная зависимость между переменными. К тому же
линейное программирование — это наиболее разработанный раздел математического
программирования, а значит один из наиболее востребованных, в настоящее время.
Целью курсовой работы является разработка
практических рекомендаций по решению некоторых типовых задач линейного
программирования в табличном процессоре.
Для достижения поставленной цели необходимо
решить следующие задачи:
— изучить и раскрыть необходимый
теоретический материал;
— провести анализ некоторых типовых
задач линейного программирования;
— проанализировать информационные
технологии, подходящие для расчета необходимых показателей;
— на примере некоторых задач
сформулировать экономико-математические модели;
— найти оптимальное решение задач с
помощью средств табличного процессора.
В работе применяются методы анализа данных по
тематике, обобщение и классификация изученного материала.
Теоретическая значимость работы выражается в
системном представлении классических задач линейного программирования.
Практическая значимость выражается в
рекомендациях по решению задач линейного программирования посредством
информационных технологий.
Структура курсовой работы включает в себя
введение, три параграфа, заключение и список использованных источников.
1. СУЩНОСТЬ ЗАДАЧИ ОПТИМИЗАЦИИ
1.1 Немного истории
Большинство задач, которые приходится решать
человеку, в процессе своей практической деятельности, являются
многовариантными, то есть предполагают наличие нескольких вариантов решения.
Всю свою жизнь человечество стремится отыскать наилучшее решение при имеющихся
ограничениях возможностей и ресурсов. Долгое время при этом он руководствовался
лишь здравым смыслом, опытом, интуицией.
На этапе индустриализации произошло резкое
увеличение масштабов производства, появилась необходимость решать задачи
управления, планирования, анализа альтернативных вариантов, выработки прогнозов
на будущее и многие другие. Очевидно, что увеличился объем обрабатываемой
информации, данных которые необходимо учитывать при решении задач такого рода.
Также нужно учитывать взаимосвязь между, казалось бы, отдельными, не связанными
между собой явлениями (загрязнение окружающей среды и промышленное
производство; характер взаимоотношений в коллективе и производственные
показатели, выполнение плана; химизация продуктов питания и уровень
онкологических заболеваний у населения и др.).
Однако, с развитием компьютерной и
вычислительной техники появилась возможность решать задачи, требующие большого объема
арифметических вычислений. Стало возможным привлечение математического
аппарата, к решению задач, решаемых ранее интуитивно и приблизительно. Стали
создаваться принципиально новые способы решения задач.
Таким образом, в 30-е годы XX в., появилась новая
математическая дисциплина — математическое программирование.
Математическое программирование — это раздел
математики, занимающийся анализом многомерных экстремальных задач управления и
планирования и разработкой теории и численных методов их решения [8].
Линейное программирование является наиболее
изученным разделом математического программирования. Термин линейного
программирования появился в работах Т. Купманса и Дж. Данцига в 1951 г[4].
1.2 Основные понятия
Математическое программирование — раздел математики,
разрабатывающий теоретическое обоснование и способы решения многомерных
экстремальных задач с ограничениями, т. е. задач на экстремум функции
нескольких переменных с ограничениями на область допустимых значений
неизвестных переменных.
Имеющиеся ресурсы представляются в виде системы
ограничений. Функцию, экстремальное значение которой нужно найти называют
целевой, показателем эффективности или критерием оптимальности. Именно эти две
составляющие являются необходимыми компонентами математической модели задачи.
В большинстве случаев модель в некотором роде
заменяет сам исследуемый объект, то есть оригинал. При решении задач вместо
исходного объекта (оригинала, словесного описания) используется его модель, в
частности математическая. Модель являлась представлением объекта в некоторой
форме, отличной от формы его реального существования.
Математическая модель задачи — это отображение
исследуемого объекта в виде систем неравенств и уравнений, функций и т. д.
Модель задачи математического программирования
включает в себя:
— совокупность неизвестных переменных,
оказывая влияние на которые, систему можно оптимизировать. Это так называемый
вектор управления, план задачи или, проще говоря, вектор решения;
— функцию цели, в некоторых источниках
она может иметь название целевой функции, показателя эффективности или же
критерия оптимальности. С помощью данного показателя эффективности
представляется возможным нахождения оптимального варианта решения задачи из
нескольких возможных решений. Наилучший план решения задачи доставляет функции
цели минимальное, либо максимальное значение. Это могут быть затраты на
грузоперевозки, количество единиц материала, доход от продажи товаров,
количество выпущенной продукции и многое другое.
Любые имеющиеся ресурсы, так или иначе ограничены,
к тому же в процессе производства, потребность в этих ресурсах сохраняется.
Именно из этого условия следуют вышеперечисленные компоненты задачи
математического программирования.
Ресурсы могут быть не только материальными или
финансовыми, но и трудовыми, техническими либо, же в качестве ресурса может
выступать научный и технологический потенциал.
Математически ограничения в ресурсах выражаются
с помощью систем уравнений или неравенств. Данная система неравенств образует
область экономических возможностей или так называемую область допустимых
решений. План, удовлетворяющий системе ограничений задачи, называется
допустимым. Допустимый план, доставляющий функции цели экстремальное значение,
называется оптимальным[13].
Модели линейного программирования широко
используются при оптимизации процессов практически во всех отраслях:
— при составлении плана производства;
— при разделении заданий и отдельных
технологических процессов по исполнителям;
— при нахождении оптимального набора
изготавливаемой продукции;
— при распределении работ по временным
промежуткам;
— при определении маршрутов
грузопотоков между потребителями и поставщиками;
— при составлении плана товарооборота
и порядка его распределении и т. д.
Наибольшее распространение методы и модели
линейного программирования получили при решении задач экономии ресурсов
(определение рациона питания, раскрой материалов, назначения), транспортных и
производственных задач.
1.3 Постановка задачи линейного
программирования
Линейное программирование — метод математического
программирования, отыскания экстремума функции, с определенными ограничениями,
выраженных в виде системы линейных неравенств или уравнений. Здесь линейность
заключается в том, что если изображать все ограничения и целевую функцию на
системе координат, то графически они будут представлены в виде прямых линий
[10].
Суть решения задачи линейного программирования
включает необходимость нахождения таких условий, которые будут приводить
функцию цели к минимуму или максимуму, то есть к экстремуму.
Условия задачи представлены в виде системы
линейных уравнений, показывающих ограничения имеющихся в наличии ресурсов:
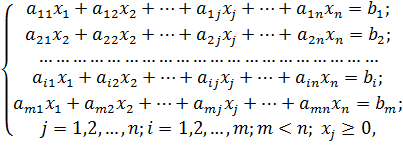
где xj— неизвестные переменные,
содержащие решение поставленной задачи;ij и bj—
известные постоянные величины, характеризующие условия задачи.
Целевая функция задается в виде:
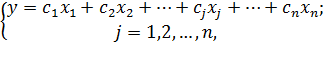
где cj—
постоянные коэффициенты стоимости.
Ограничения могут быть, заданы не только в виде
уравнений, но и в виде системы неравенств. В данном случае, для того чтобы
привести систему неравенств к виду (1.1), нужно в каждое линейное ограничение
ввести добавочные неотрицательные неизвестные: xn+1,
xn+2,
…,xn+m.
Общая математическая формулировка задачи
соответствует условиям (1.1) и (1.2).
Первая строка системы уравнений (1.1)
соответствует выражению:
,
где a11
—
количество единиц ресурсов вида 1 на первом предприятии; a12
—
количество единиц ресурсов вида 1 на втором предприятии и т.п.;b1 —
общий объем ресурсов вида 1(для всех предприятий); x1, x2
и т.д. — искомое количество предприятий типов 1, 2 и т.д.
Вторая строка системы уравнений (1.1) содержит
аналогичные величины для ресурсов вида 2 и т.д. Функция цели соответствует
формуле (1.2). Требуется обратить в минимум величину
,
где cj— показатель, характеризующий
издержки предприятий.
Пусть m — суммарное число разных типов ресурсов,
которые есть у собственника, а n — число видов предприятий, между которыми эти
ресурсы распределены. При этом известно, какое количество однородных ресурсов
различного вида (i=1, 2, …,m)
может быть реализовано на каждом из предприятий данного типа (j=1,2,…,n),
а также общее количество ресурсов данного вида (bi).
Известно также относительное значение издержек на каждом из предприятий(cj).
Задача заключается в том, чтобы наилучшим
образом разделить имеющиеся ресурсы по предприятиям, то есть найти неизвестные
величины xj.
Таким образом, особенностями линейного
программирования являются:
— линейная зависимость функции цели;
— область допустимых значений
устанавливает система линейных уравнений или неравенств.
2. ТИПОВЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Чтобы понять, откуда берутся задачи линейного
программирования, проанализируем некоторые, уже ставшие классическими, модели
подобных задач.
Основные виды задач линейного программирования:
— задача об ассортименте;
— задача о диете (рационе питания, о
смесях);
— транспортная задача;
— задача об оптимальном использовании
имеющихся мощностей;
— задача о назначениях и др.
Обязательным условием для решения задачи
линейного программирования является построение экономико-математической модели
исследуемой экономической ситуации.
.1 Задача о рационе питания (задача о диете)
Задача о смесях появляется при составлении
рациона питания животных, удовлетворяющего конкретным медицинским требованиям
так, чтобы затраты на «меню» были сведены к минимуму [13].
Допустим, что у нас в наличии есть продуктов
питания (зерно, комбикорм, сено и др.). Обозначим данные продукты с помощью.
Пусть, —
это стоимость единицы веса (например, цена килограмма) продукта Fi.
Правильная диета обязана приносить животному пользу, то есть обеспечивать его
необходимыми элементами, такими как белки, углеводы, кальций, калий, магний,
фосфор и др. Обозначим данные элементы через .
Тогда можно составить таблицу 1 указывающую, на то, какой объем каждого элемента
имеется в единице веса любого продукта.
Таблица 1 — Содержание нужных веществ в каждом
виде продукта
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получается, что величина aij
это количество i-го элемента, присутствующего в единице веса j-го продукта.
Матрица называется
матрицей питательности.
Вектор решения для рациона питания должен
показать, какое количество xi
i-го продукта должно содержаться в меню«исследуемого» животного за день (месяц,
квартал, год). Он означает, что за определенный промежуток времени животное
должно быть обеспеченоx1единиц
первого продукта, x2
единиц второго, …, xn единиц n-го
продукта.
Какие же требования могут быть предъявлены к
рациону? Выполнение конкретных медицинских требований. Они состоят в том, что
за определенный срок животное должно получить не менее необходимого количества
каждого элемента. Обозначим через bj, то минимально необходимое
количество j-го элемента, которое должно получить животное. В таком случае,
рацион питания должен соответствовать полученным ограничениям (2.1).
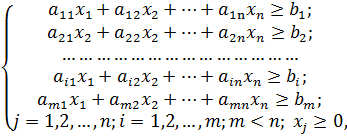
Тогда стоимость всей диеты будет составлять:
(2.2)
где —
цена единицы веса i-го продукта.
Очевидно, что затраты должны быть как можно
меньше. Поэтому задача приобретает такой вид: найти рацион (2.2) минимальной
стоимости при выполнении всех ограничений (2.1). Математически это выглядит
так:
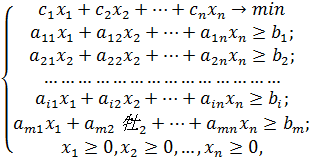
Таким образом, очевидно что:
— реальная задача приобрела строгую
математическую форму;
— функция цели (стоимость питания)
является линейной функцией;
— ограничения на значения переменных x1,
x2,
…, xn имеют вид системы
линейных неравенств.
.2 Задача о составлении плана производства
Проанализируем производственную деятельность
некоторой структурной единицы (филиал, отдел, подразделение и др.).
Предположим, что конкретная производственная единица может выпускать некоторые
продукты
Для выпуска данных товаров необходимо
использовать различные материальные ресурсы. Пусть количество этих ресурсов
будет m; обозначим их через
Технологией производства товара назовем
набор чисел показывающий,
какое количество-го ресурса необходимо для производства единицы товара .
Данные можно представить в виде таблицы 2 — технологической матрицы, которая
полностью описывает технологические потребности производства и элементами
которой являются числа aij.
Таблица 2 — Технологическая матрица
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предположим, в наличии есть
запасов каждого ресурса и планируется произвести единиц
-го ресурса. Так как невозможно превысить имеющийся лимит ресурсов, то план
производства должен
удовлетворять ограничениям:
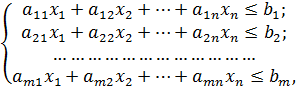
Обязательно должно соблюдаться условие
неотрицательности переменных :
Очевидно,
что прибыль, должна быть, как можно больше. Поэтому стоящая задача составления
плана производства приобретает вид:
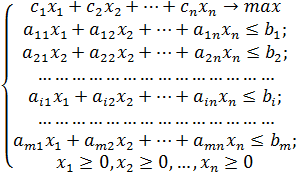
В итоге, снова получилась линейная функция цели,
и ограничения имеющихся ресурсов так же имеют характер линейных неравенств, то
есть, опять имеем дело с задачей линейного программирования.
.3 Задача о раскрое материалов
В нахождении наиболее рационального способа
раскроя имеющегося материала, (металлические стержни, бумажное полотно, ткань и
др.) состоит задача оптимального раскроя.
Нередко поиск оптимального способа раскроя
осуществляется в два этапа.
На начальном этапе находятся всевозможные
рациональные способы раскроя материала.
На II
этапе решаются задачи рациональных способов раскроя.
— Нахождение рациональных способов
раскроя материала
В задачах данного вида рассматриваются так
называемые рациональные (оптимальные по Парето) способы раскроя. Пусть, из
единицы материала можно изготовить заготовки нескольких типов.
При увеличении числа заготовок одного вида за
счет сокращения числа заготовок другого вида, способ раскроя называется
рациональным.
Пусть—
индекс типа заготовки ();
— номер способа
раскроя единицы материала ();
— количество
заготовок вида , полученных при
раскрое единицы материала -м способом.
Математически представить определение
рационального способа раскроя материала можно в таком виде: способ раскроя называется
рациональным, если для любого другого способа раскроя из
соотношений , следуют
соотношения [5].
— Определение интенсивности
использования рациональных способов раскроя.
Обозначения:
— индекс материала
();
— номер типа
заготовки ();
— индекс способа
раскроя единицы материала();
— количество
заготовок вида , полученных при
раскрое единицы -го материала -м способом;
— количество
заготовок вида в комплекте,
отправляемому заказчику;
— количество
материала-го вида;
— количество
единицу-го материала, раскраиваемых по -му способу
(интенсивность использования способа раскроя);
— величина отхода,
полученного при раскрое единицы -го материала по -му
способу;
— число комплектов
заготовок различного вида.
Имеется несколько типов моделей задач о раскрое
материала:
— Модель I(раскрой,
с минимальным расходом материалов):
где (2.6) — функция цели (минимум количества
используемых материалов);
(2.7) — система ограничений, определяющих
количество заготовок, необходимое для выполнения работы;
(2.8) — условия неотрицательности переменных.
Модель II
(раскрой, с минимальными отходами материалов):
где (2.9) — функция цели (минимум отходов при
раскрое материалов);
(2.10) — система ограничений, определяющих
количество заготовок, необходимое для выполнения заказа;
(2.11) — условия неотрицательности переменных.
— Модель III
(раскроя материала с учетом комплектации):
где (2.12) — функция цели (максимум комплектов,
включающих заготовки различных видов);
(2.13) — ограничения по количеству материалов;
(2.14) — система ограничений, определяющих количество
заготовок, необходимое для формирования комплектов;
(2.15) — условия неотрицательности переменных.
Рассмотрим несколько подробнее задачу о раскрое
материала в общем виде.
Пусть на обработку поступает a единиц сырьевого
материала одного вида (например, a листов картона одинаковых размеров). Из них
необходимо изготовить комплекты, в каждый из которых входит n видов изделий в
количестве, пропорциональном числам Имеется
m способов обработки данного материала, то есть известны величины определяющие
количество единиц j-х заготовок при i-м
способе раскроя [18].
Установить план раскроя, при котором количество
комплектов будет максимально. Согласно условиям задачи имеем, таблицу 3:
Таблица 3 -Способы раскроя
|
Вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
Пусть xi—
количество единиц сырьевого материала, раскраиваемого i-м вариантом
Тогда количество изделий 1-го вида равно:
Принимая во внимание условие комплектности,
имеем:
где y — количество комплектов.
Аналогичные равенства можно записать и для всех
остальных типов изделий, то есть условие комплектности приводит к системе
ограничений:
.
Очевидно, (на
раскрой поступает a единиц сырьевого материала), а также
Цель задачи — максимизировать количество
комплектов:
Итак, приходим к математической модели задачи о
раскрое:
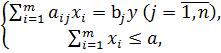
Чтобы выразить целевую функцию через переменные достаточно
воспользоваться любым из соотношений:
.4 Транспортная задача
Проанализируем задачу, в которой речь идет о
рациональной перевозке некоторого однородного продукта от производителей к
потребителям, то есть транспортную задачу.
Пусть имеется m пунктов производства однородного
продукта (добыча руды в карьерах, сборка бытовой техники, изготовление
кондитерских изделий и др.) и n пунктов потребления этого продукта. Мощности
пунктов производства составляют единиц однородного
продукта, а потребности каждого j-го пункта потребления равны единиц.
Известны затраты на перевозку едиицы
продукта от i-го поставщика j-му потребителю. Составить такой план перевозок,
при котором суммарные затраты на все перевозки были бы наименьшими. Пусть спрос
и предложение совпадают, то есть
Данную транспортную задачу называют закрытой или
сбалансированной. При этом предполагается, что вся продукция от поставщиков
будет вывезена и спрос каждого из потребителей будет удовлетворен.
Составим математическую модель задачи. Обозначим
через —
количество продукта, перевозимого из i-го пункта производства в j-й
пункт потребления. Тогда матрица: —
план перевозок.
Матрицу называют
матрицей затрат (тарифов).
Составим таблицу 4, в которую внесем все
исходные данные и перевозки xij.
Таблица 4 — Транспортная таблица
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2n |
|
|
|
|
|
Предположим, что транспортные затраты прямо
пропорциональны количеству перевозимого продукта. Тогда суммарные затраты
выразятся функцией цели:
которую необходимо минимизировать при
ограничениях: (весь продукт из
каждого i-го () пункта должен
быть, вывезен полностью),(спрос каждого j-го
()
потребителя должен быть, полностью удовлетворен).
Из условия задачи следует, что все .
Итак, математическая модель сбалансированной
транспортной задачи имеет вид:
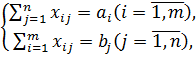
3. ПРИКЛАДНЫЕ ЗАДАЧИ ОПТИМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
РЕСУРСОВ
На основе, рассмотренной теоретической части,
необходимо составить математические модели некоторых задач линейного
программирования и найти оптимальное решение для каждой из них, с помощью
приложения MS Excel
2007.
.1 Характеристика программного средства
Для решения поставленных задач и наглядного
представления их решений была важна возможность использования математических
формул и непосредственно функции «Поиск решения».
Надстройка «Поиск решения» позволяет
найти оптимальное (максимальное или минимальное) значение для формулы
<javascript:AppendPopup(this,’xldefFormula_2_2′)>, содержащейся в целевой
ячейке. Поиск решения» работает с диапазоном ячеек, связанных с формулой в
целевой ячейке. Чтобы получить оптимальный результат по формуле из целевой
ячейки, «Поиск решения» изменяет значения в ячейках, выбранных как изменяемые.
Для конкретизации значений применяются ограничения (система неравенств),
которые могут ссылаться на другие ячейки (группы ячеек), влияющие на формулу
для ячейки с записанной целевой функцией[3].
Именно этими возможностями обладают
известные табличные процессоры Microsoft Office Excel 2007 и Open
Office Calc. В отличие от Open Office Calc MS Excel является более
распространенным и привычным для обычного пользователя, имеет более широкий
спектр поддерживаемых форматов файлов. При использовании MS Excel возникновение
несовместимости с другими программы в разы меньше, чем у Open Office. Так же в
MS Excel есть встроенный язык программирования — Visual Basic for Applications. Плюс ко
всему вышеперечисленному данное программное средство обладает более
функциональным и интуитивно понятным интерфейсом.
Надстройка «Поиск решения» в Open
Office Calc немногим отличается от похожей надстройки в MS Excel. В
последнее время эти два табличных редактора уже стали практически идентичны по
функциональному набору. Хотя стоит признать, что Calc все же уступает
конкуренту именно в наборе «Пакета анализа»[19].
Таким образом, для решения
поставленных задач использовалось программное средство Microsoft Office Excel 2007 из
пакета прикладных программ Microsoft Office.
.2 Решение задачи о рационе питания
в среде MS Excel
линейное программирование табличный
процессор
Постановка задачи:
Необходимо составить наименее затратный рацион
питания поросят, содержащий необходимое количество витаминов А, C и D.
Пищевая ценность рациона питания (в калориях) должна быть не менее необходимой.
Данная смесь изготавливается из двух видов кормов — К1 и К2.
Причем, корма вида K1 в рационе не должно быть использовано более
0,5 кг. Аналогично для корма K2
— не более 0,85 кг. Исходные данные для дальнейших расчетов приведены в таблице
5.
Таблица 5 — Содержание витаминов в кормах
|
Содержание |
Содержание |
Потребность, |
|
|
Витамин |
10 |
10 |
60 |
|
Витамин |
40 |
10 |
100 |
|
Витамин |
20 |
10 |
80 |
|
Энергетическая |
100 |
200 |
800 |
|
Стоимость |
5 |
7 |
Решение:
Построим математическую модель. За обозначим
количество корма К1, аналогично за —
объем К2.Исходя из условия задачи и
—
неотрицательные значения. Целевая функция будет стремиться к минимуму т.к.
расходы, с учетом всех необходимых условий, должны быть как можно меньше.
На основании исходных данных необходимо
составить систему ограничений. Для простоты восприятия почти все неравенства
можно сократить на положительное число, эти математические действия никак не
повлияют на конечный результат.
Из названий столбцов таблицы 5 ясно, что порции
кормов составляют по 100 грамм, а ограничение по количеству в условии задачи
дано в килограммах. Следовательно, необходимо их привести в ту же систему, что
и остальные неравенства. 0,5 кг это 500 г, а 0,85 кг — 850 г. Таким образом, .
Итак, если рассматривать всю совокупность
ограничений и целевую функцию, то математическая модель исходной задачи, примет
вид:
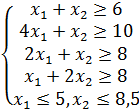
Задачу линейного программирования можно решить
как графически, так и симплекс-методом. В данном случае, воспользуемся пакетом
прикладных программ Microsoft Office, в частности MS
Excel, надстройкой
«Поиск решения».
Создадим форму для ввода данных, так решение
задачи будет представлено более наглядно, рисунок 1.
Рисунок 1 — Форма ввода данных в задаче о диете
Ячейки B3 и C3 отведены для переменных ,
пока они обнулены, но в дальнейшем они будут являться изменяемыми ячейками т.к.
именно эти значения влияют на функцию цели. В ячейку E3 введена формула для
целевой функции, которая будет стремиться к минимальному значению. В диапазоне
ячеек F7:F12 можно применить математическую функцию «Сумму произведений»
(СУММПРОИЗВ). Первый массив для всех неравенств, следовательно, его нужно
отметить знаком «$», как абсолютную ссылку, чтобы при копировании в другие
ячейки адрес этих ячеек не изменялся. Использование данной функции представлено
на рисунке 2.
Рисунок 2 — Введение формул
Далее, используем надстройку «Поиск решения».
Вызвать ее можно выбрав вкладку «Данные», закладку «Анализ». В диалоговом окне
«Поиска решения», рисунок 3, вводим ячейку цели функции, изменяемые ячейки и
все ограничения в виде неравенств, так же отмечаем маркером, что целевая
функция принимается равной минимальному значению.
Рисунок 3 — Диалоговое окно надстройки «Поиск
решения»
После нажатия кнопки «Выполнить» на экране
появляется решение задачи линейного программирования, рисунок 4.
Рисунок 4 — Результат работы «Поиска решения»
Таким образом, минимальное значение функции цели
,
то есть для составления оптимального суточного рациона питания, с минимальными
затратами и содержанием всех витаминов в полном объеме, нужно взять 400 грамм
корма К1и 200 грамм корма К2. При этом стоимость данных
витаминных добавок будет составлять 34 денежные единицы.
.3 Решение задачи о плане производства в среде
MS Excel
Постановка задачи:
Необходимо произвести изделия двух типов. Для их
изготовления имеется 120 кг алюминия. На изделиеI
типа расходуется 4 кг алюминия, а на изделиеII
типа — 2 кг. Составить план выпуска изделий, обеспечивающий получение
наибольшей прибыли от продажи изделий. Стоимость изделия I
типа установлена 4условные денежные единицы, а изделия II
типа — 5условных денежных единиц, причем изделий I
типа требуется изготовить не более 35, а изделий II
типа — не более 10.
Решение:
Обозначим количество изделийI
типа как ,
а количество, производимых по плану, изделий II
типа —.
Логично предположить, что Прибыль
от продажи изделий составит
Необходимо подобрать такой план производства,
при котором прибыль будет максимальна, то есть.
Также при составлении оптимального плана
производства нельзя не учитывать ограничения по имеющемуся ресурсу. При
производстве изделий I
типа расходуется (кг). В то время,
на производство изделий II типа используется (кг)
алюминия.Таким образом, суммарный расход алюминия составляет(кг).
Данная величина не должна превышать запасы алюминия в количестве 120 кг. В
итоге получаем неравенство:
Изделий I
типа в плане выпуска продукции должно быть не более 35 штук, то есть.
Аналогично для изделий II
типа: ,
так как по условию этих изделий должно быть не более 10.
Таким образом, математическая модель задачи
состоит из целевой функции и системы ограничений:
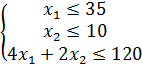
Решим задачу линейного программирования с
помощью программы MSExcel.
Для этого необходимо выполнить следующие шаги:
) создать форму для ввода исходных данных
задачи, изображенную на рисунке 5:
Рисунок 5 — Форма для ввода данных
Текст в данной форме непосредственно на ход
решения задачи не оказывает никакого влияния. Данные комментарии делают решение
задачи более понятной. Для неизвестных
и зарезервированы
ячейкиВ10
и С10.
В них после решения задачи будут внесены полученные значения. Значение функции
цели Z будет зафиксировано в ячейке G9;
2) ввести исходные данные. В диапазон В4:С6
вводим коэффициенты при переменных в системе ограничений: «Первое» —
коэффициенты 1 и 0,«Второе» — 0 и 1,«Третье» — 4 и 2.В диапазоне ячеек D4:D6 и
Н4:Н6 заносим значения свободных членов системы ограничений: 35, 10 и 120. В
диапазон ячеек В11:С11 — коэффициенты целевой функции Z, то есть 4 и 5;
3) ввести формулы для расчета целевой функции и
системы ограничений. Для вычисления значений функции цели в
ячейкуG9необходимо ввести формулу = В11*В10 + С11*С10.Здесь вместо
коэффициентов 4 и 5 записаны их адреса В11 иС11, а вместо переменных и
соответствующие
адреса В10
иС10.
Рисунок 6 — Заполненная форма
) выделить ячейку функции цели для запуска
команды «Поиск решения»;
) выбрать вкладку «Данные», в ней выбрать
закладку «Анализ», затем команду «Поиск решения»;
) в открывшемся диалоговом окне, представленном
на рисунке 7,
установить:
Рисунок 7 — Диалоговое окно команды «Поиск
решения»
— в группе «Равной»переключатель на
максимальное значение;
— в поле «Установить целевую
ячейку»ввести адрес ячейки G9,уже
содержащей формулу для расчета значения функции цели;
— в поле «Изменения ячейки»указать
ссылки на изменяемые ячейки В10
и С10,
содержащие неизвестные и
;
— в поле «Ограничения»нужно задать
необходимые ограничения, для этого необходимо нажать кнопку «Добавить»;
) в результате открывается диалоговое окно,
рисунок 8, «Добавление ограничения»:
Рисунок 8- Диалоговое окно «Добавление
ограничения»
— в поле «Ссылка на ячейку»указать
адрес левой части первого ограничения F4. Из списка выбрать нужный оператор,
означающий «не более» (<=);
— в поле «Ограничения»указать адрес
правой части первого ограничения Н4. Нажать кнопку «ОК»,
— следующие ограничения вводить
аналогично первому, нажав кнопку «Добавить».
Диалоговое окно «Поиск решения», рисунок 9, после ввода
исходных данных имеет вид:
Рисунок 9 — Форма после ввода исходных данных
) для поиска оптимального решения нажать кнопку
«Выполнить». Если задача линейного программирования имеет решение, то на экране
появятся результат работы команды «Поиск решения», как на рисунке 10.
Рисунок 10 — Результаты работы команды «Поиск
решения»
Максимальное значение целевой функции .
Оно достигается при плане производства.
Причем сырье (120 кг алюминия) используется
полностью (левая и правая части третьего ограничения равны между собой).
.4 Решение задачи о раскрое в среде MS Excel
Постановка задачи:
Для изготовления металлоконструкций используется
заготовки длиной 70, 100 и 120 см. Заготовки производят из металлических
стержней длиной 220 см. Для выполнения всего заказа требуется изготовить 102
стержня длиной 70 см, 120 стержней длиной 100 см и 80 стержней длиной 120
см.Какое минимальное количество материала необходимо использовать, чтобы
выполнить заказ?
Решение:
Сначала нужно определить все возможные способы
раскроя материала. Для наглядности представим эти данные в таблице 6:
Таблица 6 — Способы раскроя материала
|
Виды |
Способы |
||||
|
I |
II |
III |
IV |
V |
|
|
70 см |
0 |
1 |
0 |
1 |
3 |
|
100 |
1 |
0 |
2 |
1 |
0 |
|
120 см |
1 |
1 |
0 |
0 |
0 |
|
Отходы, |
0 |
30 |
20 |
50 |
10 |
Таким образом, получаем пять различных способов
раскроя материала.
Обозначим через —
количество единиц материала, раскраиваемых по -му способу (интенсивность
использования способа раскроя), то есть —
количество материала, раскраиваемого по способу 1 и так далее до .
Зададим математическую модель нахождения общего
количества металлических стержней длиной 220 см. Его минимизация является целью
решения задачи. Следовательно, целевая функция будет иметь вид:
Система ограничений примет вид:
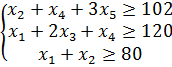
Очевидно, что количество заготовок ()
должно быть целым числом и не может быть отрицательным.
Следующим шагом будет решение задачи в MS Excel
с помощью надстройки «Поиск решения». На рисунке 11 изображено, какую
необходимо создать форму для ввода данных с занесенными в неё известными
значения.
Рисунок 11 -Форма для ввода данных
Ячейка G7 зарезервирована под функцию цели,
позже в нее будет записана формула для нахождения минимального количество
стержней длиной 220 см. В ячейках диапазона B3:F5, размещена таблица
рациональных способов раскроя материала, в диапазоне ячеек B6:F6 — величина
отходов для каждого способа раскроя, а в G3:G5 — требуемое количество стержней
заготовок различной длины. Ячейки B7:F7 заполнятся автоматически после
выполнения команды «Поиск решения», и будут равны количеству заготовок
получаемых при каждом способе раскроя.
В ячейках H3:H5необходимо указать формулы для
расчета фактического количества стержней разной длины. В ячейке H3 формула
будет иметь вид =$B$7*B3+$C$7*C3+$D$7*D3+$E$7*E3+$F$7*F3, ячейки H4 и H5
заполняются аналогично (для этого можно использовать автозаполнение т.к. в
формуле использованы абсолютные ссылки).
В ячейку G7 нужно занести целевую функцию,
вычисляющую суммарное количество единиц материала, то есть необходимое
количество стержней длиной 220 см. Таким образом, в данной ячейке будет введена
формула: =B7+C7+D7+E7+F7.
Необходимо воспользоваться надстройкой «Поиск
решения». Вызвать ее можно выбрав вкладку «Данные», закладку «Анализ». В
диалоговом окне «Поиска решения», рисунок 12, вводим ячейку целевой функции $G$7,
диапазон изменяемых ячеек:$B$7:$F$7, устанавливаем переключатель «Равной
минимальному значению».
Рисунок 12 — Диалоговое окно надстройки «Поиск
решения»
В поле «Изменяя ячейки» задается диапазон
подбираемых параметров — $B$7:$F$7.
Также нужно добавить ограничения:
— количество заготовок должно быть
целым числом ($B$7:$F$7=целое);
— количество не должно быть
отрицательным числом ($B$7:$F$7>=0);
— фактическое количество стержней
различной длины, требуемое для выполнения заказа, должно быть не менее
необходимого количества ($H$3:$F$5>=$G$3:$G$5).
В результате выполнения надстройки «Поиск
решения» получаем минимальное количество материала необходимое для выполнения
заказа в ячейке G7 — 134
единицы материала, рисунок 13:
Рисунок 13 — Результат выполнения надстройки
«Поиск решения»
Так же на рисунке 13 видно, что для этого
используются только 3 способа раскроя материала(1 способ — 80 единиц, 3 способ
— 20 единиц и 5 способ — 34 единицы).
.5 Решение транспортной задачи в среде MS Excel
Решение транспортной задачи позволяет вычислить
наиболее эффективный вариант распределения продукции. На основании, данных о
запасах и заявках, а так же о стоимости доставки 1 единиц товара, производится
поиск оптимального решения транспортной задачи.
Постановка задачи:
Существует четыре пункта производства продукта A1,
A2, A3,
A4производственные мощности которых составляют 30, 40, 50 и 30
единиц. Данный товар востребован в трех пунктах потребления B1, B2,
B3, потребности которых составляют 40, 60 и 50 единиц. Затраты на
поставку единицы товара (у.д.е.) от пунктов производства до пунктов назначения
заданы матрицей:
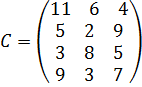
Необходимо определить план перевозок, с
минимальными транспортными затратами.
Решение:
Обозначим через количество
единиц товара перевозимых от i-го поставщика к j-му потребителю. Тогда —
план перевозок. Суммарная стоимость перевозок выразится целевой функцией,
которую необходимо будет минимизировать:
Система ограничений примет вид:
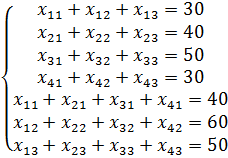
По аналогии с предыдущими задачами, создаем
форму ввода и заполняем ее исходными данными, рисунок 14:
Рисунок 14 — Форма для ввода данных к решению
транспортной задачи
Для функции цели зарезервирована ячейка H9,
для переменных — ячейки B4:B7,
D4:D7, F4:F7, в них будут занесены результаты решения задачи. В ячейки B9, D9,
F9 необходимо ввести формулы для вычисления левых частей уравнений-ограничений
по заявкам. Для потребителя B1 ограничение имеет вид уравнения:
.
Следовательно, в ячейку B9 нужно записать
формулу: =СУММ(В4:В7).
Формулы в ячейках D9 и F9 задаются таким же
образом. В ячейки I4:I7 введем формулы для вычисления левых частей уравнений по
запасам.
Для поставщика A1 уравнение имеет
следующий вид:
,
что соответствует формуле в ячейке I4:= B4 + D4
+ F4. Аналогично задаются формулы для ячеек I5, I6 и I7.
Для вычисления значения целевой функции
В ячейку H9
запишем формулу: = СУММПРОИЗВ(C4:C7;
B4:B7)
+ +СУММПРОИЗВ(E4:E7;D4:D7)+СУММПРОИЗВ(G4:G7;
F4:F7).
Необходимо воспользоваться надстройкой «Поиск
решения». Вызвать ее можно выбрав вкладку «Данные», закладку «Анализ». В
диалоговом окне «Поиска решения», рисунок 15, вводим ячейку цели функции $H$9,
диапазон изменяемых ячеек: $B$4:$B$7;$D$4:$D$7;$F$4:$F$7.
Рисунок 15 — Ввод уравнений-ограничений для
транспортной задачи
Целевая функция считается равной минимальному
значению. Введем уравнения-ограничения по заявкам:B9=B8; D9=D8; F9=F8; по
запасам:I4:I6=H4:H6. Так же нужно указать неотрицательность
переменных:В4:B7>=0;D4:D7>=0;F4:F7>=0.
В результате выполнения программы «Поиск
решения»получим на экране в ячейках B4:B6; D4:D6; F4:F6 оптимальный план
перевозок, а в ячейке Н9 — минимальную общую стоимость за все перевозки,
рисунок 16:
Рисунок 16 — Результат работы надстройки «Поиск
решения»
Таким образом, 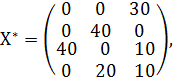
то время как .
ЗАКЛЮЧЕНИЕ
Большинство задач, которые приходится решать
человеку, в процессе своей практической деятельности, являются
многовариантными, то есть предполагают наличие нескольких вариантов решения.
Всю свою жизнь человечество стремится отыскать наилучшее решение при имеющихся
ограничениях возможностей и ресурсов. Долгое время при этом он руководствовался
лишь здравым смыслом, опытом, интуицией.
Однако, впоследствии с развитием промышленности,
увеличением обрабатываемой информации возникла потребность использования
математических методов практически во всех сферах жизни (решение задач
управления и планирования производства, задач из области логистики,
распределение и экономия ресурсов и т.д.). Многие из таких задач относятся к
одной из областей математического программирования, а именно к линейному
программированию. Для математических моделей задач, при этом должно соблюдаться
условие линейной зависимости переменных как для системы ограничений, так и для
критерия оптимальности.
Основными используемыми способами решения задач
линейного программирования являются графический и симплекс-метод. Также для
задач подобного рода найти решение можно с помощью надстройки «Поиск решения»
табличного процессора Excel2007
из пакета прикладных программ Microsoft
Office.
В данной курсовой работе в
соответствии с ее целью и задачами, была собрана и систематизирована информация
по теоретическому обоснованию моделей, приводящих к задаче линейного
программирования. На основе анализа типовых задач линейного программирования,
были сформулированы условия задач каждого вида. Решение задач осуществлялось в
табличном процессореMS
Excel 2007. К
достоинствам, решения задач таким способом, можно отнести простоту
использования, минимум вычислений. В то же время следует отметить и недостаток
данного способа, к нему относится потеря некоторых решений, в том случае если
предполагается множество решений, этого можно избежать при решении графическим
методом.
Таким образом, применение методов линейного
программирования актуально в наши дни, так как использование математических
моделей является важным направлением совершенствования планирования
производства, анализа деятельности фирм, экономии ресурсов, разработки
оптимального плана грузопотоков и многого другого. Представление условия задачи
в виде математической модели помогает структурировать информацию, моделировать
альтернативные варианты, находить рациональные решения задачи.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Бродецкий,
Г.Л. Экономико-математические методы и модели в логистике. Процедуры
оптимизации: учебник / Г.Л. Бродецкий, Д.А. Гусев. — М.: Академия, 2012. — 281
с.
2. Васильев,
А.Н. Финансовое моделирование и оптимизация средствами Excel 2007: учеб.
пособие.-СПб.: Питер, 2009.- 319 с.
. Введение
в анализ «что если» [Электронный ресурс]. — Режим
доступа:http://office.microsoft.com/ru-ru/excel-help/HA010342628.aspx (дата
обращения 20.04.2014)
. Введение
в исследование операций [Электронный ресурс]. —
http://ru.convdocs.org/docs/index-159945.html?page=9 (дата обращения
18.04.2014)
. Задача
о раскрое материалов[Электронный ресурс]. — Режим доступа:
http://edu.nstu.ru/courses/mo_tpr/files/3.1.6.html (дата обращения 18.04.2014)
. Задачи
оптимизации в Excel[Электронный
ресурс]. — Режим доступа: http://exsolver.narod.ru/LM/LM_material.html (дата
обращения 19.04.2014)
. Змеев,
О.А. Исследование операций [Электронный ресурс]. — Режим доступа:
http://abc.vvsu.ru/Books/ebooks_iskt/%D0%AD%D0%BB%D0%B5%
D0%BA%D1%82%D1%80%D0%BE%D0%BD%D0%BD%D1%8B%D0%B5%D1%83%D1%87%D0%B5%D0%B1%D0%BD%D0%B8%D0%BA%D0%B8/%D0%98%D1%81%D1%81%D0%BB%D0%B5%D0%B4%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5%20%D0%BE%D0%BF%D0%B5%D1%80%D0%B0%D1%86%D0%B8%D0%B9/fmi.asf.ru/vavilov/index.htm
(дата обращения 20.04.2014)
. Интерактивный
обучающий курс. Математика [Электронный ресурс]. — Режим доступа:
http://math.immf.ru (дата обращения 18.04.2014)
. Косарева,
А.С., Ляпина, Е.А. Использование метода линейного программирования в процессе
финансового планирования и бюджетирования // Современная наука: актуальные
проблемы теории и практики. — 2013. -№3-4. — С.20-23.
. Красс,
М.С. Математические методы и модели для магистрантов экономики: учеб. пособие.
2-е изд., дополненное / М.С. Красс, Б.П. Чупрынов — СПб.: Питер, 2013.- 486 с.
. Линейное
программирование [Электронный ресурс]. — Режим доступа: http://ecnmx.ru/article/a-27.html
(дата обращения 20.04.2014)
. Макаров,
В.И. Экономико-математические методы и модели. Задачник : учеб. пособие. — М.:
КноРус, 2009. — 208 с.
. Методы
линейного программирования [Электронный ресурс]. — Режим доступа: http://math.immf.ru/lections/302.html
(дата обращения 18.04.2014)
. Орлова,
И.В. Экономико-математические методы и модели: компьютерное моделирование :
учебное пособие для вузов/ И. В. Орлова, В. А. Половников. -2-е изд., испр.
-М.: Вузовский учебник, 2010.-365 с.
. Примеры
решения задач симплексным методом в Excel[Электронный
ресурс]. — Режим доступа: http://math.semestr.ru/simplex/excel.php
(дата обращения 18.04.2014).
. Просветов
Г.И. Математические методы в логистике: задачи и решения: учебно-практическое
пособие. — 2-е изд., доп. -М.: Альфа-Пресс, 2009. -303с.
. Решение
задач линейного программирования в Excel [Электронный ресурс]. — Режим доступа:
http://www.matburo.ru/ex_mp.php?p1=mpexcel
(дата обращения 20.04.2014)
. Решение
задач оптимизации в среде MS Excel[Электронный ресурс]. — Режим доступа:
http://ieu.udsu.ru/moodle/pluginfile.php/249/mod_resource/ content
/2/OptRas.htm (дата обращения 18.04.2014)
. Свободный
поиск. Поиск решения в OpenOffice.org Calc[Электронный ресурс]. — Режим
доступа: http://mxl4.net/blog/2009/01/svobodnyj-poisk.html(дата обращения
18.04.2014).