1. Решение задач линейного программирования в MS Excel
Подопригора Игнат Валерьевич, к.э.н.,
доцент кафедры Экономики
2. Ответы задачи
1. Шкафов А — 300; Шкафов В — 200
2. Курьерских поездов — 5; Скоростных — 7
3. Задача 1
В плановом году строительные организации города переходят к сооружению
домов типов Д-1, Д-2, Д-3 и Д-4. Данные о типах домов приведены в табл
Годовой план ввода жилой площади составляет соответственно 800, 1000, 900 и
200 квартир указанных типов.
Тип квартир
Тип дома
Д-1
Д-2
Д-3
Д-4
Однокомнатные
10
18
20
40
Двухкомнатные
Трехкомнатные
40
60
30
90
20
10
–
–
Четырехкомнатные
Плановая себестоимость,
тыс. д. е.
20
10
–
10
800
550
360
450
На жилищное строительство утвержден объем капиталовложений в размере 40
млн. д. е . Определить оптимальный план строительства на финансовый год.
4. Исходные данные
5. Считаем количество квартир
6. Вводим целевую функцию (себестоимость)
7. Поиск решения
8. Поиск решения
9. Поиск решения
10. Транспортная задача
Транспортная модель используется при
разработке плана перевозок одного вида
продукции из нескольких пунктов отправления в
пункты назначения. При построении модели
используются:
величины, характеризующие предложение в
каждом исходном пункте и спрос в каждом пункте
назначения;
стоимость перевозки единицы продукции из
каждого исходного пункта в каждый пункт
назначения.
11.
Пусть однородный продукт, сосредоточенный в m
отправления в количествах
a1 , a2 ,…, am
единиц, необходимо доставить в каждый из n
пунктов назначения в количествах
b1 , b2 ,…, bn
единиц. Стоимость перевозки единицы продукта
из i -го пункта отправления в j -й пункт
назначения равна
комбинаций i, j .
cij
и известна для всех
12.
Пусть
xij– количество продукта,
перевозимого по маршруту i, j . Задача
заключается в определении таких величин
для всех маршрутов
xij , при которых
суммарная стоимость перевозок i, j
минимальна.
13. Матрица планирования
Поставщики
Потребители
B
B2
1
c
B3 …
c
c …
A
x11
x12
x13
….
…
…
…
1
11
c
m1
12
c
m3
Am
x m1
xm 2
xm 3
Потребности
b
b
b
1
2
Bn
c
13
c
m2
Запасы
3
1n
x1n
…
…
…
c
…
xm n
b
n
a
1
…
mn
am
a b
i
j
14.
• Математическая модель транспортной задачи
сводится к минимизации целевой функции,
выражающей суммарные затраты на перевозку
всего груза
m n
Z cij xij min
i 1 j 1
15.
Систему ограничений получаем из следующих
условий задачи:
n
1. Все грузы должны быть вывезены, т.е.
xij 0;
n
j 1
xij ai , i 1,…,m .
m
j 1
n
x b
2. Все потребности должны быть удовлетворены,
i 1 j 1
ij
j
т.е.
m
xij b j , j 1,…, n .
i 1
16.
Тогда математическая модель транспортной задачи
имеет следующее.найти наименьшее значение
линейной функции при ограничениях:
m
n
Z cij xij
i 1 j 1
n
xij ai
j 1
m
xij b j
i 1
x
0
.
ij
i 1, m
j 1, n
17.
• Это есть задача ЛП с m n уравнениями и
mn неизвестными.
В рассмотренной модели предполагается, что
суммарные запасы равны суммарным потребностям
m
n
i 1
j 1
ai b j .
Такая модель называется закрытой
18.
• Теорема. Любая транспортная задача, у которой
,n
m
ai b j
i 1
имеет решение.
j 1
19. Задача
20. Задача
21. Задача
22. Копируем исходную таблицу
23. Суммируем по строкам и по столбцам таблицы
24. Считаем затраты на перевозку песка
25. Вводим Целевую Функцию
26. Поиск решения
27. Поиск решения (выбор ячеек для изменения)
28. Поиск решения. Ввод ограничения по наличию песка
29. Поиск решения. Ввод ограничения по потребности в песке
30. Поиск решения. Ввод ограничения на неотрицательность переменных
31. Поиск решения
32. Поиск решения
33. Задачи для самостоятельного решения
34. Задачи для самостоятельного решения
35. Задачи для самостоятельного решения
-
Скачать презентацию (0.87 Мб)
-
85 загрузок -
4.0 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Скачать презентацию (0.87 Мб). Тема: «Решение задач линейного программирования в MS Excel». Предмет: информатика. 28 слайдов. Для студентов. Добавлена в 2016 году. Средняя оценка: 4.0 балла из 5.
-
Формат
pptx (powerpoint)
-
Количество слайдов
28
-
Слова
-
Конспект
Отсутствует
Содержание
-
Слайд 1
Решение задач линейного программирования в MS Excel
-
Слайд 2
Общая задача линейного программирования решается симплексным методом
Симплекс (лат. simplex -простой) – простейший выпуклый многогранник в n-мерном пространстве с n+1 вершиной (например, тетраэдр в 3-мерном пространстве)
-
Слайд 3
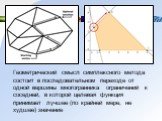
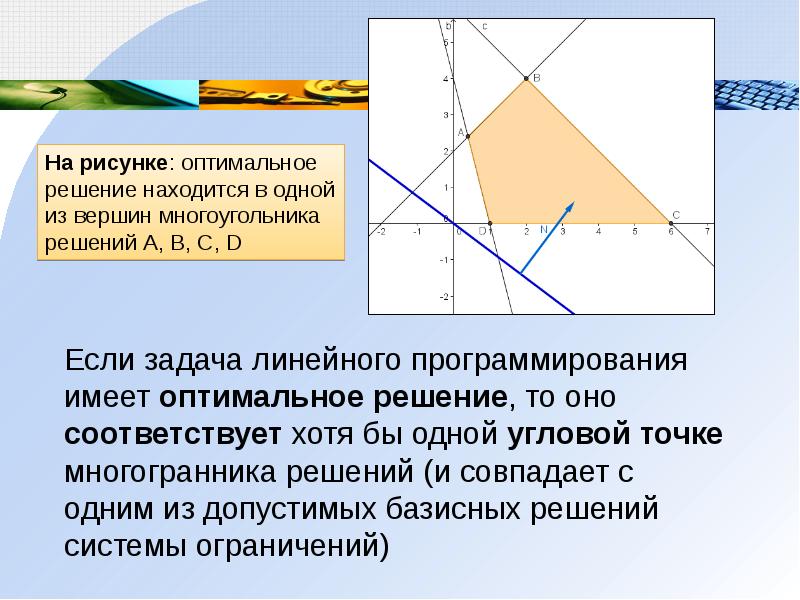
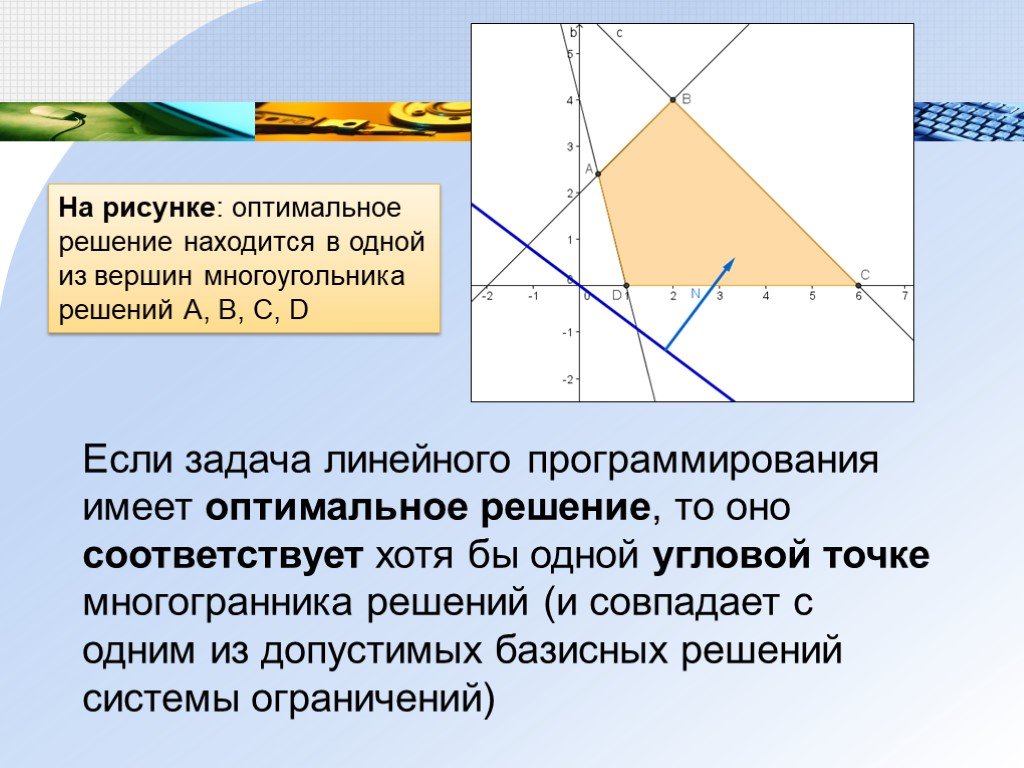
Если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений (и совпадает с одним из допустимых базисных решений системы ограничений)
На рисунке: оптимальное решение находится в одной из вершин многоугольника решений А, В, С, D -
Слайд 4
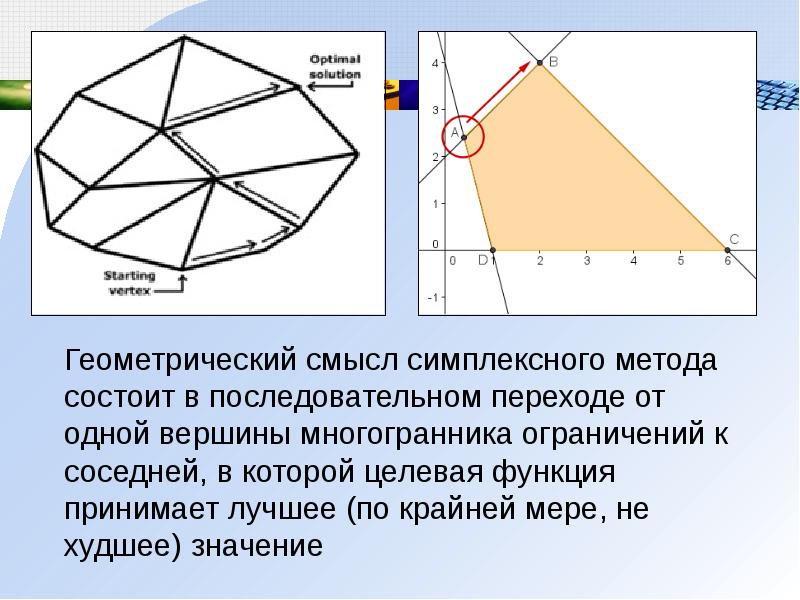
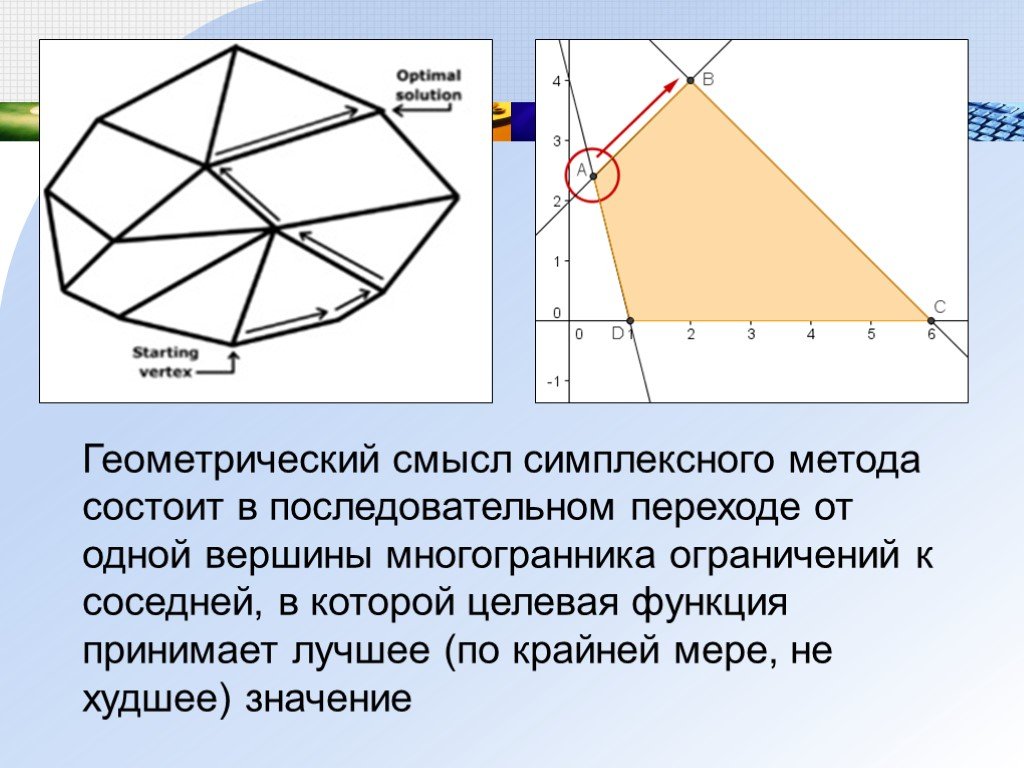
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (по крайней мере, не худшее) значение
-
Слайд 5
Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г.
Джордж Бернард Данциг (1914-2005) – американский математик, разработал симплексный алгоритм, считается основоположником методов линейного программирования
Леонид Витальевич Канторович (1912-1986) – советский математик и экономист, лауреат Нобелевской премии по экономике 1975 года «за вклад в теорию оптимального распределения ресурсов». Один из создателей линейного программирования
Идеи симплексного метода были разработаны в 1939 г. российским ученым Л.В.Канторовичем -
Слайд 6
Симплексный методпозволяетрешить любую задачу линейного программирования
В настоящее время он используется для компьютерных расчетовРассмотрим решение задачи линейного программирования в MS Excel
-
Слайд 7
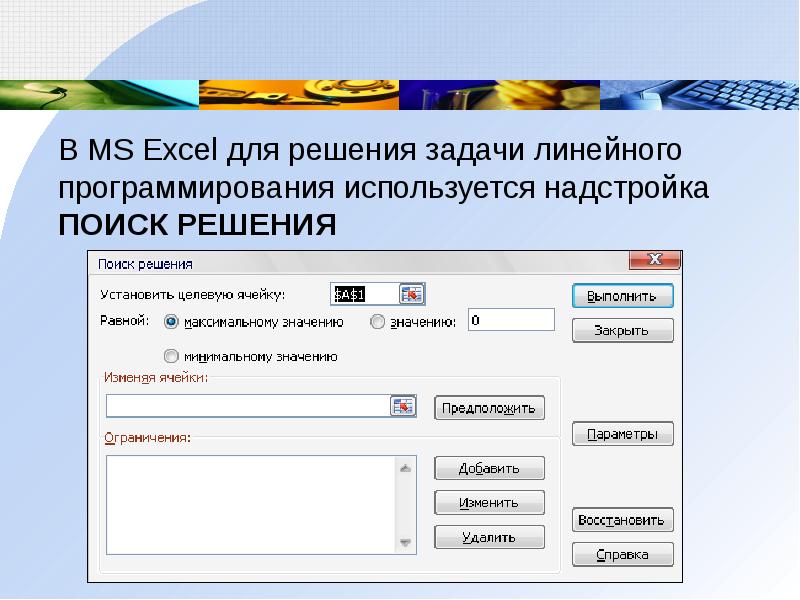
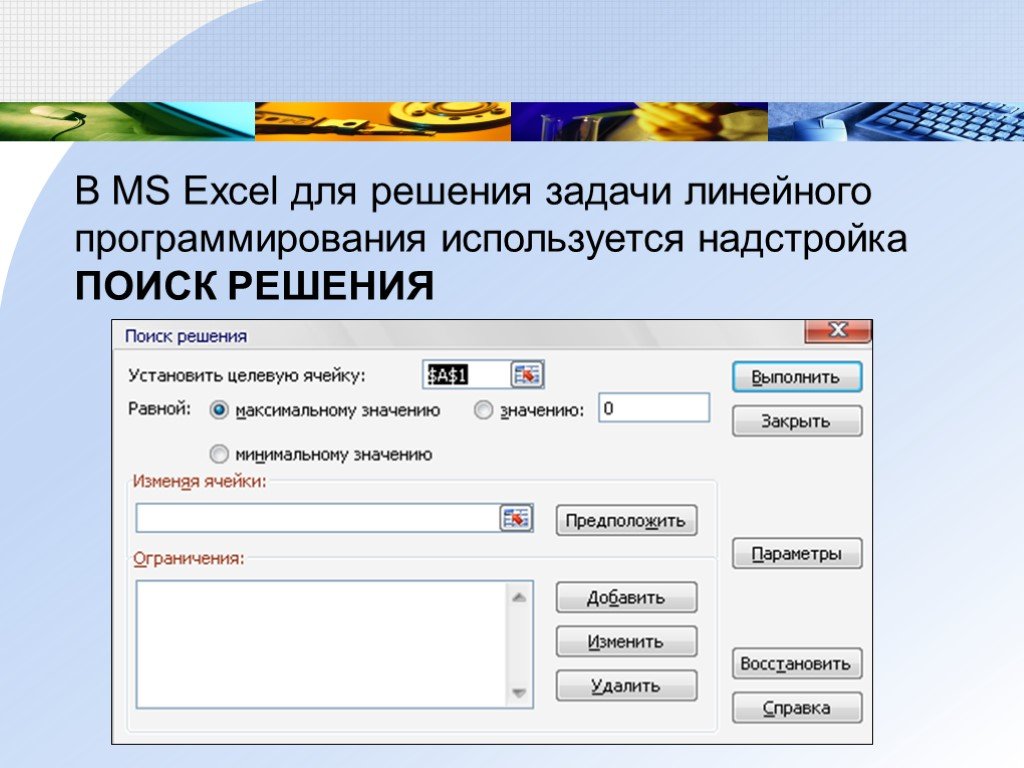
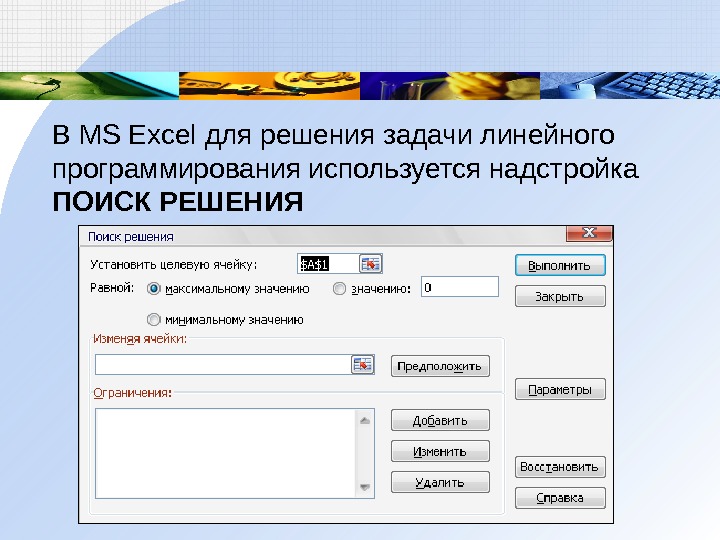
В MS Excel для решения задачи линейного программирования используется надстройка ПОИСК РЕШЕНИЯ
-
Слайд 8
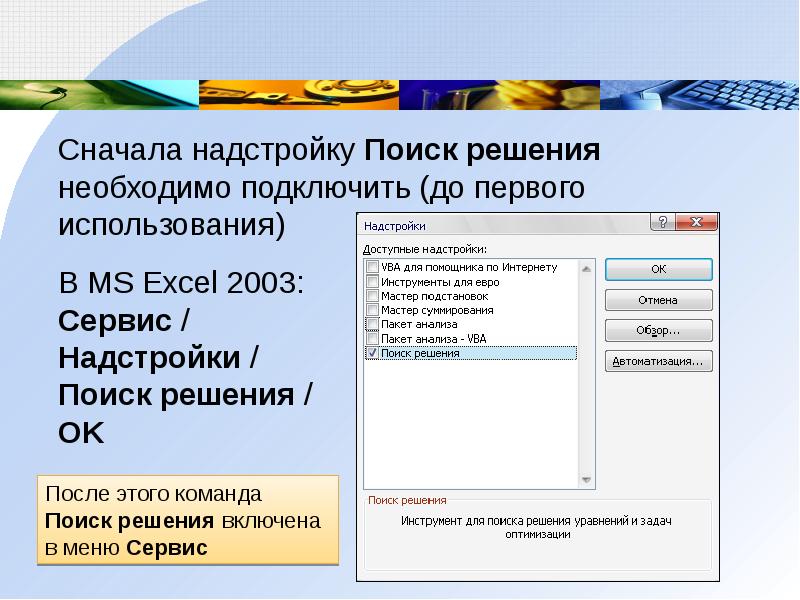
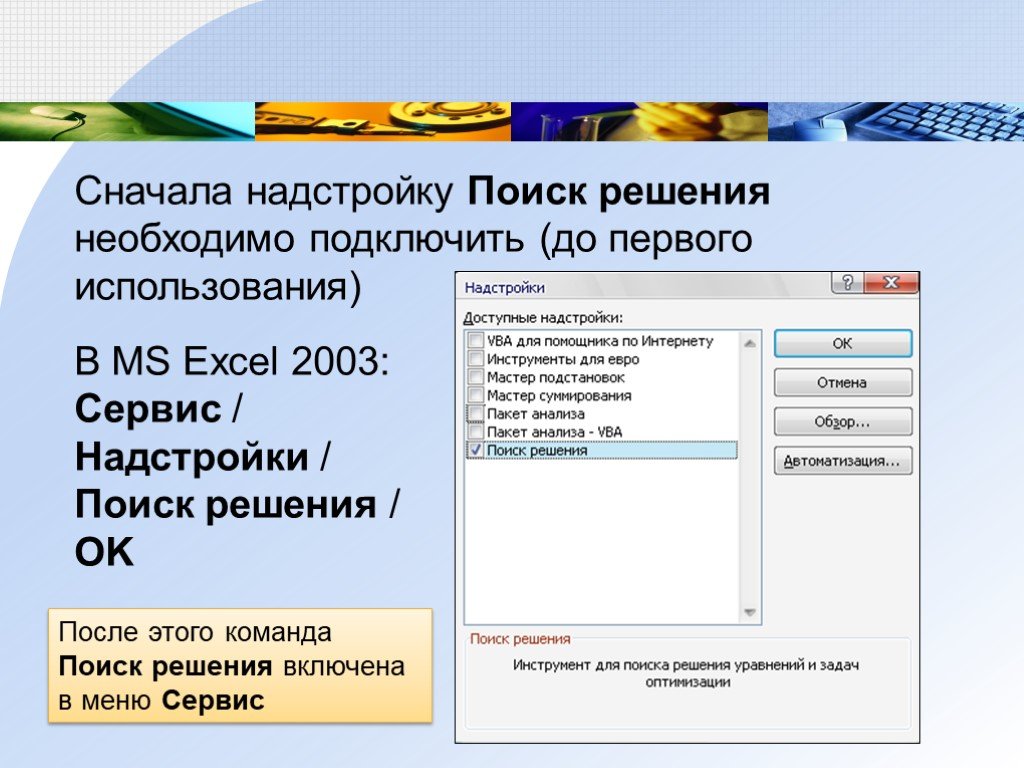
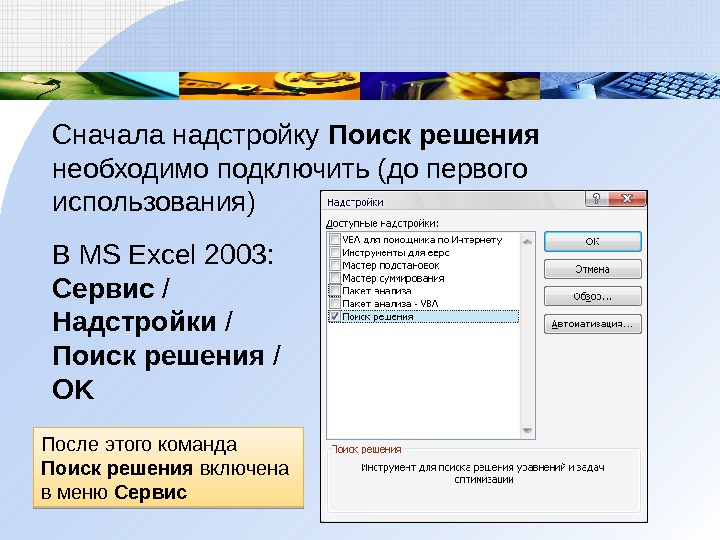
Сначала надстройку Поиск решениянеобходимо подключить (до первого использования)
В MS Excel 2003: Сервис / Надстройки / Поиск решения /
OKПосле этого команда Поиск решения включена в меню Сервис
-
Слайд 9
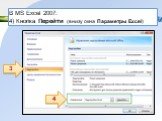
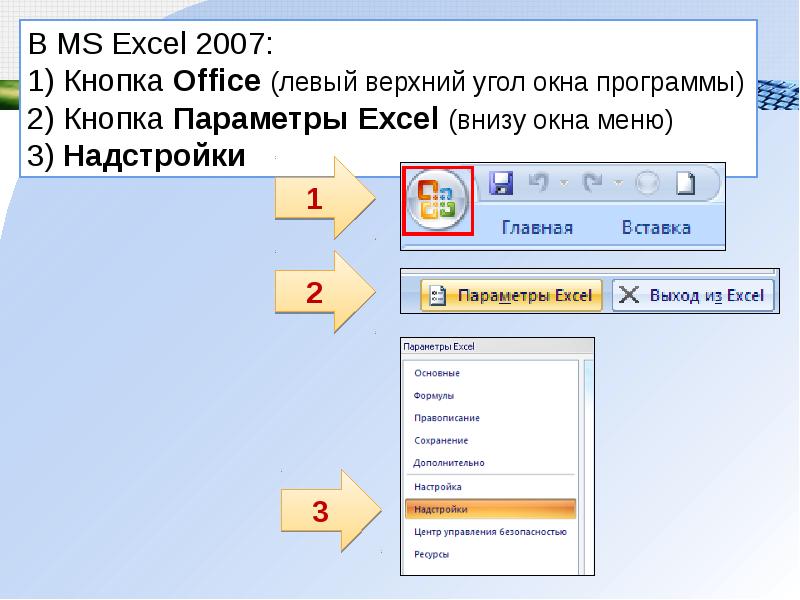
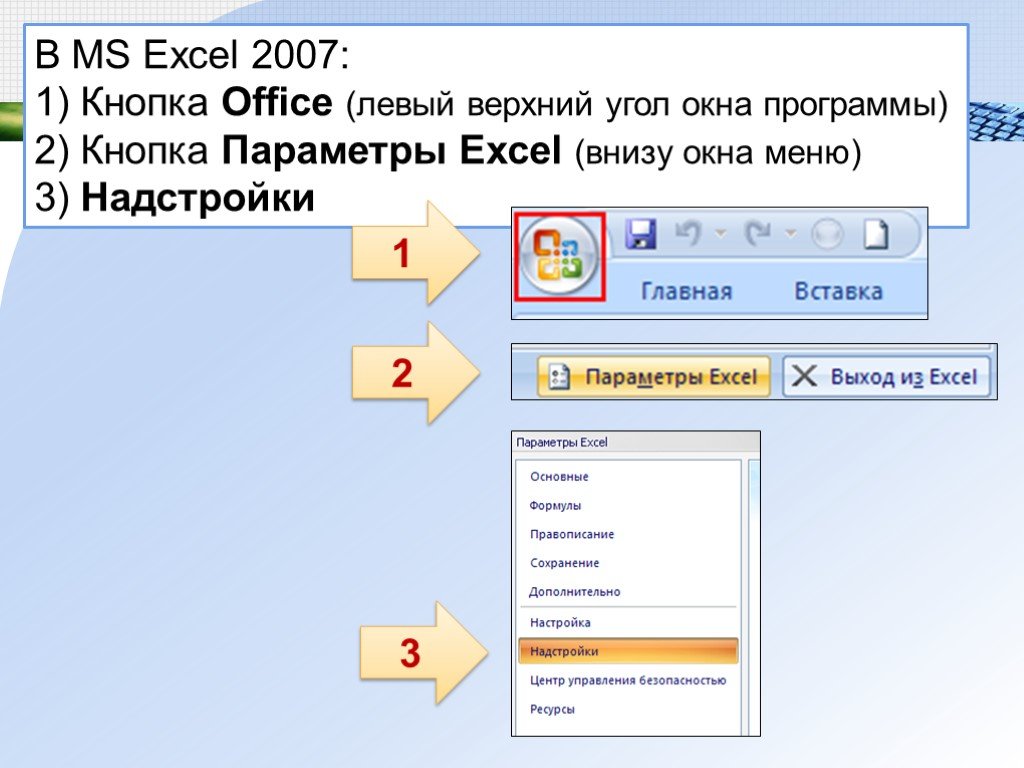
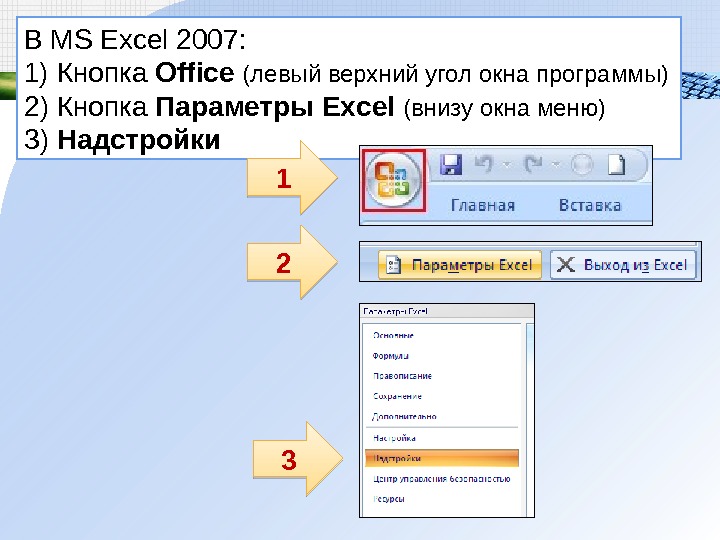
В MS Excel 2007: 1) Кнопка Office(левый верхний угол окна программы)2) Кнопка Параметры Excel(внизу окна меню)
3) Надстройки
1
2
3 -
Слайд 10
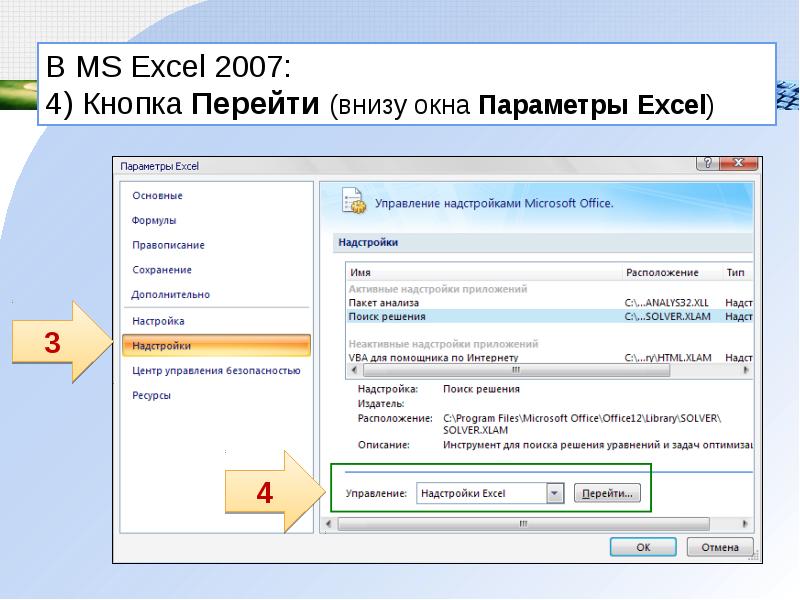
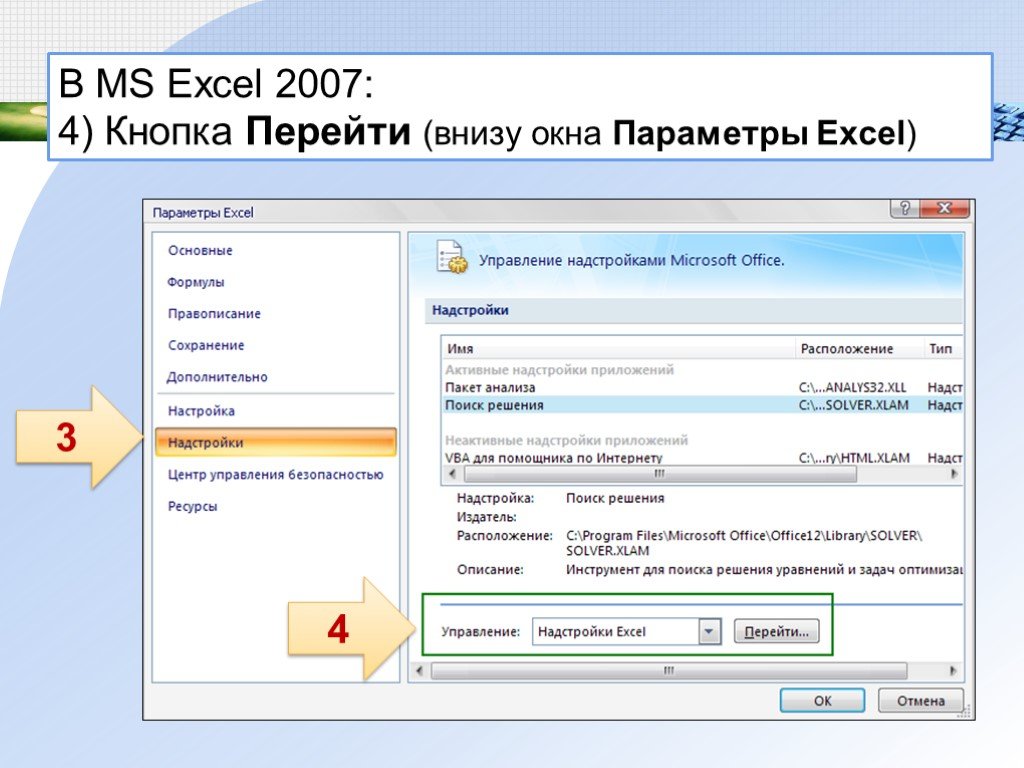
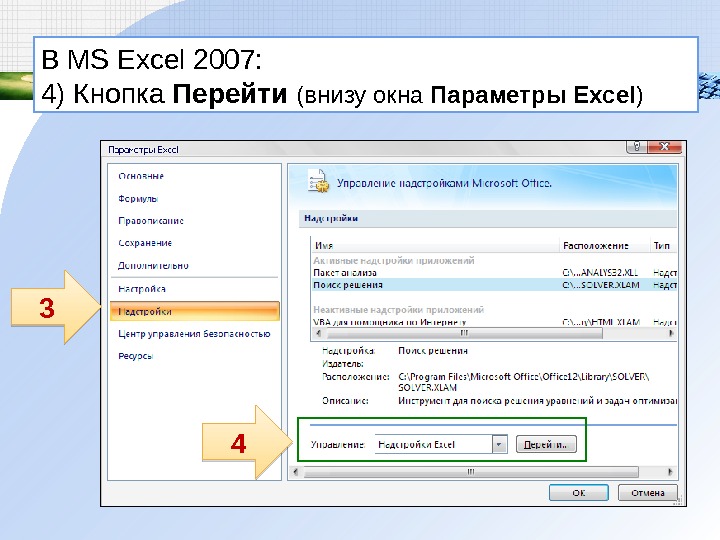
В MS Excel 2007: 4) Кнопка Перейти (внизу окна Параметры Excel)
4
3 -
Слайд 11
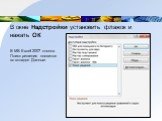
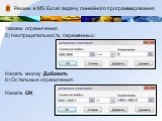
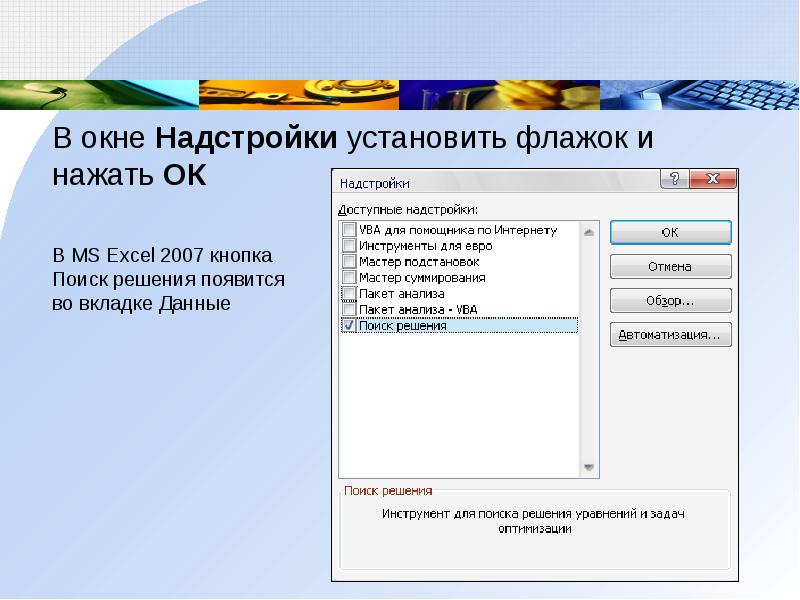
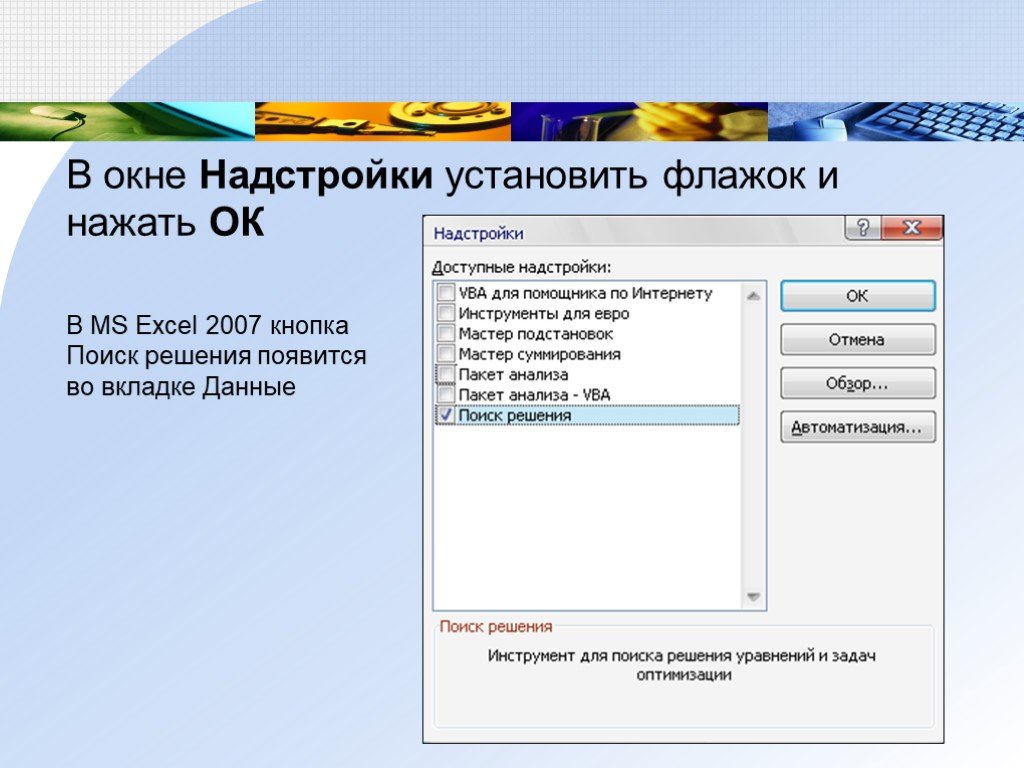
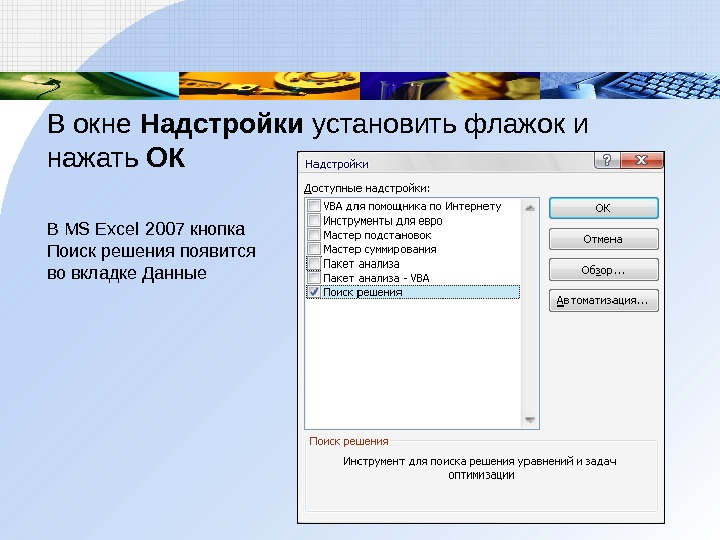
В окне Надстройки установить флажок и нажать ОК
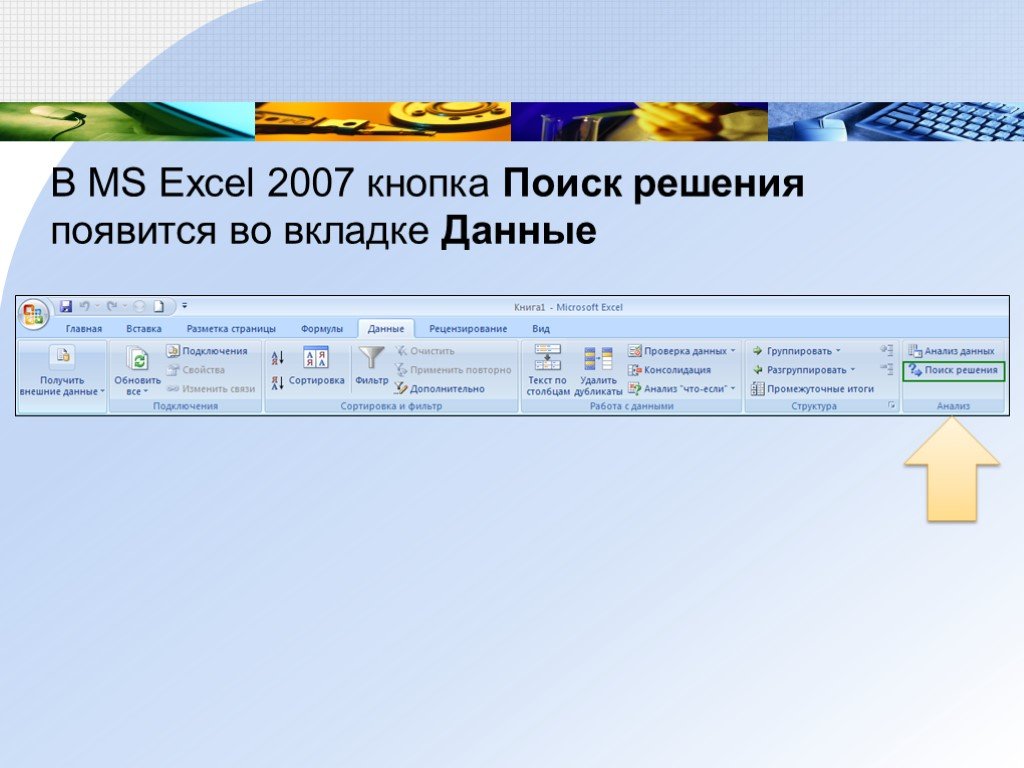
В MS Excel 2007 кнопка Поиск решения появится во вкладке Данные
-
Слайд 12
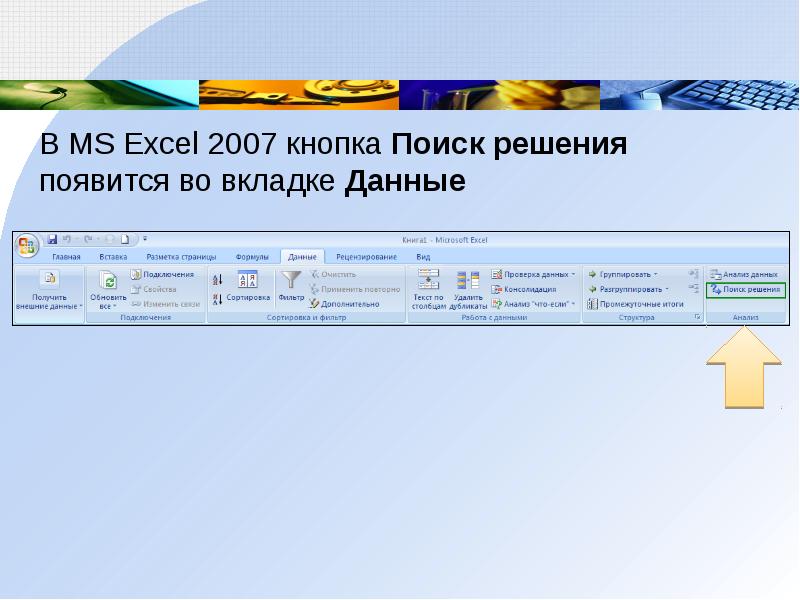
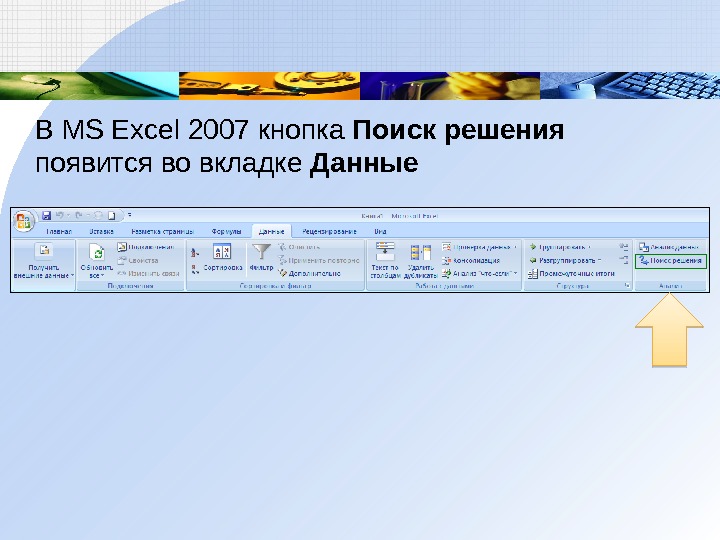
В MS Excel 2007 кнопка Поиск решения появится во вкладке Данные
-
Слайд 13
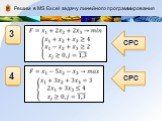
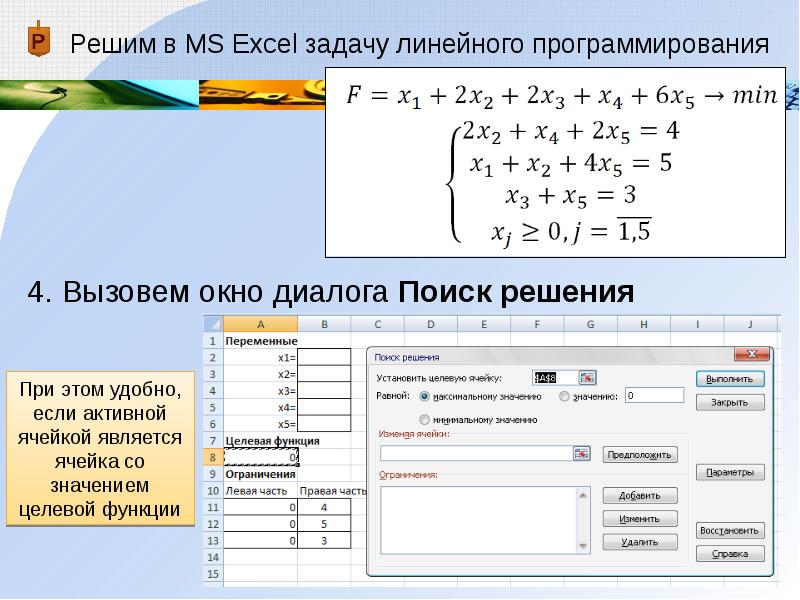
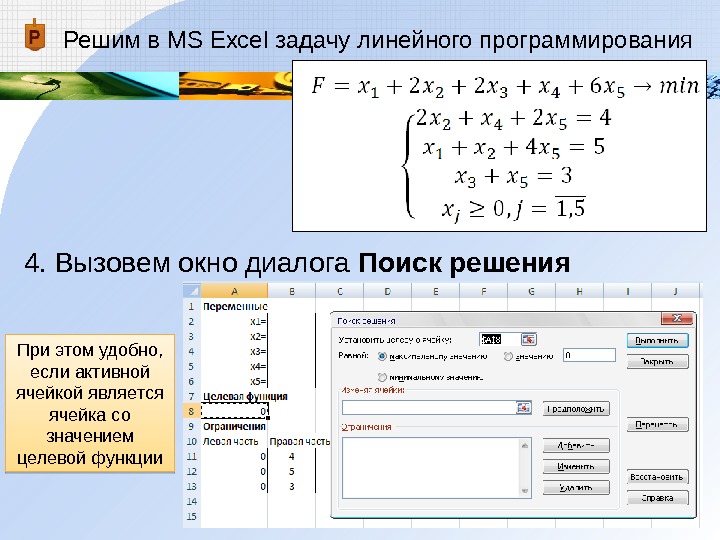
Решим в MS Excel задачу линейного программирования
1
2 -
Слайд 14
Решим в MS Excel задачу линейного программирования
3
4
СРС
СРС -
-
Слайд 16
Решим в MS Excel задачу линейного программирования
1. Создадим область переменных
Ячейки В2:В6 будут играть роль переменных
(пока они пусты) -
Слайд 17
Решим в MS Excel задачу линейного программирования
2. Введем формулу вычисления значений целевой функцииНапример, в ячейку А8
-
Слайд 18
Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем вычислять левые части ограничений в системеВ ячейках В11:В13 введем правые части ограничений системы
-
Слайд 19
Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем вычислять левые части ограничений в системе
Первое ограничение -
Слайд 20
Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем вычислять левые части ограничений в системе
Второе ограничение -
Слайд 21
Решим в MS Excel задачу линейного программирования
3. Создадим область ограничений
В ячейках А11:А13 будем вычислять левые части ограничений в системе
Третье ограничение -
Слайд 22
Решим в MS Excel задачу линейного программирования
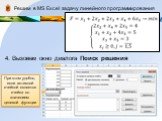
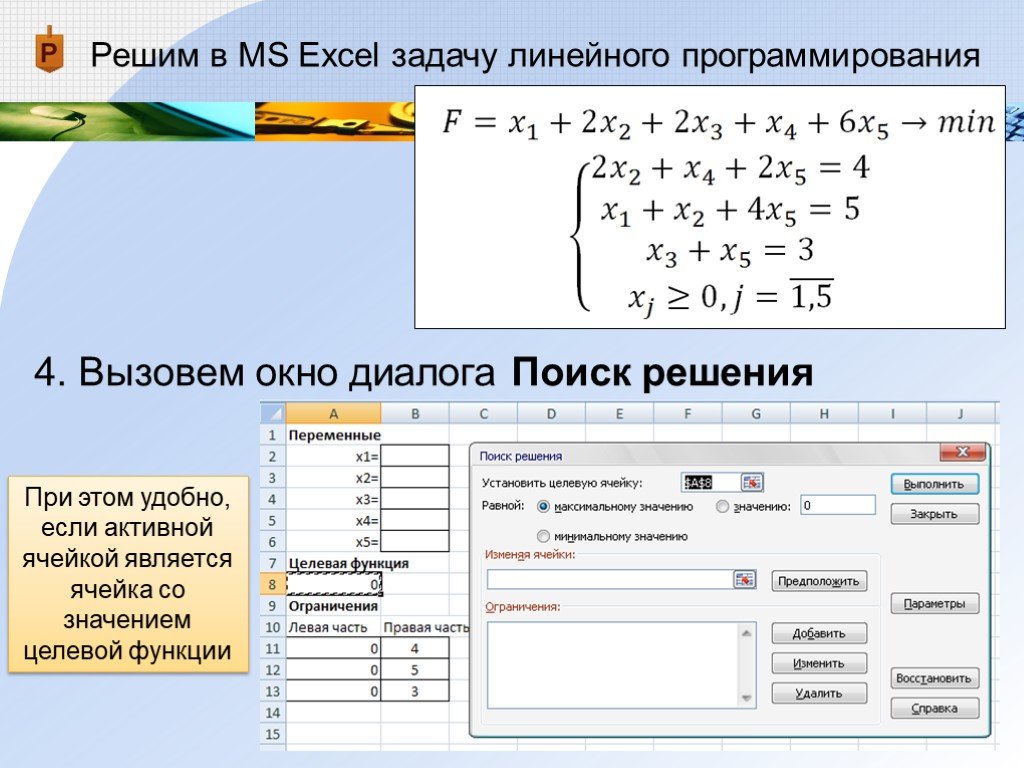
4. Вызовем окно диалога Поиск решения
При этом удобно, если активной ячейкой является ячейка со значением целевой функции -
Слайд 23
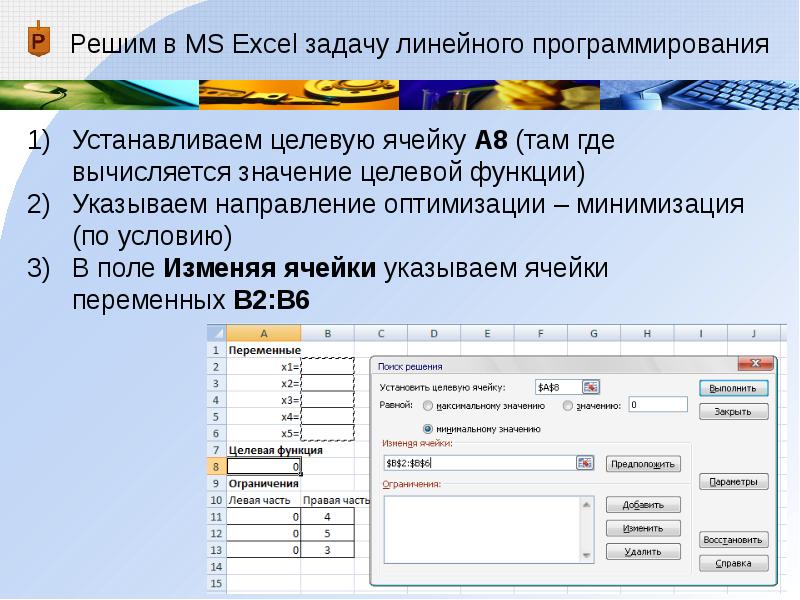
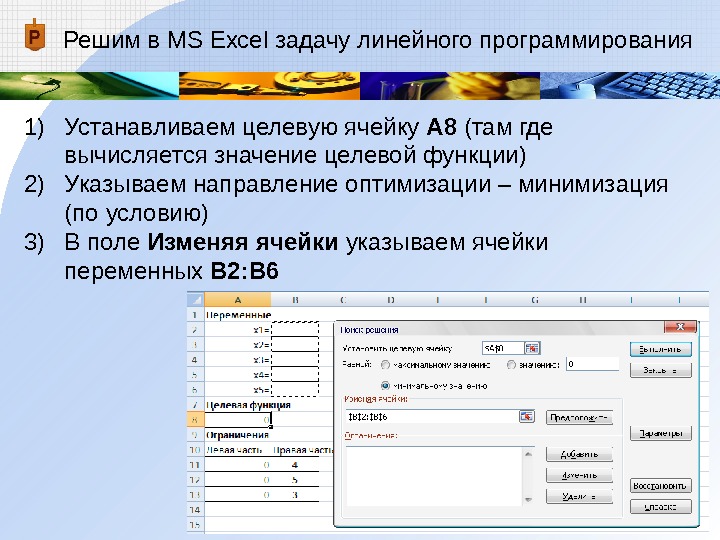
Решим в MS Excel задачу линейного программирования
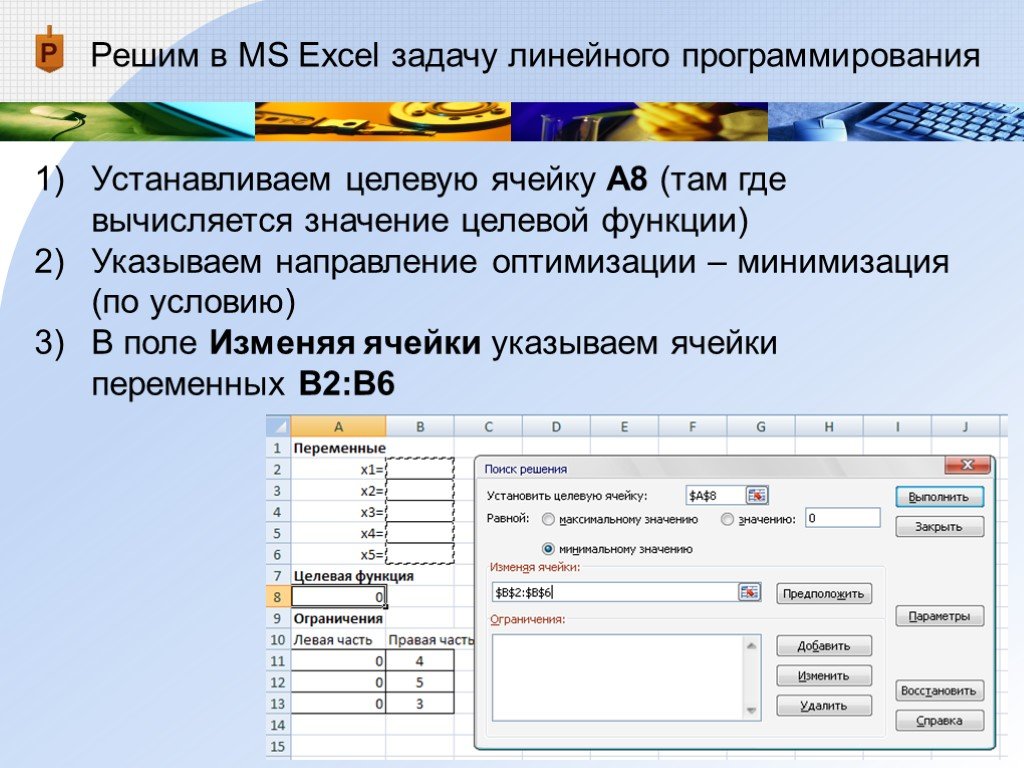
Устанавливаем целевую ячейку А8 (там где вычисляется значение целевой функции)
Указываем направление оптимизации – минимизация (по условию)
В поле Изменяя ячейки указываем ячейки переменных В2:В6 -
Слайд 24
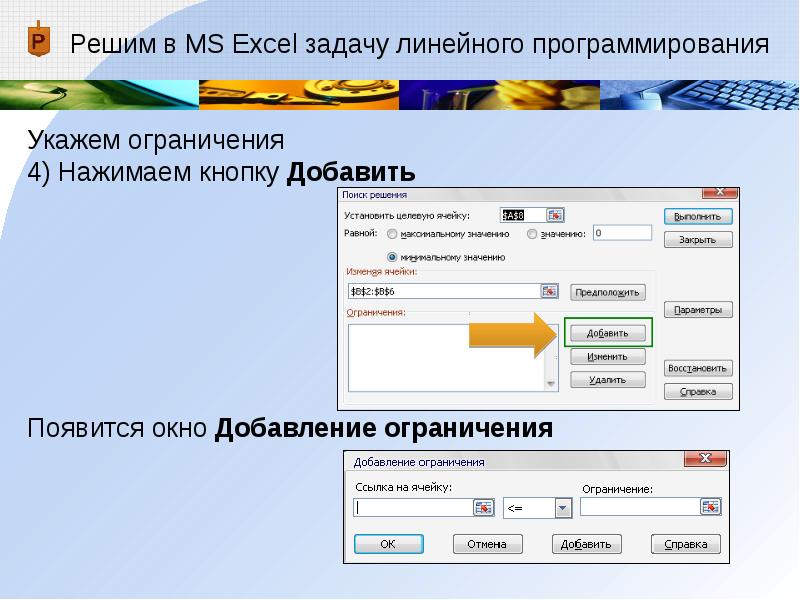
Решим в MS Excel задачу линейного программирования
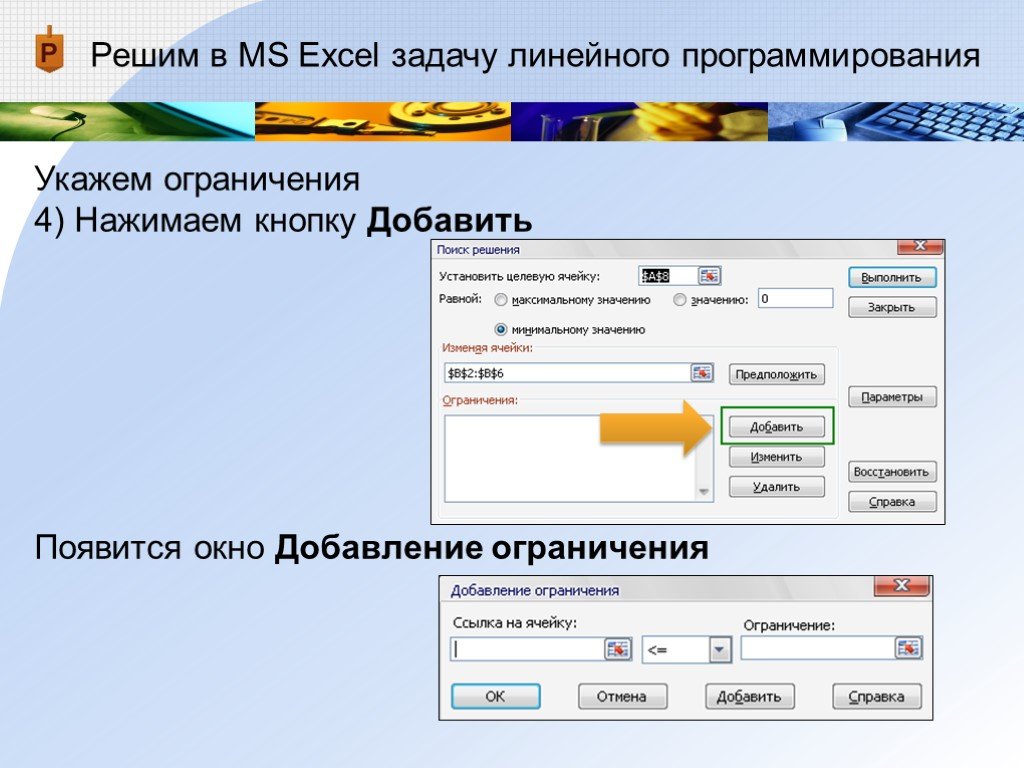
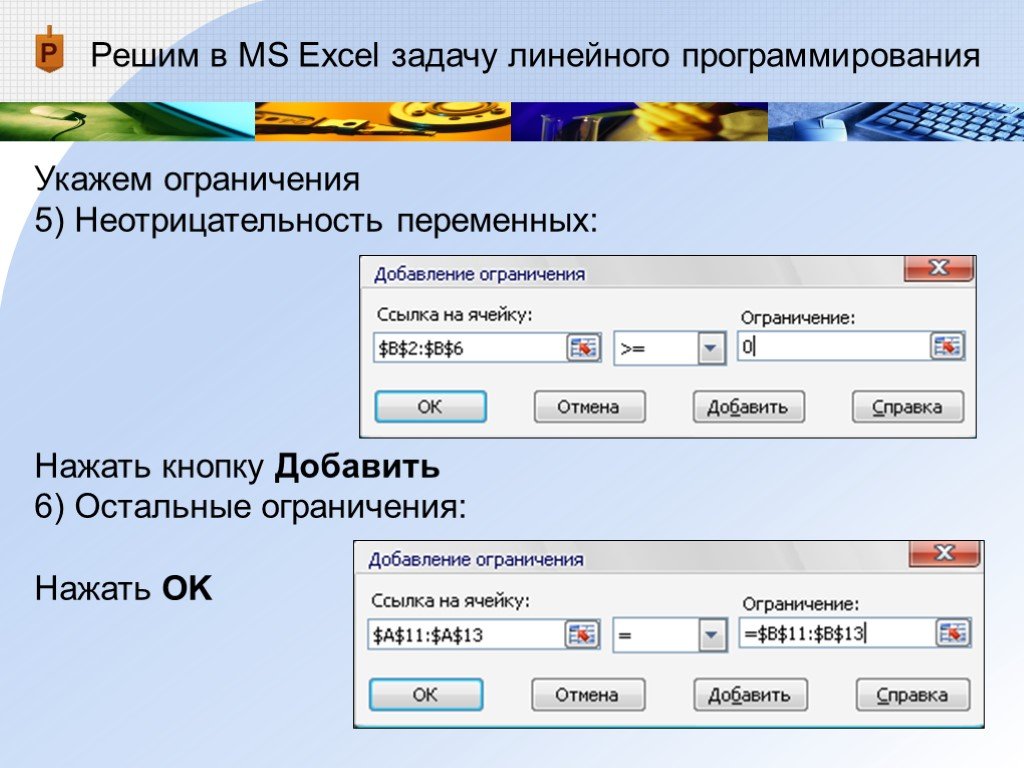
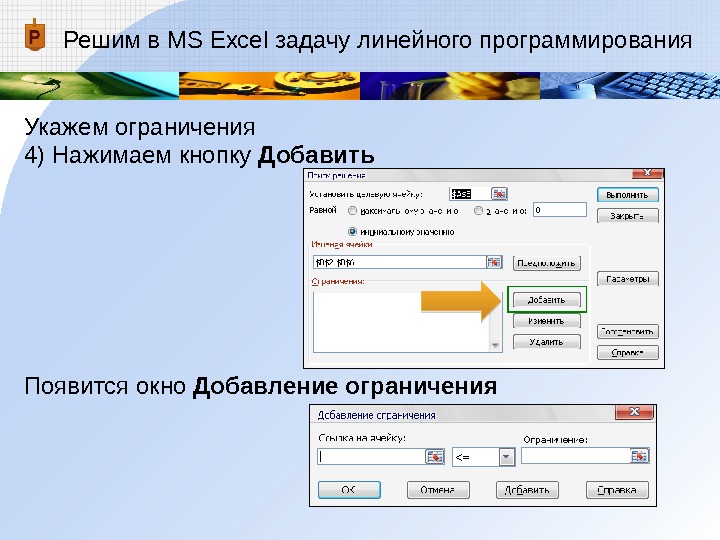
Укажем ограничения
4) Нажимаем кнопку ДобавитьПоявится окно Добавление ограничения
-
Слайд 25
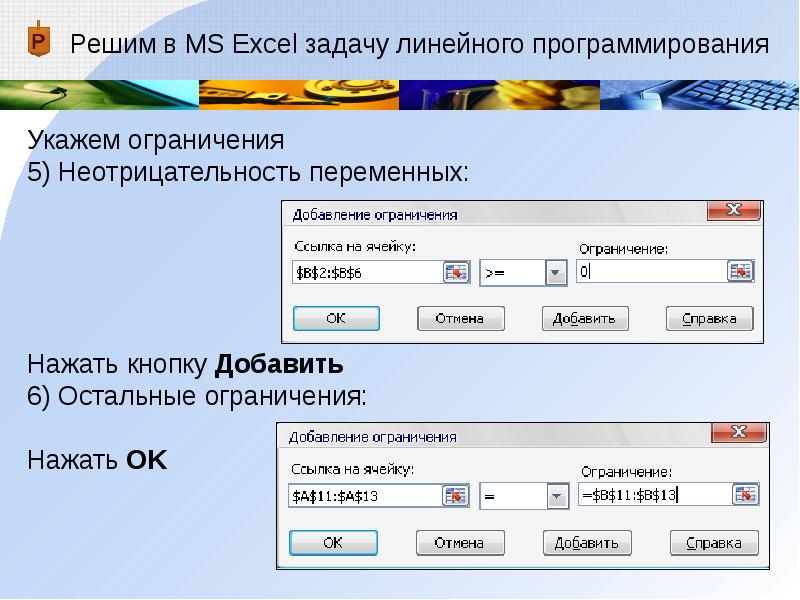
Решим в MS Excel задачу линейного программирования
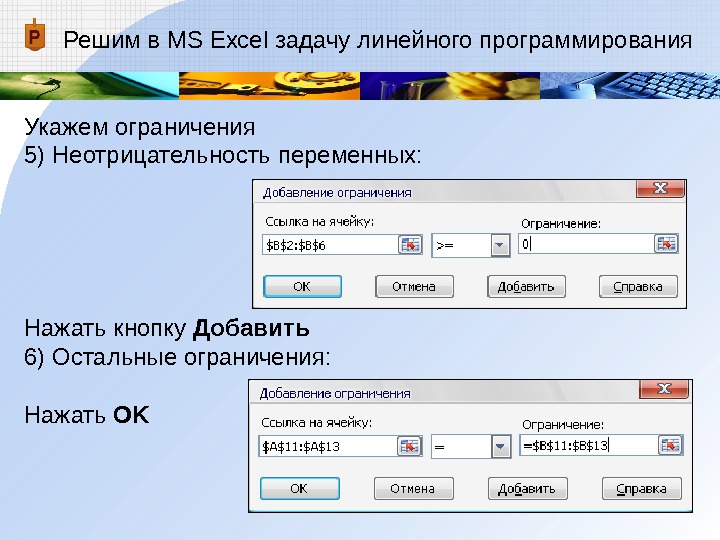
Укажем ограничения
5) Неотрицательность переменных:Нажать кнопку Добавить
6) Остальные ограничения:Нажать OK
-
Слайд 26
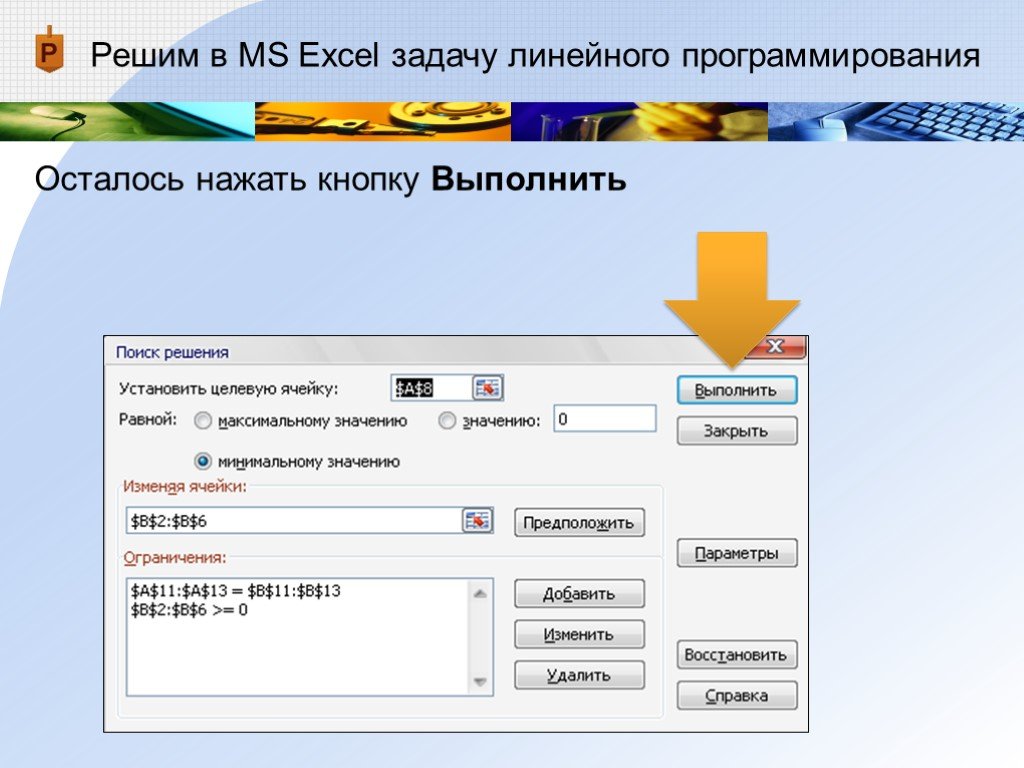
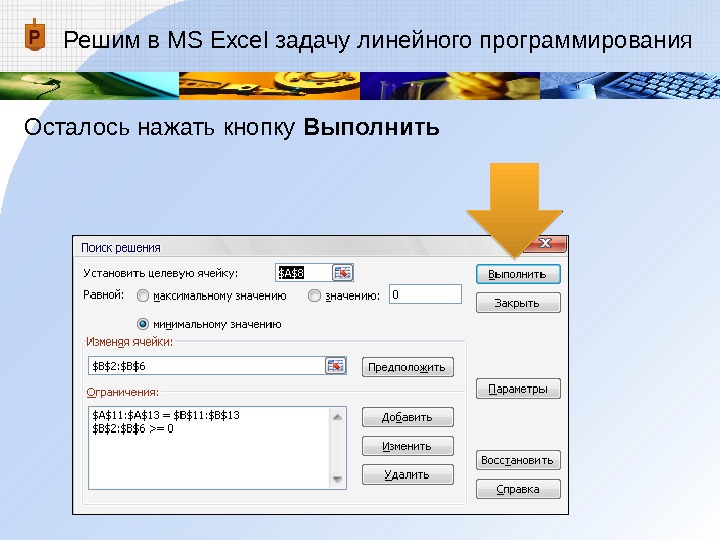
Решим в MS Excel задачу линейного программирования
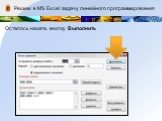
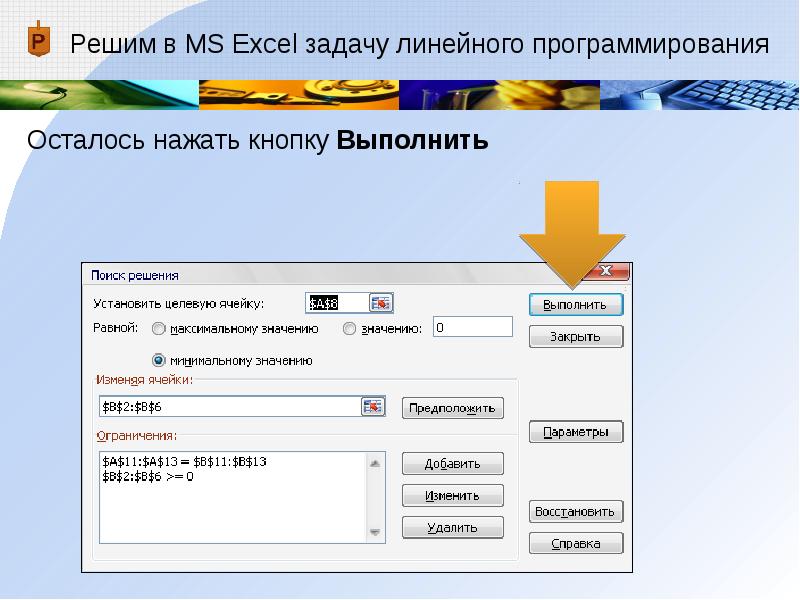
Осталось нажать кнопку Выполнить -
Слайд 27
Решим в MS Excel задачу линейного программирования
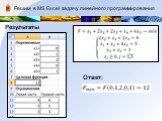
РезультатыОтвет:
-
Слайд 28
Литература
Кремер Н.Ш., Путко Б.А. Исследование операций в экономике. — М.: ЮНИТИ, 2003. — 407 с.
Красс М.С., Чупрынов Б.П. Математика для экономистов. — СПб.: Питер, 2005. — 464 с.
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации












Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте















Презентацию на тему «Решение задач линейного программирования в MS Excel»
можно скачать абсолютно бесплатно на нашем сайте. Предмет
проекта: Информатика. Красочные слайды и иллюстрации помогут вам
заинтересовать своих одноклассников или аудиторию.
Для просмотра содержимого воспользуйтесь плеером, или если вы хотите скачать доклад — нажмите на
соответствующий текст под плеером. Презентация
содержит 28 слайд(ов).
Слайды презентации
Слайд 1
Решение задач линейного программирования в MS Excel
Слайд 2
Общая задача линейного программирования решается симплексным методом Симплекс (лат. simplex — простой) – простейший выпуклый многогранник в n-мерном пространстве с n+1 вершиной (например, тетраэдр в 3-мерном пространстве)
Слайд 3
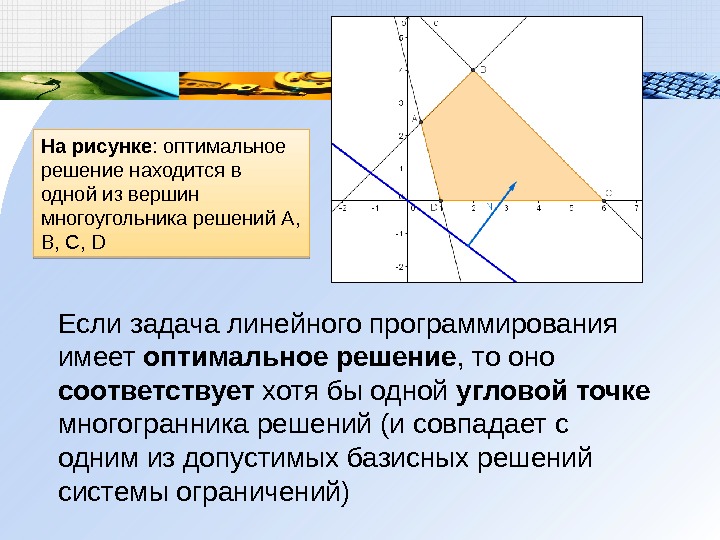
Если задача линейного программирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений (и совпадает с одним из допустимых базисных решений системы ограничений)
На рисунке: оптимальное решение находится в одной из вершин многоугольника решений А, В, С, D
Слайд 4
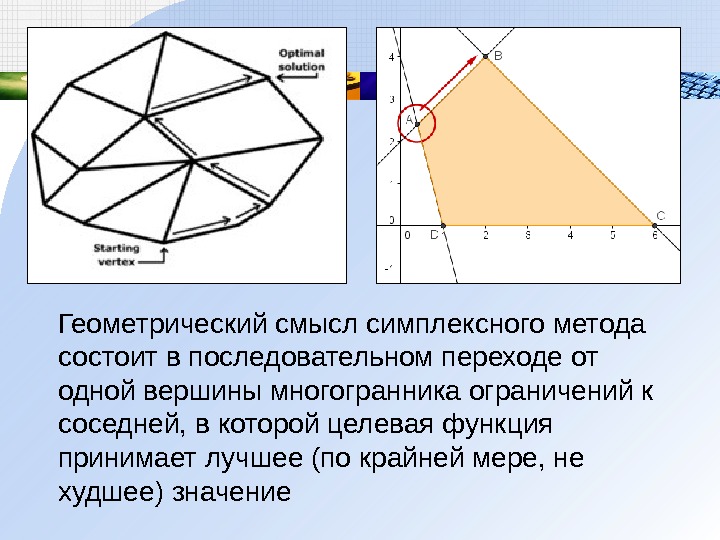
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (по крайней мере, не худшее) значение
Слайд 5
Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г.
Джордж Бернард Данциг (1914-2005) – американский математик, разработал симплексный алгоритм, считается основоположником методов линейного программирования
Леонид Витальевич Канторович (1912-1986) – советский математик и экономист, лауреат Нобелевской премии по экономике 1975 года «за вклад в теорию оптимального распределения ресурсов». Один из создателей линейного программирования
Идеи симплексного метода были разработаны в 1939 г. российским ученым Л.В.Канторовичем
Слайд 6
Симплексный метод позволяет решить любую задачу линейного программирования В настоящее время он используется для компьютерных расчетов Рассмотрим решение задачи линейного программирования в MS Excel
Слайд 7
В MS Excel для решения задачи линейного программирования используется надстройка ПОИСК РЕШЕНИЯ
Слайд 8
Сначала надстройку Поиск решения необходимо подключить (до первого использования) В MS Excel 2003: Сервис / Надстройки / Поиск решения / OK
После этого команда Поиск решения включена в меню Сервис
Слайд 9
В MS Excel 2007: 1) Кнопка Office (левый верхний угол окна программы) 2) Кнопка Параметры Excel (внизу окна меню) 3) Надстройки
1 2 3
Слайд 10
В MS Excel 2007: 4) Кнопка Перейти (внизу окна Параметры Excel)
4
Слайд 11
В окне Надстройки установить флажок и нажать ОК
В MS Excel 2007 кнопка Поиск решения появится во вкладке Данные
Слайд 12
Слайд 13
Решим в MS Excel задачу линейного программирования
Слайд 16
1. Создадим область переменных
Ячейки В2:В6 будут играть роль переменных (пока они пусты)
Слайд 17
2. Введем формулу вычисления значений целевой функции Например, в ячейку А8
Слайд 18
3. Создадим область ограничений
В ячейках А11:А13 будем вычислять левые части ограничений в системе В ячейках В11:В13 введем правые части ограничений системы
Слайд 19
В ячейках А11:А13 будем вычислять левые части ограничений в системе
Первое ограничение
Слайд 20
Второе ограничение
Слайд 21
Третье ограничение
Слайд 22
4. Вызовем окно диалога Поиск решения
При этом удобно, если активной ячейкой является ячейка со значением целевой функции
Слайд 23
Устанавливаем целевую ячейку А8 (там где вычисляется значение целевой функции) Указываем направление оптимизации – минимизация (по условию) В поле Изменяя ячейки указываем ячейки переменных В2:В6
Слайд 24
Укажем ограничения 4) Нажимаем кнопку Добавить Появится окно Добавление ограничения
Слайд 25
Укажем ограничения 5) Неотрицательность переменных: Нажать кнопку Добавить 6) Остальные ограничения: Нажать OK
Слайд 26
Осталось нажать кнопку Выполнить
Слайд 27
Результаты Ответ:
Слайд 28
Литература
Кремер Н.Ш., Путко Б.А. Исследование операций в экономике. — М.: ЮНИТИ, 2003. — 407 с. Красс М.С., Чупрынов Б.П. Математика для экономистов. — СПб.: Питер, 2005. — 464 с.
Список похожих презентаций

Решение задач оптимизации в MS Excel
Для решения задач оптимизации необходимо:. Задать целевую функцию Создать математическую модель задачи Решить задачу на компьютере. Математическая …

Решение текстовых логических задач
Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распростра-нение получили следующие три способа решения …

Решение оптимизационных задач в EXСEL
Старинная русская задача. Пошла баба на базар на людей посмотреть да кое-что продать. Сколько надо бабе на базар для продажи живых гусей, уток и кур, …

Решение математических задач в Exel
Цель урока. Показать как редактировать данные, вводить данные в готовую таблицу, строить диаграммы на основе данных. Уметь создавать и обрабатывать …

Решение логических задач
Логика — это фундаментальная основа информатики как науки. Элементы и основы математической логики заложены в логические элементы и логические устройства …

Решение логических задач
Задача № 1. Дан следующий ряд чисел: -2, 4, -12, 48, -240, … Найдите закономерность по которой составлен этот числовой ряд и продолжите его. Решение:. …

Решение логических задач
Проверка домашней работы:. § 1.3.4 РТ. № 84(б) № 88 (а). Кутепова Н.В, МОАУ «СОШ №4 г.Соль- Илецка Оренбургской обл.»2016 г. По 1 баллу. Что такое …

Решение задач. Параллельные прямые
8 9 10 11 14 15 16 17 18 1 3 4 5 6 13 19 7. Признаки параллельности прямых. Задания на проверку теоретических знаний. … по готовым чертежам. Свойства …

Решение задач с помощью графов
Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице: Определите …

Решение задач С1 ЕГЭ
Для решения задач С1 необходимо:. Проанализировать геометрический чертёж, выделив условия, ограничивающие заштрихованную область (причём в задаче …

Решение задач с условным оператором
Повторение. Какова конструкция условного оператора? Какие существуют формы условного оператора? Приведите пример условного оператора. Решение задач. …

Решение задач по теме «Вероятность»
Основные понятия. Событие — явление, которое происходит в результате осуществления какого-либо определенного комплекса условий. Эксперимент (или опыт) …
Конспекты

Excel (транспортные задачи)
Муниципальное общеобразовательное учреждение. «Средняя общеобразовательная школа № 93». Новокузнецкого района Кемеровской области. …

Табличное решение логических задач
Тема «Табличное решение логических задач». 7 класс (первый урок этой темы). Цели урока:.
систематизировать и обобщить знания учащихся по …

Табличное решение логических задач
Урок 16. Табличное решение логических задач. Планируемые образовательные результаты. :.
предметные -. умение представлять информацию в табличной …

Табличное решение логических задач
. Тема «Табличное решение логических задач». 7 класс (второй урок). Цели урока:.
систематизировать и обобщить сведения, полученные учащимися …
Советы как сделать хороший доклад презентации или проекта
- Постарайтесь вовлечь аудиторию в рассказ, настройте взаимодействие с аудиторией с помощью наводящих
вопросов, игровой части, не бойтесь пошутить и искренне улыбнуться (где это уместно). - Старайтесь объяснять слайд своими словами, добавлять дополнительные интересные факты, не нужно
просто читать информацию со слайдов, ее аудитория может прочитать и сама. - Не нужно перегружать слайды Вашего проекта текстовыми блоками, больше иллюстраций и минимум текста
позволят лучше донести информацию и привлечь внимание. На слайде должна быть только ключевая
информация, остальное лучше рассказать слушателям устно. - Текст должен быть хорошо читаемым, иначе аудитория не сможет увидеть подаваемую информацию, будет
сильно отвлекаться от рассказа, пытаясь хоть что-то разобрать, или вовсе утратит весь интерес. Для
этого нужно правильно подобрать шрифт, учитывая, где и как будет происходить трансляция презентации,
а также правильно подобрать сочетание фона и текста. - Важно провести репетицию Вашего доклада, продумать, как Вы поздороваетесь с аудиторией, что скажете
первым, как закончите презентацию. Все приходит с опытом. - Правильно подберите наряд, т.к. одежда докладчика также играет большую роль в восприятии его
выступления. - Старайтесь говорить уверенно, плавно и связно.
- Старайтесь получить удовольствие от выступления, тогда Вы сможете быть более непринужденным и будете
меньше волноваться.
Моделирование решения задач линейного программирования в Excel
Выполнила: студентка группы МДИ-117
Федюшкина В. А.
Проверила: Кормилицына Т. В.
Линейная оптимизация – это раздел математического программирования, посвящённый нахождению экстремума линейных функций нескольких переменных при дополнительных линейных ограничениях, которые налагаются на переменные.
Использование электронных таблиц широко распространено для решения многочисленных и разнообразных задач, связанных с учётом и контролем результатов управленческой деятельности.
Алгоритм решения задач линейного программирования в MS Excel
- Составить математическую модель задачи;
- Внести исходные данные задачи и ограничения;
- Выделить место под ячейки решения и целевую функцию, ввести ее формулу;
- Запустить надстройку Поиск решения;
- Установить нужные параметры решения и запустить выполнение.
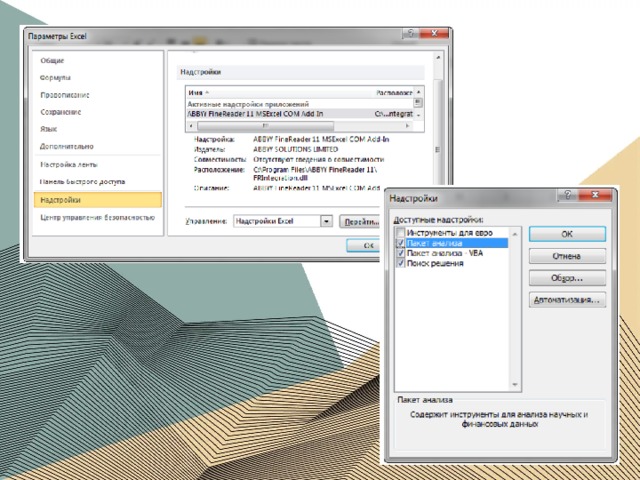
Использование надстройки Excel для решения задач линейного программирования
Поиск решения – это надстройка EXCEL, которая позволяет решать оптимизационные задачи. Если команда Поиск решения или группа Анализ отсутствует, необходимо загрузить надстройку Поиск решения.
Реализация решения задачи на определение оптимального ассортимента продукции
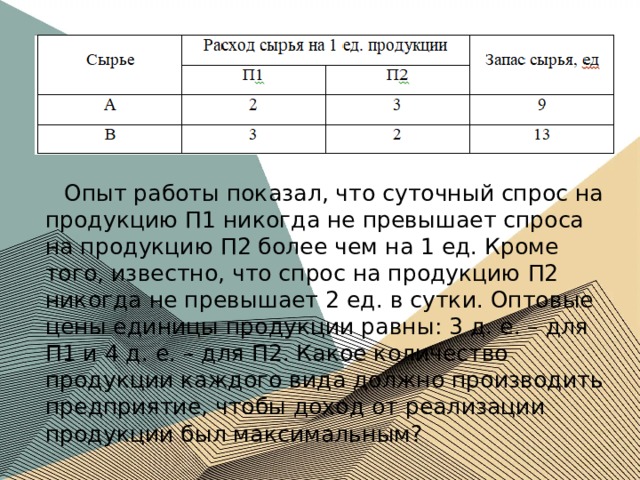
Задача. Предприятие изготавливает два вида продукции – П1 и П2, которая поступает в оптовую продажу. Для производства продукции используются два вида сырья – А и В. Максимально возможные запасы сырья в сутки составляют 9 и 13 ед. соответственно. Расход сырья на единицу продукции вида П1 и П2.
Опыт работы показал, что суточный спрос на продукцию П1 никогда не превышает спроса на продукцию П2 более чем на 1 ед. Кроме того, известно, что спрос на продукцию П2 никогда не превышает 2 ед. в сутки. Оптовые цены единицы продукции равны: 3 д. е. – для П1 и 4 д. е. – для П2. Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?
Решение
Должны выполняться следующие неравенства:
Доход составит:
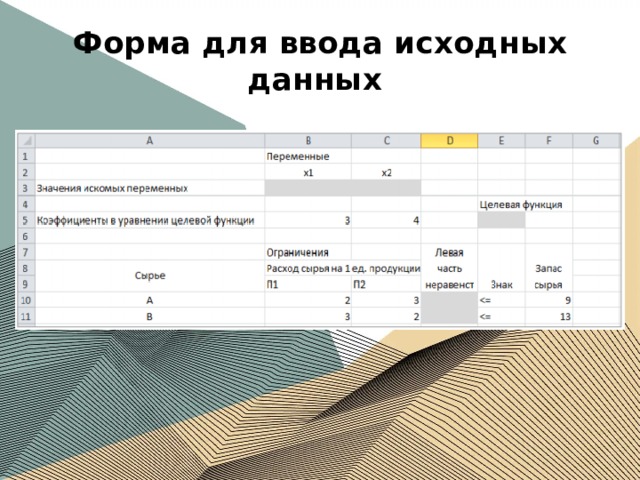
Форма для ввода исходных данных
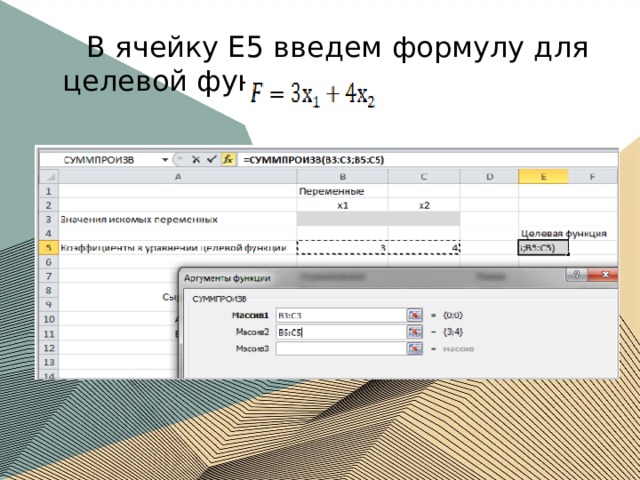
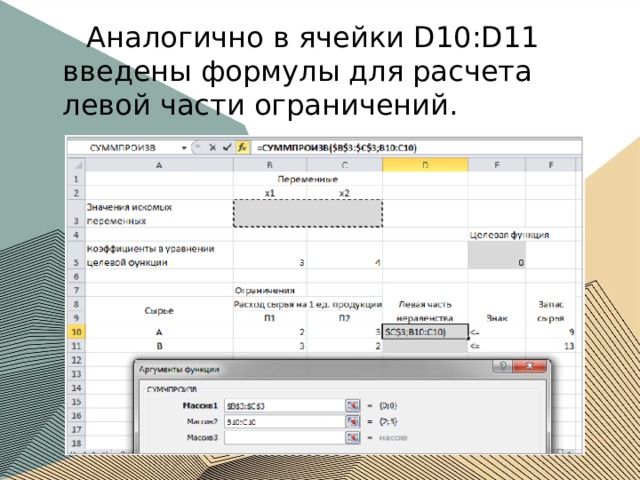
В ячейку E5 введем формулу для целевой функции:
Аналогично в ячейки D10:D11 введены формулы для расчета левой части ограничений.
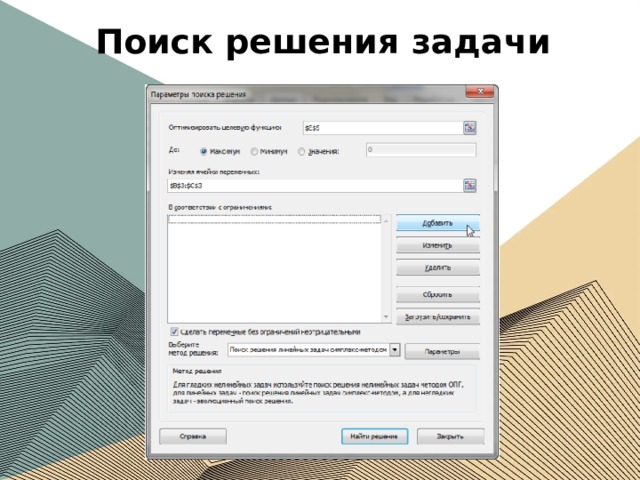
Поиск решения задачи
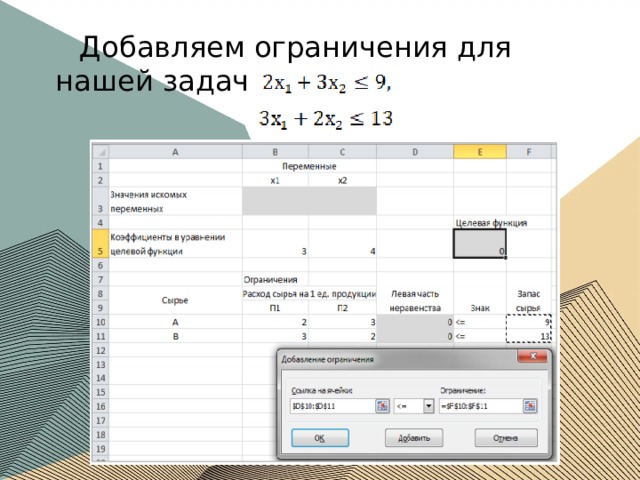
Добавляем ограничения для нашей задачи.
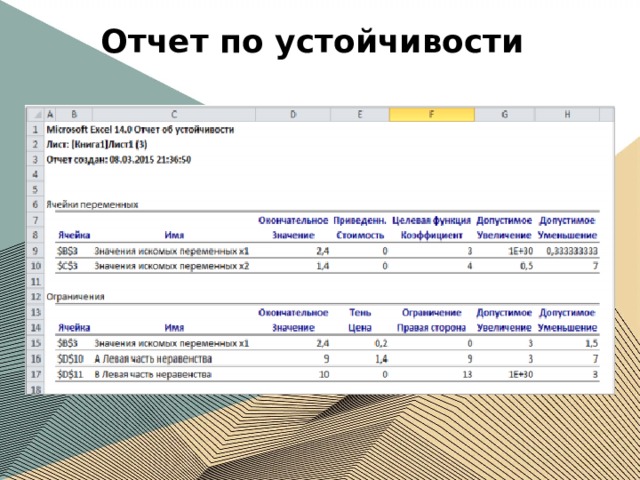
Отчет по устойчивости
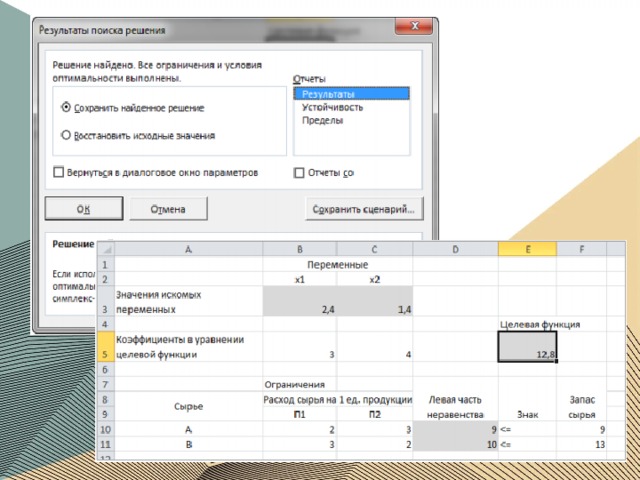
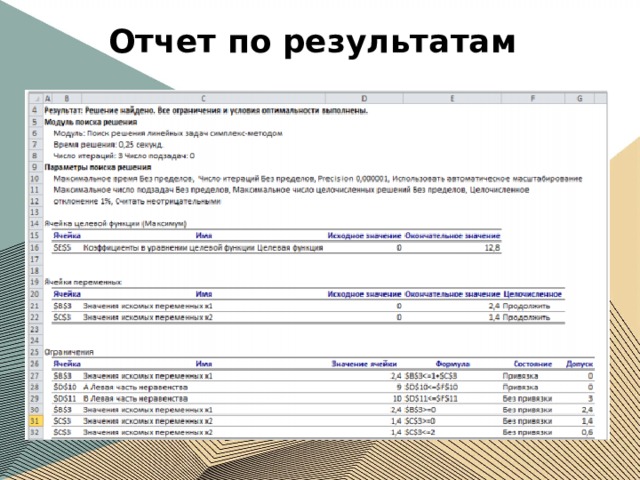
Отчет по результатам
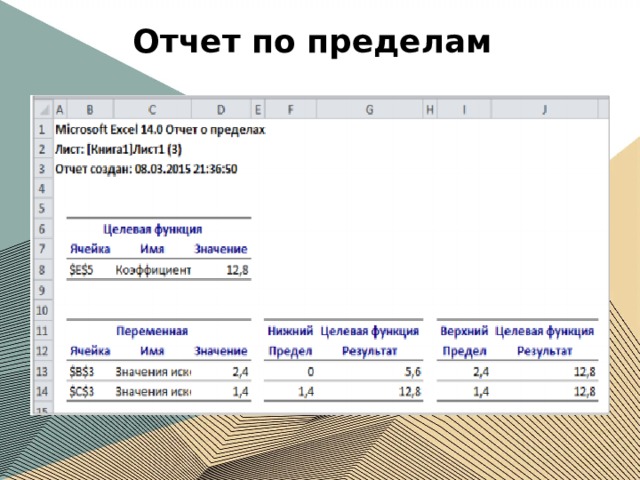
Отчет по пределам
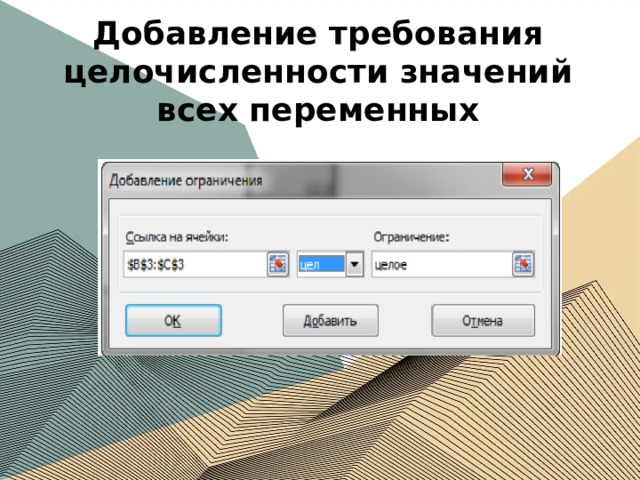
Добавление требования целочисленности значений всех переменных
Решение задачи при условии целочисленности ее переменных
Вывод
Надстройка Поиск решения в Microsoft Excel даёт возможность найти решение, оптимальное при нескольких входных значениях и наборе ограничений на решение. В результате поиска решения EXCEL выводит сообщения о том, удалось ли получить оптимальное решение задачи.
Список использованной литературы
- Акулич, И. Л. Математическое программирование в примерах и задачах : учеб. пособие для студентов экон. спец. сузов / И. Л. Акулич. – М. : Высш. шк., 1986. – 319 с.
- Банди Б. «Основы линейного программирования»: Пер. с англ. — М.: Радио и связь, 1989.
- Васильев, А. Н. Финансовое моделирование и оптимизация средствами Excel2007 / А. Н. Васильев. – СПб. : Питер, 2009. – 320 с.
- Додж М. и др. «Эффективная работа с Microsoft Excel», 2000.СПб.:Питер, 2001.
- Иванов, И. Microsoft Excel 2010 для квалифицированного пользователя / И. Иванов. – М. : Академия АЙТИ, 2011. – 244 с.
- Леоненков, А. В. Решение задач оптимизации в среде MS Excel / А. В. Леоненков. – СПб. : БХВ-Петербург, 2005. – 704 с.
- Справка и инструкции по Excel // Поддержка по Microsoft Office [Электронный ресурс]. – Режим доступа: http://office.microsoft.com/ru-ru/excel-help (дата обращения: 14.08.2014).
- Решение задач оптимизации управления с помощью MS Excel 2010 // НОУ «ИНТУИТ» [Электронный ресурс]. – Режим доступа: http://www.intuit.ru/studies/courses/4751/1020/info (дата обращения: 09.03.2015).
- Рудикова Л. В., Microsoft Excel для студента / Л. В. Рудикова – Санкт – Петербург, БХВ-Петербург, 2005;
- Уокенбах, Дж. Microsoft Excel 2010. Библия пользователя : пер. с англ. / Дж. Уокенбах. – М. : И. Д. Вильямс, 2011. – 912 с.
- Уокенбах, Дж. Формулы в Microsoft Excel 2010 : пер. с англ. / Дж. Уокенбах. – М. : И. Д. Вильямс, 2011. – 704 с.
Вы можете изучить и скачать доклад-презентацию на
тему Решение задач линейного программирования в MS Excel.
Презентация на заданную тему содержит 28 слайдов. Для просмотра воспользуйтесь
проигрывателем,
если материал оказался полезным для Вас — поделитесь им с друзьями с
помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации»
Информатика»
Презентация Решение задач линейного программирования в MS Excel
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Решение задач линейного программирования
в MS Excel
Слайд 2
Слайд 3
Слайд 4
Слайд 5
Слайд 6
Слайд 7
Слайд 8
Слайд 9
Слайд 10
Слайд 11
Слайд 12
Слайд 13
Слайд 14
Слайд 15
Слайд 16
Слайд 17
Слайд 18
Слайд 19
Слайд 20
Слайд 21
Слайд 22
Слайд 23
Слайд 24
Слайд 25
Слайд 26
Слайд 27
Слайд 28
Презентация на тему Решение задач линейного программирования в MS Excel доступна для скачивания ниже:
Отправить презентацию на почту
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
- Размер: 1.4 Mегабайта
- Количество слайдов: 28















Слайд 1Использование MS Excel для решения задач линейного программирования

Слайд 2Линейное программирование в Excel
Общие правила
1. Ввести условие задачи:
a) создать экранную форму для
ввода условия задачи:
· переменных,
· целевой функции (ЦФ),
· ограничений,
· граничных условий;

Слайд 3Линейное программирование в Excel
Общие правила
1. Ввести условие задачи:
b) ввести исходные данные в
экранную форму:
· коэффициенты ЦФ,
· коэффициенты при переменных в ограничениях,
· правые части ограничений;

Слайд 4Линейное программирование в Excel
Общие правила
1. Ввести условие задачи:
c) ввести зависимости из математической
модели в экранную форму:
· формулу для расчета ЦФ,
· формулы для расчета значений левых частей ограничений;

Слайд 5Линейное программирование в Excel
Общие правила
1. Ввести условие задачи:
d) задать ЦФ (в окне «Поиск решения»):
·
целевую ячейку,
· направление оптимизации ЦФ;

Слайд 6Линейное программирование в Excel
Общие правила
1. Ввести условие задачи:
e) ввести ограничения и граничные
условия (в окне «Поиск решения»):
· ячейки со значениями переменных,
· граничные условия для допустимых значений переменных,
· соотношения между правыми и левыми частями ограничений.

Слайд 7Линейное программирование в Excel
Общие правила
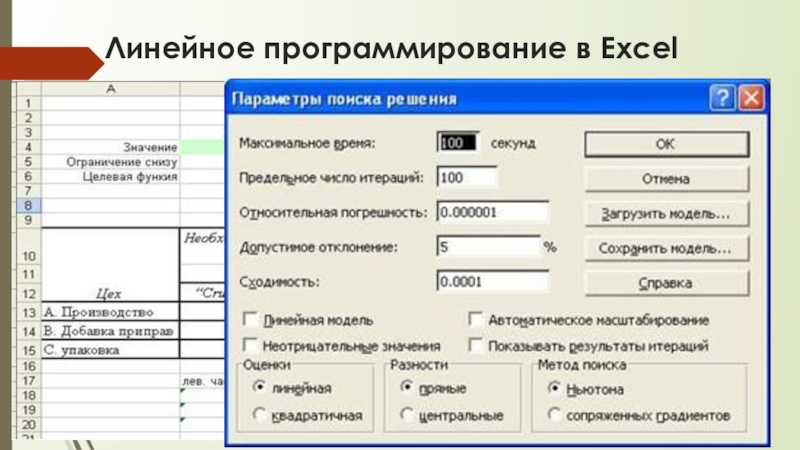
2. Решить задачу:
a) установить параметры решения задачи (в окне «Поиск
решения»);
b) запустить задачу на решение (в окне «Поиск решения»);
c) выбрать формат вывода решения (в окне «Результаты поиска решения»).

Слайд 8Линейное программирование в Excel
ПРИМЕР ЗАДАЧИ
Фабрика выпускает два вида каш для завтрака
— «C1» и «C2».
Используемые для производства обоих продуктов ингредиенты в основном одинаковы и, как правило, не являются дефицитными. Основным ограничением, накладываемым на объем выпуска, является
наличие фонда рабочего времени в каждом из трех цехов фабрики.

Слайд 9Линейное программирование в Excel
ПРИМЕР ЗАДАЧИ
Управляющему необходимо разработать план производства на месяц.
В приведенной ниже таблице указаны
общий фонд рабочего времени и
число человеко-часов, требуемое
для производства 1 т продукта.

Слайд 10Линейное программирование в Excel
ПРИМЕР ЗАДАЧИ
На настоящий момент нет никаких ограничений на
возможные объемы продаж. Имеется возможность продать всю произведенную продукцию.

Слайд 11Линейное программирование в Excel
Формальная постановка задачи
Неизвестные:
Xi – количество произведенного товара
за заданный период (i=1…2)[т]
Ограничения:
Xi >=0, i=1…2
![Презентация по решению ЗЛП в EXCEL Линейное программирование в ExcelФормальная постановка задачи Неизвестные:Xi – количество произведенного товара Линейное программирование в ExcelФормальная постановка задачи Неизвестные:Xi – количество произведенного товара за заданный период (i=1…2)[т]Ограничения:Xi >=0,](https://shareslide.ru/img/thumbs/bf1f825cc964ada2fbaef46df2f02dba-800x.jpg)
Слайд 12Линейное программирование в Excel
Формальная постановка задачи
Ограничения:
По фонду раб.времени для цеха
А
10*X1 +4*X2 <=1000

Слайд 13Линейное программирование в Excel
Формальная постановка задачи
Ограничения:
По фонду раб.времени для цеха
B
3*X1 +2*X2 <=360

Слайд 14Линейное программирование в Excel
Формальная постановка задачи
Ограничения:
По фонду раб.времени для цеха
C
2*X1 +5*X2 <=600

Слайд 15Линейное программирование в Excel
Формальная постановка задачи
Функция цели:
Прибыль 150*X1 +75*X2 ->max
Управляющему
необходимо разработать план
производ
ства на
месяц

Слайд 16Линейное программирование в Excel
Формальная постановка задачи
Неизвестные: Xi – (i=1…2)[т]
Ограничения:
Xi >=0, i=1…2;
10*X1 +4*X2 <=1000;
3*X1 +2*X2 <=360;
2*X1 +5*X2 <=600;
Функция цели: 150*X1 +75*X2 ->max
2неизв+5огр
![Презентация по решению ЗЛП в EXCEL Линейное программирование в ExcelФормальная постановка задачи Неизвестные: Xi – (i=1…2)[т]Ограничения: Линейное программирование в ExcelФормальная постановка задачи Неизвестные: Xi – (i=1…2)[т]Ограничения:](https://shareslide.ru/img/tmb/7/672663/605b9d47f80a367662f4f571b9dd3912-800x.jpg)
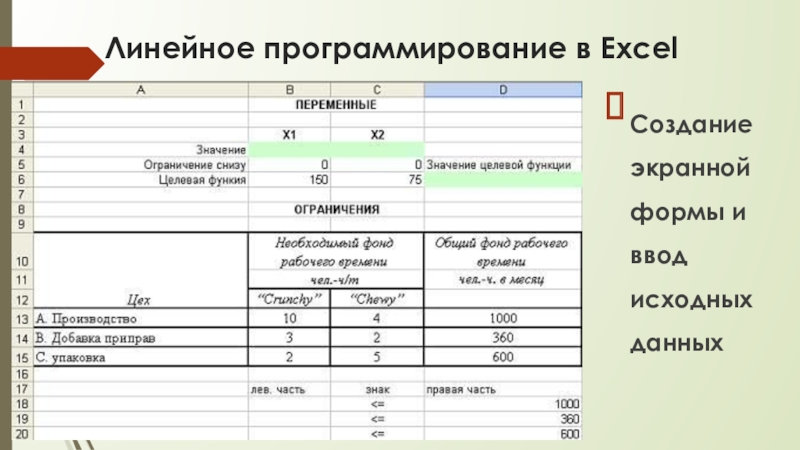
Слайд 17Линейное программирование в Excel
Создание экранной формы и ввод исходных данных
Слайд 18Линейное программирование в Excel
варьиру-емые ячейки
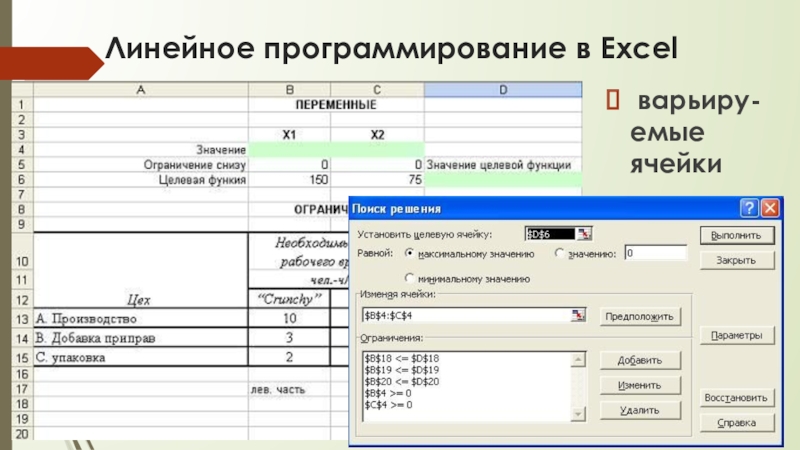
Слайд 19Линейное программирование в Excel
Формулы, описывающие ограничения модели
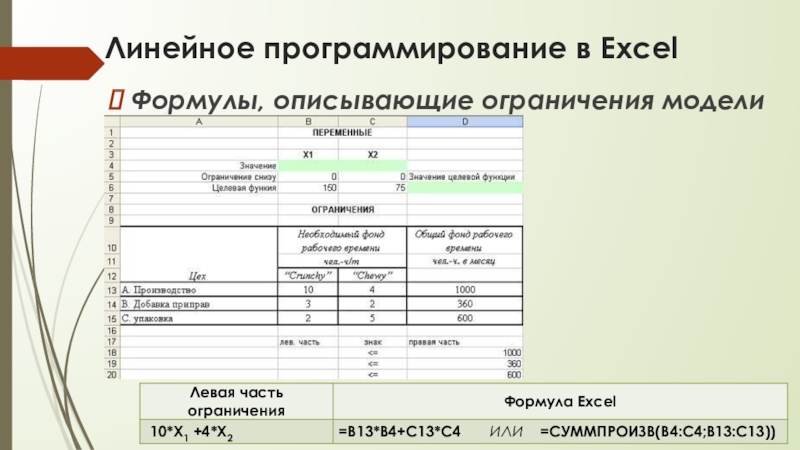
Слайд 20Линейное программирование в Excel
Формулы, описывающие ограничения модели
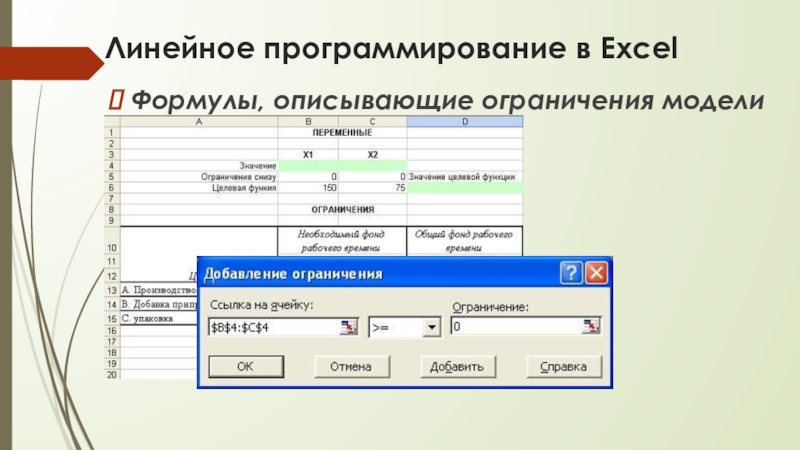
Слайд 21Линейное программирование в Excel
Формулы, описывающие ограничения модели
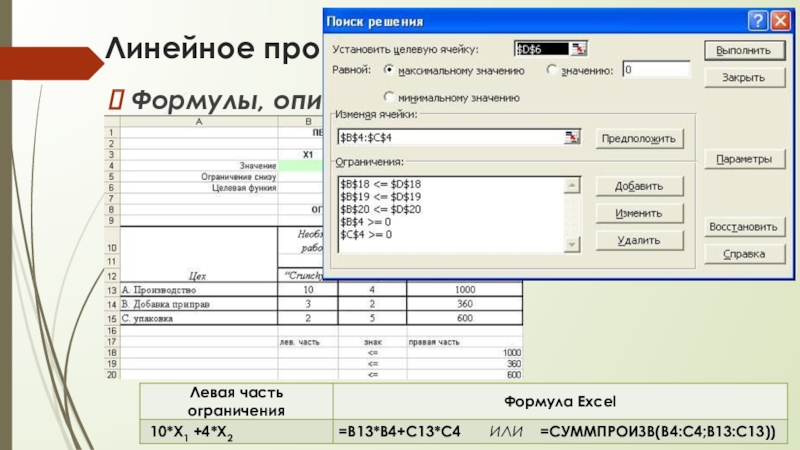
Слайд 22Линейное программирование в Excel
Установить целевую ячейку
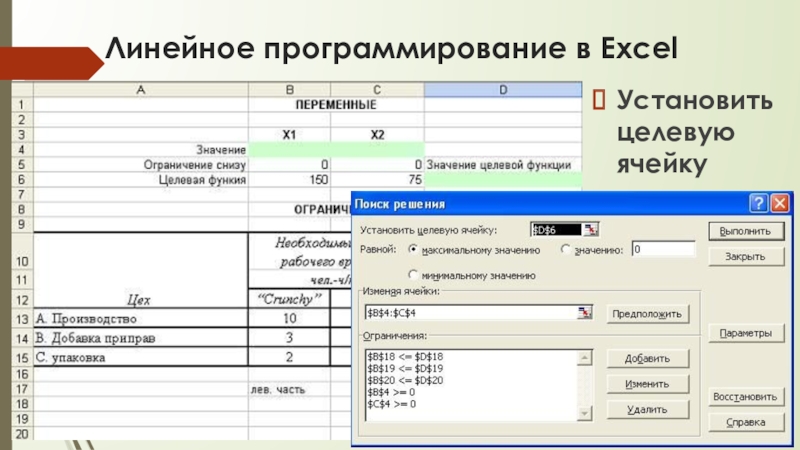
Слайд 23Линейное программирование в Excel
выполнить
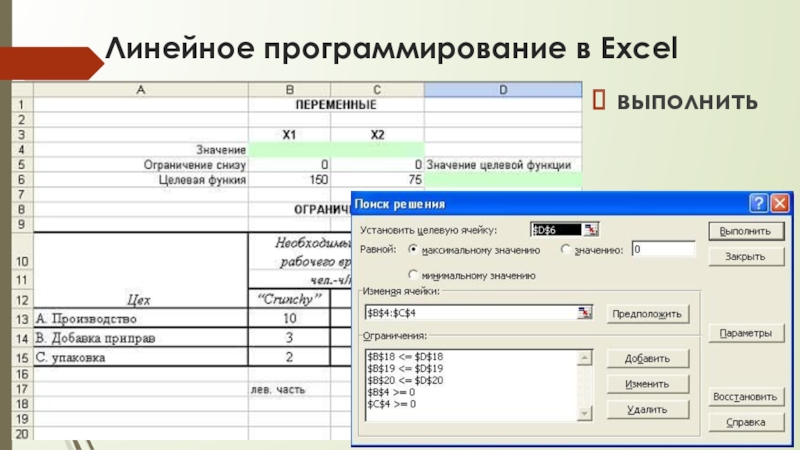
Слайд 24Линейное программирование в Excel
выполнить
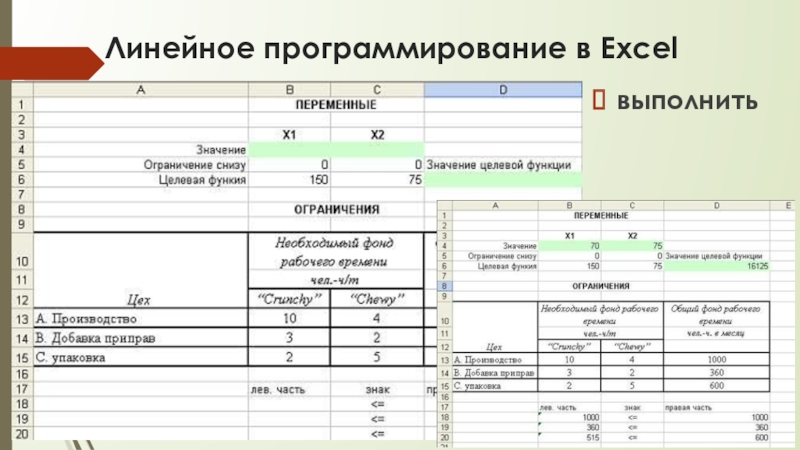
Слайд 25Линейное программирование в Excel
выполнить
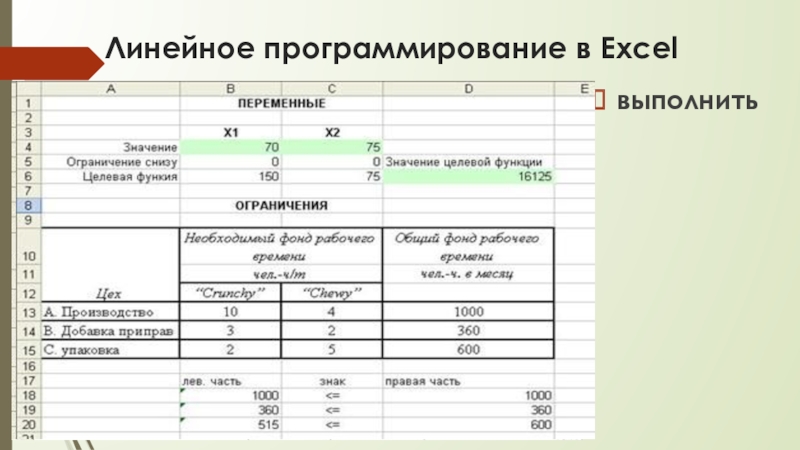
Слайд 26Линейное программирование в Excel
выполнить
Обратная связь
Если не удалось найти презентацию, то Вы можете заказать её на нашем сайте. Мы постараемся найти
нужную Вам презентацию в электронном виде и отправим ее по электронной почте.
Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: mypresentation.ru@ya.ru
Мы в социальных сетях
Социальные сети давно стали неотъемлемой частью нашей жизни. Мы узнаем из них новости, общаемся
с друзьями, участвуем в интерактивных клубах по интересам
ВКонтакте
Что такое Mypresentation.ru?
Mypresentation.ru – это сообщество, где обмениваются знаниями с помощью презентаций онлайн.
Сервис позволяет пользователям легко загружать и скачивать презентации, видео, PDF-файлы и
веб-семинары.
Для правообладателей >