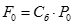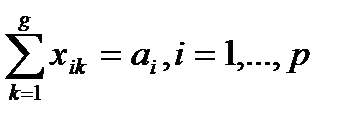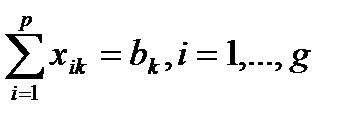Skip to content
Рассмотрим решение задачи линейного программирования с помощью симплекс-метода в Excel на примере
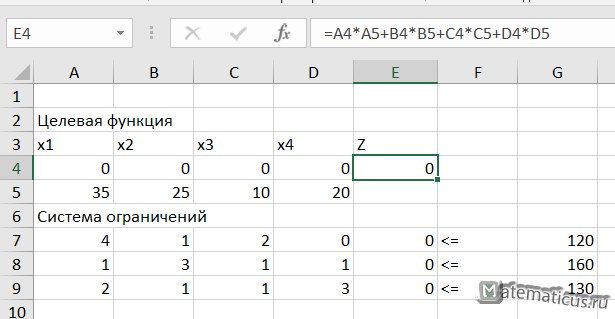
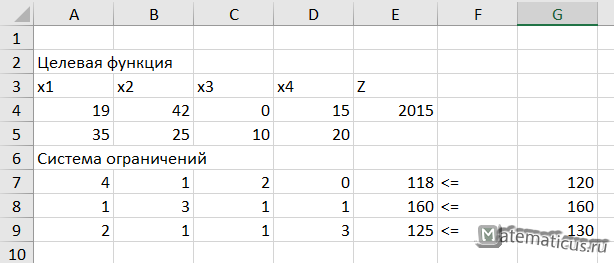
Целевая функция имеет вид
Z = 35∙x1+25∙x2+10∙x3+20∙x4→ max
Ограничения, записанные в виде системы линейных уравнений
4∙x1+1∙x2+2∙x3+0∙x4 ≤ 120
1∙x1+3∙x2+1∙x3+1∙x4 ≤ 160∙
2∙x1+1∙x2+1∙x3+3∙x4 ≤ 130
x1, x2, x3, x4 ≥ 0 – целые
Теперь данную задачу для решения запишем в Excel
В ячейке E4 вставим формулу
=A4*A5+B4*B5+C4*C5+D4*D5
Для ячейки E7, E8 и E9 формула будет иметь вид
=$A$4*A7+$B$4*B7+$C$4*C7+$D$4*D7
=$A$4*A8+$B$4*B8+$C$4*C8+$D$4*D8
=$A$4*A9+$B$4*B9+$C$4*C9+$D$4*D9
Также можно воспользоваться формулой:
=СУММПРОИЗВ(A4:D4;A7:D7)
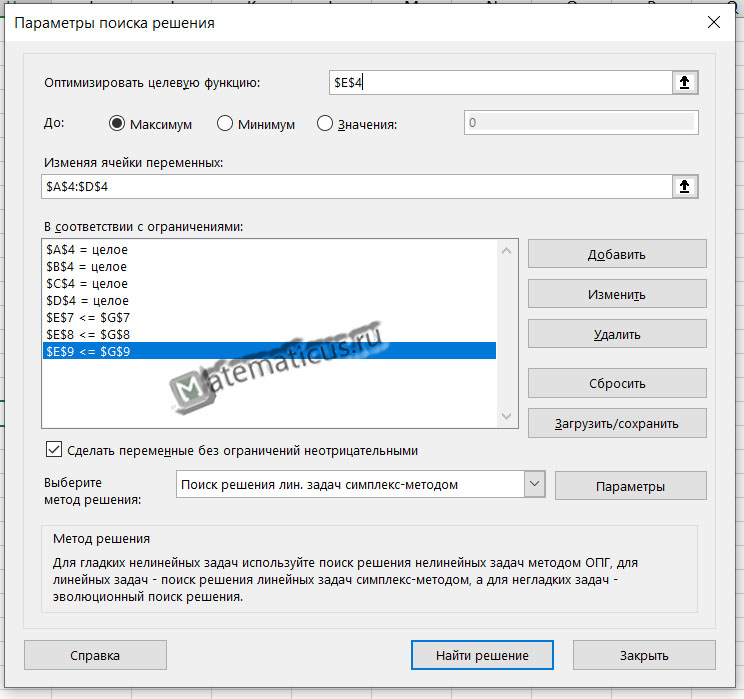
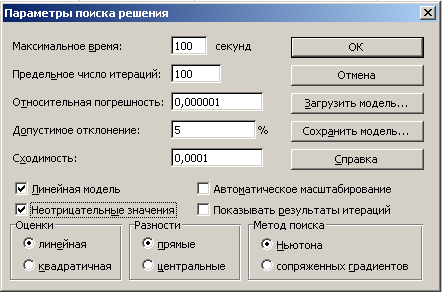
На вкладке данные переходим в Поиск решения
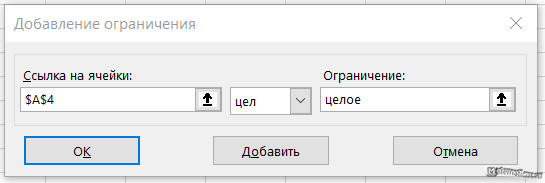
Выбираем ячейку с целевой функцией, ставим галочку максимум, далее выбираем ячейки изменяемых переменных ($A$4:$D$4) и добавляем ограничения при помощи кнопки Добавить. Также ставим галочку переменные без ограничений неотрицательные, выбираем, выбираем метод решения – симплекс-метод решения линейных задач.
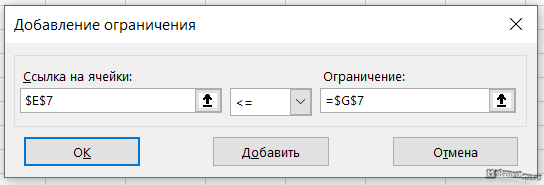
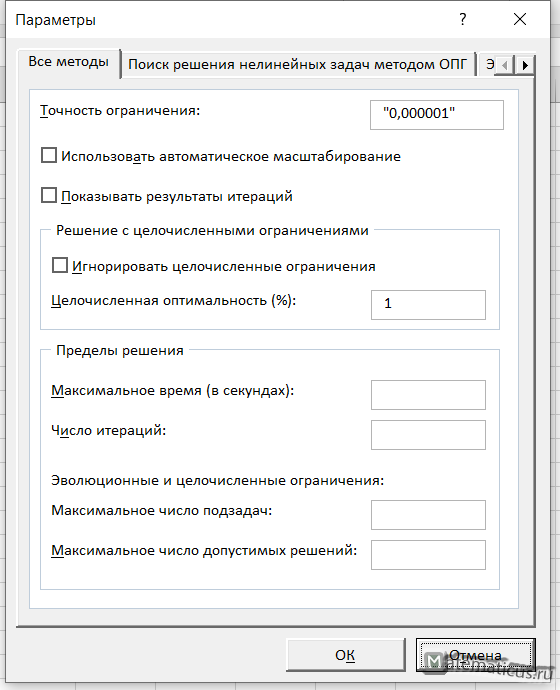
Можно также перейти в параметры и настроить точность.
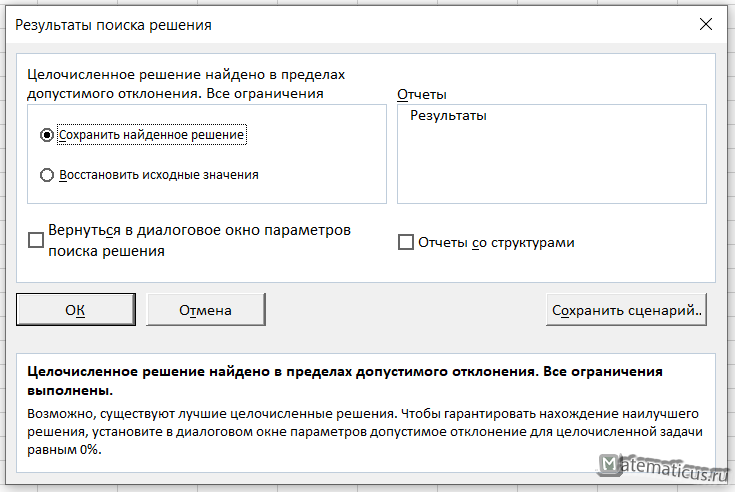
Итак, нажимаем Найти решение, появляется окно результаты поиска решений, выбираем сохранить найденное решение.
В итоги получили решения задачи
Z=2015
x1=19; x2=42; x3=0; x4=15
21595
В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel, нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel» внизу окна:
Если данная команда отсутствует в списке, необходимо выполнить команду Сервис / Надстройки
вид поиска (максимальное значение)
в поле изменяя ячейки : $B$2:$D$2
в поле Ограничения добавьте заданные ограничения
Поле должно иметь следующее содержание:
$B$2:$D$2>=0
$G$6 Выполнить
Иногда задание звучит следующим образом: расчеты осуществить на ЭВМ, привести распечатку полученных результатов.
MS Excel позволяет представить результаты поиска решения в форме отчета. Существует три типа таких отчетов:
- Результаты (Answer). В отчет включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях.
- Устойчивость (Sensitivity). Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.
- Пределы (Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.
Пример. В библиотеке работают 6 пожилых уборщиц. Каждая из них по своим физическим возможностям и состоянию здоровья может выполнять только определенные виды работ, причем с определенной производительностью. Площадь каждой из работ известна. Нужно добиться минимума времени на уборку помещений.
| ПРОИЗВОДИТЕЛЬНОСТЬ БАБУШЕК м 2 . /мин | |||||||
| Баба Аня | Белла Петровна | Баба Варя | Баба Галя | Домна Ивановна | Евгения Карловна | Площадь работ | |
| Мытье окон | 2 | 1 | 46 | ||||
| Мытье полов | 1 | 300 | |||||
| Протирка столов | 2 | 0.2 | 1 | 50 | |||
| Чистка дорожек | 2 | 4 | 100 |
Пример.На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество корма каждого вида, которое должны ежедневно получать лисицы и песцы, приведено в таблице. В ней же указаны общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца.
Найти оптимальное соотношение количества кормов и численности поголовья лис и песцов.
Для упрощения процесса вычислений при решении ЗЛП симплекс-методом можно использовать Microsoft Excel.
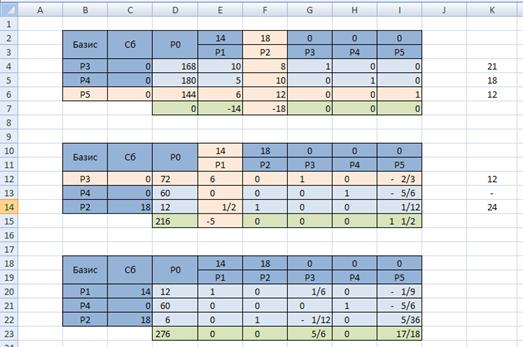
Найдем решение нашей задачи симплекс-методом с помощью Microsoft Excel.
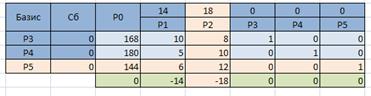
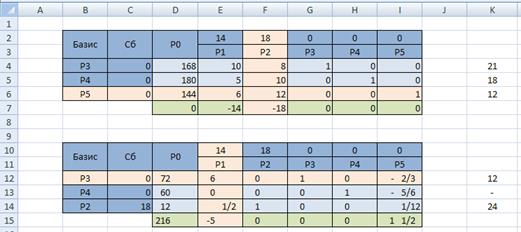
Запустите Excel и подготовьте начальную симплекс таблицу по образцу:
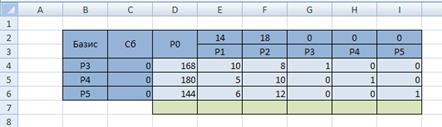
Вычислим значение 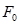
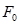
Для вычисления скалярного произведения двух векторов используется функция
СУММПРОИЗВ(массив1, [массив2], [массив3]. ),
В ячейку D7 вводится формула, вычисляющая значение 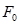
Для вычисления оценок 
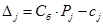
Выделите ячейку D7 и введите формулу:
Аналогично вычислите значения других оценок.
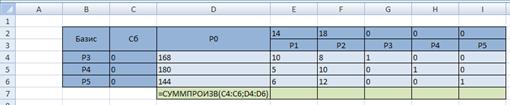
Определим разрешающий столбец – столбец с наибольшей по модулю отрицательной оценкой и найдем отношение элементов столбца 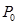
Скопируйте формулу на диапазон K4 : K6
Таким образом, разрешающий столбец – столбец 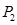
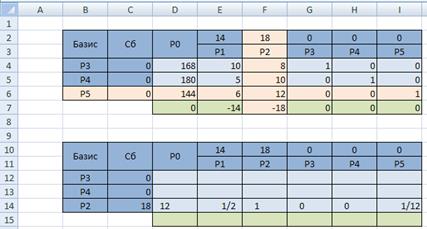
Создайте вторую симплекс-таблицу (скопируйте предыдущую и удалите все ненужно). Произведите замену в базисе вектора 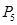
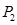
Выделите диапазон D12:I15 и укажите смените формат числовых данных на дробный
Вычислите новые элементы разрешающей строки: разделить элементы разрешающей строки на разрешающий элемент.
В ячейку D14 введите формулу
Скопируйте формулу на диапазон E14 : I14:
| В ячейку D12 введите формулу: =D14*(-$F$4)+D4 Скопируйте формулу на диапазон E12:I12. В ячейку D13 введите формулу: =D14*(-$F$5)+D5 Скопируйте формулу на диапазон E13:I13. В ячейку D15 введите формулу: =D14*(-$F$5)+D5 Скопируйте формулу на диапазон E15:I15. |  |
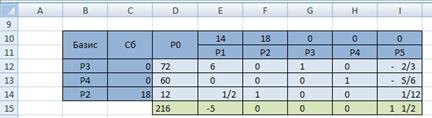
Так как строка оценок содержит отрицательное число, и соответствующий столбец содержит положительные числа, то план можно улучшить.
Выбираем разрешающую строку и разрешающий столбец:
Строим новую симплекс-таблицу и заменяем вектор 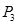
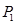
Так как строка оценок не содержит отрицательных значений, то полученный план оптимален и имеет вид:
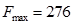
Ответ: 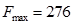
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9622 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Для решения задач линейного программирования симплекс-методом в среде MS Excel заполняются ячейки исходными данными в режиме чисел и формулами математической модели.
MS Excel позволяет получить оптимальное решение без ограничения размерности системы неравенств целевой функции.
Решим задачу о выпускаемых изделиях симплекс-методом применяя надстройку «Поиск решения» в MS Excel.
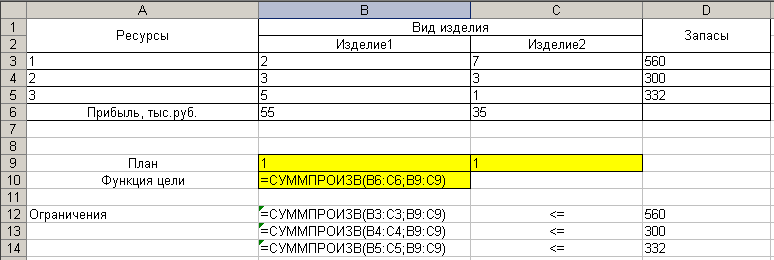
1. Заполните таблицу Excel в режиме чисел (рис.1)
2. Заполните таблицу Excel в режиме формул (рис.2)
Рис.1 Таблица в режиме чисел
Рис.1 Таблица в режиме формул
Здесь: В9:С9 – результат (оптимальное количество изделий каждого вида);
В6:С6 – коэффициенты целевой функции;
В10 – значение целевой функции;
В3:С5 – коэффициенты ограничений;
D12:D14 – правая часть ограничений;
B12:B14 – вычисляемые (фактические) значения левой части ограничений.
Решим задачу с помощью команды Данные/Поиск решения. На экране появляется диалоговое окно Поиск решения.
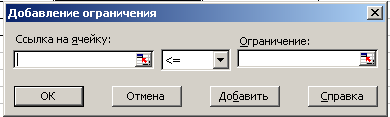
В поле Установить целевую функция будет показана ссылка на активную ячейку, т.е. на В10. Причем эта ссылка абсолютная. В секции Равной устанавливаем переключатель Максимальному (минимальному) значению в зависимости от целевой функции. Ограничения устанавливаются с помощью кнопки Добавить, которая вызывает диалоговое окно их ввода Добавление ограничения.
В поле ввода Ссылка на ячейку: указывается адрес ячейки, содержащей формулу левой части ограничения. Затем выбирается из списка знак соотношения. В поле Ограничение указывается адрес ячейки, содержащей правую часть ограничения. Щёлкаем на кнопку Добавить и повторяем до следующего ограничения. После ввода всех ограничений нажимаем ОК.
Так как все переменные несут условия неотрицательности, то их положительность задается через кнопку Параметры в окне диалога Поиск решения. После щелчка по ней, на экране окно Параметры поиска решения.
Устанавливаем флажок Сделать переменные без ограничений неотрицательными и выбрать Метод решения Поиск решения линеных задач симплекс-методом. Щёлкаем на кнопке Найти решение.
Excel предъявит окно Результаты поиска решения с сообщением о том, что решение найдено, или о том, что не может найти подходящего решения.
Если вычисления оказались успешными, Excel предъявит следующее окно итогов. Их можно сохранить или отказаться. Кроме того, можно получить один из трёх видов отчётов (Результаты,Устойчивость,Пределы), позволяющие лучше осознать полученные результаты, в том числе, оценить их достоверность.
После найденного решения, в ячейках В9:С9 появится оптимальное количество изделий каждого вида.
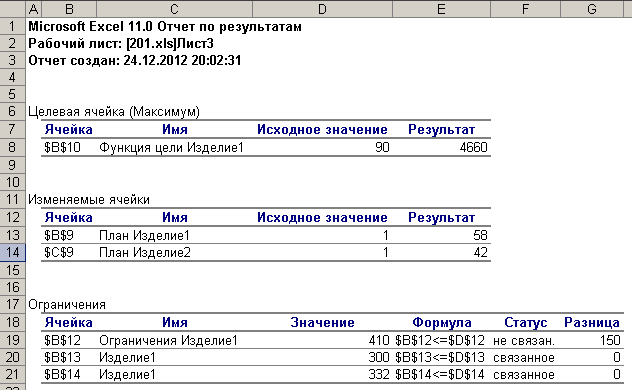
При сохранении отчета выберите – Отчет по результатам (рис.3).
Из отчета видно, что ресурс 1 не используется полностью на 150 кг, а ресурс 2 и 3 используется полностью.
В результате получен оптимальный план, при котором изделий 1 вида необходимо выпустить в количестве 58 шт., а изделий 2 вида в количестве 42 шт. При этом прибыль от их реализации максимальная и составляет 4660 тыс.руб.
Рис.3 Отчет по результатам
1. Со станции формирования ежедневно отправляются пассажирские и скорые поезда, составленные из плацкартных, купейных и мягких вагонов. Число мест в плацкартном вагоне – 54, в купейном – 36, в мягком – 18. В таблице указаны состав поезда каждого типа и количество имеющихся в парке вагонов различного типа. Определить число скорых и пассажирских поездов, которые необходимо формировать ежедневно, чтобы число перевозимых пассажиров было максимальным.
| 1 | плац | куп | мягк |
| скор | 2 | 6 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 50 | 60 | 26 |
| 2 | плац | куп | мягк |
| скор | 2 | 6 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 50 | 66 | 26 |
| 3 | плац | куп | мягк |
| скор | 2 | 6 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 55 | 60 | 26 |
| 4 | плац | куп | мягк |
| скор | 2 | 6 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 55 | 66 | 26 |
| 5 | плац | куп | мягк |
| скор | 2 | 7 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 55 | 77 | 28 |
| 6 | плац | куп | мягк |
| скор | 2 | 7 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 55 | 84 | 28 |
| 7 | плац | куп | мягк |
| скор | 4 | 6 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 60 | 60 | 26 |
| 8 | плац | куп | мягк |
| скор | 4 | 6 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 60 | 66 | 26 |
| 9 | плац | куп | мягк |
| скор | 4 | 6 | 2 |
| пасс | 5 | 2 | 2 |
| парк | 60 | 72 | 26 |
| 10 | плац | куп | мягк |
| скор | 2 | 7 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 55 | 91 | 28 |
| 11 | плац | куп | мягк |
| скор | 3 | 7 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 60 | 70 | 28 |
| 12 | плац | куп | мягк |
| скор | 2 | 6 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 50 | 72 | 26 |
| 13 | плац | куп | мягк |
| скор | 3 | 7 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 60 | 70 | 28 |
| 14 | плац | куп | мягк |
| скор | 3 | 7 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 60 | 84 | 28 |
| 15 | плац | куп | мягк |
| скор | 3 | 6 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 55 | 72 | 26 |
| 16 | плац | куп | мягк |
| скор | 3 | 7 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 60 | 91 | 28 |
| 17 | плац | куп | мягк |
| скор | 2 | 8 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 60 | 96 | 30 |
| 18 | плац | куп | мягк |
| скор | 2 | 8 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 60 | 96 | 30 |
| 19 | плац | куп | мягк |
| скор | 2 | 8 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 60 | 104 | 30 |
| 20 | плац | куп | мягк |
| скор | 2 | 8 | 2 |
| пасс | 5 | 7 | 2 |
| парк | 60 | 112 | 30 |
| 21 | плац | куп | мягк |
| скор | 1 | 8 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 55 | 96 | 30 |
| 22 | плац | куп | мягк |
| скор | 1 | 8 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 55 | 104 | 30 |
| 23 | плац | куп | мягк |
| скор | 4 | 7 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 65 | 91 | 28 |
| 24 | плац | куп | мягк |
| скор | 4 | 7 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 65 | 84 | 28 |
| 25 | плац | куп | мягк |
| скор | 4 | 7 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 65 | 70 | 28 |
| 26 | плац | куп | мягк |
| скор | 4 | 7 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 65 | 77 | 28 |
| 27 | плац | куп | мягк |
| скор | 1 | 7 | 2 |
| пасс | 5 | 3 | 2 |
| парк | 50 | 70 | 28 |
| 28 | плац | куп | мягк |
| скор | 1 | 7 | 2 |
| пасс | 5 | 4 | 2 |
| парк | 50 | 77 | 28 |
| 30 | плац | куп | мягк |
| скор | 1 | 7 | 2 |
| пасс | 5 | 6 | 2 |
| парк | 50 | 91 | 28 |
| 29 | плац | куп | мягк |
| скор | 1 | 7 | 2 |
| пасс | 5 | 5 | 2 |
| парк | 50 | 84 | 28 |
Решение транспортных задач
Транспортными задачами называются задачи определения оптимального плана перевозок груза из данных пунктов отправления в заданные пункты потребления.
| b1 | b2 | … | bk | … | bg | |
| a1 | [c11 x11 | [c12 x12 | … | [c1k x1k | … | [c1g x1g |
| a2 | [c21 x21 | [c22 X22 | … | [c2k x2k | … | [c2g x2g |
| … | … | … | … | … | … | … |
| ai | [ci2 xi2 | [ci2 xi2 | … | [cik xik | … | [cig xig |
| … | … | … | … | … | … | … |
| ap | [cp2 xp2 | [cp2 xp2 | … | [cpk xpk | … | [cpg xpg |
Если 
Переменные должны удовлетворять условиям
Суммарные затраты на перевозки
Решение такой задачи разбивается на два этапа:
1. Определение опорного (базисного) решения;
2. Построение последовательных итераций, т.е. приближение к оптимальному решению.
Для каждого из этих этапов существует несколько методов.
Для построения опорного решения чаще всего используют метод «северо-западного угла» и метод минимальных тарифов.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
Калькулятор симплекс-метода
Количество переменных:
Количество ограничений:
Очистить
Решить
В двойственную
Выполнено действий:
Как пользоваться калькулятором
- Задайте количество переменных и ограничений
- Введите коэффициенты целевой функции
- Введите коэффициенты ограничений и выберите условия (≤, = или ≥)
- Выберите тип решения
- Нажмите кнопку «Решить»
Что умеет калькулятор симплекс-метода
- Решает основную задачу линейного программирования
- Позволяет получить решение с помощью основного симплекс-метода и метода искусственного базиса
- Работает с произвольным количеством переменных и ограничений
Что такое симплекс-метод
Задача линейного программирования — это задача поиска неотрицательных значений параметров, на которых заданная линейная функция достигает своего максимума или минимума при заданных линейных ограничениях.
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Алгоритм является универсальным методом, которым можно решить любую задачу линейного программирования.
Если вам тоже ничего не понятно из этого определения, то вы на верном пути. Чаще всего статьи про симплекс-метод очень сильно углубляются в дебри теории задачи линейного программирования, из-за чего очень легко потерять суть и так ничего и не понять. Мы постараемся описать алгоритм симплекс-метода так, чтобы показать, что в нём нет ничего страшного и на самом деле он весьма простой. Но сначала нам всё-таки потребуется ввести несколько определений.
Целевая функция — функция, максимум (или минимум) которой нужно найти. Представляет собой сумму произведений коэффициентов на значения переменных: F = c1·x1 + c2·x2 + … + cn·xn
Ограничение — условие вида a1·x1 + a2·x2 + … + an·xn v b, где вместо v ставится один из знаков: ≤, = или ≥
План — произвольный набор значений переменных x1 … xn.
Алгоритм решения основной задачи ЛП симплекс-методом
Пусть в задаче есть m ограничений, а целевая функция заивисит от n основных переменных. Первым делом необходимо привести все ограничения к каноническому виду — виду, в котором все условия задаются равенствами. Для этого предварительно все неравенства с ≥ умножаются на -1, для получения неравенств с ≤.
Чтобы привести ограничения с неравенствами к каноническому виду, для каждого ограничения вводят переменную, называемую дополнительной с коэффициентом 1. В ответе эти переменные учитываться не будут, однако сильно упростят начальные вычисления. При этом дополнительные переменные являются базисными, а потому могут быть использованы для формирования начального опорного решения.
Пример 1
Привести к каноническому виду ограничения:
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 200
4·x1 + 6·x2 + 8·x3 ≥ 160
Меняем знаки у ограничений с ≥, путём умножения на -1 и добавляем дополнительные переменные к ограничениям с неравенством:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 200
-4·x1 — 6·x2 — 8·x3 + x5 = -160
Формирование начального базиса
После того как задача приведена к каноническому виду, необходимо найти начальный базис для формирования первого опорного решения. Если в процессе приведения были добавлены дополнительные переменные, то они становятся базисными.
Иначе необходимо выделить среди коэффициентов ограничений столбец, который участвует в формировании единичной матрицы в заданной строке (например, если требуется определить вторую базисную переменную, то необходимо искать столбец, в котором второе число равно 1, а остальные равны нулю). Если такой столбец найден, то переменная, соответствующая этому столбцу, становится базисной.
В противном случае можно поискать столбец, в котором все значения кроме числа в заданной строке равны нулю, и, если он будет найден, то разделить все значения строки на число, стоящее на пересечении этих строки и столбца, тем самым образовав столбец, участвующий в формировании единичной матрицы.
Пример 2
9·x1 + 5·x2 + 4·x3 + 3·x4 + 2·x5 → max
x1 — 2·x2 + 2·x3 ≤ 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 — 4·x3 + 2·x5 = 30
Для ограничения с неравенством добавляем дополнительную переменную x6.
Перепишем ограничения в каноническом виде:
x1 — 2·x2 + 2·x3 + x6 = 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 — 4·x3 + 2·x5 = 30
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Столбец 4 является частью единичной матрицы. Переменная x4 входит в начальный базис
В пятом столбце все значения кроме третьего равны нулю. Поэтому в качестве третьей базисной переменной берём x5, предварительно разделив третью строку на 2.
Симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| ? | 2 | 1 | -4 | 0 | 2 | 0 | 30 |
После преобразования получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 1 |
1 2 |
-2 | 0 | 1 | 0 | 15 |
Если такой столбец отсутствует, то для формирования базиса необходимо применить исключение Гаусса для первого ненулевого столбца, который ещё не является базисным. Для этого вся строка делится на элемент в найденном столбце, а из остальных строк вычитается полученная строка, разделённая на значение, стоящее в этом же столбце. После этой операции все значения вне данной строки будут обнулены, и столбец можно будет считать базисным.
Пример 3
4·x1 + 5·x2 + 4·x3 → max
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 160
4·x1 + 6·x2 + 8·x3 ≤ 200
Для каждого ограничения с неравенством добавляем дополнительные переменные x4 и x5.
Перепишем ограничения в каноническом виде:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 160
4·x1 + 6·x2 + 8·x3 + x5 = 200
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Начальная симплекс-таблица
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| ? | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
Для определения второй базисной переменной ищем первый ненулевой столбец, который ещё не является базисным. Первый столбец не нулевой и не является базисным. Выполняем исключение Гаусса: делим строку 2 на 4, а из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент в первом столбце.
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 3 | 6 | 1 | 0 | 240 |
| x1 | 4 | 2 | 4 | 0 | 0 | 160 |
| x5 | 4 | 6 | 8 | 0 | 1 | 200 |
После исключения получаем следующую таблицу:
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 0 | 2 | 4 | 1 | 0 | 160 |
| x1 | 1 |
1 2 |
1 | 0 | 0 | 40 |
| x5 | 0 | 4 | 4 | 0 | 1 | 40 |
После того как базис сформирован, нужно построить начальную симплекс-таблицу. Она строится следующим образом:
- Для удобства в первой строке можно записать коэффициенты Ci целевой функции (для дополнительных переменных эти коэффициенты равны нулю)
- Вторая строка формирует шапку таблицы. В ней первый столбец называется базис, а остальные перечисляют основные переменные x1..xn и дополнительные xn+1..xn+k
- Затем построчно перечисляются базисные переменные и коэффициенты ограничений
Схематично начальная таблица будет выглядеть примерно так:
| C | с1 | c2 | … | cn | 0 | 0 | … | 0 | 0 |
|---|---|---|---|---|---|---|---|---|---|
| базис | x1 | x2 | … | xn | xn+1 | xn+2 | … | xn+k | b |
| xe1 | a11 | a12 | … | a1n | a1n+1 | a1n+2 | … | a1n+k | b1 |
| xe2 | a21 | a22 | … | a2n | a2n+1 | a2n+2 | … | a2n+k | b2 |
| … | … | … | … | … | … | … | … | … | … |
| xem | am1 | am2 | … | amn | amn+1 | amn+2 | … | amn+k | bm |
Избавляемся от отрицательных свободных коэффициентов
После приведения к каноническому виду или после алгебраических преобразований при формировании базиса некоторые из свободных коэффициентов (bi) могли стать отрицательными, что не позволяет перейти к дальнейшим вычислениям. Чтобы избавиться от отрицательных значений b необходимо:
- Найти строку, в которой находится максимальное по модулю значение b. Пусть это будет строка i;
- Найти максимальный по модулю элемент в этой строке. Пусть он находится в столбце j;
- Строку i разделить на элемент, стоящий на пересечении i-ой строки и j-го столбца;
- Из каждой оставшейся строки k вычесть строку i, умноженную на элемент строки k и столбца j;
- Переменную, соответствующую найденному столбцу j, сделать базисной (добавить в базис вместо переменной, находящейся в строке i).
Этот шаг необходимо повторять до тех пор, пока все отрицательные b не станут положительными или в строке не останется отрицательных элементов. Если строка с максимальным по модулю bi не содержит отрицательных элементов, то такая задача не имеет решений и на этом алгоритм заканчивает свою работу. В противном случае все bi положительны и алгоритм переходит к следующему этапу — расчёту дельт.
Пример 4
20·x1 + 20·x2 + 10·x3 → min
4·x1 + 3·x2 + 2·x3 ≥ 33
3·x1 + 2·x2 + x3 ≥ 23
x1 + x2 + 2·x3 ≥ 12
Меняем знаки у ограничений с ≥, путём умножения на -1:
-4·x1 — 3·x2 — 2·x3 ≤ -33
— 3·x1 — 2·x2 — x3 ≤ -23
— x1 — x2 — 2·x3 ≤ -12
Для каждого ограничения с неравенством добавляем дополнительные переменные x4..x6.
Перепишем ограничения в каноническом виде:
— 4·x1 — 3·x2 — 2·x3 + x4 = -33
— 3·x1 — 2·x2 — x3 + x5 = -23
— x1 — x2 — 2·x3 + x6 = -12
Ищем начальное базисное решение:
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство, базисной будет добавленная дополнительная переменная x5
Ограничение 3 содержит неравенство, базисной будет добавленная дополнительная переменная x6
Начальная симплекс-таблица
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x4 | -4 | -3 | -2 | 1 | 0 | 0 | -33 |
| x5 | -3 | -2 | -1 | 0 | 1 | 0 | -23 |
| x6 | -1 | -1 | -2 | 0 | 0 | 1 | -12 |
В столбце b присутствуют отрицательные значения.
Максимальное по модулю |b|max = |-33| находится в первой строке.
Максимальный по модулю элемент в первой строке = -4 находится в первом столбце.
В качестве базисной переменной x4 берём x1.
Делим первую строку на -4. Из второй и третьей строк вычитаем первую, умноженную на соответствующий элемент в первом столбце.
Обновлённая таблица:
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 |
3 4 |
1 2 |
—
1 4 |
0 | 0 |
33 4 |
| x5 | 0 |
1 4 |
1 2 |
—
3 4 |
1 | 0 |
7 4 |
| x6 | 0 | —
1 4 |
—
3 2 |
—
1 4 |
0 | 1 | —
15 4 |
В столбце b присутствуют отрицательные значения.
Максимальное по модулю |b|max = |-
| находится в третьей строке.
Максимальный по модулю элемент в третьей строке = —
находится в третьем столбце.
В качестве базисной переменной x6 берём x3.
Делим третью строку на —
. Из первой и второй строк вычитаем третью, умноженную на соответствующий элемент в третьем столбце.
Обновлённая таблица:
| C | 20 | 20 | 10 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 |
2 3 |
0 | —
1 3 |
0 |
1 3 |
7 |
| x5 | 0 |
1 6 |
0 | —
5 6 |
1 |
1 3 |
1 2 |
| x3 | 0 |
1 6 |
1 |
1 6 |
0 | —
2 3 |
5 2 |
Расчёт дельт
Дельты — это параметры, на основании которых проверяется оптимальность текущего решения и улучшается функция. Они рассчитываются для каждой из переменных ограничений и записываются последней строкой таблицы.
Для расчёта дельт используется следующая формула: Δi = ce1·a1i + ce2·a2i + … + cem·ami — ci. Проще говоря, чтобы вычислить дельту по заданной i-ой переменной, нужно перемножить коэффициенты условий в i-ом столбце на коэффициенты целевой функции при соответствующих базисных переменных, сложить эти произведения и вычесть из полученной суммы коэффициент целевой функции столбца i.
Пример 5
Таблица:
| C | 3 | 0 | 2 | 0 | 0 | -6 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x2 | 2 | 1 | -3 | 0 | 0 | 6 | 18 |
| x4 | -3 | 0 | 2 | 1 | 0 | -2 | 24 |
| x5 |
1 5 |
0 |
3 5 |
0 | 1 | —
4 5 |
36 5 |
Вычисляем дельты: Δi = C2·a1i + C4·a2i + C5·a3i — Ci
Симплекс-таблица с дельтами
| C | 3 | 0 | 2 | 0 | 0 | -6 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x2 | 2 | 1 | -3 | 0 | 0 | 6 | 18 |
| x4 | -3 | 0 | 2 | 1 | 0 | -2 | 24 |
| x5 |
1 5 |
0 |
3 5 |
0 | 1 | —
4 5 |
36 5 |
| Δ | -3 | 0 | -2 | 0 | 0 | 6 | 0 |
Проверка плана на оптимальность
После того как дельты рассчитаны, необходимо проверить оптимальность текущего плана. Критерий оптимальности формулируется следующим образом:
При максимизации функции: текущее решение считается оптимальным, если в таблице отсутствуют отрицательные дельты.
При минимизации функции: текущее решение считается оптимальным, если в таблице отсутствуют положительные дельты.
Пример 6
9·x1 + 5·x2 + 4·x3 + 3·x4 + 2·x5 → max
x1 — 2·x2 + 2·x3 ≤ 6
x1 + 2·x2 + x3 + x4 = 24
2·x1 + x2 — 4·x3 + x5 = 30
Симплекс-таблица с дельтами
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Критерий оптимальности: план оптимален, если в таблице отсутствуют отрицательные дельты.
План не оптимален, так как ищется максимум функции, а Δ1 = -2 отрицательна.
Если текущий план оптимален, то алгоритм завершает свою работу. Значениям переменных соответствуют значения столбца свободных коэффициентов b. Если свободной переменной нет в базисе, то её значение считается нулевым. Значение целевой функции, принимаемой на данном наборе, находится в строке с дельтами в том же столбце. Если какое-либо из значений столбца b отрицательно, то решения задачи не существует.
Переход к более оптимальному решению
Если текущий план оказался не оптимальным, то алгоритм ищет столбец с наименьшей (с наибольшей, если ищется минимум) дельтой. После чего вычисляются симплекс-отношения Q. Для этого значения свободных коэффициентов делятся на ненулевые коэффициенты из найденного столбца. Если результат деления получается отрицательным, то такие отношение игнорируются.
Среди найденных симплекс-отношений ищется строка, в которой находится симплекс-отношение с наименьшим значением. Если таких отношений нет, то алгоритм останавливает свою работу, так как целевая функция не ограничена и решения не существует.
Пример 7
Симплекс-таблица с дельтами
| C | 2 | 1 | -2 | 0 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x1 | 1 | -5 | 0 | -3 | 0 | -1 | 25 |
| x5 | 0 | -16 | 0 | -7 | 1 | -3 | 57 |
| x3 | 0 | -6 | 1 | -2 | 0 | -1 | 17 |
| Δ | 0 | 1 | 0 | -2 | 0 | 0 | 16 |
Проверяем план на оптимальность: план не оптимален, так как ищется минимум функции, а Δ2 = 1 положительна.
Определяем разрешающий столбец — столбец, в котором находится максимальная дельта: 2, Δ2: 1
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения второго столбца
| C | 2 | 1 | -2 | 0 | 0 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x1 | 1 | -5 | 0 | -3 | 0 | -1 | 25 | — |
| x5 | 0 | -16 | 0 | -7 | 1 | -3 | 57 | — |
| x3 | 0 | -6 | 1 | -2 | 0 | -1 | 17 | — |
| Δ | 0 | 1 | 0 | -2 | 0 | 0 | 16 |
Все значения второго столбца отрицательны. Функция не ограничена. Оптимальное решение отсутствует.
В противном случае строка с наименьшим отношением считается разрешающей и, аналогично избавлению от отрицательных свободных коэффициентов, делится на разрешающий элемент, расположенный в найденных столбце и строке, и из остальных строк вычитается найденная строка, разделённая на значения, стоящие в этом же столбце соответствующей строки. Переменная, стоящая в разрешающем столбце заменяет базисную переменную, находящуюся в найденной строке.
После этого вычисляются новые дельты и проверяется новый план. Так продолжается до тех пор пока не будет выполнен критерий оптимальности плана или не будет установлено, что решение не существует.
Пример 8
Симплекс-таблица с дельтами
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b |
|---|---|---|---|---|---|---|---|
| x6 | 1 | -2 | 2 | 0 | 0 | 1 | 6 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -2 отрицательна.
Итерация 1
Определяем разрешающий столбец — столбец, в котором находится минимальная дельта: 3, Δ3: -9
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения третьего столбца
В найденном столбце ищем строку с наименьшим значением Q: Qmin = 3, строка 1.
На пересечении найденных строки и столбца находится разрешающий элемент: 2
В качестве базисной переменной x6 берём x3.
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 | 1 | -2 | 2 | 0 | 0 | 1 | 6 | 6 / 2 = 3 |
| x4 | 1 | 2 | 1 | 1 | 0 | 0 | 24 | 24 / 1 = 24 |
| x5 | 2 | 1 | -4 | 0 | 1 | 0 | 30 | — |
| Δ | -2 | 3 | -9 | 0 | 0 | 0 | 132 |
Делим первую строку на 2. Из второй и третьей строк вычитаем первую, умноженную на соответствующий элемент в третьем столбце.
Вычисляем новые дельты: Δi = C3·a1i + C4·a2i + C5·a3i — Ci
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
1 2 |
-1 | 1 | 0 | 0 |
1 2 |
3 | 3 |
| x4 |
1 2 |
3 | 0 | 1 | 0 | —
1 2 |
21 | 24 |
| x5 | 4 | -3 | 0 | 0 | 1 | 2 | 42 | — |
| Δ |
5 2 |
-6 | 0 | 0 | 0 |
9 2 |
159 |
Текущий план X: [ 0, 0, 3, 21, 42, 0 ]
Целевая функция F: 9·0 + 5·0 + 4·3 + 3·21 + 2·42 + 0·0 = 159
Проверяем план на оптимальность: план не оптимален, так как Δ2 = -6 отрицательна.
Итерация 2
Определяем разрешающий столбец — столбец, в котором находится минимальная дельта: 2, Δ2: -6
Находим симплекс-отношения Q, путём деления коэффициентов b на соответствующие значения второго столбца
В найденном столбце ищем строку с наименьшим значением Q: Qmin = 7, строка 2.
На пересечении найденных строки и столбца находится разрешающий элемент: 3
В качестве базисной переменной x4 берём x2.
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
1 2 |
-1 | 1 | 0 | 0 |
1 2 |
3 | — |
| x2 |
1 2 |
3 | 0 | 1 | 0 | —
1 2 |
21 | 21 / 3 = 7 |
| x5 | 4 | -3 | 0 | 0 | 1 | 2 | 42 | — |
| Δ |
5 2 |
-6 | 0 | 0 | 0 |
9 2 |
159 |
Делим вторую строку на 3. Из первой и третьей строк вычитаем вторую, умноженную на соответствующий элемент во втором столбце.
Вычисляем новые дельты: Δi = C3·a1i + C2·a2i + C5·a3i — Ci
| C | 9 | 5 | 4 | 3 | 2 | 0 | 0 | |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | b | Q |
|---|---|---|---|---|---|---|---|---|
| x3 |
2 3 |
0 | 1 |
1 3 |
0 |
1 3 |
10 | — |
| x2 |
1 6 |
1 | 0 |
1 3 |
0 | —
1 6 |
7 | 7 |
| x5 |
9 2 |
0 | 0 | 1 | 1 |
3 2 |
63 | — |
| Δ |
7 2 |
0 | 0 | 2 | 0 |
7 2 |
201 |
Текущий план X: [ 0, 7, 10, 0, 63, 0 ]
Целевая функция F: 9·0 + 5·7 + 4·10 + 3·0 + 2·63 + 0·0 = 201
Проверяем план на оптимальность: отрицательные дельты отсутствуют, следовательно план оптимален.
Ответ: x1 = 0, x2 = 7, x3 = 10, x4 = 0, x5 = 63, F = 201
Метод искусственного базиса
Очень часто при решении задачи линейной оптимизации бывает довольно сложно выполнять алгебраические преобразования над коэффициентами ограничений для поиска начального базиса. Для упрощения вычислений существует альтернативный метод решения, называемый методом искусственного базиса. Его суть заключается в том, что вместо того, чтобы искать базис среди имеющихся основных и дополнительных переменных, ввести так называемые искусственные переменные, которые сформируют начальный базис. Возможно, звучит сложно и непонятно, но сейчас мы всё объясним.
Подготовительный этап
Аналогично базовому симплекс-методу для всех ограничений с неравентством вводятся дополнительные переменные, причём для ограничений с ≥ они берутся с коэффициентом -1, а для ограничений с ≤ с коэффициентом 1. Ограничения с равенством остаются без изменений. Если свободный коэффициент какого-либо из ограничений меньше нуля, то такое ограничение умножается на -1 (знак неравенства при этом меняется на противоположный). После этого приступают к поиску базиса.
Пример 9
3·x1 + 2·x2 + 3·x3 → min
-2·x1 — x2 — x3 ≥ -2
3·x1 + 8·x2 + 2·x3 ≥ 8
2·x1 + x3 = 1
Меняем знаки у ограничений с отрицательными свободными коэффициентами, путём умножения на -1:
2·x1 + x2 + x3 ≤ 2
3·x1 + 8·x2 + 2·x3 ≥ 8
2·x1 + x3 = 1
Для каждого ограничения с неравенством добавляем дополнительные переменные x4 и x5.
Ограничение 1 содержит неравенство, базисной будет добавленная дополнительная переменная x4
Ограничение 2 содержит неравенство с ≥. Базисная переменная для этого ограничения будет определена позднее.
Ограничение 3 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Начальная симплекс-таблица
| C | 3 | 2 | 3 | 0 | 0 | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | b |
|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 2 |
| ?1 | 3 | 8 | 2 | 0 | -1 | 8 |
| ?2 | 2 | 0 | 1 | 0 | 0 | 1 |
Формирование начального базиса
Для того, чтобы сформировать начальный базис в первую очередь можно поискать столбец, у которого одно значение равно единице, а все значения остальные значения равны нулю, и сделать соответствующую переменную базисной для этой строки. Однако такое случается довольно редко, поэтому проще сразу перейти к следующему пункту. Для всех ограничений, не имеющих базисной переменной, добавляем искусственную переменную с коэффициентом 1. В целевую функцию добавляем эту же переменную с коэффициентов -M, если ищется максимум или с коэффициентом M, если ищется минимум. M всего лишь является очень большим числом.
Пример 10
x1 — x2 → min
2·x1 + x2 = 1
x1 — 3·x2 + x3 = 3
x1 + 11·x2 = 11
Ограничение 1 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Столбец 3 является частью единичной матрицы. Переменная x3 входит в начальный базис
Ограничение 3 содержит равенство. Базисная переменная для этого ограничения будет определена позднее.
Начальная симплекс-таблица
| C | 1 | -1 | 0 | 0 |
| базис | x1 | x2 | x3 | b |
|---|---|---|---|---|
| ?1 | 2 | 1 | 0 | 1 |
| x3 | 1 | -3 | 1 | 3 |
| ?3 | 1 | 11 | 0 | 11 |
Для ограничения 1 добавляем искусственную переменную u1 и делаем её базисной.
Для ограничения 3 добавляем искусственную переменную u2 и делаем её базисной.
В целевую функцию добавляем искусственные пременные с коэффициентом M, где M — очень большое число.
Таблица с искусственными переменными
| C | 1 | -1 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | u1 | u2 | b |
|---|---|---|---|---|---|---|
| u1 | 2 | 1 | 0 | 1 | 0 | 1 |
| x3 | 1 | -3 | 1 | 0 | 0 | 3 |
| u2 | 1 | 11 | 0 | 0 | 1 | 11 |
Перепишем условие задачи с учётом добавленных искусственных переменных:
F = 1x1 -1x2 + Mu1 + Mu2 → min
2·x1 + x2 + u1 = 1
x1 — 3·x2 + x3 = 3
x1 + 11·x2 + u2 = 11
Расчёт дельт и проверка плана на оптимальность
После того, как начальный базис сформирован необходимо вычислить дельты. Дельты вычисляются полностью аналогично базовому методу: Δi = ce1·a1i + ce2·a2i + … + cem·ami — ci. Единственным отличием будет тот факт, что результат может содержать значения с M. Когда дельты будут получены необходимо проверить текущий опорный план на оптимальность (см. проверку плана на оптимальность в базовом симплекс-методе). Если план оптимален, то алгоритм завершает свою работу, иначе формирует более оптимальное решение и повторяет процесс.
Пример 11
Таблица с искусственными переменными
| C | 3 | 2 | 3 | 0 | 0 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | u1 | u2 | b |
|---|---|---|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| u1 | 3 | 0 | 2 | 0 | -1 | 0 | 1 | 0 | 3 |
| u2 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
Вычисляем дельты: Δi = C4·a1i + C7·a2i + C8·a3i — Ci
Δ1 = C4·a11 + C7·a21 + C8·a31 — C1 = 0·2 + M·3 + M·0 — 3 = -3 + 3M
Δ2 = C4·a12 + C7·a22 + C8·a32 — C2 = 0·1 + M·0 + M·0 — 2 = -2
Δ3 = C4·a13 + C7·a23 + C8·a33 — C3 = 0·1 + M·2 + M·1 — 3 = -3 + 3M
Δ4 = C4·a14 + C7·a24 + C8·a34 — C4 = 0·1 + M·0 + M·0 — 0 = 0
Δ5 = C4·a15 + C7·a25 + C8·a35 — C5 = 0·0 + M·(-1) + M·0 — 0 = -M
Δ6 = C4·a16 + C7·a26 + C8·a36 — C6 = 0·0 + M·0 + M·(-1) — 0 = -M
Δ7 = C4·a17 + C7·a27 + C8·a37 — C7 = 0·0 + M·1 + M·0 — M = 0
Δ8 = C4·a18 + C7·a28 + C8·a38 — C8 = 0·0 + M·0 + M·1 — M = 0
Δb = C4·b1 + C7·b2 + C8·b3 — C9 = 0·2 + M·3 + M·1 — 0 = 4M
Симплекс-таблица с дельтами
| C | 3 | 2 | 3 | 0 | 0 | 0 | M | M | 0 |
| базис | x1 | x2 | x3 | x4 | x5 | x6 | u1 | u2 | b |
|---|---|---|---|---|---|---|---|---|---|
| x4 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 2 |
| u1 | 3 | 0 | 2 | 0 | -1 | 0 | 1 | 0 | 3 |
| u2 | 0 | 0 | 1 | 0 | 0 | -1 | 0 | 1 | 1 |
| Δ | -3 + 3M | -2 | -3 + 3M | 0 | -M | -M | 0 | 0 | 4M |
Текущий план X: [ 0, 0, 0, 2, 0, 0, 3, 1 ]
Целевая функция F: 3·0 + 2·0 + 3·0 + 0·2 + 0·0 + 0·0 + M·3 + M·1 = 4M
Проверяем план на оптимальность: план не оптимален, так как Δ1 = -3 + 3M положительна.