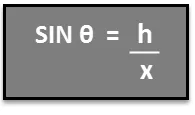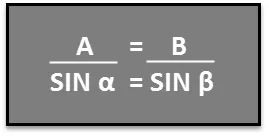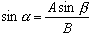Решение уравнений в excel sin - Word и Excel - помощь в работе с программами

SIN (функция SIN)

В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.

Описание

Возвращает синус заданного угла.

Синтаксис

Аргументы функции SIN описаны ниже.

Число Обязательный. Угол в радианах, для которого вычисляется синус.

Замечание

Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Тригонометрические функции SIN COS в Excel для синуса и косинуса

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

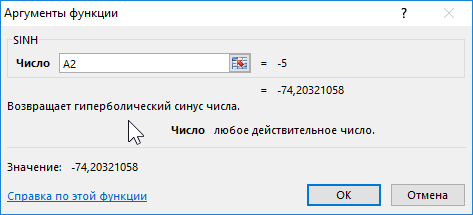
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

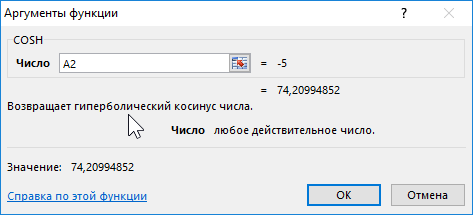
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Примеры использования функций SIN, SINH, COS и COSH в Excel

Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

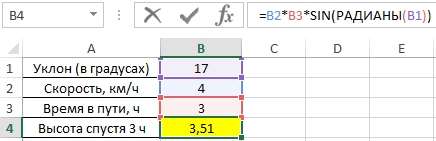
Для решения используем формулу:

B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.

Таблица синусов и косинусов в Excel

Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

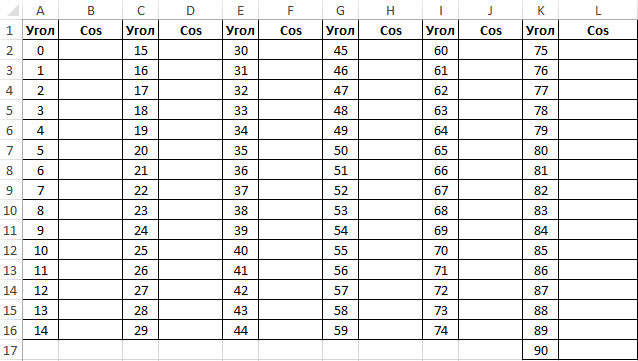
Заполним столбцы значениями углов в градусах:

Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

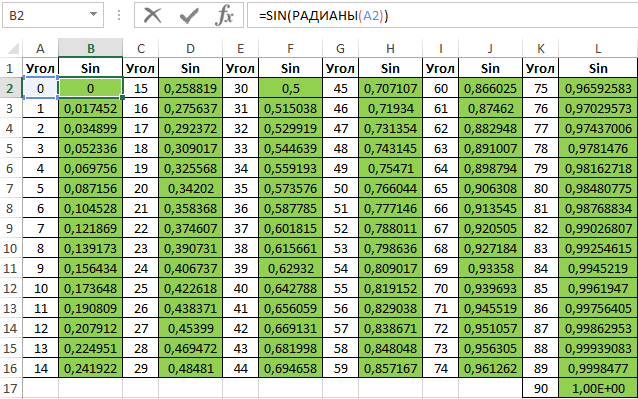
Аналогичным способом создадим таблицу синусов в Excel:

Построение графика функций SINH и COSH в Excel

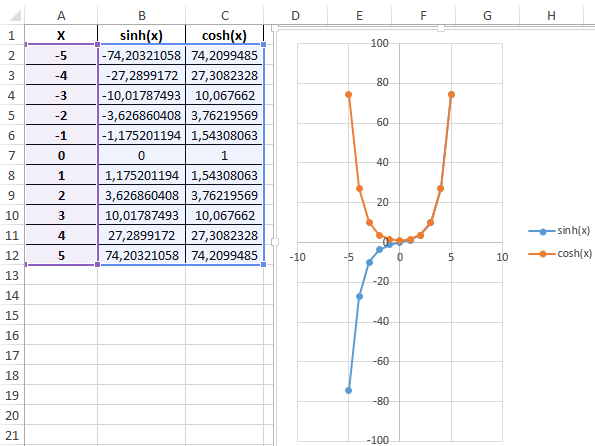
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.

Формула для нахождения синусов гиперболических:

Формула для нахождения косинусов гиперболических:

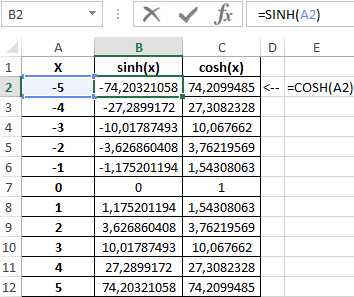
Таблица полученных значений:

Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:

Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

Синтаксис функции SINH:

Синтаксис функции COS:

Синтаксис функции COSH:

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
Все рассматриваемые функции могут быть использованы в качестве формул массива.

Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
Выражение ПИ()*угол_в_градусах/180.

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Первый метод

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

2. Переходите к инструменту и заполняете все необходимые поля

3. После проведения вычислений программа выдаст результат в ячейке с иксом.

4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Важно! В настройках оси поставьте положение по делениям.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.

Жми «Нравится» и получай только лучшие посты в Facebook ↓

источники:

http://exceltable.com/funkcii-excel/primery-funkciy-sin-sinh-cos-cosh

http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/

Источник

Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Примеры использования функций SIN, SINH, COS и COSH в Excel

Таблица данных:

Для решения используем формулу:

=B2*B3*SIN(РАДИАНЫ(B1))

Описание аргументов:

B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

Таблица синусов и косинусов в Excel

Заполним столбцы значениями углов в градусах:

Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

=COS(РАДИАНЫ(A2:A16))

Вычислим значения для всех значений углов. Полученный результат:

Аналогичным способом создадим таблицу синусов в Excel:

Построение графика функций SINH и COSH в Excel

Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.

Исходные данные:

Формула для нахождения синусов гиперболических:

=SINH(A2:A12)

Формула для нахождения косинусов гиперболических:

=COSH(A2:A12)

Таблица полученных значений:

COSH.

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

=SIN(число)

Синтаксис функции SINH:

=SINH(число)

Синтаксис функции COS:

=COS(число)

Синтаксис функции COSH:

>=COSH(число)

Примечания 1:

Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
Все рассматриваемые функции могут быть использованы в качестве формул массива.

Примечения 2:

Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

Скачать примеры тригонометрических функций SIN и COS

Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
Выражение ПИ()*угол_в_градусах/180.

Источник

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше

В этой статье описаны синтаксис формулы и использование функции SIN в Microsoft Excel.

Описание

Возвращает синус заданного угла.

Синтаксис

SIN(число)

Аргументы функции SIN описаны ниже.

Число Обязательный. Угол в радианах, для которого вычисляется синус.

Замечание

Если аргумент задан в градусах, умножьте его на ПИ()/180 или преобразуйте в радианы с помощью функции РАДИАНЫ.

Пример

Формула	Описание	Результат
=SIN(ПИ())	Синус пи радиан (0, приблизительно).	0,0
=SIN(ПИ()/2)	Синус пи/2 радиан.	1,0
=SIN(30*ПИ()/180)	Синус угла 30 градусов.	0,5
=SIN(РАДИАНЫ(30))	Синус 30 градусов.	0,5

Нужна дополнительная помощь?

Источник

Функция SIN в Excel

Функция Excel SIN (Содержание)

Функция SIN в Excel
Как использовать функцию SIN в Excel?

Функция SIN в Excel

Способность вычислять не охватывает всю математику. Это подраздел, хотя и жизненно важный в его применении. В прошедшие годы это было ограничивающим фактором, за исключением очень известных и чрезвычайно талантливых «человеческих калькуляторов», таких как Шакунтала Деви. Но компьютеры теперь позволяют сделать всю математику более интеллектуальной. Понятия и теоремы математики сейчас важнее, чем когда-либо прежде.

Excel очень искусен в обработке множества математических моделей, вооружен обширным набором математических и логических функций для поддержки различных операций. Он предоставляет целый набор тригонометрических функций, которые помогают нам, когда мы вступаем в мир тригонометрии.

Итак, для решения тригонометрической функции Sine она предоставляет функцию SIN . Это базовая тригонометрическая функция, но она очень полезна, особенно если вы работаете в сфере производства, навигации или связи. Но важно отметить, что Excel использует радианы, а не градусы для вычисления любого тригонометрического выражения. Есть два способа сделать это:

Напомним, что π = 180 °. Итак, если угол в градусах, умножьте его на π / 180 °, чтобы преобразовать его в радианы. В Excel это преобразование может быть записано как PI () / 180. Например, чтобы преобразовать 60 ° в радианы, выражение для Excel будет равно 60 * PI () / 180, что равно 1, 0472 радиан.
Excel также оснащен очень полезным инструментом, обычно называемым RADIANS. Он принимает угол в качестве аргумента, в котором угол относится к градусам, которые должны быть преобразованы в радианы. Возьмем случай, когда выражение, которое используется для преобразования 210 ° в радианы, равно «RADIANS (210)», и оно оценивается в 66519 радиан.

Наоборот, утилита DEGREES одинаково важна. Эта функция может использоваться для полной противоположности функции RADIANS путем преобразования радиан в градусы. Как пример, DEGREES (PI () / 2) оценивает 90.

Как использовать функцию SIN в Excel?

Давайте разберемся, как использовать функцию SIN в Excel, используя несколько примеров и реальных иллюстраций функции SIN в Excel.

Вы можете скачать этот шаблон SIN Function Excel здесь — Шаблон SIN Function Excel

Функция SIN в Excel — Пример № 1

Расчет значения синуса с использованием функции SIN в Excel

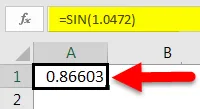
Чтобы найти синус определенного числа, мы должны сначала написать = SIN () в конкретной ячейке.

Как видно из приведенного выше снимка экрана, функция SIN в Excel ожидает ввод числа. Это число обычно представляет значение в радианах.

Так что в этом случае мы напишем «= SIN (1.0472)», где 1.0472 — это радианы, эквивалентные 60 градусам.

Как только мы сделаем это, мы получим значение SIN 60 градусов.

Функция SIN в Excel — Пример № 2

Расчет значения синуса с использованием функции SIN и RADIAN в Excel

Теперь давайте посмотрим, как мы можем использовать SIN более продуктивно, в случае, когда мы не знаем точное значение радиана для градуса.

Мы будем использовать RADIANS (), чтобы узнать значение радиана, которое мы передадим в качестве аргумента функции SIN.

Итак, начнем с более ранней версии SIN ():

Далее мы передадим RADIANS (60) в качестве аргумента функции SIN, где 60 — это значение в градусах.

Как видно из приведенного выше примера, RADIANS () принимает значение в градусах. Итак, мы передадим 60 как значение для RADIANS ().

Затем нажмите Enter. Это дает следующий результат.

Итак, мы видим, что результат такой же, как в первом примере.

Функция SIN в Excel — Пример № 3

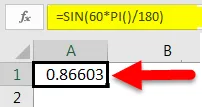
Расчет значения синуса с использованием SIN и функции PI в Excel

Существует еще один способ преобразования значения градуса в радианы для использования в функции SIN. Из школьного времени мы помним, что π = 180 °. Итак, если угол в градусах, умножьте его на π / 180 °, чтобы преобразовать его в радианы. В Excel это преобразование может быть записано как PI () / 180. Например, чтобы преобразовать 60 ° в радианы, выражение для Excel будет равно 60 * PI () / 180, что равно 1, 0472 радиан.

Давайте посмотрим, как это работает:

Мы начнем с написания функции SIN так же, как описано выше.

Далее мы напрямую передадим 60 ° в качестве аргумента функции SIN. Но это не даст нам соответствующее значение 60 градусов в радианах. Следовательно, мы умножим 60 на PI () / 180.

Это даст нам следующий результат:

Как мы видим, это то же самое, что и приведенные выше примеры.

Функция SIN в Excel — Пример № 4

Теперь давайте посмотрим на другой пример, показывающий результаты функции SIN для различных значений.

Пояснения к результатам приведены в приведенной выше таблице:

Случай 1 и 2:

3.14 — это значение Pi, и мы можем использовать оба метода, чтобы получить значение 0. Это в основном означает, что SIN для радиан Пи равно 0 .

Случай 3 и 4:

Радианы и Pi / 180 имеют одинаковое значение в математике, и, следовательно, функция SIN дает одинаковое значение. В обоих примерах SIN равен 30 градусам, что дает значение 0, 5.

Случай 5 и 6:

SIN 45 = 0, 85 — это SIN 45 радиан, что означает, что по умолчанию Excel принимает все углы в радианах, а не градусы. Чтобы преобразовать его в градусы, мы можем использовать функцию радиана и получить SIN 45 градусов, как показано в последнем ряду. т.е. SIN (RADIANS (45)) = 0, 707 или 0, 71

Функция SIN в Excel — Пример № 5

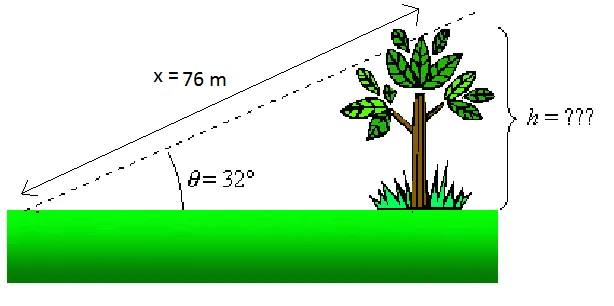
Скажем, например, мы хотим знать высоту дерева на рисунке выше. Мы знаем, что если мы стоим в 76 м от вершины дерева (x = 76 м), то линия визирования к вершине дерева составляет 32 ° по отношению к горизонту (θ = 32 °). Мы знаем это:

Следовательно, чтобы определить высоту дерева h, находим h = x SIN θ.

Функция SIN имеет только один аргумент, который является числом. Число требуется для расчета SIN этого. Следовательно, очень важно преобразовать градусы в радианы, прежде чем найти синус этого числа.

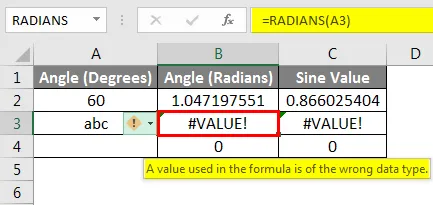
Функция SIN отображает # ЗНАЧЕНИЕ! ошибка, если ссылка, используемая в качестве аргумента функции, указывает на ячейку, содержащую текстовые данные. В приведенном ниже примере ссылка на ячейку третьей строки указывает на текстовую метку в углу (градусы) . Поскольку функции SIN поддерживают только число в качестве аргумента, SIN будет приводить к ошибке, в данном случае, #VALUE!, Если ячейка указывает на пустую ячейку, функция возвращает нулевое значение, как показано в примере ниже. Тригонометрические функции Excel интерпретируют пустые ячейки как ноль, а синус нулевых радиан равен нулю.

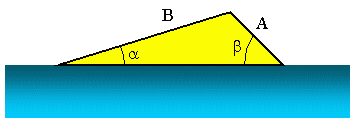
Функция SIN в Excel — Пример № 6

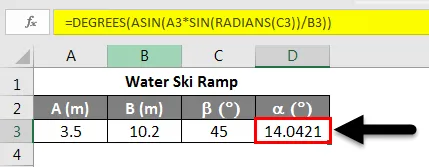
Теперь предположим, что мы хотим узнать угол запуска рампы для водных лыж, как показано на рисунке выше. Мы знаем, что A = 3, 5 м, B = 10, 2 м и b = 45, 0 °. Теперь, чтобы найти, мы можем использовать закон синусов. В этом сценарии это может быть записано как:

Мы можем реорганизовать это уравнение как:

Используя арксинус или обратный синус, мы можем узнать угол α . Применяя уравнение, показанное ниже.

Пример № 7

В нашем последнем тригонометрическом примере мы будем использовать Excel для проверки тригонометрической идентичности:

sin²θ + cos²θ = 1

Обратите внимание, что на скриншоте ниже эта идентичность сохраняется, когда θ задано в радианах и градусах.

Обратите внимание, что описание единицы измерения угла θ находится в разных ячейках, чем числа. Если мы поместим числа и единицы измерения в одну и ту же ячейку, Excel не сможет отличить число от текста, и поэтому мы не сможем ссылаться на ячейки для использования в уравнении, и это приведет к # ЗНАЧЕНИЮ! ошибка.

То, что нужно запомнить

Имейте в виду, что функция SIN в Excel по умолчанию работает с Radian.
Преобразуйте число в радианах или градусах, используя функцию RADIANS или DEGREES.
Вы можете использовать функцию PI (), чтобы получить точные результаты функции SIN при работе с π.

Рекомендуемые статьи

Это было руководство по функции SIN в Excel. Здесь мы обсудили, как использовать функцию SIN в Excel вместе с практическими примерами и загружаемым шаблоном Excel. Вы также можете просмотреть наши другие предлагаемые статьи —

Важные функции по математике в Excel (Easy)
Руководство по разделению формулы в Excel
Важные расширенные формулы и функции Excel
Шпаргалка по формулам Excel

Источник

Решение уравнений средствами Excel

	Содержание
1.	Графический способ решения нелинейных уравнений ………………………….	2
2.	Подбор параметра………………………………………………………………………………..	3
3.	Поиск решения…………………………………………………………………………………….	4
4.	Решение систем линейных уравнений методом Крамера……………………….	6
5.	Решение систем линейных матричным способом………………………………….	7
6.	Варианты заданий………………………………………………………………………………..	8
7.	Решить систему уравнений…………………………………………………………………..	9

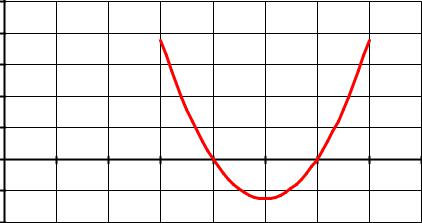
1. Графический способ решения нелинейных уравнений

Возьмем в качестве примера квадратное уравнение х2-5х+6=0. Для нахождения корней уравнения выполним следующие действия:

1.В ячейках А2:А22 введём значение аргумента x в диапазоне от 1,5

до 3,5 с шагом 0,1, то есть A2=1.5, A3=A2+0.1 и т. д. A22=A21+0.1, а

значение функции в ячейках B2:B10 – B2=A2^2-5*A2+6 и т. д.

2.Используя Мастер диаграмм, тип диаграммы – точечная построим кривую функции y(x)=х2-5х+6, точки пересечения графика функции с осью абсцисс будет решением уравнения: x1=2, x2=3 (Рис.1).

1
0,8
0,6
0,4
0,2
0
0	0,5	1	1,5	2	2,5	3	3,5	4
-0,2
-0,4

Рис. 1

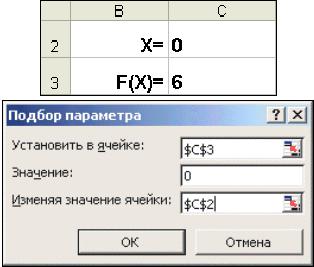
2. Подбор параметра

Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.

Возьмем в качестве примера все то же квадратное уравнение х2-5х+6=0. Для нахождения корней уравнения выполним следующие действия:

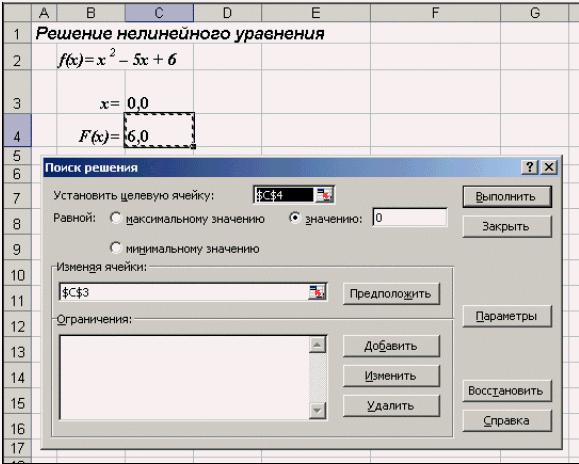
Рис. 2. Окно диалога Подбор параметра

∙В ячейку С3 (рис. 2) введем формулу для вычисления значения функции, стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.

∙В окне диалога Подбор параметра (рис. 2) в поле Установить в ячейке

введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в

которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).

∙После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.

3. Поиск решения

Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню

Сервис/Поиск решения.

Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.

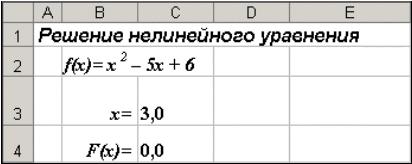
Рис. 3. Окно диалога Поиск решения

После открытия диалога Поиск решения (рис. 3) необходимо выполнить следующие действия:

1)в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем

примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;

2)для ввода значения целевой ячейки, установить переключатель значению в положение 0;

3)в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции ($С$3) (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического

поиска всех влияющих на решение ячеек используется кнопка

Предположить;

4)в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;

5)для запуска процесса поиска решения нажать кнопку Выполнить.

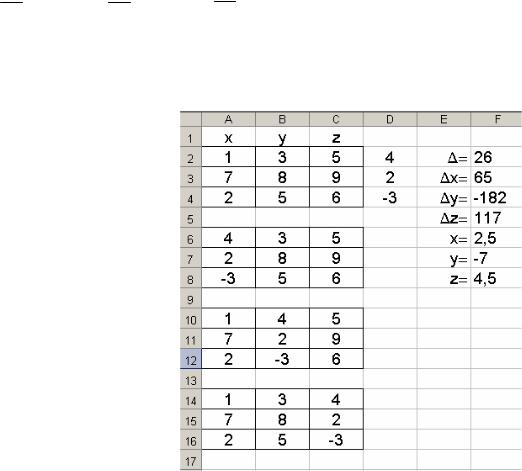
Рис. 4. Результаты поиска

Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 4. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.

4. Решение систем линейных уравнений методом Крамера

Решение систем линейных уравнений рассмотрим на примере системы трёх линейных уравнений

ì	x + 3y + 5z = 4
ï	7 x + 8 y + 9z = 2
í
ï
î2x + 5 y + 6 z = —3
			1	3	5

Тогда главный определитель будет равен =		7	8	9	= 26
			2	5	6

Дополнительные определители:
	4	3	5				1	4	5				1	3	4

x =	2	8	9	= 65 ,	y =		7	2	9	= —182 ,	z =		7	8	2	= 117 .
	— 3 5	6				2	— 3 6				2	5	— 3

Решения системы уравнений будет определяться следующими соотношениями:

x = x = 2,5 ; y = y = —7 ; z = z = 4,5 .

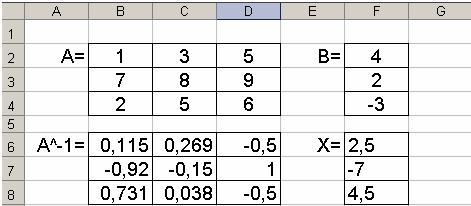
Для решения системы линейных уравнений в табличном процессоре MS Excel запишем главный определитель в ячейки A2:C4, дополнительные

– x в ячейки A6:C8, y – A10:C12, z – A14:C16. Тогда определители можно найти с помощью функции МОПРЕД:

F2 =МОПРЕД(A2:C4);

F3=МОПРЕД(A6:C8);

F4=МОПРЕД(A10:C12)

F5=МОПРЕД(A14:C12)

Решение системы уравнений будет равно:

x=F3/F2;

y=F4/F2;

z=F5/F2.

5. Решение систем линейных матричным способом

Воспользуемся предыдущей системой линейных уравнений:

ì x + 3y + 5z = 4 ïí 7 x + 8 y + 9z = 2

ïî2x + 5 y + 6 z = —3

Данную систему линейных уравнений можно записать в матричной форме:

æ1	3 5	ö		æ x ö	æ	4 ö
ç	7	8	9	÷	,	ç	÷	ç	5	÷
A× X = B , где A = ç	÷	X = ç y÷	, B = ç	÷.
ç	2	5	6	÷		ç	÷	ç	— 3	÷
è	ø		è z ø	è	ø

Решение будем искать из уравнения вида:

X = A−1 × B , где A−1 – обратная матрица матрице A.

Для системы в Excel запишем коэффициентов при неизвестных в ячейках B2:D4, матрицу столбец – F2:F4 (рис. 5).

Рис. 5

Тогда с помощью функции =МОБР(B2:D4) можно найти обратную матрицу A−1 , для чего:

1.В ячейке B6 введите функцию МОБР(B2:D4).

2.Выделите диапазон ячеек B6:D8.

3.Нажмите клавишу F2.

4.Нажмите комбинацию клавиш Shift+Ctrl+Enter.

Для нахождения решения системы уравнений надо перемножить матрицу A−1 на матрицу—столбец B . Для этого:

1.В ячейке F6 введите функцию =МУМНОЖ(B6:D8;F2:F4).

2.Выделите диапазон ячеек F6:F8.

3.Нажмите клавишу F2.

4.Нажмите комбинацию клавиш Shift+Ctrl+Enter.

6. Варианты заданий

№

f(x)

№

f(x)

варианта

ex−1 — x3 — x

0.25x3 + x — 2

x Î [0,1]

x Î [0, 2 ]

1 − x2

x —

arccos

− x

3 + sin( 3.6 x )

1 + x2

x Î [0,1]

x [ 2,3 ]

3x − 4ln x − 5

arccos x —

1—0.3x3

x Î[0,1]

x Î [ 2, 4 ]

— e− x — 2

1—0.4x2 — arcsin x

x Î[0,1]

x Î [0,1]

3x —14 + ex — e− x

— tg x

1— x

x Î[1,3]

x Î[0,1]

1− x + sin x − ln(1+ x )

2x2

+ 1,2 — cos x — 1

x Î [0,1]

x Î[0, 2]

æ 2

æ 1

— x —0,2

cosç

÷ — 2 sinç

è x

xÎ[1, 2]

x Î [1, 2]

0.1x2 — x ln x

x + 0,5 = e− x 2

Î [1, 2 ]

x Î [0,1]

7. Решить систему уравнений.

ì 2x1 — x2 — x3 = 4

ì x1 + 4x2 − x3 = 2

+ 4x2

— 2x3 = —1

+ 2x2 + 2x3 = 1

í3x1

3x1

— 2x2

+ 4x3 = 11

+ 4x2 — 2x3 = 5

î6x1

ìx1 + 3x2 + 2x3 − 4 = 0

ì x1 − x2 + 2x3 = 11

+ 6x2 + x3 — 2 = 0

+ 2x2 — x3 = 11

í2x1

í x1

+ 8x2 — x3 — 2 = 0

— 3x2 — 3x3 = 24

î4x1

ìx1 + 2x2 + 4x3 = 31

ì x1 + x2 + 2x3 = −1

+ x2 + 2x3 = 29

— x2 + 2x3 = —4

í5x1

í2x1

— x2 + x3 = 10

+ x2 + 4x3 = —2

î 3x1

î4x1

ì x1 − 3x2 − 4x3 = 4

ìx1 + 2x2 + 3x3 = 2

+ x2 — 3x3 = —1

+ x2 + 2x3 = 3

í2x1

í3x1

— 2x2

+ x3 = 11

+ 3x2 + x3 = 1

î3x1

î2x1

ì 3x1 + 2x2 + 4x3 = 6

ìx1 + 2x2 + 3x3 = 5

4x1

— 3x2

— 8x3

= 6

10.

+ x2 + 2x3

= 6

í3x1

+ 10x2

+ 8x3

= —8

= 1

î2x1

î2x1 + 3x2 + x3

ì- x1 + 3x2 + 2x3 = 6

ì 2x1 — x2 + x3 = 2

2x1 + 8x2 + x3 = 3

12.

+ 2x2 + 2x3

= —2

11. í

í3x1

+ x2

+ 2x3 = 6

2x2 + 7x3 = 17

2x1 — x2 = —1

ì x1 − x2 + 2x3 = 11

13.

+ x2

+ 2x3 = 6

14.

= 11

í3x1

í x1 + 2x2 — x3

+ 3x2 + x3 = 1

ï4x

— 3x

= 24

î2x1

ì x1 − 3x2 − 4x3 = 4

ì 3x1 + 2x2 + 4x3 = 6

15.

+ x2

— 3x3 = —1

16.

= 6

í2x1

í 4x1 — 3x2 — 8x3

3x1

— 2x2 + x3

= 11

= —8

î2x1 + 10x2 + 8x3

ì 2x1 − x

2 − x3 = 4

ì x1 + 4x2 − x3 = 2

17.

+ 4x2 — 2x3 = 11

18.

í3x1

í3x1 + 2x2 + 2x3 = 1

— 2x2 + 4x3 = 11

î3x1

î6x1 + 4x2 — 2x3 = 5

ìx1 + 2x2 + 4x3 = 31

ìx1 + 2x2 + 3x3 = 2

19.

+ x2 + 2x3 = 29

20.

= 3

í5x1

í3x1 + x2 + 2x3

3x1 — x2

+ x3 = 10

î2x1 + 3x2 + x3 = 1

				10
	ìx1 + 2x2 + 3x3 = 5		ìx1 + 3x2 + 2x3 − 4 = 0
21.	ï	+ x2 + 2x3	= 6	22.	ï	+ 6x2	+ x3 — 2 = 0
í3x1	í2x1
	ï	+ 3x2 + x3	= 1		ï	+ 8x2	— x3 — 2 = 0
	î2x1		î4x1

ì x1 + x2 + 2x3 = −1

23.ïí2x1 — x2 + 2x3 = —4 ïî4x1 + x2 + 4x3 = —2

Соседние файлы в папке Вопросы к экзаменам

Источник