Решение уравнений в excel презентация

Слайд 1

Решение уравнений в Microsoft Excel Выполнила Соколова М.А.

Слайд 2

Вариант № 13 индивидуального расчетного задания Найдите приближенное значение уравнения с точностью 0,001 Представьте графически поставленную задачу;

Слайд 3

Состав задания: Ознакомиться с теоретической частью задания; Провести расчет для своего варианта индивидуального задания в Microsoft Excel Оформить презентацию в Ms Power Point , включающую: § постановку задачи; § алгоритм расчета; § таблицу с расчетом из Ms Excel , график исходной функции; результат расчета и его анализ.

Слайд 4

Постановка задачи: Пусть дано уравнение f(x) = 0, (a, b) — интервал, на котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью. Примечание: Заметим, что если f(x) имеет k корней, то нужно выделить соответственно k интервалов.

Слайд 5

Общая постановка задачи. Найти действительные корни уравнения f ( x ) =0 , где f ( x ) –алгебраическая или трансцендентная функция. Точные методы решения уравнений подходят только к узкому классу уравнений ( квадратные, биквадратные, некоторые тригонометрические, показательные, логарифмические) Задача численного нахождения корней уравнения состоит из двух этапов: 1.Отделение(локализация) корня; 2.Приближенное вычисление корня до заданной точности (уточнение корней)

Слайд 6

6 Уточнение корня . Если искомый корень уравнения f(x)=0 , отделен, т.е. определен отрезок [ a , b ], на котором существует только один действительный корень уравнения, то далее необходимо найти приближенное значение коня с заданной точностью. Такая задача называется уточнения корня. Уточнения корня можно производить различными методами: 1)Метод половинного деления(бисекции); 2)Метод итераций; 3)Метод хорд(секущих); 4)Метод касательных(Ньютона); 5)Комбинированные методы.

Слайд 7

индивидуальное расчетное задание Дано: Найти: Отделить корень заданного уравнения, пользуясь графическим методом, и вычислите один корень с точностью 0,001 при помощи программы Microsoft Excel

Слайд 8

Графический метод: Для отделения корней уравнения естественно приме­нять графический метод. График функции у = f ( х ) с уче­том свойств функции дает много информации для опре­деления числа корней уравнения f ( х ) = 0. До настоящего времени графический метод предлага­лось применять для нахождения грубого значения корня или интервала, содержащего корень, затем применять итерационные методы, т. е. методы последовательных приближений для уточнения значения корня. С появле­нием математических пакетов и электронных таблиц ста­ло возможным вычислять таблицы значений функции с любым шагом и строить графики с высокой точностью. Это позволяет уточнять очередной знак в приближенном значении корня при помощи следующего алгоритма: 1) если функция f ( x ) на концах отрезка [ а , b ] значения разных принимает значения разных знаков то делим отрезок на 10 равных частей и находим ту часть, которая содержит корень (таким способом мы можем уменьшить длину отрезка, содержащего корень, в 10 раз); 2) повторим действия предыдущего пункта для полу­ченного отрезка. Этот процесс можно продолжать до тех пор, пока длина отрезка не станет меньше заданной погрешности.

Слайд 9

Графический метод:

Слайд 10

Метод половинного деления: Постановка задачи: Пусть дано уравнение f(x) = 0, (a, b) — интервал, на котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью. Примечание: Заметим, что если f(x) имеет k корней, то нужно выделить соответственно k интервалов. Метод половинного деления или дихотомии ): Метод основан на той идее, что корень лежит либо на середине интервала (a, b) , либо справа от середины, либо — слева, что следует из существования единственного корня на интервале (a, b) . Алгоритм для программной реализации: а:=левая граница b:= правая граница m:= ( a+b )/2 середина определяем f(a) и f(m) если f(a)*f(m)<0 то b:=m иначе a:=m если (a-b)/2>e повторяем , начиная с пункта2 m- искомый корень.

Слайд 11

Расчет уравнения по методу половинного деления:

Слайд 12

Метод простой итерации: Смысл метода простой итерации состоит в том, что мы представляем уравнение f(x) в виде и по формуле будем строить итерации, которые сходятся к искомому корню с интересующей степенью точности, но тут есть проблемы: возможно f(x) очень сложно представить в таком виде, да и не факт, что любая будет строить сходящиеся итерации, поэтому алгорим сводится к тому, чтобы оптимально найт и . Подготовка: Ищем числа m и M такие, что на (a, b) ; Представляем , где ; Алгоритм: 1. Выбираем х 0 из (a, b) ; 2.Вычисляем ; 3.Проверяем условие , где q=(M-m)/( M+m ) ; 4.Если оно ложно, то переходим к пункту 7; 5. х 0 =х 1 ; 6.Переходим к пункту 2 ; 7. х 1 –искомый корень.

Слайд 13

Расчет уравнения по методу простой итерации:

Слайд 14

Метод хорд Метод хорд заключается в замене кривой у = f ( x ) отрезком прямой, проходящей через точки ( а , f ( a )) и ( b , f ( b )) . Абсцисса точки пересечения прямой с осью ОХ принимается за очередное приближение. Чтобы получить расчетную формулу метода хорд, за­пишем уравнение прямой, проходящей через точки ( a , f ( a )) и ( b , f ( b )) и, приравнивая у к нулю, найдем х : Алгоритм метода хорд : 1) П усть k = 0; 2) В ычислим следующий номер итерации: k = k + 1. Найдем очередное k -e приближение по формуле: x k = a — f ( a )( b — a )/( f ( b ) — f ( a )). Вычислим f ( x k ); 3) Е сли f ( x k )= 0 (корень найден), то переходим к п. 5. Если f ( x k ) × f ( b )>0, то b = x k , иначе a = x k ; 4) Е сли |x k – x k -1 | > ε , то переходим к п. 2; 5) В ыводим значение корня x k ; 6) К онец.

Слайд 15

Расчет уравнения по методу хорд:

Слайд 16

Метод касательных В точке пересечения касательной с осью Оx переменная у = 0. Приравнивая у к нулю, выразим х и получим формулу метода касательных: Теорема. Пусть на отрезке [а, b]выполняются условия: 1) функция f(x)и ее производные f ‘(х)и f »(x)непрерывны; 2) производные f ‘(x)и f »(x)отличны от нуля и сохраняют определенные постоянные знаки; 3) f(a)× f(b) < 0 (функция f(x)меняет знак на отрезке). Тогда существует отрезок [α, β], содержащий искомый корень уравнения f(x) = 0, на котором итерационная последовательность сходится. Если в качестве нулевого приближения х0 выбрать ту граничную точку [α, β], в которой знак функции совпадает со знаком второй производной, т.е. f(x0)× f»(x0)>0, то итерационная последовательность сходится монотонно

Слайд 17

Расчет уравнения по методу касательных:

Слайд 18

Вывод о проделанной работе: Вывод: Решение уравнения в Microsoft Excel Было выполнено: графическим методом, методом половинного деления , хорд, касательных, простой итерации. Графический метод самый неточный, чем остальные методы. метод половинного деления быстрее графического метода, а метод простой итерации намного точнее предыдущих. Метод хорд более точный, чем все остальных методы. Метод касательный относительно быстрее и точнее всех методов.

Слайд 19

Список использованной литературы и интернет-источников Зенков , А.В. ЧИСЛЕННЫЕ МЕТОДЫ /А.В. Зенков . — Екатеринбург: Издательство Уральского университета, 2016. — 127с. Вычислительные методы // Википедия. [2010—2019]. Дата обновления: 31.01.2019. URL: https://ru.wikipedia.org/?oldid=97827303 (дата обращения: 20.05.2019); Численное решение уравнений // Википедия. [2010—2018]. Дата обновления: 01.01.2018. URL: https://ru.wikipedia.org/?oldid=89982922 (дата обращения: 20.05.2019);

1. Решение уравнений в Ms Excel

Решение уравнений в Excel производится в два
этапа:
● локализация корней, т. е. определение
приближенного значения корня или интервала
его нахождения (аналитически или графически);
● уточнение корней с помощью инструмента
Подбор параметра.

2.

Пример 4. Решить уравнение
.
Решение:
3
x
ln | x | 2
2
.
1) Преобразуйте уравнение к стандартной форме f(x) = 0:
3
x
ln | x | 2 0
2
2) С целью отделения корней создайте столбец значений
переменной x, изменяющейся в диапазоне [–5; 5] с шагом
0,5, и столбец соответствующих значений функции
3
x
f x ln | x | 2
2

3.

x
f(x)
-5
-4,5
-4
-3,5
-3
-2,5
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
6,5
-19,23443791
-14,8947024
-11,38629436
-8,612137968
-6,473612289
-4,869415732
-3,693147181
-2,827340108
-2,125
-1,322477819
#ЧИСЛО!
-1,291227819
-1,875
-1,983590108
-1,693147181
-0,963165732
0,276387711
2,106612032
4,613705639
7,886547603
12,01556209
17,09212691
23,20824053
30,45632282
x
-5
=C4+0,5
=C5+0,5
=C6+0,5
=C7+0,5
=C8+0,5
=C9+0,5
=C10+0,5
=C11+0,5
=C12+0,5
=C13+0,5
=C14+0,5
=C15+0,5
=C16+0,5
f(x)
=СТЕПЕНЬ(C4/2;3)-LN(ABS(C4))-2
=СТЕПЕНЬ(C5/2;3)-LN(ABS(C5))-2
=СТЕПЕНЬ(C6/2;3)-LN(ABS(C6))-2
=СТЕПЕНЬ(C7/2;3)-LN(ABS(C7))-2
=СТЕПЕНЬ(C8/2;3)-LN(ABS(C8))-2
=СТЕПЕНЬ(C9/2;3)-LN(ABS(C9))-2
=СТЕПЕНЬ(C10/2;3)-LN(ABS(C10))-2
=СТЕПЕНЬ(C11/2;3)-LN(ABS(C11))-2
=СТЕПЕНЬ(C12/2;3)-LN(ABS(C12))-2
=СТЕПЕНЬ(C13/2;3)-LN(ABS(C13))-2
=СТЕПЕНЬ(C14/2;3)-LN(ABS(C14))-2
=СТЕПЕНЬ(C15/2;3)-LN(ABS(C15))-2
=СТЕПЕНЬ(C16/2;3)-LN(ABS(C16))-2
=СТЕПЕНЬ(C17/2;3)-LN(ABS(C17))-2

4.

Обратите внимание, что при
x [2,5; 3]
функция f(x) меняет знак с минуса на плюс.
Следовательно, корень уравнения f(x) = 0
находится в интервале x от 2,5 до 3.
Этап отделения корней завершен.

5. Уточним корни, используя инструмент ПОДБОР ПАРАМЕТРА

1) Подбор параметра
2) Точное значение корня
2,905712
-4,9E-06

6. Решение систем линейных уравнений в Excel

В Excel имеется ряд функций для обработки
двумерных массивов.
Формулы – Вставить функцию или кнопка
Категория Математические содержит функции:

7.

МОБР (массив) − возвращает обратную матрицу для
выбранного диапазона ячеек, хранящего значения
элементов квадратной матрицы;

8.

МОПРЕД (массив) − возвращает
определитель матрицы (матрица хранится в
массиве);
МУМНОЖ(массив1; массив2) − возвращает
произведение матриц;

9.

ТРАНСП(массив) – преобразует вертикальный
диапазон ячеек в горизонтальный, или наоборот;
ЧИСЛСТОЛБ(массив) – возвращает число
столбцов в массиве;
ЧСТРОК(массив) – возвращает число строк в
массиве.
Перечисленные функции позволяют реализовать
решение системы линейных алгебраических
уравнений методом обратной матрицы.

10.

.
МОПРЕД
Так как определитель матрицы отличен от нуля, то система
линейных уравнений имеет единственное решение,
определяемое по формуле
1
X A b

11.

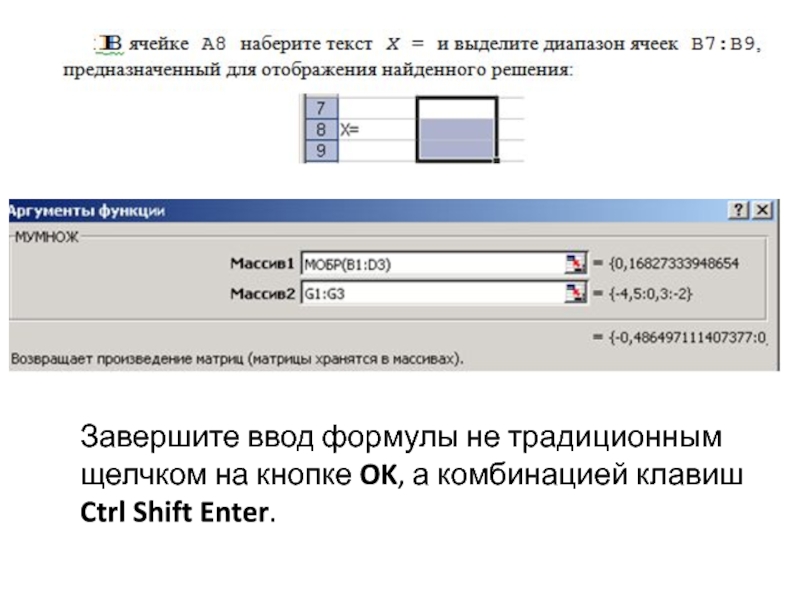
Завершите ввод формулы не традиционным
щелчком на кнопке OK, а комбинацией клавиш
Ctrl Shift Enter.

1


РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ MS EXCEL

2


Решение линейных уравнений уравнений с помощью средства «Подбор параметра» Пример 1 Найти все корни уравнения 3cos2x-sinx = 0 при x [0;3]

3


Шаг 1 Табулируем функцию 3cos2x-sinx = 0 с шагом 0,3 на отрезке [0;3] !!! При решении уравнений с помощью средства Подбор параметра значения переменной должны быть заданы числом

4


Из таблицы значений видно, что функция на [0;3] меняет знак два раза: при х [0,6;0,9] и х [2,4;2,7], на этих отрезках есть точки пересечения функции с осью Х

5


Найдем корни полинома методом последовательных приближений с помощью средства поиск решения: Сервис > Подбор параметра

6


Скопируйте формулу из ячейки В2 в F2 (теперь формула ссылается на пустую ячейку Е2, поэтому в F2 отражается 0) Установите в ячейку Е2 значение переменной из [0,6;0,9], например х=0,7

7


Зададим относительную погрешность вычислений 0,00001 и предельное число итераций 1000 Сервис > Параметры > Вычисления

8

9


В качестве начальных значений приближений к корням можно взять любые точки из отрезков локализации корней, например 0,7 и 2,5

10


Установите курсорную рамку в ячейку F2 и выполните Сервис, Подбор параметра Аналогично найдите второй корень уравнения

11


РЕШЕНИЕ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ В СРЕДЕ MS EXCEL С ИСПОЛЬЗОВАНИЕМ СРЕДСТВА «ПОИСК РЕШЕНИЯ»

12


Пара (х;у) является решением системы уравнений тогда и только тогда, когда она является решением следующего уравнения с двумя неизвестными: (х 2 +у 2 -3) 2 +(2х+3у-1) 2 =0

13


Решением системы — точки пересечения окружности r=3 и прямой уравнение имеет не более двух различных решений Определяемое значение нелинейной задачи зависит от начального приближения

14


Для локализации корней протабулируем левую часть уравнения (х 2 +у 2 -3) 2 + (2х+3у-1) 2 = 0 по переменным х и у на [-3;3] шагом 1,5

15


Протабулируем функцию с помощью таблицы подстановки F(x;y)=(х 2 +у 2 -3) 2 +(2х+3у-1) 2

16


Из таблицы видно, что начальное приближение к корню следует выбрать следующие пары значений (-1,5;1,5), (1,5;0) и (1,5;1,5)

17


Для нахождения корней уравнения введем соответствующие пары значений (х; у) для первого корня в ячейки в А10, А11 для второго корня в ячейки в А14,А15 для третьего корня в ячейки в А17,А18 F(x;y) соответственно в ячейки В13, В16, В19

18


Найдем первый корень. 1.Установить курсорную рамку в ячейке В15 2.Выполнить Сервис > Поиск Решения

19

20


В окне Поиск решения установить целевую ячейку В13, равной значению 0, изменяя ячейки $A$11:$A$12 Нажмите кнопку Параметры и убедитесь, что снят флажок Линейная модель

21


После нажатия кнопки Выполнить средство Поиск решения находит решение, которое помещает в ячейки А11, А12 Аналогично находим второй и третий корни. Решением уравнения будут две пары значений (-1,269;1,179) (1,576;-0,717)

22


РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ

23


Простейшие операции над массивами МАССИВ — объект Excel, используемый для получения нескольких значений в результате вычисления одной формулы или для работы с набором аргументов, расположенных в различных ячейках и сгруппированных по строкам или столбцам.

24


Два типа массивов Microsoft Excel : диапазон массива — непрерывный диапазон ячеек, использующих общую формулу; диапазон констант — набор констант, используемых в качестве аргументов функций.

25


диапазон констант — набор констант, используемых в качестве аргументов функций диапазон массива — непрерывный диапазон ячеек, использующих общую формулу;

26


Массив констант может включать: Числа (целые, с десятичной точкой или в экспоненциальном формате) Текст (должен быть взят в двойные кавычки) Логические значения (ИСТИНА, ЛОЖЬ или значения ошибок например #Н/Д) Элементы разного типа{1,3,4;ИСТИНА,ЛОЖЬ,ИСТИНА}. Массив констант не может содержать Формулы. $ (знак доллара) Скобки % (знак процента) Ссылки на ячейки Столбцы или строки разной длины

27


Для умножения (деления) массива на число: 1.Выделить диапазон ячеек того же размера 2.Ввести в первую ячейку диапазона формулу =Е1:G3*100 и нажать комбинацию клавиш SHIFT+ CTRL+ENTER Если в формуле используется ссылка на ячейку в которой хранится число, то ссылка на эту ячейку должна быть абсолютной

28


Формула массива обрабатывает несколько наборов значений (аргументов массива). Каждый аргумент массива должен включать одинаковое число строк и столбцов. Формула массива создается так же, как и другие формулы, только что для ввода такой формулы используются комбинация клавиш SHIFT+ CTRL+ENTER

29


Пример Перемножение массивов: 1.Выделить область такого же размера как перемножаемые массивы 2.Ввести в первую ячейку формулу =А1:С3*А1:С7 3.Для ввода массива нажать комбинацию SHIFT+ CTRL+ENTER Сложение, вычитание, деление, вычисление каждого элемента как результата некоторой функции производится аналогично. При вводе формулы массива Microsoft Excel автоматически заключает ее в фигурные скобки

30


Формула массива может выполнить несколько вычислений, а затем вернуть одно значение или группу значений. Пример Рассчитать суммарный балл оценки экспертом качества услуги по формуле: Si — суммарный балл Wi – вес критерия Ci – оценка критерия экспертом N – количество критериев

31


Способ решения 1 1.Введите в ячейку D2 формулу =В2*С2 и скопируйте ее в ячейки диапазона D3:D7 2.Введите в ячейку D8 формулу = СУММ(D2:D7) 3.В ячейке D9 вычислите значение S = D86

32


Функция – заранее созданная формула, позволяющая выполнять сложные вычисления, знак = в начале формулы означает, что это формула а не текст. Функция состоит из двух частей: Имя функции — описывает операцию Аргумент – задает значение или ячейки, используемые функцией. Аргумент всегда заключается в скобки При использовании в функции нескольких аргументов их разделяют знаком «;» (не более 30 аргументов) Между именем и аргументом пробелов или других символов не ставится, иначе в ячейке отображается сообщение об ошибке #ИМЯ? Общая длина формулы не более 1024 символа

33


Функцию можно ввести в ячейку с клавиатуры или с помощью средства Мастер функций Каждая функция выводится в стандартном окне диалога Для ввода аргумента достаточно указать в соответствующих полях числовые значения аргументов, адреса ячеек или адреса диапазонов ячеек

34


Способ решения 2 Используем функцию Excel из категории Математические СУММПРОИЗВ(массив1;массив2;массив3;…) Массив1, массив2,… массив30 — перемножаются поэлементно, а затем произведения складываются. Аргументы, которые являются массивами, должны иметь одинаковые размерности, в противном случае функция СУММПРОИЗВ() возвращает значение ошибки #ЗНАЧ!. Нечисловые элементы массивов функция СУММПРОИЗВ() трактует как нулевые

35


Окно диалога функции Суммпроизв() Результат вычисления формулы — число

36


Функции для работы с массивами МУМНОЖ(массив1;массив2) — перемножает массивы. Массивы (матрицы) должны быть одной размерности и оба массива должны содержать только числа.

37


МОБР(массив)- возвращает обратную матрицу для матрицы, хранящейся в массиве

38


ТРАНСП(массив) — используется для того, чтобы поменять ориентацию массива на рабочем листе с вертикальной на горизонтальную и наоборот.

39


МОПРЕД(массив) — возвращает определитель матрицы (матрица хранится в массиве). Определитель матрицы — это число, вычисляемое на основе значений элементов массива. Для массива A1:C3, состоящего из трех сток и тех столбцов, определитель вычисляется следующим образом: = A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)

40


СУММСУММКВ(массив_x;массив_y) — возвращает сумму сумм квадратов соответствующих элементов двух массивов. Сумма сумм квадратов — это распространенный термин во многих статистических вычислениях. Массив_x — это первый массив или интервал значений. Массив_y — это второй массив или интервал значений.

41


СРГЕОМ(число1;число2;…) — возвращает среднее геометрическое значений массива или интервала положительных чисел. Например, функцию СРГЕОМ можно использовать для вычисления средних темпов роста, если задан составной доход с переменными ставками. СУММКВРАЗН(массив_x;массив_y) — возвращает сумму квадратов разностей с оответствующих значений в двух массивах. Массив_x — это первый массив или интервал значений. Массив_y — это второй массив или интервал значений.

42


ЧИСЛСТОЛБ(массив) — возвращает количество столбцов в ссылке или массиве: =ЧИСЛСТОЛБ(A1:D9) в ячейке отображается число 4 ЧСТРОК(массив) — возвращает количество строк в ссылке или массиве. = ЧСТРОК (A1:D9) в ячейке отображается число 9 Статистические функции, который используются для прогнозирования Тенденция(), Рост(), Предсказ(), Линейн() также используют правило ввода значений массива

43


Решение матричных уравнений в EXCEL Найти решение уравнения А*Х=В А-матрица коэффициентов В- столбец (вектор) свободных членов Х-столбец (вектор)неизвестных Решение линейной системы имеет вид: Х=А -1 *В А -1 – обратная матрица

44


Шаг 1. Вычислим А -1 с помощью функции =МОБР(массив) Шаг 2. Выделить диапазон К2:К4 для элементов массива вектора Х и ввести формулу =МУМНОЖ(E2:G4;I2:I4) Для вставки массива нажать комбинацию клавиш SHIFT+ CTRL+ENTER

45


Шаг 3. Проверка. Умножим матрицу А на найденный вектор Х В результате мы должны получить вектор В Выделим диапазон М2:М4 и введем функцию = МУМНОЖ(А2:С4;К2:К4) Для вставки массива нажать комбинацию клавиш SHIFT+ CTRL+ENTER

46


Самостоятельно решить системы линейных уравнений А 2 *Х=В и А 3 *Х=В

47


Решить уравнение Z=Х т A X А-матрица, Х-вектор, Х T — транспонированный вектор Шаг1. Найти транспонированный вектор Х T Выделать диапазон G2:I2 и ввести формул =ТРАНСП(E2:E4) для ввода массива значений нажать SHIFT+ CTRL+ENTER

48


Шаг2. Умножить полученную строку Х T на матрицу Авыделить диапазон К2:М2 и ввести формулу =МУМНОЖ(G2:I2;A2:C4) Шаг 3. В отдельную ячейку введите формулу =МУМНОЖ(K2:M2;E2:E4) – результат вычисления число 227, но для ввода нажать SHIFT+ CTRL+ENTER

49


Это же решение можно получить путем ввода в ячейку одной формулы, содержащей вложенные функции: =МУМНОЖ(МУМНОЖ(ТРАНСП(E2:E4);A2:C4);E2:E4) Самостоятельно решить уравнения: 1. Z=Y т A т AY 2. Z=Y т A т A 2 Y

50


Решение системы линейных уравнений методом Гаусса

51


1. Ввести матрицу коэффициентов в ячейки рабочего листа MS Excel 2. Скопировать первую строчку (диапазон А1:Е6) в диапазоны А6:Е6 А11:Е11 А16:Е16

52

53


3. Выделить диапазон А7:Е7 и введите формулу, которая обращает в 0 коэффициент при х 1 во втором уравнении системы: =A2:E2-$A$1:$E$1*(A2/$A$1) Для вставки элементов массива нажать SHIFT+ CTRL+ENTER Выделить диапазон А7:Е7 и протащить маркер автозаполнения этого диапазона, чтобы заполнить диапазоны А7:Е7 в диапазон А8:Е8 и А9:Е9. Это обратит в 0 коэффициенты при х 1 в третьем и четвертом уравнениях системы.

54


4. Выделить диапазон А7:Е7 и скопируйте значения в буфер Выделите диапазон А12:Е12 и выполните вставку значений без формул используйте команду Правка, специальная вставка Аналогично вставьте значения в диапазон А17:Е17

55


5. Выделите диапазон А13:Е13 и введите формулу массива, которая обращает в 0 коэффициент при х 2 третьего и четвертого уравнений системы =A8:E8-$A$7:$E$7*(B8/$B$7) Для вставки элементов массива нажать SHIFT+ СTRL+ENTER Затем скопировать массив А13:Е13 в диапазон А14:Е14

56


5. Выделите диапазон А19:Е19 и введите формулу массива, которая обращает в 0 коэффициент при х 3 =A14:E14-$A$13:$E$13*(C14/$C$13) Для вставки элементов массива нажать SHIFT+ СTRL+ENTER Прямая прогонка метода Гаусса завершена

57


Обратная прогонка заключается в вводе формул : В диапазон G4:K4 =A19:E19/D19 В диапазон G3:K3 =(A18:E18-G4:K4*D18)/C18 В диапазон G2:K2 =(A17:E17-G4:K4*D17-G3:K3*C17)/B17 В диапазон G1:K1 =(A16:E16-G4:K4*D16-G3:K3*C16-G2:K2*B16)/A16

58


В диапазоне получено решение системы

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Численное решение уравнений с помощью электронных таблиц Microsoft Excel
  Выполнила Соколова М.А.

• 

  2 слайд

  Введение:
  В общем случае процесс решения задачи с использованием ЭВМ состоит из следующих этапов:

  1.Постановка задачи и построение математической модели (этап моделирования);
  2.Выбор метода и разработка алгоритма (этап алгоритмизации);
  3.Запись алгоритма на языке, понятном ЭВМ (этап программирования);
  4.Отладка и использования программы на ЭВМ (этап реализации);
  5.Анализ полученных результатов (этап интерпретации).

• 

  3 слайд

  Вариант № 10
  индивидуального расчетного задания
  Найдите приближенное значение уравнения 𝑥 3 +9𝑥+1=0 с точностью е=0,001.
  Представьте графически поставленную задачу;

• 

  4 слайд

  Состав задания:
  Ознакомиться с теоретической частью задания;
  Провести расчет для своего варианта индивидуального задания в Microsoft Excel
  Оформить презентацию в Ms Power Point , включающую:
  постановку задачи;
  алгоритм расчета;
  таблицу с расчетом из Ms Excel, график исходной функции;
  результат расчета и его анализ.

• 

  5 слайд

  Постановка задачи:
  Пусть дано уравнение   f(x) = 0, (a, b) — интервал, на котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью.
  Примечание: Заметим, что если   f(x) имеет k корней, то нужно выделить соответственно k интервалов.

• 

  6 слайд

  Общая постановка задания:
  Найти действительные корни уравнения f(x) =0 ,
  где f(x) –алгебраическая или трансцендентная функция.

  Точные методы решения уравнений подходят только к узкому классу уравнений ( квадратные, биквадратные,
  некоторые тригонометрические, показательные, логарифмические)

  Задача численного нахождения корней уравнения
  состоит из двух этапов:

  Отделение(локализация) корня;

  Приближенное вычисление корня до заданной точности
  (уточнение корней).

• 

  7 слайд

  Уточнение корня.
  Если искомый корень уравнения f(x)=0, отделен, т.е. определен
  отрезок [a,b], на котором существует только один действительный корень уравнения, то далее необходимо найти приближенное значение коня с заданной точностью.

  Такая задача называется уточнение корня.

  Уточнение корня можно производить различными методами:

  Метод половинного деления(бисекции);
  Метод итераций;
  Метод хорд(секущих);
  Метод касательных(Ньютона);
  Комбинированные методы.

• 

  8 слайд

  Индивидуальное расчетное задание
  Дано:
  𝑥 3 +9𝑥+1=0

  Найти: Отделить корень заданного уравнения, пользуясь графическим методом, и с помощью численных методов вычислить один корень с точностью 0,001 при помощи программы Microsoft Excel

• 

  9 слайд

  Графический метод
  Для отделения корней уравнения естественно приме­нять графический метод. График функции у = f (х) с уче­том свойств функции дает много информации для опре­деления числа корней уравнения f (х) = 0.
  До настоящего времени графический метод предлага­лось применять для нахождения грубого значения корня или интервала, содержащего корень, затем применять итерационные методы, т. е. методы последовательных приближений для уточнения значения корня. С появле­нием математических пакетов и электронных таблиц ста­ло возможным вычислять таблицы значений функции с любым шагом и строить графики с высокой точностью.
  Это позволяет уточнять очередной знак в приближенном значении корня при помощи следующего алгоритма:
  1) если функция f(x) на концах отрезка [а,b] значения разных принимает значения разных знаков то делим отрезок на 10 равных частей и находим ту часть, которая содержит корень (таким способом мы можем уменьшить длину отрезка, содержащего корень, в 10 раз);
  2) повторим действия предыдущего пункта для полу­ченного отрезка.
  Этот процесс можно продолжать до тех пор, пока длина отрезка не станет меньше заданной погрешности.

• 

  10 слайд

  Графический метод:
  X=-0,11096 ,Отрезок [-1;0]

• 

  11 слайд

  Метод половинного деления
  Постановка задачи: Пусть дано уравнение   f(x) = 0, (a, b) — интервал, на котором f(x) имеет единственный корень. Нужно приближенно вычислить этот корень с заданной точностью.
  Примечание: Заметим, что если   f(x) имеет k корней, то нужно выделить соответственно k интервалов.
  Метод половинного деления или дихотомии (дихотомия — сопоставленность или противопоставленность двух частей целого): Метод основан на той идее, что корень лежит либо на середине интервала (a, b), либо справа от середины, либо — слева, что следует из существования единственного корня на интервале (a, b).
  Алгоритм для программной реализации:
  а:=левая граница b:= правая граница  
   m:= (a+b)/2    середина
  определяем f(a) и f(m)
  если f(a)*f(m)<0  то b:=m иначе a:=m
  если (a-b)/2>e повторяем , начиная с пункта2
  m- искомый корень.

• 

  12 слайд

  Расчет уравнения по методу половинного деления: x=-0,11096

• 

  13 слайд

  Метод простой итерации:
  Смысл метода простой итерации состоит в том, что мы представляем уравнение f(x) в виде 𝑥 𝑛 =𝜑( 𝑥 𝑛−1 ) и по формуле x=𝜑 𝑥 будем строить итерации, которые сходятся к искомому корню с интересующей степенью точности, но тут есть проблемы: возможно f(x) очень сложно представить в таком виде, да и не факт, что любая 𝜑(𝑥) будет строить сходящиеся итерации, поэтому алгорим сводится к тому, чтобы оптимально найти x=𝜑(𝑥).
  Подготовка:
  Ищем числа m и M такие, что 0<𝑚≤ 𝑓 1 𝑥 ≥𝑀 на (a, b);
  Представляем 𝜑(𝑥) =𝑥−𝑎∗𝑓(𝑥), где a= 2 𝑀+𝑛 ;

• 

  14 слайд

  Алгоритм:

  Выбираем х0 из (a, b);
  Вычисляем;
  Проверяем условие, где q=(M-m)/(M+m) ;
  Если оно ложно, то переходим к пункту 7;
  х0=х1;
  Переходим к пункту 2;
  х1–искомый корень.

• 

  15 слайд

  Расчет уравнения по методу простой итерации : 𝑥 3 +9𝑥+1=0,x=-0,11096

• 

  16 слайд

  Метод хорд
  Метод хорд заключается в замене кривой у = f(x) отрезком прямой, проходящей через точки (а, f(a)) и (b, f(b)) . Абсцисса точки пересечения прямой с осью ОХ принимается за очередное приближение.
  Чтобы получить расчетную формулу метода хорд, за­пишем уравнение прямой, проходящей через точки (a, f(a)) и (b, f(b)) и, приравнивая у к нулю, найдем х:

• 

  17 слайд

  Алгоритм

  Пусть k = 0;
  Вычислим следующий номер итерации: k = k + 1.
  Найдем очередное k-e приближение по формуле:xk = a — f(a)(b — a)/(f(b) — f(a)). Вычислим f(xk);
  Если f(xk)= 0 (корень найден), то переходим к п. 5.
  Если f(xk) ×f(b)>0, то b = xk, иначе a = xk;
  Если |xk – xk-1| > ε, то переходим к п. 2;
  Выводим значение корня xk;
  Конец.

• 

  18 слайд

  Расчет уравнения по методу хорд:
  x=-0,11096

• 

  19 слайд

  Метод касательных
  В точке пересечения касательной с осью Оx переменная у = 0. Приравнивая у к нулю, выразим х и получим формулу метода касательных:
  𝑥 𝑛+1 = 𝑥 𝑛 − 𝑓( 𝑥 𝑛 ) 𝑓 | ( 𝑥 𝑛 )
  Теорема. Пусть на отрезке [а, b]выполняются условия:
  1) функция f(x)и ее производные f ‘(х)и f »(x)непрерывны;
  2) производные f ‘(x)и f »(x)отличны от нуля и сохраняют определенные постоянные знаки;
  3) f(a)× f(b) < 0 (функция f(x)меняет знак на отрезке).
  Тогда существует отрезок [α, β], содержащий искомый корень уравнения f(x) = 0, на котором итерационная последовательность сходится. Если в качестве нулевого приближения х0 выбрать ту граничную точку [α, β], в которой знак функции совпадает со знаком второй производной, т.е. f(x0)× f»(x0)>0, то итерационная последовательность сходится монотонно

• 

  20 слайд

  Расчетное уравнение по методу касательных: x=-0,11096

• 

  21 слайд

  Вывод:
  Численное решение уравнений с помощью электронных таблиц Microsoft Excel можно получить различными методами:
  Графический метод;
  Метод половинного деления;
  Метод хорд ;
  Метод касательных;
  Метод простой итераций.

• 

  22 слайд

  Список использованной литературы и интернет-источников
  Зенков, А.В. ЧИСЛЕННЫЕ МЕТОДЫ /А.В. Зенков. — Екатеринбург: Издательство Уральского университета, 2016. — 127с.
  Вычислительные методы // Википедия. [2010—2019]. Дата обновления: 31.01.2019. URL: https://ru.wikipedia.org/?oldid=97827303 (дата обращения: 20.05.2019);
  Численное решение уравнений // Википедия. [2010—2018]. Дата обновления: 01.01.2018. URL: https://ru.wikipedia.org/?oldid=89982922 (дата обращения: 20.05.2019);

Краткое описание документа:

Представлена презентация по дисциплине Численные методы » Численное решение уравнений с помощью электронных таблиц Microsoft Excel » рассмотрены различные методы решения уравнения: 1.Графический метод; 2.Метод половинного деления; 3.Метод хорд ; 4.Метод касательных; 5.Метод простой итерации.

В общем случае процесс решения задачи с использованием ЭВМ состоитиз следующих этапов:

•1.Постановка задачи и построение математической модели (этап моделирования);

•2.Выбор метода и разработка алгоритма (этап алгоритмизации);

•3.Запись алгоритма на языке, понятном ЭВМ (этап программирования);

•4.Отладка и использования программы на ЭВМ (этап реализации);

•5.Анализ полученных результатов (этап интерпретации).

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 212 200 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»

• Курс повышения квалификации «Облачные технологии в образовании»

• Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»

• Курс повышения квалификации «Использование компьютерных технологий в процессе обучения в условиях реализации ФГОС»

• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

• Курс повышения квалификации «Современные тенденции цифровизации образования»

• Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»