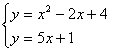Практическое занятие
Математические задачи. Решение уравнений и систем уравнений.
Пояснения к работе
Excel включает
большое число надстроек – откомпилированных программ, добавляющих табличному
процессору новые функциональные возможности. К таким надстройкам относятся
«Подбор параметра», «Поиск решения».
«Подбор параметра» помогает
находить в общем случае приближенные решения уравнений вида f(x)
= 0. Решим простое уравнение:
f(x) = x2 — 5x + 6 = 0
Для решения этого уравнения
подготовим рабочий лист. Ячейка B4 будет содержать значение неизвестной x, а
ячейка B5 – значение функции f(x).
Для этого в B5
поместим формулу = B4* B4 — 5* B4+6, как показано на рис. 1
Рис. 1. Подготовка к решению уравнения
Выберем команду. Сервис/Подбор
параметра. Excel отобразит диалоговое окно Подбор
параметра, приведенное на рисунке 2.В этом окне заполним все три окна в
соответствии с результатом, который мы хотим получить. В поле Установить в
ячейке введем адрес формулы (B5),
результаты которой будут подобраны. В поле Значение введем желаемый
результат вычисления формулы (0). Наконец, используя поле Изменяя значения
ячейки, определим адрес ячейки, которая содержит значение, которое нужно
изменить.
Рис. 2. Заполнение окна Подбор
параметра
После щелчка кнопкой Ok Excel выполнит необходимые вычисления и
выведет диалоговое окно Результат подбора параметра.
Рис. 3. Результат Подбора параметра
Ячейка B4 будет содержать найденный корень
уравнения.
Примечание. В нашем случае уравнение имеет
два корня x1 =2 и x2 = 3. Excel всегда дает только один корень в
зависимости от начального значения изменяемой ячейки.
Примечание. Решение уравнений можно выполнить,
представив функцию в табличном виде. Построив график функции на некотором
отрезке с заданным шагом изменения аргумента, грубо приближенно можно
определить корень уравнения. Затем, используя метод Подбора параметра,
уточнить корень уравнения.
Решение систем уравнений.
Для решения систем уравнений с несколькими
неизвестными используется надстройка «Поиск решения». Пусть требуется решить
систему уравнений
x2 + 5y = 29
5x + y2 = 31
Подготовим рабочий лист так, как показано
на рис. 4. Ячейки D4 и D5
содержат формулы, выражающие левые части уравнений, ячейки E1 и E2 – значения неизвестных x и y
(изменяемые ячейки).
Рис. 4. Подготовка к решению системы
уравнений
Выполним команду Сервис/Поиск решения, на
экране откроется диалоговое окно Поиск решения (рис.5).
Рис. 5. Поиск решения. Надстройки
Установим в поле Установить целевую ячейку
адрес первой формулы D4, в поле Равной значению – число 29 (правая
часть первого уравнения), а в поле Изменяя ячейки диапазон E1:E2 (рис.
6)
Рис. 6. Поиск решения
Второе уравнение мы запишем как ограниченное в поле Ограничения.
Для этого нажмите кнопку Добавить в открывшемся диалоговом окне Добавить
ограничения. Заполним соответствующие поля как показано на рис. 7
Рис. 7. Результат поиска решения
После нажатия кнопки ОК произойдет возврат в окно Поиск
решения. Нам остается только щелкнуть по кнопке Выполнить.
Результат поиска решения показан на рис. 7. Полученные
результаты можно сохранить, нажав кнопку ОК.
Чтобы решить систему из более, чем двух уравнений,
надо одно из них, например первое, выбрать как целевое, т.е. адрес
соответствующей формулы внести в поле Установить целевую ячейку, а
остальные как ограничения.
Надстройка «Поиск решения» как и «Выбор параметра»
позволяет находить только одно решение системы.
Надстройка «Поиск решения» помогает решать довольно
сложные задачи на экстремумы функций нескольких переменных при наличии
ограничений на эти переменные.
Варианты заданий
Задание 1

Определить, сколько точек попадает в заданную фигуру, рис. 1а.
Результат определения принадлежности точек и подсчет
количества точек, принадлежащих заданной фигуре, представлен на рис. 2. В
ячейку C4 помещена формула для определения принадлежности
точек фигуре.
Рис. 2. Подсчет количества точек
Количество точек
находим с помощью автосуммы.
Задание 2. Решить
уравнения и системы уравнений
1.
x3 – x2 + 4 cos πx/2 = 0
2.
x = log x + 5
3.
x2 + xy = 7 –y2
x + 5y2 = 9 –x/3
4.
2x2 + 3y
= 10
—x
+ 6y2 =4
5.
3x
-4y = 3
6.
x3 – sinx – 0,5 = 0
7.
x2 –sinx + 0,1 = 0
8.
x3 + x2
-12x = 0
9.
x3 -19 x – 30 = 0
10.
x3 – x2 +
3x – 10 = 0
Практическая работа «Графический метод решения уравнений в Excel»

Найти графическим методом корень уравнения 10sin(x)-2x 2 +5=0.
Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).
Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.
Приближенное решение уравнения: -0.5 и 2.5.
Просмотр содержимого документа
«Практическая работа «Графический метод решения уравнений в Excel»»
Графический метод решения уравнений.
Найти графическим методом корень уравнения 10sin(x)-2x 2 +5=0.
Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).
Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.
Приближенное решение уравнения: -0.5 и 2.5.
Исследование физических моделей
Рассмотрим процесс решения задачи на конкретном примере: Тело брошено с некоторой высоты с начальной скоростью, направленной под углом к горизонту. Определить угол, при котором дальность полета будет максимальной.
Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.
1) Описательная модель. Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:
тело мало по сравнению с Землей, поэтому его можно считать материальной точкой;
изменение высоты тела не велико, поэтому ускорение свободного падения считать постоянной величиной g = 9,8 м/с 2 и движение по оси OY можно считать равноускоренным;
скорость движения мала, поэтому сопротивлением воздуха можно пренебречь.
2) Формальная модель. Из курса физики известно, что описанное выше движение является равноускоренным. Координаты тела в любой момент времени можно найти по формулам:
Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости и и угле бросания а значения координат дальности полета х и высоты у от времени можно описать следующими формулами:


3) Компьютерная модель. Преобразуем формальную модель в компьютерную с использованием электронных таблиц. Выделим ячейки для ввода начальных данных: нач. скорость, нач. высота, угол. Построим таблицу для вычисления координат x и y.
Координата x: =$B$1*COS($B$3*3,14/180)*A6 .
Координата y: =$B$2+$B$1*SIN($B$3*3,14/180)*A6-9,8*A6*A6/2.
Визуализируем модель построив график движения тела (зависимость y от x).
4) Исследуем модель и определим искомый угол.
Практические работы «Решение систем уравнений в среде Microsoft Excel» и «Стандартные функции Microsoft Excel»
Практическая работа по теме “Решение систем уравнений в среде Microsoft Excel”
Цель работы:
- освоить основные приемы работы с Мастером диаграмм в MS Excel;
- научиться решать системы уравнений с помощью электронных таблиц.
Используемые программные средства: табличный процессор MS Excel.
Содержание работы:
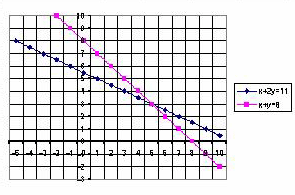
Задача 1. Решить графически систему уравнений
Основное задание. Найти решение системы уравнений
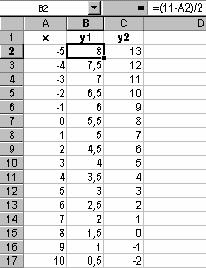
1. Заполните таблицу, как показано на рисунке 1:
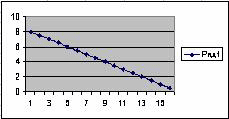
2. Выделите блок В2:В17. Постройте диаграмму – график, как показано на рис.2.
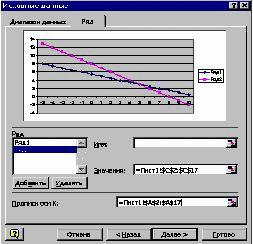
3. ПКМ вызовите вкладку Исходные данные. Выполните Ряд, Добавить, Значения. ЛКМ выделите блок С2 : С17.
4. В окне Подписи оси Х занесите значения x, выделив блок А2 : А17. Завершите построение диаграммы и найдите решение системы. Решение запишите в тетрадь. (Рис. 3)
Дополнительное задание. Оформите решение.
1. Выбрав вкладку Параметры диаграммы ПКМ, добавить основные линии сетки по осям OX и OY.
2. В “Исходных данных” во вкладке Ряд добавить имена рядов: 

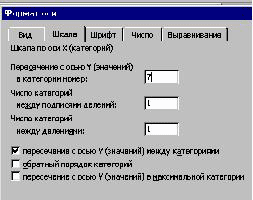
3. Щелкнув ПКМ по оси OX, выбрать меню Формат оси, Шкала; установить соответствующие значения. (Рис.4)
4. Щелкнув ПКМ по оси OY, установить цену основных делений 1 и во вкладке Шрифт уменьшить размер шрифта.
5. Щелкнув ПКМ, выбрать Формат области построения, во вкладке Вид поставить флажок Заливка прозрачная.
6. Сравните полученный результат с образцом, представленным на рисунке 5.
Задача 2. Решить графически систему уравнений
Практическая работа по теме “Стандартные функции Microsoft Excel”
Цель работы:
- освоить основные приемы работы со стандартными функциями в MS Excel;
- научиться решать задачи табулирования функции с помощью электронных таблиц.
Используемые программные средства: табличный процессор MS Excel.
Содержание работы:
Функции
Для записи формул в электронных таблицах можно использовать стандартные функции. Всё множество встроенных функций табличного процессора делится на несколько групп: математические, статистические, функции даты и времени и т.д. В различных табличных процессорах наборы стандартных функций различаются.
Таблица некоторых стандартных функций Excel
| SIN() | синус |
| COS() | косинус |
| TAN() | тангенс |
| КОРЕНЬ()(SQRT) | корень |
| ABS() | модуль |
| СУММА() | сумма |
| СРЗНАЧ()(AVERAGE) | среднее значение |
| МАКС()(MAX) | максимум |
| МИН(MIN) | минимум |
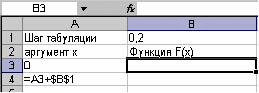
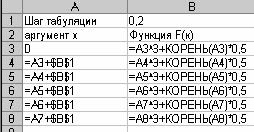
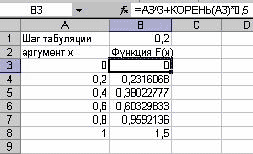
Задача 1. На отрезке [0;1] вычислить значения функции 
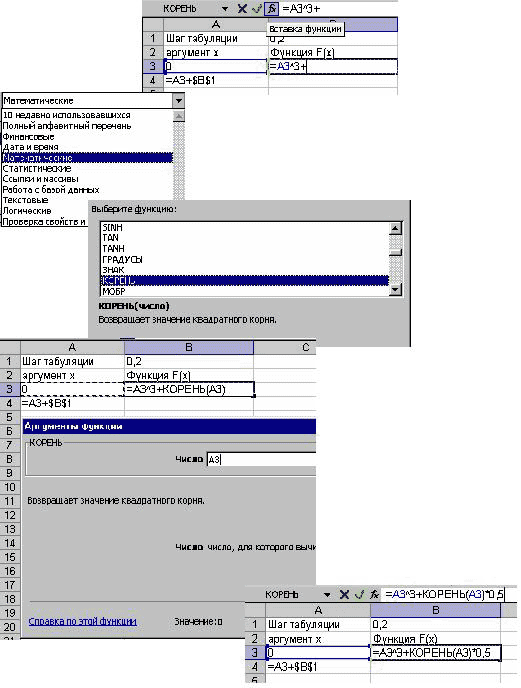
1. Заполните таблицу, как показано ниже на рисунках 1 и 2.
2. Скопируйте формулу из ячейки А4 в ячейки А5 : А8, а формулу из ячейки В3 в ячейки В4 : В8.
При копировании абсолютный адрес $B$1, содержащий значение шага табуляции, не будет изменяться.
3. Загрузите режим отображения формул: Сервис/параметры/вид/формулы.
В режиме отображения формул таблица будет выглядеть так, как показано на рисунке 3:
4. Отмените режим отображения формул. В режиме отображения значений таблица будет выглядеть так, как показано на рисунке 4:
Задачи для самостоятельной работы:
Задача 2. На отрезке [1,2; 2] вычислить значения функции 
Задача 3. На отрезке [2;4] вычислить значения функции 
Информатика Практическое занятие Excel Подбор параметра. Решение уравнений.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Математические задачи. Решение уравнений и систем уравнений.
Пояснения к работе
Excel включает большое число надстроек – откомпилированных программ, добавляющих табличному процессору новые функциональные возможности. К таким надстройкам относятся «Подбор параметра», «Поиск решения».
«Подбор параметра» помогает находить в общем случае приближенные решения уравнений вида f ( x ) = 0. Решим простое уравнение:
Для решения этого уравнения подготовим рабочий лист. Ячейка B 4 будет содержать значение неизвестной x , а ячейка B 5 – значение функции f ( x ). Для этого в B 5 поместим формулу = B 4* B 4 — 5* B 4+6, как показано на рис. 1
Рис. 1. Подготовка к решению уравнения
Выберем команду. Сервис/Подбор параметра . Excel отобразит диалоговое окно Подбор параметра, приведенное на рисунке 2.В этом окне заполним все три окна в соответствии с результатом, который мы хотим получить. В поле Установить в ячейке введем адрес формулы ( B 5), результаты которой будут подобраны. В поле Значение введем желаемый результат вычисления формулы (0). Наконец, используя поле Изменяя значения ячейки , определим адрес ячейки, которая содержит значение, которое нужно изменить.
Рис. 2. Заполнение окна Подбор параметра
После щелчка кнопкой Ok Excel выполнит необходимые вычисления и выведет диалоговое окно Результат подбора параметра.
Рис. 3. Результат Подбора параметра
Ячейка B 4 будет содержать найденный корень уравнения.
Примечание . В нашем случае уравнение имеет два корня x 1 =2 и x 2 = 3. Excel всегда дает только один корень в зависимости от начального значения изменяемой ячейки.
Примечание . Решение уравнений можно выполнить, представив функцию в табличном виде. Построив график функции на некотором отрезке с заданным шагом изменения аргумента, грубо приближенно можно определить корень уравнения. Затем, используя метод Подбора параметра , уточнить корень уравнения.
Решение систем уравнений.
Для решения систем уравнений с несколькими неизвестными используется надстройка «Поиск решения». Пусть требуется решить систему уравнений
Подготовим рабочий лист так, как показано на рис. 4. Ячейки D 4 и D 5 содержат формулы, выражающие левые части уравнений, ячейки E 1 и E 2 – значения неизвестных x и y (изменяемые ячейки).
Рис. 4. Подготовка к решению системы уравнений
Выполним команду Сервис/Поиск решения , на экране откроется диалоговое окно Поиск решения (рис.5).
Рис. 5. Поиск решения. Надстройки
Установим в поле Установить целевую ячейку адрес первой формулы D 4, в поле Равной значению – число 29 (правая часть первого уравнения), а в поле Изменяя ячейки диапазон E 1: E 2 (рис. 6)
Рис. 6. Поиск решения
Второе уравнение мы запишем как ограниченное в поле Ограничения. Для этого нажмите кнопку Добавить в открывшемся диалоговом окне Добавить ограничения. Заполним соответствующие поля как показано на рис. 7
Рис. 7. Результат поиска решения
После нажатия кнопки ОК произойдет возврат в окно Поиск решения. Нам остается только щелкнуть по кнопке Выполнить.
Результат поиска решения показан на рис. 7. Полученные результаты можно сохранить, нажав кнопку ОК.
Чтобы решить систему из более, чем двух уравнений, надо одно из них, например первое, выбрать как целевое, т.е. адрес соответствующей формулы внести в поле Установить целевую ячейку , а остальные как ограничения.
Надстройка «Поиск решения» как и «Выбор параметра» позволяет находить только одно решение системы.
Надстройка «Поиск решения» помогает решать довольно сложные задачи на экстремумы функций нескольких переменных при наличии ограничений на эти переменные.
На плоскости заданы координаты точек. Определить, сколько точек попадает в заданную фигуру, рис. 1а.
Результат определения принадлежности точек и подсчет количества точек, принадлежащих заданной фигуре, представлен на рис. 2. В ячейку C 4 помещена формула для определения принадлежности точек фигуре.
Рис. 2. Подсчет количества точек
Количество точек находим с помощью автосуммы .
Задание 2. Решить уравнения и системы уравнений
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 949 человек из 80 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Курс добавлен 23.11.2021
- Сейчас обучается 48 человек из 28 регионов
Курс повышения квалификации
Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Курс добавлен 31.01.2022
- Сейчас обучается 33 человека из 19 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 565 603 материала в базе
Другие материалы
- 29.05.2018
- 258
- 1
- 29.05.2018
- 6308
- 44
- 29.05.2018
- 5991
- 16
- 29.05.2018
- 1261
- 0
- 29.05.2018
- 256
- 0
- 29.05.2018
- 180
- 0
- 29.05.2018
- 1174
- 22
- 29.05.2018
- 855
- 1
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 29.05.2018 2901
- DOCX 79.2 кбайт
- 48 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Метлина Наталия Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 4 года и 4 месяца
- Подписчики: 0
- Всего просмотров: 41138
- Всего материалов: 22
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
У 76% российских учителей оклад ниже МРОТ
Время чтения: 2 минуты
Профессия педагога на третьем месте по популярности среди абитуриентов
Время чтения: 1 минута
Объявлен конкурс дизайн-проектов для школьных пространств
Время чтения: 2 минуты
В России могут объявить Десятилетие науки и технологий
Время чтения: 1 минута
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
источники:
http://urok.1sept.ru/articles/312409
http://infourok.ru/informatika-prakticheskoe-zanyatie-ecel-podbor-parametra-reshenie-uravneniy-3073646.html
Практическая работа по теме “Решение
систем уравнений в среде Microsoft Excel”
Цель работы:
- освоить основные приемы работы с Мастером
диаграмм в MS Excel; - научиться решать системы уравнений с помощью
электронных таблиц.
Используемые программные средства: табличный
процессор MS Excel.
Содержание работы:
Задача 1. Решить графически
систему уравнений
Основное задание. Найти решение системы
уравнений
Решение:
1. Заполните таблицу, как показано на рисунке 1:
Рис. 1
2. Выделите блок В2:В17. Постройте диаграмму –
график, как показано на рис.2.
Рис. 2
3. ПКМ вызовите вкладку Исходные данные.
Выполните Ряд, Добавить, Значения. ЛКМ
выделите блок С2 : С17.
4. В окне Подписи оси Х занесите значения x,
выделив блок А2 : А17. Завершите построение
диаграммы и найдите решение системы. Решение
запишите в тетрадь. (Рис. 3)
Рис. 3
Дополнительное задание. Оформите решение.
1. Выбрав вкладку Параметры диаграммы ПКМ,
добавить основные линии сетки по осям OX и OY.
2. В “Исходных данных” во вкладке Ряд добавить
имена рядов: и
.
3. Щелкнув ПКМ по оси OX, выбрать меню Формат
оси, Шкала; установить соответствующие
значения. (Рис.4)
Рис. 4
4. Щелкнув ПКМ по оси OY, установить цену основных
делений 1 и во вкладке Шрифт уменьшить размер
шрифта.
5. Щелкнув ПКМ, выбрать Формат области
построения, во вкладке Вид поставить
флажок Заливка прозрачная.
6. Сравните полученный результат с образцом,
представленным на рисунке 5.
Рис. 5
Задача 2. Решить графически
систему уравнений
Практическая работа по теме
“Стандартные функции Microsoft Excel”
Цель работы:
- освоить основные приемы работы со стандартными
функциями в MS Excel; - научиться решать задачи табулирования функции
с помощью электронных таблиц.
Используемые программные средства:
табличный процессор MS Excel.
Содержание работы:
Функции
Для записи формул в электронных таблицах можно
использовать стандартные функции. Всё множество
встроенных функций табличного процессора
делится на несколько групп: математические,
статистические, функции даты и времени и т.д. В
различных табличных процессорах наборы
стандартных функций различаются.
Таблица некоторых стандартных
функций Excel
| SIN() | синус |
| COS() | косинус |
| TAN() | тангенс |
| КОРЕНЬ()(SQRT) | корень |
| ABS() | модуль |
| СУММА() | сумма |
| СРЗНАЧ()(AVERAGE) | среднее значение |
| МАКС()(MAX) | максимум |
| МИН(MIN) | минимум |
Задача 1. На отрезке [0;1] вычислить
значения функции с шагом 0,2.
Решение:
1. Заполните таблицу, как показано ниже на
рисунках 1 и 2.
Рис. 1
Рис. 2
2. Скопируйте формулу из ячейки А4 в ячейки А5 : А8,
а формулу из ячейки В3 в ячейки В4 : В8.
При копировании абсолютный адрес $B$1, содержащий
значение шага табуляции, не будет изменяться.
3. Загрузите режим отображения формул:
Сервис/параметры/вид/формулы.
В режиме отображения формул таблица будет
выглядеть так, как показано на рисунке 3:
Рис. 3
4. Отмените режим отображения формул. В режиме
отображения значений таблица будет выглядеть
так, как показано на рисунке 4:
Рис. 4
Задачи для самостоятельной работы:
Задача 2. На отрезке [1,2; 2]
вычислить значения функции с шагом 0,1.
Задача 3. На отрезке [2;4] вычислить
значения функции с шагом 0,2.
Графический метод решения уравнений.
Найти графическим методом корень уравнения 10sin(x)-2x2+5=0.
Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).
Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.
Приближенное решение уравнения: -0.5 и 2.5.
Исследование физических моделей
Рассмотрим процесс решения задачи на конкретном примере: Тело брошено с некоторой высоты с начальной скоростью, направленной под углом к горизонту. Определить угол, при котором дальность полета будет максимальной.
Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.
1) Описательная модель. Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:
-
тело мало по сравнению с Землей, поэтому его можно считать материальной точкой;
-
изменение высоты тела не велико, поэтому ускорение свободного падения считать постоянной величиной g = 9,8 м/с2 и движение по оси OY можно считать равноускоренным;
-
скорость движения мала, поэтому сопротивлением воздуха можно пренебречь.
2) Формальная модель. Из курса физики известно, что описанное выше движение является равноускоренным. Координаты тела в любой момент времени можно найти по формулам:
Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости и и угле бросания а значения координат дальности полета х и высоты у от времени можно описать следующими формулами:
или
или
3) Компьютерная модель. Преобразуем формальную модель в компьютерную с использованием электронных таблиц. Выделим ячейки для ввода начальных данных: нач. скорость, нач. высота, угол. Построим таблицу для вычисления координат x и y.
Координата x: =$B$1*COS($B$3*3,14/180)*A6 .
Координата y: =$B$2+$B$1*SIN($B$3*3,14/180)*A6-9,8*A6*A6/2.
Визуализируем модель построив график движения тела (зависимость y от x).
4) Исследуем модель и определим искомый угол.
5) Проанализируем полученные результаты.
Практическая работа №5. Решение уравнений средствами
программы MS Excel.
Цель: изучив
возможности MS Excel, научиться вычислять корни уравнений высших степеней
методом подбора параметра.
Анализ
данных с использованием метода наименьших квадратов.
1. В собственном
каталоге создайте файл с именем «lab_5.xls»
2. Первый
лист рабочей книги назовите «Задача1», аналогично назовите следующие
листы указывая номер очередной задачи.
Задача №1.
а) Найти
решения уравнения x3-3x2+x=-1.
Порядок
действий..
- Занесите в ячейку
А1 значение 0. - Занесите в ячейку
В1 левую часть уравнения, используя в качестве независимой переменной
ссылку на ячейку А1. Соответствующая формула может, например, иметь вид
=A1^3-3*A1^2+A1. - Дайте
команду Сервис-Подбор параметра. - В поле Установить
в ячейке укажите В1, а в поле Значение задайте
–1, в поле Изменяя значение ячейки укажите А1. - Щелкните ОК и
посмотрите на результат подбора, отображаемый в диалоговом окне Результата
подбора параметра. Щелкните на кнопке ОК, чтобы сохранить полученные
значения ячеек, участвовавших в операции. - Повторите расчет,
задавая в ячейке А1 другие начальные значения, например 0,5 или 2. Совпали
ли результаты вычислений? Чем можно объяснить различия? - Для того чтобы
определить начальные значения аргумента, можно протабулировать функцию и
выяснить при каких значениях аргумента функция меняет знак. Например
|
x |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
f(x)=x3-3x2+x+1 |
-329 |
-204 |
-115 |
-56 |
-21 |
-4 |
1 |
0 |
-1 |
4 |
21 |
56 |
115 |
На
промежутке от –1 до 0, от 1 до 2 функция меняет знак, поэтому в качестве
начального параметра можно взять 0 и 2. При аргументе 1 функция равна 0, т.е.
это корень, его приближенное значение мы получили, взяв в качестве начального
параметра 0,5.
б) Найдите
все действительные корни уравнения x^5+3*x^2-1=0.
Задача №2
Через год
Вы хотели бы иметь на счете в банке сумму 3210 рублей. Известно, что банк
начисляет 4% процента в конце каждого месяца на сумму лежащую в данный момент
на счете. Сколько денег необходимо положить в банк, чтобы в конце года получить
нужную сумму (задача решается с помощью подбора параметра)?
Задача №3
Некто решил
купить компьютер стоимостью 1000 долларов. На его счете в банке в данный момент
числятся 567,82 долларов, при этом банк начисляет каждый месяц 3% на текущую
сумму. На сколько месяцев придется отложить покупку, если дополнительных
вложений денег не будет, а компьютеры номинально дешевеют на 2% в месяц?
Задача №4
а) Для
заданного набора пар значений независимой переменной и функции определить
наилучшие линейное приближение в виде прямой с уравнением y=ax+b.
Предположим,
что небольшая фирма имела продажи на сумму 3100 руб., 4500 руб., 4400 руб.,
5400 руб., 7500 руб. и 8100 руб. за первые шесть месяцев отчетного года.
Оценить объем продаж в девятом месяце.
В качестве
аргументов возьмем порядковые номера месяца, будем считать объемы продаж
значениями некоторой линейной функции y=ax+b. Определим коэффициенты этой
функции (a и b), затем, взяв х=9, определим объем продаж соответственно в
девятом месяце.
Порядок
действий.
- В интервал А1:А6
введите значения с 1 по 6, в ячейку А7 запишите 9. - В интервал В1:В6
введите объемы продаж. - Выделите ячейку С1
и щелкните на кнопке Изменить формулу в строке формул. Раскройте список на
левом краю строки формул и выберите пункт Другие функции. - В окне мастера
функций выберите категорию Ссылки и массивы и функцию ИНДЕКС. В новом
диалоговом окне выберите первый вариант набора параметров. - Установите
текстовый курсор в первое поле для ввода параметров в палитре формул и
снова выберите пункт Другие Функции в раскрывающемся списке в строке
формул. - С помощью мастера
функций выберите функцию ЛИНЕЙН категории Статистические. - В качестве первого
параметра функции ЛИНЕЙН выберите диапазон, содержащий значения функции
(В1:В6). - В качестве второго
параметра функции ЛИНЕЙН выберите диапазон, содержащий значения
независимой переменной (А1:А6). - Переместите
текстовый курсор в строке формул, чтобы он стоял на имени функции ИНДЕКС.
В качестве второго параметра функции ИНДЕКС задайте число 1. Щелкните ОК
на палитре формул. - Функция ЛИНЕЙН
возвращает коэффициенты уравнения прямой в виде массива из двух элементов.
С помощью функции ИНДЕКС выбирается нужный элемент. - Выделите ячейку
D1. Повторите операции указанные выше, чтобы в итоге в этой ячейке
появилась формула: =ИНДЕКС(ЛИНЕЙН(В1:В6;А1:А6);2). Ее можно ввести
вручную. Теперь в ячейках С1 и D1 вычислены, соответственно, коэффициенты
a и b уравнения прямой. - Выделите ячейку В7
и введите формулу для подсчета прогнозируемого результата: =С1*А7+D1.
б) Фирма
желает приобрести земельный надел в июле следующего года. Для этого сотрудники
собирают информацию о ценах за последние 12 месяцев на типичный земельный
надел. Эти значения равны соответственно 133 890 руб., 135 000 руб., 135 790
руб., 137 300 руб., 138 130 руб., 139 100 руб., 139 900 руб., 141 120 руб.,
141890 руб., 143 230 руб., 144 000 руб., 145 290 руб. Каков прогноз цены на
земельный участок?
Задача №5
Создайте
базу данных с информацией о своём взводе с полями: фамилия, имя, год рождения,
день рождения, знак зодиака, любимый цвет. Отсортируйте полученный список по
знаку зодиака. Выведите на экране информацию только о тех, кто родился летом и
при этом любит желтый цвет. Задание выполните сначала с помощью автофильтра, а
затем с помощью расширенного фильтра.