Содержание
- Варианты решений
- Способ 1: матричный метод
- Способ 2: подбор параметров
- Способ 3: метод Крамера
- Способ 4: метод Гаусса
- Вопросы и ответы
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
- Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
- Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
=МОБР(массив)Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
- Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
- Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
- Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
- Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
- В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
- Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
- После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Урок: Обратная матрица в Excel
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
3x^2+4x-132=0
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
=3*x^2+4*x-132Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
- Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
- Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
- После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
- Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Урок: Подбор параметра в Excel
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
- Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
- Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
=МОПРЕД(массив)Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
- Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
- Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
- Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
- Аналогичным образом производим подсчет определителей для остальных трех таблиц.
- На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
- Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
- Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
=B8:E8-$B$7:$E$7*(B8/$B$7)Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
- После этого копируем полученную строку и вставляем её в строчку ниже.
- Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
- Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
- В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
=B13:E13-$B$12:$E$12*(C13/$C$12)После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
=B17:E17/D17Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
- Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
=(B16:E16-B21:E21*D16)/C16Жмем привычное уже нам сочетание клавиш для применения формулы массива.
- Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
=(B15:E15-B20:E20*C15-B21:E21*D15)/B15Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Еще статьи по данной теме:
Помогла ли Вам статья?
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12683 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
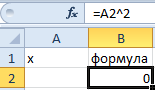
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
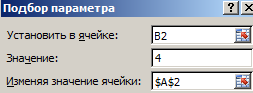
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
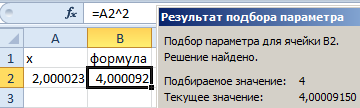
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
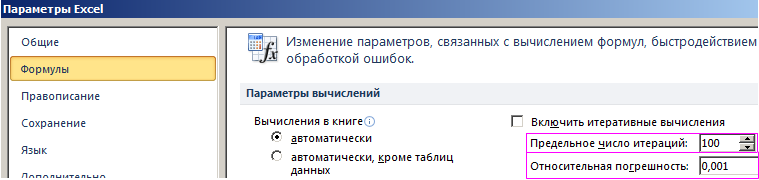
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://exceltable.com/otchety/reshenie-uravneniy
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.
В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:
Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?
Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 
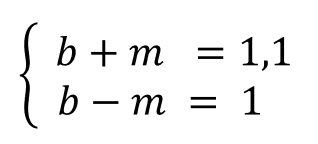
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:
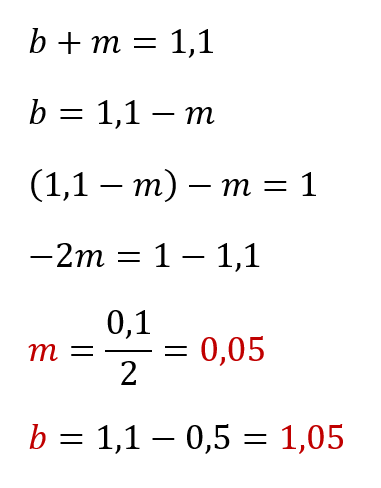
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).
Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):
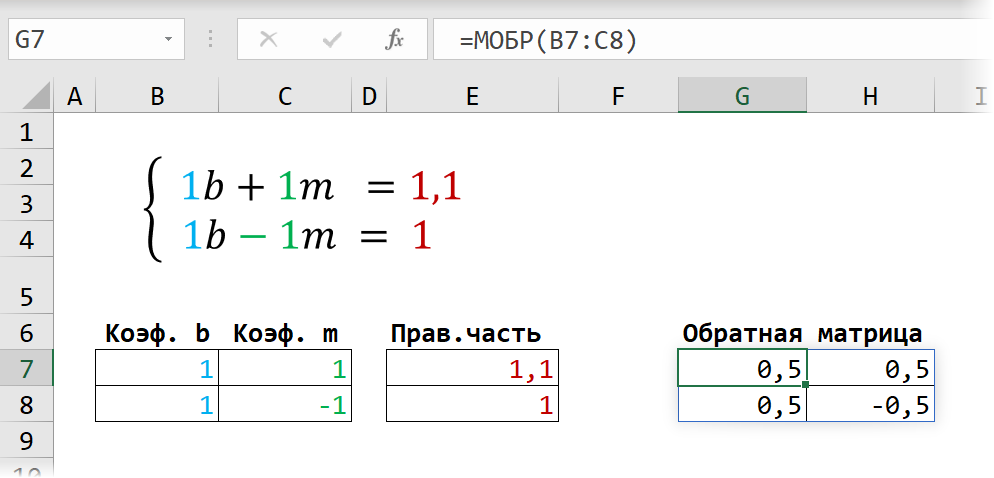
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов — G7:H8
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
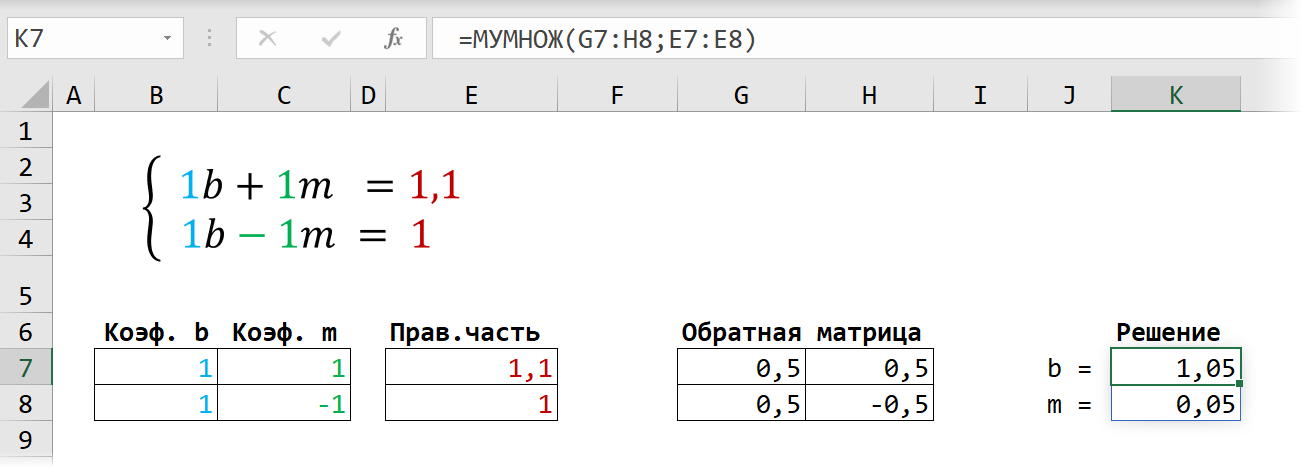
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
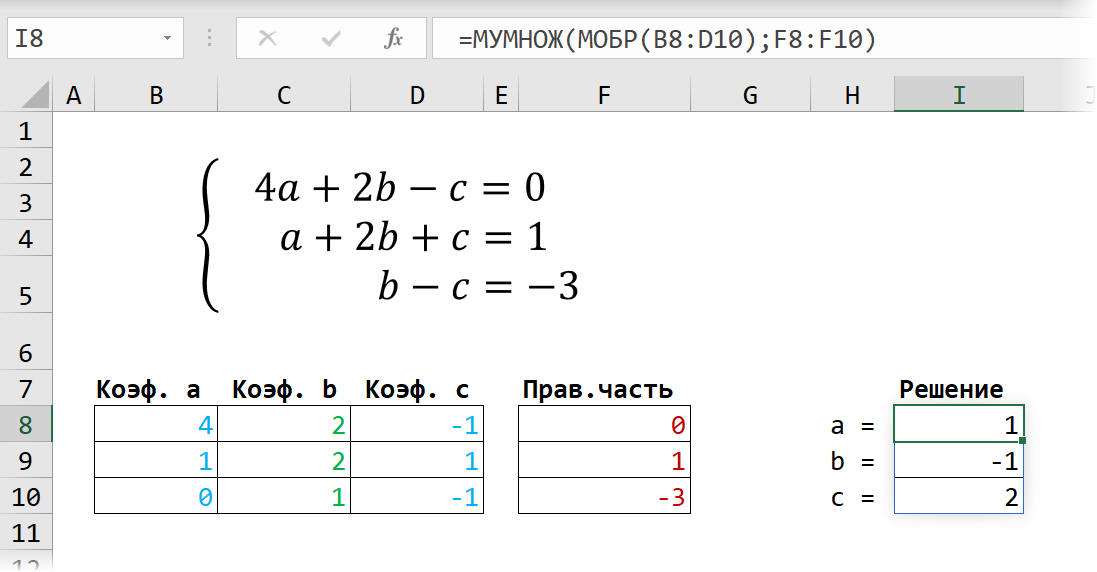
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.
Способ 2. Подбор надстройкой «Поиск решения» (Solver)
Принципиально другой способ решения подобных задач — это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins).
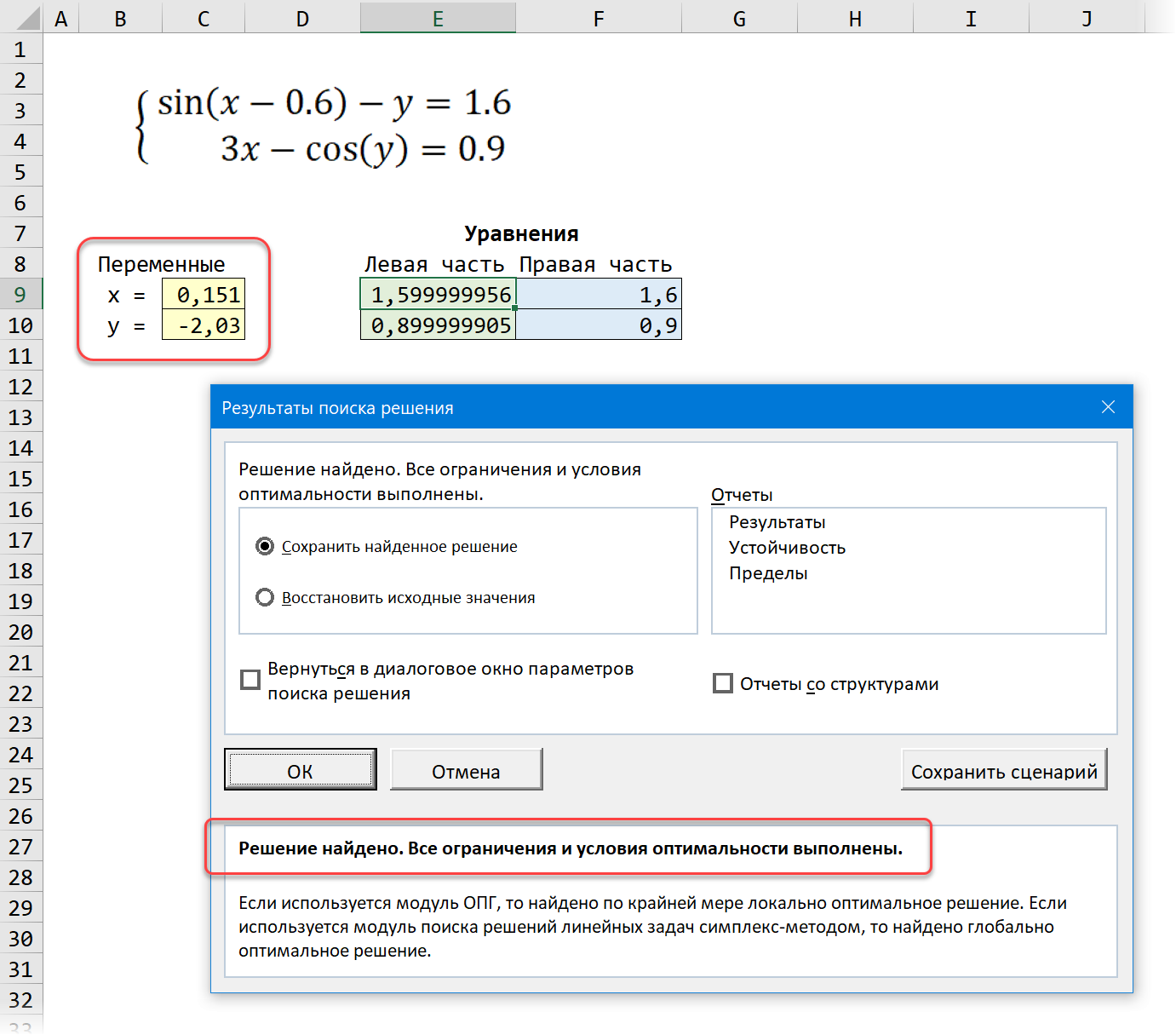
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
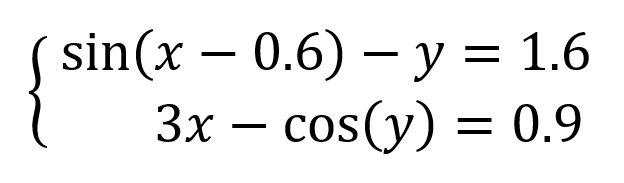
Подготавливаем основу для оптимизации в Excel:

Здесь:
- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
- В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:
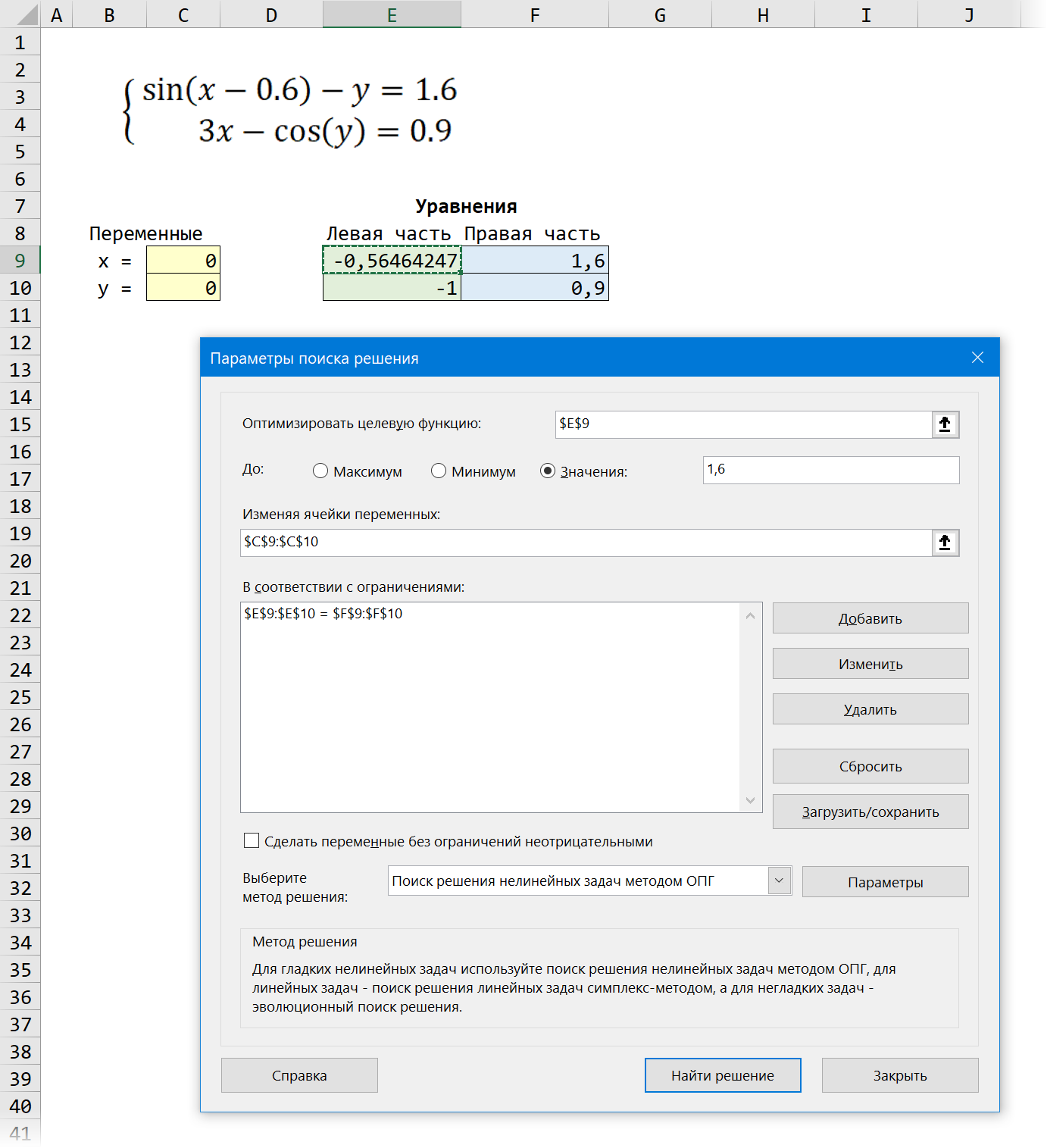
- Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
- Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Пахомов Н.А. 1Селищев Д.В. 1
1МБОУ «СОШ №12»
Утяганова З.З. 1
1МБОУ «СОШ № 12»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
ВВЕДЕНИЕ
Постановка проблемы и актуальность исследования. Школьный курс математики, начиная с начальной ступени и до 11 класса, включает в себя большое количество способов решения различных видов уравнений и систем уравнений. Некоторые уравнения решаются нестандартными методами, которые применить может небольшая часть выпускников школ. Анализ изученной литературы показал, что уравнения и системы уравнений встречаются в различных отраслях промышленности и экономики. И как правило, эти уравнения выглядят не так привлекательно, как школьные, и имеют нецелые решения. Чтобы автоматизировать процесс решения уравнений и систем уравнений, мы решили найти способы с помощью электронных таблиц. Электронные таблицы широко используются в профессиональной деятельности специалистов самых разных областей науки, производства и сферы услуг, в различных государственных и коммерческих организациях и фирмах. Кроме того, электронные таблицы могут быть использованы при решении бытовых задач, таких, как создание домашней картотеки книг или компакт-дисков, ведение учета коммунальных платежей или домашнего бюджета и т.п.
К настоящему времени существует достаточное количество различных учебных материалов, где подробно раскрываются способы решения производственных задач с помощью уравнений и систем уравнений [1, 3, 7, 8, 9], а также методы их решения с помощью электронных таблиц [2, 4, 5, 7-9].
Тем не менее, в ходе исследования было обнаружено, что недостаточно исследованы способы решения уравнений высших степеней, а также уравнений, имеющих бесконечное множество решений (например, тригонометрических).
Актуальность обозначенной проблемы определила выбор темы исследования: «Решение уравнений средствами приложения Microsoft Excel».
Цель работы: исследовать инструменты приложения Microsoft Excel для решения уравнений разного порядка.
Объект исследования: приложение Microsoft Excel.
Предмет исследования: применение инструментов ПОДБОР ПАРАМЕТРА и ПОИСК РЕШЕНИЯ приложения Microsoft Excel при решении уравнений.
Гипотеза исследования: использование инструментов приложения MS Excel ПОДБОР ПАРАМЕТРА и ПОИСК РЕШЕНИЯ значительно упрощает процесс решения уравнений различного вида.
Задачи исследования:
Изучить литературу по применению уравнений при решении производственных задач.
Изучить литературу по использованию приложения Microsoft Excel в практической деятельности.
Рассмотреть способы решения уравнений с помощью инструментов ПОДБОР ПАРАМЕТРА и ПОИСК РЕШЕНИЯ приложения Microsoft Excel.
Создать видеокурсы по решению различных видов уравнений.
Теоретическая значимость: проведен анализ ряда источников по возможностям приложения Microsoft Excel при решении уравнений разного порядка.
Практическая значимость: предложены способы решения уравнений высших порядков и тригонометрических уравнений с помощью приложения MS Excel, систематизирован и обобщен материал в форме видеокурсов.
Методы исследования: теоретический анализ и обобщение научной литературы и материалов сети Интернет; проведение экспериментов по решению уравнений различного вида с помощью инструментов Подбор параметра и Поиск решения; создание видеокурсов по использованию инструментов Подбор параметра и Поиск решения при решении различных уравнений.
УРАВНЕНИЯ В РАЗЛИЧНЫХ ОТРАСЛЯХ
В современном обществе уравнения нашли свое применение во многих отраслях хозяйства и производства, а также практически во всех новейших технологиях. Конечно, математика, как и любая другая наука, не стоит на месте. Уже выработано достаточно способов решения различных видов уравнений различных степеней. Появление компьютеров и стремительное развитие информационных технологий позволило в несколько раз упростить задачи нахождения корней различных уравнений. В данной главе, в качестве примеров, нами представлены виды уравнений, решаемых в некоторых отраслях хозяйства и производства.
1.1. Уравнения при решении экономических задач
Пример 1.1.1. Рассчитать, с какого возраста необходимо уплачивать по 1000 рублей в качестве дополнительных страховых взносов, чтобы получить прибавку к пенсии в 2000 рублей за счет участия в государственной программе софинансирования?
Входные данные:
ежемесячные отчисления – 1000 руб.;
период уплаты дополнительных страховых взносов – расчетная величина (пенсионный возраст (в примере – для мужчины) минус возраст участника программы на момент вступления);
пенсионные накопления – расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза;
ожидаемый период выплаты трудовой пенсии – 228 мес. (19 лет);
желаемая прибавка к пенсии – 2000 руб.
пенсионные накопления – расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза).
Пусть х – возраст, с которого необходимо производить отчисления. Тогда прибавка к пенсии (в размере 2000 рублей) будет рассчитана по формуле:
Получили линейное уравнение, в котором необходимо найти параметр x.
Пример 1.1.2. Пусть дана структура цены договора: собственные расходы, прибыль, НДС. Известно, что собственные расходы составляют 150 000,00 руб., НДС 18%, а целевая стоимость договора 200 000,00 руб. Необходимо подобрать такое значение прибыли, при которой стоимость договора равна Целевой (то есть Расхождение должно равняться нулю) [8].
Пусть х – прибыль. Тогда цену продукции будем рассчитывать как сумму Собственных расходов и Прибыли: 150000+х. НДС от цены продукции будет равен (150000+х)*0,18. Стоимость договора вычислим как сумму Цены продукции и НДС: (150000+х)+ (150000+х)*0,18=(150000+х)*1,18.
Итак, получили уравнение (150000+х)*1,18=2000.
Пример 1.1.3., решение которого также сводится к линейному уравнению. Определить максимальную сумму кредита, которую мы можем себе позволить взять в банке, если известно, что ежемесячно мы можем выплачивать сумму в размере 1 800,00 руб. Известны также процентная ставка по кредиту и срок, на который мы хотим взять кредит (количество месяцев) [8].
Пример 1.1.4, решение которого сводится к системе линейных уравнений. Предприятию для изготовления наборов елочных украшений необходимо изготовить их составные части — шар, колокольчик, мишура [9].
В свою очередь для изготовления этих составных частей необходимы три вида сырья — стекло (в г), папье-маше (в г), фольга (в г), потребности в котором отражены в таблице.
Требуется:
1) определить потребности в сырье для выполнения плана по изготовлению комплектов первого, второго, третьего и четвертого вида в количестве соответственно x1, x2, x3 и x4 штук;
2) провести подсчеты для значений x1 = 500, x2 = 400, x3 = 300 и x4=200.
Для решения данной задачи необходимо найти корни системы линейных уравнений:
y1 = 5· (5x1 + 6x2 + 8x3 + 10x4) = 25x1 + 30x2 + 40x3 + 50x4
y2 = 4· (3x1 + 4x2 + 6x3) = 12x1 + 16x2 + 24x3
y3 = 3· (5x1 + 6x2 + 8x3 + 10x4) + 75· (3x2 + 5x3 + 8x4) = 15x1 + 243x2 + 399x3 + 630x4
Уравнения в электроэнергетике
Рассмотрим применение уравнений в электроэнергетике [3, С. 11].
Пример 1.2.1. Приведена схема электрической цепи постоянного тока. Найти токи в ветвях цепи.
Для решения данной задачи необходимо составить и решить систему линейных уравнений на основе законов Кирхгофа (здесь не рассматривается процесс составления системы уравнений):
Уравнения в транспортной отрасли
Пример 1.3.1. Для решения задач проектирования транспортных сооружений и принятия обоснованных решений при планировании, контроле и управлении технологическими процессами дорожного строительства необходимо выявлять взаимосвязи между параметрами, определяющими ход этих процессов, и представлять их в количественной форме – в виде математических моделей. В связи с этим на практике часто применяется регрессионный анализ.
Регрессионный анализ – метод моделирования измеряемых данных и исследования их свойств путем выявления взаимосвязи между зависимой переменной y и одной или несколькими независимыми переменными x1, x2, …, xn.
Независимые переменные иначе называют факторами, аргументами, или регрессорами, а зависимые переменные – функциями, откликами, результирующими, объясняемыми.
На практике уравнение регрессии чаще всего подбирается в виде линейной и нелинейной функции (наиболее простые – гипербола, экспонента и парабола) [1, С.7-8].
Пример 1.3.2. Транспортная задача
Требуется составить план перевозок, при котором все запасы (строительных материалов или конструкций) поставщиков (АБЗ, ЦБЗ, карьеры) будут вывезены, спрос потребителей (объекты дорожных работ, участки) полностью удовлетворен, и при этом суммарные транспортные издержки будут минимальными (стоимость перевозок, сроки, другие ресурсы).
При решении данной задачи составляется система линейных уравнений относительно xij – количества груза (материалов), перевозимого из пункта i в пункт j [1, С. 14].
Уравнения в строительной отрасли
Пример 1.4.1. Вычислить стрелу прогиба ( в середине) прямоугольной пластины. Прямоугольная пластина загружена равномерно распределенной нагрузкой интенсивностью q. Пластина защемлена по контуру, края неподвижны [7].
Стрела прогиба вычисляется как корень нелинейного уравнения на интервале [0; 0,05]:
Пример 1.4.2. Определить критическую силу для стальной колонны двутаврового сечения, если известны длина колонны L, модуль упругости стали Е, коэффициент жесткости упругой опоры С, момент инерции I.
Критическая сила вычисляется по формуле:
где – коэффициент приведения длины колонны, который определяется по формуле
Параметр находится из решения уравнения
на интервале [3,2; 4,6].
ИСПОЛЬЗОВАНИЕ ИНСТРУМЕНТА ПОДБОР ПАРАМЕТРА ПРИ РЕШЕНИИ УРАВНЕНИЙ
При решении производственных задач достаточно часто возникает проблема подбора параметра. Например, в экономических расчётах применяются алгоритмы расчёта стоимости товара, расчёта фонда заработной платы, прибыли от деятельности предприятия, которые, в свою очередь, зависят от множества изменяемых и неизменяемых факторов [4, 5].
Пример 2.1. Итак, сначала, с целью изучения принципа работы надстройки ПОДБОР ПАРАМЕТРА, рассмотрим решение линейного уравнения вида Ах+В=С с помощью приложения Microsoft Excel.
В ячейку В3 введем любое первоначальное значение переменной x, например, 0, а в ячейку С1 введем левую часть уравнения в виде формулы: =B1*B3+B2. Вызовем диалоговое окно ПОДБОР ПАРАМЕТРА с помощью команд Данные – Анализ «что-если» — Подбор параметра. В этом окне в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение – ожидаемый результат (т.е. 7), в поле Изменяя значение в ячейке – ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
Рисунок 1 – Диалоговое окно ПОДБОР ПАРМЕТРА
После нажатия кнопки ОК, получим результат.
Рисунок 2 – Решение линейного уравнения с помощью диалогового окна ПОДБОР ПАРАМЕТРА
Известно, что инструмент Подбор параметра в основном используется при решении линейного уравнения. Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (которое имеет два корня), то инструмент найдет решение, но только одно, то, которое ближе к начальному значению.
Пример 2.2. Рассмотрим пример решения квадратного уравнения. Найдем корни квадратного уравнения . Сначала создадим первоначальную таблицу.
Рисунок 3 – Первоначальные данные квадратного уравнения
Зададим любое первоначальное значение х, например, 0. Далее воспользуемся инструментом ПОДБОР ПАРАМЕТРА.
Получили результат: 2.
Второй корень найдем, задав другое начальное значение, например, 5. И проделаем те же действия.
ИСПОЛЬЗОВАНИЕ НАДСТРОЙКИ ПОИСК РЕШЕНИЯ ПРИ РЕШЕНИИ УРАВНЕНИЙ
Пример 3.1. Рассмотрим решение квадратного уравнения (с предыдущей главы) с помощью инструмента ПОИСК РЕШЕНИЯ.
Введем начальные данные
Рисунок 4 – Первоначальные данные квадратного уравнения
Вызываем инструмент ПОИК РЕШЕНИЯ, выбрав команду ДАННЫЕ.
Рисунок 5 – Надстройка ПОИСК РЕШЕНИЯ при решении квадратного уравнения
В поле «Установить целевую ячейку» выбираем ячейку с формулой квадратного уравнения С1. Далее установим переключатель в положение «Равной значению 0». В поле «Изменяя ячейки» добавим ячейку В4. Нажмем кнопку «Выполнить». Получили решение.
Рисунок 6 – Решение квадратного уравнения, найденного с помощью надстройки ПОИСК РЕШЕНИЯ
При решении данным способом также получили только один корень.
Для нахождения второго корня зададим другое начальное значение переменной х, например, равно 1.
Однако, на любом производстве чаще всего приходится сталкиваться с уравнениями высших степеней.
Пример 3.2. Рассмотрим уравнение пятой степени –3x5+x3+2x2–3x–3=0.
Прежде чем находить корни уравнения (а у этого уравнения должно быть максимум 5 корней), выясним, в каких интервалах содержатся эти корни. Воспользуемся графиком функции, с помощью которого мы наглядно увидим промежутки расположения корней уравнения.
Построим график функции. Для этого в ячейке А1 введем «х», в ячейке В1 введем «у». Значения х внесем в ячейки А2:А22, значения у будем рассчитывать в ячейках В2:В22 соответственно.
Рисунок 7 – Формула уравнения пятой степени
Известно, что корень уравнения (уравнение записано в виде f(x)=0) – это такое значение аргумента, при котором значение функции равно нулю. В графическом представлении – это может быть точка пересечения или касания графика функции с осью абсцисс.
Построим график функции.
Рисунок 8 – График функции на промежутке [–10; 10] с шагом 1
График функции показывает, что уравнение, имеет единственный действительный корень (остальные – комплексные), который находится в промежутке [–1; 0].
Найдем его с помощью инструмента ПОИСК РЕШЕНИЯ. Для этого в таблице выберем точку, близкую к решению уравнения, например, –0,7.
Рисунок 9 – Нахождение корня уравнения с помощью надстройки
ПОИСК РЕШЕНИЯ
Установим с помощью команды «Формат ячеек» относительную погрешность 0,0001.
Итак, решением уравнения является х≈ –0,668.
Таким образом, получили алгоритм решения уравнения высшей степени:
поиск интервалов, в которых содержится только по одному корню;
уточнение корня в выбранном интервале (определением значения корня с заданной точностью).
Тригонометрические уравнения
Особенность тригонометрических уравнений заключается в том, что они имеют бесконечно много решений, и все решения отличаются между собой на определенный период.
Пример решения одного из тригонометрических уравнений подробно рассмотрен в Приложении 1.
В Приложении 2 также рассмотрен пример нахождения решений системы линейных уравнений.
ЗАКЛЮЧЕНИЕ
В результате проведенной исследовательской работы было выявлено, что решение различных уравнений и систем уравнений применяется во многих отраслях экономики и промышленности.
В ходе исследований мы научились находить корни уравнений и систем линейных уравнений с помощью инструментов ПОИСК РЕШЕНИЯ и ПОДБОР ПАРАМЕТРА приложения Microsoft Excel, создали видеокурсы по решению уравнений с помощью приложения Microsoft Excel.
Таким образом, поставленные цель и задачи данного исследования были выполнены.
Кроме того, экспериментальным путём, было выявлено, что использование инструментов ПОИСК РЕШЕНИЯ и ПОДБОР ПАРАМЕТРА приложения Microsoft Excel значительно упрощает процесс нахождения корней уравнений и систем уравнений. Таким образом, поставленная в начале исследования гипотеза подтвердилась.
Результаты выполненной работы позволят использовать возможности изученных инструментов в будущей профессиональной деятельности, особенно если выполнение задания будет содержать сложные расчеты.
Исследование может быть полезно не только учащимся в учебной деятельности, но и специалистам различных отраслей экономики и промышленности, занимающимся проектированием объектов.
Результаты проведенной работы могут быть использованы при изучении других возможностей приложения Microsoft Excel.
На этом исследование не закончено. Мы планируем продолжить рассмотреть способы решения систем нелинейных уравнений с помощью Microsoft Excel.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ:
Богомолов, С.В. Экономико-математические методы проектирования транспортных сооружений [Электронный ресурс] : методические указания к практическим занятиям и самостоятельной работе для студентов специальности 270205 «Автомобильные дороги и аэродромы» всех форм обучения / С.В. Богомолов. – Электрон. дан. – Кемерово: КуГТУ, 2013. – 30 с.
Информатика для экономистов. Практикум: учебное пособие для бакалавров / под ред. В.П. Полякова, В.П. Косарева. – М.: Издательство Юрайт, 2013. – 343 с.
Митрофанов, С.В. Использование системы MathCAD при решении задач электротехники и электромеханики : методические указания к выполнению РГЗ по дисциплине «Прикладные задачи программирования» / С.В. Митрофанов, А.С. Падеев. – Оренбург: ГОУ ОГУ, 2005. – 40 с.
Репкин, Д.А. Применение MS EXCEL для решения прикладных задач в экономике: учебное пособие для студентов направления 080100 «Экономика» всех профилей подготовки, всех форм обучения / Д.А. Репкин. — Киров: ПРИП ФГБОУ ВПО «ВятГУ», 2012. [Электронный ресурс]
Федулов, С.В. Использование MS Excel в финансовых вычислениях : учеб.-метод. пособие / С.В. Федулов. – Екатеринбург: Изд-во УрГУПС, 2013. – 94 с.
Численные методы. Часть 1: Методические указания к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика» / Сост. Ф.Г. Ахмадиев, Ф.Г. Габбасов, Р.Ф. Гизяятов, И.В. Маланичев. – Казань: Изд-во казан. гос. архитект-строит. ун-та, 2013 – 34 с.
Решение нелинейных уравнений в Excel https://www.altstu.ru/media/f/lr3nelin-uravn.pdf – сайт Алтайского государственного технического университета им. И.И. Ползунова
http://excel2.ru/articles/podbor-parametra-v-ms-excel – сайт Excel2.ru
https://knowledge.allbest.ru/mathematics/3c0b65625b3ad68b4c43a89421306d37_0.html – сайт allbest
Приложение 1
Решение тригонометрического уравнения с помощью инструмента ПОИСК РЕШЕНИЯ
Найдем решения уравнения .
Решать данное уравнение будем аналогично примеру 3.1. То есть:
Протабулируем функцию и построим ее график;
Уточним корни уравнения.
Протабулируем функцию на промежутке [-10; 10]. Сначала в ячейках А2:А22 зададим значения аргумента x и найдем значения функции в данных точках, которые запишем в ячейки В2:В22.
В ячейке В2 укажем формулу: =A2*TAN(A2)-1
Рисунок 1 – Таблица значений аргумента и функции
на отрезке [-10; 10] с шагом 1
Построим график функции на данном отрезке.
Рисунок 2 – График заданной тригонометрической фнкции
Проанализировав график и таблицу значений функции, видим, что корни уравнения расположены в промежутках (–10; –9), (–7; –6); (–4; –3) и т.п., то есть на тех промежутках, где функция меняет знак и пересекает ось Ох.
Уточним первый корень уравнения. Для этого установим курсор в ячейке В2 и вызовем инструмент ПОИСК РЕШЕНИЯ.
Рисунок 3 – Надстройка ПОИСК РЕШЕНИЯ
Итак, первый корень получен.
Рисунок 4 – Решение тригонометрического уравнения
Аналогично, найдем корень уравнения, задав начальное значение х=–7 и х= –4.
Рисунок 5 – Три корня тригонометрического уравнения
Учитывая, что период функции тангенса равен π, найдем разницу между корнями уравнения: получили 3,04 и 3,01. Итак, разность между корнями равна примерно 3. Следовательно, следующие корни уравнения: – 0,4; 2,6; и т.п.
Таким образом, для нахождения корней тригонометрического уравнения, необходимо проделать те же действия, что и при решении уравнений высших степеней.
Приложение 2
Использование инструмента ПОИСК РЕШЕНИЯ при решении систем линейных уравнений
С помощью инструмента ПОИСК РЕШЕНИЯ можно решить и систему линейных уравнений [6, С. 31].
Пример 4.1. Решим следующую систему линейных уравнений
Для этого зададим ячейки, где будут записаны решения системы уравнений. Пусть это будут ячейки A2:D2.
Рисунок 1 – Создание таблицы для решения системы линейных уравнений
Введем в ячейки, предназначенные для решения (А2:D2) произвольные величины, лежащие в области определения (начальные значения).
В ячейки (А3:D3) внесем формулы, по которым должны вычисляться правые части уравнений: (=8*A2+4*B2-6*C2; =–2*А2–4*С2–6*D2; =6*А2+4*В2+4*С2+6*D2; = 4*А2+6*В2+8*С2+8*D2)
Рисунок 2 – Первоначальная таблица для решения системы линейных уравнений
Запустим ПОИСК РЕШЕНИЯ из меню ДАННЫЕ. Выберем одну из ячеек, содержащих формулы, в качестве целевой ячейки (например, А3), сделаем её равной –18.
В поле ИЗМЕНЯЯ ЯЧЕЙКИ вставим ячейки А2:D2. Добавим ограничения, нажимая на кнопку ДОБАВИТЬ: В3=–2; С3=–14; D3=–6.
Рисунок 3 – Диалоговое окно надстройки ПОИСК РЕШЕНИЯ
Рисунок 4 – Диалоговое окно ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ
Нажмем на кнопку ВЫПОЛНИТЬ. Получим решение:
Рисунок 5 – Решение системы линейных уравнений
Таким образом, решение системы линейных уравнений найдено. Если проверить решение (х1=–5, х2=1, х3=–3, х4=4) подстановкой, то получим верные равенства.
Просмотров работы: 2160
Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.
Подбор параметра и решение уравнений в Excel
Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:
2x+1=7
- y=7 является функцией x;
- нам известно значение y, следует узнать при каком значении x мы получим y вычисляемый формулой.
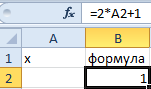
Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:
- Заполните ячейки листа, так как показано на рисунке:
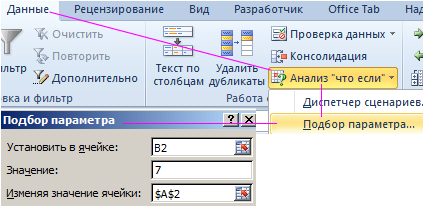
- Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
- В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:
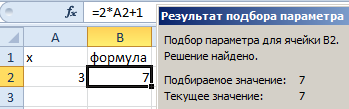
В результате мы получили правильное значение 3.
Получили максимально точный результат: 2*3+1=7
Второй пример использования подбора параметра для уравнений
Немного усложним задачу. На этот раз формула выглядит следующим образом:
x2=4
Решение:
- Заполните ячейку B2 формулой как показано на рисунке:
- Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
- Сравните 2 результата вычисления:
Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.
Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:
x=(7-1)/2
Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:
Таким образом, если нас не устраивает результат вычислений, можно:
- Увеличить в настройках параметр предельного числа итераций.
- Изменить относительную погрешность.
- В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).
Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.
О подборе нескольких параметров в Excel узнаем из примеров следующего урока.