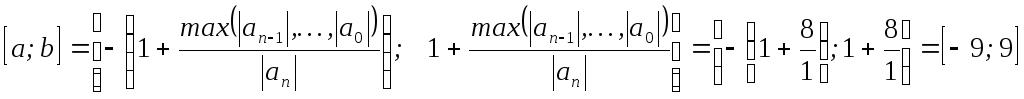Открытый урок по математике и информатике «Решение уравнений высших степеней в MS Excel»
Научить учащихся решать уравнения 3, 4, 5 и т.д. степени в редакторе электронных таблиц MS EXEL.
1. Актуализация знаний.
Ребята! На прошлом уроке мы с вами занимались построением графиков функций в MS EXEL. Сегодняшний урок – продолжение изучения того материала, который мы начали на предыдущем уроке. Тема нашего урока «Решение уравнений высших степеней в МS EXСEL».
Откройте тетради и запишите тему урока. Обратите внимание на тему – она состоит из двух частей: уравнения высших степеней(математика) и МS EXСEL(информатика). Сегодня на уроке мы должны связать и объединить два предмета – математику и информатику. Но чтобы приступить к изучению нового материала, мы должны вспомнить материал из математики – способы и методы изучения уравнений высших степеней. Поможет нам с вами в этом плакат.
На плакате 5 способов решения уравнений(к каждому способу предлагается пример уравнения):
- Способ разложения на множители;
- Графический способ;
- Схема Горнера;
- Метод неопределённых коэффициентов;
- Метод сведения к системе уравнений.
— Какие способы решения вы помните и знаете?
— На примере уравнения вспомним этот способ.
— Все слагаемые переносятся в левую часть. Применяются способы разложения на множители: вынесение общего множителя за скобки, группировка, формулы сокращенного умножения. В конце применяется правило: произведение множителей равно нулю, когда хотя бы один из множителей равен нулю.
-Ещё какой способ вам знаком?
— Объясним на примере уравнения этот способ решения.
— Левая часть уравнения делится на две части так, чтобы хорошо строились графики функций обеих частей. Строятся графики левой и правой части уравнений, находятся точки пересечения графиков. Абсциссы точек пересечения графиков – решения уравнения.
— И ещё один способ мы изучили на факультативных занятиях – схему Горнера. По этому способу находятся все делители свободного члена, отыскивается среди них корень уравнения- а, затем левая часть уравнения делится на х-а, получаем в частном квадратный трёхчлен. Левая часть уравнения раскладывается на множители и применяется правило равенства нулю правой части уравнения. Остальные способы рассмотрим на следующих факультативных занятиях.
— Согласитесь , что школьная программа предоставляет нам мало способов решения уравнений высших степеней, а ведь с такими уравнениями мы часто с вами сталкиваемся при исследовании функций, решении иррациональных уравнений, систем уравнений и не можем найти выход из создавшихся проблемных ситуаций.
— Сейчас я вам напишу на доске уравнение, посмотрите на него и подумайте, как бы вы его стали решать в рамках школьной программы: х 4 -4х 3 -10х 2 +3х-14=0
Идут рассуждения учеников по решению уравнения. Ученики соглашаются, что решить его школьной программой невозможно.
2. Объяснение нового материала
— Где же искать выход из создавшейся проблемной ситуации? Ещё разок посмотрите на тему урока. Так где же мы будем искать сегодня выход? В МS EXСEL. В начале урока я вам сказала, что сегодняшний урок – продолжение изучения материала прошлого урока. Ещё разок вспомним, чем мы занимались на предыдущем уроке – построением графиков функций. Давайте подумаем, как же решить это уравнение графически в МS EXСEL.
Дети предлагают построить график функции левой части уравнения.
— Посмотрите, что стоит в правой части уравнения? Число – 0. Значит задача сводится к нахождению нулей функции или точек пересечения с осью х. Это вы делать умеете.
— Перед вами практическая работа, которая позволит решить это уравнение. 1 и 2 часть практической работы построение графика функции и смещение оси у вы сможете выполнить, точки пересечения (приближённые) с осью х тоже сможете найти. Кто быстро построит график функции, попробует выполнить 3 часть практической работы – найти корни уравнения с точностью до 5,6 знаков после запятой.
3. Практическая работа «Решение уравнений высших степеней с помощью MS EXEL”.
Решите уравнение х 4 -4х 3 -10х 2 +37х-14=0
1. Строим график функции у=х 4 -4х 3 -10х 2 +3х-14=0 на промежутке [-4;6] с шагом h=0,5.
| х | у |
| -4 | 190 |
| -3,5 | 55,5625 |
| -3 | 26 |
| -2,5 | -67,4375 |
| 2 | -80 |
| -1,5 | -73,4375 |
| -1 | -56 |
| -0,5 | -34,4375 |
| 0 | -14 |
| 0,5 | 1,5625 |
| 1,5 | 10,5625 |
| 2 | 4 |
| 2,5 | -7,4375 |
| 3 | -20 |
| 3,5 | -28,4375 |
| 4 | -26 |
| 4,5 | -4,4375 |
| 5 | 46 |
| 5,5 | 136,5625 |
| 6 | 280 |
- Выделяем значения функции у
- Вставка-Диаграмма-Нестандартные-Гладкие графики-Далее
- Выбрать вкладку РЯД
- Выбрать Подписи оси Х , установить в ней курсор и провести мышью при нажатой левой кнопкепо всему ряду значений аргумента Х таблицы.
2. Смещение оси У на место.
- Выделяем ось Х
- Формат-Выделенная ось-Шкала-Пересечение с осью У
- Подбираем значения для нужного смещения оси
- ОК
Из таблицы и графика можно определить промежутки, в которых находятся корни этого уравнения: х1є[-3,5;-3], х2є[0;0,5], х3є[2;2,5], х4є[4,5;5]. Затем с помощью команды Сервис, Подбор параметра можно уточнить значение корней. Для этого следует активизировать со значением функции у=55,5625 (например, С8), соответствующим значению аргумента х=3,5, или ячейку со значением у= -26, соответствующим х=-3, и выполнить команду Сервис, Подбор параметра. Появится одноименное диалоговое окно с тремя строками:
В первой указан адрес выбранного значения функции. Во второй нужно установить курсор и занести подбираемое значение функции, указанное в правой части данного уравнения( в нашем случае – число 0). А затем, установив курсор в третьей строке, надо щёлкнуть левой кнопке мыши на ячейке с соответствующим значением аргумента (В8 или В9), чтобы получить абсолютное значение этого адреса или щёлкнуть мышью по кнопке ОК.
После выполнения нескольких итераций и по достижении значения функции, близкого к подбираемому значению, в адресе аргумента установится значение корня х1=-3, 192582. Запишем его в тетрадь. В появившемся окне Результат подбора параметра необходимо щёлкнуть мышью по кнопке Отмена для восстановления прежних значений аргумента и функции. Аналогично находим значение остальных корней.
3 часть практической работы выполняется вместе с учителем.
Учащимся предлагается выполнить индивидуальные задания на решение уравнения по карточкам.
4. Домашнее задание – переписать в тетрадь 3 часть практической работы.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Excel. Решение уравнений n-ой степени
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
ПОИСК РЕШЕНИЯ В EXCEL
Программа Microsoft Office Excel предназначена и широко используется для вычислений, предполагающих представление данных в табличном виде.
На уроках алгебры часто приходится решать квадратные, кубические уравнения, системы уравнений.
Цель — решать уравнения n -ой степени и системы уравнений с помощью Excel .
Для достижения данной цели поставим следующие задачи :
изучить возможности инструмента «Поиск решения»;
создать в Excel шаблоны для решения различных типов задач;
разработать инструкции нахождения решений;
Программа « Поиск решения» позволяет получить результат на основе изменения значения нескольких ячеек. Кроме того, при выполнении поиска решения можно задать условия – ввести ограничения. Эти возможности позволяют использовать программу Excel для решения системы уравнений и уравнений, при решении которых необходимо учитывать область допустимых значений, для нахождения точек, в которых достигается максимум или минимум значения целевой функции нескольких переменных, определенных на множестве с линейными и нелинейными ограничениями. Другими словами – находить оптимальное решение задачи с ограничениями.
Модели всех задач на оптимизацию состоят из следующих элементов:
Переменные — неизвестные величины, которые нужно найти при решении задачи.
Целевая функция — величина, которая зависит от переменных и является целью, ключевым показателем эффективности или оптимальности модели.
Ограничения — условия, которым должны удовлетворять переменные.
Поиск решения рассмотрим на примерах.
Найти минимальное значение функции 
В 
Получен результат: минимальное значение функции 
Найти максимальное значение функции 

источники:
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
http://infourok.ru/ecel-reshenie-uravneniy-noy-stepeni-1487724.html
Цели урока:
- Формирование умений и навыков, носящих в современных условиях общенаучный и обще интеллектуальный характер.
- Развитие у школьников теоретического, творческого мышления, а также формирование операционного мышления, направленного на выбор оптимальных решений.
- Научить учащихся применять современное программное обеспечение в решении нестандартных задач.
- Повторение пройденного материала.
Задачи урока:
- Воспитательная – развитие познавательного интереса, воспитание информационной культуры.
- Учебная – изучить и закрепить основные навыки работы с электронными таблицами.
- Развивающая – развитие логического мышления, расширение кругозора.
Оборудование: персональные компьютеры (ПК), раздаточный материал, доска, маркеры, проектор.
План урока
- Организационный момент.
- Фронтальный опрос для проверки уровня подготовки учащихся к усвоению нового материала.
1) Какие дополнительные возможности есть у программы Excel?
2) Как вы понимаете термин деловая графика?
3) Какими возможностями для создания деловой графики обладает Excel?
4) При помощи какой команды меню можно построить диаграммы и графики в Excel?
5) Как задать автоматическое вычисление в таблице значений ячеек по определенной формуле?
6) Каким образом можно занести формулу в несколько ячеек, т.е. скопировать ее? - Объяснение нового материала. Проводится одновременно с работой учеников на ПК синхронно с учителем.
- Самостоятельная работа учащихся на компьютерах.
- Сравнение результатов, полученных графическим способом (Excel) и аналитическим (Qbasic).
- Выполнение индивидуальных заданий.
- Подведение итогов.
- Выставление оценок.
- Домашнее задание.
Ход урока
1. Организационный момент.
2. Фронтальный опрос.
1) Для чего нужна программа Excel?
Ответ: для создания таблиц, вычисляемых таблиц, диаграмм и графиков (деловой графики).
2) Какими возможностями для создания деловой графики обладает Excel?
Ответ: с помощью библиотеки диаграмм можно составлять диаграммы и графики разных видов (гистограммы, круговые диаграммы, столбчатые, графики и др.), их можно снабжать заголовками и пояснениями, можно задавать цвет и вид штриховки в диаграммах, редактировать их, печатать их на бумаге, изменяя размеры и расположение на листе, вставлять диаграммы в нужное место листа.
3) При помощи какой команды меню можно построить диаграммы и графики в Excel?
Ответ: с помощью вызова Мастера диаграмм (по команде Вставка-Диаграмма или с помощью кнопки Мастер диаграмм).
4) Как задать автоматическое вычисление в таблице значений ячеек по определенной формуле?
Ответ: активизировать нужную ячейку, затем ввести знак «=» и формулу, которая может содержать адреса ячеек, знаки арифметических операций и функции. Контролировать и редактировать ввод формулы можно с помощью строки ввода формулы, которая расположена в верхней части окна программы.
5) Каким образом можно занести формулу в несколько ячеек, т.е. скопировать ее.
Ответ: ввести формулу в ячейку, установить курсор на нижнем правом маркере ячейки (при этом курсор должен принять вид маленького черного крестика) и протянуть его до последней ячейки в нужном диапазоне.
3. Объяснение нового материала (проводится одновременно с работой учеников на компьютерах синхронно с учителем).
Тема урока «Применение табличного процессора Excel для графического решения уравнений n-ой степени».
Из курса математики нам известно, что корнями уравнения являются значения точек пересечения графика функции (то есть нашего уравнения) с осью абсцисс. Если же мы решаем систему уравнений, то ее решениями будут координаты точек пересечения графиков функций. Этот метод нахождения корней называется графическим. На прошлом занятии мы узнали, что с помощью программы Excel можно строить практически любые графики. Воспользуемся этими знаниями для нахождения корней системы уравнений графическим методом.
Для примера рассмотрим решение следующей системы уравнений:
Y — X2 = 0
Y – 2X = 9
Преобразуем данную систему в приведенную:
Y = X2
Y = 2X + 9
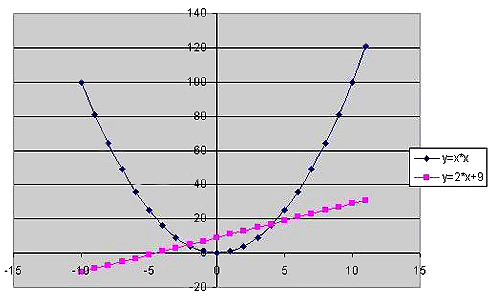
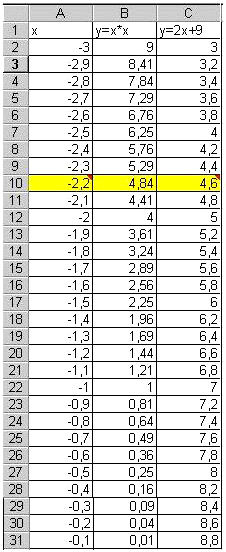
Для оценки решений воспользуемся диаграммой, на которой отобразим графики обеих функций. Сначала построим таблицу 1 (рисунок 1).
Таблица 1
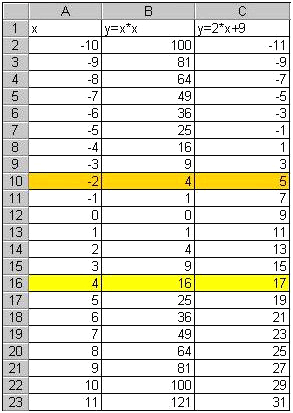
Рисунок 1
- Первая строка – строка заголовков. Далее для построения таблицы используем формулы.
- При заполнении столбца А: в ячейку А2 заносится начальное значение аргумента Х=-10, для автоматического заполнения всего столбца нужно в ячейку А3 занести формулу А2+1 и скопировать ее до ячейки А23.
- При заполнении столбца В в ячейку В2 заносится формула А2*А2, которая затем копируется до ячейки В23.
- При заполнении столбца С в ячейку С2 заносится формула 2*А2+9, и также копируется до С23.
- Выделяем таблицу вместе со строкой заголовка и помощью мастера диаграмм выберем тип диаграмм Точечная и построим черновую диаграмму первоначальной оценки решений.
- Вводим заголовок «Диаграмма оценки решения» и обозначения осей x, y (поле ввода текста).
- Добавляем основные линии сетки по оси X и по оси Y (выставляем флажки).
- Размещаем легенду справа от графиков (выставляем флажок «добавить легенду» и включаем переключатель «размещение справа»).
- Размещаем графики на имеющемся листе.
- Подписываем лист 1 «Диаграмма оценки решения» (рисунок 2).
Диаграмма оценки решения
Рисунок 2
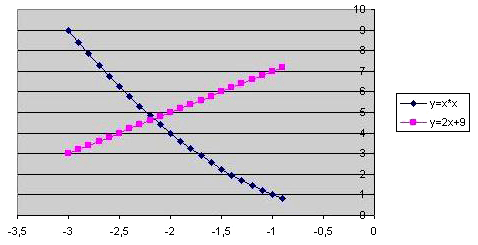
На диаграмме видно, что оба графика имеют точки пересечения – эти координаты точек и есть решения системы. Так как шаг изменения аргумента был достаточно велик, то мы получили приближенные значения решений. Уточним их, построив два графика в интервалах от –3 до 0, где находится первое решение, и от 3 до 5 – где находится второе. Составим новые таблицы.
Для первого решения (таблица 2, рисунок 3).
Таблица 2
Рисунок 3
- При заполнении столбца А: в ячейку А2 заносится начальное значение аргумента Х=-3, для автоматического заполнения всего столбца нужно в ячейку А3 занести формулу А2+0,1(в этом случае мы уменьшаем шаг изменения аргумента для более точного построения) и скопировать ее до ячейки А23.
- При заполнении столбца В в ячейку В2 заносится формула А2*А2, которая затем копируется до ячейки В23.
- При заполнении столбца С в ячейку С2 заносится формула 2*А2+9, и также копируется до С23.
- Выделяем таблицу вместе со строкой заголовка и помощью мастера диаграмм
- выберем тип диаграмм Точечная и построим диаграмму для первого решения.
- Вводим заголовок «Первое решение» и обозначения осей x, y (поле ввода текста).
- Добавляем основные линии сетки по оси X и по оси Y (выставляем флажки).
- Размещаем легенду справа от графиков (выставляем флажок «добавить легенду» и включаем переключатель «размещение справа»).
- Размещаем графики на имеющемся листе.
- Подписываем лист 2 «Первое решение» (рисунок 4).
Первое решение
Рисунок 4
4. Самостоятельная работа.
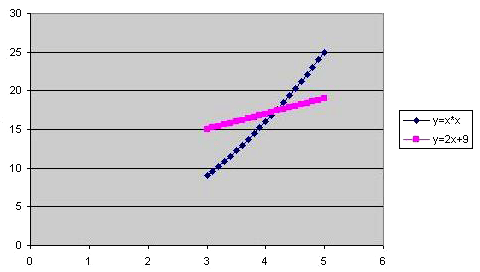
Для второго решения ребята самостоятельно строят таблицу (таблица 3, рисунок 5), выбрав правильно промежуток. Затем по таблице строят диаграмму для второго решения (рисунок 6). Учитель проходит и проверяет правильность выполнения работы. И если нужна помощь, то в индивидуальном порядке оказывает ее.
Таблица 3
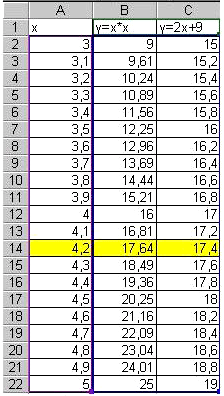
Рисунок 5
Второе решение
Рисунок 6
Решением нашей системы будут координаты точек пересечения графиков: X1=-2,1; Y1=4,8; X2=4,2; Y2=17,4.
Как вы уже поняли, графическое решение системы дает приблизительные результаты.
5. Сравнение результатов, полученных графическим способом (Excel) и аналитическим (Qbasic).
Учитель предлагает решить данную систему уравнений аналитическим способом, используя ранее полученную на уроках информатики программу решения квадратного уравнения. К доске приглашается ученик, который преобразует систему в квадратное уравнение:
X^2-2*X-9=0
Выделяем коэффициенты a, b, c, (a=1, b=-2,c=-9) и подставляем в программу
(ребята открывают программу, которая была составлена ранее на уроках программирования).
REM Решение квадратного уравнения
INPUT «Введите коэффициенты a, b, с»; a, b,c
d= b^2-4*a*c
IF d<0 THEN PRINT «Решений нет»: GOTO 90
IF d=0 THEN x=-b/(2*a): PRINT «x=»; x: GOTO 90
X1=(-b-SQR(d))/(2*a)
X2=(-b+SQR(d))/(2*a)PRINT “x1=”; x1, “x2=”; x2
90 END
Подставив коэффициенты в программу, получаем точное значение абсцисс:
x1=-2,162278
x2= 4,162278
Сравниваем решения системы, полученные графическим способом и аналитическим. Делаем выводы.
6. Выполнение индивидуальных заданий.
1. C помощью табличного процессора Excel решить графически систему:
Y=X2
Y=4X+12
2. C помощью табличного процессора Excel решить графически систему:
Y=X2+5
Y=6X+12
3. C помощью табличного процессора Excel решить графически систему:
Y=X2+4
Y=X+12
4. C помощью табличного процессора Excel решить графически систему:
Y=X2+5
Y=4X+4
5. C помощью табличного процессора Excel решить графически систему:
Y=X2+5
Y=3X+12
6. C помощью табличного процессора Excel решить графически систему:
Y=X3+5
Y=2X2+4X+12
7. C помощью табличного процессора Excel решить графически систему:
Y=X2
Y=8X+12
8. C помощью табличного процессора Excel решить графически систему:
Y=X3+5
Y=X+12
9. C помощью табличного процессора Excel решить графически систему:
Y=X2+3
Y=5X+1
10. C помощью табличного процессора Excel решить графически систему:
Y=X2+2
Y=X+12
11. C помощью табличного процессора Excel решить графически систему:
Y=X3+5
Y=4X2+12
12. C помощью табличного процессора Excel решить графически систему:
Y=X3+5
Y=X2+4X+12
7. Подведение итогов.
Распечатка отчетов.
8. Выставление оценок.
9. Домашнее задание.
Проанализировать и проверить свои индивидуальные задания и оформить отчеты на листочках.
Разнообразные
проблемы механики, физики, техники
сводятся к вопросу о нахождении корней
многочлена, причем, иногда достаточно
высоких степеней. Точные решения известны
для квадратных уравнений, кубических
(формула Кардано) и уравнений 4-й степени
(метод Феррари). Для уравнений выше 5-й
степени не существует формул для
выражения корней многочлена. Однако в
технических приложениях обычно достаточно
знать лишь приближенные значения корней
с некоторой заранее заданной точностью.
В
общем
же
случае
надежд
на
простое
аналитическое
решение
нет. Более
того,
доказано,
что
даже
алгебраическое
уравнение
выше
четвертой
степени
неразрешимо
в
элементарных
функциях.
Поэтому
решение
уравнения
проводят
численно
в
два
этапа
(здесь
разговор
идет
лишь
о
вещественных
корнях
уравнения).
На
первом
этапе
производится
отделение
корней
– поиск
интервалов,
в
которых
содержится
только
по
одному
корню.
Второй
этап
решения
связан
с
уточнением
корня
в
выбранном
интервале
(определением
значения
корня
с
заданной
точностью).
В
общем виде уравнение n-й
степени выглядит следующим образом:
,
где
n
− некоторое положительное число,
− произвольные числа, причем старший
коэффициентдолжен быть не равен нулю.
Выражение
называется многочленом (полиномом)n
− й степени от неизвестного x.
Если
при некотором x
= x0
выполняется равенство
,
тоx0
называется корнем многочлена
.
Приведем
некоторые рекомендации по отысканию
действительных корней многочленов с
действительными коэффициентами:
-
Действительными
корнями многочлена будут абсциссы
точек пересечения его графика с осью
Х
и только они; -
Число
положительных корней многочлена равно
числу перемен знаков в системе
коэффициентов этого многочлена
(коэффициенты, равные нулю, не учитываются)
или меньше этого числа на четное число; -
Число
отрицательных корней многочлена равно
числу сохранения знаков в системе
коэффициентов этого многочлена или
меньше этого числа на четное число; -
Если
многочлен не имеет отрицательных
коэффициентов, то многочлен не имеет
положительных корней; -
О
трезок
локализации всех корней многочлена
определяется по выражению:
Для границы a
формула справедлива если
Решение
отыскания корней многочлена с помощью
электронной таблицы MS
Excel
предполагает следующие шаги:
-
Провести
табулирование заданного многочлена
на интервале
.
-
Выявить
интервалы локализации каждого корня
многочлена (перемена знака в значении
).
При необходимости, следует использовать
табуляцию многочлена, неоднократно
уменьшая шаг табуляции для более точных
оценок. -
После
локализации корней произвести их
уточнение.
При последующем
уточнении корня на обнаруженном
интервале не надейтесь никогда найти
точное
значение и добиться обращения функции
в нуль при использовании калькулятора
или компьютера, где сами числа
представлены ограниченным числом
знаков. Здесь критерием может служить
приемлемая абсолютная
или относительная
погрешность
корня. Если корень близок к нулю, то лишь
относительная погрешность даст
необходимое число значащих цифр. Если
же он весьма велик по абсолютной величине,
то критерий абсолютной погрешности
часто дает совершенно излишние верные
цифры. Для функций, быстро изменяющихся
в окрестности корня, может быть
привлечен и критерий: абсолютная
величина значения функции
не превышает заданной допустимой
погрешности.
Пример
Найти
все действительные корни уравнения:
f(x)
= Х5
+
2Х4
+
5Х3
+
8Х2
−
7Х –
3
= 0,
где
а5
= 1, а4
= 2, а3
= 5, а2
= 8, а1
= −7, а0
= −3.
-
Число сохраненных
знаков =
4 (в уравнение отрицательных корней 4
или 2) -
Число перемены
знаков = 1 (в уравнение один положительный
корень) -
Определяем отрезок
[a;
b],
на котором существуют корни уравнения..
-
Выполняем
приближенное табулирование функции
на отрезке [−9; 9]
с шагом 1. -
Определяем, что
функция меняет знак на отрезке [−3; 1]. -
Производим
табулирование функции на отрезке [−3;
1] с шагом 0,1. -
Строим график
функции. -
Используя, таблицу
и график функции определяем положение
корней уравнения (на рис. 1. отрезки
локализации корней выделены желтым
цветом).
Р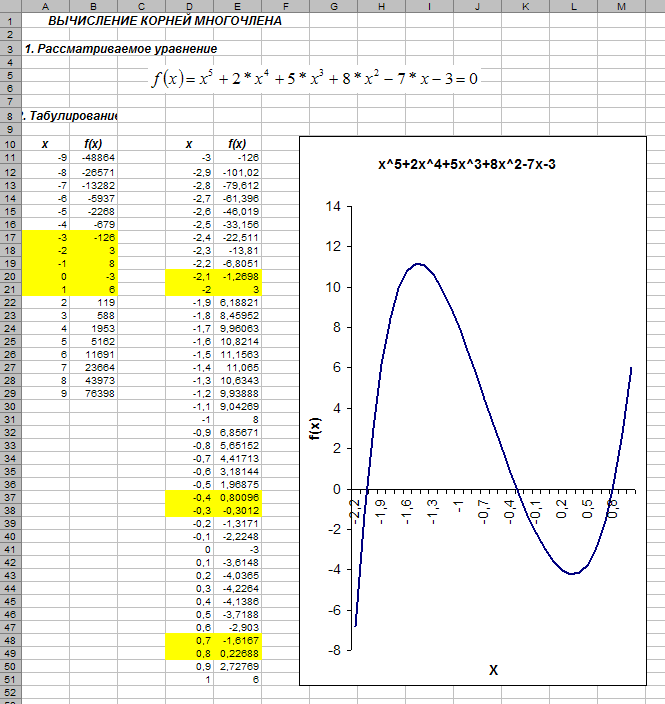
1. Локализация корней уравнения
Из таблицы и графика
видно, что многочлен f(x)
содержит 3 корня, находящихся в границах
отрезков: 1-й корень
,
;
2-й корень,
;
3 — й корень,
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подписи к слайдам:
Графическое решение уравнений
n-ой степени средствами
Microsoft Excel
- Козырева И. Н., ЯНАО, п. Харп
Повторение
- Для чего используется табличный процессор Microsoft Excel?
Повторение
- 2. Что означает термин «деловая графика»?
Повторение
- 3. Какими возможностями обладает Microsoft Excel для создания деловой графики?
Повторение
- 4. Что такое диаграмма? Назовите типы диаграмм.
Повторение
- 5. С помощью какой команды панели инструментов можно построить диаграммы и графики в Excel?
Повторение
- 6. Как задать автоматическое вычисление в таблице значений ячеек по определенной формуле?
- =
- 3*А2-2
- =3*А2-2
Повторение
- 7. Как заполнить диапазон ячеек последовательностью чисел, например, от 1 до 8 с шагом 1?
Повторение
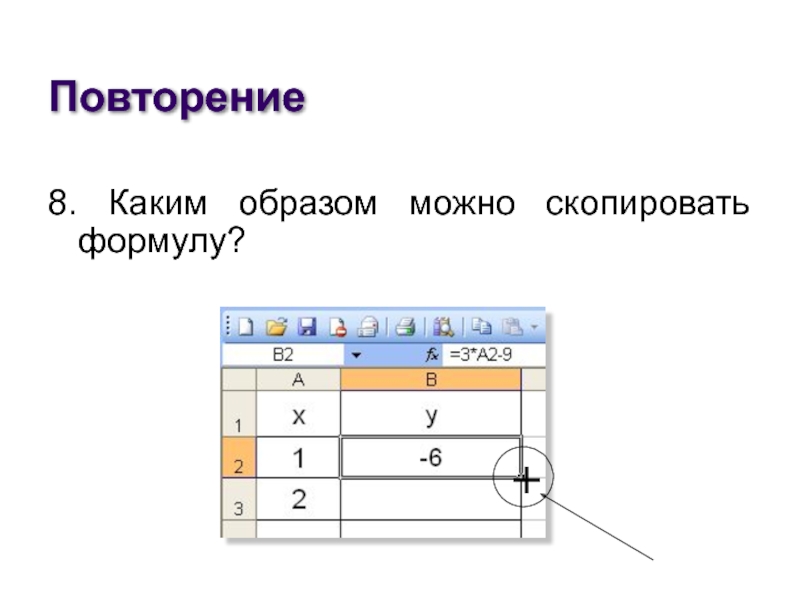
- 8. Каким образом можно скопировать формулу?
Применение Excel для графического решения
системы уравнений
- Корнями уравнения являются значения точек пересечения графика функции с осью абсцисс.
- Решением системы уравнений являются точки пересечения графиков функций.
- Такой метод нахождения корней называется графическим.
- При помощи табличного процессора можно решать уравнения и системы уравнений. Для графического решения подойдут средства построения диаграмм.
- Применение Excel для графического решения
системы уравнений
- Найти решение системы уравнений:
- 1. Преобразуем данную систему:
- Ответ записать с точностью до 0,1.
- Задание
- 2. Для оценки решений воспользуемся диаграммой, на которой отобразим графики обеих функций.
- 1 строка – строка заголовков
- Заполняем столбец А: заполняем ячейки А2:А22 числами от -10 до 10 с шагом 1.
- При заполнении столбца В в ячейку В2 заносим формулу =А2*А2, которую затем копируем до ячейки В22.
- При заполнении столбца С в ячейку С2 заносим формулу =2*А2+4, копируем ее до ячейки С22.
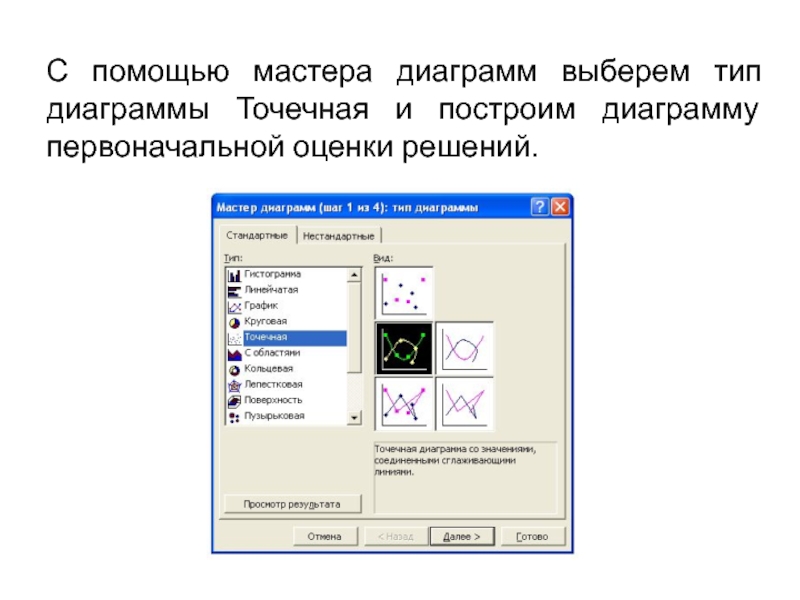
- С помощью мастера диаграмм выберем тип диаграммы Точечная и построим диаграмму первоначальной оценки решений.
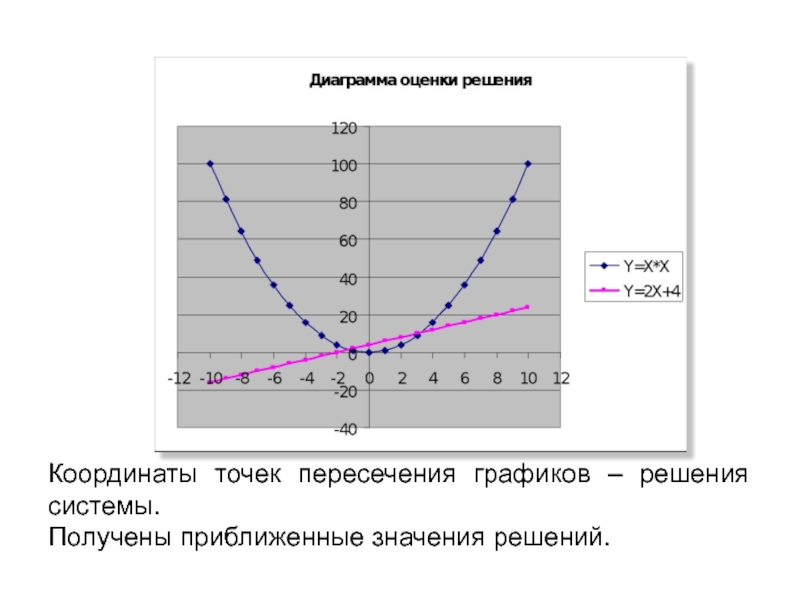
- Координаты точек пересечения графиков – решения системы.
- Получены приближенные значения решений.
- Для уточнения значения решений построим графики в интервалах от -2 до 0, где находится первое решение,
- и от 2 до 4, где находится второе решение.
- 3. Составляем новую таблицу для
— 2 ≤ x ≤ 0.
- Проверка:>
- 3. Составляем новую таблицу для
— 2 ≤ x ≤ 0.
- Строим точечную диаграмму для получения первого решения
- 4. Составляем новую таблицу для
2 ≤ x ≤ 4.
- Проверка>
- 4. Составляем новую таблицу для
2 ≤ x ≤ 4.
- Строим точечную диаграмму для получения второго решения
- Решением нашей системы будут координаты точек пересечения графиков.
- Какие?
- X1= -1.2 Y1= 1.5
- Графическое решение системы уравнений является приближенным.
- !!!
- X2= 3.3 Y2= 10.8
- Выполнение индивидуальных заданий (по карточкам).
- Подготовка отчетов.
Домашнее задание:- Подготовить задание из учебника алгебры. Проанализировать его (определить интервал для построения диаграммы оценки решений).
Спасибо!
Урок завершен.
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Содержание
-
1.
Графическое решение уравнений n-ой степени средствами Microsoft Excel -
2.
ПовторениеДля чего используется табличный процессор Microsoft Excel? -
3.
Повторение2. Что означает термин «деловая графика»? -
4.
Повторение3. Какими возможностями обладает Microsoft Excel для создания деловой графики? -
5.
Повторение4. Что такое диаграмма? Назовите типы диаграмм. -
6.
Слайд 6 -
7.
Слайд 7 -
8.
Слайд 8 -
9.
Слайд 9 -
10.
Слайд 10 -
11.
Повторение5. С помощью какой команды панели инструментов можно построить диаграммы и графики в Excel? -
12.
Повторение6. Как задать автоматическое вычисление в таблице значений ячеек по определенной формуле?=3*А2-2=3*А2-2 -
13.
Повторение7. Как заполнить диапазон ячеек последовательностью чисел, например, от 1 до 8 с шагом 1? -
14.
Повторение8. Каким образом можно скопировать формулу? -
15.
Применение Excel для графического решения системы -
16.
При помощи табличного процессора можно решать уравнения -
17.
Найти решение системы уравнений:1. Преобразуем данную систему:Ответ записать с точностью до 0,1.Задание -
18.
2. Для оценки решений воспользуемся диаграммой, на -
19.
При заполнении столбца В в ячейку В2 -
20.
С помощью мастера диаграмм выберем тип диаграммы Точечная и построим диаграмму первоначальной оценки решений. -
21.
Координаты точек пересечения графиков – решения системы. Получены приближенные значения решений. -
22.
Для уточнения значения решений построим графики в -
23.
3. Составляем новую таблицу для -
24.
3. Составляем новую таблицу для -
25.
Строим точечную диаграмму для получения первого решения -
26.
4. Составляем новую таблицу для -
27.
4. Составляем новую таблицу для -
28.
Строим точечную диаграмму для получения второго решения -
29.
Решением нашей системы будут координаты точек пересечения -
30.
Выполнение индивидуальных заданий (по карточкам).Подготовка отчетов. -
31.
Спасибо! Урок завершен. -
32.
Скачать презентанцию
ПовторениеДля чего используется табличный процессор Microsoft Excel?
Слайды и текст этой презентации
Слайд 1Козырева И. Н., ЯНАО, п. Харп
Графическое решение уравнений
n-ой степени
средствами
Microsoft Excel

Слайд 2Повторение
Для чего используется табличный процессор Microsoft Excel?

Слайд 3Повторение
2. Что означает термин «деловая графика»?

Слайд 4Повторение
3. Какими возможностями обладает Microsoft Excel для создания деловой графики?

Слайд 5Повторение
4. Что такое диаграмма? Назовите типы диаграмм.

Слайд 11Повторение
5. С помощью какой команды панели инструментов можно построить диаграммы
и графики в Excel?

Слайд 12Повторение
6. Как задать автоматическое вычисление в таблице значений ячеек по
определенной формуле?
=
3*А2-2
=3*А2-2

Слайд 13Повторение
7. Как заполнить диапазон ячеек последовательностью чисел, например, от 1
до 8 с шагом 1?

Слайд 14Повторение
8. Каким образом можно скопировать формулу?
Слайд 15Применение Excel для графического решения
системы уравнений
Корнями уравнения являются значения
точек пересечения графика функции с осью абсцисс.
Решением системы уравнений
являются точки пересечения графиков функций.
Такой метод нахождения корней называется графическим.

Слайд 16
При помощи табличного процессора можно решать уравнения и системы уравнений.
Для графического решения подойдут средства построения диаграмм.
Применение Excel для графического
решения
системы уравнений

Слайд 17Найти решение системы уравнений:
1. Преобразуем данную систему:
Ответ записать с точностью
до 0,1.
Задание

Слайд 182. Для оценки решений воспользуемся диаграммой, на которой отобразим графики
обеих функций.
1 строка – строка заголовков
Заполняем столбец А: заполняем ячейки
А2:А22 числами от -10 до 10 с шагом 1.

Слайд 19При заполнении столбца В в ячейку В2 заносим формулу =А2*А2,
которую затем копируем до ячейки В22.
При заполнении столбца С в
ячейку С2 заносим формулу =2*А2+4, копируем ее до ячейки С22.

Слайд 20С помощью мастера диаграмм выберем тип диаграммы Точечная и построим
диаграмму первоначальной оценки решений.
Слайд 21Координаты точек пересечения графиков – решения системы.
Получены приближенные значения
решений.
Слайд 22Для уточнения значения решений построим графики в интервалах от -2
до 0, где находится первое решение,
и от 2 до
4, где находится второе решение.

Слайд 233. Составляем новую таблицу для
— 2 ≤ x
≤ 0.
Проверка:Проверка:>

Слайд 25Строим точечную диаграмму для получения первого решения

Слайд 264. Составляем новую таблицу для
2 ≤ x ≤
4.
ПроверкаПроверка>

Слайд 28Строим точечную диаграмму для получения второго решения
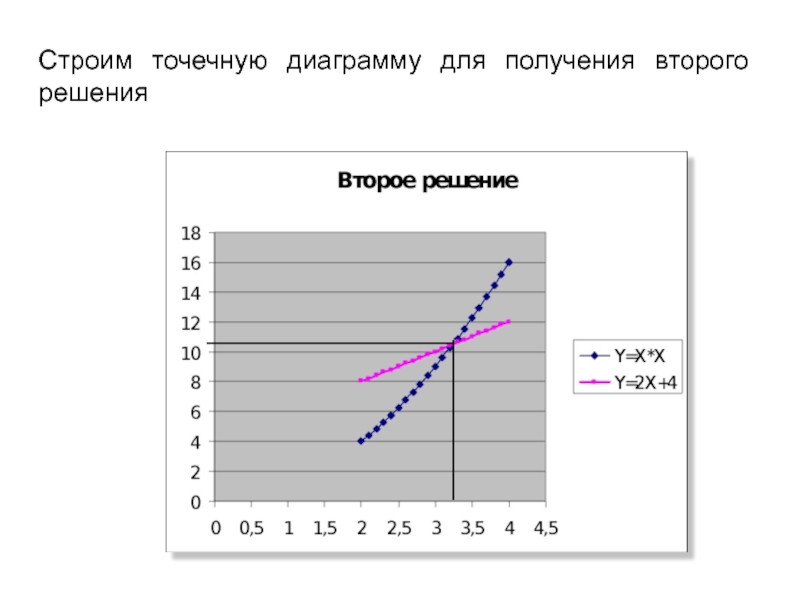
Слайд 29Решением нашей системы будут координаты точек пересечения графиков.
Какие?
X1= -1.2
Y1= 1.5
Графическое решение системы уравнений является приближенным.
!!!
X2= 3.3
Y2= 10.8

Слайд 30Выполнение индивидуальных заданий (по карточкам).
Подготовка отчетов.
Домашнее задание:
Подготовить задание из
учебника алгебры. Проанализировать его (определить интервал для построения диаграммы оценки
решений).




























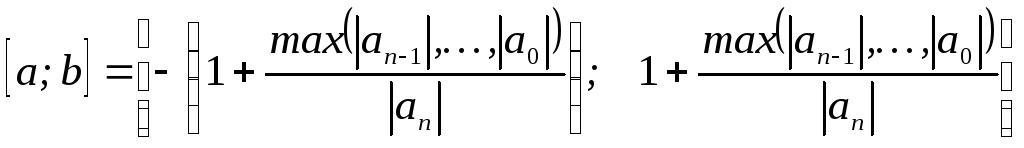 трезок
трезок