Решение уравнений excel cos

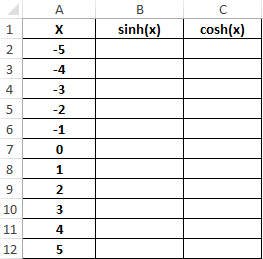
Функция COS

В этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.

Описание

Возвращает косинус заданного угла.

Синтаксис

Аргументы функции COS описаны ниже.

Число — обязательный аргумент. Угол в радианах, для которого определяется косинус.

Замечания

Если угол задан в градусах, умножьте его на ПИ()/180 или воспользуйтесь функцией РАДИАНЫ, чтобы преобразовать его в радианы.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Функция COS Excel

Функция COS Excel — это встроенная тригонометрическая функция в Excel, которая используется для вычисления значения косинуса заданного числа или в терминах или тригонометрии значения косинуса заданного угла, здесь угол — это число в Excel, и эта функция принимает только один аргумент. который является предоставленным входным номером.

Функция COS Excel

Это встроенная функция в MS Excel. Он относится к категории «Математические функции в MS Excel». Функция возвращает косинус угла в радианах. Параметр — это значение угла, для которого должен быть вычислен косинус. Угол можно рассчитать с помощью функции РАДИАНЫ или умножив его на PI () / 180.

Формула COS

Формула COS в Excel выглядит следующим образом:

Формула COS в Excel имеет один аргумент, который является обязательным параметром.

• количество= Это обязательный параметр. Он указывает угол, для которого должен быть вычислен косинус.

Как использовать функцию COS в Excel?

COS можно использовать в листе Excel как функцию листа (WS), а также в Excel VBA. Как функцию WS, ее можно ввести как часть формулы COS в ячейку рабочего листа. В качестве функции VBA ее можно ввести в код VBA.

Обратитесь к примерам, приведенным ниже, чтобы лучше понять.

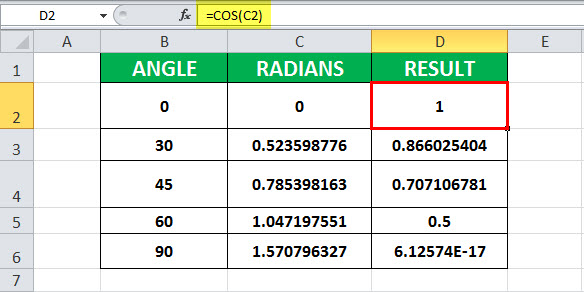
Пример №1 — Вычислить значение cos (0)

В этом примере ячейка B2 содержит значение угла, для которого должен быть вычислен косинус. С ячейкой C2 связана формула COS — РАДИАНЫ. COS в Excel назначается ячейке D2. РАДИАНЫ (B2) равны 0. Далее, COS применяется к 0, то есть 1.

Следовательно, результирующая ячейка D2 имеет значение 1, поскольку COS (0) равно 1.

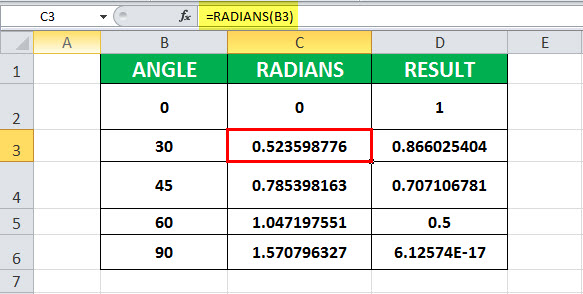
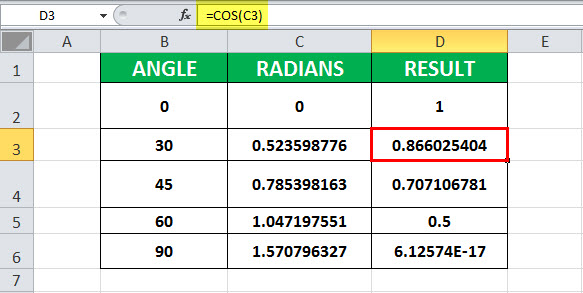
Пример №2 — Вычислить значение cos (30)

В этом примере ячейка B3 содержит значение угла, для которого должен быть вычислен косинус. С ячейкой C3 связана формула COS — РАДИАНЫ. COS в Excel назначается ячейке D3. РАДИАНЫ (B3) — 0,523598776. Далее, COS применяется к 0,523598776, что составляет 0,866025404.

Следовательно, результирующая ячейка D3 имеет значение 1, поскольку COS (0,523598776) равно 1.

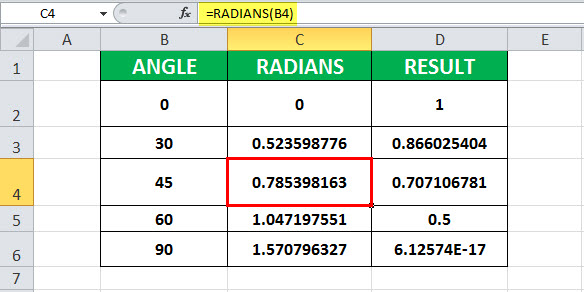
Пример №3 — Вычислить значение cos (45)

В этом примере ячейка B4 содержит значение угла, для которого должен быть вычислен косинус. С ячейкой C4 связана формула COS — РАДИАНЫ. COS назначается ячейке D4. РАДИАНЫ (B3) — 0,523598776. Далее, COS применяется к 0,785398163, что составляет 0,707106781.

Следовательно, результирующая ячейка D4 имеет значение 1, поскольку COS (0,707106781) равно 1.

Пример №4 — Вычислить значение cos (60)

В этом примере ячейка B5 содержит значение угла, для которого должен быть вычислен косинус. С ячейкой C5 связана формула COS — РАДИАНЫ. COS назначается ячейке D5. РАДИАНЫ (B5) — 1.047197551. Далее, COS применяется к 1.047197551, что составляет 0,5.

Следовательно, результирующая ячейка D5 имеет значение 0,5, поскольку COS (1,047197551) равно 0,5.

Пример # 5 — Вычислить значение cos (90)

В этом примере ячейка B6 содержит значение угла, для которого нужно вычислить косинус. С ячейкой C6 связана формула COS: B6 * PI () / 180. COS назначается ячейке D6. 90 * PI () / 180 равно 1,570796327. Значение PI () равно 3,14159. Итак, это 90 * (3,14159 / 180) = 1,570796327. Далее, COS применяется к 1.570796327, то есть 6.12574E-17..

Следовательно, результирующая ячейка D6 имеет 6.12574E-17, поскольку COS (1.570796327) равен 6.12574E-17.

Что нужно помнить о COS Функция в Excel

• COS в Excel всегда ожидает радиан в качестве параметра, для которого должен быть вычислен косинус.
• Если угол указывается в градусах, его необходимо вычислить с помощью функции РАДИАНЫ или умножить угол на PI () / 180.

Использование функции COS в Excel VBA

COS в Excel можно использовать в Excel VBA следующим образом. Он служит той же цели, которая заключается в получении значения косинуса заданного угла.

Пример VBA # 1

Здесь val1 — переменная. Он объявлен как Double, что означает, что он может хранить данные с типом данных double. Косинус 0 равен 1. Следовательно, val1 имеет значение 1.

Пример VBA # 2

Здесь угол 45 преобразуется в радианы с использованием той же формулы COS, которая используется в листе Excel.

Если для Cos в excel указано нечисловое значение, оно вернет Несоответствие типов ошибка в коде Excel VBA.

Как найти косинус угла с помощью функции COS в Excel

Если вам нужно найти косинус угла, используйте функцию COS в Microsoft Excel. Независимо от угла в градусах или радианах, это решение работает с небольшими изменениями. Следуйте этому пошаговому руководству, чтобы узнать, как легко воспользоваться преимуществами быстрых математических навыков Excel.

Инструкции в этой статье относятся к Excel 2019, 2016, 2013, 2010, 2007; Excel для Mac, Excel 365, Excel Online, Excel для Android, Excel для iPad и Excel для iPhone.

Найти косинус угла в Excel

Тригонометрическая функция косинуса, как синус и тангенс, основана на прямоугольном треугольнике (треугольник, содержащий угол, равный 90 градусам), как показано на рисунке ниже.

В математическом классе косинус угла определяется путем деления длины стороны, прилегающей к углу, на длину гипотенузы. В Excel косинус угла можно найти с помощью функции COS, если этот угол измеряется в радианах.

Функция COS экономит вам много времени и, возможно, много царапает голову, поскольку вам больше не нужно помнить, какая сторона треугольника примыкает к противоположному углу, а какая – к гипотенузе.

Понять градусы против радианов

Использование функции COS для определения косинуса угла может быть проще, чем делать это вручную, но, как уже упоминалось, важно понимать, что при использовании функции COS угол должен быть в радианах а не градусов.

Радианы связаны с радиусом круга. Один радиан составляет примерно 57 градусов.

Чтобы упростить работу с COS и другими функциями триггера Excel, используйте функцию Excel RADIANS для преобразования измеряемого угла из градусов в радианы, как показано в ячейке B2 на изображении выше. В этом примере угол 60 градусов преобразуется в 1,047197551 радиан.

Другие варианты преобразования градусов в радианы включают в себя вложение функции RADIANS внутри функции COS (как показано в строке 3 на изображении примера) и использование функции PI в формуле (как показано в строке 4 на изображении примера).

Тригонометрическое использование в Excel

Тригонометрия фокусируется на отношениях между сторонами и углами треугольника, и хотя многим из нас не нужно использовать его ежедневно, тригонометрия находит применение в ряде областей, включая архитектуру, физику, инженерию и геодезию.

Архитекторы, например, используют тригонометрию для расчетов, связанных с затенением от солнца, структурной нагрузкой и уклонами крыши.

Синтаксис и аргументы функции Excel COS

Синтаксис функции относится к макету функции и включает в себя имя функции, скобки и аргументы. Синтаксис для функции COS:

Число . Рассчитываемый угол в радианах. Для этого аргумента можно ввести размер угла в радианах или вместо него можно указать ссылку на ячейку для расположения этих данных на листе.

Используйте функцию Excel COS

Пример в этой статье охватывает шаги, используемые для ввода функции COS в ячейку C2 на изображении выше, чтобы найти косинус угла 60 градусов или 1,047197551 радиан.

Варианты входа в функцию COS включают ввод вручную всей функции или использование диалогового окна «Аргументы функции», как описано ниже.

Введите функцию COS

Выберите ячейку C2 на рабочем листе, чтобы сделать ее активной.

Выберите вкладку Формулы на панели ленты.

Выберите Math & Trig на ленте, чтобы открыть раскрывающийся список функций.

Выберите COS в списке, чтобы открыть диалоговое окно «Аргументы функции». В Excel для Mac откроется построитель формул.

В диалоговом окне поместите курсор в числовую строку.

Выберите ячейку B2 на листе, чтобы ввести ссылку на эту ячейку в формулу.

Выберите ОК , чтобы завершить формулу и вернуться на лист. За исключением Excel для Mac, где вы выбираете Готово .

Ответ 0.5 появляется в ячейке C2, , которая является косинусом угла 60 градусов.

Выберите ячейку C2, чтобы увидеть полную функцию в строке формул над рабочим листом.

Устранение неполадок с функцией Excel COS

#VALUE! Ошибки

Функция COS отображает # ЗНАЧЕНИЕ!ошибка, если ссылка, используемая в качестве аргумента функции, указывает на ячейку, содержащую текстовые данные. Переключите тип данных ячейки на Числа, чтобы исправить ошибку.

Результаты пустых ячеек

Если ячейка указывает на пустую ячейку, функция возвращает значение единицы. Триггерные функции Excel интерпретируют пустые ячейки как ноль, а косинус нулевых радиан равен единице. Исправьте ошибку, указав свою функцию в правой ячейке.

Функция COS

В этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.

Описание

Возвращает косинус заданного угла.

Синтаксис

Аргументы функции COS описаны ниже.

Число — обязательный аргумент. Угол в радианах, для которого определяется косинус.

Замечания

Если угол задан в градусах, умножьте его на ПИ()/180 или воспользуйтесь функцией РАДИАНЫ, чтобы преобразовать его в радианы.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Тригонометрические функции SIN COS в Excel для синуса и косинуса

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

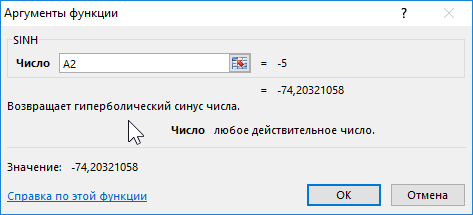
Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

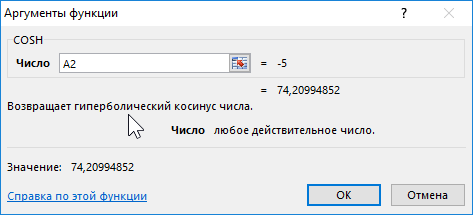
Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Примеры использования функций SIN, SINH, COS и COSH в Excel

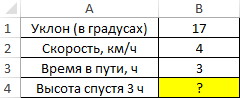
Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

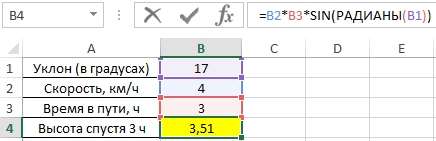
Для решения используем формулу:

• B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
• SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.

Таблица синусов и косинусов в Excel

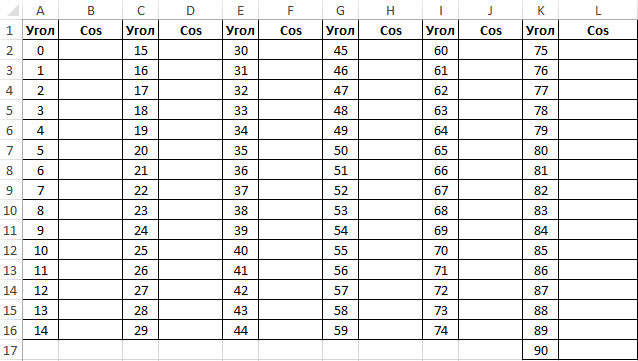
Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

Заполним столбцы значениями углов в градусах:

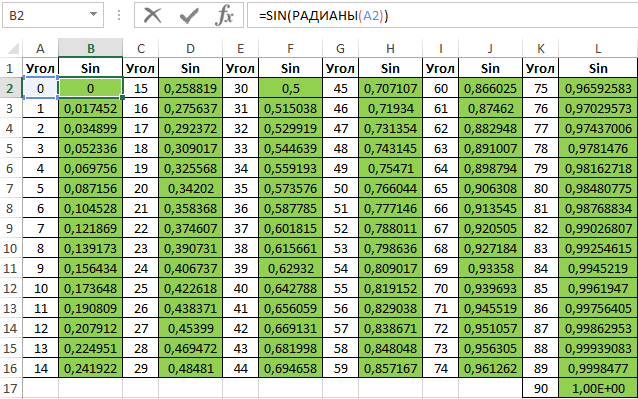
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

Аналогичным способом создадим таблицу синусов в Excel:

Построение графика функций SINH и COSH в Excel

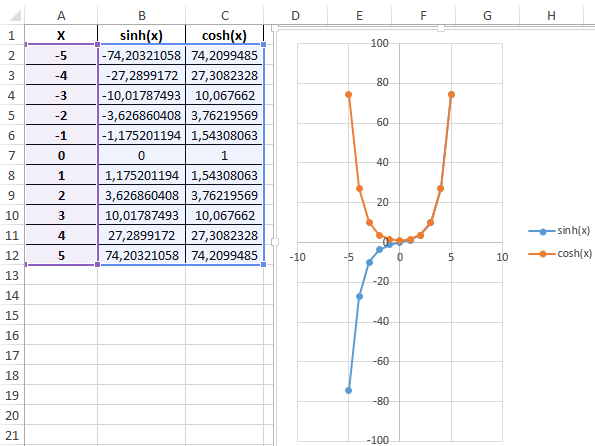
Пример 3. Построить графики функций sinh(x) и cosh(x) для одинаковых значений независимой переменной и сравнить их.

Формула для нахождения синусов гиперболических:

Формула для нахождения косинусов гиперболических:

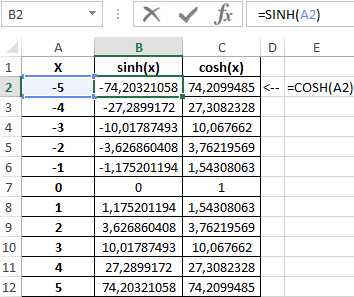
Таблица полученных значений:

Построим графики обеих функций на основе имеющихся данных. Выделите диапазон ячеек A1:C12 и выберите инструмент «ВСТАВКА»-«Диаграммы»-«Вставь точечную (X,Y) или пузырьковую диаграмму»-«Точечная с гладкими кривыми и маркерами»:

Как видно, графики совпадают на промежутке (0;+∞), а в области отрицательных значений x части графиков являются зеркальными отражениями друг друга.

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

Синтаксис функции SINH:

Синтаксис функции COS:

Синтаксис функции COSH:

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

1. Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
2. В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
3. Все рассматриваемые функции могут быть использованы в качестве формул массива.

1. Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
2. Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
3. При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

• Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
• Выражение ПИ()*угол_в_градусах/180.

Как найти косинус угла с помощью функции COS в Excel

Если вам нужно найти косинус угла, используйте функцию COS в Microsoft Excel. Независимо от угла в градусах или радианах, это решение работает с небольшими изменениями. Следуйте этому пошаговому руководству, чтобы узнать, как легко воспользоваться преимуществами быстрых математических навыков Excel.

Инструкции в этой статье относятся к Excel 2019, 2016, 2013, 2010, 2007; Excel для Mac, Excel 365, Excel Online, Excel для Android, Excel для iPad и Excel для iPhone.

Найти косинус угла в Excel

Тригонометрическая функция косинуса, как синус и тангенс, основана на прямоугольном треугольнике (треугольник, содержащий угол, равный 90 градусам), как показано на рисунке ниже.

В математическом классе косинус угла определяется путем деления длины стороны, прилегающей к углу, на длину гипотенузы. В Excel косинус угла можно найти с помощью функции COS, если этот угол измеряется в радианах.

Функция COS экономит вам много времени и, возможно, много царапает голову, поскольку вам больше не нужно помнить, какая сторона треугольника примыкает к противоположному углу, а какая – к гипотенузе.

Понять градусы против радианов

Использование функции COS для определения косинуса угла может быть проще, чем делать это вручную, но, как уже упоминалось, важно понимать, что при использовании функции COS угол должен быть в радианах а не градусов.

Радианы связаны с радиусом круга. Один радиан составляет примерно 57 градусов.

Чтобы упростить работу с COS и другими функциями триггера Excel, используйте функцию Excel RADIANS для преобразования измеряемого угла из градусов в радианы, как показано в ячейке B2 на изображении выше. В этом примере угол 60 градусов преобразуется в 1,047197551 радиан.

Другие варианты преобразования градусов в радианы включают в себя вложение функции RADIANS внутри функции COS (как показано в строке 3 на изображении примера) и использование функции PI в формуле (как показано в строке 4 на изображении примера).

Тригонометрическое использование в Excel

Тригонометрия фокусируется на отношениях между сторонами и углами треугольника, и хотя многим из нас не нужно использовать его ежедневно, тригонометрия находит применение в ряде областей, включая архитектуру, физику, инженерию и геодезию.

Архитекторы, например, используют тригонометрию для расчетов, связанных с затенением от солнца, структурной нагрузкой и уклонами крыши.

Синтаксис и аргументы функции Excel COS

Синтаксис функции относится к макету функции и включает в себя имя функции, скобки и аргументы. Синтаксис для функции COS:

Число . Рассчитываемый угол в радианах. Для этого аргумента можно ввести размер угла в радианах или вместо него можно указать ссылку на ячейку для расположения этих данных на листе.

Используйте функцию Excel COS

Пример в этой статье охватывает шаги, используемые для ввода функции COS в ячейку C2 на изображении выше, чтобы найти косинус угла 60 градусов или 1,047197551 радиан.

Варианты входа в функцию COS включают ввод вручную всей функции или использование диалогового окна «Аргументы функции», как описано ниже.

Введите функцию COS

Выберите ячейку C2 на рабочем листе, чтобы сделать ее активной.

Выберите вкладку Формулы на панели ленты.

Выберите Math & Trig на ленте, чтобы открыть раскрывающийся список функций.

Выберите COS в списке, чтобы открыть диалоговое окно «Аргументы функции». В Excel для Mac откроется построитель формул.

В диалоговом окне поместите курсор в числовую строку.

Выберите ячейку B2 на листе, чтобы ввести ссылку на эту ячейку в формулу.

Выберите ОК , чтобы завершить формулу и вернуться на лист. За исключением Excel для Mac, где вы выбираете Готово .

Ответ 0.5 появляется в ячейке C2, , которая является косинусом угла 60 градусов.

Выберите ячейку C2, чтобы увидеть полную функцию в строке формул над рабочим листом.

Устранение неполадок с функцией Excel COS

#VALUE! Ошибки

Функция COS отображает # ЗНАЧЕНИЕ!ошибка, если ссылка, используемая в качестве аргумента функции, указывает на ячейку, содержащую текстовые данные. Переключите тип данных ячейки на Числа, чтобы исправить ошибку.

Результаты пустых ячеек

Если ячейка указывает на пустую ячейку, функция возвращает значение единицы. Триггерные функции Excel интерпретируют пустые ячейки как ноль, а косинус нулевых радиан равен единице. Исправьте ошибку, указав свою функцию в правой ячейке.

Лабораторная работа

Отделение корней
нелинейного уравнения

Пусть имеется
нелинейное уравнение .

Требуется найти
корни этого уравнения. Численный процесс приближенного решения поставленной
задачи разделяют два этапа: отделение корня и уточнение корня.

Для отделения
корня необходимо определить промежуток аргумента , где
содержится один и только один корень уравнения. Одна из точек этого промежутка
принимается за начальное приближение корня. В зависимости от метода, который
предполагается использовать для уточнения корня, требуется определение
некоторых свойств отделенного корня и поведения функции на отрезке отделения.
Например, при использовании метода деления пополам, необходимо и достаточно
установить лишь непрерывность функции на отрезке отделения.

Этап отделения
корня уравнения алгоритмизирован только для некоторых классов уравнений
(наиболее известным из которых является класс алгебраических уравнений),
поэтому отделение корней нелинейных уравнений, обычно, выполняется «вручную» с
использованием всей возможной информации о функции . Часто
применяется графический метод отделения действительных корней, обладающий
большой наглядностью.

Методы
отделения корней

Отделение корней
во многих случая можно произвести графически. Учитывая, что действительные
корни уравнения F(x)=0 – это есть точки пересечения графика
функции y=F(x) с осью абсцисс y=0, нужно построить
график функции y=F(x) и на оси OX отметить отрезки,
содержащие по одному корню. Но часто для упрощения построения графика функции y=F(x)
исходное уравнение заменяют равносильным ему уравнением f₁(x)=f₂(x).
Далее строятся графики функций y₁=f₁(x)
и y₂=f₂(x), а затем по оси OX
отмечаются отрезки, локализующие абсциссы точек пересечения двух графиков.

На практике
данный способ реализуется следующим образом: например, требуется отделить корни
уравнения cos(2x)+x-5=0 графически на отрезке    [–10;10],
используя Excel.

1 способ

Построим график функции f(x)=cos(2x)+x-5
в декартовой системе координат. Для этого нужно:

1.                
Ввести в
ячейку A1 текст х.

2.                
Ввести в
ячейку B1 текст y=cos(2x)+x-5.

3.                
Ввести в
ячейку А2 число -10, а в ячейку А3 число -9.

4.                
Выделить
ячейки А2 и А3.

5.                
Навести
указатель «мыши» на маркер заполнения в правом нижнем углу рамки, охватывающий
выделенный диапазон. Нажать левую кнопку «мыши» и перетащить маркер так, чтобы
рамка охватила диапазон ячеек А2:А22.

6.                
Ячейки
автоматически заполняются цифрами :

7.                
Ввести в
ячейку В2 формулу =COS(2*A2)+A2-5.

8.                
Методом
протягивания заполнить диапазон ячеек В3:В22.

9.                
Вызвать
«Мастер диаграмм» и выбрать диаграмму график (первый вид), нажать
«далее».

10.           
Указать
диапазон данных, для этого щелкнуть кнопку в поле «Диапазон» и выбрать диапазон
данных В2:В22.

11.           
Выбрать
вкладку ряд, указать имя ряда, щелкнув кнопку в поле «ряд» и выбрав В1.

12.           
В поле
«подписи по оси Х», щелкнуть кнопку и выбрать диапазон А2:А22, нажать «далее».

13.           
Подписать
названия осей x и y соответственно, нажать «далее».

14.           
Вывести
диаграмму на том же листе, что и таблица, нажать кнопку «готово».

В итоге получаем следующее
(рисунок 1):

Рисунок 1 – Локализация корня

Анализируя полученное
изображение графика, можно сказать, что уравнение cos(2x)+x-5=0
имеет один корень – это видно из пересечения графика функции y=cos(2x)+x-5
с осью OX. Можно выбрать отрезок, содержащий данный корень:[5;6] – отрезок локализации.

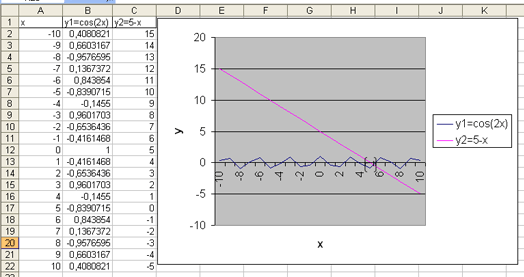
2 способ

Для подтверждения полученных
данных, можно решить эту же задачу вторым способом. Для этого необходимо
уравнение cos(2x)+x-5=0 преобразовать к виду: cos(2x)=5-x.
Затем следует каждую часть уравнения рассмотреть как отдельную функцию. Т. е. y₁=cos(2x)
и y₂=5-x. Для решения этой задачи в  Excel необходимо
выполнить следующие действия:

1.                
Вести в
ячейки А1:C1 соответственно текст: «x», «y₁=cos(2_x)»,
«y₂=5-x».

2.                
A2:A22
заполнить так же как при решении задачи первым способом.

3.                
В В2
ввести формулу =COS(2*A2).

4.                
Методом
протягивания заполнить диапазон ячеек В3:В22.

5.                
В С2
ввести =5-A2.

6.                
Методом
протягивания заполнить диапазон ячеек С3:С22.

7.                
С помощью
Мастера диаграмм выбрать график (первый вид).

8.                
В данном
случае диапазон данных следует указывать для построения двух графиков. Для
этого нужно нажать кнопку в поле «Диапазон» и выделить ячейки В2:В22, затем
нажать Ctrl (на клавиатуре) и выделить следующий диапазон C2:C22.

9.                
Перейти
на вкладку ряд, где выбрать именем ряда 1 ячейку В1, а именем ряда 2 ячейку С2.

10.           
Подписать
ось x , выбрав диапазон А2:А22.

11.           
Подписать
соответственно оси x и y.

12.           
Поместить
диаграмму на имеющемся листе.

Результат представлен на
рисунке 2: Анализируя
полученный результат, можно сказать, что точка пересечения двух графиков
попадает на тот же самый отрезок локализации [5;6], что и при решении задачи
первым способом.

Рисунок 2 – Локализация корня

Аналитический способ отделения
корней

Аналитический
способ отделения корней основан на следующей теореме, известной из курса математического
анализа.

ТЕОРЕМА: Если непрерывная на  функция ,
определяющая уравнение , на концах отрезка  принимает значения разных знаков, т.е. , то на этом отрезке содержится, по
крайней мере, один корень уравнения. Если же функция  непрерывна
и дифференцируема и ее производная сохраняет знак внутри отрезка , то на этом отрезке находится только один
корень уравнения.

В случае, когда
на концах интервала функция имеет одинаковые знаки, на этом интервале корни
либо отсутствуют, либо их четное число.

Для отделения корней
аналитическим способом выбирается отрезок , на
котором находятся все интересующие вычислителя корни уравнения. Причем на
отрезке  функция F(x) определена, непрерывна и  F(a)*F(b)<0.
Требуется указать все частичные отрезки ,
содержащие по одному корню.

Будем вычислять
значение функции F(x),
начиная с точки x=a, двигаясь вправо с некоторым шагом h. Если F(x)*F(x+h)<0,
то на отрезке [x;x+h] существует корень (рисунок 3).

Рисунок 3 –
Аналитический способ локализации корней

Если F(x_k)=0,
x_k-точный корень. 

Доказательство существования
и единственности корня на отрезке.

В качестве примера рассмотрим
функцию f(x)=cos(2x)+x-5.

1.      Ввести в ячейки А1, В1 и С1
соответственно «x», «y=cos(2x)+x-5» и «ответ».

2.      В А2 и А3 ввести граничные
значения отрезка изоляции.

3.      В В2 ввести формулу
=COS(2*A2)+A2-5 и методом протягивания заполнить В3.

4.      В С2 ввести формулу
=ЕСЛИ(B2*B3<0;»корень существует»;»корень не
существует»).

Таким образом, на отрезке
изоляции корень существует:

Рисунок 4 – Проверка существования корня на отрезке

Для доказательства
единственности корня на отрезке изоляции необходимо выполнить следующие
действия:

1.                
Продолжить
работу в том же документе MS Excel.

2.                
Заполнить
D1 и E1 соответственно: «y’=-sin(2x)*2+1» и «ответ» (причем выражение
y’=-sin(2x)*2+1 – это производная первого порядка от функции y=cos(2x)+x-5).

3.                
Ввести в
D2 формулу =-SIN(2*A2)*2+1 и методом протягивания заполнить D3.

4.                
Ввести в
E2 =ЕСЛИ(D2*D3>0;»корень на данном отрезке единственный»;»Корень
не единственный»).

В результате получаем
(рисунок 5):

Рисунок 5 –
Доказательство единственности корня на отрезке

Таким образом доказано
существование и единственность корня на отрезке изоляции.

Рассмотрим
решение задачи отделения корней уравнения 
cos(2x)+x-5=0 аналитическим
способом с шагом 1 на отрезке [-10;10].

Чтобы отделить корни
уравнения аналитическим способом с помощью Excel, необходимо выполнить
следующее:

1.                
Заполнить
ячейки A1:D1 соответственно: «x», «y=cos(2x)+x-5»,
«h», «ответ».

2.                
В С2
ввести значение 1.

3.                
Ввести в
А2 значение -10.

4.                
Ввести в
А3 =A2+$C$2 и методом протягивания заполнить ячейки А4:А22.

5.                
В В2
ввести =COS(2*A2)+A2-5 и методом протягивания заполнить диапазон В3:В22.

6.                

В С3 ввести формулу
=ЕСЛИ(B2*B3<0;»Корень на отрезке существует»;ЕСЛИ(B3=0;»точный
корень»;»-«)) и методом протягивания заполнить диапазон ячеек
С4:С22.

В результате получаем
следующее (рисунок 6):

Рисунок 6 –
Отделение корня

Следующий пример (рисунок
7) демонстрирует отделение нескольких корней. Пусть исследуется функция cos(x)=0,1x на интервале [–10;10] с шагом
1.

Табулирование
функции и построение графика осуществляется как в предыдущих примерах. Видно,
что на заданном отрезке имеем 7 корней, находящихся внутри отрезков: [-10;-9];
[-9;-8]; [-5;-4]; [-2;-1]; [1;2]; [5;6]; [7;8].

Рисунок 7 – Отделение корней

Обратим внимание
на то, что надежность рассмотренного алгоритма отделения корней уравнения
зависит как от характера функции F(x), так и от выбранной величины шага h.
Для повышения надежности следует выбирать при отделении корней достаточно малые
значения h.

Задание

1. Выполнить отделение корней
следующих функций:

№ п/п	Уравнение	A	B
1	tg(x) = 1/x	0	n/2
2	e -x = x	0	1
3	ln(x) = 1/x	1	2
4	2 +ln(x) = 1/x	0	1
5	x — x3 + 1 =0	1	2

2. Выполнить индивидуальные задания

Вариант 1

1	ctg(x) = —x2	1,6	4,5
2	2ln(x)+sin(x) =e x	0	2
3	lg(x) = 2 x-x3	0	10
4	cos(x) = 1/x	0	p/2
5	cos(x) = ln(1+x)	0	p/2

Вариант 2

1	tg(x) = 1/x—x2	1,6	4,5
2	2ln(x) =e x	0	2
3	lg(x) = sin(x)	0	10
4	cos(x)+x2 = 1/x	0	p/2
5	cos2(x) = ln(1+x2)	0	p/2

Вариант 3

1	cos2(x) = x	0	p/2
2	1 — 3 x + x3=0	0	1
3	1 — 3x + x4=0	0	1
4	1 — 3 x + x5=0	0	1
5	tg(x) = 1/x2	0	p/2

Вариант 4

1	ln(x) = sin(x)	1	3
2	e — x = sin(x)	0	p/2
3	e x = 1 /sin(x)	0	p/2
4	e — x = x2	0	1
5	2 + ln(x) = 1/x2	0	1

Вариант 5

1	ln(x) = Sin (x)	0	p/2
2	x — x3 + 2 =0	1	2
3	x +5 = x3	1	2
4	x 2—  0,5 x-2=0	0	0,5
5	ln(x -1)+  x-2=0	1	3

Вариант 6

1	ln(x+3) = Sin (x)	0	p/2
2	2x — x3 + 3 =0	1	2
3	x +8 = x3+x2	1	2
4	x —  0,5 x2+4=0	0	0,5
5	(x -1)2—  x=0	1	3

Вариант 7

1	x +0,5 = e -x	0	1
2	2 — x + x3=0	-2	0
3	sin(x) = 1/x	0	p/2
4	sin(x) = x/2	п/2	п
5	ln(x) = e -x	0	2

Вариант 8

1	lg(x) = e — x	0	1
2	cos(x) = x	0	p/2
3	cos(x) = ln(x)	0	p/2
4	cos(x) = tg(x)	0	p/2
5	cos(x) = x3	0	p/2

Вариант 9

1	1 — 5 x + x3=0	0	1
2	1 — 5 x + x4=0	0	1
3	1 — 3 x + x5=0	1	2
4	4cos(x) = x+x2	0	p/2
5	cos(x) = ln(x)-x2	0	p/2

Вариант 10

1	ln(x) = cos (x)	0	p/2
2	x2 — x3 + 2 =0	1	2
3	cosx +5 = x3	1	2
4	x  0,5—   x=0	0	0,5
5	(x -1)2—   x=5	1	3

Вариант 11

1	ln(x+3) =sin (x)-x	0	p/2
2	2x — x3 + 3 =ln(x)	1	2
3	cos(x) +2 = x3+x2	1	2
4	3x —  0,5 x2+cosx=0	0	0,5
5	(x -1)2—  x+tg(x-1)=0	1	3

Вариант 12

1	x2 +0,5 = e -x	0	1
2	2 – sin(x) + x3=0	-2	0
3	sin(x) = 1/x-x2	0	p/2
4	sin(x) = x/2+cos(x)	п/2	п
5	ln(x)-x = e -x	0	2

Вариант 13

1	lg(x)+2sin2(x) = e — x	0	1
2	cos(x+p/2) = x+x2	0	p/2
3	cos(x) = ln(x)-x2	0	p/2
4	cos(x) = tg(x)+sin(2x-p/2)	0	p/2
5	cos(x) = x3-log(x2)	0	p/2

Вариант 14

1	1 — 5 cos(x) + x3=0	0	1
2	1 — 5 tg(x) + x4=0	0	1
3	1 – 3( x-2)2 + x5=0	1	2
4	4cos(x) = cos(x)+x2	0	p/2
5	cos(x) = ln(x)-x2+x	0	p/2