Решение транспортной задачи в excel практическая работа - Word и Excel

Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.

Содержание

Транспортная задача: описание
Подготовительный этап: включение функции “Поиск решения”
Пример задачи и ее решение
- Условия
- Алгоритм решения
Заключение

Транспортная задача: описание

С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.

Транспортные задачи бывают двух типов:

Закрытая – совокупное предложение продавца равняется общему спросу.
Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).

Подготовительный этап: включение функции “Поиск решения”

Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:

Открываем меню “Файл”.
В перечне слева выбираем пункт “Параметры”.
В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.

Пример задачи и ее решение

Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.

Условия задачи

Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.

Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).

Алгоритм решения

Итак, приступи к решению нашей задачи:

Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
На экране отобразится окно, в котором нужно заполнить аргументы:
- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
- по готовности жмем OK.
Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
Перед нами появится окно с параметрами функции:
- в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
- для параметра “До” выбираем вариант – “Минимум”.
- в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
- нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
- становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
- затем выбираем знак “равно”.
- в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
- щелкаем OK по готовности.
Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
- больше или равно нулю;
- целое число.
В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.

Заключение

Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.

Источник

Министерство
общего и профессионального образования

Свердловской
области

Государственное
бюджетное профессиональное образовательное учреждение

Свердловской
области

«Нижнетагильский
железнодорожный техникум»

«РЕШЕНИЕ ТРАНСПОРТНЫХ ЗАДАЧ В ЭЛЕКТРОННЫХ
ТАБЛИЦАХ EXCEL»

Автор:
Мызникова Ирина Викторовна

Нижний
Тагил
2016

Аннотация

В данной методической разработке
рассматривается поэтапное внедрение элементов технологии интегрированного
обучения в ходе повторения учебного материала, при этом интегративный характер
занятия реализуется в рамках требований примерной программы учебной
дисциплины ЕН.02 Информатика «Учебно — методический центр по образованию на
железнодорожном транспорте», рекомендованной экспертным советом по
профессиональному образованию Федерального государственного автономного
учреждения «Федеральный институт развития образования» (ФГАУ «ФИРО») 2012,
Москва.

Занятия по дисциплине
«Информатика» — это универсальное связующее звено, позволяющее «соединить»
практически все дисциплины. Поэтому в основе данной методической разработки
лежит личный опыт организации и проведения интегрированных занятий.

Занятие разработано для студентов II
курса, осваивающих дисциплины по программе подготовки специалистов среднего
звена 23.02.01 Организация перевозок и управление на транспорте (по видам) (автомобильный
транспорт).

Данную методическую разработку
можно использовать для проведения учебных занятий по дисциплинам «ЕН.02
Информатика» и «ЕНв.03 Экология автомобиля», а также в качестве мастер-класса для
демонстрации технологии интегрированного обучения.

Пояснительная
записка

Новые
требования, выдвинутые в рамках Федерального государственного образовательного
стандарта 3 поколения, ставят для всей системы профессионального образования
основную задачу – подготовку компетентного специалиста, способного самостоятельно и критически мыслить, умеющего видеть и творчески
решать возникающие проблемы. Поэтому очень важен переход от исполнительной,
репродуктивной деятельности обучающихся к творческой, поисковой деятельности на
всех этапах учебного процесса [7].

В инновационном образовательном
процессе студент должен иметь высокий образовательный уровень, гибкое мышление,
профессиональную мобильность, осуществлять поиск, анализ и оценку информации,
необходимой для решения профессиональных задач, то есть обладать определенными
профессиональными и общими компетенциями.

Реализовать все вышеназванное
помогает внедрение технологии интегрированного обучения.

Интеграция предметов –
это организация предметной деятельности, предполагающая использование
системного подхода, ориентированного на формирование системного типа мышления.
Главное в интегрированном занятии — вычленить проблему. Проблема должна быть
комплексной, жизненной, социально значимой [10].

Интегрированные занятия предполагают возможность вовлечения
каждого обучающегося в активный познавательный процесс, причём процесс не
пассивного овладения знаниями, а активной познавательной самостоятельной
деятельности каждого обучающегося, т.к. каждый имеет возможность проявить себя
в той области, которая ему ближе и применить на практике полученные знания [5].

В данной методической
разработке интегрированного занятия по теме «Решение
транспортных задач в электронных таблицах Excel» приводится и технологическая
карта учебного занятия и общая структура.

Одним из условий проведения интегрированного занятия является правильное вычленение
междисциплинарного объекта изучения, который должен быть актуальным и
проблемным, содержать естественную взаимосвязь. Таким объектом была выбрана «транспортная
задача», для решения которой использовались межпредметные связи дисциплин «ЕН.02
Информатика» и «ЕНв.03 Экология автомобиля».

Основной целью учебного занятия является инициирование
творческой активности, развитие признаков общих и профессиональных компетенций
обучающихся. Стратегическая задача занятия — попытка достижения современного
качества образования и высокая мотивация студентов к выполнению заданий.

Ориентированная основа деятельности на таком занятии
является одним из условий формирования компетенций. Для выполнения практических
работ обучающимся предлагаются ориентиры, при опоре на которые они могут
безошибочно действовать в практическом плане (см. Приложение).

В процессе решения транспортной
задачи студентами проводится анализ эффективности использования того или иного
вида топлива, а также его влияние на окружающую среду. Включение заданий и
вопросов экологического характера в содержательную часть занятия способствует
формированию у студентов навыков экологически оправданного поведения в природе,
уверенность в своих силах, позитивное отношение к себе и окружающему миру. На
основе синтеза и сопоставления знаний двух дисциплин, делаются обобщающие
выводы и вносятся предложения.

При интеграции нескольких дисциплин, связанных единой
темой, непроизвольно идет усовершенствование отдельных сторон педагогического опыта,
т.к. материалы различных дисциплин взаимопроникают друг в друга (см.
Интегративная карта), сокращается общее время преподавания дисциплин,
увеличивается время для других сторон учебного занятия: средств обучения,
применения различных видов деятельности, самостоятельной работы обучающихся, в
их комбинаторике и применении современных технологий [3].

Используемая технология обучения
позволяет не только умело овладеть информацией обучающимися, но и критически ее
оценить, осмыслить, применить.

Ожидаемые результаты реализации
интегрированного занятия:

1. расширение тематики изучаемого
материала, необходимость более глубокой и детальной проработки содержания
учебных дисциплин;

2. активизация познавательной
деятельности обучающихся, возрастание роли самостоятельной работы, инициативы в
проведении исследовательской деятельности, и как следствие формирование и
развитие общих и профессиональных компетенций.

Разработка интегрированного
учебного занятия достаточно трудоемка, но всегда сопровождается позитивной
мотивацией и интересом обучающихся к учебно — познавательной деятельности.

Содержание

1. Технологическая
карта учебного занятия

Тема занятия: «Решение транспортных задач в
электронных таблицах Excel».

Цель занятия:
создание условий для решения задач по определению затрат на перевозки грузов в
электронных таблиц Excel, и
определение степени влияния разных видов топлива на окружающую среду.

Задачи занятия:

·
закрепить
знания правил записи арифметических выражений и формул в электронных таблицах;

·
проверить
умения строить диаграммы с помощью электронных таблиц Excel;

·
закрепить
умения и навыки редактирования содержимого ячеек таблицы;

·
обеспечить
осмысление влияния разных видов топлива на окружающую среду;

·
показать
взаимосвязь двух дисциплин – ЕН.02 Информатика и ЕНв.03 Экология
автомобиля;

·
продемонстрировать
применение диаграмм в профессиональной деятельности.

·
развивать
познавательный интерес обучающихся;

·
развивать
логическое мышление (умение анализировать, сравнивать, обобщать, делать
выводы);

·
развивать
умения работать с имеющейся информацией в необычной ситуации;

·
развивать
самооценку самостоятельной деятельности на учебном занятии, развивать умения
анализировать свои ошибки и исправлять их в процессе решения задач;

·
развивать
коммуникативные навыки.

·
воспитывать
умения слушать друг друга;

·
воспитывать
добросовестное отношение к дисциплинам, ответственность, честность,
сопереживание успехам и неудачам одногруппников.

Педагогические
технологии: технология системно — деятельностного подхода, проблемное обучение,
элементы технологии взаимного обучения, технологии критического мышления.

Вид занятия:
интегрированный.

Тип занятия: повторительно
— обобщительный.

Форма организации
учебного занятия: фронтальная работа, работа в парах.

Методы обучения:

·
информационно-практический;

·
проблемно-поисковый;

·
вопросно-ответный;

·
наглядный.

Методические
приемы:

·
осуществление
взаимосвязи дисциплин: ЕН.02 Информатика, ЕНв.03Экология автомобиля,

·
мультимедийное
представления в формате программ Microsoft Power Point, Excel, Word;

·
индивидуальная
работа;

·
тьюторство;

·
создание
атмосферы комфорта и взаимопонимания.

Информационное
обеспечение: раздаточный материал (алгоритмы выполнения задания),
информационные буклеты.

Техническое и
программное обеспечение: мультимедийная установка, приложения MS Power Point,
MS Excel, MS Word.

Формируемые
компетенции:

Блок самоорганизации
и самообучения:

· ОК 1.
Понимать сущность и социальную значимость своей будущей профессии, проявлять к
ней устойчивый интерес.

· ОК 2.
Организовывать собственную деятельность, выбирать типовые методы и способы
выполнения профессиональных задач, оценивать их эффективность и качество.

· ОК 3.
Принимать решение в стандартных и нестандартных ситуациях и нести за них
ответственность.

·
ОК
8. Самостоятельно определять задачи профессионального и личностного развития,
заниматься самообразованием, осознанно планировать повышение квалификации.

·
ОК
9. Ориентироваться в условиях частой смены технологий в профессиональной
деятельности.

·
ПК
2.2 Планировать и организовывать производственные работы.

·
ПК
2.3 Выбирать оптимальные решения в нестандартных ситуациях.

Информационный блок:

·
ОК 4. Осуществлять поиск и
использование информации, необходимой для эффективного выполнения
профессиональных задач, профессионального и личностного развития.

·
ОК 5. Использовать
информационно-коммуникационные технологии в профессиональной деятельности.

·
ПК 1.3. Оформлять
документы, регламентирующие организацию перевозочного процесса с применением
современных информационных технологий управления перевозками.

Коммуникационный блок

·
ОК 6. Работать в
коллективе и команде, эффективно общаться с коллегами, руководством,
потребителями

·
ОК 7. Брать на себя
ответственность за работу членов команды (подчиненных), за результат выполнения
заданий.

Учебный продукт: практическая работа «Решение
транспортных задач в среде MS Excel, исследовательская работа «влияние разных
видов топлива на окружающую среду».

Интегративная
карта

Тема
занятия:

Информатика

Экология
автомобиля

«Решение
транспортных задач в электронных таблицах Excel»

Тема
программы:

—
«Электронные
таблицы Excel». Выполнение вычислительных операций. Абсолютная и
относительная адресация ячеек. Построение диаграмм.

Тема
программы:

-Воздействие
автомобильного транспорта на экологические системы. Загрязнение окружающей
среды отходами автомобильного транспорта

2. Дидактическая
структура занятия

Этапы занятия, время	Цель	Деятельность преподавателя, его функции	Деятельность студента, форма организации деятельности обучающегося	Методы, приемы	Методы контроля	Формируемые компетенции
Организационный момент (3 мин)	Сообщение темы, постановка цели, задач занятия.	Проверка готовности к занятию, сообщение темы, постановка целей учебного занятия, рекомендации по организации работы на занятии.	Осмысление целей и задач занятия.	Словесный Фронтальная работа	Наблюдение	ОК 2
Актуализация знаний (Планерка 12 мин)	Подготовка к восприятию нового учебного материала.	Обеспечение контроля выполнения задания	Контроль и корректировка своих знаний. Работа в среде MS Power Point. Представление организации, по сфере деятельности и структуре.	Словесно-наглядный, практический Работа в парах, фронтальная работа	Практический, словесно-наглядный	ОК 1 ОК 2 ОК 3 ОК 5 ОК 6 ОК 7 ПК 1.3
Операционно-исполнительный. Практическая работа с элементами исследования (50 мин)	Понимание значимости информационных технологий для решения производственных задач.	Создание условий для решения проблемного вопроса восприятия с помощью информационного обеспечения (программа Excel), раздаточного материала, обеспечение контроля выполнения задания	Восприятие проблемного вопроса, его анализ. Решение задач, построение диаграмм с помощью MS Excel [3]. Проводят исследование по оценке экономичного вида топлива. Показывают результаты работы через проектор. Проводят анализ последствия деятельности фирм. Учатся договариваться, взаимодействовать друг с другом. Принимать общее решение.	Проблемно-поисковый, наглядный. Практический.	Взаимоконтроль. Оценка практической работы по дисциплине «Информатика», оценка исследовательской работы по дисциплине «Экология автомобиля»	ОК 1 ОК 2 ОК 3 ОК 5 ОК 6 ОК 7 ОК 8 ОК9 ПК 1.3 ПК 2.2 ПК 2.3
Рефлексивно-оценочный. Подведение итогов занятия, рефлексия, самооценка. (15 мин)	Рефлексия: осмысление студентами своих действий, развитие способности к самооценке.	Характеристика работы студентов на занятии	Подготовка документа, отражающий эмоциональное настроение на занятии. Заполнение листа самооценки.	Соотнесение результатов деятельности с поставленной целью, показ конечного результата своей работы на занятии. Индивидуальная и фронтальная работа	Наблюдение, самопроверка, устный опрос.	ОК 2 ОК 6

3.
Характеристика
структурных компонентов

1.
Актуализация
знаний

Планерка

Каждой паре предлагается вытянуть конверт с названием
организации

1. Фирма «Лесоруб»

2. Фирма «Мастер»

3. ИП «Маша»

4. Компания «Дачник»

5. Мебельная фабрика

6. Мебельный комбинат

Разработка презентации в среде Power Point, содержащей
название, деятельность и структуру компании.

2.
Операционно-исполнительный

Рабочий день

Каждой группе предлагается решить транспортную задачу
по перевозке грузов с использованием электронных таблиц EXCEL, а
именно:

·
решить
задачу (в электронных таблицах EXCEL);

·
построить
диаграмму;

·
оценить
затраты на использование разных видов топлива

·
анализ
деятельности последствия работы организации, формулировка выводов.

(см.
Приложение 1)

Каждая команда выводит отчет по работе организации на
экран через проектор. Даёт анализ своей работы.

Одним из отрицательных последствий работы фирм
является вырубка леса и влияние каждого вида топлива на окружающую среду.

Студенты выступают с сообщениями о том, как влияет
определенный вид топлива на окружающую среду.

Далее демонстрируется фильм «Вырубка леса и его
последствия на окружающую среду», после просмотра которого, студенты предлагают
пути выхода из сложившейся ситуации и делают следующие выводы:

1. необходимо находить и использовать новые
альтернативные виды топлива;

2. вырубка лесов приводит к негативным последствиям на
нашей планете: разрушению озонового слоя, возникновению « парникового эффекта»,
исчезновению многих видов растений и животных, опустыниванию и др;

3.каждый человек должен задуматься о своем влиянии на
окружающую среду и об экологических последствиях.

3.
Рефлексивно-оценочный.

Подведение итогов рабочего дня.

Создание документа в текстовом редакторе Word, отражающего
эмоциональное настроение на конец занятия, с использованием объекта WordArt и
панели рисования; заполнение листа самооценки (см. Приложение 2)

4.
Список
литературы

1. Барвенов С. А.
Компьютерные технологии в организации самостоятельной работы
студентов-гуманитариев / Высшая школа. – 2004. – № 4. – С. 35–37.

2. Воронина,
Т. П. Образование в эпоху новых информационных технологий / Т. П. Воронина.-
М.: АМО, 2008.-147с.

3. Глинская,
Е. А. Межпредметные связи в обучении / Е.А. Глинская, С.В. Титова. – 3-е изд. –
Тула: Инфо, 2007. — 44 с.

4. Данилюк,
Д. Я. Учебный предмет как интегрированная система /Д.Я. Данилюк //Педагогика. —
2007. — № 4. — С. 24-28.

5. Дик, Ю.И.
Интеграция учебных предметов / Ю.И. Дик //Современная педагогика. — 2008. — №
9. — С. 42-47

6. Екжанова
Е. Основы интегрированного обучения. Издательство: Дрофа, Москва. — 2008.

7. Ломакина
Т.Ю., Сергеева М.Г. Педагогические технологии в профессиональных учебных
заведениях / Т.Ю. Ломакина, М.Г. Сергеева.- М.: Наука, 2008.

8. Ливанский В. М.
«Ресурсный подход становления интегрированного школьного и внешкольного
образовательного пространства // Завуч. -2006г.-№5. — С. 118

9. Макарова Н. В.
Информатика и информационно-коммуникационные технологии. 10-11 кл. СПб.: Питер,
2006. — 224с.

10. Пузанкова Е.Н.,
Бочкова Н. В. Современная педагогическая интеграция, ее характеристики///
Образование и общество. — 2009. — N 1. — С. 9-13.

Приложение 1.

Фирма «Лесоруб» организует
поставку леса в разные населенные пункты на бортовом автомобиле «Фермер». В
качестве горючего используются дизельное топливо и бензин. Определите затраты
на горючее до каждого населенного пункта.

Постойте гистограмму, отражающую значения столбцов
затраты на горючее с подписями данных и круговую диаграмму по ячейкам общей
денежной суммы.

Оцените, использование какого горючего экономичнее?

Фирма «Мастер» в Нижнем
Тагиле закупила у фирмы «Лесоруб» лес. 10000 рублей было потрачено на подвоз
леса к пилораме. Далее, обработанный лес оправился по разным пунктам назначения
на бортовом автомобиле «Фермер». В качестве горючего используются дизельное
топливо и бензин.

Определите затраты на горючее в литрах до каждого
пункта назначения и общую денежную сумму потраченную на доставку.

Постойте гистограмму, отражающую значения столбцов
затраты на топливо и бензин с подписями данных и круговую диаграмму по ячейкам
затраты на горючее в рублях.

Оцените, использование какого вида горючего
экономичнее?

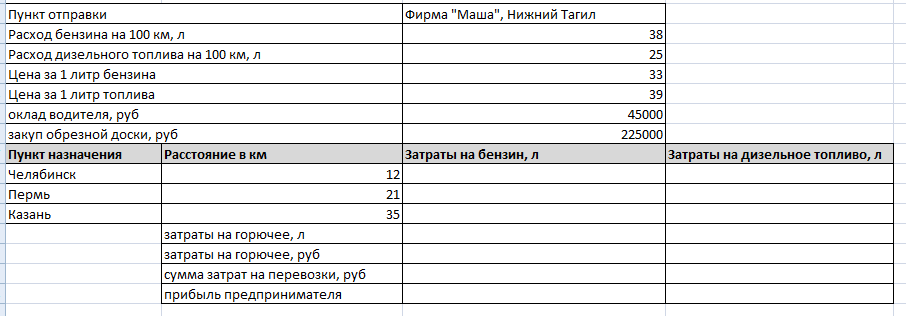
ИП «Маша» по перевозке
грузов закупила в фирме «Мастер» обрезную доску на сумму 225 000 рублей. Для
получения прибыли ее продают в разные города. Нанимаются водители с окладом в
45000 рублей каждый, осуществляющих перевозку на бортовом автомобиле «Фермер».
В качестве горючего используются дизельное топливо и бензин.

В Челябинске выручка от продажи составила 300000
рублей, в Перми — 470000 рублей, в Первоуральске -120000 рублей. Определите:
а) сумму затрат перевозки с учетом расхода на горючее; б) прибыль
предпринимателя.

Постойте гистограмму, отражающую значения столбцов
затраты на горючее с подписями данных и круговую диаграмму затраты на горючее в
рублях.

Оцените, использование какого горючего экономичнее?

Оцените, использование какого вида горючего
экономичнее?

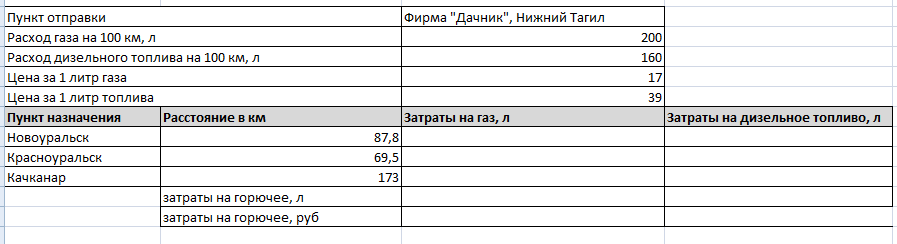
Фирма «Дачник» закупила оптом
доску обрезную для строительства дач в Свердловской области. Пункты доставки
следующие: Красноуральск, Новоуральск, Качканар. Доставка осуществляется
автомобилем Белаз.

Постойте гистограмму, отражающую значения столбцов
затраты на топливо и газ с подписями данных, а также круговую диаграмму
затраты на горючее в рублях.

Оцените, использование какого вида горючего экономичнее?

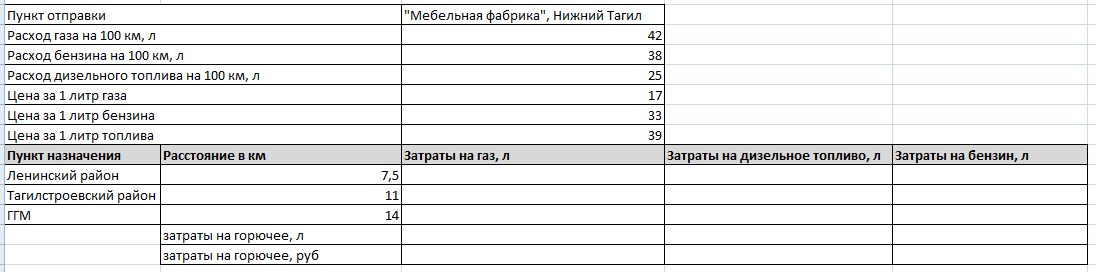
Мебельная фабрика
занимается закупкой леса у фирмы «Лесоруб», изготовлением мебели и её
поставкой в разные районы города. Доставка осуществляется автомобилем Зил,
работающем на разном виде топлива.

Постойте гистограмму, отражающую значения столбцов
затраты на горючее с подписями данных, а также круговую диаграмму затраты на
горючее в рублях.

Оцените, использование какого вида горючего
экономичнее?

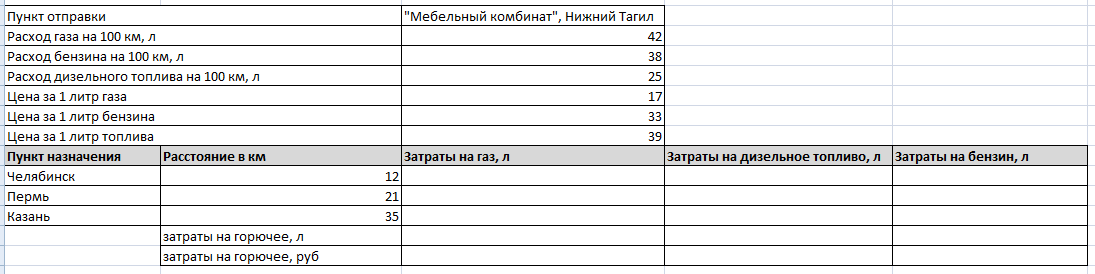
Мебельный комбинат занимается
изготовлением мягкой и корпусной мебели, доставкой её по всей России. Доставка
осуществляется автомобилем Зил, работающем на разном виде топлива.

Оцените, использование какого вида горючего
экономичнее?

Приложение 2.

Лист
самооценки проявления компетенций

ФИ
студента_______________

Группа
___________________

	Признаки проявления компетенций	Баллы
общие	ОК 1. Понимаю сущность и социальную значимость своей будущей профессии, проявляю к ней устойчивый интерес.
ОК 2. Организовываю собственную деятельность, выбираю типовые методы и способы выполнения профессиональных задач, оцениваю их эффективность и качество: · оцениваю влияние различных видов топлива на окружающую среду.
ОК 3. Принимаю решение в стандартных и нестандартных ситуациях и несу за них ответственность: · умею решать поставленную проблему.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использую информационно-коммуникационные технологии в профессиональной деятельности:
· оформляю документы с применением современных информационных технологий управления перевозками;
· владею приемами работы с презентацией Power Point;
· умею устанавливать нужный формат ячейки;
· умею производить расчеты в электронных таблицах Excel;
· использую абсолютную адресацию ячеек при вводе формул;
· строю диаграммы и графики в соответствии с предложенным заданием;
· умею воспроизводить, совершенствовать средства и способы получения и воспроизведения информации в электронном виде, пользоваться современными компьютерными технологиями;
· владею навыками работы в текстовом редакторе Word;
· использую панель рисования в текстовом редакторе Word.
ОК 6. Работаю в коллективе и команде, эффективно общаюсь с одногруппниками, преподавателями.
ОК 7. Беру на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий: · умею обобщить результаты работы группы и презентовать их.
ОК 8. Самостоятельно определяю задачи профессионального и личностного развития, занимаюсь самообразованием: · планирую свою деятельность по самостоятельному изучению материала и подготовке к занятию.
ОК 9. Ориентируюсь в условиях частой смены технологий в профессиональной деятельности: · владею навыками работы MS Excel.
профессиональные	ПК 1.3. Оформляю документы, регламентирующие организацию перевозочного процесса с применением современных информационных технологий управления перевозками.
ПК 2.2 Планирую и организую производственные работы.
ПК 2.3 Выбираю оптимальные решения в нестандартных ситуациях
	Суммарный балл:
	Оценка:

Критерии оценивания:

0 б — признак не проявляется;

1 б — признак проявляется частично;

2 б — признак проявляется в полном объеме

Максимальное количество баллов:

38-42 б – компетентен

22-37 б – частично компетентен

21 и менее – не компетентен

Балл	Оценка
38-42	5
30-37	4
22-29	3
21 и менее	2

Источник

Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.

Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.

Виды транспортных задач

Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.

Условия транспортной задачи можно представить двумя способами:

в виде схемы;
в виде матрицы.

В процессе решения могут быть ограничения (либо задача решается без них).

По характеру условий различают следующие типы транспортных задач:

открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).

Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.

Пример решения транспортной задачи в Excel

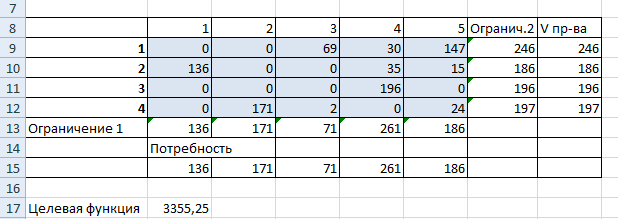
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.

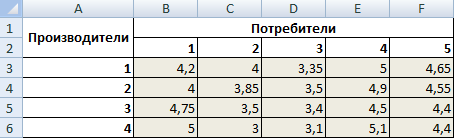
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:

Производители	Потребители	Объем производства
	В1	В2	В3	В4	В5
А1	4,2	4	3,35	5	4,65	246
А2	4	3,85	3,5	4,9	4,55	186
А3	4,75	3,5	3,4	4,5	4,4	196
А4	5	3	3,1	5,1	4,4	197
Объем потребления	136	171	71	261	186

Задача: минимизировать транспортные расходы по перевозке продукции.

Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.

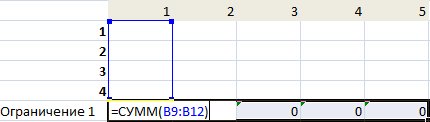
Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.

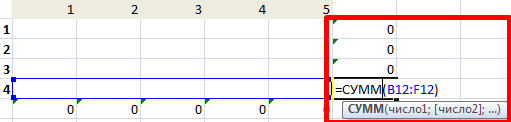
Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.

Вносим известные значения потребности в товаре и объема производства.

Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
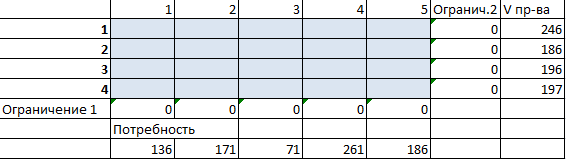
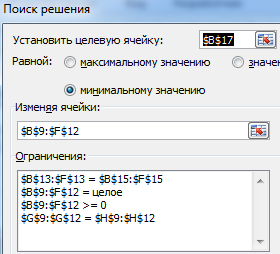
Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.

Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.

Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.

Решение открытой транспортной задачи в Excel

При таком типе возможны два варианта развития событий:

суммарный объем производства превышает суммарную потребность в товаре;
суммарная потребность больше суммы запасов.

Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.

Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.

Единица перевозки груза для фиктивного участника равняется 0.

Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.

Читайте также по теме: решение транспортной задачи методом потенциалов в Excel.

Источник

Министерство общего и профессионального образования

Свердловской области

Государственное бюджетное профессиональное образовательное учреждение

Свердловской области

«Нижнетагильский железнодорожный техникум»

«РЕШЕНИЕ ТРАНСПОРТНЫХ ЗАДАЧ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ EXCEL»

Авторы: Мызникова Ирина Викторовна

Трапезникова Наталья Владимировна

Нижний Тагил 2016

Аннотация

В данной методической разработке рассматривается поэтапное внедрение элементов технологии интегрированного обучения в ходе повторения учебного материала, при этом интегративный характер занятия реализуется в рамках требований примерной программы учебной дисциплины ЕН.02 Информатика «Учебно — методический центр по образованию на железнодорожном транспорте», рекомендованной экспертным советом по профессиональному образованию Федерального государственного автономного учреждения «Федеральный институт развития образования» (ФГАУ «ФИРО») 2012, Москва.

Занятия по дисциплине «Информатика» — это универсальное связующее звено, позволяющее «соединить» практически все дисциплины. Поэтому в основе данной методической разработки лежит личный опыт организации и проведения интегрированных занятий.

Занятие разработано для студентов II курса, осваивающих дисциплины по программе подготовки специалистов среднего звена 23.02.01 Организация перевозок и управление на транспорте (по видам) (автомобильный транспорт).

Данную методическую разработку можно использовать для проведения учебных занятий по дисциплинам «ЕН.02 Информатика» и «ЕНв.03 Экология автомобиля», а также в качестве мастер-класса для демонстрации технологии интегрированного обучения.

Пояснительная записка

Новые требования, выдвинутые в рамках Федерального государственного образовательного стандарта 3 поколения, ставят для всей системы профессионального образования основную задачу – подготовку компетентного специалиста, способного самостоятельно и критически мыслить, умеющего видеть и творчески решать возникающие проблемы. Поэтому очень важен переход от исполнительной, репродуктивной деятельности обучающихся к творческой, поисковой деятельности на всех этапах учебного процесса [7].

В инновационном образовательном процессе студент должен иметь высокий образовательный уровень, гибкое мышление, профессиональную мобильность, осуществлять поиск, анализ и оценку информации, необходимой для решения профессиональных задач, то есть обладать определенными профессиональными и общими компетенциями.

Реализовать все вышеназванное помогает внедрение технологии интегрированного обучения.

Интеграция предметов – это организация предметной деятельности, предполагающая использование системного подхода, ориентированного на формирование системного типа мышления. Главное в интегрированном занятии — вычленить проблему. Проблема должна быть комплексной, жизненной, социально значимой [10].

Интегрированные занятия предполагают возможность вовлечения каждого обучающегося в активный познавательный процесс, причём процесс не пассивного овладения знаниями, а активной познавательной самостоятельной деятельности каждого обучающегося, т.к. каждый имеет возможность проявить себя в той области, которая ему ближе и применить на практике полученные знания [5].

В данной методической разработке интегрированного занятия по теме «Решение транспортных задач в электронных таблицах Excel» приводится технологическая карта учебного занятия и общая структура.

Одним из условий проведения интегрированного занятия является правильное вычленение междисциплинарного объекта изучения, который должен быть актуальным и проблемным, содержать естественную взаимосвязь. Таким объектом была выбрана «транспортная задача», для решения которой использовались межпредметные связи дисциплин «ЕН.02 Информатика» и «ЕНв.03 Экология автомобиля».

Основной целью учебного занятия является инициирование творческой активности, развитие признаков общих и профессиональных компетенций обучающихся. Стратегическая задача занятия — попытка достижения современного качества образования и высокая мотивация студентов к выполнению заданий.

Ориентированная основа деятельности на таком занятии является одним из условий формирования компетенций. Для выполнения практических работ обучающимся предлагаются ориентиры, при опоре на которые они могут безошибочно действовать в практическом плане (см. Приложение).

В процессе решения транспортной задачи студентами проводится анализ эффективности использования того или иного вида топлива, а также его влияние на окружающую среду. Включение заданий и вопросов экологического характера в содержательную часть занятия способствует формированию у студентов навыков экологически оправданного поведения в природе, уверенность в своих силах, позитивное отношение к себе и окружающему миру. На основе синтеза и сопоставления знаний двух дисциплин, делаются обобщающие выводы и вносятся предложения.

При интеграции нескольких дисциплин, связанных единой темой, непроизвольно идет усовершенствование отдельных сторон педагогического опыта, т.к. материалы различных дисциплин взаимопроникают друг в друга (см. Интегративная карта), сокращается общее время преподавания дисциплин, увеличивается время для других сторон учебного занятия: средств обучения, применения различных видов деятельности, самостоятельной работы обучающихся, в их комбинаторике и применении современных технологий [3].

Используемая технология обучения позволяет не только умело овладеть информацией обучающимися, но и критически ее оценить, осмыслить, применить.

Ожидаемые результаты реализации интегрированного занятия:

1. расширение тематики изучаемого материала, необходимость более глубокой и детальной проработки содержания учебных дисциплин;

2. активизация познавательной деятельности обучающихся, возрастание роли самостоятельной работы, инициативы в проведении исследовательской деятельности, и как следствие формирование и развитие общих и профессиональных компетенций.

Разработка интегрированного учебного занятия достаточно трудоемка, но всегда сопровождается позитивной мотивацией и интересом обучающихся к учебно — познавательной деятельности.

Содержание

Технологическая карта учебного занятия

Тема занятия: «Решение транспортных задач в электронных таблицах Excel».

Цель занятия: создание условий для решения задач по определению затрат на перевозки грузов в электронных таблиц Excel, и определение степени влияния разных видов топлива на окружающую среду.

Задачи занятия:

закрепить знания правил записи арифметических выражений и формул в электронных таблицах;
проверить умения строить диаграммы с помощью электронных таблиц Excel;
закрепить умения и навыки редактирования содержимого ячеек таблицы;
обеспечить осмысление влияния разных видов топлива на окружающую среду;
показать взаимосвязь двух дисциплин – ЕН.02 Информатика и ЕНв.03 Экология автомобиля;
продемонстрировать применение диаграмм в профессиональной деятельности.

развивать познавательный интерес обучающихся;
развивать логическое мышление (умение анализировать, сравнивать, обобщать, делать выводы);
развивать умения работать с имеющейся информацией в необычной ситуации;
развивать самооценку самостоятельной деятельности на учебном занятии, развивать умения анализировать свои ошибки и исправлять их в процессе решения задач;
развивать коммуникативные навыки.

воспитывать умения слушать друг друга;
воспитывать добросовестное отношение к дисциплинам, ответственность, честность, сопереживание успехам и неудачам одногруппников.

Педагогические технологии: технология системно — деятельностного подхода, проблемное обучение, элементы технологии взаимного обучения, технологии критического мышления.

Вид занятия: интегрированный.

Тип занятия: повторительно — обобщительный.

Форма организации учебного занятия: фронтальная работа, работа в парах.

Методы обучения:

информационно-практический;
проблемно-поисковый;
вопросно-ответный;
наглядный.

Методические приемы:

осуществление взаимосвязи дисциплин: ЕН.02 Информатика, ЕНв.03Экология автомобиля,
мультимедийное представления в формате программ Microsoft Power Point, Excel, Word;
индивидуальная работа;
тьюторство;
создание атмосферы комфорта и взаимопонимания.

Информационное обеспечение: раздаточный материал (алгоритмы выполнения задания), информационные буклеты.

Техническое и программное обеспечение: мультимедийная установка, приложения MS Power Point, MS Excel, MS Word.

Формируемые компетенции:

Блок самоорганизации и самообучения:

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решение в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
ПК 2.2 Планировать и организовывать производственные работы.
ПК 2.3 Выбирать оптимальные решения в нестандартных ситуациях.

Информационный блок:

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ПК 1.3. Оформлять документы, регламентирующие организацию перевозочного процесса с применением современных информационных технологий управления перевозками.

Коммуникационный блок

ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.

Учебный продукт: практическая работа «Решение транспортных задач в среде MS Excel, исследовательская работа «влияние разных видов топлива на окружающую среду».

Интегративная карта

Тема занятия:

Информатика

Экология автомобиля

«Решение транспортных задач в электронных таблицах Excel»

Тема программы:

«Электронные таблицы Excel». Выполнение вычислительных операций. Абсолютная и относительная адресация ячеек. Построение диаграмм.

Тема программы:

-Воздействие автомобильного транспорта на экологические системы. Загрязнение окружающей среды отходами автомобильного транспорта

Дидактическая структура занятия

Этапы занятия, время	Цель	Деятельность преподавателя, его функции	Деятельность студента, форма организации деятельности обучающегося	Методы, приемы	Методы контроля	Формируемые компетенции
Организационный момент (3 мин)	Сообщение темы, постановка цели, задач занятия.	Проверка готовности к занятию, сообщение темы, постановка целей учебного занятия, рекомендации по организации работы на занятии.	Осмысление целей и задач занятия.	Словесный Фронтальная работа	Наблюдение	ОК 2
Актуализация знаний (Планерка 12 мин)	Подготовка к восприятию нового учебного материала.	Обеспечение контроля выполнения задания	Контроль и корректировка своих знаний. Работа в среде MS Power Point. Представление организации, по сфере деятельности и структуре.	Словесно-наглядный, практический Работа в парах, фронтальная работа	Практический, словесно-наглядный	ОК 1 ОК 2 ОК 3 ОК 5 ОК 6 ОК 7 ПК 1.3
Операционно-исполнительный. Практическая работа с элементами исследования (50 мин)	Понимание значимости информационных технологий для решения производственных задач.	Создание условий для решения проблемного вопроса восприятия с помощью информационного обеспечения (программа Excel), раздаточного материала, обеспечение контроля выполнения задания	Восприятие проблемного вопроса, его анализ. Решение задач, построение диаграмм с помощью MS Excel [3]. Проводят исследование по оценке экономичного вида топлива. Показывают результаты работы через проектор. Проводят анализ последствия деятельности фирм. Учатся договариваться, взаимодействовать друг с другом. Принимать общее решение.	Проблемно-поисковый, наглядный. Практический.	Взаимоконтроль. Оценка практической работы по дисциплине «Информатика», оценка исследовательской работы по дисциплине «Экология автомобиля»	ОК 1 ОК 2 ОК 3 ОК 5 ОК 6 ОК 7 ОК 8 ОК9 ПК 1.3 ПК 2.2 ПК 2.3
Рефлексивно-оценочный. Подведение итогов занятия, рефлексия, самооценка. (15 мин)	Рефлексия: осмысление студентами своих действий, развитие способности к самооценке.	Характеристика работы студентов на занятии	Подготовка документа, отражающий эмоциональное настроение на занятии. Заполнение листа самооценки.	Соотнесение результатов деятельности с поставленной целью, показ конечного результата своей работы на занятии. Индивидуальная и фронтальная работа	Наблюдение, самопроверка, устный опрос.	ОК 2 ОК 6

Характеристика структурных компонентов

Актуализация знаний

Планерка

Каждой паре предлагается вытянуть конверт с названием организации

1. Фирма «Лесоруб»

2. Фирма «Мастер»

3. ИП «Маша»

4. Компания «Дачник»

5. Мебельная фабрика

6. Мебельный комбинат

Разработка презентации в среде Power Point, содержащей название, деятельность и структуру компании.

Операционно-исполнительный

Рабочий день

Каждой группе предлагается решить транспортную задачу по перевозке грузов с использованием электронных таблиц EXCEL, а именно:

решить задачу (в электронных таблицах EXCEL);
построить диаграмму;
оценить затраты на использование разных видов топлива
анализ деятельности последствия работы организации, формулировка выводов.

(см. Приложение 1)

Каждая команда выводит отчет по работе организации на экран через проектор. Даёт анализ своей работы.

Одним из отрицательных последствий работы фирм является вырубка леса и влияние каждого вида топлива на окружающую среду.

Студенты выступают с сообщениями о том, как влияет определенный вид топлива на окружающую среду.

Далее демонстрируется фильм «Вырубка леса и его последствия на окружающую среду», после просмотра которого, студенты предлагают пути выхода из сложившейся ситуации и делают следующие выводы:

1. необходимо находить и использовать новые альтернативные виды топлива;

2. вырубка лесов приводит к негативным последствиям на нашей планете: разрушению озонового слоя, возникновению «парникового эффекта», исчезновению многих видов растений и животных, опустыниванию и др;

3.каждый человек должен задуматься о своем влиянии на окружающую среду и об экологических последствиях.

Рефлексивно-оценочный.

Подведение итогов рабочего дня.

Создание документа в текстовом редакторе Word, отражающего эмоциональное настроение на конец занятия, с использованием объекта WordArt и панели рисования; заполнение листа самооценки (см. Приложение 2)

Список литературы

Барвенов С. А. Компьютерные технологии в организации самостоятельной работы студентов-гуманитариев / Высшая школа. – 2004. – № 4. – С. 35–37.
Воронина, Т. П. Образование в эпоху новых информационных технологий / Т. П. Воронина.- М.: АМО, 2008.-147с.
Глинская, Е. А. Межпредметные связи в обучении / Е.А. Глинская, С.В. Титова. – 3-е изд. – Тула: Инфо, 2007. — 44 с.
Данилюк, Д. Я. Учебный предмет как интегрированная система /Д.Я. Данилюк //Педагогика. — 2007. — № 4. — С. 24-28.
Дик, Ю.И. Интеграция учебных предметов / Ю.И. Дик //Современная педагогика. — 2008. — № 9. — С. 42-47
Екжанова Е. Основы интегрированного обучения. Издательство: Дрофа, Москва. — 2008.
Ломакина Т.Ю., Сергеева М.Г. Педагогические технологии в профессиональных учебных заведениях / Т.Ю. Ломакина, М.Г. Сергеева.- М.: Наука, 2008.
Ливанский В. М. «Ресурсный подход становления интегрированного школьного и внешкольного образовательного пространства // Завуч. -2006г.-№5. — С. 118
Макарова Н. В. Информатика и информационно-коммуникационные технологии. 10-11 кл. СПб.: Питер, 2006. — 224с.
Пузанкова Е.Н., Бочкова Н. В. Современная педагогическая интеграция, ее характеристики// Образование и общество. — 2009. — N 1. — С. 9-13.

Приложение 1.

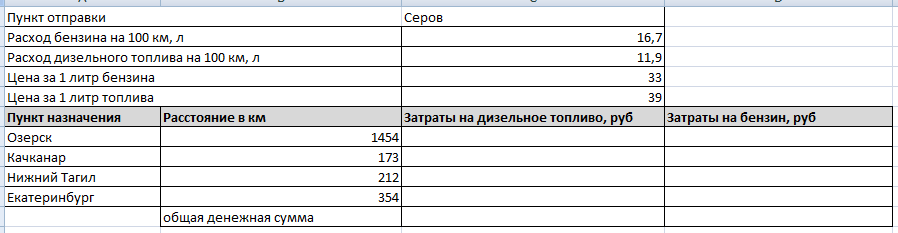
Фирма «Лесоруб» организует поставку леса в разные населенные пункты на бортовом автомобиле «Фермер». В качестве горючего используются дизельное топливо и бензин. Определите затраты на горючее до каждого населенного пункта.

Постойте гистограмму, отражающую значения столбцов затраты на горючее с подписями данных и круговую диаграмму по ячейкам общей денежной суммы.

Оцените, использование какого горючего экономичнее?

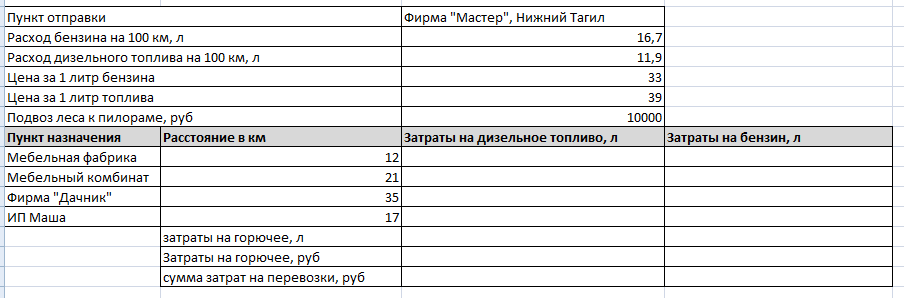
Фирма «Мастер» в Нижнем Тагиле закупила у фирмы «Лесоруб» лес. 10000 рублей было потрачено на подвоз леса к пилораме. Далее, обработанный лес оправился по разным пунктам назначения на бортовом автомобиле «Фермер». В качестве горючего используются дизельное топливо и бензин.

Определите затраты на горючее в литрах до каждого пункта назначения и общую денежную сумму потраченную на доставку.

Постойте гистограмму, отражающую значения столбцов затраты на топливо и бензин с подписями данных и круговую диаграмму по ячейкам затраты на горючее в рублях.

Оцените, использование какого вида горючего экономичнее?

ИП «Маша» по перевозке грузов закупила в фирме «Мастер» обрезную доску на сумму 225 000 рублей. Для получения прибыли ее продают в разные города. Нанимаются водители с окладом в 45000 рублей каждый, осуществляющих перевозку на бортовом автомобиле «Фермер». В качестве горючего используются дизельное топливо и бензин.

В Челябинске выручка от продажи составила 300000 рублей, в Перми — 470000 рублей, в Первоуральске -120000 рублей. Определите: а) сумму затрат перевозки с учетом расхода на горючее; б) прибыль предпринимателя.

Постойте гистограмму, отражающую значения столбцов затраты на горючее с подписями данных и круговую диаграмму затраты на горючее в рублях.

Оцените, использование какого горючего экономичнее?

Оцените, использование какого вида горючего экономичнее?

Фирма «Дачник» закупила оптом доску обрезную для строительства дач в Свердловской области. Пункты доставки следующие: Красноуральск, Новоуральск, Качканар. Доставка осуществляется автомобилем Белаз.

Постойте гистограмму, отражающую значения столбцов затраты на топливо и газ с подписями данных, а также круговую диаграмму затраты на горючее в рублях.

Оцените, использование какого вида горючего экономичнее?

Мебельная фабрика занимается закупкой леса у фирмы «Лесоруб», изготовлением мебели и её поставкой в разные районы города. Доставка осуществляется автомобилем Зил, работающем на разном виде топлива.

Постойте гистограмму, отражающую значения столбцов затраты на горючее с подписями данных, а также круговую диаграмму затраты на горючее в рублях.

Оцените, использование какого вида горючего экономичнее?

Мебельный комбинат занимается изготовлением мягкой и корпусной мебели, доставкой её по всей России. Доставка осуществляется автомобилем Зил, работающем на разном виде топлива.

Постойте гистограмму, отражающую значения столбцов затраты на горючее с подписями данных и круговую диаграмму по ячейкам общей денежной суммы.

Оцените, использование какого вида горючего экономичнее?

Приложение 2.

Лист самооценки проявления компетенций

ФИ студента_______________

Группа ___________________

	Признаки проявления компетенций	Баллы
общие	ОК 1. Понимаю сущность и социальную значимость своей будущей профессии, проявляю к ней устойчивый интерес.
ОК 2. Организовываю собственную деятельность, выбираю типовые методы и способы выполнения профессиональных задач, оцениваю их эффективность и качество: оцениваю влияние различных видов топлива на окружающую среду.
ОК 3. Принимаю решение в стандартных и нестандартных ситуациях и несу за них ответственность: умею решать поставленную проблему.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использую информационно-коммуникационные технологии в профессиональной деятельности:
оформляю документы с применением современных информационных технологий управления перевозками;
владею приемами работы с презентацией Power Point;
умею устанавливать нужный формат ячейки;
умею производить расчеты в электронных таблицах Excel;
использую абсолютную адресацию ячеек при вводе формул;
строю диаграммы и графики в соответствии с предложенным заданием;
умею воспроизводить, совершенствовать средства и способы получения и воспроизведения информации в электронном виде, пользоваться современными компьютерными технологиями;
владею навыками работы в текстовом редакторе Word;
использую панель рисования в текстовом редакторе Word.
ОК 6. Работаю в коллективе и команде, эффективно общаюсь с одногруппниками, преподавателями.
ОК 7. Беру на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий: умею обобщить результаты работы группы и презентовать их.
ОК 8. Самостоятельно определяю задачи профессионального и личностного развития, занимаюсь самообразованием: планирую свою деятельность по самостоятельному изучению материала и подготовке к занятию.
ОК 9. Ориентируюсь в условиях частой смены технологий в профессиональной деятельности: владею навыками работы MS Excel.
профессиональные	ПК 1.3. Оформляю документы, регламентирующие организацию перевозочного процесса с применением современных информационных технологий управления перевозками.
ПК 2.2 Планирую и организую производственные работы.
ПК 2.3 Выбираю оптимальные решения в нестандартных ситуациях
	Суммарный балл:
	Оценка:

Критерии оценивания:

0 б — признак не проявляется;

1 б — признак проявляется частично;

2 б — признак проявляется в полном объеме

Максимальное количество баллов:

38-42 б – компетентен

22-37 б – частично компетентен

21 и менее – не компетентен

Балл	Оценка
38-42	5
30-37	4
22-29	3
21 и менее	2

Источник

Транспортная
задача –
это задача о минимизации транспортных
расходов, связанных с обеспечением
пунктов потребления определенным
количеством однородной продукции,
производимой в нескольких пунктах
производства [1, 3, 7]. В общем виде задача
может быть сформулирована следующим
образом.

Однородный
продукт, сосредоточенный в

пунктах производства, необходимо
распределить между

пунктами потребления. Стоимость перевозки
единицы продукции известна для всех
маршрутов. Необходимо составить такой
план перевозок, при котором запросы
всех пунктов потребления были бы
удовлетворены за счет имеющихся продуктов
в пунктах производства и общие транспортные
расходы по доставке продуктов были бы
минимальными.

Примем
следующие обозначения: i
– номер пункта производства, j
–номер пункта потребления,
–
количество продукта, имеющееся в i-ом
пункте производства,

– количество продукта, необходимое для
j-го
пункта потребления,

– стоимость перевозки единицы продукта
из i-го
пункта производства в j-й
пункт потребления,

– количество груза, планируемого к
перевозке из i-го
пункта производства в j-й
пункт потребления, i=1,2,…,m;
j=1,2,…,n.
Математическая модель транспортной
задачи будет выглядеть следующим
образом:

Условия
задачи удобно записывать в виде таблицы,
которая называется матрицей
планирования:

с₁₁
с₁₂…
с₁_n

. . .

с_m₁
с_m₂…
с_mn

a₁

…

a_m

b₁

b₂…

b_n

Рассмотрим решение
транспортной задачи в табличном
процессоре MS
Excel.
Так как транспортная задача является
частным случаем задачи линейного
программирования, то эту задачу можно
решать так, как описано выше. Однако
благодаря свойствам задачи, ее можно
записать в более компактной форме.

Рассмотрим
транспортную задачу, матрица планирования
которой имеет вид:

B_j A_i	B₁	B₂	B₃	B₄	B₅
A₁	14	25	18	19	23	33
A₂	2	17	16	24	2	25
A₃	29	3	7	15	22	25
A₄	5	20	17	23	10	17
	33	11	11	11	34	b_ja_i

Для решения
транспортной задачи введем данные, как
показано на рис.6.

Рис.6.
Исходные данные транспортной задачи.

В
ячейки
B2
: F5
введем стоимость перевозок. Ячейки B8
: F11
отведены под значения объемов перевозок,
пока неизвестные. В ячейки H8
: H11
введены объемы производства, а в ячейки
B13
: F13
— потребности (спрос) в продукции в
пунктах потребления.

В
ячейку G12
вводится целевая функция

=
СУММПРОИЗВ (B2
: F5;
B8
: F11)
.

В
ячейки B12
: F12
вводятся формулы

=
СУММ (B8
: B11),

=
СУММ (C8
: C11),

=
СУММ (D8
: D11),

=
СУММ (E8
: E11),

=
СУММ (F8
: F11),

определяющие объем
продукции, ввозимой в пункты потребления.
В ячейки

G8
: G11
введены формулы

= СУММ (B8
: F8),

= СУММ (B9
: F9),

= СУММ (B10
: F10),

= СУММ (B11
: F11),

характеризующие
объем продукции, вывозимой из пунктов
производства.

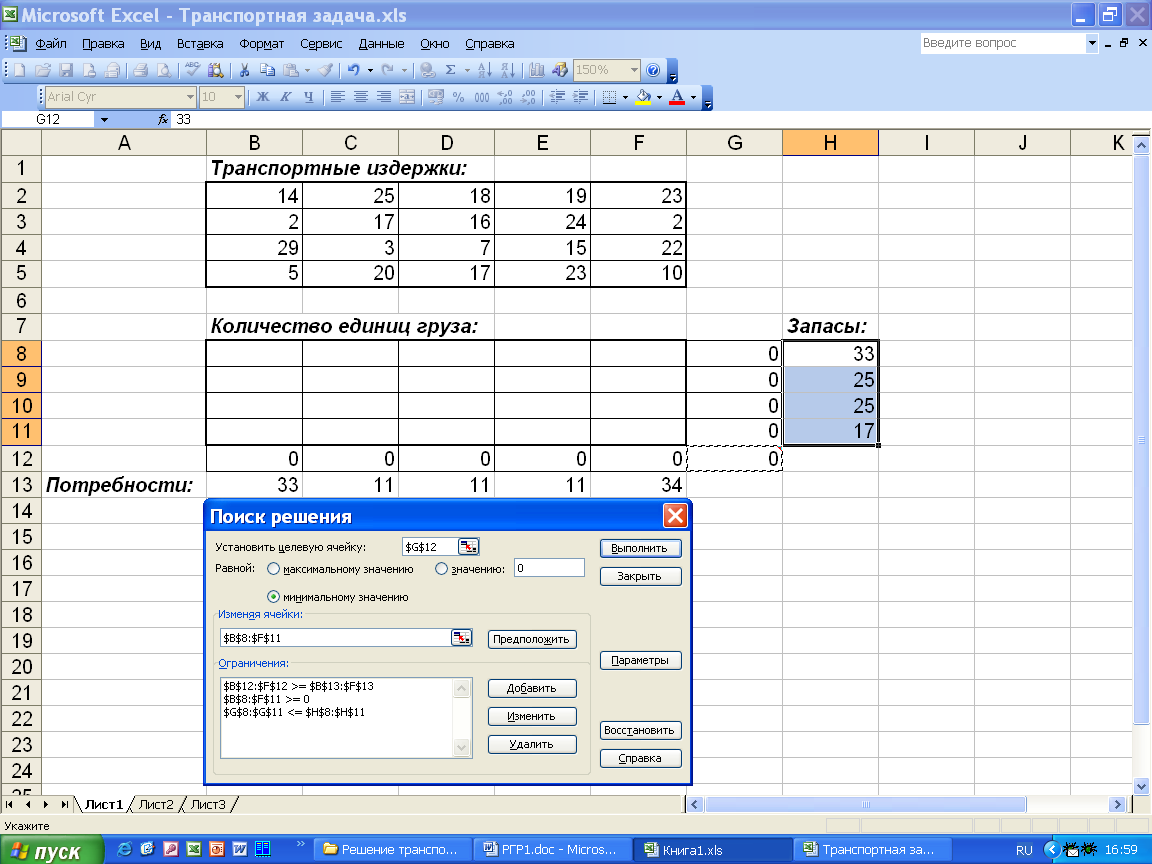
Далее выбираем
команду Сервис,
Поиск решения и
заполняем
открывшееся диалоговое окно Поиск
решения, как
показано на рис.7.

Рис.7.
Диалоговое окно Поиск
решения
для транспортной задачи.

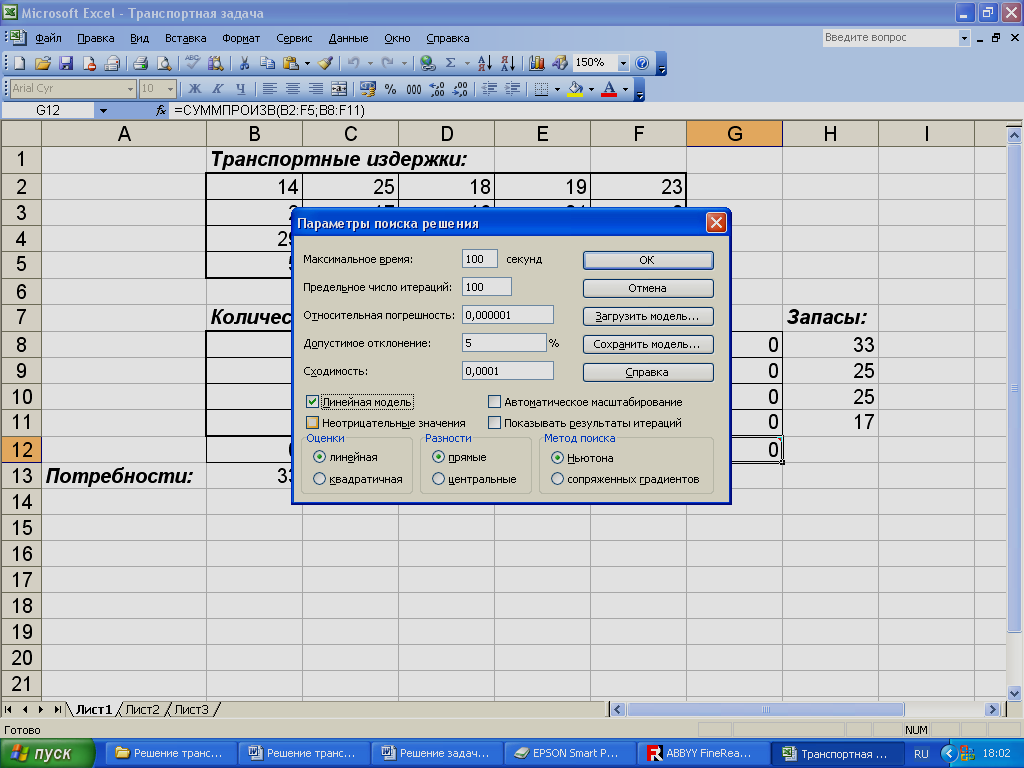
В диалоговом окне
Параметры
поиска решения установить
флажок Линейная
модель (рис.8).

Рис.8.
Диалоговое окно Параметры
поиска решений.

После нажатия
кнопки Выполнить
получаем
оптимальный план поставок продукции
и соответствующие ему транспортные
расходы (рис. 9).

Рис.9.
Оптимальное решение транспортной
задачи.

Соседние файлы в папке 5_Практикум

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

Источник

Содержание

Введение

§1. Постановка Транспортной задачи (ТЗ) для n переменных

§2. Пример решения Транспортной задачи

§3. Транспортные задачи по различным критериям

§4. Решение транспортной задачи в Excel

Список литературы

Введение

Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Классическая транспортная задача – задача о наиболее экономном плане перевозок однородного продукта или взаимозаменяемых продуктов из пунктов производства в пункты потребления, встречается чаще всего в практических приложениях линейного программирования. Линейное программирование является одним из разделов математического программирования – области математики, разрабатывающей теорию и численные методы решения многомерных экстремальных задач с ограничениями.

Огромное количество возможных вариантов перевозок затрудняет получение достаточно экономного плана эмпирическим или экспертным путем. Применение математических методов и вычислительных в планировании перевозок дает большой экономический эффект. Транспортные задачи могут быть решены симплексным методом однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его получить оптимальное решение.

В зависимости от способа представления условий транспортной задачи она может быть представлена в сетевой (схематичной) или матричной (табличной) форме. Транспортная задача может также решаться с ограничениями и без ограничений.

§1. Постановка Транспортной задачи (ТЗ) для nпеременных

Пусть имеется несколько поставщиков однородной продукции (каждый с определенным запасом) и несколько потребителей этой продукции (с известными потребностями у каждого). Задана также сеть коммуникаций (дорог, рек, воздушных линий и т.д.) связывающая каждого поставщика с каждым потребителем. На каждой коммуникации задана цена перевозки – стоимость перевозки единицы продукции. Если какая – либо коммуникация отсутствует, то считаем, что она есть, но цену перевозки на ней устанавливаем равной бесконечности (+∞). Это соглашение сделает невыгодным перевозку по ней и автоматически исключит данную коммуникацию из плана перевозок.

Таким образом, требуется составить план перевозок продукции от поставщиков к потребителям так, чтобы потребности потребителей были бы удовлетворены за счет вывоза запаса от поставщиков. Цель – минимизация суммарной стоимости всех перевозок.

Транспортные задачи бывают:

1) открытые m ≠ n (суммарный запас продукции, имеющейся у поставщиков, не совпадает с суммарной потребностью в продукции у потребителей.)

2) закрытые m = n (суммарный запас продукции, имеющейся у поставщиков, совпадает с суммарной потребностью в продукции у потребителей.)

Метод потенциалов «работает» только для закрытых ТЗ, причем, закрытая ТЗ всегда разрешима.

Открытую ТЗ сводят к закрытой ТЗ путем прибавления к суммарному запасу продукции или суммарной потребности продукции недостающих единиц до равенства суммарного запаса продукции и суммарной потребности продукции.

Закрытая транспортная задача формулируется как Задача Линейного Программирования (ЗЛП) следующего вида:

/>/>

/>, где

/>— запас i– го поставщика

/>— потребность j– го потребителя

/>— цена перевозки единицы продукции по коммуникациям (i,j)

(от i– го поставщика к j– му потребителю)

/>— объем перевозки продукции (неизвестный) по коммуникациям (i,j).

Для вывода критерии оптимальности транспортной задачи построим двойственную задачу.

Структура матрицы ограничений транспортной задачи такова, что столбец, соответствующей переменной />содержит ровно два ненулевых элемента: единицу в строке с номером iи единицу в строке m+ i.

Вектор двойственных переменных Y= (/>,…,/>,/>,…,/>) имеет m+ nкомпонент (по числе ограничений ТЗ), которые называются потенциалами: переменные />,/>,…,/>— потенциалы поставщиков; переменные />,/>…,/>— потенциалы потребителей.

Используя схему для построения двойственной задачи к ЗЛП в стандартной форме, имеем: />

В полученной двойственной задаче n·mограничений, соответствующих каждой переменной />ТЗ. Вспоминая, что невязка между левой и правой частью в ограничений двойственной задачи есть оценка для соответствующей переменной исходной задачи, запишем условия оптимальности текущего плана перевозок в ТЗ:

/>.

Неизвестные потенциалы />и />(их общее количество равно m+ n) могут быть найдены (и именно так отыскиваются) из условия равенства нулю оценок для базисных переменных (заполненных клеток таблицы) ТЗ (таких равенств (m+n— 1), что следует из замечания ниже).

для заполненных клеток (i,j) таблицы ТЗ.

Решение полученной системы (содержащей неизвестных на единицу больше, чем число уравнений) ищется, когда одно из неизвестных (вообще говоря, любое) полагается равным некоторому числу (тоже, вообще говоря, любому). После этого оставшаяся система имеет единственное решение.

§2. Пример решения Транспортной задачи

Метод потенциалов представляет из себя модификацию симплекс-метода, учитывающую специфику транспортной задачи, поэтому его алгоритм не отличается от алгоритма симплекс-метода, за исключением шага проверки целевой функции на неограниченность на множестве решений. Отсутствие указанного шага в методе потенциалов обусловлено теоремой о том, что закрытая ТЗ всегда разрешима. Итак, алгоритм метода потенциалов для решения ТЗ состоит из следующих шагов:

ШАГ 1. Построение начального плана перевозок.

ШАГ 2. Проверка текущего плана на оптимальность.

Если план оптимален, то алгоритм завершен.

ШАГ 3. Улучшение плана перевозок. Переход к шагу 1.

Опишем алгоритм по шагам, иллюстрируя каждый шаг

ШАГ 1. Построение начального плана перевозок.

Построение начального решения (как и последующие расчеты) проводят в таблице, имеющей следующий вид:

Клетка ( i, j ) таблицы соответствует коммуникации, связывающей i-го поставщика сj-м потребителем.

—PAGE_BREAK—

Построить начальный план перевозок означает — назначить объемы перевозок в клетки таблицы таким образом, чтобы:

а)число заполненных клеток было (m+n-1). (Тогда план перевозок будет отвечать базисному решению ЗЛП);

б)сумма перевозок в любой строке должна быть равна запасу соответствующего поставщика, а сумма перевозок в каждом столбце равна потребности потребителя. (Условие выполнения ограничений ТЗ). Существует несколько способов нахождения начального решения, которые отличаются только выбором клетки, в которую назначается очередная перевозка. Так, в способе северо-западного угла (СЗУ) для очередного назначения перевозки выбирается левая верхняя клетка таблицы (при этом никак не учитываются цены перевозок). Наоборот, в способе минимальной стоимости (МС) для заполнения выбирается клетка текущей таблицы с минимальной ценой перевозки, что в большинстве случаев (но не всегда) приводит к более дешевому (а значит и более близкому к оптимальному) начальному плану перевозок.

Мы будем пользоваться способом минимальной стоимости (МС).

Изложим теперь алгоритм нахождения начального решения.

ШАГ 1. Определенным способом выбираем клетку в текущей таблице. Пусть она имеет индексы (i, j) (i -номер поставщика, j — номер потребителя).

ШАГ 2. В качестве перевозок в эту клетку назначаем наименьшую из ai и потребности bj.

xij = min{ai,bj }

ШАГ З. Уменьшим запас ai и потребность bj на величину перевозки xij, т.е.

ai = ai — xij,

bj =bj -xij

ШАГ 4. При исчерпании запаса (ai = 0) запрещаем к перевозке оставшиеся свободные клетки i-ой строки, а при исчерпании потребности

(bj =0) запрещаем такие же клетки вj-ом столбце.

В случае одновременного исчерпания запасов потребностей (ai =bj = 0) запрещаем перевозки или в строке (тогда считаем, что у потребителя осталась потребность в количестве равном нулю, которую необходимо удовлетворить), или в столбце (в этом случае считаем, что у поставщика остается запас равный нулю, который необходимо вывезти). Это делается для того, чтобы при одновременном запрещении перевозок в строке и столбце количество заполненных клеток таблицы не стало меньшим, чем m+n-1.

Получим новую текущую таблицу, в которую не входят заполненные и запрещенные клетки. Если таблица не пуста, переходим к шагу 1. (При исчерпании таблицы — конец).

Способ минимальной стоимости.

1.Клетки с минимальной ценой (3,1), (3,2) и (3,3). Выбираем, например, (3,2). (Далее все шаги, как в предыдущем способе).

2. x32 = min{50,60} = 50

3. a ‘3 =50-50=0, b ‘2 = 100-50=50

4.Запрещаем строку 3.

Клетка с min ценой ~ (2,3)

x23 = min{70,80} = 70

a2=70-70=0, b’3 = 80-70=10

Запрещаем строку 2.

—

Клетка с min ценой ~ (1,1)

x 11=min{120,60} = 60

a 1’=120-60 = 60, b1’= 0

4.В первом столбце запрещать уже нечего. Текущая таблица содержит две клетки (1,2) и (1,3).

1.Выбираем клетку (1,2)

2.x 12 =min{110,100} = 100

3.a 1 =110-100 = 10, b’1 = 0

4.Текущая таблица содержит одну клетку (1,3).

1. Выбираем последнюю клетку(1,3)

2. x13=min{10,10} = 10

3.a1′ = b3 = 0

4.Таблица исчерпана. Конец.

Переходим к описанию следующего шага метода потенциалов.

ШАГ 2. Проверка текущего плана на оптимальность.

Признаком того, что текущий план перевозок является оптимальным, служит условие

(1)ui +vj -cij ≤0

которое выполняется для всех клеток таблицы. Неизвестные здесь величины ui и vj (называемые потенциалами) определяются из условий

(2)ui + vj = cij

Условие (1) означает невозможность появления «спекулятивной» цены. Само же название «потенциалы» заимствовано из физического закона о том, что работа по перемещению заряда в электростатическом поле равна разности потенциалов в данных точках поля (У нас: «… цена перевозки единицы продукции по коммуникации равна разности цен в конце и в начале пути»)

Так как заполненных клеток в таблице (m+n-1) штук, а неизвестных и (m+n) штук, то для их определения имеется система из (m+n-1) уравнений относительно (m+n) неизвестных. Чтобы найти решение (хотя бы какое-нибудь) такой системы, достаточно положить одно из неизвестных (произвольное) равным некоторому произвольно выбранному числу. Тогда остальные определяются единственным образом. Можно решать эту систему непосредственно (продолжаем работать с нашим «старым» примером и найдем потенциалы для начального плана, построенного способом МС).

Заполненные клетки Уравнения

(1,1) u1+ v1=5

продолжение
—PAGE_BREAK—

(1,2)u1+ v2=10

(1,3)u1+ v3=12

(2,3) u2+v3=4

(3,2)u3+v2=0

Положим, например, неизвестное u 1 равным 0 (через него можно из первых трех уравнений найти v1, v2 и v3). Последовательно из них находим u 2 ,u 3.

Этот метод можно сформулировать в виде единого правила:

Неизвестный потенциал находится вычитанием известного из цены перевозки в заполненной клетке

Применим это правило для определения u и v в нашем примере и получим:

u1 =0, u2 =-8, u3 =-6

v1 =5, v2 =10, v3 =12

Переходим к проверке условий оптимальности (1). Достаточно проверять их для незаполненных клеток, так как для клеток заполненных эти условия выполняются как равенства. Для проверки берется незаполненная клетка, складываются соответствующие ей потенциалы (первый элемент строки и последний элемент столбца) и из них вычитается цена перевозки в данной клетке. Если полученное число отрицательное (или ноль), то оптимальность в данной клетке не нарушается (в случае выполнения условия (1) для всех незаполненных клеток, имеем оптимальный план перевозок). Если же в таблице встретилась хотя бы одна клетка, для которой это число положительно, тогда решение не является оптимальным и может быть улучшено.

Проверим на оптимальность имеющееся решение

(2,1) u2+v1-c21=-8+5-8=-11<0

(2,2)u 2+v2-c22=-8+10-6=-4<0

(3,1) u 3 +v1 -c31=-10+ 5-0=-5<0

(3,3) u 3 +v3 -c33=-10+12-0=2>0

Следовательно, условие оптимальности нарушено в клетке (3,3).

Имеющийся план перевозок можно улучшить.

Дадим описание заключительного шага алгоритма метода потенциалов.

ШАГ 3 Улучшение плана перевозок.

Улучшение плана происходит путем назначения перевозки θ>0 в ту клетку (i, j) таблицы, в которой нарушилось условие оптимальности. Но назначение ненулевой перевозки нарушает условия баланса вывоза продукции от поставщика i (вывозит весь запас и еще плюсθ>0 ) и условия баланса привоза продукции к потребителю j (получает все что можно и еще плюс θ > 0). Условия баланса восстанавливают путем уменьшения вывоза от i-поставщика к какому-то другому потребителю j (уменьшают на θ перевозку в какой-то заполненной клетке (i, j) строки i). При этом нарушается баланс привоза продукции к потребителю j (получает на θ меньше, чем ему требуется). Восстанавливают баланс в столбце j, тогда он нарушается в некоторой строке i и т.д. до тех пор, пока цикл перемещения перевозок не замкнется на клетке, в которой нарушалось условие оптимальности. Продемонстрируем эти рассуждения на нашем примере.

120

50+Ө

10-Ө

—

50— Ө

* + Ө

100

120

-(0)

—

* 10

100

1. Оптимальность нарушена в клетке (3,3). Назначим в нее перевозку θ>0 (+θ означает, увеличение на θ).

2.Нарушается баланс вывоза от поставщика 3 (вывозит 50+ θ, а это больше его запаса!). Уменьшаем на θ перевозку в заполненной клетке строки 3 (вне заполненной уменьшать нельзя, так как это приведет к отрицательной перевозке).

Рассмотрим те клетки цикла в которых уменьшаем на θ перевозку и берём минимум из вычетаемых, у нас это min{10- θ ,50- θ }=10.

И данное число надо подставить в цикл

§3. Транспортные задачи по различным критериям

Транспортная задача по критерию времени

Иногда возникает ситуация, когда в условиях (ТЗ) необходимо минимизировать не стоимость перевозок, а время их выполнения (Срочные грузы, перевозки скоропортящихся продуктов, работа «скорой помощи» и т.д.)

Имеется mпоставщиков />однородного груза и nпотребителей />груза. Для каждой пары (/>,/>) известно время />, за которое груз перевозится от />к />. Требуется составить такой план перевозок, при котором все запасы поставщиков будут вывезены, а все запросы потребителей будут полностью удовлетворенны и наибольшее время доставки всех грузов будет минимизирован.

продолжение
—PAGE_BREAK—

Задача о назначениях (Венгерский метод)

Имеется n видов работ и n рабочих. Каждый рабочий может выполнить любую из n работ за некоторое время (цена рабочего). Требуется распределить все работы между всеми рабочими так, чтобы время выполнения работ было минимальным, а каждую работу выполнял только один рабочий.

§4. Решение транспортной задачи в Excel

В качестве примера я рассмотрел транспортную задачу для 2 складов и 5 магазинов.

В ячейки C4:C5 записал объемы продукции, имеющиеся на 2 складах.

В ячейки E5:I5 — заявки на продукцию, поступившие от магазинов.

В ячейки B8:F9 — матрицу транспортных расходов, задающую расходы на перевозку из I-го склада в J-й магазин единицы продукции.

В ячейки B13:F14 — план перевозок — матрицу, задающую количество товара, перевезенного из I-го склада в J-й магазин. Начальное распределение плана задано по принципу «каждой сестре по серьге», равномерно распределив всю имеющуюся на складе продукцию по магазинам. Эти ячейки являются регулируемыми и Решатель должен найти более подходящее решение, изменив значения в этих ячейках.

В ячейку D15 — записал целевую функцию:

{ =СУММ((B8:F8*B13:F13)+(B9:F9*B14:F14))}

В ячейки D17:H17 записал ограничения, задающие требование о точном выполнении заявки каждого магазина. Как обычно, я записал соответствующую формулу в первую из этих ячеек:

{=СУММ(B13:B14) — E5 }

Затем скопировал ее. При копировании формула автоматически меняется, задавая нужное ограничение. Правда, нужно следить при этом за правильной ориентацией данных. Например, в данном случае формулу нужно копировать в строку, а не в столбец.

Затем задал следующую группу ограничений. Эти ограничения отвечают тому естественному условию, что со склада нельзя увести больше продукции, чем там имеется. Формула, помещенная в ячейку D18, имеет вид:

{=C4 — СУММ(B13:F13)}

Эта формула скопирована уже по столбцу в ячейку D19. Подготовительный этап завершен — можно вызывать Решатель.

При вызове Решателя и задании параметров в его диалоговом окне выполнялась стандартная работа по указанию ячейки с целевой функцией, диапазоном регулируемых ячеек и заданием ограничений. Заметьте, помимо двух групп ограничений я задал и ограничения целочисленности переменных. Предполагается, что продукция может перевозиться только целыми единицами — бочками, мешками, ящиками. Такие ограничения в Решателе создаются совсем просто, — достаточно среди операторов, связывающих левую и правую части ограничения, выбрать оператор int. Взгляните, как выглядят результаты моей работы:

Рис. 2.21.Окно Решателя при решении транспортной задачи

Прежде чем дать команду на решение задачи, я провел настройку параметров в окне Options. В частности я включил флажки, указывающие на линейность модели и положительность переменных. Кроме того, я увеличил точность решения целочисленной задачи, задав в окне Tolerance значение в 1% вместо 5%, принятых по умолчанию.

Рис. 2.22.Настройка в окне параметров Решателя при решении транспортной задачи

Осталось щелкнуть кнопку «Solve» и получить оптимальный план перевозок. Вы можете проанализировать, насколько оптимальный план отличается от равномерного распределения, предложенного в качестве первоначального варианта, и как уменьшились транспортные расходы:

Рис. 2.23.Решение транспортной задачи

Параметры, управляющие работой Решателя

Рассмотрим возможности управления работой Решателя, задаваемые в окне Параметры (Options):

Максимальное время (MaxTime) — ограничивает время, отведенное на процесс поиска решения. По умолчанию задано 100 секунд, что обычно достаточно для задач небольшой размерности, имеющих около 10 ограничений. Для задач большой размерности придется это значение увеличивать.

Предельное число итераций (Iterations) — еще один способ ограничения времени поиска путем задания максимального числа итераций. По умолчанию задано 100, но это число можно увеличивать до 32767. Чаще всего, если решение не получено за 100 итераций, надежд получить его при увеличении этого значения мало. Лучше попытаться изменить начальное приближение и запустить процесс поиска заново.

Относительная погрешность (Precision) — задает точность выполнения ограничений. Иногда проще изменить ограничение, отодвинув границу, чем пытаться выполнить ограничения с высокой точностью.

Сходимость (Convergence) — задается десятичной дробью, меньшей единицы, позволяя остановить процесс поиска при сходимости решения к неподвижной точке, когда относительные изменения в течение последних 5 итераций не превышают заданную дробь.

Линейная модель (Assume Linear Model) — этот флажок следует включать, когда целевая функция и ограничения — линейные функции. Эта дополнительная информация позволяет Решателю упростить процесс поиска решения.

Неотрицательные значения (Assume Non-Negative) — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.

Показывать результаты итераций (Show Iteration Results) — флажок, позволяющий включить пошаговый процесс поиска, показывая на экране результаты каждой итерации. В сложных ситуациях, когда Решатель не находит решения автоматически, рекомендуется включать этот флажок, так как иногда можно найти точку, от которой процесс поиска уклонился в сторону.

Автоматическое масштабирование (Use Automating Scaling) — флажок автоматического изменения масштаба следует включать, когда масштаб значений входных переменных и целевой функции и ограничений отличается, возможно, на порядки. Например, переменные задаются в штуках, а целевая функция, задающая суммарную стоимость, измеряется в миллионах рублей.

Относительная погрешность (Tolerance) — задается в процентах. Указанное значение имеет смысл только для задач с целочисленными ограничениями. Решатель в таких задачах вначале находит оптимальное не целочисленное решение, а потом пытается найти ближайшую целочисленную точку, решение в которой отличалось бы от оптимального не более чем на указанное данным параметром количество процентов. Если такая точка найдена, Решатель сообщает об успехе. При большом допуске (по умолчанию 5%) может быть потеряно лучшее целочисленное решение, правда, отличающееся от найденного Решателем в пределах допуска. Для целочисленных задач допуск имеет смысл уменьшить, что я и сделал при решении транспортной задачи. Хочу еще раз обратить внимание на эту особенность решения задач целочисленного программирования. Если значение параметра Tolerance задать большим, то Решатель может остановиться раньше времени, не найдя лучшего целочисленного решения. Если же его взять малым, то наилучшее целочисленное решение будет отличаться от оптимального нецелочисленного решения на величину большую, чем ту, которая задается параметром Tolerance. В этом случае формально решение заканчивается неуспехом, поскольку найденное решение не удовлетворяет всем требованиям. Конечно, параметр Tolerance играет служебную роль, и «умный» Решатель, найдя наилучшее целочисленное решение, должен был бы уведомлять, что решение найдено, но ограничение по Tolerance не выполнено. Этого, однако, не происходит. Мы еще столкнемся с этой ситуацией при рассмотрении следующей задачи.

Сохранить модель (Save Model) — командная кнопка; позволяет открыть диалоговое окно, где можно указать имя сохраняемой модели. Имеет смысл использовать эту возможность, когда на рабочем листе несколько моделей, так как единственная модель запоминается автоматически.

Загрузить модель (Load Model) — позволяет загрузить одну из сохраненных моделей.

Есть еще несколько более специальных параметров, которыми можно управлять, варьируя процедурами, применяемыми в процессе поиска. К ним следует прибегать в тяжелых ситуациях, когда решение найти не удается.

Источник