Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Содержание
- Транспортная задача: описание
- Подготовительный этап: включение функции “Поиск решения”
- Пример задачи и ее решение
- Условия
- Алгоритм решения
- Заключение
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
- Закрытая – совокупное предложение продавца равняется общему спросу.
- Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
- Открываем меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
- В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
- В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
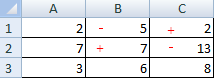
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
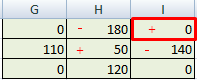
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
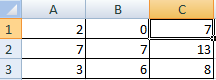
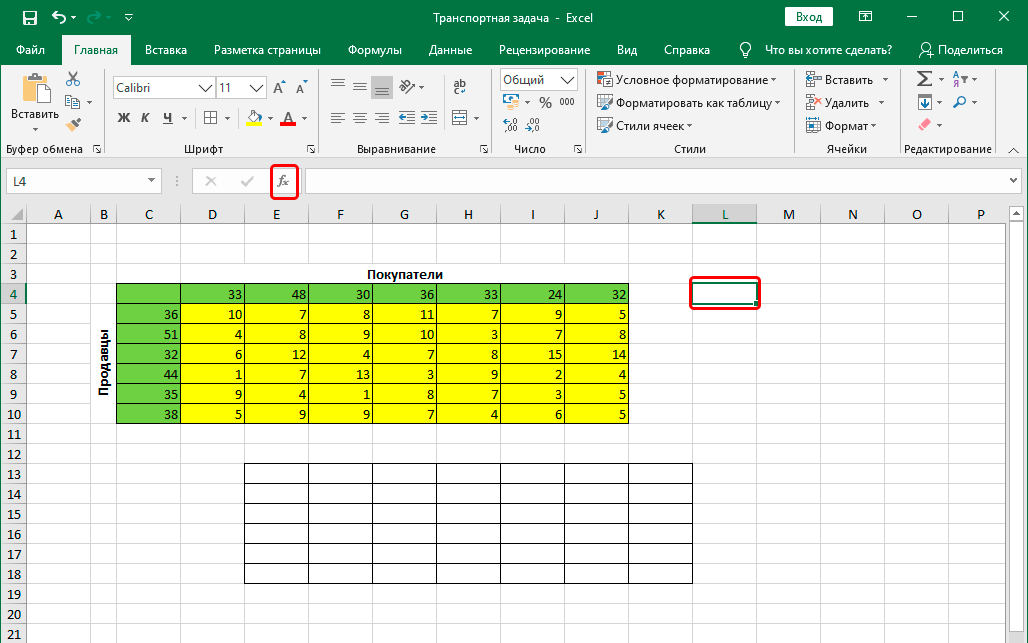
- Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
- Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
- В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
- На экране отобразится окно, в котором нужно заполнить аргументы:
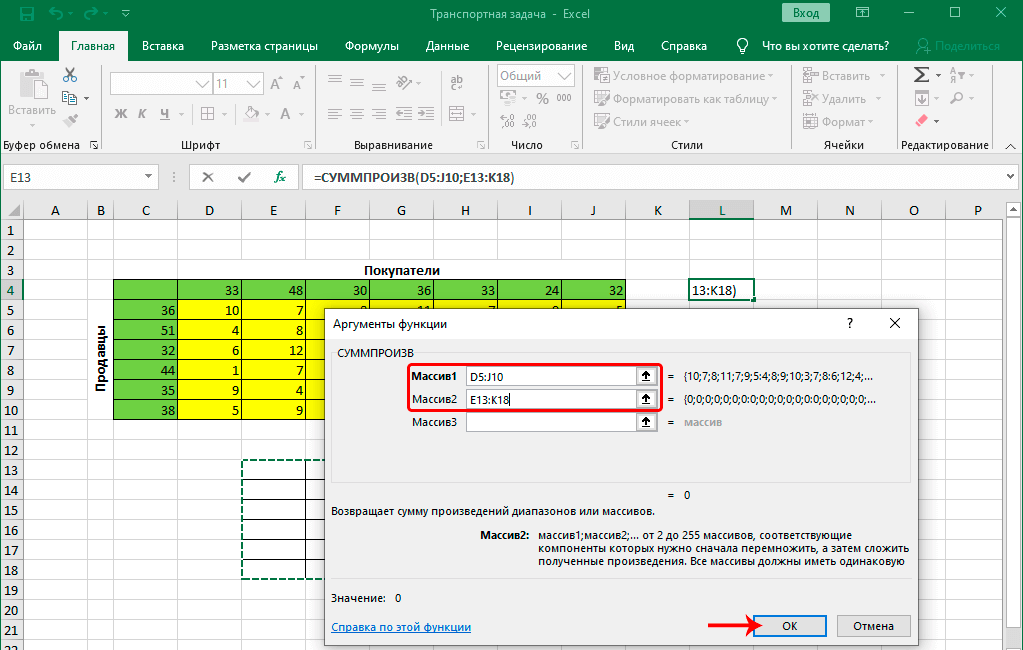
- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
- по готовности жмем OK.
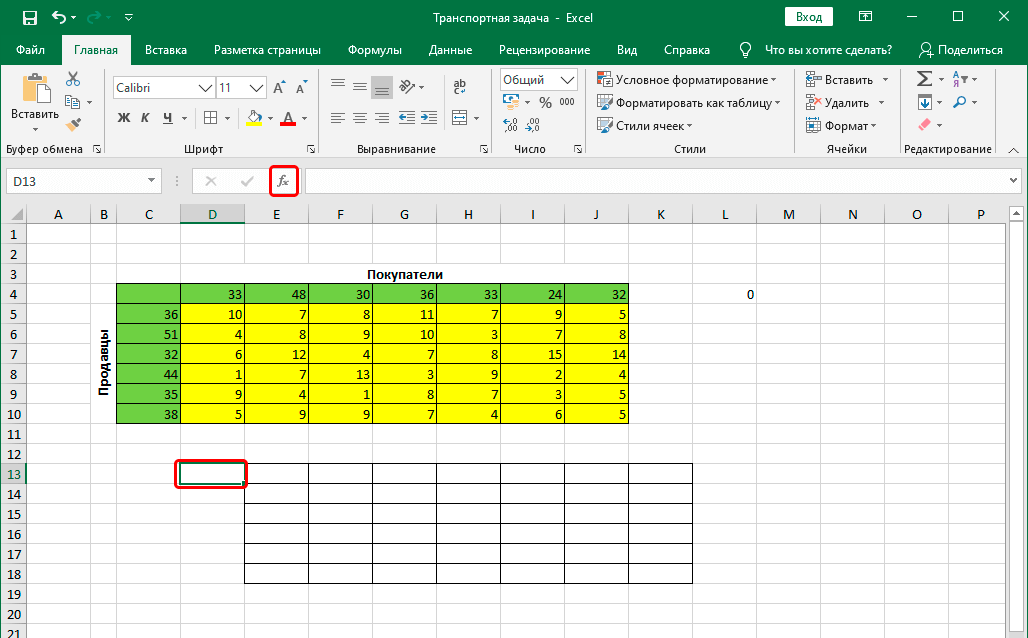
- Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
- На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
- Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
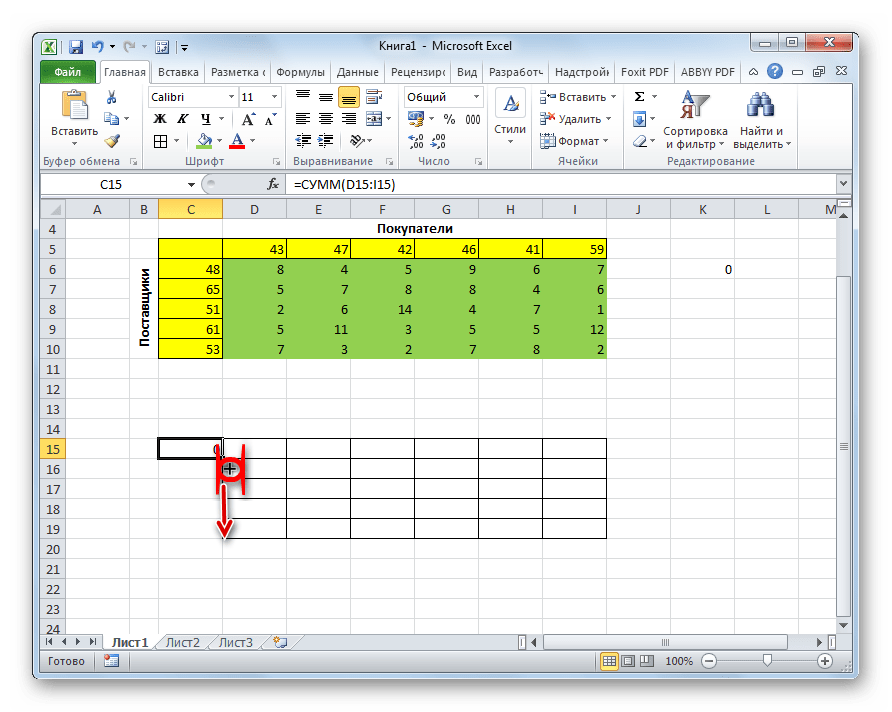
- В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
- Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
- Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
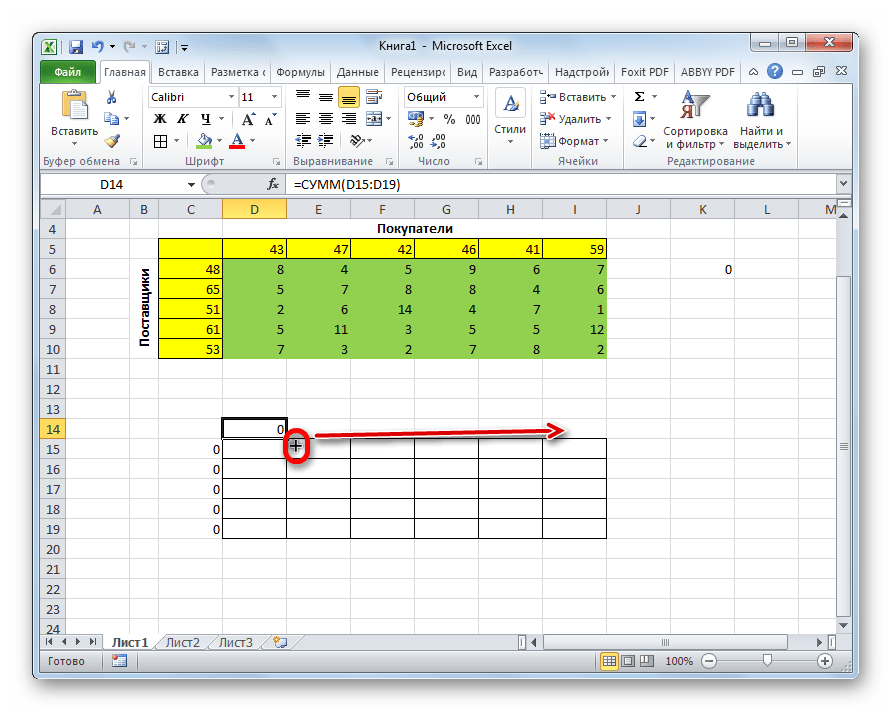
- В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
- С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
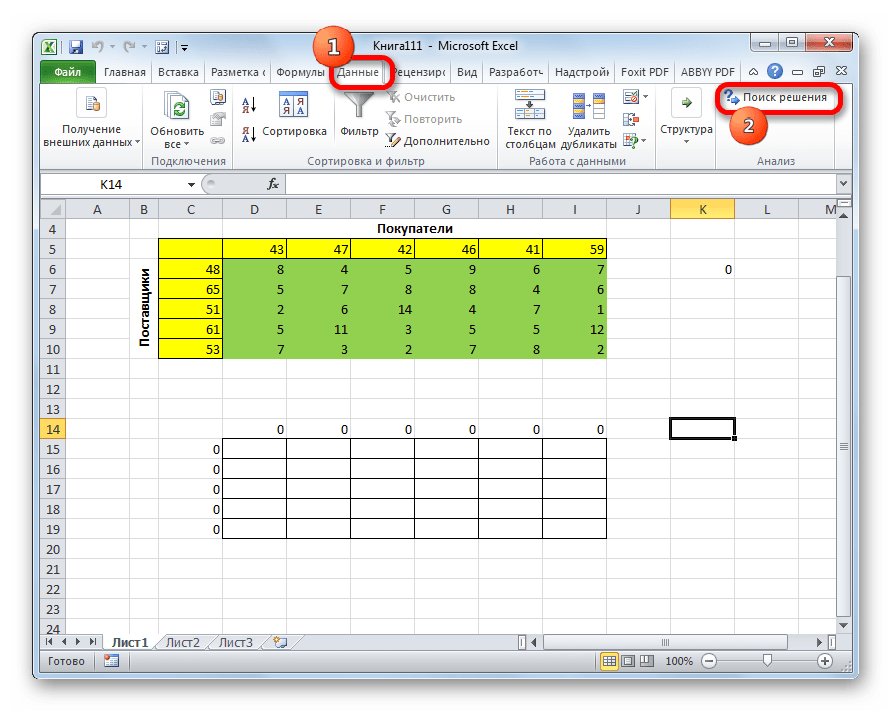
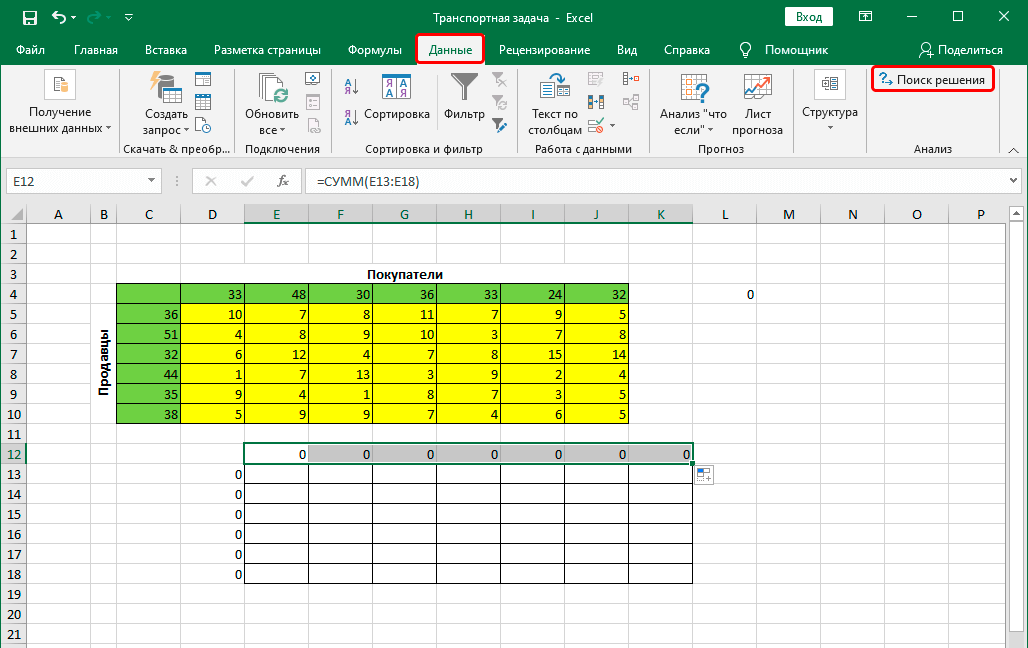
- Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
- Перед нами появится окно с параметрами функции:
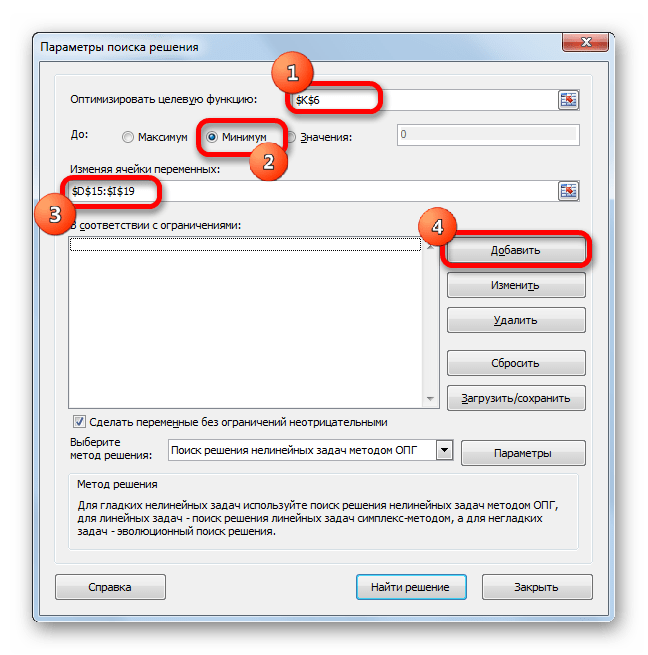
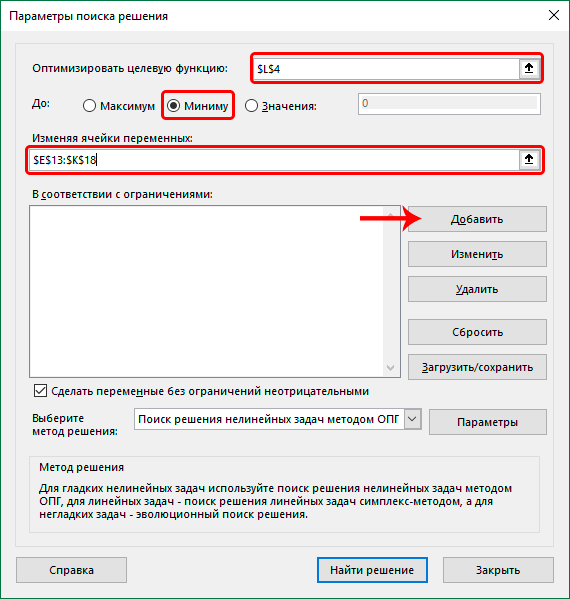
- в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
- для параметра “До” выбираем вариант – “Минимум”.
- в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
- нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
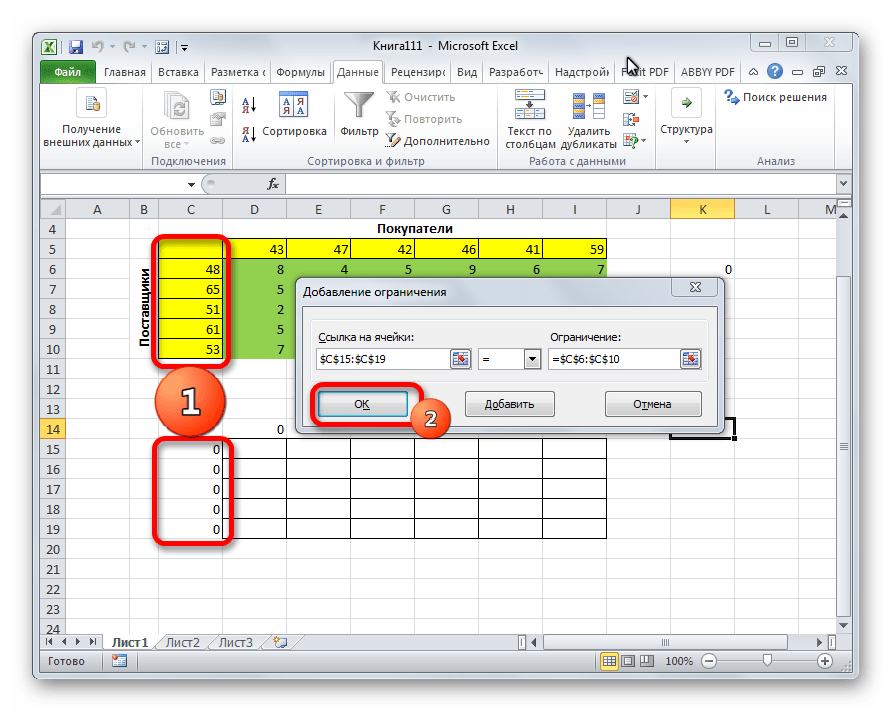
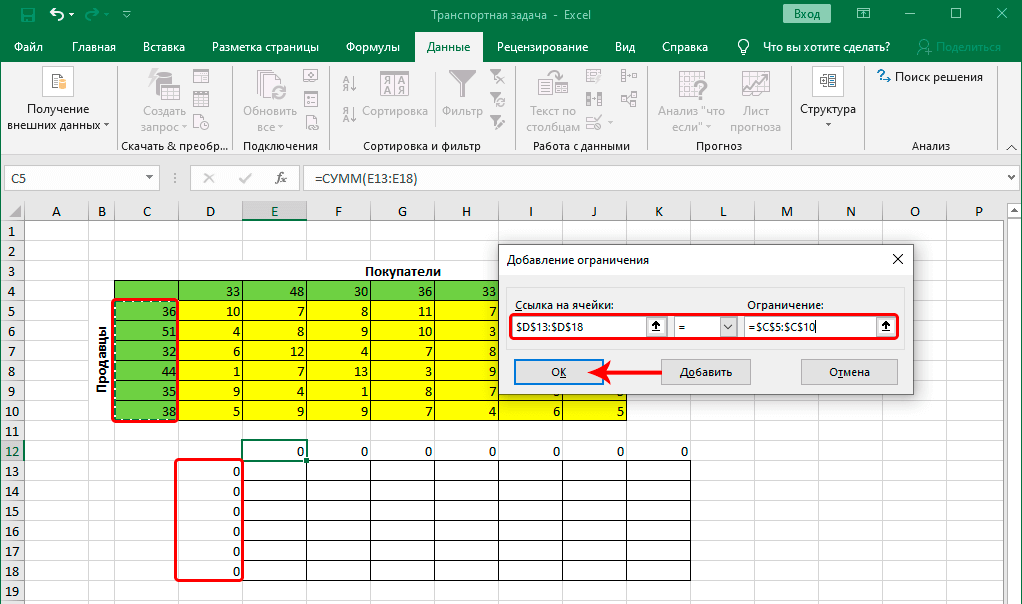
- Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
- становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
- затем выбираем знак “равно”.
- в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
- щелкаем OK по готовности.
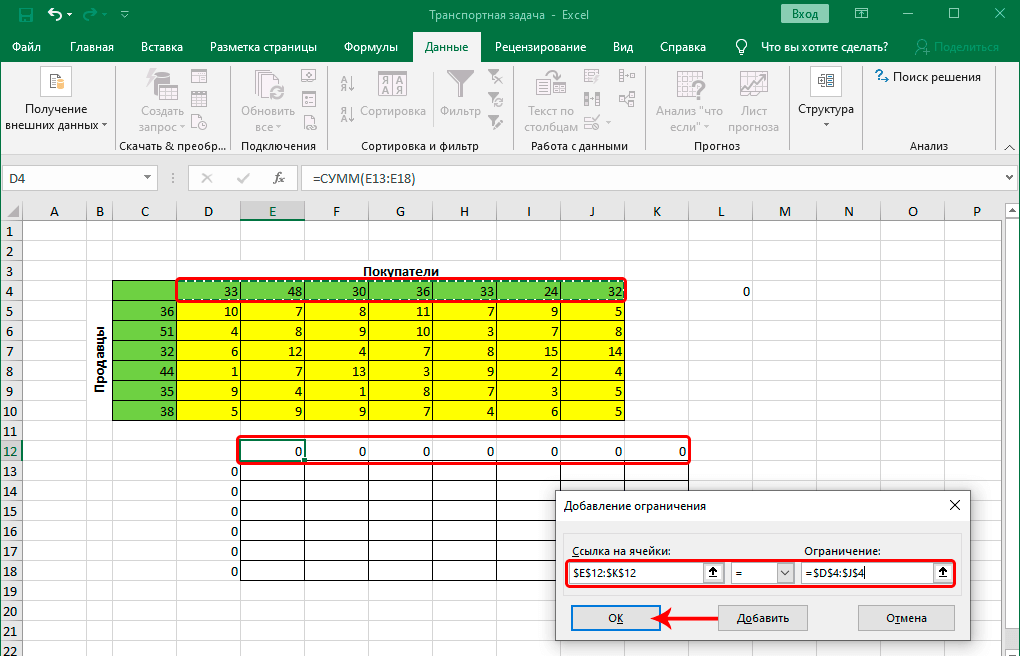
- Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
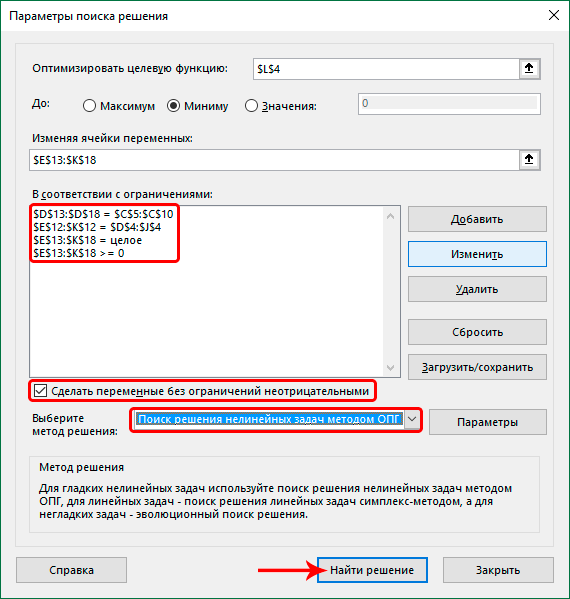
- Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
- больше или равно нулю;
- целое число.
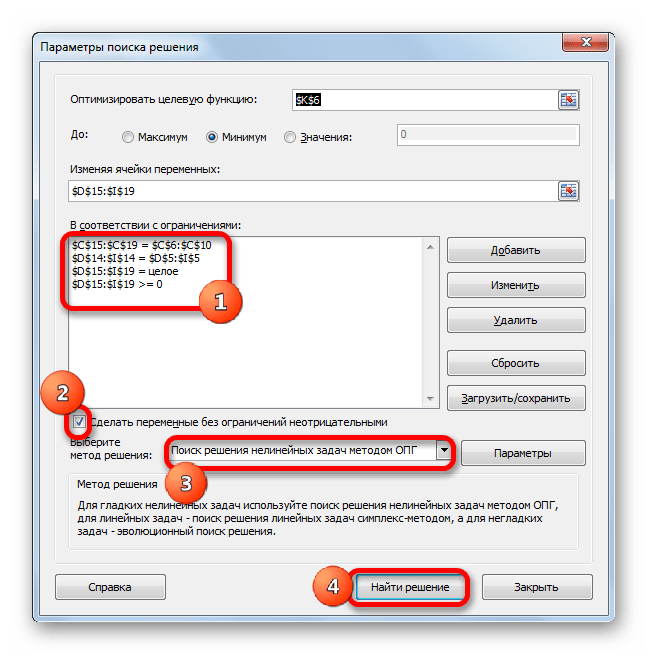
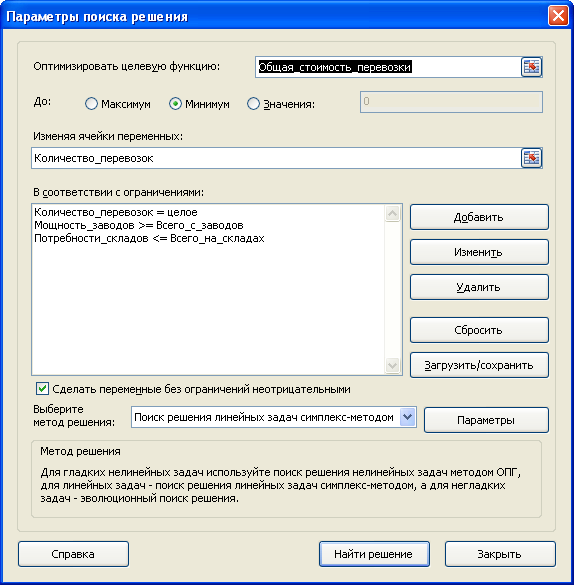
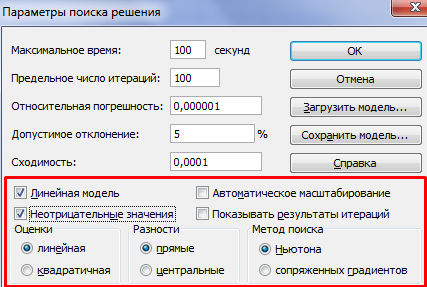
- В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
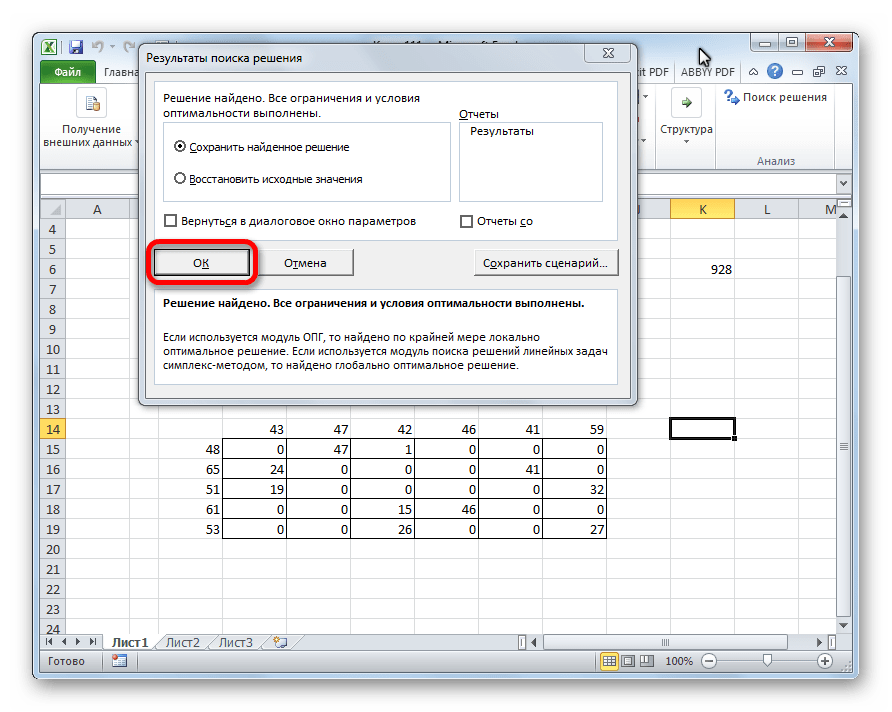
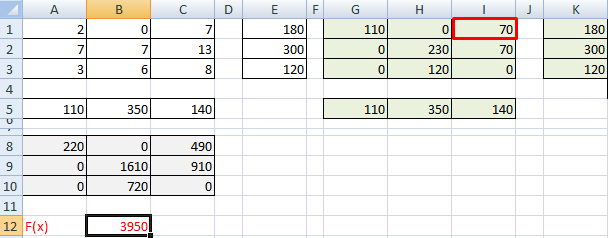
- В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
- Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.
Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
- в виде схемы;
- в виде матрицы.
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
- открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
- закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
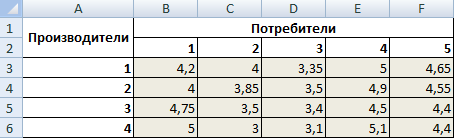
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 |
Задача: минимизировать транспортные расходы по перевозке продукции.
- Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
- Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
- Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
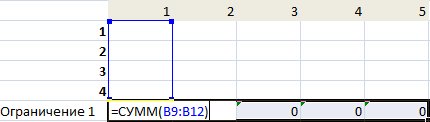
- Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
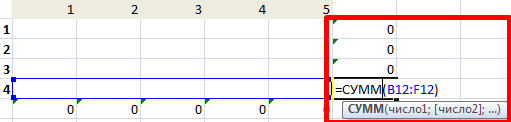
- Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
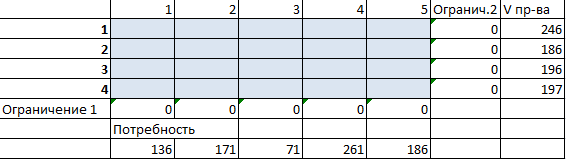
- Вносим известные значения потребности в товаре и объема производства.
- Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
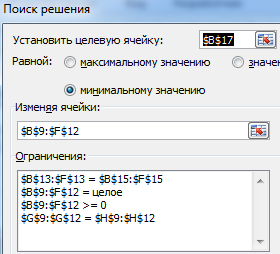
- Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
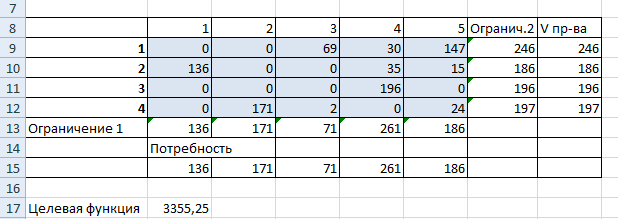
- Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
- суммарный объем производства превышает суммарную потребность в товаре;
- суммарная потребность больше суммы запасов.
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Читайте также по теме: решение транспортной задачи методом потенциалов в Excel.
Содержание
- Общее описание транспортной задачи
- Инструменты для решения транспортной задачи в Эксель
- Пример решения транспортной задачи в Excel
- Условия задачи
- Решение задачи
- Вопросы и ответы
Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.
Общее описание транспортной задачи
Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.
Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.
Инструменты для решения транспортной задачи в Эксель
Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.
- Делаем перемещение во вкладку «Файл».
- Кликаем по подразделу «Параметры».
- В новом окне переходим по надписи «Надстройки».
- В блоке «Управление», который находится внизу открывшегося окна, в выпадающем списке останавливаем выбор на пункте «Надстройки Excel». Делаем клик по кнопке «Перейти…».
- Запускается окно активации надстроек. Устанавливаем флажок возле пункта «Поиск решения». Кликаем по кнопке «OK».
- Вследствие этих действий во вкладке «Данные» в блоке настроек «Анализ» на ленте появится кнопка «Поиск решения». Она нам и понадобится при поиске решения транспортной задачи.
Урок: функция «Поиск решения» в Экселе
Теперь давайте разберем конкретный пример решения транспортной задачи.
Условия задачи
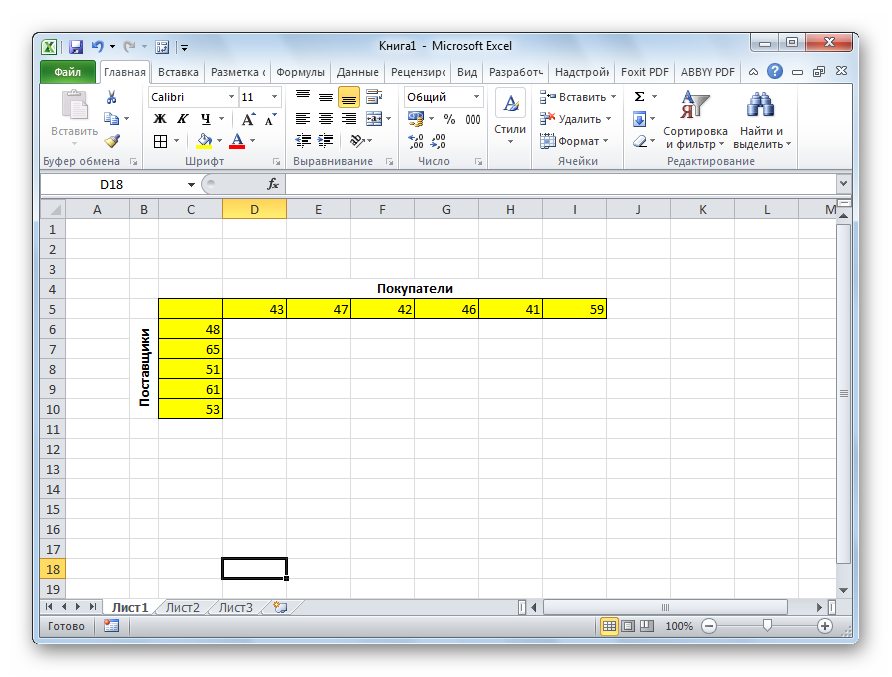
Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.
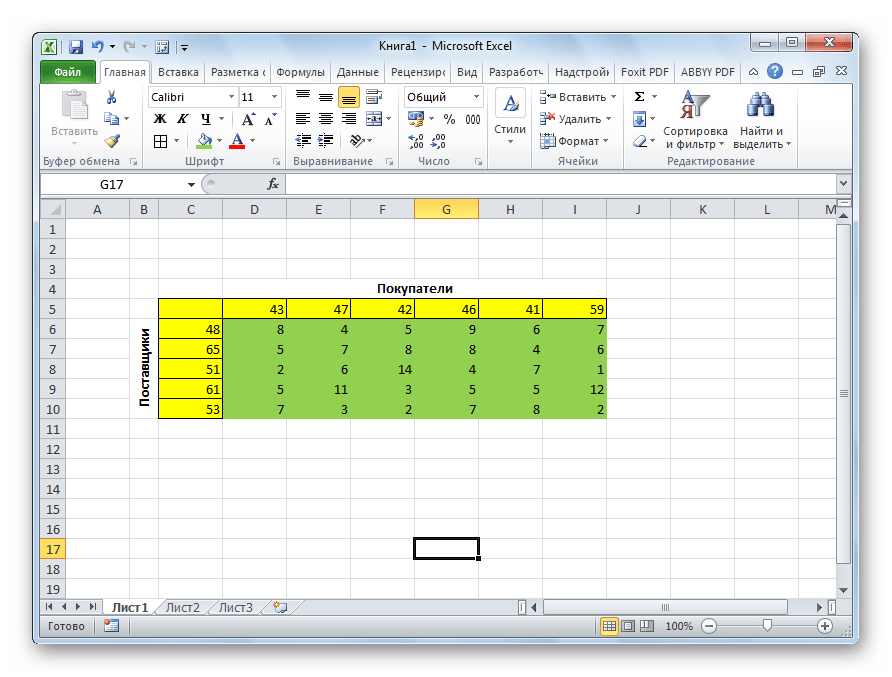
Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.
Решение задачи
Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.
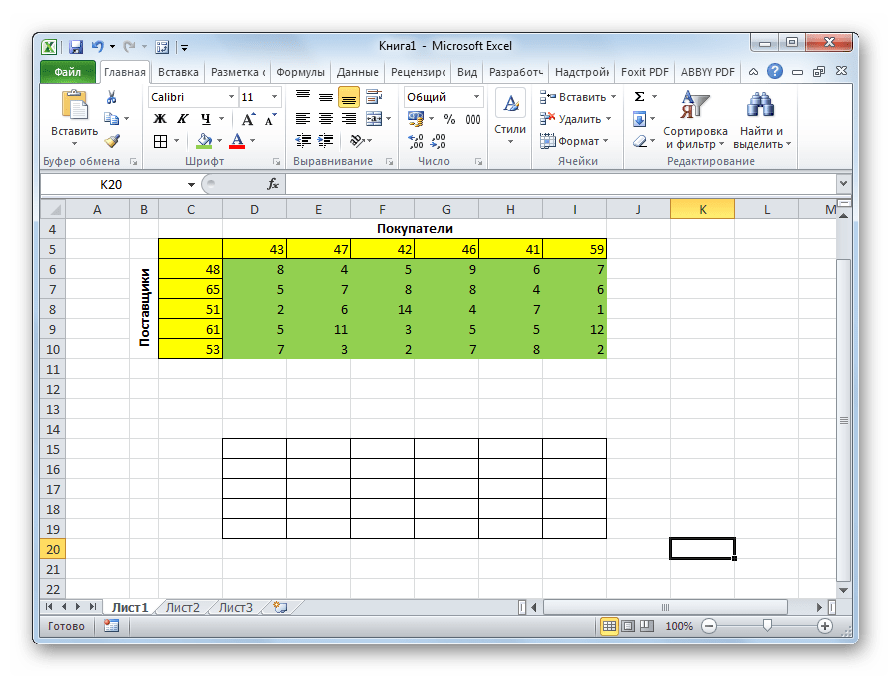
- Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.
- Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.
- Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».
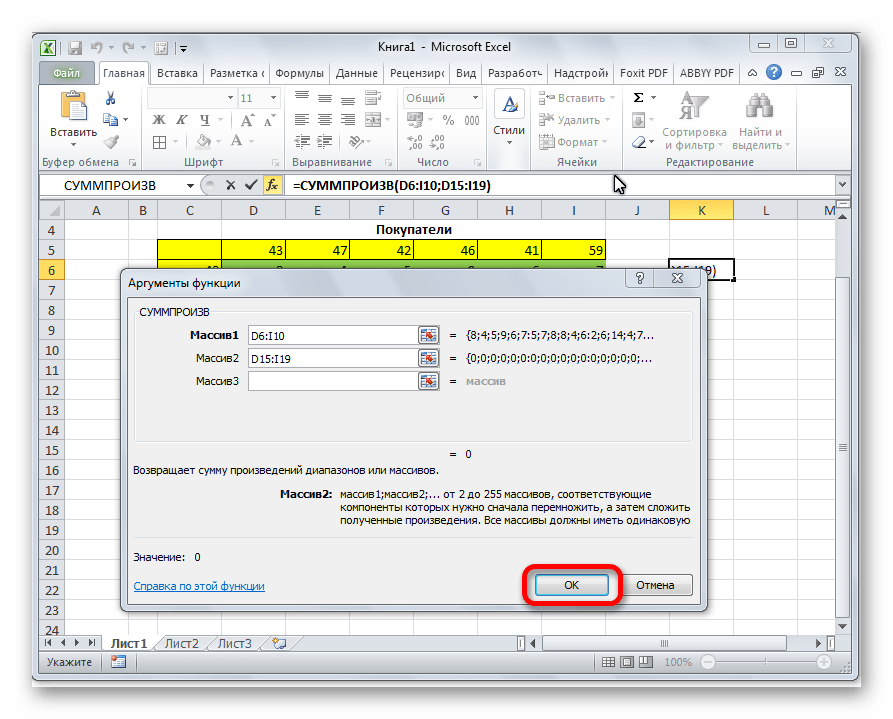
- Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».
- Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».
- Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.
- Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».
- Копируем маркером заполнения формулу на всю строку.
- Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».
- Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.
- Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».
- Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».
- После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».
Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.
Еще статьи по данной теме:
Помогла ли Вам статья?
Содержание
- Решение транспортных задач ЛП в Excel
- Как решить транспортную задачу в Excel
- Алгоритм решения ТЗ в Эксель
- Транспортные задачи: примеры в Excel
- Транспортная задача в Microsoft Excel
- Общее описание транспортной задачи
- Инструменты для решения транспортной задачи в Эксель
- Пример решения транспортной задачи в Excel
- Условия задачи
- Решение задачи
- Решение транспортной задачи в Excel с примером и описанием
- Виды транспортных задач
- Пример решения транспортной задачи в Excel
- Решение открытой транспортной задачи в Excel
Решение транспортных задач ЛП в Excel
На этой странице разберем подробные решения транспортной задачи (алгоритм и примеры разных типов) с использованием пакета электронных таблиц MS Excel (надстройка Поиск решения).
Как решить транспортную задачу в Excel
Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).
Использовать можно любую версию программы — 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).
Алгоритм решения ТЗ в Эксель
- Составить математическую модель транспортной задачи — то есть получить таблицу со стоимостью перевозок, запасами груза у поставщиков и потребностями потребителей (и, возможно, дополнительными ограничениями).
- Если задача открытая (несбалансированная), то добавить потребителя или поставщика с нулевыми тарифами перевозки.
- Внести на лист таблицы Excel данную модель в виде матрицы тарифов (затрат).
- Создать рядом на листе еще одну таблицу, где будут выводиться искомые перевозки (такой же размерности, что и таблица тарифов). Просуммировать перевозки по строкам и столбцам (чтобы сравнивать с аналогичными ячейками — предельными ограничениями задачи — запасами поставщиков и потребностями потребителей).
- Ввести в ячейку формулу, подсчитывающую суммарную стоимость перевозок (это число мы должны минимизировать по смыслу транспортной задачи)
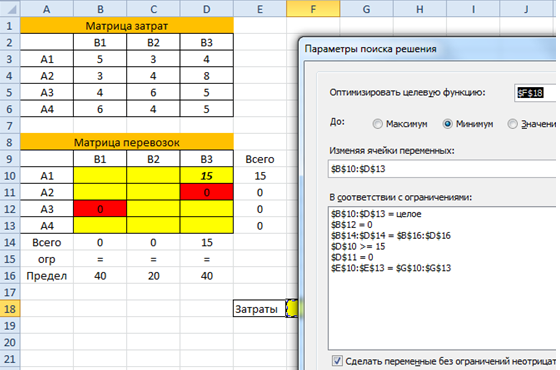
В режиме формул таблица будет выглядеть так: - Запустить надстройку Поиск решения и указать а) ячейку, которую мы минимизируем, б) все ограничения на запасы поставщиков и потребности потребителей, в) дополнительные ограничения (иногда бывают запреты перевозок или требования по минимальному объему груза между определенными пунктами, как в данном случае).
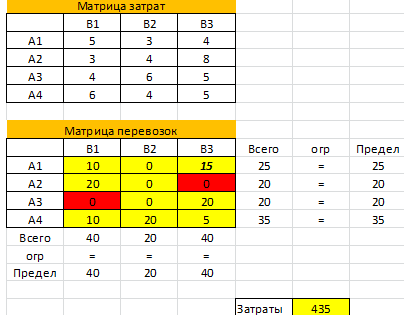
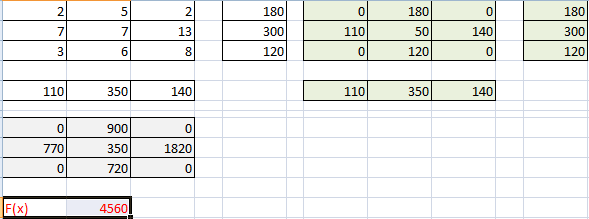
- Получить решение транспортной задачи: в целевой ячейке вы увидите минимальную стоимость перевозок (в примере 435), а в таблице перевозок — искомые значения объема перевозимого груза (см. желтые ячейки).
- Проанализировать решение, если требуется и записать более подробно, например
Минимальные затраты на перевозку составят 435. План перевозок:
Из 1 карьера 10 тонн везем на 1-й участок, 15 тонн на 3-й.
Из 2 карьера 20 тонн везем на 1-й участок.
Из 3 карьера 20 тонн везем на 3-й.
Из 4 карьера 10 тонн везем на 1-й участок, 20 тонн на 2-й, 5 тонн на 3-й.
Транспортные задачи: примеры в Excel
Задача 1. Решить транспортную задачу вручную (методом потенциалов) и в программе Эксель.
Задача 2. Исходные данные задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху — мощности потребителей.
Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя Поиск решений.
Задача 3. Имеется 3 нефтеперерабатывающих завода, 4 спиртовых завода, 3 завода по производству синтетического каучука.
Схема кооперационных связей (см. файл).
Далее приведены производственные показатели предприятий.
Также заданы расстояния между предприятиями.
Необходимо найти решение транспортной задачи с ориентацией на спрос СК и минимизацией транспортных суммарных затрат.
Задача 4. Используя метод потенциалов, решить транспортную задачу. Выполнить проверку, используя табличный редактор Microsoft Excel Компания владеет тремя заводами А1, А2, А3. Соответствующие объемы производства равны 600, 300 и 330 единиц продукции. Компания обязалась поставить в города В1, В2, В3 и В4 соответственно 350, 350, 230 и 300 единиц. При заданных в таблице стоимостях перевозок единицы продукции составьте план ее распределения, чтобы общая стоимость перевозок была наименьшей.
Задача 5. Свести задачу к виду ТЗ и решить с помощью надстройки «Поиск решения»
Четыре ремонтные мастерские могут за год отремонтировать соответственно 400, 500, 450 и 550 машин при себестоимости ремонта одной машины в 500, 700, 650 и 600 рублей. Планируется годовая потребность в ремонте пяти автобаз: 550, 350, 300, 375 и 400 машин.
Ремонт машин с 1 автобазы должен осуществляться в 100% случаев силами ремонтных мастерских.
На 4 АБ возможно самостоятельное проведение ремонтных работ (бесплатное) в объеме, не превышающем 8% от планируемой годовой потребности этой мастерской. Платное (на стороне) — совсем не возможно.
Вторая, третья и пятая АБ могут «ремонтироваться» на стороне, стоимость ремонта +трансп.расходы каждой машины в таком случае составит 695 руб.
Дана матрица, характеризующая транспортные расходы на доставку машины с j-й автобазы в i-ю ремонтную мастерскую. Определить минимальную годовую потребность в кредитах на выполнение указанного объема работ по всем автобазам
Источник
Транспортная задача в Microsoft Excel
Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.
Общее описание транспортной задачи
Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.
Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.
Инструменты для решения транспортной задачи в Эксель
Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.
- Делаем перемещение во вкладку «Файл».
- Кликаем по подразделу «Параметры».
Пример решения транспортной задачи в Excel
Теперь давайте разберем конкретный пример решения транспортной задачи.
Условия задачи
Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.
Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.
Решение задачи
Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.
- Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.
- Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.
- Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».
- Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».
- Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».
- Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.
- Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».
- Копируем маркером заполнения формулу на всю строку.
- Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».
- Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.
- Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».
- Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».
- После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».
Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.
Источник
Решение транспортной задачи в Excel с примером и описанием
Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
- открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
- закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 |
Задача: минимизировать транспортные расходы по перевозке продукции.
- Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
- Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
- Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
- Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
- Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
- Вносим известные значения потребности в товаре и объема производства.
- Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
- Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
- Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
- суммарный объем производства превышает суммарную потребность в товаре;
- суммарная потребность больше суммы запасов.
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Источник
При
решении транспортной задачи в EXCEL
задача должна быть предварительно
сбалансирована.
1.
Ввод
данных. Вводим
данные табл. 1 и 2 в ячейки EXCEL
(рис. 5.1).
В
ячейках ВЗ:Е5 введены стоимости перевозок
(табл. 1).
В
ячейках F3:F5
находится число прибывающих туристов,
а в ячейках В6:Е6 находится число мест в
отелях. Ячейки В8:Е10 — рабочие (изменяемые)
ячейки, в которых будут вычисляться
значения переменных задачи Xij
В
ячейках F8:F10
нужно записать формулы для вычисления
левых частей ограничений (3) – (5):
в
F8
должна быть сумма ячеек В8:Е8;
в
F9
должна быть сумма ячеек В9:Е9;
в
F10
должна быть сумма ячеек В10:Е10.
Формулы
для вычисления левых частей ограничений
(6) – (9) введем в ячейки В11:Е11:
в
В11 должна быть сумма ячеек В8:В10;
в
СП должна быть сумма ячеек С8:С10;
в
D11
должна быть сумма ячеек D8:D10;
в
Е11 должна быть сумма ячеек Е8:Е10;
Целевую
функцию поместим в ячейку G3:
G3:СУММПРОИЗВ
(ВЗ:Е5; В8:Е10). Для этого во вкладке «Формулы»
найдем «Математические», а среди них
выберем «СУММПРОИЗВ». Отметим необходимые
ячейки.
Таблица
исходных данных имеет вид (рис. 5.1):
Рис.
5.1. Исходные данные для решения задачи
-
Заполнение окна процедуры «Поиск решения».
Во
вкладке «Данные» найдем «Поиск решения».
Если команда «Поиск решения» отсутствует,
необходимо загрузить настройку «Поиск
решения». На вкладке «Файл»
выберите команду «Параметры»,
а затем — категорию «Надстройки».
В поле «Управление»
выберите значение «Надстройки
Excel»
и нажмите кнопку «Перейти».
В поле «Доступные
надстройки»
установите флажок рядом с пунктом «Поиск
решения»
и нажмите кнопку ОК.
В
появившемся окне (рис. 3) нужно установить
адрес целевой ячейки G3,
содержащую формулу для вычисления
целевой функции, установитьи другие
ограничения:
Целевая
функция: G3.
Значение
целевой функции: min.
Изменяемые
ячейки: В8:Е10.
Ограничения
задачи:
F8:F10
= F3:F5
(формулы (3) – (5));
В11:Е11
= В6:Е6 (формулы (6) – (9));
В8:Е10
> 0 (1) и В8:Е10 – целые числа (2).
Чтобы
ввести ограничения задачи, нужно нажать
кнопку «Добавить». В появившемся
диалоговом окне (рис. 5.2) слева ввести
адрес F8:F10,
затем выбрать знак = и в правой части
ввести F3:F5.
После ввода нажать кнопку «Добавить»
и аналогично ввести другие ограничения.
Рис.
5.2. Диалоговое окно для ввода ограничений
В
окне «Параметры» установить «Поиск
решения линейных задач симплекс-методом».
Результаты заполнения окна показаны
на рис. 5.3.
Рис.
5.3. Окно процедуры «Поиск решения»
Выполнив
процедуру «Поиск решения», получим
следующие результаты (рис. 5.4).
Рис.
5.4. Результаты решения транспортной
задачи
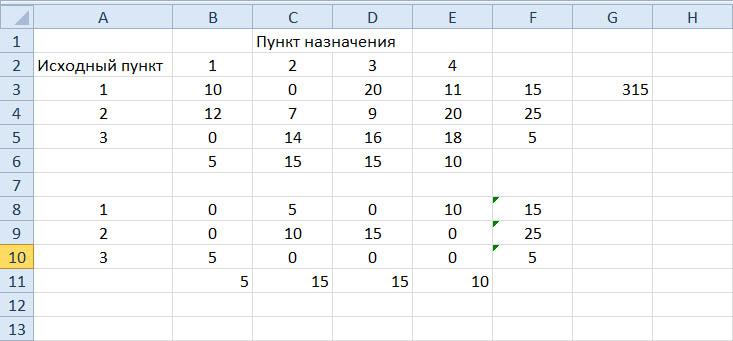
Таким
образом, с железнодорожного вокзала
(исходный пункт 1) следует
10 туристов отвезти в отель «Уютный»
(пункт 4) и 5 туристов в отель «Солнечный»
(пункт назначения 2); из аэропорта
(исходный пункт 2) 10
туристов отвезти в отель «Солнечный»
(пункт назначения 2) и 15 туристов
в отель «Слава» (пункт назначения 3);
туристов прибывающих на морской
вокзал (исходный пункт 3) нужно отправить
в отель «Морской» (пункт
назначения 1). Все эти результаты видны
в конечной таблице (рис.
4). При этом суммарная стоимость
транспортных расходов составит
315 тыс. руб. (ячейка G3).
Варианты
для самостоятельного решения
Задание.
Продукция
определенного типа производится в
городах А1,
А2,
А3
и потребляется в городах В1,
В2,
В3,
В4.
В
таблице вашего варианта указаны: объем
производства, спрос, стоимость перевозки
единицы продукции.
-
Составить
оптимальный план перевозки продукции,
при котором стоимость всех перевозок
будет минимальна. -
Предварительно
следует проверить, сбалансирована ли
данная транспортная задача. Если задача
не сбалансирована, то нужно ввести
фиктивных потребителей или производителей,
добавляя к исходной таблице столбцы
или строки. -
Решенную
задачу в распечатанном виде сдать
преподавателю и сделать вывод.
Вариант
1.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
20 |
47 |
31 |
13 |
49 |
|
А2 |
3 |
38 |
44 |
10 |
18 |
|
А3 |
11 |
32 |
46 |
17 |
68 |
|
Спрос |
45 |
30 |
10 |
45 |
Вариант
2.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
47 |
31 |
13 |
45 |
34 |
|
А2 |
20 |
47 |
31 |
13 |
44 |
|
А3 |
4 |
42 |
41 |
2 |
68 |
|
Спрос |
30 |
45 |
41 |
80 |
Вариант
3.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
31 |
13 |
45 |
35 |
48 |
|
А2 |
38 |
44 |
10 |
33 |
48 |
|
А3 |
20 |
47 |
31 |
13 |
44 |
|
Спрос |
40 |
41 |
45 |
44 |
Вариант
4.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
13 |
45 |
35 |
7 |
49 |
|
А2 |
47 |
31 |
13 |
45 |
47 |
|
А3 |
32 |
46 |
17 |
27 |
68 |
|
Спрос |
45 |
80 |
44 |
45 |
Вариант
5.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
45 |
35 |
7 |
43 |
48 |
|
А2 |
44 |
10 |
33 |
46 |
41 |
|
А3 |
42 |
41 |
2 |
38 |
49 |
|
Спрос |
44 |
12 |
88 |
44 |
Вариант
6.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
35 |
7 |
43 |
39 |
45 |
|
А2 |
31 |
13 |
45 |
35 |
33 |
|
А3 |
47 |
31 |
13 |
45 |
19 |
|
Спрос |
6 |
10 |
30 |
41 |
Вариант
7.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
7 |
43 |
39 |
10 |
41 |
|
А2 |
10 |
33 |
46 |
16 |
22 |
|
А3 |
46 |
17 |
27 |
47 |
61 |
|
Спрос |
38 |
30 |
19 |
87 |
Вариант
8.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
43 |
39 |
10 |
40 |
34 |
|
А2 |
13 |
45 |
35 |
7 |
18 |
|
А3 |
41 |
2 |
38 |
44 |
86 |
|
Спрос |
48 |
45 |
5 |
30 |
Вариант
9.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
39 |
10 |
40 |
43 |
26 |
|
А2 |
33 |
46 |
16 |
28 |
18 |
|
А3 |
31 |
13 |
45 |
35 |
58 |
|
Спрос |
15 |
50 |
10 |
2 |
Вариант
10.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
20 |
40 |
43 |
6 |
16 |
|
А2 |
45 |
35 |
7 |
43 |
27 |
|
А3 |
17 |
27 |
47 |
23 |
68 |
|
Спрос |
31 |
44 |
24 |
42 |
Вариант
11.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
40 |
43 |
6 |
36 |
15 |
|
А2 |
46 |
16 |
288 |
47 |
39 |
|
А3 |
2 |
38 |
44 |
9 |
71 |
|
Спрос |
50 |
28 |
36 |
1 |
Вариант
12.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
43 |
6 |
36 |
45 |
14 |
|
А2 |
35 |
7 |
44 |
39 |
48 |
|
А3 |
13 |
45 |
35 |
7 |
22 |
|
Спрос |
23 |
16 |
45 |
10 |
Вариант
13.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
6 |
36 |
45 |
13 |
24 |
|
А2 |
16 |
28 |
47 |
22 |
52 |
|
А3 |
27 |
47 |
23 |
22 |
85 |
|
Спрос |
24 |
18 |
49 |
20 |
Вариант
14.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
36 |
45 |
13 |
31 |
34 |
|
А2 |
7 |
43 |
39 |
10 |
52 |
|
А3 |
38 |
44 |
9 |
34 |
81 |
|
Спрос |
50 |
38 |
49 |
80 |
Вариант
15.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
45 |
13 |
31 |
46 |
42 |
|
А2 |
28 |
47 |
22 |
23 |
47 |
|
А3 |
45 |
35 |
7 |
43 |
72 |
|
Спрос |
30 |
49 |
44 |
88 |
Вариант
16.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
13 |
31 |
46 |
19 |
49 |
|
А2 |
43 |
39 |
10 |
40 |
88 |
|
А3 |
47 |
33 |
22 |
47 |
58 |
|
Спрос |
17 |
48 |
35 |
45 |
Вариант
17.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
31 |
46 |
19 |
26 |
58 |
|
А2 |
47 |
22 |
23 |
47 |
24 |
|
А3 |
44 |
9 |
34 |
46 |
78 |
|
Спрос |
49 |
36 |
21 |
49 |
Вариант
18.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
46 |
19 |
26 |
47 |
54 |
|
А2 |
39 |
10 |
40 |
43 |
19 |
|
А3 |
35 |
7 |
43 |
39 |
44 |
|
Спрос |
36 |
15 |
6 |
50 |
Вариант
19.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
19 |
26 |
47 |
25 |
52 |
|
А2 |
22 |
23 |
47 |
28 |
13 |
|
А3 |
23 |
22 |
47 |
29 |
12 |
|
Спрос |
10 |
19 |
10 |
48 |
Вариант
20.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
26 |
47 |
25 |
20 |
48 |
|
А2 |
10 |
40 |
43 |
6 |
28 |
|
А3 |
9 |
34 |
46 |
15 |
71 |
|
Спрос |
47 |
81 |
25 |
44 |
Вариант
21.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
47 |
25 |
20 |
47 |
41 |
|
А2 |
23 |
47 |
28 |
17 |
41 |
|
А3 |
7 |
43 |
39 |
10 |
79 |
|
Спрос |
40 |
46 |
88 |
37 |
Вариант
22.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
25 |
20 |
47 |
30 |
32 |
|
А2 |
40 |
43 |
6 |
36 |
49 |
|
А3 |
22 |
47 |
29 |
16 |
46 |
|
Спрос |
13 |
50 |
46 |
28 |
Вариант
23.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
20 |
47 |
30 |
14 |
22 |
|
А2 |
47 |
28 |
17 |
46 |
58 |
|
А3 |
34 |
46 |
15 |
29 |
78 |
|
Спрос |
43 |
42 |
50 |
18 |
Вариант
24.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
47 |
30 |
14 |
45 |
10 |
|
А2 |
43 |
6 |
36 |
45 |
61 |
|
А3 |
43 |
39 |
10 |
40 |
60 |
|
Спрос |
44 |
23 |
48 |
6 |
Вариант
25.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
30 |
14 |
45 |
35 |
10 |
|
А2 |
28 |
17 |
46 |
33 |
44 |
|
А3 |
47 |
29 |
16 |
46 |
41 |
|
Спрос |
15 |
43 |
41 |
6 |
Вариант
26.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
14 |
45 |
35 |
7 |
22 |
|
А2 |
3 |
36 |
45 |
13 |
83 |
|
А3 |
46 |
15 |
29 |
47 |
56 |
|
Спрос |
39 |
24 |
30 |
18 |
Вариант
27.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
45 |
35 |
7 |
43 |
83 |
|
А2 |
17 |
46 |
33 |
10 |
18 |
|
А3 |
39 |
10 |
40 |
43 |
82 |
|
Спрос |
47 |
42 |
15 |
29 |
Вариант
28.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
4 |
5 |
6 |
13 |
530 |
|
А2 |
8 |
6 |
3 |
8 |
405 |
|
А3 |
7 |
10 |
4 |
11 |
540 |
|
Спрос |
425 |
415 |
335 |
400 |
Вариант
29.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
3 |
7 |
4 |
8 |
513 |
|
А2 |
9 |
6 |
4 |
4 |
448 |
|
А3 |
6 |
10 |
5 |
8 |
522 |
|
Спрос |
437 |
417 |
333 |
396 |
Вариант
30.
|
Производители |
Потребители |
Объем |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
А1 |
35 |
30 |
10 |
10 |
53 |
|
А2 |
21 |
41 |
53 |
10 |
28 |
|
А3 |
39 |
32 |
27 |
20 |
61 |
|
Спрос |
47 |
38 |
23 |
24 |
Создадим модель для решения Транспортной задачи (Transportation Problem, Shipping Routes). Решение Транспортной задачи позволяет определить самые недорогие маршруты для перевозки товаров от производителей на склад. Расчет будем проводить с помощью надстройки Поиск решения.
Рассмотрим Транспортную задачу на основе примера из файла solvsamp.xls (при установленном MS EXCEL 2010 файл находится в папке C:Program FilesMicrosoft OfficeOffice14SAMPLES).
Вводная статья про
Поиск решения
в MS EXCEL 2010
находится здесь
.
Задача
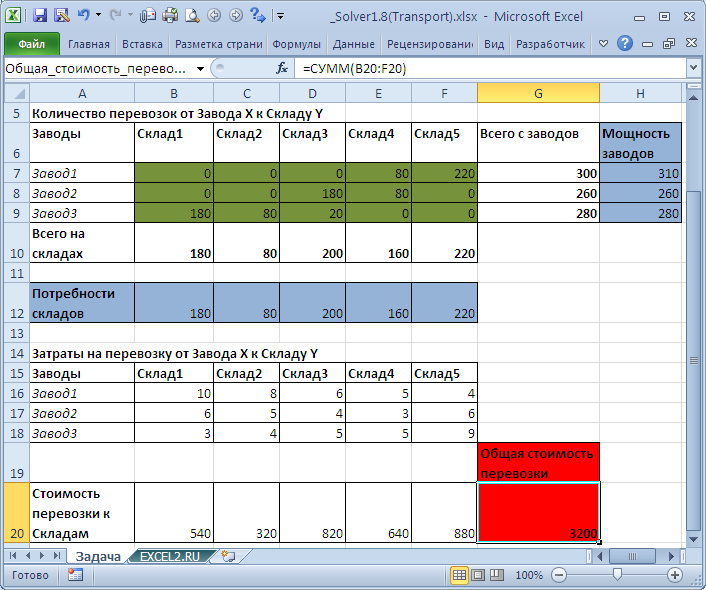
Компания доставляет товары с трех заводов на пять региональных складов. Товары могут доставляться с любого завода на любой склад, однако, очевидно, что стоимость доставки на большее расстояние будет б
о
льшей. Требуется определить объемы перевозок между заводами и складами, в соответствии с потребностями складов и производственными возможностями (мощностями) заводов, при которых транспортные расходы минимальны.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см.
файл примера
).
Переменные (выделено зеленым)
. В качестве переменных модели следует взять объемы перевозок между заводами и складами.
Ограничения
(выделено синим).
Потребности складов должны быть удовлетворены (т.е. суммарные поставки на склад должны быть больше или равны потребности). Суммарные объемы перевозок с завода не должны превосходить его мощности.
Целевая функция (выделено красным)
. Суммарные транспортные расходы должны быть минимальны.
Убедитесь, что метод решения соответствует линейной задаче.
Теперь в диалоговом окне можно нажать кнопку
Найти решение
.
Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.
Общее описание транспортной задачи
Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.
Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.
Инструменты для решения транспортной задачи в Эксель
Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.
-
Делаем перемещение во вкладку «Файл».
Кликаем по подразделу «Параметры».
В блоке «Управление», который находится внизу открывшегося окна, в выпадающем списке останавливаем выбор на пункте «Надстройки Excel». Делаем клик по кнопке «Перейти…».
Запускается окно активации надстроек. Устанавливаем флажок возле пункта «Поиск решения». Кликаем по кнопке «OK».
Пример решения транспортной задачи в Excel
Теперь давайте разберем конкретный пример решения транспортной задачи.
Условия задачи
Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.
Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.
Решение задачи
Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.
-
Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.
Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.
Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».
Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».
Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».
Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.
Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».
Копируем маркером заполнения формулу на всю строку.
Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».
Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.
Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».
Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».
Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Решение транспортной задачи в Excel с примером и описанием
Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
- в виде схемы;
- в виде матрицы.
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
- открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
- закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 |
Задача: минимизировать транспортные расходы по перевозке продукции.
- Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
- Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
- Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
- Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
- Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
- Вносим известные значения потребности в товаре и объема производства.
- Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
- Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
- Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
- суммарный объем производства превышает суммарную потребность в товаре;
- суммарная потребность больше суммы запасов.
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Как решить транспортную задачу в Excel
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
- Закрытая – совокупное предложение продавца равняется общему спросу.
- Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
- Открываем меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
- В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
- В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
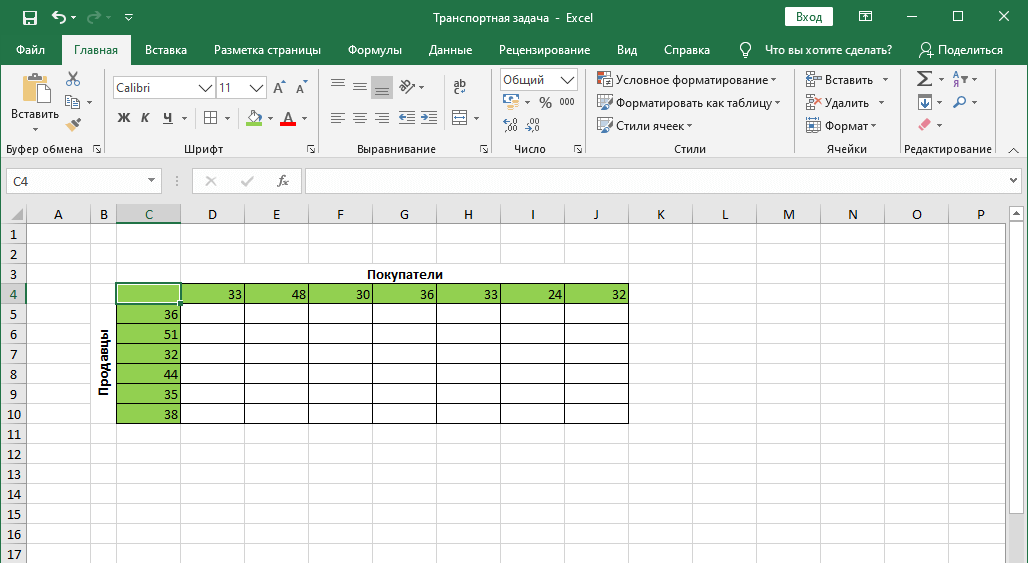
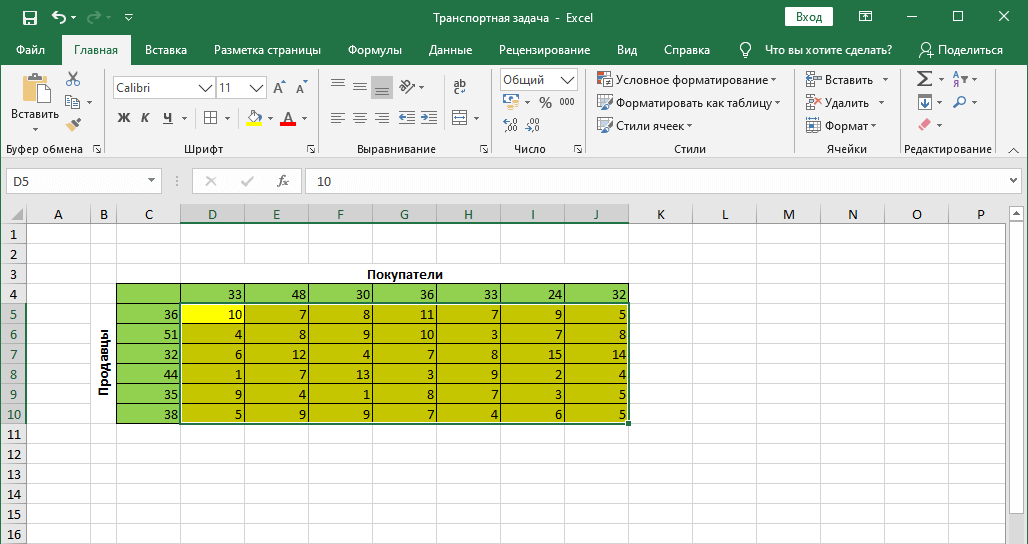
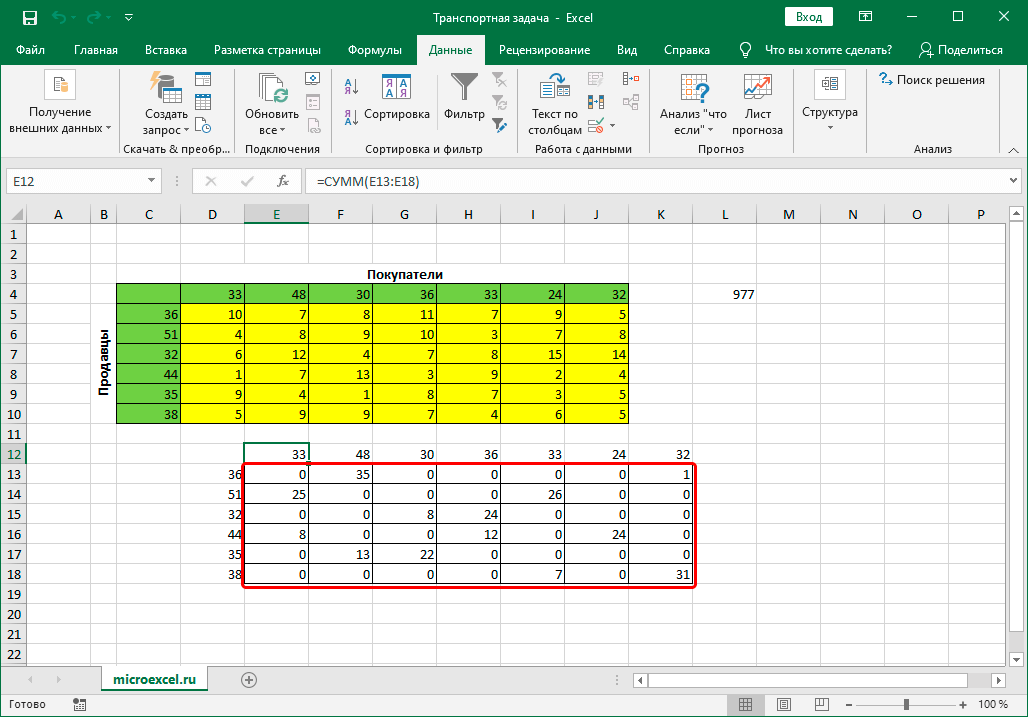
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
-
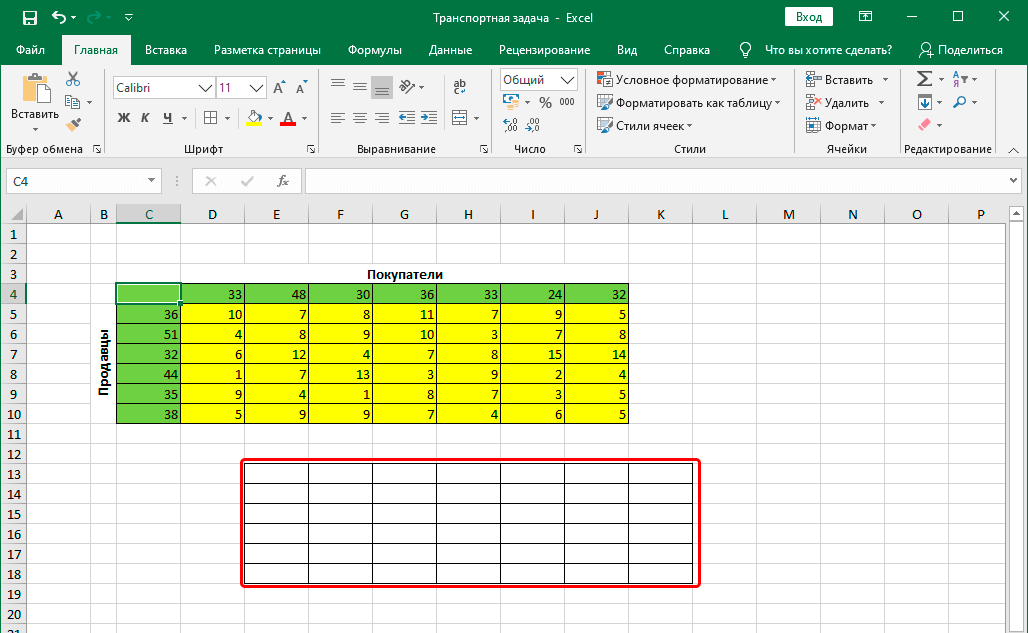
Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.


- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).










- в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
- для параметра “До” выбираем вариант – “Минимум”.
- в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
- нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
- становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
- затем выбираем знак “равно”.
- в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
- щелкаем OK по готовности.

- больше или равно нулю;
- целое число.



Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.
Решение транспортной задачи в Excel (стр. 1 из 3)
§1. Постановка Транспортной задачи (ТЗ) для n переменных
§2. Пример решения Транспортной задачи
§3. Транспортные задачи по различным критериям
§4. Решение транспортной задачи в Excel
Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Классическая транспортная задача – задача о наиболее экономном плане перевозок однородного продукта или взаимозаменяемых продуктов из пунктов производства в пункты потребления, встречается чаще всего в практических приложениях линейного программирования. Линейное программирование является одним из разделов математического программирования – области математики, разрабатывающей теорию и численные методы решения многомерных экстремальных задач с ограничениями.
Огромное количество возможных вариантов перевозок затрудняет получение достаточно экономного плана эмпирическим или экспертным путем. Применение математических методов и вычислительных в планировании перевозок дает большой экономический эффект. Транспортные задачи могут быть решены симплексным методом однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его получить оптимальное решение.
В зависимости от способа представления условий транспортной задачи она может быть представлена в сетевой (схематичной) или матричной (табличной) форме. Транспортная задача может также решаться с ограничениями и без ограничений.
§1. Постановка Транспортной задачи (ТЗ) для n переменных
Пусть имеется несколько поставщиков однородной продукции (каждый с определенным запасом) и несколько потребителей этой продукции (с известными потребностями у каждого). Задана также сеть коммуникаций (дорог, рек, воздушных линий и т.д.) связывающая каждого поставщика с каждым потребителем. На каждой коммуникации задана цена перевозки – стоимость перевозки единицы продукции. Если какая – либо коммуникация отсутствует, то считаем, что она есть, но цену перевозки на ней устанавливаем равной бесконечности (+∞). Это соглашение сделает невыгодным перевозку по ней и автоматически исключит данную коммуникацию из плана перевозок.
Таким образом, требуется составить план перевозок продукции от поставщиков к потребителям так, чтобы потребности потребителей были бы удовлетворены за счет вывоза запаса от поставщиков. Цель – минимизация суммарной стоимости всех перевозок.
Транспортные задачи бывают:
1) открытые m ≠ n (суммарный запас продукции, имеющейся у поставщиков, не совпадает с суммарной потребностью в продукции у потребителей.)
2) закрытые m = n (суммарный запас продукции, имеющейся у поставщиков, совпадает с суммарной потребностью в продукции у потребителей.)
Метод потенциалов «работает» только для закрытых ТЗ, причем, закрытая ТЗ всегда разрешима.
Открытую ТЗ сводят к закрытой ТЗ путем прибавления к суммарному запасу продукции или суммарной потребности продукции недостающих единиц до равенства суммарного запаса продукции и суммарной потребности продукции.
Закрытая транспортная задача формулируется как Задача Линейного Программирования (ЗЛП) следующего вида:
Решение транспортной задачи в Excel
В этом материале попробуем разобраться, как решить транспортную задачу в Excel. Среда решения – Excel. Данный материал подходит для версий программы: 2007, 2010, 2013, 2016.
Постановка задачи и подготовка таблиц
Цель задачи сводится к математическому моделированию минимизации грузопотоков. Довольно часто студенты пишут рефераты на тему поиска решения транспортной задачи. Этот пример можно взять за основу реферата. Рассмотрим решение на конкретном примере.
Задача
В хозяйстве имеются 5 складов минеральных удобрений и 4 пункта, в которые необходимо доставить удобрения. Потребность каждого пункта в удобрениях различна, а так же запасы на каждом складе ограничены. Требуется определить, с какого склада, в какой пункт поставлять, сколько удобрений для минимализации грузооборота перевозок.
Наличие минеральных удобрений (либо иной продукции) на складах.
| Склады | Наличие удобрений, т. |
| Склад № 1 | 200 |
| Склад № 2 | 190 |
| Склад № 3 | 220 |
| Склад № 4 | 145 |
| Склад № 5 | 280 |
Потребность в минеральных удобрениях на различных пунктах.
| Пункты | Потребность в удобрениях |
| 1 пункт | 200 |
| 2 пункт | 150 |
| 3 пункт | 220 |
| 4 пункт | 330 |
Расстояние между складами и пунктами доставки
| Пункт 1 | Пункт 2 | Пункт 3 | Пункт 4 | |
| Склад № 1 | 6 | 4 | 5 | 11 |
| Склад № 2 | 12 | 6 | 4 | |
| Склад № 3 | 15 | 7 | 10 | 4 |
| Склад № 4 | 9 | 5 | 12 | 5 |
| Склад № 5 | 3 | 7 | 12 | 11 |
Данные в таблицах. На пересечении столбца конкретного пункта доставки со строкой склада находится информация о расстоянии между этим пунктом доставки и складом. Например, расстояние между 3 пунктом и складом № 3 равно 10 километрам.
Пошаговое решение в Excel
Подготовим таблицы для решения задачи.
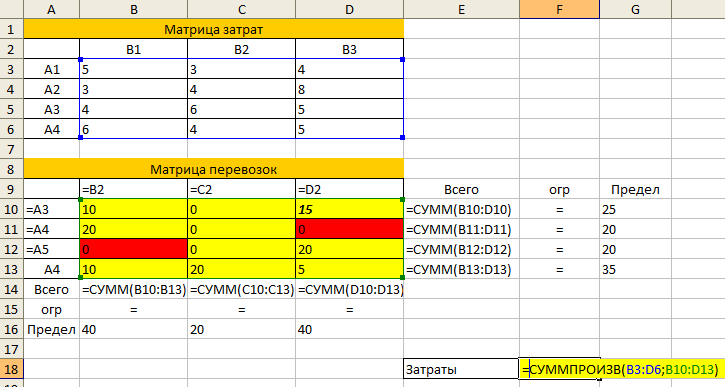
Значения ячеек в столбце B с третьей по седьмую определяют сумму значения соответствующих строк со столбца C до столбца F.
Например, значение ячейки B3=СУММ(C4:F4)
Аналогично значения в восьмой строке, складываются из суммы соответствующих столбцов. Далее создадим еще одну таблицу.
В строке 16 по столбцам C-F определим грузооборот по каждому пункты доставки. Например, для пункта 1 (ячейка С16) это рассчитывается по формуле:
Либо, это можно рассчитать с помощью функции СУММПРОИЗВ:
В ячейке B4 находится количество минеральных удобрений, перевозимых со склада № 1 в 1 пункт доставки, а в ячейке C11 — расстояние от склада №1 до 1 пункта доставки. Соответственно первое слагаемое в формуле означает полный грузооборот по данному маршруту. Вся же формула вычисляет полный грузооборот перевозок минеральных удобрений в 1 пункт доставки.
В ячейке B16 по формуле =СУММ(C16:F16) будет вычисляться общий объем грузооборота минеральных удобрений. Рабочий лист примет следующий вид.
Для решения транспортной задачи воспользуемся процедурой Поиск решения, которая находится на вкладке Данные. Если у вас нет процедуры Поиск решения, необходимо зайти в Параметры Excel -> Надстройки — > Поиск решения.
После выбора данной процедуры на вкладке Данные откроется диалоговое окно.
Выберем целевую ячейку $B$16, установим ее равной минимальному значению, что бы минимизировать значение конечной ячейки, путем изменения влияющих ячеек, изменяя ячейки, выберем диапазон с единицами $C$3:$F$7.
Если запустить процесс, то мы получим параметры равные нулям. Для получения необходимых значений установим некоторые ограничения:
- $B$3:$B$7 = 0
- $C$8:$F$8 >= $C$10:$F$10
После всех установок нажмем «Выполнить» и получаем результат.
Решение транспортной задачи методом потенциалов в Excel с примером
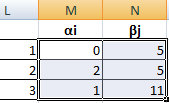
Решим транспортную задачу методом потенциалов. Нам известны торговые запасы, потребительские запросы и стоимость доставки за единицу продукции. Сделаем три исходные таблицы.
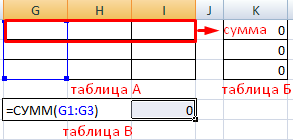
Построим опорный план транспортной задачи с помощью инструмента «Поиск решений». Рядом составим такие же по объему таблицы с пустыми ячейками. Таблица А – аналог стоимостной, Б – «запасов», В – «спроса».
Элементы таблицы Б – сумма соответствующих строк в таблице А. Элементы таблицы В – сумма соответствующих столбцов в таблице А.
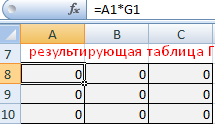
Отдельно составим результирующую таблицу Г. В ней отразятся оптимальные транспортные расходы. Каждый элемент таблицы Г – произведение элемента А и соответствующего элемента стоимостной таблицы.
В отдельном месте листа введем формулу функции: =СУММПРОИЗВ(A1:C3;G1:I3)
Первый массив – стоимостная таблица, второй – диапазон А.
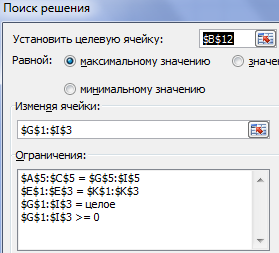
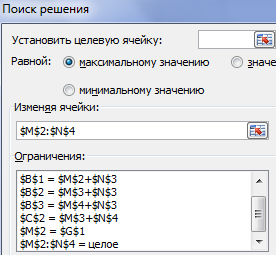
Ставим курсор в ячейку со значением функции. Вызываем инструмент «Поиск решения». Заполняем диалоговое окно:
- Целевая ячейка – ссылка на ячейку со значением функции.
- Она должна быть равна «максимальному значению», как наиболее выгодному для перевозчика.
- Команда изменяет значения ячеек в таблице А. Значения – целые числа.
- Диапазон таблицы Б = «Запасам».
- Диапазон В = «Потребительскому спросу».
В открытом диалоговом окне нажимаем кнопку «Параметры» и устанавливаем следующие настройки:
Жмем ОК – «Выполнить». Получаем опорный план транспортной задачи:
Он залит бледно-зеленым цветом. Ячейки со значениями выше нуля называются «базисными», «занятыми». Ячейки со значением 0 – «свободными».
Далее действуем по плану:
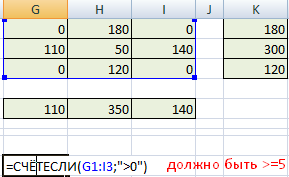
Посчитаем число занятых клеток с помощью функции СЧЕТЕСЛИ.
Так как результат равен 5, опорный план является не вырожденным. Проверим оптимальность опорного плана – найдем потенциалы по занятым клеткам.
Нужно составить систему уравнений. Предполагается, что αj = 0, а αi + βj = сij (стоимость доставки единицы груза). Вызываем команду «Поиск решения». Вносим условия системы уравнений в качестве ограничений.
Заполненное диалоговое окно:
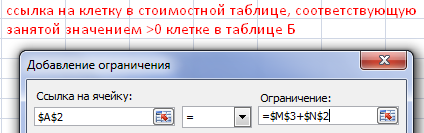
Результат работы инструмента «Поиск решения»:
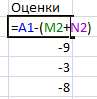
Посчитаем оценки свободных клеток. Формула: сij – (αi + βj). Берем свободную клетку из таблицы А. Смотрим ее значение в стоимостной таблице. Это будет сij. Далее смотрим, какие потенциалы соответствуют данной клетке. Вставляем их значения в формулу.
В программе Excel найдем оценки с помощью математических операторов и ссылок на соответствующие ячейки.
План считается оптимальным, если оценки больше или равны 0. В нашем случае получились отрицательные значения – план не является оптимальным. Поэтому двигаемся дальше.
Находим, какой клетке в таблице А соответствует минимальная оценка. Строим для этой клетки цикл – замкнутую ломаную линию. Условия: обязательно чередование вертикального и горизонтального направления, только по базисным клеткам.
В исходной клетке (с минимальной оценкой) ставим знак «+». Далее чередуем: «-», «+» и т.д.
В таблице стоимости находим минимальное значение со знаком «-».
В нашем примере – это «5», ячейка В1. Эту клетку нужно убрать из базиса. А ячейку с минимальной оценкой сделать базисной.
С учетом изменившихся данных вновь строим опорный план транспортной задачи. Применяем инструмент «Поиск решения». Пересчитанный план перевозок выглядит так:
Обратите внимание: ячейка I1 (где была минимальная оценка) стала базисной, занятой.
Проводим те же расчеты для нового плана (с пункта №1): находим потенциалы, оценки свободных клеток для проверки оптимальности. И так до тех пор, пока оценки свободных клеток не будут больше или равны 0.
Excel – очень функциональная программа. Она может использоваться для решения огромного пласта задач, с которыми приходится сталкиваться в бизнесе. Одна из самых распространённых – транспортная задача. Представим, что нам нужно понять, какой способ перевозки от производителя к конечному покупателю самый оптимальный по затратам времени, денег и других ресурсов. Эта проблема довольно популярная, независимо от того, в какой сфере работает бизнес. Поэтому давайте более подробно разберемся, как её реализовать с помощью Excel.
Содержание
- Описание транспортной задачи
- Как включить функцию “Поиск решения” в Excel
- Пример решения транспортной задачи в Excel
- Условия задачи
- Решение – пошаговый алгоритм
- Заключение
Описание транспортной задачи
Итак, у нас есть два контрагента, которые постоянно взаимодействуют друг с другом. В нашем случае это покупатель и продавец. Нам нужно посчитать, как перевозить товары таким образом, чтобы издержки были минимальны. Для этого нужно представить все данные в схематической или матричной форме. В Эксель используем последний вариант. В целом, выделяют два типа транспортных задач:
- Закрытые. В этом случае спрос и предложение находятся в балансе.
- Открытые. Здесь нет равенства между спросом и предложением. Чтобы получить решение этой задачи, нужно сперва ее привести к первому типу, уравняв спрос и предложение. Для этого нужно ввести дополнительный показатель – наличие условного покупателя или продавца. Кроме этого, нужно внести определенные изменения в таблицу издержек.
Как включить функцию “Поиск решения” в Excel
Для решения транспортных задач в Excel существует специальная функция, которая называется «Поиск решения». Она не активирована по умолчанию, поэтому нужно сделать следующие шаги:
- Открыть меню «Файл», которое находится в левом верхнем углу окна программы.
- После этого нажимаем на кнопку с параметрами.
- Далее находим подраздел «Настройки» и переходим в меню управления надстройками. Это маленькие программы, которые выполняются в рамках среды Microsoft Excel. Видим, что сначала мы нажали на меню «Надстройки», а потом в правой части внизу выставили пункт «Надстройки Excel» и нажали на кнопку «Перейти». Все нужные действия выделены красными прямоугольниками и стрелочками.
- Далее включаем надстройку «Поиск решения», после чего подтверждаем свои действия нажатием клавиши ОК. Исходя из описания настройки, мы видим, что она предназначена для анализа сложных данных, таких как научные и финансовые.
- После этого переходим во вкладку «Данные», где видим новую кнопку, которая называется так же, как и надстройка. Ее можно найти в группе инструментов «Анализ».
Осталось только кликнуть по этой кнопке, и мы переходим к решению транспортной задачи. Но перед этим следует немного подробнее поговорить про инструмент «Поиск решения» в Excel. Это специальное дополнение Эксель, которое дает возможность находить самое быстрое решение задачи. Характерная особенность – учет ограничений, которые пользователь задает на этапе подготовки. Если говорить простым языком, это подпрограмма, дающая возможность определить самый лучший способ достижения определенной задачи. К таким задачам могут относиться следующие:
- Инвестирование, загрузка склада или любая другая подобная деятельность. В том числе, и доставка товара.
- Лучший способ. Сюда входят такие задачи, как достижение максимальной прибыли при минимальных издержках, способы достижения самого лучшего качества при имеющихся ресурсах и так далее.
Кроме транспортных задач, эта надстройка используется и для таких целей:
- Разработка плана производства. То есть, сколько нужно выработать единиц товара, чтобы достичь максимального дохода.
- Найти распределение рабочих сил по разным видам работ, чтобы суммарные затраты на производство товара или услуг были самыми маленькими.
- Установить, сколько минимально времени понадобится на то, чтобы выполнить все работы.
Как видим, задачи бывают самыми разными. Универсальное правило применения этой надстройки – необходимо перед решением задачи создать модель, которая бы соответствовала ключевым характеристикам поставленной проблемы. Моделью является совокупность функций, которые используют переменные в качестве своих аргументов. То есть, значения, которые могут изменяться.
Важно учесть, что оптимизация набора значений осуществляется исключительно по одному показателю, который называется целевой функцией.
Надстройка «Поиск решения» осуществляет перебор разных значений переменных, которые передаются целевой функции таким образом, чтобы она была максимальной, минимальной или равной определенному значению (именно это и является ограничением). Есть еще одна функция, которая несколько похожая по своему принципу действия, и какую нередко путают с «Поиском решения». Называется она «Подбор параметра». Но если копнуть более глубоко, то разница между ними колоссальная:
- Функция «Подбор параметра» не работает больше, чем с одной переменной.
- Она не предусматривает возможности задавать ограничения для переменных.
- Способна определять только равенство целевой функции определенному значению, но не дает возможности находить максимум и минимум. Поэтому для нашей задачи она не подходит.
- Способна эффективно вычислять лишь если модельно линейного типа. Если модель нелинейная, то она находит значение, которое наиболее близкое к изначальному.
Транспортная задача по своей структуре значительно сложнее, поэтому надстройки «Подбор параметра» для этого недостаточно. Давайте разберемся более детально, как реализовать на практике функцию «Поиск решения» на примере транспортной задачи.
Пример решения транспортной задачи в Excel
Для того, чтобы наглядно продемонстрировать, как на практике решать транспортные задачи в Excel, давайте приведем пример.
Условия задачи
Предположим, у нас есть 6 продавцов и 7 покупателей. Спрос и предложение между ними распространяется соответственно следующим способом: 36, 51, 32, 44, 35 и 38 единиц – продавцы и 33, 48, 30, 36, 33, 24 и 32 единицы – покупатели. Если просуммировать все эти значения, то обнаружится, что спрос и предложение находятся в балансе. Следовательно, эта задача закрытого типа, которая решается очень просто.
Кроме этого, у нас есть информация о том, сколько нужно потратить на перевозку из пункта А в пункт Б (они на примере выделены желтыми ячейками).
Решение – пошаговый алгоритм
Теперь, после того, как мы ознакомились с таблицами с исходными данными, можем воспользоваться следующим алгоритмом, чтобы решить эту задачу:
- Сперва делаем таблицу, состоящую из 6 строк и 7 колонок.
- После этого переходим в какую-угодно ячейку, не содержащую никаких значений и при этом лежащую за пределами новосозданной таблицы и вставляем функцию. Для этого нажимаем на кнопку fx, которая находится слева от строки ввода функции.
- У нас появляется окно, в котором нам нужно выбрать категорию «Математические». А какая функция нас интересует? Та, которая выделена на этом скриншоте. Функция СУММИПРОИЗВ умножает диапазоны или массивы между собой и суммирует их. Как раз то, что нам нужно. После этого нажимаем клавишу ОК.
- Далее на экране появится окно, в котором необходимо указать параметры функции. Они следующие:
- Массив 1. Это первый аргумент, в котором записываем тот диапазон, который выделен жёлтым цветом. Задать параметры функции можно как используя клавиатуру, так и выделив соответствующую область с помощью левой кнопки мыши.
- Массив 2. Это второй аргумент, в качестве которого выступает новосозданная таблица. Действия выполняются аналогичным образом.
Подтверждаем свое действие нажатием клавиши ОК.
- После этого делаем левый клик мыши по той ячейке, которая служит верхней левой в новосозданной таблице. Теперь снова нажимаем кнопку вставки функции.
- Выбираем ту же категорию, что и в предыдущем случае. Но на этот раз нас интересует функция СУММ.
- Теперь наступил этап заполнения аргументов. В качестве первого аргумента записываем верхнюю строку таблицы, которую мы создали в начале. Точно так же, как и раньше, это можно сделать путем выделения этих ячеек на листе, так и вручную. Подтверждаем свои действия нажатием клавиши ОК.
- Увидим результаты в ячейке с функцией. В данном случае это ноль. Далее переносим курсор в правый нижний угол, после чего появится маркер автозаполнения. Выглядит он, как маленький чёрный плюсик. Если он появился, зажимаем левую кнопку мыши и перемещаем курсор до последней ячейки в нашей таблице.
- Это дает нам возможность перенести формулу во все остальные ячейки и получить правильные результаты без необходимости выполнения дополнительных расчетов.
- Следующий шаг – выбор левой верхней ячейки и вставка функции СУММ в нее. После этого заносим аргументы и с помощью маркера автозаполнения заполняем все оставшиеся ячейки.
- После этого приступаем непосредственно к решению задачи. Для этого воспользуемся дополнением, которое мы включили ранее. Переходим на вкладку «Данные», и там находим инструмент «Поиск решения». Нажимаем по этой кнопке.
- Теперь перед нашим взором появилось окошко, через которое можно настроить параметры нашего дополнения. Давайте каждый из этих параметров разберем:
- Оптимизировать целевую функцию. Здесь нам нужно выбрать ячейку, содержащую функцию СУММПРОИЗВ. Видим, что эта опция дает возможность выбрать функцию, для которой будет осуществляться поиск решения.
- До. Здесь выставляем опцию «Минимум».
- Изменяя ячейки переменных. Здесь указываем диапазон, соответствующий той таблице, которую мы создавали в самом начале (за исключением суммирующей строки и столбца).
- В соответствии с ограничениями. Здесь нам нужно добавить ограничения, нажав кнопку «Добавить».
- Мы помним, какое ограничение нам нужно создать – сумма значений спросов покупателей и предложений продавцов должны быть одинаковыми.
- Задача ограничений осуществляется следующим образом:
- Ссылка на ячейки. Здесь заносим диапазон таблицы для расчётов.
- Условия. Это математическая операция на предмет соответствия которой проверяется диапазон, заданный в первом поле ввода.
- Значение условия или ограничение. Сюда заносим подходящую колонку в исходной таблице.
- После того, как все действия будут выполнены, нажимаем кнопку ОК, тем самым подтверждая наши действия.
Точно такие же операции производим для верхних строк, задавая следующее условие: они должны быть равны.
Следующий этап – задание условий. Нам необходимо установить следующие критерии для суммы ячеек в таблице – больше или равно нулю, целое число. В результате у нас появляется такой перечень условий, при которых задача решается. Здесь нужно убедиться, что поставлен флажок возле опции «Сделать переменные без ограничений неотрицательными». Также в нашей ситуации требуется, чтобы был выбран метод решения задачи – «Поиск решения нелинейных задач методов ОПГ». Теперь можно смело говорить, что настройка осуществлена. Поэтому осталось только выполнить расчеты. Для этого нажимаем на кнопку «Найти решение».
После этого все данные будут рассчитаны автоматически, а потом Эксель покажет окно с результатами. Оно необходимо для того, чтобы перепроверить работу компьютера, поскольку возможны ошибки, если условия ранее были заданы неверно. Если все правильно, то нажимаем кнопку «ОК» и видим готовую таблицу.
Если же оказывается, что у нас задача стала открытого типа, то это плохо, поскольку нужно отредактировать исходную таблицу так, чтобы задача превратилась в закрытую. Тем не менее, когда это сделать, оставшийся алгоритм будет такой же.
Заключение
Как видим, Excel может использоваться и для очень сложных вычислений, которые на первый взгляд не доступны простой компьютерной программе, которая установлена почти у каждого. Тем не менее, это так. Сегодня мы уже рассмотрели продвинутый уровень использования. Данная тема не такая простая, но как говорится, дорогу осилит идущий. Главное – следовать плану действий, и точно выполнять все действия, указанные выше. Тогда ошибок не возникнет, а программа самостоятельно выполнит все необходимые расчеты. Не нужно будет думать, какую функцию использовать и так далее.
Оцените качество статьи. Нам важно ваше мнение: