Решение транспортной задачи онлайн в excel онлайн - Word и Excel

Содержание

Общее описание транспортной задачи
Инструменты для решения транспортной задачи в Эксель
Пример решения транспортной задачи в Excel
- Условия задачи
- Решение задачи
Вопросы и ответы

Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.

Общее описание транспортной задачи

Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.

Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.

Инструменты для решения транспортной задачи в Эксель

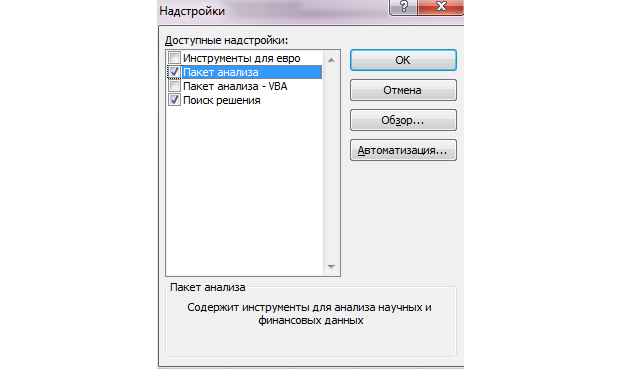
Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.

Делаем перемещение во вкладку «Файл».

Кликаем по подразделу «Параметры».

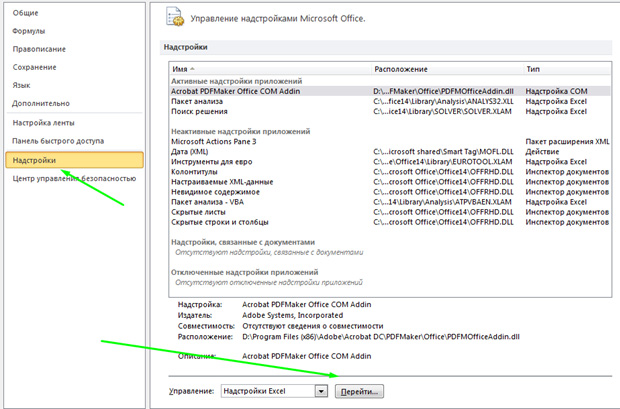
В новом окне переходим по надписи «Надстройки».

В блоке «Управление», который находится внизу открывшегося окна, в выпадающем списке останавливаем выбор на пункте «Надстройки Excel». Делаем клик по кнопке «Перейти…».

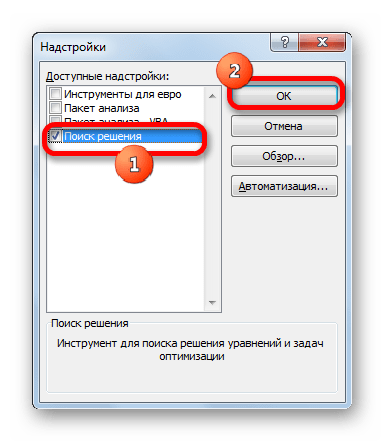
Запускается окно активации надстроек. Устанавливаем флажок возле пункта «Поиск решения». Кликаем по кнопке «OK».

Вследствие этих действий во вкладке «Данные» в блоке настроек «Анализ» на ленте появится кнопка «Поиск решения». Она нам и понадобится при поиске решения транспортной задачи.

Урок: функция «Поиск решения» в Экселе

Теперь давайте разберем конкретный пример решения транспортной задачи.

Условия задачи

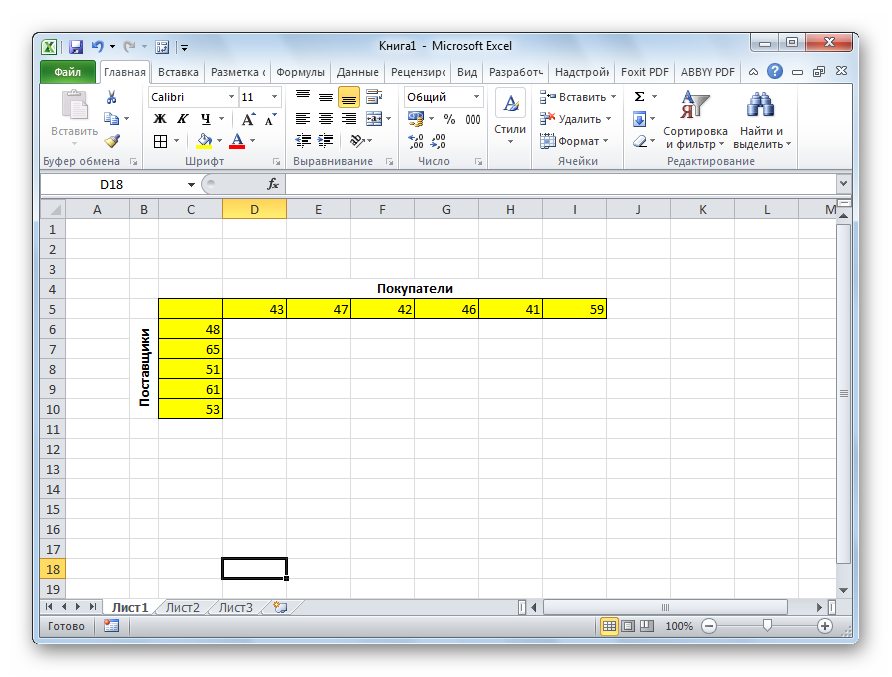
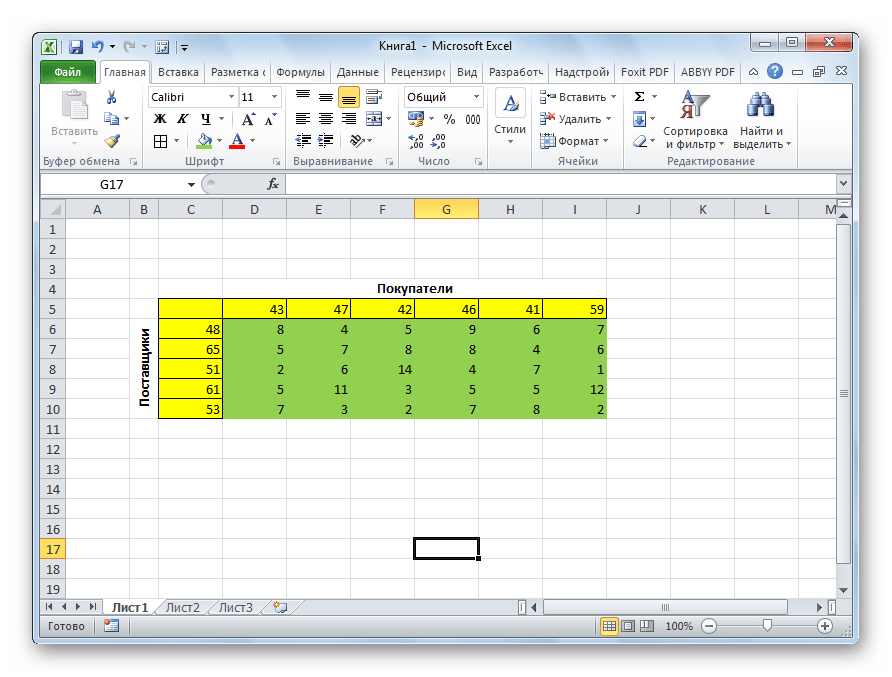
Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.

Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.

Решение задачи

Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.

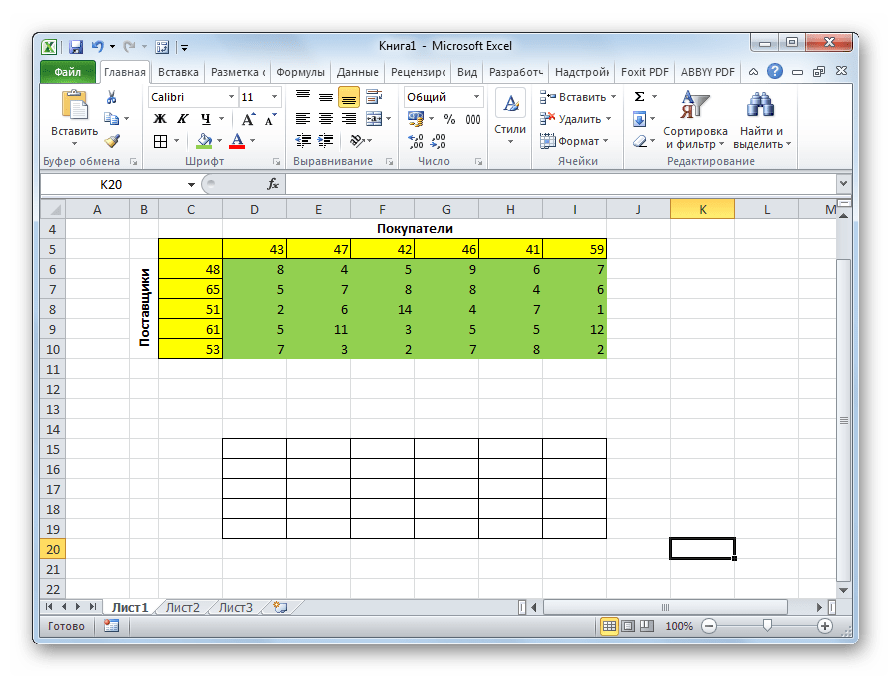
Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.

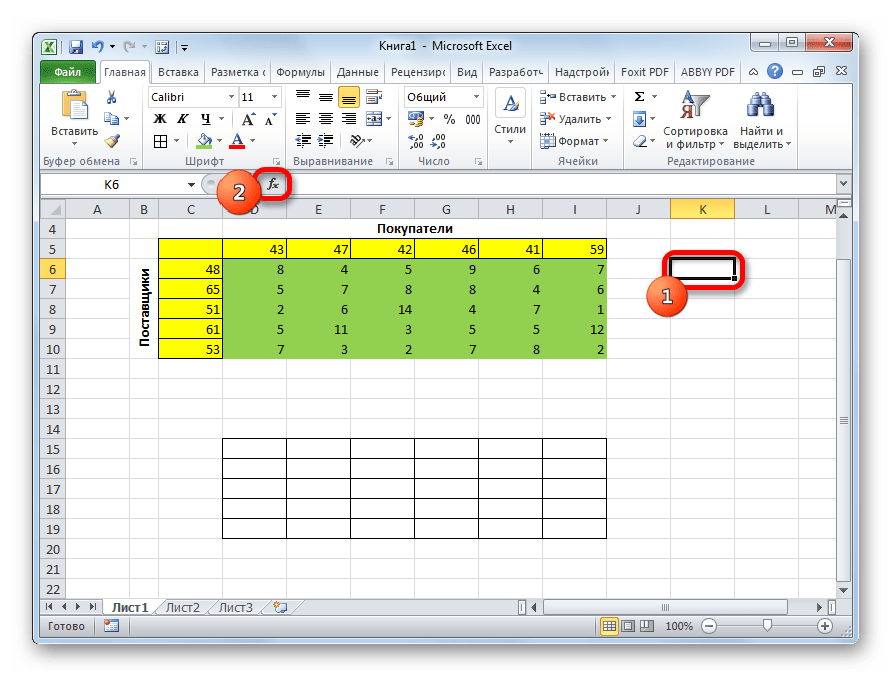
Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.

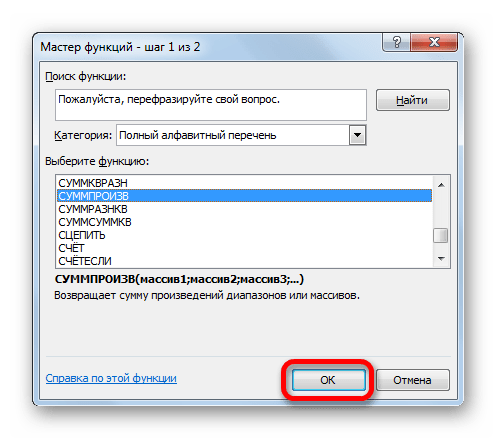
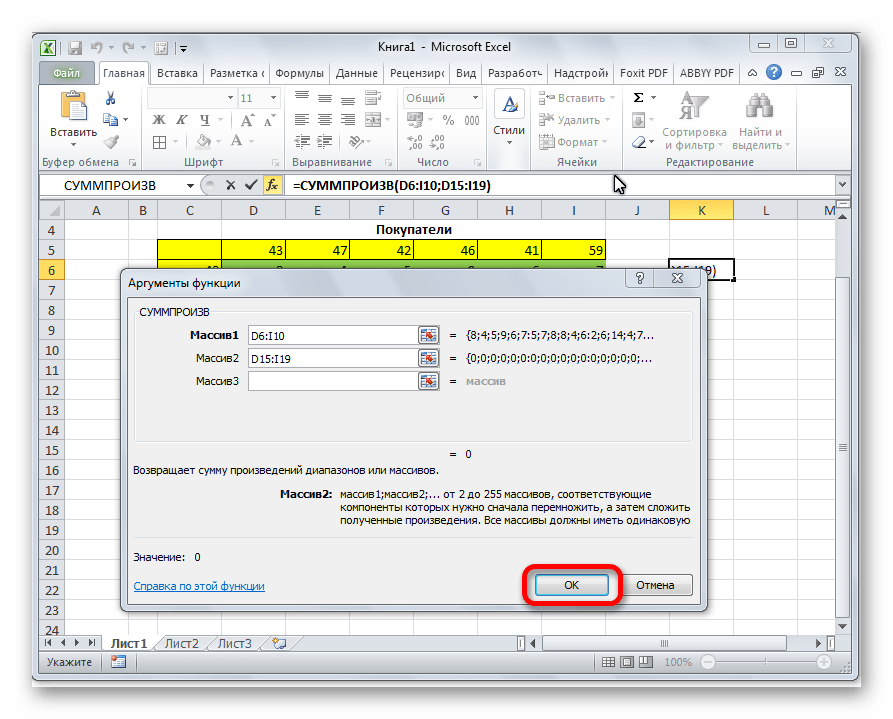
Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».

Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».

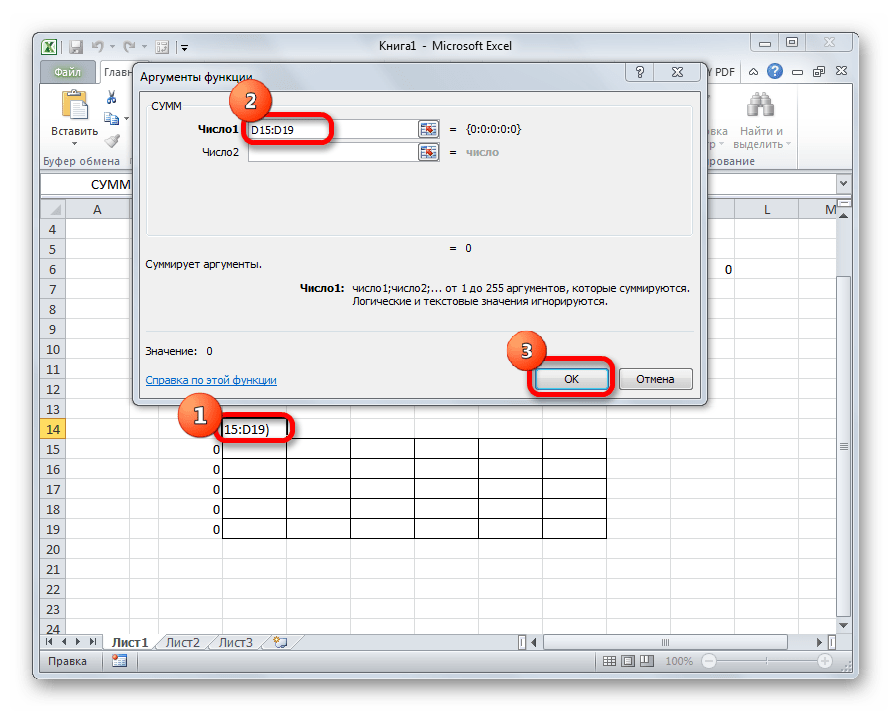
Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».

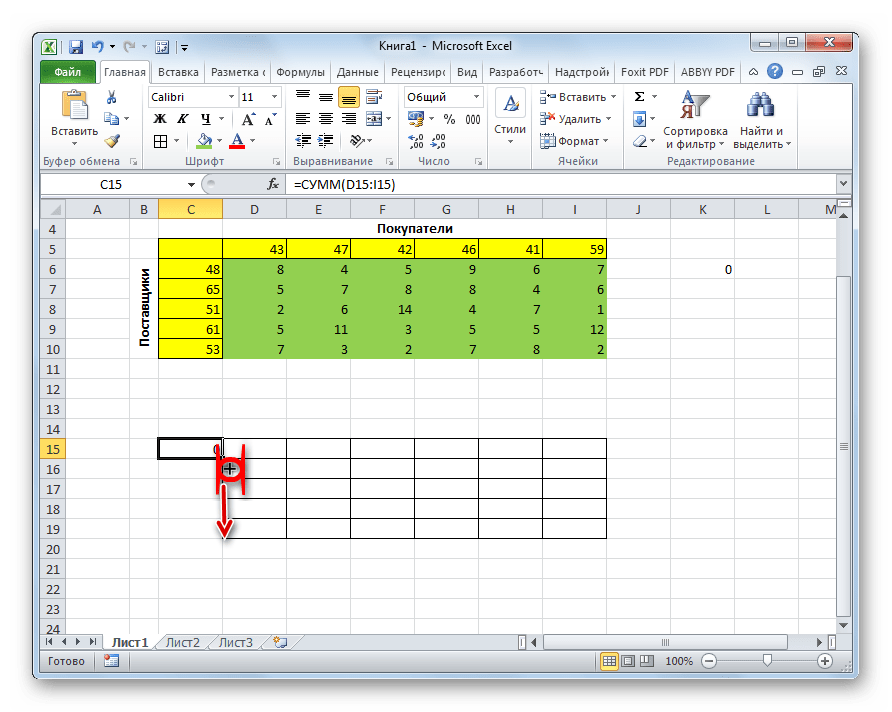
Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.

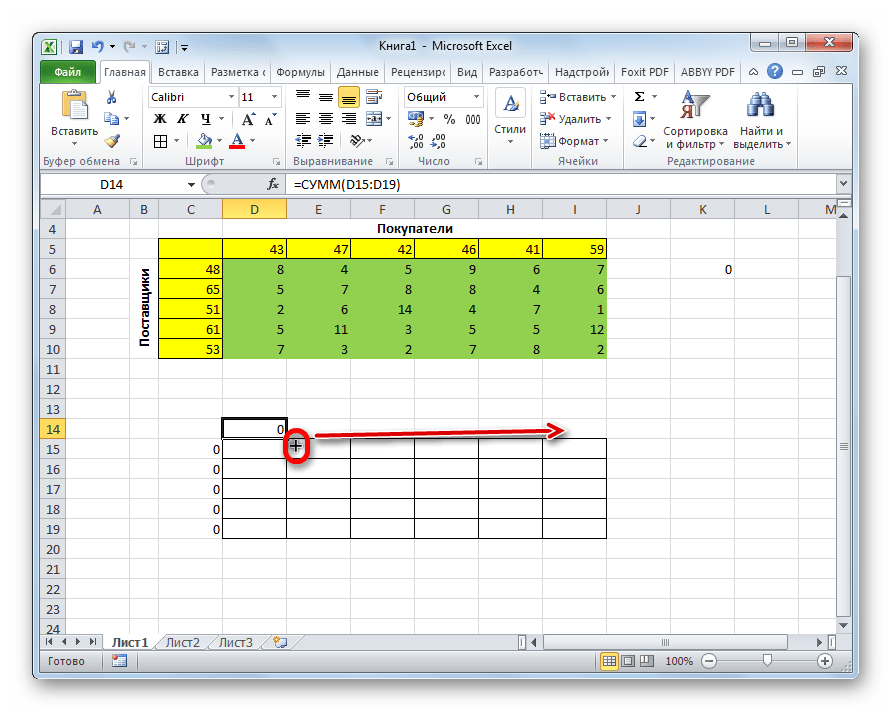
Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».

Копируем маркером заполнения формулу на всю строку.

Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».

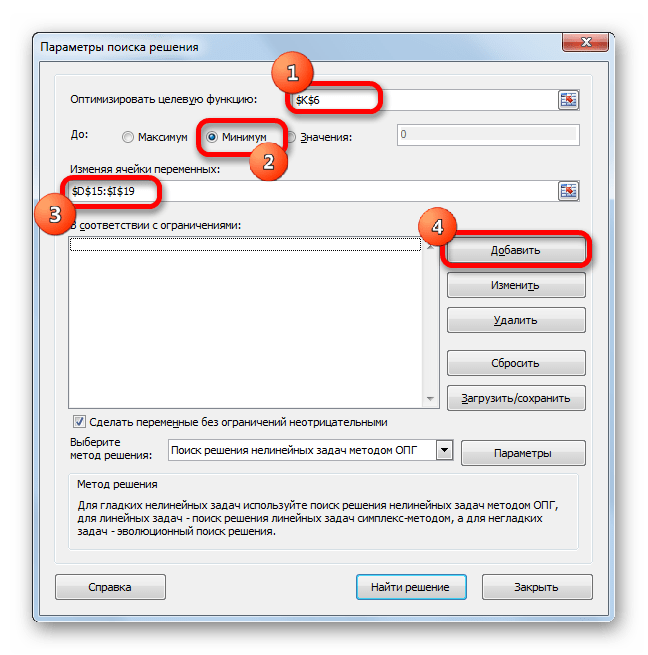
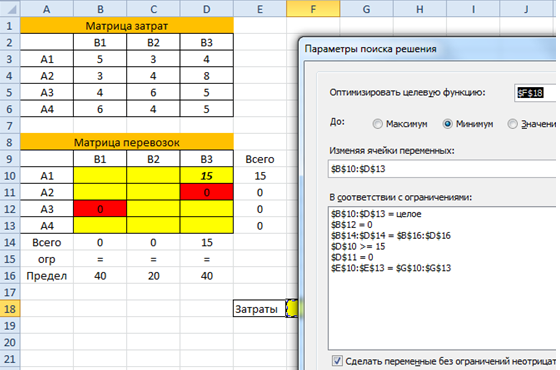
Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.

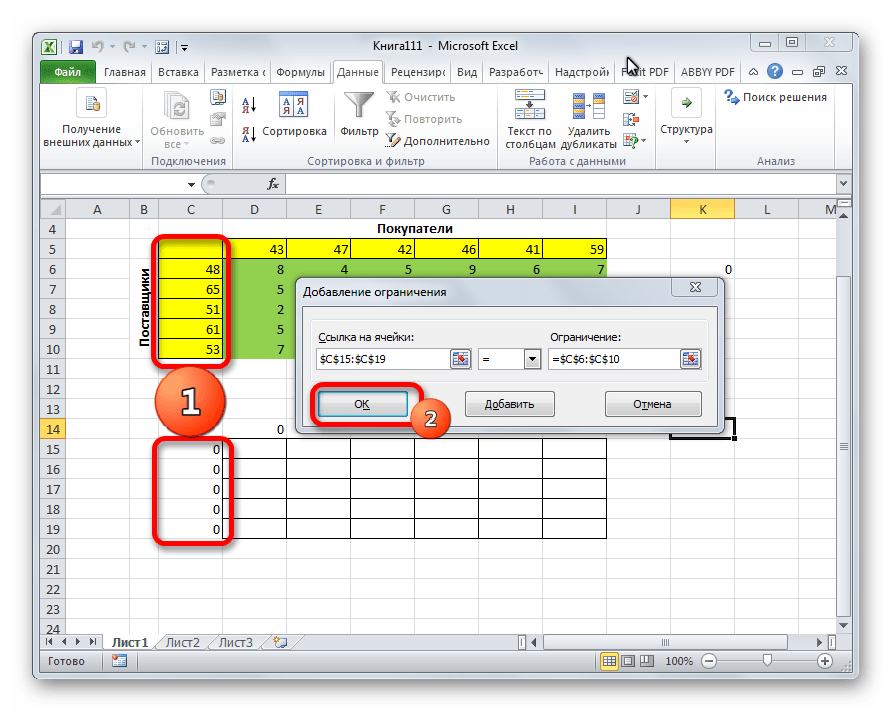
Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».

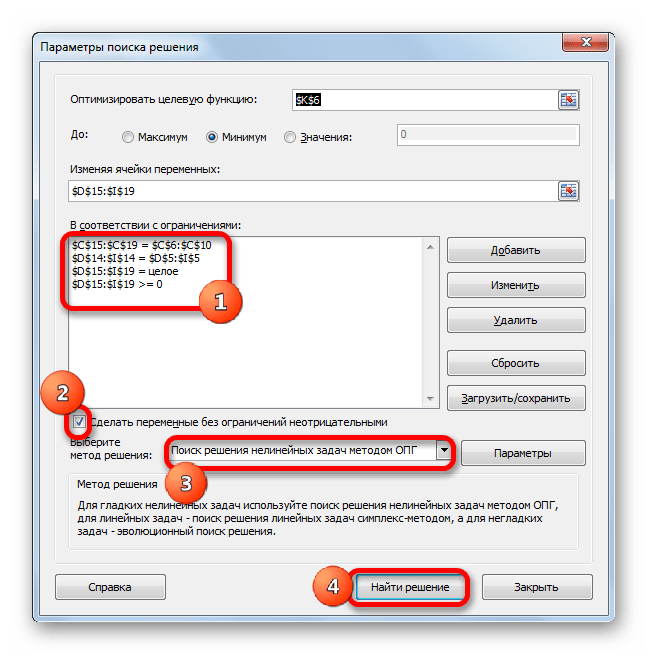
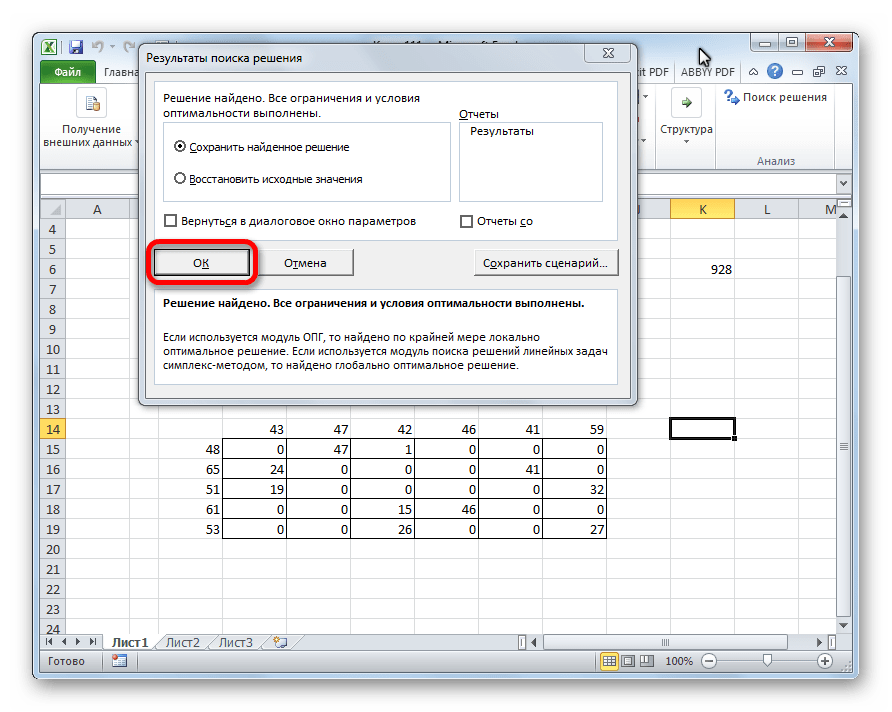
Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».

После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».

Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Еще статьи по данной теме:

Помогла ли Вам статья?

Источник

Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.

Содержание

Транспортная задача: описание
Подготовительный этап: включение функции “Поиск решения”
Пример задачи и ее решение
- Условия
- Алгоритм решения
Заключение

Транспортная задача: описание

С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.

Транспортные задачи бывают двух типов:

Закрытая – совокупное предложение продавца равняется общему спросу.
Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).

Подготовительный этап: включение функции “Поиск решения”

Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:

Открываем меню “Файл”.
В перечне слева выбираем пункт “Параметры”.
В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.

Пример задачи и ее решение

Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.

Условия задачи

Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.

Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).

Алгоритм решения

Итак, приступи к решению нашей задачи:

Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
На экране отобразится окно, в котором нужно заполнить аргументы:
- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
- по готовности жмем OK.
Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
Перед нами появится окно с параметрами функции:
- в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
- для параметра “До” выбираем вариант – “Минимум”.
- в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
- нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
- становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
- затем выбираем знак “равно”.
- в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
- щелкаем OK по готовности.
Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
- больше или равно нулю;
- целое число.
В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.

Заключение

Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.

Источник

Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.

Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.

Виды транспортных задач

Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.

Условия транспортной задачи можно представить двумя способами:

в виде схемы;
в виде матрицы.

В процессе решения могут быть ограничения (либо задача решается без них).

По характеру условий различают следующие типы транспортных задач:

открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).

Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.

Пример решения транспортной задачи в Excel

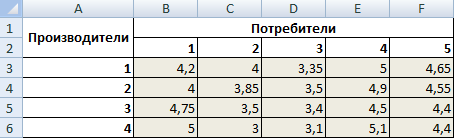
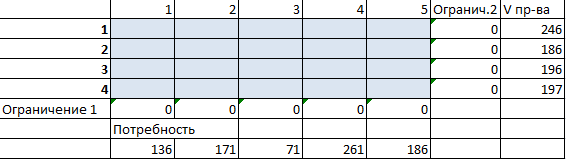
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.

Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:

Производители	Потребители	Объем производства
	В1	В2	В3	В4	В5
А1	4,2	4	3,35	5	4,65	246
А2	4	3,85	3,5	4,9	4,55	186
А3	4,75	3,5	3,4	4,5	4,4	196
А4	5	3	3,1	5,1	4,4	197
Объем потребления	136	171	71	261	186

Задача: минимизировать транспортные расходы по перевозке продукции.

Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.

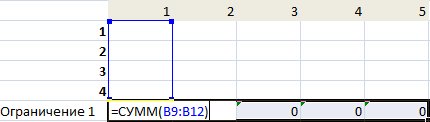
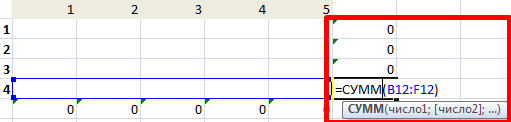
Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.

Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.

Вносим известные значения потребности в товаре и объема производства.

Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
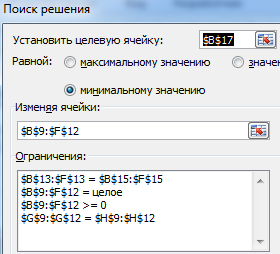
Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.

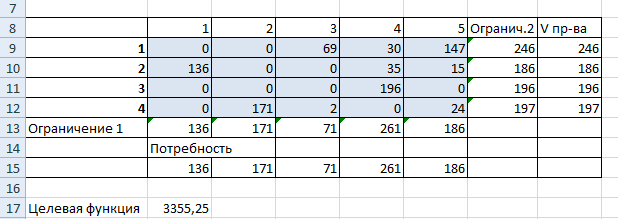
Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.

Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.

Решение открытой транспортной задачи в Excel

При таком типе возможны два варианта развития событий:

суммарный объем производства превышает суммарную потребность в товаре;
суммарная потребность больше суммы запасов.

Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.

Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.

Единица перевозки груза для фиктивного участника равняется 0.

Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.

Читайте также по теме: решение транспортной задачи методом потенциалов в Excel.

Источник

На этой странице разберем подробные решения транспортной задачи (алгоритм и примеры разных типов) с использованием пакета электронных таблиц MS Excel (надстройка Поиск решения).

Как решить транспортную задачу в Excel

Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).

Использовать можно любую версию программы — 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).

Алгоритм решения ТЗ в Эксель

Составить математическую модель транспортной задачи — то есть получить таблицу со стоимостью перевозок, запасами груза у поставщиков и потребностями потребителей (и, возможно, дополнительными ограничениями).

Если задача открытая (несбалансированная), то добавить потребителя или поставщика с нулевыми тарифами перевозки.

Внести на лист таблицы Excel данную модель в виде матрицы тарифов (затрат).

Создать рядом на листе еще одну таблицу, где будут выводиться искомые перевозки (такой же размерности, что и таблица тарифов). Просуммировать перевозки по строкам и столбцам (чтобы сравнивать с аналогичными ячейками — предельными ограничениями задачи — запасами поставщиков и потребностями потребителей).

Ввести в ячейку формулу, подсчитывающую суммарную стоимость перевозок (это число мы должны минимизировать по смыслу транспортной задачи)

В режиме формул таблица будет выглядеть так:

Запустить надстройку Поиск решения и указать а) ячейку, которую мы минимизируем, б) все ограничения на запасы поставщиков и потребности потребителей, в) дополнительные ограничения (иногда бывают запреты перевозок или требования по минимальному объему груза между определенными пунктами, как в данном случае).

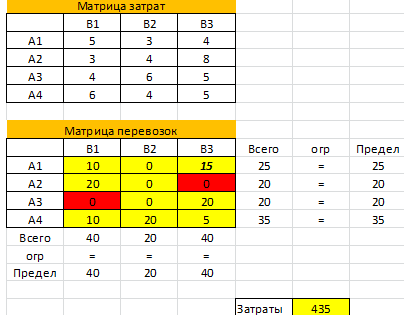
Получить решение транспортной задачи: в целевой ячейке вы увидите минимальную стоимость перевозок (в примере 435), а в таблице перевозок — искомые значения объема перевозимого груза (см. желтые ячейки).

Проанализировать решение, если требуется и записать более подробно, например
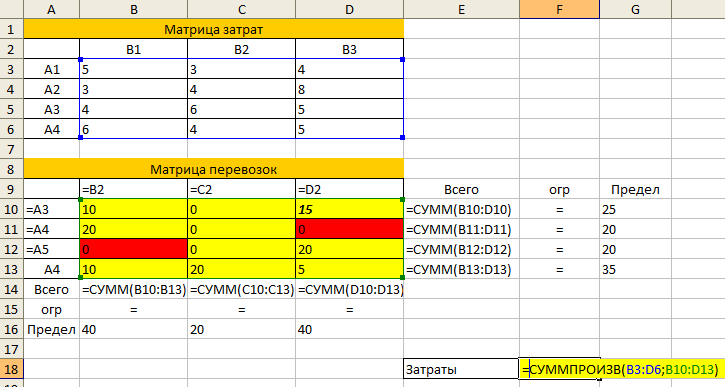
Минимальные затраты на перевозку составят 435. План перевозок:
Из 1 карьера 10 тонн везем на 1-й участок, 15 тонн на 3-й.
Из 2 карьера 20 тонн везем на 1-й участок.
Из 3 карьера 20 тонн везем на 3-й.
Из 4 карьера 10 тонн везем на 1-й участок, 20 тонн на 2-й, 5 тонн на 3-й.

Спасибо за ваши закладки и рекомендации

Транспортные задачи: примеры в Excel

Задача 1. Решить транспортную задачу вручную (методом потенциалов) и в программе Эксель.

Задача 2. Исходные данные задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху — мощности потребителей.
Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя Поиск решений.

Задача 3. Имеется 3 нефтеперерабатывающих завода, 4 спиртовых завода, 3 завода по производству синтетического каучука.
Схема кооперационных связей (см. файл).
Далее приведены производственные показатели предприятий.

Также заданы расстояния между предприятиями.

Необходимо найти решение транспортной задачи с ориентацией на спрос СК и минимизацией транспортных суммарных затрат.

Задача 4. Используя метод потенциалов, решить транспортную задачу. Выполнить проверку, используя табличный редактор Microsoft Excel Компания владеет тремя заводами А1, А2, А3. Соответствующие объемы производства равны 600, 300 и 330 единиц продукции. Компания обязалась поставить в города В1, В2, В3 и В4 соответственно 350, 350, 230 и 300 единиц. При заданных в таблице стоимостях перевозок единицы продукции составьте план ее распределения, чтобы общая стоимость перевозок была наименьшей.

Задача 5. Свести задачу к виду ТЗ и решить с помощью надстройки «Поиск решения»
Четыре ремонтные мастерские могут за год отремонтировать соответственно 400, 500, 450 и 550 машин при себестоимости ремонта одной машины в 500, 700, 650 и 600 рублей. Планируется годовая потребность в ремонте пяти автобаз: 550, 350, 300, 375 и 400 машин.
Ремонт машин с 1 автобазы должен осуществляться в 100% случаев силами ремонтных мастерских.
На 4 АБ возможно самостоятельное проведение ремонтных работ (бесплатное) в объеме, не превышающем 8% от планируемой годовой потребности этой мастерской. Платное (на стороне) — совсем не возможно.
Вторая, третья и пятая АБ могут «ремонтироваться» на стороне, стоимость ремонта +трансп.расходы каждой машины в таком случае составит 695 руб.
Дана матрица, характеризующая транспортные расходы на доставку машины с j-й автобазы в i-ю ремонтную мастерскую. Определить минимальную годовую потребность в кредитах на выполнение указанного объема работ по всем автобазам

Решаем транспортные задачи любой сложности

Полезные ссылки

Транспортная задача: решение вручную
Решение линейного программирования в Excel

Решенные контрольные по ЛП
Онлайн учебник по оптимальным решениям

Источник

Транспортная задача — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.

Цитата взята с википедии.

Решение транспортной задачи рассматривается практически на всех специальностях, где хоть как-то присутствует курс математики. Решить транспортную задачу можно различными способами и программными средствами. Причем если решение такой задачи в математических пакетах типа Mathcad или MATLAB обыденное дело, то решение такой задачи в программе 1С:Предприятие 8.2 уже интересная диковинка.

Смотрите также видео версию статьи «Решение транспортной задачи в Excel (сбалансированная задача)».

Сегодня мы рассмотрим решение сбалансированной транспортной задачи в табличном процессоре MS Excel.

Постановка задачи

Есть запасы однотипной продукции у поставщиков A1, A2, A3, A4.

Существует потребность в этой продукции B1, B2, B3

Стоимость доставки единицы продукции от поставщиков к потребителям представлена в таблице.

Поставщик	Потребитель	Запас
В1	В2	В2
А1	6	5	2	250
А2	3	7	4	100
А3	7	8	1	80
А4	2	2	3	120
Потребность	150	150	250

Необходимо составить такой план перевозок, который бы удовлетворил все потребности и имел минимальную стоимость.

Решение задачи

Для решения данной задачи в табличном процессоре необходимо составить две таблицы, приведенные выше, но вторую таблицу не заполнять данными.

Для решения транспортной задачи потребуются функции: СУММПРОИЗВ, СУММ и надстройка «Поиск решения».

Для отображения формул необходимо на вкладке «Формулы» в группе «Зависимости формул» выбрать «Показать формулы» либо горячее сочетание клавиш «Ctrl+` (тильда)».

Дальше выбираем команду «Поиск решения» на вкладке «Данные»

Кстати, если дать имена диапазонам ячеек, то окно поиска решения будет выглядеть следующим образом:

Решение поставленной задачи представлено ниже.

Источник

Содержание

Постановка задачи и подготовка таблиц
Виды транспортных задач
Общее описание транспортной задачи
Инструменты для решения транспортной задачи в Эксель
Постановка задачи
Решение задачи
Условие
Варианты решения
Транспортная задача в Экселе
Пример задачи
Как решить транспортную задачу в Excel
Алгоритм решения транспортной задачи распределительным методом
Что такое симплекс-метод
Алгоритм решения основной задачи ЛП симплекс-методом
Вводная часть, с которой желательно ознакомиться
О чем говорится в определении транспортной задачи?
Общий план решения транспортной задачи методом потенциалов
Подробная инструкция по решению транспортной задачи

Постановка задачи и подготовка таблиц

Цель задачи сводится к математическому моделированию минимизации грузопотоков. Довольно часто студенты пишут рефераты на тему поиска решения транспортной задачи. Этот пример можно взять за основу реферата.

Виды транспортных задач

Условия транспортной задачи можно представить двумя способами:

в виде схемы;
в виде матрицы.

В процессе решения могут быть ограничения (либо задача решается без них).

По характеру условий различают следующие типы транспортных задач:

открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).

Общее описание транспортной задачи

Инструменты для решения транспортной задачи в Эксель

Делаем перемещение во вкладку «Файл».

Кликаем по подразделу «Параметры».

В новом окне переходим по надписи «Надстройки».

В блоке «Управление», который находится внизу открывшегося окна, в выпадающем списке останавливаем выбор на пункте «Надстройки Excel». Делаем клик по кнопке «Перейти…».

Запускается окно активации надстроек. Устанавливаем флажок возле пункта «Поиск решения». Кликаем по кнопке «OK».

Вследствие этих действий во вкладке «Данные» в блоке настроек «Анализ» на ленте появится кнопка «Поиск решения». Она нам и понадобится при поиске решения транспортной задачи.

Постановка задачи

Есть запасы однотипной продукции у поставщиков A1, A2, A3, A4.

Существует потребность в этой продукции B1, B2, B3

Стоимость доставки единицы продукции от поставщиков к потребителям представлена в таблице.

Поставщик	Потребитель	Запас
В1	В2	В2
А1	6	5	2	250
А2	3	7	4	100
А3	7	8	1	80
А4	2	2	3	120
Потребность	150	150	250

Решение задачи

Для решения транспортной задачи потребуются функции: СУММПРОИЗВ, СУММ и надстройка «Поиск решения».

Дальше выбираем команду «Поиск решения» на вкладке «Данные»

Кстати, если дать имена диапазонам ячеек, то окно поиска решения будет выглядеть следующим образом:

Решение поставленной задачи представлено ниже.

Условие

Есть некие предприятия и склады с грузом. Каждое предприятие, нуждается в определённом объёме нашего груза. Каждый склад доставляет тонну груза по собственному тарифу. Таким образом, нужно составить маршрут, по которому мы развезём объём груза, удовлетворяющий каждое предприятие, и при этом затратим меньше всего средств.
Так транспортная задача выглядит в своём наиболее общем и типовом виде.

С – это цена за тонну. X – это то, сколько мы привезём тонн со склада на предприятие. Например, если мы примем X11 равным 5, это будет значить, что со склада А1 к потребителю B1 мы повезём 5 тонн по цене C11. Вот нам и нужно как-то распределить всё так, чтобы потратить меньше всего денег.

Варианты решения

Транспортную задачу можно решить «вручную». Существует несколько подходов к её решению на бумаге. Среди них:

Метод опорного плана;
Метод минимального элемента;
Метод Фогеля.

Решение транспортных задач

Как правило, решая задачу одним из этих способов, вы получаете решение, находите потенциалы для него и понимаете, что в числе потенциалов есть положительные значения. Соответственно, это говорит о том, что вы нашли неверное решение. Далее вам нужно действовать, что называется, наугад. Вы переставляете различные цифры в таблице, пробуете разные варианты, словом, ищите решение методом «научного тыка». Далее снова пересчитываете потенциалы, и снова ничего не срастается.
Однозначного алгоритма, работающего безотказно в любых условиях, к сожалению, пока не придумали.
Однако для решения транспортной задачи или проверки полученного нами на бумаге результата, мы можем воспользоваться функционалом MS Excel.

Транспортная задача в Экселе

Для решения нам потребуется надстройка «Поиск решения». Возможно, она не будет активирована в вашем редакторе по умолчанию, поэтому, проделываем следующую очередность действий:

Жмём «Файл»;
В появившемся меню нажимаем по предпоследней кнопке «Параметры»;
Вновь находим предпоследний пункт «Надстройки» и переходим в «Управление»:

Ставим галочку в появившемся окне рядом с пунктов «Поиск решения» и жмём «ОК».

Поиск решения активирован. Далее он будет нами использован.

Пример задачи

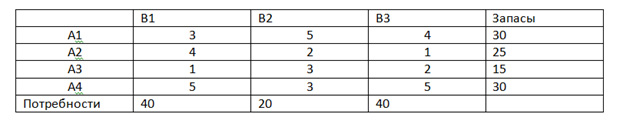
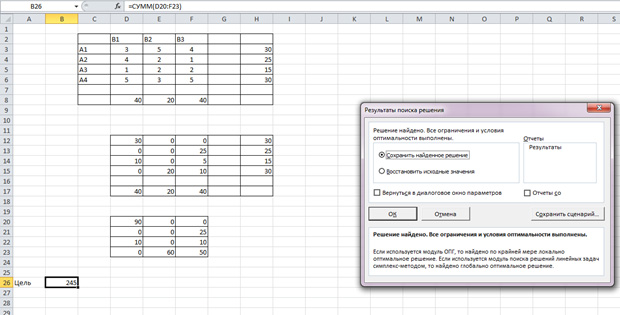
На складах A1 — A4 есть суммарно 100 тонн зерна, и их нужно развести по текущим расценкам в пункты B1 – B3, потратив как можно меньше средств на доставку. Тарифы на доставку указаны в центре таблицы.

Использовать можно любую версию программы – 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).

Алгоритм решения транспортной задачи распределительным методом

Резюмируя выполненные выше решения, сформулируем алгоритм решения транспортной задачи распределительным методом (поиска оптимального плана транспортной задачи).

Проверить, является ли план перевозок оптимальным. Если оценки всех “свободных мест” неотрицательны, то план перевозок является оптимальным. В противном случае можно найти новый план перевозок с меньшим значением линейной формы.
Найти “свободное место” с наименьшей негативной оценкой (наибольшее по модулю отрицательное число). В новом плане перевозок соответствующая клетка становится “занятым местом”.
Вдоль цикла, соответствующего “свободному месту” из предыдущего пункта, отметить вершины знаками “плюс” и “минус” пройденные вершины (“кружочки”) по принципу: знаком “плюс” отмечаются нечётные вершины, знаком “минус” – чётные.
Вдоль цикла, упомянутого в предыдущем пункте, выбрать наименьшее из чисел в кружочке, отмеченное знаком “минус” и обозначить его буквой “тэта”.
Произвести перенаправление грузов для нового плана перевозок. Для этого число “тэта”, упомянутое в предыдущем пункте, прибавить к стоимостям перевозок в правых нижних углах клеток со знаком “плюс” и вычесть из стоимостей перевозок в правых нижних углах клеток со знаком “минус”. Стоимости в клетках, не входящих в цикл, не меняются.
Вычислить значение линейной формы для нового плана перевозок. Для этого вычисляется “экономия”: число “тэта” умножается на число, стоящее в кружочке в соответствующей клетке. “Экономия” (отрицательное число) прибавляется к значению линейной формы предыдущего плана.
В таблице, соответствующей новому плану, построить циклы, соответствующие “свободным местам” и вычислить оценки этих “свободных мест”. Для этого двигаться только по “занятым местам” и при каждом шаге поворот делать только под прямым углом. Каждый шаг вдоль цикла отмечать знаком “плюс” или “минус” по принципу: знаком “плюс” отмечаются нечётные вершины, знаком “минус” – чётные.

Эти шаги следует повторять до тех пор, пока оценки всех “свободных мест” не станут положительными.

Если в ходе решения транспортной задачи появились вырожденные (сингулярные) планы, то возможно, что число “тэта” равно нулю. Тогда на соответствующей итерации решения значение линейной формы не меняется (что и было показано в примере 2).

Что такое симплекс-метод

Задача линейного программирования — это задача поиска неотрицательных значений параметров, на которых заданная линейная функция достигает своего максимума или минимума при заданных линейных ограничениях.

Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Алгоритм является универсальным методом, которым можно решить любую задачу линейного программирования.

Если вам тоже ничего не понятно из этого определения, то вы на верном пути. Чаще всего статьи про симплекс-метод очень сильно углубляются в дебри теории задачи линейного программирования, из-за чего очень легко потерять суть и так ничего и не понять. Мы постараемся описать алгоритм симплекс-метода так, чтобы показать, что в нём нет ничего страшного и на самом деле он весьма простой. Но сначала нам всё-таки потребуется ввести несколько определений.

Целевая функция — функция, максимум (или минимум) которой нужно найти. Представляет собой сумму произведений коэффициентов на значения переменных: F = c₁·x₁ + c₂·x₂ + … + c_n·x_n

Ограничение — условие вида a₁·x₁ + a₂·x₂ + … + a_n·x_n v b, где вместо v ставится один из знаков: ≤, = или ≥

План — произвольный набор значений переменных x₁ … x_n.

Алгоритм решения основной задачи ЛП симплекс-методом

Пусть в задаче есть m ограничений, а целевая функция заивисит от n основных переменных. Первым делом необходимо привести все ограничения к каноническому виду — виду, в котором все условия задаются равенствами. Для этого предварительно все неравенства с ≥ умножаются на -1, для получения неравенств с ≤.

Чтобы привести ограничения с неравенствами к каноническому виду, для каждого ограничения вводят переменную, называемую дополнительной с коэффициентом 1. В ответе эти переменные учитываться не будут, однако сильно упростят начальные вычисления. При этом дополнительные переменные являются базисными, а потому могут быть использованы для формирования начального опорного решения.

Пример 1

Привести к каноническому виду ограничения:
2·x₁ + 3·x₂ + 6·x₃ ≤ 240
4·x₁ + 2·x₂ + 4·x₃ = 200
4·x₁ + 6·x₂ + 8·x₃ ≥ 160
Меняем знаки у ограничений с ≥, путём умножения на -1 и добавляем дополнительные переменные к ограничениям с неравенством:
2·x₁ + 3·x₂ + 6·x₃ + x₄ = 240
4·x₁ + 2·x₂ + 4·x₃ = 200
-4·x₁ – 6·x₂ – 8·x₃ + x₅ = -160

Вводная часть, с которой желательно ознакомиться

Существует несколько методов решения транспортной задачи. Мы будем подробно рассматривать два из них:

решение транспортной задачи методом потенциалов (рассмотрен в данной статье)
решение транспортной задачи с использованием симплекс метода.

Решение задачи методом потенциалов происходит в несколько этапов:

Определение опорного решения.
Применение к найденному опорному решению самого метода потенциалов.
Проверка единственности решения.

Определение опорного плана, в свою очередь, можно выполнить несколькими способами. Мы рассмотрим два из них:

метод северо-западного угла
метод минимальных стоимостей

(не путать с методами решения самой транспортной задачи!!!)

О чем говорится в определении транспортной задачи?

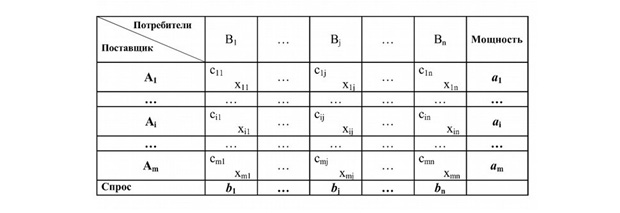
У нас есть некоторый груз, который находится на складах: склад 1, склад 2, …, склад – это пункты отправления.

Этот груз нам необходимо развести по магазинам: магазин 1, магазин 2, …, магазин k – это пункты назначения.

Нам выгоднее как можно эффективнее выполнить работу, т.е. найти такой вариант перевозки, при котором затраты будут минимальными.

Общий план решения транспортной задачи методом потенциалов

Решить транспортную задачу можно различными методами, начиная от симплекс-метода и простого перебора, и заканчивая методом графов. Один из наиболее применяемых и подходящих для большинства случаев методов – итерационное улучшение плана перевозок.

Суть его в следующем: находим некий опорный план и проверяем его на оптимальность (Z → min). Если план оптимален – решение найдено. Если нет – улучшает план столько раз, сколько потребуется, пока не будет найден оптимальный план.

Подробная инструкция по решению транспортной задачи

Строим таблицу, где указываем запасы материалов, имеющиеся на складах поставщиков (Ai), и потребности заводов (Bj) в этих материалах.

В нижний правый угол ячеек таблицы заносим значение тарифов на перевозку груза (Cij).

2. Проверка задачи на закрытость

Обозначим суммарный запас груза у всех поставщиков символом A, а суммарную потребность в грузе у всех потребителей – символом B.

Тогда:

Транспортная задача называется закрытой, если A = B . Если же A ≠ B , то транспортная задача называется открытой. В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.

Проверим задачу на закрытость:

A = 10 + 20 + 30 = 60

B = 15 + 20 + 25 = 60

A = B, следовательно данная транспортная задача – закрытая.

3. Составление опорного плана

Составляет предварительный (опорный) план перевозок. Он не обязательно должен быть оптимальный. Это просто своеобразный «черновик», «набросок», улучшая который мы постепенно придем к плану оптимальному.

Есть разные методы нахождения опорного плана. Наиболее распространены следующие:

а) Метод Северо-Западного угла.

Суть метода проста – ячейки транспортной таблицы последовательно заполняются максимально возможными объемами перевозок, в направлении сверху вниз и слева направо. То есть сперва заполняется самая верхняя левая ячейка (“северо-западная” ячейка), потом следующая справа и т.д. Затем переходят на новую строку и вновь заполняют ее слева направо. И так пока таблица не будет заполнена полностью.

Подробное описание метода и пример можно посмотреть здесь.

б) Метод минимального элемента.

Метод заключается в том, что для заполнения ячеек транспортной таблицы выбирается клетка с минимальным значением тарифа. Затем выбирается следующая клетка с наименьшим тарифом и так продолжается до тех пор, пока таблица не будет заполнена (все запасы и потребности при этом обнулятся).
Подробное описание метода и пример можно посмотреть здесь

в) Аппроксимация Фогеля.

Основа метода в нахождении разности(по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем в строке или столбце с наибольшейразностью заполняется клетка с наименьшимтарифом. Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки.
Подробное описание аппроксимации Фогеля и пример можно посмотреть онлайн

г) Метод двойного предпочтения.

Суть метода в том, что отмечаются клетки с наименьшим тарифом по строкам, а затем по столбцам. Затем ячейки заполняются в следующей очередности: сначала клетки с двумя отметками, потом с одной, наконец без отметок.
Подробное описание метода и пример можно посмотреть здесь

4. Проверка опорного плана на вырожденность

Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) – свободными.

План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n -1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся). Однако проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим!

План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ниже приведен пример цикла:

Ломаная линия может иметь точки самопересечения, но не в клетках цикла.

Кол-во базисных клеток = 5

m + n – 1 = 3 + 3 – 1 = 5

Следовательно, первоначальный план перевозок – невырожденный.

5. Вычисление потенциалов для плана перевозки

Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.

Этот метод улучшения плана перевозок называется методом потенциалов. Есть другие методы итерационного улучшения плана перевозок, но здесь мы их рассматривать не будем.

Итак, сопоставим каждому поставщику Ai и каждому потребителю Bj величины Ui и Vj соответственно так, чтобы для всех базисных клеток плана было выполнено соотношение:

Ui + Vj = Cij

Добавим к транспортной таблице дополнительную строку и столбец для Ui и Vj.

Предположим, что U1 = 0.

Тогда мы сможем найти V3 = C13 – U1 = 1 – 0 = 1.

Зная V3, мы теперь можем найти U3:

По аналогии вычисляем все оставшиеся потенциалы:

6. Проверка плана на оптимальность методом потенциалов

Для каждой свободной клетки плана вычислим разности

ΔCij = Cij – (Ui + Vj )

и запишем полученные значения в левых нижних углах соответствующих ячеек.

План является оптимальным, если все разности ΔCij ≥ 0.

В данном случае план – неоптимальный (ΔC22 < 0), и его следует улучшить путем перераспределения поставок.

7. Перераспределение поставок

Найдем ячейку с наибольшей по абсолютной величине отрицательной разностью ΔCij и построим цикл, в котором кроме этой клетки все остальные являются базисными. Такой цикл всегда существует и единственен.

Отметим ячейку с отрицательной разностью ΔCij знаком «+», следующую знаком «-», и так далее, поочередно.

Затем находим минимальной значение груза в ячейках цикла имеющих знак «-» (здесь это 5) и вписываем его в свободную ячейку со знаком «+». Затем последовательно обходим все ячейки цикла, поочередно вычитая и прибавляя к ним минимальное значение (в соответствии со знаками, которыми эти ячейки помечены: где минус – вычитаем, где плюс – прибавляем).

Получим новый опорный планперевозок:

Так как базисных клеток стало больше, чем m + n – 1, то базисную клетку с нулевым значением делаем свободной:

Снова вычисляем значения потенциалов и разности ΔCij:

На этот раз все разности ΔCij ячеек положительные, следовательно, найдено оптимальное решение.

8. Если оптимальное решение найдено, переходим к п. 9, если нет – к п. 5.

У нас оптимальное решение найдено, поэтому переходим к пункту 9.

9. Вычисление общих затрат на перевозку груза

Вычислим общие затраты на перевозку груза (Z), соответствующие найденному нами оптимальному плану, по формуле:

Zmin = 10 ∙ 1 + 15 ∙ 3 + 5 ∙ 2 + 15 ∙ 1 + 15 ∙ 2 = 110 ден. ед.

Общие затраты на доставку всей продукции, для оптимального решения, составляют 110 ден. ед.

10. Построение графа перевозок

Найдя оптимальный план перевозок, построим граф. Вершинами графа будут «склады» и «магазины». В вершинах укажем соответствующие объемы запасов и потребностей. Дугам, соединяющим вершины графа, будут соответствовать ненулевые перевозки. Каждую такую дугу подпишем, указав объем перевозимого груза.

В результате получится граф, аналогичный изображенному ниже:

Источники

https://abuzov.ru/reshenie-transportnoj-zadachi-excel/
https://exceltable.com/otchety/reshenie-transportnoy-zadachi
https://lumpics.ru/the-solution-of-the-transportation-problem-in-excel/
https://msoffice-prowork.com/reshenie-transportnojj-zadachi-v-excel-sbalansirovannaya-zadacha/
https://Reshatel.org/reshenie-zadach/transportnaya-zadacha-v-excel/
https://www.MatBuro.ru/ex_mp.php?p1=tzexcel
https://function-x.ru/zadacha_transportnaja_raspredelitelnyi_metod.html
https://programforyou.ru/calculators/simplex-method
http://matecos.ru/mat/matematika/kak-reshit-transportnuyu-zadachu-2.html
http://galyautdinov.ru/post/transportnaya-zadacha

Источник

В этой статье мы пошагово рассмотрим, как решить транспортную задачу посредством функций MS Excel. Задачи данного типа изучаются студентами на таких дисциплинах, как исследование операций и методы оптимальных решений.

Условие

Так транспортная задача выглядит в своём наиболее общем и типовом виде.

С – это цена за тонну. X – это то, сколько мы привезём тонн со склада на предприятие. Например, если мы примем X11 равным 5, это будет значить, что со склада А1 к потребителю B1 мы повезём 5 тонн по цене C11. Вот нам и нужно как-то распределить всё так, чтобы потратить меньше всего денег.

Варианты решения

Транспортную задачу можно решить «вручную». Существует несколько подходов к её решению на бумаге. Среди них:

Метод опорного плана;
Метод минимального элемента;
Метод Фогеля.

Однозначного алгоритма, работающего безотказно в любых условиях, к сожалению, пока не придумали.

Однако для решения транспортной задачи или проверки полученного нами на бумаге результата, мы можем воспользоваться функционалом MS Excel.

Транспортная задача в Экселе

Жмём «Файл»;
В появившемся меню нажимаем по предпоследней кнопке «Параметры»;
Вновь находим предпоследний пункт «Надстройки» и переходим в «Управление»:

Ставим галочку в появившемся окне рядом с пунктов «Поиск решения» и жмём «ОК».

Поиск решения активирован. Далее он будет нами использован.

Пример задачи

Шаг 1

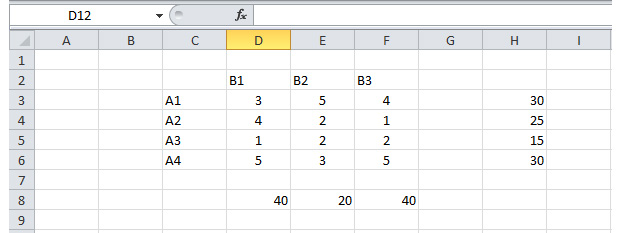
Дублируем нашу таблицу в Excel.

Шаг 2

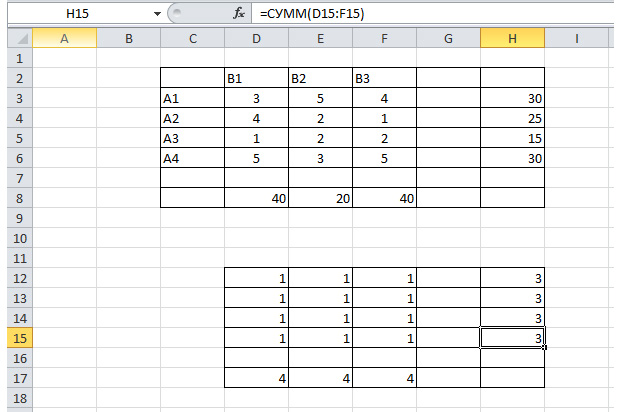
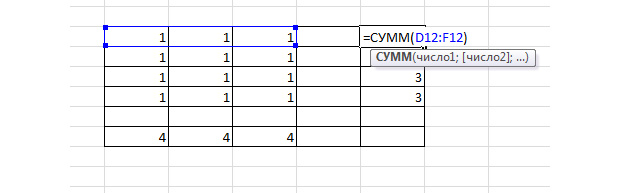
Рисуем другую таблицу.

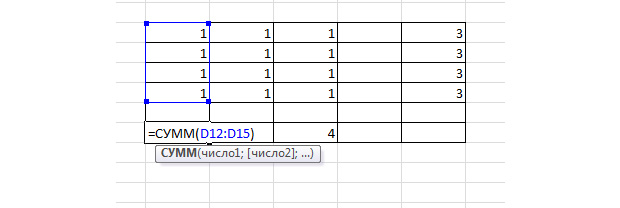
Диапазон ячеек D12 – F15 заполняем единицами. Эти значения мы впоследствии будем изменять, чтобы найти самый дешёвый вариант перевозки. В диапазоне H12 – H15 должна быть сумма трёх единиц таблицы в строке D12 – F12, а в D17 – F17 – сумма четырёх единиц в столбце. Так напротив каждой строки и каждого столбца

Шаг 3

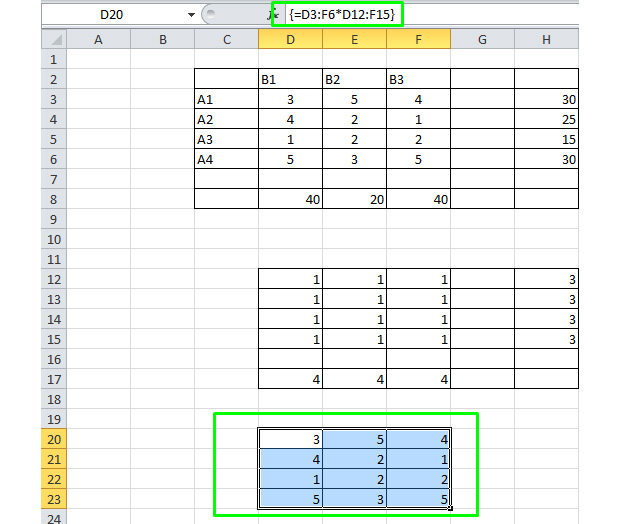
Рисуем третью таблицу, которая перемножит соответствующие ячейки первых двух таблиц.

Для этого выделяем диапазон 3 на 4 клетки, жмём на кнопку « = », выделяем диапазон D3-F6, жмём на клавиатуре « * », выделяем D12 – F15 и зажимаем сочетание клавиш Ctrl + Shift + Enter. Всё, вы перемножили значения.

Шаг 4

Теперь суммируем все значения последней таблицы. Для этого просто выберите произвольную свободную ячейку в MS Excel. Введите в неё « =СУММ( » и выделите третью таблицу. Нажмите Enter.

Шаг 5

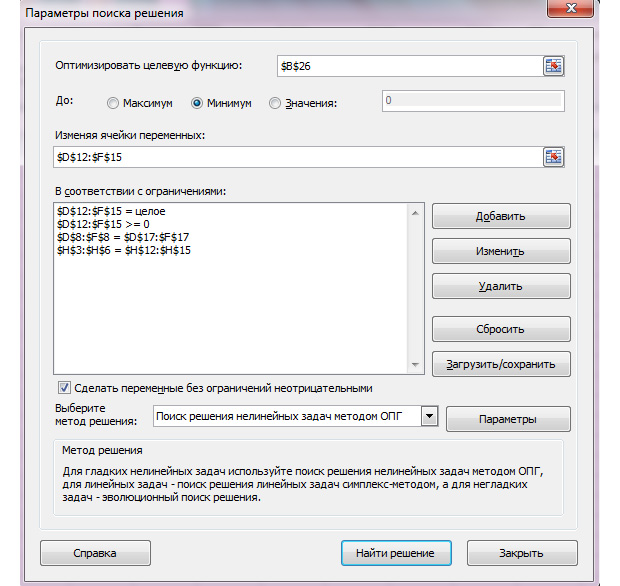
Переходим во вкладку «Данные» и находим там «Поиск решения».

Щелкаем по данной кнопке. Далее всё делаем, как представлено на рисунке.

Описываю сверху вниз всё окно. Выберите целевую ячейку ту, которую мы сделали в 4-ом шаге нашего решения. Далее выберите минимум. В поле «Изменяя ячейки переменных» выберите диапазон, где мы проставили единицы. Выставляем ограничения. Значения, которые будут находиться вместо единиц, должны быть больше нуля и целыми, а потребности не должны превысить запасов. Жмём «Найти решение».

Получаем следующий результат.

Если вы всё сделали правильно, то у вас должно быть всё точно так же.

Заключение

По второй таблице сверху вы видите, сколько тонн и куда мы повезём. В третьей таблице вы видите, сколько это будет стоить. Например, мы повезём 30 тонн в B1 со склада A1 и 10 тонн со склада A3, так как спрос у пункта B1 равен 40. Аналогично и с другими пунктами.

Источник