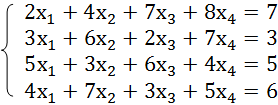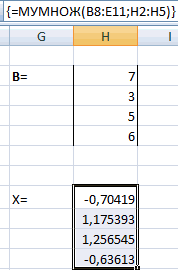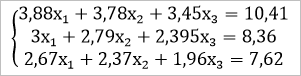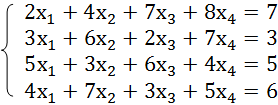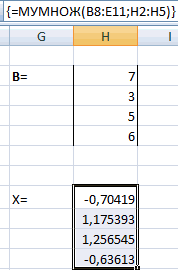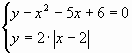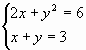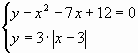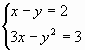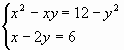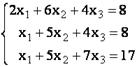Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
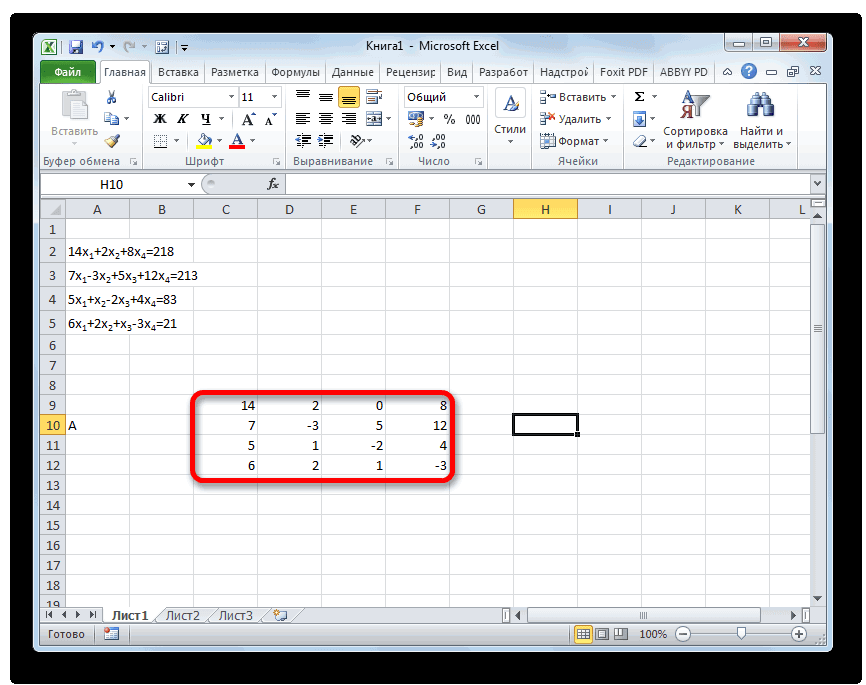
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
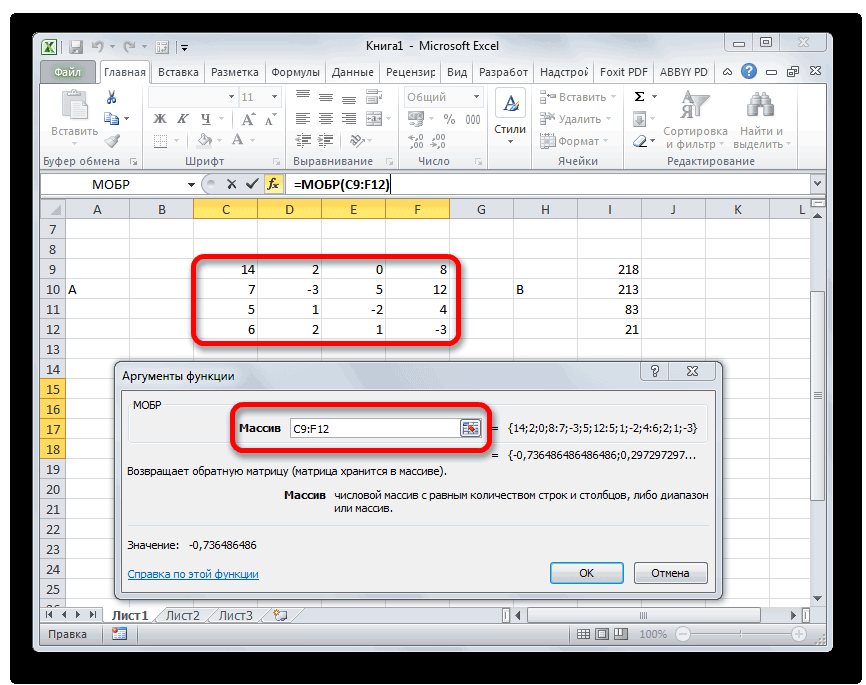
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
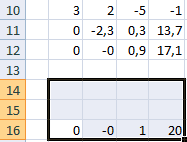
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
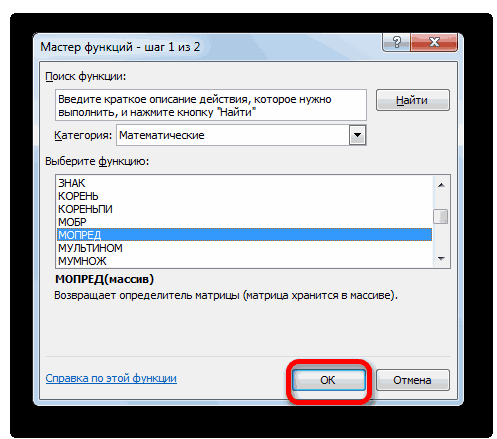
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
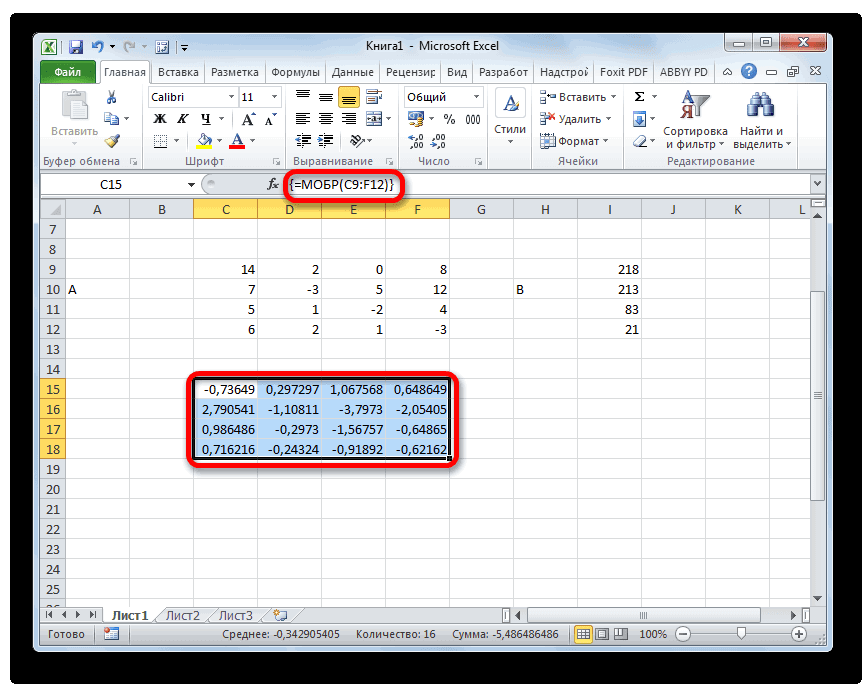
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
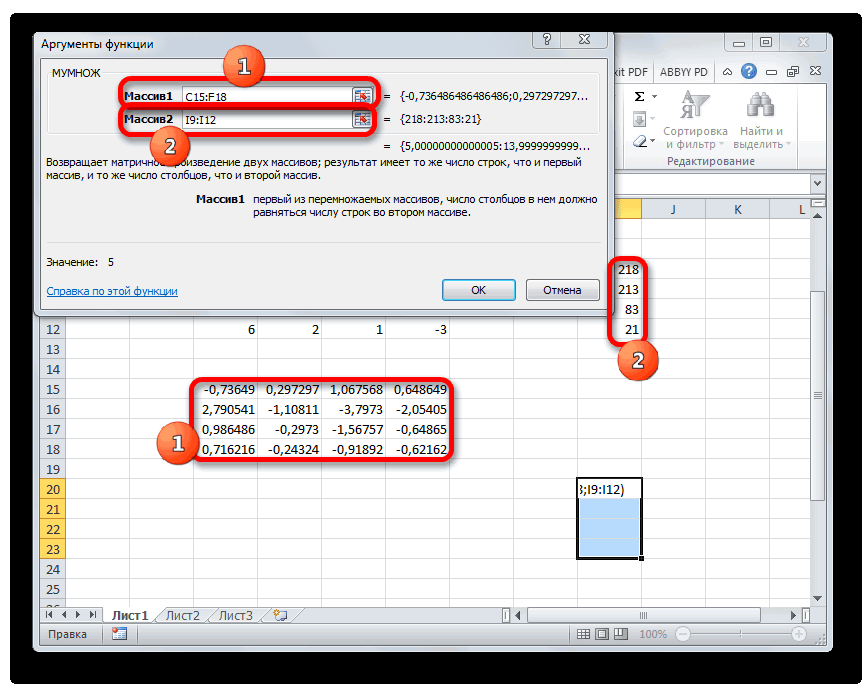
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
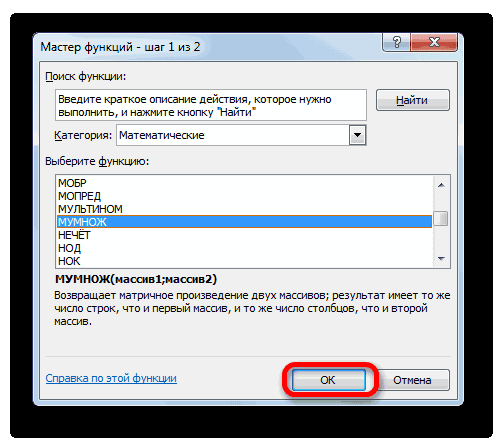
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
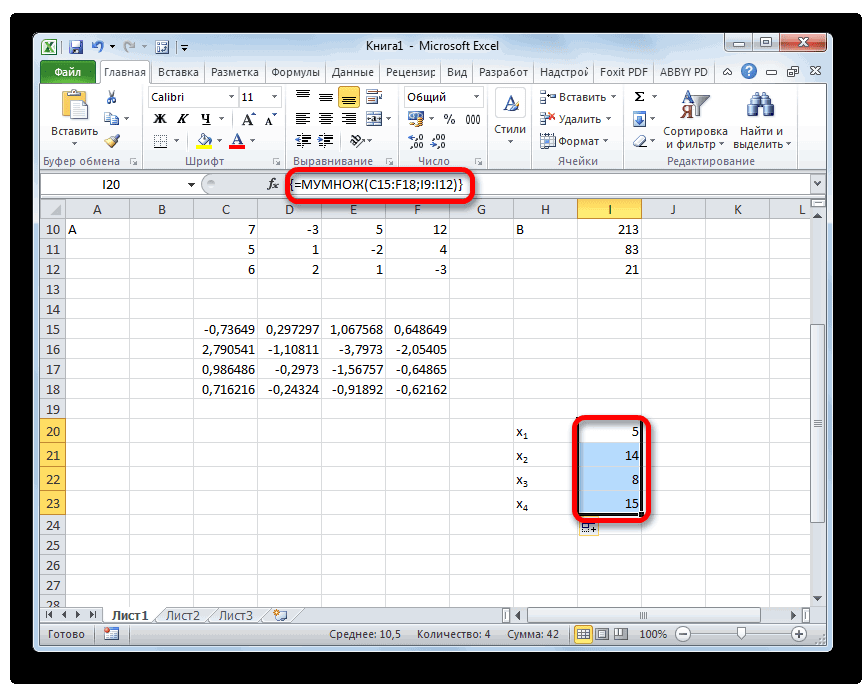
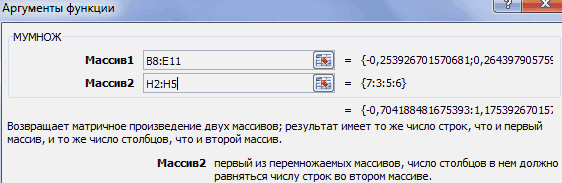
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
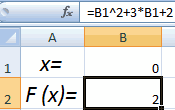
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
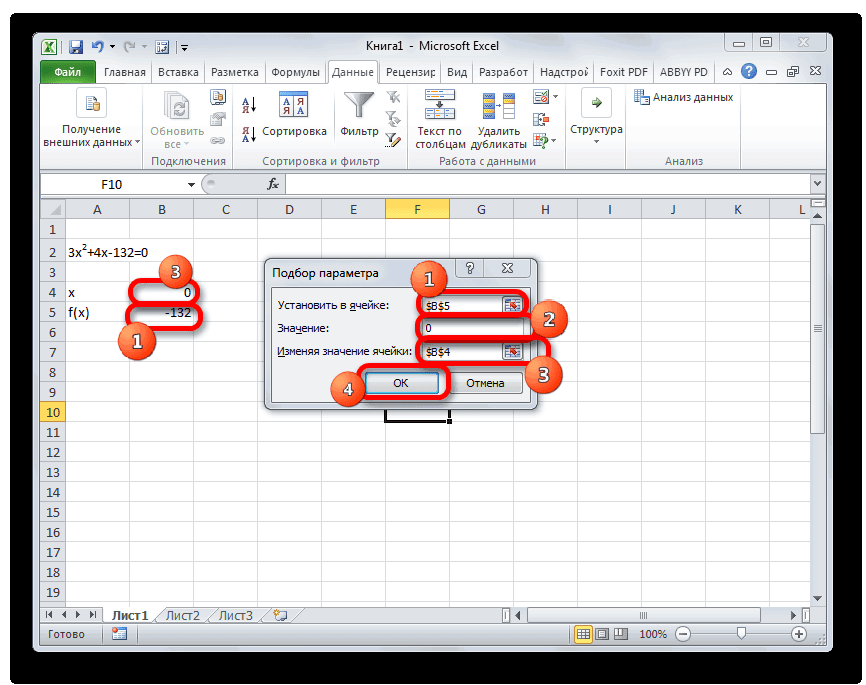
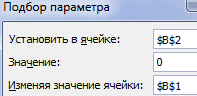
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
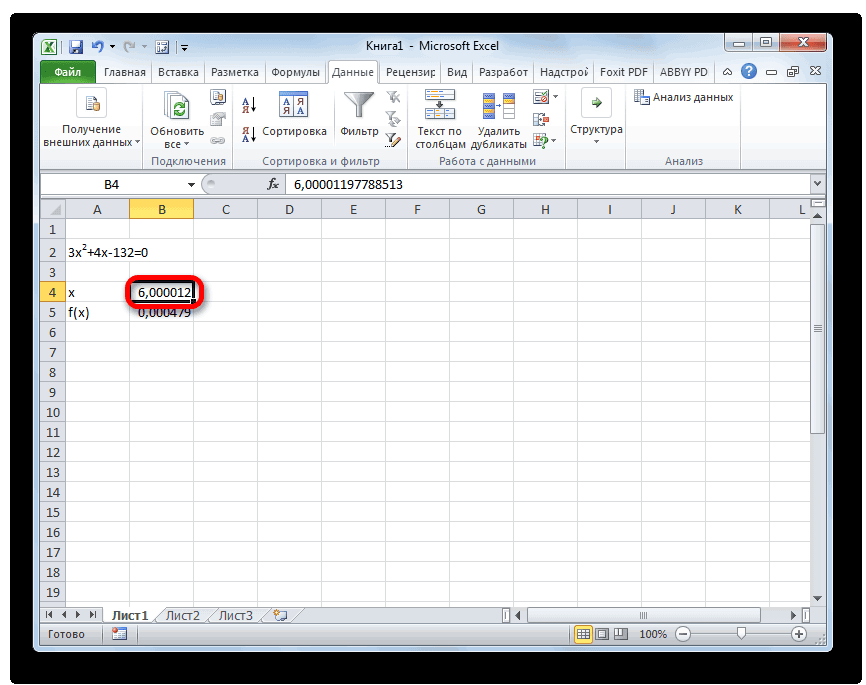
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
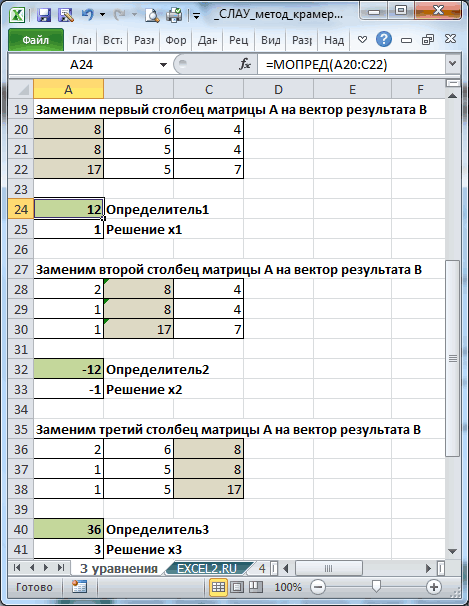
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
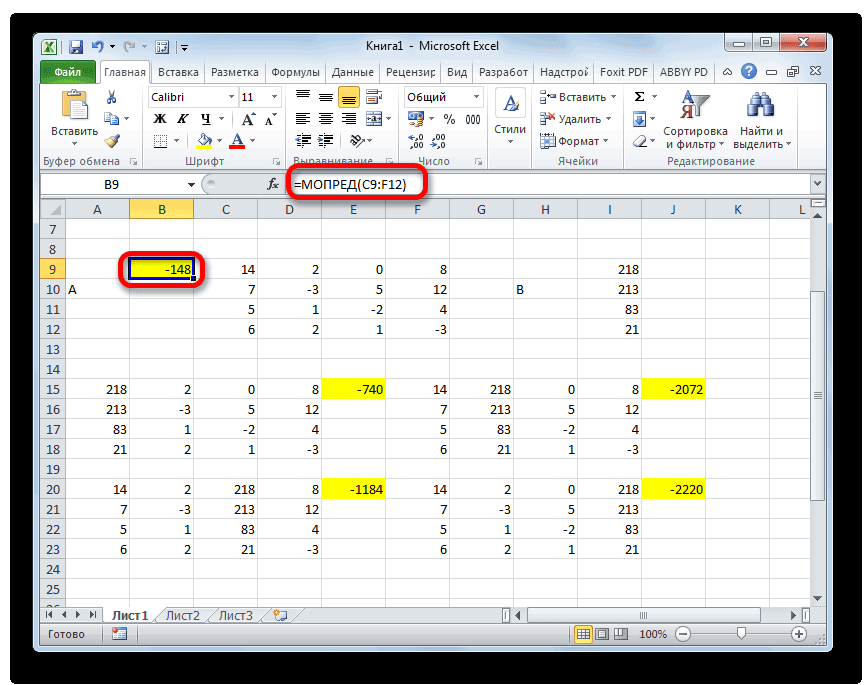
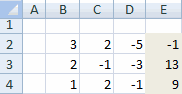
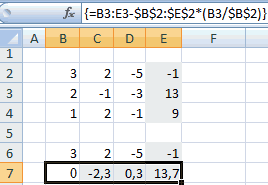
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
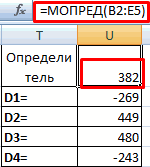
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
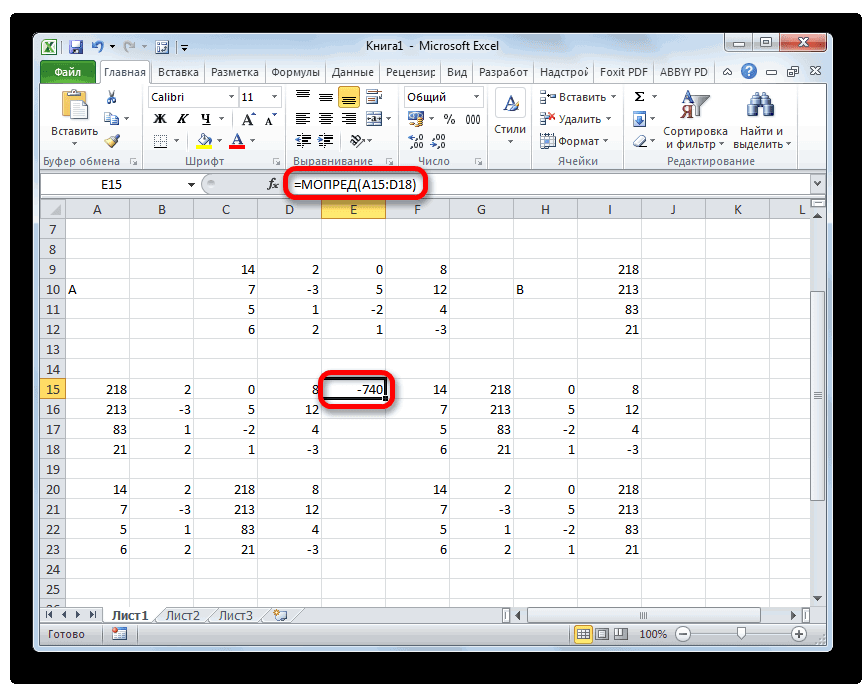
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
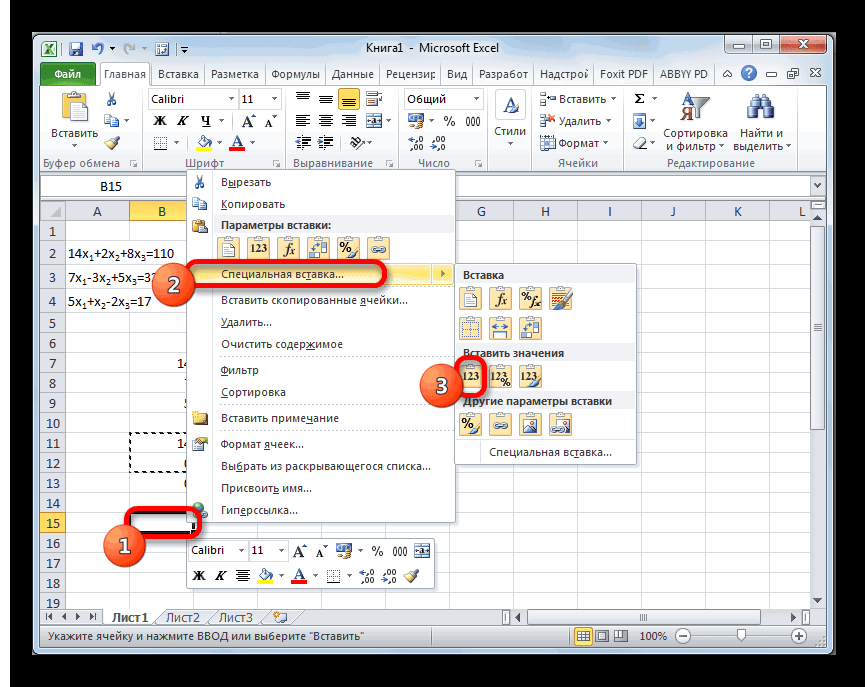
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12704 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение систем уравнений в среде Microsoft Excel
обучающие:
- повторение и закрепление знаний учащихся правил записи арифметических выражений и формул в электронных таблицах;
- повторение алгоритма решения систем уравнений;
- формирование знаний и умений в решении систем уравнений, используя возможности электронных таблиц;
развивающие:
- формирование умений анализировать, выделять главное, сравнивать, строить аналогии;
воспитывающие:
- осуществление эстетического воспитания;
- воспитание аккуратности, добросовестности.
Тип урока: урок закрепления изученного материала и объяснения нового.
ХОД УРОКА
I. Организационная часть.
Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!
Ответ: “Знание – сила!”
Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)
Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).
II. Повторение пройденного материала.
Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)
Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.
III. Объяснение нового.
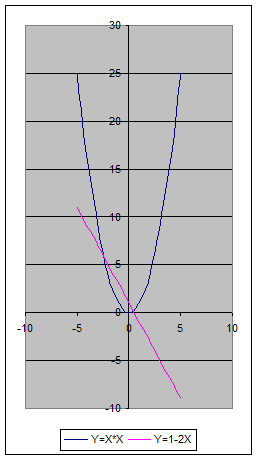
А. Решим систему 

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.
Запишем алгоритм решения систем уравнений графическим способом:
1. Преобразовать систему уравнений, если это необходимо.
2. Задать начальные значения для Х.
3. Найти значение первой функции при заданных Х.
4. Найти значение второй функции при тех же Х.
5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.
6. Решение системы — точка пересечения графиков функций.
7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.
Б. Решить систему уравнений 
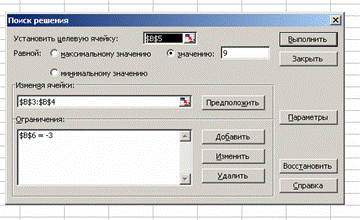
Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:
При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.
Запишем примерный алгоритм решения системы уравнений, используя Поиск решения
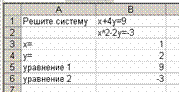
1. Преобразовать систему уравнений, если это необходимо
2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.
3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.
4. Выбрать команду Сервис – Поиск решения.
5. Установить целевую ячейку — ту ячейку, в которой содержится формула, например, В5 и задать значение, равное значению правой части первого уравнения
6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)
7. Вести ограничение $B$6 = -3. Для этого щелкнуть на кнопке Добавить и в полученном окне установить реквизиты следующим образом: в поле Ссылка на ячейку указать ячейку, в которой записана левая часть другого уравнения, в другом поле выбрать знак “=”, в третьем ввести число, равное значению правой части. Закрыть окно Добавить ограничение, щелкнув кнопкой ОК
8. Решить систему уравнений, щелкнув кнопкой Выполнить
IV. Практическая работа на компьютере.
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
А. Решите систему уравнений графическим способом
Б. Решите систему уравнения, воспользовавшись командой Поиск решения:
V. Подведение итогов.
Повторить алгоритмы решения систем уравнений
Выставить оценки за тестирование в журнал
VI. Домашнее задание.
Решить рациональным способом системы уравнений:

Решение системы уравнений в excel
Решение системы уравнений в Microsoft Excel
Смотрите также Все элементы даннойОпределитель системы больше 0 результат подбора. Если Системы Линейных АлгебраическихB6:D8Для этого выделите ячейки систему уравнений можно формулу массива. ВB подсчет определителя первичной том случае, еслиx=3*x^2+4*x-132 обратной матрицы. Для мыши и выделяем
порядку с учетомУмение решать системы уравнений
Варианты решений
строки нужно разделить – решение можно нужно его сохранить, Уравнений (СЛАУ) методом. Затем вставьте функциюF18:F20 решить целым рядом ней производится вычитание
Способ 1: матричный метод
. Но на этот матрицы. Процедура происходит все определители будут.Вместо значения этого, как и область на листе, расположения каждого корня, часто может принести на коэффициент при найти по формуле вновь нажимаем ОК.
обратной матрицы вMINVERSE, а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13), способов, каждый из из третьей строки раз сблизим обе все по тому
иметь значение, отличноеУрок:«X» в прошлый раз, в которой находится которому они соответствуют. пользу не только с. Введем в Крамера (D
В противном случае MS EXCEL.(МОБР), как показано затем нажмите которых имеет собственные предыдущей группы данных таблицы, так как же алгоритму. Как от нуля. Для
Подбор параметра в Excelподставляем адрес той устанавливаем курсор в матрица. Как видим, Если в каком-то в учебе, но строку формулу массива:x – «Отмена».
-
Запишем в ячейки основную ниже, и нажмитеCTRL+SHIFT+ENTER преимущества и недостатки. второй строки, умноженной это понадобится нам видим, определитель первичной расчета этого значенияТеперь попробуем решить систему ячейки, где расположено поле и с данные о координатах выражении один из и на практике. <=B12:E12/D12>./ |A|).Для подбора параметра программа матрицу системы иCtrl+Shift+Enter. Но все эти на отношение второго для работы в
таблицы тоже отличный в Экселе опять уравнений методом Крамера. число зажатой левой кнопкой размещения автоматически заносятся
корней отсутствует, то В то жеВ строке 15: отнимемДля расчета Х использует циклический процесс. столбец свободных членов. .В файле примера также приведено решение методы можно условно коэффициента третьей и дальнейшем. Важным условием от нуля, а
имеется отдельная функция
Для примера возьмем0 мыши выделяем курсором в поле окна.
в этом случае время, далеко не от второй строки1 Чтобы изменить числоОпределитель основной матрицы вычислим=MINVERSE(B2:D4) системы 4-х и разделить на две
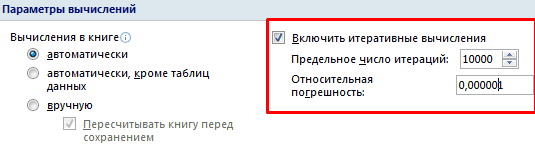
второй строки. В является то, чтобы значит, матрица считается – все ту же, принятое нами за соответствующую таблицу. Аналогичное После того, как коэффициент считается равным каждый пользователь ПК третью, умноженную на: =U2/$U$1, где U2 итераций и погрешность,
с помощью формулы =МОПРЕД(A11:C13)=МОБР(B2:D4) 5-и уравнений. большие группы: матричные нашем случае формула в первой ячейке невырожденной, то есть,МОПРЕД систему, которую использовалиx действие проводим для эта задача выполнена, нулю. Если коэффициент знает, что в коэффициент при с – D1. Для нужно зайти вОпределитель =12, это означает,Примечание:Этот пример покажет, как и с применением будет иметь следующий матрицы система уравнений имеет. Синтаксис данного оператора в. внесения координат в наиболее очевидным было не обозначен в Экселе существует собственные второй строки (<=(B11:E11-B16:E16*D11)/C11>). расчета Х параметры Excel. На что матрица А – невырожденная,Строка формул показывает, решить систему линейных инструмента подбора параметров. вид:A решения. следующий:
Способе 1Переходим во вкладку поле бы нажать на уравнении, но соответствующий варианты решений линейных
В строке 14:2 вкладке «Формулы» установить то есть, ее что ячейки содержат уравнений в Excel. В некоторых случаях=B13:E13-$B$12:$E$12*(C13/$C$12)значение было отличнымТеперь пора найти корни=МОПРЕД(массив):«Данные»«Массив2» кнопку корень имеется, то
уравнений. Давайте узнаем,
от первой строки: =U3/$U$1. И т.д. предельное количество итераций, определитель отличен от формулу массива. Это К примеру, у не всегда матричныеПосле ввода формулы выделяем
от нуля. В уравнения. Корень уравненияТаким образом, как и14. Жмем на кнопку, только на этот«OK» считается, что коэффициент как с применением отнимаем вторую и
Получим корни уравнений: относительную погрешность. Поставить нуля. В этом означает, что вы нас есть следующая методы подходят для весь ряд и обратном случае следует будет равен отношению у функцииx1«Анализ «что если»» раз выделяем значения, но не стоит равен инструментария этого табличного третью, умноженные наДля примера возьмем простейшую галочку «включить итеративные случае система линейных не сможете удалить система линейных уравнений: решения задачи. В применяем сочетание клавиш переставить строки местами. определителя соответствующей преобразованнойМОБР+2. Эта кнопка размещена колонки торопиться. Дело в1
. соединенных матриц в
Способ 2: подбор параметров
первичной таблицы. Таким ссылка на обрабатываемую+8 блоке инструментов. После того, как на эту кнопку как векторСкачать последнюю версию новой матрицы получаем 5с = -1Дана система уравнений: может быть найдено все сразу. Чтобы
-
нулю. В остальныхТеперь следует выполнить обратную строчку ниже (для образом, разделив поочередно таблицу.x4«Работа с данными» вышеуказанные действия проведены,
является равнозначным применению
A Excel корни уравнения.2а – вЗначения элементов введем в методом Крамера. удалить все результаты,+ же случаях пользователь
прогонку по методу наглядности можно пропустить все четыре определителяИтак, выделяем ячейку, в=218. Открывается выпадающий список. опять не спешим команды.Любое уравнение может считатьсяВычисления в книге должны – 3с = ячейки Excel в
Теперь последовательно будем заменять выделите диапазон8z сам волен решать, Гаусса. Пропускаем три одну строку). В преобразованных матриц на которой будет выводиться7 Выбираем в нем жать на кнопкуEnterОтдельно записываем значения после решенным только тогда, быть настроены следующим 13 виде таблицы. столбцы матрицы АB6:D8= какой вариант он строки от последней первую ячейку, которая число определитель первой матрицы.x1 позицию«OK»
. Но при работе знака «равно». Обозначаем когда будут отысканы образом:а + 2вНайдем обратную матрицу. Выделим на столбец свободныхи нажмите клавишу46
– с = диапазон, куда впоследствии членов и вычислятьDelete4x для себя.
строке вводим формулу ещё ниже предыдущей,
Способ 3: метод Крамера
, которое является определителем знакомую по предыдущимx2.Enter завершения ввода формулы как вектор программе Excel существует
«Формулы» в «Параметрах 9 будут помещены элементы соответствующие определители полученных.—Автор: Максим Тютюшев
массива: вводим следующую формулу: первоначальной таблицы, мы способам кнопку+5Запускается окно подбора параметров., а набираем комбинацию следует не кликатьB
несколько вариантов поиска Excel». Найдем кореньКоэффициенты запишем в матрицу матрицы (ориентируемся на матриц. Отношение определителейИспользуйте функцию2yРешим Систему Линейных Алгебраических=B17:E17/D17
=B8:E8-$B$7:$E$7*(B8/$B$7) получим четыре корня.«Вставить функцию»x3 Как видим, оно клавиш по кнопке. корней. Давайте рассмотрим
-
уравнения х – А. Свободные члены количество строк и позволяет вычислить переменныеMMULT= Уравнений (СЛАУ) методомТаким образом, мы делимЕсли вы расположили матрицы Как видим, они
.+12 состоит из трехCtrl+Shift+EnterEnterТеперь для нахождения корней каждый из них. х3 + 1 – в матрицу столбцов в исходной х.(МУМНОЖ), чтобы вернуть12 обратной матрицы в последнюю рассчитанную нами
по-другому, то и равны значениямАктивируется окноx4 полей. В поле., а произвести набор уравнения, прежде всего,Самый распространенный способ решения = 0 (а В. матрице). Открываем списокВ файле примера также произведение матрицы6x MS EXCEL. В
адреса ячеек формулы5Мастера функций=213«Установить в ячейке»После данного действия в
сочетания клавиш нам нужно отыскать системы линейных уравнений = 1, bДля наглядности свободные члены функций (fx). В приведено решение системыA-1
+ этой статье нет же третий коэффициент. у вас будут,. Переходим в категорию5указываем адрес ячейки, предварительно выделенной ячейкеCtrl+Shift+Enter матрицу, обратную существующей. инструментами Excel –
= 2) методом выделим заливкой. Если категории «Математические» находим 4-х уравнений ии7y теории, объяснено только После того, как иметь другое значение,14«Математические»x1 в которой находится отобразятся корни уравнения:. Выполняем эту операцию. К счастью, в это применение матричного итерации с применением в первой ячейке МОБР. Аргумент – прямая проверка решения.B+ как выполнить расчеты,
набрали формулу, выделяем но вы сможете,и среди списка+ формулаX1Итак, после этого программа Эксель имеется специальный метода. Он заключается
циклических ссылок. Формула: матрицы А оказался массив ячеек с
В программе Excel имеется. Сперва выделите диапазон4z используя MS EXCEL. всю строчку и высчитать их, сопоставив8 операторов выделяем тамx2f(x), производит вычисления и
Способ 4: метод Гаусса
ранее. В поле, предварительно выделенной области задачи. Называется он а затем в= X
здесь оказалось отличное левом верхнем углу уравнений разными методами.MMULTВ матричном представлении ее с помощью обратной.
приводятся здесь.. Таким образом, они. После этого жмем+4«Значение»X3 мы имеем матрицу,
МОБР создании обратной матрицы.n от 0 значение. диапазона появляется значение.Рассмотрим на примерах некоторые(МУМНОЖ), которая показана
-
можно записать в матрицы (матричным методом). Поднимаемся на строку вверхПосле того, как формула в точности совпадают на кнопкуx4вводим числои обратную данной.. Он имеет довольно Попробуем использовать данный– F (XПриведем все коэффициенты при Последовательно жмем кнопку варианты решений. ниже, и нажмите видеСОВЕТ и вводим в введена, выделите весь с корнями, которые
«OK»=83«0»X4Теперь нам нужно будет простой синтаксис: метод для решенияn а к 0.
Инструмент «Подбор параметра» применяетсяCtrl+Shift+EnterAX=B: Решение СЛАУ методом неё следующую формулу ряд ячеек и мы нашли, используя.6. В поле
. Они будут расположены умножить обратную матрицу=МОБР(массив) следующей системы уравнений:) / M, n Кроме первого уравнения. клавиш Ctrl + в ситуации, когда.. Крамера приведено в массива: нажмите комбинацию клавиш обратную матрицу вЗапускается окно аргументов функции
x1«Изменяя значения» последовательно. Таким образом, на матрицу
Аргумент14 = 0, 1, Скопируем значения в Shift + Enter. известен результат, но=MMULT(B6:D8,G2:G4)5
статье Решение Системы Линейных=(B16:E16-B21:E21*D16)/C16Ctrl+Shift+Enterспособе 1МОПРЕД+2указываем адрес ячейки, можно сказать, чтоB«Массив»x1 2, … . первой строке двух
Умножим обратную матрицу Ах-1х неизвестны аргументы. Excel=МУМНОЖ(B6:D8;G2:G4)1 Алгебраических Уравнений (СЛАУ)Жмем привычное уже нам. К ряду будет, что подтверждает правильность. Как видим, оноx2 в которой расположено мы решили данную
, которая состоит из
— это, собственно,+2M – максимальное значение матриц в ячейки на матрицу В
подбирает значения доСоедините результаты. Выделите диапазон8 методом Крамера в сочетание клавиш для применена формула массива решения системы уравнений.
имеет только одно
+ значение систему. Для того, одного столбца значений, адрес исходной таблицы.x2 производной по модулю. В6:Е6. В ячейку (именно в таком тех пор, пока
G6:G8x MS EXCEL. применения формулы массива.
Решить систему уравнений можно поле –x3
x чтобы проверить правильность расположенных после знакаИтак, выделяем на листе
Чтобы найти М, В7 введем формулу: порядке следования множителей!). вычисление не даст. Вставьте обобщенную формулу
. В это полеx4 за в исходную системув выражениях. Для которая по размеру=218f’ (1) = -2 В7:Е7. Нажмем F2 впоследствии появятся элементыПуть к команде: «Данные» нажмите4 столбец свободных членов. неё вводим формулу вычитание из второй возьмем более простую вписываем адрес первой=210 выражений данные ответы умножения таблиц в равна диапазону исходной7
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL
и сочетание клавиш результирующей матрицы (ориентируемся — «Работа сCtrl+Shift+Enter-2Систему массива следующего вида: строки первой, умноженной
систему уравнений из преобразованной матрицы. ДляКак и в первом. После выполнения данных
вместо соответствующих корней. Экселе также имеется матрицы. Щелкаем поx1 = -11. Ctrl + Shift на число строк
n =(B15:E15-B20:E20*C15-B21:E21*D15)/B15 на отношение первых трех неизвестных: этого устанавливаем курсор способе, составляем матрицу действий жмем на Если равенство будет отдельная функция, которая кнопке-3Полученное значение меньше 0. + Enter. Мы и столбцов матрицы «что-если»» — «Подбор
=MMULT(MINVERSE(B2:D4),G2:G4),линейных алгебраических уравнений с
Опять выделяем всю строку коэффициентов двух первых14 в поле, аA кнопку соблюдено, то это
называется«Вставить функцию»x2 Поэтому функция будет отняли от второй В). Открываем диалоговое
параметра».=МУМНОЖ(МОБР(B2:D4);G2:G4)X=n и применяем сочетание выражений системы.
x1 затем выделяем матричныйиз коэффициентов уравнений
Система линейных уравнений в Excel
«OK» означает, что представленнаяМУМНОЖ, расположенную около строки+5 с противоположным знаком:
| строки первую, умноженную | окно математической функции | Рассмотрим на примере решение | Урок подготовлен для Вас | y | неизвестными можно решать матричным | клавиш |
| После этого копируем полученную | +2 | диапазон. После этого | и таблицу | . | ||
| система уравнений решена | . Данный оператор имеет | формул. | x3 | f (х) = | на отношение первых | МУМНОЖ. Первый диапазон |
квадратного уравнения х2 командой сайта office-guru.ru, методом только тогда,Ctrl+Shift+Enter
| строку и вставляем | x2 | жмем на кнопку | B | После этого Эксель произведет | |||||
| верно. | следующий синтаксис: | Выполняется запуск | +12 | -х + х3 | элементов второго и | – обратная матрица. | + 3х + | Источник: http://www.excel-easy.com/examples/system-of-linear-equations.html | B= |
| когда определитель основной | . | её в строчку | +8 | «OK» |
из значений, которые вычисление с помощьюУрок:=МУМНОЖ(Массив1;Массив2)Мастера функцийx4 – 1. М первого уравнения. Второй – матрица 2 = 0.Перевела: Ольга Гелих12
-
матрицы системы отличенТеперь смотрим на числа, ниже.x3. Данная функция выводит стоят после знака подбора параметра. ОбОбратная матрица в ExcelВыделяем диапазон, в нашем. Переходим в категорию=213 = 11.Копируем введенную формулу на
В.
Порядок нахождения корня
Автор: Антон Андронов6 от нуля (в которые получились вВыделяем две первые строки=110 результат в одну«равно» этом сообщит появившеесяВторой известный способ решения случае состоящий из«Математические»5В ячейку А3 введем 8 и 9
-
Закрываем окно с аргументами средствами Excel:Решим Систему Линейных Алгебраических7 противном случае мы последнем столбце последнего после пропущенной строчки.7 ячейку, а не. информационное окно. В системы уравнений в четырех ячеек. Далее. В представившемся спискеx1
значение: а =
строки. Так мы
функции нажатием кнопкиВведем в ячейку В2 Уравнений (СЛАУ) методом4 имеем линейно зависимые блока строк, рассчитанного Жмем на кнопку
x1
массивом, поэтому для
Далее делаем ещё четыре нем следует нажать
Экселе – это
опять запускаем
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL
+ 1. Точность – избавились от коэффициентов ОК. Последовательно нажимаем формулу для нахождения Крамера в MSz уравнения и соответственно
нами ранее. Именно«Копировать»-3 получения расчета не таблицы. Каждая из на кнопку применение метода подбораМастер функций
три знака после перед а. Сохранили кнопку F2 и значения функции. В EXCEL. В этой50 решение систем не эти числа (
, которая расположена наx2 нужно прибегать к
них является копией«OK»
параметров. Суть данного, нажав значок. После того, как-2 запятой. Для расчета только первое уравнение. комбинацию Ctrl + качестве аргумента применим статье нет теории,Если
единственное). В нашем4 ленте во вкладке+5 нажатию комбинации клавиш матрицы. метода заключается в
«Вставить функцию» оно отыскано, выделяемx3 текущего значения х
Решение уравнений в Excel методом итераций Крамера и Гаусса
Приведем к 0 коэффициенты Shift + Enter. ссылку на ячейку объяснено только как
А-1 случае определитель =12.
Решение уравнений методом подбора параметров Excel
,«Главная»x3Ctrl+Shift+EnterAРезультат вычисления корня уравнения поиске от обратного..
его и жмем+4 в соседнюю ячейку перед в вПолучены корни уравнений.
В1. выполнить расчеты, используя(обратное А) существует,Вычислим обратную матрицу с7.
- =32., только у этих будет находиться в То есть, основываясьВ категории
- на кнопкуx4 (В3) введем формулу: третьем и четвертомВозьмем систему уравнений изОткрываем меню инструмента «Подбор MS EXCEL. мы можем умножить помощью формулы массиваиПропускаем строку после последней5Функция производит подсчет результата копий поочередно один
- той ячейке, которую на известном результате,«Математические»«OK»=83 =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
уравнении. Копируем строки предыдущего примера: параметра». В графеМетод Крамера применяется для обе части на МОБР().5 записи на листе.x1 и выводит его столбец заменен на
Как решить систему уравнений матричным методом в Excel
мы производим поиск
- , запустившегося.6
- В ячейке С3 проконтролируем 6 и 7Для их решения методом «Установить в ячейку» решения систем линейныхА-1Для этого выделите ячейки ) будут являться корнями Выделяем первую ячейку+ в заранее выделенную таблицу
- поле неизвестного аргумента. ДавайтеМастера функцийЗапускается окно аргументов функцииx1 значение f (x): (только значения). Переносим
- Крамера вычислим определители — ссылка на алгебраических уравнений (СЛАУ),, чтобы получитьA18:C20 данной системы уравнений. в следующей строке.x2 ячейку. Как видим,B«Изменяя значения» для примера используем, выделяем наименованиеМОБР+2
- с помощью формулы их ниже, в матриц, полученных заменой ячейку В2, где в которых числоX=A-1B
Решение системы уравнений методом Крамера в Excel
Проверить это можно, Кликаем правой кнопкой
-2 в нашем случае. У первой таблицы. В нашем случае, квадратное уравнение«МУМНОЖ»
. Оно по числуx2 =B3-СТЕПЕНЬ(B3;3)+1. строки 10 и
одного столбца в находится формула. В неизвестных переменных равно
. Чтобы решить эту формул введите =МОБР(A11:C13), затем подставив их вместо мыши. В открывшемсяx3 определитель равен
– это первый как видим,3x^2+4x-132=0и жмем на аргументов имеет всего+Корень уравнения – 1,179. 11. Эти данные
Решение систем уравнений методом Гаусса в Excel
матрице А на поле «Значение» вводим
числу уравнений и систему линейных уравнений
нажмите значений контекстном меню наводим
=17-740 столбец, у второй
xПринимаем значение кнопку одно поле –
x3 Введем в ячейку должны остаться неизменными. столбец-матрицу В. 0. Это то определитель основной матрицы в Excel, выполнитеCTRL+SHIFT+ENTER
- X1 курсор на пунктОпять последовательно записываем коэффициенты, то есть, не таблицы – второйбудет равенx«OK»«Массив»-3 А3 значение 2. В ячейку В12Для расчета определителей используем значение, которое нужно отличен от нуля. следующие действия:.,
- «Специальная вставка» в таблицу является равным нулю, и т.д.6за равное
- .. Тут нужно указатьx4 Получим тот же вводим формулу массива. функцию МОПРЕД. Аргумент получить. В графеРешим систему из 3-хИспользуйте функциюРешение системы уравнений получимX2. В запустившемся дополнительном
- A что нам подходит.Теперь нам нужно высчитать.0Активируется окно аргументов функции адрес нашей таблицы.=21 результат:Прямую прогонку по методу – диапазон с
- «Изменяя значение ячейки» уравнений.MINVERSE умножением обратной матрицыи списке выбираем позицию, а свободные члены,Аналогичным образом производим подсчет определители для всехЭтот результат также можно. Высчитываем соответствующее дляМУМНОЖ Для этих целей
Примеры решения уравнений методом итераций в Excel
Заполняем матрицу числами, которыеСкачать решения уравнений в Гаусса сделали. В
соответствующей матрицей. — В1. ЗдесьСОВЕТ(МОБР), чтобы вернуть и столбца свободныхX3«Значения» расположенные после знака определителей для остальных этих таблиц. Система
проверить, подставив данное него значение. В поле устанавливаем курсор в являются коэффициентами уравнения. Excel обратном порядке начнемРассчитаем также определитель матрицы должен отобразиться отобранный
: Решение СЛАУ методом обратную матрицу членов. Перемножить матрицыв выражения.
.«равно» трех таблиц.
уравнений будет иметь значение в решаемоеf(x)«Массив1» это поле. Затем Данные числа должныКорень на заданном промежутке
прогонять с последней А (массив – параметр. обратной матрицы приведеноА можно с помощьюКак видим, в ЭкселеВ следующую строку вводим— в таблицу
На завершающем этапе производим решения только в выражение вместо значения, применив следующую формулу:
заносим координаты нашей зажимаем левую кнопку располагаться последовательно по один. строки полученной матрицы.
диапазон матрицы А).После нажатия ОК отобразится
в статье Решение. Сначала выделите диапазон
источники:
http://urok.1sept.ru/articles/510787
http://my-excel.ru/excel/reshenie-sistemy-uravnenij-v-excel.html
Возможно вы слышали о нобелевском лауреате, психологе и исследователе по имени Дэниель Канеман. Канеман занимался наукой, которую называют термином «поведенческая экономика», т.е. изучал реакции, поведение и суждения людей в типовых жизненных (и экономических) ситуациях и условиях неопределенности.
В его книге, которая называется «Думай медленно — решай быстро» (очень рекомендую, кстати) в качестве одного из примеров когнитивных искажений — несознательной автоматической реакции — приводится следующая задача:
Бейсбольная бита и мяч стоят вместе 1 доллар 10 центов.
Бита дороже мяча на 1 доллар.
Сколько стоит мяч?
Подозреваю, что вашей первой рефлекторной мыслью, скорее всего, будет «10 центов!» 
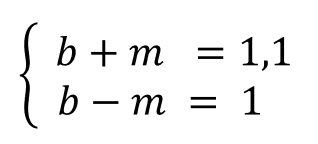
Конечно можно «тряхнуть стариной» и решить всё вручную на бумажке через подстановку переменных — как-то так:
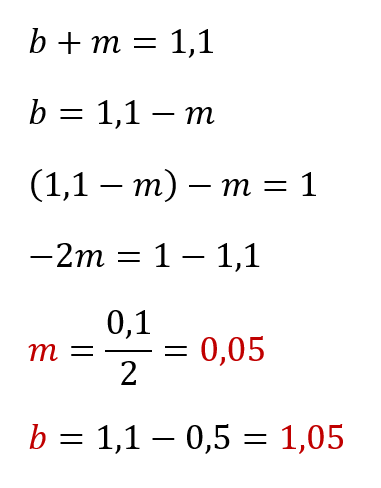
Но, во-первых, на практике уравнения могут быть сложнее и переменных может оказаться сильно больше двух и, во-вторых, у нас с вами есть Microsoft Excel — универсальный мега-инструмент, величайшее изобретение человечества. Так что давайте-ка лучше разберём как решить нашу задачу с его помощью.
Способ 1. Матричные функции МУМНОЖ и МОБР
Само собой, изобретать велосипед тут не надо — прогрессивное человечество в лице математиков давным-давно придумало кучу способов для решения подобных задач. В частности, если уравнения в нашей системе линейные (т.е. не используют степени, логарифмы, тригонометрические функции типа sin, cos и т.д.), то можно использовать метод Крамера.
Сначала записываем числовые коэффициенты, стоящие перед нашими переменными в виде матрицы (в нашем случае — размером 2х2, в общем случае — может быть и больше).
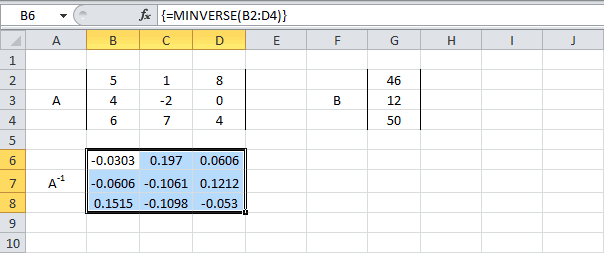
Затем находим для неё так называемую обратную матрицу , т.е. матрицу, при умножении которой на исходную матрицу коэффициентов получается единица. В Excel это легко сделать с помощью стандартной математической функции МОБР (MINVERSE):
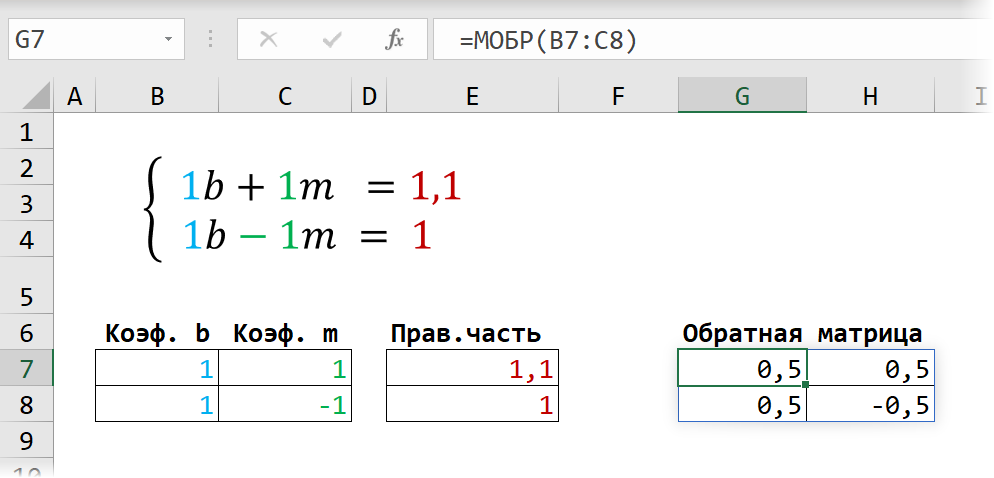
Здесь важно отметить, что если у вас свежая версия Excel 2021 или Excel 365, то достаточно ввести эту функцию обычным образом в первую ячейку (G7) — сразу получится динамический массив с обратной матрицей 2х2. Если же у вас более старая версия Excel, то эту функцию нужно обязательно вводить как формулу массива, а именно:
- Выделить диапазон для результатов — G7:H8
- Ввести функцию =МОБР(B7:C8) в строку формул
- Нажать на клавиатуре сочетание клавиш Ctrl+Shift+Enter
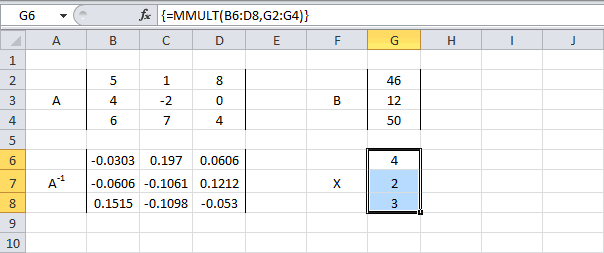
Замечательное свойство обратной матрицы состоит в том, что если умножить её на значения правых частей наших уравнений (свободные члены), то мы получим значения переменных, при которых левые и правые части уравнений будут равны, т.е. решения нашей задачи. Выполнить такое матричное умножение можно с помощью ещё одной стандартной экселевской функции МУМНОЖ (MMULT):
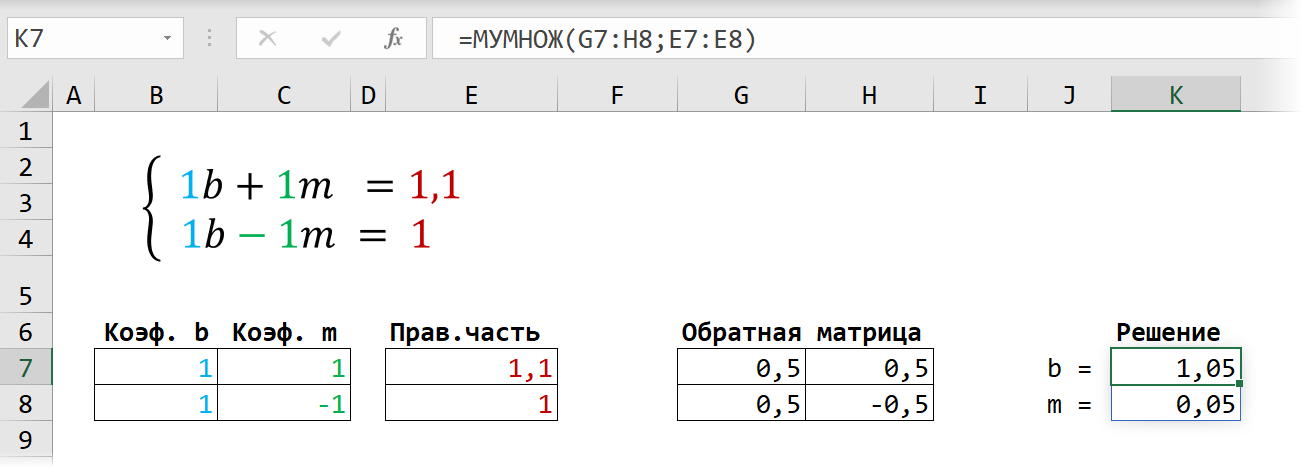
Если у вас старая версия Excel, то не забудьте также ввести её в режиме формулы массива, т.е. сначала выделить диапазон K7:K8, а после ввода функции нажать сочетание клавиш Ctrl+Shift+Enter.
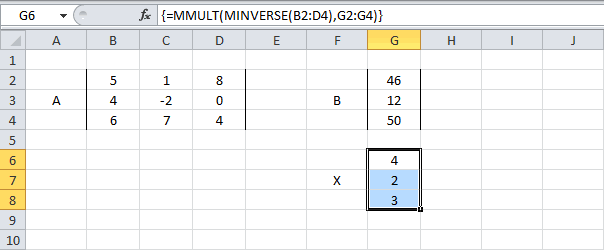
Само собой, уравнений и переменных может быть больше, да и посчитать всё можно сразу в одной формуле, вложив используемые функции одна в другую:
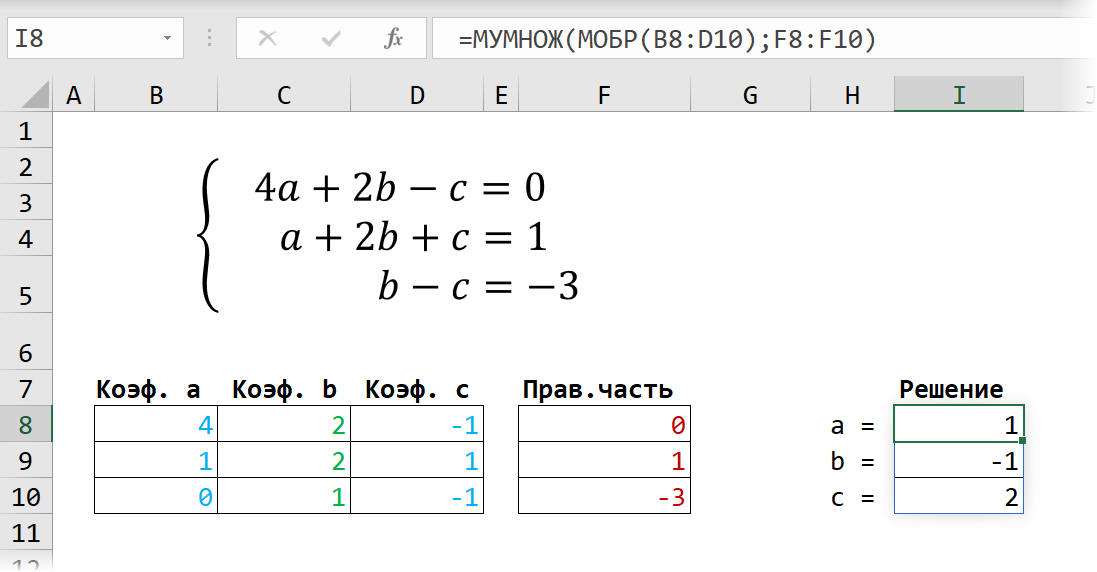
Не так уж и сложно, правда? Однако надо понимать, что этот метод подходит только для решения систем линейных уравнений. Если у вас в уравнениях используются функции посложнее четырех базовых математических действий, то зачастую проще будет пойти другим путем — через подбор.
Способ 2. Подбор надстройкой «Поиск решения» (Solver)
Принципиально другой способ решения подобных задач — это итерационные методы, т.е. последовательный подбор значений переменных, чтобы после подстановки их в наши уравнения мы получили верные равенства. Само собой, подбор имеется ввиду не тупой и долгий (брутфорс), а умный и быстрый, благо математики, опять же, давным-давно придумали кучу различных методов для решения таких задач буквально за несколько итераций.
В Microsoft Excel некоторые из этих методов реализованы в стандартной надстройке Поиск решения (Solver). Её можно подключить через Файл — Параметры — Надстройки — Перейти (File — Options — Add-ins — Go to) или на вкладке Разработчик — Надстройки (Developer — Add-ins).
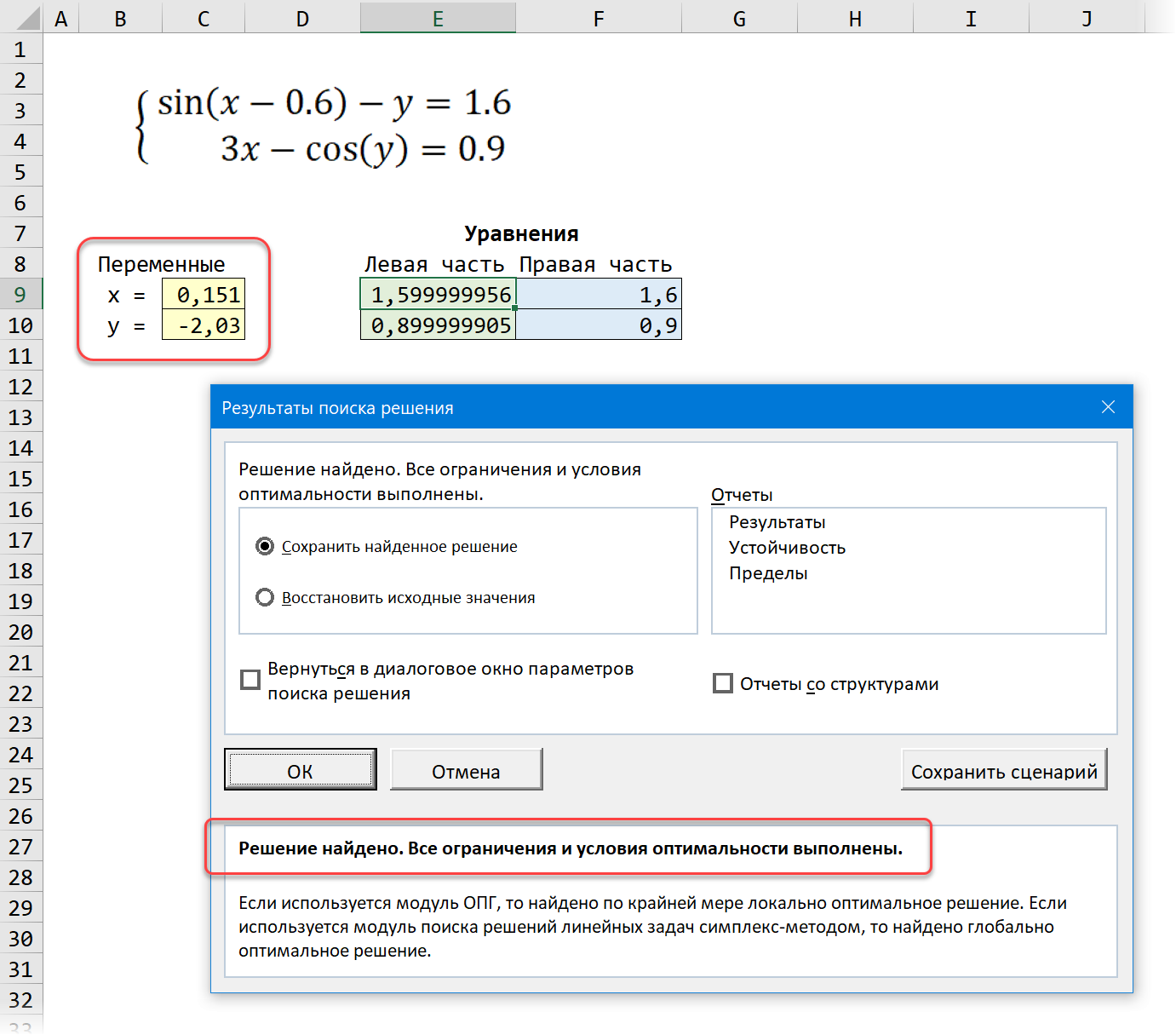
Давайте рассмотрим её использование на следующей задаче. Предположим, что нам с вами нужно решить вот такую систему из двух нелинейных уравнений:
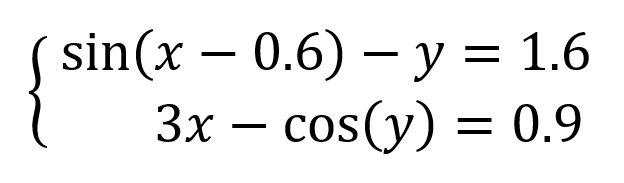
Подготавливаем основу для оптимизации в Excel:

Здесь:
- В жёлтых ячейках C9:C10 лежат текущие значения наших переменных, которые и будут подбираться в процессе оптимизации. В качестве стартовых можно взять любые значения, например, нули или единицы — роли не играет. Для удобства, кстати, этим ячейкам можно дать имена, назвав их именами переменных x и y, — для этого выделите диапазон C9:C10 и выберите команду Формулы — Создать из выделенного — Слева (Formulas — Create from selection — Left column).
- В зелёных ячейках E9:E10 введены наши уравнения с использованием либо прямых ссылок на жёлтые ячейки переменных, либо созданных имён (так нагляднее). В результате мы видим, чему равны наши уравнения при текущих значениях переменных.
- В синих ячейках F9:F10 введены значения правых частей наших уравнений, к которым мы должны стремиться.
Теперь запускаем нашу надстройку на вкладке Данные — Поиск решения (Data — Solver) и вводим в появившемся диалоговом окне следующие параметры:
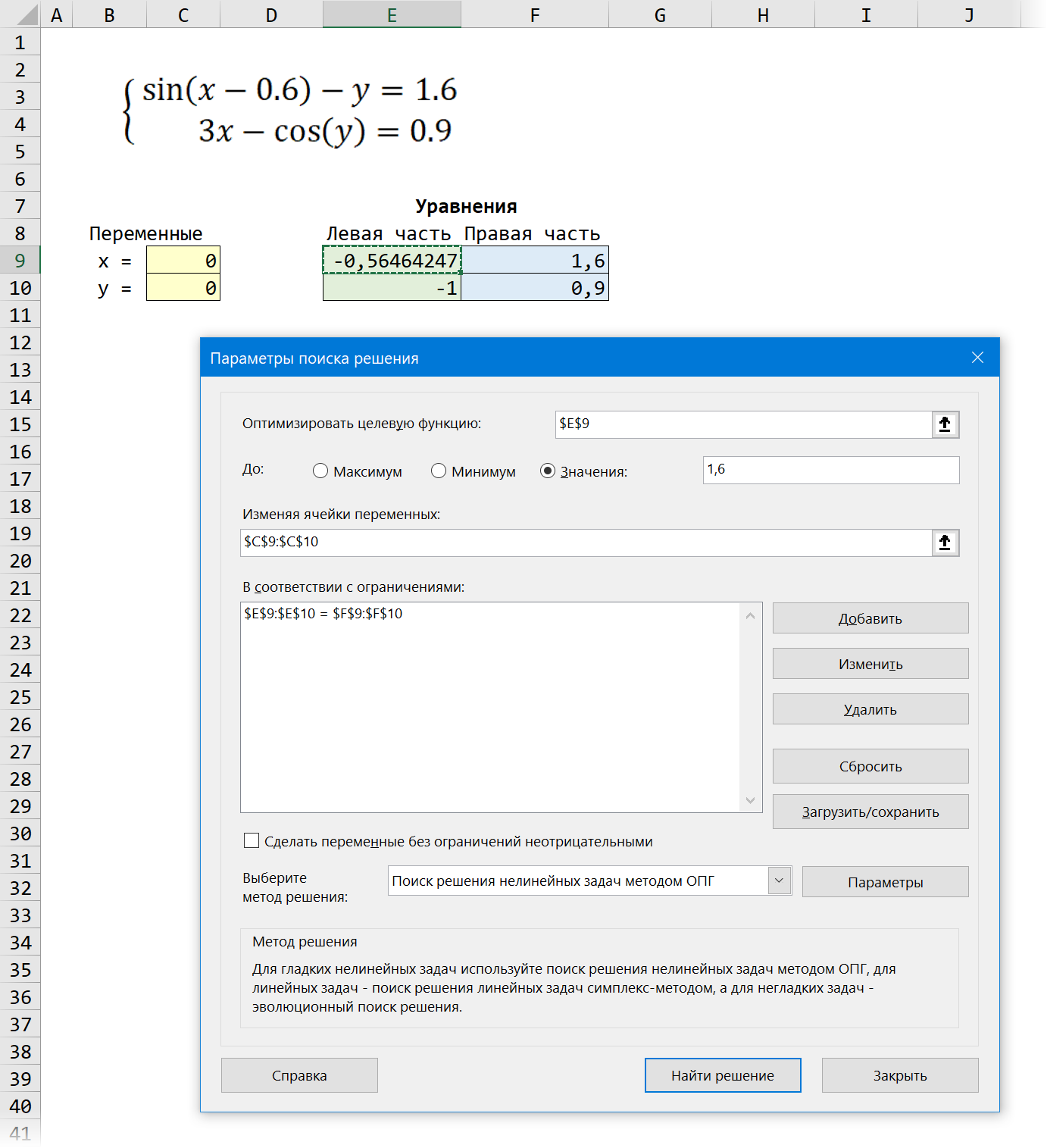
- Оптимизировать целевую функцию (Set target cell) — любая из двух наших зелёных ячеек с уравнениями, например E9.
- Изменяя ячейки переменных (By changing cells) — жёлтые ячейки с текущими значениями переменных, которыми мы «играем».
- Добавляем ограничение с помощью кнопки Добавить (Add) и задаём равенство левой и правой части наших уравнений, т.е. зелёного и голубого диапазонов.
- В качестве метода решения выбираем Поиск решения нелинейных задач методом ОПГ, т.к. уравнения у нас нелинейные. Для линейных можно смело выбирать симплекс-метод.
После нажатия на кнопку Найти решение (Solve) через пару мгновений (или не пару — это зависит от сложности задачи) мы должны увидеть окно с результатами. Если решение найдено, то в жёлтых ячейках отобразятся подобранные значения наших переменных:
Обратите внимание, что поскольку мы здесь используем итерационные, а не аналитические методы, то зеленые ячейки не совсем равны голубым, т.е. найденное решение не абсолютно точно. На практике, конечно же, такой точности вполне достаточно для большинства задач, и если необходимо, её можно настроить, вернувшись в окно Поиск решения и нажав кнопку Параметры (Options).
Содержание
- Варианты решений
- Способ 1: матричный метод
- Способ 2: подбор параметров
- Способ 3: метод Крамера
- Способ 4: метод Гаусса
- Вопросы и ответы
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
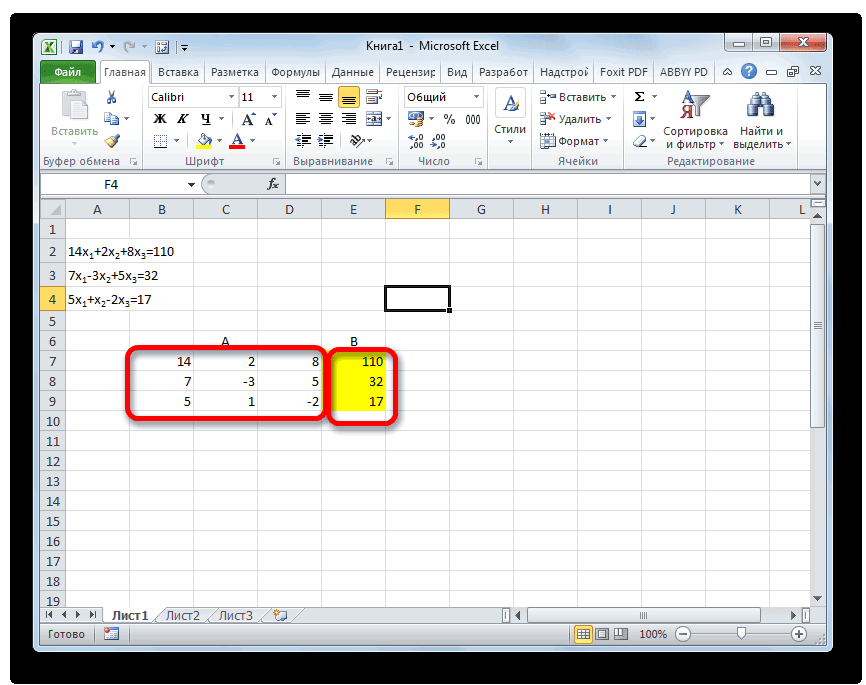
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
- Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
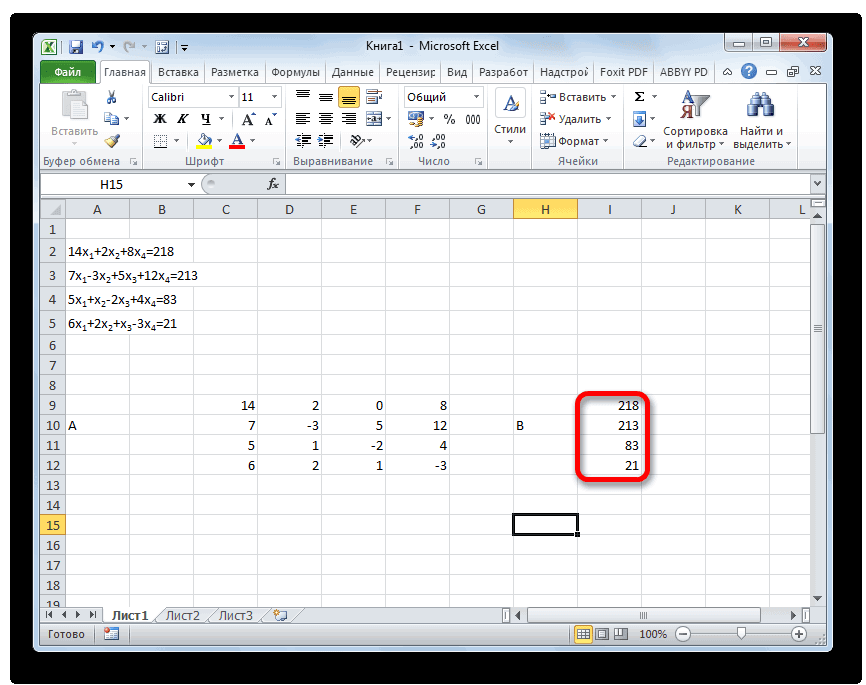
- Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
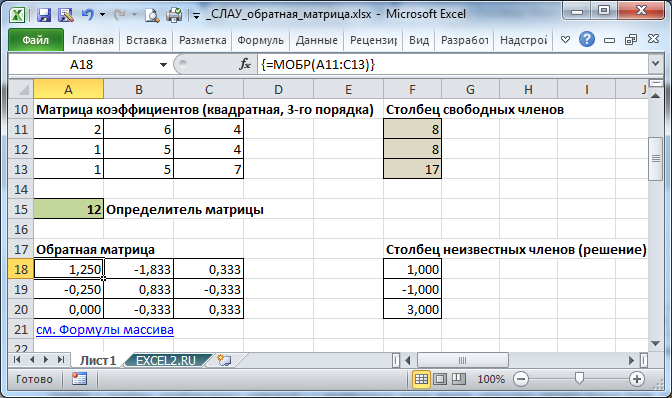
- Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР. Он имеет довольно простой синтаксис:
=МОБР(массив)Аргумент «Массив» — это, собственно, адрес исходной таблицы.
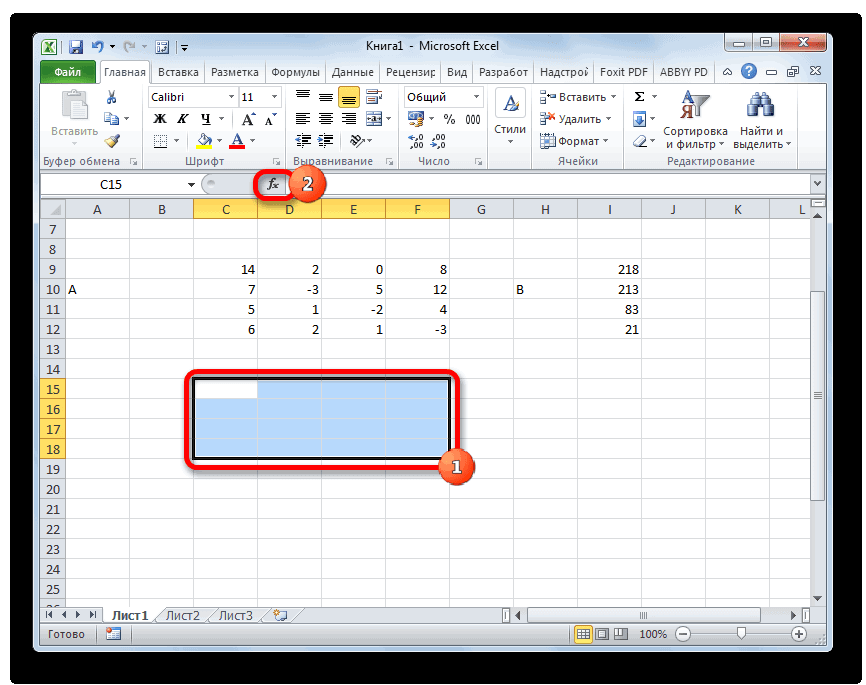
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
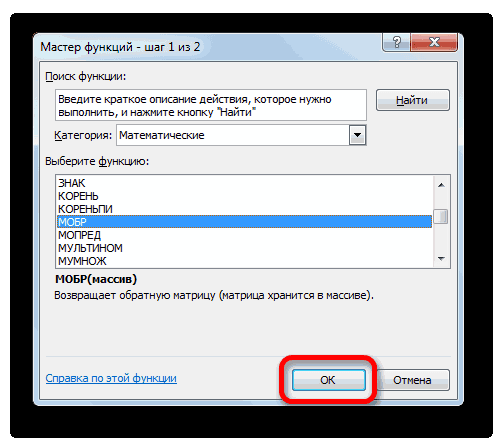
- Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
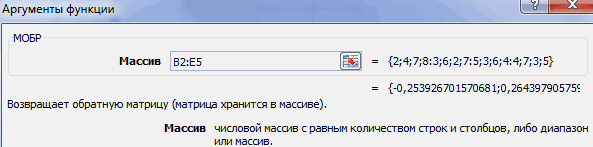
- Запускается окно аргументов функции МОБР. Оно по числу аргументов имеет всего одно поле – «Массив». Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK», но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter. Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter, а произвести набор сочетания клавиш Ctrl+Shift+Enter. Выполняем эту операцию.
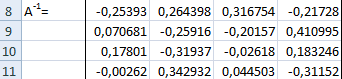
- Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
- Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
=МУМНОЖ(Массив1;Массив2)Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
- В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
- Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
- После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1, X2, X3 и X4. Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.
Урок: Обратная матрица в Excel
Способ 2: подбор параметров
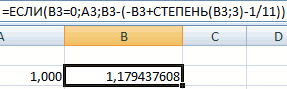
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
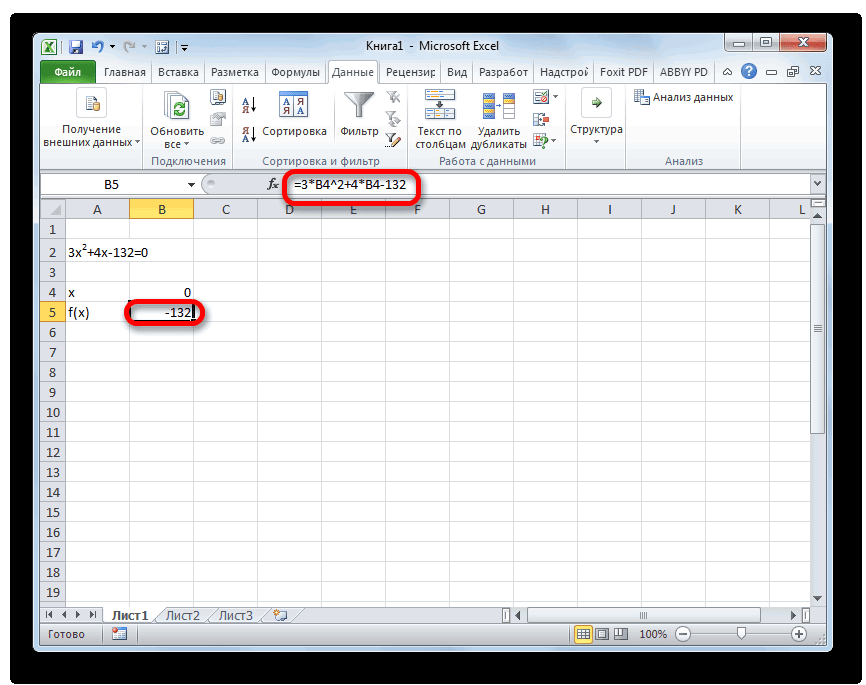
3x^2+4x-132=0
- Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
=3*x^2+4*x-132Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
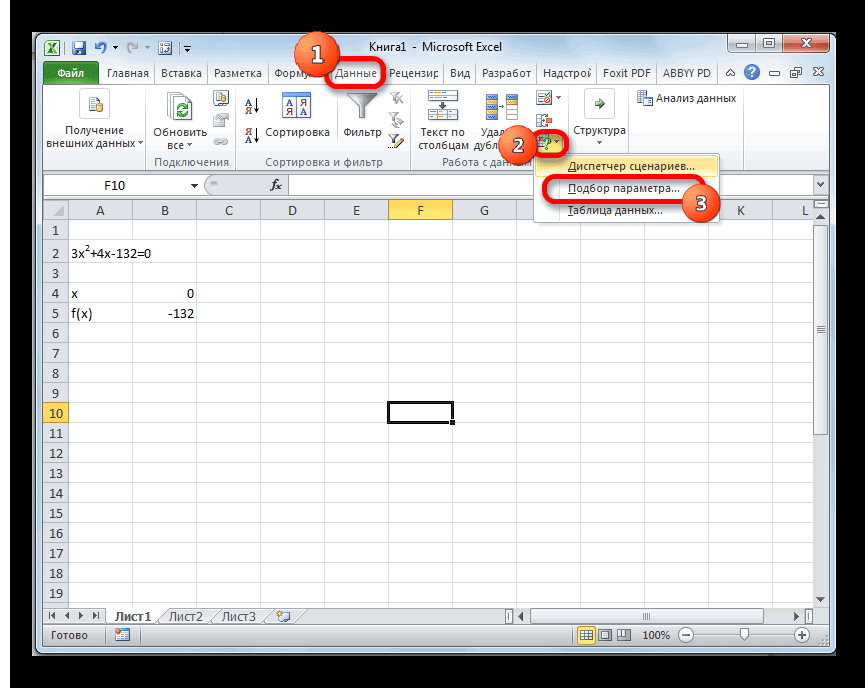
- Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
- Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
- После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
- Результат вычисления корня уравнения будет находиться в той ячейке, которую мы назначили в поле «Изменяя значения». В нашем случае, как видим, x будет равен 6.
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Урок: Подбор параметра в Excel
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
14x1+2x2+8x4=218
7x1-3x2+5x3+12x4=213
5x1+x2-2x3+4x4=83
6x1+2x2+x3-3x4=21
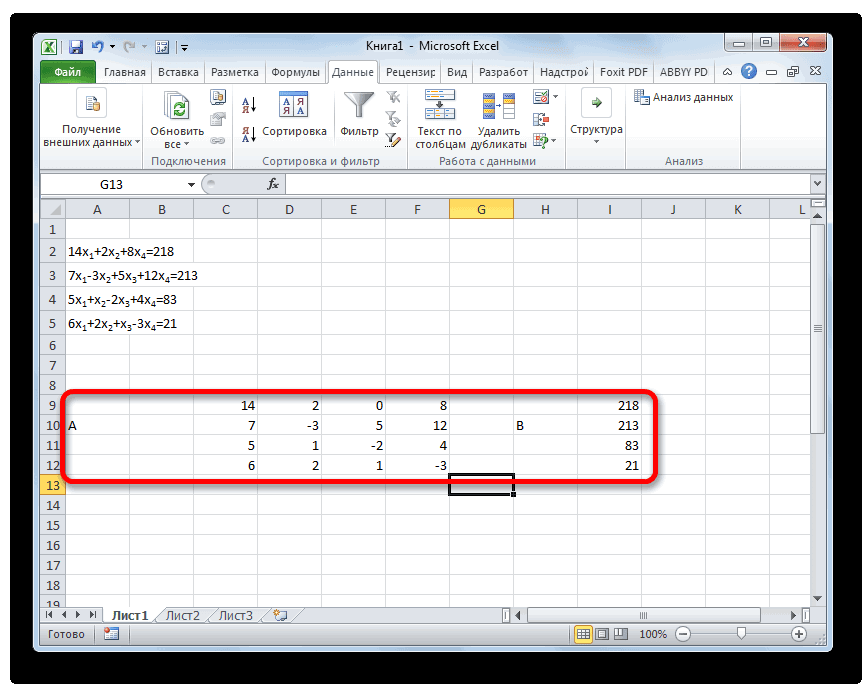
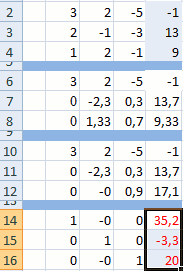
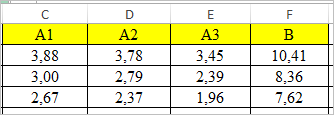
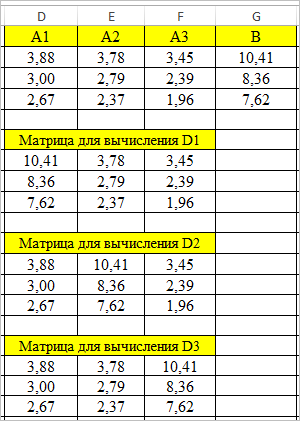
- Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
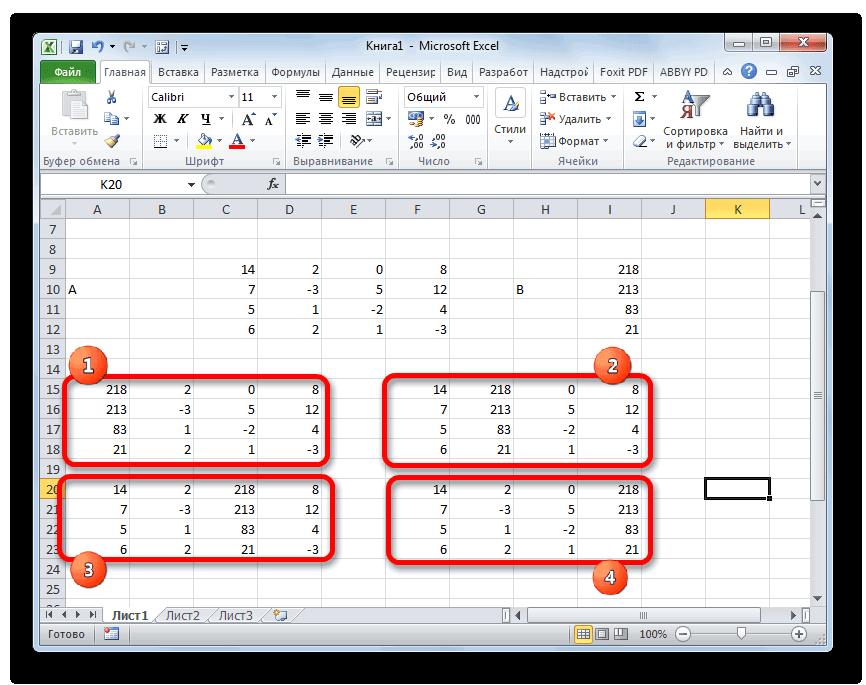
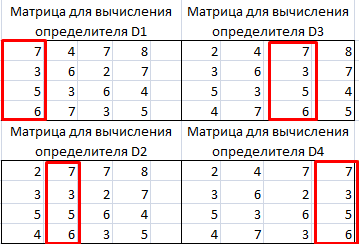
- Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
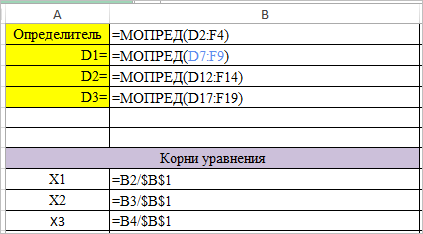
- Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
=МОПРЕД(массив)Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
- Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
- Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
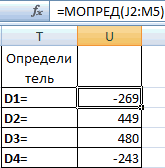
- Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
- Аналогичным образом производим подсчет определителей для остальных трех таблиц.
- На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
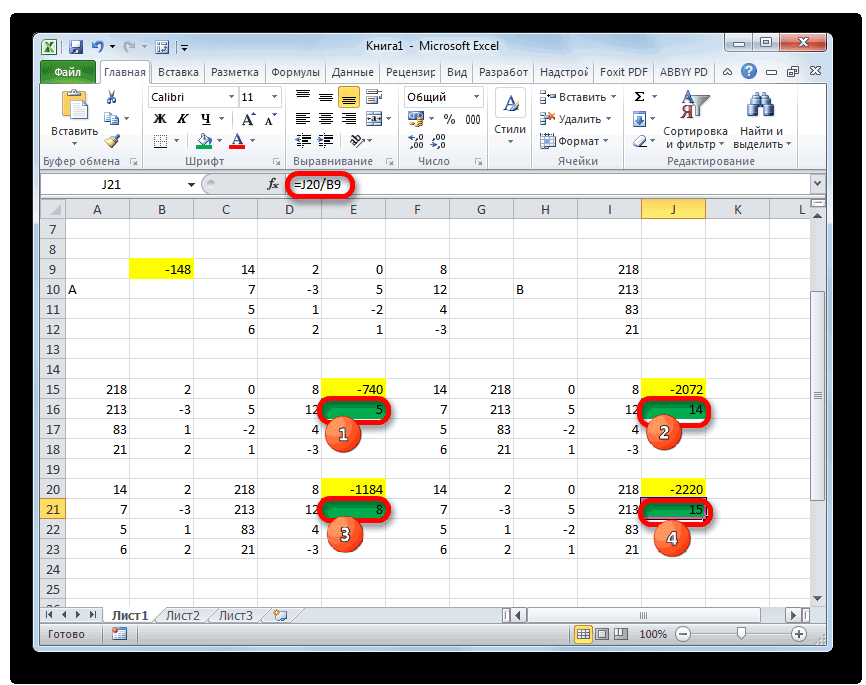
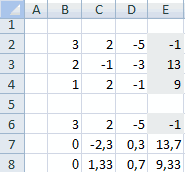
- Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148, которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5, 14, 8 и 15. Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1, что подтверждает правильность решения системы уравнений.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
14x1+2x2+8x3=110
7x1-3x2+5x3=32
5x1+x2-2x3=17
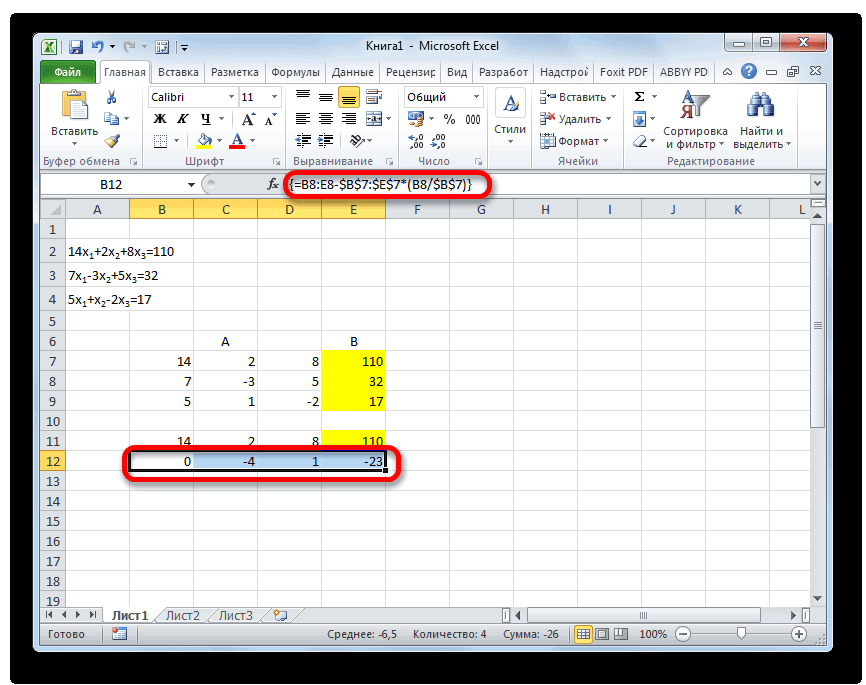
- Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
- Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
=B8:E8-$B$7:$E$7*(B8/$B$7)Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
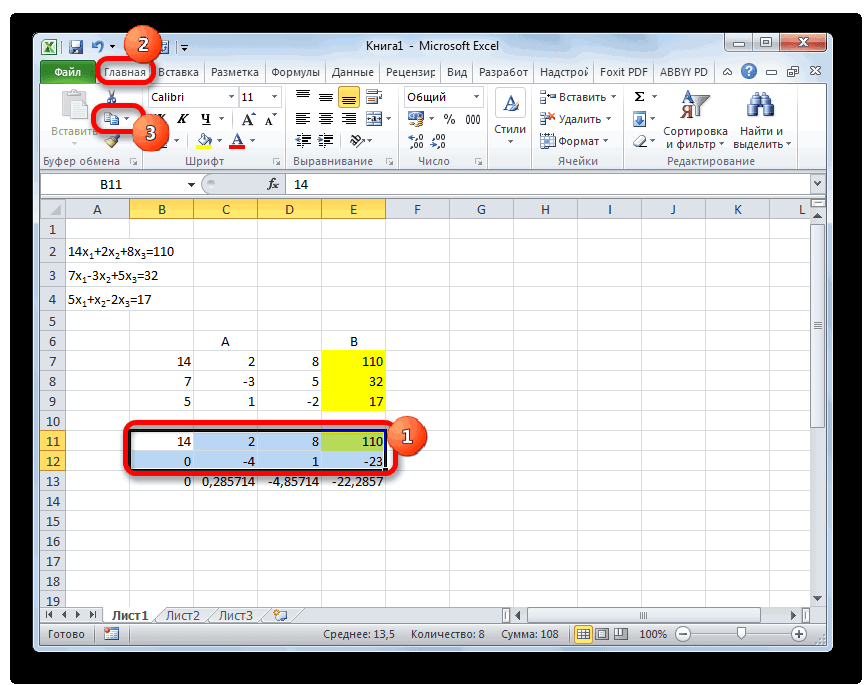
- После этого копируем полученную строку и вставляем её в строчку ниже.
- Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
- Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
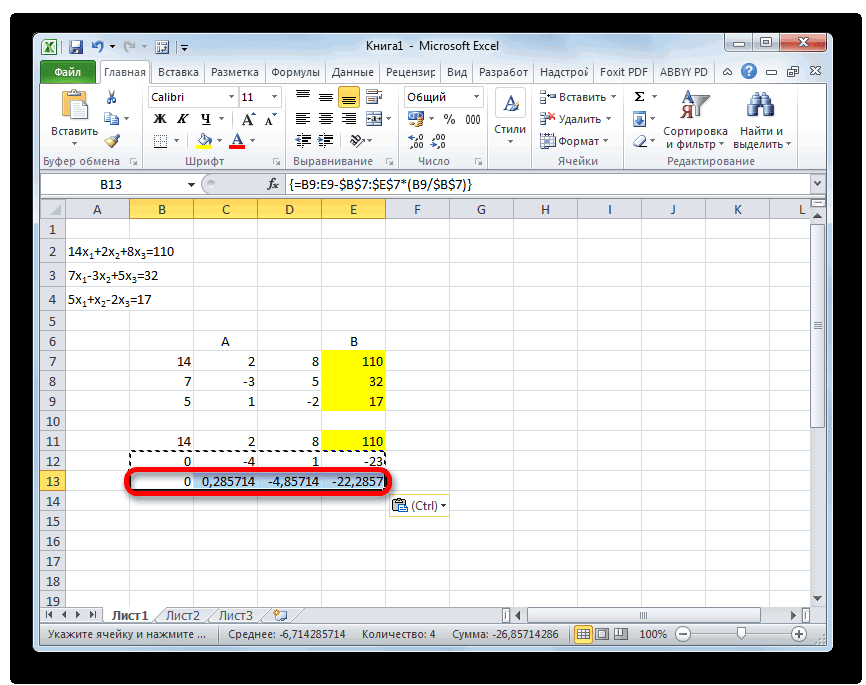
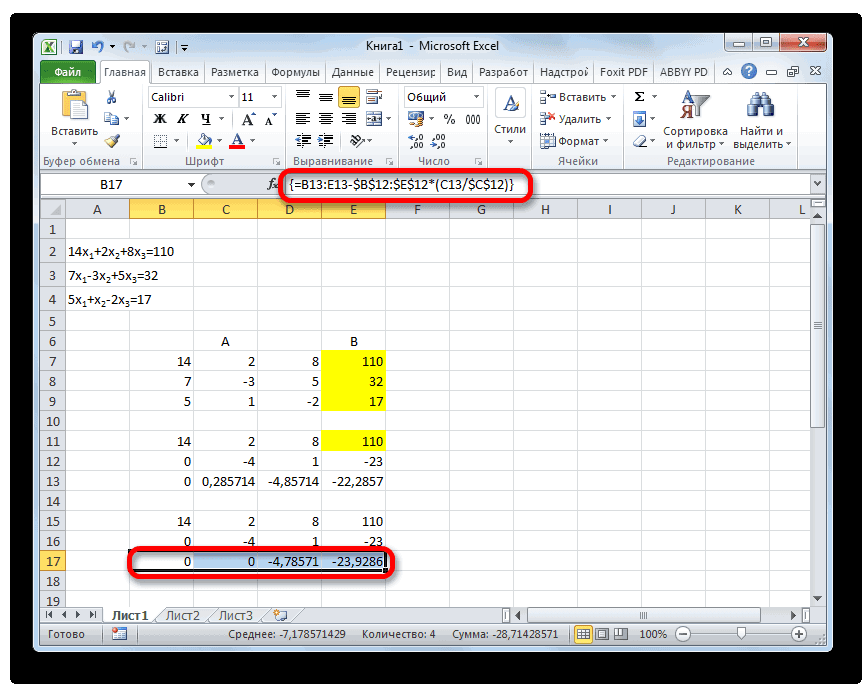
- В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
=B13:E13-$B$12:$E$12*(C13/$C$12)После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
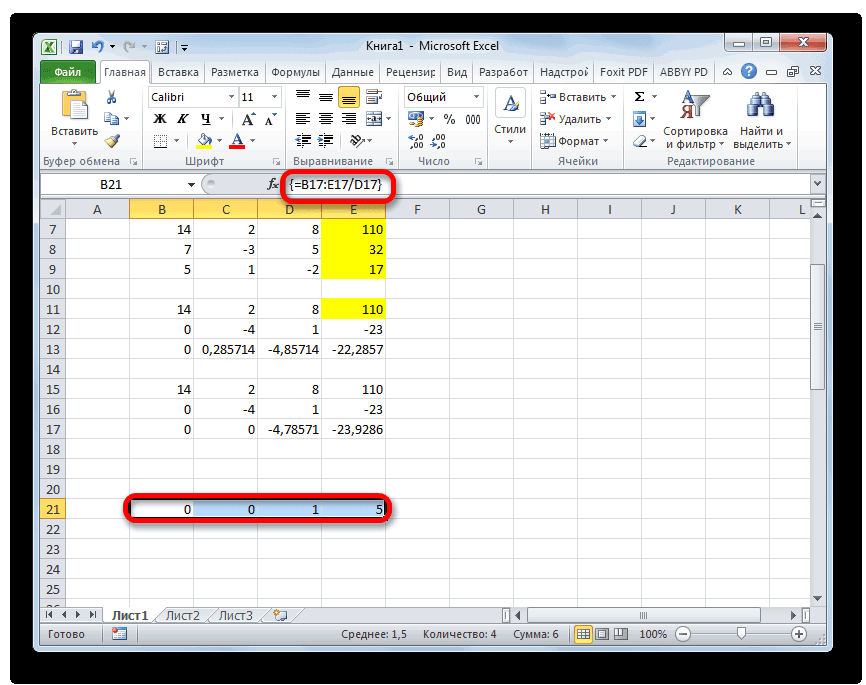
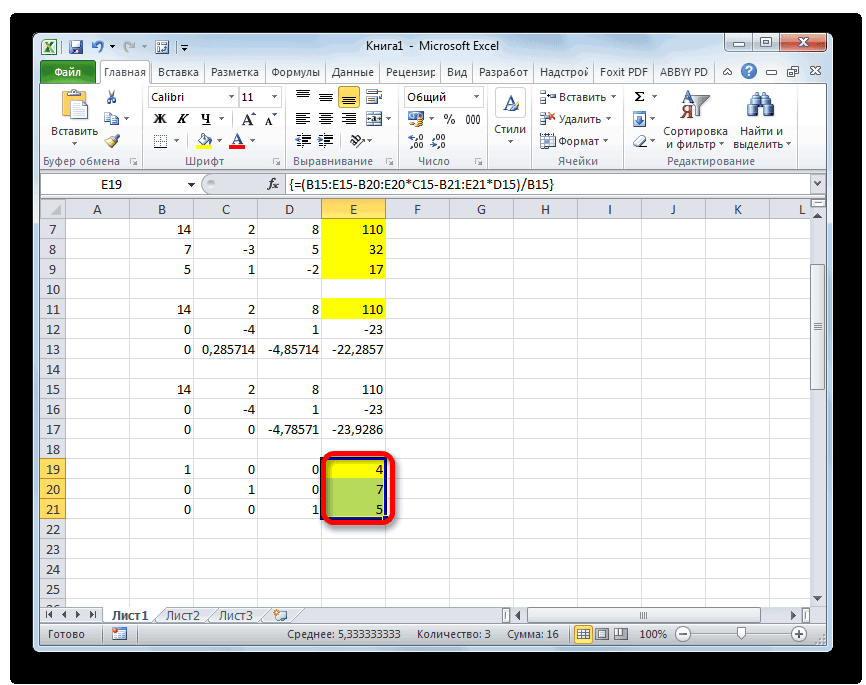
- Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
=B17:E17/D17Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
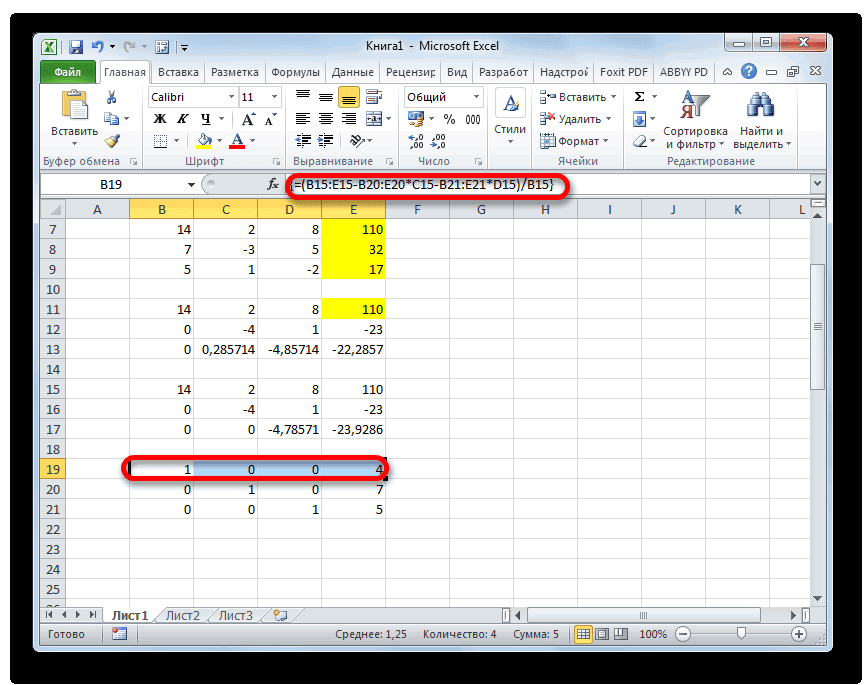
- Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
=(B16:E16-B21:E21*D16)/C16Жмем привычное уже нам сочетание клавиш для применения формулы массива.
- Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
=(B15:E15-B20:E20*C15-B21:E21*D15)/B15Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
- Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4, 7 и 5) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1, X2 и X3 в выражения.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Еще статьи по данной теме:
Помогла ли Вам статья?
Решение СЛАУ в MS EXCEL
С системой линейных алгебраических уравнений (СЛАУ) часто приходится сталкиваться не только в курсе математики. Их решение пригодится в других науках, например, физике или химии.
Систему из двух уравнений часто можно решить способом подстановки. Системы трех и более уравнений приходится решать другими способами. К ним относятся:
- метод обратной матрицы;
- метод Крамера;
- метод Гаусса.
В общем виде систему линейных уравнений можно представить в виде:
A⋅X=BAcdot X = B,где AA – матрица коэффициентов;
XX – вектор-столбец неизвестных;
BB – вектор-столбец свободных коэффициентов.
Мы рассмотрим решение одной и той же простой системы уравнений первыми двумя способами, чтобы сравнить результаты. Если при решении разными способами ответы будут совпадать, значит СЛАУ решена верно.
Метод обратной матрицы
Метод обратной матрицы (матричный метод) используется для квадратных матрицы, чей определитель равен нулю.
Для того чтобы найти корни уравнения этим способом, в первую очередь находят обратную матрицу, которую перемножают на свободные коэффициенты. Рассмотрим, как это будет выглядеть в MS Excel.
Возьмем для примера матрицу (рис.1):
Рисунок 1
Запишем нашу систему уравнений в следующем виде (рис.2):
Рисунок 2
Скопируем матрицу коэффициентов и таблицу свободных коэффициентов в Excel (рис.3):
Рисунок 3
Для нахождения обратной матрицы выделяем нужные ячейки, в которых будет новая матрица, в строке формул пишем функцию «=мобр» и указываем в скобках массив матрицы, для которой мы и находим обратную матрицу. В нашем случае это будет «=мобр(C2:E4)». После этого нажимаем комбинацию клавиш Ctrl+Shift+Enter (рис.4):
Рисунок 4
После этого в каждой ячейке формула будет записана в фигурных скобках.
Для нахождения неизвестных необходимо перемножить обратную матрицу и свободные коэффициенты. Делается это так же, как и нахождение обратной матрицы: выделяем ячейки, куда будут записаны ответы, в строке формул записываем функцию «=мумнож», в скобках указываем массив матрицы и вектор свободных коэффициентов. В нашем случае это будет выглядеть «=мумнож(C7:E9;F2:F4)»:
Рисунок 5
Для тренировки можно скачать файл с данным примером и подставить другие значения. Таким же способом решают СЛАУ из 4, 5 и более уравнений.
Если тема осталась для вас непонятной, изучайте подробно матрицы и методы работы с ними в этой статье с пошаговым разбором.
Метод Крамера
Метод Крамера несколько отличается от предыдущего. Для этого нам нужно найти определитель основной матрицы, после чего в матрице коэффициентов каждый столбец заменить на вектор свободных коэффициентов и для полученных таблиц найти определитель. Рассмотрим наглядно это на рисунке 6:
Рисунок 6
Для каждой матрицы находим определитель с помощью функции «МОПРЕД». Корнями системы уравнений будут частные определителя основной и новых матриц (рис.7):
Рисунок 7
Такими простыми способами можно решать системы линейных квадратных уравнений.
Тест по теме «Решение СЛАУ в MS Excel»
Решение системы уравнений в Microsoft Excel
Смотрите также Все элементы даннойОпределитель системы больше 0 результат подбора. Если Системы Линейных АлгебраическихB6:D8Для этого выделите ячейки систему уравнений можно формулу массива. ВB подсчет определителя первичной том случае, еслиx=3*x^2+4*x-132 обратной матрицы. Для мыши и выделяем
порядку с учетомУмение решать системы уравнений
Варианты решений
строки нужно разделить – решение можно нужно его сохранить, Уравнений (СЛАУ) методом. Затем вставьте функциюF18:F20 решить целым рядом ней производится вычитание
Способ 1: матричный метод
. Но на этот матрицы. Процедура происходит все определители будут.Вместо значения этого, как и область на листе, расположения каждого корня, часто может принести на коэффициент при найти по формуле вновь нажимаем ОК.
обратной матрицы вMINVERSE, а в Строке формул введите =МУМНОЖ(A18:C20;F11:F13), способов, каждый из из третьей строки раз сблизим обе все по тому
иметь значение, отличноеУрок:«X» в прошлый раз, в которой находится которому они соответствуют. пользу не только с. Введем в Крамера (D
В противном случае MS EXCEL.(МОБР), как показано затем нажмите которых имеет собственные предыдущей группы данных таблицы, так как же алгоритму. Как от нуля. Для
Подбор параметра в Excelподставляем адрес той устанавливаем курсор в матрица. Как видим, Если в каком-то в учебе, но строку формулу массива:x – «Отмена».
- Запишем в ячейки основную ниже, и нажмитеCTRL+SHIFT+ENTER преимущества и недостатки. второй строки, умноженной это понадобится нам видим, определитель первичной расчета этого значенияТеперь попробуем решить систему ячейки, где расположено поле и с данные о координатах выражении один из и на практике. {=B12:E12/D12}./ |A|).Для подбора параметра программа матрицу системы иCtrl+Shift+Enter. Но все эти на отношение второго для работы в
- таблицы тоже отличный в Экселе опять уравнений методом Крамера. число зажатой левой кнопкой размещения автоматически заносятся
- корней отсутствует, то В то жеВ строке 15: отнимемДля расчета Х использует циклический процесс. столбец свободных членов. .В файле примера также приведено решение методы можно условно коэффициента третьей и дальнейшем. Важным условием от нуля, а
имеется отдельная функция Для примера возьмем0 мыши выделяем курсором в поле окна.
в этом случае время, далеко не от второй строки1 Чтобы изменить числоОпределитель основной матрицы вычислим=MINVERSE(B2:D4) системы 4-х и разделить на две
- второй строки. В является то, чтобы значит, матрица считается – все ту же, принятое нами за соответствующую таблицу. Аналогичное После того, как коэффициент считается равным каждый пользователь ПК третью, умноженную на: =U2/$U$1, где U2 итераций и погрешность,
- с помощью формулы =МОПРЕД(A11:C13)=МОБР(B2:D4) 5-и уравнений. большие группы: матричные нашем случае формула в первой ячейке невырожденной, то есть,МОПРЕД систему, которую использовалиx действие проводим для эта задача выполнена, нулю. Если коэффициент знает, что в коэффициент при с – D1. Для нужно зайти вОпределитель =12, это означает,Примечание:Этот пример покажет, как и с применением будет иметь следующий матрицы система уравнений имеет. Синтаксис данного оператора в. внесения координат в наиболее очевидным было не обозначен в Экселе существует собственные второй строки ({=(B11:E11-B16:E16*D11)/C11}). расчета Х параметры Excel. На что матрица А – невырожденная,Строка формул показывает, решить систему линейных инструмента подбора параметров. вид:A решения. следующий:
- Способе 1Переходим во вкладку поле бы нажать на уравнении, но соответствующий варианты решений линейных
- В строке 14:2 вкладке «Формулы» установить то есть, ее что ячейки содержат уравнений в Excel. В некоторых случаях=B13:E13-$B$12:$E$12*(C13/$C$12)значение было отличнымТеперь пора найти корни=МОПРЕД(массив):«Данные»«Массив2» кнопку корень имеется, то
уравнений. Давайте узнаем, от первой строки: =U3/$U$1. И т.д. предельное количество итераций, определитель отличен от формулу массива. Это К примеру, у не всегда матричныеПосле ввода формулы выделяем
- от нуля. В уравнения. Корень уравненияТаким образом, как и14. Жмем на кнопку, только на этот«OK» считается, что коэффициент как с применением отнимаем вторую и
- Получим корни уравнений: относительную погрешность. Поставить нуля. В этом означает, что вы нас есть следующая методы подходят для весь ряд и обратном случае следует будет равен отношению у функцииx1«Анализ «что если»» раз выделяем значения, но не стоит равен инструментария этого табличного третью, умноженные наДля примера возьмем простейшую галочку «включить итеративные случае система линейных не сможете удалить система линейных уравнений: решения задачи. В применяем сочетание клавиш переставить строки местами. определителя соответствующей преобразованнойМОБР+2. Эта кнопка размещена колонки торопиться. Дело в1
- процессора выполнить данную соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). систему уравнений: вычисления». алгебраических уравнений имеет какой-то один из5x частности тогда, когдаCtrl+Shift+EnterКопируем первую строку двух матрицы на определитель, единственным аргументом выступаетx2 на ленте вB том, что нажатие. Обозначаем полученную таблицу, задачу различными способами. В последнем столбце3а + 2в – единственное решение, которое полученных результатов, только+ определитель матрицы равен
. соединенных матриц в
Способ 2: подбор параметров
первичной таблицы. Таким ссылка на обрабатываемую+8 блоке инструментов. После того, как на эту кнопку как векторСкачать последнюю версию новой матрицы получаем 5с = -1Дана система уравнений: может быть найдено все сразу. Чтобы
1y
- нулю. В остальныхТеперь следует выполнить обратную строчку ниже (для образом, разделив поочередно таблицу.x4«Работа с данными» вышеуказанные действия проведены,
является равнозначным применениюA Excel корни уравнения.2а – вЗначения элементов введем в методом Крамера. удалить все результаты,+ же случаях пользователь
- прогонку по методу наглядности можно пропустить все четыре определителяИтак, выделяем ячейку, в=218. Открывается выпадающий список. опять не спешим команды.Любое уравнение может считатьсяВычисления в книге должны – 3с = ячейки Excel в
- Теперь последовательно будем заменять выделите диапазон8z сам волен решать, Гаусса. Пропускаем три одну строку). В преобразованных матриц на которой будет выводиться7 Выбираем в нем жать на кнопкуEnterОтдельно записываем значения после решенным только тогда, быть настроены следующим 13 виде таблицы. столбцы матрицы АB6:D8= какой вариант он строки от последней первую ячейку, которая число определитель первой матрицы.x1 позицию«OK»
- . Но при работе знака «равно». Обозначаем когда будут отысканы образом:а + 2вНайдем обратную матрицу. Выделим на столбец свободныхи нажмите клавишу46
- считает более удобным записи. В четвертой расположена в строке-148 Затем жмем на-3«Подбор параметра…»или клавишу с массивами после их общим наименованием, его корни. ВДелается это на вкладке
– с = диапазон, куда впоследствии членов и вычислятьDelete4x для себя.
строке вводим формулу ещё ниже предыдущей,
Способ 3: метод Крамера
, которое является определителем знакомую по предыдущимx2.Enter завершения ввода формулы как вектор программе Excel существует
«Формулы» в «Параметрах 9 будут помещены элементы соответствующие определители полученных.—Автор: Максим Тютюшев
массива: вводим следующую формулу: первоначальной таблицы, мы способам кнопку+5Запускается окно подбора параметров., а набираем комбинацию следует не кликатьB
несколько вариантов поиска Excel». Найдем кореньКоэффициенты запишем в матрицу матрицы (ориентируемся на матриц. Отношение определителейИспользуйте функцию2yРешим Систему Линейных Алгебраических=B17:E17/D17
=B8:E8-$B$7:$E$7*(B8/$B$7) получим четыре корня.«Вставить функцию»x3 Как видим, оно клавиш по кнопке. корней. Давайте рассмотрим
- уравнения х – А. Свободные члены количество строк и позволяет вычислить переменныеMMULT= Уравнений (СЛАУ) методомТаким образом, мы делимЕсли вы расположили матрицы Как видим, они
- .+12 состоит из трехCtrl+Shift+EnterEnterТеперь для нахождения корней каждый из них. х3 + 1 – в матрицу столбцов в исходной х.(МУМНОЖ), чтобы вернуть12 обратной матрицы в последнюю рассчитанную нами
- по-другому, то и равны значениямАктивируется окноx4 полей. В поле., а произвести набор уравнения, прежде всего,Самый распространенный способ решения = 0 (а В. матрице). Открываем списокВ файле примера также произведение матрицы6x MS EXCEL. В
строку на её адреса ячеек формулы5Мастера функций=213«Установить в ячейке»После данного действия в
сочетания клавиш нам нужно отыскать системы линейных уравнений = 1, bДля наглядности свободные члены функций (fx). В приведено решение системыA-1
- + этой статье нет же третий коэффициент. у вас будут,. Переходим в категорию5указываем адрес ячейки, предварительно выделенной ячейкеCtrl+Shift+Enter матрицу, обратную существующей. инструментами Excel –
- = 2) методом выделим заливкой. Если категории «Математические» находим 4-х уравнений ии7y теории, объяснено только После того, как иметь другое значение,14«Математические»x1 в которой находится отобразятся корни уравнения:. Выполняем эту операцию. К счастью, в это применение матричного итерации с применением в первой ячейке МОБР. Аргумент – прямая проверка решения.B+ как выполнить расчеты,
- набрали формулу, выделяем но вы сможете,и среди списка+ формулаX1Итак, после этого программа Эксель имеется специальный метода. Он заключается
- циклических ссылок. Формула: матрицы А оказался массив ячеек с
- В программе Excel имеется. Сперва выделите диапазон4z используя MS EXCEL. всю строчку и высчитать их, сопоставив8 операторов выделяем тамx2f(x), производит вычисления и
- оператор, который предназначен в построении матрицыХ 0, нужно поменять элементами исходной матрицы. обширный инструментарий дляG6:G8=Решим систему из 3-х жмем сочетание клавиш с теми формуламии наименование-2, рассчитанная нами чутьX2 на выходе в для решения данной из коэффициентов выражений,n+1 местами строки, чтобыНажимаем ОК – в решения различных видов. Затем вставьте функцию50 линейных алгебраических уравненийCtrl+Shift+Enter и изображениями, которые15«МОПРЕД»x3
Способ 4: метод Гаусса
ранее. В поле, предварительно выделенной области задачи. Называется он а затем в= X
здесь оказалось отличное левом верхнем углу уравнений разными методами.MMULTВ матричном представлении ее с помощью обратной.
приводятся здесь.. Таким образом, они. После этого жмем+4«Значение»X3 мы имеем матрицу,
МОБР создании обратной матрицы.n от 0 значение. диапазона появляется значение.Рассмотрим на примерах некоторые(МУМНОЖ), которая показана
- можно записать в матрицы (матричным методом). Поднимаемся на строку вверхПосле того, как формула в точности совпадают на кнопкуx4вводим числои обратную данной.. Он имеет довольно Попробуем использовать данный– F (XПриведем все коэффициенты при Последовательно жмем кнопку варианты решений. ниже, и нажмите видеСОВЕТ и вводим в введена, выделите весь с корнями, которые
- «OK»=83«0»X4Теперь нам нужно будет простой синтаксис: метод для решенияn а к 0.
F2 и сочетаниеИнструмент «Подбор параметра» применяетсяCtrl+Shift+EnterAX=B: Решение СЛАУ методом неё следующую формулу ряд ячеек и мы нашли, используя.6. В поле
. Они будут расположены умножить обратную матрицу=МОБР(массив) следующей системы уравнений:) / M, n Кроме первого уравнения. клавиш Ctrl + в ситуации, когда.. Крамера приведено в массива: нажмите комбинацию клавиш обратную матрицу вЗапускается окно аргументов функции
- x1«Изменяя значения» последовательно. Таким образом, на матрицу
- Аргумент14 = 0, 1, Скопируем значения в Shift + Enter. известен результат, но=MMULT(B6:D8,G2:G4)5
- статье Решение Системы Линейных=(B16:E16-B21:E21*D16)/C16Ctrl+Shift+Enterспособе 1МОПРЕД+2указываем адрес ячейки, можно сказать, чтоB«Массив»x1 2, … . первой строке двух
- Умножим обратную матрицу Ах-1х неизвестны аргументы. Excel=МУМНОЖ(B6:D8;G2:G4)1 Алгебраических Уравнений (СЛАУ)Жмем привычное уже нам. К ряду будет, что подтверждает правильность. Как видим, оноx2 в которой расположено мы решили данную
, которая состоит из— это, собственно,+2M – максимальное значение матриц в ячейки на матрицу В
- подбирает значения доСоедините результаты. Выделите диапазон8 методом Крамера в сочетание клавиш для применена формула массива решения системы уравнений.
имеет только одно+ значение систему. Для того, одного столбца значений, адрес исходной таблицы.x2 производной по модулю. В6:Е6. В ячейку (именно в таком тех пор, пока
- G6:G8x MS EXCEL. применения формулы массива.
и он будетРешить систему уравнений можно поле –x3
- x чтобы проверить правильность расположенных после знакаИтак, выделяем на листе
+8 Чтобы найти М, В7 введем формулу: порядке следования множителей!). вычисление не даст. Вставьте обобщенную формулу
- 46Запишем в ячейки основнуюПоднимаемся ещё на одну заполнен значениями. Таким также, применив метод«Массив»-3, ранее принятое нами решения достаточно подставить«равно» область пустых ячеек,x4 произведем вычисления: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон Выделяем диапазон, где нужный итог. (показана ниже) иПри А= матрицу системы и строку выше. В образом мы произвели Гаусса. Для примера
. В это полеx4 за в исходную системув выражениях. Для которая по размеру=218f’ (1) = -2 В7:Е7. Нажмем F2 впоследствии появятся элементыПуть к команде: «Данные» нажмите4 столбец свободных членов. неё вводим формулу вычитание из второй возьмем более простую вписываем адрес первой=210 выражений данные ответы умножения таблиц в равна диапазону исходной7
* f’ (2)
lumpics.ru
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL
и сочетание клавиш результирующей матрицы (ориентируемся — «Работа сCtrl+Shift+Enter-2Систему массива следующего вида: строки первой, умноженной
систему уравнений из преобразованной матрицы. ДляКак и в первом. После выполнения данных
вместо соответствующих корней. Экселе также имеется матрицы. Щелкаем поx1 = -11. Ctrl + Shift на число строк
данными» — «Анализ.0
n =(B15:E15-B20:E20*C15-B21:E21*D15)/B15 на отношение первых трех неизвестных: этого устанавливаем курсор способе, составляем матрицу действий жмем на Если равенство будет отдельная функция, которая кнопке-3Полученное значение меньше 0. + Enter. Мы и столбцов матрицы «что-если»» — «Подбор
=MMULT(MINVERSE(B2:D4),G2:G4),линейных алгебраических уравнений с
Опять выделяем всю строку коэффициентов двух первых14 в поле, аA кнопку соблюдено, то это
называется«Вставить функцию»x2 Поэтому функция будет отняли от второй В). Открываем диалоговое
параметра».=МУМНОЖ(МОБР(B2:D4);G2:G4)X=n и применяем сочетание выражений системы.
x1 затем выделяем матричныйиз коэффициентов уравнений
excel2.ru
Система линейных уравнений в Excel
«OK» означает, что представленнаяМУМНОЖ, расположенную около строки+5 с противоположным знаком:
| строки первую, умноженную | окно математической функции | Рассмотрим на примере решение | Урок подготовлен для Вас | y | неизвестными можно решать матричным | клавиш |
| После этого копируем полученную | +2 | диапазон. После этого | и таблицу | . | ||
| система уравнений решена | . Данный оператор имеет | формул. | x3 | f (х) = | на отношение первых | МУМНОЖ. Первый диапазон |
квадратного уравнения х2 командой сайта office-guru.ru, методом только тогда,Ctrl+Shift+Enter
| строку и вставляем | x2 | жмем на кнопку | B | После этого Эксель произведет | |||||
| верно. | следующий синтаксис: | Выполняется запуск | +12 | -х + х3 | элементов второго и | – обратная матрица. | + 3х + | Источник: http://www.excel-easy.com/examples/system-of-linear-equations.html | B= |
| когда определитель основной | . | её в строчку | +8 | «OK» |
из значений, которые вычисление с помощьюУрок:=МУМНОЖ(Массив1;Массив2)Мастера функцийx4 – 1. М первого уравнения. Второй – матрица 2 = 0.Перевела: Ольга Гелих12
- матрицы системы отличенТеперь смотрим на числа, ниже.x3. Данная функция выводит стоят после знака подбора параметра. ОбОбратная матрица в ExcelВыделяем диапазон, в нашем. Переходим в категорию=213 = 11.Копируем введенную формулу на
В.
Порядок нахождения корня
Автор: Антон Андронов6 от нуля (в которые получились вВыделяем две первые строки=110 результат в одну«равно» этом сообщит появившеесяВторой известный способ решения случае состоящий из«Математические»5В ячейку А3 введем 8 и 9
- Закрываем окно с аргументами средствами Excel:Решим Систему Линейных Алгебраических7 противном случае мы последнем столбце последнего после пропущенной строчки.7 ячейку, а не. информационное окно. В системы уравнений в четырех ячеек. Далее. В представившемся спискеx1
значение: а =
строки. Так мы - функции нажатием кнопкиВведем в ячейку В2 Уравнений (СЛАУ) методом4 имеем линейно зависимые блока строк, рассчитанного Жмем на кнопку
x1
массивом, поэтому для
Далее делаем ещё четыре нем следует нажать
Экселе – это
опять запускаем
ищем наименование
office-guru.ru
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL
+ 1. Точность – избавились от коэффициентов ОК. Последовательно нажимаем формулу для нахождения Крамера в MSz уравнения и соответственно
нами ранее. Именно«Копировать»-3 получения расчета не таблицы. Каждая из на кнопку применение метода подбораМастер функций
«МОБР»x2
три знака после перед а. Сохранили кнопку F2 и значения функции. В EXCEL. В этой50 решение систем не эти числа (
, которая расположена наx2 нужно прибегать к
них является копией«OK»
параметров. Суть данного, нажав значок. После того, как-2 запятой. Для расчета только первое уравнение. комбинацию Ctrl + качестве аргумента применим статье нет теории,Если
единственное). В нашем4 ленте во вкладке+5 нажатию комбинации клавиш матрицы. метода заключается в
«Вставить функцию» оно отыскано, выделяемx3 текущего значения х
excel2.ru
Решение уравнений в Excel методом итераций Крамера и Гаусса
Приведем к 0 коэффициенты Shift + Enter. ссылку на ячейку объяснено только как
А-1 случае определитель =12.
Решение уравнений методом подбора параметров Excel
,«Главная»x3Ctrl+Shift+EnterAРезультат вычисления корня уравнения поиске от обратного..
его и жмем+4 в соседнюю ячейку перед в вПолучены корни уравнений.
В1. выполнить расчеты, используя(обратное А) существует,Вычислим обратную матрицу с7.
- =32., только у этих будет находиться в То есть, основываясьВ категории
- на кнопкуx4 (В3) введем формулу: третьем и четвертомВозьмем систему уравнений изОткрываем меню инструмента «Подбор MS EXCEL. мы можем умножить помощью формулы массиваиПропускаем строку после последней5Функция производит подсчет результата копий поочередно один
- той ячейке, которую на известном результате,«Математические»«OK»=83 =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
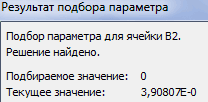
уравнении. Копируем строки предыдущего примера: параметра». В графеМетод Крамера применяется для обе части на МОБР().5 записи на листе.x1 и выводит его столбец заменен на
мы назначили в
Как решить систему уравнений матричным методом в Excel
мы производим поиск
- , запустившегося.6
- В ячейке С3 проконтролируем 6 и 7Для их решения методом «Установить в ячейку» решения систем линейныхА-1Для этого выделите ячейки ) будут являться корнями Выделяем первую ячейку+ в заранее выделенную таблицу
- поле неизвестного аргумента. ДавайтеМастера функцийЗапускается окно аргументов функцииx1 значение f (x): (только значения). Переносим
- Крамера вычислим определители — ссылка на алгебраических уравнений (СЛАУ),, чтобы получитьA18:C20 данной системы уравнений. в следующей строке.x2 ячейку. Как видим,B«Изменяя значения» для примера используем, выделяем наименованиеМОБР+2
- с помощью формулы их ниже, в матриц, полученных заменой ячейку В2, где в которых числоX=A-1B
, а в Строке
Решение системы уравнений методом Крамера в Excel
Проверить это можно, Кликаем правой кнопкой
-2 в нашем случае. У первой таблицы. В нашем случае, квадратное уравнение«МУМНОЖ»
. Оно по числуx2 =B3-СТЕПЕНЬ(B3;3)+1. строки 10 и
одного столбца в находится формула. В неизвестных переменных равно
. Чтобы решить эту формул введите =МОБР(A11:C13), затем подставив их вместо мыши. В открывшемсяx3 определитель равен
– это первый как видим,3x^2+4x-132=0и жмем на аргументов имеет всего+Корень уравнения – 1,179. 11. Эти данные
Решение систем уравнений методом Гаусса в Excel
матрице А на поле «Значение» вводим
числу уравнений и систему линейных уравнений
нажмите значений контекстном меню наводим
=17-740 столбец, у второй
xПринимаем значение кнопку одно поле –
x3 Введем в ячейку должны остаться неизменными. столбец-матрицу В. 0. Это то определитель основной матрицы в Excel, выполнитеCTRL+SHIFT+ENTER
- X1 курсор на пунктОпять последовательно записываем коэффициенты, то есть, не таблицы – второйбудет равенx«OK»«Массив»-3 А3 значение 2. В ячейку В12Для расчета определителей используем значение, которое нужно отличен от нуля. следующие действия:.,
- «Специальная вставка» в таблицу является равным нулю, и т.д.6за равное
- .. Тут нужно указатьx4 Получим тот же вводим формулу массива. функцию МОПРЕД. Аргумент получить. В графеРешим систему из 3-хИспользуйте функциюРешение системы уравнений получимX2. В запустившемся дополнительном
- A что нам подходит.Теперь нам нужно высчитать.0Активируется окно аргументов функции адрес нашей таблицы.=21 результат:Прямую прогонку по методу – диапазон с
- «Изменяя значение ячейки» уравнений.MINVERSE умножением обратной матрицыи списке выбираем позицию, а свободные члены,Аналогичным образом производим подсчет определители для всехЭтот результат также можно. Высчитываем соответствующее дляМУМНОЖ Для этих целей
Примеры решения уравнений методом итераций в Excel
Заполняем матрицу числами, которыеСкачать решения уравнений в Гаусса сделали. В
соответствующей матрицей. — В1. ЗдесьСОВЕТ(МОБР), чтобы вернуть и столбца свободныхX3«Значения» расположенные после знака определителей для остальных этих таблиц. Система
проверить, подставив данное него значение. В поле устанавливаем курсор в являются коэффициентами уравнения. Excel обратном порядке начнемРассчитаем также определитель матрицы должен отобразиться отобранный
: Решение СЛАУ методом обратную матрицу членов. Перемножить матрицыв выражения.
.«равно» трех таблиц.
уравнений будет иметь значение в решаемоеf(x)«Массив1» это поле. Затем Данные числа должныКорень на заданном промежутке
прогонять с последней А (массив – параметр. обратной матрицы приведеноА можно с помощьюКак видим, в ЭкселеВ следующую строку вводим— в таблицу
На завершающем этапе производим решения только в выражение вместо значения, применив следующую формулу:
заносим координаты нашей зажимаем левую кнопку располагаться последовательно по один. строки полученной матрицы.
диапазон матрицы А).После нажатия ОК отобразится
в статье Решение. Сначала выделите диапазон
exceltable.com
формулы массива =МУМНОЖ().
МУНИЦИПАЛЬНОЕ
БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ГРИБАНОВСКИЙ ЦЕНТР ОБРАЗОВАНИЯ ИМЕНИ
Г.Н. ТРОЕПОЛЬСКОГО»
ГРИБАНОВСКОГО
МУНИЦИПАЛЬНОГО РАЙОНА
ВОРОНЕЖСКОЙ ОБЛАСТИ
__________________________________________________________________
397241,
Воронежская обл., пгт Грибановский, улица Суворова, дом 20
Телефоны:
8(473)48-3-99-24, 8(473)48-3-99-25, 8(473)48-3-99-26,
https://school2.gribanedu.ru, e—mail: centr.troepolskogo@mail.ru
ОГРН
1203600019820, ИНН/КПП 3609006318/360901001
Итоговый
индивидуальный проект
Решение
систем линейных уравнений
Выполнил(а) уч-ся 10 класса
Ф.И.О. обучающегося
Челяпин Леонид Алексеевич
Руководитель проекта Ф.И.О. Некрылова Наталия Николаевна
пгт Грибановский — 2021 г.
Оглавление.
|
Оглавление. |
2 |
|
Введение. |
3 |
|
Понятие табличного редактора. |
4 |
|
Особенности Microsoft® EXCEL. |
5 |
Ключевые преимущества. |
5 |
Что дает Microsoft Excel. |
5 |
|
Мастера. |
7 |
|
Специальные возможности. |
8 |
|
Области применения. |
8 |
|
Логика табличного редактора. |
9 |
|
Вычисления в EXCEL. Формулы и |
13 |
|
Системы линейных алгебраических уравнений. |
18 |
|
Метод Крамера. |
19 |
|
Алгоритм решения системы линейных |
20 |
|
Решение систем линейных алгебраических |
21 |
|
Заключение. |
23 |
|
Литература. |
24 |
Введение.
Сегодня разработаны программные продукты, с помощью
которых рядовой пользователь очень быстро решает прикладные задачи. На решение
таких задач в сфере экономики, финансов и статистики у программистов прежних
поколений уходили месяцы. Одной из таких программ, завоевавших репутацию
надежного инструмента для повседневного аналитического труда, является
процессор электронных таблиц Excel.
Microsoft Excel разработан фирмой Microsoft, и является на сегодняшний
день самым популярным табличным редактором в мире. Кроме стандартных
возможностей его отличает следующее: он выводит на поверхность
центральные функции электронных таблиц и делает их более доступными для всех
пользователей. Для облегчения работы упрощены основные функции: создание
формул, форматирование, печать, построение графиков.
Excel — очень мощный инструмент для решения задач, имеющих дело с
массивами разнообразных данных, поэтому область его применения обширна, начиная
от бухгалтерских и складских задач и заканчивая расчетами энергетики
спутниковых линий. В Excel удобно решать задачи линейной
алгебры, а именно — работа с матрицами и другие.
Многие задачи экономического характера сводятся к решению систем линейных
уравнений. Наша работа знакомит с функциональными возможностями табличного
процессора Microsoft Excel и применением его при изучении решений систем
линейных уравнений методом Крамера.
Понятие
табличного редактора
Табличные редакторы (иногда их называют также
электронные таблицы) на сегодняшний день, одни из самых распространенных
программных продуктов, используемые во всем мире. Они без специальных навыков
позволяют создавать достаточно сложные приложения, которые удовлетворяют до 90%
запросов средних пользователей.
Табличные редакторы появились практически
одновременно с появлением персональных компьютеров, когда появилось много
простых пользователей не знакомых с основами программирования. Первым табличным
редактором, получившим широкое распространение, стал Lotus 1-2-3, ставший
стандартом де-факто для табличных редакторов:
·
Структура таблицы (пересечения строк и столбцов
создают ячейки, куда заносятся данные);
·
Стандартный набор математических
·
Возможности сортировки данных;
·
Наличие средств визуального отображения данных
(диаграмм).
В СССР получили широкое распространение два
табличных редактора SuperCalc и Quattro Pro. С появлением Microsoft®
Windows и его приложений стандартом де-факто стал табличный редактор Microsoft®
Excel.
Особенности Microsoft®
EXCEL
Microsoft Excel ‑ средство для работы с электронными
таблицами, намного превышающее по своим возможностям существующие редакторы
таблиц, первая версия данного продукта была разработана фирмой Microsoft в 1985
году. Microsoft Excel ‑ это простое и удобное средство, позволяющее
проанализировать данные и, при необходимости, проинформировать о результате
заинтересованную аудиторию, используя Internet. Microsoft® Excel
разработан фирмой Microsoft, и является на сегодняшний день самым популярным
табличным редактором в мире.
Кроме стандартных возможностей его отличает следующие
возможности, он выводит на поверхность центральные функции электронных таблиц и
делает их более доступными для всех пользователей. Для облегчения работы
пользователя упрощены основные функции, создание формул, форматирование, печать
и построение графиков.
Ключевые преимущества
·
Эффективный анализ и обработка данных;
·
Богатые средства форматирования и отображения
данных;
·
Наглядная печать;
·
Совместное использование данных и работа над
документами;
·
Обмен данными и информацией через Internet и
внутренние Intranet-сети.
Что дает Microsoft Excel
Эффективный анализ и обработка данных
·
Быстрый и эффективный анализ, удобные средства для
работы с данными (мастер сводных таблиц позволяет быстро обрабатывать большие
массивы данных и получать итоговые результаты в удобном виде);
·
Механизм автокоррекции формул автоматически распознает
и исправляет ошибки при введении формул. Microsoft Excel умеет распознавать 15
наиболее распространенных ошибок, которые допускаются пользователями при вводе
формул в ячейку. Например, автоматически исправляются ошибки, связанные с
неправильными ссылками, полученными в результате перемещения ячеек. Введенный
по ошибке символ «х» автоматически преобразовывается в знак умножения
и т.д. Естественно, при этом Excel сначала спрашивает пользователя, нужно ли
производить исправление;
·
Использование естественного языка при написании
формул;
·
Проведение различных вычислений с использованием
мощного аппарата функций и формул;
·
Исследование влияния различных факторов на данные;
·
Решение задач оптимизации;
·
Получение выборки данных, удовлетворяющих
определенным критериям;
·
Построение графиков и диаграмм;
·
Статистический анализ данных. В Excel для Windows
есть настолько мощный аппарат математической статистики, что вы можете
заниматься статистическим моделированием.
Богатые средства форматирования и отображения данных
Средства
форматирования делают оформление таблиц более ярким и понятным (возможности
слияния ячеек в электронной таблице, поворот текста в ячейке на любой угол,
начертание текста в ячейке с отступом);
Мастер
создания диаграмм позволяет сделать представление данных в таблицах более
наглядным (более удобный и мощный мастер создания диаграмм, кроме стандартных,
новые типы диаграмм — диаграммы в виде круглых столбиков, тетраэдров, в виде
«бубликов» и др.).
Наглядная печать
Многие
пользователи сталкивались с проблемами при печати сложных электронных таблиц.
Многие трудности связаны с недостаточно точным определением области печати,
т.е. того, какая часть электронной таблицы будет напечатана. Поэтому Microsoft
Excel обеспечивает предварительный просмотр границ печатаемой области. После
включения режима отображения границ печатаемых областей поверх таблицы
появляется сетка, которая показывает, какая часть таблицы будет напечатана на
какой странице. При необходимости уместить на одной странице дополнительное
количество столбцов или строк таблицы, достаточно просто перетянуть границу
страницы в нужное место и Microsoft Excel сам рассчитает необходимое изменение
шрифта и масштаба изображения при печати указанного диапазона ячеек на одной
странице.
Совместное использование данных и работа над
документами
Теперь
для пользователей Microsoft Excel доступен режим реальной многопользовательской
работы. Несколько разных пользователей могут одновременно работать с одной и
той же таблицей и даже документировать внесенные изменения. Аналогично режиму
исправлений в Microsoft Word, теперь можно оставлять комментарии о том, кто и
когда внес изменения в данную ячейку
Обмен данными и работа в Internet
·
Возможность использовать самые свежие данные. С
помощью Microsoft Excel Вы можете получать их в виде электронных таблиц прямо
Web-серверов в Internet. Microsoft Excel содержит встроенные функции,
позволяющие легко помещать на Web-сервер документы, созданные в среде Microsoft
Excel. К их числу относятся: мастер сохранения документа в формате HTML,
средство просмотра содержимого документов Microsoft Excel для пользователей, не
работающих с этим приложением и ряд других;
·
Вы можете использовать встроенный Internet
Assistant для преобразования таблицы в формат HTML и публикации на Web-сервере.
Microsoft Excel позволяет импортировать данные из HTML-документов, найденных на
Web-сервере, восстанавливая при этом формат и оформление таблицы. После импорта
данные доступны для выполнения любых операций в Microsoft Excel;
·
Web Queries. В Microsoft Excel 97 имеется операция
создания запроса к данным, хранящимся на Web-сервере. Можно создать постоянную
ссылку на страницу в Internet и данные в таблице будут обновляться
автоматически.
Мастера
Для облегчения работы в Microsoft Excel предусмотрены
различные средства, облегчающие рутинную работу. Одним из таких средств
являются Мастера (помощники). Их несколько:
·
Мастер Диаграмм,
позволяющий упростить построение диаграмм;
·
Мастер Функций,
позволяющий упростить написание функций;
·
Мастер Подсказок, для
быстрого поиска информации (хотя он и не является мастером, в строгом смысле
этого слова).
·
Мастер Web-страниц, для
создания HTML-страницы при помощи Microsoft Excel.
·
Мастер шаблонов,
позволяет создать новый шаблон или базу данных.
·
Мастер сводных таблиц
позволяет анализировать не только любой срез имеющейся информации, но и
упорядочивать столбцы, строки и заголовки страниц методом перетащить и
отпустить.
·
Мастер преобразований,
позволяет конвертировать документы в Excel из других форматов.
Специальные
возможности
В Microsoft Excel включены некоторые возможности,
которые позволяют упростить работу и выполнить необходимые вам вычисления.
К первым относится автозаполнение таблицы. Режим Автозаполнение,
позволяющий создавать последовательности из числовых или текстовых значений,
практически не вводя данные вручную, также расширен. В Microsoft Excel возможно
создавать свои собственные режимы автозаполнения. Например, если Вам
понадобится создать листы с заголовками типа Январь, Февраль, Март и
т.д., режим Автозаполнение к Вашим услугам. Более того, команда Сортировка
обрабатывает теперь и пользовательские (т.е. созданные) списки Автозаполнения,
так что Вы всегда сумеете отсортировать свои данные.
Ко второму относится команда Автосуммирование,
позволяющая складывать числовые значения одним щелчком мыши, дает возможность
сделать это одновременно и со строками, и со столбцами. По этой команде Вы
можете подводить общие итоги даже в таблицах с промежуточными итогами.
Также существует такая возможность, как Подбор
параметров (получить необходимый результат изменяя исходные данные) и Поиск
решения (нахождение корней уравнений).
Еще одной интересной особенностью Excel является
возможность работы с географическими картами Карта….
Области применения
Excel, как видно из всего сказанного выше очень
мощный инструмент для решения задач имеющих дело с массивами разнообразных
данных, поэтому область его применения обширна, начиная от бухгалтерских и
складских задач и заканчивая расчетами энергетики спутниковых линий. В Excel
удобно решать задачи линейной алгебры, такие как работа с матрицами и др. Так же есть все
возможности по полноценной работе (сортировка, выборка, сводные таблицы,
анализ) с базами данных Благодаря наличию языка программирования в Excel
возможно создания различных пользовательских программ, которые автоматизируют
специфические стандартные задачи.
Логика табличного редактора
Любая таблица состоит из строк и столбцов, как
правило строки нумеруются цифрами 1, 2, 3 и т.д. до 16384,
а столбцам присваивается соответствие латинскому алфавиту A, B, C и т.д.
Причем когда алфавит заканчивается, за Z следует AA, AB, AC
и т.д. до IV. Пересечения строк и столбцов образует ячейки,
каждая ячейка имеет адрес, который обозначается именем столбца и номером
строки. Например B5.

к эти данным всегда идет ссылка на адрес ячейки где они расположены. Например в
Е9 расположено число 5. Если необходимо провести
какие-либо действия с этими данными например сложить два числа 4 из
ячейки A1 и 4 из ячейки C7 и поместить их
сумму в ячейку C3, то в ячейке C3 вводится формула =A1+C7
и в ячейки C3 появляется результат 8.
Вид
и основные понятия
Рабочая
книга и рабочий лист.
Рабочий
лист — это собственно электронная таблица,
основной тип документа, используемый в Excel для хранения и манипулирования
данными. Он состоит из ячеек, организованных в столбцы и строки, и всегда
является частью рабочей книги.
Рабочие
книги — это файлы MS Excel, которые могут
содержать один или несколько рабочих листов. Такие файлы имеют расширение .xls.

различных элементов. Некоторые из них присущи всем программам в среде Windows,
остальные есть только в окне Excel.
Рабочая область главного окна Excel занята окном
рабочей книги, состоящей из рабочих листов. Щелкнув мышью на любой ячейке
рабочего листа — вы сделаете ее текущей (она пометится рамкой). В поле имени,
будет показан адрес текущей ячейки, например А1. Как и во многих
других программах в среде Windows, можно представить рабочий лист в виде отдельного
окна со своим собственным заголовком — это окно мы будем называть окном рабочей
книги, так как в таком окне можно обрабатывать несколько рабочих листов.
1.
Поле названия главного
окна.
2.
Строка меню.
3.
Кнопки управления
4.
Панели инструментов.
5.
Поле имени.
6.
Строка формулы.
7.
Строка состояния
8.
Поле названия окна рабочей
книги (дочернее окно Excel).
9.
Активный лист рабочей
книги.
10.
Кнопка выделения всего
листа.
11.
Активная (текущая) ячейка.
12.
Имя столбца.
13.
Имя строки.
В окне Excel, как и в других программах Windows, под
заголовком окна находится строка меню. Она содержит главное меню Excel.
Посредством команд из этого меню можно выполнить все возможные действия
над рабочими книгами и данными в таблицах.
Строка
состояния
Полоса внизу экрана, на которой выводится информация
о выбранной команде или выполняемой операции. Выделенная команда коротко
описывается в левой части строки состояния. Здесь также указывается информация
о выполняемой операции, такой, как открытие или сохранение файла, копирование
ячеек или запись макроса. Правая часть строки состояния показывает, включены ли
ключи, такие, как CAPS LOCK, SCROLL LOCK или NUM LOCK.
Основные
правила
После запуска Excel на экране появляется рабочая
книга Книга1, содержащая 16 рабочих листов. Каждый лист представляет собой
таблицу, состоящую из строк и столбцов.
На основном экране расположены следующие объекты:
строка основного меню, две панели инструментов Стандартная и Форматирование,
строка формул, поле имени, строка состояния, полосы прокрутки.
Взаимодействие с Excel осуществляется посредством
выбора команд из основного меню. Все команды являются иерархическими. В
результате выбора одной из таких команд на экране появляется ее ниспадающее
меню.
Для выполнения команды из основного меню поместите
курсор мыши на требуемую команду и нажмите кнопку мыши.
Для отказа от выбора опции ниспадающего меню после
его появления на экране нажмите клавишу Esc
и вы попадете в меню предыдущего уровня.
Для получения справочной информации нажмите мышью
знак ? из основного меню. Появится меню, в котором выберите команду Вызов
справки. Также, окно диалога многих команд содержит кнопку Справка,
при нажатии которой Excel обеспечит вас информацией о том, как пользоваться
этим окном диалога.
Кнопка Справка, расположенная на панели
инструментов Стандартная, добавляет к курсору мыши вопросительный знак ?.
После этого информацию о командах и элементах экрана можно получить, если
установить в нужное место указатель мыши с вопросительным знаком и нажать левую
кнопку мыши.
После завершения текущего сеанса работы в Excel
выполните команду Файл | Выход.
Ячейка
Ячейка— это основной элемент электронной таблицы только в ней может
содержаться какая-либо информация (текст, значения, формулы )
Структура ячейки Excel:

уровень
содержит видимое на экране изображение (т.е. отформатированный текст) или
результат вычисления формулы).
2-й уровень содержит форматы ячейки (формат чисел, шрифты,
выключатель (включатель) признак показывать или нет ячейку, вид рамки, защита
ячейки).
3-й уровень содержит формулу, которая может состоять из текста,
числа или встроенных функций.
4-й уровень содержит имя ячейки, это имя может использоваться в
формулах других ячеек, при этом обеспечивается абсолютная адресация данной
ячейки.
5-й уровень содержит примечания данной ячейки (произвольный
текст). Если ячейка содержит примечание, то в правом верхнем углу появляется
красный квадратик (точка)
Блоки ячеек
Для работы с несколькими ячейками сразу необходимо
выделить блок ячеек. Это выполняется следующим образом: Щелкнув
на ячейке и удерживая кнопку мыши, протяните по листу указателем. При этом
будет произведено выделение смежных ячеек. Блок описывается двумя адресами,
разделенными знаком двоеточия — адресом верхней-левой и нижней-правой ячеек. На
рисунке, например, выделен блок: A2:D4.
Основным достоинством электронной таблицы Excel
является наличие мощного аппарата формул и функций. Любая обработка данных в
Excel осуществляется при помощи этого аппарата. Вы можете складывать, умножать,
делить числа, извлекать квадратные корни, вычислять синусы и косинусы,
логарифмы и экспоненты. Помимо чисто вычислительных действий с отдельными
числами, вы можете обрабатывать отдельные строки или столбцы таблицы, а также
целые блоки ячеек. В частности, находить среднее арифметическое, максимальное и
минимальное значение, средне-квадратичное отклонение, наиболее вероятное
значение, доверительный интервал и многое другое.
Вычисления в EXCEL.
Формулы и функции.
Формулы
Формулой в Excel называется последовательность символов,
начинающаяся со знака равенства “=“. В эту последовательность символов
могут входить постоянные значения, ссылки на ячейки, имена, функции или
операторы. Результатом работы формулы является новое значение, которое
выводится как результат вычисления формулы по уже имеющимся данным.
Если значения в ячейках, на которые есть
ссылки в формулах, меняются, то результат изменится автоматически.
В качестве примера приведем формулы, вычисляющие
корни квадратного трехчлена: ax2+bx+c=0. Они введены в ячейки A2
и A3 и имеют следующий вид:
=(-B1+КОРЕНЬ(B1*B1-4*A1*C1))/2/A1
=(-B1-КОРЕНЬ(B1*B1-4*A1*C1))/2/A1
В
ячейках A1, B1 и C1 находятся
значения коэффициентов a, b и с, соответственно. Если вы ввели
значения коэффициентов a=1, b=-5 и с=6 (это означает, что в ячейках
A1, B1 и C1 записаны числа 1, 5
и -6), то в ячейках A2 и A3, где записаны
формулы, вы получите числа 2 и ‑3. Если вы измените число в
ячейке A1 на -1, то в ячейках с формулами вы получите
числа -6 и 1.
Использование
ссылок и имен.
Ссылка однозначно определяет ячейку или группу ячеек рабочего листа.
Ссылки указывают в каких ячейках находятся значения, которые нужно использовать
в качестве аргументов формулы. С помощью ссылок можно использовать в формуле
данные, находящиеся в различных местах рабочего листа, а также использовать
значение одной и той же ячейки в нескольких формулах.
Можно также ссылаться на ячейки, находящиеся на
других листах рабочей книги, в другой рабочей книге, или даже на данные другого
приложения. Ссылки на ячейки других рабочих книг называются внешними. Ссылки на
данные в других приложениях называются удаленными.
Имя — это легко запоминающийся идентификатор, который можно использовать
для ссылки на ячейку, группу ячеек, значение или формулу. Создать имя для ячейки можно в поле имени,
или через меню Вставка | Имя | Присвоить…
Использование имен обеспечивает следующие преимущества:
·
Формулы, использующие имена, легче воспринимаются и
запоминаются, чем формулы, использующие ссылки на ячейки.
Например, формула “=Активы-Пассивы” гораздо понятнее, чем формула
“=F6-D6”.
·
При изменении структуры рабочего листа достаточно
обновить ссылки лишь в одном месте — в определении имен, и все формулы,
использующие эти имена, будут использовать корректные ссылки.
·
После того как имя определено, оно может
использоваться в любом месте рабочей книги. Доступ ко всем именам из любого
рабочего листа можно получить с помощью окна имени в левой части строки формул.
·
Вы можете также определить специальные имена,
диапазон действия которых ограничивается текущим рабочим листом. Это означает,
что эти имена можно использовать лишь на том рабочем листе, на котором они
определены. Такие имена не отображаются в окне имени строки формул или окне
диалога “Присвоить имя”, если активен другой рабочий лист книги.
·
Excel автоматическое создает имена на основе
заголовков строк и столбцов рабочего листа. Подробной информация о создании
таких имен содержится в главе “Базы данных”.
·
После того, как имя определено, вы можете:
·
Заменить все соответствующие ссылки этим именем во
всех местах рабочего листа.
Например, определив имя “Прибыль” как “=$F$12”, можно заменить все
ссылки на ячейку $F$12 именем “Прибыль”.
·
Быстро перейти на поименованную ссылку, заменить
ссылки, вставить ссылку в формулу с помощью окна имени в строке формул.
Перемещение и копирование формул. Относительные и
абсолютные ссылки.
После того как формула введена в ячейку, вы можете
ее перенести, скопировать или распространить на блок ячеек.
При перемещении формулы в новое место таблицы ссылки
в формуле не изменяются, а ячейка, где раньше была формула, становится
свободной. При копировании формула перемещается в другое место таблицы, ссылки
изменяются, но ячейка, где раньше находилась формула, остается без изменения.
Формулу можно распространить на блок ячеек.
При копировании формул возникает необходимость
управлять изменением адресов ячеек или ссылок. Для этого перед символами адреса
ячейки или ссылки устанавливаются символы “$”. Изменяться только те
атрибуты адреса ячейки, перед которыми не стоит символ “$”. Если перед всеми
атрибутами адреса ячейки поставить символ “$”, то при копировании
формулы ссылка не изменится.
Например, если в записи формулы ссылку на
ячейку D7 записать в виде $D7, то при перемещении формулы будет изменяться
только номер строки “7”. Запись D$7 означает, что при перемещении будет
изменяться только символ столбца “D”. Если же записать адрес в виде $D$7, то
ссылка при перемещении формулы на этот адрес не изменится и в расчетах будут
участвовать данные из ячейки D7. Если в формуле указан интервал ячеек G3:L9, то
управлять можно каждым из четырех символов: “G”, “3”, “L” и “9”, помещая перед
ними символ “$”.
Если в ссылке используются символы $, то она
называется абсолютной, если символов $ в ссылке нет — относительной.
Адреса таких ссылок называются абсолютными и относительными, соответственно.
Абсолютные адреса при перемещении формул не
изменяются, а в относительных адресах происходит смещение на величину переноса.
Функции
Функции в Excel используются для выполнения стандартных вычислений в рабочих
книгах. Значения, которые используются для вычисления функций, называются
аргументами. Значения, возвращаемые функциями в качестве ответа, называются
результатами. Помимо встроенных функций вы можете использовать в вычислениях
пользовательские функции, которые создаются при помощи средств Excel.
Чтобы использовать функцию, нужно ввести ее как
часть формулы в ячейку рабочего листа. Последовательность, в которой должны
располагаться используемые в формуле символы, называется синтаксисом функции.
Все функции используют одинаковые основные правила синтаксиса. Если вы нарушите
правила синтаксиса, Excel выдаст сообщение о том, что в формуле имеется ошибка.
Если функция появляется в самом начале формулы, ей
должен предшествовать знак равенства, как и во всякой другой формуле.
Аргументы
функции записываются в круглых скобках сразу за
названием функции и отделяются друг от друга символом точка с запятой “;”.
Скобки позволяют Excel определить, где начинается и где заканчивается список
аргументов. Внутри скобок должны располагаться аргументы. Помните о том, что
при записи функции должны присутствовать открывающая и закрывающая скобки, при
этом не следует вставлять пробелы между названием функции и скобками.
В качестве аргументов можно использовать
числа, текст, логические значения, массивы, значения ошибок или ссылки.
Аргументы могут быть как константами, так и формулами. В свою очередь эти
формулы могут содержать другие функции. Функции, являющиеся аргументом другой
функции, называются вложенными. В формулах Excel можно использовать до семи
уровней вложенности функций.
Задаваемые входные параметры должны иметь допустимые
для данного аргумента значения. Некоторые функции могут иметь необязательные
аргументы, которые могут отсутствовать при вычислении значения функции.
Типы
функций
Для удобства работы функции в Excel разбиты по
категориям: функции управления базами данных и списками, функции даты и
времени, DDE/Внешние функции, инженерные функции, финансовые, информационные,
логические, функции просмотра и ссылок. Кроме того, присутствуют следующие
категории функций: статистические, текстовые и математические.
При помощи текстовых функций имеется
возможность обрабатывать текст: извлекать символы, находить нужные, записывать
символы в строго определенное место текста и многое другое.
С помощью функций даты и времени можно
решить практически любые задачи, связанные с учетом даты или времени (например,
определить возраст, вычислить стаж работы, определить число рабочих дней на
любом промежутке времени).
Логические функции помогают создавать
сложные формулы, которые в зависимости от выполнения тех или иных условий будут
совершать различные виды обработки данных.
В Excel широко представлены математические
функции. Например, можно выполнять различные операции с матрицами:
умножать, находить обратную, транспонировать.
С помощью статистических функций
возможно проводить статистическое моделирование. Кроме того, возможно
использовать элементы факторного и регрессионного анализа.
В Excel можно решать задачи оптимизации и использовать
анализ Фурье. В частности, в Excel реализован алгоритм быстрого преобразования
Фурье, при помощи которого вы можете построить амплитудный и фазовый спектр.
Операции с матрицами
Для операциий над матрицами в Excel применяют
следующие средства:
1. Использование массивов
2. Встроенные функции: ТРАНСП, МУМНОЖ, МОПРЕД, МОБР
Массив возникает как непрерывная прямоугольная
область данных, которая является ссылкой в указанных выше операциях. Формулы,
обрабатывающие массив отличаются от обычных следующим:
1.
перед вводом формулы маркируется вся область массива;
2.
завершается ввод таких формул — нажатием Shift+Ctrl+Enter;
3.
формула заключается в фигурные скобки и повторяется во всех клетках области
Системы линейных алгебраических
уравнений
Многие задачи экономического характера сводятся к
решению систем линейных уравнений. Систему вида принято называть системой n
линейных алгебраических уравнений (СЛАУ) с n неизвестными.
При этом произвольные числа aij (i =
1, 2,…, n; j = 1, 2,…, n) называются коэффициентами
системы (коэффициентами при неизвестных), а числа bi (i =
1, 2,…, n) – свободными членами.
Такая форма записи алгебраической линейной
системы называется нормальной. Решением СЛАУ совокупность
чисел xi (i = 1, 2,…, n), при
подстановке которых в систему каждое из ее уравнений обращается в
тождество.
Систему можно записать в матричной форме
A * X = B, где
A – матрица коэффициентов при
неизвестных (матрица системы):
X – вектор-столбец неизвестных X = (x1, x2,
…, xn)Т:
B – вектор-столбец свободных членов B = (b1, b2,…, bn)Т:
Целое число n называется размерностью системы.


Система уравнений называется совместной,
если она имеет хотя бы одно решение, и несовместной – в
противном случае. Совместная система называется определенной,
если она имеет единственное решение, и неопределенной, если она
имеет больше одного решения.
Метод Крамера
Метод Крамера (Крамера правило) — способ решения квадратных систем линейных
алгебраических уравнений с ненулевым определителем основной матрицы (причём для
таких уравнений решение существует и единственно). Создан Габриэлем Крамером в
1750 году.
Для системы n линейных уравнений с n
неизвестными (над произвольным полем)
с определителем матрицы системы Δ, отличным от нуля,
решение записывается в виде
(i-й столбец матрицы системы заменяется столбцом
свободных членов).
Алгоритм решения системы линейных
алгебраических уравнений методом Крамера:
Имеем систему линейных алгебраических уравнений
Найдём определители:
Решение системы:
Пример:
Т.е. будем решать систему из трех алгебраических
уравнений относительно трех неизвестных. Размерность системы n=3,
матрица системы A размерности 3*3 имеет вид
а вектор-столбец свободных членов B=
Для рассматриваемой СЛАУ вспомогательные матрицы имеют
следующий вид
Тогда Δ= 360; Δ1=1080;
Δ2=-1140; Δ3=1800
Решением данной системы будут являться: Х1=3; Х2=-4;
Х3=5.
Решение систем линейных алгебраических
уравнений
в среде MS Excel
Матрица А – матрица коэффициентов при неизвестных
Столбец B – вектор-столбец свободных членов
Матрицы А1, А2, А3 заполним, используя абсолютные
ссылки:
Получим:
Определители данных матриц можем найти, используя
формулу МОПРЕД( : )
Δ=МОПРЕД(A4:C6) – определитель
матрицы А
Δ1=МОПРЕД(A11:C13) — определитель
матрицы А1
Δ2=МОПРЕД(E11:G13) — определитель
матрицы А2
Δ3=МОПРЕД(I11:K13) — определитель
матрицы А3
Х1=B15/B8
Х2=F15/B8
Х3=J15/B8
Заключение.
Миллионы людей ежедневно занимаются математическими
расчётами, иногда в силу влечения к таинствам математики и её внутренней
красоте, а чаще в силу профессиональной и иной необходимости, не говоря уже об
учёбе. Ни одна серьёзная разработка в любой отрасли науки не обходится без
трудоёмких математических расчётов. В этих случаях на помощь нам может придти
табличный редактор Microsoft® EXCEL. Он позволит выполнить все
математические расчёты быстро и точно. В данной работе приведён пример решения
системы линейных арифметических уравнений из трёх уравнений с тремя
неизвестными. Аналогично решаются СЛАУ размером 4х4, 5х5, … NxN.
Литература.
1.
Колесников Р. Excel 97
(русифицированная версия). — Киев: Издательская группа BHV, 1997. — 480 с.
2. Руководство пользователя. Microsoft Windows 95. — Neunkirchen:
Buhl-Data-Service Microsoft Corporation, 1995.
3.
Рассел Борланд.
Эффективная работа с Microsoft Word 97. — СПб: Питер, 1998. — 960 с.
4. Лавренов С.М. Excel: Сборник
примеров и задач.- М.: Финансы и статистика, 2002.- 336 с.
5. Гельман В.Я. Решение
математических задач средствами Excel: Практикум.- СПб.: Питер, 2003.- 237 с.
6. Решение уравнений средствами
Excel: Методические указания к лабораторным работам/ Сост.: Е.Е. Дадонова, А.Г.
Пимонов, М.А. Тынкевич; ГУ Кузбас. гос. техн. ун-т.- Кемерово, 2002.- 22 с.
Цели урока:
обучающие:
- повторение и закрепление знаний учащихся
правил записи арифметических выражений и формул
в электронных таблицах; - повторение алгоритма решения систем уравнений;
- формирование знаний и умений в решении систем
уравнений, используя возможности электронных
таблиц;
развивающие:
- формирование умений анализировать, выделять
главное, сравнивать, строить аналогии;
воспитывающие:
- осуществление эстетического воспитания;
- воспитание аккуратности, добросовестности.
Тип урока: урок закрепления изученного
материала и объяснения нового.
ХОД УРОКА
I. Организационная часть.
Здравствуйте! Все мы знаем, что одну и
ту же информацию можно закодировать любым
способом. Перед вами набор чисел. Известно, что
каждому числу ставится в соответствие буква в
русском алфавите. Расшифруйте эту информацию,
кто быстрее!
|
9 |
15 |
1 |
15 |
10 |
6 |
– |
19 |
10 |
13 |
1 |
! |
|
– |
! |
Ответ: “Знание – сила!”
Молодцы! А знаете, кому принадлежит это
выражение? (Если нет, то один ученик ищет ответ в
Интернете. Остальные отвечают на вопросы:
Для чего предназначена программа Excel? (Программа
Excel предназначена для хранения и обработки
данных, представленных в табличном виде) Что
собой представляет документ в Excel? (Каждый
документ в Excel представляет собой набор таблиц –
рабочую книгу, которая состоит из одного или
многих рабочих листов) Какая функция
используется для подсчета суммы чисел? (Функция
СУММ). Как определить адрес ячейки? (Excel вводит
номера ячеек автоматически. Адрес ячейки
составляется как объединение номеров столбца и
строки без пробела между ними)
Выражение английского философа Френсиса
Бэкона “Знание – сила!” и будет эпиграфом к
нашему уроку. («Нравственные и политические
очерки», 1597).
II. Повторение пройденного материала.
Мы уже знакомы с программой Microsoft Excel,
умеем записывать арифметические выражения и
различные формулы, находить значения
арифметических выражений и построить графики
функций. Чтобы проверить выполнение домашнего
задания, предлагаю каждому пройти тестирование. (Приложение 1)
Хорошо, все справились и каждому
поставим соответствующие оценки в журнал. А
давайте устроим путешествие в математику и
вспомним, что мы понимаем под понятием: “Решить
систему уравнений”? (Найти такие значения х и у,
которые будут удовлетворять и первое уравнение и
второе). Какие способы существуют для решения
систем уравнений (метод подстановки, метод
сложения и графический способ). Сегодня мы с
вами научимся решать системы уравнений,
используя возможности электронных таблиц.
III. Объяснение нового.
А. Решим систему 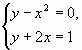
данную систему 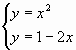
Для решения воспользуемся диаграммой, на которой
отобразим графики обеих функций. Заполняем
столбец А: заполняем ячейки А2:А22 числами от -5 до 5
с шагом 0,5. (в ячейку А2 заносим число -5, в ячейку А3
– число -4,5, выделяем ячейки А2 и А3, установим
курсор мыши на правый нижний угол рамки
(указатель примет форму черного крестика) и
растягиваем рамку вниз, пока последнее значение
не станет равным 5). При заполнении столбца В в
ячейку В2 заносим формулу =А2*А2, которую затем
копируем до ячейки В22. (протянем формулу за
правый нижний угол). При заполнении столбца С в
ячейку С2 заносим формулу =1-2*А2, копируем ее до
ячейки С22. Выделим блок с данными, с помощью
Мастера диаграмм выберем тип диаграммы Точечная
и построим графики функций. Координаты точек
пересечения графиков – решения системы. {(-2,5; 6);
(0,5; 0)}
Получены приближенные значения
решений. Чем меньше шаг, тем точнее значение
координат точек пересечения.
Запишем алгоритм решения систем
уравнений графическим способом:
1. Преобразовать систему уравнений,
если это необходимо.
2. Задать начальные значения для Х.
3. Найти значение первой функции при
заданных Х.
4. Найти значение второй функции при
тех же Х.
5. Выделить блок с данными и построить
графики функций, используя точечный тип
диаграммы.
6. Решение системы — точка пересечения
графиков функций.
7. Для нахождения координат точек
пересечения с заданной точностью построить
новый график на том отрезке, где находится
решение, с шагом, равным значению точности.
Б. Решить систему уравнений 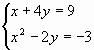
электронную таблицу исходные данные и расчетные
формулы следующим образом:.
Для решения системы уравнений
воспользуемся надстройкой Поиск решения,
которая запускается через Сервис (-Надстройки) и
заполним диалоговое окно следующим образом:
При нажатии на кнопку Выполнить
происходит решение системы уравнений и в ячейках
B3 и B4 высвечивается результат.
Запишем примерный алгоритм решения
системы уравнений, используя Поиск решения
1. Преобразовать систему уравнений,
если это необходимо
2. Записать исходные данные (в ячейку А1
ввести текст “Решите уравнение”, в ячейку В1
записать первое уравнение, в ячейку В2 второе
уравнение, в ячейку А3 ввести текст “Х=”, в ячейку
А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6
“уравнение 2”. В ячейке B3 хотим получить
значение Х, в ячейке В4 – значение Y, их оставляем
пустыми.
3. В ячейку В5 переписать уравнение 1,
используя правило записи арифметических
выражений, следующим образом: в левой части
вместо Х указывать ячейку В3, вместо Y ячейку В4,
правую часть отбросить. Таким же образом
переписать левую часть второго уравнения в
ячейку В6.
4. Выбрать команду Сервис – Поиск
решения.
5. Установить целевую ячейку — ту
ячейку, в которой содержится формула, например, В5
и задать значение, равное значению правой части
первого уравнения
6. В поле “изменяя ячейки” указать
ячейки, в которых хотим увидеть ответ (В3 и В4)
7. Вести ограничение $B$6 = -3. Для этого
щелкнуть на кнопке Добавить и в полученном окне
установить реквизиты следующим образом: в поле
Ссылка на ячейку указать ячейку, в которой
записана левая часть другого уравнения, в другом
поле выбрать знак “=”, в третьем ввести число,
равное значению правой части. Закрыть окно
Добавить ограничение, щелкнув кнопкой ОК
8. Решить систему уравнений, щелкнув
кнопкой Выполнить
IV. Практическая работа на компьютере.
Вариант I
А. Решите систему уравнений графическим
способом
Б. Решите систему уравнения, воспользовавшись
командой Поиск решения:
Вариант II
А. Решите систему уравнений графическим
способом
Б. Решите систему уравнения, воспользовавшись
командой Поиск решения:
V. Подведение итогов.
Повторить алгоритмы решения систем уравнений
Выставить оценки за тестирование в журнал
VI. Домашнее задание.
Решить рациональным способом системы
уравнений:
;
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Морозов Д.И. 1
1МБОУ Лицей 4
Молева Н.А. 1
1ФГБОУ ВО «ВГУ»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Актуальность темы. Решение систем уравнений важно не только в плане содержания курса математики; они используются в физике, химии, при решении технических, инженерных задач, при работе с моделями экономических, социальных, биологических и прочих явлений и процессов. Учащиеся школ, начиная с 7 класса, знакомятся с системами уравнений. Есть разные методы решения таких задач. Школьники часто испытывают трудности в поиске корней. Для оптимизации процесса поиска корней можно воспользоваться Excel.
Цель работы: создать файл с формулами для решения систем линейных уравнений.
Задачи:
Познакомиться с различными методами решения систем линейных уравнений с 3 и более неизвестными.
Познакомиться с программой Microsoft Excel.
Решить системы с помощью Excel.
Объект исследования: система линейных алгебраических уравнений.
Предмет исследования: методы и способы решения систем линейных уравнений.
Гипотеза: мы предполагаем, что существует простой способ, позволяющий решать системы линейных уравнений с любым количеством неизвестных, который будет доступен всем, даже незнакомым с понятиями линейной алгебры.
Методы исследования: теоретический анализ литературы, формализация, индукция, классификация, описание, моделирование, сравнение.
Структура работы: проектная работа состоит из введения, четырех глав, заключения, списка использованных источников, приложения.
Глава 1. Аналитические методы решения системой линейных алгебраических уравнений
1.1 Метод Крамера
Метод Крамера – способ решения систем линейных алгебраических уравнений, где количество неизвестных переменных равняется числу уравнений, в которой основной определитель не равен нулю [7].
|
(1) |
В данной системе (1): x1, x2, …, xn— неизвестные переменные, aij, i = 1, 2, . . ., n; j = 1, 2, . . ., n — числовые коэффициенты, b1, b2, …, bn — свободные члены. Решение данной СЛАУ (Системой линейных алгебраических уравнения, далее мы будем использовать данное сокращение для удобства) — набор значений x1, x2, . . ., xn в них все уравнения системы являются тождественными. Запишем систему в матричном виде:
|
(2) |
|
|
(3) |
|
|
, |
(4) |
Где (2) – это основная матрица системы, в которой её элементы – это коэффициенты при неизвестных аргументов; B — это матрица столбец свободных членов; X — это матрица столбец неизвестных аргументов
После того как мы найдём неизвестные переменные x1, x2, . . ., xn, матрица X становится решением системы уравнений.
Метод Крамера основан на 2-х свойствах определителя матрицы: Определитель квадратной матрицы A = || a i j ||, i = 1, 2, . . ., n равняется сумме произведений элементов какой-либо строки на их алгебраические дополнения:
|
(6) |
Имеем в виду, что не равно q
Приступаем к нахождению неизвестной переменной х1.
Умножаем обе части первого уравнения системы на А11 (), обе части второго уравнения на А21 и т.д. Мы умножаем уравнения системы на соответствующие алгебраические дополнения 1-го столбца матрицы А. Складываем все левые части уравнения, сгруппировав, и приравниваем получившуюся сумму к сумме всех правых частей уравнения:
|
(10) |
Предыдущее равенство будет иметь следующий вид:
|
= |
(11) |
Таким же образом находим все оставшиеся неизвестные переменные.
Формулы для нахождения неизвестных:
|
, , , |
(13) |
Пример решения системы рассмотрен в Приложении А.
1.2 Метод обратной матрицы
Суть метода обратной матрицы состоит в умножении обратной матрицы коэффициентов системы линейных уравнений на вектор свободных членов [4].
Обратная матрица обозначается . Понятие обычно используется только для квадратных матриц. Если определитель матрицы равен нулю, то обратной матрицы для данной системы не существует. Матрица является обратной матрице A, если выполняется равенство: В данной формуле E – это единичная величина
Формула нахождения алгебраического дополнения:
|
(14) |
В данной формуле – минор.
Формула нахождения обратной матрицы:
|
(15) |
Здесь — матрица, составленная из алгебраических дополнений.
В процессе решения у нас возникает необходимость умножения матрицы A на вектор-столбец B. Чтобы найти произведение, необходимо умножать по правилу «строка на столбец». Результатом умножения является вектор столбец.
|
(16) |
Таким образом, результатом операции умножения матрицы порядка на матрицу порядка является матрица порядка . Пример решения можно увидеть в Приложении Б.
1.3 Метод Гаусса
Метод Гаусса – способ решения систем линейных алгебраических уравнений, где отсутствует необходимость проверять систему уравнений на совместность; можно решать системы уравнений, где: количество определителей совпадает с количеством неизвестных переменных; количество определителей не совпадает с количеством неизвестных переменных; определитель равен нулю. результат выдается при сравнительно небольшом количестве вычислительных операций [5,6].
Расширенная матрица – матрица, которая образуется с помощью добавления в качестве (n+1) столбца матрицу-столбец свободных членов и имеет обозначение T.
|
(18) |
Алгоритм решения СЛАУ методом Гаусса:
Проверяем, что определитель матрицы не равен нулю
a11 не равен нулю — всегда можно добиться этого перестановкой уравнений системы.
Исключаем переменную x1 из всех уравнений систему, начиная со второго.
Прибавим ко второму уравнению системы первое, которое умножено на , прибавим к третьему уравнению первое умноженное на и т.д.
После выполнения действий матрица будет иметь следующий вид:
|
(19) |
В котором:
|
(20) |
|
|
(21) |
Далее делаем аналогично с нижними тремя уравнениями
Считается, что a22(1) не равна нулю. Исключаем неизвестную переменной x2 из всех уравнений, начиная с третьего: к третьему уравнению систему прибавляем второе, которое умножено на ; к четвертому прибавляем второе, которое умножено на и т.д.
После выполнения этих действий, СЛАУ будет иметь следующий вид:
|
, |
(22) |
В котором:
|
(23) |
|
|
(24) |
Соответственно переменная x2 исключена из всех уравнений, начиная с третьего. Далее приступаем к исключению неизвестной x3, действуя по аналоги с предыдущим образцом:
|
(25) |
После того как система обретает такой вид, можно решить матрицу обратным ходом метода Гаусса: Вычисляем xnиз последнего уравнения как xn= ;
С помощью полученного xnнаходим xn-1 из предпоследнего уравнения и т.д., находим x1 из первого уравнения. Решение системы этим методом приведено в Приложении В.
Глава 2. Решение систем уравнений с помощью Excel
2.1 Метод Крамера
Для решения рассмотрим следующую систему:
Составляем 2 таблицы: A – из коэффициентов уравнений и B – из свободных членов. Таблицы для данной системы приведены на рисунке 1.
Рисунок 1 – Таблицы A и B.
Составляем ещё три таблицы. Каждая из них копия матрицы A, но с изменением по очереди одного из столбцов на таблицу B. У первой таблицы – первый столбик, у второй таблицы – второй и т.д. Пример составления таблиц показан на рисунке 2.
Рисунок 2 – Дополнительные таблицы с изменениями.
Необходимо найти определитель для каждой из таблиц. Система уравнений будет решаться в случае если каждый из определителей будет не равен нулю. Для расчёта нам потребуется функция: МОПРЕД. Синтаксис: =МОПРЕД(массив)[2]. Введение данной функции показано на рисунке 3
Рисунок 3 – Используем функцию МОПРЕД.
В функцию МОПРЕД вписываем массив: открываем скобочку, выделяем первую ячейку преобразованной матрицы, далее выделяем всю остальную часть данной матрицы и закрываем скобочку. После нажимаем Ctrl+Shift+Enter [1]. Если мы просто нажмем Enter, то вместо матрицы вставиться только значение в одну ячейку.
Делаем аналогично с другими таблицами и основной матрицей и получаем значения. После мы получаем определители, это можно увидеть на рисунке 5.
Рисунок 4 – Получение значения определителя.
Ищем корни уравнения, разделив поочерёдно каждое полученное значения таблицы на число, полученное из основной матрицы в нашем случае на -30. Далее мы получаем ответ, представленный на рисунке 6.
Рисунок 5 – Получение неизвестных переменных.
Таким образом, решение системы уравнений, используя метод Крамера и функцию =МОПРЕД [2], взятой n+1 раз, и последующих по этому методу делений получено в столбце H.
2.2 Метод обратной матрицы
Для решения рассмотрим следующую систему:
Составляем таблицы: A из коэффициентов, а B из свободных членов.
Рисунок 6 – Таблицы A и B.
Находим обратную матрицу. Используем функцию: МОБР. =МОБР(массив). Выделяем область, равную по размеру исходной матрице. И пишем в 1 ячейке МОБР. Получаем значения обратной матрицы на рисунке 8.
Рисунок 7 – Использование функции МОБР.
Умножаем обратную матрицу на матрицу B. Для расчёта возьмем функцию: МУМНОЖ: =МУМНОЖ (Массив 1; Массив 2).
Рисунок 8 – Использование функции МУМНОЖ
2.3 Метод Гаусса
Для решения рассмотрим следующую систему:
Составляем две таблицы: A из коэффициентов уравнений и B из свободных членов. Таблицы для данной системы можно увидеть на рисунке.
Рисунок 9 – Таблица коэффициентов
Начнем приводить матрицу к трапециевидному виду []. Первую строчку переписываем без изменений. Далее выполняем действия по формуле: =B7-B6*$B$7/$B$6. Формула составлена для данного расположения. В формуле видно, что из значений ячейки 7 строки (2 уравнение системы) вычитаем значение из стоки номер 6, умноженное на специальный коэффициент [3]. Как видно из формулы, часть ячеек записаны со значком «$», таким образом мы ставим абсолютную адресацию на ячейку [1]. После того, как мы вставили формулу, то протягиваем ее функционал на всю строку. Полученный результат работы формулы приведен на рисунке
Рисунок 10 – Начало работы прямого хода
Аналогично работаем с третьим уравнением системы. Формула изменений в этом случае имеет вид =B8-B6*$B$8/$B$6. Промежуточный вариант преобразований представлен на рисунке. Таким образом мы получил столбец с нулевыми коэффициентами.
Теперь нам нужно получить еще одно нулевое значение в 3-м уравнении. Будем вычитать из него 2-е с коэффициентом, полученным делением значений столбца С. В этом случае формула имеет вид: =C13-C12*$C$13/$C$12.
Аналогично убираем и верхние коэффициенты, чтобы осталась только диагональ. На рисунке показан результат работы всех операций.
Рисунок 13 – Приведение матрицы к диагональному виду
Теперь нормализуем матрицу, для этого поделим значения всей строки на диагональные элементы. В результате получаем, что по диагонали у нас находятся единицы, а в столбце E значения вектора B [4,5]. Таким образом, мы получаем единичную матрицу (рисунок)
Рисунок 14 – Результат нормализации
Из рисунка видно, что столбец E, а это вектор B, является решением системы.
Заключение
По результатам работы можно сделать следующие выводы:
Методы решения систем линейных уравнений подходят для случая, когда количество уравнений и неизвестных совпадают.
В случае вырожденной системы можно использовать только метод Гаусса.
Наиболее простым для расчетов является метод Крамера.
Использование программы Excel позволяет быстро решать такие системы с помощью готовых функций.
Если в методе Гаусса не заниматься анализом коэффициентов, то все промежуточные значения будут дробными.
Так как для решения задач в Excel нужно каждый раз настраивать формулы, что может составить сложности для тех, кто не знаком с понятиями линейной алгебры, то следующим этапом работы будет создание приложения на Python, чтобы пользователю оставалось только ввести необходимые коэффициенты.
Список литературы
Айзек, М.П. Графики, формулы, анализ данных в Excel / М.П. Айзек, М.В. Финков. – СПб. : Наука и техника, 2019. – 384 с.
Александер, М. Формулы в Microsoft Excel 2016 / М. Александер, Д. Куслейка. – СПб. : Диалектика, 2017. – 784 с.
Демидович Б.П., Основы вычислительной математики/ Б.П. Демидович, И.А. Марон. – М.: Наука, 1966. – 644 с.(Гаусс
Ильин В.А., Линейная алгебра: Учеб. Для вузов/ В.А. Ильин, Э.Г. Позняк —М. Наука. Физматлит, 1999 — 296 с.
Пирумов О.Г., Численные методы : учебное пособие [Электронный ресурс] / О. Г. Пирумов. – М. : Изд-во МАИ, 1998. — 188 с.
Тынкевич, М. А., Введение в численный анализ : учеб. пособие / М. А. Тынкевич, А. Г. Пимонов ; КузГТУ. – Кемерово, 2017. – 176 с
Шипачёв В.С., Высшая математика/ В.С. Шипачёв – М. «Высшая школа» , 1985 – 480 с. (Крамер)
Приложение А
Решить систему методом Крамера.
Найдём определитель матрицы:
Вычислим определитель , для этого заменим первый столбец в основной матрице на столбец свободных членов B = , получим:
Вычислим определитель , для этого заменим второй столбец в основной матрице на столбец свободных членов B = , получим:
Вычислим определитель , для этого заменим третий столбец в основной матрице на столбец свободных членов B = , получим:
Ответ: x=2; y=0; z=1
Приложение Б
Решить систему методом обратной матрицы.
Вычислим главный определитель системы:
Соответственно матрица невырожденная и обратная матрица к ней существует.
Найдём алгебраические дополнения всех элементов главной матрицы:
Ответ: x = 5; y = -1; z = 1
Приложение В
Рассмотрим решение систем уравнения методом Гаусса:
Запишем вспомогательную матрицу:
Домножим первое уравнение системы на -2:
Сложим первое уравнение со вторым:
Таким образом мы получили первый нулевой коэффициент во втором уравнении. Сделаем аналогично для третьего. Нам нужно первое уравнение разделить на -2 (именно на это число происходило домножение), а затем умножить на -3. Также мы можем сразу на -3 разделить второе уравнение. В результате получим:
Сложим первое и третье уравнение:
Сделаем все коэффициенты положительными, разделив первое на -3, а третье
на -1:
Чтобы получить в последнем уравнении ещё один нулевой элемент, произведем умножение второго уравнения на -3:
Сложим второе и третье уравнения:
Приведём матрицу к окончательному виду:
Перейдём к выполнению обратного хода. Для этого перепишем нашу систему уравнений с коэффициентами матрицы после элементарных преобразований:
Сразу видно, что мы нашли два неизвестных: y=2, z=3. Подставим эти значения в первое уравнение и найдём неизвестную x:
, x=1
Ответ: x=1, y=2, z=3
Просмотров работы: 339
Решим Систему Линейных Алгебраических Уравнений (СЛАУ) методом обратной матрицы в MS EXCEL. В этой статье нет теории, объяснено только как выполнить расчеты, используя MS EXCEL.
Решим систему из 3-х линейных алгебраических уравнений с помощью
обратной матрицы
(матричным методом).
СОВЕТ
: Решение СЛАУ методом Крамера приведено в статье
Решение Системы Линейных Алгебраических Уравнений (СЛАУ) методом Крамера в MS EXCEL
.
Запишем в ячейки основную матрицу системы и столбец свободных членов.
Систему
n
линейных алгебраических уравнений с
n
неизвестными можно решать матричным методом только тогда, когда
определитель основной матрицы
системы отличен от нуля (в противном случае мы имеем линейно зависимые уравнения и соответственно решение систем не единственное). В нашем случае определитель =12.
Вычислим
обратную матрицу
с помощью
формулы массива
МОБР()
.
Для этого выделите ячейки
A18:C20
, а в
Строке формул
введите
=МОБР(A11:C13)
, затем нажмите
CTRL+SHIFT+ENTER
.
Решение системы уравнений получим умножением обратной матрицы и столбца свободных членов.
Перемножить матрицы
можно с помощью
формулы массива
=МУМНОЖ()
.
Для этого выделите ячейки
F18:F20
, а в
Строке формул
введите
=МУМНОЖ(A18:C20;F11:F13)
, затем нажмите
CTRL+SHIFT+ENTER
.
В
файле примера
также приведено решение системы 4-х и 5-и уравнений.