Создадим модель для нахождения наилучшего распределения ресурсов, при котором минимизируются затраты, понесенные за несколько периодов (Allocation Problem). Расчет будем проводить с помощью надстройки Поиск решения.
Задача оптимального распределения ресурсов (распределительная задача) заключается в отыскании наилучшего распределения ресурсов, при котором либо максимизируется результат, либо минимизируются затраты. Задача, в которой минимизируются затраты, понесенные в одном периоде решена в статье
Поиск решения MS EXCEL (1.2). Распределение ресурсов (ограничение по количеству оборудования)
, и имеет смысл предварительно познакомиться с изложенным там материалом. В этой статье мы решим аналогичную задачу, но для случая работы оборудования в нескольких периодах (пример с сайта
www.solver.com
).
Вводная статья про
Поиск решения
в MS EXCEL 2010
находится здесь
.
Задача
Предприятие выпускает монопродукт (только один вид изделия и ничего более) и ему необходимо выполнить заказ клиента. Выпуск продукции осуществляется в течение 5 дней. Отгрузка заказа ежедневная. На предприятии 3 типа оборудования. Каждый тип оборудования выпускает один и тот же продукт. Производительность каждого типа оборудования разная. Каждый тип оборудования имеет постоянную и переменную часть расходов. Переменная часть расходов пропорциональна количеству произведенных изделий. Имеется ограниченное количество единиц оборудования каждого типа (но общее количество оборудования избыточно для выполнения заказа). Требуется минимизировать расходы на оборудование при условии выполнения заказа.
Создание модели
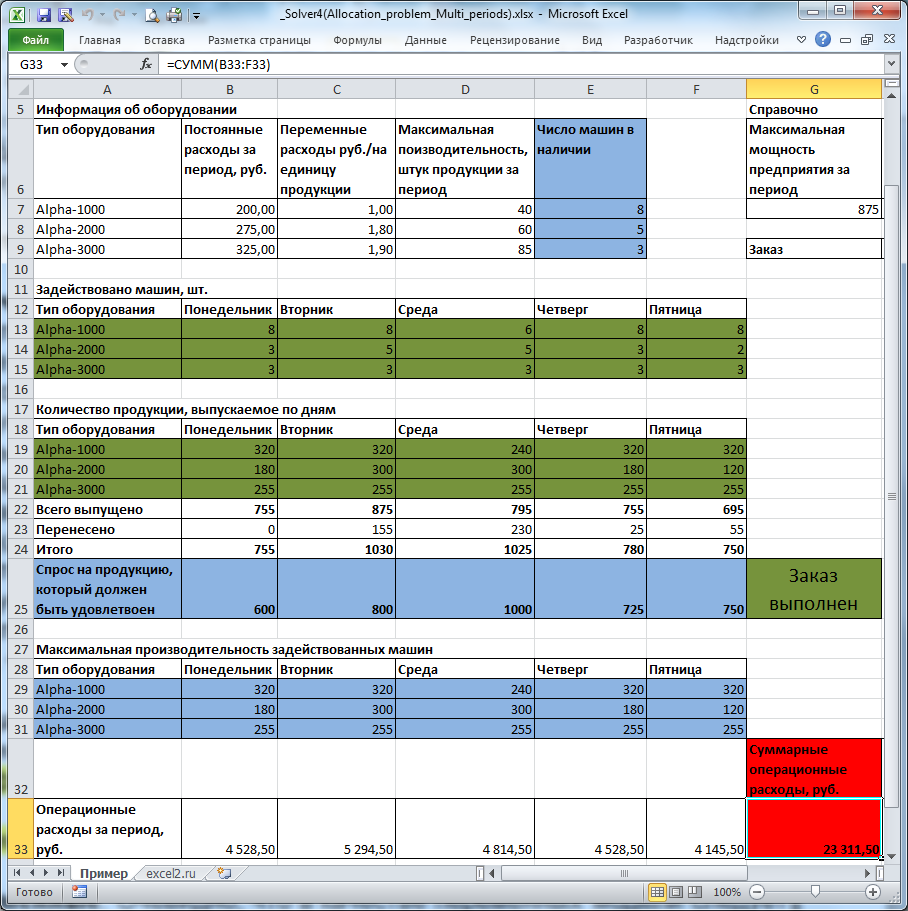
На рисунке ниже приведена модель, созданная для решения задачи (см.
файл примера
).
Предприятие несет расходы в зависимости от типа оборудования: использование оборудования типа Alpha-3000 самое дорогое в эксплуатации, но оно и самое производительное. Оборудование типа Alpha-1000 самое дешевое в эксплуатации, но оно и менее производительное. Задача
Поиска решения
выбрать наиболее дешевое оборудование, так чтобы заказ был выполнен (мощностей Alpha-1000 не хватит для выполнения заказа). Казалось бы, решение очевидно (взять по максимуму дешевое оборудование, остальную производительность обеспечить более дорогим). Однако, если учесть, что из-за низкой производительности дешевых машин приходится их брать больше, неся существенные постоянные расходы, то решение уже не кажется очевидным.
Переменные (выделено зеленым)
. В качестве переменных модели следует взять количество задействованных единиц оборудования каждого типа и суммарное количество продукции, выпущенное на каждом типе оборудования (производительность задается не для каждой единицы, а для типа в целом). Для наглядности диапазонам ячеек, содержащих переменные, присвоены
имена
Машин_Задействовано
и
Продукции_выпущено.
Ограничения (выделено синим)
. Количество задействованных машин должно быть целым числом. Количество задействованных машин каждого типа должно быть не больше, чем имеется в наличии (используются
именованные диапазоны
Alpha
XXXX
_Задействовано
и
Alpha
XXXX
_в_наличии
). Всего должно быть выпущено продукции не меньше чем величина заказа (используется
именованный диапазон
Продукции выпущено_Итого
). В день возможно производить больше продукции, чем требуется в день заказа, излишек переносится на следующий день. Также необходимо ограничить производительность задействованного оборудования. Производительность задается не для каждой единицы, а для типа в целом (используются
именованные диапазоны
Продукции выпущено
и
Макс_производительность_задейств_машин
).
Целевая функция (выделено красным)
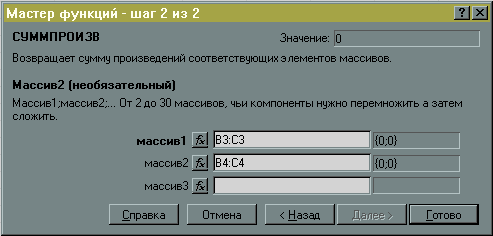
. Целевая функция – это сумма операционных расходов за 5 дней. Операционные расходы, понесенные за день, задается формулой
=СУММПРОИЗВ(B19:B21; Расходы_переменные)+ СУММПРОИЗВ(B13:B15; Расходы_постоянные)
B19:B21
– количество продукции, выпущенной в определенный день.
B13:B15
— количество задействованных машин в определенный день.
Это суммарные операционные расходы (переменная и постоянные части). Сумма операционных расходов за 5 дней должна быть минимизирована.
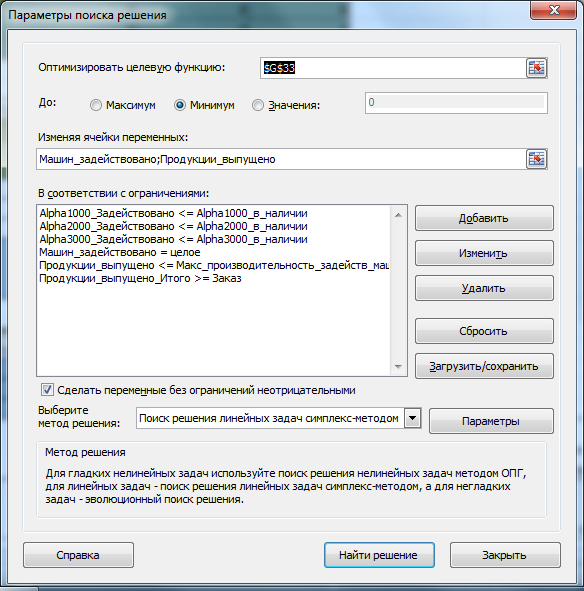
Убедитесь, что метод решения соответствует линейной задаче. Параметры
Поиска решения
были выбраны следующие:
Теперь в диалоговом окне можно нажать кнопку
Найти решение
.
Результаты расчетов
Поиск решения
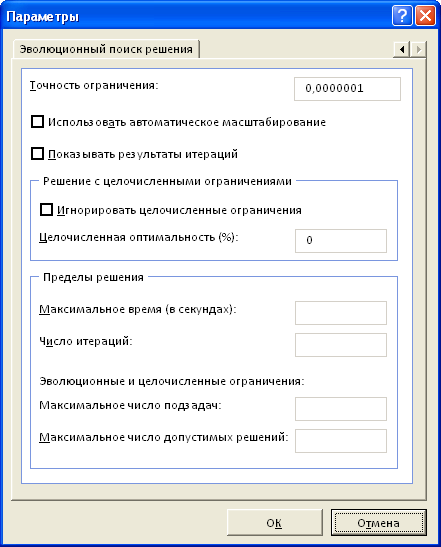
подберет оптимальный набор единиц оборудования по типам и их производительность, при котором операционные расходы будут минимальные, а заказ выполнен. В нашей задаче было установлено целочисленное ограничение, что существенно усложняет задачу поиска и, соответственно, сказывается на скорости расчета. Как показано на рисунке выше,
Целочисленная оптимальность
была выбрана 0% (
Целочисленная оптимальность
(Integer Optimality) позволяет
Поиску решения
остановить поиск, в случае, если он найдет целочисленное решение, в пределах указанного процента от оптимального). В нашем случае (0%), требуется найти лучшее из известных
Поиску решения
решений. Поиск в этом случае занял 8 секунд, результат 23 311,50. Установив
Целочисленную оптимальность
1%, поиск займет 0,2 сек, результат 23 370,50 (отличие на 0,3%). Это информация к размышлению: стоит ли увеличение точности на 0,3% уменьшения скорости расчетов более чем на порядок? Решать Вам. В любом случае, первые расчеты модели лучше проводить при
Целочисленной оптимальности
не равной 0%.
Содержание
- Постановка задачи и подготовка таблиц
- Виды транспортных задач
- Общее описание транспортной задачи
- Инструменты для решения транспортной задачи в Эксель
- Постановка задачи
- Решение задачи
- Условие
- Варианты решения
- Транспортная задача в Экселе
- Пример задачи
- Как решить транспортную задачу в Excel
- Алгоритм решения транспортной задачи распределительным методом
- Что такое симплекс-метод
- Алгоритм решения основной задачи ЛП симплекс-методом
- Вводная часть, с которой желательно ознакомиться
- О чем говорится в определении транспортной задачи?
- Общий план решения транспортной задачи методом потенциалов
- Подробная инструкция по решению транспортной задачи
Постановка задачи и подготовка таблиц
Цель задачи сводится к математическому моделированию минимизации грузопотоков. Довольно часто студенты пишут рефераты на тему поиска решения транспортной задачи. Этот пример можно взять за основу реферата.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
- в виде схемы;
- в виде матрицы.
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
- открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
- закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Общее описание транспортной задачи
Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.
Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.
Инструменты для решения транспортной задачи в Эксель
Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.
- Делаем перемещение во вкладку «Файл».
- Кликаем по подразделу «Параметры».
- В новом окне переходим по надписи «Надстройки».
- В блоке «Управление», который находится внизу открывшегося окна, в выпадающем списке останавливаем выбор на пункте «Надстройки Excel». Делаем клик по кнопке «Перейти…».
- Запускается окно активации надстроек. Устанавливаем флажок возле пункта «Поиск решения». Кликаем по кнопке «OK».
- Вследствие этих действий во вкладке «Данные» в блоке настроек «Анализ» на ленте появится кнопка «Поиск решения». Она нам и понадобится при поиске решения транспортной задачи.
Постановка задачи
Есть запасы однотипной продукции у поставщиков A1, A2, A3, A4.
Существует потребность в этой продукции B1, B2, B3
Стоимость доставки единицы продукции от поставщиков к потребителям представлена в таблице.
|
Поставщик |
Потребитель |
Запас |
||
| В1 | В2 | В2 | ||
| А1 | 6 | 5 | 2 | 250 |
| А2 | 3 | 7 | 4 | 100 |
| А3 | 7 | 8 | 1 | 80 |
| А4 | 2 | 2 | 3 | 120 |
|
Потребность |
150 | 150 | 250 |
Необходимо составить такой план перевозок, который бы удовлетворил все потребности и имел минимальную стоимость.
Решение задачи
Для решения данной задачи в табличном процессоре необходимо составить две таблицы, приведенные выше, но вторую таблицу не заполнять данными.
Для решения транспортной задачи потребуются функции: СУММПРОИЗВ, СУММ и надстройка «Поиск решения».
Для отображения формул необходимо на вкладке «Формулы» в группе «Зависимости формул» выбрать «Показать формулы» либо горячее сочетание клавиш «Ctrl+` (тильда)».
Дальше выбираем команду «Поиск решения» на вкладке «Данные»
Кстати, если дать имена диапазонам ячеек, то окно поиска решения будет выглядеть следующим образом:
Решение поставленной задачи представлено ниже.
Условие
Есть некие предприятия и склады с грузом. Каждое предприятие, нуждается в определённом объёме нашего груза. Каждый склад доставляет тонну груза по собственному тарифу. Таким образом, нужно составить маршрут, по которому мы развезём объём груза, удовлетворяющий каждое предприятие, и при этом затратим меньше всего средств.
Так транспортная задача выглядит в своём наиболее общем и типовом виде.
С – это цена за тонну. X – это то, сколько мы привезём тонн со склада на предприятие. Например, если мы примем X11 равным 5, это будет значить, что со склада А1 к потребителю B1 мы повезём 5 тонн по цене C11. Вот нам и нужно как-то распределить всё так, чтобы потратить меньше всего денег.
Варианты решения
Транспортную задачу можно решить «вручную». Существует несколько подходов к её решению на бумаге. Среди них:
- Метод опорного плана;
- Метод минимального элемента;
- Метод Фогеля.
Решение транспортных задач
Как правило, решая задачу одним из этих способов, вы получаете решение, находите потенциалы для него и понимаете, что в числе потенциалов есть положительные значения. Соответственно, это говорит о том, что вы нашли неверное решение. Далее вам нужно действовать, что называется, наугад. Вы переставляете различные цифры в таблице, пробуете разные варианты, словом, ищите решение методом «научного тыка». Далее снова пересчитываете потенциалы, и снова ничего не срастается.
Однозначного алгоритма, работающего безотказно в любых условиях, к сожалению, пока не придумали.
Однако для решения транспортной задачи или проверки полученного нами на бумаге результата, мы можем воспользоваться функционалом MS Excel.
Транспортная задача в Экселе
Для решения нам потребуется надстройка «Поиск решения». Возможно, она не будет активирована в вашем редакторе по умолчанию, поэтому, проделываем следующую очередность действий:
- Жмём «Файл»;
- В появившемся меню нажимаем по предпоследней кнопке «Параметры»;
- Вновь находим предпоследний пункт «Надстройки» и переходим в «Управление»:
- Ставим галочку в появившемся окне рядом с пунктов «Поиск решения» и жмём «ОК».
Поиск решения активирован. Далее он будет нами использован.
Пример задачи
На складах A1 — A4 есть суммарно 100 тонн зерна, и их нужно развести по текущим расценкам в пункты B1 – B3, потратив как можно меньше средств на доставку. Тарифы на доставку указаны в центре таблицы.
Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).
Использовать можно любую версию программы – 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).
Алгоритм решения транспортной задачи распределительным методом
Резюмируя выполненные выше решения, сформулируем алгоритм решения транспортной задачи распределительным методом (поиска оптимального плана транспортной задачи).
- Проверить, является ли план перевозок оптимальным. Если оценки всех “свободных мест” неотрицательны, то план перевозок является оптимальным. В противном случае можно найти новый план перевозок с меньшим значением линейной формы.
- Найти “свободное место” с наименьшей негативной оценкой (наибольшее по модулю отрицательное число). В новом плане перевозок соответствующая клетка становится “занятым местом”.
- Вдоль цикла, соответствующего “свободному месту” из предыдущего пункта, отметить вершины знаками “плюс” и “минус” пройденные вершины (“кружочки”) по принципу: знаком “плюс” отмечаются нечётные вершины, знаком “минус” – чётные.
- Вдоль цикла, упомянутого в предыдущем пункте, выбрать наименьшее из чисел в кружочке, отмеченное знаком “минус” и обозначить его буквой “тэта”.
- Произвести перенаправление грузов для нового плана перевозок. Для этого число “тэта”, упомянутое в предыдущем пункте, прибавить к стоимостям перевозок в правых нижних углах клеток со знаком “плюс” и вычесть из стоимостей перевозок в правых нижних углах клеток со знаком “минус”. Стоимости в клетках, не входящих в цикл, не меняются.
- Вычислить значение линейной формы для нового плана перевозок. Для этого вычисляется “экономия”: число “тэта” умножается на число, стоящее в кружочке в соответствующей клетке. “Экономия” (отрицательное число) прибавляется к значению линейной формы предыдущего плана.
- В таблице, соответствующей новому плану, построить циклы, соответствующие “свободным местам” и вычислить оценки этих “свободных мест”. Для этого двигаться только по “занятым местам” и при каждом шаге поворот делать только под прямым углом. Каждый шаг вдоль цикла отмечать знаком “плюс” или “минус” по принципу: знаком “плюс” отмечаются нечётные вершины, знаком “минус” – чётные.
Эти шаги следует повторять до тех пор, пока оценки всех “свободных мест” не станут положительными.
Если в ходе решения транспортной задачи появились вырожденные (сингулярные) планы, то возможно, что число “тэта” равно нулю. Тогда на соответствующей итерации решения значение линейной формы не меняется (что и было показано в примере 2).
Что такое симплекс-метод
Задача линейного программирования — это задача поиска неотрицательных значений параметров, на которых заданная линейная функция достигает своего максимума или минимума при заданных линейных ограничениях.
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Алгоритм является универсальным методом, которым можно решить любую задачу линейного программирования.
Если вам тоже ничего не понятно из этого определения, то вы на верном пути. Чаще всего статьи про симплекс-метод очень сильно углубляются в дебри теории задачи линейного программирования, из-за чего очень легко потерять суть и так ничего и не понять. Мы постараемся описать алгоритм симплекс-метода так, чтобы показать, что в нём нет ничего страшного и на самом деле он весьма простой. Но сначала нам всё-таки потребуется ввести несколько определений.
Целевая функция — функция, максимум (или минимум) которой нужно найти. Представляет собой сумму произведений коэффициентов на значения переменных: F = c1·x1 + c2·x2 + … + cn·xn
Ограничение — условие вида a1·x1 + a2·x2 + … + an·xn v b, где вместо v ставится один из знаков: ≤, = или ≥
План — произвольный набор значений переменных x1 … xn.
Алгоритм решения основной задачи ЛП симплекс-методом
Пусть в задаче есть m ограничений, а целевая функция заивисит от n основных переменных. Первым делом необходимо привести все ограничения к каноническому виду — виду, в котором все условия задаются равенствами. Для этого предварительно все неравенства с ≥ умножаются на -1, для получения неравенств с ≤.
Чтобы привести ограничения с неравенствами к каноническому виду, для каждого ограничения вводят переменную, называемую дополнительной с коэффициентом 1. В ответе эти переменные учитываться не будут, однако сильно упростят начальные вычисления. При этом дополнительные переменные являются базисными, а потому могут быть использованы для формирования начального опорного решения.
Пример 1
Привести к каноническому виду ограничения:
2·x1 + 3·x2 + 6·x3 ≤ 240
4·x1 + 2·x2 + 4·x3 = 200
4·x1 + 6·x2 + 8·x3 ≥ 160
Меняем знаки у ограничений с ≥, путём умножения на -1 и добавляем дополнительные переменные к ограничениям с неравенством:
2·x1 + 3·x2 + 6·x3 + x4 = 240
4·x1 + 2·x2 + 4·x3 = 200
-4·x1 – 6·x2 – 8·x3 + x5 = -160
Вводная часть, с которой желательно ознакомиться
Существует несколько методов решения транспортной задачи. Мы будем подробно рассматривать два из них:
- решение транспортной задачи методом потенциалов (рассмотрен в данной статье)
- решение транспортной задачи с использованием симплекс метода.
Решение задачи методом потенциалов происходит в несколько этапов:
- Определение опорного решения.
- Применение к найденному опорному решению самого метода потенциалов.
- Проверка единственности решения.
Определение опорного плана, в свою очередь, можно выполнить несколькими способами. Мы рассмотрим два из них:
- метод северо-западного угла
- метод минимальных стоимостей
(не путать с методами решения самой транспортной задачи!!!)
О чем говорится в определении транспортной задачи?
У нас есть некоторый груз, который находится на складах: склад 1, склад 2, …, склад – это пункты отправления.
Этот груз нам необходимо развести по магазинам: магазин 1, магазин 2, …, магазин k – это пункты назначения.
Нам выгоднее как можно эффективнее выполнить работу, т.е. найти такой вариант перевозки, при котором затраты будут минимальными.
Общий план решения транспортной задачи методом потенциалов
Решить транспортную задачу можно различными методами, начиная от симплекс-метода и простого перебора, и заканчивая методом графов. Один из наиболее применяемых и подходящих для большинства случаев методов – итерационное улучшение плана перевозок.
Суть его в следующем: находим некий опорный план и проверяем его на оптимальность (Z → min). Если план оптимален – решение найдено. Если нет – улучшает план столько раз, сколько потребуется, пока не будет найден оптимальный план.
Подробная инструкция по решению транспортной задачи
Строим таблицу, где указываем запасы материалов, имеющиеся на складах поставщиков (Ai), и потребности заводов (Bj) в этих материалах.
В нижний правый угол ячеек таблицы заносим значение тарифов на перевозку груза (Cij).
2. Проверка задачи на закрытость
Обозначим суммарный запас груза у всех поставщиков символом A, а суммарную потребность в грузе у всех потребителей – символом B.
Тогда:
Транспортная задача называется закрытой, если A = B . Если же A ≠ B , то транспортная задача называется открытой. В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.
Проверим задачу на закрытость:
A = 10 + 20 + 30 = 60
B = 15 + 20 + 25 = 60
A = B, следовательно данная транспортная задача – закрытая.
3. Составление опорного плана
Составляет предварительный (опорный) план перевозок. Он не обязательно должен быть оптимальный. Это просто своеобразный «черновик», «набросок», улучшая который мы постепенно придем к плану оптимальному.
Есть разные методы нахождения опорного плана. Наиболее распространены следующие:
а) Метод Северо-Западного угла.
Суть метода проста – ячейки транспортной таблицы последовательно заполняются максимально возможными объемами перевозок, в направлении сверху вниз и слева направо. То есть сперва заполняется самая верхняя левая ячейка (“северо-западная” ячейка), потом следующая справа и т.д. Затем переходят на новую строку и вновь заполняют ее слева направо. И так пока таблица не будет заполнена полностью.
Подробное описание метода и пример можно посмотреть здесь.
б) Метод минимального элемента.
Метод заключается в том, что для заполнения ячеек транспортной таблицы выбирается клетка с минимальным значением тарифа. Затем выбирается следующая клетка с наименьшим тарифом и так продолжается до тех пор, пока таблица не будет заполнена (все запасы и потребности при этом обнулятся).
Подробное описание метода и пример можно посмотреть здесь
в) Аппроксимация Фогеля.
Основа метода в нахождении разности(по модулю) между парой минимальных тарифов в каждой строке и столбце. Затем в строке или столбце с наибольшейразностью заполняется клетка с наименьшимтарифом. Затем все эти действия повторяются заново, только при этом уже не учитываются заполненные клетки.
Подробное описание аппроксимации Фогеля и пример можно посмотреть онлайн
г) Метод двойного предпочтения.
Суть метода в том, что отмечаются клетки с наименьшим тарифом по строкам, а затем по столбцам. Затем ячейки заполняются в следующей очередности: сначала клетки с двумя отметками, потом с одной, наконец без отметок.
Подробное описание метода и пример можно посмотреть здесь
4. Проверка опорного плана на вырожденность
Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) – свободными.
План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n -1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся). Однако проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим!
План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ниже приведен пример цикла:
Ломаная линия может иметь точки самопересечения, но не в клетках цикла.
Кол-во базисных клеток = 5
m + n – 1 = 3 + 3 – 1 = 5
Следовательно, первоначальный план перевозок – невырожденный.
5. Вычисление потенциалов для плана перевозки
Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.
Этот метод улучшения плана перевозок называется методом потенциалов. Есть другие методы итерационного улучшения плана перевозок, но здесь мы их рассматривать не будем.
Итак, сопоставим каждому поставщику Ai и каждому потребителю Bj величины Ui и Vj соответственно так, чтобы для всех базисных клеток плана было выполнено соотношение:
Ui + Vj = Cij
Добавим к транспортной таблице дополнительную строку и столбец для Ui и Vj.
Предположим, что U1 = 0.
Тогда мы сможем найти V3 = C13 – U1 = 1 – 0 = 1.
Зная V3, мы теперь можем найти U3:
По аналогии вычисляем все оставшиеся потенциалы:
6. Проверка плана на оптимальность методом потенциалов
Для каждой свободной клетки плана вычислим разности
ΔCij = Cij – (Ui + Vj )
и запишем полученные значения в левых нижних углах соответствующих ячеек.
План является оптимальным, если все разности ΔCij ≥ 0.
В данном случае план – неоптимальный (ΔC22 < 0), и его следует улучшить путем перераспределения поставок.
7. Перераспределение поставок
Найдем ячейку с наибольшей по абсолютной величине отрицательной разностью ΔCij и построим цикл, в котором кроме этой клетки все остальные являются базисными. Такой цикл всегда существует и единственен.
Отметим ячейку с отрицательной разностью ΔCij знаком «+», следующую знаком «-», и так далее, поочередно.
Затем находим минимальной значение груза в ячейках цикла имеющих знак «-» (здесь это 5) и вписываем его в свободную ячейку со знаком «+». Затем последовательно обходим все ячейки цикла, поочередно вычитая и прибавляя к ним минимальное значение (в соответствии со знаками, которыми эти ячейки помечены: где минус – вычитаем, где плюс – прибавляем).
Получим новый опорный планперевозок:
Так как базисных клеток стало больше, чем m + n – 1, то базисную клетку с нулевым значением делаем свободной:
Снова вычисляем значения потенциалов и разности ΔCij:
На этот раз все разности ΔCij ячеек положительные, следовательно, найдено оптимальное решение.
8. Если оптимальное решение найдено, переходим к п. 9, если нет – к п. 5.
У нас оптимальное решение найдено, поэтому переходим к пункту 9.
9. Вычисление общих затрат на перевозку груза
Вычислим общие затраты на перевозку груза (Z), соответствующие найденному нами оптимальному плану, по формуле:
Zmin = 10 ∙ 1 + 15 ∙ 3 + 5 ∙ 2 + 15 ∙ 1 + 15 ∙ 2 = 110 ден. ед.
Общие затраты на доставку всей продукции, для оптимального решения, составляют 110 ден. ед.
10. Построение графа перевозок
Найдя оптимальный план перевозок, построим граф. Вершинами графа будут «склады» и «магазины». В вершинах укажем соответствующие объемы запасов и потребностей. Дугам, соединяющим вершины графа, будут соответствовать ненулевые перевозки. Каждую такую дугу подпишем, указав объем перевозимого груза.
В результате получится граф, аналогичный изображенному ниже:
Источники
- https://abuzov.ru/reshenie-transportnoj-zadachi-excel/
- https://exceltable.com/otchety/reshenie-transportnoy-zadachi
- https://lumpics.ru/the-solution-of-the-transportation-problem-in-excel/
- https://msoffice-prowork.com/reshenie-transportnojj-zadachi-v-excel-sbalansirovannaya-zadacha/
- https://Reshatel.org/reshenie-zadach/transportnaya-zadacha-v-excel/
- https://www.MatBuro.ru/ex_mp.php?p1=tzexcel
- https://function-x.ru/zadacha_transportnaja_raspredelitelnyi_metod.html
- https://programforyou.ru/calculators/simplex-method
- http://matecos.ru/mat/matematika/kak-reshit-transportnuyu-zadachu-2.html
- http://galyautdinov.ru/post/transportnaya-zadacha
Примеры
задач, решаемых в процедуре «Поиск
решения» Excel.
Задача
распределения ресурсов.
Пример
1
Предприятие
изготавливает и продает краску двух
видов: для внутренних и внешних работ.
Для производства краски используется
два исходных продукта A
и B.
Расходы продуктов A
и B
на 1 т. соответствующих красок и запасы
этих продуктов на складе приведены в
таблице:
|
Исходный |
Расход |
Запас |
|
|
продукт |
краска |
краска |
складе ( |
|
A |
1 |
2 |
3 |
|
B |
3 |
1 |
3 |
Продажная
цена за 1 тонну краски для внутренних
работ составляет 2 000 рублей, краска для
наружных работ продается по 1 000 рублей
за 1 тонну. Требуется определить какое
количество краски каждого вида следует
производить предприятию, чтобы получить
максимальный
доход.
Рассмотрим
поэтапное решение этой задачи несколькими
способами: графическим, алгебраическим
и с использованием процедуры « Поиск
решения » Excel.
IV.
Решение задачи распределения ресурсов
в EXCEL.
-
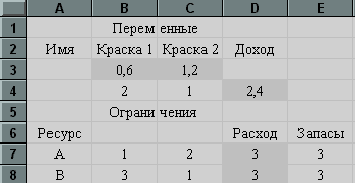
Ввод
данных примера 1 в таблицу EXCEL
(рис.4).
Рис.4
На
рис.4 «краска 1» обозначает краску для
внутренних работ, «краска 2» – краску
для наружных работ.
Для
переменных задачи x1
и x2
отведены ячейки B3
и C3.
Эти ячейки называются рабочими
или изменяемыми
ячейками. В изменяемые ячейки ничего
не заносится
и в результате решения задачи в этих
ячейках будет оптимальные значения
переменных.
В
ячейку D4
вводится формула для вычисления целевой
функции задачи (дохода) Z=2x1+x2.
Чтобы сделать это надо выполнить
следующие действия:
курсор
в D4;
курсор
на кнопку fx
(мастер функций);
В
появившемся окне выбрать “Математические”
и “СУММПРОИЗВ” (рис. 5).
Рис.5.
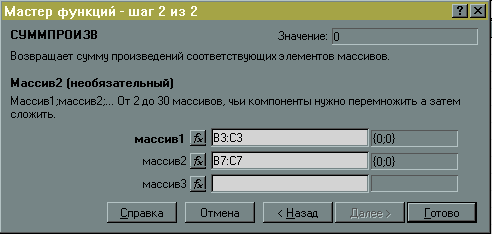
В
окне мастера функций нажать Далее>,
в появившемся окне (рис.6) в поле “массив
1” ввести (протаскивая курсор мыши по
ячейкам) адреса изменяемых ячеек B3:C3.
В поле “массив 2” вводятся адреса ячеек
содержащих цены на краски B4:C4,
после нажать Готово
.
Рис.6
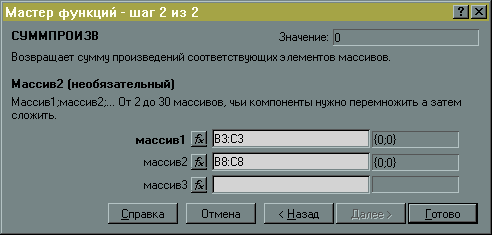
В
ячейку D7
вводится формула для вычисления
израсходованного количества продукта
А: x1+2x2,
а в ячейку D8
вводится формула для израсходованного
количества продукта B:
3x1+x2.
Обе формулы вводятся аналогично целевой
функции (рис.7
и 8).
Рис.7
Проверить
результаты ввода можно следующим
образом: при установке курсора в ячейку
D4
в строке ввода должно появиться:
“=СУММПРОИЗВ(B3:C3
; B4:C4)”;
в ячейки D7:
“=СУММПРОИЗВ(B3:C3
; B7:C7)”;
в ячейки D8:
“=СУММПРОИЗВ(B3:C3
; B8:C8)”.
Окончательно
после ввода формул и данных экран имеет
вид (рис.9):
Рис.9
2)
Работа в окне “Поиск решения”
В
меню “Сервис” выбираем процедуру
“Поиск решения”
В
появившемся окне (рис.10) нужно установить
адрес целевой ячейки D4,
значение целевой ячейки: максимальное,
адреса изменяемых ячеек B3:C3.
Рис.10
Чтобы
ввести ограничения задачи, нажать кнопку
«Добавить». В появившемся диалоговом
(рис.11) окне слева ввести адрес D7
(израсходованное количество продукта
А), затем выбрать знак <= и в правой
части количество продукта А на складе,
равное 3 (или адрес ячейки E7).
Рис.11
После
ввода нажать кнопку «Добавить» и
аналогично ввести второе ограничение:
D8
<= 3. Снова нажать кнопку «Добавить» и
ввести ограничение: B3:C3
>= 0 (соответствующее ограничению x1,
x2
>= 0). После ввода последнего ограничения
нажать ОК.
После ввода ограничений окно «Поиска
решений имеет» будет иметь вид (рис.
12):
Рис.12
3)
Настройка параметров решения задачи.
В
окне «Поиск решения» нажать «Параметры»
в появившемся окне (рис. 13) установить
флажок в пункте «Линейная модель». В
этом случае при решении задачи будет
использоваться симплекс — метод. Остальные
значения можно оставить без изменения.
После нажать кнопку ОК
Рис.13
Для
решения задачи в окне «Поиск решения»
нажать кнопку «Выполнить».
Если решение найдено появляется окно
(рис.14):
Рис.14
Для
просмотра результатов выбираем тип
отчета: «Результаты» и нажимаем кнопку
ОК.
В появившихся трех таблицах (рис.15)
приводятся результаты поиска. Из этих
таблиц видно, что в оптимальном решении:
производство
краски 1 = B3
= 0.6 ;
производство
краски 2 = С3 = 1.2 ;
при
этом доход = D4
= 2.4 ;
расход
ресурса A
= D7
= 3 ;
расход
ресурса B
= D8
= 3 ;
таким
образом, оба ресурса дефицитные
(соответствующие ограничения называются
связанными).
|
Целевая |
||||||
|
Ячейка |
Имя |
Исходно |
Результат |
|||
|
$D$4 |
Доход |
2,4 |
2,4 |
|||
|
Изменяемые |
||||||
|
Ячейка |
Имя |
Исходно |
Результат |
|||
|
$B$3 |
Краска |
0,6 |
0,6 |
|||
|
$C$3 |
Краска |
1,2 |
1,2 |
|||
|
Ограничения |
||||||
|
Ячейка |
Имя |
Значение |
Формула |
Состояние |
Разница |
|
|
$D$7 |
A |
3 |
$D$7<=$E$7 |
связанное |
0 |
|
|
$D$8 |
B |
3 |
$D$8<=$E$8 |
связанное |
0 |
|
|
$B$3 |
Краска |
0,6 |
$B$3>=0 |
не |
0,6 |
|
|
$C$3 |
Краска |
1,2 |
$C$3>=0 |
не |
1,2 |
Рис.15
«Отчет
по результатам» состоит из трех таблиц
(рис.15):
в таблице 1 приводятся
сведения о целевой функции;
в таблице 2 приводятся
значения переменных задачи;
в таблице 3 показаны
результаты поиска для ограничений
задачи.
Первоначальная
таблица EXCEL
заполняется результатами, полученными
при решении (на рис.16 появившиеся значения
в темных ячейках).
Рис.16
Соседние файлы в папке 1 задача
- #
- #
- #
02.03.20169.52 Кб38Книга1.xlsx
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.