Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.
Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Скачать примеры
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12689 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
1. Решение нелинейных уравнений в MS Excel
1.1 Отделение корней
В общем виде любое уравнение одной переменной принято записывать так 

Например , для уравнения 

Рисунок 1. График функции 
1.2 Решение уравнений, используя инструмент “Подбор параметра”
Используя возможности Excel , можно находить корни нелинейного уравнения вида f ( x )=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:
1. Производится вычисление значений функции в диапазоне вероятного существования корней от значений аргумента, изменяющегося с определенным шагом;
2. В таблице выделяются ближайшие приближения к значениям корней (пары соседних значений функции с разными знаками);
3. Используя средство Excel Подбор параметра, вычисляются корни уравнения.
2. Работа с матрицами в MS Excel . Решение систем уравнений.
Нахождение определителя матрицы
Перед нахождением определителя необходимо ввести матрицу в диапазон ячеек Excel в виде таблицы.
Для нахождения определителя матрицы в Excel необходимо:
· сделать активной ячейку, в которой в последующем будет записан результат;
· в меню Вставка – Функция в категории Математические выбрать функцию МОПРЕД и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы матрицы, и нажать OK .
Нахождение обратной матрицы
Для нахождения обратной матрицы необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы матрицы ( количество строк и количество столбцов должны равняться соответствующим параметрам исходной матрицы).
· в меню Вставка – Функция в категории Математические выбрать функцию МОБР и нажать OK ;
· на втором шаге задать диапазон ячеек, в котором содержатся элементы исходной матрицы, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Для перемножения матриц необходимо
· выделить диапазон ячеек, в которых в последующем будут записаны элементы результирующей матрицы.
· в меню Вставка – Функция в категории Математические выбрать функцию МУМНОЖ и нажать OK ;
· на втором шаге задать два диапазона ячеек с элементами перемножаемых матриц, и нажать OK .
· после появления значения в левом верхнем углу выделенного диапазона последовательно нажать клавишу F 2 и комбинацию клавиш Ctrl + Shift + Enter .
Решение системы уравнений в Excel .
Решение системы уравнений при помощи нахождения обратной матрицы.
Пусть дана линейная система уравнений.

Данную систему уравнений можно представить в матричной форме:




Матрица неизвестных вычисляется по формуле

где A -1 – обратная матрица по отношению к A .
Для вычисления уравнения в Excel необходимо:
· ввести матрицу A;
· ввести матрицу B;
· вычислить обратную матрицу по отношению к А ;
· перемножить полученную обратную матрицу с матрицей B .
Порядок выполнения работы
Задание 1
Найти все корни уравнения 2x 3 -15sin( x )+0,5x-5=0 на отрезке [-3 ; 3].
1. Построить таблицу значений функции f ( x ) для значений x от –3 до 3, шаг 0,2.
Для этого ввести первые два значения переменной x , выделить эти две ячейки, с помощью маркера автозаполнения размножить значения до 3.
Затем ввести формулу для вычисления f ( x ). Скопировать формулу с использованием маркера автозаполнения на весь столбец.
Из полученной таблицы находим, что значение функции трижды меняет знак, следовательно, исходное уравнение имеет на заданном отрезке три корня.
2. Выделить цветом пары значений x и f ( x ), где f ( x ) меняет знак (см .р исунок 2).
3. Построить график функции f ( x ).
Рисунок 2. Поиск приближенных значений корней уравнения
4. Скопировать рядом с таблицей произвольную пару выделенных значений x и f ( x ) (см .р исунок 3).
5. Выполнить команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 3) заполнить следующие поля:
þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;
þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);
þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.
Рисунок 3. Диалоговое окно Подбор параметра для поиска первого корня
6. После щелчка на ОК должно получиться значение первого корня -1,65793685 .
7. Выполнить последовательно операции, аналогичные предыдущим, для вычисления значений остальных корней: -0,35913476 и 2,05170101 .
Задание 2
Решить систему уравнений:

1. Ввести значения элементов матриц A и B уравнения в ячейки Excel .
2. Вычислить обратную матрицу с помощью матричной функции МОБР.
3. Перемножить обратную матрицу A -1 на матрицу B с помощью матричной функции МУМНОЖ (Порядок умножения важен – первой должна идти матрица A -1 а второй B .)
4. Проверить правильность полученной матрицы корней X .
Контрольные вопросы
1. Порядок действий для решения нелинейного уравнения с помощью инструмента Подбор параметра MS Excel .
2. Порядок действий для решения системы уравнений матричным методом в MS Excel .
источники:
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
http://zf.bsut.by/it/fbo/zb1/lab2.htm
Цель урока: продолжить формирование
навыков работы с электронными таблицами.
Задачи:
- обучающие: формировать умения создания,
редактирования, форматирования и выполнения
простейших вычислений в электронных таблицах. - развивающие: расширить представления
учащихся о возможных сферах применения
электронных таблиц; развивать навыки
аналитического мышления, речи и внимания. - воспитательные: формировать и воспитывать
познавательный интерес; прививать навыки
самостоятельности в работе.
План урока.
- Организационный момент.
- Актуализация знаний учащихся.
- Проверка домашнего задания.
- Решение задач.
- Самостоятельное решение задачи.
- Подведение итогов. Оценки.
- Домашнее задание.
Ход урока
1. Организационный момент.
Сообщить тему урока, сформулировать цели и
задачи урока.
Сегодня мы вновь окажемся в гостях у маленького
великана Васи в Сказочной стране. Ему, как всегда,
требуется ваша помощь, ребята.
Сможете ли вы помочь Васе? Сейчас проверим!
2. Актуализация знаний учащихся.
1) Устно ответить на вопросы.
| A | B | C | D | |
| 1 | 2 | 1 | =A1+3*B1 | =A1^2+B1 |
| 2 | 4 | 6 | =A2+3*B2 | =A2^2+B2 |
- Что такое электронная таблица?
- Какие основные элементы электронной таблицы
вам известны? - Как задается имя ячейки (строки, столбца) в
электронной таблице? - Что может быть содержимым ячейки?
- Число 1 находится в столбце …, в строке …, в
ячейке с адресом … - Число 4 находится в ячейке с адресом …
- Каковы правила записи формул в ячейках?
- Чему равно значение, вычисляемое по формуле, в
ячейке С1? - Чему равно значение, вычисляемое по формуле, в
ячейке D2?
2) Какой результат будет получен в ячейках с
формулами?
| А | В | |
| 1 | 25 | 4 |
| 2 | 2 | =A1*B1/2 |
| 3 |
Ответ: 25*4/2=50
| A | B | C | D | |
| 1 | 5 | 2 | 1 | |
| 2 | 6 | 8 | 3 | |
| 3 | 8 | 3 | 4 | |
| 4 | =СУММ(B1:D3) |
- Что означает запись =СУММ(В1:D3)?
- Сколько элементов содержит блок В1:D3? Ответ: 9.
- Содержимое ячейки D3? Ответ: 5+2+1+6+8+3+8+3+4= 40
3) Проверка домашнего задания
Результаты соревнований по плаванию
Один ученик рассказывает, как он выполнил
домашнее задание (через проектор).
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3.23 | 3.44 | 3.30 | |||
| 2 | Моржов | 3.21 | 3.22 | 3.24 | |||
| 3 | Акулов | 3.17 | 3.16 | 3.18 | |||
| 4 | Рыбин | 3.24 | 3.20 | 3.18 | |||
| 5 | Черепахин | 3.56 | 3.44 | 3.52 | |||
| Лучший результат соревнований |
|||||||
| Среднее время участников соревнований |
|||||||
| Максимальное отклонение |
- Среднее время для каждого спортсмена находится
как среднее арифметическое трех его заплывов. - В ячейку «Лучшее время» записывается
минимальный результат из 3 заплывов. - В ячейку «Лучший результат соревнований»
записывается минимальное время из столбца. - В столбец «Отклонение» записывается
разность между лучшим временем спортсмена и
лучшим результатом соревнований. - В ячейку «Максимальное отклонение»
записывается максимальное значение столбца.
| Результаты соревнований по плаванию |
|||||||
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3,23 | 3,44 | 3,30 | 3,23 | 3,32 | 0,07 |
| 2 | Моржов | 3,21 | 3,22 | 3,24 | 3,21 | 3,22 | 0,05 |
| 3 | Акулов | 3,17 | 3,16 | 3,18 | 3,16 | 3,17 | 0,00 |
| 4 | Рыбин | 3,24 | 3,20 | 3,18 | 3,18 | 3,21 | 0,02 |
| 5 | Черепахин | 3,56 | 3,44 | 3,52 | 3,44 | 3,51 | 0,28 |
| Лучший результат соревнований |
3,16 | ||||||
| Среднее время участников соревнований |
3,29 | ||||||
| Максимальное отклонение | 0,28 |
4) Решение простых задач.
Маленький великан Вася решил отремонтировать
забор вокруг своего огорода и вскопать его под
посадку овощей (наступила очередная весна),
разметить грядки прямоугольной формы. Для работы
ему потребовалось найти длину забора и площадь
участка. Но ведь в школе он никогда не учился.
Поможем Васе.
№ 1. Вычислить периметр и площадь
прямоугольника со сторонами:
а) 3 и 5; б) 6 и 8; в) 10 и 7.
Эту задачу обсуждаем совместно с детьми:
- Как оформить таблицу?
- Какие формулы использовать?
- Как использовать уже записанные формулы для
следующего прямоугольника?
Оформление таблицы – на доске и в тетрадях.
В то же время другой ученик самостоятельно
решает следующую задачу и представляет свое
решение учащимся (через проектор).
№ 2. Маленький великан Вася решил
подсчитать, через сколько дней в его копилке
будет 100 руб., если ежедневно он стал класть туда
на 5 руб. больше, чем в предыдущий день. Помогите
Васе. Сейчас в его копилке 2,02 руб.
Обсудив решение задачи № 2, переходим к решению
следующей.
Один ученик показывает, как работать с
формулами, другой – как использовать функцию
суммирования, числовой формат (общий, денежный) и
т.д. (Таблица уже готова, ученикам предстоит
ввести формулы, использовать суммирование и
получить ответ).
№ 3. Посчитайте, используя ЭТ, хватит ли
Васе 150 рублей, чтобы купить все продукты, которые
ему заказала мама, и хватит ли на чипсы за 10
рублей? Сдачу мама разрешила положить в копилку.
Сколько рублей попадет в копилку?
Предполагаемое решение:
| № | Наименование | Цена в рублях | Количество | Стоимость |
| 1 | Хлеб | 9,6 | 2 | =C2*D2 |
| 2 | Кофе | 2,5 | 5 | =C3*D3 |
| 3 | Молоко | 13,8 | 2 | =C4*D4 |
| 4 | Пельмени | 51,3 | 1 | =C5*D5 |
|
Итого: |
=СУММ(E2:E5) | |||
| После покупок останется | =150-E6 | |||
| После покупки чипсов останется |
=D7-10 |
5) Самостоятельное решение задачи.
Маленький великан Вася часто бывал в гостях у
жителей Цветочного города.
Собираясь на пляж, веселые человечки решили
запастись прохладительными напитками. Незнайка
взял с собой 2 литра кваса, 1 литр газировки и 1
литр малинового сиропа, Пончик – 3 литра
газировки и 2 литра малинового сиропа, Торопыжка
– 2 литра газировки, доктор Пилюлькин – 1 литр
кваса и 1 литр касторки.
- Сколько литров напитков каждого вида взяли все
человечки вместе? - Сколько всего литров напитков взял с собой
каждый из человечков? - Сколько всего литров напитков взяли все
человечки вместе?
Оформите таблицу произвольно и сохраните в
своей личной папке.
Результат работы.
| Веселые человечки. Напитки. |
|||||
| Напиток | Незнайка | Пончик | Торопыжка | Пилюлькин | Всего |
| Квас, л | 2 | 0 | 0 | 1 | 3 |
| Газировка, л | 1 | 3 | 2 | 0 | 6 |
| Сироп, л | 1 | 2 | 0 | 0 | 9 |
| Касторка, л | 0 | 0 | 0 | 1 | 1 |
| ИТОГО: | 4 | 5 | 2 | 2 | 13 |
7) Подведение итогов. Оценки.

Подумайте и решите эту задачу, если известны
еще следующие величины.
Как изменится таблица? Какие формулы появятся?
Известно, что 1 литр кваса в Цветочном городе
стоит 1 монету, 1 литр газировки – 3 монеты, 1 литр
малинового сиропа – 6 монет, 1 литр касторки – 2
монеты.
- Сколько монет истратил на покупку напитков
каждый человечек? - Сколько монет затрачено на покупку напитков
каждого вида? - Сколько потрачено денег всеми человечками
вместе?
Литература
- Информатика. Задачник-практикум в 2 т. /Под ред.
И.Г.Семакина, Е.К.Хеннера – М.: Лаборатория
Базовых Знаний, 2010. - Ефимова О. Курс компьютерной технологии с
основами информатики. – М.: ООО “издательство
АСТ”; АВF, 2005.
Презентация
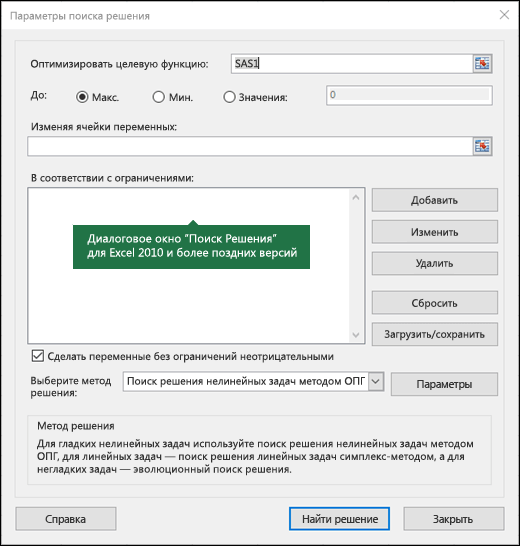
«Поиск решения» — это надстройка для Microsoft Excel, которую можно использовать для анализ «что если». С ее помощью можно найти оптимальное значение (максимум или минимум) формула, содержащейся в одной ячейке, называемой целевой, с учетом ограничений на значения в других ячейках с формулами на листе. Надстройка «Поиск решения» работает с группой ячеек, называемых ячейками переменных решения или просто ячейками переменных, которые используются при расчете формул в целевых ячейках и ячейках ограничения. Надстройка «Поиск решения» изменяет значения в ячейках переменных решения согласно пределам ячеек ограничения и выводит нужный результат в целевой ячейке.
Проще говоря, с помощью надстройки «Поиск решения» можно определить максимальное или минимальное значение одной ячейки, изменяя другие ячейки. Например, вы можете изменить планируемый бюджет на рекламу и посмотреть, как изменится планируемая сумма прибыли.
Примечание: В версиях надстройки «Поиск решения», выпущенных до Excel 2007, ячейки переменных решения назывались изменяемыми или регулируемыми. В Excel 2010 надстройка «Поиск решения» была значительно улучшена, так что работа с ней в Excel 2007 будет несколько отличаться.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка F5), пока общая прибыль (целевая ячейка F7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке F7, =СУММ (Q1 Прибыль:Q2 Прибыль).
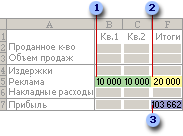
1. Ячейки переменных
2. Ячейка с ограничениями
3. Целевая ячейка
После выполнения процедуры получены следующие значения.

-
На вкладке Данные в группе Анализ нажмите кнопку Поиск решения.
-
В поле Оптимизировать целевую функцию введите ссылка на ячейку или имя целевой ячейки. Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
-
Чтобы значение целевой ячейки было максимальным из возможных, установите переключатель в положение Макс.
-
Чтобы значение целевой ячейки было минимальным из возможных, установите переключатель в положение Мин.
-
Чтобы задать для целевой ячейки конкретное значение, установите переключатель в положение Значение и введите в поле нужное число.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми. Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить. Для этого выполните указанные ниже действия.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Щелкните связь (<=, =, >=, int,binили dif), которая требуется между ячейкой, на которую ссылается ссылка, и ограничением. Если щелкнуть int, в поле Ограничение появится integer. Если щелкнуть бин,в поле Ограничение появится двоичное поле. Если нажать кнопку dif,в поле Ограничение появится ссылкаalldifferent.
-
Если в поле Ограничение было выбрано отношение <=, = или >=, введите число, ссылку на ячейку (или имя ячейки) или формулу.
-
Выполните одно из указанных ниже действий.
-
Чтобы принять данное ограничение и добавить другое, нажмите кнопку Добавить.
-
Чтобы принять ограничение и вернуться в диалоговое окно Параметрырешения, нажмите кнопку ОК.
Примечание Отношения int,binи dif можно применять только в ограничениях для ячеек переменных решения.Чтобы изменить или удалить существующее ограничение, выполните указанные ниже действия.
-
-
В диалоговом окне Параметры поиска решения щелкните ограничение, которое требуется изменить или удалить.
-
Нажмите кнопку Изменить и внесите изменения либо нажмите кнопку Удалить.
-
-
Нажмите кнопку Найти решение и выполните одно из указанных ниже действий.
-
Чтобы сохранить значения решения на листе, в диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
-
Чтобы восстановить исходные значения перед нажатием кнопки Найти решение, выберите вариант Восстановить исходные значения.
-
Вы можете прервать поиск решения, нажав клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных решения.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, будут доступны только некоторые отчеты или они вообще не будут доступны.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех найденных решений, в диалоговом окне Параметры установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из указанных ниже действий.
-
Чтобы остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения, нажмите кнопку Стоп.
-
Чтобы продолжить процесс поиска решения и просмотреть следующий вариант решения, нажмите кнопку Продолжить.
-
-
В диалоговом окне Параметры поиска решения нажмите кнопку Параметры.
-
В диалоговом окне на вкладках Все методы, Поиск решения нелинейных задач методом ОПГ и Эволюционный поиск решения выберите или введите значения нужных параметров.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Загрузить/сохранить.
-
Введите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить или сохранить для сохранения задач по отдельности.
В диалоговом окне Параметры поиска решения можно выбрать любой из указанных ниже алгоритмов или методов поиск решения.
-
Нелинейный метод обобщенного понижающего градиента (ОПГ). Используется для гладких нелинейных задач.
-
Симплекс-метод. Используется для линейных задач.
-
Эволюционный метод Используется для негладких задач.
В приведенном ниже примере количество проданных единиц в каждом квартале зависит от уровня рекламы, что косвенно определяет объем продаж, связанные издержки и прибыль. Надстройка «Поиск решения» может изменять ежеквартальные расходы на рекламу (ячейки переменных решения B5:C5) до ограничения в 20 000 рублей (ячейка D5), пока общая прибыль (целевая ячейка D7) не достигнет максимального значения. Значения в ячейках переменных используются для вычисления прибыли за каждый квартал, поэтому они связаны с формулой в целевой ячейке D7, =СУММ (Q1 Прибыль:Q2 Прибыль).
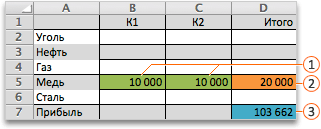
В результате выполнения получены следующие значения:

-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
В разделе Оптимизировать целевую функцию, введите ссылка на ячейку или имя целевой ячейки.
Примечание: Целевая ячейка должна содержать формулу.
-
Выполните одно из следующих действий.
Задача
Необходимые действия
Сделать так, чтобы значение целевой ячейки было максимальным из возможных
Выберите значение Макс.
Сделать так, чтобы значение целевой ячейки было минимальным из возможных
Выберите значение Мин.
Сделать так, чтобы целевая ячейка имела определенное значение
Щелкните Значение, а затем введите нужное значение в поле.
-
В поле Изменяя ячейки переменных введите имена диапазонов ячеек переменных решения или ссылки на них. Несмежные ссылки разделяйте запятыми.
Ячейки переменных должны быть прямо или косвенно связаны с целевой ячейкой. Можно задать до 200 ячеек переменных.
-
В поле В соответствии с ограничениями введите любые ограничения, которые требуется применить.
Для этого выполните следующие действия:
-
В диалоговом окне Параметры поиска решения нажмите кнопку Добавить.
-
В поле Ссылка на ячейку введите ссылку на ячейку или имя диапазона ячеек, на значения которых налагаются ограничения.
-
Во всплывающем меню <= задайте требуемое отношение между целевой ячейкой и ограничением. Если вы выбрали <=, =, или >= в поле Ограничение, введите число, имя ячейки, ссылку на нее или формулу.
Примечание: Отношения int, бин и раз можно использовать только в ограничениях для ячеек, в которых находятся переменные решения.
-
Выполните одно из указанных ниже действий.
Задача
Необходимые действия
Принять ограничение и добавить другое
Нажмите кнопку Добавить.
Принять ограничение и вернуться в диалоговое окно Параметры поиска решения
Нажмите кнопку ОК.
-
-
Нажмите кнопку Найти решение и выполните одно из следующих действий:
Задача
Необходимые действия
Сохранить значения решения на листе
В диалоговом окне Результаты поиска решения выберите вариант Сохранить найденное решение.
Восстановить исходные значения
Щелкните Восстановить исходные значения.
Примечания:
-
Чтобы прервать поиск решения, нажмите клавишу ESC. Лист Excel будет пересчитан с учетом последних найденных значений для ячеек переменных.
-
Чтобы создать отчет, основанный на найденном решении, выберите тип отчета в поле Отчеты и нажмите кнопку ОК. Отчет будет помещен на новый лист книги. Если решение не найдено, отчет не будет доступен.
-
Чтобы сохранить значения ячейки переменной решения в качестве сценария, который можно будет отобразить позже, нажмите кнопку Сохранить сценарий в диалоговом окне Результаты поиска решения, а затем введите имя этого сценария в поле Название сценария.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
После постановки задачи нажмите кнопку Параметры в диалоговом окне Параметры поиска решения.
-
Чтобы просмотреть значения всех предварительных решений, установите флажок Показывать результаты итераций и нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение.
-
В диалоговом окне Показать предварительное решение выполните одно из следующих действий:
Задача
Необходимые действия
Остановить поиск решения и вывести на экран диалоговое окно Результаты поиска решения
Нажмите кнопку Стоп.
Продолжить поиск и просмотреть следующее предварительное решение
Нажмите кнопку Продолжить.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Нажмите кнопку Параметры, а затем в диалоговом окне Параметры или Поиск решения выберите один или несколько из следующих вариантов:
Задача
Необходимые действия
Настроить время решения и число итераций
На вкладке Все методы в разделе Пределы решения в поле Максимальное время (в секундах) введите количество секунд, в течение которых можно будет искать решение. Затем в поле Итерации укажите максимальное количество итераций, которое вы хотите разрешить.
Примечание: Если будет достигнуто максимальное время поиска решения или количество итераций, а решение еще не будет найдено, средство «Поиск решения» выведет диалоговое окно Показать предварительное решение.
Задать точность
На вкладке Все методы введите в поле Точность ограничения нужное значение погрешности. Чем меньше число, тем выше точность.
Задать степень сходимости
На вкладке Поиск решения нелинейных задач методом ОПГ или Эволюционный поиск решения в поле Сходимость укажите, насколько должны отличаться результаты последних пяти итераций, чтобы средство прекратило поиск решения. Чем меньше число, тем меньше должно быть изменение.
-
Нажмите кнопку ОК.
-
В диалоговом окне Параметры поиска решения нажмите кнопку Найти решение или Закрыть.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Щелкните Загрузить/сохранить, укажите диапазон ячеек для области модели и нажмите кнопку Сохранить или Загрузить.
При сохранении модели введите ссылку на первую ячейку вертикального диапазона пустых ячеек, в котором следует разместить модель оптимизации. При загрузке модели введите ссылку на весь диапазон ячеек, содержащий модель оптимизации.
Совет: Чтобы сохранить последние параметры, настроенные в диалоговом окне Параметры поиска решения, вместе с листом, сохраните книгу. Каждый лист в книге может иметь свои параметры надстройки «Поиск решения», и все они сохраняются. Кроме того, для листа можно определить более одной задачи, если нажимать кнопку Загрузить/сохранить для сохранения задач по отдельности.
-
В Excel 2016 для Mac: выберите пункты Данные > Поиск решения.
В Excel 2011 для Mac: на вкладке Данные в группе Анализ выберите Поиск решения.
-
Во всплывающем меню Выберите метод решения выберите одно из следующих значений:
|
Метод решения |
Описание |
|---|---|
|
Нелинейный метод обобщенного понижающего градиента (ОПГ) |
Используется по умолчанию для моделей со всеми функциями Excel, кроме ЕСЛИ, ВЫБОР, ПРОСМОТР и другие ступенчатые функции. |
|
Поиск решения линейных задач симплекс-методом |
Используйте этот метод для задач линейного программирования. В формулах модели, которые зависят от ячеек переменных, должны использоваться функции СУММ, СУММПРОИЗВ, +, — и *. |
|
Эволюционный поиск решения |
Этот метод, основанный на генетических алгоритмах, лучше всего подходит в том случае, если в модели используются функции ЕСЛИ, ВЫБОР и ПРОСМОТР с аргументами, которые зависят от ячеек переменных. |
Примечание: Авторские права на части программного кода надстройки «Поиск решения» версий 1990–2010 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Поскольку надстройки не поддерживаются в Excel в Интернете, вы не сможете использовать надстройку «Поиск решения» для анализа данных «что если», чтобы найти оптимальные решения.
Если у вас есть Excel, вы можете нажать кнопку Открыть в Excel, чтобы открыть книгу для использования надстройки «Поиск решения».
Дополнительная справка по надстройке «Поиск решения»
За дополнительной справкой по надстройке «Поиск решения» обращайтесь по этим адресам:
Frontline Systems, Inc.
P.O. Box 4288
Incline Village, NV 89450-4288
(775) 831-0300
Веб-сайт: http://www.solver.com
Электронная почта: info@solver.com
«Решение» на www.solver.com.
Авторские права на части программного кода надстройки «Поиск решения» версий 1990-2009 принадлежат компании Frontline Systems, Inc. Авторские права на части версии 1989 принадлежат компании Optimal Methods, Inc.
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
См. также
Использование «Решения» для бюджетов с использованием средств на счете вех
Использование «Решение» для определения оптимального сочетания продуктов
Введение в анализ гипотетических вариантов
Полные сведения о формулах в Excel
Рекомендации, позволяющие избежать появления неработающих формул
Обнаружение ошибок в формулах
Сочетания клавиш в Excel
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Содержание
- Поиск решения задач в Excel с примерами
- Решение задач оптимизации в Excel
- Решение финансовых задач в Excel
- Решение эконометрики в Excel
- Решение логических задач в Excel
- Решение математических задач в Excel
- Проект «Решение задач при помощи электронных таблиц»
- Реализация межпредметных связей при обучении математике в системе основного и среднего общего образования
- Организация учебно-исследовательской деятельности учащихся как средство развития познавательной активности при обучении математике в условиях реализации ФГОС ООО и ФГОС СОО
- Ментальная арифметика: отрицательные числа, дроби, возведение в квадрат, извлечение квадратного корня
- Обучение школьников 5-9 классов решению текстовых задач по математике различными способами
- Описание презентации по отдельным слайдам:
- Опытные онлайн-репетиторы
- IV Международный практический «Инфофорум» для педагогов
- 2023 год педагога и наставника: вызовы и решения
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Онлайн-занятия с репетиторами
- Подарочные сертификаты
Поиск решения задач в Excel с примерами
Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.
Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.
Решение задач оптимизации в Excel
Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).
В Excel для решения задач оптимизации используются следующие команды:
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
- Количество изделий нам пока неизвестно. Это переменные.
- В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
- Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
- Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.
Решение финансовых задач в Excel
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
- Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
- Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
- Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
- Тип – 0.
- БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.
Решение эконометрики в Excel
Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.
Дано 2 диапазона значений:
Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.
Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).
Решение логических задач в Excel
В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.
- Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
- Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
- Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».
Решение математических задач в Excel
Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).
Условие учебной задачи. Найти обратную матрицу В для матрицы А.
- Делаем таблицу со значениями матрицы А.
- Выделяем на этом же листе область для обратной матрицы.
- Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
- В поле аргумента «Массив» вписываем диапазон матрицы А.
- Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.
Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.
Источник
Проект «Решение задач при помощи электронных таблиц»

Курс повышения квалификации
Реализация межпредметных связей при обучении математике в системе основного и среднего общего образования
- Сейчас обучается 21 человек из 13 регионов

Курс повышения квалификации
Организация учебно-исследовательской деятельности учащихся как средство развития познавательной активности при обучении математике в условиях реализации ФГОС ООО и ФГОС СОО
- Сейчас обучается 22 человека из 14 регионов

Курс повышения квалификации
Ментальная арифметика: отрицательные числа, дроби, возведение в квадрат, извлечение квадратного корня
- Сейчас обучается 92 человека из 37 регионов

Обучение школьников 5-9 классов решению текстовых задач по математике различными способами
Описание презентации по отдельным слайдам:
Решение задач при помощи электронных таблиц
Автор: Коротков Павел, 8 класс
Руководитель: Гончарук А.В.
МОУ Непецинская СОШ
Целью моей работы было рассмотреть задачи, решаемых при помощи электронных таблиц. Определить роль Excel в различных сферах деятельности, ведь знание Microsoft Excel стало обязательным требованием для офисных рабочих.
Для чего нужен EXCEL?
Во первых excel это самая популярная программа для быстрого и эффективного решения самых разных задач.
Программа способна создавать графики, решать самые различные рода задач: финансовые, экономические, математические, логические, оптимизационные и многие другие.
Например: если получать кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?
РЕШЕНИЕ УРАВНЕНИЙ МЕТОДОМ ПОДБОРА ПАРАМЕТРОВ EXCEL
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
2. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
3. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
4. После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
РЕШЕНИЕ ЗАДАЧ ОПТИМИЗАЦИИ В EXCEL
Подбор параметров («Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра») – находит значения, которые обеспечат нужный результат.
Поиск решения (надстройка Microsoft Excel; «Данные» — «Анализ») – рассчитывает оптимальную величину, учитывая переменные и ограничения. Диспетчер сценариев («Данные» — «Работа с данными» — «Анализ «что-если»» — «Диспетчер сценариев») – анализирует несколько вариантов исходных значений, создает и оценивает наборы сценариев.
Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».
Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.
Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:
На основании этих данных составим рабочую таблицу:
Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.
Активизируем команду «Поиск решения» и вносим параметры.
После нажатия кнопки «Выполнить» программа выдает свое решение.
Оптимальный вариант – сконцентрироваться на выпуске
йогурта «3» и «1». Йогурт «2» производить не стоит.
РЕШЕНИЕ ФИНАНСОВЫХ ЗАДАЧ В EXCEL
Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
ПОСТРОЕНИЕ ГРАФИКОВ В EXCEL ПО ДАННЫМ ТАБЛИЦЫ
Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
ЗАКЛЮЧЕНИЕ
Excel – это самое полезное, универсальное и многофункциональное программное средство из пакета Office. Основное назначение Excel – хранение, анализ и визуализация данных, создание отчетов и проведение сложных расчетов.
СПАСИБО ЗА ВНИМАНИЕ!

Лучшее для учеников, педагогов и родителей
Опытные
онлайн-репетиторы
- По любым предметам 1-11 классов
- Подготовка к ЕГЭ и ОГЭ
Рабочие листы и материалы для учителей и воспитателей
Более 7 500 дидактических материалов для школьного и домашнего обучения
IV Международный практический «Инфофорум» для педагогов
2023 год педагога и наставника: вызовы и решения
Ценности гуманной педагогики
Открытая сессия для учителей и руководителей образовательных организаций
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 168 730 материалов в базе
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 31.05.2018 3940
- PPTX 407.4 кбайт
- 65 скачиваний
- Рейтинг: 1 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Гончарук Анастасия Викторовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 9133
- Всего материалов: 7
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 490 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Онлайн-занятия с репетиторами
для весеннего интерьера
Как преуспеть в роли репетитора: запланируйте неудачу, чтобы проект получился удачным
Методическое сопровождение образовательного процесса
Оказание первой помощи при наружных кровотечениях и травмах
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник