Цель урока:
- Познакомить
с основными технологическими приемами при решении задач оптимизации; - Приобрести
навыки работы с надстройками Excel; - Научить использовать инструменты Excel Поиск решения и Подбор
параметра.
Задача учителя: Показать
приемы использования функций Excel Поиск решения и Подбор
параметра.
Методика проведения
урока
Excel позволяет не только
производить расчеты, но и решать сложные задачи из различных сфер деятельности,
такие как решение уравнений, задачи прогнозирования и оптимизации и другие. Решение
задач такого вида может быть осуществлено с помощью инструмента Поиск
решения.
Формулировка таких задач
может представлять собой систему уравнений с несколькими неизвестными и набор
ограничений на решения. Поэтому решение
задачи надо начинать с построения соответствующей модели.
Для того чтобы
надстройка Поиск решения загружалась
сразу при запуске Excel:
- Выберите
команду Кнопка Office, Параметры Excel; - В
диалоговом окне слева выберите команду Надстройки,
а справа выделите команду Поиск решения и
нажмите ОК.
Для того чтобы команда Подбор параметра находилась на панели
быстрого доступа необходимо:
- Выберите
команду Кнопка Office, Параметры Excel; - Слева
в диалоговом окне выберите команду Настройки,
справа – все команды и ОК; - В
окне команд выберите команду Подбор
параметра и нажмите Добавить.
Познакомимся с этими командами на примере.
Задача. Предположим, что мы решили производить 2
вида полок А и В. На изготовление модели А требуется 3 м3 досок, на
изготовление модели В — 4 м3 досок. За неделю можно получить не более 1800 м3 досок.
На изготовление модели А требуется – 15 минут, модели
В – 30 минут. Рабочая неделя для 4 сотрудников составляет 160 часов. Сколько
полок А и В надо изготовить, чтобы получить
максимальную прибыль, если полка А стоит 3500 рублей, полка В – 4800 рублей.
Технология
работы:
- Запустите
табличный процессор Excel. - Заполните
таблицу в соответствии с образцом:А
В
1
Наименование
2
А
3
В
4
5
Прибыль
6
7
Затраты на материалы
8
Затраты по времени
9
- Щелкните
правой кнопкой мыши по ячейке В2 и переименуйте ее в x, так как сначала у нас
количество полок вида А равно x. Аналогично
переименуйте ячейку В3 в y. - Целевая
функция, определяющая нашу прибыль, выглядит следующим образом: ПРИБЫЛЬ=3500*x+4800*y. - Затраты
по материалам равны 3*x+4*y. Затраты по
времени равны 0,25*x+0,5*y. - Выделим
ячейку В5 и выберем меню Данные, после чего активизируем команду Поиск решения. Заполним
ячейки этого окна следующим образом:и нажмем Выполнить. Если все сделано правильно,
то решение будет таким, как указано
ниже:
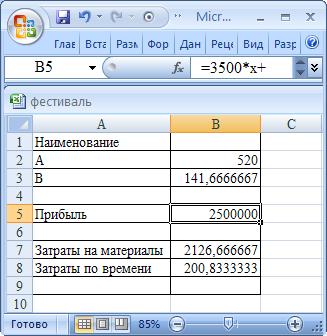
Введем эти данные в нашу
таблицу и получим:
|
А |
В |
|
|---|---|---|
|
1 |
Наименование |
|
|
2 |
А |
|
|
3 |
В |
|
|
4 |
||
|
5 |
Прибыль |
=3500*x+4800*y |
|
6 |
||
|
7 |
Затраты на материалы |
=3*x+4*y |
|
8 |
Затраты по времени |
=0,25*x+0,5*y |
|
9 |
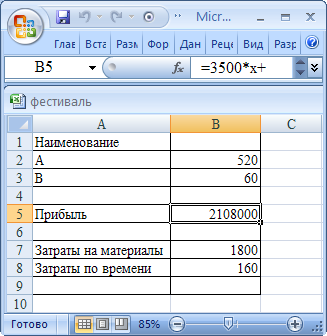
Из решения видно, что
оптимальный план выпуска полок составляет 520 штук вида А
и 60 штук вида В. Полученная максимальная прибыль составит 2108000 рублей.
Покажем применение еще
одной команды для решения этой задачи. Пусть мы хотим получать максимальную
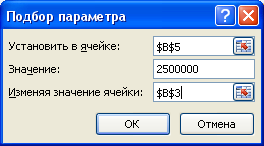
прибыль в размере 2500000 рублей. Используем
функцию Подбор параметра для
определения новых значений. Выберем эту команду и заполним ячейки окна
следующим образом:
и нажмем ОК. Получим следующее решение:
В данном случае изменяли
количество полок вида В. Заметим, что необходимо увеличить затраты по времени и
затраты по материалам, т.е. надо получать не менее 2127 м3 досок
в неделю.
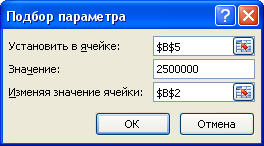
Можно выбрать в качестве Изменяя значения ячейки количество полок
вида А.
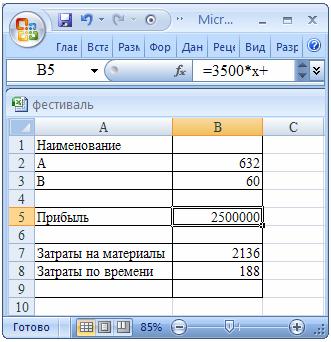
Тогда при решении
получим следующие значения:
В данном случае также
необходимо будет увеличить затраты на материалы – потребуется 2136 м3 досок
и затраты по времени.
Анализ данного примера показывает, что с помощью Excel
можно решать различные экономические задачи. Можно найти все оптимальные
решения и выбрать наиболее подходящее с точки зрения дополнительных критериев.
Т. о. рассматривается
важная задача, как формирование умений и навыков при решении практических задач
в экономике.
Литература:
1. Макарова, Н. В. Информатика. Задачник по моделированию. —
9 класс. – СПб.: Питер, 2001.
2. Чернов, А. А., Чернов, А. Ф. Информатика. Сборник
элективных курсов. – 9 класс. – Волгоград: Учитель, 2007.
XXX
республиканский методически фестиваль
«Уроки математики и информатики, физики и
астрономии
в современной школе»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
ОТКРЫТОГО УРОКА
«Решение прикладных задач в ЭТ MS Excel»
|
по дисциплине |
ИНФОРМАТИКА |
|
|
для студентов |
1 |
курса |
СОСТАВИТЕЛЬ
Баранова М.М.
преподаватель информатики,
информационных технологий
Чебоксарский техникум строительства и городского
хозяйства Минобразования Чувашской Республики (ГАПОУ ЧР «ЧТСГХ»)
Чебоксары
2019
г.
Содержание
Содержание
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
МЕТОДИЧЕСКАЯ КАРТА УЧЕБНОГО ЗАНЯТИЯ
Литература
Содержание и последовательность
учебного занятия
1. Организационный момент
2. Мотивация
3. Актуализация
знаний студентов.
4. Пояснение
преподавателя по ходу выполнения практической работы.
5. Выполнение
студентами практической работы.
6. Тестирование
7. Рефлексия.
Подведение итогов
ПОЯСНИТЕЛЬНАЯ
ЗАПИСКА
Методическая разработка составлена на проведение
открытого занятия в рамках аттестации преподавателя Барановой М.М. по теме «Решение
прикладных задач в ЭТ MS Excel».
Урок проводится со студентами 1 курса по специальности
08.02.01 «Строительство и эксплуатация зданий и сооружений». Группа активна,
полна творческой энергии, уровень развития средний; отношения между студентами
доброжелательные.
Тип занятия: урок повторения и закрепления материала.
Занятия в данной группе проводятся по рабочей
программе учебной дисциплины «Информатика» для специальностей среднего
профессионального образования.
Раздел и тема по календарно-тематическому
планированию (КТП), предшествующие данному уроку по дисциплине «Информатика»,
раздел 4 Прикладные программные средства Практическое занятие №8. «Организация
расчетов в табличном процессоре MS Excel»; Практическое занятие №9. «Создание
расчетных таблиц с использованием различных типов адресации в MS Excel», а сам
урок соответствует по КТП практическое занятие №12 «Решение прикладных задач в
ЭТ»
Выбранное занятие является завершением темы «Табличный
процессор» после изучения теоретического материала и выполнения практических
работ. В ходе выполнения практической работы студенты закрепляют полученные
знания: осуществлять ввод и редактирование данных, применять различные форматы и
типы данных; автоматизировать экономическо-финансовую деятельность; выполнять вычислительные
операции при помощи формул, вычислять значения математических функций; строить
различные графики и диаграммы.
Продолжительность занятия – 45 мин.
В начале занятия проводится повторение
пройденного теоретического курса на тему «Электронные таблицы» в виде кроссворда
в группах.
На уроке применяются фронтальная,
групповая и индивидуальная формы работы, используются как
объяснительно-иллюстративные, так и репродуктивные методы обучения.
В групповой учебной деятельности воспитывается
взаимопонимание, взаимопомощь, коллективность, ответственность,
самостоятельность, культура ведения диалога.
Выполнение
повторения знаний студентов предполагает групповую деятельность, студенты
разбиваются на группы и вместе разгадывают кроссворд на своих карточках, после
обмениваются карточками между группами и проверяются и обсуждаются вместе с
преподавателем. Правильные ответы высвечиваются на экране. Это проводится с
целью установления пробелов в знаниях студентов, а также ликвидации этих
пробелов. Выставляются оценки, которые будут учитываться при выставлении общей
оценки. Выполнение самостоятельной работы предполагает выполнение
индивидуальной работы.
В конце занятия подводятся итоги работы,
выставляются оценки. На наш взгляд в учебном процессе основное внимание должно
быть уделено процессу осознания субъектом образования своей деятельности. Ведь
без понимания способов своего учения, механизмов познания и мыследеятельности студенты
не смогут присвоить себе добытые ими знания. Рефлексия помогает студентам
сформулировать получаемые результаты, переопределить цели дальнейшей работы,
скорректировать свой образовательный путь. Рефлексивная деятельность позволяет
осознать студенту свою индивидуальность, уникальность и предназначение. В
личностно — ориентированном обучении, в обогащающей модели обучения
рефлексивная деятельность выступает на первый план. Ребята оценивают, достигли
ли они поставленных целей в начале урока. За урок студенты получат оценку по информатике.
Данная методическая разработка может быть
использована преподавателями информатики при подготовке к проведению учебного
занятия по всем специальностям НПО и СПО при изучении программы MS Excel.
МЕТОДИЧЕСКАЯ
КАРТА УЧЕБНОГО ЗАНЯТИЯ
Дисциплина: ЕН.02 Информатика
Группа: С27у-15
Преподаватель: Баранова Мальвина Михайловна
Дата: 10.11.2016 г.
Тема занятия: «Решение прикладных задач в ЭТ MS Excel»
Тип занятия: закрепление и систематизация знаний и умений
Вид занятия: урок-практикум
Цели занятия:
1.
Образовательная
цель:
закрепление знаний и умений выполнения расчетов в ЭТ MS Excel
Задачи:
—
повторить
знания и умения студентов по основам работы в ЭТ MS Excel;
—
проверить
уровень сформированности умений работы в ЭТ;
—
закрепить
умения и навыки на практических примерах
2.
Развивающая цель: развитие познавательной
деятельности студентов, логического мышления.
Задачи:
—
развивать
познавательные процессы (память, восприятие, мышление);
—
развивать
умения применять знания на практике.
3.
Воспитательная
цель:
воспитание ответственного отношения к
выполняемому заданию, умение работать в коллективе
Задачи:
—
способствовать
повышению добросовестного отношения к выполняемой деятельности и ее результату;
—
формировать навыки работы в группе и индивидуально;
—
побуждать студентов к активности.
Ожидаемый результат: знать и уметь применять электронные таблицы MS Excel
при решении прикладных задач профессиональной направленности.
Виды ОК:
ОК
2. Организовывать собственную деятельность, выбирать типовые методы и способы
выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения
в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 5. Использовать
информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в
коллективе и в команде, эффективно общаться с коллегами, руководством,
потребителями.
Организационная
деятельность на уроке:
индивидуальная и групповая
Методы обучения:
Объяснительно-иллюстративный, репродуктивный,
алгоритмический, частично-поисковый
Межпредметные связи:
МДК 02.01 Тема 1.9 Ценообразование и
проектно-сметное дело в строительстве
ОП.08 Системы автоматизированного
проектирования в строительстве проектно-сметное дело в строительство
Внутрипредметные связи: Тема 4.2 Электронные таблицы, Практические занятия
№9 — №13.
Средства обучения: Мультимедийная презентация, ПК, раздаточный материал,
программное обеспечение: MS Excel.
Содержание и последовательность учебного
занятия:
1.
Организационный момент.
2.
Мотивация
3.
Актуализация знаний студентов,
повторение.
4.
Пояснение преподавателя по
ходу выполнения практической работы.
5.
Выполнение студентами
практической работы.
6.
Рефлексия. Подведение
итогов
7.
Домашнее задание
Методы контроля: кроссворд, практическая работа, беседа
Тип контроля: самоконтроль, взаимоконтроль, оперативный
контроль
Самостоятельная работа: выполнение практических заданий
Задание на дом: определить, какое количество плиток потребуется на
ремонт 2-х комнатной квартиры. Какая сумма денег будет потрачена.
Литература
1.
Н.В. Макарова Информатика и ИКТ. Задачник по моделированию
9-11 класс. Базовый уровень — Питер 2007-192с.
2.
С. Цветкова, Л.С.
Великович Информатика и ИКТ.
[Текст] –М: Издательский центр «Академия», 2013. – 352с.
3.
Михеева, Е.В. Практикум по информатике [Текст]: учебник /
Е.В. Михеева – М.: Академия, 2011. – 192 с.
4.
Михеева, Е.В. Информатика [Текст]: учебник / Е.В. Михеева,
О.И. Титова, – М.: Академия, 2011. – 352с.
Дополнительные источники:
1.
Угринович Н.Д. Информатика и информационные технологии.
Учебник для 10-11 классов. М.: БИНОМ. Лаборатория знаний, 2010.
Интернет-ресурсы:
1.
www.википедия
2.
www.openclass.ru
3.
http://nsportal.ru
4.
http://festival.1september.ru
5.
http://www.metod-kopilka.ru
6.
www.youtube
|
Преподаватель |
М.М. Баранова |
Содержание и последовательность
учебного занятия
1. Организационный момент
2. Мотивация
3. Актуализация знаний студентов.
4. Пояснение преподавателя по ходу выполнения
лабораторной работы.
5. Выполнение студентами
практической работы.
6. Рефлексия. Подведение итогов
ХОД
УРОКА
1. Организационный момент
Преподаватель:
Добрый день Дорогие гости и участники урока!
Сегодня у нас открытый урок, поэтому жду от вас активного участия на уроке.
Преподаватель:
Тема нашего сегодняшнего занятия «Решение прикладных задач в ЭТ MS Excel».
Прикладную задачу разберем на примере «Вычисление расходов на материалы для
осуществления капитального ремонта в двухкомнатной квартире в ЭТ MS Excel».
2. Мотивация
Преподаватель: Что такое ЭТ?
Студенты: ЭТ – программа, позволяющая проводить вычисления с данными.
Преподаватель: Что такое ячейка?
Студенты: на пересечении строк и столбцов находятся ячейки
Преподаватель: На прошлых занятиях мы уже познакомились с принципом
работы в MS Excel.
– Перечислите, что вы научились
делать, изучая табличный процессор MS EXCEL?
Студенты:
Мы научились
выполнять ввод и редактирование
данных, изменять форматы данных, виды функций, выполняли вычислительные операции при помощи
формул, решили массу задач различного содержания, составляли много различных
таблиц и диаграмм.
Преподаватель: Что называется
формулой в ЭТ? Что она включает в себя?
Студенты: это
математическое выражение, записанное поп правилам, установленным в среде
табличного процессора. Формула включает в себя операторы, ссылки на ячейки,
константы, переменные, знаки арифметических операций, функции и должна
начинаться со знака равенства (=)
Преподаватель: Что такое
ссылка в ЭТ? И какие они бывают?
Студенты: Ссылка – это
адрес объекта (ячейки, блока ячеек) используемый при записи формулы.
Относительные
ссылки: изменяются при копировании в зависимости от нового положения
формулы.
Абсолютные ссылки: не изменяются при
копировании.
Смешанная ссылка используется, когда при
копировании формулы может изменяться только одна какая-то часть ссылки, либо
буква столбца, либо номер строки.
Цель нашего урока можно связать с цитатой Конфуция: «Скажи мне – и я
забуду, покажи мне – и я запомню, дай мне сделать – и я пойму» (всё, что мы с вами услышали и увидели на
теоретических занятиях, очень важно закрепить практически).
Т.е. мы сегодня закрепим полученные знания и
умения, при выполнении расчетов в ЭТ MS Excel.
Вашим домашним заданием было повторить конспект
лекций по Табличному процессору MS
Excel.
Преподаватель: Приведите пример, где
применяются ЭТ?
Студенты: в области экономики,
выполняются в табличной форме: балансы, расчётные ведомости, сметы расходов
и т. п.
Это – наука, производство бухгалтерия, торговля, статистика,
экология, математика, физика. Вывод: области применения электронных таблиц очень
разнообразны, без них не может обойтись практически ни один современный
специалист.
Преподаватель:
– Можно ли ее связать с вашей
профессией?
Студенты:
Да, можно. При расчете (варианты
студентов)
3. Актуализация знаний студентов.
Преподаватель:
Давайте проведем разминку, для того чтобы вспомнить
пройденный материал. У вас на парте лежит карточка с вопросами кроссворда,
нужно его разгадать, время ограниченно, выполнение на 5 минуты.
Студентам предлагается кроссворд на тему «Электронные таблицы»,
на выполнение – 5 минут.
Выполнение
повторения знаний студентов предполагает групповую деятельность, студенты
разбиваются на группы и вместе разгадывают кроссворд на своих карточках, после
обмениваются карточками между группами и проверяются и обсуждаются вместе с
преподавателем. Правильные ответы высвечиваются на экране. Это проводится с
целью установления пробелов в знаниях студентов, а также ликвидации этих
пробелов. Выставляются оценки, которые будут учитываться при выставлении общей
оценки.
ВОПРОСЫ
РАЗМИНКИ:
1.
Часть рабочей
книги Excel, имеющая вид таблицы из строк и
столбцов, в которых хранятся данные (Лист)
2.
Графическое
представление числовой информации, содержащейся в таблице.
3.
Так называется
ссылка, которая не меняется при копировании или перемещении формулы
4.
Запись,
используемая для выполнения операций над содержимым ячеек.
5.
Основной
структурный элемент таблицы.
6.
Переменная
величина, значение которой зависит от значений других величин.
7.
Блок ячеек
таблицы.
ОТВЕТЫ:
1.
Лист
2.
Диаграмма.
3.
Абсолютная
4.
Формула.
5.
Ячейка.
6.
Функция.
7.
Диапазон.
Преподаватель:
Сейчас я попрошу командам поменяться
карточками между группами, чтобы оценить ваш выполненный кроссворд. Правильные
ответы, проверим на экране. Для этого подсчитайте количество верных ответов,
6-7 — оценка «отлично», 5- соответственно «хорошо», 3-4- «удовлетворительно»,
менее трех верных ответов – «неудовлетворительно». После проверки верните
карточки обратно, с проставленными оценками. Поднимите руки те, кто справился
на «отлично». (Преподаватель выставляет оценки, но поясняет, что обязательно
сравнит их с результатами своей проверки ответов).
4. Пояснение преподавателя по ходу выполнения практической работы.
На данном этапе урока преподаватель поясняет принципы
работы.
Преподаватель: Сейчас
мы перейдем к выполнению практической работы.
Задание: Необходимо сделать ремонт в двухкомнатной квартире. В квартире решили
обновить обои во всех комнатах. Определить какое количество обоев потребуется,
какая сумма денег будет потрачена на приобретение материала. Построить
диаграмму (гистограмму), отображающую сумму, потраченную на обои в каждой
комнате.
Примечание: ширина, высота окна и двери необходимо взять с таблицы неоклеиваемя
поверхность.
Порядок выполнения
практической работы.
1.
Откройте
документ Смета расходов 1 и 2 варианты с Папки: Компьютер/Диск Н.
Для правильного
подсчета используйте схему квартиры:
1
вариант
1 вариант
|
Смета расходов по отделке стен комнат 1 вариант |
Неоклеиваемая поверхность |
||||||||||||||||
|
Обои |
Окна: |
Ширина |
Высота |
||||||||||||||
|
№ |
Комната |
Длина (м) |
Ширина (м) |
Высота (м) |
Площадь стен (м2) |
Длина рулона |
Ширина рулона |
Площадь рулона |
Количество рулонов |
Цена за 1 рулон обоев |
Сумма за обои (руб) |
ОК1 |
1,5 |
м |
1,5 |
м |
|
|
ОК2 |
1,8 |
м |
|||||||||||||||
|
1 |
Прихожая |
||||||||||||||||
|
2 |
Зал |
Двери: |
Ширина |
Высота |
|||||||||||||
|
3 |
Кухня |
Д1 |
1,0 |
м |
2,1 |
м |
|||||||||||
|
4 |
Спальня |
Д2 |
0,7 |
м |
|||||||||||||
|
Итого |
Д3 |
0,9 |
м |
||||||||||||||
|
Максимальная сумма |
|||||||||||||||||
|
Минимальная сумма |
2 вариант
|
Смета расходов по отделке стен комнат 1 вариант |
Неоклеиваемая поверхность |
||||||||||||||||
|
Обои |
Окна: |
Ширина |
Высота |
||||||||||||||
|
№ |
Комната |
Длина (м) |
Ширина (м) |
Высота (м) |
Площадь стен (м2) |
Длина рулона |
Ширина рулона |
Площадь рулона |
Количество рулонов |
Цена за 1 рулон обоев |
Сумма за обои (руб) |
ОК1 |
1,5 |
м |
1,5 |
м |
|
|
ОК2 |
1,8 |
м |
|||||||||||||||
|
1 |
Прихожая |
||||||||||||||||
|
2 |
Зал |
Двери: |
Ширина |
Высота |
|||||||||||||
|
3 |
Кухня |
Д1 |
1,0 |
м |
2,1 |
м |
|||||||||||
|
4 |
Спальня |
Д2 |
0,7 |
м |
|||||||||||||
|
Итого |
Д3 |
0,9 |
м |
||||||||||||||
|
Максимальная сумма |
|||||||||||||||||
|
Минимальная сумма |
2.
Рассчитайте
ПЛОЩАДЬ СТЕН.
При расчете площади
стен в каждой комнате, нужно учитывать неоклеиваемую поверхность, т.е. вычесть
окна и дверей.
В прямоугольной
комнате 2 стены по длине Площадь = Длину * Высоту, и 2 стены по ширине Площадь
= Ширину * Высоту, тогда формула будет следующая:
Но необходимо
учитывать неоклеиваемую площадь (НП) окон и дверей:
где В – высота стены, Д – длина стены, Ш –
ширина, Шо – ширина окна, Во – высота окна, Шдв
– ширина двери, Вдв – высота двери. Т.к. ширина и высота окон и
дверей одинакова во всех комнатах, то необходимо применить абсолютную
адресацию.
При
расчете Площади Стен в прихожей, нужно учесть, что там 6 дверей:
з двери марки Д3, 2 двери марки Д2, одна дверь
марки Д1 и окон нет.
В ячейку F5 написать формулу: =2*$E$5*(C5+D5)-$O$7*$Q$7-2*$O$8*$Q$7-3*$O$9*$Q$7
При расчете Площади
Стен в зале, необходимо учесть, что дверь марки Д3
и окно марки ОК2.
В ячейку F6 написать формулу: =2*$E$5*(C5+D5)-$O$7*$Q$7-2*$O$8*$Q$7-3*$O$9*$Q$7
При расчете Площади
Стен в спальне и на кухне, необходимо учесть, что дверь марки Д3
и окно марки ОК1.
В ячейку F7 написать формулу: =2*$E$5*(C7+D7)-$O$9*$Q$7-$O$3*$Q$3
И маркером
автозаполнения заполнить ячейку F8.
3.
Рассчитайте
ПЛОЩАДЬ РУЛОНА.
Площадь рулона
=Ширина рулона*длину рулона.
В ячейку I5 написать формулу: =G5*H5.
И маркером
автозаполнения заполнить остальные ячейки.
4.
Рассчитайте
КОЛИЧЕСТВО РУЛОНОВ.
Количество рулонов: 
учесть что N – целое число, т.к. нам в магазине не смогут продать 4,3 рулона,
то мы используем в MS Excel
математическую функцию ОКРУГЛВВЕРХ(число; число разрядов)
В ячейку J5 написать формулу:
=ОКРУГЛВВЕРХ(F5/I5;0).
И маркером
автозаполнения заполнить остальные ячейки.
5.
Рассчитайте
СУММУ НА ОБОИ.
Сумма на обои =
Количество рулонов* Стоимость 1 рулона.
В ячейку L5 написать формулу: =K5*J5
6.
Найдите
МАКС и МИН суммы денег, потраченные на обои, для этого воспользуемся в MS Excel статистической функцией.
7.
Построить
диаграмму, отображающую сумму, потраченную на обои в каждой комнате. Для этого
необходимо выделить столбец Комната и зажав клавишу Ctrl выделить столбец Сумма за обои (руб). Отпустить
клавишу Ctrl. Выполнить команду Вставка/Диаграмма/Гистограмма
Полученные
результаты:
1 вариант
2 вариант
5. Выполнение студентами
практической работы.
После того, как студенты заполнили половину
таблицы, преподаватель просит сделать предварительный анализ полученных
результатов, а также сравнить данные с целью направить работу студентов и
выявить, правильно ли производятся подсчеты.
6.
Тестирование
После выполнения работы студенты проходят
тестирование в Google-форме
7. Рефлексия. Подведение итогов
Преподаватель:
Какую цель мы ставили в начале урока?
Студенты:
Закрепить полученные знания и умения
выполнения расчетов в ЭТ MS Excel.
Преподаватель:
Мы ее выполнили, как вы считаете?
Студенты:
Да.
Преподаватель:
Что было трудно выполнить в ходе работы?
Преподаватель:
Что понравилось?
Преподаватель:
Что не понравилось?
(Отвечают на вопросы)
Ребята по кругу высказываются одним предложением, выбирая начало фразы
из рефлексивного экрана на доске:
Домашнее задание
Дополнить таблицу. Рассчитать какое количество
линолеумов потребуется.
Муниципальное образовательное учреждение
Октябрьская средняя общеобразовательная школа
Радищевского района Ульяновской области
Реферат на тему:
«Решение прикладных (экономических) задач
в Excel»
Работу выполнил:
Учащийся 11 класса
Чахоян Каруш
Руководитель:
Учитель информатики
Юдахина Т. М.
П. Октябрьский. 2007 г
Оглавление:
1. Введение. Обоснование выбора темы реферата…………………………….3
2. Решение прикладных задач в Excel………….…………………………………3
3. Задачи оптимизации …………………………………………………………..6
4. Прогнозирование ……………………………………………………………..11
5. Заключение. Актуальность выбранной темы……………………………….13
6. Используемая литература………………………………….…………………14
7. ПРИЛОЖЕНИЕ (файлы таблицы Excel) ……………………………………..…… 15
- ВВЕДЕНИЕ
Обоснование выбора темы реферата.
Целью данной работы является использование функций Excel для решения экономических задач. Данные задачи будут решаться с помощью программ табличного процессора Excel. Microsoft Excel средство для работы с электронными таблицами, намного превышающее по своим возможностям существующие редакторы таблиц, первая версия данного продукта была разработана фирмой Microsoft в 1985 году. Табличные процессоры — удобный инструмент для экономистов, бухгалтеров, инженеров, научных работников — всех тех, кому приходится работать с большими массивами числовой информации. Эти программы позволяют создавать таблицы, которые являются динамическими, т. е. содержат так называемые вычисляемые поля, значения которых автоматически пересчитываются по заданным формулам при изменении значений исходных данных, содержащихся в других полях. В дальнейшем ее можно просматривать, изменять, записывать на магнитный диск для хранения, печатать на принтере. Microsoft Excel – это программа управления электронных таблицами общего назначения, которая используется для вычислений, организации и анализа деловых данных. Многие фирмы разработчики программного обеспечения для ПК создали свои версии табличных процессоров. Из них наибольшую известность приобрели Lotus 1-2-3 фирмы Lotus Development, Supercalc фирмы Computer Associates.
Excel — очень мощный инструмент для решения задач, имеющих дело с массивами разнообразных данных, поэтому область его применения обширна, начиная от бухгалтерских и складских задач и заканчивая расчетами энергетики спутниковых линий. В Excel удобно решать задачи линейной алгебры, такие как работа с матрицами и др. Также есть все возможности по полноценной работе (сортировка, выборка, сводные таблицы, анализ) с базами данных. Благодаря наличию языка программирования в Excel возможно создание различных пользовательских программ, которые автоматизируют специфические стандартные задачи.
Мне интересна данная тема именно в использовании электронной таблицы в ведении бухгалтерии. Я собираюсь связать свою профессию с экономикой. Наша семья имеет частный магазин. Поэтому я взялся за данную тему. Я уже сейчас занимаюсь экономическими и бухгалтерскими расчетами, помогая отцу в содержании магазина и организации его эффективной работы. Использование компьютера очень помогает мне быстро и правильно производить расчеты и строить перспективы на дальнейшую работу.
2. Решение прикладных задач в Excel
В данном разделе вы убедитесь, что Excel позволяет не только производить расчеты, но и решать сложные задачи в различных сферах деятельности, такие как решение уравнений, задачи оптимизации, прогнозирования. Решение этих задач может быть существенно облегчено с помощью инструмента Поиск решения (Solver в английских версиях Excel).
Формулировка таких задач может представлять собой систему уравнений с несколькими неизвестными и набор ограничений на решения. Поэтому решение задачи необходимо начинать с построения соответствующей модели.
Если надстройка Поиск решения (Solver) не была установлена при первоначальной установке Excel, то следует запустить процесс установки повторно и выбрать только эту настройку.
Для того чтобы надстройка Поиск решения (Solver) загружалось сразу при запуске Excel:
-выберите команду Сервис, Надстройки;
-в диалоговом окне Надстройки в списке надстроек установите флажок напротив надстройки Поиск решения. Если в списке нет элемента Поиск решения, то нажмите кнопку Обзор, чтобы самостоятельно найти файл Solver.XLA.
Виды математических моделей.
При решении оптимизационных задач с помощью надстройки Поиск решения необходимо различать линейные и нелинейные модели. Под линейными понимаются модели, в которых связь между входными значениями переменных и результирующими значениями описывается линейными функциями. Например:
Y=A*X1+B*X2+C*X3+…
В этом выражении А,В,С — константы, Х1,Х2,Х3-переменные, Y-результат.
Если выражение для целевой величины и выражение для ограничений являются линейными, то можно применять быстрые и надежные методы поиска решения. Для использования именно линейных методов следует установить параметр Линейная модель в окне Параметры поиска решения. Если этот параметр не установить, то даже для линейной задачи будут использоваться общие, более медленные методы.
Ограничения в задачах.
Под ограничениями понимаются соотношения типа A1>=B1, A2=B2, A3>0.
По крайней мере, одна из ячеек в соотношении, определяющем ограничение, должна зависеть от переменных задачи, в противном случае это ограничение не может влиять на процесс решения. Часто ограничения записываются сразу для групп ячеек, например:
A1:A10<=B1:B10 или A1:E1>=0.
Правильная формулировка ограничений является наиболее ответственной частью при формировании модели для поиска решения.
В одних случаях ограничения просты и очевидны, например ограничения на количество сырья. Другие ограничения менее очевидны и могут быть указаны неверно или , хуже того, оказаться пропущенными.
Решение уравнений.
Часто при решении практических задач возникают ситуации, когда необходимо достичь какой-то конкретной цели. Например, необходимо, чтобы себестоимость продукции составляло 20 у. е.
Специфика таких задач состоит в том, что в вашем распоряжении есть математическая модель исследуемого процесса, например закон ценообразования, но вы не знаете, при каком значении входящего в нее параметра можно достичь поставленной цели.
Решение таких задач можно искать методом перебора, однако на это уходит много времени (в лучшем случае).
Можно предложить другие способы решения. В Excel они реализованы как поиск значения параметра формулы, удовлетворяющего ее конкретному значению.
Эта процедуру используют для поиска такого значения ячейки, при котором значение другой ячейки, вычисляемая по формуле, заранее задано. В формуле должна быть ссылка на ячейку, значение которой ищут. Ограничения на искомое значение ячейки не налагают.
Познакомимся с этой процедурой на примере составления штатного расписания.
Задача 1. Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующий хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 10 000 у. е. Необходимо определить, какими должны быть оклады сотрудников больницы.
Построим модель решения этой задачи. За основу возьмем оклад санитарки, а остальное оклады будем вычислять, исходя из него: во сколько-то раз или на сколько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада санитарки: Ai*C+Bi, где С- оклад санитарки; Ai и Bi-коэффициенты, которые для каждой должности определяются следующим образом:
-медсестра получает в 1,5 раза больше санитарки (А2=1,5; В2=0);
-врач в 3раза больше санитарки (А3=3;В3=0);
-заведующий отделением –на 30у.е. больше, чем врач (А4=3;В4=30);
-заведующий аптекой- в 2 раза больше санитарки (А5=2;В5=0);
-заведующий хозяйством – на 40 у. е. больше медсестры (А6=1,5; В6=40);
-главный врач — в 4 раза больше санитарки (А7=4; В7=0);
-заведующий больницей — на 20 у.е больше главного врача (А8=4;В8=20).
Зная количество человек на каждой должности, нашу модель можно записать как уравнение:
N1*A1*C+N2(A2*C+B2)+…+N8*(A8*C+B8)=10000, где N1-число санитарок, N2-число медсестер и т. д.
В этом уравнений нам известны А1…А8, В1…В8 и N1…N8, а С неизвестно.
Анализ уравнения показывает, что задача составления расписания свелась к решению линейного уравнения относительно С.
Решим его.
Технология работы:
-Запустите табличный процессор Excel.
-Заполните таблицу в соответствии с образцом в таблице (файл hospital.xls) cм Приложения
В столбце D вычислите заработную плату для каждой должности. Например, для ячейки D2 формула расчета имеет вид =B2*$G$2+C2.Затем заполните вниз.
В столбце F вычислите заработную плату всех работающих на данной должности. Например, для ячейки F2 формула расчета имеет вид =D2*Е2. Затем заполните вниз.
В ячейке F10 вычислите суммарный фонд заработной платы больницы. Рабочий лист электронной таблицы будет выглядеть, как показано ниже: (файл hospital 1.xls) cм Приложения
Как видите, взяв оклад санитарки за 150, мы превысили месячный фонд зарплаты. Определите оклад санитарки так, чтобы расчетный фонд был равен заданному. Для этого:
-активизируйте команду Подбор параметра из меню Сервис;
-в поле «Установить в ячейке» появившегося окна введите ссылку на ячейку F10, содержащую формулу;
-в поле «Значение» наберите искомый результат 10000.
В поле «Изменяя значение ячейки» введите ссылку на изменяемую ячейку G2 и щелкните кнопкой ОК. Таблица будет выглядеть следующим образом: (Таблица сохранена в каталоге Приложения под именем hospital2.xls.)
Анализ задачи показывает, что с помощью Excel можно решать линейные уравнения. Конечно, такое уравнение может решить любой школьник. Однако благодаря этому простому примеру стало очевидно, что поиск значения параметра формулы, удовлетворяющего ее конкретному значению, — это не что иное, как численное решение уравнений. Другими словами, используя Excel, можно решить любые уравнения с одной переменной.
3.Задачи оптимизации
Иногда интересует не конкретный результат, а минимально или максимально возможный. Например, как минимизировать затраты на содержание персонала или максимизировать прибыли от реализации продукции?
Такие задачи в Excel также решаются с помощью Поиска решения.
Если математическая модель исследуемого процесса и ограничения на значения ее параметров линейны, то задача достижения цели является задачей линейного программирования.
Познакомимся с решением этих задач на следующем примере.
Задача 2. Составление штатного расписания.
Усложним рассмотренную ранее задачу. Пусть известно, что для нормальной работы больницы необходимо 5-7 санитарок, 8-10 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующий хозяйством и заведующий больницей. Общий месячный фонд зарплаты должен быть минимален, Необходимо определить, какими должны быть оклады сотрудников больницы, при условии, что оклад санитарки не должен быть меньше прожиточного минимума — 80у.е.
В качестве модели решения этой задачи возьмем, как и раньше, линейную. Запишем ее так:
N1*A1*C+N2*(A2*C+B2)+…+N8*(A8*C+B8)=Минимум.
В этом уравнений нам не известно число санитарок (N1), медсестер (N2), врачей (N3) и оклад санитарки (C).
Используя Поиск решения, найдем их.
Откройте созданный в предыдущей задаче (файл hospital 1.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения.
В окне установить целевую ячейку укажите ячейку F10, содержащую модель.
Поскольку необходимо минимизировать общий месячный фонд зарплаты, то активизируйте радиокнопку Минимальному значению.
Используя кнопку Добавить, опишите ограничения задачи.
$E$2<=7
$E$2>=5
$E$3<=10
$E$3>=8
$G$2>=80
Щелкните кнопкой ОК, затем — Выполнить.
Решение приведено ниже: (файл hospital3.xls) см Приложения
Оно тривиально: чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд заработной платы.
Задача 3. План выгодного производства
Предположим, что мы решили производить несколько видов конфет. Назовем их условно «А», «В», «С». Известно, что реализация 10 килограммов конфет «А» дает прибыль 9 у. е., «В»-10 у. е., «С»-16 у.е.
Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограммов необходимо произвести, чтобы общая прибыль от реализаций была максимальной.
Нормы расхода сырья на производство 10 кг конфет каждого вида приведены ниже.
|
Сырье |
Нормы расхода |
Запас |
||
|
А |
B |
C |
||
|
Какао |
18 |
15 |
12 |
360 |
|
сахар |
6 |
4 |
8 |
192 |
|
наполнитель |
5 |
3 |
3 |
180 |
|
прибыль |
9 |
10 |
16 |
Решение.
Технология работы:
-Запустите табличный процессор Excel.
-Заполните таблицу в соответствии с данными задачи (таблица файл konfetki.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:
$A$10<=360
$B$10<=192
$B$3>=0
$B$4>=0
$B$5>=0
$C$10<=180.
Не забудьте указать, что изменяются ячейки $B$3:$B$5 и в Параметрах на Линейность модели.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано в таблице (файл konfetki 1.xls) см. Приложения
Из решения видно, что оптимальный план выпуска предусматривает изготовление 80 кг конфет «В» и 20 кг конфет «С». Конфеты «А» производить не стоит. Полученная вами прибыль составит 400 у. е.
Задача 4. Ваше предприятие выпускает изделия 1, изделия 2, изделия 3, используя общий склад комплектующих. Каждое изделие состоит из деталей, имеющихся на складе. В связи с ограниченностью запаса необходимо найти оптимальное соотношение объемов выпуска изделий. Прибыль, получаемая от каждого изделия, равна соответственно 47,32; 31,55; 22,08. Число деталей, идущих на каждое изделие, указано в таблице.
|
Наличие на складе |
Изделие1 |
Изделие 2 |
Изделие 3 |
|
|
Деталь 1 |
450 |
1 |
1 |
0 |
|
Деталь 2 |
250 |
1 |
0 |
0 |
|
Деталь 3 |
800 |
2 |
2 |
1 |
|
Деталь 4 |
450 |
1 |
1 |
0 |
|
Деталь 5 |
600 |
2 |
1 |
1 |
Решение.
Технология работы:
-Запустите табличный процессор Excel.
-Заполните таблицу в соответствий с образцом: (файл detali.xls) см Приложения
В ячейках D4:F8 указывается, из какого числа деталей состоит каждое изделие.
В ячейках D2:F2 указываем примером количество изделий, которые собирается выпускать.
В ячейках В4:В8 указывается число деталей на складе.
В ячейках С4:С8 подсчитываем число деталей, взятых со склада для изготовления изделий.
В ячейках D11:G11 подсчитываем прибыль, полученную от изготовления каждого изделия, и общую прибыль.
В меню Сервис активизируйте команду Поиск решения и опешите его ограничения, как указано ниже:
$B$4:$B$8>=$C$4:$C$8
$D$2:$F$2>=0.
Самостоятельно укажите изменяемые ячейки.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано в таблице (файл detali1.xls) cм. Приложения
Задача 5. Найти оптимальный объём перевозок товаров с 3 заводов на 5 региональных складов. То есть минимизировать затраты на перевозку грузов от заводов – производителей на торговые склады.
Производительность каждого завода и затраты на перевозку от завода на каждый склад приведены в таблице:
|
Заводы |
Поставки |
затраты |
||||
|
Склад 1 |
Склад 2 |
Склад3 |
Склад4 |
Склад5 |
||
|
Завод1 |
310 |
10 |
8 |
6 |
5 |
4 |
|
Завод2 |
260 |
6 |
5 |
4 |
3 |
6 |
|
6Завод3 |
280 |
3 |
4 |
5 |
5 |
9 |
Решение
Технология работы:
-Запустите табличный процессор Excel.
Заполните таблицу в соответствии с образцом: (файл sklad.xls) см Приложения
Допускаем, что от каждого завода на каждый склад перевозиться единица продукций. Ячейки $C$6:$G$6.
В меню Сервис активизируйте команду Поиск решения и опешите его ограничения, как указано ниже:
$B$2:$B$4>=$B$10:$B$12 Количество перевезенных грузов не может превышать производственных возможностей заводов.
$C$6:$G$6>=$C$8:$G$8 Количество доставляемых грузов не должно быть меньше потребностей складов. То есть производство должно быть не меньше потребностей.
$C$2:$G$4>=0 Число перевозок не может быть отрицательным.
Целевая ячейка $B$14. Изменяемые ячейки $C$2:$G$4.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл sklad1.xls) см Приложения
Обратите внимание, что с первого завода вывезена не вся изготовленная продукция, а склады заполнены полностью. Измените потребности складов, затраты на перевозку от заводов к складу, и вы получите другое решение.
Задача 6. Парк отдыха обслуживается семью группами сотрудников. (Группы обозначены А, Б, В, Г, Д, Е, Ж..) Каждая группа имеет разные выходные дни. Выходных дней для каждой группы должно быть не менее двух, выходные следуют подряд. Один сотрудник входит только в одну группу. Известна потребность в сотрудниках в каждый из дней. Все сотрудники имеют одинаковый размер недельной оплаты, который не зависит от графика работы. Необходимо подобрать такую численность сотрудников в каждой группе, чтобы добиться минимизации затрат на оплату труда при выполнении требования по числу сотрудников на каждый день. Дневная зарплата сотрудников 40 у. е.
Решение
Технология работы:
-Запустите табличный процессор Excel.
-Заполните таблицу в соответствии с образцом (файл sоtrudniki.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:
$C$2:$C$8>=0 Количество сотрудников в группе не может быть отрицательным.
$C$2:$C$8= целое. Число сотрудников должно быть целым.
$D$10:$J$10>=$D$12:$J$12. Число ежедневно занятых сотрудников не должно быть меньше ежедневной потребности.
Целевая ячейка $C$15. Изменяемые ячейки $C$2:$C$8.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл sоtrudniki1.xls) см Приложения
Вот тут-то и начинается самое интересное!
Важной особенностью этой задачи является наличие нескольких оптимальных решений, каждое из которых обеспечивает достижение целевой функций при выполнений всех ограничений.
Вызовите диалоговое окно Поиск решения и вновь выполните расчет. Вы получите новое оптимальное решение. Но общее число сотрудников в любом из решении равно 25. Таким образом, можно найти все оптимальные решения и выбрать наиболее подходящее с точки зрения дополнительных критериев.
Задача7. В нескольких пунктах (пункты отправки) скопились транспортные средства (ТС). Эти ТС необходимо перегнать в другие пункты (пункты приемки). Необходимо составить такой план перегона, чтобы общая стоимость перегона была минимальной.
В этой задаче мы имеем следующие значимые факторы:
-число ТС, имеющихся на каждом из трех пунктов отправки:
|
Пункты |
Скопилось ТС |
|
А1 |
120 |
|
А2 |
110 |
|
А3 |
130 |
-необходимые количества ТС для каждого из пяти пунктов приема:
|
Пункты приема |
В1 |
В2 |
В3 |
В4 |
В5 |
|
Требуется ТС |
80 |
60 |
70 |
100 |
50 |
-стоимость перегона одного ТС по каждому из пятнадцати маршрутов:
|
Пункты отправки |
В1 |
В2 |
В3 |
В4 |
В5 |
|
А1 |
2 |
4 |
1 |
6 |
7 |
|
А2 |
3 |
10 |
5 |
4 |
2 |
|
А3 |
8 |
9 |
8 |
3 |
4 |
Решение.
Технология работы:
-Запустите табличный процессор Excel.
-Заполните таблицу в соответствий с образцом: (файл transport.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:
$B$6:$F$6=$B$11:$F$11 Исходные данные – требуемое число ТС по каждому маршруту и число принятых ТС должно быть одинаковым.
$B$8:$F$10>=0 и $B$8:$F$10=целое. Изменяемые данные должны быть целыми и положительными.
$G#3:$G$5=$G$8:$G$10 Исходные данные – количество ТС, скопившихся в каждом из пунктов отравления и отправляемых из этого пункта.
Целевая ячейка $G$16. Изменяемые ячейки $B$8:$F$10.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл transport1.xls) см Приложения
В заключение отметим, что при некоторых исходных данных задача может иметь несколько оптимальных решений.
Задача 8. Для некоторого технологического процесса требуется использование угля с определенным содержанием фосфора и пепла. Доступны три сорта угля – А, В, С. Как их следует смешать, чтобы удовлетворить ограничения на примеси и минимизировать цену? Характеристики каждого угля приведены в таблице:
|
Сорт угля |
Содержание примеси фосфора, % |
Содержание примеси пепла, % |
Цена |
|
А |
0,06 |
2,00 |
30,00 |
|
В |
0,04 |
4,00 |
30,00 |
|
С |
0,02 |
3,00 |
45,00 |
Смесь угля должна иметь следующие характеристики:
|
Содержание примеси фосфора в смеси не более, % |
0,03 |
|
Содержание примеси пепла в смеси не более, % |
3,25 |
Технология работы:
Запустите табличный процессор Excel.
Заполните таблицу в соответствии с образцом: (файл ugol.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:
Целевая ячейка $E$11. Изменяемые ячейки: $B$8:$B$10.
Ограничения:
$B$11=1 Сумма долей угля от разных поставщиков равна единице.
$C$11<=$E$1 Суммарные доли примесей фосфора не должны быть больше предельно допустимых.
$D$11<=$E2 Суммарные доли примесей пепла не должны быть больше предельно допустимых.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл ugol1.xls) см Приложения
Попробуйте выяснить, несколько дешевым должен стать уголь сорта «А», чтобы стало целесообразным его покупать.
Задача 9. Задача о рюкзаке.
Имеется 4 предмета, каждый из которых характеризуется весом и ценой. Нужно выбрать из них такие и столько, чтобы их общий вес не превышал 83, а суммарная цена была максимальной.
Решение.
Введите исходные данные и формулы в электронную таблицу, как указано ниже (в режиме просмотра формул): (файл rukzak.xls) см Приложения
В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:
Целевая ячейка $G$7. Находим максимальное значение.
Изменяемые ячейки: $E$3:$E$6.
Ограничения:
$E$3:$E$6>=0 Количество предметов не может быть отрицательным.
$E$3:$E$6= целое Предметы не разделяются.
$F$7<=B$1 общий вес не должен превышать предельно допустимый.
Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл rukzak1.xls) см Приложения
4. Прогнозирование
Иногда нам хочется знать, «что будет», заранее. Это облегчает принятие предстоящих решений в свою пользу. Как принято говорить, мы хотим «подстелить соломку».
В науке предвидения называют прогнозированием. Основой прогнозирования являются наблюдения. Точнее, не сами наблюдения, а числовые значения неких состояний наблюдаемого явления. Например, курс ценных бумаг. Фиксируя значения курса во времени, мы получим табличное описание процесса изменения курса. Понятно, что если описать аналитический этот процесс, то есть поставить ему в соответствие некую функциональную зависимость:
ПРОГНОЗ=f(x), где х – некий момент времени, то ПРОГНОЗ будет не чем иным, как значением f(x) в некоторой наперед заданный момент времени х.
Аппроксимация позволяет описать наблюдаемые результаты аналитической функцией.
Продемонстрируем возможность прогнозирования на примере определения зависимости высоты от времени свободного падения тела.
Заполните данными рабочий лист электронной таблицы, как показано ниже:
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
|
|
1 |
Время |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
2 |
Высота |
5.1 |
19.4 |
45.2 |
78.4 |
122.8 |
176.3 |
238.6 |
312.9 |
396.9 |
499.6 |
Постройте диаграмму зависимости высоты от времени свободного падения.
Аппроксимируйте полученную кривую с помощью степенной зависимости. Для этого:
-выделите данные диаграммы, установив курсор на графике и щелкнув правой кнопкой мыши;
-выберите из меню команду Формат линий тренда. На экране появится окно выбора линий тренда.
Сделайте настройку линий тренда:
-выберите на вкладе «Тип» степенную аппроксимацию;
-выберите на вкладе «Параметры» «Показать уравнение на диаграмме»;
-щелкните кнопкой ОК.
Результат аппроксимации показан на рисунке (файл prognoz.xls) см Приложения
Как видно, получена следующая аппроксимирующая функция: y=5,0118x 1,9895
Если бы мы не знали из школьного курса физики, что точная зависимость y=gx2/2, то по полученной с помощью Excel зависимости можно было бы предсказать, например, что за время х=20с тело пролетит 1962 м.
Это же можно проверить и с помощью Excel, выбрав на вкладе «Параметры» «Прогноз вперед на … периодов».
Таким образом, как показывает рассмотренный пример, Excel позволяет не только определить аналитические выражение зависимости таблично представляемых данных, но и предсказать тенденцию их изменения.
Заключение.
Актуальность выбранной темы:
Данная тема актуальна потому, что табличные редакторы на сегодняшний день — одни из самых распространенных программных продуктов, используемых во всем мире. Они без специальных навыков позволяют создавать достаточно сложные приложения, которые удовлетворяют до 90% запросов средних пользователей.
Я выбрал эту тему из-за того, что мне нравится использовать сложные формулы в Excel и решать экономические задачи, не прилагая больших усилий и не требуя обширных знаний в области экономики.
Надеюсь, что данная работа заинтересует, поможет разобраться в решении достаточно сложных задач. А главное — даст возможность убедиться, что Excel – одна из самых интересных и полезных программ, используемых пользователями разного уровня!
Список литературы
1. Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов.-М.: Высш. шк., 1986.
2. Microsoft Excel. Руководство пользователя. — Корпорация Microsoft, 1993.
3. Гусева О.Л., Миронова Н. Н. Excel для Windows. Практические работы //Информатика и образование. 1996 №3.
4. Электронные учебники по Excel.
- Cайты учителей
- Все блоги
- Все файлы
- Все тесты
-
1 - Войти
- Зарегистрироваться / Создать сайт


СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 13.04.2023 09:27

Устюгова Екатерина Владимировна
Преподаватель информатики
41 год
929
44 039
15.06.2015 17:08
Решение прикладных задач с помощью программы MS Excel. Цель урока — освоить основные этапы и методы решения прикладных задач с помощью MS Excel. Решать системы уравнией с помощью программы MS Excel.
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
И. Л. СОБОЛЕВА
МОУ «ТВЕРСКОЙ ЛИЦЕЙ»
РЕШЕНИЕ ПРИКЛАДНЫХ ЗАДАЧ В EXCEL
В Тверском лицее изучение Информационных технологий осуществляется в течение нескольких лет. По программе на эту тему отводится в 8 и 9 классе всего 12 часов, в 10 физико-математическом классе – еще 12 часов. На средней ступени изучаются основные возможности электронных таблиц, а именно, основные типы и форматы данных, относительные, абсолютные и смешанные ссылки, использование формул, встроенные функции, построение диаграмм различных типов. Все эти вопросы изучаются на простых доступных примерах. На старшей ступени в физико-математическом классе наряду с повторением пройденного материала изучаются и другие возможности программы Excel, например, использование сложных (вложенных) функций, в том числе логических.
Программа Excel предназначена и широко используется для вычислений, предполагающих представление данных в табличном виде. Для творческого использования возможностей Excel на уровне лицеистов необходимо не только познакомить детей с различными вычислительными возможностями программы, но и показать примеры практического применения процессора, например, на уроках математики. Наша задача – обеспечить грамотный подход и развить творческое отношение детей к решению разнообразных задач. Такими задачами могут быть: построение графиков функций, решение квадратного уравнения, решение системы уравнений, приближенное определение площадей фигур, ограниченных графиком функции, задачи оптимизации, прогнозирования и др. Некоторые из этих задач можно решать с помощью инструмента «Поиск решения».
Решение таких задач на уроках информатики позволяет осуществлять основные принципы педагогической деятельности:
-
Научность является обязательным дидактическим принципом, т. к. в основе изучения темы лежат современные компьютерные технологии.
-
Знакомство и изучение научной литературы по соответствующей тематике.
-
Изучение накопленного педагогического опыта.
-
Ведущая роль теоретических знаний в содержании обучения.
-
Изучение требований ВУЗов по предмету.
-
Проблемный подход, направленный на формирование творческого отношения к решению задач.
-
Связь обучения с практикой.
-
Использование межпредметных связей при изучении темы.
-
Систематичность и последовательность преподавания и усвоения знаний.
-
Доступность.
-
Наглядность.
-
Индивидуализация и дифференциация обучения.
-
Сознательность и активность учащихся в обучении достигается благодаря развитию и постоянному подкреплению интереса к предмету, возможностей использования полученных знаний в различных сферах деятельности.
-
Прочность усвоения знаний.
-
Развитие навыков самостоятельной работы.
-
Формирование творческого отношения к учебе и работе.
Использование программы «Поиск решения»
Программа «Поиск решения» позволяет получить результат на основе изменения значения нескольких ячеек. Кроме того, при выполнении поиска решения можно задать условия – ввести ограничения. Эти возможности позволяют использовать программу Excel для решения системы уравнений и уравнений, при решении которых необходимо учитывать область допустимых значений, для нахождения точек, в которых достигается максимум или минимум значения целевой функции нескольких переменных, определенных на множестве с линейными и нелинейными ограничениями. Другими словами – находить оптимальное решение задачи с ограничениями.
Модели всех задач на оптимизацию состоят из следующих элементов:
-
Переменные — неизвестные величины, которые нужно найти при решении задачи.
-
Целевая функция — величина, которая зависит от переменных и является целью, ключевым показателем эффективности или оптимальности модели.
-
Ограничения — условия, которым должны удовлетворять переменные.
Поиск решения такой модели рассмотрим на примерах.
Пример 1. Решить уравнение 5x — 8lnx = 8
Для решения данного уравнения с помощью инструмента «Поиск решения» нужно:
-
В
ячейку C7 занести значение x=0,0000001(исходное значение параметра). Присвоить этой ячейке имя X.
-
В ячейку B7 записать формулу
=5*X-8*LN(X) (Рис. 1). Рис.1 -
В меню Сервис выбрать пункт Поиск решения… Если этого пункта в меню нет, то его следует загрузить, выполнив команду меню Сервис — Надстройки. В открывшемся диалоговом окне следует поставить флажок Поиск решения. В результате выполнения этой команды появится окно Поиск решения.
-
В
поле Установить целевую ячейку указать ссылку на ячейку с целевой функцией, значение которой необходимо оптимизировать, т. е. $B$7 (Рис.2). При поиске решения целевая ячейка должна содержать формулу и быть прямо или косвенно связанной с ячейками с изменяемыми значениями. Рис.2
-
В поле Изменяя ячейки: указать ячейки, отведенные под переменные целевой функции – это ячейка X, ее адрес $C$7.
-
Кнопка Удалить удаляет ограничение из списка, а кнопка Редактировать дает возможность вносить изменения.
-
Кнопка Параметры вызывает окно диалога «Параметры поиска решения», в котором вы можете изменять параметры целевой функции.
-
В
списке Ограничения: указать дополнительные условия, которые необходимо учитывать при поиске решения. Ограничения вводятся с помощью кнопки Добавить (Рис.3).
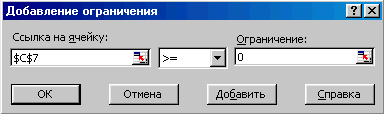
Рис.3 Рис.4
-
В ячейке параметр (X) получим решение данного уравнения (Рис.4).
Таким образом, с помощью Excel можно решать любые уравнения с одной переменной. Мы рассмотрели задачу поиска значения параметра, позволяющего достичь конкретной цели. Но решаемые задачи могут быть более сложными. Например, поиск нескольких параметров, обеспечивающих некоторый, наперед заданный результат.
Пример 2. Решить систему уравнений x1 + 5x2 + x3 = -7
2x1 – x2 – x3 = 0
x1 – 2x2 – x3 = 2
Д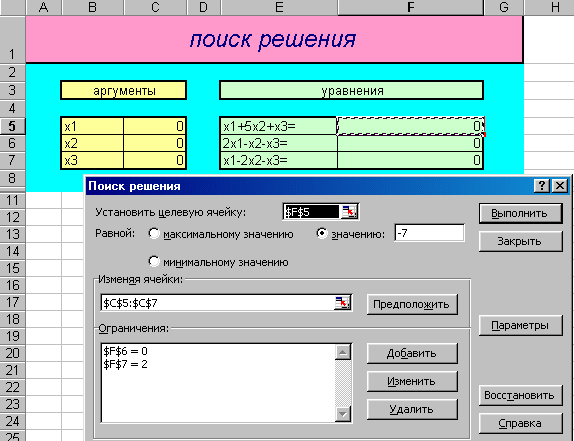
)
Рис.5 Рис.6
Результаты решения системы уравнений появятся в соответствующих ячейках (Рис.6).
Кроме того, зачастую нас интересует не конкретный результат, а минимально или максимально возможный. В таких задачах при поиске решения также накладываются дополнительные условия. Такие задачи в Excel решают с помощью инструмента «Поиск решения».
Дети, обучающиеся в лицее, заинтересованы в получении разносторонних и глубоких знаний. Решение разнообразных задач позволит расширить представление старшеклассников о возможностях электронных таблиц, продемонстрировать практическое применение программы Excel на уроках математики. Кроме того, возможность получать новые знания способствуют развитию творческого отношения детей к решению разнообразных задач. Полученные знания будут полезны нашим выпускникам для успешного и комфортного изучения информатики в ВУЗах.
СПИСОК ЛИТЕРТУРЫ
-
Безручко В.Т. Практикум по курсу «Информатика». Работа в Windows, Word, Excel: Учеб. пособие. — М.: Финансы и статистика, 2002.
-
Информатика. 9 класс. Простейшие статистические характеристики. Начальные сведения из теории вероятностей. Решение прикладных (экономических) задач в Excel: сборник элективных курсов / авт.-сост. А.А.Чернов. — Волгоград: Учитель, 2006.
5

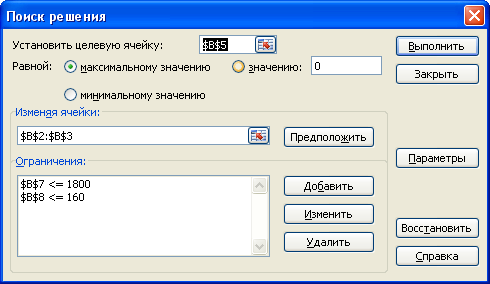









 ячейку C7 занести значение x=0,0000001(исходное значение параметра). Присвоить этой ячейке имя X.
ячейку C7 занести значение x=0,0000001(исходное значение параметра). Присвоить этой ячейке имя X.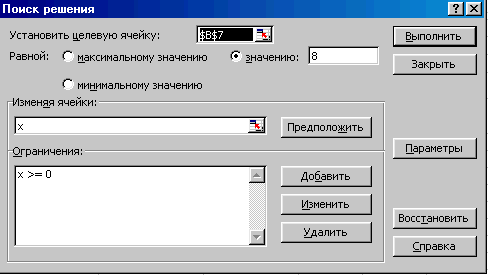 поле Установить целевую ячейку указать ссылку на ячейку с целевой функцией, значение которой необходимо оптимизировать, т. е. $B$7 (Рис.2). При поиске решения целевая ячейка должна содержать формулу и быть прямо или косвенно связанной с ячейками с изменяемыми значениями. Рис.2
поле Установить целевую ячейку указать ссылку на ячейку с целевой функцией, значение которой необходимо оптимизировать, т. е. $B$7 (Рис.2). При поиске решения целевая ячейка должна содержать формулу и быть прямо или косвенно связанной с ячейками с изменяемыми значениями. Рис.2 списке Ограничения: указать дополнительные условия, которые необходимо учитывать при поиске решения. Ограничения вводятся с помощью кнопки Добавить (Рис.3).
списке Ограничения: указать дополнительные условия, которые необходимо учитывать при поиске решения. Ограничения вводятся с помощью кнопки Добавить (Рис.3).