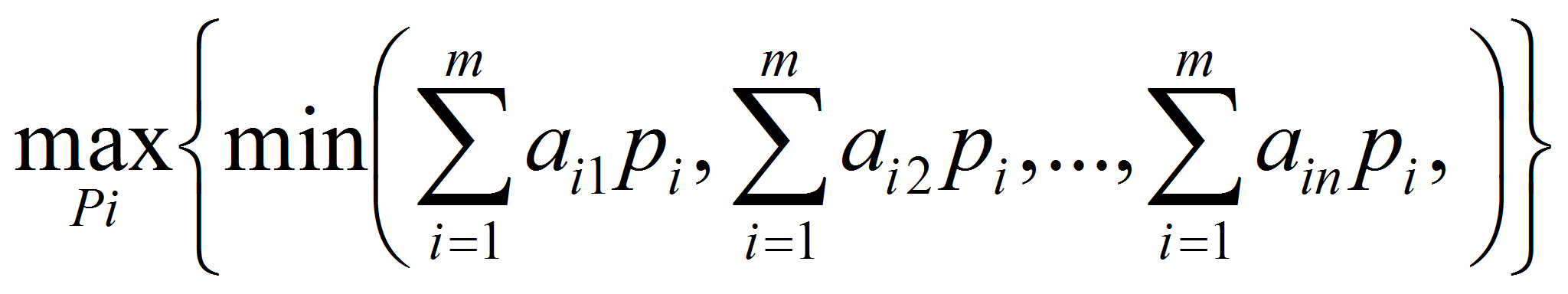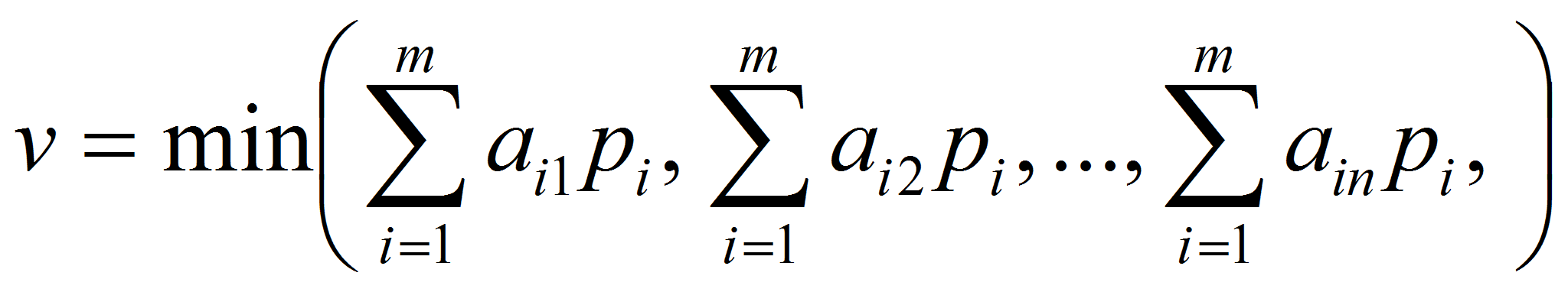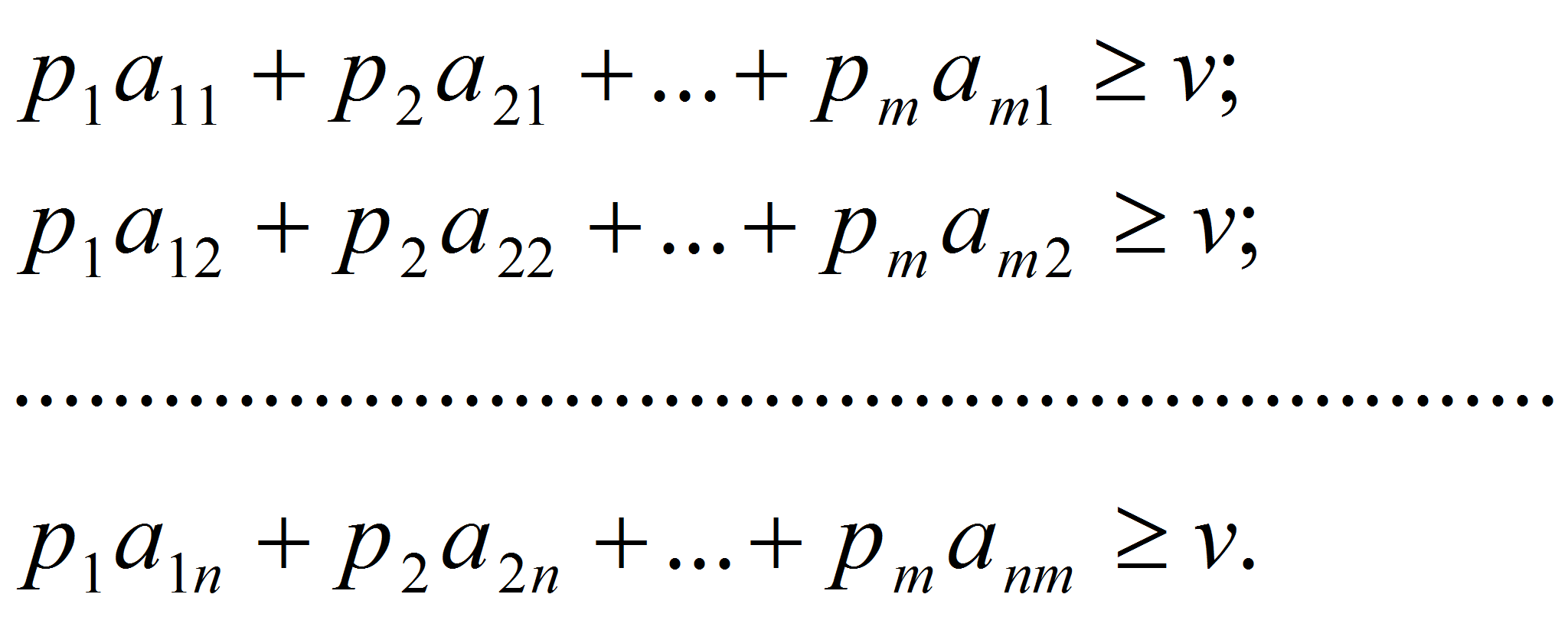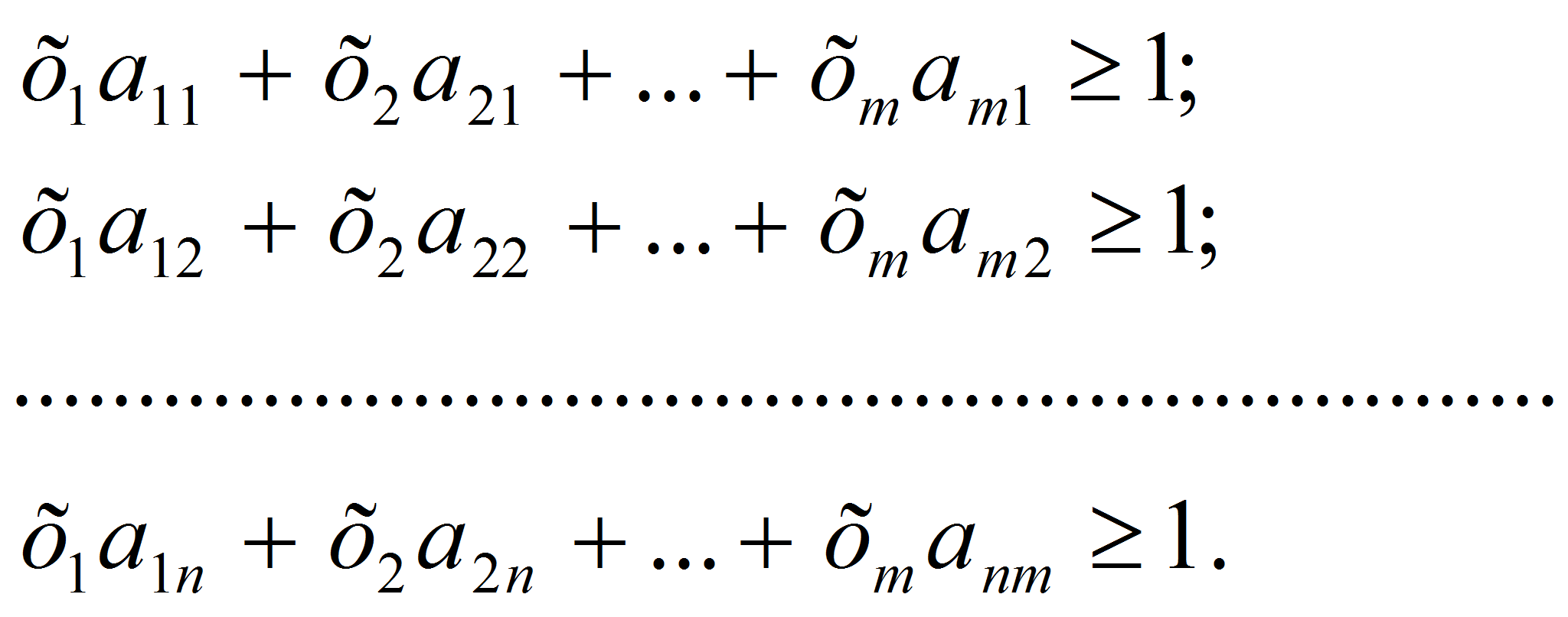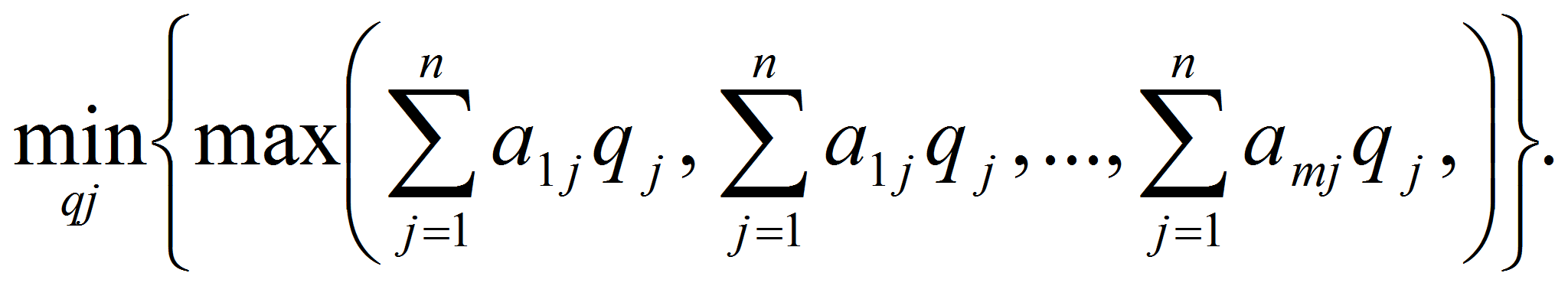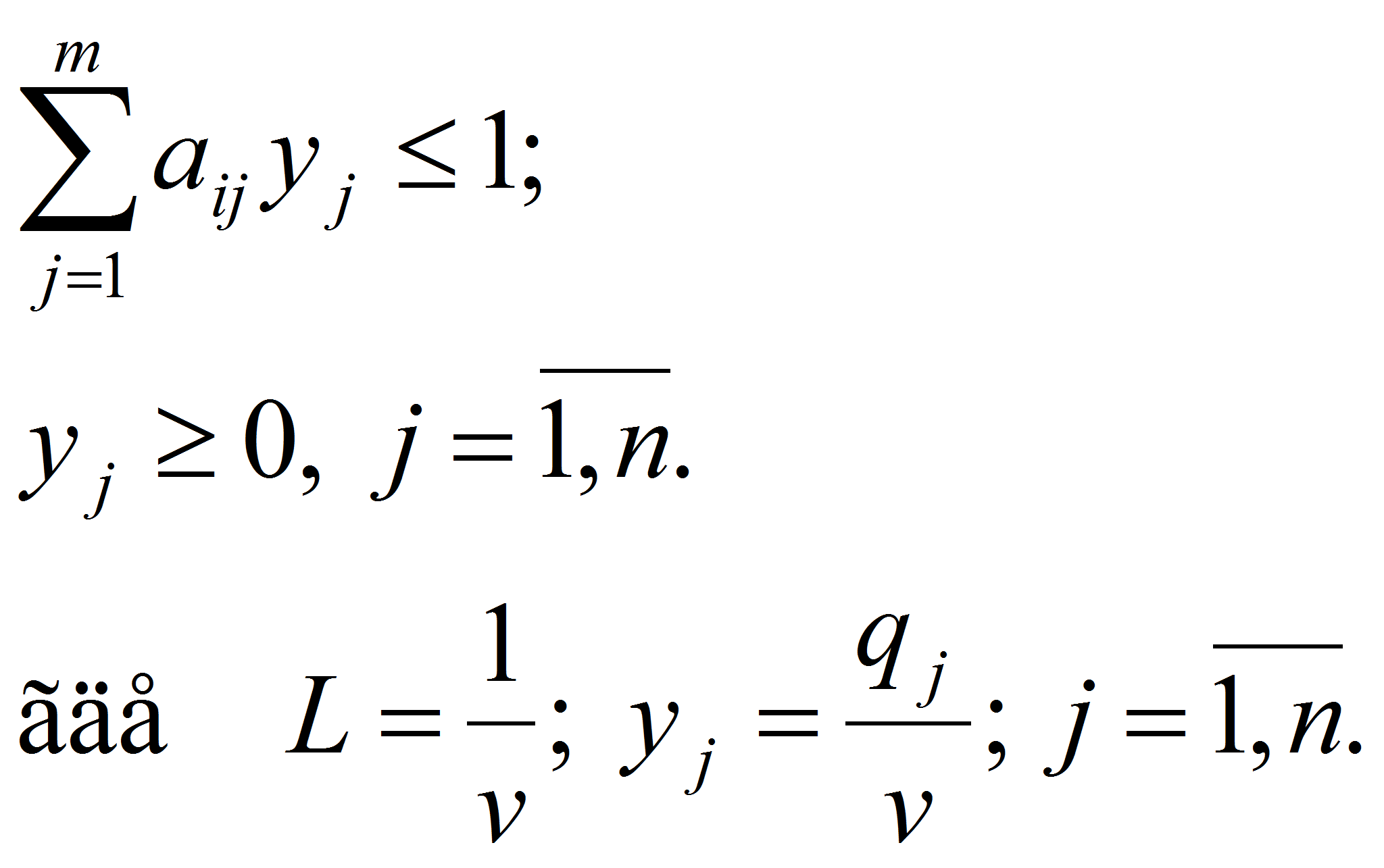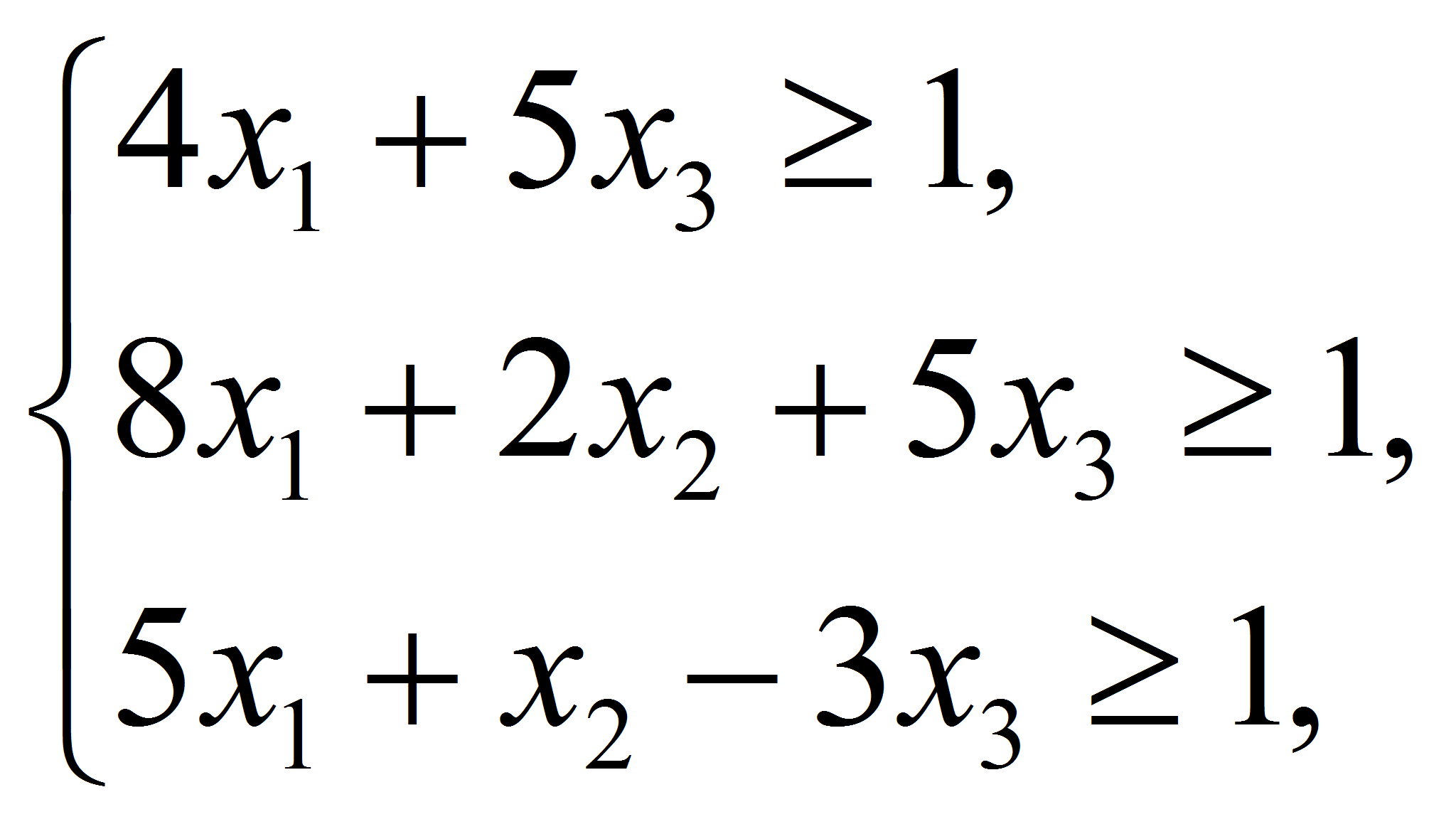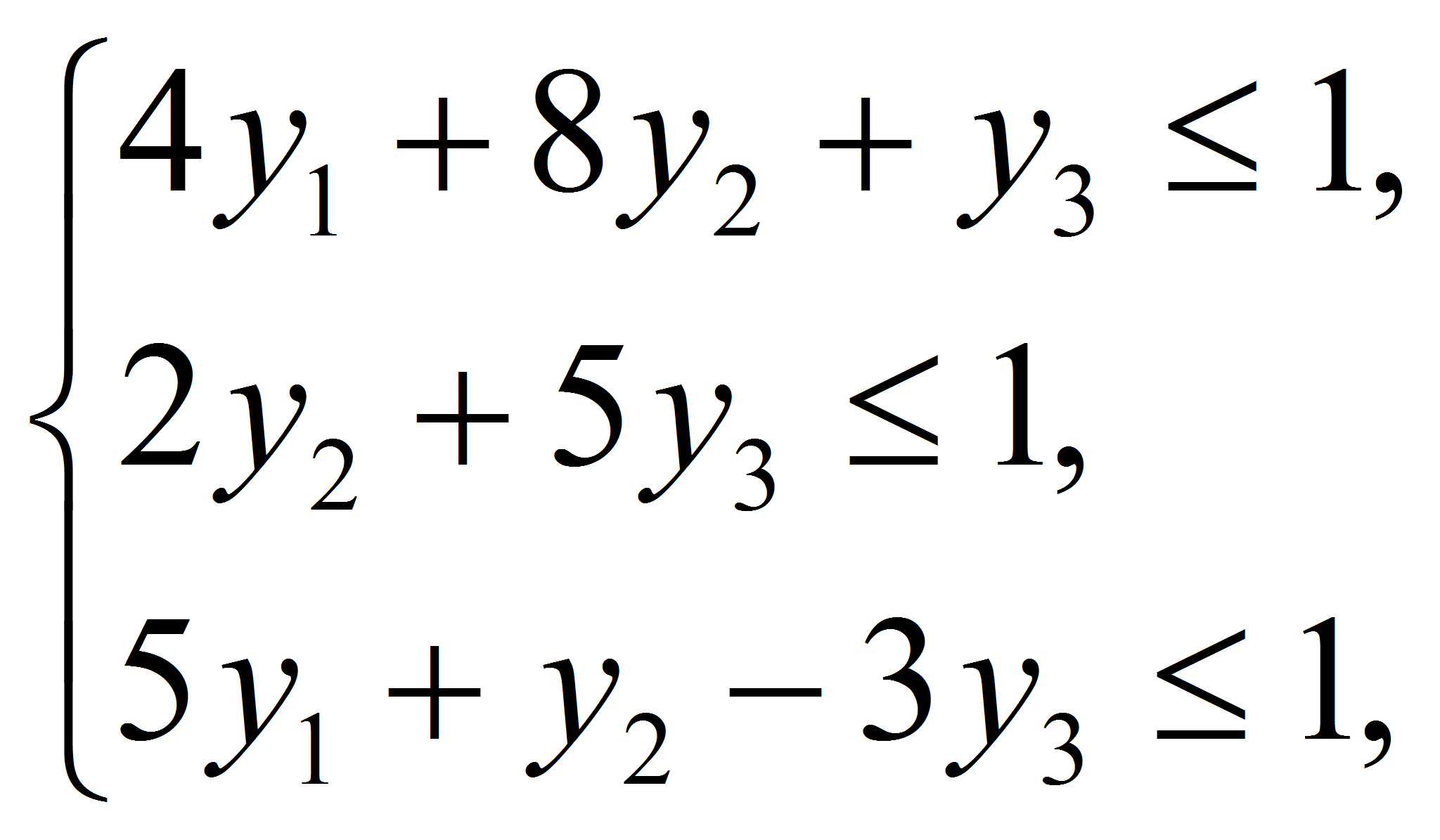Решим, используя надстройку
«Поиск решения» Excel игру, заданную
матрицей
.
Нижняя
и верхняя цены игры:
=
max(l;3)
= 3;
не совпадают, поэтому применяем смешанные
стратегии.
Для
нахождения оптимальной стратегии
первого игрока решаем задачу линейного
программирования: найти
минимальное значение функциипри ограничениях

;
,
.
Здесь
,
где
вероятность выбора первой строки
вероятность выбора второй строки,
цена игры.
Для
ее решения на рабочем листе Excel выполним
указанный выше алгоритм. Вводим исходные
данные в виде таблицы
|
A |
B |
C |
D |
|
|
1 |
u1 |
u2 |
L |
|
|
2 |
||||
|
3 |
1 |
1 |
||
|
4 |
1 |
6 |
1 |
|
|
5 |
9 |
3 |
1 |
Вводим зависимости для целевой функции
и системы ограничений. Для этого в ячейку
С2 вводим формулу =СУММПРОИЗВ(A2:B2;A3:B3). В
ячейки С4 и С5 соответственно формулы:
=СУММПРОИЗВ(A2:B2;A4:B4) и =СУММПРОИЗВ(A2:B2;A5:B5).
В результате получаем таблицу.
|
A |
B |
C |
D |
|
|
1 |
u1 |
u2 |
L |
|
|
2 |
0 |
|||
|
3 |
1 |
1 |
||
|
4 |
1 |
6 |
0 |
1 |
|
5 |
9 |
3 |
0 |
1 |
Запускаем команду «Поиск решения» и
заполняем появившееся окно Поиск
решения следующим образом. В поле
«Оптимизировать целевую функцию» вводим
ячейку С2. Выбираем оптимизации значения
целевой ячейки «Минимум».
В поле «Изменяя ячейки переменных»
вводим изменяемые ячейки A2:B2. В поле «В
соответствии с ограничениями» вводим
заданные ограничения с помощью кнопки
«Добавить». Ссылки на ячейку $C$4:$C$5
Ссылки на ограничения =$D$4:$D$5 между ними
знак => затем кнопку «ОК».
Ставим флажок в поле «Сделать переменные
без ограничений неотрицательными».
Выбрать метод решения «Поиск решения
линейных задач симплекс-методом».
Нажатием кнопки «Найти решение»
запускается процесс решения задачи. В
итоге появляется диалоговое окно
«Результаты поиска решения» и исходная
таблица с заполненными ячейками для
значений переменных и оптимальным
значением целевой функции.
|
A |
B |
C |
D |
|
|
1 |
u1 |
u2 |
L |
|
|
2 |
0,058824 |
0,156863 |
0,215686 |
|
|
3 |
1 |
1 |
||
|
4 |
1 |
6 |
1 |
1 |
|
5 |
9 |
3 |
1 |
1 |
В диалоговом окне «Результаты поиска
решения» сохраняем результат u1=0,058824,
u2=0,156863,
L=0,215686-равный
минимальному значению целевой функции.
Заметим, что нужное количество знаков
после запятой можно ввести, выбрав
команду Формат ячеек.
Так
как
и
,
,
то находим, что=4,63637,
=0,272728
0,27,
=0,727274
0,73
с такими вероятностями первый игрок
должен выбирать первую и вторую строки.
Находим
оптимальную стратегию второго игрока,
т.е. находим наибольшее
значение функции
и соответствующие значения
неотрицательных переменных
,
,
если выполняются
неравенства:
Здесь
,
где
вероятность выбора первогостолбца
вероятность выбора второго столбца,
цена игры.
Решение этой задачи с использованием
надстройки «Поиск решения» Excel дано в
таблице
|
A |
B |
C |
D |
|
|
1 |
t1 |
t2 |
L |
|
|
2 |
0,117647 |
0,098039 |
0,215686 |
|
|
3 |
1 |
1 |
||
|
4 |
1 |
9 |
1 |
1 |
|
5 |
6 |
3 |
1 |
1 |
Так
как
и
,
,
то находим, что=4,63637,
=0,545455
0,55,
=0,454546
0,45
с такими вероятностями второй игрок
должен выбирать первый столбец и второй.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Библиографическое описание:
Захарова, Т. Н. Решение игровых задач с нулевой суммой с помощью Microsoft Excel / Т. Н. Захарова. — Текст : непосредственный // Актуальные задачи педагогики : материалы I Междунар. науч. конф. (г. Чита, декабрь 2011 г.). — Чита : Издательство Молодой ученый, 2011. — С. 176-181. — URL: https://moluch.ru/conf/ped/archive/20/1343/ (дата обращения: 17.04.2023).
Рассмотрим
общий случай игровой задачи m
x
n
с нулевой суммой, когда модель задачи не имеет седловой точки. Такую
модель можно представить в виде матрицы (табл.1):
Таблица 1. Общая таблица стратегий
|
Стратегии |
В1 |
В2 |
… |
Вn |
|
A1 |
a11 |
a12 |
a1n |
|
|
A2 |
a21 |
a22 |
a2n |
|
|
…. |
||||
|
Am |
am1 |
am2 |
amn |
Оптимальное
решение необходимо искать в области смешанных стратегий. Обозначим
вероятности применения стратегий первого игрока (игрока А) через
,
а цену игры — через v.
Оптимальная смешанная стратегия игрока А определяется из условия
Пусть
Поскольку при
оптимальной стратегии средний выигрыш не меньше v
при любой стратегии противника, то справедлива система n
неравенств:
Или
(1)
Тогда задача отыскания
оптимальной смешанной стратегии игрока А может быть сформулирована в
виде задачи линейного программирования.
Для этого
необходимо максимизировать целевую функцию F
=v
при ограничениях
(2)
Введем новые
неизвестные:
Поскольку
Разделим левую и
правую части неравенств (1) и (2) на v, получим:
(3)
В силу того что
max
v
= min
1/v
= min{x1+x2+…+xm}.
задача принимает вид
F=
x1+x2+…+xm
→
min
(4)
при ограничениях
(5)
Для
второго игрока (игрока В) оптимальная стратегия определяется из
условия:
при условии
q1+q2+…+qn
= 1
Эта задача
записывается как симметричная двойственная задача линейного
программирования к задаче игрока A
(4), (5):
L=
y1
+y2+…
+yn
→
max
(6)
при ограничениях
(7)
Задачи игроков A
и В решают симплекс-методом.
Использование
возможностей Microsoft
Excel
позволяет существенно облегчить и ускорить решение этой задачи.
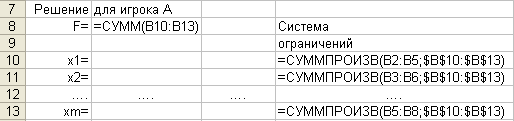
Сначала нужно создать исходную таблицу:
Затем, на основе этой таблицы записать
формулы для нахождения решения:
Для нахождения
решения используется надстройка Поиск решения. Нужно выделить ячейку,
в которой вычисляется значение функции F
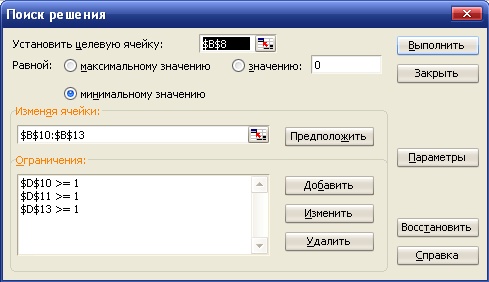
и вызвать надстройку Поиск решения. Заполнить окно поиска решения:
В поле Ограничения
нужно задать формулы для всех ограничений. Затем нажать кнопку
Параметры и отметить поля Линейная модель и Неотрицательные значения.
Нажать кнопку ОК, затем Выполнить.
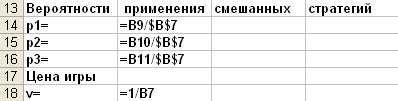
Чтобы найти значения вероятностей и цену
игры нужно записать формулы:
Решение задачи для
игрока В выполняется по аналогичной схеме согласно формулам (6), (7).
Рассмотрим пример
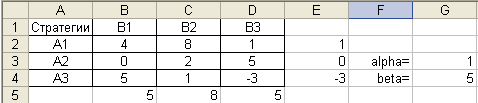
решения задачи. Найдем
решение игры, заданной матрицей
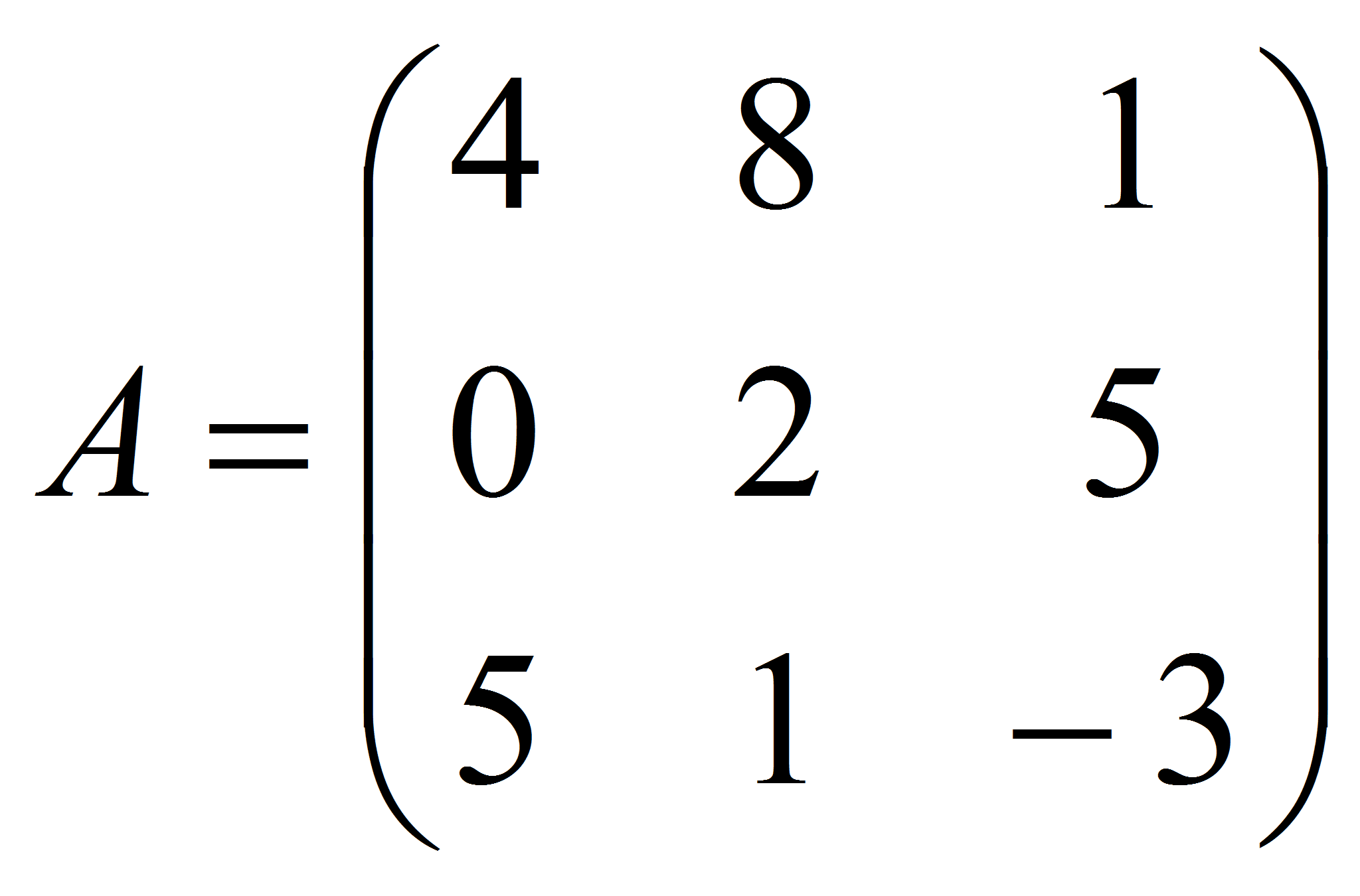
Проверим наличие седловой точки.
В режиме отображения
формул эта запись имеет вид:
Поскольку нижняя цена
игры (минимальный выигрыш игрока А) и верхняя цена игры (максимальный
проигрыш игрока В) не равны, то модель данной задачи не имеет
седловой точки. Поэтому решение следует искать в смешанных
стратегиях. Составим задачи линейного программирования для нахождения
решений игроков А (согласно формулам (4), (5)) и В(согласно формулам
(6), (7)):
для игрока А и
для игрока В.
Для решения этих систем используем
надстройку «Поиск решения». Сначала оформим задачу для
поиска решения игрока А:
В режиме отображения формул:
Затем нужно активировать ячейку В7 и
запустить надстройку Поиск решения. Далее заполнить окно Поиска
решения:
Затем нажать кнопку Параметры и отметить
поля Линейная модель и Неотрицательные значения. Нажать кнопку ОК,
затем Выполнить.
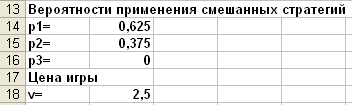
Получим результат:
Вероятности применения смешанных
стратегий и цену игры найдем по формулам: pi=xi/F,
v=1/F.
В режиме отображения формул:
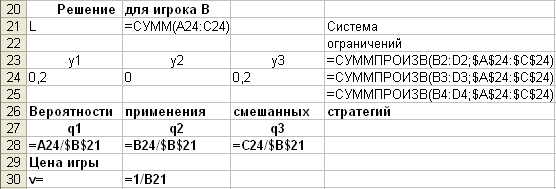
Аналогично найдем решение для игрока В:
В режиме отображения формул:
Литература:
1. Акулич И.Л. Математическое
программирование в примерах и задачах. М. «Высшая школа»,
1993г.
2. Агальцов В.П., Волдайская И.В.
Математические методы в программировании М. ИД «Форум» —
ИНФРА-М, 2006г.
3. Бережная Е.В., Бережной В.И.
Математические методы моделирования экономических систем М. «Финансы
и статистика», 2003г.
4. Партыка Т.Л., Попов И.И.
Математические методы М. ИД «Форум» — ИНФРА-М, 2007г.
Основные термины (генерируются автоматически): игрок А, Поиск решения, режим отображения формул, игрок В, линейное программирование, цена игры, кнопка ОК, Линейная модель, оптимальная смешанная стратегия, оптимальная стратегия.
Похожие статьи
Создание и использование программы для статистического…
стратегия, игра, игрок, матричная игра, цена игры, решение игры, нулевая сумма, участник, верхняя цена игры, платежная матрица. Поиск решения как средство решения задач оптимизации…
Теория игр: основные понятия, типы игр, примеры
Для второго игрока самой оптимальной смешанной стратегией является стратегия . Запишем цену игры
Алгоритм. Иначе цена игры находится в промежутке и решение игры находится в смешанных стратегиях.
Поиск решения как средство решения задач оптимизации…
Получится запись как на рис.1. В диалоговом окне Поиск решения нажать кнопку Параметры, установить флажок Линейная модель и задать условия неотрицательности переменных, установив флажок
Нажать кнопку ОК и перейти в диалоговое окно Поиск решения.
Математическое моделирование оптимальных стратегий…
‒ аспект оптимальных решений — теория математических моделей принятия оптимальных решений вусловиях конфликтов.
игрок, функция распределения, стратегия, конфликтная ситуация, функция, математическая модель, непрерывная игра, обычный риманов интеграл…
Интеграл Стильтьеса в теории игр | Статья в журнале…
Аналогичным образом с помощью интеграла Стильтьеса находится цена непрерывной игры и оптимальная смешанная стратегия для обоих игроков-стратегов. Предположим, что есть платежная функция (или функция выигрыша)…
Целочисленное решение задач линейного программирования…
Оптимальное решение в примере, в принципе, не может быть получено каким-либо округлением решения соответствующей задачи линейного программирования.
Решение многокритериальных задач линейного…
Рис. 1. Оптимальное решение задачи.
Основные термины (генерируются автоматически): критерий, задача, учет уступок, полученное решение, поиск решения, матрица коэффициентов, важность критерия, допустимая уступка, линейное программирование.
Применение метода линейного программирования для решения…
Метод линейного программирования при решении текстовых задач графически имеет следующий алгоритм
Литература: 1. Шикин Е. В., Чхартишвили А. Г. Математические методы и модели.
Линейное программирование | Статья в журнале «Молодой…»
Модель линейного программирования имела бы множество переменных решений
Решение задач оптимального раскроя средствами MS Excel. Симплекс-метод, основанный на идеях Л. В. Канторовича, был описан и детально разработан рядом ученых из США в середине 20 века.
10.7. Практическое задание. Решение
матричных игр с помощью табличного процессора MS Excel
Решение матричных игр в чистых стратегиях
Решение игры в чистых
стратегиях для матрицы определенной размерности
легко автоматизировать, разработав электронную таблицу. Обучаемые
при этом закрепляют навыки работы в табличном редакторе (наиболее
распространенным изучаемом в курсе «Информатика и математика» текстовым
редактором является MS Excel). Используемые функции в MS Excel для нахождения цены игры: МАКС, МИН,
ЕСЛИ.
Справка по используемым функция MS ExcelЕСЛИ —
Возвращает одно значение, если заданное условие при вычислении дает
значение ИСТИНА, и другое значение, если ЛОЖЬ. Функция ЕСЛИ используется при
проверке условий для значений и формул.
Синтаксис: ЕСЛИ(лог_выражение;
значение_если_истина; значение_если_ложь).
Лог_выражение — это любое значение или
выражение, принимающее значения ИСТИНА или ЛОЖЬ. Значение_если_истина —
это значение, которое возвращается, если лог_выражение
равно ИСТИНА. Значение_если_истина может быть числом,
текстом, формулой. Значение_если_ложь —
это значение, которое возвращается, если лог_выражение
равно ЛОЖЬ. Значение_если_ложь
и Значение_если_истина может быть числом, текстом, формулой.МИН — Возвращает наименьшее значение в списке аргументов. Синтаксис: МИН(число1;число2; …) Число1, число2, … — это
от 1 до 30 чисел, среди которых ищется минимальное значение.
МАКС —
Возвращает наибольшее значение в списке аргументов. Синтаксис: МАКС(число1;число2;
…) Число1, число2, … — это от 1 до 30 чисел, среди которых
ищется максимальное значение.
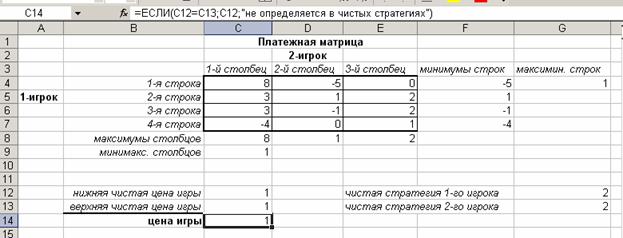
Схема алгоритма решения матричной
игры в чистых стратегиях для платежной матрицы размерностью 3´4.
Рис. 10.3 Пример решения матричной игры в чистых стратегиях в MS Excel
На основании созданной
электронной таблицы решить несколько игр в чистых стратегиях.
Решение матричных игр, описываемых платежной матрицей 2´2, в смешанных стратегиях
Формулы
для нахождения вероятностей применения стратегий игроков и цены игры легко
запрограммировать в электронной таблице (рис. 10.4). Однако использовать разработанную
электронную таблицу для нахождения решения матричных игр во всех задачах не
рекомендуется. Обучаемые не должны терять навык вычисления «вручную», используя
для этого необходимые формулы или вышеуказанный алгоритм.
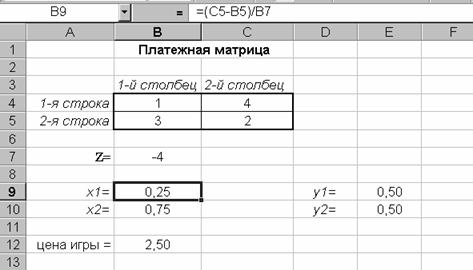
Рис.10.4.
Пример электронной таблицы для расчета вероятностей применения стратегий
игроков и цены игры
На основании созданной
электронной таблицы получить решение несколько игр в смешанных стратегиях.
Определить какие результаты выдает таблица, если платежная матрица не
соответствует игре в смешанных стратегиях.
Предыдущая | Главная | Глава 10 | Следующая