Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12686 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение уравнений в Excel методом итераций Крамера и Гаусса
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х 2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах -1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: <=B12:E12/D12>.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки (<=(B11:E11-B16:E16*D11)/C11>). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты (<=(B10:E10-B15:E15*C10-B16:E16*D10)/B10>). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х 3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х 3 – 1. М = 11.
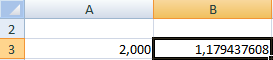
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
источники:
http://lumpics.ru/how-solve-system-equations-excel/
http://exceltable.com/otchety/reshenie-uravneniy
Решение уравнений средствами Excel
|
Содержание |
||
|
1. |
Графический способ решения нелинейных уравнений …………………………. |
2 |
|
2. |
Подбор параметра……………………………………………………………………………….. |
3 |
|
3. |
Поиск решения……………………………………………………………………………………. |
4 |
|
4. |
Решение систем линейных уравнений методом Крамера………………………. |
6 |
|
5. |
Решение систем линейных матричным способом…………………………………. |
7 |
|
6. |
Варианты заданий……………………………………………………………………………….. |
8 |
|
7. |
Решить систему уравнений………………………………………………………………….. |
9 |
2
1. Графический способ решения нелинейных уравнений
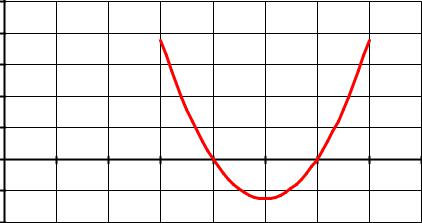
Возьмем в качестве примера квадратное уравнение х2-5х+6=0. Для нахождения корней уравнения выполним следующие действия:
1.В ячейках А2:А22 введём значение аргумента x в диапазоне от 1,5
до 3,5 с шагом 0,1, то есть A2=1.5, A3=A2+0.1 и т. д. A22=A21+0.1, а
значение функции в ячейках B2:B10 – B2=A2^2-5*A2+6 и т. д.
2.Используя Мастер диаграмм, тип диаграммы – точечная построим кривую функции y(x)=х2-5х+6, точки пересечения графика функции с осью абсцисс будет решением уравнения: x1=2, x2=3 (Рис.1).
|
1 |
||||||||
|
0,8 |
||||||||
|
0,6 |
||||||||
|
0,4 |
||||||||
|
0,2 |
||||||||
|
0 |
||||||||
|
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
|
-0,2 |
||||||||
|
-0,4 |
Рис. 1
3
2. Подбор параметра
Когда желаемый результат вычислений по формуле известен, но неизвестны значения, необходимые для получения этого результата, можно воспользоваться средством Подбор параметра, выбрав команду Подбор параметра в меню Сервис. При подборе параметра Excel изменяет значение в одной конкретной ячейке до тех пор, пока вычисления по формуле, ссылающейся на эту ячейку, не дадут нужного результата.
Возьмем в качестве примера все то же квадратное уравнение х2-5х+6=0. Для нахождения корней уравнения выполним следующие действия:
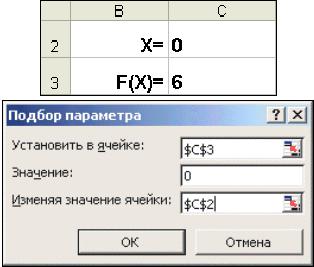
Рис. 2. Окно диалога Подбор параметра
∙В ячейку С3 (рис. 2) введем формулу для вычисления значения функции, стоящей в уравнении слева от знака равенства. В качестве аргумента используем ссылку на ячейку С2, т.е. =С2^2-5*C2+6.
∙В окне диалога Подбор параметра (рис. 2) в поле Установить в ячейке
введем ссылку на ячейку с формулой, в поле Значение — ожидаемый результат, в поле Изменяя значения ячейки — ссылку на ячейку, в
которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).
∙После нажатия на кнопку Ok Excel выведет окно диалога Результат подбора параметра. Если подобранное значение необходимо сохранить, то нажмите на Оk, и результат будет сохранен в ячейке, заданной ранее в поле Изменяя значения ячейки. Для восстановления значения, которое было в ячейке С2 до использования команды Подбор параметра, нажмите кнопку Отмена.
4
3. Поиск решения
Команда Подбор параметра является удобной для решения задач поиска определенного целевого значения, зависящего от одного неизвестного параметра. Для более сложных задач следует использовать команду Поиск решения (Решатель), доступ к которой реализован через пункт меню
Сервис/Поиск решения.
Рассмотрим, как воспользоваться Поиском решения на примере того же квадратного уравнения.
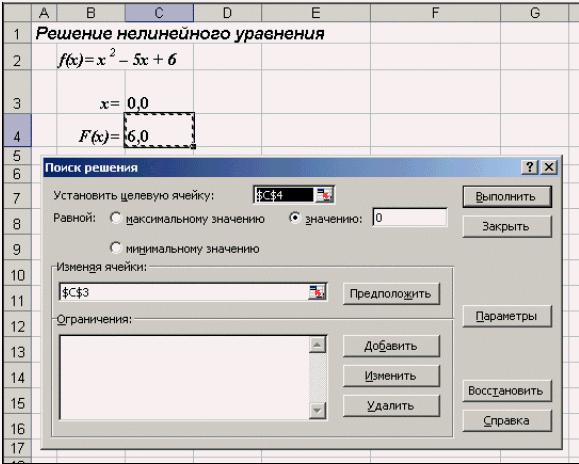
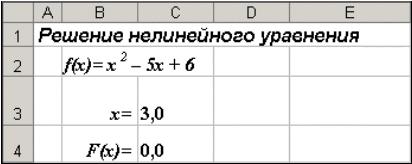
Рис. 3. Окно диалога Поиск решения
После открытия диалога Поиск решения (рис. 3) необходимо выполнить следующие действия:
1)в поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу для вычисления значений оптимизируемой функции, в нашем
примере целевая ячейка — это С4, а формула в ней имеет вид: = C3^2 — 5*C3 + 6;
2)для ввода значения целевой ячейки, установить переключатель значению в положение 0;
3)в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргументов целевой функции ($С$3) (или щелкая мышью при нажатой клавише Сtrl на соответствующих ячейках), для автоматического
поиска всех влияющих на решение ячеек используется кнопка
Предположить;
5
4)в поле Ограничения с помощью кнопки Добавить ввести все ограничения, которым должен отвечать результат поиска: для нашего примера ограничений задавать не нужно;
5)для запуска процесса поиска решения нажать кнопку Выполнить.
Рис. 4. Результаты поиска
Для сохранения полученного решения необходимо использовать переключатель Сохранить найденное решение в открывшемся окне диалога Результаты поиска решения. После чего рабочий лист примет вид, представленный на рис. 4. Полученное решение зависит от выбора начального приближения, которое задается в ячейке С4 (аргумент функции). Если в качестве начального приближения в ячейку С4 ввести значение, равное 1,0, то с помощью Поиска решения найдем второй корень, равный 2,0.
6
4. Решение систем линейных уравнений методом Крамера
Решение систем линейных уравнений рассмотрим на примере системы трёх линейных уравнений
|
ì |
x + 3y + 5z = 4 |
|||||
|
ï |
7 x + 8 y + 9z = 2 |
|||||
|
í |
||||||
|
ï |
||||||
|
î2x + 5 y + 6 z = —3 |
||||||
|
1 |
3 |
5 |
||||
|
Тогда главный определитель будет равен = |
7 |
8 |
9 |
= 26 |
||
|
2 |
5 |
6 |
|
Дополнительные определители: |
|||||||||||||||||
|
4 |
3 |
5 |
1 |
4 |
5 |
1 |
3 |
4 |
|||||||||
|
x = |
2 |
8 |
9 |
= 65 , |
y = |
7 |
2 |
9 |
= —182 , |
z = |
7 |
8 |
2 |
= 117 . |
|||
|
— 3 5 |
6 |
2 |
— 3 6 |
2 |
5 |
— 3 |
Решения системы уравнений будет определяться следующими соотношениями:
x = x = 2,5 ; y = y = —7 ; z = z = 4,5 .
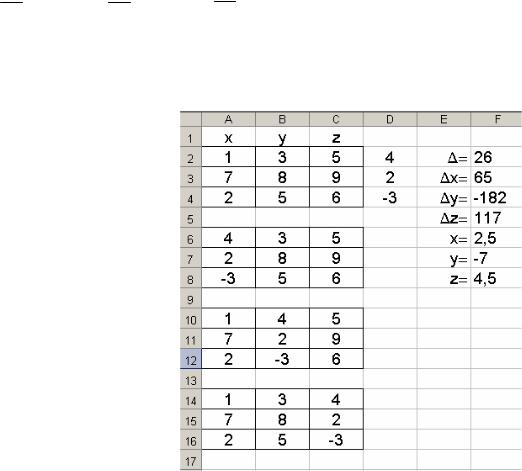
Для решения системы линейных уравнений в табличном процессоре MS Excel запишем главный определитель в ячейки A2:C4, дополнительные
– x в ячейки A6:C8, y – A10:C12, z – A14:C16. Тогда определители можно найти с помощью функции МОПРЕД:
F2 =МОПРЕД(A2:C4);
F3=МОПРЕД(A6:C8);
F4=МОПРЕД(A10:C12)
F5=МОПРЕД(A14:C12)
Решение системы уравнений будет равно:
x=F3/F2;
y=F4/F2;
z=F5/F2.
7
5. Решение систем линейных матричным способом
Воспользуемся предыдущей системой линейных уравнений:
ì x + 3y + 5z = 4 ïí 7 x + 8 y + 9z = 2
ïî2x + 5 y + 6 z = —3
Данную систему линейных уравнений можно записать в матричной форме:
|
æ1 |
3 5 |
ö |
æ x ö |
æ |
4 ö |
|||||
|
ç |
7 |
8 |
9 |
÷ |
, |
ç |
÷ |
ç |
5 |
÷ |
|
A× X = B , где A = ç |
÷ |
X = ç y÷ |
, B = ç |
÷. |
||||||
|
ç |
2 |
5 |
6 |
÷ |
ç |
÷ |
ç |
— 3 |
÷ |
|
|
è |
ø |
è z ø |
è |
ø |
Решение будем искать из уравнения вида:
X = A−1 × B , где A−1 – обратная матрица матрице A.
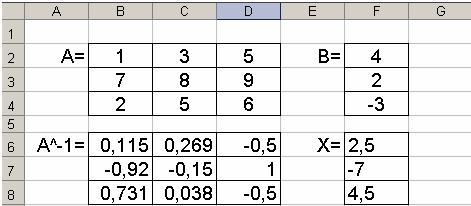
Для системы в Excel запишем коэффициентов при неизвестных в ячейках B2:D4, матрицу столбец – F2:F4 (рис. 5).
Рис. 5
Тогда с помощью функции =МОБР(B2:D4) можно найти обратную матрицу A−1 , для чего:
1.В ячейке B6 введите функцию МОБР(B2:D4).
2.Выделите диапазон ячеек B6:D8.
3.Нажмите клавишу F2.
4.Нажмите комбинацию клавиш Shift+Ctrl+Enter.
Для нахождения решения системы уравнений надо перемножить матрицу A−1 на матрицу—столбец B . Для этого:
1.В ячейке F6 введите функцию =МУМНОЖ(B6:D8;F2:F4).
2.Выделите диапазон ячеек F6:F8.
3.Нажмите клавишу F2.
4.Нажмите комбинацию клавиш Shift+Ctrl+Enter.
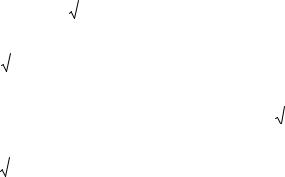
8
6. Варианты заданий
|
№ |
f(x) |
№ |
f(x) |
|||||||||||||||
|
варианта |
варианта |
|||||||||||||||||
|
1 |
ex−1 — x3 — x |
9 |
0.25x3 + x — 2 |
|||||||||||||||
|
x Î [0,1] |
x Î [0, 2 ] |
|||||||||||||||||
|
1 |
1 − x2 |
|||||||||||||||||
|
x — |
arccos |
− x |
||||||||||||||||
|
2 |
3 + sin( 3.6 x ) |
10 |
1 + x2 |
|||||||||||||||
|
x Î [0,1] |
x [ 2,3 ] |
|||||||||||||||||
|
3x − 4ln x − 5 |
||||||||||||||||||
|
3 |
arccos x — |
1—0.3x3 |
11 |
|||||||||||||||
|
x Î[0,1] |
x Î [ 2, 4 ] |
|||||||||||||||||
|
ex |
— e− x — 2 |
|||||||||||||||||
|
4 |
1—0.4x2 — arcsin x |
12 |
||||||||||||||||
|
x Î[0,1] |
x Î [0,1] |
|||||||||||||||||
|
3x —14 + ex — e− x |
— tg x |
|||||||||||||||||
|
5 |
13 |
1— x |
||||||||||||||||
|
x Î[1,3] |
x Î[0,1] |
|||||||||||||||||
|
1− x + sin x − ln(1+ x ) |
||||||||||||||||||
|
6 |
2x2 |
+ 1,2 — cos x — 1 |
14 |
|||||||||||||||
|
x Î [0,1] |
x Î[0, 2] |
|||||||||||||||||
|
æ 2 |
ö |
æ 1 |
ö |
+ |
1 |
x5 |
— x —0,2 |
|||||||||||
|
7 |
cosç |
÷ — 2 sinç |
÷ |
x |
15 |
|||||||||||||
|
è x |
ø |
è x |
ø |
xÎ[1, 2] |
||||||||||||||
|
x Î [1, 2] |
||||||||||||||||||
|
8 |
0.1x2 — x ln x |
16 |
x + 0,5 = e− x 2 |
|||||||||||||||
|
x |
Î [1, 2 ] |
x Î [0,1] |
||||||||||||||||
|
9 |
|||||||||||||||||
|
7. Решить систему уравнений. |
|||||||||||||||||
|
ì 2x1 — x2 — x3 = 4 |
ì x1 + 4x2 − x3 = 2 |
||||||||||||||||
|
1. |
ï |
+ 4x2 |
— 2x3 = —1 |
2. |
ï |
+ 2x2 + 2x3 = 1 |
|||||||||||
|
í3x1 |
í3x1 |
||||||||||||||||
|
ï |
3x1 |
— 2x2 |
+ 4x3 = 11 |
ï |
+ 4x2 — 2x3 = 5 |
||||||||||||
|
î |
î6x1 |
||||||||||||||||
|
ìx1 + 3x2 + 2x3 − 4 = 0 |
ì x1 − x2 + 2x3 = 11 |
||||||||||||||||
|
3. |
ï |
+ 6x2 + x3 — 2 = 0 |
4. |
ï |
+ 2x2 — x3 = 11 |
||||||||||||
|
í2x1 |
í x1 |
||||||||||||||||
|
ï |
+ 8x2 — x3 — 2 = 0 |
ï |
— 3x2 — 3x3 = 24 |
||||||||||||||
|
î4x1 |
î4x1 |
||||||||||||||||
|
ìx1 + 2x2 + 4x3 = 31 |
ì x1 + x2 + 2x3 = −1 |
||||||||||||||||
|
5. |
ï |
+ x2 + 2x3 = 29 |
6. |
ï |
— x2 + 2x3 = —4 |
||||||||||||
|
í5x1 |
í2x1 |
||||||||||||||||
|
ï |
— x2 + x3 = 10 |
ï |
+ x2 + 4x3 = —2 |
||||||||||||||
|
î 3x1 |
î4x1 |
||||||||||||||||
|
ì x1 − 3x2 − 4x3 = 4 |
ìx1 + 2x2 + 3x3 = 2 |
||||||||||||||||
|
7. |
ï |
+ x2 — 3x3 = —1 |
8. |
ï |
+ x2 + 2x3 = 3 |
||||||||||||
|
í2x1 |
í3x1 |
||||||||||||||||
|
ï |
— 2x2 |
+ x3 = 11 |
ï |
+ 3x2 + x3 = 1 |
|||||||||||||
|
î3x1 |
î2x1 |
||||||||||||||||
|
ì 3x1 + 2x2 + 4x3 = 6 |
ìx1 + 2x2 + 3x3 = 5 |
||||||||||||||||
|
9. |
ï |
4x1 |
— 3x2 |
— 8x3 |
= 6 |
10. |
ï |
+ x2 + 2x3 |
= 6 |
||||||||
|
í |
í3x1 |
||||||||||||||||
|
ï |
+ 10x2 |
+ 8x3 |
= —8 |
ï |
= 1 |
||||||||||||
|
î2x1 |
î2x1 + 3x2 + x3 |
||||||||||||||||
|
ì- x1 + 3x2 + 2x3 = 6 |
ì 2x1 — x2 + x3 = 2 |
||||||||||||||||
|
ï |
2x1 + 8x2 + x3 = 3 |
12. |
ï |
+ 2x2 + 2x3 |
= —2 |
||||||||||||
|
11. í |
í3x1 |
||||||||||||||||
|
ï |
x1 |
+ x2 |
+ 2x3 = 6 |
ï |
2x2 + 7x3 = 17 |
||||||||||||
|
î |
î |
||||||||||||||||
|
ì |
2x1 — x2 = —1 |
ì x1 − x2 + 2x3 = 11 |
|||||||||||||||
|
13. |
ï |
+ x2 |
+ 2x3 = 6 |
14. |
ï |
= 11 |
|||||||||||
|
í3x1 |
í x1 + 2x2 — x3 |
||||||||||||||||
|
ï |
+ 3x2 + x3 = 1 |
ï4x |
— 3x |
— 3x |
= 24 |
||||||||||||
|
î2x1 |
2 |
3 |
|||||||||||||||
|
î |
1 |
||||||||||||||||
|
ì x1 − 3x2 − 4x3 = 4 |
ì 3x1 + 2x2 + 4x3 = 6 |
||||||||||||||||
|
15. |
ï |
+ x2 |
— 3x3 = —1 |
16. |
ï |
= 6 |
|||||||||||
|
í2x1 |
í 4x1 — 3x2 — 8x3 |
||||||||||||||||
|
ï |
3x1 |
— 2x2 + x3 |
= 11 |
ï |
= —8 |
||||||||||||
|
î |
î2x1 + 10x2 + 8x3 |
||||||||||||||||
|
ì 2x1 − x |
2 − x3 = 4 |
ì x1 + 4x2 − x3 = 2 |
|||||||||||||||
|
17. |
ï |
+ 4x2 — 2x3 = 11 |
18. |
ï |
|||||||||||||
|
í3x1 |
í3x1 + 2x2 + 2x3 = 1 |
||||||||||||||||
|
ï |
— 2x2 + 4x3 = 11 |
ï |
|||||||||||||||
|
î3x1 |
î6x1 + 4x2 — 2x3 = 5 |
||||||||||||||||
|
ìx1 + 2x2 + 4x3 = 31 |
ìx1 + 2x2 + 3x3 = 2 |
||||||||||||||||
|
19. |
ï |
+ x2 + 2x3 = 29 |
20. |
ï |
= 3 |
||||||||||||
|
í5x1 |
í3x1 + x2 + 2x3 |
||||||||||||||||
|
ï |
3x1 — x2 |
+ x3 = 10 |
ï |
||||||||||||||
|
î |
î2x1 + 3x2 + x3 = 1 |
|
10 |
|||||||
|
ìx1 + 2x2 + 3x3 = 5 |
ìx1 + 3x2 + 2x3 − 4 = 0 |
||||||
|
21. |
ï |
+ x2 + 2x3 |
= 6 |
22. |
ï |
+ 6x2 |
+ x3 — 2 = 0 |
|
í3x1 |
í2x1 |
||||||
|
ï |
+ 3x2 + x3 |
= 1 |
ï |
+ 8x2 |
— x3 — 2 = 0 |
||
|
î2x1 |
î4x1 |
ì x1 + x2 + 2x3 = −1
23.ïí2x1 — x2 + 2x3 = —4 ïî4x1 + x2 + 4x3 = —2
Соседние файлы в папке Вопросы к экзаменам
- #
- #
- #
- #
- #
- #
В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.
Рассмотрим на примерах некоторые варианты решений.
Решение уравнений методом подбора параметров Excel
Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.
Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».
Рассмотрим на примере решение квадратного уравнения х2 + 3х + 2 = 0. Порядок нахождения корня средствами Excel:
- Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
- Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
- После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».
Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».
Как решить систему уравнений матричным методом в Excel
Дана система уравнений:
- Значения элементов введем в ячейки Excel в виде таблицы.
- Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
- Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
- Умножим обратную матрицу Ах-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
- Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.
Получены корни уравнений.
Решение системы уравнений методом Крамера в Excel
Возьмем систему уравнений из предыдущего примера:
Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.
Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.
Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).
Определитель системы больше 0 – решение можно найти по формуле Крамера (Dx / |A|).
Для расчета Х1: =U2/$U$1, где U2 – D1. Для расчета Х2: =U3/$U$1. И т.д. Получим корни уравнений:
Решение систем уравнений методом Гаусса в Excel
Для примера возьмем простейшую систему уравнений:
3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9
Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.
Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.
- Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
- Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
- Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
- Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
- В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.
Примеры решения уравнений методом итераций в Excel
Вычисления в книге должны быть настроены следующим образом:
Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х3 + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:
Хn+1 = Xn– F (Xn) / M, n = 0, 1, 2, … .
M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:
f’ (1) = -2 * f’ (2) = -11.
Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х3 – 1. М = 11.
В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).
В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.
Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:
Скачать решения уравнений в Excel
Корень на заданном промежутке один.
Применение табличного процессора calc для решения уравнений
В работе представлена технология решения уравнений методом подбора параметра в табличном процессоре LibreOffice Calc. Выделены методические рекомендации по изучению данного метода. Приведены задачи для самостоятельного изучения.
УЧЕБНЫЙ ПРОЦЕСС, РЕШЕНИЕ УРАВНЕНИЙ, МЕТОД ПОДБОРА ПАРАМЕТРА, ЭЛЕКТРОННЫЕ ТАБЛИЦЫ, LIBREOFFICE CALC, ТАБЛИЧНЫЙ ПРОЦЕССОР
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Представлены модели для решения квадратных уравнений с помощью алгебраического метода, по теореме Виета и графического метода, а также построила модель биквадратного уравнения. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
В данном проекте затрагиваются вопросы решения квадратных и биквадратных уравнений с помощью табличного процессора MS Excel. Я попыталась построить модель для решения квадратных уравнений с помощью алгебраического метода, по теореме Виета и графического метода, а также построила модель биквадратного уравнения.
- При решении уравнений необходимо обратить внимание учащихся на то, что в ячейке B1 мы изначально вносим произвольное значение переменной x, входящее в область допустимых значений уравнения!;
- Приведенные задания можно усложнить:
- предложить решить аналогичное уравнение, но содержащее в правой части не 0, а какое-либо целое число;
- предложить решить аналогичное уравнение, содержащее в правой части какое-либо выражение, зависящее от x; в этом случае, учащимся потребуется сначала перенести все слагаемые из правой части уравнения в левую и только потом воспользоваться возможностями программы.
Франсуа Виет заметил некоторую закономерность между корнями квадратного уравнения и его коэффициентами. Сегодня эта теорема в школьном учебнике алгебры звучит так: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
При решении уравнений необходимо обратить внимание учащихся на то, что в ячейке B1 мы изначально вносим произвольное значение переменной x, входящее в область допустимых значений уравнения. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Данный метод является удобным средством для решения задач, которые имеют точное целевое значение, зависящее от одного неизвестного параметра. В связи с этим, целесообразно использовать данный метод для решения уравнений различной сложности.
Применение табличного процессора calc для решения уравнений — NovaInfo 51
Это окно служит для задания абсолютного адреса рабочей ячейки, на которую ссылается расчетная функция (ячейка D2). В случае вертикальной организации таблицы подстановки ссылку на рабочую ячейку необходимо ввести в поле Подставлять значения по строкам.
Решение нелинейных уравнений с помощью средства MS Excel Подбор параметра
Постановка задачи. Дано уравнение: x 3 –0,01x 2 –0,7044x+0,139104 = 0. Необходимо решить его с помощью средства MS Excel Подбор параметра с точностью 0,001 [6].
Выполнение. Для начала решим уравнение графически. Известно, что графическим решением уравнения f(x) = 0является точка пересечения графика функции f(x) с осью абсцисс, т. е. такое значение x, при котором функция обращается в ноль.
Проведем табулирование нашего полинома на интервале от -1 до 1 с шагом 0,2. Результаты вычислений приведены на рис.1, где в ячейку В2 была введена формула: = A2^3-0,01*A2^2-0,7044*A2+0,139104.
На графике видно, что функция три раза пересекает ось Оx, а так как полином третьей степени имеет не более трех вещественных корней, то графическое решение поставленной задачи найдено: была проведена локализация корней, т. е. определены интервалы, на которых находятся корни данного полинома: [-1,-0.8], [0.2,0.4] и [0.6,0.8].
Теперь можно найти корни полинома методом последовательных приближений с помощью команды: Сервис → Подбор параметра. Относительная погрешность вычислений и предельное число итераций (например, 0,00001 и 1000) задаются на вкладке Сервис → Параметры.
После ввода начальных приближений и значений функции можно обратиться к пункту меню Сервис → Подбор параметра и заполнить диалоговое окно следующим образом (рис.2.).
После нажатия кнопки ОК появится диалоговое окно Результат подбора параметра (рис. 3.) с сообщением об успешном завершении поиска решения приближенное значение корня будет помещено в ячейку А14.
Два оставшихся корня находим аналогично. Результаты вычислений будут помещены в ячейки А15 и А16 (см. рис.4.).
Постановка задачи. Дано уравнение: e x – (2x – 1) 2 = 0.
Необходимо решить его с помощью средства MS Excel Подбор параметра – с точностью 0,001.
Выполнение.Проведем локализацию корней нелинейного уравнения.
т. е. e x = (2x -1) 2 или f(x) = e x ,g(x) = (2x – 1) 2 и решим графически.
будет точка пересечения линий f(x) и g(x).
Построим графики f(x) и g(x). Для этого в диапазон А3:А18 введем значения аргумента. В ячейку В3 введем формулу для вычисления значений функции:
Результаты вычислений и построение графиков f(x) и g(x) в одной графической области показаны на рис.5.
Рис. 5. Результаты вычислений и построение графиков f(x) и g(x)
На графике видно, что линии f(x) и g(x) пересекаются дважды, т. е. данное уравнение имеет два решения. Одно из них тривиальное и может быть вычислено точно:
Для второго можно определить интервал изоляции корня: 1,5 < x < 2.
Теперь можно найти корень уравнения на отрезке [1.5,2] методом последовательных приближений.
Введём начальное приближение в ячейку Н17 = 1,5 и само уравнение (со ссылкой на начальное приближение) в ячейку I17 = EXP(H17) – (2*H17–1)^2 (рис. 5).
Далее воспользуемся пунктом меню Сервис → Подбор параметра и заполним диалоговое окно Подбор параметра (рис.6).
Результат поиска решения будет выведен в ячейку Н17 (рис.).
1. Можно ли произвольно задавать значения на отрезке по оси х для определения корней?
2. Что при определении корней называют критическими точками?
3. Сколько корней может быть у функции, если у нее существует лишь одна критическая точка?
4. Какие основные проблемы могут встретиться при аналитическом определении корней?
Мнение эксперта
Витальева Анжела, консультант по работе с офисными программами
Со всеми вопросами обращайтесь ко мне!
Задать вопрос эксперту
Если же что-то в расчетах вас не устраивает, то необходимо отменить результат кнопочка Отмена , вернуться к предыдущему состоянию нашей таблицы и исправить допущенные ошибки. Если же вам нужны дополнительные объяснения, обращайтесь ко мне!
Поскольку порядок действия известен, то начинаем создавать необходимую нам таблицу с данными и формулами. Расположение ячеек, как и ранее, вы можете установить на свое усмотрение. Или же воспользоваться нашим
Использование поиска решений в Excel 2010 для решения сложных задач
значение_если_ложь – это альтернативное значение или формула, которая возвращается при невыполнении условия. Данное поле не обязательно заполнять. В этом случае при наступлении альтернативного события функция вернет значение ЛОЖЬ.
Практическое занятие
Математические задачи. Решение уравнений и систем уравнений.
Пояснения к работе
Excel включает
большое число надстроек – откомпилированных программ, добавляющих табличному
процессору новые функциональные возможности. К таким надстройкам относятся
«Подбор параметра», «Поиск решения».
«Подбор параметра» помогает
находить в общем случае приближенные решения уравнений вида f(x)
= 0. Решим простое уравнение:
f(x) = x2 — 5x + 6 = 0
Для решения этого уравнения
подготовим рабочий лист. Ячейка B4 будет содержать значение неизвестной x, а
ячейка B5 – значение функции f(x).
Для этого в B5
поместим формулу = B4* B4 — 5* B4+6, как показано на рис. 1
Рис. 1. Подготовка к решению уравнения
Выберем команду. Сервис/Подбор
параметра. Excel отобразит диалоговое окно Подбор
параметра, приведенное на рисунке 2.В этом окне заполним все три окна в
соответствии с результатом, который мы хотим получить. В поле Установить в
ячейке введем адрес формулы (B5),
результаты которой будут подобраны. В поле Значение введем желаемый
результат вычисления формулы (0). Наконец, используя поле Изменяя значения
ячейки, определим адрес ячейки, которая содержит значение, которое нужно
изменить.
Рис. 2. Заполнение окна Подбор
параметра
После щелчка кнопкой Ok Excel выполнит необходимые вычисления и
выведет диалоговое окно Результат подбора параметра.
Рис. 3. Результат Подбора параметра
Ячейка B4 будет содержать найденный корень
уравнения.
Примечание. В нашем случае уравнение имеет
два корня x1 =2 и x2 = 3. Excel всегда дает только один корень в
зависимости от начального значения изменяемой ячейки.
Примечание. Решение уравнений можно выполнить,
представив функцию в табличном виде. Построив график функции на некотором
отрезке с заданным шагом изменения аргумента, грубо приближенно можно
определить корень уравнения. Затем, используя метод Подбора параметра,
уточнить корень уравнения.
Решение систем уравнений.
Для решения систем уравнений с несколькими
неизвестными используется надстройка «Поиск решения». Пусть требуется решить
систему уравнений
x2 + 5y = 29
5x + y2 = 31
Подготовим рабочий лист так, как показано
на рис. 4. Ячейки D4 и D5
содержат формулы, выражающие левые части уравнений, ячейки E1 и E2 – значения неизвестных x и y
(изменяемые ячейки).
Рис. 4. Подготовка к решению системы
уравнений
Выполним команду Сервис/Поиск решения, на
экране откроется диалоговое окно Поиск решения (рис.5).
Рис. 5. Поиск решения. Надстройки
Установим в поле Установить целевую ячейку
адрес первой формулы D4, в поле Равной значению – число 29 (правая
часть первого уравнения), а в поле Изменяя ячейки диапазон E1:E2 (рис.
6)
Рис. 6. Поиск решения
Второе уравнение мы запишем как ограниченное в поле Ограничения.
Для этого нажмите кнопку Добавить в открывшемся диалоговом окне Добавить
ограничения. Заполним соответствующие поля как показано на рис. 7
Рис. 7. Результат поиска решения
После нажатия кнопки ОК произойдет возврат в окно Поиск
решения. Нам остается только щелкнуть по кнопке Выполнить.
Результат поиска решения показан на рис. 7. Полученные
результаты можно сохранить, нажав кнопку ОК.
Чтобы решить систему из более, чем двух уравнений,
надо одно из них, например первое, выбрать как целевое, т.е. адрес
соответствующей формулы внести в поле Установить целевую ячейку, а
остальные как ограничения.
Надстройка «Поиск решения» как и «Выбор параметра»
позволяет находить только одно решение системы.
Надстройка «Поиск решения» помогает решать довольно
сложные задачи на экстремумы функций нескольких переменных при наличии
ограничений на эти переменные.
Варианты заданий
Задание 1

Определить, сколько точек попадает в заданную фигуру, рис. 1а.
Результат определения принадлежности точек и подсчет
количества точек, принадлежащих заданной фигуре, представлен на рис. 2. В
ячейку C4 помещена формула для определения принадлежности
точек фигуре.
Рис. 2. Подсчет количества точек
Количество точек
находим с помощью автосуммы.
Задание 2. Решить
уравнения и системы уравнений
1.
x3 – x2 + 4 cos πx/2 = 0
2.
x = log x + 5
3.
x2 + xy = 7 –y2
x + 5y2 = 9 –x/3
4.
2x2 + 3y
= 10
—x
+ 6y2 =4
5.
3x
-4y = 3
6.
x3 – sinx – 0,5 = 0
7.
x2 –sinx + 0,1 = 0
8.
x3 + x2
-12x = 0
9.
x3 -19 x – 30 = 0
10.
x3 – x2 +
3x – 10 = 0