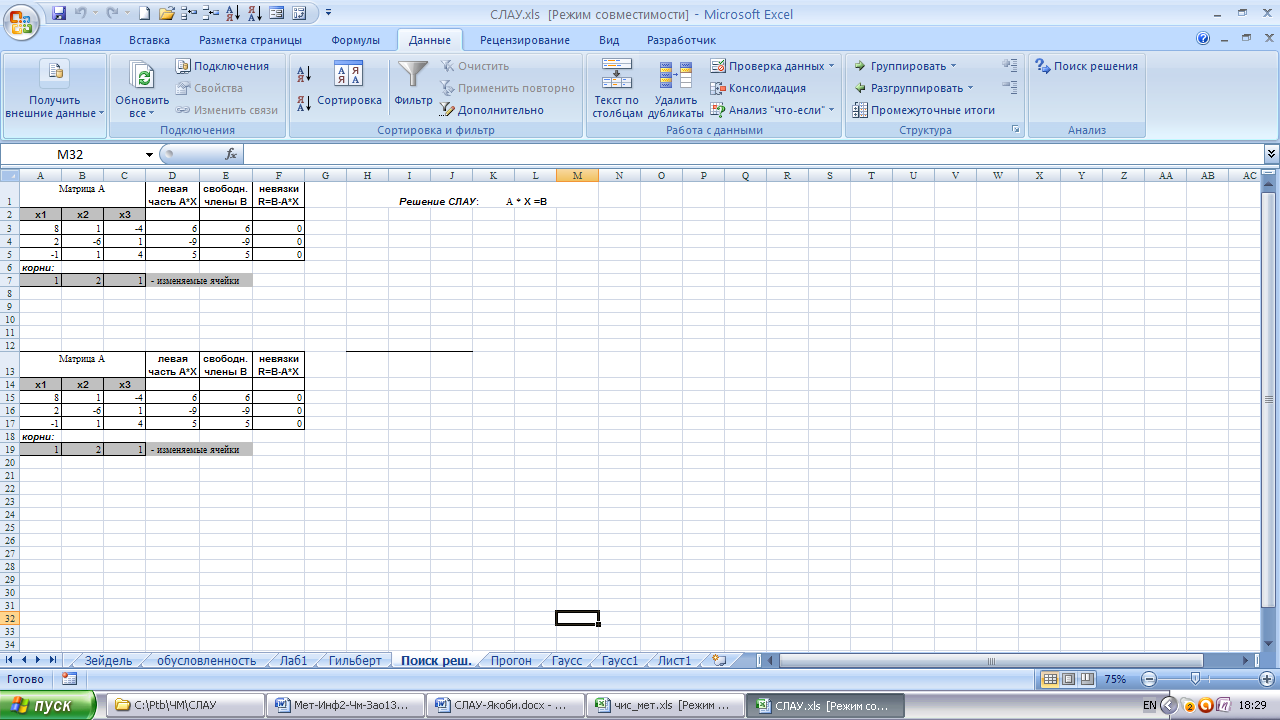
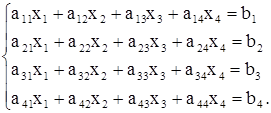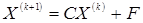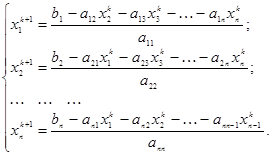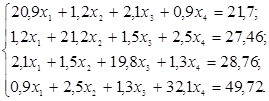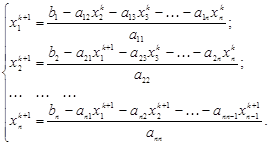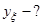Решение СЛАУ с помощью надстройки «Поиск решения»
Систему линейных алгебраических уравнений можно также решить, используя надстройку «Поиск решения». При использовании данной надстройки строится последовательность приближений 
Назовем вектором невязок следующий вектор:
Задача Excel заключается в том, чтобы найти такое приближение 

В качестве примера рассмотрим СЛАУ (3.27).
Последовательность действий:
1. Оформим таблицу, как показано на рис.3.4. Введем коэффициенты системы (матрицу А) в ячейки А3:С5.
Рис.3.4. Решение СЛАУ с помощью надстройки «Поиск решения»
2. В ячейках А8:С8 будет сформировано решение системы (х1, х2, х3). Первоначально они остаются пустыми, т.е. равными нулю. В дальнейшем будем их называть изменяемыми ячейками.. Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например, единицы. Эти значения можно рассматривать как нулевое приближение решения системы, 
3. В столбец D введем выражения для вычисления левых частей исходной системы. Для этого в ячейкуD3 введем и затем скопируем вниз до конца таблицы формулу:
Используемая функция СУММПРОИЗВ принадлежит категории Математические.
4. В столбец Е запишем значения правых частей системы (матрицу В).
5. В столбец F введем невязки в соответствии с формулой (3.29), т.е. введем формулу F3=D3-E3 и скопируем ее вниз до конца таблицы.
6. Будет не лишним проверить правильность вычислений для случая 
7. Выберем команду ДанныеАнализПоиск решения.
Рис. 3.5. Окно надстройки «Поиск решения»
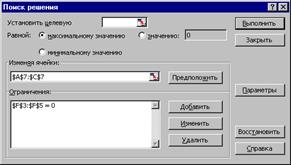
В окне Поиск решения (рис.3.5) в поле Изменяемые ячейки укажем блок $А$8:$С$8, а в поле Ограничения – $F$3:$F$5=0. Далее щелкнем по кнопке Добавить и введем эти ограничения. И затем — кнопка Выполнить
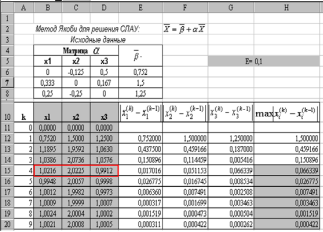
Реализация метода Якоби средствами приложения MS Excel
В качестве примера рассмотрим систему уравнений (3.19), решение которой методом Якоби получено выше (пример 3.2)
Приведем эту систему к нормальному виду:
Последовательность действий
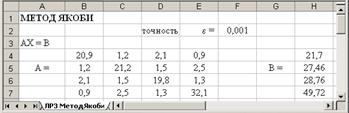
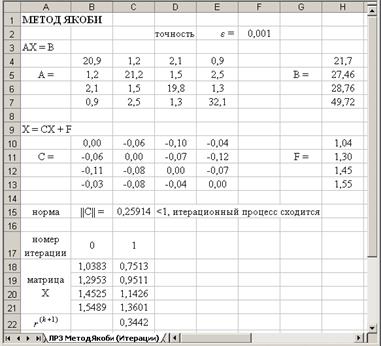
1. Оформим таблицу, как показано на рис.3.6.:
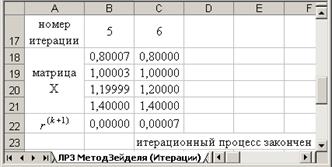
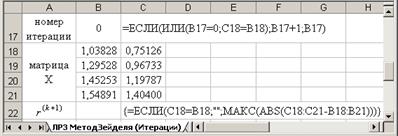
• Матрицы 
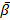
• Значение e–в Н5.
• Номер итерации k сформируем в столбце А таблицы с помощью автозаполнения.
• В качестве нулевого приближения выберем вектор

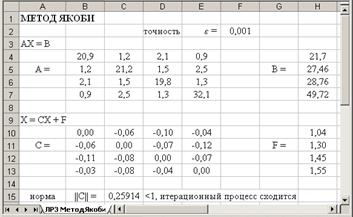
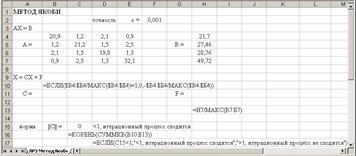
2. Используя выражения (3.29), в ячейки В12:D12 запишем формулы для вычисления первого приближения:
Эти формулы можно записать иначе, используя функцию Excel СУММПРОИЗВ.
В ячейку Е12 введем формулу: E12=ABS(B11-B12) и скопируем ее вправо, в ячейки F12:G12.
Рис.3.6. Схема решения СЛАУ методом Якоби
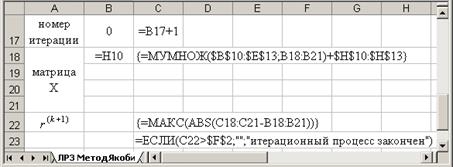
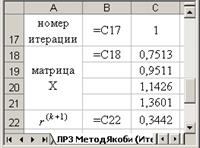
3. В ячейку Н12 введем формулу для вычисления M (k) , используя выражение (3.18): Н12 = МАКС(E12:G12). Функция МАКС находится в категории статистические.
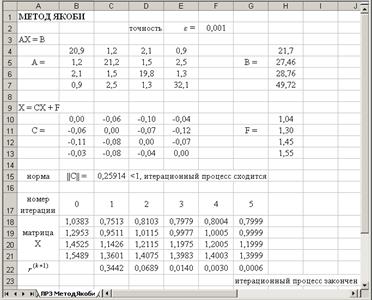
4. Выделим ячейки В12:Н12 и скопируем их вниз до конца таблицы. Таким образом, получим k приближений решения СЛАУ.
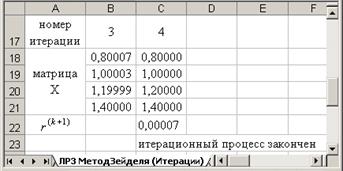
5. Определим приближенное решение системы и количество итераций, необходимое для достижения заданной точности e.
Для этого оценим степень близости двух соседних итераций по формуле (3.18). Воспользуемся Условным форматированиемв ячейках столбца.
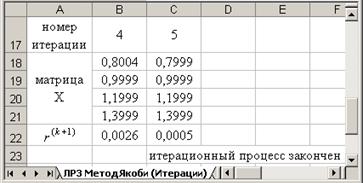
Результат такого форматирования виден на рис.3.6. Ячейки столбца Н, значения которых удовлетворяют условию (3.18), т.е. меньше e=0,1, тонированы.
Анализируя результаты, принимаем за приближенное решение исходной системы с заданной точностью e=0,1 четвертую итерацию, т.е.
Исследуем характер итерационного процесса. Для этого выделим блок ячеек А10:D20 и, используя Мастер диаграмм, построим графики изменения каждой компоненты вектора решения в зависимости от номера итерации,
Приведенные графики (рис.3.7) подтверждают сходимость итерационного процесса.
Рис. 3.7. Иллюстрация сходящегося итерационного процесса
Изменяя значение eв ячейке Н5, получим новое приближенное решение исходной системы с новой точностью.
Реализация метода прогонки средствами приложения Excel
Рассмотрим решение следующей системы линейных алгебраических уравнений методом «прогонки», используя таблицы Excel.
Векторы:
Последовательность действий
1. Оформим таблицу, как показано на рис.3.8. Исходные данные расширенной матрицы системы (3.30), т.е. вектора 

2. Про гоночные коэффициенты U0=0 и V0=0 введем в ячейки G4 и H4 соответственно.
3. Вычислим прогоночные коэффициенты Li, Ui, Vi. Для этого в ячейках F5, G5, H5 вычислим L1, U1, V1. по формуле (3.8). Для этого введем формулы:
F5 = B5*G4+C5; G5=-D5/F5, H5 = (E5-B5*H4)/F5, и затем скопируем их вниз.
Рис.3.8. Расчетная схема метода «прогонки»
4. В ячейке I10 вычислим x6 по формуле (3.10)
5. По формуле (3.7) вычислим все остальные неизвестные x5 x4, x3, x2, x1. Для этого в ячейке I9 вычислим x5 по формуле (3.6): I9=G9*I10+H9 . А далее копируем эту формуле вверх.
Контрольные вопросы
1. Система линейных алгебраических уравнений (СЛАУ). Что является решением СЛАУ. Когда существует единственное решение СЛАУ.
2. Общая характеристика прямых (точных) методов решения СЛАУ. Методы Гаусса и прогонки.
3. Общая характеристика итерационных методов решения СЛАУ. Методы Якоби (простых итераций) и Гаусса-Зейделя.
4. Условия сходимости итерационных процессов.
5. Что понимают под терминами обусловленности задач и вычислений, корректности задачи решения СЛАУ.
Глава 4.
Численное интегрирование
При решении достаточно большого круга технических задач приходится сталкиваться с необходимостью вычисления определенного интеграла:
Вычисление площадей, ограниченных кривыми, работы, моментов инерции, перемножение эпюр по формуле Мора и т.д. сводится к вычислению определенного интеграла.
Если непрерывная на отрезке [a, b] функция y = f(x) имеет на этом отрезке первообразную F(x), т.е. F ’ (x) = f(x) , то интеграл (4.1) может быть вычислен по формуле Ньютона – Лейбница:
Однако, только для узкого класса функций y=f(x) первообразная F(x) может быть выражена в элементарных функциях. Кроме того, функция y=f(x) может задаваться графически или таблично. В этих случаях применяют различные формулы для приближенного вычисления интегралов.
Такие формулы называют квадратурными формулами или формулами численного интегрирования.
Формулы численного интегрирования хорошо иллюстрируются графически. Известно [1, 12], что значение определенного интеграла (4.1) пропорционально площади криволинейной трапеции, образованной подынтегральной функцией y=f(x), прямыми х=а и х=b, осью ОХ (рис.4.1).
Задачу вычисления определенного интеграла (4.1) заменяем задачей вычисления площади этой криволинейной трапеции. Однако задача нахождения площади криволинейной не является простой.
Отсюда идея численного интегрирования [3, 6] будет заключатся в замене криволинейной трапеции фигурой, площадь которой вычисляется достаточно просто.
Рис.4.1. Геометрическая интерпретация численного интегрирования
Для этого отрезок интегрирования [a, b] разобьем на n равных элементарных отрезков [xi ,xi+1] (i=0, 1, 2, …. n-1), с шагом h=(b-a)/n. При этом криволинейная трапеция разобьется на n элементарных криволинейных трапеций с основаниями равными h (рис.4.1).
Каждая элементарная криволинейная трапеция заменяется фигурой, площадь которой вычисляется довольно просто. Обозначим эту площадь Si . Сумма всех этих площадей называется интегральной суммой и вычисляется по формуле
Тогда приближенная формула вычисления определенного интеграла (4.1) имеет вид
Точность вычисления по формуле (4.4) зависит от шага h, т.е. от числа разбиений n. С увеличением n интегральная сумма 
Это хорошо проиллюстрировано на рис.4.2.
Точное значение интеграла
Рис.4.2. Зависимость точности вычисления интеграла
от числа разбиений
В математике доказывается теорема: если функция y=f(x) непрерывна на [a, b], то предел интегральной суммы бn существует и не зависит от способа разбиения отрезка [a,b] на элементарные отрезки.
Формулу (4.4) можно использовать, если известна степень точности такого приближения. Существуют различные формулы для оценки погрешности выражения (4.4), но, как правило, они достаточно сложны. Будем проводить оценку точности приближения (4.4) методом половинного шага.
Решение системы уравнений в Microsoft Excel
Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.
Варианты решений
Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.
Способ 1: матричный метод
Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:
-
Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1. Обозначаем полученную таблицу, как вектор A.
Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B.
Аргумент «Массив» — это, собственно, адрес исходной таблицы.
Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.
Выполняется запуск Мастера функций. Переходим в категорию «Математические». В представившемся списке ищем наименование «МОБР». После того, как оно отыскано, выделяем его и жмем на кнопку «OK».
Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.
Теперь нам нужно будет умножить обратную матрицу на матрицу B, которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ. Данный оператор имеет следующий синтаксис:
Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».
В категории «Математические», запустившегося Мастера функций, выделяем наименование «МУМНОЖ» и жмем на кнопку «OK».
Активируется окно аргументов функции МУМНОЖ. В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2», только на этот раз выделяем значения колонки B. После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter, а набираем комбинацию клавиш Ctrl+Shift+Enter.
Способ 2: подбор параметров
Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение
-
Принимаем значение x за равное 0. Высчитываем соответствующее для него значение f(x), применив следующую формулу:
Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.
Переходим во вкладку «Данные». Жмем на кнопку «Анализ «что если»». Эта кнопка размещена на ленте в блоке инструментов «Работа с данными». Открывается выпадающий список. Выбираем в нем позицию «Подбор параметра…».
Запускается окно подбора параметров. Как видим, оно состоит из трех полей. В поле «Установить в ячейке» указываем адрес ячейки, в которой находится формула f(x), рассчитанная нами чуть ранее. В поле «Значение» вводим число «0». В поле «Изменяя значения» указываем адрес ячейки, в которой расположено значение x, ранее принятое нами за 0. После выполнения данных действий жмем на кнопку «OK».
После этого Эксель произведет вычисление с помощью подбора параметра. Об этом сообщит появившееся информационное окно. В нем следует нажать на кнопку «OK».
Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.
Способ 3: метод Крамера
Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:
-
Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно».
Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A, только у этих копий поочередно один столбец заменен на таблицу B. У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.
Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД. Синтаксис данного оператора следующий:
Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.
Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».
Активируется окно Мастера функций. Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД». После этого жмем на кнопку «OK».
Запускается окно аргументов функции МОПРЕД. Как видим, оно имеет только одно поле – «Массив». В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK». Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter.
Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740, то есть, не является равным нулю, что нам подходит.
Аналогичным образом производим подсчет определителей для остальных трех таблиц.
На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.
Способ 4: метод Гаусса
Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:
-
Опять последовательно записываем коэффициенты в таблицу A, а свободные члены, расположенные после знака «равно» — в таблицу B. Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.
Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:
Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.
После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.
После этого копируем полученную строку и вставляем её в строчку ниже.
Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать», которая расположена на ленте во вкладке «Главная».
Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка». В запустившемся дополнительном списке выбираем позицию «Значения».
В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:
После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.
Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:
Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.
Поднимаемся на строку вверх и вводим в неё следующую формулу массива:
Жмем привычное уже нам сочетание клавиш для применения формулы массива.
Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:
Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.
Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.
Помимо этой статьи, на сайте еще 12677 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Решение систем линейных уравнений
Эта страничка поможет решить Системы Линейных Алгебраических Уравнений (СЛАУ) методом Гаусса, матричным методом или методом Крамера, исследовать их на совместность (теорема Кронекера-Капелли), определить количество решений, найти общее, частное и базисные решения.
Введите коэффициенты при неизвестных в поля. Если Ваше уравнение имеет меньшее количество неизвестных, то оставьте пустыми поля при переменных, не входящих в ваше уравнение. Можно использовать дроби ( 13/31 ).
источники:
http://lumpics.ru/how-solve-system-equations-excel/
http://matrixcalc.org/slu.html
Методы решения систем линейных алгебраических уравнений хорошо описаны
в учебнике «Основы вычислительной математики. Демидович Б.П., Марон И.А. 1966».
Скачать — 11Мб
1. Метод обратной матрицы (решение в Excel)
Если дано уравнение:
A*X = B, где A — квадратная матрица, X,B — вектора;
причем B — известный вектор (т е столбец чисел), X — неизвестный вектор,
то решение X можно записать в виде:
X = A-1*B, где A-1 — обратная от А матрица.
В MS Excel обратная матрица вычисляется функцией МОБР(), а перемножаются матрицы
(или матрица на вектор) — функцией МУМНОЖ().
Имеются «тонкости» использования этих матричных действий в Excel. Так, чтобы вычислить
обратную матрицу от матрицы А, нужно:
1. Мышкой выделить квадратную область клеток, где будет размещена обратная матрица. 2. Начать вписывать формулу =МОБР( 3. Выделить мышкой матрицу А. При этом правее скобки впишется соответствующий диапазон клеток. 4. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter 5. Должна вычислиться обратная матрица и заполнить предназначенную для неё область
Чтобы умножить матрицу на вектор:
1. Мышкой выделить область клеток, где будет размещён результат умножения 2. Начать вписывать формулу =МУМНОЖ( 3. Выделить мышкой матрицу - первый сомножитель. При этом правее скобки впишется соответствующий диапазон клеток. 4. С клавиатуры ввести разделитель ; (точка с запятой) 5. Выделить мышкой вектор- второй сомножитель. При этом правее скобки впишется соответствующий диапазон клеток. 6. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter 7. Должно вычислиться произведение и заполнить предназначенную для него область
Есть и другой спососб, при котором используется кнопка построителя функции Excel.
Пример СЛАУ 4-го порядка
Скачать документ Excel, в котором этот пример решён различными методами.
2. Метод Гаусса
Метод Гаусса подробно (по шагам) выполняется только в учебных целях, когда нужно показать, что Вы это умеете. А чтобы решить реальную СЛАУ, лучше применить в Excel метод обратной матрицы
или воспользоваться специальными программами, например, этой
Краткое описание.
- Решаю систему уравнений: A*X=B, где A — квадратная матрица n-го порядка,
X,B — вектора - К матрице A справа приписываю вектор B. Получаю расширенную матрицу A
- В дальнейшем A обозначает расширенную матрицу (n строк, n+1 столбец)
- Aij — обозначает элемент матрицы, находящийся на i-й строке и j-м столбце
- Делю 1-ю строку на A11, т е A’1j = A1j/A11 (j = 1..n+1). В результате A’11 = 1. A’ обозначает преобразованную строку
- Преобразую остальные строки по формуле: A’ij = Aij — A’1j*Ai1 (i = 2..n; j = 1..n+1)
- В результате 1-й столбец в строках 2..n заполнится нулями
- Отметим, что все эти преобразования не нарушают правильность уравнений
- Аналогичные действия проводим для обнуления 2-го столбца в строках 3..n, то есть:
- Делю 2-ю строку на A’22, т е A»2j = A’2j/A’22 (j = 2..n+1). В результате A»22 = 1. A» обозначает резельтат 2-го преобразования строки
- Преобразую остальные строки по формуле: A»ij = A’ij — A»2j*A’i2 (i = 3..n; j = 2..n+1)
- В результате 2-й столбец в строках 3..n заполнится нулями
- Аналогичные действия проводим далее
- В результате левые n столбцов матрицы A превращаютс в верхнюю треугольную
матрицу, т е ниже главной диагонали находятся только нули (а на главной диагонали — единицы) — см Рис 1. На этом рисунке вектор B — слева, S — номер шага - Затем выполняется «обратный ход», начиная с нижней строки, из которой можно вычислить Xn = Bn/Ann, например: Х4 = 9,55741/68,6388 = 0,13924 (рис. 1)
- Затем можно вычислить X3 = (0,9065 — 2,40919*0,13924) = 0,57059
- Затем из второй строки: X2 + 2,83562*X3 + 8,17808*X4 = 2,47945 вычисляю X2, и т д
3. Метод Якоби (метод простых итераций)
Для применения метода Якоби (и метода Зейделя) необходимо, чтобы диагональные компоненты матрицы А были больше суммы остальных компонент той же строки. Заданная система не обладает таким свойством, поэтому выполняю предварительные преобразования.
Далее номер в скобках означает номер строки.
Новую первую строку получаю сложением старой первой строки с другими строками, умноженными на специально подобранные коэффициенты. Записываю это в виде формулы:
(1)’ = (1) + 0,43*(2) - 0,18*(3) – 0,96*(4) (2)’ = (2) + 0,28*(1) – 1,73*(3) + 0,12*(4) (3)’ = (3) – 0,27*(1) - 0,75*(2) + 0,08*(4) (4)’ = (4) + 0,04*(1) – 6,50*(2) + 8,04*(3) Примечание: подбор коэффицентов выполнен на листе "Анализ". Решаются системы уравнений, цель которых - обратить внедиагональные элементы в нуль. Коэффиценты - это округлённые результаты решения таких систем уравнений. Конечно, это не дело. В результате получаю систему уравнений:
Для применения метода Якоби систему уравнений нужно преобразовать к виду:
X = B2 + A2*X Преобразую:
Далее делю каждую строку на множитель левого столбца, то есть на 16, 7, 3, 70 соответственно. Тогда матрица А2 имеет вид :
А вектор В2:
Скачать
|
||||
|
||||
|
3.1. |
||||
|
Метод
Система
В
где
Система
Предполагаем,
(3.3)
т.е.
Предполагаем,
Преобразуем
Система
Введём
Систему
где
Систему
За т.е.
Используя
Таким
Если
На
Критерий
Если условие (3.9)
Условия
Прежде
Доказывается
Если |
||||
|
3.2. |
||||
|
Для
МУМНОЖ(<матрица1>;<матрица2>)
МОБР(<матрица>)
МОПРЕД(<матрица>)
Порядок
Кроме
СУММПРОИЗВ(<вектор1>,<вектор2>) |
||||
|
||||
|
Задание
1.
2.
В
Задача
Последовательность |
||||
|
Оформите
Введите
|
Рис.3.1. |
|||
|
Выберите
Решение |
Рис. |
|||
|
3.4. |
||||
|
Задание
Проверим, Приведем
или где
|
||||
Соседние файлы в папке Информатика_2
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 06.11.2019 Сообщений: 39 |
|
|
1 |
|
Уравнение методом Якоби23.05.2020, 14:33. Показов 1381. Ответов 1
Здравствуйте уважаемые пользователи форума! Не могу понять как решить уравнение в EXEL методом Якоби. Буду безмерно благодарен за помощь! Заранее большое спасибо! Уравнение прикрепил картинкой. Миниатюры
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
23.05.2020, 14:33 |
|
Ответы с готовыми решениями: Система линейных уравнений методом Якоби или Зейделя Риккати, Дарбу, Якоби (дифф.уравнение)!
Решить уравнение любым методом(методом половинного деления,методом простой интеграции,методом касательных) 1 |
|
1557 / 791 / 182 Регистрация: 10.09.2013 Сообщений: 3,103 Записей в блоге: 3 |
|
|
23.05.2020, 17:07 |
2 |
|
0 |
Содержание
- 4.2. Решение слау, используя метод «Поиск решения. » (пункт главного меню «Сервис») ms Excel
- 4.3. Решение слау методом Крамера (методом определителей)
- Решение СЛАУ с помощью надстройки Поиск решения
4.2. Решение слау, используя метод «Поиск решения. » (пункт главного меню «Сервис») ms Excel
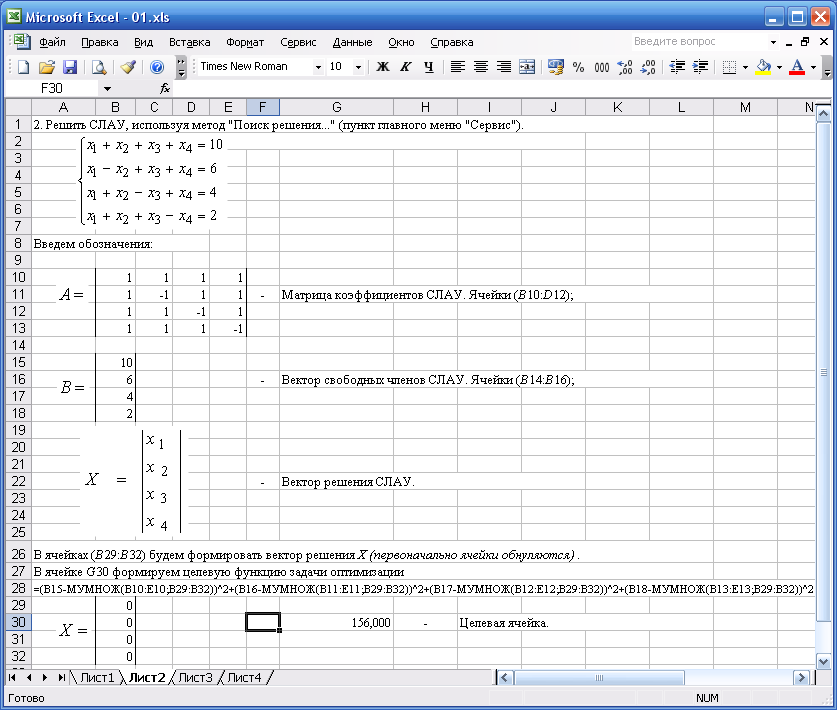
Рассмотрим использование метода «Поиск решения. » на исходных данных представленных на рис. 4.1.
Для использования метода «Поиск решения. » необходимо свести задачу решения СЛАУ к задаче оптимизации. Введем целевую функцию вида

где bi – i-й элемент вектора свободных членов СЛАУ;
n – количество уравнений в СЛАУ.
Ограничений на вектор решения X накладывать не будем.
Тогда математически задачу поиска вектора решения СЛАУ X можно записать

Подобная задача (4.5) легко решается использованием метода «Поиск решения. » MS Excel (см. рис. 4.2) следующим образом:
обнуляем ячейки (B29:B32), в которых будем формировать вектор решения СЛАУ X;
для ячейки G30 в строке формул запишем =(B15-МУМНОЖ(B10:E10;B29:B32))^2+(B16-МУМНОЖ(B11:E11;B29:B32))^2+(B17-МУМНОЖ(B12:E12;B29:B32))^2+(B18-МУМНОЖ(B13:E13;B29:B32))^2 (см. 4.5) правую часть целевой функции (4.4) для исходных данных нашей задачи;
Рис. 4.2. Решение СЛАУ, используя метод «Поиск решения. » (пункт главного меню «Сервис») MS Excel
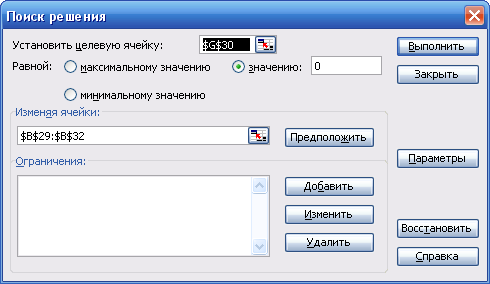
в пункте главного меню MS Excel «Сервис» выбираем подпункт «Поиск решения. » (см. рис. 4.3).
При открытии окна «Поиск решения» напротив метки «Установить целевую ячейку:» будет отражен адрес активной ячейки (ячейки, в которой был установлен курсор при открытии окна). В ячейке $G$30 (G30) должна быть записана формула вычисления правой части целевой функции (4.4). Также в окне «Поиск решения» ниже метки «Изменяя ячейки:» необходимо задать адрес вектора решения СЛАУ X ($B$29:$B$32) (B29:B32). Адреса целевой ячейки и вектора решения СЛАУ можно формировать в режиме конструктора. Для этого необходимо поместить курсор в ячейку формирования соответствующего адреса и на листе MS Excel выделить ячейку или массив ячеек;
нажать кнопку «Выполнить». После чего появится окно «Результаты поиска решения» и в ячейках (B29:B32) сформируется вектор решения СЛАУ X.
Рис. 4.3. Окно “Поиск решения…”
Лист MS Excel, представленный на рис. 4.2 позволяет получить вектор решения для любой СЛАУ, состоящей из четырех уравнений. Описанная технология решения СЛАУ легко позволяет решить задачу любой размерности (для любого количества уравнений в СЛАУ).
4.3. Решение слау методом Крамера (методом определителей)
СЛАУ из n уравнений задается матрицей коэффициентов СЛАУ A и вектором свободных членов СЛАУ B.


bi – i-й элемент вектора свободных членов СЛАУ.
Суть метода Крамера в следующем: сначала вычисляется определитель матрицы коэффициентов СЛАУ

за тем вычисляются еще n определителей
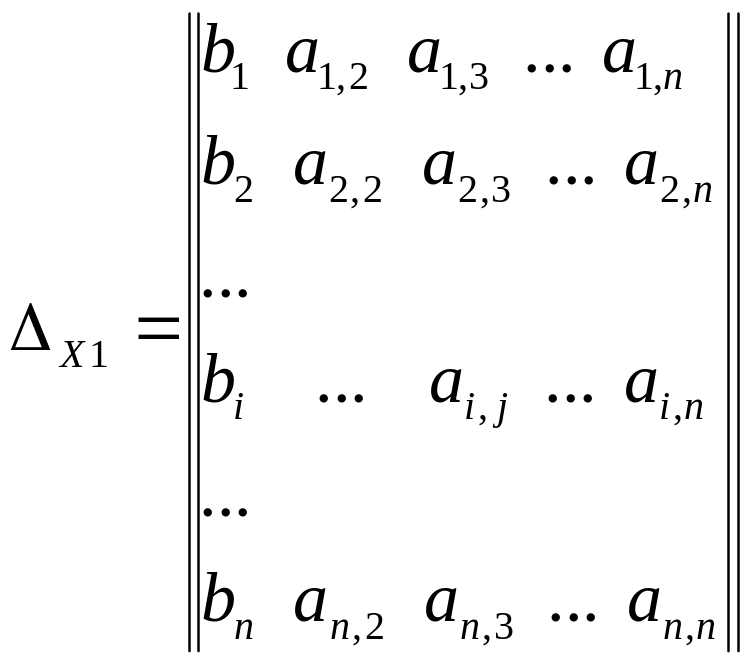


т.е. определитель вычисляется для матрицы, полученной из матрицы коэффициентов СЛАУ путем замены j-го столбца матрицы коэффициентов СЛАУ вектором свободных членов СЛАУ.
Тогда элементы вектора решения СЛАУ xj, j = 1, …, n определяются по формуле

В MS Excel существует формула =МОПРЕД(левый_верхний_элемент_исходной_матрицы: правый_нижний_элемент_исходной_матрицы) для вычисления значений определителей квадратных матриц.
Решение СЛАУ методом Крамера (методом определителей) представлено на рис. 4.4.
Рис. 4.4. Решение СЛАУ методом Крамера
Строки с 1 по 25 на рис. 4.4 не показаны, потому что они полностью совпадают с соответствующими строками рис. 4.1, 4.2.
Необходимо сформировать матрицы для вычисления определителей , X1, X2, X3 в ячейках (B27:E30), (B32:E35), (B37:E40), (B42:E45), (B47:E50), соответственно. Алгоритм формирования матриц для вычисления определителей представлен в табл. 4.2.
Алгоритм формирования матриц для вычисления определителей
Щелкнуть левой кнопкой манипулятора “мышь” по ячейке
Набрать в строке формул … и нажать Enter
Формирование матрицы для вычисления определителя
Источник
Решение СЛАУ с помощью надстройки Поиск решения
Пример 1.2: Найти решение СЛАУ из примера 1.1, используя надстройку Поиск решения.
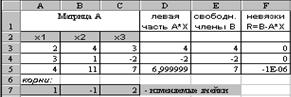
При решении СЛАУ 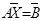
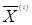

Задача Excel заключается в том, чтобы найти такое приближение 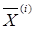
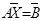
Последовательность действий
1.
Возьмем новый лист (а можно и на том же). Заготовим таблицу, как показано на рис.1.2.
2. Заготовим ячейки А7:С7, где будет сформировано решение системы (х1, х2, х3). Первоначально они остаются пустыми, т.е. равными нулю. Однако для контроля правильности вводимых далее формул, удобно ввести в эти ячейки какие-либо значения, например единицы. Эти значения можно рассматривать как нулевое приближение решения системы, 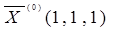
3. Введем коэффициенты системы (матрицу А) в ячейки А3:С5.
4. В столбец D введем выражения для вычисления левых частей исходной системы. Для этого в ячейке D3 введем и скопируем вниз до конца таблицы формулу: D3=СУММПРОИЗВ (A3:C3;$A$7:$C$7).
Используемая функция СУММПРОИЗВ принадлежит категории Математические.
5. В столбец Е запишем значения правых частей системы матрицу 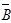
6. 
7. Будет не лишним проверить правильность вычислений для случая 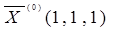
8. Зададим команду меню СервисПоиск решения. В окне Поиск решения (рис.1.3) в поле Изменяя ячейки укажем блок $А$7:$С$7, а в поле Ограничения – $F$3:$F$5=0. Для этого надо щелкнуть на кнопке Добавить и ввести эти ограничения.
9. Щелкнем на кнопке Выполнить.
Полученное решение системы (1.8) х1=1; х2=-1 х3=2 записано в ячейках А7:С7, рис.1.2.
1) Как отделяются корни уравнения?
2) Как используется функция СУММПРОИЗВ?
3) Какой должна быть величина шага при отделении корней?
4) Какие условия должны быть выполнены для применения метода половинного деления отрезка?
Задания к лабораторным работам № 5-7
Найти решение данной системы
| № варианта | Коэффициенты при неизвестных | Свободные члены | ||
 |
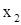 |
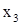 |
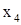 |
|
| 0,11270 | -2,39990 | 8,95146 | 0,75000 | 8,60527 |
| 9,58778 | -3,45350 | 0,24300 | 1,46840 | 16,40216 |
| 0,86400 | 4,23700 | -2,50200 | -1,72927 | -15,88846 |
| -0,28427 | -4,58674 | -1,85970 | 0,14940 | 10,90588 |
| 1,11270 | -3,02270 | -10,91328 | 1,06140 | 11,56420 |
| 8,40446 | -3,45350 | 0,12430 | 0,84560 | 5,25400 |
| -0,33640 | 5,11230 | -1,83880 | 16,03250 | -11,79026 |
| -0,28427 | 5,85754 | -2,48250 | -0,16200 | -13,67224 |
| 1,42410 | -2,71130 | 9,60540 | 0,43860 | 6,30236 |
| 0,33853 | -5,34326 | -2,17110 | -0,16200 | 12,83405 |
| -0,02500 | 5,11230 | -2,46160 | -16,71758 | -11,58650 |
| 8,40446 | -2,83070 | 0,43570 | 1,15700 | 15,77090 |
| 0,28640 | 5,11230 | -2,15020 | 16,60758 | -12,52887 |
| 0,80130 | -2,39990 | -8,29752 | 0,75000 | 7,078579 |
| 8,52378 | -2,83070 | -0,18710 | 1,46840 | -2,20182 |
| 0,33853 | 4,72046 | -1,85970 | -0,16200 | -11,78629 |
| 0,11270 | -2,71130 | -9,60540 | 0,75000 | 8,93943 |
| -8,99612 | -3,45350 | 0,12430 | 1,15700 | 1,07023 |
| 0,02500 | 5,11230 | -2,15020 | 16,03250 | -11,77124 |
| -0,28427 | 5,23474 | -2,17110 | -0,16200 | -12,58937 |
| 0,80130 | -2,71130 | 9,60540 | 1,06140 | 6,16237 |
| 8,52378 | -3,14210 | -0,18710 | 1,15700 | 16,18665 |
| 0,02500 | 8,00900 | -1,83880 | -14,66234 | -10,15728 |
| 0,02713 | -5,34326 | -2,17110 | -0,47340 | 14,18018 |
| 0,86400 | 4,80090 | -2,46160 | 16,60758 | -12,88453 |
| 1,42410 | -2,39990 | -8,95146 | 0,43860 | 6,53240 |
| -10,17944 | -3,45350 | 0,3570 | 1,46840 | -0,61624 |
| -0,28427 | 5,23474 | -1,85970 | -0,47340 | -12,05482 |
| 0,80130 | -3,02270 | 9,60540 | 0,75000 | 5,53137 |
| -0,28427 | -5,85754 | -2,48250 | -0,16200 | 15,60785 |
| -0,33640 | 5,11230 | -2,15020 | -16,71758 | -13,11164 |
| 8,52378 | -3,45350 | -0,18710 | 0,84560 | 15,88634 |
| -0,33640 | 5,42370 | -2,46160 | -10,08774 | -14,95126 |
| 1,42410 | -3,02270 | 10,25934 | 0,43860 | 4,97590 |
| 8,99612 | -3,45350 | 0,43570 | 8,45600 | 15,15486 |
| -0,28427 | -5,83234 | -2,48250 | 0,14940 | 13,79060 |
| 8,01300 | -2,71130 | -8,95146 | 0,75000 | 9,11636 |
| 0,28427 | 5,20954 | -2,17110 | 0,14940 | -13,29494 |
| 0,02300 | 5,42370 | -2,15020 | 16,71758 | -10,78791 |
| -9,11544 | -3,45350 | -0,18710 | 1,15700 | 1,72450 |
| 1,42410 | -2,71130 | -10,25934 | 0,75000 | 9,42647 |
| 0,33853 | 3,18060 | -2,17110 | 0,14940 | -11,34148 |
| 0,02500 | 5,42370 | -2,50200 | 16,71758 | -9,13914 |
| 8,40446 | -2,83070 | 0,43570 | 1,15700 | -2,82800 |
| 0,28640 | 5,42370 | -2,46160 | -17,97774 | -15,96309 |
| 1,12700 | -2,39990 | 8,29752 | 0,43860 | 6,97586 |
| 8,99612 | -3,14210 | 0,12430 | 1,46840 | 16,54115 |
| 0,02713 | -4,07246 | -1,85970 | 0,14940 | 9,91665 |
| 0,80130 | -3,02270 | -9,60540 | 0,75000 | 11,60641 |
| 7,93212 | -3,14210 | -0,18710 | 0,84560 | 0,64655 |
| -0,33640 | 5,42370 | -2,15020 | 17,40266 | -10,64578 |
| 0,02713 | 5,31806 | -2,28250 | 0,14940 | -12,89141 |
| 0,80130 | -2,39990 | 8,95146 | 1,06140 | 6,70370 |
| 0,28427 | -5,23474 | -1,85970 | -0,47340 | 13,31273 |
| 0,28640 | 4,80090 | -1,83800 | -15,23742 | -10,10485 |
| 9,70710 | -3,45350 | -0,1871 | 1,46840 | 16,57743 |
| 0,33640 | 4,80090 | -1,83880 | 15,34742 | -12,65950 |
| 1,42410 | -3,02270 | 11,56722 | 1,06140 | 11,39202 |
| -8,99612 | -3,45350 | 0,43570 | 0,84560 | 0,29410 |
| -0,28427 | 6,48034 | -2,48250 | -0,47340 | -14,12547 |
| 1,42410 | -2,39990 | 10,25934 | 1,06140 | 6,91312 |
| 0,33853 | -5,34326 | -1,85970 | -0,47340 | 12,56925 |
| 0,28640 | 4,80090 | -1,83880 | -15,23742 | -8,55119 |
| 8,99612 | -2,83070 | 0,43570 | 1,46840 | 16,28011 |
| 0,80130 | -2,39990 | 8,29752 | 0,75000 | 6,86659 |
| 9,11544 | -3,14210 | -0,18710 | 1,46840 | 16,68709 |
| 0,28640 | 4,80090 | -2,15020 | -15,92250 | -9,97026 |
| 0,02713 | -4,72046 | -1,85970 | -0,47340 | 12,24497 |
| 1,42410 | -3,02270 | -10,91328 | 0,75000 | 11,45227 |
| -8,40446 | -3,14210 | 0,35700 | 8,45600 | -12,16038 |
| -0,33640 | 8,00900 | -2,15020 | 16,03250 | -12,70757 |
| 0,02713 | 5,96606 | -2,48250 | -0,73400 | -27,01020 |
| 1,42410 | -2,39990 | 8,95146 | 0,43860 | 6,84369 |
| 9,58778 | -3,14210 | 0,43570 | 1,46840 | 16,40812 |
| 0,86400 | 5,11230 | -2,46160 | -17,29266 | -11,66944 |
| 0,02713 | -4,09766 | -1,85970 | -0,16200 | 9,32315 |
| 0,02500 | 4,80090 | -2,50200 | 15,34742 | -12,64048 |
| 1,42410 | -2,11300 | -10,25934 | 0,75000 | 8,76250 |
| -9,58778 | -3,45350 | 0,43570 | 1,15700 | -0,16016 |
| -0,28427 | 5,85754 | -2,17110 | -0,47340 | -13,13770 |
| 0,28640 | 5,42370 | -1,83880 | 16,60758 | -9,22557 |
| 1,42410 | -2,39990 | -10,25934 | 0,61400 | 6,77157 |
| 10,17944 | -3,45350 | 0,43570 | 1,46840 | -0,16779 |
| 0,28427 | 4,58674 | -1,85970 | 0,14940 | -10,62107 |
| 1,42410 | -2,71130 | -9,13280 | 1,06140 | 9,36148 |
| 8,99612 | -3,14210 | 0,35700 | 1,57000 | -1,40821 |
| 0,25000 | 5,42870 | -1,83880 | 6,03250 | -9,30032 |
| 0,02713 | 4,69526 | -2,17110 | 0,49400 | -10,27949 |
| 1,42410 | -3,02270 | -11,56722 | 1,06140 | 2,15109 |
| 0,38530 | 9,40860 | -2,48250 | 0,19400 | -12,32926 |
| -0,33640 | 5,42370 | -1,83880 | 16,71758 | -9,25325 |
| 8,12800 | -2,83070 | 0,35700 | 0,84560 | -2,28724 |
| 0,80130 | -3,02270 | -10,25934 | 1,06140 | 11,73637 |
| -0,28427 | 5,83234 | -2,48250 | 0,49400 | -14,47291 |
| -0,33640 | 5,42370 | -1,83880 | 16,71758 | -10,80692 |
| -8,52378 | -3,45350 | -0,18710 | 0,84560 | 2,17967 |
| 0,80130 | -2,71130 | -8,29752 | 0,43860 | 9,08626 |
| -8,52378 | -3,14210 | -0,18710 | 1,15700 | 0,10103 |
| -0,02500 | 5,42370 | -2,46160 | 17,40266 | -10,62675 |
| 0,02713 | 4,69526 | -2,17110 | 0,14940 | -11,71343 |
| 0,28640 | 4,80090 | -1,83880 | 15,23742 | -13,39031 |
| 1,11270 | -2,39990 | -9,60540 | 1,06140 | 6,73204 |
| -8,99612 | -3,14210 | 0,12430 | 1,46840 | -1,25720 |
| 0,02713 | 4,72046 | -1,85970 | -0,47340 | -11,35118 |
| 0,80130 | -2,39990 | -7,64358 | 0,43860 | 6,89578 |
| -0,28427 | 4,58674 | -1,85970 | 0,14940 | -12,02186 |
| 0,26640 | 5,42370 | -2,46160 | 17,07774 | -10,64711 |
| -9,70710 | 3,45350 | -0,18710 | 1,46840 | 1,26392 |
| -0,33640 | 4,80090 | -2,46160 | -16,71758 | -8,98045 |
| 1,11270 | -3,02270 | 9,60540 | 0,43860 | 5,41943 |
| 7,81280 | -3,14210 | 0,12430 | 0,84560 | 14,99671 |
| 0,02713 | -5,96606 | -2,48250 | -0,47340 | 15,29948 |
| 1,11270 | -2,71130 | 8,95146 | 0,43860 | 6,06062 |
| 8,99612 | -3,45350 | 0,12430 | 1,15700 | 15,49607 |
| -0,02500 | 4,80090 | -2,46160 | -16,03250 | -9,14355 |
| -0,28427 | -5,85754 | -2,17110 | -0,47340 | 14,35349 |
| 1,42410 | -3,02270 | 11,56722 | 1,06140 | 4,74101 |
| 8,40446 | -3,14210 | 0,43570 | 0,84560 | 15,12192 |
| -0,33640 | 5,11230 | -1,83880 | -16,03250 | 11,68307 |
| 0,02713 | -5,34326 | -2,48250 | -0,16200 | 12,90826 |
| 0,33640 | 5,11230 | -2,15020 | 16,71758 | -11,73373 |
| 0, 11270 | -3,02270 | -10,25934 | 0,75000 | 11,52934 |
| 7,81280 | -3,14210 | 0,24300 | 0,84560 | 0,05805 |
| 0,02713 | 5,34326 | -2,48250 | -0,16200 | -12,16925 |
| 0,02500 | 4,80090 | -2,15020 | -15,34742 | -10,02268 |
| 0,80130 | -2,71130 | 8,95146 | 0,75000 | 6,42511 |
| 7,93212 | -2,83070 | -0,18710 | 1,15700 | 16,02528 |
| 0,33853 | -5,96606 | -2,17110 | -0,73400 | 16,13629 |
| 1,11270 | -2,39990 | -8,29752 | 0,43860 | 6,71409 |
| -9,58778 | -3,45350 | 0,12430 | 1,46840 | 0,61506 |
| 0,26400 | 5,11230 | -2,46160 | 17,29266 | -11,82287 |
| -0,28427 | 4,61194 | -1,85970 | -0,16200 | -11,41139 |
| 1,11270 | -3,02270 | 10,25934 | 0,75000 | 5,00928 |
| 8,40446 | -3,45350 | 0,12430 | 0,84560 | 15,03841 |
| -0,33640 | 4,80090 | -2,15020 | -16,03250 | -9,11502 |
| -0,28427 | -6,48034 | -2,48250 | -0,47340 | 6,28870 |
| -0,02500 | 5,11230 | -2,46150 | 16,71758 | -11,71470 |
| 1,11270 | -2,71130 | -8,95146 | 0,43860 | 9,00442 |
| -8,40446 | -3,14210 | 0,12430 | 1,15700 | -0,48746 |
| 0,02713 | 4,72046 | -2,17110 | -0,16200 | -11,08638 |
| -0,33640 | 5,42370 | -1,83880 | -16,71758 | -15,78430 |
| 1,11270 | -3,02270 | 9,13280 | 1,06140 | 5,26310 |
| 7,81280 | -3,14210 | 0,12430 | 0,84560 | 15,25495 |
| 0,02713 | -5,31806 | -2,48250 | 0,14940 | 13,69198 |
| 0,25000 | 5,42370 | -2,15020 | -16,71758 | -15,71771 |
| 1,11270 | -2,71130 | 9,60540 | 0,75000 | 6,31920 |
| 8,40446 | -3,14210 | 0,12430 | 1,15700 | 15,89804 |
| 0,02713 | -4,69526 | -2,17110 | 0,14940 | 11,75676 |
| 1,11270 | -2,71130 | 2,59340 | 1,06140 | 6,10400 |
| 8,99612 | -3,45350 | 0,12430 | 1,57000 | 15,84940 |
| -0,02500 | 5,42370 | -1,83880 | -16,03250 | -15,64308 |
| -0,84270 | -2,09540 | -2,17110 | 0,14940 | 12,74599 |
Лабораторная работа 6. Итерационные методы решения систем линейных уравнений
Цель:Ознакомиться с итерационными методами решения систем линейных уравнений и их реализацией в MS Excel.
Задание:Решить систему линейных уравнений с точностью ε одним из методов:
1) Якоби, e = 10 –3 ;
Алгоритмы методов и их реализация в ms excel
Алгоритм
1. Выписать для системы 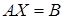
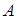
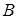
2. Преобразовать исходную систему к виду 
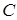

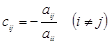
элементы столбца 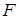
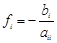
3. Проверить условие сходимости: имеет ли матрица 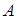

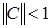
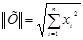
5. Задать вектор нулевого приближения 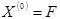
6. Вычислить координаты вектора следующего, более точного приближения к решению по итерационной формуле:
7. Окончание итерационного процесса:
оценить погрешность 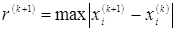
итерационный процесс заканчивается, как только 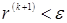
Реализация в MS Excel
1.Решить систему линейных алгебраических уравнений:
8. Расположить на листе исходные данные:
9. Рассчитать элементы матрицы 
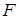
Вид рабочего листа с результатом расчета
Вид рабочего листа с формулами
10. Уточнение корней системы линейных уравнений методом Якоби с помощью таблицы вычислений (в качестве начального приближения выбрать значения столбца 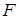
Вид рабочего листа с результатом расчета
Вид рабочего листа с формулами
Примечание: Фигурные скобки означают, что соответствующая формула выводится массивом, т. е. с использованием комбинации Ctrl + Shift + Enter.
Уточнение корня с использованием режима Итерации MS Excel (вручную):
создать копию листа: Правка – Переместить/Скопировать лист…, на которой удалить ячейки с итерационным процессом:
настроить MS Excel на выполнение итераций вручную: Сервис – Параметры – Вычисления – вручную; итерации разрешить, Предельное число итераций – 1, Относительная погрешность – 0,001;
организовать в таблице циклические ссылки: в ячейках, где хранились старые значения корней, поставить ссылку на ячейки, где рассчитаны новые, более точные значения корней:
нажимать клавишу F9, наблюдая за поведением погрешности:
После окончания вычислительного процесса выполнить: Сервис – Параметры – Вычисления и вернуть предустановленные настройки.
Лабораторная работа 7. Итерационные методы решения систем линейных уравнений
Цель:Ознакомиться с итерационными методами решения систем линейных уравнений и их реализацией в MS Excel.
Задание:Решить систему линейных уравнений с точностью ε одним из методов:
1) Зейделя, e = 10 –6 ;
Алгоритм
Выписать для системы 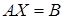
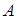
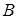
Преобразовать исходную систему к виду 
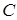
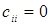
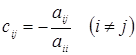
элементы столбца 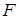
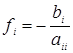
Проверить условие сходимости: имеет ли матрица 

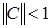
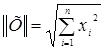
Задать вектор нулевого приближения 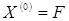
Вычислить координаты вектора следующего, более точного приближения к решению по итерационным формулам:
Окончание итерационного процесса:
оценить погрешность 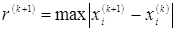
итерационный процесс заканчивается, как только 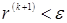
Реализация в MS Excel
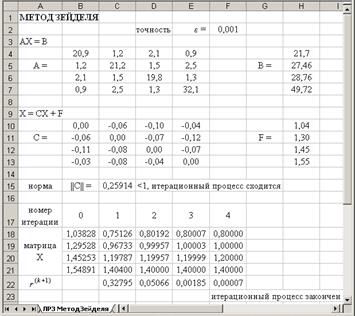
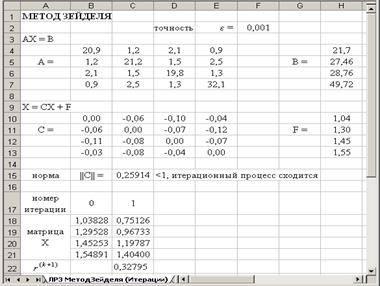
Расположить на листе исходные данные и уточнить корни системы линейных уравнений методом Зейделя с помощью таблицы вычислений (в качестве начального приближения выбрать значения столбца F):
Вид рабочего листа с результатом расчета
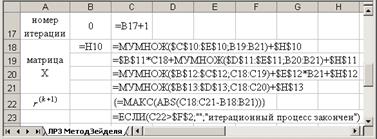
Вид рабочего листа с формулами
Уточнение корня с использованием режима Итерации MS Excel (вручную):
создать копию листа: Правка – Переместить/Скопировать лист…, на которой удалить ячейки с итерационным процессом:
настроить MS Excel на выполнение итераций вручную: Сервис – Параметры – Вычисления – вручную; итерации разрешить, Предельное число итераций – 1, Относительная погрешность – 0,001;
организовать в таблице циклические ссылки: в ячейках, где хранились старые значения корней, поставить ссылку на ячейки, где рассчитаны новые, более точные значения корней:
нажимать клавишу F9, наблюдая за поведением погрешности:
После окончания вычислительного процесса выполнить: Сервис – Параметры – Вычисления и вернуть предустановленные настройки.
Поскольку подсчет номера итерации и расчет погрешности работают некорректно, следует модифицировать формулы:
и снова провести расчет:
После окончания вычислительного процесса выполнить: Сервис – Параметры – Вычисления и вернуть предустановленные настройки.
Лабораторная работа 8. Теория приближений функций
Цель: Ознакомиться с численными методами получения аналитической зависимости по экспериментальным точкам и их реализацией в MS Excel.
1)Найти приближенное значение функции при заданном значении аргумента 
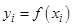
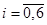
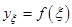
2)Оценить погрешность полученного значения.
Вопросы самоконтроля.
1) Постановка задачи интерполирования. Геометрическая иллюстрация.
2) В чем различие между задачами интерполяции и задачами экстраполяции?
3) Привести формулу Лагранжа. Дать оценку погрешности.
4) Как выглядит формула Лагранжа для равностоящих узлов?
5) От чего зависит точность получаемого формулой Лагранжа результата?
6) Когда полином 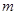
Источник


















































 , (3.1)
, (3.1)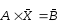 , (3.2)
, (3.2)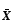




 (3.4)
(3.4)
 (3.5)
(3.5) (3.6)
(3.6)

 (3.7)
(3.7) . (3.8)
. (3.8) ,
, (3.9)
(3.9) .
. (3.10)
(3.10)

 ,
,
 .
. .
.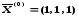 .
.

 , (3.12)
, (3.12) ,
, ,
,

 ,
,
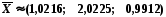


 Обыкновенное дифференциальное уравнение (легкое) аналитическим методом и методом рунге-кутта 2-го пор
Обыкновенное дифференциальное уравнение (легкое) аналитическим методом и методом рунге-кутта 2-го пор